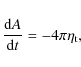| Issue |
A&A
Volume 506, Number 1, October IV 2009
The CoRoT space mission: early results
|
|
|---|---|---|
| Page(s) | 263 - 268 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200911895 | |
| Published online | 28 July 2009 | |
The CoRoT space mission: early results
On the differential rotation of CoRoT-2a![[*]](/icons/foot_motif.png)
H.-E. Fröhlich1 - M. Küker1 - A. P. Hatzes2 - K. G. Strassmeier1
1 - Astrophysikalisches Institut Potsdam (AIP),
An der Sternwarte 16, 14482 Potsdam, Germany
2 -
Thüringer Landessternwarte Tautenburg,
Karl-Schwarzschild-Observatorium (TLS), Sternwarte 5, 07778 Tautenburg, Germany
Received 20 February 2009 / Accepted 15 July 2009
Abstract
We apply a robust spot model to fit the light curve of CoRoT-2a. The spots are assumed to be long-living and each has its own rotation period. A model with three circular spots reproduces the basic features of the longitude-time spot coverage map. One of the spots exhibits a noticeably lower rotational frequency than the other two. From the rotational frequencies of the three dark features we infer a differential rotation of above 0.11 rad/d, in rough agreement with theoretical models. Mean field models of angular momentum transport by convection and meridional flow lead to an equatorial rotational frequency that exceeds that of the poles by 0.09 rad/d. The spot decay corresponds to a turbulent magnetic diffusivity of
![]() cm2/s.
cm2/s.
Key words: stars: activity - stars: individual: CoRoT-2a - stars: interiors - stars: late-type - stars: rotation - starspots
1 Introduction
The second detection of a transit planet by the CoRoT satellite belongs to a young
(![]() 0.5 Gyr) main-sequence G7 star (Bouchy et al. 2008).
The orbital period of the ``hot'' Jupiter is 1.743 days
(Alonso et al. 2008). The parent star rotates with a period of 4.5 days.
The star's inclination is
0.5 Gyr) main-sequence G7 star (Bouchy et al. 2008).
The orbital period of the ``hot'' Jupiter is 1.743 days
(Alonso et al. 2008). The parent star rotates with a period of 4.5 days.
The star's inclination is
![]() (Alonso et al. 2008).
(Alonso et al. 2008).
By relying on similarity to the Sun, Lanza et al. (2009, L09) applied their
maximum-entropy (ME) technique to fit the time variability of the total solar
irradiance (Lanza et al. 2003) and analyzed the CoRoT-2a
photometric white light data correspondingly in terms of short living
(![]() 3.2 days) surface features: dark spots and bright faculae with a
constant ratio between them. Assuming a short surface activity timescale, they
divided the 142 day time span into 45 intervals and, by applying ME regularization,
mapped the evolution in surface brightness inhomogeneities. Even without taking into account the
effect of bright faculae they were able to produce an excellent fit (
3.2 days) surface features: dark spots and bright faculae with a
constant ratio between them. Assuming a short surface activity timescale, they
divided the 142 day time span into 45 intervals and, by applying ME regularization,
mapped the evolution in surface brightness inhomogeneities. Even without taking into account the
effect of bright faculae they were able to produce an excellent fit (![]() 0.2 mmag) to the data.
The results indicate that there are two ``active longitudes'', which are slowly converging (by
0.2 mmag) to the data.
The results indicate that there are two ``active longitudes'', which are slowly converging (by
![]() over the whole interval). From the relative motion, they were able to infer a minimal differential rotation of below one percent.
over the whole interval). From the relative motion, they were able to infer a minimal differential rotation of below one percent.
CoRoT-2a's photometric variability of 0.07 mag exceeds the solar level by a factor of 20, even at solar maximum. If the spots are larger than their solar counterparts, then, for purely dimensional reasons, one expects longer lifetimes. In the following we adopt a multi-spot modeling approach to analyze the measured white-light light curve of CoRoT-2a. Admittedly the CoRoT-2a light curve looks complex, but there is regularity in this complexity and one can see a regular pattern that can be easily identified with a few spots. The two- and three-spot modeling was carried out with the code of Dorren (1987), assuming circular spots and a linear limb-darkening law. Bright features were not modeled. According to L09, in the case of CoRoT-2a, the surface inhomogeneities are dominated by dark spots, not bright faculae. A Markov-Chain Monte Carlo method (MCMC) was applied to analyze in a Bayesian manner the multi-dimensional parameter space.
We note that CoRoT-2a is a slow rotator and not amenable to the Doppler imaging technique. We were therefore compelled to use photometric modeling and draw conclusions with the proper caveats.
2 Theory: differential rotation
Current models of stellar rotation predict a weak increase in the surface differential rotation with increasing rotation frequency and a modest increase with effective temperature (Küker & Rüdiger 2008). From Doppler imaging, Barnes et al. (2005) found a strong dependence on temperature and no systematic dependence on rotation. These results were confirmed by Reiners (2006) with the Fourier transform method. With the effective temperature of CoRoT-2a that is only 150 K lower than that of the Sun, we do not expect to observe a drastic difference between the rotation patterns of both stars. We note that this holds only for the total value of the differential rotation,
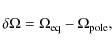 |
(1) |
where the subscripts eq and pole refer to values at the equator and the poles, respectively. The corresponding values for the solar differential rotation and the lapping time are 0.07 rad/d and 90 d, respectively.
We investigate this problem by computing the rotation pattern and meridional flow for a young Sun from the evolutionary track used in Küker & Stix (2008). The model star has one solar mass, an age of 0.55 Gyr, a luminosity of 0.745 solar luminosities, and a radius of 0.9 solar radii. The effective temperature is 5640 K and the base of the convection zone is located at a fractional radius of 0.73.
We use the mean field formulation of fluid dynamics, which takes into account the effect of small-scale motions on the large-scale flow, rotation, and heat transport without treating the small-scale motions in detail. For the convective heat transport in a non-rotating convection zone, this approach leads to the well-known mixing length theory. The description that we use here is identical for slow rotation but takes into account the effect of the Coriolis force on the convective motions. Similar descriptions can be found for the momentum transport, which is expressed in terms of the Reynolds stress. The transport coefficients describing the effect of the small-scale flows were computed by Kitchatinov & Rüdiger (1993), Kitchatinov et al. (1994), and Kitchatinov & Rüdiger (2005). The numerical scheme is a modified version of that in Küker & Stix (2001) as described in Bonanno et al. (2007).
The differential rotation is caused by a non-diffusive term in the Reynolds stress and a tilt of the heat transport vector towards the rotation axis, both caused by the Coriolis force. The polar region is slightly warmer than the equator throughout the convection zone. The difference is 10 K at the bottom and about 2.4 K at the top. That temperature gradient balances the differential rotation as a driving force of meridional flow and allows an equilibrium to be established without the requirement of constant rotation period along cylindrical surfaces for much faster rotation than with a strictly spherical stratification.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{11895fg1.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg11.png) |
Figure 1: Angular velocity versus latitude on the stellar surface. The unit is rad/d. |
| Open with DEXTER | |
The surface rotation law predicted by our model is shown in Fig. 1. It is of the same type as that on the solar surface with the equator rotating faster than the polar caps. The difference of
![]() rad/d between the rotation rates at the equator and the poles corresponds to a lapping time of 71 days.
rad/d between the rotation rates at the equator and the poles corresponds to a lapping time of 71 days.
The level of differential rotation found in our model exceeds the (admittedly) minimal value given by L09 by an order of magnitude. We ask whether the rotation can be made more rigid by adjusting free parameters. The only two parameters that can be varied are the mixing length parameter and the anisotropy of the ![]() effect in the surface layer. Both are set to a value of two in our standard calibration, which is motivated by reproducing the internal solar rotation as measured by helioseismology. Setting the anisotropy parameter to zero decreases the surface shear to less than half the value that we find with our standard model but this would imply the assumption of predominantly horizontal gas motions in the top layer and lead to unrealistic results if applied to the Sun. Lowering the mixing length parameter to a value of 1.5 lowers the surface differential rotation by about 1/6th but reduces the meridional flow speed by 50 percent. As with the anisotropy parameter, application to the Sun does not yield the closest agreement with observations. We conclude that for our model to be valid the differential rotation of CoRoT-2a must be much stronger than the lower limit found by L09.
effect in the surface layer. Both are set to a value of two in our standard calibration, which is motivated by reproducing the internal solar rotation as measured by helioseismology. Setting the anisotropy parameter to zero decreases the surface shear to less than half the value that we find with our standard model but this would imply the assumption of predominantly horizontal gas motions in the top layer and lead to unrealistic results if applied to the Sun. Lowering the mixing length parameter to a value of 1.5 lowers the surface differential rotation by about 1/6th but reduces the meridional flow speed by 50 percent. As with the anisotropy parameter, application to the Sun does not yield the closest agreement with observations. We conclude that for our model to be valid the differential rotation of CoRoT-2a must be much stronger than the lower limit found by L09.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{11895fg2.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg14.png) |
Figure 2: The turbulence magnetic diffusivity versus the fractional radius in the convection zone of CoRoT-2a for a rotation period of 4.5 days. The unit is 1013 cm2 s-1. |
| Open with DEXTER | |
Besides a measure of differential rotation, precision photometry of star spots provides
decay times, which should be compared with theoretical ones.
The decay of sunspots follows approximately the linear decay law (Krause & Rüdiger 1975)
where A is the spot area and
Figure 2 shows the magnetic diffusivity from our model of the convection zone of CoRoT-2a. As the Coriolis number increases with depth, the lower parts of the convection zone are affected more by rotational quenching of the transport coefficients. The surface value of
![]() cm2 s-1 is the same as from standard mixing-length theory, but in the lower part the diffusion coefficient is significantly reduced.
cm2 s-1 is the same as from standard mixing-length theory, but in the lower part the diffusion coefficient is significantly reduced.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{11895fg3new.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg18.png) |
Figure 3:
Robust fit of the light curve by three dark circular spots
differing in rotational frequency. The residuals, shown at the top,
are |
| Open with DEXTER | |
3 Observations
The CoRoT photometric satellite Baglin et al. (2006) observed CoRoT-2a during the first long run from May 16 to October 5, 2007. The 142 d run covers about 30 consecutive rotations of CoRoT-2a. For further detail the reader is referred to L09.
Transits were removed according to the ephemeris given by Alonso et al. (2008), creating gaps of 2.7 h every 1.743 days. The remaining data points were binned in time bins of ![]() 0.4 h duration, which is roughly a quarter of the satellite's orbital period (103 min). The reason for this high-resolution binning was that in the case of the CP star HD 50 773 an excellent fit to the data by a simple spot model could be
achieved after removing a sinusoidal signal (at the 100 ppm level) at the
CoRoT orbital frequency and its overtones (Lüftinger et al. 2009).
A similar artifact in the CoRoT-2a data should be detectable
by a binning with a time resolution shorter than the orbital period of the
satellite. However, in the framework of our simplified three-spot model the residuals are much too large for the CoRoT effect to be detected. After binning, 7669 normal points remain. The median of all the contributing
measurements within a time bin has been used to calculate the flux value of a normal point.
The weight of a normal point increases with the number of original measurement values.
As in L09, white-light data were used. As the color information hints at a
linear trend of the time series in at least one color band, one also has to allow
for a systematic linear trend in the white light.
0.4 h duration, which is roughly a quarter of the satellite's orbital period (103 min). The reason for this high-resolution binning was that in the case of the CP star HD 50 773 an excellent fit to the data by a simple spot model could be
achieved after removing a sinusoidal signal (at the 100 ppm level) at the
CoRoT orbital frequency and its overtones (Lüftinger et al. 2009).
A similar artifact in the CoRoT-2a data should be detectable
by a binning with a time resolution shorter than the orbital period of the
satellite. However, in the framework of our simplified three-spot model the residuals are much too large for the CoRoT effect to be detected. After binning, 7669 normal points remain. The median of all the contributing
measurements within a time bin has been used to calculate the flux value of a normal point.
The weight of a normal point increases with the number of original measurement values.
As in L09, white-light data were used. As the color information hints at a
linear trend of the time series in at least one color band, one also has to allow
for a systematic linear trend in the white light.
The precision light curve (Fig. 3) spanning 142 days exhibits an overall variation of 0.07 mag.
4 Bayesian spot modeling
Any ME method involves estimating a large number of free parameters. Here we prefer a more robust approach. We try to fit the light curve by assuming two and three, respectively, long-living circular dark features differing in rotational period. We also allow for some spot evolution. Our most ambitious model, with three spots, is described by 29 parameters.
To estimate all these parameters, a Bayesian method was applied. This provides a straightforward way of estimating parameters and their uncertainties from the data alone. From the marginal distribution of a particular parameter, all other quantities follow (e.g. mean, median, mode, standard deviation, and confidence regions). The marginal distribution is what remains if the likelihood function is integrated over all parameters apart from the particular one under study, taking into account proper prior distributions. The Bayesian approach is indeed so attractive because one can draw the marginal distribution from the data alone without relying on Monte Carlo simulations that use artificial data. Although deriving a best set of parameter values is comparatively easy, assigning mean values and error bars is computationally demanding, but becomes quite feasible with the Markov-Chain Monte-Carlo (MCMC) technique (see Press et al. 2007), which is related to the famous Metropolis formalism (Metropolis et al. 1953). This method has already been successful in analyzing high-precision photometric data from the MOST space satellite (Croll 2006; Fröhlich 2007).
For a migrating circular spot, the light curve is determined by at least four
parameters: starting longitude, final longitude, latitude, and
spot radius. Longitudes are defined with respect to a rigidly rotating coordinate system.
To describe the basic rotation of the star, the same reference period
as L09 has been taken, namely 4.5221 days. Longitude increases in the direction of stellar rotation. The zero point is the central meridian facing the observer at the beginning
of the time series. The inclination of the star (87.84
![]() )
is given.
The spot intensity with respect to the unspotted atmosphere and the parameter for the linear limb-darkening law are assumed to be adjustable.
)
is given.
The spot intensity with respect to the unspotted atmosphere and the parameter for the linear limb-darkening law are assumed to be adjustable.
The rotational frequency of a spot may change slightly with time. To allow for this, an additional parameter enters: the longitude value at the half-way point - at the middle of the time span. A spot's longitude at any time is interpolated quadratically by a Lagrange three-point formula from these three longitude values. Spot overlapping is not allowed.
Three parameters are considered to be nuisance parameters:
zeropoint, slope, and measurement error.
Spotted stars that are geometrically similar exhibit the same light curve,
except for an offset in magnitude. In what follows, this offset is considered
irrelevant and removed by integration. This is justifiable, because the magnitude of the
unspotted star, i.e., the zeropoint, is in almost all cases unknown.
The data may also exhibit a long-term trend, caused by an instrumental effect.
The Bayesian analysis allows the presence of an unknown slope simply by trying all
possible slopes. As with the zeropoint, dependence on this parameter is eliminated by integration.
These two integrations (with respect to zeropoint as well as slope) can be done even
analytically if one assumes that the distribution of the measurement error is
Gaussian in magnitude (see Sect. A).
The magnitude error in the ith normal
point can be written as
![]() ,
where Ni is the number of
measurements contributing to the ith time bin. We assume that nothing is known about
,
where Ni is the number of
measurements contributing to the ith time bin. We assume that nothing is known about ![]() .
The likelihood depends strongly on
.
The likelihood depends strongly on ![]() ,
so it is perhaps a good idea not to fix its value, but to allow for a large range of
,
so it is perhaps a good idea not to fix its value, but to allow for a large range of ![]() values.
We have eliminated the
values.
We have eliminated the ![]() parameter by integration using Jeffreys
parameter by integration using Jeffreys ![]() prior.
Hence, the likelihood function considered is a mean likelihood with respect to
photometric offset, slope, and measurement error. In short, the method itself
determines photometric offset, long-term trend, and ``measurement'' error
from the data (strictly speaking, the residuals, in any case, are considered as
Gaussian noise).
prior.
Hence, the likelihood function considered is a mean likelihood with respect to
photometric offset, slope, and measurement error. In short, the method itself
determines photometric offset, long-term trend, and ``measurement'' error
from the data (strictly speaking, the residuals, in any case, are considered as
Gaussian noise).
In the following a flat prior distribution over the parameter space is
presumed. For this reason, longitudes are restricted to the interval
![]() ,
instead of the latitude its sine is considered, and instead of spot radius (or area) its logarithm is used. The last replacement ensures that the posterior distribution for a radius is consistent with that for an area, i.e., it makes no difference whether one prefers radii or areas. A latitude prior that is constant over the sine of the latitude takes into account that there is a greater possibility of locating by chance a spot near the equator than near the poles.
,
instead of the latitude its sine is considered, and instead of spot radius (or area) its logarithm is used. The last replacement ensures that the posterior distribution for a radius is consistent with that for an area, i.e., it makes no difference whether one prefers radii or areas. A latitude prior that is constant over the sine of the latitude takes into account that there is a greater possibility of locating by chance a spot near the equator than near the poles.
Spot evolution is described by a simple ansatz: the spot area is assumed to evolve linearly with time. For a decaying spot, this prescription allows an estimate of the turbulent magnetic diffusivity according to Eq. (2). In the case of both, increasing as well as decreasing area, five parameters are needed to describe area evolution: the maximal area and the time of that, two time derivatives (for increase and decrease, resp.), and a smoothing parameter that prevents a sharp bend at the time of maximal extent.
5 Results
Table 1:
Spot parameters: expectation values
and 1-![]() uncertainties are listed.
uncertainties are listed.
In the framework of our spot model, an acceptable fit needs at least three spots. Some results for the two- and the three-spot solution are given in the Table 1. The mean differential rotation exploits the starting and the ending longitudes of the slowest and the fastest spot only. It is considered to be an additional delineated parameter and its marginal distribution is computed in the same way as for the independent parameters. The maximal differential rotation takes into account the ``half-way'' longitudes as well when computing the time-dependent frequencies. It is given for the ``best'' model in each case. Therefore, no error estimate is possible.
The residuals of the two-spot model exceed that of our three-spot model more then twice. A gain in the goodness-of-fit as high as this speaks for itself. It justifies the enlargement of the parameter space from 20 to 29 parameters beyond a doubt, and hence we believe that use of the three-spot model is most appropriate. The high degree of differential rotation in the three-spot model, 0.13 rad/d, is due to the third spot located near the southern pole. Without the third spot, the differential rotation would be as low as 1.6 percent.
6 Discussion and conclusions
There are other reasons why we should discard the two-spot solution: Both spots are located at very high latitudes, and the other delineated parameter values are also not convincing: both the spot rest intensity and the limb darkening value assume extreme values.
Admittedly, even in the three-spot case the estimates of rest intensity (brightness contrast) of the spots and linear limb darkening coefficient look unrealistic. We have repeated the calculations with these two parameters fixed to the same values as in Lanza et al., i.e.,
![]() .
The residuals are then only one percent larger. So, as in the case of the latitudes (see below), these two parameters are ill-defined, notwithstanding their formally small error bars.
.
The residuals are then only one percent larger. So, as in the case of the latitudes (see below), these two parameters are ill-defined, notwithstanding their formally small error bars.
Although the star is seen nearly equator-on, the spot latitudes are surprisingly well defined. This, of course, is because we have assumed that the spots are completely circular with sharp boundaries to the unperturbed photosphere. Due to lack of analytical formulae, we are unable to do the same MCMC calculations with other than circular shapes. The ``spots'' are probably not so simple. Perhaps our idealized model spots describe in reality dark features, which would be more appropriately described by groups of spots or even extended active regions.
Distrusting the latitudes derived from the data, we do not try to compute the full equator-pole span of differential rotation. The differential rotation extracted from the data represents, therefore, a lower bound. Nevertheless, the latitudinal ordering of the spots makes sense. As expected for a solar-like star, the fastest spot (no. 2) is the closest to the equator, the slowest (no. 3) near the pole. In contrast to latitudinal information, the longitudinal information that can be drawn easily from the nearly 5-month-long light curve seems to be highly reliable. It is this kind of information on which the inferred rotational periods rely.
![\begin{figure}
\includegraphics[width=12.5cm,clip]{11895fg4.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg26.png) |
Figure 4: Plotted over Fig. 4 of L09 are the migration paths of our three spots. They outline the same activity pattern! Besides the two ``active longitudes'' a slowly rotating feature (red) is evident. The longitudinal extent corresponds to the diameter of the spots if they were located at the equator. We thank Antonino Lanza and coworkers for kindly providing their longitude versus time ME activity data. |
| Open with DEXTER | |
In Fig. 4, the migration paths of the three spots are overplotted
on the longitude-time diagram of L09 (their Fig. 4) showing how
longitudinal spot coverage evolves with time. Our three-spot model outlines the same activity
pattern! Besides the two ``active longitudes'' - our fast rotating
spots - a slowly rotating feature is discernible already in the spot
coverage ME map of L09.
The cyclic behavior noticed by Lanza et al. can be naturally explained, at least
partly, by a beat phenomenon. Unfortunately, the duration of the time series is too short to settle this issue.
From the migration paths, one finds a minimal period of 4.535 d (spot no. 2, close to longitude
![]() )
and a maximal one of 5.000 d (spot no. 3). From both these extreme values, a maximal shear of 0.13 rad/d follows.
This corresponds to a beat period of 49 d.
It seems to be noticeable that the rotational period of the 3rd spot
increases with time by 2.3 percent.
)
and a maximal one of 5.000 d (spot no. 3). From both these extreme values, a maximal shear of 0.13 rad/d follows.
This corresponds to a beat period of 49 d.
It seems to be noticeable that the rotational period of the 3rd spot
increases with time by 2.3 percent.
By accepting a decrease in goodness-of-fit, one can look for a solution without period
change, i.e., in which migration paths are straight
lines in the longitude-versus-time map. In that case, the number of longitudes to
be determined is reduced to two per spot. The residuals are larger by three per
cent, which is substantial in view of the 7669 normal points involved,
but the degree of differential rotation is slightly lower at 0.11 rad/d,
corresponding to a lapping time of 55 days, which is closer to the theoretical expectation of
0.09 rad/d. It is that case for which Fig. 5 shows the posterior
probability distribution of the angular velocity difference, a derived parameter.
This marginal distribution is surprisingly well confined.
What does this mean? It means that, given the
model is true, i.e., that of three circular spots (no more, no less)
with unknown but constant periods, a linear limb-darkening law,
and parameterized spot evolution, then the
minimal value of the rotational shear is very well constrained by the data to be
![]() rad/d. It seems to be an advantage of Bayesian reasoning
that one has to state explicitly and beforehand all the assumptions and prejudices inherent to the modeling.
rad/d. It seems to be an advantage of Bayesian reasoning
that one has to state explicitly and beforehand all the assumptions and prejudices inherent to the modeling.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11895fg5.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg29.png) |
Figure 5:
The marginal distribution for the shear
|
| Open with DEXTER | |
Spot evolution is depicted in Fig. 6. We emphasize that it is the imposed restriction in spot evolution that enables us to estimate the degree of differential rotation. The longevity assumption is essential to our approach, and it seems to us reasonable because of the large size of the spots assuming that there are a few spots only. Surely, one can, as L09 have done, fit the data with short-living surface features, but the information on differential rotation is then mostly lost.
A by-product of considering spot evolution is an estimate of the turbulent magnetic
diffusivity from the inferred spot decay. To derive a robust estimate,
all spots are assumed to decay likewise. This further reduces the
number of free parameters. The residuals are increased by merely 0.2 percent. So the assumption of a common decay law seems justified. Assuming a stellar radius of
![]() (Alonso et al. 2008), one arrives at a diffusivity of
(Alonso et al. 2008), one arrives at a diffusivity of
![]() ,
twice the
theoretical value.
,
twice the
theoretical value.
![\begin{figure}
\includegraphics[width=8cm,clip]{11895fg6.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg32.png) |
Figure 6:
The evolution in the area of the three spots. The decreasing parts of spot
area evolution exhibit nearly the same slope. From this a
turbulent magnetic diffusivity can be computed. The third
spot is so large because of the latitude that the MCMC method
assigns to it:
|
| Open with DEXTER | |
Acknowledgements
This work has been conducted in the framework of the CoRoT additional program on ``Stellar variability and microvariability. II. Spot maps and modeling''. The authors thank the CoRoT instrument team for providing such excellent photometric data, A.F. Lanza for valuable suggestions, and an anonymous Referee for helping to improve the paper.
Appendix A: Bayesian spot modeling
Our starting point is the likelihood function. For the time being, it depends on
all kinds of parameters, nuisance parameters as well as ``real'' ones.
In case of N data points, it reads:
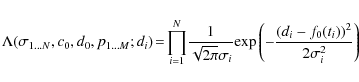 |
(A.1) |
The signal
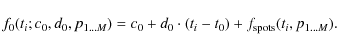
The offset c0 describes our ignorance concerning the unspotted brightness of the star, and the linear trend d0 accounts for any instrumental effects.
We set
![]() .
Relative errors si are normalized according to
.
Relative errors si are normalized according to
![]() .
Now, one can integrate
.
Now, one can integrate ![]() over the unknown
over the unknown ![]() using Jeffreys'
using Jeffreys'
![]() -prior:
-prior:
![$\displaystyle \Lambda^\prime\left(c_0,d_0,p_{1},\dots{} ;d_i\right) = \int_0^\i...
... N}\sum_{i=1}^N\left({d_i-f_0\left(t_i\right)}\over
s_i\right)^2\right]^{N/2}},$](/articles/aa/full_html/2009/40/aa11895-09/img38.png) |
(A.2) |
where
Integration over c0 provides
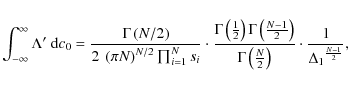 |
(A.3) |
where A1=1,
Obeying the convention
![]() the
integration over d0 yields:
the
integration over d0 yields:
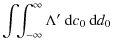 |
= | ||
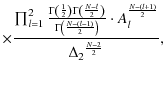 |
(A.4) |
where
References
- Alonso, R., Auvergne, M., Baglin, A., et al. 2008, A&A, 482, L21 [CrossRef] [EDP Sciences] (In the text)
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, 36th COSPAR Scientific Assembly, 36, 3749 (In the text)
- Barnes, J. R., Collier Cameron, A., Donati, J.-F., et al. 2005, MNRAS, 357, L1 [NASA ADS] (In the text)
- Bonanno, A., Küker, M., & Paternò, L. 2007, A&A, 462, 1031 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bouchy, F., Queloz, D., Deleuil, M., et al. 2008, A&A, 482, L25 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Croll, B. 2006, PASP, 118, 1351 [NASA ADS] [CrossRef] (In the text)
- Dorren, J. D. 1987, ApJ, 320, 756 [NASA ADS] [CrossRef] (In the text)
- Fröhlich, H.-E. 2007, Astron. Nachr., 328, 1037 [NASA ADS] [CrossRef] (In the text)
- Kitchatinov, L. L., & Rüdiger, G. 1993, A&A, 276, 96 [NASA ADS] (In the text)
- Kitchatinov, L. L., & Rüdiger, G. 2005, Astron. Nachr., 326, 379 [NASA ADS] [CrossRef] (In the text)
- Kitchatinov, L. L., Pipin, V. V., & Rüdiger, G. 1994, Astron. Nachr., 315, 157 [NASA ADS] [CrossRef] (In the text)
- Krause, F., & Rüdiger, G. 1975, Sol. Phys., 42, 107 [NASA ADS] [CrossRef] (In the text)
- Küker, M., & Rüdiger, G. 2008, J. Phys. Conf. Ser., 118, 012029 [NASA ADS] [CrossRef] (In the text)
- Küker, M., & Stix, M. 2001, A&A, 366, 668 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lanza, A. F., Rodonò, M., Pagano, I., Barge, P., & Llebaria, A. 2003, A&A, 403, 1135 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lanza, A. F., Bonomo, A. S., & Rodonò, M. 2007, A&A, 464, 741 [NASA ADS] [CrossRef] [EDP Sciences]
- Lanza, A. F., Pagano, I., Leto, G., et al. 2009, A&A, 493, 193 [NASA ADS] [CrossRef] [EDP Sciences] (L09) (In the text)
- Lüftinger, T., Fröhlich, H.-E., Weiss, W., et al. 2009, A&A, submitted (In the text)
- Metropolis, N., Rosenbluth, A, Rosenbluth, M., et al. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] (In the text)
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical Recipes, 3rd edn. (Cambridge: Cambridge Univ. Press) (In the text)
- Reiners, A. 2006, A&A, 446, 267 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Footnotes
- ... CoRoT-2a
![[*]](/icons/foot_motif.png)
- Based on observations obtained with CoRoT. The CoRoT space mission, launched on December 27th 2006, has been developed by CNES, with the contribution of Austria, Belgium, Brazil, ESA, Germany and Spain.
All Tables
Table 1:
Spot parameters: expectation values
and 1-![]() uncertainties are listed.
uncertainties are listed.
All Figures
![\begin{figure}
\par\includegraphics[width=6cm,clip]{11895fg1.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg11.png) |
Figure 1: Angular velocity versus latitude on the stellar surface. The unit is rad/d. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{11895fg2.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg14.png) |
Figure 2: The turbulence magnetic diffusivity versus the fractional radius in the convection zone of CoRoT-2a for a rotation period of 4.5 days. The unit is 1013 cm2 s-1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{11895fg3new.eps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg18.png) |
Figure 3:
Robust fit of the light curve by three dark circular spots
differing in rotational frequency. The residuals, shown at the top,
are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=12.5cm,clip]{11895fg4.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg26.png) |
Figure 4: Plotted over Fig. 4 of L09 are the migration paths of our three spots. They outline the same activity pattern! Besides the two ``active longitudes'' a slowly rotating feature (red) is evident. The longitudinal extent corresponds to the diameter of the spots if they were located at the equator. We thank Antonino Lanza and coworkers for kindly providing their longitude versus time ME activity data. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11895fg5.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg29.png) |
Figure 5:
The marginal distribution for the shear
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8cm,clip]{11895fg6.ps}
\end{figure}](/articles/aa/full_html/2009/40/aa11895-09/Timg32.png) |
Figure 6:
The evolution in the area of the three spots. The decreasing parts of spot
area evolution exhibit nearly the same slope. From this a
turbulent magnetic diffusivity can be computed. The third
spot is so large because of the latitude that the MCMC method
assigns to it:
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.