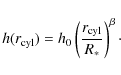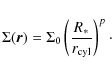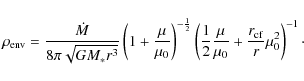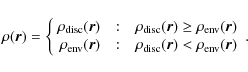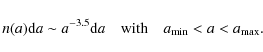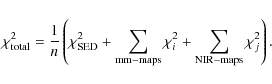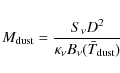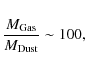| Issue |
A&A
Volume 505, Number 3, October III 2009
|
|
|---|---|---|
| Page(s) | 1167 - 1182 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200912397 | |
| Published online | 18 August 2009 | |
The circumstellar disc in the Bok globule CB 26
Multi-wavelength observations and modelling of the dust disc and envelope
J. Sauter1,2 - S. Wolf1 - R. Launhardt2 - D. L. Padgett3 - K. R. Stapelfeldt4 - C. Pinte5,6 - G. Duchêne7,6 - F. Ménard6 - C.-E. McCabe 3 - K. Pontoppidan8 - M. Dunham9 - T. L. Bourke10 - J.-H. Chen9
1 - Christian-Albrechts-Universität zu Kiel, Institut für Theoretische Physik und Astrophysik, Leibnizstr. 15, 24098 Kiel, Germany
2 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
3 - California Institute of Technology, 1200 E California Blvd, Mail code 220-6, Pasadena, CA 91125, USA
4 - JPL, 4800 Oak Grove Drive, Mail Stop 183-900, Pasadena, CA 91109, USA
5 - School of Physics, University of Exeter, Stocker Road, Exeter EX4 4QL, UK
6 - Laboratoire d'Astrophysique de Grenoble, CNRS/UJF UMR 5571, B.P. 53, 38041 Grenoble Cedex 9, France
7 - Astronomy Department, University of California Berkeley, 601 Campbell Hall, Berkeley CA 94720-3411, USA
8 - California Institute of Technology, Division of Geological and Planetary Sciences, MS 150-21, Pasadena, CA 91125, USA
9 - Department of Astronomy, University of Texas at Austin, 1 University Station C1400, Austin, TX 78712, USA
10 - Harvard-Smithonian Center for Astrophysics, 60 Garden St., Cambridge MA02138, USA
Received 27 April 2009 / Accepted 6 July 2009
Abstract
Context. Circumstellar discs are expected to be the nursery of planets. Grain growth within such discs is the first step in the planet formation process. The Bok globule CB 26 harbours such a young disc.
Aims. We present a detailed model of the edge-on circumstellar disc and its envelope in the Bok globule CB 26.
Methods. The model is based on HST near-infrared maps in the I, J, H, and K bands, OVRO and SMA radio maps at
![]() ,
,
![]() and
and
![]() ,
and the spectral energy distribution (SED) from
,
and the spectral energy distribution (SED) from
![]() to 3 mm.
New photometric and spectroscopic data from the Spitzer Space Telescope and the Caltech Submilimeter Observatory are also part of our analysis. Using the self-consistent radiative transfer code MC3D, the model we construct is able to discriminate between parameter sets and dust properties of both envelope and disc.
to 3 mm.
New photometric and spectroscopic data from the Spitzer Space Telescope and the Caltech Submilimeter Observatory are also part of our analysis. Using the self-consistent radiative transfer code MC3D, the model we construct is able to discriminate between parameter sets and dust properties of both envelope and disc.
Results. We find that the data are fit by a disc that has an inner hole with a radius of
![]() .
Based on a dust model including silicate and graphite, the maximum grain size needed to reproduce the spectral millimetre index is
.
Based on a dust model including silicate and graphite, the maximum grain size needed to reproduce the spectral millimetre index is
![]() .
Features seen in the near-infrared images, dominated by scattered light, can be described as a result of a rotating envelope.
.
Features seen in the near-infrared images, dominated by scattered light, can be described as a result of a rotating envelope.
Conclusions. Successful employment of ISM dust in both the disc and envelope hint that grain growth may not yet play a significant role for the appearance of this system. A large inner hole implies that CB 26 is a circumbinary disc.
Key words: circumstellar matter - planetary systems: protoplanetary disks - radiative transfer - stars: formation - stars: individual: CB 26
1 Introduction
CB 26 is a small cometary-shaped Bok globule located about ![]() north of the Taurus/Auriga dark cloud at a distance of 140 pc (Launhardt & Sargent 2001).
An IRAS point source (IRAS 04559+5200) at its southwest rim suggests an embedded Class I young stellar object (YSO) (Stecklum et al. 2004) source.
Launhardt & Henning (1997) found an unresolved 1.3 mm continuum source associated with the IRAS source.
north of the Taurus/Auriga dark cloud at a distance of 140 pc (Launhardt & Sargent 2001).
An IRAS point source (IRAS 04559+5200) at its southwest rim suggests an embedded Class I young stellar object (YSO) (Stecklum et al. 2004) source.
Launhardt & Henning (1997) found an unresolved 1.3 mm continuum source associated with the IRAS source.
Interferometric observations by Launhardt & Sargent (2001) showed that the major fraction of thermal dust emission at millimetre wavelengths has its origin in a young circumstellar disc with a diameter of about 400 AU and a mass of about
![]() .
This disc is seen almost edge-on, so the central star is not visible directly.
However, the spectral energy distribution suggests a Class I YSO with
.
This disc is seen almost edge-on, so the central star is not visible directly.
However, the spectral energy distribution suggests a Class I YSO with
![]() (Stecklum et al. 2004).
From the 13CO line emission and the Keplerian rotation curve, Launhardt & Sargent (2001) derive a central stellar mass of
(Stecklum et al. 2004).
From the 13CO line emission and the Keplerian rotation curve, Launhardt & Sargent (2001) derive a central stellar mass of
![]() .
Furthermore, Launhardt et al. (2008) detected a jet-like molecular outflow emanating perpendicular to the plane of the disc.
This outflow seems to be co-rotating with the disc.
.
Furthermore, Launhardt et al. (2008) detected a jet-like molecular outflow emanating perpendicular to the plane of the disc.
This outflow seems to be co-rotating with the disc.
We present new observations and a model for this source that accounts for spatially resolved data sets over more than 3 orders of magnitude as well as for the unresolved SED of the object.
Our modelling is based on spatially resolved maps of CB 26 in the millimetre regime from the Sub-millimetre Array (SMA) and the Owens Valley Radio Observatory (OVRO), high resolution images in the I,J,H, and K bands obtained with the the Near Infrared Camera and Multi-Object Spectrometer (NICMOS) and the Advanced Camera for Surveys (ACS) instruments on the Hubble Space Telescope (HST). The photometric data for the spectral energy distribution (SED) upon our model is based are provided by the Multiband Imaging Photometer for Spitzer (MIPS) and the Infrared Array Camera (IRAC) aboard the Spitzer Space Telescope (SST) and millimetre photometry. We also obtained a spectrum with the Infra-Red Spectrograph (IRS) aboard the SST.
In this paper, we use all available NIR to mm continuum data on CB 26 to develop a self-consistent model of the source. This model consists of two parts. First, an optically thick dust disc which accounts for the dark lane seen in images obtained with the HST of the object and the significantly elongated intensity profiles in the mm range. The second component is an optically thin envelope that reproduces the near-infrared scattered light nebulosity. While the millimetre observations are sensitive only to radiation being emitted from dust in the dense region within the disc, the near-infrared images are dominated by scattered stellar light from dust in the circumstellar envelope and the disc's upper optically thin layers, often referred to as the ``disc surface''. These observations trace different physical processes in different regions of the circumstellar environment, but they are both strongly related to the dust properties in the system.
Thus, we are in the position not only to model observations on the common basis of one set of parameters, but we are also able to investigate whether the dust properties are different in the disc and the envelope. This has been suggested by investigations of dust evolution in circumstellar discs where dust grain growth alters the dust grain properties in the circumstellar disc quite considerably whilst it is of less importance in the low-density envelope. Evidence for grain growth has been found, for instance, for the circumstellar discs IM Lupi (Pinte et al. 2008), GG Tau (Duchêne et al. 2004; Pinte et al. 2007), HH 30 (Watson & Stapelfeldt 2004), IRAS 04302+2247 (Wolf et al. 2003), and VV Serpens (Alonso-Albi et al. 2008).
In order to compare our model with the available observations, we use the self-consistent radiative transfer code MC3D (Wolf 2003b; Wolf et al. 1999) in a parameter space study on the free parameters of the model. We aim at finding the best-fit model, which we define to be the model that reproduces certain predefined features among the observational data (such as width of the dark lane; see below for further details) best.
2 Observations and data reduction
In the case of the disc in the Bok Globule CB 26, we are in the fortunate situation of having a large variety of observational data at hand.
This data includes not only the SED from
![]() to
to
![]() ,
but also resolved maps in the near-infrared and millimetre regimes.
We will now briefly discuss those observations and the data reduction in this section.
,
but also resolved maps in the near-infrared and millimetre regimes.
We will now briefly discuss those observations and the data reduction in this section.
2.1 HST imaging
The NICMOS and ACS data were taken by the GEODE![]() team. An overview of the complete program, its objects, and its objectives can be found in Padgett et al. (2009, in preparation).
team. An overview of the complete program, its objects, and its objectives can be found in Padgett et al. (2009, in preparation).
2.1.1 ACS
CB 26 was observed with the Advanced Camera for Surveys Wide Field Channel on 2005 September 09. Two 1250 s exposures were made in the F814W filter (
![]() ,
,
![]() ), corresponding to Johnson I band. With a pixel scale of
), corresponding to Johnson I band. With a pixel scale of
![]() ,
the ACS provides a field of view of
,
the ACS provides a field of view of
![]() .
The images were reduced, combined to reject cosmic rays, and corrected for geometric distortion by the STScI pipeline. Residual hot pixels and cosmic rays were manually removed by replacing the affected pixels by local median values.
.
The images were reduced, combined to reject cosmic rays, and corrected for geometric distortion by the STScI pipeline. Residual hot pixels and cosmic rays were manually removed by replacing the affected pixels by local median values.
2.1.2 NICMOS
CB 26 was observed using NICMOS on 2005 September 15 with the F110W (
![]() ,
,
![]() ), F160W (
), F160W (
![]() ,
,
![]() ) and F205W (
) and F205W (
![]() ,
,
![]() )
filters on the NIC2 array.
With a pixel scale of
)
filters on the NIC2 array.
With a pixel scale of
![]() ,
the NIC2 array provides a field of view of
,
the NIC2 array provides a field of view of
![]() on a side. All data were taken in a MULTIACCUM step = 128 sequence, with total exposure times of 512 s for the F110W data and 384 s for the F160W and F205W data. The observations were dithered by
on a side. All data were taken in a MULTIACCUM step = 128 sequence, with total exposure times of 512 s for the F110W data and 384 s for the F160W and F205W data. The observations were dithered by
![]() for bad pixel removal.
for bad pixel removal.
All three of the NICMOS data sets were taken less than 1900 s after emergence from the South Atlantic Anomaly (SAA) and therefore suffer from significant cosmic ray persistence. The data were re-reduced using the most recent calibration files available. The standard STScI CALNICA pipeline was used as a basis for the re-reduction, in addition to which, we employed both the biaseq and pedsub IRAF routines to remove the pedestal effects visible in each of the quadrants. The biaseq task removes the time-dependent variations in the bias level for each quadrant, and the pedsub task then removes the fixed bias offset. After the data have had the pedestal effect removed, we used the IDL SAACLEAN program to model and iteratively remove the persistent cosmic rays in the image. After emerging from the SAA, NICMOS powers back up and takes 2 dark frames. These dark frames provide the model for the cosmic ray persistence pattern; SAACLEAN takes this model and iteratively removes it from the data until the noise in the background reaches a global minimum. Further details on this procedure can be found in Bergeron & Dickinson (2003) (ISR 2003-010). Following the SAACLEAN procedure, the data are run through a second round of pedestal subtraction, have any remaining bad pixels removed, and are then run through the CALNICB pipeline procedure to generate the final mosaics.
2.2 Spitzer photometry and spectroscopy
Mid- and far-infrared photometry for CB 26 were retrieved from the Spitzer Archive.
IRAC observations were carried out under GTO program 94 (PI: Charles Lawrence). The data were taken 2004 February 11, AOR key 4916224 using the high dynamic range mode to obtain 5 dithered exposures of 30 s each.
Aperture photometry was measured from the Spitzer pipeline ``post-BCD'' mosaics (version 11.0.2), using a standard 10 pixel radius aperture for the source and background annulus with 12-20 pixel radius.
MIPS observations were made under GTO program 53 (PI: George Rieke) on 2005 March 08, AOR key 12020480. A medium scan map covering
![]() was performed, providing multiple dithered 4 s exposures and total integration times of 168, 84, and 16 s at 24, 70, and 160
was performed, providing multiple dithered 4 s exposures and total integration times of 168, 84, and 16 s at 24, 70, and 160
![]() ,
respectively. Spitzer post-BCD pipeline mosaics (version 14.4.0) were used for aperture photometry.
Photometry was measured in apertures whose radii and background annuli were 7
,
respectively. Spitzer post-BCD pipeline mosaics (version 14.4.0) were used for aperture photometry.
Photometry was measured in apertures whose radii and background annuli were 7
![]() (24
(24 ![]() m), 35
m), 35
![]() (70
(70 ![]() m), and 48
m), and 48
![]() (160
(160 ![]() m) with aperture correction factors as given by Gordon et al. (2007); Engelbracht et al. (2007); Stansberry et al. (2007).
m) with aperture correction factors as given by Gordon et al. (2007); Engelbracht et al. (2007); Stansberry et al. (2007).
We carried out our own Spitzer low-resolution spectroscopy of CB 26 on 2006 October 18 under program 30765, AOR key 18964992.
The ramp duration and number of observing cycles used were
![]() s,
s,
![]() s,
s,
![]() s, and
s, and
![]() s for the SL2, SL1, LL2, and LL1 modules of the IRS (respectively).
The spectra were processed beginning with the intermediate droopres products from pipeline version 15.3.0.
The 2D images were co-added, and the nod pairs subtracted to remove stray light and other additive artifacts, as well as rogue pixels.
1D spectra of each nodding beam were then extracted using a fixed aperture of 5 pixels.
Following Bouwman et al. (2008), the spectra were flux calibrated using a spectral response function determined by comparing standard star observations with template spectra.
These response functions are also used with the ``C2D'' Legacy data set (e.g. Kessler-Silacci et al. 2006).
It was not necessary to apply any scaling to match the short-low and long-low modules, indicating that the source is unresolved at the IRS wavelengths.
s for the SL2, SL1, LL2, and LL1 modules of the IRS (respectively).
The spectra were processed beginning with the intermediate droopres products from pipeline version 15.3.0.
The 2D images were co-added, and the nod pairs subtracted to remove stray light and other additive artifacts, as well as rogue pixels.
1D spectra of each nodding beam were then extracted using a fixed aperture of 5 pixels.
Following Bouwman et al. (2008), the spectra were flux calibrated using a spectral response function determined by comparing standard star observations with template spectra.
These response functions are also used with the ``C2D'' Legacy data set (e.g. Kessler-Silacci et al. 2006).
It was not necessary to apply any scaling to match the short-low and long-low modules, indicating that the source is unresolved at the IRS wavelengths.
2.3 Millimetre and sub-millimetre measurements
2.3.1 SMA
Observations at 270 GHz (
![]() )
with the Sub-Millimetre Array (SMA, Ho et al. 2004) were made in December 2006, in two configurations providing baselines in the range 12-62 k
)
with the Sub-Millimetre Array (SMA, Ho et al. 2004) were made in December 2006, in two configurations providing baselines in the range 12-62 k![]() .
Typical system temperatures were 350-500 K. The quasar 3C279 was used for bandpass calibration, and the quasars B0355+508 and 3C111 for gain calibration. Uranus was used for absolute flux calibration, which is accurate to 20-30%. The data were calibrated using the IDL MIR package (Qi 2005) and imaged using MIRIRAD Sault et al. (1995). The cleaned and restored 1.1 mm continuum map was constructed with robust uv-weighting using line-free channels in both sidebands. Here we only use the continuum map.
The observations together with the molecular line data are described in more detail in a forthcoming paper (Launhardt et al. in prep.).
.
Typical system temperatures were 350-500 K. The quasar 3C279 was used for bandpass calibration, and the quasars B0355+508 and 3C111 for gain calibration. Uranus was used for absolute flux calibration, which is accurate to 20-30%. The data were calibrated using the IDL MIR package (Qi 2005) and imaged using MIRIRAD Sault et al. (1995). The cleaned and restored 1.1 mm continuum map was constructed with robust uv-weighting using line-free channels in both sidebands. Here we only use the continuum map.
The observations together with the molecular line data are described in more detail in a forthcoming paper (Launhardt et al. in prep.).
2.3.2 OVRO
CB 26 was also observed with the Owens Valley Radio Observatory (OVRO) between January 2000 and December 2001. Four configurations of the six 10.4 m antennas provided baselines in the range 6-180 k![]() at 2.7 mm (110 GHz) and 12-400 k
at 2.7 mm (110 GHz) and 12-400 k![]() at 1.3 mm (232 GHz). Average SSB system temperatures of the SIS receivers were 300-400 K at 110 GHz and 300-600 K at 232 GHz. The raw data were calibrated and edited using the MMA software package (Scoville et al. 1993).
Mapping and data analysis were performed with the MIRIAD toolbox.
Observing parameters are described in detail in Launhardt & Sargent (2001).
The data presented here include additional observations conducted in 2001.
All maps are generated with robust uv-weighting, cleared, and restored with a clean beam.
Effective synthesised beam sizes of all interferometric millimetre continuum
maps used here are summarised in Table 1.
at 1.3 mm (232 GHz). Average SSB system temperatures of the SIS receivers were 300-400 K at 110 GHz and 300-600 K at 232 GHz. The raw data were calibrated and edited using the MMA software package (Scoville et al. 1993).
Mapping and data analysis were performed with the MIRIAD toolbox.
Observing parameters are described in detail in Launhardt & Sargent (2001).
The data presented here include additional observations conducted in 2001.
All maps are generated with robust uv-weighting, cleared, and restored with a clean beam.
Effective synthesised beam sizes of all interferometric millimetre continuum
maps used here are summarised in Table 1.
2.3.3 CSO
Submillimeter observations of CB 26 at 350 ![]() m were obtained with the Submillimeter High Angular Resolution Camera II (SHARC-II) at the Caltech Submillimeter Observatory (CSO) on 2007 October 21.
SHARC-II is a
m were obtained with the Submillimeter High Angular Resolution Camera II (SHARC-II) at the Caltech Submillimeter Observatory (CSO) on 2007 October 21.
SHARC-II is a
![]() element bolometer array giving a
element bolometer array giving a
![]() field of view (Dowell et al. 2003).
The beam-size at 350
field of view (Dowell et al. 2003).
The beam-size at 350 ![]() m is 8.5
m is 8.5
![]() .
.
We used the Lissajous observing mode to map a region approximately 1![]()
![]() 0.5
0.5![]() ,
centred at the position of the source. We obtained two scans, each 10 mn long, for a total integration time of 20 min in good weather (
,
centred at the position of the source. We obtained two scans, each 10 mn long, for a total integration time of 20 min in good weather (
![]() ). During both scans the Dish Surface Optimisation System (DSOS)
). During both scans the Dish Surface Optimisation System (DSOS)![]() was used to correct the dish surface for gravitational deformations as the dish moves in elevation.
was used to correct the dish surface for gravitational deformations as the dish moves in elevation.
The raw scans were reduced with version 1.61 of the Comprehensive Reduction Utility for SHARC-II (CRUSH), a publicly available![]() , Java-based software package. CRUSH iteratively solves a series of models that attempt to reproduce the observations, taking into account both instrumental and atmospheric effects (Kovács et al. 2006; Kovács 2006; Beelen et al. 2006). Pointing corrections to each scan were applied in reduction based on a publicly available
, Java-based software package. CRUSH iteratively solves a series of models that attempt to reproduce the observations, taking into account both instrumental and atmospheric effects (Kovács et al. 2006; Kovács 2006; Beelen et al. 2006). Pointing corrections to each scan were applied in reduction based on a publicly available![]() model fit to all available pointing data. Pixels at the edges of the map with a total integration time less than 25% of the maximum were removed to compensate for the increased noise in these pixels. We then used Starlink's stats package to assess the rms noise of the map, calculated using all pixels in the off-source regions. The final map has a 1
model fit to all available pointing data. Pixels at the edges of the map with a total integration time less than 25% of the maximum were removed to compensate for the increased noise in these pixels. We then used Starlink's stats package to assess the rms noise of the map, calculated using all pixels in the off-source regions. The final map has a 1![]() rms noise of 70 mJy beam-1.
rms noise of 70 mJy beam-1.
Table 1: Overview of the beam sizes in the millimetre-maps.
Photometry was measured in a 20
![]() aperture centred at the peak position of the source.
Calibration was performed according to the method used by Wu et al. (2007); Shirley et al. (2000).
This method is based on the requirement that a point source should have the same flux density in all apertures with diameters greater than the beam FWHM (8.5
aperture centred at the peak position of the source.
Calibration was performed according to the method used by Wu et al. (2007); Shirley et al. (2000).
This method is based on the requirement that a point source should have the same flux density in all apertures with diameters greater than the beam FWHM (8.5
![]() for these observations).
To briefly summarise, a flux conversion factor (FCF) is calculated for a 20
for these observations).
To briefly summarise, a flux conversion factor (FCF) is calculated for a 20
![]() aperture by dividing the total flux density of a calibration source in Jy by the calculated flux density in the native instrument units of
aperture by dividing the total flux density of a calibration source in Jy by the calculated flux density in the native instrument units of ![]() V in a 20
V in a 20
![]() aperture.
Flux densities of science targets are then derived by multiplying the 20
aperture.
Flux densities of science targets are then derived by multiplying the 20
![]() aperture flux density (in the instrument units) of the source by the FCF. We measure a 350
aperture flux density (in the instrument units) of the source by the FCF. We measure a 350 ![]() m flux density for CB 26 of
m flux density for CB 26 of
![]() Jy.
Jy.
3 Results from observations - basis for modeling
The focus of this section are the results by the previously described observations. The presented data set forms the basis of our modeling.
3.1 Images
The maps from the HST in I, J, H, and K bands are shown in Fig. 1. All all four images have been rotated in order to align the major axis of the dark lane with the horizontal axis. The emission seen on these maps is scattered light from the central star. A dark shadowy linear feature that intersects the bipolar structure is present in all images. The dependence of its width on the wavelength is clearly visible. Since one expects the circumstellar disc to be optically thick at these wavelengths, the dark lane is interpreted as the disc's shadow in the encompassing envelope structure. The bipolar nebula also shows a complex morphology far above and especially below the disc. For further discussion we refer the interested reader to Padgett et al. (2009, in preparation).
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[width=4.5cm]{12397f1a.eps...
...=4.5cm]{12397f1c.eps}
\includegraphics[width=4.5cm]{12397f1d.eps}}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg74.png) |
Figure 1:
Inverse HST images obtained with ACS and NICMOS in the I, J, H and K band. The colour scale is |
| Open with DEXTER | |
The interferometric millimetre continuum maps at 1.1 mm, 1.3 mm, and 2.7 mm, together with the dirty beam maps (see also Table 1), are shown in Fig. 2. For the ease of modelling, these images have been rotated ![]() in order to align the major axis of the elongated structure with the horizontal axis. While the source is unresolved vertically in all images, it is well-resolved along its horizontal axis, especially in the highest-resolution map at 1.3 mm. The 1.3 mm map also recovers some extended emission from the envelope that might be related to a disc wind (see Launhardt & Sargent 2001). For all images shown, radio and NIR, North is the same direction.
in order to align the major axis of the elongated structure with the horizontal axis. While the source is unresolved vertically in all images, it is well-resolved along its horizontal axis, especially in the highest-resolution map at 1.3 mm. The 1.3 mm map also recovers some extended emission from the envelope that might be related to a disc wind (see Launhardt & Sargent 2001). For all images shown, radio and NIR, North is the same direction.
Figure 3 shows an overlay of a NIR colour-composite image and the
![]() dust continuum emission. The spatial co-location of the millimetre dust emission and the dark lane in the scattered light images confirms the hypothesis of an edge-on optically thick disc as explanation for the observed features. However, the HST pointing is only good to about 1 arcsec. Due to the high extinction in the cloud core and the small NICMOS field of view, there are no reference stars in the image that could be used to correct for this pointing uncertainty.
dust continuum emission. The spatial co-location of the millimetre dust emission and the dark lane in the scattered light images confirms the hypothesis of an edge-on optically thick disc as explanation for the observed features. However, the HST pointing is only good to about 1 arcsec. Due to the high extinction in the cloud core and the small NICMOS field of view, there are no reference stars in the image that could be used to correct for this pointing uncertainty.
![\begin{figure}
\par\resizebox{9cm}{!}{
\includegraphics[width=4.5cm]{12397f2a.e...
....5cm]{12397f2e.eps}
\includegraphics[width=4.5cm]{12397f2f.eps}}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg75.png) |
Figure 2:
Inverse, reconstructed images from millimetre interferometric observations (left column) and corresponding dirty beam maps (right column), linear colour scale. All images have been rotated by |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12397f3a.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg76.png) |
Figure 3:
Overlay of the OVRO
|
| Open with DEXTER | |
3.2 Spectral energy distribution
The results of photometric measurements are presented in Table 2 and Fig. 4. The spectrum we obtained from the IRS compliments the photometric points as seen in Fig. 4.
As is evident in this Figure, the 350 ![]() m SHARC-II flux density is lower than expected based on comparison to the complete SED.
This discrepancy can be explained by the fact that the Lissajous observing mode is insensitive to extended emission, as noted by Wu et al. (2007).
This issue will be explored in more detail by Dunham et al. (2009, in preparation), but preliminary results suggest that flux densities measured from this particular observing mode may underestimate the true flux density by up to a factor of 2, even for relatively compact objects.
m SHARC-II flux density is lower than expected based on comparison to the complete SED.
This discrepancy can be explained by the fact that the Lissajous observing mode is insensitive to extended emission, as noted by Wu et al. (2007).
This issue will be explored in more detail by Dunham et al. (2009, in preparation), but preliminary results suggest that flux densities measured from this particular observing mode may underestimate the true flux density by up to a factor of 2, even for relatively compact objects.
Table 2: Photometric data points for CB 26.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12397f4a.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg98.png) |
Figure 4: Spectral energy distribution. Data with error-bars from Table 2. The IRS spectrum is the solid line. The dashed-dotted line corresponds to the best-fit model. The dashed line is the best-fit model with the dust screen. |
| Open with DEXTER | |
4 Model and modeling
In this section, we provide the reader with an introduction to the concepts and techniques we use.
4.1 The model
First, we discuss the various components of our model, i.e., the disc and envelope dust density distribution. The employment of both these parts in the model is readily suggested by the data.
4.1.1 The disc
The main part of our model for CB 26 is a parametrised disc. The disc is seen as the radially extended luminous structure in the millimetre maps. The dark lane in the near-infrared maps is another indication for a disc as it can be understood as the disc's shadow on the surrounding envelope.
We employ a parametric approach to such a disc which can be written as
where z is the usual cylindrical coordinate with z = 0 corresponding to the disc midplane and
Here the quantities
Integrating Eq. (1) along the z axis yields the surface density
Comparison with Eq. (1) yields the following relation between the exponent of the surface density power law and the geometrical parameters of the ansatz
The radial size of the disc
4.1.2 The envelope
In order to reproduce the pattern of scattered light we see in the I, J, H, and K observations, we add an envelope-like dust distribution to the model. The HST optical and NIR data show while the envelope has a high enough density to produce scattered light, it is orders of magnitude lower than the density of the circumstellar disc which is optically thick enough to obscure the central star completely. Further evidence for the low density in the envelope are the millimetre maps where the envelope cannot be seen.
For the model of the envelope structure we follow the ideas of Ulrich (1976).
We thus implement a model for a rotating envelope resulting from infalling matter similar to Whitney et al. (2003); Eisner et al. (2005):
Here
Hence, we are using
![]() as a fitting parameter. To avoid introducing a constant like
as a fitting parameter. To avoid introducing a constant like
![]() with no direct physical interpretation into the discussion later on, we shall in this work refer to M* and
with no direct physical interpretation into the discussion later on, we shall in this work refer to M* and ![]() separately.
separately.
As a criterion to decide whether the disc dust distribution or the envelope dust distribution at a given point should be considered, we compare the two densities and choose the larger value:
In this manner, we embed the disc into the envelope and guarantee a smooth transition from the disc to the envelope without the need to alter the density structure of the optically thick, millimetre-bright part of the object. For the radius of the complete model space we take twice the outer radius of the disc. Since we do employ a maximum size for the outer disc radius
4.1.3 The dust
Since gas is optically thin![]() in the wavelength regime we deal with, we limit ourselves to radiative transfer through the dust.
For the mass relation of dust and gas we assume the standard value of
in the wavelength regime we deal with, we limit ourselves to radiative transfer through the dust.
For the mass relation of dust and gas we assume the standard value of
![]() which is in agreement with the findings of Glauser et al. (2008) in another disc surrounding a low-mass T Tauri star.
Therefore, it is the dust whose density structure is described by Eqs. (1) and (5) in the disc and the envelope, respectively. The dust grain properties in our model can be divided in three groups: The shape of the dust grains, their chemical composition, and their size distribution.
which is in agreement with the findings of Glauser et al. (2008) in another disc surrounding a low-mass T Tauri star.
Therefore, it is the dust whose density structure is described by Eqs. (1) and (5) in the disc and the envelope, respectively. The dust grain properties in our model can be divided in three groups: The shape of the dust grains, their chemical composition, and their size distribution.
Grain shape:
We assume the dust grains to be homogeneous spheres. Real dust grains, of course, are expected to feature a much more complex and fractal structure. As discussed by Voshchinnikov (2002), chemical composition, size and shape of dust grains cannot be determined separately, but only as a combination. We therefore limit our model to the less complex but also less ambiguous approach of spherical, non-aligned and non-orientated dust grains.
Grain chemistry:
For the chemical composition of the dust grains we employ a model that incorporates both silicate and graphite material. This grain model has already been used to model the ``Butterfly star'' by Wolf et al. (2003). For the optical data, we use the complex refractive indices of ``smoothed astronomical silicate'' and graphite as published by Weingartner & Draine (2001). Since the longest wavelength considered in our modeling is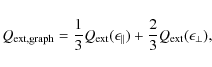 |
(7) |
where
Grain sizes:
For the grain size distribution we assume a power law of the formHere, a is the dust grain radius and n(a) the number of dust grains with a specific radius. For
To model the different grain sizes and chemical populations, one has to consider an arbitrary number of separate dust grain sizes within a given interval
![]() .
But, the observables derived from radiative transfer considering each grain species separately are close to the observables resulting from radiative transfer (RT) simulations based on weighted mean dust grain parameters of the dust grain ensemble (Wolf 2003a).
Thus, we use weighted mean values for the efficiencies factors, cross sections, albedo, and scattering matrix elements.
For each dust grain ensemble, 1000 logarithmically equidistantly distributed grain sizes within the interval
.
But, the observables derived from radiative transfer considering each grain species separately are close to the observables resulting from radiative transfer (RT) simulations based on weighted mean dust grain parameters of the dust grain ensemble (Wolf 2003a).
Thus, we use weighted mean values for the efficiencies factors, cross sections, albedo, and scattering matrix elements.
For each dust grain ensemble, 1000 logarithmically equidistantly distributed grain sizes within the interval
![]() have been taken into account for each chemical component in the averaging process.
have been taken into account for each chemical component in the averaging process.
There are arguments that the grain size can not be governed by a power law as in Eq. (8). Furthermore, in the complex environment of a circumstellar disc, we expect dust settling and grain growth to make the grain size distribution quite dependent on the location within the disc. Unfortunately, a consideration of grain sizes that takes into account the effects of e.g. dust settling requires more than just one parameter as Eq. (8) does. Given the data we have, we are not able to disentangle these parameters in our study. Therefore, we assume that the power law distribution (8) to be valid in the whole disc and envelope structure and only use the maximum grain size as a parameter in our modeling efforts.
It will turn out that even with these simplifying assumptions we are able to model observational data of the system, although different
![]() in the disc and envelope have been found for other objects (e.g. Wolf et al. 2003).
We assume an average grain mass density of
in the disc and envelope have been found for other objects (e.g. Wolf et al. 2003).
We assume an average grain mass density of
![]() .
This density does not have any influence on the optical properties of the dust, as they are governed by the chemical composition and the particle size of the grains. The average grain mass density merely controls, together with the disc mass and particle size, the number of dust grains in the disc.
.
This density does not have any influence on the optical properties of the dust, as they are governed by the chemical composition and the particle size of the grains. The average grain mass density merely controls, together with the disc mass and particle size, the number of dust grains in the disc.
4.1.4 Heating sources
There are two sources of energy for the disc that need our attention. The disc can be heated by stellar radiation and/or accretion of in-falling matter.
Accretion heating
: Our model involves a parameter with the dimensionality of an ``accretion rate'':Besides matter infall in the envelope, accretion in the disc might be an important source of energy. As shown by Wolf et al. (2003), the accretion luminosity from within the disc is about two of magnitude smaller than the stellar contribution. As the model setup here is similar, we neglect accretion heating as a significant source of energy.
Stellar heating
: The discussion above leaves the star as the only primary source of energy in our model. Its radiation heats the dust which then in turn itself re-emits at longer wavelengths. In this sense the disc in our model is passive. That is, we neglect accretion or turbulent processes within the disc as a possible other primary energy source.We do not observe the star directly. This is for the following two reasons:
- 1.
- in the far infrared and at longer wavelengths, where the disc becomes less opaque with increasing wavelength, the contribution to the spectral energy distribution from the dust is orders of magnitude larger than that coming from the star;
- 2.
- in the optical, near, and mid-infrared bands, the disc becomes opaque, and the star is shielded from our direct view.
Both of these parameters have been kept fixed in our parameter study to avoid degeneracies between parameters of the model. Except for the total flux, this choice has no impact on the near-infrared images.
As Natta (1993) showed, under certain conditions stellar light scattered back to the disc can have significant implications for the thermal structure of the disc. Here, the outer envelope regions
![]() are shown to be of importance.
An important assumption in the argument is that the scattering phase function is independent of the scattering angle.
However, in our modeling framework, the scattering phase function is highly asymmetrical and favours forward scattering by orders of magnitude.
Thus, the amount of radiation scattered back to the disc from the envelope outside our model space, i.e. at distance larger then
are shown to be of importance.
An important assumption in the argument is that the scattering phase function is independent of the scattering angle.
However, in our modeling framework, the scattering phase function is highly asymmetrical and favours forward scattering by orders of magnitude.
Thus, the amount of radiation scattered back to the disc from the envelope outside our model space, i.e. at distance larger then
![]() ,
can be neglected.
,
can be neglected.
4.2 Means of modeling
In this section we discuss how we proceed with the model. We discuss the free parameters, their range, and the sampling of the resulting parameter space. Finally, we review the constraints imposed upon our model by the various observations and give a criterion for the best-fit model.
4.2.1 Radiative transfer
For our continuum radiative transfer simulations, we made use of the program MC3D (Wolf 2003b; Wolf et al. 1999).
It is based on the Monte-Carlo method and solves the continuum radiative transfer problem self-consistently.
It estimates the dust temperature distribution taking into account any heating sources, which in our case is the central star's radiation.
It makes use of the temperature correction technique as described by Bjorkman & Wood (2001), the absorption concept as introduced by Lucy (1999), and the enforced scattering scheme as proposed by Cashwell & Everett (1959).
The optical properties of the dust grains (scattering, extinction and absorption cross sections, scattering phase function) and their interaction with the radiation field is calculated using Mie theory.
Multiple and anisotropic scattering is considered.
The phase function is highly asymmetrical (e.g. at the peak of stellar emission at
![]() one has
one has
![]() ), strongly favouring forward-scattering.
), strongly favouring forward-scattering.
In order to derive a spatially resolved dust temperature distribution, the model space has to be subdivided into volume elements inside which a constant temperature is assumed. Both the symmetry of the density distribution and the density gradient distribution have to be taken into account. For the present study, we use a spherical model space, centred on the illuminating star and an equidistant subdivision of the model in the ![]() -direction, whilst a logarithmic radial scale is chosen in order to resolve the temperature gradient at the very dense inner region of the disc.
The required spatial resolution at the disc inner radius rim of our model ranges from
-direction, whilst a logarithmic radial scale is chosen in order to resolve the temperature gradient at the very dense inner region of the disc.
The required spatial resolution at the disc inner radius rim of our model ranges from
![]() up to
up to
![]() ,
and every grid cell outwards is 1% larger than its next inner neighbour.
,
and every grid cell outwards is 1% larger than its next inner neighbour.
The radiative transfer is simulated at 101 wavelengths.
The first 100 wavelengths are logarithmically distributed in the wavelength range
![]() .
The longest wavelength used is
.
The longest wavelength used is
![]() .
.
With MC3D we compute observables from the model. These observables are then compared to the observed data in the quest for the best-fit model. Namely, the quantities we derive with MC3D from the model are:
- 1.
- images in the NIR, that is in the I, J, H, and K Band;
- 2.
- images in the millimetre regime at 1.1 mm, 1.3 mm and 2.7 mm,
- 3.
- 101 points for the SED accordingly to the above wavelength distribution.
4.2.2 Constraints from observations
Given the broad variety of available observational data, there are primary features are that we want to reproduce with our model. This also determines the criteria for the best-fit model. The case is simple for the spectral energy distribution. There, we aim at reproducing the complete spectrum over three orders of magnitudes from the optical bands down to the millimetre regime. We can divide the maps of the disc in two major groups: the maps in the millimetre regime, and the maps in the near-infrared. Both groups trace different physical processes and different spatial regions of the object.
Millimetre maps:
For resolved images, the issue is not as simple as for the SED. Our model is rotationally symmetric and thus does not provide for any related asymmetry as seen in observations.
The morphology of the millimetre maps has its origin in the dust that is heated by the star and re-emits light at those wavelengths.
Although the images at
![]() ,
,
![]() and
and
![]() are rather simply structured they impose two major features that constrain our models.
These are:
are rather simply structured they impose two major features that constrain our models.
These are:
- 1.
- the peak flux and;
- 2.
- the spatial brightness distribution.
Maps in the near-infrared:
The four images in the near-infrared show more structures and details than the millimetre maps. In addition to the disc, which appears as a dark lane in the near-infrared, there is also a complex, wavelength-dependent morphology of the surrounding envelope.Considering that the circumstellar disc CB 26 is located at the edge of a Bok globule, one realises that the environment of the disc can account for the majority of the substructure seen on these maps; yet the Bok Globule itself is not part of our model. Hence, we have to restrict ourselves to the following two points that we want to reproduce with our model:
- 1.
- the dependence of the width of the dark dust lane on wavelength and;
- 2.
- the relative peak height of the brightness distribution above and below the dust lane.
4.2.3 Quality of the fit
For each comparison between model and observation on the aforesaid points, we get an individual
![]() .
The total
.
The total ![]() of one model is then just the sum over all the individual
of one model is then just the sum over all the individual ![]() s:
s:
Here, n=8 as we have one
Based on
![]() we get from Eq. (9), we give our modeling errors as the range where we can alter the parameter values without changing
we get from Eq. (9), we give our modeling errors as the range where we can alter the parameter values without changing
![]() more than 10%. This value is rather arbitrary as there is no mathematical reasoning behind it.
Yet, it has proved within our study to reflect quite well the adjustability of the model. Allowing for a larger variation of
more than 10%. This value is rather arbitrary as there is no mathematical reasoning behind it.
Yet, it has proved within our study to reflect quite well the adjustability of the model. Allowing for a larger variation of
![]() than
than ![]() gives generally worse results.
gives generally worse results.
4.2.4 Parameter space study
Based on the model laid out in the previous sections, we are left with ten adjustable parameters to reproduce the characteristics as described in the previous section. If not stated otherwise, we choose the range of a parameter for our study based on modeling of other similar objects (see e.g. Wolf et al. 2003). Then, we first sample that range of an individual parameter in four coarse steps, select the two best values, and go with the same procedure to the next parameter. Second, we take the results as an indicator how to refine the stepping in a smaller range. This process is iterated to reach our final results. As the starting values in our parameter space study we chose the values obtained for IRAS 04302+2247 which has a similar appearance to CB 26.
Table 3: Overview of parameter ranges and best-fit values.
In detail, the parameters we use are:
- 1.
- the exponents
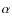 and
and 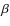 which describe the radial density profile of the disc (see Eq. (1) for details). From D'Alessio et al. (1999), we choose for the flaring parameter
which describe the radial density profile of the disc (see Eq. (1) for details). From D'Alessio et al. (1999), we choose for the flaring parameter
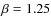 and obtain a corresponding value for
and obtain a corresponding value for
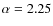 from the relation
from the relation
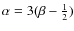 ,
which is a result of accretion disc physics (see e.g. Shakura & Syunyaev 1973). Those values are taken as a starting point and we then look for agreement between observations and modeling at and beyond those values in steps of 0.1 and 0.2, respectively;
,
which is a result of accretion disc physics (see e.g. Shakura & Syunyaev 1973). Those values are taken as a starting point and we then look for agreement between observations and modeling at and beyond those values in steps of 0.1 and 0.2, respectively;
- 2.
- the scale height h0 of the disc at a given radius.
In the following, we fix the scale height at a radial distance from the star of
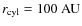 and consider the cases
and consider the cases
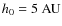 ,
,
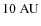 ,
,
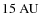 ,
,
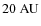 ,
and
,
and
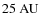 ;
;
- 3.
- from the density Eq. (5) for the envelope, we have the centrifugal radius
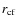 and;
and;
- 4.
- the coupling constant
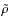 which is a function of the mass accretion rate
which is a function of the mass accretion rate 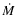 and the mass of the central star M*.
For the centrifugal radius, we probe values in the range
and the mass of the central star M*.
For the centrifugal radius, we probe values in the range
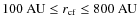 .
As for
.
As for
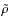 ,
we chose for the accretion rate values from the interval
,
we chose for the accretion rate values from the interval
![$\dot{M}~\in~[10^{-5}~{M}_\odot~{\rm yr}^{-1};10^{-10}~{M}_\odot~{\rm yr}^{-1}]$](/articles/aa/full_html/2009/39/aa12397-09/img184.png) and calculate
and calculate
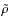 under the consideration of the stellar mass by Launhardt et al. (2008). In this paper a dynamical mass of
under the consideration of the stellar mass by Launhardt et al. (2008). In this paper a dynamical mass of
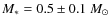 is derived;
is derived;
- 5.
- the inner and outer disc radius. The inner radius was initially set to
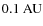 ,
which is approximately the dust sublimation radius. However, we do not get good agreement especially with the
,
which is approximately the dust sublimation radius. However, we do not get good agreement especially with the
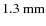 map unless we choose values of
map unless we choose values of 
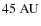 .
For the outer radius, we chose a value of
.
For the outer radius, we chose a value of
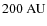 but also considered configurations with
but also considered configurations with
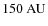 and
and
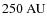 ;
;
- 6.
- the disc mass. We consider 7 different disc dust masses in the range from
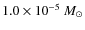 up to
up to
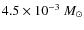 ;
;
- 7.
- the disc's inclination is such that the system is seen almost edge-on. We restrict the range for
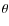 to be part of our parameter space to values between
to be part of our parameter space to values between 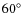 and
and 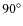 with a stepping of
with a stepping of 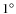 between
between 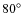 and
and 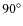 ;
;
- 8.
- the maximum grain size
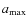 .
Grain growth is a major issue for protoplanetary discs as it is the first step towards the formation of planets from the dust in the interstellar medium. We allow for a maximum grain size of
.
Grain growth is a major issue for protoplanetary discs as it is the first step towards the formation of planets from the dust in the interstellar medium. We allow for a maximum grain size of
 .
.
![\begin{figure}
\par\resizebox{9cm}{!}{
\includegraphics[]{12397f5a.eps} }
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg197.png) |
Figure 5: Sketch showing all components of our model and their spatial arrangement. All sizes are not to scale. |
| Open with DEXTER | |
5 Results
The values of the parameters of our best-fit model can be found in Table 3. Our geometrical parameters ![]() and
and ![]() of the disc density structure yield with the Eq. (4) a surface density power-law exponent of p=-0.8.
of the disc density structure yield with the Eq. (4) a surface density power-law exponent of p=-0.8.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12397f6a.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg199.png) |
Figure 6:
Upper plot: contours of dust density distribution on a plane perpendicular to the midplane normalised to the peak density of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12397f7a.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg201.png) |
Figure 7:
Radial profiles of density (upper plot) and temperature (lower plot) in the midplane along r (solid line) and along z/r=0.1 (dashed line). The latter profile is chosen in order to include the scale height h0 at
|
| Open with DEXTER | |
In Fig. 6 the density and temperature distribution of the best-fit model is shown while in Fig. 7 radial profiles of the density and temperature distribution in the midplane and 20 ![]() above are shown. It is apparent that the high density in the midplane on the inner rim provides enough opacity so that material behind it in the midplane is not being heated up directly by the stellar radiation.
The highest dust temperature at the inner disc rim amounts to
above are shown. It is apparent that the high density in the midplane on the inner rim provides enough opacity so that material behind it in the midplane is not being heated up directly by the stellar radiation.
The highest dust temperature at the inner disc rim amounts to ![]() 90 K and is reached
90 K and is reached ![]() 20
20 ![]() above the midplane.
However, due to the high density in the midplane, the stellar radiation does not penetrate deep into the midplane which results in a steep temperature gradient. In the less dense upper (and lower) layers of the disc, the stellar radiation also heats more distant parts of the disc resulting in a less steep temperature gradient.
above the midplane.
However, due to the high density in the midplane, the stellar radiation does not penetrate deep into the midplane which results in a steep temperature gradient. In the less dense upper (and lower) layers of the disc, the stellar radiation also heats more distant parts of the disc resulting in a less steep temperature gradient.
An average dust temperature of
![]() is obtained from the temperature distribution by weighting it with the mass distribution.
This goes nicely with Fig. 6 if one bears in mind that the bulk of the dust is located in the midplane and is well shielded against stellar radiation by inner parts of the disc. High temperatures are only reached in a very narrow region at the inner disc rim and in the very low density regions of the disc and, thus, contributes little to the mass averaged dust temperature.
is obtained from the temperature distribution by weighting it with the mass distribution.
This goes nicely with Fig. 6 if one bears in mind that the bulk of the dust is located in the midplane and is well shielded against stellar radiation by inner parts of the disc. High temperatures are only reached in a very narrow region at the inner disc rim and in the very low density regions of the disc and, thus, contributes little to the mass averaged dust temperature.
Since our dust grain model only uses refractive indices, an effective dust grain opacity can be calculated by re-arranging
and assuming gas-to-dust ratio of 100. Here,
Figure 4 shows the spectral energy distribution of the best-fit model in comparison with the spectral data.
We achieve quite a good match to the observational data except for the optical wavelengths.
Since the circumstellar disc is embedded in the Bok globule CB 26 we need to consider the dust outside our model space as well.
Thus, we add a screen that mimics the effect of foreground extinction between the object and the observer.
For this screen, we assume the extinction properties of interstellar dust grains. Such a screen is described in detail by Cardelli et al. (1989). Using ![]() as a parameter with a minimum value of 2, we find in our study that a screen with a visual extinction of
as a parameter with a minimum value of 2, we find in our study that a screen with a visual extinction of
![]() can easily account for the missing flux in the optical. The result is shown in Fig. 4 as the dashed curve, whereas the dashed-dotted line corresponds to the best-fit model without the screen.
can easily account for the missing flux in the optical. The result is shown in Fig. 4 as the dashed curve, whereas the dashed-dotted line corresponds to the best-fit model without the screen.
It needs to be stressed that this screen only applies extinction law to all observable quantities.
It is not subject to any radiative transfer or thermal re-emission.
We estimated the possible contribution to re-emitted radiation of a such a screen with
![]() composed of ISM grains at the same distance as CB 26 with a temperature of 16 K. We found that the screen is clearly optically thin (e.g.
composed of ISM grains at the same distance as CB 26 with a temperature of 16 K. We found that the screen is clearly optically thin (e.g.
![]() )
and has only enough mass to have about
)
and has only enough mass to have about ![]() 1% of the observed flux in the millimetre regime.
1% of the observed flux in the millimetre regime.
Furthermore, the spectral energy distribution of the model shows that the contribution of the envelope is quite important for shorter wavelengths. In this regime, the main contribution to the spectral energy distribution comes from the envelope whilst in the radio regime the flux comes completely from the dust in the disc which glows at those wavelengths. Figure 8 illustrates this.
 |
Figure 8:
Contributions to the spectral energy distribution from disc (dashed line) and envelope (solid line). The transition from envelope to disc as the major source of radiation (re-emission and scattering) is at
|
| Open with DEXTER | |
6 Discussion
6.1 Grain size and growth
It needs to be pointed out that we have found a model capable of explaining all major elements of the observations without the need to increase the maximum grain size in our parameter study significantly. The maximum grain size of our best fit model is
![]() .
While this is a factor ten larger than the smallest maximum grain size considered in our parameter space, the value found is only marginally larger then upper grain sizes given for the ISM in the literature.
In fact, this is only true for the dust in the the disc component of our model. The maximum grain size in the envelope is the same as in found in the ISM,
.
While this is a factor ten larger than the smallest maximum grain size considered in our parameter space, the value found is only marginally larger then upper grain sizes given for the ISM in the literature.
In fact, this is only true for the dust in the the disc component of our model. The maximum grain size in the envelope is the same as in found in the ISM,
![]() .
If the maximum grain size in the envelope were bigger, then the short wavelength part of the SED could not be reproduced.
.
If the maximum grain size in the envelope were bigger, then the short wavelength part of the SED could not be reproduced.
The disc grain size we determine is certainly smaller by several orders of magnitude than the maximum grain size in other disc models such as in the work of Pinte et al. (2008). There, a maximum size of a few millimetres has been found. In contrast, models in our parameter space featuring values of
![]() fail to fit the SED in the millimetre regime as the slope of the model SED is not steep enough. Also, we did not succeed in reproducing the default value for the maximum grain size of
fail to fit the SED in the millimetre regime as the slope of the model SED is not steep enough. Also, we did not succeed in reproducing the default value for the maximum grain size of
![]() of ISM. In particular, the model would be off by a factor of ten for the SED data point at
of ISM. In particular, the model would be off by a factor of ten for the SED data point at
![]() .
.
One needs to discuss why the change for
![]() from
from
![]() to
to
![]() allows for a fit in the millimetre part of the SED - at wavelengths three orders of magnitude larger than the largest grains in the model. Intuitively, one would expect the millimetre part of the SED to remain unaltered by a change of grain size at that level.
However, this expectation is based on the assumption that the absorption efficiency of the grains
allows for a fit in the millimetre part of the SED - at wavelengths three orders of magnitude larger than the largest grains in the model. Intuitively, one would expect the millimetre part of the SED to remain unaltered by a change of grain size at that level.
However, this expectation is based on the assumption that the absorption efficiency of the grains
![]() in the millimetre regime is also insensitive to a change in the grain size at the micrometre level.
Yet, this only holds true for only two of the three dust species in the model. For the astronomical silicate and the graphite component with an alignment of the crystals' optical axis perpendicular to the propagation direction of the electromagnetic field
in the millimetre regime is also insensitive to a change in the grain size at the micrometre level.
Yet, this only holds true for only two of the three dust species in the model. For the astronomical silicate and the graphite component with an alignment of the crystals' optical axis perpendicular to the propagation direction of the electromagnetic field
![]() has the same slope in the millimetre regime for grain size distributions with a maximum grain size of
has the same slope in the millimetre regime for grain size distributions with a maximum grain size of
![]() and
and
![]() .
But for the third dust species, namely the graphite component with the crystals' optical axis aligned with the electromagnetic field, this is different. Here, the slope of
.
But for the third dust species, namely the graphite component with the crystals' optical axis aligned with the electromagnetic field, this is different. Here, the slope of
![]() is significantly larger for
is significantly larger for
![]() than for
than for
![]() .
This effect is large enough to dominate the sensitivity of the SED to changes in the maximum grain size even at the level discussed despite the fact that the dust species responsible for this behaviour has only a 12.5% share of the total dust. This is due to the fact that graphite is a far more effective absorber than silicate.
.
This effect is large enough to dominate the sensitivity of the SED to changes in the maximum grain size even at the level discussed despite the fact that the dust species responsible for this behaviour has only a 12.5% share of the total dust. This is due to the fact that graphite is a far more effective absorber than silicate.
A look on the millimetre spectral index of the data yields
![]() .
The corresponding millimetre opacity slope is
.
The corresponding millimetre opacity slope is
![]() ,
if the millimetre emission is assumed to be optically thin.
A
,
if the millimetre emission is assumed to be optically thin.
A
![]() and smaller is understood to indicate dust grain particles larger than in the interstellar medium to be present.
A value of
and smaller is understood to indicate dust grain particles larger than in the interstellar medium to be present.
A value of
![]() is expected if only ISM grains were present in the disc.
The latter is true only for grains whose absorption efficiency
is expected if only ISM grains were present in the disc.
The latter is true only for grains whose absorption efficiency
![]() behaves like silicate.
The value of
behaves like silicate.
The value of
![]() we obtain from data and model of CB 26 close to what is expected for large grains despite having still only micrometre sized grains in the model is due to the unorthodox behaviour of the parallel graphite component on the one hand side and on the other hand side to the non-vanishing optical depth in the millimetre regime (e.g.
we obtain from data and model of CB 26 close to what is expected for large grains despite having still only micrometre sized grains in the model is due to the unorthodox behaviour of the parallel graphite component on the one hand side and on the other hand side to the non-vanishing optical depth in the millimetre regime (e.g.
![]() ).
).
Draine (2006) considered also the behaviour of the millimetre opacity slope
![]() for dust mixtures of graphite and silicate.
There, no dependency of the opacity index as in our work was found.
However, in this analysis not crystalline graphite was used but the optical properties of amorphous carbonaceous solids instead.
for dust mixtures of graphite and silicate.
There, no dependency of the opacity index as in our work was found.
However, in this analysis not crystalline graphite was used but the optical properties of amorphous carbonaceous solids instead.
We summarise that we do not need mm sized grains to model the circumstellar disc CB 26 but grains with a maximum grain size still close to what is found in the ISM. This is in contrast to the modelling of the Butterfly star (see Wolf et al. 2003) as well as for the circumstellar disc HH 30 (see Wood et al. 2002) where in both cases the authors found it necessary, to have their largest grains at least four times larger than the largest grain of the interstellar matter. Of course, this result is based directly on the choice of the grain model we made. For another model, especially one without graphite, larger grains might be needed to fit the observed SED. Yet, due to the poorly constrained dust composition of circumstellar discs - in particular in the disc interior - this degeneracy between dust model and grain size must remain. As the dust model used in this work is also used in the context of other studies of circumstellar discs such as the Butterfly star (Wolf et al. 2003), it is a reasonable choice as it keeps the models of similar objects comparable as they are built on common assumptions.
6.2 Inner hole
 |
Figure 9:
Horizontal cut through the spatial brightness distribution at
|
| Open with DEXTER | |
The most unexpected result of our modeling is the inner disc radius for the model. In Fig. 9 the solid line shows the flux profile along the disc midplane at
![]() as seen by OVRO whilst the thin solid line is the PSF of the observation. At the centre of the disc, the profile shows a plateau in the brightness distribution. There are two possible explanations for this dip.
as seen by OVRO whilst the thin solid line is the PSF of the observation. At the centre of the disc, the profile shows a plateau in the brightness distribution. There are two possible explanations for this dip.
First, the minimum could indicate that emitting dust in that region is present but not visible. If the optical depth in the midplane is sufficiently high, the flux contribution from the inner parts of the disc compared to the contribution of the optically thin parts on the disc's surface would be smaller.
A high optical depth can easily be reached in regions of high dust densities.
For a given total disc mass, a disc with small inner radius yields higher densities than the model with the large inner radius.
Hence, the smaller the inner radius in our model, the more matter we find to be close to the star and thus reaching higher optical depths in the inner disc regions. However, even for the smallest inner radius of our parameter space,
![]() we did not reach an optical depth that obscures enough flux from the disc centre to reproduce our observations.
we did not reach an optical depth that obscures enough flux from the disc centre to reproduce our observations.
This behaviour would also be more obvious when compared with maps at shorter wavelengths since the optical depth increases with decreasing wavelength.
But in the images at
![]() and
and
![]() we do not observe a dip at the centre of the disc. Unfortunately, the other available images do not help us to conclude whether the absence of the dip is really an indicator for a substantial void in the disc. This is because the point spread function at those two images is far too large to resolve the feature (see Table 1). Wolf et al. (2008) reasoned this way in the case of IRAS 04302+2247 where they found a similar dip in the brightness distribution at
we do not observe a dip at the centre of the disc. Unfortunately, the other available images do not help us to conclude whether the absence of the dip is really an indicator for a substantial void in the disc. This is because the point spread function at those two images is far too large to resolve the feature (see Table 1). Wolf et al. (2008) reasoned this way in the case of IRAS 04302+2247 where they found a similar dip in the brightness distribution at
![]() but not at
but not at
![]() .
.
The second possible cause for the spatial brightness distribution in the
![]() map is the actual lack of dust in the inner region of the disc.
Whilst we started with an inner radius in the order of magnitude of a few tens of the stellar radius, it was not possible to match the plateau structure of the
map is the actual lack of dust in the inner region of the disc.
Whilst we started with an inner radius in the order of magnitude of a few tens of the stellar radius, it was not possible to match the plateau structure of the
![]() map.
On this account, we allow the inner disc radius to be as large as
map.
On this account, we allow the inner disc radius to be as large as
![]() .
Unfortunately, within our model and parameter framework we are not at liberty to increase the total mass, and hence the density at the disc centre, because the flux at
.
Unfortunately, within our model and parameter framework we are not at liberty to increase the total mass, and hence the density at the disc centre, because the flux at
![]() already sets an upper limit for the total disc dust mass.
This is because at this wavelength any model is optically thin, so we see the total matter of the disc.
already sets an upper limit for the total disc dust mass.
This is because at this wavelength any model is optically thin, so we see the total matter of the disc.
Another way to think about the issue is to consider the optical depth of the disc at
![]() .
We have run one simulation of the disc with exactly the same parameter values as for our best-fit model except for the inner radius. For the comparison model we chose
.
We have run one simulation of the disc with exactly the same parameter values as for our best-fit model except for the inner radius. For the comparison model we chose
![]() .
For both runs we computed the optical depth along the line of sight from the observer through the disc. As a result, for the large inner radius we have
.
For both runs we computed the optical depth along the line of sight from the observer through the disc. As a result, for the large inner radius we have
![]() ,
and for the small inner radius
,
and for the small inner radius
![]() .
In the first case we deal with an optically thin system, while for the second, the optical depth is borderline. An optical depth of 1.9 means that the initial flux is reduced by a factor of e
-1.9=0.15. A much larger value of
.
In the first case we deal with an optically thin system, while for the second, the optical depth is borderline. An optical depth of 1.9 means that the initial flux is reduced by a factor of e
-1.9=0.15. A much larger value of ![]() along the line of sight would be required to hide all emitting dust in the central region and produce the observed plateau structure. Thus, in our study, we were not able to fit the millimetre profile with a small inner radius.
along the line of sight would be required to hide all emitting dust in the central region and produce the observed plateau structure. Thus, in our study, we were not able to fit the millimetre profile with a small inner radius.
We are therefore forced to conclude that in the millimetre regime we do see the entire disc. Hence, the plateau structure rises from the wide spatial separation of the inner rim from the star, whereas a disc with a small inner radius would have a central peak in the brightness distribution.
Based on this line of arguments, our model provides predictive power for high resolution images at wavelengths longer than
![]() .
Since we conclude that the plateau structure in the brightness profile is due to lack of dust, it should also be visible at longer wavelengths.
There, the dust becomes more optically thin and thus provides us with literal insight inside the disc. Now, if the lack of flux in the disc centre is due to an optical depth effect, the central trough should vanish with longer wavelengths, and the brightness profile should have one central peak instead of a plateau-structure. Unfortunately, the image at
.
Since we conclude that the plateau structure in the brightness profile is due to lack of dust, it should also be visible at longer wavelengths.
There, the dust becomes more optically thin and thus provides us with literal insight inside the disc. Now, if the lack of flux in the disc centre is due to an optical depth effect, the central trough should vanish with longer wavelengths, and the brightness profile should have one central peak instead of a plateau-structure. Unfortunately, the image at
![]() has a point spread function far too large to allow us to disentangle between the two possibilities. Future observations of the disc CB 26 with higher spatial resolution will provide a perfect opportunity to confirm this prediction.
Figure 10 shows what we expect the disc to look like at different wavelengths according to our model with the inner void.
With the Atacama Large Millimeter Array (ALMA) it will be quite easy to confirm our findings.
has a point spread function far too large to allow us to disentangle between the two possibilities. Future observations of the disc CB 26 with higher spatial resolution will provide a perfect opportunity to confirm this prediction.
Figure 10 shows what we expect the disc to look like at different wavelengths according to our model with the inner void.
With the Atacama Large Millimeter Array (ALMA) it will be quite easy to confirm our findings.
![\begin{figure}
\resizebox{9cm}{!}{
\includegraphics[width=4.5cm]{12397fAa.eps}...
...397fAc.eps} \\
\includegraphics[width=4.5cm]{12397fAd.eps} \\
}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg234.png) |
Figure 10: Predicted appearance of the inner region of the disc. |
| Open with DEXTER | |
It needs to be pointed out that the spectral energy distribution of CB 26 does not hint at the presence of a large inner hole. Its general shape is similar to SEDs of other edge-on discs. This is because the inner regions of the disc which completely dominate the disc emission in the 1-20 micron regime are completely hidden from view in the edge-on configuration. Scattered starlight from the outer disc and/or the envelope accounts for the short wavelength bump of the SED, irrespective of the amount of emission from the disc itself. Only the quality of the OVRO map at 1.3 mm provides us with the need to postulate about an inner clearing.
A possible explanation for a large void with
![]() in diameter is that the disc in the Bok globule CB 26 is actually a circumbinary disc.
Binarity is also a possible explanation for the rotating molecular outflow described by Launhardt et al. (2008). However, a detailed dynamical study is not the scope of this paper.
in diameter is that the disc in the Bok globule CB 26 is actually a circumbinary disc.
Binarity is also a possible explanation for the rotating molecular outflow described by Launhardt et al. (2008). However, a detailed dynamical study is not the scope of this paper.
Of course, another idea might be that the dust in the inner region has already bean processed to planetesimals, or at least to bodies that are large enough to decouple from the disc and its dynamics, and do not contribute to the mm-flux. However, a first indicator for a low age of the system is the fact that it is still deeply embedded in its parental cloud.
Another indication to the young age of the system is the absence of dust grains larger than found in the interstellar medium. Hence, we do not expect that we may be dealing with a so called ``transitional disc''![]() and a planet population in the centre that has already cleaned up formerly dusty regions.
and a planet population in the centre that has already cleaned up formerly dusty regions.
6.3 Disc mass
Within our model a rather high disc mass is needed to account for the observed flux in the millimetre regime.
With a total of about
![]() and dust-to-gas ratio of
and dust-to-gas ratio of
we end up with a total disc mass of
6.3.1 The dust grain structure, temperature and density
The radiative transfer in our modeling is performed under the assumption of spherical dust grains to avoid equivocalities. It would be possible to have a lower estimate of the dust mass if we dismiss this assumption. This very much complicates the radiative transfer calculations since we now need to take into account all the possible fractal grain shapes as well as the spatial orientation of every grain. So far, we do not have the ability to do such a simulation. But, we can make a gedankenexperiment on parts of the results. Of course, one expects strong changes in the scattering behaviour of dust grains with complex shapes. But, besides that, one also can think of a plenitude of dust grains with almost the same absorption cross section as spherical dust grains but with much less mass. Voshchinnikov et al. (2007) discusses very fluffy particles with a porosity up to 90%.
We furthermore point out that the grain density
![]() is not one of the fitting parameters.
The disc mass is proportional to this density and the number of grains.
We only can constrain within our study the disc structure, the grain size, and their number, but not the density of one grain. For our investigation of the system, we used
is not one of the fitting parameters.
The disc mass is proportional to this density and the number of grains.
We only can constrain within our study the disc structure, the grain size, and their number, but not the density of one grain. For our investigation of the system, we used
![]() ,
but it might well be less than this value.
In turn, this will alter our estimate for the disc mass by the same factor.
,
but it might well be less than this value.
In turn, this will alter our estimate for the disc mass by the same factor.
6.3.2 The snow line
For the estimation of the total disc mass of gas and dust, we make use of the canonical relation (11). This relation assumes that there is some gas and dust of the disc inside the snow line and some outside. The snow line indicates the largest radius for which the temperature in the disc is high enough to keep water from freezing onto the dust grains. This line is usually set at a radius where the disc temperature drops to 170 K. As reported above, the maximum temperature we reach within our disc is about 90 K, and the average is only 16 K. This means, that our entire disc is outside the snow line. Thus we need to adjust the dust to gas ratio (11) to about 50 as published by Kokubo & Ida (2002).
However, the very same dust model we made use of in this work was also built upon in other modeling projects (e.g. Wolf et al. 2003). In order to allow comparison of our model for CB 26 with those models, we also give consideration to the disc stability when we keep the dust model.
6.3.3 Stability, binarity and dynamics
A criterion for a disc to become unstable was first shown by Toomre (1964).
In order to allow self-gravity of the disc to take over, it must satisfy
where
![\begin{figure}
\par\resizebox{9cm}{!}{
\includegraphics[width=0.8\textwidth]{12397fBa.eps}}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg244.png) |
Figure 11: Contour lines of the Toomre parameter Q (see Eq. (12)). The lines, from right to left, are at levels of Q = 0.1, 0.3, 0.5, 0.7. |
| Open with DEXTER | |
Yet, the Toomre criterion only can be consistently employed for a system that is formed by a central star and a surrounding disc.
As discussed above, the inner hole we find in CB 26 can be an indication for a binary. An example for such a system would be the young binary system GG Tau. Here, a dusty ring around the central stars has been observed by Guilloteau et al. (1999) with a total ring mass of
![]() ,
which is about a factor of two smaller than the total mass of CB 26. The discussion of stability of a binary system is quite delicate and not the topic of the present paper.
,
which is about a factor of two smaller than the total mass of CB 26. The discussion of stability of a binary system is quite delicate and not the topic of the present paper.
However, if one assumes a single central star, there are still effects that we did not consider in our model but which might be important for the system's stability.
Following the discussion in the paper of Gammie (2001), discs violating the Toomre criterion are not stable but nevertheless might be in a steady gravoturbulent state.
The paper investigates gravitationally unstable thin Keplerian discs and concludes that the actual outcome of the instability depends on the cooling time
![]() .
.
However, the parametric model we use does not account for any dynamical interaction within the dust. Therefore, it would be interesting to couple our radiative transfer code MC3D with hydrodynamic simulations of circumstellar discs in a future study.
6.4 The width of the dark lane and envelope structure
![\begin{figure}
\par\resizebox{9cm}{!}{
\includegraphics[width=4.5cm]{12397fCa.e...
...4.5cm]{12397fCc.eps}
\includegraphics[width=4.5cm]{12397fCd.eps}}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg251.png) |
Figure 12:
Vertical cuts at the horizontal centre through the near-infrared scattered light images. The solid line is from observational data, and the dashed line is from our best-fit model. For an illustration where those cuts are obtained in the respective maps, see Fig. 13.
The plots are normalised to 1. In case of the I-Band, this corresponds to
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12397fDa.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg253.png) |
Figure 13:
Inverse H-Band image from HST/NICMOS. The contour lines are from our best-fit model.
From the outer to the inner lines they are at 27%, 41%, 68% of the peak height. The second dark lane is not
reproduced by our modeling as we did not account for envelope asymmetries.
The PSF for those images is rather small |
| Open with DEXTER | |
Another aim of our modeling efforts was to mimic the chromaticity of the dust lane, which narrows with increasing wavelength. Figure 12 shows cuts from north to south through the centre of the NIR maps from modeling and observations. Our model of the spherical envelope is quite successful in reproducing the overall flux at each wavelength. Also, the wavelength-dependent width of the dark lane is correctly reproduced.
Figure 13 shows an overlay of the HST/NICMOS H-band image with the contours given by the best-fit model. The figure clearly shows that the dark lane is well reproduced. Since our envelope model, Eq. (5), is axially symmetric, we cannot expect the asymmetries of the lower lobe to be modeled as well. Thus, the model yields the seen discrepancy to the observation.
A second effect of the neglect of asymmetry is that the lower lobe flux, which in the image is concentrated on the left hand side, is in the model distributed among the complete lower lobe. Since both fluxes are equal in magnitude, we end up with a smaller maximum in the model which also can be seen in Fig. 13.
6.4.1 Alternative model for the envelope
Besides the rotating, infalling envelope model as described in Eq. (5), we also tested a spherical symmetric density distribution as a model for the envelope:
This brings two parameters into the model,
- 1.
- The spatial flux distribution as seen in the I, J, H, and K images cannot be reproduced. In fact, we obtain a much more concentrated flux distribution above and below the dark lane than what we see in Fig. 3. Figure 14 illustrates this.
- 2.
- In the SED appears a strong silicate emission feature between
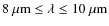 .
We are not able to have the feature disappearing as required by observations except for the inclination approaching values
.
We are not able to have the feature disappearing as required by observations except for the inclination approaching values
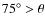 .
But this clearly contradicts the edge-on nature of the system.
.
But this clearly contradicts the edge-on nature of the system.
| |
Figure 14: J Band image from a simulation with a power-law envelope structure (left) and from rotating envelope (right). See also Fig. 1 for the observation. |
| Open with DEXTER | |
6.5 Inclination of the disc
Within our study, we considered two ways to determine disc inclination. The first is to infer it from the millimetre observations, and the second way is to constrain it from the maps in the near-infrared.
In Fig. 15, the spatial brightness distribution along a horizontal cut in the 1.3 mm map from the best-fit model at different inclinations is shown. For inclination values in the range of
![]() the profile does not change substantially.
For inclinations smaller than
the profile does not change substantially.
For inclinations smaller than ![]() ,
the profile gets lower.
This is because for an observer the warm inner rim of the disc looks at exactly
,
the profile gets lower.
This is because for an observer the warm inner rim of the disc looks at exactly ![]() like a line and becomes more and more a circle as one goes from edge-on to face-on orientation.
As long as the complete rim fits into the size of the point spread function, one cannot distinguish between the different inclinations.
But as soon as the rim gets less ellipsoidal and is no longer within the scope of one beam, the flux in the centre decreases.
This is what can be seen in Fig. 15.
Thus, from the comparison of models at different inclinations with the observations, we can infer an value for theta in the aforesaid range of
like a line and becomes more and more a circle as one goes from edge-on to face-on orientation.
As long as the complete rim fits into the size of the point spread function, one cannot distinguish between the different inclinations.
But as soon as the rim gets less ellipsoidal and is no longer within the scope of one beam, the flux in the centre decreases.
This is what can be seen in Fig. 15.
Thus, from the comparison of models at different inclinations with the observations, we can infer an value for theta in the aforesaid range of
![]() .
Naturally, this way of reasoning is only valid for systems optically thin in the millimetre.
As outlined earlier, this is assumed the case for CB 26.
.
Naturally, this way of reasoning is only valid for systems optically thin in the millimetre.
As outlined earlier, this is assumed the case for CB 26.
![\begin{figure}
\par\resizebox{9cm}{!}{
\includegraphics[width=0.8\textwidth]{12397fFa.eps}}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg263.png) |
Figure 15:
Dependency of the brightness distribution along a central cut on the inclination. All the curves for
|
| Open with DEXTER | |
The second way to determine the disc's inclination is to compare the relative peak heights from vertical cuts through the spatial brightness distributions in the near-infrared. Assuming a symmetric system one expects that both peaks exhibit the same height if the inclination is exactly edge-on. From an analysis of the actual peak heights (see Fig. 12) in the HST/NICMOS images we deduce an inclination of
![]() which is in good agreement with the numbers we obtained from the millimetre maps.
which is in good agreement with the numbers we obtained from the millimetre maps.
6.6 Comparison with similar objects
In general our model has disc and envelope parameters that are comparable with those of the circumstellar environment of other young stellar objects. Yet, there are not many edge-on seen circumstellar discs in the sky for which the same richness of observational data is available for modeling as it is for CB 26. Hence, the number of comparable multi-wavelength studies on edge-on discs is equally limited. Two objects, HH 30 and the ``Butterfly-star'', share a large number of features with the disc in CB 26. All three are seen circumstellar discs seen almost edge-on.
Wolf et al. (2003) has compiled a similar data set for a model for IRAS 04302+2247, the so called ``Butterfly-star''.
The data set includes millimetre maps and high-resolution near-infrared images obtained with HST/NICMOS.
Utilising the same techniques as in this study, the authors' main result is that the dust properties must be different in the circumstellar disc and in the envelope. Whilst a grain size distribution with grain radii up to
![]() is required to reproduce the millimetre observations of the disc, the envelope is dominated by smaller grains similar to those of the interstellar medium.
This is quite in contrast to our model, where we find grains with almost ISM-like properties are needed in both disc and envelope.
However, the original millimetre maps of the model do not suggest any presence of a large inner void as the spatial resolution is not good enough.
In a later investigation (Wolf et al. 2008) on the ``Butterfly-star'' with the Sub-Millimetre Array the authors as well discover a ``dip'' in the horizontal brightness distribution.
According to the model however, in this case the effect is attributed to an effect of the optical depth rather than an inner void.
is required to reproduce the millimetre observations of the disc, the envelope is dominated by smaller grains similar to those of the interstellar medium.
This is quite in contrast to our model, where we find grains with almost ISM-like properties are needed in both disc and envelope.
However, the original millimetre maps of the model do not suggest any presence of a large inner void as the spatial resolution is not good enough.
In a later investigation (Wolf et al. 2008) on the ``Butterfly-star'' with the Sub-Millimetre Array the authors as well discover a ``dip'' in the horizontal brightness distribution.
According to the model however, in this case the effect is attributed to an effect of the optical depth rather than an inner void.
HH 30 was identified as a circumstellar disc with a large inner void present by HH 30 by Guilloteau et al. (2008). The authors found a inner hole of radius
![]() and an outer disc radius of
and an outer disc radius of
![]() .
At this numbers HH 30 and CB 26 are quite comparable.
The separation of two central stars is postulated to be about
.
At this numbers HH 30 and CB 26 are quite comparable.
The separation of two central stars is postulated to be about
![]() ,
so this might also be good guess for CB 26.
Yet, in contrast to our model for CB 26, no envelope structure is needed to explain the appearance of HH 30 in the near-infrared bands.
This suggests that CB 26 is less dynamically evolved than HH 30.
Both systems drive a molecular outflow, but CB 26 shows clear signatures of outflow rotation (Launhardt et al. 2008), while HH 30 does not (Pety et al. 2006).
The reason for this difference remains unclear, though the early dynamically state of CB 26 as compared to HH 30 may provide the key.
Yet another difference between HH 30 and our object is that the presence of cm size grains is needed to model the value for
,
so this might also be good guess for CB 26.
Yet, in contrast to our model for CB 26, no envelope structure is needed to explain the appearance of HH 30 in the near-infrared bands.
This suggests that CB 26 is less dynamically evolved than HH 30.
Both systems drive a molecular outflow, but CB 26 shows clear signatures of outflow rotation (Launhardt et al. 2008), while HH 30 does not (Pety et al. 2006).
The reason for this difference remains unclear, though the early dynamically state of CB 26 as compared to HH 30 may provide the key.
Yet another difference between HH 30 and our object is that the presence of cm size grains is needed to model the value for
![]() (Wood et al. 2002).
In summary, although all three objects, CB 26, HH 30, and IRAS 04302+2247, feature the same interior structure, our investigation suggests that the systems are at different evolutionary states.
(Wood et al. 2002).
In summary, although all three objects, CB 26, HH 30, and IRAS 04302+2247, feature the same interior structure, our investigation suggests that the systems are at different evolutionary states.
6.7 Errors and caveats
A matter that has not been touched so far is the uniqueness of our model. Despite the simplifications we applied, the volume of the parameter space is still too vast to be completely scanned in a single study. We therefore employed the above described step-by-step technique for the parameters to find our best-fit model.
For instance, we began by modeling the millimetre maps as for those the envelope structure is not a dominant contribution. Thus, we obtained information about the disc total mass as well as its inner and outer radius and the apparent absence of large dust grains. The exploration of the near infrared images then showed the requirement for a rotational envelope structure rather then a simple power law distribution. By treating the parameters in this independent and serial manner, the order in which they are fitted might become an important issue. For instance, the study could first have focused on the near infrared images and wideness of the dust lane. As we know from our experience from modeling other objects this wideness usually requires small grains at least in the envelope. Modeling the SED in the millimetre regime as a second step would still have lead us to the overall usage of ISM grains.
This raises the question if our model is really a global minimum in the parameter space or just a local one, and if there exists in that space a model that reproduces the observations on CB 26 even better.
We exclude this possibility.
The model we obtained exhibits some unexpected features. In the framework of our model set we thoroughly explored the range of those parameters upon which these features sensitively depend.
For example, we explored the combinations for values of the inner radius and the scale height and disc mass.
If adjusted accordingly, all three can produce the plateau observed in the
![]() image.
However, only the larger inner radius prevailed.
A small scale height might squeeze the dust tight enough for high optical depth, but clearly contradicts the wavelength dependence of the dark lane in the NIR images.
The same holds for the maximum grain size.
In addition, we do not even have the possibility of mimicking ISM behaviour by means of disc geometry.
image.
However, only the larger inner radius prevailed.
A small scale height might squeeze the dust tight enough for high optical depth, but clearly contradicts the wavelength dependence of the dark lane in the NIR images.
The same holds for the maximum grain size.
In addition, we do not even have the possibility of mimicking ISM behaviour by means of disc geometry.
As a remaining issue, we need to consider parameters not varied at all in our modeling effort.
As explained in sections above, model assumptions such as spherical grains versus fractal grains can hold the key to the mass problem of the disc.
However, this would not alter the model we have at hand or provide a hint to the ``real'' global ![]() -minimum if one thinks the model is trapped in a local minimum.
-minimum if one thinks the model is trapped in a local minimum.
Degeneracy might also be an issue for the stellar parameters. Varying the luminosity and effective temperature of the embedded T Tauri star in general changes the total energy throughput in the radiative transfer and the location of the peak of the stellar spectrum in the wavelength space. Deviations from our assumed ``typical'' T Tauri star of course will affect the numbers of our best-fit model. For instance, the total mass critically depends on the flux in the millimetre regime and this flux on the total energy provided by the central star. Also, the screen introduced to mimic interstellar extinction is affected by the choice of surface temperature. However, no choice of stellar parameters is able to affect the main conclusions of our model. These are the presence of ISM grains in the disc and the disc inner hole.
Despite the discussed caveats, the fact we actually found a good model suggest that we do not need to introduce more complex physics, such as grain growth or dust settling. The data do not require this.
7 Summary
For a large span of wavelengths, we have compiled a high quality data set for the circumstellar disc in the Bok globule CB 26. We obtained images in the near infrared and in the millimetre regime as well as photometric data and spectra. Together with literature values, we have constructed a detailed model that allows interpretation of observations with one single set of parameters. The conclusions we obtained are as follows:
- 1.
- In order to account for the brightness distribution in the
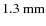 map we needed to include an inner hole with a radius of 45 AU. Future observations, especially in the sub-millimetre regime, are required to confirm our interpretation of a low optical depth along the line of site at
map we needed to include an inner hole with a radius of 45 AU. Future observations, especially in the sub-millimetre regime, are required to confirm our interpretation of a low optical depth along the line of site at
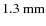 .
.
- 2.
- Our model very nicely reproduces the prominent chromaticity of the dark lane as seen in the near infrared images.
- 3.
- Based on the chosen dust composition (astronomical silicate, graphite) and the resulting opacity structure of the best-fit disc model, we find that the millimetre SED indicates that the grains feature the same grain size distribution and almost the same upper limit to the grain size as the interstellar medium.
- 4.
- The disc is massive with a total dust and gas mass of
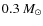 under the assumption of spherical grains and
under the assumption of spherical grains and
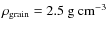 ,
compared to a mass of the central T Tauri star with
,
compared to a mass of the central T Tauri star with
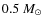 ,
and therefore is possibly, but not inevitably, unstable.
We discussed that, due to possible grain fractal structure and other effects, the real disc mass may be small enough to have a stable system.
,
and therefore is possibly, but not inevitably, unstable.
We discussed that, due to possible grain fractal structure and other effects, the real disc mass may be small enough to have a stable system.
Acknowledgements
The authors thank all members of the GEODE-team for their help in this project. J. Sauter thanks Owen Matthews, Jens Rodmann, and Arjan Bik for enlightening discussions. This work is supported by the DFG through the research group 759 ``The Formation of Planets: The Critical First Growth Phase''. F. Menard thanks financial support from Programme national de Physique Stellaire (PNPS) of CNRS/INSU, France and from Agence Nationale pour la Recherche of France under contract ANR-07-BLAN-0221. This work has been supported by NASA funding from the Space Telescope Science Institute, HST general observer program 10603; and by NASA funding from the Jet Propulsion Laboratory, under Spitzer general observer program 30765. C. Pinte acknowledges the funding from the European Commission's Seventh Framework Program as a Marie Curie Intra-European Fellow (PIEF-GA-2008-220891). The Submillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica.
References
- Alonso-Albi, T., Fuente, A., Bachiller, R., et al. 2008, ApJ, 680, 1289 [NASA ADS] [CrossRef] (In the text)
- Beckwith, S. V. W., Sargent, A. I., Chini, R. S., et al. 1990, AJ, 99, 924 [NASA ADS] [CrossRef]
- Beelen, A., Cox, P., Benford, D. J., et al. 2006, ApJ, 642, 694 [NASA ADS] [CrossRef]
- Bergeron, L. E., & Dickinson, M. E. 2003, Instrument Science Report NICMOS 2003-010 (Baltimore: STScI) (In the text)
- Bjorkman, J. E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef] (In the text)
- Bouwman, J., Henning, T., Hillenbrand, L. A., et al. 2008, ArXiv e-prints, 802 (In the text)
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] (In the text)
- Cashwell, E. D., & Everett, C. J. 1959, A practical manual on the Monte Carlo Method for random walk problems (Pergamon) (In the text)
- D'Alessio, P., Cantó, J., Hartmann, L., Calvet, N., & Lizano, S. 1999, ApJ, 511, 896 [NASA ADS] [CrossRef] (In the text)
- Dowell, C. D., Allen, C. A., Babu, R. S., et al. 2003, in SPIE Conf. Ser. 4855, ed. T. G. Phillips, & J. Zmuidzinas, 73 (In the text)
- Draine, B. T. 2006, ApJ, 636, 1114 [NASA ADS] [CrossRef] (In the text)
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [NASA ADS] [CrossRef]
- Draine, B. T., & Lee, H. M. 1987, ApJ, 318, 485 [NASA ADS] [CrossRef]
- Draine, B. T., & Malhotra, S. 1993, ApJ, 414, 632 [NASA ADS] [CrossRef] (In the text)
- Duchêne, G., McCabe, C., Ghez, A. M., et al. 2004, ApJ, 606, 969 [NASA ADS] [CrossRef]
- Eisner, J. A., Hillenbrand, L. A., Carpenter, J. M., et al. 2005, ApJ, 635, 396 [NASA ADS] [CrossRef]
- Engelbracht, C. W., Blaylock, M., Su, K. Y. L., et al. 2007, PASP, 119, 994 [NASA ADS] [CrossRef]
- Gammie, C. F. 2001, ApJ, 553, 174 [NASA ADS] [CrossRef] (In the text)
- Glauser, A. M., Ménard, F., Pinte, C., et al. 2008, A&A, 485, 531 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gordon, K. D., Engelbracht, C. W., Fadda, D., et al. 2007, PASP, 119, 1019 [NASA ADS] [CrossRef]
- Guilloteau, S., Dutrey, A., Pety, J., et al. 2008, A&A, 478, L31 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Guilloteau, S., Dutrey, A., & Simon, M. 1999, A&A, 348, 570 [NASA ADS] (In the text)
- Gullbring, E., Hartmann, L., Briceno, C., et al. 1998, ApJ, 492, 323 [NASA ADS] [CrossRef] (In the text)
- Ho, P. T. P., Moran, J. M., & Lo, K. Y. 2004, ApJ, 616, L1 [NASA ADS] [CrossRef] (In the text)
- Hughes, A. M., Wilner, D. J., Kamp, I., et al. 2008, ApJ, 681, 626 [NASA ADS] [CrossRef] (In the text)
- Kessler-Silacci, J., Augereau, J.-C., Dullemond, C. P., et al. 2006, ApJ, 639, 275 [NASA ADS] [CrossRef] (In the text)
- Kokubo, E., & Ida, S. 2002, ApJ, 581, 666 [NASA ADS] [CrossRef] (In the text)
- Kovács, A. 2006, Ph.D. Thesis, AA(Caltech), attila@submm.caltech.edu
- Kovács, A., Chapman, S. C., Dowell, C. D., et al. 2006, ApJ, 650, 592 [NASA ADS] [CrossRef]
- Launhardt, R., & Henning, T. 1997, A&A, 326, 329 [NASA ADS] (In the text)
- Launhardt, R., & Sargent, A. I. 2001, ApJ, 562, L173 [NASA ADS] [CrossRef] (In the text)
- Launhardt, R., Pavlyuchenkov, Y., Gueth, F., et al. 2008, VizieR Online Data Catalog, 34940147 (In the text)
- Lucy, L. B. 1999, A&A, 344, 282 [NASA ADS] (In the text)
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] (In the text)
- Natta, A. 1993, ApJ, 412, 761 [NASA ADS] [CrossRef] (In the text)
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS]
- Pety, J., Gueth, F., Guilloteau, S., et al. 2006, A&A, 458, 841 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pinte, C., Fouchet, L., Ménard, F., Gonzalez, J.-F., & Duchêne, G. 2007, A&A, 469, 963 [NASA ADS] [CrossRef] [EDP Sciences]
- Pinte, C., Padgett, D. L., Menard, F., et al. 2008, ArXiv e-prints, 808 (In the text)
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433 (In the text)
- Scoville, N. Z., Carlstrom, J. E., Chandler, C. J., et al. 1993, PASP, 105, 1482 [NASA ADS] [CrossRef] (In the text)
- Shakura, N. I., & Syunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] (In the text)
- Shirley, Y. L., Evans, II, N. J., Rawlings, J. M. C., et al. 2000, ApJS, 131, 249 [NASA ADS] [CrossRef]
- Stansberry, J. A., Gordon, K. D., Bhattacharya, B., et al. 2007, PASP, 119, 1038 [NASA ADS] [CrossRef]
- Stapelfeldt, K. R., Krist, J. E., Menard, F., et al. 1998, ApJ, 502, L65 [NASA ADS] [CrossRef]
- Stapelfeldt, K. R., Ménard, F., Watson, A. M., et al. 2003, ApJ, 589, 410 [NASA ADS] [CrossRef] (In the text)
- Stecklum, B., Launhardt, R., Fischer, O., et al. 2004, ApJ, 617, 418 [NASA ADS] [CrossRef] (In the text)
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] (In the text)
- Ulrich, R. K. 1976, ApJ, 210, 377 [NASA ADS] [CrossRef] (In the text)
- Voshchinnikov, N. V. 2002, in Optics of Cosmic Dust, ed. G. Videen, & M. Kocifaj, 1 (In the text)
- Voshchinnikov, N. V., Videen, G., & Henning, T. 2007, Appl. Opt., 46, 4065 [NASA ADS] [CrossRef] (In the text)
- Watson, A. M., & Stapelfeldt, K. R. 2004, ApJ, 602, 860 [NASA ADS] [CrossRef] (In the text)
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] (In the text)
- Whitney, B. A., Wood, K., Bjorkman, J. E., et al. 2003, ApJ, 591, 1049 [NASA ADS] [CrossRef]
- Wolf, S. 2003a, ApJ, 582, 859 [NASA ADS] [CrossRef] (In the text)
- Wolf, S. 2003b, Comp. Phys. Commun., 150, 99 [NASA ADS] [CrossRef]
- Wolf, S., Henning, T., & Stecklum, B. 1999, A&A, 349, 839 [NASA ADS]
- Wolf, S., Padgett, D. L., & Stapelfeldt, K. R. 2003, ApJ, 588, 373 [NASA ADS] [CrossRef] (In the text)
- Wolf, S., Schegerer, A., Beuther, H., Padgett, D. L., & Stapelfeldt, K. R. 2008, ApJ, 674, L101 [NASA ADS] [CrossRef] (In the text)
- Wood, K., Wolff, M. J., Bjorkman, J. E., et al. 2002, ApJ, 564, 887 [NASA ADS] [CrossRef] (In the text)
- Wu, J., Dunham, M. M., Evans, II, N. J., Bourke, T. L., & Young, C. H. 2007, AJ, 133, 1560 [NASA ADS] [CrossRef]
Footnotes
- ... GEODE
![[*]](/icons/foot_motif.png)
- Group for edge-on disc exploration.
- ... System (DSOS)
![[*]](/icons/foot_motif.png)
- See www.cso.caltech.edu/dsos/DSOS_MLeong.html
- ... available
![[*]](/icons/foot_motif.png)
- See www.submm.caltech.edu/~sharc/crush/index.htm
- ... available
![[*]](/icons/foot_motif.png)
- See www.submm.caltech.edu/~sharc/analysis/pmodel/
- ... thin
![[*]](/icons/foot_motif.png)
- This implies that we neglect line emission and absorption by the gas. We do not aim at modeling those throughout the entire disc since the dust is by far the dominant coolant of the disc. Hence, thermal equilibrium obtained in radiative transfer calculations based on dust only will provide a reliable description of the disc's thermal. structure.
- ... disc''
![[*]](/icons/foot_motif.png)
- Those discs are considered to be predecessors of evolved debris-type discs.
All Tables
Table 1: Overview of the beam sizes in the millimetre-maps.
Table 2: Photometric data points for CB 26.
Table 3: Overview of parameter ranges and best-fit values.
All Figures
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[width=4.5cm]{12397f1a.eps...
...=4.5cm]{12397f1c.eps}
\includegraphics[width=4.5cm]{12397f1d.eps}}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg74.png) |
Figure 1:
Inverse HST images obtained with ACS and NICMOS in the I, J, H and K band. The colour scale is |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{
\includegraphics[width=4.5cm]{12397f2a.e...
....5cm]{12397f2e.eps}
\includegraphics[width=4.5cm]{12397f2f.eps}}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg75.png) |
Figure 2:
Inverse, reconstructed images from millimetre interferometric observations (left column) and corresponding dirty beam maps (right column), linear colour scale. All images have been rotated by |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12397f3a.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg76.png) |
Figure 3:
Overlay of the OVRO
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12397f4a.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg98.png) |
Figure 4: Spectral energy distribution. Data with error-bars from Table 2. The IRS spectrum is the solid line. The dashed-dotted line corresponds to the best-fit model. The dashed line is the best-fit model with the dust screen. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{
\includegraphics[]{12397f5a.eps} }
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg197.png) |
Figure 5: Sketch showing all components of our model and their spatial arrangement. All sizes are not to scale. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12397f6a.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg199.png) |
Figure 6:
Upper plot: contours of dust density distribution on a plane perpendicular to the midplane normalised to the peak density of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12397f7a.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg201.png) |
Figure 7:
Radial profiles of density (upper plot) and temperature (lower plot) in the midplane along r (solid line) and along z/r=0.1 (dashed line). The latter profile is chosen in order to include the scale height h0 at
|
| Open with DEXTER | |
| In the text | |
 |
Figure 8:
Contributions to the spectral energy distribution from disc (dashed line) and envelope (solid line). The transition from envelope to disc as the major source of radiation (re-emission and scattering) is at
|
| Open with DEXTER | |
| In the text | |
 |
Figure 9:
Horizontal cut through the spatial brightness distribution at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\resizebox{9cm}{!}{
\includegraphics[width=4.5cm]{12397fAa.eps}...
...397fAc.eps} \\
\includegraphics[width=4.5cm]{12397fAd.eps} \\
}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg234.png) |
Figure 10: Predicted appearance of the inner region of the disc. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{
\includegraphics[width=0.8\textwidth]{12397fBa.eps}}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg244.png) |
Figure 11: Contour lines of the Toomre parameter Q (see Eq. (12)). The lines, from right to left, are at levels of Q = 0.1, 0.3, 0.5, 0.7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{
\includegraphics[width=4.5cm]{12397fCa.e...
...4.5cm]{12397fCc.eps}
\includegraphics[width=4.5cm]{12397fCd.eps}}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg251.png) |
Figure 12:
Vertical cuts at the horizontal centre through the near-infrared scattered light images. The solid line is from observational data, and the dashed line is from our best-fit model. For an illustration where those cuts are obtained in the respective maps, see Fig. 13.
The plots are normalised to 1. In case of the I-Band, this corresponds to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12397fDa.eps}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg253.png) |
Figure 13:
Inverse H-Band image from HST/NICMOS. The contour lines are from our best-fit model.
From the outer to the inner lines they are at 27%, 41%, 68% of the peak height. The second dark lane is not
reproduced by our modeling as we did not account for envelope asymmetries.
The PSF for those images is rather small |
| Open with DEXTER | |
| In the text | |
| |
Figure 14: J Band image from a simulation with a power-law envelope structure (left) and from rotating envelope (right). See also Fig. 1 for the observation. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{
\includegraphics[width=0.8\textwidth]{12397fFa.eps}}
\end{figure}](/articles/aa/full_html/2009/39/aa12397-09/Timg263.png) |
Figure 15:
Dependency of the brightness distribution along a central cut on the inclination. All the curves for
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}\rho_{\rm disc}(\vec{r})= \rho_0 \left( \frac{R_*}{r_{\rm cyl...
...pha \exp \left(-\frac{1}{2}\left[ \frac{z}{h}\right]^2 \right)
\end{displaymath}](/articles/aa/full_html/2009/39/aa12397-09/img99.png)