| Issue |
A&A
Volume 505, Number 3, October III 2009
|
|
|---|---|---|
| Page(s) | 1099 - 1113 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200911827 | |
| Published online | 02 July 2009 | |
A double stellar generation in the globular cluster NGC 6656 (M 22)![[*]](/icons/foot_motif.png)
Two stellar groups with different iron and s-process element abundances
A. F. Marino1,2 - A. P. Milone1 - G. Piotto1 - S. Villanova3 - L. R. Bedin4 - A. Bellini1,4 - A. Renzini5
1 - Dipartimento di Astronomia, Università di Padova,
Vicolo dell'Osservatorio 3, 35122 Padova, Italy
2 -
P. Universidad Católica de Chile, Departamento de
Astronomía y Astrofísica, Casilla 306, Santiago 22, Chile
3 -
Departamento de Astronomia, Universidad de Concepcion, Casilla
160-C, Concepcion, Chile
4 -
Space Telescope Science Institute, 3700 San Martin Drive,
Baltimore, MD 21218, USA
5 -
Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5,
35122 Padova, Italy
Received 11 February 2009 / Accepted 17 May 2009
Abstract
We present a chemical abundance analysis
based on high resolution UVES spectra of seventeen
bright giant stars in the Globular Cluster (GC) M 22.
We obtained an average iron abundance of
![]() (internal errors only)
and an
(internal errors only)
and an ![]() enhancement of
enhancement of
![]() (internal errors only).
Na and O, and Al and O follow the well known
anticorrelations found in many other GCs.
We identified two
groups of stars with significantly different abundances of the s-process
elements Y, Zr, and Ba. The relative numbers of the two group
members are very similar
to the ratio of the number of stars in the two sub giant branches
(SGB) of M 22. Y and Ba abundances
do not correlate with Na, O, and Al. The s-element rich stars
are also richer in iron and have higher Ca abundances.
The results from high resolution spectra were
confirmed by analyses of lower resolution GIRAFFE spectra of fourteen
additional M 22 stars. The analyses of the GIRAFFE spectra also show that the
Eu - a pure r-process element - abundance is not related
to the iron content.
We discuss the chemical abundance pattern of M 22 stars
in the context of GC multiple stellar populations phenomenon.
(internal errors only).
Na and O, and Al and O follow the well known
anticorrelations found in many other GCs.
We identified two
groups of stars with significantly different abundances of the s-process
elements Y, Zr, and Ba. The relative numbers of the two group
members are very similar
to the ratio of the number of stars in the two sub giant branches
(SGB) of M 22. Y and Ba abundances
do not correlate with Na, O, and Al. The s-element rich stars
are also richer in iron and have higher Ca abundances.
The results from high resolution spectra were
confirmed by analyses of lower resolution GIRAFFE spectra of fourteen
additional M 22 stars. The analyses of the GIRAFFE spectra also show that the
Eu - a pure r-process element - abundance is not related
to the iron content.
We discuss the chemical abundance pattern of M 22 stars
in the context of GC multiple stellar populations phenomenon.
Key words: stars: abundances - galaxy: globular clusters: individual: NGC 6656
1 Introduction
Globular Clusters (GC) are generally chemically homogeneous in their Fe-peak elements, while they show star-to-star abundance variations in light elements such as C, N, O, Na, Mg, and Al among others. In some cases, these chemical inhomogeneities produce clearly defined anticorrelations. For example, all GCs for which Na and O abundances have been measured, show a clearly defined NaO anticorrelation (see Carretta et al. 2006, 2008, for an update), often associated with an anticorrelation between Mg and Al content. The origin of these variations has not yet been well understood, since both a primordial and an evolutionary explanation, or a combination of both have been proposed (see Gratton et al. 2004, for a recent review).
Interestingly, abundance anomalies have also been found among stars in the lower part of the red giant branch (RGB) or even the main sequence (MS). For instance, Cannon et al. (1998) found a CN bimodality in MS and subgiant branch (SGB) stars in 47 Tuc, and the NaO anti-correlation was observed for the MS turn off (TO) and SGB in M 13 (Cohen & Melendez 2005), NGC 6397 and NGC 6752 (Carretta et al. 2005; Gratton et al. 2001), and NGC 6838 (Ramírez & Cohen 2002). By themselves, these results suggest the possibility of a primordial origin for abundance inhomogeneities.
More recent results, made possible by a significant improvement in the photometric precision of data from HST images, provide evidence of multimodal sequences in the color-magnitude diagrams (CMD) of some GCs (Bedin et al. 2004; Piotto et al. 2007; Milone et al. 2008; and Piotto et al. in preparation) further confirming that at least in some GCs, there is more than one generation of stars formed from material chemically contaminated by previous generations.
Among the clusters with multiple stellar populations,
![]() Centauri is the most complex and interesting case. This
object is the only one for which variations in iron-peak elements have
been reliably identified (Freeman & Rodgers 1975; Norris et al. 1996; Suntzeff & Kraft 1996). The Fe multimodal distribution
is at least in part responsible for the multiple RGB (Lee et al. 1999;
Pancino et al. 2000) of
Centauri is the most complex and interesting case. This
object is the only one for which variations in iron-peak elements have
been reliably identified (Freeman & Rodgers 1975; Norris et al. 1996; Suntzeff & Kraft 1996). The Fe multimodal distribution
is at least in part responsible for the multiple RGB (Lee et al. 1999;
Pancino et al. 2000) of ![]() Cen. The MS of this GC also divides
into three sequences as shown by Bedin et al. (2004). Among the two
principal MSs, the bluest one is more metal rich than the redder one
(Piotto et al. 2005). So far, the only way of explaining the
photometric and spectroscopic properties of the MS of
Cen. The MS of this GC also divides
into three sequences as shown by Bedin et al. (2004). Among the two
principal MSs, the bluest one is more metal rich than the redder one
(Piotto et al. 2005). So far, the only way of explaining the
photometric and spectroscopic properties of the MS of ![]() Cen is
to assume that the bluest MS is also strongly He-enhanced.
Villanova et al. (2007) also showed that the SGB divides in at least
four branches with a wide age difference (greater than 1 Gyr) between
the different populations.
Cen is
to assume that the bluest MS is also strongly He-enhanced.
Villanova et al. (2007) also showed that the SGB divides in at least
four branches with a wide age difference (greater than 1 Gyr) between
the different populations.
NGC 2808 was the second (in time) cluster in which a MS divided into three branches was found (Piotto et al. 2007). In this case, the MS multimodality was also associated with different values of helium, of stars following the observed multimodal distribution of the NaO anti-correlation, where three groups of stars with different O (and Na) contents were found by Carretta et al. (2006) on the RGB.
In NGC 1851, Yong & Grundahl (2008) found abundance variations in various elements by studying a sample of 8 RGB stars. Sodium and oxygen follow the NaO anticorrelation. There is also some evidence of two groups of stars of different s-process element content, as well as of two groups of stars with different CN-strengths, that are possibly related to the two sequences photometrically identified by Milone et al. (2008) along the SGB. The split SGB of NGC 1851 can be explained by the presence of two stellar populations. The stars in the fainter SGB could be part of either a population about 1 Gyr older than the bright SGB ones, or could indeed be slightly younger but strongly enriched in total C + N + O content (Cassisi et al. 2008).
Further evidence of a primordial origin of abundance variations related to the presence of different populations of stars was provided by Marino et al. (2008). By studying a large sample of RGB stars in the GC M 4, they found two distinct groups of stars with a different sodium content, which also display a remarkable difference in the strength of the CN-band. These two spectroscopic groups were found to populate two different regions along the RGB. They also noted that the RGB spread is present from the base of the RGB to the RGB-tip, suggesting that the spread must be related to the presence of two distinct stellar generations.
At the basis of the present investigation, there is a result by our group, who identified a bimodal distribution of the stars in the SGB of the GC NGC 6656 (Piotto 2009, see also Fig. 18 of the present paper).
Located at a distance from the Sun of ![]() 3.2 kpc (Harris 1996),
NGC 6656 (M 22) is a particularly interesting GC, because a large
number of photometric and spectroscopic studies imply that it
contains a complex
metallicity spread, similar to, albeit significantly smaller than,
that found in
3.2 kpc (Harris 1996),
NGC 6656 (M 22) is a particularly interesting GC, because a large
number of photometric and spectroscopic studies imply that it
contains a complex
metallicity spread, similar to, albeit significantly smaller than,
that found in ![]() Centauri. In particular, it has often been
suggested, although never convincingly confirmed, that M 22 may
also have a spread in the abundance of iron.
Centauri. In particular, it has often been
suggested, although never convincingly confirmed, that M 22 may
also have a spread in the abundance of iron.
The first evidence of a spread in metallicity came from the
significant spread along the RGB (Hesser et al. 1977; Peterson &
Cudworth 1994) observed both in (B-V) and in Strömgren colors.
However, it remains still uncertain whether this spread can be
attributed to either a
metallicity spread or reddening variations.
Because of its location on the sky,
close to the Galactic plane and toward the Galactic bulge
[
![]() ], M 22
is affected by high and spatially varing
interstellar absorption, with a reddening in the interval
0.3 <E(B-V)< 0.5.
This differential reddening creates a degeneracy in measuring
metallicity when the atmospheric parameters of the stars are derived
from their color.
Spectroscopic studies are divided between those that conclude that no
significant metallicity variations is present in M 22 (Cohen 1981; based on 3 stars; Gratton 1982, 4 stars)
and studies claiming a spread in iron, with
], M 22
is affected by high and spatially varing
interstellar absorption, with a reddening in the interval
0.3 <E(B-V)< 0.5.
This differential reddening creates a degeneracy in measuring
metallicity when the atmospheric parameters of the stars are derived
from their color.
Spectroscopic studies are divided between those that conclude that no
significant metallicity variations is present in M 22 (Cohen 1981; based on 3 stars; Gratton 1982, 4 stars)
and studies claiming a spread in iron, with
![]() (Pilachowsky et al. 1984; 6 stars; Lehnert et al. 1991, 4 stars).
(Pilachowsky et al. 1984; 6 stars; Lehnert et al. 1991, 4 stars).
Particularly interesting are the findings about CN-band strengths.
Norris & Freeman (1983) showed that CN variations in M 22 were
correlated with Ca, H, and K line variations, similar to those in
![]() Cen. By studying a sample of 4 stars, Lehnert et al. (1991)
found Ca and Fe variations that also correlated with variations in CH and CN band strength.
However, Brown & Wallerstein (1992) found no Ca abundance differences
between CN-strong and CN-weak stars, although they observed differences in
[Fe/H] correlating with the CN-strength. Kayser et al. (2008) found some indications of a CN-CH anti-correlation in SGB stars,
which was perhaps diluted by large uncertainties introduced by differential
reddening.
Cen. By studying a sample of 4 stars, Lehnert et al. (1991)
found Ca and Fe variations that also correlated with variations in CH and CN band strength.
However, Brown & Wallerstein (1992) found no Ca abundance differences
between CN-strong and CN-weak stars, although they observed differences in
[Fe/H] correlating with the CN-strength. Kayser et al. (2008) found some indications of a CN-CH anti-correlation in SGB stars,
which was perhaps diluted by large uncertainties introduced by differential
reddening.
In the present study, we analyse high resolution UVES spectra for a sample of seventeen RGB stars in M 22 to study the chemical abundances and possible relations to the identified split in the SGB. To increase the statistical significance and reinforce our findings, we also added the results from a sample of fourteen RGB stars from medium resolution, high S/N GIRAFFE spectra. In Sect. 2, we provide an overview of the observations and the data analysis, and in Sect. 3 we describe the procedure used to derive the chemical abundances. Our results about the chemical composition of M 22 are presented in Sect. 4, and a discussion of them is provided in Sect. 5. In Sect. 6, we look for possible connections between our spectroscopic results and the two stellar populations photometrically observed by Piotto (2009). A comparison between the results of this paper and those of Marino et al. (2008) on the GC M 4 is provided in Sect. 7. In Sect. 8, we present a brief discussion of the results obtained from GIRAFFE spectra. Section 9 summarizes the most relevant properties of the two stellar populations of M 22.
2 Observations and membership analysis
Table 1: Right ascension, declination, heliocentric radial velocity, and magnitude for the analysed stars.
Our data set consists of spectra of seventeen RGB stars retrieved from the ESO archive. The observations were obtained
using UVES (Dekker et al. 2000) and FLAMES@UVES (Pasquini et al. 2002). The spectra cover the wavelength range 4800-6800 Å,
are of resolution
![]() ,
and have a typical
,
and have a typical
![]() .
.
Data were reduced using the UVES pipeline (Ballester et al. 2000),
including bias subtraction, flat-field correction, wavelength
calibration, and spectral rectification. The
membership of the analysed stars was established from the radial
velocities obtained using the IRAF-FXCOR task, which cross-correlates
the object spectrum with a template. As template, we used a
synthetic spectrum obtained from the spectral synthesis code
SPECTRUM![]() , using a Kurucz model atmosphere with roughly the mean
atmospheric parameters of our stars
, using a Kurucz model atmosphere with roughly the mean
atmospheric parameters of our stars
![]() K,
K,
![]() ,
,
![]() km s-1, and
km s-1, and
![]() .
In the
end, each radial velocity was corrected to the heliocentric system.
We obtained a mean radial velocity of
.
In the
end, each radial velocity was corrected to the heliocentric system.
We obtained a mean radial velocity of ![]() km s-1 from all the
selected spectra, which agrees well with the values in the literature
(Peterson & Cudworth 1994). To within 2
km s-1 from all the
selected spectra, which agrees well with the values in the literature
(Peterson & Cudworth 1994). To within 2![]() ,
where
,
where ![]() is our measured velocity dispersion of 10 km s-1, all our
stars are members.
The list of the analysed stars,
their coordinates, radial velocities, and magnitudes, are reported in Table 1.
Figure 1 shows the location of the target stars in the CMD of M 22.
is our measured velocity dispersion of 10 km s-1, all our
stars are members.
The list of the analysed stars,
their coordinates, radial velocities, and magnitudes, are reported in Table 1.
Figure 1 shows the location of the target stars in the CMD of M 22.
We also analysed a sample of stars observed with GIRAFFE HR09, HR13,
and HR15 set-ups at a resolution of
![]() -25 000.
These spectra were reduced by using the pipeline developed by Geneva
observatory (Blecha et al. 2000).
More details about these data and their analysis are
provided in Sect. 8.
-25 000.
These spectra were reduced by using the pipeline developed by Geneva
observatory (Blecha et al. 2000).
More details about these data and their analysis are
provided in Sect. 8.
3 Abundance analysis
Abundances of all elements, with the exception of oxygen, were measured by an equivalent width analysis by using the local thermodynamical equilibrium (LTE) program MOOG (freely distributed by Sneden, University of Texas at Austin). The atmospheric parameters, i.e., temperature, microturbolence, and gravity were determined from Fe lines by removing trends in the excitation potential (EP) and equivalent widths (EW) as a function of abundance respectively, and satisfying the ionization equilibrium.
In contrast to other elements, we measured the O content by comparing observed with synthetic spectra, because of the blending of the target O line at 6300 Å with other spectral features.
More details about the linelist, atmospheric parameters, and abundance measurements can be found in Marino et al. (2008). In Table 2, we report the reference chemical abundances obtained for the Sun used in this paper. The stellar parameters obtained for the M 22 stars analysed are listed in Table 3.
Table 2:
Measured solar abundances
![]() .
.
Table 3: Atmospheric parameters for the analysed stars.
We note that the method employed for the measurements of the atmospheric parameters is based on the spectra, and hence our temperatures are not color dependent. This is an important advantage when analysing GCs, such as M 22, that are affected by high differential reddening.
In Fig. 1, we mark with red symbols the location of our seventeen UVES target stars on the B as a function of (B-I) CMD. Photometry was obtained with the Wide Field Imager (WFI) camera at the ESO/MPI 2.2 m telescope by Monaco et al. (2004) and stars with the highest photometric quality were carefully selected. Magnitudes were corrected for sky concentration (i.e. the increase in the background level in frames near the center because of light reflected back from the detector to the optics) by using the most accurate available solution (Bellini et al. 2009). Since the photometry is affected by spatially variable interstellar reddening, we corrected the CMD for this effect (by using the method described in Sarajedini et al. 2007). To separate probable asymptotic giant branch (AGB) from RGB stars, we drow by hand the black dashed line of Fig. 1. On the basis of their position in the CMD, stars that are possible AGB stars, are marked as triangles, while RGB stars are marked by circles.
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827fg1.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg48.png) |
Figure 1: Distribution of the UVES target stars (red symbols) on the B vs. (B-I) CMD corrected for differential reddening. Data for the star #200083 are not plotted because the B magnitude is not available for this star. The stars observed with GIRAFFE are shown by blue crosses. |
| Open with DEXTER | |
3.1 Internal errors associated with chemical abundances
The primary goal of this paper is to study the intrinsic variation in chemical abundances of M 22 stars.
The differences in the measured chemical abundances between stars
are a consequence of both measurement errors and intrinsic variations
in their chemical composition. In this section, we attempt to
differentiate between internal errors, caused by measurement uncertainties,
and true variations in the chemical content of the stars.
We compare the observed dispersion in the chemical abundances
![]() ,
listed in Table 4, with that produced by
internal errors
,
listed in Table 4, with that produced by
internal errors
![]() .
Since we wish to study the
star-to-star intrinsic abundance variations, we do not consider
possible external sources of errors that do not affect relative
abundances.
.
Since we wish to study the
star-to-star intrinsic abundance variations, we do not consider
possible external sources of errors that do not affect relative
abundances.
There are two primary sources of errors contributing to
![]() :
the
uncertainties in the EWs, and the uncertainties in the
atmospheric parameters.
:
the
uncertainties in the EWs, and the uncertainties in the
atmospheric parameters.
To derive the typical error in the EWs, we considered two stars (#200101 and #71) with similar atmospheric parameters and roughly the same iron abundance. In this way, any difference in the EWs of the iron spectral lines can be attributed to measurement errors. The dispersion in the distribution of the differences between the EWs of the iron lines for the two selected stars, that is 2.3 mÅ, was taken as our estimate of the typical error in the EW measurement. The corresponding error in the chemical abundances was calculated by varying the EWs of a star (#200101) at intermediate temperature, representative of our sample, by 2.3 mÅ. The variations in the obtained abundances for each chemical species, listed in Table 5 (Col. 7), were taken as our most reliable estimate of the internal errors introduced by uncertainties in the EWs.
We used the same procedure described in Marino et al. (2008)
to estimate the uncertainties associated with the atmospheric
parameters, and the corresponding errors related to chemical
abundances. From our analysis, the derived uncertainties related to
atmospheric parameters are:
![]() K,
K,
![]() ,
and
,
and
![]() km s-1.
These internal errors in the atmospheric parameters translate into the
errors in chemical abundances listed in Table 5 (Cols. 2-4).
km s-1.
These internal errors in the atmospheric parameters translate into the
errors in chemical abundances listed in Table 5 (Cols. 2-4).
We also investigated the influence of a variation in the total
metallicity ([A/H]) of the model atmosphere on the derived
abundances. By varying the metallicity of the model by 0.10 dex, that
is the iron observed dispersion, the element
abundances change by the amount listed in Col. 5 of Table 5. A
variation in the metallicity of the model atmosphere changes mainly
the ionization equilibrium, and hence the values of log (g), since we
used the ionization equilibrium between FeI and FeII to derive
gravities. We calculated that by increasing [A/H] by
0.10 dex, log (g) decreases by ![]() 0.06, while temperature and
microturbolence do not change significantly. Since we are interested
in the search for possible small star-to-star variations in the iron
abundances, we measured the effect on the [Fe/H] abundances of
this change in gravity in a model atmosphere with increasing
metallicity, and verified that it does not affect the derived iron
abundances by more than 0.01 dex. By increasing
the total metallicity by 0.2 dex, the FeII abundances change by
0.06, while temperature and
microturbolence do not change significantly. Since we are interested
in the search for possible small star-to-star variations in the iron
abundances, we measured the effect on the [Fe/H] abundances of
this change in gravity in a model atmosphere with increasing
metallicity, and verified that it does not affect the derived iron
abundances by more than 0.01 dex. By increasing
the total metallicity by 0.2 dex, the FeII abundances change by
![]() 0.06 dex, and we have to decrease log (g) by
0.06 dex, and we have to decrease log (g) by ![]() 0.12 to
re-establish the ionization equilibrium between FeI and
FeII. In this case, the effect on the iron abundances is also smaller
than 0.01 dex.
0.12 to
re-establish the ionization equilibrium between FeI and
FeII. In this case, the effect on the iron abundances is also smaller
than 0.01 dex.
Table 4: The average abundances for M 22 stars.
Column 8 of Table 5 reports the quadratic sum (
Since the oxygen abundance was calculated from the same spectral line
and the spectra are of similar S/N, we assume as an estimate of the
error related to [O/Fe], the
![]() calculated in
Marino et al. (2008) for M 4 red giants.
This error, for M 4 stars, was calculated to be the dispersion in O of the
O-rich stars, i.e., the Na-poor group, assumed to
be homogeneous in oxygen content.
calculated in
Marino et al. (2008) for M 4 red giants.
This error, for M 4 stars, was calculated to be the dispersion in O of the
O-rich stars, i.e., the Na-poor group, assumed to
be homogeneous in oxygen content.
4 The chemical composition of M 22
4.1 Iron-peak and 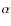 elements
elements
The wide spectral range of UVES data allows us to obtain chemical
abundances for fifteen chemical species. Table 4
gives the mean abundance for each element (Col. 2), the rms of the mean
of the abundances
![]() (Col. 3), and the number of stars (
(Col. 3), and the number of stars (
![]() )
used to
calculate the mean (Col. 4).
In Table 4, we associate with each average abundance an
uncertainty that is the rms scatter (
)
used to
calculate the mean (Col. 4).
In Table 4, we associate with each average abundance an
uncertainty that is the rms scatter (
![]() )
divided by
)
divided by
![]() ,
although some of the distributions are clearly not Gaussians.
A plot of our measured abundances is
shown in Fig. 2, where, for each box, the central
horizontal line is the mean value for each element, and the upper
and lower lines
contain the 68.27% of the distribution around the mean.
The points represent individual measurements.
,
although some of the distributions are clearly not Gaussians.
A plot of our measured abundances is
shown in Fig. 2, where, for each box, the central
horizontal line is the mean value for each element, and the upper
and lower lines
contain the 68.27% of the distribution around the mean.
The points represent individual measurements.
Our results confirm M 22 to be a metal poor GC of a mean metallicity
We measured the chemical abundances of five ![]() elements: O, Mg,
Si, Ca and Ti. The corresponding mean abundances are listed in
Table 4. Here we consider only Mg, Si, Ca, and Ti. The results
for oxygen will be discussed in Sect. 4.2.
These four
elements: O, Mg,
Si, Ca and Ti. The corresponding mean abundances are listed in
Table 4. Here we consider only Mg, Si, Ca, and Ti. The results
for oxygen will be discussed in Sect. 4.2.
These four ![]() elements are all overabundant
with respect to solar values, with an
average of
elements are all overabundant
with respect to solar values, with an
average of
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827fg2.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg79.png) |
Figure 2: Box plot for M 22 star element abundances. The points are the individual measurements. The central horizontal line of each box is the mean of the data; the upper and lower lines represent the 68.27% levels of the distribution around the mean value. |
| Open with DEXTER | |
Table 5:
Sensitivity of derived UVES abundances to the atmospheric parameters
and EWs. We reported the error
![]() caused by the
uncertainties in the atmospheric parameters
(
caused by the
uncertainties in the atmospheric parameters
(
![]() ,
,
![]() log (g),
log (g),
![]() ,
and
,
and ![]() ([A/H])), related to the error in EW measurements
(
([A/H])), related to the error in EW measurements
(
![]() ), the squared sum of the two (
), the squared sum of the two (
![]() ), and the
observed dispersion (
), and the
observed dispersion (
![]() )
for each element.
)
for each element.
4.2 NaO anticorrelation
As displayed in Fig. 3, sodium and oxygen exhibit the well
established NaO
anti-correlation found in RGB stars in all GCs for which Na and O have been
measured so far (see Carretta et al. 2006).
The [Na/Fe] values range from ![]() -0.25 to
-0.25 to ![]() 0.7 dex,
with a dispersion
0.7 dex,
with a dispersion
![]() ,
and [O/Fe] abundances ranging from
,
and [O/Fe] abundances ranging from ![]() -0.10 to
-0.10 to ![]() +0.5 dex, with a dispersion
+0.5 dex, with a dispersion
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm]{figure/11827fg3.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg101.png) |
Figure 3: The anticorrelation between [Na/Fe] and [O/Fe] abundance ratios. Triangles indicate stars that, on the basis of their position on the CMD, should be AGB. |
| Open with DEXTER | |
As discussed in Sect. 6, Piotto (2009) demonstrated that the SGB of M 22 is split into two separate branches, indicating the presence of two stellar populations. In Fig. 4, we compare the Na versus O trend for M 22 with those observed in other four GCs where multiple stellar populations have been identified: NGC 2808 (data from Carretta et al. 2006), NGC 1851 (data from Yong & Grundahl 2008), NGC 6388 (data from Carretta et al. 2007), and M 4 (data from Marino et al. 2008).
In NGC 2808, the presence of multiple stellar populations is inferred
by the triple MS (Piotto et al. 2007). The three MS branches may be
associated with the complexities of the cluster horizontal branch
(D'Antona & Caloi 2004) and its oxygen abundance distribution
(Carretta et al. 2006).
In contrast, the MS of
M 22 is narrow and any spread or split, must be
smaller than 0.02 mag in
![]() color
(see Piotto 2009).
Figure 4 shows that NGC 2808 stars cover almost the same
range of Na abundances as M 22, but span a range of O abundance at
least two times larger.
color
(see Piotto 2009).
Figure 4 shows that NGC 2808 stars cover almost the same
range of Na abundances as M 22, but span a range of O abundance at
least two times larger.
In M 4, the presence of multiple populations is inferred by the
bimodal distribution of the Na abundance (Marino et al. 2008). In
addition, stars from the two groups of different Na content populate
two distinct RGB sequences in the U vs. U-B CMD.
Moreover, no split in either the MS or SGB has been identified.
Interestingly, in M 4, the
maximum variations in [Na/Fe] and [O/Fe] are 0.39 and 0.31 dex respectively smaller than those observed in M 22. In
particular, a few O-poor stars with [O/Fe] ![]() 0.00 and
[Na/Fe]
0.00 and
[Na/Fe] ![]() 0.50 are present among M 22 stars but not in M 4.
0.50 are present among M 22 stars but not in M 4.
As in M 22, in NGC 1851 (Milone et al. 2008) and NGC 6388 (Piotto 2008; Moretti et al. 2009; Piotto 2009) the presence of multiple populations is inferred from a split in the SGB. Unfortunately, for both of these clusters, the available chemical measurements from high resolution spectroscopy are limited to seven RGB stars for NGC 6388 (Carretta et al. 2007) and eight RGB stars for NGC 1851 (Yong & Grundahl 2008). In the case of NGC 6388, the stars are located in a portion of the NaO plane that is not populated by any M 22 star in our sample, since the stars in NGC 6388 are systematically O-poorer. In contrast, the range of NaO anticorrelation in NGC 1851 matches quite well that of M 22.
At variance with the case of M 4 and NGC 2808, both NGC 1851 and M 22 seem to show a continuum distribution in [Na/Fe], without any hint of multi-modalities; this is in spite of the small number of stars studied in this paper and in Yong & Grundahl (2008) for NGC 1851, preventing us from definitively excluding the presence of discontinuities in the [Na/Fe] or [O/Fe] distribution.
![\begin{figure}
\par\includegraphics[width=7.8cm]{figure/11827fg4.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg105.png) |
Figure 4: NaO anticorrelation for M 22 stars superimposed on a collection of stars of four GCs that host multiple stellar populations. |
| Open with DEXTER | |
4.3 Aluminum and magnesium
The abundances of aluminum and magnesium were determined from Al lines at 6696 Å, and 6698 Å, from the Mg doublet at 6318-6319 Å, and the Mg line at 5711 Å.
Figure 5 shows the [Mg/Fe] ratio as a function of [ Al/Fe]. There is no clear MgAl correlation, despite the presence of a clearly defined NaO anticorrelation, and a clear AlNa correlation, as shown in Fig. 6. Assuming that the Na enhancement is caused by proton capture process at the expense of Ne, we also expect to observe a MgAl anticorrelation, since Al forms at the expense of Mg. This means that we expect a decrease in Mg abundance with increasing Al content. We do not observe this effect but, given our uncertainties, it could be too small to be detected. The lack of this correlation was also found for M 4 by Marino et al. (2008). However, they found a small difference in Mg content among stars with a large range of Na abundances, according to the scenario proposed by Ivans et al. (1999), who predicted that a decrease of only 0.05 dex in Mg is required to explain the increase in abundance of Al (see their Sect. 4.2.2).
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827fg5.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg106.png) |
Figure 5: [Mg/Fe] as a function of [Al/Fe] abundance ratios. Symbols are as in Fig. 3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{figure/11827fg6.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg107.png) |
Figure 6: [Al/Fe] as a function of [Na/Fe] abundance ratios. Symbols are as in Fig. 3, dashed line is the best least squares fitting straight line. |
| Open with DEXTER | |
4.4 s-process elements
We measured abundance for three s-process elements: yttrium, zirconium, and barium, all of which span a wide range of abundance values. The maximum variations in [Y/Fe], [Zr/Fe], and [Ba/Fe] are of amplitudes 0.87, 0.73, and 0.65 dex, respectively, despite the small estimated internal error (In Fig. 7, we show [Zr/Fe] and [Ba/Fe] as a function of [Y/Fe] (left and central panels), and [Ba/Fe] as a function of [Zr/Fe] (right panel). A clear correlation between each pair of s-process elements is evident, and the slopes of the best fitting lines are also similar.
Most importantly, the s-process elements clearly show a bimodal
distribution: one group is overabundant in s-elements
with average values of [Y/Fe] = +0.34 ![]() 0.05,
[Zr/Fe] = +0.60
0.05,
[Zr/Fe] = +0.60 ![]() 0.04, and [Ba/Fe] = +0.43
0.04, and [Ba/Fe] = +0.43 ![]() 0.04.
This group contains seven out of seventeen stars
(i.e.,
0.04.
This group contains seven out of seventeen stars
(i.e., ![]() 40% of the entire sample studied in this paper). The remaining ten
stars have [Y/Fe] = -0.16
40% of the entire sample studied in this paper). The remaining ten
stars have [Y/Fe] = -0.16 ![]() 0.03, [Zr/Fe] = +0.20
0.03, [Zr/Fe] = +0.20 ![]() 0.03, and
[Ba/Fe] = +0.02
0.03, and
[Ba/Fe] = +0.02 ![]() 0.04.
0.04.
Figure 7 suggests that we can isolate a s-process element rich group, and a s-process element poor one, by selecting stars with [Y/Fe] greater and smaller than 0, respectively. Stars rich in s-process elements are represented by red filled symbols, while s poor stars by the black empty ones. In Table 6, we list the mean abundances of all the elements studied in this paper, calculated separately for each of these two groups. There are few remarkable differences in the average abundances for the two groups.
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/11827f7a.ps}\includegrap...
...igure/11827f7b.ps}\includegraphics[width=5.6cm]{figure/11827f7c.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg109.png) |
Figure 7: From left to right: [Zr/Fe] and [Ba/Fe] versus [Y/Fe] and [Ba/Fe] versus [Zr/Fe] abundance ratios. Red filled symbols represent the s element rich stars, and the black empty ones represent the s poor stars. The red and the black crosses with error bars indicate the average abundances of stars in each group, dashed lines are the best least squares fitting straight lines. Triangles indicate probable AGB stars. |
| Open with DEXTER | |
As an example, in Fig. 8 we show the [Y/Fe] ratio as a function of the [Na/Fe], [Al/Fe] and [O/Fe] ratios. There is no clear correlation between Y, as well as Ba, and Zr abundances and Na, O or Al. However, stars enriched in s-process elements are all Na-rich and Al-rich, while the group of stars with lower s-process element abundances spans almost all the values of Na and Al.
The bimodality in s-process elements in M 22 resembles the case of NGC 1851. In NGC 1851, Yong & Grundahl (2008) noted that the abundances of the s-process elements Zr and La appear to cluster around two distinct values. They suggested that the two corresponding groups of stars should be related to the two stellar populations photometrically observed by Milone et al. (2008) along the SGB. In NGC 1851, the s-element abundance also appears to correlate with the Na, Al, and O abundance.
Because of the similarity between our results and those of Yong & Grundahl (2008) for NGC 1851, it is tempting to associate the presence of the two groups of stars with different s-process element contents, with the two populations of stars isolated along the SGB of M 22 by Piotto (2009, see also Fig. 18). Barium, yttrium, and zirconium can be considered as a signature of the s processes that occur in intermediate mass AGB stars (Busso et al. 2001), whose wind could have polluted the primordial material from which the second generation of stars in M 22 and NGC 1851 formed. The s-element rich stars may also to be appear rich in Na and Al because of the pollution from intermediate mass AGB stars, although the lack of a clear correlation is more difficult to interpret.
We note that the results of Piotto et al. (2005) about the
metal content of the stars in the two main MSs of
![]() Centauri can be interpreted within this scenario. Piotto
et al. (2005) measured [Ba/Fe]
Centauri can be interpreted within this scenario. Piotto
et al. (2005) measured [Ba/Fe] ![]() 0.5 for the metal-poorer ([
Fe/H] = -1.68) red MS, and [Ba/Fe]
0.5 for the metal-poorer ([
Fe/H] = -1.68) red MS, and [Ba/Fe] ![]() 0.8 for the
metal-richer ([Fe/H] = -1.37) bluer MS.
This result was confirmed by Villanova et al. (2007), who observed that SGB metal-poor stars have a Ba content lower
than intermediate-metallicity ones by about 0.2 dex.
The relationship between the s-process element abundance and the iron content
of M 22 is the subject of the following section.
0.8 for the
metal-richer ([Fe/H] = -1.37) bluer MS.
This result was confirmed by Villanova et al. (2007), who observed that SGB metal-poor stars have a Ba content lower
than intermediate-metallicity ones by about 0.2 dex.
The relationship between the s-process element abundance and the iron content
of M 22 is the subject of the following section.
Table 6: Average abundances of s-element process poor and rich stars.
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/11827f8a.ps}\includegrap...
...igure/11827f8b.ps}\includegraphics[width=5.6cm]{figure/11827f8c.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg114.png) |
Figure 8: From the left to the right: [Y/Fe] as a function of [Na/Fe], [Al/Fe] and [O/Fe] abundance ratios. Symbols are as in Fig. 7. |
| Open with DEXTER | |
5 The spread in Fe of M 22
As discussed in Sect. 1, for a long time, the existence of
an intrinsic Fe spread
in M 22 has been debated in the literature (see Ivans et al. 2004,
for a review), since photometric and spectroscopic studies have
yielded conflicting results. Some spectroscopic studies have found no
significant variations (Gratton 1982; Ivans et al. 2004), whereas others seem to find a
variation in [Fe/H] of up to ![]() 0.5 dex (Pilachowsky et al. 1984).
Photometric studies have derived similarly controversial results. Undoubtedly,
the RGB of M 22 has a large
spread in color. This spread is observed both in BVI and
Strömgren photometry, but can be interpreted in terms of either
metallicity variation or differential reddening, or a combination of both.
0.5 dex (Pilachowsky et al. 1984).
Photometric studies have derived similarly controversial results. Undoubtedly,
the RGB of M 22 has a large
spread in color. This spread is observed both in BVI and
Strömgren photometry, but can be interpreted in terms of either
metallicity variation or differential reddening, or a combination of both.
We emphasize that the [Fe/H] measurements presented in this paper are not based on photometric data, and therefore do not suffer the effects of differential reddening. For this reason, they represent an appropriate tool to measure the [Fe/H] variations in M 22.
From Table 5, we see that the observed dispersion
![]() in iron is comparable with the estimated internal error
in iron is comparable with the estimated internal error
![]() ,
i.e., the observed star-to-star metallicity
scatter could be interpreted as being caused by measurement errors only.
This demonstrates the difficulty in establishing the statistical
significance of any intrinsic spread in [Fe/H].
In this paper, we can tackle the problem of the iron dispersion
in M 22 in a different way.
The observed dispersion in iron content alone could
be a poor indicator of any intrinsic metallicity dispersion. First of
all, because of the abundance measurement errors.
In addition, we note that if anomalies in [Fe/H] affect only a
small fraction of M 22 stars, their effect on the iron
dispersion of the entire sample of stars could be negligible.
,
i.e., the observed star-to-star metallicity
scatter could be interpreted as being caused by measurement errors only.
This demonstrates the difficulty in establishing the statistical
significance of any intrinsic spread in [Fe/H].
In this paper, we can tackle the problem of the iron dispersion
in M 22 in a different way.
The observed dispersion in iron content alone could
be a poor indicator of any intrinsic metallicity dispersion. First of
all, because of the abundance measurement errors.
In addition, we note that if anomalies in [Fe/H] affect only a
small fraction of M 22 stars, their effect on the iron
dispersion of the entire sample of stars could be negligible.
A visual inspection of some spectra reinforces the suggestion that there may be star-to-star iron variations. As an example, in Fig. 9, we show spectra of two pairs of stars with very similar stellar atmospheric parameters. The two spectral lines in Fig. 9 are iron lines. The upper panel shows the spectra of the stars #200068 and #200083 for which we measured an iron abundance [Fe/H] = -1.84 and [Fe/H] = -1.63, respectively (see Table 3). The line depths differ significantly and, because of the similarity in their atmospheric parameters, must be indicative of an intrinsic iron difference. For comparison, in the bottom panel we plot the same spectral region for two stars (#200101 and #71) of almost the same iron content.
![\begin{figure}
\par\includegraphics[width=8cm]{figure/11827fg9.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg115.png) |
Figure 9: The upper panel shows the spectra of the metal-poor star #200068 ([Fe/H] = -1.84) and of the metal-rich star #200083 ([Fe/H] = -1.63) centered on the lines of FeI. The stellar parameters are very similar, although, the Fe lines differ significantly. The bottom panel shows the same lines for stars #200101 and #71 with similar metallicity and stellar parameters. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/1827f10a.ps}\includegrap...
...igure/1827f10b.ps}\includegraphics[width=5.6cm]{figure/1827f10c.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg116.png) |
Figure 10: From the left to the right: [Na/Fe], [Al/Fe], and [O/Fe] as a function of [Fe/H] abundance ratios. Symbols are as in Fig. 7 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/1827f11a.ps}\includegrap...
...igure/1827f11b.ps}\includegraphics[width=5.6cm]{figure/1827f11c.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg117.png) |
Figure 11: [Y/Fe] ( left), [Zr/Fe] ( center), and [Ba/Fe] ( right) as a function of [Fe/H]. Symbols are as in Fig. 7, dashed lines are the best least squares fitting straight lines. |
| Open with DEXTER | |
Figure 10 shows that the Fe abundance is not significantly correlated with the Al, Na, and O abundances, elements that, on the other hand, exhibit clearly defined correlations, as discussed in Sect. 4.2.
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827f12.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg118.png) |
Figure 12: Simulation of 100 000 stars with the properties of the two observed groups of stars. The red and the blue histograms represent the s-rich and the s-poor groups of stars, respectively. |
| Open with DEXTER | |
However, when we compare the iron abundances with the s-process element
abundances, we find a strong correlation, with s-process element
rich stars
having systematically higher [Fe/H], as shown in the
three panels of Fig. 11.
The two s-process
element rich and poor groups have average [
Fe/H]
![]() 1.68
1.68 ![]() 0.02 and [
Fe/H]
0.02 and [
Fe/H]
![]() = -1.82
= -1.82 ![]() 0.02, respectively
(
0.02, respectively
(![]() [Fe/H] = 0.14
[Fe/H] = 0.14 ![]() 0.03).
0.03).
We emphasize that the significance of the Fe variation can be appreciated only when we consider the average iron content of the two groups characterized by a different s-element content. This is demonstrated by a simple test that we computed whose results are summarized in Fig. 12. We simulated 100 000 stars with an iron content, and iron abundance dispersion identical to that of observed stars, i.e., 41% of the sample are s-process element rich stars (red Gaussian) and a 59% are s-process element poor ones (blue Gaussian) with a mean [Fe/H] of -1.82 and -1.68 dex, respectively. The dispersion in iron content of each group was taken to be equal to 0.09 dex, that is the error that we estimated for the iron abundance (see Table 5). The resulting metallicity abundance dispersion for the entire sample is 0.11 dex, which is close to, and only marginally greater, than the dispersion expected from the measurement errors.
![\begin{figure}
\par\includegraphics[width=8cm]{figure/11827f13.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg122.png) |
Figure 13: [Ca/Fe] as a function [Fe/H]. Symbols are as in Fig. 7. |
| Open with DEXTER | |
The presence of two groups of stars, one of which is enriched in both
s-process elements and iron, is analogous to the case of
![]() Centauri discussed in Sect. 4.4,
where Piotto et al. (2005) and Villanova et al. (2007) found that the more metal rich,
He-enriched stars also have a higher Ba content.
Centauri discussed in Sect. 4.4,
where Piotto et al. (2005) and Villanova et al. (2007) found that the more metal rich,
He-enriched stars also have a higher Ba content.
As shown in Fig. 13, the iron abundances are also well correlated
with calcium abundances, and the Ca content correlates with the
s-process element abundance. A similar behavior is again
present in
![]() Centauri, where a spread in Ca was first detected by Freeman &
Rodgers (1975). Villanova et al. (2007) showed that the
SGB population with [Fe/H]
Centauri, where a spread in Ca was first detected by Freeman &
Rodgers (1975). Villanova et al. (2007) showed that the
SGB population with [Fe/H] ![]() -1.2 has a mean [Ca/Fe] that is higher by
-1.2 has a mean [Ca/Fe] that is higher by
![]() 0.1 dex, than that found for the more metal-poor population.
However, the
0.1 dex, than that found for the more metal-poor population.
However, the ![]() abundance of the most metal-rich population in
abundance of the most metal-rich population in
![]() Centauri is still debated, since Pancino et al. (2002) found
the metal-rich stars to be
Centauri is still debated, since Pancino et al. (2002) found
the metal-rich stars to be ![]() -poor.
-poor.
In M 22, evidence of a calcium spread was noted
by Norris & Freeman (1983), who showed a correlation between CN variations and Ca, similar to those in ![]() Centauri.
By studying a sample of 4 stars, Lehnert et al. (1991), found both Ca
and Fe variations that were correlated with the CN-band strengths.
Centauri.
By studying a sample of 4 stars, Lehnert et al. (1991), found both Ca
and Fe variations that were correlated with the CN-band strengths.
Our abundance measurements indicate that both calcium and iron correlate with the s-process elements (Fig. 14 and Fig. 11). As shown in Fig. 15, we also found that calcium, like iron, is not clearly correlated with Na, although the stars with an higher Ca content seem to be slightly Na rich.
In Figs. 7, 11, 13, and 14, six out of seven probable AGB stars, represented by triangles, belong to the s-poor group. We emphasize that our selection of the probable AGB stars is based only on a visual inspection of the stars on the CMD, without consideration of the photometric errors. In any case, assuming that all these stars are indeed true AGB members, our s-poor sample would include both RGB and AGB stars. If there is really a group of AGB stars in our s-poor sample, they could represent the evolved low mass stars of the primordial population, which did not experience the third dredge-up and enrich their surfaces with s-process elements. Hence they should trace the primordial composition of the cluster. Because of their higher iron abundance, stars with higher s element abundances may have systematically redder colors than s-process element poor stars and have a low probability of being shifted by photometric errors into the AGB region.
Figure 16 shows [Mg/Fe] and [Si/Fe] as a function of [Fe/H]. Both Mg and Si are slightly overabundant in s-process element rich stars with respect to s-process element poor ones (see also Table 6). This seems to suggest that core-collapse SNe (CCSNe) are the most probable candidates to produce the iron excess of the second generation of stars. If iron was produced instead by Type Ia SNe, we would expect lower [Mg/Fe] and [Si/Fe] ratios for the group of stars enriched in s-process elements than the first generation of (s-process element poor) stars. SNe Ia events are selectively enriched in iron (although a modest quantity of Si is also produced). In contrast, CCSNe in addition to iron, also produce Mg and Si in higher quantities than SNe Ia.
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/1827f14a.ps}\includegrap...
...igure/1827f14b.ps}\includegraphics[width=5.6cm]{figure/1827f14c.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg123.png) |
Figure 14: [Y/Fe] ( left), [Zr/Fe] ( center), and [Ba/Fe] ( right) as a function of [Ca/Fe]. Symbols are as in Fig. 7, dashed lines are the best least squares fitting straight lines. |
| Open with DEXTER | |
With a present day mass of ![]()
![]()
![]() ,
(Pryor & Meylan 1993)
NGC 6656 is one of the most massive GCs in the Milky Way.
Its s-element rich population of mass
,
(Pryor & Meylan 1993)
NGC 6656 is one of the most massive GCs in the Milky Way.
Its s-element rich population of mass
![]()
![]() and iron abundance [
Fe/H] =
and iron abundance [
Fe/H] =
![]() dex, includes
dex, includes ![]() 1.5
1.5
![]() of
fresh iron if we assume that
of
fresh iron if we assume that
![]() .
Each
CCSN on average
produces
.
Each
CCSN on average
produces ![]() 0.07
0.07
![]() of iron (Hamuy
2003), therefore about twenty SNe are needed to produce the fresh
iron in the second stellar population.
In this scenario, the fainter SGB (and TO) of this second generation of stars
is caused by
their different chemical mixture, rather than an age difference.
of iron (Hamuy
2003), therefore about twenty SNe are needed to produce the fresh
iron in the second stellar population.
In this scenario, the fainter SGB (and TO) of this second generation of stars
is caused by
their different chemical mixture, rather than an age difference.
6 Can the iron abundance spread account for the SGB split?
Figure 18 from Piotto (2009) shows that the SGB of M 22 splits into two branches. In the previous section, we have shown that there are two groups of stars in M 22 with both different s-process element abundances, and two different average iron contents. In this section, we investigate whether the variation in iron content can explain the split of the SGB.
In Fig. 19, we compare two isochrones from Pietrinferni
et al. (2004) in the ACS/WFC plane
![]() vs.
vs.
![]() of Fig. 18. Both of them have an
age of 14 Gyr, but different metallicities.
The black line corresponds to the mean
metallicity of the group of s-process element poor stars
([Fe/H] = -1.82) and the dashed red line is an isochrone with the
average [Fe/H] = -1.68 of the s-process element
rich stars. The different metallicity reflects mainly
in a split in both the RGB and the SGB. In the inset, we show a
zoom of the SGB region. At
of Fig. 18. Both of them have an
age of 14 Gyr, but different metallicities.
The black line corresponds to the mean
metallicity of the group of s-process element poor stars
([Fe/H] = -1.82) and the dashed red line is an isochrone with the
average [Fe/H] = -1.68 of the s-process element
rich stars. The different metallicity reflects mainly
in a split in both the RGB and the SGB. In the inset, we show a
zoom of the SGB region. At
![]() ,
the difference in magnitude
,
the difference in magnitude
![]() between the two isochrones is
between the two isochrones is
![]() ,
about 0.07 mag smaller than
that observed by Piotto (2009).
We conclude that the observed difference in [Fe/H] can contribute to
produce the split of the SGB observed by Piotto (2009), but that it is
not sufficient. On the other hand, the entire shape of
the turn off-SGB-RGB region is difficult to reproduce with standard,
alpha-enhanced
isochrones. This probably indicates that the reason for the SGB split
may be far more complicated and also involve the NaCNO abundances,
as suggested by Cassisi et al. (2008) for the case of NGC 1851.
,
about 0.07 mag smaller than
that observed by Piotto (2009).
We conclude that the observed difference in [Fe/H] can contribute to
produce the split of the SGB observed by Piotto (2009), but that it is
not sufficient. On the other hand, the entire shape of
the turn off-SGB-RGB region is difficult to reproduce with standard,
alpha-enhanced
isochrones. This probably indicates that the reason for the SGB split
may be far more complicated and also involve the NaCNO abundances,
as suggested by Cassisi et al. (2008) for the case of NGC 1851.
7 Comparison with M 4
We compare the chemical abundances obtained in this paper for M 22 with the abundance measurements of M 4 RGB stars derived by Marino et al. (2008) to highlight the complexity of the multiple populations in different clusters.
This comparison is instructive, first of all, because M 4, in a similar way to M 22, is affected by high differential reddening (Lyons et al. 1995; Ivans et al. 1999), and moreover, their spectra were analysed employing the same procedure. We also note that the UVES spectra of M 4 were collected with the same set-up and have almost the same S/N ratio as the M 22 spectra analysed in this work.
Marino et al. (2008) demonstrated that
M 4 hosts two distinct stellar populations,
characterized by different Na contents, and different CN-band strengths.
These two groups of stars also define two sequences along the RGB,
although there is no split detected in the SGB.
In disagreement with the results for M 22, M 4 does not show any
evidence of an intrinsic Fe spread.
Marino et al. (2008) set an upper limit to the [Fe/H] spread of 0.05 dex (1![]() )
in M 4.
In the case of M 22, as discussed in
Sect. 4.2, we identified a clearly
NaO anticorrelation, but found no evidence of a dichotomy in
Na distribution similar to that found in M 4.
We found a dichotomy instead, in the s-process elements
and that the SGB is split into two branches.
)
in M 4.
In the case of M 22, as discussed in
Sect. 4.2, we identified a clearly
NaO anticorrelation, but found no evidence of a dichotomy in
Na distribution similar to that found in M 4.
We found a dichotomy instead, in the s-process elements
and that the SGB is split into two branches.
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827f15.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg133.png) |
Figure 15: [Na/Fe] as a function of [Ca/Fe]. Symbols are as in Fig. 7. |
| Open with DEXTER | |
For comparison purposes, we show in Fig.17 the Fe
abundances as
a function of Ba and Ca in M 4, using the same scale used for the same plots
as our M 22 targets (Fig. 11, right panel, and
Fig. 13 respectively). In the case of M 4, there is no
evidence of a chemical spread in
[Ba/Fe] versus [Fe/H] nor in [Ca/Fe] versus [Fe/H].
We note that the rms of the calcium abundance in M 4 is 0.04 dex, to
be compared with
the
![]() (see Table 5) that we found for the
same element in M 22.
We find a rms in the calcium abundance almost
equal to that found in M 4 when we divide our stellar sample into the two s-process element rich and poor groups
(
(see Table 5) that we found for the
same element in M 22.
We find a rms in the calcium abundance almost
equal to that found in M 4 when we divide our stellar sample into the two s-process element rich and poor groups
(
![]() for both the two s groups).
for both the two s groups).
The two stellar populations in M 4 and M 22 are apparently of different origin, or the mechanisms responsible for this dichotomy must have been operating with different efficiencies in the two clusters.
8 An independent check of our results
We have presented clear evidence of a spread in [Fe/H] and the presence of a bimodal distribution in the s-process element abundances of M 22 stars. These results are based on high resolution UVES spectra of seventeen stars. Because of the high relevance of these results to the ongoing lively debate about the multipopulation phenomenon in star clusters, we searched the ESO archive for additional spectra of M 22 stars to strengthen the statistical significance of our results for UVES data. We found GIRAFFE spectra data for 121 stars which we reduced. Data for only fourteen were in the appropriate RGB location to have high enough S/N to pass all of our quality checks (see the following discussion) and be useful to the abundance measurements. In any case, we were able to double the original UVES sample of stars.
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/1827f16a.ps}\includegraphics[width=5.6cm]{figure/1827f16b.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg135.png) |
Figure 16: [Mg/Fe] ( left), and [Si/Fe] ( right) as a function of [Fe/H]. Symbols are as in Fig. 7. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/1827f17a.ps}\includegraphics[width=5.6cm]{figure/1827f17b.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg136.png) |
Figure 17: [Ba/Fe] ( left), and [Ca/Fe] as a function [Fe/H] ( right) for 104 stars in the GC M 4 (from Marino et al. 2008). |
| Open with DEXTER | |
Each star was observed with HR09, HR13, and HR15 set-ups, which
provided a resolution
of about
![]() -25 000 in the wavelength ranges of 514-535,
612-640, and 660-696 nm, respectivelly.
Data were reduced using the last version of the pipeline
developed by Geneva observatory (Blecha et al. 2000),
and were bias-subtracted, flat-field corrected, and
extracted by applying a wavelength calibration derived with
ThAr lamps. Each spectrum was then normalized.
Finally, for each star we obtained a radial velocity
and applied a membership criterion as performed for the UVES
data. Spectra of each member star were then shifted to a
velocity rest-frame and combined together.
We also performed a test to verify the influence of scattered
light on the spectral line shape, which could alter the final abundances.
We also reduced some spectra covering the whole GIRAFFE CCD
with and without scattered-light subtraction
and compared spectral features. We found that scattered-light
has no significant influence on the line strengths.
-25 000 in the wavelength ranges of 514-535,
612-640, and 660-696 nm, respectivelly.
Data were reduced using the last version of the pipeline
developed by Geneva observatory (Blecha et al. 2000),
and were bias-subtracted, flat-field corrected, and
extracted by applying a wavelength calibration derived with
ThAr lamps. Each spectrum was then normalized.
Finally, for each star we obtained a radial velocity
and applied a membership criterion as performed for the UVES
data. Spectra of each member star were then shifted to a
velocity rest-frame and combined together.
We also performed a test to verify the influence of scattered
light on the spectral line shape, which could alter the final abundances.
We also reduced some spectra covering the whole GIRAFFE CCD
with and without scattered-light subtraction
and compared spectral features. We found that scattered-light
has no significant influence on the line strengths.
For GIRAFFE data analysis, we followed the same procedure
for UVES, i.e., obtaining atmospheric parameters only from
spectroscopy and not from photometry, which can be altered
by differential reddening.
This approach has the advantage of placing the abundance determinations from
the two data sets
on the same abundance scale, avoiding systematic effects.
However, this choice,
coupled with the selection of stars located only in the RGB,
required the rejection of
103 spectra because of their low
![]() .
A high S/N ratio
is necessary to measure a sufficient number of isolated FeI/II lines
in GIRAFFE spectra, which
have lower resolution and cover a smaller wavelength range than UVES.
In addition, the brightest stars were not analysed because of their very low
temperature
(
.
A high S/N ratio
is necessary to measure a sufficient number of isolated FeI/II lines
in GIRAFFE spectra, which
have lower resolution and cover a smaller wavelength range than UVES.
In addition, the brightest stars were not analysed because of their very low
temperature
(
![]() ). In this
). In this
![]() regime metal poor
stars (as in the case of M 22) also have very strong lines, which are
blended in the GIRAFFE data, preventing a reliable EW measurement.
regime metal poor
stars (as in the case of M 22) also have very strong lines, which are
blended in the GIRAFFE data, preventing a reliable EW measurement.
After a star had passed our selection criteria, atmospheric parameters (and Fe content) were obtained by the EW method, as for the UVES data, using the same linelist for the spectral lines in common between the two set-ups.
Some comparisons are needed
between the results obtained for data from the two spectrographs.
Since we have only one star (#51) in common between the two data-sets,
we could not compare the results directly (apart for this star).
In Table 7, we list the chemical abundances in common
obtained for this
star from the two different data sets. We note that the atmospheric
parameters are in agreement within the errors calculated for the UVES
data, the
values of Fe and Y abundances agree within the
![]() margins of error
listed in Table 5, while for the other elements there are larger
discrepancies probably because of the errors associated with the
GIRAFFE results (that we have not considered here).
Since the comparison of one star is not enough to verify the
compatibility between the two sets of abundances,
we compared the atmospheric parameters and the mean metallicity.
margins of error
listed in Table 5, while for the other elements there are larger
discrepancies probably because of the errors associated with the
GIRAFFE results (that we have not considered here).
Since the comparison of one star is not enough to verify the
compatibility between the two sets of abundances,
we compared the atmospheric parameters and the mean metallicity.
Table 7: Atmospheric parameters and chemical abundances for the star #51 obtained from UVES and GIRAFFE data.
Figure 20 summarizes our tests. Filled circles represent
GIRAFFE results and open squares the UVES ones.
In the upper left panel, we plot log (g) as a function of
![]() ,
while
the upper right panel shows
,
while
the upper right panel shows ![]() versus log (g).
Both gravity as a function of temperature and
microturbolence velocity as a function of gravity follow the same
general trend for the two datasets, with similar dispersions.
Further tests are shown in the two lower panels.
The lower left one shows the Fe abundance vs. V magnitude (i.e.,
as a function of the
evolutionary state of the star along the RGB). No correlation
is apparent, meaning that no systematic errors due to the different
evolutionary phase are present.
The lower right panel reports
versus log (g).
Both gravity as a function of temperature and
microturbolence velocity as a function of gravity follow the same
general trend for the two datasets, with similar dispersions.
Further tests are shown in the two lower panels.
The lower left one shows the Fe abundance vs. V magnitude (i.e.,
as a function of the
evolutionary state of the star along the RGB). No correlation
is apparent, meaning that no systematic errors due to the different
evolutionary phase are present.
The lower right panel reports
![]() vs. B-V color.
The line is the empirical relation by Alonso et al. (1999),
obtained by assuming a reddening
E(B-V)=0.34 (Harris 1996).
In this case good agreement was also found, not only for
the zeropoint of the relations (i.e., the absolute average reddening of
the cluster), but also for the shape of the relations themselves.
vs. B-V color.
The line is the empirical relation by Alonso et al. (1999),
obtained by assuming a reddening
E(B-V)=0.34 (Harris 1996).
In this case good agreement was also found, not only for
the zeropoint of the relations (i.e., the absolute average reddening of
the cluster), but also for the shape of the relations themselves.
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827f18.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg139.png) |
Figure 18: ACS/WFC CMD of M 22 from Piotto (2009). |
| Open with DEXTER | |
An important test comes from the comparison of the mean iron content obtained from the two data-sets. From the fourteen GIRAFFE stars, we obtain
A rough estimate of errors in the atmospheric parameters can be made as in
Marino et al. (2008), assuming that stars of the same V
magnitude (corrected
for differential reddening) have the same parameters.
In this way, we obtain:
![]() K,
K,
![]() ,
and
,
and
![]() km s-1.
We can see that the errors are a bit larger, but still comparable
with UVES ones.
km s-1.
We can see that the errors are a bit larger, but still comparable
with UVES ones.
All the other elements, with the exception of Ti, in GIRAFFE data were measured by spectral synthesis because of the severe blends with other lines. In addition to Fe and Ti, we measured O (from the forbidden line at 630 nm), Na (from the doublet at 615 nm), Y (from the doublet at 520 nm), Ba (from the line at 614 nm), Nd (from the line at 532 nm), and Eu (from the line at 665 nm).
After verifying the good agreement between the atmospheric parameters and the iron content obtained from the two data-sets, we proceed by verifying whether the results for the GIRAFFE data agree with our UVES results. For this reason, in Fig. 21 we show some of the trends discussed in the previous sections. Filled circles are GIRAFFE measurements, while open circles are UVES ones. It is clear from this comparison that UVES results are fully confirmed. In particular, we can confirm the Y-Ba bimodality (central panel), as well as the different Fe content for the two s-element rich and s-element poor groups of stars (see leftmost and rightmost middle panels).
In addition, from GIRAFFE data we also measured Nd (a combined s and r element) and Eu (a pure r element) lines. Their abundances as a function of [Fe/H] are shown in the central and right lower panels. No trend is evident for [Eu/Fe], while [Nd/Fe] clearly correlates with [Fe/H]. This is further evidence that the iron enrichment of the s-process rich group is caused by core-collapse SNe.
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827f19.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg144.png) |
Figure 19: Red and blue lines are theoretical isochrones from Pietrinferni et al. (2004), with [Fe/H] = -1.68 and [ Fe/H] = -1.82. The difference in metallicity produces in the CMD a split of the RGB and the SGB. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{figure/11827f20.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg145.png) |
Figure 20: Check of the atmospheric parameters used in this paper. Filled circles are GIRAFFE stars, while open squares are UVES ones. See Sect. 8 for a full explanation. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{figure/11827f21.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg146.png) |
Figure 21: Comparison of our final results we obtained for UVES (open circles) and GIRAFFE (filled circles). |
| Open with DEXTER | |
9 Conclusions
We have presented a high resolution spectroscopic analysis of seventeen RGB stars in the GC M 22 from UVES and FLAMES+UVES data.
We confirm that M 22 is a metal poor GC, with a mean iron content
of [Fe/H] =
![]() (weighted mean between UVES and
GIRAFFE) and a mean
(weighted mean between UVES and
GIRAFFE) and a mean ![]() -enhancement [
-enhancement [![]() /Fe] =
/Fe] =
![]() .
Sodium and oxygen follow the well known
anticorrelation, while there is no evidence of a MgAl
anticorrelation. A clear correlation was found between Na and Al.
.
Sodium and oxygen follow the well known
anticorrelation, while there is no evidence of a MgAl
anticorrelation. A clear correlation was found between Na and Al.
We found a clear dichotomy in the distribution of the s-process
elements barium, yttrium, and zirconium. Most importantly, we found
that the abundance of these
elements is correlated with the iron abundance. Stars enriched in
s-process elements also exhibit systematically higher values of [Fe/H], by
![]() 0.14 dex. The
s-process element abundance correlates with calcium, and the calcium with
the iron abundance. No clear correlation is present between s-process
elements and sodium, and between iron and sodium, but we noted that
s-element and Fe enriched stars show higher values of sodium.
These stars also show an overabundance of magnesium and silicon.
The correlation between s-process elements, and Ca abundances, with [Fe/H] is the strongest support for
the presence of two groups of stars with a different Fe content in M 22.
All these results have been confirmed for a sample of
fourteen lower resolution
GIRAFFE spectra, which has allowed us to double our original UVES sample.
0.14 dex. The
s-process element abundance correlates with calcium, and the calcium with
the iron abundance. No clear correlation is present between s-process
elements and sodium, and between iron and sodium, but we noted that
s-element and Fe enriched stars show higher values of sodium.
These stars also show an overabundance of magnesium and silicon.
The correlation between s-process elements, and Ca abundances, with [Fe/H] is the strongest support for
the presence of two groups of stars with a different Fe content in M 22.
All these results have been confirmed for a sample of
fourteen lower resolution
GIRAFFE spectra, which has allowed us to double our original UVES sample.
According to theoretical models by Pietrinferni et al. (2004),
a difference in metallicity of
0.14 dex should cause a difference of
![]() 0.10 mag in the F606W ACS/WFC band at the level
of the SGB. Piotto (2009) indeed found that the SGB of M 22 is
separated into two, distinct branches. However, the average separation in
F606W band is of the order of
0.17 mag: it appears that the SGB split cannot be
caused by a difference in [Fe/H] alone.
0.10 mag in the F606W ACS/WFC band at the level
of the SGB. Piotto (2009) indeed found that the SGB of M 22 is
separated into two, distinct branches. However, the average separation in
F606W band is of the order of
0.17 mag: it appears that the SGB split cannot be
caused by a difference in [Fe/H] alone.
The fraction of stars on the bright SGB (bSGB) corresponds to
62% ![]() 5% of the total SGB population, while the faint SGB (fSGB) includes
the remaining 38%
5% of the total SGB population, while the faint SGB (fSGB) includes
the remaining 38% ![]() 5% of the SGB stars (Piotto 2009). In the stellar sample of the present paper,
the fraction of Ba-strong, Y-strong, Zr-strong stars is
5% of the SGB stars (Piotto 2009). In the stellar sample of the present paper,
the fraction of Ba-strong, Y-strong, Zr-strong stars is ![]() 41%.
It is therefore tempting to connect the
s-process element poor sample to the bright SGB stars, while the faint SGB
stars could be the stars with enhanced s-process elements. The correct reproduction
of the two SGBs requires an accurate determination of the NaCNO abundances,
as shown by Cassisi et al. (2008) for the analogous case of NGC 1851.
He variations between the two populations can also affect the SGB morphology.
We note that M 22 shares similarities with
41%.
It is therefore tempting to connect the
s-process element poor sample to the bright SGB stars, while the faint SGB
stars could be the stars with enhanced s-process elements. The correct reproduction
of the two SGBs requires an accurate determination of the NaCNO abundances,
as shown by Cassisi et al. (2008) for the analogous case of NGC 1851.
He variations between the two populations can also affect the SGB morphology.
We note that M 22 shares similarities with ![]() Centauri and
NGC 1851: these clusters, where multiple stellar populations have
been photometrically identified along the SGB,
exhibit a large range, not only in C, N, O, Na, Al, but also in
s-process element abundance.
M 22 is the only globular, apart from
Centauri and
NGC 1851: these clusters, where multiple stellar populations have
been photometrically identified along the SGB,
exhibit a large range, not only in C, N, O, Na, Al, but also in
s-process element abundance.
M 22 is the only globular, apart from ![]() Centauri, where some
evidence of an intrinsic spread in iron has been observed.
Some hints
(even if very uncertain due to the low number statistics of the analysed
sample) of a some iron spread in NGC 1851 was suggested by Yong & Grundahl
(2008).
NGC 1851,
Centauri, where some
evidence of an intrinsic spread in iron has been observed.
Some hints
(even if very uncertain due to the low number statistics of the analysed
sample) of a some iron spread in NGC 1851 was suggested by Yong & Grundahl
(2008).
NGC 1851, ![]() Centauri, and M 22 show a large
variation in the Strömgren index, traditionally used as a
metallicity indicator. All of these three GCs exhibit a splitted SGB.
Centauri, and M 22 show a large
variation in the Strömgren index, traditionally used as a
metallicity indicator. All of these three GCs exhibit a splitted SGB.
From our observations and the results of Piotto (2009), it is tempting to speculate that the SGB split could be related to the presence of two groups of stars with different s-process element contents and a difference, albeit small, in iron. According to this interpretation, s-process element poor stars would correspond to the brighter SGB stars and constitute the first M 22 population. The second stellar generation should have been formed after the AGB winds of this first stellar generation had polluted the protocluster interstellar medium with s-process elements. This second generation may have formed from material that was also enriched by core-collapse supernovae ejecta, as indicated by their higher iron, magnesium, and silicon content, and the lack of correlation of the iron content with a pure r-process element (Eu). A detailed analysis of the C, N, and O abundances of SGB stars in M 22 is strongly needed to resolve this problem.
Acknowledgements
We warmly thank the referee, J. Cohen, for her comments and suggestions which surely helped to strengthen the results presented in this paper. We also thank P. Marigo for useful discussion. A.F.M., A.P.M., A.B., A.R., and G.P. acknowledge the support by the MIUR-PRIN2007 prot. 20075TP5K9. AFM acknowledges partial support by Fondazione A. Gini. APM acknowledges partial support by ASI. A.B. acknowledgments the support of the CA.RI.PA.RO. foundation, and the STScI under the 2008 graduate research assistentship program.
References
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1999, A&A, 140, 261 [NASA ADS] [CrossRef] (In the text)
- Ballester, P., Modigliani, A., Boitquin, O., et al. 2000, ESO Messenger, 101, 31 [NASA ADS] (In the text)
- Bellini, A., Piotto, G., Bedin, L. R., et al. 2009, A&A, 493, 959 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] (In the text)
- Blecha, A., Cayatte, V., North, P., Royer, F., & Simond, G. 2000, Proc. SPIE, 4008, 467 [NASA ADS] (In the text)
- Brown, J. A., & Wallerstein, G. 1992, AJ, 104, 1818 [NASA ADS] [CrossRef] (In the text)
- Busso, M., Gallino, R., Lambert, D. L., Travaglio, C., & Smith, V. V. 2001, ApJ, 557, 802 [NASA ADS] [CrossRef] (In the text)
- Cannon, R. D., Croke, B. F. W., Bell, R. A., Hesser, J. E., & Stathakis, R. A. 1998, MNRAS, 298, 601 [NASA ADS] [CrossRef] (In the text)
- Carretta, E., Gratton, R. G., Lucatello, S., Bragaglia, A., & Bonifacio, P. 2005, A&A, 433, 597 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2006, A&A, 450, 523 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2007, A&A, 464, 967 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Carretta, E., Bragaglia, A., Gratton, R. G., & Lucatello, S. 2008 [arXiv:0811.3591] (In the text)
- Cassisi, S., Salaris, M., Pietrinferni, A., et al. 2008, ApJ, 672, L115 [NASA ADS] [CrossRef] (In the text)
- Cohen, J. G. 1981, ApJ, 247, 869 [NASA ADS] [CrossRef] (In the text)
- Cohen, J. G., & Meléndez, J. 2005, AJ, 129, 303 [NASA ADS] [CrossRef] (In the text)
- D'Antona, F., & Caloi, V. 2004, ApJ, 611, 871 [NASA ADS] [CrossRef] (In the text)
- Dekker, H., D'Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, Proc. SPIE, 4008, 534 [NASA ADS] (In the text)
- Freeman, K. C., & Rodgers, A. W. 1975, ApJ, 201, L71 [NASA ADS] [CrossRef] (In the text)
- Gratton, R. G. 1982, A&A, 115, 171 [NASA ADS] (In the text)
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gratton, R., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] (In the text)
- Hamuy, M. 2003, ApJ, 582, 905 [NASA ADS] [CrossRef] (In the text)
- Harris, W. E. 1996, VizieR Online Data Catalog, 7195, 0 (In the text)
- Hesser, J. E., Hartwick, F. D. A., & McClure, R. D. 1977, ApJS, 33, 471 [NASA ADS] [CrossRef] (In the text)
- Ivans, I. I., Sneden, C., Kraft, R. P., et al. 1999, ApJ, 118, 1273 [NASA ADS] (In the text)
- Ivans, I. I., Sneden, C., Wallerstein, G., et al. 2004, Mem. Soc. Astron. Ital., 75, 286 [NASA ADS] (In the text)
- Kayser, A., Hilker, M., Grebel, E. K., & Willemsen, P. G. 2008, A&A, 486, 437 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lee, Y.-W., Joo, J.-M., Sohn, Y.-J., et al. 1999, Nature, 402, 55 [NASA ADS] [CrossRef] (In the text)
- Lehnert, M. D., Bell, R. A., & Cohen, J. G. 1991, ApJ, 367, 514 [NASA ADS] [CrossRef] (In the text)
- Lyons, M. A., Bates, B., Kemp, S. N., & Davies, R. D. 1995, MNRAS, 277, 113 [NASA ADS] (In the text)
- Marino, A. F., Villanova, S., Piotto, G., et al. 2008, A&A, 490, 625 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Milone, A. P., Bedin, L. R., Piotto, G., et al. 2008, ApJ, 673, 241 [NASA ADS] [CrossRef] (In the text)
- Monaco, L., Pancino, E., Ferraro, F. R., & Bellazzini, M. 2004, MNRAS, 349, 1278 [NASA ADS] [CrossRef] (In the text)
- Moretti, A., Piotto, G., Arcidiacono, C., et al. 2009, A&A, 493, 539 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Norris, J. E., & Freeman, K. C. 1983, ApJ, 266, 130 [NASA ADS] [CrossRef] (In the text)
- Norris, J. E., Freeman, K. C., & Mighell, K. J. 1996, ApJ, 462, 241 [NASA ADS] [CrossRef] (In the text)
- Pancino, E., Ferraro, F. R., Bellazzini, M., Piotto, G., & Zoccali, M. 2000, ApJ, 534, L83 [NASA ADS] [CrossRef] (In the text)
- Pancino, E., Pasquini, L., Hill, V., Ferraro, F. R., & Bellazzini, M. 2002, ApJ, 568, L101 [NASA ADS] [CrossRef] (In the text)
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] (In the text)
- Peterson, R. C., & Cudworth, K. M. 1994, ApJ, 420, 612 [NASA ADS] [CrossRef] (In the text)
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] (In the text)
- Pilachowski, C., Wallerstein, G., Leep, E. M., & Peterson, R. C. 1984, ApJ, 263, 187 [NASA ADS] [CrossRef]
- Piotto, G. 2008, Mem. Soc. Astron. Ital., 79, 334 [NASA ADS] (In the text)
- Piotto, G. 2009 [arXiv:0902.1422] (In the text)
- Piotto, G. et al. 2009, in preparation
- Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef] (In the text)
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] (In the text)
- Pryor, C., & Meylan, G. 1993, Structure and Dynamics of Globular Clusters, ASP, 50, 357 (In the text)
- Ramírez, S. V., & Cohen, J. G. 2002, AJ, 123, 3277 [NASA ADS] [CrossRef] (In the text)
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [NASA ADS] [CrossRef] (In the text)
- Suntzeff, N. B., & Kraft, R. P. 1996, AJ, 111, 1913 [NASA ADS] [CrossRef] (In the text)
- Villanova, S., Piotto, G., King, I. R., et al. 2007, ApJ, 663, 296 [NASA ADS] [CrossRef] (In the text)
- Yong, D., & Grundahal, F. 2008, ApJ, 672, L39 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... (M 22)
![[*]](/icons/foot_motif.png)
- Based on data collected at the European Southern Observatory with the VLT-UT2, Paranal, Chile.
- ...
SPECTRUM
![[*]](/icons/foot_motif.png)
- See http://www.phys.appstate.edu/spectrum/spectrum.html for more details.
All Tables
Table 1: Right ascension, declination, heliocentric radial velocity, and magnitude for the analysed stars.
Table 2:
Measured solar abundances
![]() .
.
Table 3: Atmospheric parameters for the analysed stars.
Table 4: The average abundances for M 22 stars.
Table 5:
Sensitivity of derived UVES abundances to the atmospheric parameters
and EWs. We reported the error
![]() caused by the
uncertainties in the atmospheric parameters
(
caused by the
uncertainties in the atmospheric parameters
(
![]() ,
,
![]() log (g),
log (g),
![]() ,
and
,
and ![]() ([A/H])), related to the error in EW measurements
(
([A/H])), related to the error in EW measurements
(
![]() ), the squared sum of the two (
), the squared sum of the two (
![]() ), and the
observed dispersion (
), and the
observed dispersion (
![]() )
for each element.
)
for each element.
Table 6: Average abundances of s-element process poor and rich stars.
Table 7: Atmospheric parameters and chemical abundances for the star #51 obtained from UVES and GIRAFFE data.
All Figures
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827fg1.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg48.png) |
Figure 1: Distribution of the UVES target stars (red symbols) on the B vs. (B-I) CMD corrected for differential reddening. Data for the star #200083 are not plotted because the B magnitude is not available for this star. The stars observed with GIRAFFE are shown by blue crosses. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827fg2.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg79.png) |
Figure 2: Box plot for M 22 star element abundances. The points are the individual measurements. The central horizontal line of each box is the mean of the data; the upper and lower lines represent the 68.27% levels of the distribution around the mean value. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{figure/11827fg3.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg101.png) |
Figure 3: The anticorrelation between [Na/Fe] and [O/Fe] abundance ratios. Triangles indicate stars that, on the basis of their position on the CMD, should be AGB. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm]{figure/11827fg4.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg105.png) |
Figure 4: NaO anticorrelation for M 22 stars superimposed on a collection of stars of four GCs that host multiple stellar populations. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827fg5.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg106.png) |
Figure 5: [Mg/Fe] as a function of [Al/Fe] abundance ratios. Symbols are as in Fig. 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{figure/11827fg6.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg107.png) |
Figure 6: [Al/Fe] as a function of [Na/Fe] abundance ratios. Symbols are as in Fig. 3, dashed line is the best least squares fitting straight line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/11827f7a.ps}\includegrap...
...igure/11827f7b.ps}\includegraphics[width=5.6cm]{figure/11827f7c.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg109.png) |
Figure 7: From left to right: [Zr/Fe] and [Ba/Fe] versus [Y/Fe] and [Ba/Fe] versus [Zr/Fe] abundance ratios. Red filled symbols represent the s element rich stars, and the black empty ones represent the s poor stars. The red and the black crosses with error bars indicate the average abundances of stars in each group, dashed lines are the best least squares fitting straight lines. Triangles indicate probable AGB stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/11827f8a.ps}\includegrap...
...igure/11827f8b.ps}\includegraphics[width=5.6cm]{figure/11827f8c.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg114.png) |
Figure 8: From the left to the right: [Y/Fe] as a function of [Na/Fe], [Al/Fe] and [O/Fe] abundance ratios. Symbols are as in Fig. 7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{figure/11827fg9.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg115.png) |
Figure 9: The upper panel shows the spectra of the metal-poor star #200068 ([Fe/H] = -1.84) and of the metal-rich star #200083 ([Fe/H] = -1.63) centered on the lines of FeI. The stellar parameters are very similar, although, the Fe lines differ significantly. The bottom panel shows the same lines for stars #200101 and #71 with similar metallicity and stellar parameters. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/1827f10a.ps}\includegrap...
...igure/1827f10b.ps}\includegraphics[width=5.6cm]{figure/1827f10c.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg116.png) |
Figure 10: From the left to the right: [Na/Fe], [Al/Fe], and [O/Fe] as a function of [Fe/H] abundance ratios. Symbols are as in Fig. 7 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/1827f11a.ps}\includegrap...
...igure/1827f11b.ps}\includegraphics[width=5.6cm]{figure/1827f11c.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg117.png) |
Figure 11: [Y/Fe] ( left), [Zr/Fe] ( center), and [Ba/Fe] ( right) as a function of [Fe/H]. Symbols are as in Fig. 7, dashed lines are the best least squares fitting straight lines. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827f12.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg118.png) |
Figure 12: Simulation of 100 000 stars with the properties of the two observed groups of stars. The red and the blue histograms represent the s-rich and the s-poor groups of stars, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{figure/11827f13.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg122.png) |
Figure 13: [Ca/Fe] as a function [Fe/H]. Symbols are as in Fig. 7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/1827f14a.ps}\includegrap...
...igure/1827f14b.ps}\includegraphics[width=5.6cm]{figure/1827f14c.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg123.png) |
Figure 14: [Y/Fe] ( left), [Zr/Fe] ( center), and [Ba/Fe] ( right) as a function of [Ca/Fe]. Symbols are as in Fig. 7, dashed lines are the best least squares fitting straight lines. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827f15.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg133.png) |
Figure 15: [Na/Fe] as a function of [Ca/Fe]. Symbols are as in Fig. 7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/1827f16a.ps}\includegraphics[width=5.6cm]{figure/1827f16b.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg135.png) |
Figure 16: [Mg/Fe] ( left), and [Si/Fe] ( right) as a function of [Fe/H]. Symbols are as in Fig. 7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.6cm]{figure/1827f17a.ps}\includegraphics[width=5.6cm]{figure/1827f17b.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg136.png) |
Figure 17: [Ba/Fe] ( left), and [Ca/Fe] as a function [Fe/H] ( right) for 104 stars in the GC M 4 (from Marino et al. 2008). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827f18.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg139.png) |
Figure 18: ACS/WFC CMD of M 22 from Piotto (2009). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm]{figure/11827f19.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg144.png) |
Figure 19: Red and blue lines are theoretical isochrones from Pietrinferni et al. (2004), with [Fe/H] = -1.68 and [ Fe/H] = -1.82. The difference in metallicity produces in the CMD a split of the RGB and the SGB. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{figure/11827f20.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg145.png) |
Figure 20: Check of the atmospheric parameters used in this paper. Filled circles are GIRAFFE stars, while open squares are UVES ones. See Sect. 8 for a full explanation. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{figure/11827f21.ps}
\end{figure}](/articles/aa/full_html/2009/39/aa11827-09/Timg146.png) |
Figure 21: Comparison of our final results we obtained for UVES (open circles) and GIRAFFE (filled circles). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


