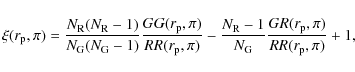| Issue |
A&A
Volume 505, Number 2, October II 2009
|
|
|---|---|---|
| Page(s) | 463 - 482 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200912314 | |
| Published online | 03 August 2009 | |
The zCOSMOS survey. The dependence of clustering on luminosity and stellar mass at z=0.2-1![[*]](/icons/foot_motif.png)
B. Meneux1,2 - L. Guzzo3 - S. de la Torre3,4,5 - C. Porciani6,7 - G. Zamorani8 - U. Abbas9 - M. Bolzonella8 - B. Garilli5 - A. Iovino10 - L. Pozzetti8 - E. Zucca8 - S. J. Lilly7 - O. Le Fèvre4 - J.-P. Kneib4 - C. M. Carollo7 - T. Contini11 - V. Mainieri12 - A. Renzini13 - M. Scodeggio5 - S. Bardelli8 - A. Bongiorno1 - K. Caputi7 - G. Coppa8,14 - O. Cucciati4 - L. de Ravel4 - P. Franzetti5 - P. Kampczyk7 - C. Knobel7 - K. Kovac7 - F. Lamareille11 - J.-F. Le Borgne11 - V. Le Brun4 - C. Maier7 - R. Pellò11 - Y. Peng7 - E. Perez Montero11 - E. Ricciardelli13 - J. D. Silverman7 - M. Tanaka12 - L. Tasca4,5 - L. Tresse4 - D. Vergani8 - D. Bottini5 - A. Cappi8 - A. Cimatti14 - P. Cassata4 - M. Fumana5 - A. M. Koekemoer15 - A. Leauthaud16 - D. Maccagni5 - C. Marinoni17 - H. J. McCracken18 - P. Memeo5 - P. Oesch7 - R. Scaramella19
1 -
Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstrasse, 85748 Garching-bei-München,
Germany
2 - Universitäts-Sternwarte, Scheinerstrasse 1, Munich 81679,
Germany
3 - INAF - Osservatorio Astronomico di Brera, Via
Bianchi 46, 23807 Merate (LC), Italy
4 - Laboratoire
d'Astrophysique de Marseille, UMR 6110 CNRS Université de
Provence, BP8, 13376 Marseille Cedex 12, France
5 - INAF -
Istituto di Astrofisica Spaziale e Fisica Cosmica, Via Bassini 15,
20133 Milano, Italy
6 - Argelander Institute for Astronomy, Auf
dem Hügel 71, 53121 Bonn, Germany
7 - Institute of Astronomy, ETH
Zurich, Zurich, Switzerland
8 - INAF - Osservatorio Astronomico
di Bologna, Bologna, Italy
9 - INAF - Osservatorio Astronomico
di Torino, Strada Osservatorio 20, 10025 Pino Torinese (TO), Italy
10 - INAF - Osservatorio Astronomico di Brera, via Brera 28,
Milano, Italy
11 - Laboratoire d'Astrophysique de
Toulouse-Tarbes, Université de Toulouse, CNRS Toulouse, 31400,
France
12 - European Southern Observatory, Garching,
Germany
13 - Dipartimento di Astronomia, Università di
Padova, Padova, Italy
14 - Dipartimento di Astronomia,
Università degli Studi di Bologna, Bologna, Italy
15 - Space
Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD
21218, USA
16 - Berkeley Lab & Berkeley Center for Cosmological
Physics, University of California, Berkeley, CA 94720, USA
17 -
Centre de Physique Theorique, UMR 6207 CNRS Université de
Provence, 13288 Marseille, France
18 - Institut d'Astrophysique
de Paris, Université Pierre & Marie Curie, Paris, France
19 -
INAF - Osservatorio Astronomico di Roma, via di Frascatti 33,
00040 Monte Porzio Catone, Italy
Received 9 April 2009 / Accepted 15 June 2009
Abstract
Aims. We study the dependence of galaxy clustering on luminosity and stellar mass at redshifts ![]() [0.2-1], using the first 10K redshifts from the zCOSMOS spectroscopic survey of the COSMOS field.
[0.2-1], using the first 10K redshifts from the zCOSMOS spectroscopic survey of the COSMOS field.
Methods. We measured the redshift-space correlation functions
![]() and
and ![]() and the projected function,
and the projected function,
![]() for subsamples covering different luminosity, mass, and redshift ranges. We explored and quantified in detail the observational selection biases from the flux-limited nature of the survey, using ensembles of realistic semi-analytic mock samples built from the Millennium simulation. We used the same mock data sets to carefully check our covariance and error estimate techniques, comparing the performances of methods based on the scatter in the mocks and on bootstrapping schemes. We finally compared our measurements to the cosmological model predictions from the mock surveys.
for subsamples covering different luminosity, mass, and redshift ranges. We explored and quantified in detail the observational selection biases from the flux-limited nature of the survey, using ensembles of realistic semi-analytic mock samples built from the Millennium simulation. We used the same mock data sets to carefully check our covariance and error estimate techniques, comparing the performances of methods based on the scatter in the mocks and on bootstrapping schemes. We finally compared our measurements to the cosmological model predictions from the mock surveys.
Results. At odds with other measurements at similar redshift and in the local Universe, we find a weak dependence of galaxy clustering on luminosity in all three redshift bins explored. A mild dependence on stellar mass is instead observed, in particular on small scales, which becomes particularly evident in the central redshift bin (0.5<z<0.8), where
![]() shows strong excess power on scales >1 h-1 Mpc. This is reflected in the shape of the full
shows strong excess power on scales >1 h-1 Mpc. This is reflected in the shape of the full
![]() that we interpret as produced by dominating structures almost perpendicular to the line of sight in the survey volume. Comparing to
that we interpret as produced by dominating structures almost perpendicular to the line of sight in the survey volume. Comparing to ![]() measurements, we do not see any significant evolution with redshift of the amplitude of clustering for bright and/or massive galaxies.
measurements, we do not see any significant evolution with redshift of the amplitude of clustering for bright and/or massive galaxies.
Conclusions. This is consistent with previous results and the standard picture in which the bias evolves more rapidly for the most massive haloes, which in turn host the highest-stellar-mass galaxies. At the same time, however, the clustering measured in the zCOSMOS 10K data at 0.5<z<1 for galaxies with
![]() is only marginally consistent with the predictions from the mock surveys. On scales larger than
is only marginally consistent with the predictions from the mock surveys. On scales larger than ![]() 2 h-1 Mpc, the observed clustering amplitude is compatible only with
2 h-1 Mpc, the observed clustering amplitude is compatible only with ![]() 1% of the mocks. Thus, if the power spectrum of matter is
1% of the mocks. Thus, if the power spectrum of matter is ![]() CDM with standard normalisation and the bias has no ``unnatural'' scale-dependence, this result indicates that COSMOS has picked up a particularly rare,
CDM with standard normalisation and the bias has no ``unnatural'' scale-dependence, this result indicates that COSMOS has picked up a particularly rare, ![]() 2-3
2-3![]() positive fluctuation in a volume of
positive fluctuation in a volume of ![]() 106 h-1 Mpc3. These findings underline the need for larger surveys of the
106 h-1 Mpc3. These findings underline the need for larger surveys of the ![]() Universe to appropriately characterise the level of structure at this epoch.
Universe to appropriately characterise the level of structure at this epoch.
Key words: cosmology: observations - large-scale structure of Universe - surveys - Galaxy: evolution
1 Introduction
In the canonical scenario of galaxy formation, galaxies are thought to form through the cooling of baryonic gas within extended dark matter haloes (White & Rees 1978). The mass of the hosting halo is expected to play a significant role in the definition of the visible properties of the galaxy, as the total mass in gas and stars, its luminosity, colour, star formation rate, and possibly, morphology.Since it is the baryons that form the visible fabric of the Universe, a major challenge in testing the galaxy formation paradigm is to build clear connections between these observed properties and those of the hosting dark-matter haloes. This is a difficult task, as any direct connection initially existing between the dark-matter mass and the baryonic component cooling within the halo is modified by all subsequent dynamical processes affecting the halo-galaxy system, such as merging or dynamical friction. This is confirmed by simulations, which also show however that galaxy luminosity and stellar mass do in fact retain memory of the ``original'' (not actual) halo mass, i.e. before it experiences a major merger or is accreted by a larger halo (Conroy et al. 2006; Wang et al. 2006,2007). This gives some hope that by measuring the dependence of the galaxy distribution on galaxy properties one is actually constraining the relationship between the dark and luminous components of galaxies.
Measurements of first
moments, such as the luminosity function (LF) or the stellar mass
function, provide a way to understand how these are related to the
total halo mass functions, which can be obtained from analytic
predictions (e.g. Press & Schechter 1974) or n-body
simulations (e.g. Warren et al. 2006). Similar investigations
can be made on the second moment, i.e. the two-point correlation
function (e.g. Springel et al. 2006). Studies of galaxy
clustering in large local surveys have shown how clustering at
![]() does depend significantly on several specific properties.
These include luminosity
(Hamilton 1988; Maurogordato & Lachieze-Rey 1991; Iovino et al. 1993; Benoist et al. 1996; Guzzo et al. 2000; Norberg et al. 2001; Norberg et al. 2002; Zehavi et al. 2005),
colour or spectral type
(Willmer et al. 1998; Norberg et al. 2002; Zehavi et al. 2002), morphology
(Davis & Geller 1976; Giovanelli et al. 1986; Guzzo et al. 1997), stellar
mass (Li et al. 2006), and environment
(Abbas & Sheth 2006).
does depend significantly on several specific properties.
These include luminosity
(Hamilton 1988; Maurogordato & Lachieze-Rey 1991; Iovino et al. 1993; Benoist et al. 1996; Guzzo et al. 2000; Norberg et al. 2001; Norberg et al. 2002; Zehavi et al. 2005),
colour or spectral type
(Willmer et al. 1998; Norberg et al. 2002; Zehavi et al. 2002), morphology
(Davis & Geller 1976; Giovanelli et al. 1986; Guzzo et al. 1997), stellar
mass (Li et al. 2006), and environment
(Abbas & Sheth 2006).
In recent years it has become possible to extend these
investigations to high redshift, obtaining first indicative
results on how these dependences evolve with time
(Meneux et al. 2006,2008; Pollo et al. 2006; Daddi et al. 2003; Coil et al. 2006; Phleps et al. 2006).
The VIMOS-VLT Deep Survey (VVDS) (Pollo et al. 2006) and the
DEEP2 survey (Coil et al. 2006) in particular, have provided new
insights into the way galaxies of different luminosity cluster at
![]() .
More specifically, Pollo et al. (2006) have shown that
at these epochs galaxies already show a luminosity segregation,
with more luminous galaxies being more clustered than faint
objects. At the same time, however, a significant steepening with
luminosity of the shape of their two-point correlation function
for separations <1-2 h-1 Mpc, is observed. This behaviour
is at variance with that at
.
More specifically, Pollo et al. (2006) have shown that
at these epochs galaxies already show a luminosity segregation,
with more luminous galaxies being more clustered than faint
objects. At the same time, however, a significant steepening with
luminosity of the shape of their two-point correlation function
for separations <1-2 h-1 Mpc, is observed. This behaviour
is at variance with that at ![]() .
A similar trend has been
observed at the same redshift by the DEEP2 survey
(Coil et al. 2006). In addition, Meneux et al. (2008) have shown a
positive trend of clustering with stellar mass also at
.
A similar trend has been
observed at the same redshift by the DEEP2 survey
(Coil et al. 2006). In addition, Meneux et al. (2008) have shown a
positive trend of clustering with stellar mass also at ![]() ,
with clear evidence of a stronger evolution of the bias factor for
the most massive galaxies (see also Brown et al. 2008; Wake et al. 2008).
,
with clear evidence of a stronger evolution of the bias factor for
the most massive galaxies (see also Brown et al. 2008; Wake et al. 2008).
Interpreting the evolution in shape and amplitude of
![]() with
respect to luminosity and redshift is particularly interesting in
the context of the halo model for galaxy formation. In this
framework, the observed shape of
with
respect to luminosity and redshift is particularly interesting in
the context of the halo model for galaxy formation. In this
framework, the observed shape of ![]() (or
(or
![]() )
is
interpreted as being composed of the sum of two components: a) the
1-halo term, which dominates on small scales (<1-2 h-1 Mpc
at the current epoch), where correlations are dominated by pairs
of galaxies living within the same dark-matter halo (i.e. in a
group or cluster); b) the 2-halo term on large scales, which is
characterised by pairs of galaxies occupying different dark-matter
haloes (see Cooray & Sheth (2002) for a review).
Zheng et al. (2007) have modelled the luminosity-dependent
)
is
interpreted as being composed of the sum of two components: a) the
1-halo term, which dominates on small scales (<1-2 h-1 Mpc
at the current epoch), where correlations are dominated by pairs
of galaxies living within the same dark-matter halo (i.e. in a
group or cluster); b) the 2-halo term on large scales, which is
characterised by pairs of galaxies occupying different dark-matter
haloes (see Cooray & Sheth (2002) for a review).
Zheng et al. (2007) have modelled the luminosity-dependent
![]() from both the DEEP2 (at
from both the DEEP2 (at ![]() )
and SDSS (at
)
and SDSS (at ![]() )
surveys, within such Halo Occupation Distribution (HOD)
framework. In this way they establish evolutionary connections
between galaxies and dark-matter haloes at these two epochs,
providing a self-consistent scenario in which the growth of the
stellar mass depends on the halo mass. Similar results have been
obtained more recently in a combined analysis of the VVDS-Deep and
SDSS data (Abbas et al. 2009).
)
surveys, within such Halo Occupation Distribution (HOD)
framework. In this way they establish evolutionary connections
between galaxies and dark-matter haloes at these two epochs,
providing a self-consistent scenario in which the growth of the
stellar mass depends on the halo mass. Similar results have been
obtained more recently in a combined analysis of the VVDS-Deep and
SDSS data (Abbas et al. 2009).
1 In this paper we use the first 10 000 redshifts from the zCOSMOS
redshift survey (the ``10K sample'') to further explore these
high-redshift trends of clustering with luminosity and mass based
on a new, independent sample. Although shallower than VVDS-Deep
and DEEP2 (
![]() vs. 24 and 23.5, respectively), zCOSMOS
covers a significantly larger area and samples a volume of
vs. 24 and 23.5, respectively), zCOSMOS
covers a significantly larger area and samples a volume of
![]()
![]() h-1 Mpc to redshift z=1.2. This should
hopefully help reducing the effect of cosmic variance (still
strong for samples this size, Garilli et al. 2008; Stringer et al. 2009),
while providing a better sampling of the high-end tail of the
luminosity and mass functions. However, one main result of this
analysis will be the explicit demonstration of the strength of the
cosmic variance within volumes of this size. The clustering
properties of the zCOSMOS sample in the volume contained within
the redshift range 0.4-1 seem to lie at the extreme high end of
the distribution of fluctuations on these scales, as already
suggested by the angular clustering of the COSMOS data
(McCracken et al. 2007). As we shall see, these results and those
presented in the zCOSMOS series of clustering papers
de la Torre et al. 2009; Porciani et al., in
prep.; Abbas et al., in prep. indicate how cautious
one should be in drawing far-reaching conclusions from the
modelling of current clustering results from deep galaxy surveys.
h-1 Mpc to redshift z=1.2. This should
hopefully help reducing the effect of cosmic variance (still
strong for samples this size, Garilli et al. 2008; Stringer et al. 2009),
while providing a better sampling of the high-end tail of the
luminosity and mass functions. However, one main result of this
analysis will be the explicit demonstration of the strength of the
cosmic variance within volumes of this size. The clustering
properties of the zCOSMOS sample in the volume contained within
the redshift range 0.4-1 seem to lie at the extreme high end of
the distribution of fluctuations on these scales, as already
suggested by the angular clustering of the COSMOS data
(McCracken et al. 2007). As we shall see, these results and those
presented in the zCOSMOS series of clustering papers
de la Torre et al. 2009; Porciani et al., in
prep.; Abbas et al., in prep. indicate how cautious
one should be in drawing far-reaching conclusions from the
modelling of current clustering results from deep galaxy surveys.
A significant part of this paper is dedicated to discussing these cosmic-variance effects in detail, together with the impact of incompleteness on the derived results. This is particularly important when constructing mass-limited subsamples from a magnitude-limited survey, which introduces a mass incompleteness that depends on redshift and stellar mass. The intrinsic scatter in the galaxy mass-luminosity relation determines a progressive loss of faint galaxies with high mass-to-light ratio. We study the effect of this incompleteness on the measured clustering in detail using both the data themselves and mock samples built from the Millennium simulation. At the same time, we explore in quite some detail our ability to characterise measurement errors and the covariance matrix of our data, comparing estimates from the mock samples to those from bootstrap resamplings of the data.
The paper is organised as follows. In Sects. 2 and 3 we describe the zCOSMOS survey and the simulated mock samples used in the analysis, while in Sect. 4 we describe the selection of luminosity- and mass-limited subsamples, discussing extensively the incompleteness related to this operation. In Sect. 5 we describe our clustering estimators, while in Sect. 6 we discuss the observational biases and selection effects in detail, as well as how we account for them and what is their effect on the measured quantities; in Sect. 7 we explore the error budget and how to estimate the covariance properties of our measurements; in Sects. 8 and 9 we present our measurements of clustering as a function of luminosity and mass, respectively; in Sect. 10 we compare these results with those from other surveys and with simple model predictions; finally, in Sect. 11 we place these findings in a broader context and discuss future developments.
Throughout the paper we adopt a cosmology with
![]() ,
,
![]() .
When needed, we also adopt a value
.
When needed, we also adopt a value
![]() for the normalisation of the matter power spectrum;
this is chosen for consistency with the Millennium simulation,
also used for comparison to model predictions. The Hubble constant
is parameterised via h=H0/100 to ease comparison with previous
works. Stellar masses are quoted in unit of h=1. All length
values are quoted in co-moving coordinates.
for the normalisation of the matter power spectrum;
this is chosen for consistency with the Millennium simulation,
also used for comparison to model predictions. The Hubble constant
is parameterised via h=H0/100 to ease comparison with previous
works. Stellar masses are quoted in unit of h=1. All length
values are quoted in co-moving coordinates.
![\begin{figure}\par\includegraphics[width=12cm]{12314f01.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg39.png) |
Figure 1:
Distribution on the sky of the |
| Open with DEXTER | |
2 The zCOSMOS survey data
The zCOSMOS survey (Lilly et al. 2007) is being performed with the VIMOS multi-object spectrograph at the ESO Very Large Telescope (Le Fèvre et al. 2003). Six hundred hours of observation have been allocated to this programme. These are being invested to measure spectra for galaxies in the COSMOS field (Scoville et al. 2007a), targeting: a)
Observations were performed using the
medium-resolution RED grism, corresponding to ![]() and
covering the spectral range 5550-9650 Å. The average error on
the redshift measurements was estimated from the repeated
observations of 632 galaxies and found to be
and
covering the spectral range 5550-9650 Å. The average error on
the redshift measurements was estimated from the repeated
observations of 632 galaxies and found to be ![]() 100 km s-1(Lilly et al. 2009). This corresponds roughly to a radial
distance error of 1 h-1 Mpc. The reduction of the data to the
redshift assignment was carried out independently at two
institutes before a reconciliation process to solve discrepancies.
The quality of each measured redshift was then quantified via a
quality flag that provides us with a confidence level
(see Lilly et al. 2009,2007, for definition). For the
present work, we only use redshifts with flags 1.5-4.5 and
9.3-9.5, corresponding to confidence levels greater than 98%.
100 km s-1(Lilly et al. 2009). This corresponds roughly to a radial
distance error of 1 h-1 Mpc. The reduction of the data to the
redshift assignment was carried out independently at two
institutes before a reconciliation process to solve discrepancies.
The quality of each measured redshift was then quantified via a
quality flag that provides us with a confidence level
(see Lilly et al. 2009,2007, for definition). For the
present work, we only use redshifts with flags 1.5-4.5 and
9.3-9.5, corresponding to confidence levels greater than 98%.
The zCOSMOS survey benefits the large multi-wavelength coverage of the COSMOS field (Capak et al. 2007), which with the latest additions now comprises 30 photometric bands (Ilbert et al. 2009) extending well into the infrared. These include, in particular, accurate K-band and Spitzer-IRAC photometry over the whole area, which have allowed us to derive relevant physical properties as rest-frame luminosity and stellar mass with unprecedented accuracy (Pozzetti et al. 2009; Bolzonella et al. 2009; Zucca et al. 2009).
![\begin{figure}\par\includegraphics[width=12cm]{12314f02.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg43.png) |
Figure 2: Selection boundaries of the different subsamples of the zCOSMOS 10K survey used in this paper. Left: luminosity-redshift selection, which accounts for the average luminosity evolution of galaxies; Right: mass-redshift selection. |
| Open with DEXTER | |
3 Mock survey catalogues
In this paper we make intense use of mock surveys constructed from the Millennium simulation (Springel et al. 2005). This was done a) to understand the effect of our selection criteria on the measured quantities (Sect. 6.3) and b) to estimate the measurement errors and covariance of the data (Sect. 7).
We used two sets of light cones, constructed as explained in
Kitzbichler & White (2007) and Blaizot et al. (2005) by combining
dark-matter halo trees from the Millennium run to the Munich
semi-analytic model of galaxy formation
(De Lucia & Blaizot 2007). The two sets contain 24
![]() deg2 mocks built by Kitzbichler & White (2007) and
40
deg2 mocks built by Kitzbichler & White (2007) and
40 ![]() deg2 mocks built by De Lucia & Blaizot (2007),
which we name KW24 and DLB40, respectively. The main difference
between the two sets, in addition to the different survey area, is
that the DLB40 set contains all galaxies irrespective of any
criteria down to the simulation limit that corresponds roughly to
deg2 mocks built by De Lucia & Blaizot (2007),
which we name KW24 and DLB40, respectively. The main difference
between the two sets, in addition to the different survey area, is
that the DLB40 set contains all galaxies irrespective of any
criteria down to the simulation limit that corresponds roughly to
![]() ,
up to redshift z=1.7, whereas the KW24 set only
contains galaxies brighter than
,
up to redshift z=1.7, whereas the KW24 set only
contains galaxies brighter than ![]() .
This implies that the
DLB40 set allowed us to select in stellar mass down to very low
masses and to test selection effects. The observing strategy of
the zCOSMOS 10K sample was only applied to the KW24 set, allowing
us to do careful error analysis of our measurements.
.
This implies that the
DLB40 set allowed us to select in stellar mass down to very low
masses and to test selection effects. The observing strategy of
the zCOSMOS 10K sample was only applied to the KW24 set, allowing
us to do careful error analysis of our measurements.
The Millennium run contains N=21603 particles of mass
![]() h-1
h-1 ![]() in a cubic box of size
500 h-1 Mpc. The simulation was built with a
in a cubic box of size
500 h-1 Mpc. The simulation was built with a ![]() CDM
cosmological model with
CDM
cosmological model with
![]() ,
,
![]() ,
,
![]() and H0=73 km s-1 Mpc-1.
and H0=73 km s-1 Mpc-1.
4 Luminosity- and mass-selected subsamples
4.1 Luminosity selection
Absolute magnitudes were derived for the 10K galaxies using the code ALF (Zucca et al. 2009; Ilbert et al. 2005), which is based on fitting a spectral energy distribution (SED) to the observed multi-band photometry. There are various sources of uncertainties to take into account (errors on apparent magnitudes, number of available photometric bands, method used, etc.). A direct comparison with absolute magnitudes derived with the independent code ZEBRA (Feldmann et al. 2006) shows consistent estimates with a small dispersion of-2 For our analysis, the goal is to define luminosity-limited samples that are as close as possible to truly volume-limited samples, i.e. with a constant number density. This might be done within a few independent redshift ranges. The size of the redshift slices in which to split the sample has to be chosen as a compromise between two aspects: a) large enough to have sufficient statistics and provide a good measurement of clustering and b) not too large to avoid significant evolution within each redshift bin.
We know, however, that the luminosity of galaxies evolves through the redshift range covered by the zCOSMOS survey (0.2<z<1.1), with a clear change in the characteristic parameters of the LF (Ilbert et al. 2005). This evolution does depend on the morphological/spectral type of the galaxy considered. To be able to select a nearly volume-limited sample within a given redshift interval, we need to take the corresponding evolution into account. This can only be done realistically in a statistical way by looking at the population-averaged evolution of the global LF.
We therefore considered the observed LF measured from the same
data (Zucca et al. 2009) and modelled its change with redshift
as a pure luminosity evolution (i.e. keeping a constant slope
![]() and normalisation factor
and normalisation factor ![]() ), which is a fair
description of the observed behaviour. We find that the
characteristic absolute magnitude M*(z) evolves with redshift
as
), which is a fair
description of the observed behaviour. We find that the
characteristic absolute magnitude M*(z) evolves with redshift
as
| M*(z) = M*0 + A z, | (1) |
where
We therefore defined our luminosity-limited samples by an
effective absolute magnitude cut at z=0,
![]() ,
including all galaxies with
,
including all galaxies with
![]() .
The resulting selection loci for different values of
.
The resulting selection loci for different values of
![]() are plotted over the data in the
luminosity-redshift plane in the left panel of
Fig. 2. As is evident in the figure, the
faintest allowed threshold
are plotted over the data in the
luminosity-redshift plane in the left panel of
Fig. 2. As is evident in the figure, the
faintest allowed threshold
![]() depends on the
redshift range considered, i.e. z= [0.2-0.5],
z= [0.5-0.8], and z= [0.8-1.0]. The details of the
resulting samples are described in Table 1.
depends on the
redshift range considered, i.e. z= [0.2-0.5],
z= [0.5-0.8], and z= [0.8-1.0]. The details of the
resulting samples are described in Table 1.
Table 1: Properties of the luminosity-selected samples.
Table 2: Properties of the mass-selected samples.
| |
Figure 3: The observed relationship between stellar mass and luminosity for galaxies in the 10K sample, within the three redshift ranges studied in this paper. The left panel shows an aspect of the galaxy bimodality, with red galaxies more massive and brighter than blue ones. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f04.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg60.png) |
Figure 4:
Estimate of how the completeness in stellar mass changes
as a function of redshift, due to the survey flux limit
(
|
| Open with DEXTER | |
4.2 Mass selection
Stellar mass has become a quantity routinely measured in recent
years, thanks to surveys with multi-wavelength photometry,
extending to the near-infrared (e.g. Rettura et al. 2006),
although some uncertainties related to the detailed modelling of
stellar evolution remain (Pozzetti et al. 2007). This has made
studies of clustering as a function of stellar mass possible for
large statistical samples. We used stellar masses estimated by
fitting the SED, as sampled by the large multi-band photometry,
with a library of stellar population models based on
Bruzual & Charlot (2003). We used the code Hyperzmass, a modified
version of the photometric redshift code Hyperz
(Bolzonella et al. 2000). The typical error on stellar masses is
![]() 0.2 dex. The method and accuracy of these measurements are
fully described in Bolzonella et al. (2009) and
Pozzetti et al. (2009).
0.2 dex. The method and accuracy of these measurements are
fully described in Bolzonella et al. (2009) and
Pozzetti et al. (2009).
We have thus constructed a set of mass-selected samples, containing galaxies more massive than a given threshold. We chose the same redshift ranges as used for the luminosity-selected samples. The properties of the selected subsamples are summarised in Table 2 and represented in Fig. 2.
4.3 Mass completeness
The flux-limited nature of surveys like zCOSMOS (
![]() )
mean that the lowest-mass samples are affected to varying degrees
by incompleteness related to the scatter in the mass-luminosity
relation (Fig. 3). This introduces a
bias against objects that would be massive enough to enter the
mass-selected samples, but too faint to fulfil the
apparent-magnitude limit of the survey. These missed high
mass-to-light ratio galaxies will be those dominated by
low-luminosity stars, i.e. the red and faint objects. Clearly, if
this is not accounted for in some way, it would inevitably affect
the estimated clustering properties, with respect to a truly
complete, mass-selected sample (Meneux et al. 2008). It is
therefore necessary to understand the effective completeness level
in detail in the stellar mass of the samples that we defined for
our analysis.
)
mean that the lowest-mass samples are affected to varying degrees
by incompleteness related to the scatter in the mass-luminosity
relation (Fig. 3). This introduces a
bias against objects that would be massive enough to enter the
mass-selected samples, but too faint to fulfil the
apparent-magnitude limit of the survey. These missed high
mass-to-light ratio galaxies will be those dominated by
low-luminosity stars, i.e. the red and faint objects. Clearly, if
this is not accounted for in some way, it would inevitably affect
the estimated clustering properties, with respect to a truly
complete, mass-selected sample (Meneux et al. 2008). It is
therefore necessary to understand the effective completeness level
in detail in the stellar mass of the samples that we defined for
our analysis.
Meneux et al. (2008) have used two different methods to explore and
quantify the completeness limit in stellar mass as a function of
redshift. The first is based on the observed scatter in the
mass-luminosity relation, obtained from the data themselves and
extrapolated to fainter fluxes. The second instead makes use of
mock survey samples, under the hypothesis that they provide a
realistic description of the mass-luminosity relation and its
scatter: the DLB40 set of mock survey catalogues that are complete
in stellar mass are ``observed'' under the same conditions as the
real data, i.e. selected at ![]() .
The completeness is then
simply defined, for a given redshift range and mass threshold, as
the ratio of the number of galaxies brighter than the zCOSMOS flux
limit over those at any flux. Interestingly, even if this method
is model-dependent (in particular, on the prescription of galaxy
formation used in the semi-analytic models), this approach leads
to similar completeness limits to the first one. The results of
this second exercise are shown as a function of redshift and mass
threshold and for a flux limit
.
The completeness is then
simply defined, for a given redshift range and mass threshold, as
the ratio of the number of galaxies brighter than the zCOSMOS flux
limit over those at any flux. Interestingly, even if this method
is model-dependent (in particular, on the prescription of galaxy
formation used in the semi-analytic models), this approach leads
to similar completeness limits to the first one. The results of
this second exercise are shown as a function of redshift and mass
threshold and for a flux limit ![]() ,
in
Fig. 4. Completeness is estimated in
narrow redshift ranges (
,
in
Fig. 4. Completeness is estimated in
narrow redshift ranges (
![]() )
for different mass
thresholds
)
for different mass
thresholds
![]() increasing from 108 to
1011.7
increasing from 108 to
1011.7
![]() with a step of
100.01
with a step of
100.01
![]() .
A large fraction of low-mass objects
are clearly missed at high redshift.
.
A large fraction of low-mass objects
are clearly missed at high redshift.
We also add in Fig. 4 the
completeness limit estimated from the observed scatter in the M/L
relation of the data, and defined at each redshift as the lower
boundary,
![]() ,
including above it 95% of the mass
distribution (Pozzetti et al. 2009). It is very encouraging to
notice the very good agreement between this independent estimation
from the data and that based on the DLB40 set of mock catalogues.
This adds confidence in the use of the simulated samples.
Table 3 summarises the completeness estimates
derived from these mock catalogues for each of the 10 zCOSMOS
galaxy samples defined in Table 2. The sample M2.1
shows the strongest incompleteness: 65.1% of the galaxies more
massive than 109
,
including above it 95% of the mass
distribution (Pozzetti et al. 2009). It is very encouraging to
notice the very good agreement between this independent estimation
from the data and that based on the DLB40 set of mock catalogues.
This adds confidence in the use of the simulated samples.
Table 3 summarises the completeness estimates
derived from these mock catalogues for each of the 10 zCOSMOS
galaxy samples defined in Table 2. The sample M2.1
shows the strongest incompleteness: 65.1% of the galaxies more
massive than 109
![]() are fainter than I=22.5at z= [0.5-0.8] and then, not included in our sample.
In Sect. 6.3 we discuss the effects of
this incompleteness on the galaxy clustering
measurement.
are fainter than I=22.5at z= [0.5-0.8] and then, not included in our sample.
In Sect. 6.3 we discuss the effects of
this incompleteness on the galaxy clustering
measurement.
Table 3: The completeness in stellar mass of mass-selected mock subsamples reproducing the properties and selection criteria of our 10K data samples.
5 Estimating the two-point correlation function
The two-point correlation function is the
simplest estimator for quantifying galaxy clustering, because it
is related to the second moment of the galaxy distribution, i.e.
its variance. In practice, it describes the excess probability
![]() of observing a pair of galaxies at a given separation
r, with respect to that of a random distribution
(Peebles 1980). Here we estimate the redshift-space
correlation function
of observing a pair of galaxies at a given separation
r, with respect to that of a random distribution
(Peebles 1980). Here we estimate the redshift-space
correlation function
![]() ,
which allows one to incorporates the
effect of peculiar motions on the pure Hubble recession velocity.
In this case, galaxy separations are split into the tangential and
radial components,
,
which allows one to incorporates the
effect of peculiar motions on the pure Hubble recession velocity.
In this case, galaxy separations are split into the tangential and
radial components, ![]() and
and ![]() (Fisher et al. 1994; Davis & Peebles 1983).
(Fisher et al. 1994; Davis & Peebles 1983).
The real-space correlation function ![]() can be recovered by
projecting
can be recovered by
projecting
![]() along the line of sight, as
along the line of sight, as
For a power-law correlation function,
![]() ,
this integral can be solved
analytically and fitted to the observed
,
this integral can be solved
analytically and fitted to the observed
![]() to find the
best-fitting values of the correlation length
r0 and slope
to find the
best-fitting values of the correlation length
r0 and slope ![]() (e.g. Davis & Peebles 1983). In computing
(e.g. Davis & Peebles 1983). In computing
![]() ,
a finite upper integration limit has to be chosen in
practice. Its value has to be high enough as to include most of
the clustering signal dispersed along the line of sight by
peculiar motion. However, it must not be too high to avoid adding
only noise, which is dominant above a certain
,
a finite upper integration limit has to be chosen in
practice. Its value has to be high enough as to include most of
the clustering signal dispersed along the line of sight by
peculiar motion. However, it must not be too high to avoid adding
only noise, which is dominant above a certain ![]() .
Previous
works (Pollo et al. 2005) have shown that, for similar data, the
best results are obtained with an integration limit
.
Previous
works (Pollo et al. 2005) have shown that, for similar data, the
best results are obtained with an integration limit
![]() between 20 and 40 h-1 Mpc. Our tests show
that the scatter in the recovered
between 20 and 40 h-1 Mpc. Our tests show
that the scatter in the recovered
![]() is obtained using the
lowest value in this range. This can introduce a 5-10%
underestimate in the recovered large-scale amplitude, which can be
accounted for when fitting a model to
is obtained using the
lowest value in this range. This can introduce a 5-10%
underestimate in the recovered large-scale amplitude, which can be
accounted for when fitting a model to
![]() .
In the following, we
in general use
.
In the following, we
in general use
![]() h-1 Mpc and show examples
of how the amplitude is biased by this choice for the real data.
h-1 Mpc and show examples
of how the amplitude is biased by this choice for the real data.
To estimate
![]() from each galaxy sample, we used
the standard estimator of Landy & Szalay (1993):
from each galaxy sample, we used
the standard estimator of Landy & Szalay (1993):
where
6 Observational biases and selection effects
6.1 Correction of VIMOS angular footprint and varying sampling
To properly estimate the correlation function from the 10K zCOSMOS data, we need to correct for its spatial sampling rate, which is on average
![\begin{figure}\par\includegraphics[width=12cm]{12314f05.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg77.png) |
Figure 5:
Overall radial distribution of the zCOSMOS 10K sample,
compared to three different smoothed distributions. These are
obtained by filtering the observed data with a Gaussian kernel of
increasing |
| Open with DEXTER | |
We tested three different algorithms to correct for the angular selection function of the survey and obtained comparable results. Other weighting schemes use in particular the angular correlation functions of the 10K sample and the photometric catalogue to correct for the nonuniform spatial sampling rate. These methods are discussed in the parallel clustering analyses by de la Torre et al. (2009) and Porciani et al. (in preparation). In the latter paper in particular, comparative tests of the three algorithms are presented.
Since the subsamples analysed in this work are essentially volume-limited (above the luminosity/mass completeness limits), we did not need to apply any further minimum-variance weighting scheme (as e.g. the J3 weighting, Fisher et al. 1994). This is normally necessary for purely flux-limited surveys in which the selection function varies significantly as a function of redshift, such that different parts of the volume are sampled by galaxies with different luminosities and number densities (e.g. Li et al. 2006).
6.2 Construction of reference random samples
A significant source of uncertainty that we encountered in estimating two-point functions from our 10K subsamples is related to the construction of the random sample and in particular to its redshift distribution. We soon realised that the strongly clustered nature of the COSMOS field along the line of sight, with several dominating structures at different redshifts, required some particular care so as not to generate systematic biases in the random sample. These superclusters are already evident as vertical stripes in Fig. 2 and even more clearly so in the redshift histogram of Fig. 5. We point out the big ``walls'' at z=0.35, 0.75, and 0.9, which are also clearly identified by the density field reconstruction of Kovac et al. (2009).
![\begin{figure}\par\includegraphics[width=12cm]{12314f06.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg78.png) |
Figure 6:
The radial distribution of the luminosity-selected sample
L2.1 compared to a smoothed curved (with a kernel of
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f07.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg79.png) |
Figure 7:
The effect of stellar mass incompleteness
on the measured
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f08.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg80.png) |
Figure 8:
Ratio of the diagonal errors on
|
| Open with DEXTER | |
A standard way to generate a random redshift coordinate accounting
for the radial selection function of the data uses a
Gaussian-filtered version of the data themselves. This is normally
obtained using smoothing kernels with a dispersion ![]() (in
co-moving coordinates) in the range 150-250 h-1 Mpc. The
results of applying this technique to the current 10K data are
shown in Fig. 5. One notes how for smoothing
scales of 150 and 250 h-1 Mpc, the curves still retain memory
of the two largest galaxy fluctuations. These are only erased
when a very strong smoothing filter (450 h-1 Mpc) is adopted.
However, in this case the smoothed curve is unable to correctly
follow the global shape of the distribution, overestimating the
number density in the lowest and highest redshift ranges. The
situation for our specific analysis, however, is somewhat simpler
than this general case. Our luminosity-limited or mass-limited
samples are in principle ``volume-limited'', i.e. samples that -
if properly selected - should have a constant density within the
specific redshift bin. One such case is shown in the zoom of
Fig. 6, where the redshift
distribution in the range
z=[0.5,0.8] is plotted.
(in
co-moving coordinates) in the range 150-250 h-1 Mpc. The
results of applying this technique to the current 10K data are
shown in Fig. 5. One notes how for smoothing
scales of 150 and 250 h-1 Mpc, the curves still retain memory
of the two largest galaxy fluctuations. These are only erased
when a very strong smoothing filter (450 h-1 Mpc) is adopted.
However, in this case the smoothed curve is unable to correctly
follow the global shape of the distribution, overestimating the
number density in the lowest and highest redshift ranges. The
situation for our specific analysis, however, is somewhat simpler
than this general case. Our luminosity-limited or mass-limited
samples are in principle ``volume-limited'', i.e. samples that -
if properly selected - should have a constant density within the
specific redshift bin. One such case is shown in the zoom of
Fig. 6, where the redshift
distribution in the range
z=[0.5,0.8] is plotted.
An alternative way to generate the radial distribution of the random sample is to integrate the galaxy LF in steps along the redshift direction, computing at each step a value for the density of galaxies expected at that redshifts. Ideally, the LF can be measured from the sample itself and would include any detected evolution of its parameters. This is what we did here, using the evolving LF parameters presented in the companion dedicated paper (Zucca et al. 2009). The dashed red line in Fig. 6 shows the result one obtains if smoothing with a kernel of 450 h-1 Mpc, compared to the one obtained from the integration of the LF. The latter is fully consistent with what is expected from a truly volume-limited sample with the given selection criteria, with the number of objects increasing as the square of the radial co-moving distance.
6.3 Effect of mass incompleteness on

As discussed in
Sect. 4.3 when we constructed our
mass-limited samples, a fraction of the galaxies more massive than
the formal mass threshold are in fact lost because of the limiting
The ratio of these two estimates (``true'' over
``observed'') averaged over the 40 mock catalogues is
shown in Fig. 7. For a mass
selection that is 100% complete within the given redshift bin, we
would measure
![]() at all separations. We can see
that the only mass range for which this is strictly happening at
any redshift is the one with
at all separations. We can see
that the only mass range for which this is strictly happening at
any redshift is the one with
![]() .
For lower
mass samples, we see a clear reduction of the clustering
amplitude. However, we can also see that, for most samples, the
shape of
.
For lower
mass samples, we see a clear reduction of the clustering
amplitude. However, we can also see that, for most samples, the
shape of
![]() is distorted mainly only below <1 h-1 Mpc.
Above this scale, the mass incompleteness introduces an amplitude
reduction up to
is distorted mainly only below <1 h-1 Mpc.
Above this scale, the mass incompleteness introduces an amplitude
reduction up to ![]() 20% in the worst cases. This will have to
be considered when comparing our measurements with models
(although keeping in mind that these estimates come from simulated
data, not from real observations). For general comparisons,
however, the amount of amplitude reduction of
20% in the worst cases. This will have to
be considered when comparing our measurements with models
(although keeping in mind that these estimates come from simulated
data, not from real observations). For general comparisons,
however, the amount of amplitude reduction of
![]() is typically
negligible on scales larger than
is typically
negligible on scales larger than ![]() 1 h-1 Mpc, given the
statistical errors of the data measurements.
1 h-1 Mpc, given the
statistical errors of the data measurements.
7 Systematic and statistical errors on correlation estimates
The derivation of realistic errors on the galaxy correlation
function has been the subject of debate since its early
measurements (see e.g. Bernstein 1994). In particular, it
is well known that the measured values of the two-point
correlation function are not independent on different scales. This
means that, the bins of
![]() have a degree of correlation among
them, which needs to be taken into account when fitting a model to
the observed values. This can be done if we are able to
reconstruct the
have a degree of correlation among
them, which needs to be taken into account when fitting a model to
the observed values. This can be done if we are able to
reconstruct the ![]() covariance (or correlation) matrix of
the N bins (Fisher et al. 1994).
covariance (or correlation) matrix of
the N bins (Fisher et al. 1994).
In a recent paper,
Norberg et al. (2009) compare in detail three different methods for
estimating the covariance matrix of a given set of measurements.
These use a) the ensemble variance from a set of mock catalogues,
reproducing as accurately as possible the clustering properties
and selection function of the real data; b) a set of bootstrap resamplings of the volume containing the data; and c) a
so-called jack-knife subset of volumes of the survey. In
this latest case, the survey volume is divided into ![]() subvolumes and the statistics under study recomputed each time
excluding one of the subparts. In the ``block-wise'' incarnation
of the bootstrap technique (Porciani & Giavalisco 2002, method
``b''), instead, N subvolumes are selected each
time with repetition, i.e. excluding some of them, but
counting two or more times some others as to always get a global
sample with the same total volume. We note, however, that there
are historically two possible ways of resampling internally the
data set. The classical ``old'' bootstrap (Ling et al. 1986)
entailed boot-strapping the sample ``galaxy-by-galaxy''. This
means each time randomly picking a sample of
subvolumes and the statistics under study recomputed each time
excluding one of the subparts. In the ``block-wise'' incarnation
of the bootstrap technique (Porciani & Giavalisco 2002, method
``b''), instead, N subvolumes are selected each
time with repetition, i.e. excluding some of them, but
counting two or more times some others as to always get a global
sample with the same total volume. We note, however, that there
are historically two possible ways of resampling internally the
data set. The classical ``old'' bootstrap (Ling et al. 1986)
entailed boot-strapping the sample ``galaxy-by-galaxy''. This
means each time randomly picking a sample of ![]() galaxies among
our data set of
galaxies among
our data set of ![]() galaxies, allowing repetitions. In this way,
within one bootstrap realisation a galaxy can be selected more
than once, while some others are never selected. This technique
has been shown to generally lead to some underestimation of the
diagonal errors (Fisher et al. 1994). Here we also directly test
this aspect.
galaxies, allowing repetitions. In this way,
within one bootstrap realisation a galaxy can be selected more
than once, while some others are never selected. This technique
has been shown to generally lead to some underestimation of the
diagonal errors (Fisher et al. 1994). Here we also directly test
this aspect.
The advantage of using mock samples is that, under the assumption that these are a realistic realisation of the real data, they allow us to obtain a true ensemble average and standard deviation from samples with the same size as the data sample, including both Poissonian noise and cosmic variance. Unfortunately, the covariance properties derived from mock samples are not necessarily a good description of those of the real data, thus making the use of the derived covariance matrix (e.g. in model fitting) doubtful. Conversely, depending on the sample size, jack-knife or volume-bootstrap covariance matrices can exacerbate the peculiarities of some subregions, again not adequately representing the true covariance properties of the data.
| |
Figure 9: -2 Mean of the 24 correlation matrix derived resampling the galaxies of eack KW24 mocks ( left), or resampling 8 equal subvolumes ( center). These are compared to the correlation matrix derived directly from the KW24 mocks ( right). The redshift range considered here is z= [0.5-0.8]. The averaging over the 24 realisations of the 2 left matrices suppress the negative off-diagonal terms, which are sometimes present for a given mock catalogues. Correlation coefficients are then colour-coded from 0 to 1. |
| Open with DEXTER | |
For the present investigation, we put
considerable effort in understanding how to best estimate a
sensible covariance matrix for our
![]() measurements. The
available mock samples were crucial for allowing us to perform
direct comparisons of the performances of the different
techniques. After some initial attempts, we excluded the jack-knife method because of the limited size of the survey
volume. We then directly compared the covariance matrices derived
through the bootstrap technique and from the KW24 mock catalogues.
For the bootstrap method, we decided to directly test how galaxy-
and volume-bootstrap were performing. We concentrated on the
redshift range z= [0.5-0.8] by selecting simulated galaxies
brighter than
measurements. The
available mock samples were crucial for allowing us to perform
direct comparisons of the performances of the different
techniques. After some initial attempts, we excluded the jack-knife method because of the limited size of the survey
volume. We then directly compared the covariance matrices derived
through the bootstrap technique and from the KW24 mock catalogues.
For the bootstrap method, we decided to directly test how galaxy-
and volume-bootstrap were performing. We concentrated on the
redshift range z= [0.5-0.8] by selecting simulated galaxies
brighter than
![]() .
After computing the
correlation function
.
After computing the
correlation function
![]() for all 24 mock samples, we
constructed for each of them a) 100 galaxy-galaxy-bootstrap
samples and b) 100 volume-volume-bootstrap samples. In the latter
case, we considered 8 equal subvolumes, defined as redshift slices
within the redshift range considered. The number of subvolumes was
chosen as the best compromise between having enough of them and
not having volumes that were too small. With this choice, their
volume is
for all 24 mock samples, we
constructed for each of them a) 100 galaxy-galaxy-bootstrap
samples and b) 100 volume-volume-bootstrap samples. In the latter
case, we considered 8 equal subvolumes, defined as redshift slices
within the redshift range considered. The number of subvolumes was
chosen as the best compromise between having enough of them and
not having volumes that were too small. With this choice, their
volume is ![]()
![]() for the samples
with
for the samples
with
![]() and
and
![]() and
and
![]()
![]() for
for
![]() .
The
two bootstrap techniques led to a total of 4800 samples and
corresponding estimates of
.
The
two bootstrap techniques led to a total of 4800 samples and
corresponding estimates of
![]() .
We then calculated the
covariance (and correlation) matrices for each of these two cases,
along with the one derived from the correlation function of the 24
mocks themselves.
.
We then calculated the
covariance (and correlation) matrices for each of these two cases,
along with the one derived from the correlation function of the 24
mocks themselves.
In Fig. 8 we compare the standard
deviations derived from the two bootstrap techniques, to those
derived from the 24 mocks. In each case, these values correspond
by definition to the square root of the diagonal elements of the
covariance matrix. In the plot we show the mean (over the 24
mocks) of the ratio of
![]() from the bootstrap to the
``true'' one from the ensemble of mock surveys. This shows
clearly how the rms values obtained with the
single-galaxy-bootstrap grossly underestimate the true variance,
up to one order of magnitude on large scales. Bootstrapping by
volumes produces a better result, providing a realistic
estimate of
from the bootstrap to the
``true'' one from the ensemble of mock surveys. This shows
clearly how the rms values obtained with the
single-galaxy-bootstrap grossly underestimate the true variance,
up to one order of magnitude on large scales. Bootstrapping by
volumes produces a better result, providing a realistic
estimate of
![]() between 0.1 and 1 h-1 Mpc, and a
20-25% underestimate on larger scales.
between 0.1 and 1 h-1 Mpc, and a
20-25% underestimate on larger scales.
Each element of the the correlation matrix rij is obtained
from the corresponding element of the covariance matrix
![]() as
as
![]() .
By definition, the off-diagonal terms of the
correlation matrix will then range between -1 and 1, indicating
the degree of correlation between different scales of the function
.
By definition, the off-diagonal terms of the
correlation matrix will then range between -1 and 1, indicating
the degree of correlation between different scales of the function
![]() .
Considering the redshift range z= [0.5-0.8], we
show in Fig. 9 the mean of the 24
correlation matrices derived by resampling the galaxies
(left panel) or by resampling 8 equal subvolumes (centre), 100
times each. These are compared to the correlation matrix directly
derived from the 24 mocks (right panel). The first case shows a
mainly diagonal correlation matrix where off-diagonal terms are
mostly noise. In the second case they instead decrease smoothly
from 1 to 0 as a function of bin separation. The matrix derived
from the 24 mocks shows high correlation on all scales.
.
Considering the redshift range z= [0.5-0.8], we
show in Fig. 9 the mean of the 24
correlation matrices derived by resampling the galaxies
(left panel) or by resampling 8 equal subvolumes (centre), 100
times each. These are compared to the correlation matrix directly
derived from the 24 mocks (right panel). The first case shows a
mainly diagonal correlation matrix where off-diagonal terms are
mostly noise. In the second case they instead decrease smoothly
from 1 to 0 as a function of bin separation. The matrix derived
from the 24 mocks shows high correlation on all scales.
Table 4: The five main eigenvalules of the correlation matrix derived with the bootstrap resampling of galaxies (first column) and subvolumes (Col. 2), and from the ensemble variance of the 24 mocks (Col. 3).
In order to directly compare the properties of the correlation
matrices derived with the 3 methods, we compute the principal
components and the amplitudes of the corresponding eigenvalues
![]() (i= 1-12) for each of the 24+24+1 matrices. The
sum of the eigenvalues of a correlation matrix is always equal to
its dimension, i.e. 12 in our case. We report in
Table 4 the values of the five main eigenvalues
obtained with the 24 mocks (first column) compared to the averages
over the 24 mocks of those obtained with the two resampling
methods. The numbers show that the correlation matrix derived from
the 24 mocks essentially contains four principal components and is
mostly dominated by one of them. This indicates a strong
correlation in the data. The bootstrap matrices, instead, show
more than five non-negligible components, with the fifth one the
same order of magnitude as the second in the mock matrix. This
implies a lower correlation. We note, however, that volume
resampling tends to produce a matrix whose structure is closer to
that of the mocks, with 1-2 dominant components. This is another
indication of how volume-bootstrapping, although not perfectly
reproducing the intrinsic covariance properties of the sample,
better estimates the variance and correlation in the data than
does a galaxy-galaxy-bootstrap.
(i= 1-12) for each of the 24+24+1 matrices. The
sum of the eigenvalues of a correlation matrix is always equal to
its dimension, i.e. 12 in our case. We report in
Table 4 the values of the five main eigenvalues
obtained with the 24 mocks (first column) compared to the averages
over the 24 mocks of those obtained with the two resampling
methods. The numbers show that the correlation matrix derived from
the 24 mocks essentially contains four principal components and is
mostly dominated by one of them. This indicates a strong
correlation in the data. The bootstrap matrices, instead, show
more than five non-negligible components, with the fifth one the
same order of magnitude as the second in the mock matrix. This
implies a lower correlation. We note, however, that volume
resampling tends to produce a matrix whose structure is closer to
that of the mocks, with 1-2 dominant components. This is another
indication of how volume-bootstrapping, although not perfectly
reproducing the intrinsic covariance properties of the sample,
better estimates the variance and correlation in the data than
does a galaxy-galaxy-bootstrap.
![\begin{figure}\par\includegraphics[width=12cm]{12314f10.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg102.png) |
Figure 10:
Projected correlation function
|
| Open with DEXTER | |
These experiments are extended and further discussed in our
parallel accompanying papers, in particular Porciani et al. (in
preparation). The bottom-line result of our extensive
investigations is that a volume-bootstrap provides a good enough
reconstruction of the intrinsic covariance matrix of the data set,
if enough resamplings are used. This is obtained at the expense of
a slightly less accurate account of cosmic variance on large scale
than what can be obtained from the scatter among mock samples,
where wavelengths longer than the survey size can be sampled.
However, we have shown (Fig. 8) that this
effect on scales ![]() 10 h-1 Mpc is limited to
10 h-1 Mpc is limited to ![]() 20%.
20%.
8 Dependence of galaxy clustering on luminosity
8.1 Luminosity dependence at fixed redshift
Figure 10 shows the projected correlation
function
![]() estimated for our nine luminosity-selected
subsamples at different redshifts. Error bars correspond to the
estimated for our nine luminosity-selected
subsamples at different redshifts. Error bars correspond to the
![]() dispersion provided by 200 volume-bootstrap resamplings,
as extensively discussed in Sect. 7.
dispersion provided by 200 volume-bootstrap resamplings,
as extensively discussed in Sect. 7.
No clear dependence on luminosity is observed within any of the
three redshift ranges. Also, in the shape of
![]() ,
there is some
hint of the usual ``shoulder'', i.e. a change in slope around
1 h-1 Mpc, but no clear separation between the
expected 1-halo term on small scales and the 2-halo
component above this scale (see the Introduction for definitions).
In particular, in the intermediate-redshift bin, all subsamples
show a rather flat large-scale slope, with no evidence of the
usual breakdown above
,
there is some
hint of the usual ``shoulder'', i.e. a change in slope around
1 h-1 Mpc, but no clear separation between the
expected 1-halo term on small scales and the 2-halo
component above this scale (see the Introduction for definitions).
In particular, in the intermediate-redshift bin, all subsamples
show a rather flat large-scale slope, with no evidence of the
usual breakdown above ![]() 2 h-1 Mpc.
2 h-1 Mpc.
| |
Figure 11:
Iso-correlation contours of
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f12.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg104.png) |
Figure 12:
Sensitivity of the projected function
|
| Open with DEXTER | |
To try to understand the origin of the observed flat shape, it is
interesting to look directly at the contour plots of the
bi-dimensional redshift-space correlation function
![]() .
These are shown in Fig. 11 for the three
luminosity-selected subsamples L1.4, L2.2 and L3.1 (see
Table 1 for definitions), which include galaxies
brighter than
.
These are shown in Fig. 11 for the three
luminosity-selected subsamples L1.4, L2.2 and L3.1 (see
Table 1 for definitions), which include galaxies
brighter than
![]() .
The three contour
plots show some interesting features. First, one clearly notices
the much stronger distortion along the line of sight
.
The three contour
plots show some interesting features. First, one clearly notices
the much stronger distortion along the line of sight ![]() ,
in the
central panel. At the same time,
a much more extended signal is
also observed along the perpendicular direction
,
in the
central panel. At the same time,
a much more extended signal is
also observed along the perpendicular direction ![]() in the same
redshift range. It is tempting to interpret both these effects as
produced in some way by the two dominating structures that we
showed in Fig. 6. The excess
signal along the line of sight is very plausibly due to the
distortions by ``Fingers of God'', due to an anomalous number of
virialised systems (groups and clusters) within these structures.
At the same time, the extension along
in the same
redshift range. It is tempting to interpret both these effects as
produced in some way by the two dominating structures that we
showed in Fig. 6. The excess
signal along the line of sight is very plausibly due to the
distortions by ``Fingers of God'', due to an anomalous number of
virialised systems (groups and clusters) within these structures.
At the same time, the extension along ![]() indicates that there
is also an excess of pairs perpendicular to the line of sight,
with respect to an isotropic distribution. In fact, we know
(Scoville et al. 2007b; Guzzo et al. 2007) that the large-scale structure
at
indicates that there
is also an excess of pairs perpendicular to the line of sight,
with respect to an isotropic distribution. In fact, we know
(Scoville et al. 2007b; Guzzo et al. 2007) that the large-scale structure
at
![]() extends over a large part of the COSMOS area.
This evidently biases the observed number of pairs along
extends over a large part of the COSMOS area.
This evidently biases the observed number of pairs along ![]() ,
for simple geometrical reasons. We cannot exclude that part of the
large-scale compression observed in
,
for simple geometrical reasons. We cannot exclude that part of the
large-scale compression observed in
![]() is also
generated by an excess of galaxy infall onto this structure, thus
producing what is known as the Kaiser effect
(Kaiser 1987). This effect is proportional to the growth
of structure (see e.g. Guzzo et al. 2008, for a recent direct
estimate at similar redshift) and can be extracted when the
underlying clustering can be assumed to be isotropic. In this case
it is in practice impossible to disentangle this dynamical
distortion from the geometrical anisotropy generated by having one
dominating structure elongated perpendicular to the line of sight.
is also
generated by an excess of galaxy infall onto this structure, thus
producing what is known as the Kaiser effect
(Kaiser 1987). This effect is proportional to the growth
of structure (see e.g. Guzzo et al. 2008, for a recent direct
estimate at similar redshift) and can be extracted when the
underlying clustering can be assumed to be isotropic. In this case
it is in practice impossible to disentangle this dynamical
distortion from the geometrical anisotropy generated by having one
dominating structure elongated perpendicular to the line of sight.
The flatter shape in
![]() in Fig. 10 is also consistent
with the overdense samples of Abbas & Sheth (2007), who notice not only a higher amplitude
for the most overdense (10% and 30%) samples of mock and SDSS galaxies,
but also a flattening in the correlation function compared to the full sample.
This is another line of evidence favouring the hypothesis that the zCOSMOS field is
centred on an overdensity.
in Fig. 10 is also consistent
with the overdense samples of Abbas & Sheth (2007), who notice not only a higher amplitude
for the most overdense (10% and 30%) samples of mock and SDSS galaxies,
but also a flattening in the correlation function compared to the full sample.
This is another line of evidence favouring the hypothesis that the zCOSMOS field is
centred on an overdensity.
The plots of Fig. 11 also explicitly show
the reasons for our choice of
![]() h-1 Mpc as
the upper integration limit in computating
h-1 Mpc as
the upper integration limit in computating
![]() ,
a value that
provides a reasonable compromise between including most of the
signal and excluding the noisiest regions in the upper part the
diagrams. In the central redshift bin, however, some real
clustering power may still be present above this scale, for small
,
a value that
provides a reasonable compromise between including most of the
signal and excluding the noisiest regions in the upper part the
diagrams. In the central redshift bin, however, some real
clustering power may still be present above this scale, for small
![]() 's. In Fig. 12 we show directly how
's. In Fig. 12 we show directly how
![]() changes, when
changes, when
![]() is extended from 20 to
30 h-1 Mpc. We see that, somewhat counter
intuitively, below 1 h-1 Mpc, no extra amplitude is
gained, while - as indicated by the mock experiments (see
Sect. 5) - the scatter is increased.
Conversely, one can see the slight scale-dependent bias on the
amplitude at larger separations, which gets up to
is extended from 20 to
30 h-1 Mpc. We see that, somewhat counter
intuitively, below 1 h-1 Mpc, no extra amplitude is
gained, while - as indicated by the mock experiments (see
Sect. 5) - the scatter is increased.
Conversely, one can see the slight scale-dependent bias on the
amplitude at larger separations, which gets up to ![]() 10% at
15 h-1 Mpc when increasing
10% at
15 h-1 Mpc when increasing
![]() .
.
8.2 Redshift evolution at fixed (evolving) luminosity
In Sect. 4.1 we discussed how our luminosity selection was devised such as to account for the average evolution in the luminosity of galaxies, assuming this to be the dominant effect in modifying the mean density of objects at any given luminosity. Under this assumption, it is then interesting to test how
9 Dependence of galaxy clustering on stellar mass
The relation of clustering properties to galaxy stellar masses is in principle more informative and straightforward for interpreting because stellar mass is a more fundamental physical parameter than luminosity.
9.1 Mass dependence at fixed redshift
Also in the case of stellar mass dependence, it is interesting to look at the shape of the full correlation function
![\begin{figure}\par\includegraphics[width=12cm]{12314f13.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg107.png) |
Figure 13:
Evolution of the projected function
|
| Open with DEXTER | |
| |
Figure 14:
Example of full redshift-space correlation function
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f15.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg109.png) |
Figure 15:
The projected correlation function
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f16.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg110.png) |
Figure 16:
Evolution of the projected function
|
| Open with DEXTER | |
Figure 15 shows the projected correlation function
![]() of the 10 mass-selected samples. The plotted points are
not corrected for the residual stellar mass incompleteness (see
Sect. 6.3). Errors are estimated as in the
luminosity case using 200 bootstrap resamplings of 8 equal
subvolumes of each data set. The figure shows a weak mass
dependence of clustering in the low- and high-redshift bins, in
particular at small separations. At the same time, a strong
dependence at all separations is evident in the
intermediate-redshift slice. There, the slope of
of the 10 mass-selected samples. The plotted points are
not corrected for the residual stellar mass incompleteness (see
Sect. 6.3). Errors are estimated as in the
luminosity case using 200 bootstrap resamplings of 8 equal
subvolumes of each data set. The figure shows a weak mass
dependence of clustering in the low- and high-redshift bins, in
particular at small separations. At the same time, a strong
dependence at all separations is evident in the
intermediate-redshift slice. There, the slope of
![]() remains
extremely flat out to the largest explored scales, even more
strongly than in the luminosity-selected cases. Finally, in the
low- and high-redshift bins there is evidence of a
steeper ``1-halo term'' contribution at
remains
extremely flat out to the largest explored scales, even more
strongly than in the luminosity-selected cases. Finally, in the
low- and high-redshift bins there is evidence of a
steeper ``1-halo term'' contribution at
![]() h-1 Mpc (with no clear indication of an evolution in
redshift of the transition scale to the 2-halo term). Conversely,
the central redshift range seems to be characterised by the same,
flat power-law shape down to 0.2 h-1 Mpc, where a sudden
steepening is then observed. The slope below 0.2 h-1 Mpc
seems to depend directly on the limiting mass, with more massive
galaxies showing a steeper correlation function. In summary, no
clear overall trend can be shown among the three redshift ranges,
with the central volume again displaying peculiar clustering
properties that apparently dominate any possible cosmological
effect.
h-1 Mpc (with no clear indication of an evolution in
redshift of the transition scale to the 2-halo term). Conversely,
the central redshift range seems to be characterised by the same,
flat power-law shape down to 0.2 h-1 Mpc, where a sudden
steepening is then observed. The slope below 0.2 h-1 Mpc
seems to depend directly on the limiting mass, with more massive
galaxies showing a steeper correlation function. In summary, no
clear overall trend can be shown among the three redshift ranges,
with the central volume again displaying peculiar clustering
properties that apparently dominate any possible cosmological
effect.
9.2 Clustering evolution at fixed stellar mass
It is also interesting to directly compare the evolution of
![\begin{figure}\par\includegraphics[width=12cm]{12314f17.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg114.png) |
Figure 17:
The measured projected function
|
| Open with DEXTER | |
10 Comparison with independent measurements and models
10.1 Redshift evolution of

An accurate ![]() reference measurement of
reference measurement of
![]() as a
function of stellar mass has been obtained by the SDSS
(Li et al. 2006). Meneux et al. (2008) do find evidence for
evolution of the amplitude of
as a
function of stellar mass has been obtained by the SDSS
(Li et al. 2006). Meneux et al. (2008) do find evidence for
evolution of the amplitude of
![]() for galaxies less massive
than 1010.5
for galaxies less massive
than 1010.5
![]() ,
when comparing this to the
measurements from VVDS-Deep at
,
when comparing this to the
measurements from VVDS-Deep at ![]() .
The SDSS and zCOSMOS
stellar masses were derived with the same initial mass function
(Chabrier 2003) and normalised to h=1. They are
directly comparable. The SDSS clustering measurements were
obtained within differential stellar mass ranges
(Li et al. 2006), while ours correspond to galaxies that are
more massive than a given threshold. However, from
Fig. 2 we see that the zCOSMOS sample
includes a very small number of galaxies that are more massive
than 1011
.
The SDSS and zCOSMOS
stellar masses were derived with the same initial mass function
(Chabrier 2003) and normalised to h=1. They are
directly comparable. The SDSS clustering measurements were
obtained within differential stellar mass ranges
(Li et al. 2006), while ours correspond to galaxies that are
more massive than a given threshold. However, from
Fig. 2 we see that the zCOSMOS sample
includes a very small number of galaxies that are more massive
than 1011
![]() ,
due to the much smaller volume
than for the SDSS. Any of our mass-selected samples has
therefore, in practice, an upper bound at this value of mass. This
implies that we can coherently compare two of the SDSS
measurements of
,
due to the much smaller volume
than for the SDSS. Any of our mass-selected samples has
therefore, in practice, an upper bound at this value of mass. This
implies that we can coherently compare two of the SDSS
measurements of
![]() (for their galaxy samples with stellar
masses in the ranges [10.0-10.5] and [10.5-11.0]) to those from
our samples M3.1 and M3.2, which include galaxies more massive
than 1010 and
1010.5
(for their galaxy samples with stellar
masses in the ranges [10.0-10.5] and [10.5-11.0]) to those from
our samples M3.1 and M3.2, which include galaxies more massive
than 1010 and
1010.5
![]() ,
,
respectively, within the redshift range z= [0.8-1.0].
This comparison (Fig. 17) does not show
a clear evolution with redshift. For both samples, the large-scale
amplitude of
![]() is virtually the same as in the local SDSS
samples. Considering a simple evolution of structures, this
implies that the bias for galaxies more massive than
1010
is virtually the same as in the local SDSS
samples. Considering a simple evolution of structures, this
implies that the bias for galaxies more massive than
1010
![]() has evolved significantly between
has evolved significantly between
![]() and today, as to keep their apparent clustering
amplitude substantially unchanged. This implies in practice that
the bias b(z) must evolve in such a way that
and today, as to keep their apparent clustering
amplitude substantially unchanged. This implies in practice that
the bias b(z) must evolve in such a way that
![]() ,
where D(z) is the linear growth rate of density
fluctuations. In the standard model, this implies that, at the
approximate mean redshifts of our redshift bins,
z=0.35, 0.75,
0.9, the bias of massive galaxies must have been, respectively,
1.2, 1.44, and 1.53 times its value at the current epoch.
Meneux et al. (2008) observed the same effect at
,
where D(z) is the linear growth rate of density
fluctuations. In the standard model, this implies that, at the
approximate mean redshifts of our redshift bins,
z=0.35, 0.75,
0.9, the bias of massive galaxies must have been, respectively,
1.2, 1.44, and 1.53 times its value at the current epoch.
Meneux et al. (2008) observed the same effect at
![]() in the VVDS data but only for galaxies
more massive than
in the VVDS data but only for galaxies
more massive than ![]() 1010.5
1010.5
![]() ,
with
lower-mass objects showing a weaker bias evolution. A lack of any
evolution of the clustering of the most massive galaxies was also
noticed in the NDWFS (Brown et al. 2008) and 2SLAQ surveys
(Wake et al. 2008).
,
with
lower-mass objects showing a weaker bias evolution. A lack of any
evolution of the clustering of the most massive galaxies was also
noticed in the NDWFS (Brown et al. 2008) and 2SLAQ surveys
(Wake et al. 2008).
![\begin{figure}\par\includegraphics[width=12cm]{12314f18.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg117.png) |
Figure 18: Direct comparison of the dependence of clustering on stellar mass in the VVDS-Deep and zCOSMOS samples, over a similar redshift range. |
| Open with DEXTER | |
10.2 Observed and predicted shape of
 at 0.5<z<1
at 0.5<z<1
The only available
measurement of clustering as a function of stellar mass at
redshifts comparable to those explored by our sample comes from
the VVDS-Deep survey (Meneux et al. 2008) at 0.5<z<1.2.
VVDS-Deep goes 1.5 magnitude deeper (although over a smaller area
of ![]() 0.5 deg2), which allows the analysis to be extended
beyond z=1. To provide a qualitative, yet meaningful comparison
of these two data sets, we can recompute the correlation function
for the 10K data within the widest usable redshift range
overlapping with the VVDS interval, i.e. [0.5-1.0]. We applied
the same stellar mass selection limits, keeping in mind the
residual incompleteness that will affect the highest redshift part
of the sample. The result is shown in
Fig. 18, where the VVDS and zCOSMOS
mass-selected samples are directly compared. The difference in
shape and amplitude in the
0.5 deg2), which allows the analysis to be extended
beyond z=1. To provide a qualitative, yet meaningful comparison
of these two data sets, we can recompute the correlation function
for the 10K data within the widest usable redshift range
overlapping with the VVDS interval, i.e. [0.5-1.0]. We applied
the same stellar mass selection limits, keeping in mind the
residual incompleteness that will affect the highest redshift part
of the sample. The result is shown in
Fig. 18, where the VVDS and zCOSMOS
mass-selected samples are directly compared. The difference in
shape and amplitude in the
![]() derived from the two data sets
is rather striking. The zCOSMOS points show in general a much
flatter relation than those from the VVDS. The amplitudes for a
given mass selection also seem to be incompatible at several
standard deviations between the two samples, especially above
1 h-1 Mpc.
derived from the two data sets
is rather striking. The zCOSMOS points show in general a much
flatter relation than those from the VVDS. The amplitudes for a
given mass selection also seem to be incompatible at several
standard deviations between the two samples, especially above
1 h-1 Mpc.
![\begin{figure}\par\includegraphics[width=12cm]{12314f19.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg118.png) |
Figure 19:
The zCOSMOS (solid circles) and VVDS-Deep (open
circles)
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f20.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg119.png) |
Figure 20:
The redshift-space, angle-averaged correlation function
|
| Open with DEXTER | |
10.3 Comparison to analytic and semi-analytic models
At this point, it is relevant to compare the available
observations from zCOSMOS and VVDS with model predictions in a
standard ![]() CDM scenario. We can do this in two ways. We
first used the HALOFIT public code (Smith et al. 2003),
which uses the halo model to compute the expected nonlinearly
evolved power spectrum at z=0.8, which we take as a reasonable
mean redshift for the two samples. Our conclusions would not
differ at all if predictions for z=0.7 or 0.9 were used. The
corresponding projected function
CDM scenario. We can do this in two ways. We
first used the HALOFIT public code (Smith et al. 2003),
which uses the halo model to compute the expected nonlinearly
evolved power spectrum at z=0.8, which we take as a reasonable
mean redshift for the two samples. Our conclusions would not
differ at all if predictions for z=0.7 or 0.9 were used. The
corresponding projected function
![]() is then computed by
Fourier-transforming the power spectrum and projecting the
resulting real-space correlation function. The result gives the
expected
is then computed by
Fourier-transforming the power spectrum and projecting the
resulting real-space correlation function. The result gives the
expected
![]() of the mass density field at z=0.8. Second, we
can compute the expectation value and the scatter expected in the
same redshift range (0.5<z<1) for
of the mass density field at z=0.8. Second, we
can compute the expectation value and the scatter expected in the
same redshift range (0.5<z<1) for
![]() using the available
semi-analytic mock surveys built from the Millennium run. To this
end, we used the DLB40 mocks for which we have full control over
stellar masses, selecting simulated galaxies with
using the available
semi-analytic mock surveys built from the Millennium run. To this
end, we used the DLB40 mocks for which we have full control over
stellar masses, selecting simulated galaxies with
![]() and
and
![]() and reproducing the sampling rate of
the 10K data. In Fig. 19 we plot the
HALOFIT prediction both for the dark matter and for an
arbitrarily biased population of haloes with
and reproducing the sampling rate of
the 10K data. In Fig. 19 we plot the
HALOFIT prediction both for the dark matter and for an
arbitrarily biased population of haloes with
![]() ,
together with the DLB40 mean
,
together with the DLB40 mean
![]() and
the corresponding
and
the corresponding ![]() and
and ![]() scatter corridor from
the 40 mock surveys. As a consistency check, we note the rather
good agreement between the analytic HALOFIT result and the
expected value from the full N-body plus semi-analytic simulation.
On these model predictions, we overplot the corresponding zCOSMOS
and VVDS estimates. The zCOSMOS points agree with the models at
better than 68% confidence in both shape and amplitude on scales
smaller than 1 h-1 Mpc. On larger scales, however, the
observed
scatter corridor from
the 40 mock surveys. As a consistency check, we note the rather
good agreement between the analytic HALOFIT result and the
expected value from the full N-body plus semi-analytic simulation.
On these model predictions, we overplot the corresponding zCOSMOS
and VVDS estimates. The zCOSMOS points agree with the models at
better than 68% confidence in both shape and amplitude on scales
smaller than 1 h-1 Mpc. On larger scales, however, the
observed
![]() would require a strongly scale-dependent bias to
be compatible with the model predictions. This scale-dependence
would also behave contrary to what models and very general
considerations suggest, implying a bias that grows with scale,
rather than declines. From the plot we see in fact that the 10K
data are compatible with
would require a strongly scale-dependent bias to
be compatible with the model predictions. This scale-dependence
would also behave contrary to what models and very general
considerations suggest, implying a bias that grows with scale,
rather than declines. From the plot we see in fact that the 10K
data are compatible with
![]() on small scales, but would
require
on small scales, but would
require
![]() on 10 h-1 Mpc scales. The shaded area
shows that this large-scale excess is marginally compatible with
the model predictions, representing a very strong positive
fluctuation. A few percent of volumes this size would show this
high clustering amplitude (on these scales and for this kind of
galaxies), in a
on 10 h-1 Mpc scales. The shaded area
shows that this large-scale excess is marginally compatible with
the model predictions, representing a very strong positive
fluctuation. A few percent of volumes this size would show this
high clustering amplitude (on these scales and for this kind of
galaxies), in a ![]() CDM Universe.
CDM Universe.
It is interesting to note, at the same time, how the VVDS
measurements lie on the opposite side of the distribution, at
about 1.5-2![]() from the mean, but with a shape that is
compatible with the model prediction over the whole range
(corresponding to a linear bias
from the mean, but with a shape that is
compatible with the model prediction over the whole range
(corresponding to a linear bias ![]() ).
Based on the results of Abbas &
Sheth (2007), one would also conclude that the central volume
of the COSMOS survey is dominated by overdense regions,
while these should be slightly under-represented in the
corresponding volume of the VVDS survey.
).
Based on the results of Abbas &
Sheth (2007), one would also conclude that the central volume
of the COSMOS survey is dominated by overdense regions,
while these should be slightly under-represented in the
corresponding volume of the VVDS survey.
These results show how a full HOD model fitting to the
![]() measured from the 10K data - originally planned for this paper -
would add no meaningful information to the current analysis. Our
first experiments with HOD models based on the universal halo mass
function indicate that rather unrealistic sets of parameters are
required to reproduce the observed function. An interesting
possibility would be to use in such modelling a halo mass function
that depends on local environment (e.g.
Abbas & Sheth 2005,2006), to consider the evidence that a
large part of this sample is dominated by an overdensity. We plan
to explore this possibility using the larger 20K zCOSMOS sample
that is now nearly complete.
measured from the 10K data - originally planned for this paper -
would add no meaningful information to the current analysis. Our
first experiments with HOD models based on the universal halo mass
function indicate that rather unrealistic sets of parameters are
required to reproduce the observed function. An interesting
possibility would be to use in such modelling a halo mass function
that depends on local environment (e.g.
Abbas & Sheth 2005,2006), to consider the evidence that a
large part of this sample is dominated by an overdensity. We plan
to explore this possibility using the larger 20K zCOSMOS sample
that is now nearly complete.
11 Discussion
Together with previous analyses (McCracken et al. 2007; Kovac et al. 2009),
these results suggest that a significant fraction of the volume of
Universe bounded by the COSMOS field is indeed characterised by
particularly extreme density fluctuations. We have seen how, in
statistical terms, these seem to lie at the ![]() limit of the
distribution of amplitudes expected in volumes of a few
106 h-3 Mpc3. We should consider, however, that these
conclusions are drawn from measurements that are strongly affected
by the angular distribution of structure. The McCracken et al. (2007)
result is based on the angular correlation function, while here we
studied the projected function
limit of the
distribution of amplitudes expected in volumes of a few
106 h-3 Mpc3. We should consider, however, that these
conclusions are drawn from measurements that are strongly affected
by the angular distribution of structure. The McCracken et al. (2007)
result is based on the angular correlation function, while here we
studied the projected function
![]() .
Although making use of the
redshift information, the latter is in practice a clustering
measure dominated by galaxy pairs lying almost perpendicular to
the line of sight. The underlying assumption when measuring
.
Although making use of the
redshift information, the latter is in practice a clustering
measure dominated by galaxy pairs lying almost perpendicular to
the line of sight. The underlying assumption when measuring
![]() is that the geometrical distribution of structures within the
sample being analysed is completely isotropic, in other words,
that there are superclusters aligned along several directions,
such that the only remaining radial signal is produced by
galaxy-peculiar velocities. The very reason for using
is that the geometrical distribution of structures within the
sample being analysed is completely isotropic, in other words,
that there are superclusters aligned along several directions,
such that the only remaining radial signal is produced by
galaxy-peculiar velocities. The very reason for using
![]() is
indeed to get rid of the distortions introduced in the shape of
is
indeed to get rid of the distortions introduced in the shape of
![]() (the redshift-space, angle-averaged correlation function)
by galaxy motions. If this is true, and only in this case, then
(the redshift-space, angle-averaged correlation function)
by galaxy motions. If this is true, and only in this case, then
![]() is fully equivalent to an integral over the real-space
correlation function
is fully equivalent to an integral over the real-space
correlation function ![]() ,
so it carries the same cosmological
information. However, if, as in the case we have encountered here,
there is one or more dominating structures extending
preferentially along one direction, then the use of
,
so it carries the same cosmological
information. However, if, as in the case we have encountered here,
there is one or more dominating structures extending
preferentially along one direction, then the use of
![]() to
infer cosmological information is inappropriate.
to
infer cosmological information is inappropriate.
![\begin{figure}\par\includegraphics[width=12cm]{12314f21.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg125.png) |
Figure 21:
Comparison of the redshift-space correlation function for galaxies with
|
| Open with DEXTER | |
One may thus wonder whether more robust cosmological information
could instead be inferred by looking directly at the simplest,
angle-averaged redshift-space correlation function ![]() .
The
expectation is that the average over all directions
reduces the weight of the excess pair counts produced by just a
few structures oriented along one preferred direction. In such
case any analytic modelling (e.g. with HOD models) should also
include an appropriate model for the linear and nonlinear redshift
distortions (Tinker et al. 2007; Scoccimarro 2004). More simply,
we can use the available mock samples in redshift-space to compute
the nonlinear redshift-space
.
The
expectation is that the average over all directions
reduces the weight of the excess pair counts produced by just a
few structures oriented along one preferred direction. In such
case any analytic modelling (e.g. with HOD models) should also
include an appropriate model for the linear and nonlinear redshift
distortions (Tinker et al. 2007; Scoccimarro 2004). More simply,
we can use the available mock samples in redshift-space to compute
the nonlinear redshift-space ![]() and its variance and compare
it to the data, as we did for
and its variance and compare
it to the data, as we did for
![]() .
In Fig. 20 we
first plot
.
In Fig. 20 we
first plot ![]() for the 10K sample, computed for the usual
four mass ranges in the broad redshift range 0.5<z<1. The four
data sets show a smooth power-law behaviour, with some evidence of
a mass dependence of the clustering amplitude, in particular at
the upper mass limit. The overall shape is well described by a
rather flat power-law
for the 10K sample, computed for the usual
four mass ranges in the broad redshift range 0.5<z<1. The four
data sets show a smooth power-law behaviour, with some evidence of
a mass dependence of the clustering amplitude, in particular at
the upper mass limit. The overall shape is well described by a
rather flat power-law
![]() ,
with slope
,
with slope
![]() and a correlation length s0 between 6 and
and a correlation length s0 between 6 and
![]() 10 h-1 Mpc. These values for the shape and amplitude of
10 h-1 Mpc. These values for the shape and amplitude of
![]() are similar to those measured for luminous red galaxies
at z=0.55 in the 2SLAQ survey (see Fig. 7 in Ross et al. 2007)
and for luminous early-type galaxies in the 2dFGRS
(Norberg et al. 2002). This is consistent with the most massive
objects in the 10K sample being predominantly red, early-type
galaxies that show moderate or no evolution in the overall
clustering amplitude with redshift.
are similar to those measured for luminous red galaxies
at z=0.55 in the 2SLAQ survey (see Fig. 7 in Ross et al. 2007)
and for luminous early-type galaxies in the 2dFGRS
(Norberg et al. 2002). This is consistent with the most massive
objects in the 10K sample being predominantly red, early-type
galaxies that show moderate or no evolution in the overall
clustering amplitude with redshift.
In Fig. 21, instead, we compare ![]() of our
``reference'' sample with
of our
``reference'' sample with
![]() ,
with the mean
and scatter (at
,
with the mean
and scatter (at ![]() and
and ![]() confidence, respectively)
of the similarly-selected set of DLB40 mocks. Despite the angular
average, we note a behaviour that is similar to what is observed
in
confidence, respectively)
of the similarly-selected set of DLB40 mocks. Despite the angular
average, we note a behaviour that is similar to what is observed
in
![]() ,
although now the agreement extends to slightly larger
scales. The observed clustering is compatible with the predictions
of the standard model (to better than the 68% level) on scales
smaller than
,
although now the agreement extends to slightly larger
scales. The observed clustering is compatible with the predictions
of the standard model (to better than the 68% level) on scales
smaller than ![]() 2 h-1 Mpc. On larger scales,
2 h-1 Mpc. On larger scales, ![]() also
shows excess power with respect to the models, which places the
zCOSMOS volume at the upper
also
shows excess power with respect to the models, which places the
zCOSMOS volume at the upper ![]() limit of the statistical
distribution obtained from the mocks. This exercise shows that,
even after angle-averaging our clustering estimator, the amount of
structure present in this specific volume of the Universe remains
outstanding in comparison to the model expectations. The
conclusion can only be that we have either been very unlucky in
the selection of the COSMOS field and picked up a fluctuation with
a probability of
limit of the statistical
distribution obtained from the mocks. This exercise shows that,
even after angle-averaging our clustering estimator, the amount of
structure present in this specific volume of the Universe remains
outstanding in comparison to the model expectations. The
conclusion can only be that we have either been very unlucky in
the selection of the COSMOS field and picked up a fluctuation with
a probability of ![]() 1% to be found in such a volume or
fluctuations with this amplitude are in reality more common than
what the standard cosmology predicts.
1% to be found in such a volume or
fluctuations with this amplitude are in reality more common than
what the standard cosmology predicts.
12 Summary
We used the 10K zCOSMOS spectroscopic sample to study galaxy clustering as a function of galaxy luminosity and stellar mass, in the range of redshift [0.2,1]. To this end, we built luminosity and mass-selected samples from the 10K catalogue sampling three separate redshift ranges. We used mock catalogues to quantify the effect of stellar mass incompleteness on the measured clustering, as a function of redshift. We carefully checked our covariance and error estimate techniques, comparing the performances of methods based on the scatter in the mocks and on bootstrapping schemes. We adopted the latter, based on 200 resamplings of 8 subvolumes of the survey, as the most appropriate description of the covariance properties of the data.
By measuring the redshift-space correlation functions ![]() and
and
![]() and the projected function
and the projected function
![]() for these
subsamples, we found the following results.
for these
subsamples, we found the following results.
- Surprisingly, we do
not see any clear dependence on luminosity of the correlation
function at all redshifts. This is at odds with
results in the local Universe by the 2dFGRS and with
mesurements at similar redshift by the VVDS and DEEP2 surveys, which
found a significant steepening of
 with luminosity.
with luminosity.
- We find a mildly more evident (although not striking)
dependence of
 on stellar mass, especially on small scales.
The central redshift bin (0.5<z<0.8) displays in general a more
evident effect, with a very flat shape of
on stellar mass, especially on small scales.
The central redshift bin (0.5<z<0.8) displays in general a more
evident effect, with a very flat shape of
 on scales
on scales
 [1-10] h-1 Mpc. The overall shape of the corresponding
map of
[1-10] h-1 Mpc. The overall shape of the corresponding
map of
 shows strong distortions that we interpret as
the effect of dominant structure extending preferentially
perpendicular to the line of sight.
shows strong distortions that we interpret as
the effect of dominant structure extending preferentially
perpendicular to the line of sight.
- From comparison to
the SDSS measurements at
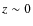 ,
we do not
see any significant evolution with redshift of the
amplitude of clustering for bright and/or massive galaxies. Together
with previous results from VVDS, this is consistent with a more
rapid evolution of the linear bias for the most massive objects with
respect to the general population. In the zCOSMOS sample, this
invariance in the clustering amplitude between
,
we do not
see any significant evolution with redshift of the
amplitude of clustering for bright and/or massive galaxies. Together
with previous results from VVDS, this is consistent with a more
rapid evolution of the linear bias for the most massive objects with
respect to the general population. In the zCOSMOS sample, this
invariance in the clustering amplitude between  and
and  seems to remain valid down to lower masses than in the VVDS, an
effect easily explained by the overall larger clustering amplitude
observed in general for z>0.5 in this sample. This is shown
by a much flatter shape (higher amplitude) of
seems to remain valid down to lower masses than in the VVDS, an
effect easily explained by the overall larger clustering amplitude
observed in general for z>0.5 in this sample. This is shown
by a much flatter shape (higher amplitude) of
 of zCOSMOS
galaxies with respect to VVDS galaxies, when selected with the same
criteria.
of zCOSMOS
galaxies with respect to VVDS galaxies, when selected with the same
criteria.
- This particularly high level of structure is confirmed by
comparing the measured
 and
and 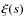 at 0.5<z<1 with model
predictions, concentrating on the sample with
at 0.5<z<1 with model
predictions, concentrating on the sample with
 .
On scales smaller than
.
On scales smaller than  1-2 h-1 Mpc, the
observations agree very well with the model expectation values in the standard
1-2 h-1 Mpc, the
observations agree very well with the model expectation values in the standard
 CDM scenario for a linear bias
CDM scenario for a linear bias
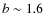 .
On these
scales, the measured values are compatible to better than 68% with
the DLB40 mocks. On larger scales, however, the observed clustering
amplitude is reproduced in only a few percent of the mocks. In
other words, if the shape of the power spectrum is that of
.
On these
scales, the measured values are compatible to better than 68% with
the DLB40 mocks. On larger scales, however, the observed clustering
amplitude is reproduced in only a few percent of the mocks. In
other words, if the shape of the power spectrum is that of
 CDM and the bias has no ``innatural'' scale-dependence,
COSMOS has picked up a volume of the Universe that is rare,
2-3
CDM and the bias has no ``innatural'' scale-dependence,
COSMOS has picked up a volume of the Universe that is rare,
2-3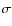 positive fluctuation. This conclusion is also corroborated
by comparison with the VVDS measurements, which on the other
hand lie on the lower side of the distribution, at about 1.5-2
positive fluctuation. This conclusion is also corroborated
by comparison with the VVDS measurements, which on the other
hand lie on the lower side of the distribution, at about 1.5-2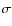 .
.
Acknowledgements
We thank the anonymous referee for a detailed review of the manuscript that helped to improve the paper. We thank G. De Lucia, J. Blaizot, S. Phleps, and A. Sànchez for their thorough comments on an early version of the manuscript. This work was supported by Grant ASI/COFIS/WP3110 I/026/07/0.
References
- Abbas, U., & Sheth, R. K. 2005, MNRAS, 364, 1327 [NASA ADS] [CrossRef]
- Abbas, U., & Sheth, R. K. 2006, MNRAS, 372, 1749 [NASA ADS] [CrossRef] (In the text)
- Abbas, U., & Sheth, R. K. 2007, MNRAS, 378, 641 [NASA ADS] [CrossRef] (In the text)
- Abbas, U., de la Torre, S., Le Fèvre, O., et al. 2009, A&A, submitted (In the text)
- Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences]
- Bell, E. F., Naab, T., McIntosh, D. H., et al. 2006, ApJ, 640, 241 [NASA ADS] [CrossRef]
- Benoist, C., Maurogordato, S., da Costa, L. N., Cappi, A., & Schaeffer, R. 1996, ApJ, 472, 452 [NASA ADS] [CrossRef] (In the text)
- Bernstein, G. M. 1994, ApJ, 424, 569 [NASA ADS] [CrossRef] (In the text)
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] (In the text)
- Bolzonella, M., Kovac, K., Pozzetti, L., et al. 2009, A&A, submitted [arXiv:0907.0013]
- Blaizot, J., Wadadekar, Y., Guiderdoni, B. et al. 2005, MNRAS, 360, 159 [NASA ADS] [CrossRef] (In the text)
- Brown, M. J. I., Zheng, Z., White, M., et al. 2008, ApJ, 682, 937 [NASA ADS] [CrossRef] (In the text)
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] (In the text)
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] (In the text)
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] (In the text)
- Coil, A. L., Newman, J. A., Cooper, M. C., et al. 2006, ApJ, 644, 671 [NASA ADS] [CrossRef]
- Coil, A. L., Newman, J. A., Croton, D., et al. 2008, ApJ, 672, 153 [NASA ADS] [CrossRef]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] (In the text)
- Conroy, C., Wechsler, R. H., & Kravtsov, A. V. 2006, ApJ, 647, 201 [NASA ADS] [CrossRef]
- Daddi, E., Röttgering, H. J. A., Labbé, I., et al. 2003, ApJ, 588, 50 [NASA ADS] [CrossRef]
- Davis, M., & Geller, M. J. 1976, ApJ, 208, 13 [NASA ADS] [CrossRef] (In the text)
- Davis, M., & Peebles, J. P. E. 1983, ApJ, 267, 465 [NASA ADS] [CrossRef]
- de la Torre, S., Le Fèvre, O., et al. 2009, A&A, submitted (In the text)
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] (In the text)
- Feldmann, R., Carollo, C. M., Porciani, C., et al. 2006, MNRAS, 372, 565 [NASA ADS] [CrossRef] (In the text)
- Fisher, K. B., Davis, M., Strauss, M. A., Yahil, A., & Huchra, J. 1994, MNRAS, 266, 50 [NASA ADS]
- Garilli, B., Le Fèvre, O., Guzzo, L., et al. 2008, A&A, 486, 683 [NASA ADS] [CrossRef] [EDP Sciences]
- Giacconi, R., Zirm, A., Wang, J., et al. 2002, ApJS, 139, 369 [NASA ADS] [CrossRef]
- Giovanelli, R., Haynes, M. P., & Chincarini, G. L. 1986, ApJ, 300, 77 [NASA ADS] [CrossRef] (In the text)
- Guzzo, L., Strauss, M. A., Fisher, K. B., Giovanelli, R., & Haynes, M. P. 1997, ApJ, 489, 37 [NASA ADS] [CrossRef] (In the text)
- Guzzo, L., Bartlett, J. G., Cappi, A., et al. 2000, A&A, 355, 1 [NASA ADS] (In the text)
- Guzzo, L., Cassata, P., Finoguenov, A., et al. 2007, ApJS, 172, 254 [NASA ADS] [CrossRef]
- Guzzo, L., Pierleoni, M., Meneux, B., et al. 2008, Nature, 451, 541 [NASA ADS] [CrossRef] (In the text)
- Hamilton, A. J. S. 1988, ApJ, 331, L59 [NASA ADS] [CrossRef] (In the text)
- Iovino, A., Giovanelli, R., Haynes, M., Chincarini, G., & Guzzo, L. 1993, MNRAS, 265, 21 [NASA ADS] (In the text)
- Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] (In the text)
- Kaiser, N. 1987, MNRAS, 227, 1 [NASA ADS] (In the text)
- Kitzbichler, M. G., & White, S. D. M. 2007, MNRAS, 376, 2 [NASA ADS] [CrossRef] (In the text)
- Kovac, K., Lilly, S. J., Cucciati, O., et al. 2009, ApJ, submitted [arXiv:0903.3409] (In the text)
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] (In the text)
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, Proc. SPIE, 4841, 1670 [NASA ADS] (In the text)
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005a, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Le Fèvre, O., Guzzo, L., Meneux, B., et al. 2005b, A&A, 439, 877 [NASA ADS] [CrossRef] [EDP Sciences]
- Li, C., Kauffmann, G., Jing, Y. P., et al. 2006, MNRAS, 368, 21 [NASA ADS] (In the text)
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] (In the text)
- Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, submitted (In the text)
- Ling, E. N., Barrow, J. D., & Frenk, C. S. 1986, MNRAS, 223, 21 [NASA ADS] (In the text)
- Maurogordato, S., & Lachieze-Rey, M. 1991, ApJ, 369, 30 [NASA ADS] [CrossRef] (In the text)
- McCracken, H. J., Peacock, J. A., Guzzo, L., et al. 2007, ApJS, 172, 314 [NASA ADS] [CrossRef] (In the text)
- McCracken, H. J., Ilbert, O., Mellier, Y., et al. 2008, A&A, 479, 321 [NASA ADS] [CrossRef] [EDP Sciences]
- Meneux, B., Le Fèvre, O., Guzzo, L., et al. 2006, A&A, 452, 387 [NASA ADS] [CrossRef] [EDP Sciences]
- Meneux, B., Guzzo, L., Garilli, B., et al. 2008, A&A, 478, 299 [NASA ADS] [CrossRef] [EDP Sciences]
- Norberg, P., Baugh, C. M., Hawkins, E., et al. 2001, MNRAS, 328, 64 [NASA ADS] [CrossRef] (In the text)
- Norberg, P., Baugh, C. M., Hawkins, E., et al. 2002, MNRAS, 332, 827 [NASA ADS] [CrossRef] (In the text)
- Norberg, P., Baugh, C. M., Gaztanaga, E., & Croton, D. J. 2009, MNRAS, 396, 19 [NASA ADS] [CrossRef] (In the text)
- Peebles, P. J. E. 1980, The Large Scale Structure of the Universe (Princeton: Princeton University Press) (In the text)
- Phleps, S., Peacock, J. A., Meisenheimer, K., & Wolf, C., 2006, A&A, 457, 145 [NASA ADS] [CrossRef] [EDP Sciences]
- Pollo, A., Meneux, B., Guzzo, L., et al. 2005, A&A, 439, 887 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pollo, A., Guzzo, L., Le Fèvre, O., et al. 2006, A&A, 451, 409 [NASA ADS] [CrossRef] [EDP Sciences]
- Porciani, C., & Giavalisco, M. 2002, ApJ, 565, 24 [NASA ADS] [CrossRef] (In the text)
- Pozzetti, L., Bolzonella, M., Lamareille, F., et al. 2007, A&A, 474, 443 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2009, A&A, submitted
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] (In the text)
- Rettura, A., Rosati, P., Strazzullo, V., et al. 2006, A&A, 458, 717 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ross, N. P., da Ângela, J., Shanks, T., et al. 2007, MNRAS, 381, 573 [NASA ADS] [CrossRef] (In the text)
- Scoccimarro, R. 2004, Phys. Rev. D, 70, 083007 [NASA ADS] [CrossRef]
- Scoville, N., Abraham, R. G., Aussel, H., et al. 2007a, ApJS, 172, 38 [NASA ADS] [CrossRef] (In the text)
- Scoville, N., Aussel, H., Benson, A., et al. 2007b, ApJS, 172, 150 [NASA ADS] [CrossRef]
- Skibba, R. A., Sheth, R. K., & Martino, M. C. 2007, MNRAS, 382, 1940 [NASA ADS]
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311 [NASA ADS] [CrossRef] (In the text)
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] (In the text)
- Springel, V., Frenk, C. S., & White, S. D. M. 2006, Nature, 440, 1137 [NASA ADS] [CrossRef] (In the text)
- Stringer, M. J., Benson, A. J., Bundy, K., Ellis, R. S., & Quetin, E. L. 2009, MNRAS, 143
- Tinker, J. L., Norberg, P., Weinberg, D. H., & Warren, M. S. 2007, ApJ, 659, 877 [NASA ADS] [CrossRef]
- Wake, D. A., Sheth, R. K., Nichol, R. C., et al. 2008, MNRAS, 387, 1045 [NASA ADS] [CrossRef] (In the text)
- Wang, L., Li, C., Kauffmann, G., & De Lucia, G. 2006, MNRAS, 371, 537 [NASA ADS] [CrossRef]
- Wang, L., Li, C., Kauffmann, G., & De Lucia, G. 2007, MNRAS, 377, 1419 [NASA ADS] [CrossRef]
- Warren, M. S., Abazajian, K., Holz, D. E., & Teodoro, L. 2006, ApJ, 646, 881 [NASA ADS] [CrossRef] (In the text)
- Willmer, C. N. A., da Costa, L. N., & Pellegrini, P. S. 1998, AJ, 115, 869 [NASA ADS] [CrossRef] (In the text)
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] (In the text)
- Zehavi, I., Blanton, M. R., Frieman, J. A., et al. 2002, ApJ, 571, 172 [NASA ADS] [CrossRef] (In the text)
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2005, ApJ, 630, 1 [NASA ADS] [CrossRef] (In the text)
- Zheng, Z., Coil, A., & Zehavi, I. 2007, ApJ, 667, 760 [NASA ADS] [CrossRef] (In the text)
- Zucca, E., Ilbert, O., Bardelli, S., et al. 2006, A&A, 455, 879 [NASA ADS] [CrossRef] [EDP Sciences]
- Zucca, E., Bardelli, S., Bolzonella, M., et al. 2009, A&A, submitted
Footnotes
- ...=0.2-1
![[*]](/icons/foot_motif.png)
- Based on observation at the European Southern Observatory (ESO) Very Large Telescope (VLT) under Large Program 175.A-0839. Also based on observations with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, operated by the Association of Universities for Research in Astronomy, Inc. (AURA Inc.), under NASA contract NAS 5-26555, with the Subaru Telescope, operated by the National Astronomical Observatory of Japan, with the telescopes of the National Optical Astronomy Observatory, operated by the AURA under cooperative agreement with the National Science Foundation, and with the Canada-France-Hawaii Telescope, operated by the National Research Council of Canada, the Centre Nationla de la Recherche Scientifique de France and the University of Hawaii.
All Tables
Table 1: Properties of the luminosity-selected samples.
Table 2: Properties of the mass-selected samples.
Table 3: The completeness in stellar mass of mass-selected mock subsamples reproducing the properties and selection criteria of our 10K data samples.
Table 4: The five main eigenvalules of the correlation matrix derived with the bootstrap resampling of galaxies (first column) and subvolumes (Col. 2), and from the ensemble variance of the 24 mocks (Col. 3).
All Figures
![\begin{figure}\par\includegraphics[width=12cm]{12314f01.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg39.png) |
Figure 1:
Distribution on the sky of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f02.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg43.png) |
Figure 2: Selection boundaries of the different subsamples of the zCOSMOS 10K survey used in this paper. Left: luminosity-redshift selection, which accounts for the average luminosity evolution of galaxies; Right: mass-redshift selection. |
| Open with DEXTER | |
| In the text | |
| |
Figure 3: The observed relationship between stellar mass and luminosity for galaxies in the 10K sample, within the three redshift ranges studied in this paper. The left panel shows an aspect of the galaxy bimodality, with red galaxies more massive and brighter than blue ones. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f04.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg60.png) |
Figure 4:
Estimate of how the completeness in stellar mass changes
as a function of redshift, due to the survey flux limit
(
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f05.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg77.png) |
Figure 5:
Overall radial distribution of the zCOSMOS 10K sample,
compared to three different smoothed distributions. These are
obtained by filtering the observed data with a Gaussian kernel of
increasing |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f06.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg78.png) |
Figure 6:
The radial distribution of the luminosity-selected sample
L2.1 compared to a smoothed curved (with a kernel of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f07.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg79.png) |
Figure 7:
The effect of stellar mass incompleteness
on the measured
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f08.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg80.png) |
Figure 8:
Ratio of the diagonal errors on
|
| Open with DEXTER | |
| In the text | |
| |
Figure 9: -2 Mean of the 24 correlation matrix derived resampling the galaxies of eack KW24 mocks ( left), or resampling 8 equal subvolumes ( center). These are compared to the correlation matrix derived directly from the KW24 mocks ( right). The redshift range considered here is z= [0.5-0.8]. The averaging over the 24 realisations of the 2 left matrices suppress the negative off-diagonal terms, which are sometimes present for a given mock catalogues. Correlation coefficients are then colour-coded from 0 to 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f10.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg102.png) |
Figure 10:
Projected correlation function
|
| Open with DEXTER | |
| In the text | |
| |
Figure 11:
Iso-correlation contours of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f12.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg104.png) |
Figure 12:
Sensitivity of the projected function
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f13.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg107.png) |
Figure 13:
Evolution of the projected function
|
| Open with DEXTER | |
| In the text | |
| |
Figure 14:
Example of full redshift-space correlation function
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f15.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg109.png) |
Figure 15:
The projected correlation function
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f16.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg110.png) |
Figure 16:
Evolution of the projected function
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f17.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg114.png) |
Figure 17:
The measured projected function
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f18.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg117.png) |
Figure 18: Direct comparison of the dependence of clustering on stellar mass in the VVDS-Deep and zCOSMOS samples, over a similar redshift range. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f19.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg118.png) |
Figure 19:
The zCOSMOS (solid circles) and VVDS-Deep (open
circles)
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f20.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg119.png) |
Figure 20:
The redshift-space, angle-averaged correlation function
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}\par\includegraphics[width=12cm]{12314f21.ps} \end{figure}](/articles/aa/full_html/2009/38/aa12314-09/Timg125.png) |
Figure 21:
Comparison of the redshift-space correlation function for galaxies with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}w_{\rm p}(r_{\rm p}) \equiv 2 \int\limits_0^\infty \xi(r_{\rm...
...fty
\xi_{\rm R}\left[(r_{\rm p}^2+y^2)^{1/2}\right] {\rm d}y.
\end{displaymath}](/articles/aa/full_html/2009/38/aa12314-09/img65.png)