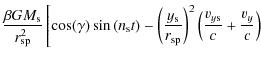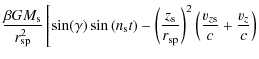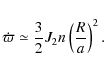EDP Sciences
Home All issues Volume 505 / No 2 (October II 2009) A&A, 505 2 (2009) 845-852 Full HTML
Free Access
Issue
A&A
Volume 505, Number 2, October II 2009
Page(s) 845 - 852
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/200911886
Published online 11 August 2009

Orbital evolution of the $\mu $ and $\nu $ dust ring particles of Uranus

R. Sfair - S. M. Giuliatti Winter

UNESP-São Paulo State University, C.P. 205, Guaratinguetá, CEP 12516-410, SP, Brazil

Received 19 February 2009 / Accepted 24 June 2009

Abstract
The $\mu $ and $\nu $ rings of Uranus form a secondary ring-moon system with the satellites Puck, Mab, Portia, and Rosalind. These rings are tenuous and dominated by micrometric particles, which can be strongly disturbed by dissipative forces, such as the solar radiation pressure. In the region of these rings, the solar radiation force and the planetary oblateness change the orbital evolution of these dust particles significantly. In this work, we performed a numerical analysis of the orbital evolution of a sample of particles with radii of 1, 3, 5, and $10~\mu$m under the influence of these perturbations, combined with the gravitational interaction with the close satellites. As expected, the Poynting-Robertson component of the solar radiation force causes the collapse of the orbits on a timescale between $3.1\times10^5$ and $3.6\times10^6$ years, while the radiation pressure causes an increase in the eccentricity of the particles. The inclusion of Uranus's oblateness prevents a large variation in the eccentricity, confining the particles in the region of the rings. The encounters with the close satellites produce variations in the semimajor axis of the particles, leading them to move inward and outward within the ring region. These particles can either remain within the region of the rings or collide with a neighbouring satellite. The number of collisions depends on the size of both the particles and the satellites, and the radial width of the ring. For the time span analysed, the percentage of particles that collide with a satellite varies from 43% to 94% for the $\nu $ring, and from 12% to 62% for the $\mu $ ring. Our study shows that all collisions with Portia and Rosalind have the value of impact velocity comparable to the escape velocity, which could result in the deposition of material onto the surface of the satellite. Collisions between Puck and particles larger than $1~\mu$m also occur at an impact velocity comparable to the value of the escape velocity. The exception is Mab, which is hit by particles with velocities several times larger than the escape velocity. These collisions are energetic enough to eject material and supply material to the $\mu $ ring. However, only a few particles (3%) collide with the surface of the satellite Mab at such a velocity.

Key words: planets: rings - planets and satellites: individual: Uranus - methods: N-body simulations

1 Introduction

Until 1977, the only known planet surrounded by rings was Saturn. In this year, during the occultation of the star SAO 158687, four narrow rings around Uranus were discovered (Elliot et al. 1977), and further observations from Voyager II found six more rings and faint dust bands between the rings (Smith et al. 1986). The $\epsilon $ring orbits at 51 149 km ( $2~R_{\rm p}$), the outer edge of the main ring system.

Showalter & Lissauer (2006) obtained several images with long exposure times of the Uranian system using the Hubble Space Telescope (HST), which discovered two rings, $\mu $ and $\nu $, which represented a secondary ring-moon system orbiting outside the main rings. Both rings are very faint and their radial profiles, defined in terms of the brightness of the ring as a function of the distance from the planet's centre, show a distinguished triangular profile. Their orbits are closely related with satellites: the peak, which corresponds to the distance from the planet's centre of maximum normal value of I/F (measurement of the brightness of the ring that would be observed from a perpendicular point of view), of $\mu $ ring is almost aligned with the orbit of the satellite Mab, while the inner edge of the ring coincides with the orbit of Puck. The $\nu $ ring peak does not match the orbit of any satellite, but the ring orbits between the satellites Rosalind and Portia. Figure 1 shows a schematic view of the $\mu $ and $\nu $ rings and the closest satellites. The radial extension of each ring is represented by shadow areas, and the solid lines correspond to the orbits of Puck, Mab, Rosalind, and Portia. All distances are represented in units of Uranus' radius ($R_{\rm p}$), and the solid line at $2~R_{\rm p}$indicates the position of the $\epsilon $ ring, the outermost ring of the main system.

 \begin{figure}\par\includegraphics[width=8cm]{11886f1.eps}\end{figure} Figure 1:

Schematic view of the secondary ring-moon system of Uranus. The solid lines correspond to the satellites orbits and the rings are represented by shadow areas. The planet (shadow area until 1 $R_{\rm p}$) and the $\epsilon $ ring are also indicated. All distances are scaled in units of Uranus' radius ($R_{\rm p}$).

Open with DEXTER

The $\mu $ and $\nu $ rings are radially wide and predominantly forward scattering, indicating that they are dominated by micrometric dust (de Pater et al. 2006). Dust particles can be disturbed by several non-gravitational forces, such as the solar radiation force, the solar tidal, and the planetary oblateness. These forces are much weaker than the gravity force of the planet. However, they change the orbital energy of the particle, which can be important to its long-term evolution.

In this paper, we analyse the orbital evolution of a sample of dust particles, located at the secondary ring system of Uranus, affected by the solar radiation pressure, the oblateness of the planet, and the gravitational perturbations of the satellites. In Sect. 2, we analyse the strength of the solar radiation pressure and the oblateness of the planet, and in Sect. 3, we describe the numerical method. The effects of these perturbations on the ring particles and the orbital evolution of them are analysed in Sects. 4 and 5, respectively. Section 6 deals with the collisions between the particles and the satellites. Our final conclusions are presented in the last section.

2 Force parameter

Hamilton & Krivov (1996) presented a way to compare the strength of the perturbation forces using dimensionless parameters that depend on the dust particles' semimajor axis, and the physical properties of the dust and the planet. Following their notation, we calculated the values of the solar tidal (A), oblateness (W), and radiation pressure (C) parameters. The solar tidal parameter A is defined as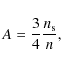

\begin{displaymath}A = \frac{3}{4}\frac{n_{\rm s}}{n}, \end{displaymath} (1)

where $n_{\rm s}$ is the mean motion of the planet around the Sun and n is the mean motion of the particle.

The parameter W, which describes the strength of the planetary oblateness, is written as

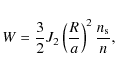\begin{displaymath}W = \frac{3}{2} J_2 \left(\frac{R}{a}\right)^2\frac{n_{\rm s}}{n}, \end{displaymath} (2)

where J2 denotes the second zonal harmonic coefficient, R is the radius of the planet, and a is the semimajor axis of the particle.

The ratio $\sigma$ of the radiative force to the planets' gravity of a particle with radius r and density $\rho$ is

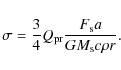\begin{displaymath}\sigma= \frac{3}{4} Q_{\rm pr}\frac{F_{\rm s} a}{GM_{\rm s}c\rho r}. \end{displaymath} (3)

In this equation, $Q_{\rm pr}$ is the radiation pressure coefficient, $F_{\rm s}$ is the incoming solar flux at the planet, $GM_{\rm s}$ is the planet's gravitational constant, and c is the speed of light.

Using the previous definition of $\sigma$, the perturbation caused by radiation pressure is written as

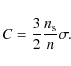\begin{displaymath}C = \frac{3}{2}\frac{n_{\rm s}}{n} \sigma. \end{displaymath} (4)

All of these parameters were calculated for a dust particle around Uranus, and the results are presented in Fig. 2.

 \begin{figure}\par\includegraphics[width=8cm]{11886f2.eps}\end{figure} Figure 2:

Parameters values as a function of the distance of the planet: A (solar tide), W (planetary oblateness), and C(radiation pressure). The vertical bars denote the radial extent of the $\mu $ and $\nu $ rings. We assumed a spherical grain with radius of $1~\mu$m and uniform density of 1.0 g cm-3.
Open with DEXTER

As can be seen in Fig. 2, the solar tide is relevant to particles located faraway from the planet (>50 $R_{\rm p}$), thus it can be safely ignored in the region of the $\mu $ and $\nu $ rings. On the other hand, for these rings the effects of radiation pressure and oblateness are appreciable and must be taken into account. In the following sections, we present our results for a numerical study of the evolution of a sample of particles disturbed by the gravitational effects of the closest satellites to each ring, the solar radiation pressure, and the oblateness of Uranus.

2.1 Solar radiation force

Most of the planetary ring systems are coplanar to the orbital plane of the planet, that is, the inclination i of the ring particle is $i \leq \gamma$, where $\gamma$ is the obliquity of the planet (Hamilton 1993). In these cases, the problem can be treated as bidimensional, when the Sun and the ring particle are located in the same plane.

Although Uranus's dusty rings describe equatorial orbits, the obliquity of Uranus is $97.8^\circ$ (Murray & Dermott 1999). Therefore, this problem requires a three-dimensional approach, since the Sun and the ring particle do not share the same orbital plane.

For a particle that describes an orbit around a planet with obliquity $\gamma$, the components of the solar radiation force, in a Cartesian inertial frame centred on the planet, can be written as (Mignard 1984)


 
                                  Fx = $\displaystyle \frac{\beta G M_{\rm s}}{r_{\rm sp}^2} \left[ \cos\left(n_{\rm s}... ...{v_x}{c} \right) - \left( \frac{v_{x{\rm s}}}{c}+\frac{v_x}{c} \right) \right],$ (5)
Fy = $\displaystyle \frac{\beta G M_{\rm s}}{r_{\rm sp}^2} \left[ \cos(\gamma)\sin\le... ...r_{\rm sp}}\right)^2 \left( \frac{v_{y{\rm s}}}{c}+\frac{v_y}{c} \right)\right.$  
    $\displaystyle - \left.\left( \frac{v_{y{\rm s}}}{c}+\frac{v_y}{c} \right) \right],$ (6)
Fz = $\displaystyle \frac{\beta G M_{\rm s}}{r_{\rm sp}^2} \left[ \sin(\gamma)\sin\le... ..._{\rm sp}}\right)^2 \left( \frac{v_{z{\rm s}}}{c}+\frac{v_z}{c} \right) \right.$  
    $\displaystyle - \left. \left( \frac{v_{z{\rm s}}}{c}+\frac{v_z}{c} \right) \right],$ (7)

where $r_{\rm sp}$ is the module of the Sun-planet vector, and ($x_{\rm s}$, $y_{\rm s}$, $z_{\rm s}$) are the components of $r_{\rm sp}$. The components of the velocity of the particle are (vx, vy, vz), and ( $v_{x{\rm s}}$, $v_{y{\rm s}}$, $v_{z{\rm s}}$) are the components of the velocity of the planet around the Sun. In these equations, the term independent of the velocities is called the radiation pressure (RP hereafter) and the remaining terms correspond to the Poynting-Robertson drag (PR drag).

If we assume that a spherical particle obeys geometrical optics, the parameter $\beta$ defined earlier as the ratio of the radiation force to the solar gravitational force can be written as (Burns et al. 1979)

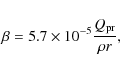\begin{displaymath}\beta = 5.7\times 10^{-5} \frac{Q_{\rm pr}}{\rho r}, \end{displaymath} (8)

where $Q_{\rm pr}$, the radiation pressure coefficient, is assumed to be equal to the unit to represent the value of an ideal material.

3 Numerical simulations

We performed a numerical study of the evolution of a sample of particles located at the $\mu $ and $\nu $ rings influenced by the gravity field of Uranus, the solar radiation force, and the gravitational perturbation of the closest satellites.

The numerical integrations were carried out using the variable timestep Bulirsch-Stoer algorithm from the Mercury package (Chambers 1999). The Mercury package allows the inclusion of a user-defined force such as Eqs. (5)-(7). It can also handle the case of a non-spherical central body including terms for the multipole expansion of the gravity field. We restricted our analysis to the first term of the expansion (J2) for Uranus, a reasonable approximation when higher terms of the expansion are at least two orders of magnitude smaller.

In our model, the planet is in a circular orbit around the Sun, thus $n_{\rm s}$ is constant, as well as the solar flux. We did not take into account the reflection from the planet, when the contribution of this effect was at least an order of magnitude weaker than those produced by the direct radiation (Hamilton & Krivov 1996). For the same reason, we ignored the effects of the grain rotation (Yarkovsky effect).

The semimajor axis (a), eccentricity (e), inclination (i), pericentre ($\omega$), ascending node ($\Omega$), and the radius of the satellites used in the numerical simulations are listed in Table 1. All orbital elements were derived from Showalter & Lissauer (2006), and the density of all satellites was assumed to be 1.3 g cm-3, equivalent to those for the satellite Miranda. Table 2 (adapted from Showalter & Lissauer 2006) summarizes the information for the $\mu $ and $\nu $ rings orbital radii. The rings were assumed to be in circular and equatorial orbits. Uranus's parameters used in the numerical simulations (radius, mass, semimajor axis, and J2coefficient) were derived from Murray & Dermott (1999).

The gravitational effects of the other satellites of the Portia family were not taken into account since these satellites are small and far from the $\mu $ and $\nu $ rings.

No information has so far regarding the particle size distribution of the $\mu $ and $\nu $ rings. Since de Pater et al. (2006) showed that these rings are dominated by micrometric dust, we assumed spherical particles of size 1, 3, 5, and 10 $\mu $m with density of 1 g cm-3 (pure solid ice). For each ring, an ensemble of 10 000 particles of each size were radially and azimuthally distributed within the ring region. The initial conditions of the particles were chosen following a random normal distribution.

Each particle was numerically integrated for a time span of 1000 years. When the distance between the particle and a satellite was less than the satellite's radius, a collision was detected. In this case, the particle is removed from the system and the impact parameters (position and velocity) were recorded.

Table 1:   Satellite orbital elements and physical parameters used in the numerical simulations.

Table 2:   The $\mu $ and $\nu $ rings radii.

4 Solar radiation force and planetary oblateness effects

Firstly, we analysed the effects of each component of the solar radiation force on the orbital elements of the particle, and how accounting for the planetary oblateness modified these effects.

As expected, if the oblateness of the planet is not taken into account, the radiation pressure component causes a variation of a few kilometres in the semimajor axis and induces large variations in the eccentricity of a dust particle. Figure 3 shows how RP changes the eccentricity of four particles with identical initial conditions but different sizes. Figure 3a shows the evolution in the eccentricity of particles located at the $\mu $ ring, and Fig. 3b for those particles at the $\nu $ ring.

 \begin{figure}\mbox{ \subfigure[]{ \includegraphics[angle=-90,width=8.5cm]{11886... ...bfigure[]{ \includegraphics[angle=-90,width=8.5cm]{11886f3b.eps} }} \end{figure} Figure 3:

Evolution of the eccentricity due to the radiation pressure component for ring particles with identical initial conditions: a) for the $\mu $ ring and b) for the $\nu $ ring.
Open with DEXTER

The overall behaviour of the eccentricity variation caused by the radiation pressure component for both $\mu $ and $\nu $ rings is the same. For larger particles, the period of oscillation is approximately equal to the orbital period of the planet ($\sim$84 years). The concavities seen in Fig. 3 are related to a highly inclined Uranus' equatorial plane. A local minimum appears approximately at the half of the orbital period of the planet, as the Sun crosses the ring plane.

It can be seen that the eccentricity of the 1 $\mu $m particle reaches a value higher than 0.5, which is enough to cause a collision with the $\epsilon $ ring. Before colliding with the main ring system, the particles of the $\mu $ and $\nu $ rings should cross the orbits of several satellites of the Portia family and may collide with one of these satellites.

In contrast to the radiation pressure, the Poynting-Robertson component causes no secular change in the eccentricity. The main effect of the PR drag is a decrease in the semimajor axis caused by the energy loss experienced by the particle. A $1~\mu$m particle initially located at a=97 500 km (approximately at the peak of the $\mu $ ring) decays 23 km in about 100 years, while the variation in the semimajor axis of a $10~\mu$m particle is roughly 2 km (Fig. 4). If we assume a constant decay rate, the time until the orbits collapse varies from $3.1\times10^5$ to $3.6\times10^6$ years, depending on the size of the particle. Burns et al. (1979) provide an analytical expression to calculate the lifetime of a circumplanetary particle in an equatorial orbit and the values derived from our numerical simulations are accurate to about 5% for particles of all sizes.

 \begin{figure}\par\includegraphics[angle=-90,width=8.6cm]{11886f4.eps} \end{figure} Figure 4:

Evolution of the semimajor axis due to the PR drag for $1~\mu$m and $10~\mu$m sized particles of $\mu $ ring with identical initial conditions. $\Delta a=0$corresponds to the initial semimajor axis of the particle.
Open with DEXTER

The next step was to analyse the effects of the solar radiation force and a non-spherical central body. The oblateness of Uranus adds a short-period variation in the semimajor axis disturbed by the Poynting-Robertson component, although the decay rate remains the same (Fig. 5).

 \begin{figure}\par\includegraphics[angle=-90,width=8.6cm]{11886f5.eps}\end{figure} Figure 5:

Evolution of the semimajor axis under the effects of the PR drag and the planetary oblateness. The initial conditions of the particles are the same as in Fig. 4.
Open with DEXTER

The effect of the oblateness is more evident in the eccentricity of the particle under the effects of the radiation pressure component. Figure 6 shows the variation in the eccentricity for particles of different sizes and identical initial conditions as presented in Fig. 3a. A comparison between Figs. 3a and 6 shows that the oblateness causes a ``damping'' in the eccentricity variation.

 \begin{figure}\par\includegraphics[angle=-90,width=8.6cm]{11886f6.eps}\end{figure} Figure 6:

Evolution of the eccentricity due to the radiation pressure and the planetary oblateness (J2 term) for those particles located at the $\mu $ ring. The initial conditions are identical to those presented in Fig. 3a.
Open with DEXTER

The decrease in the amplitude is enhanced as the distance to the planet decreases, when the rate of precession can be described by an inverse square law (cf. Eq. (9)). The reduction is more evident for the $\nu $ ring particles. Figure 7a and b illustrates the variation in the eccentricity for $1~\mu$m and $10~\mu$m sized particles of the $\nu $ ring with the same initial conditions as the particles shown in Fig. 3b.

 \begin{figure}\mbox{ \subfigure[]{ \includegraphics[angle=-90,width=8.6cm]{11886... ...bfigure[]{ \includegraphics[angle=-90,width=8.6cm]{11886f7b.eps} }} \end{figure} Figure 7:

Evolution of the eccentricity due to the radiation pressure component and the planetary oblateness for $\nu $ ring particles. The size of the particles are a) $1~\mu$m and b) $10~\mu$m, and the initial conditions are the same as in Fig. 3b.
Open with DEXTER

This decrease in the eccentricity keeps the particle within the region of the rings. A similar process occurs in the Saturn's F-ring, where the damping in the eccentricity avoids the particles leaving the ring region (Sfair et al. 2009).

The effects of the planetary oblateness on a particle, already disturbed by the solar radiation pressure, can lead to different outcomes. For dust particles located close to Phobos and Deimos (Mars' satellites), the oblateness of the planet enhances the variation in the eccentricity produced by RP component (Hamilton & Krivov 1996), while for those particles at the ring system of Neptune (Foryta & Sicardy 1996) and Saturn (Sfair et al. 2009) the effect is the opposite. The values of the eccentricity are ``damped'' when the planetary oblateness is considered.

The damping in the eccentricity occurs when the precession due to the oblateness is faster than the planet's mean motion. In this case, the forced eccentricity induced by the radiation pressure has insufficient time to develop fully and tends to disappear (Mignard 1984).

The period of oscillation also changes and becomes shorter. The period of the eccentricity is modulated by the coupling of three frequencies: $n_{\rm s}$, $\dot\varpi$, and a short-period frequency related to the inclusion of the J2 term, where $\dot\varpi$ is the pericentre precession rate, which can be written as (Murray & Dermott 1999)

\begin{displaymath}\dot\varpi \simeq \frac{3}{2}J_2 n \left(\frac{R}{a}\right)^2. \end{displaymath} (9)

The time rate of $\varpi$ varies from 1.87 to 8.86 degrees per year for the innermost and outermost particles, respectively. These values agree fairly well with those obtained by means of numerical simulations.

5 Orbital evolution

In addition to the effects of the solar radiation pressure and the oblateness of Uranus, the dust ring particles are also perturbed by the closest satellites. The $\mu $ ring particles are perturbed by the satellites Puck and Mab, and the $\nu $ ring particles suffer the gravitational effects of Portia and Rosalind. Because of the large number of particles analysed, we present some representative plots of the $1~\mu$m and $10~\mu$m sized particles.

Figures 8 and 9 show the evolution of the semimajor axis of two $\mu $ ring particles. In each plot, the y-axis represents the semimajor axis displacement from its initial value as a function of time (x-axis). All particles were integrated for a time span of 1000 years, unless a collision occurs.

 \begin{figure}\par\subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f8a.ep... ... \subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f8b.eps} } \end{figure} Figure 8:

Temporal evolution of the semimajor axis of two $1~\mu$m sized particles located in $\mu $ ring under the effects of the solar radiation force, the planetary oblateness, and the satellites Puck and Mab. In a) the particle collides with Puck after 635 years. The outer and inner edges of the ring are located at 5485 km and -11 515 km, respectively; the particle represented in b) remains within the ring region for the time span of 1000 years. The outer and inner edges of the ring are located at 5027 km and -11 970 km, respectively. In each plot, $\Delta a=0$ corresponds to the initial semimajor axis of the particle.

Open with DEXTER

 \begin{figure}\par\subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f9a.ep... ... \subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f9b.eps} } \end{figure} Figure 9:

Temporal evolution of the semimajor axis of two $10~\mu$m particles located in $\mu $ ring under the effects of the solar radiation force, the planetary oblateness, and the satellites Mab and Puck. The particle represented in a) collides with Mab after 950 years. The outer and inner edges of the ring are located at 8700 km and -8300 km, respectively. The particle represented in b) survived within the ring region for the time span of 1000 years. The outer and inner edges of the ring are located at 1392 km and -10 708 km, respectively.
Open with DEXTER

 \begin{figure}\par\subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f10.ep... ... \subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f11.eps} } \end{figure} Figure 10:

Evolution of the semimajor axis of $1~\mu$m particles of the $\nu $ ring disturbed by the solar radiation force, planetary oblateness, and gravitational influence of Portia and Rosalind. In a) the particle collides with Portia after 80 years. The outer and inner edges of the ring are located at 682 km and -3118 km, respectively. The particle represented in b) collides with Rosalind in approximately 690 years. The outer and inner edges of the ring are located at 3053 km and -747 km, respectively. In each plot, $\Delta a=0$ corresponds to the initial semimajor axis of the particle.

Open with DEXTER

 \begin{figure}\par\subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f12.ep... ... \subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f13.eps} } \end{figure} Figure 11:

The same as Fig. 10 for $10~\mu$m particles. The particle represented in a) collides with Portia in 125 years. The outer and inner edges of the ring are located at 3053 km and -747 km, respectively. The particle represented in b) survived inside the ring region for the time span that we analysed. The outer and inner edges of the ring are located at 1541 km and -2259 km, respectively.

Open with DEXTER

The amplitude of the variation in the eccentricity, caused by the gravitational perturbation of the satellites, is $\mathcal{O}(10^{-4})$. It is, at least, two orders of magnitude smaller than the variation produced by the RP component. Therefore, the evolution of the eccentricity is dominated by this component of the solar radiation force. The eccentricity can reach values higher than 0.01. Such values are high enough to cause close encounters with the satellites, which cause sudden variations (jumps) of the semimajor axis. The $1~\mu$m particles exhibit amounts of these axis large variations, sometimes of hundreds of kilometres (Fig. 8), while the majority of the $10~\mu$m particles exhibit ``jumps'' of a few kilometres (Fig. 9). Even those particles initially faraway from the neighbourhood of the satellites can experience close encounters with them, especially small particles, which are more sensitive to the effects of the radiation pressure.

In the cases shown in Figs. 8 and 9, the particles have different orbital evolution. The variation in the semimajor axis of the particles, due to close encounters with the satellites, in combination with the eccentricity oscillation, allow the orbit of the particle to cross the orbit of the satellite, leading to an eventual collision. For example, the semimajor axis of the particle represented in Fig. 8 has a variation larger than 300 km, implying that a collision with Puck will occur in $\sim$360 years.

A similar behaviour was found for the $\nu $ ring particles. Figures 10 and 11 show the evolution of the semimajor axis of four $\nu $ ring particles, orbiting an oblate Uranus, affected by the solar radiation force and the gravitational perturbations of Portia and Rosalind.

As expected, the strength of the planetary oblateness is stronger in the $\nu $ ring region (Fig. 2), which makes the eccentricity damping more effective. However, even a small a variation in the eccentricity leads to close encounters with one of the satellites (Fig. 10). Some $10~\mu$m sized particles of the $\nu $ ring undergo deviations of some hundreds of kilometres in semimajor axis (Fig. 11a), as a consequence of the proximity with Portia and Rosalind.

The global behaviour of the representative sample of the particles with 3 $\mu $m and $5~\mu$m sizes do not differ from the cases presented here. The eccentricity varies according to the combination of the J2 term and the RP component. The close encounters between the particle and the satellite produce variations (jumps) in the semimajor axis within the ring region.

6 Collisions between satellites and particles

Since the oblateness prevents the overstated increase in the eccentricity, the complete ensemble of particles remains within the region of the rings for the time span of 1000 years. However, some particles cross the orbit and can collide with the close satellite. Tables 3 and 4 summarize the number of collisions between the particles and the satellites in the numerical simulations. $N_\%$ is the percentage of the particles that collide with the satellite, $\overline{T}$ is the mean time of the collision, and $\overline{v}$ is the mean impact velocity.

For both rings, the percentage of the number of collisions ($N_\%$) and the mean time ( $\overline{T}$) exhibit a correlation with the size of the particle. This is because of the different values of the eccentricity, produced by the effect of the RP component. Small particles, which are more sensitive to this effect, exhibit large variations in their eccentricity. The orbits of $1~\mu$m sized particles cross a broad region of the ring, increasing the probability of collision with a close satellite.

By comparing both ring systems, we can verify that the particles located at the $\nu $ ring have a shorter lifetime. After 1000 years, $94\%$ of the $1~\mu$m sized particles collided with Portia or Rosalind. Meanwhile, the number of collisions with Puck and Mab is roughly $60\%$ of the total number of particles. This difference is caused mainly by the radial extension of the $\nu $ ring, which is $\sim$4.5 times narrower than the $\mu $ ring. All particles that did not suffer any collision with the satellites remained within the region of the rings.

The number of collisions with the satellites Portia and Puck depends, primarily, on the size and location of the satellites. The decrease in the semimajor axis, due to the PR drag, increases the collision between the satellites, located close to the inner edge of the ring, and the particles. Portia and Puck are both larger than the satellites Mab and Rosalind. It can be seen from Table 1 that Puck is $\sim$7 larger than Mab, which increases the superficial area of Puck and consequently the probability of collision with the particles. More than 50% of the $\mu $ ring particles collide with Puck.

When a particle hits the surface of the satellite, it may be absorbed or it can produce dust ejecta. At the time of the collision, we computed the relative velocities of the satellite and the particle, which allows us to calculate the impact velocity. The impact velocity is a reliable measurement of the energy carried by the particle. Depending on the impact velocity, the particle can be absorbed or dust ejecta can be produced.

The escape velocities ( ${v}_{\rm esc}$) of Puck, Mab, Portia, and Rosalind are approximately 70 m s-1, 10 m s-1, 60 m s-1, and 30 m s-1, respectively. Most of the collisions where $\overline{v} \gg {v}_{\rm esc}$ can generate ejecta debris that can escape from the parent satellite. The fate of these debris depends strongly on the size of the satellite and the geometry during impact. Tables 3 and 4 show that most of the values of the impact velocity of the ring particles are comparable to the escape velocity of the satellite. Collisions that could produce dust ejecta are those between $1~\mu$m sized particles and the satellites. All dust particles that collide with Mab have $\overline{v} \gg {v}_{\rm esc}$. However, this means of suppling dust particles to the ring is insufficient, since the number of collisions is less than 3% of the total amount of analysed particles.

7 Final discussion

We have performed a numerical analysis to determine the orbital evolution of a sample of dust particles, located at the $\mu $ and $\nu $ rings, under the combined effects of the solar radiation force, the oblateness of Uranus, and the gravitational perturbation of the closest satellites.

Each component of the solar radiation force is responsible for a distinctive effect in the orbit of the particle. The semimajor axis of the particles decays due to PR drag, and the RP component causes large variations in the eccentricity. The effects on the semimajor axis of the particles does not change considerably when the oblateness of Uranus is taken into account. However, the damping of the eccentricity, due to the J2 term, keeps the particles within the region of the rings and prevent the collision with the $\epsilon $ ring.

The close encounters with the satellites induce sudden variations in the semimajor axis of the particles, although the particles still do not leave the ring region. Consecutive encounters increase the probability of collisions between the particles and the satellites, especially for $1~\mu$m particles, which are more sensitive to the effects of RP component. The number of collisions and the mean time of the collision depend on both the size of the particle and the width of the rings.

The total number of collisions is higher for the inner satellites Puck and Portia. All collisions with Portia and Rosalind have an impact velocity comparable to the value of the escape velocity, which could deposit material onto the surface of the satellite. Collisions between Puck and particles larger than $1~\mu$m also have an impact velocity comparable to the value of the escape velocity. However, the impact velocity of those $1~\mu$m particles that collide with Puck is almost seven times higher than the escape velocity. Further analysis is required in order to verify whether these collisions can produce dust ejecta. Only a few particles (3%) hit the surface of the satellite Mab at a velocity that can cause the ejection of material in the $\mu $ ring.

Other mechanisms of dust production, such as bombardment by micrometeoroids, will have to be introduced to explain the origin of the micrometric particles in the $\mu $ and $\nu $ rings. This study is under investigation.

Table 3:   Results of the collision between $\mu $ ring particles and the close satellites (Mab and Puck) after 1000 years.

Table 4:   Results of the collision between $\nu $ ring particles and the close satellites (Rosalind and Portia) after 1000 years.

Acknowledgements
The authors thank FAPESP, CAPES, and CNPq for the financial support. We also thank the anonymous referee for its helpful comments.

References

All Tables

Table 1:   Satellite orbital elements and physical parameters used in the numerical simulations.

Table 2:   The $\mu $ and $\nu $ rings radii.

Table 3:   Results of the collision between $\mu $ ring particles and the close satellites (Mab and Puck) after 1000 years.

Table 4:   Results of the collision between $\nu $ ring particles and the close satellites (Rosalind and Portia) after 1000 years.

All Figures

  \begin{figure}\par\includegraphics[width=8cm]{11886f1.eps}\end{figure} Figure 1:

Schematic view of the secondary ring-moon system of Uranus. The solid lines correspond to the satellites orbits and the rings are represented by shadow areas. The planet (shadow area until 1 $R_{\rm p}$) and the $\epsilon $ ring are also indicated. All distances are scaled in units of Uranus' radius ($R_{\rm p}$).

Open with DEXTER
In the text

  \begin{figure}\par\includegraphics[width=8cm]{11886f2.eps}\end{figure} Figure 2:

Parameters values as a function of the distance of the planet: A (solar tide), W (planetary oblateness), and C(radiation pressure). The vertical bars denote the radial extent of the $\mu $ and $\nu $ rings. We assumed a spherical grain with radius of $1~\mu$m and uniform density of 1.0 g cm-3.
Open with DEXTER
In the text

  \begin{figure}\mbox{ \subfigure[]{ \includegraphics[angle=-90,width=8.5cm]{11886... ...bfigure[]{ \includegraphics[angle=-90,width=8.5cm]{11886f3b.eps} }} \end{figure} Figure 3:

Evolution of the eccentricity due to the radiation pressure component for ring particles with identical initial conditions: a) for the $\mu $ ring and b) for the $\nu $ ring.
Open with DEXTER
In the text

  \begin{figure}\par\includegraphics[angle=-90,width=8.6cm]{11886f4.eps} \end{figure} Figure 4:

Evolution of the semimajor axis due to the PR drag for $1~\mu$m and $10~\mu$m sized particles of $\mu $ ring with identical initial conditions. $\Delta a=0$corresponds to the initial semimajor axis of the particle.
Open with DEXTER
In the text

  \begin{figure}\par\includegraphics[angle=-90,width=8.6cm]{11886f5.eps}\end{figure} Figure 5:

Evolution of the semimajor axis under the effects of the PR drag and the planetary oblateness. The initial conditions of the particles are the same as in Fig. 4.
Open with DEXTER
In the text

  \begin{figure}\par\includegraphics[angle=-90,width=8.6cm]{11886f6.eps}\end{figure} Figure 6:

Evolution of the eccentricity due to the radiation pressure and the planetary oblateness (J2 term) for those particles located at the $\mu $ ring. The initial conditions are identical to those presented in Fig. 3a.
Open with DEXTER
In the text

  \begin{figure}\mbox{ \subfigure[]{ \includegraphics[angle=-90,width=8.6cm]{11886... ...bfigure[]{ \includegraphics[angle=-90,width=8.6cm]{11886f7b.eps} }} \end{figure} Figure 7:

Evolution of the eccentricity due to the radiation pressure component and the planetary oblateness for $\nu $ ring particles. The size of the particles are a) $1~\mu$m and b) $10~\mu$m, and the initial conditions are the same as in Fig. 3b.
Open with DEXTER
In the text

  \begin{figure}\par\subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f8a.ep... ... \subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f8b.eps} } \end{figure} Figure 8:

Temporal evolution of the semimajor axis of two $1~\mu$m sized particles located in $\mu $ ring under the effects of the solar radiation force, the planetary oblateness, and the satellites Puck and Mab. In a) the particle collides with Puck after 635 years. The outer and inner edges of the ring are located at 5485 km and -11 515 km, respectively; the particle represented in b) remains within the ring region for the time span of 1000 years. The outer and inner edges of the ring are located at 5027 km and -11 970 km, respectively. In each plot, $\Delta a=0$ corresponds to the initial semimajor axis of the particle.

Open with DEXTER
In the text

  \begin{figure}\par\subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f9a.ep... ... \subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f9b.eps} } \end{figure} Figure 9:

Temporal evolution of the semimajor axis of two $10~\mu$m particles located in $\mu $ ring under the effects of the solar radiation force, the planetary oblateness, and the satellites Mab and Puck. The particle represented in a) collides with Mab after 950 years. The outer and inner edges of the ring are located at 8700 km and -8300 km, respectively. The particle represented in b) survived within the ring region for the time span of 1000 years. The outer and inner edges of the ring are located at 1392 km and -10 708 km, respectively.
Open with DEXTER
In the text

  \begin{figure}\par\subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f10.ep... ... \subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f11.eps} } \end{figure} Figure 10:

Evolution of the semimajor axis of $1~\mu$m particles of the $\nu $ ring disturbed by the solar radiation force, planetary oblateness, and gravitational influence of Portia and Rosalind. In a) the particle collides with Portia after 80 years. The outer and inner edges of the ring are located at 682 km and -3118 km, respectively. The particle represented in b) collides with Rosalind in approximately 690 years. The outer and inner edges of the ring are located at 3053 km and -747 km, respectively. In each plot, $\Delta a=0$ corresponds to the initial semimajor axis of the particle.

Open with DEXTER
In the text

  \begin{figure}\par\subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f12.ep... ... \subfigure[]{\includegraphics[angle=-90,width=8cm]{11886f13.eps} } \end{figure} Figure 11:

The same as Fig. 10 for $10~\mu$m particles. The particle represented in a) collides with Portia in 125 years. The outer and inner edges of the ring are located at 3053 km and -747 km, respectively. The particle represented in b) survived inside the ring region for the time span that we analysed. The outer and inner edges of the ring are located at 1541 km and -2259 km, respectively.

Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.