| Issue |
A&A
Volume 505, Number 2, October II 2009
|
|
|---|---|---|
| Page(s) | 695 - 706 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200810972 | |
| Published online | 24 July 2009 | |
Results from DROXO![[*]](/icons/foot_motif.png)
II. [Ne II] and X-ray emission from  Ophiuchi young stellar
objects
Ophiuchi young stellar
objects
E. Flaccomio1 - B. Stelzer1 - S. Sciortino1 - G. Micela1 - I. Pillitteri1,2 - L. Testi3,4
1 - INAF - Osservatorio Astronomico di Palermo,
Piazza del Parlamento 1,
90134 Palermo, Italy
2 -
Dip. di Scienze Fisiche e Astronomiche, Sez. di Astronomia, Università di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
3 -
INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
4 -
ESO, Karl Schwarzschild Str. 2, 85748 Garching bei München, Germany
Received 17 September 2008 / Accepted 16 June 2009
Abstract
Context. The infrared [Ne II] and [Ne III] fine structure lines at 12.81 ![]() m and 15.55
m and 15.55 ![]() m have recently been theoretically predicted to trace the circumstellar disk gas subject to X-ray heating and ionization.
m have recently been theoretically predicted to trace the circumstellar disk gas subject to X-ray heating and ionization.
Aims. We observationally investigate the origin of the neon fine structure line emission by comparing observations with models of X-ray irradiated disks and by searching for empirical correlations between the line luminosities and stellar and circumstellar parameters.
Methods. We select a sample of 28 young stellar objects in the ![]() Ophiuchi star formation region for which good quality infrared spectra and X-ray data have been obtained, the former with the Spitzer/IRS and the latter with the deep rho Ophiuchi XMM-Newton observation (DROXO). We measure neon line fluxes and X-ray luminosities; we complement these data with stellar/circumstellar parameters obtained by fitting the spectral energy distributions of our objects (from optical to millimeter wavelengths) with star/disk/envelope models.
Ophiuchi star formation region for which good quality infrared spectra and X-ray data have been obtained, the former with the Spitzer/IRS and the latter with the deep rho Ophiuchi XMM-Newton observation (DROXO). We measure neon line fluxes and X-ray luminosities; we complement these data with stellar/circumstellar parameters obtained by fitting the spectral energy distributions of our objects (from optical to millimeter wavelengths) with star/disk/envelope models.
Results. We detect the [Ne II] and the [Ne III] lines in 10 and 1 cases, respectively. Line luminosities show no correlation with X-ray emission. The luminosity of the [Ne II] line for one star, and that of both the [Ne II] and [Ne III] lines for a second star, match the predictions of published models of X-ray irradiated disks; for the remaining 8 objects the [Ne II] emission is 1-3 dex higher than predicted on the basis of their ![]() .
However, the stellar/circumstellar characteristics assumed in published models do not match those of most of the stars in our sample. Class I objects show significantly stronger [Ne II] lines than Class II and Class III ones. A correlation is moreover found between the [Ne II] line emission and the disk mass accretion rates estimated from the spectral energy distributions. This might point toward a role of accretion-generated UV emission in the generation of the line or to other mechanisms related to mass inflows from circumstellar disks and envelopes and/or to the associated mass outflows (winds and jets).
.
However, the stellar/circumstellar characteristics assumed in published models do not match those of most of the stars in our sample. Class I objects show significantly stronger [Ne II] lines than Class II and Class III ones. A correlation is moreover found between the [Ne II] line emission and the disk mass accretion rates estimated from the spectral energy distributions. This might point toward a role of accretion-generated UV emission in the generation of the line or to other mechanisms related to mass inflows from circumstellar disks and envelopes and/or to the associated mass outflows (winds and jets).
Conclusions. The X-ray luminosity is clearly not the only parameter that determines the [Ne II] emission. For more exacting tests of X-ray irradiated disk models, these must be computed for the stellar and circumstellar characteristics of the observed objects. Explaining the strong [Ne II] emission of Class I objects likely requires the inclusion in the models of additional physical components such as the envelope, inflows, and outflows.
Key words: stars: activity - stars: formation - stars: circumstellar matter - stars: planetary systems: protoplanetary disks - stars: pre-main sequence
1 Introduction
The first million years in the formation of a low-mass star are characterized by several complex and still not fully understood phenomena involving the circumstellar envelope, the disk, and the central protostar, e.g., envelope and disk mass accretion, outflows, disk evolution including planet formation, star/disk magnetic interactions, and other manifestations of the magnetic field such as the intense X-ray emission from hot magnetically confined plasma. The first studies of young stellar objects (YSOs) have often neglected important interactions between these phenomena. A noteworthy example is the effect of X-rays from the central object on the surrounding molecular cloud, the accretion envelope, and the disk. YSOs, indeed, have stronger X-ray emission than main sequence stars (Feigelson & Montmerle 1999).
The origin of magnetic phenomena in YSOs, and of their X-ray emission in particular, is an intriguing and still poorly understood problem. Renewed interest in YSO X-ray emission comes from the recent recognition that X-rays may ionize and modify in several other ways the thermal and chemical structure of star forming clouds (Lorenzani & Palla 2001), circumstellar disks (e.g. Ilgner & Nelson 2006; Glassgold et al. 1997; Gorti & Hollenbach 2008; Meijerink et al. 2008; Ercolano et al. 2008), and planetary atmospheres (Cecchi-Pestellini et al. 2006). Here we focus on the response of YSO disks to X-ray irradiation by the central (proto)star.
The structure and temporal evolution of circumstellar disks is of paramount importance for the understanding of the star- and planet-formation process. The structure of the gas-phase component, by far more massive than the dust component, is particularly uncertain, being more stongly affected by high energy radiation (far/extreme ultraviolet and X-ray). Glassgold et al. (1997) have shown that, in a protostellar disk illuminated by a central X-ray source, X-ray ionization dominates over that of galactic cosmic rays, giving rise to a vertically layered ionization structure with an outer active surface and a mostly neutral inner dead zone (Gammie 1996; Glassgold et al. 1997). Ilgner & Nelson (2006) calculated the disk ionization structure as a function of the X-ray luminosity and emitting plasma temperature, and found that the disk is divided into three distinct radial zones: an inner active region, a central region where the depth of the dead-zone depends on the X-ray spectral and temporal characteristics, and an outer region with a non-variable dead-zone. In addition to ionization, X-rays can heat the external layers of disk atmospheres, as shown by Glassgold et al. (2004) who predict temperatures of the order of 5000 K.
Theoretical calculations depend critically on several ingredients: the
disk model, the chemical network, the spectral and temporal
characteristics of the X-ray source and its assumed spatial location
with respect to the disk. Observational tests are therefore highly
desirable and could help constrain the model assumptions. The lines of
ionized neon are particularly useful as a proxy of the effect of high
energy radiation, as its 1st and 2nd ionization potential
are 21.56 and 41 eV, respectively and therefore ionization can occur
only by photons in the EUV and X-ray range. Moreover, due to its
closed shell configuration, the Ne chemistry is particularly simple.
Glassgold et al. (2007), Meijerink et al. (2008, hereafter MGN 08), Gorti & Hollenbach (2008, hereafter
GH 08), and Ercolano et al. (2008) have recently calculated the
strength of fine structure emission lines from ionized neon
originating in a disk exposed to stellar X-rays. Glassgold et al. (2007)
estimate that in low-mass YSOs the ionization of neon is dominated by
X-rays, because the photospheres of these stars emit few UV photons
and cosmic rays are removed by the strong winds. Ne II and Ne III
ions, predominantly resulting from K-shell photoionization of neutral
neon by X-rays with energy E>0.87 keV, give rise to magnetic dipole
transitions at 12.81 ![]() m and 15.55
m and 15.55 ![]() m, respectively. The
predicted line luminosities are, for the reference disk/star models of
MGN 08 and GH 08, and for X-ray luminosities of
m, respectively. The
predicted line luminosities are, for the reference disk/star models of
MGN 08 and GH 08, and for X-ray luminosities of ![]()
![]() erg s-1, of the order of 1028 and 1027 erg s-1 for [Ne II] and [Ne III], respectively. MGN 08 predict
that the line luminosities increase with X-ray luminosity following a
steeper-than-linear relation. Ercolano et al. (2008) predict, with respect to
MGN 08 and GH 08, lower luminosities by a factor of 3-5. The
theoretical models are far from unique: other recent calculations of
[Ne II] line emission from an EUV-induced photoevaporative disk wind,
that neglect X-ray irradiation, yield luminosities similar to those
obtained by MGN 08 and GH 08 for their reference models
(Alexander 2008). The observation of line shifts and broadenings,
accessible through ground-based high resolution spectrographs, may
help to discriminate among the different proposed emission mechanisms
(e.g. van Boekel et al. 2009; Herczeg et al. 2007).
erg s-1, of the order of 1028 and 1027 erg s-1 for [Ne II] and [Ne III], respectively. MGN 08 predict
that the line luminosities increase with X-ray luminosity following a
steeper-than-linear relation. Ercolano et al. (2008) predict, with respect to
MGN 08 and GH 08, lower luminosities by a factor of 3-5. The
theoretical models are far from unique: other recent calculations of
[Ne II] line emission from an EUV-induced photoevaporative disk wind,
that neglect X-ray irradiation, yield luminosities similar to those
obtained by MGN 08 and GH 08 for their reference models
(Alexander 2008). The observation of line shifts and broadenings,
accessible through ground-based high resolution spectrographs, may
help to discriminate among the different proposed emission mechanisms
(e.g. van Boekel et al. 2009; Herczeg et al. 2007).
Detection of the [Ne II] 12.81 ![]() m line was first reported by
Pascucci et al. (2007) for four stars out of a sample of 6 transition-disk
systems. Lahuis et al. (2007) detected the line in 15 more T-Tauri stars and
Espaillat et al. (2007) added three more detections. The relation of the line
strengths to X-ray luminosity and other system parameters has remained
unclear: Pascucci et al. (2007) report a correlation of the [Ne II] line
luminosity with
m line was first reported by
Pascucci et al. (2007) for four stars out of a sample of 6 transition-disk
systems. Lahuis et al. (2007) detected the line in 15 more T-Tauri stars and
Espaillat et al. (2007) added three more detections. The relation of the line
strengths to X-ray luminosity and other system parameters has remained
unclear: Pascucci et al. (2007) report a correlation of the [Ne II] line
luminosity with ![]() and an anticorrelation with mass accretion
rate
and an anticorrelation with mass accretion
rate![]() ,
,
![]() ;
Espaillat et al. (2007), complementing the Pascucci et al. (2007) data with
their own, fail to confirm the correlation with
;
Espaillat et al. (2007), complementing the Pascucci et al. (2007) data with
their own, fail to confirm the correlation with ![]() and find a
possible direct correlation with
and find a
possible direct correlation with ![]() ;
the sample of
Lahuis et al. (2007) had only sparse X-ray data; in all cases the samples are
small and inhomogeneous, comprising stars in different star-forming
regions with different ages and distances.
;
the sample of
Lahuis et al. (2007) had only sparse X-ray data; in all cases the samples are
small and inhomogeneous, comprising stars in different star-forming
regions with different ages and distances.
Table 1: Observation parameters for the Spitzer/IRS and DROXO data.
In this contribution, we investigate the connections between the neon fine structure line emission and the stellar/circumstellar properties, with particular reference to the X-ray luminosity. We choose to focus onThis paper is organized as follows: we first introduce, in Sect. 2, the main X-ray and NIR data, as well as additional data both original and from the literature; in Sect. 3 we derive the quantities used for the subsequent analysis. We then compare the theoretical prediction for the X-ray ionization proxies with the observations (Sect. 4) and look for physically meaningful correlations between these and other stellar/circumstellar properties. Section 5 summarizes our results and presents our conclusions. An Appendix describes our method to characterize the YSOs in our sample by fitting theoretical models to their spectral energy distributions.
2 DROXO/Spitzer sample
In order to correlate the [Ne II] and [Ne III] line strengths with
the stellar X-ray emission and with the properties of the
circumstellar material, we decided to focus on a physically
homogeneous and well characterized sample of YSOs. Our sample includes
YSOs that: i) belong to the ![]() Ophiuchi star forming region, and
are therefore both young and relatively coeval; ii) have been
observed with the Spitzer/IRS in high resolution mode; iii)
fall in the field of view of DROXO, and have therefore well
characterized X-ray emission.
Ophiuchi star forming region, and
are therefore both young and relatively coeval; ii) have been
observed with the Spitzer/IRS in high resolution mode; iii)
fall in the field of view of DROXO, and have therefore well
characterized X-ray emission.
2.1 Spitzer/IRS data
We started by searching the Spitzer archive for IRS observations
of ![]() Ophiuchi members in the XMM-Newton field (cf. Sect. 2.2) performed with the short-high module (SH:
Ophiuchi members in the XMM-Newton field (cf. Sect. 2.2) performed with the short-high module (SH:
![]()
![]() m;
m; ![]() ;
slit
size = 4.7
;
slit
size = 4.7
![]()
![]() 11.3
11.3
![]() ). Excluding GY 65, which was
identified by Luhman & Rieke (1999) as a background star, our sample consists
of 28 YSOs. Table 1 lists these objects, the
Spitzer program(s) under which they were observed, the total IRS
(SH) exposure times and the details of the observing strategy: the
number of exposures, the number of data collecting events (DCE) per
exposure, and the integration time for each DCE. Note that four
objects were targeted by two separate programs and have therefore been
observed twice.
). Excluding GY 65, which was
identified by Luhman & Rieke (1999) as a background star, our sample consists
of 28 YSOs. Table 1 lists these objects, the
Spitzer program(s) under which they were observed, the total IRS
(SH) exposure times and the details of the observing strategy: the
number of exposures, the number of data collecting events (DCE) per
exposure, and the integration time for each DCE. Note that four
objects were targeted by two separate programs and have therefore been
observed twice.
We downloaded the short-wavelength, high-resolution Basic Calibrated
Data (BCD) for the 28 stars in our sample from the Spitzer
archive. In order to produce final spectra, we used the tools
suggested on the Spitzer Science Center web
pages![]() .
Specifically, after removing bad pixels with IRSCLEAN v 1.9 we
extracted the spectra of each DCE in the Spitzer IRS Custom
Extraction (SPICE) v 2.0.4 environment. We then added all the
spectra from a given observation of a given target, from a minimum of
two (the two nod positions) up to 72. This leaves us with 32 spectra
(28 + 4 for the objects that were observed twice). Finally, we used
IRSFRINGE v 1.1 for the defringing. The background (sky)
emission as a function of wavelength was estimated using SPOT
.
Specifically, after removing bad pixels with IRSCLEAN v 1.9 we
extracted the spectra of each DCE in the Spitzer IRS Custom
Extraction (SPICE) v 2.0.4 environment. We then added all the
spectra from a given observation of a given target, from a minimum of
two (the two nod positions) up to 72. This leaves us with 32 spectra
(28 + 4 for the objects that were observed twice). Finally, we used
IRSFRINGE v 1.1 for the defringing. The background (sky)
emission as a function of wavelength was estimated using SPOT![]() , in steps
of 0.5
, in steps
of 0.5 ![]() m for
m for
![]() -19
-19 ![]() m and 0.01
m and 0.01 ![]() m for
m for
![]() -12.87
-12.87 ![]() m (the region of the [Ne II] line). These
values, computed for the sky coordinates of the objects and the
observation date, include the expected contributions from the Zodiacal
light, the interstellar medium, and the cosmic infrared
background
m (the region of the [Ne II] line). These
values, computed for the sky coordinates of the objects and the
observation date, include the expected contributions from the Zodiacal
light, the interstellar medium, and the cosmic infrared
background![]() .
They do not consider any eventual extended emission in the target
proximity. Note, however, that this should not affect our main
purpose, i.e. measuring the [Ne II] and [Ne III] line fluxes, since
emission from these lines is not expected from the cold molecular
cloud in the absence of hot ionizing stars. Previous observations of
YSOs have moreover indicated that the emission of these lines is
spatially unresolved at the Spitzer resolution (Lahuis et al. 2007).
Any continuum emission from the molecular cloud, if present, will thus
be subtracted along with the stellar continuum when measuring line
fluxes. However, multiple emission components, if present
within the Spitzer beam (4-5
.
They do not consider any eventual extended emission in the target
proximity. Note, however, that this should not affect our main
purpose, i.e. measuring the [Ne II] and [Ne III] line fluxes, since
emission from these lines is not expected from the cold molecular
cloud in the absence of hot ionizing stars. Previous observations of
YSOs have moreover indicated that the emission of these lines is
spatially unresolved at the Spitzer resolution (Lahuis et al. 2007).
Any continuum emission from the molecular cloud, if present, will thus
be subtracted along with the stellar continuum when measuring line
fluxes. However, multiple emission components, if present
within the Spitzer beam (4-5
![]() ), will obviously be included
in the [Ne II] and [Ne III] fluxes, including e.g. those that may be
associated with outflows as shown by van Boekel et al. (2009) for the T Tauri
system.
), will obviously be included
in the [Ne II] and [Ne III] fluxes, including e.g. those that may be
associated with outflows as shown by van Boekel et al. (2009) for the T Tauri
system.
Table 2: Stellar/circumstellar data for the objects in our sample (see Sect. 2.3).
Table 3: Parameters from SED fits(cf. Sect. A.2).
2.2 X-ray data
The deep rho Ophiuchi XMM-Newton observation (DROXO) is the most
sensitive X-ray exposure of the ![]() Oph star forming region
performed so far (Sciortino et al. 2006). It consists of an observation of
Core F performed with the XMM-Newton X-ray telescope
(Jansen et al. 2001). The nominal pointing position was
Oph star forming region
performed so far (Sciortino et al. 2006). It consists of an observation of
Core F performed with the XMM-Newton X-ray telescope
(Jansen et al. 2001). The nominal pointing position was
![]() :27:16.5,
:27:16.5,
![]() :40:06.8. The
observation, interrupted only by the constraints of the satellite
orbit, was carried out in five subsequent revolutions
(# 0961...# 0965), for a total exposure time of 515 ks. Here
we use data from the European Photon Imaging Camera
(EPIC; Strüder et al. 2001; Turner et al. 2001), consisting of three almost co-pointed
imaging detectors (MOS1, MOS2, and pn) sensitive to 0.3-10.0 keV
photons and with a combined field of view of
:40:06.8. The
observation, interrupted only by the constraints of the satellite
orbit, was carried out in five subsequent revolutions
(# 0961...# 0965), for a total exposure time of 515 ks. Here
we use data from the European Photon Imaging Camera
(EPIC; Strüder et al. 2001; Turner et al. 2001), consisting of three almost co-pointed
imaging detectors (MOS1, MOS2, and pn) sensitive to 0.3-10.0 keV
photons and with a combined field of view of ![]() 0.2 square degrees.
Source detection resulted in a list of 111 X-ray emitters, 60 of
which are identified with a mid-infrared object detected by
Bontemps et al. (2001) with ISOCAM at 6.7 and/or 14.3
0.2 square degrees.
Source detection resulted in a list of 111 X-ray emitters, 60 of
which are identified with a mid-infrared object detected by
Bontemps et al. (2001) with ISOCAM at 6.7 and/or 14.3 ![]() m. Details of the
data reduction and general results from DROXO are found in Pillitteri
et al. (2009, submitted). The present study is limited to the 28 YSOs with Spitzer/IRS coverage (see Sect. 2.1).
m. Details of the
data reduction and general results from DROXO are found in Pillitteri
et al. (2009, submitted). The present study is limited to the 28 YSOs with Spitzer/IRS coverage (see Sect. 2.1).
Twenty-two of our 28 YSOs are positionally matched with a DROXO source
using a 5
![]() identification radius. All the identifications are
unambiguous. Columns 5-7 of Table 4 list the
DROXO source numbers from Pillitteri et al. (2009) and, for all 28
objects, off-axis angles and effective exposure times at the YSO
position for the three EPIC detectors
identification radius. All the identifications are
unambiguous. Columns 5-7 of Table 4 list the
DROXO source numbers from Pillitteri et al. (2009) and, for all 28
objects, off-axis angles and effective exposure times at the YSO
position for the three EPIC detectors![]() . Six YSOs
are not detected in DROXO (see Sect. 3.1.2). In three
cases we used Chandra ACIS data from the literature. In the
remaining three cases, we have computed upper limits for the count
rate as described in Pillitteri et al. (2009). Chandra ACIS data
were also used for one of the DROXO-detected sources, IRS42/GY252. In
the DROXO data the photon extraction region for this object is
contaminated by a nearby bright source. The higher spatial resolution
Chandra data are not affected by this problem.
. Six YSOs
are not detected in DROXO (see Sect. 3.1.2). In three
cases we used Chandra ACIS data from the literature. In the
remaining three cases, we have computed upper limits for the count
rate as described in Pillitteri et al. (2009). Chandra ACIS data
were also used for one of the DROXO-detected sources, IRS42/GY252. In
the DROXO data the photon extraction region for this object is
contaminated by a nearby bright source. The higher spatial resolution
Chandra data are not affected by this problem.
2.3 Ancillary data and SED fits
We have collected additional data for our targets from which we derive
relevant physical parameters. A summary of the results is given in
Table 2. Column 2 lists the ISOCAM source number
from Bontemps et al. (2001); Col. 3 the YSO Class derived both from the
spectral slope between ![]() m and
m and ![]() m (reported from
Bontemps et al. 2001) and from our own model fitting of the SED (see below and
Appendix A). As detailed below, the two
classifications agree for 70% of the sources.
m (reported from
Bontemps et al. 2001) and from our own model fitting of the SED (see below and
Appendix A). As detailed below, the two
classifications agree for 70% of the sources.
Stellar parameters for Class II and III sources (according to our own classification based on SED fits) were estimated from the near-IR (2MASS) photometry. The procedure we have used follows closely that adopted by Bontemps et al. (2001) and improved by Natta et al. (2006). We assume that the J-band emission from these sources is dominated by the stellar photosphere and that it is only marginally contaminated by the emission from circumstellar material and that the IR colors of Class II sources can be approximated by emission from a passive circumstellar disk, as described by Meyer et al. (1997). These assumptions obviously do not apply to Class I sources and for this reason we do not derive photospheric parameters for these sources.
Our procedure starts with the dereddening of each object in the J-Hvs. H-K diagram to the locus of cTTS. As opposed to the procedure used by Natta et al. (2006), we have used the Cardelli et al. (1989) extinction law. Two sources have colors slightly bluer than those of reddened main-sequence stars, presumably due to photometric uncertainties. Dereddening these sources extrapolating the colors of Class II and III sources would produce an overestimation of the extinction. To minimize this effect, we have dereddened these sources to J-H=0.578.
The values we derive for the J-band extinction AJ (Col. 4 of Table 2) are very similar to the numbers in Natta et al. (2006). The one exception is WL 16 for which our procedure produces a significantly higher extinction.
Bolometric luminosities (Col. 5 of Table 2)
were estimated from the dereddened J band magnitudes and the
bolometric correction used by Natta et al. (2006):
![]() .
Stellar masses and effective temperatures
(Cols. 6 and 7) were obtained from
.
Stellar masses and effective temperatures
(Cols. 6 and 7) were obtained from
![]() assuming that stars
lie on the 0.5 Myr isochrone of the D'Antona & Mazzitelli (1997) evolutionary
tracks.
assuming that stars
lie on the 0.5 Myr isochrone of the D'Antona & Mazzitelli (1997) evolutionary
tracks.
As part of the DROXO program, we have obtained complementary IR
spectroscopy at the VLT using the ISAAC instrument and the same
observing modes described in Natta et al. (2006). Low-resolution spectra
(
![]() )
in the J or K band were obtained
for 12 of the 13 YSOs in our sample that had not been observed by
Natta et al. (2006), the exception being WL 19/GY 277. These spectra
comprise the Pa
)
in the J or K band were obtained
for 12 of the 13 YSOs in our sample that had not been observed by
Natta et al. (2006), the exception being WL 19/GY 277. These spectra
comprise the Pa![]() and Br
and Br![]() lines that we use to measure
accretion luminosities and mass accretion rates. For the reduction of
the ISAAC data and the measurements of the Pa
lines that we use to measure
accretion luminosities and mass accretion rates. For the reduction of
the ISAAC data and the measurements of the Pa![]() or Br
or Br![]() line we followed the procedures described by Natta et al. (2006). Accretion
luminosities (or upper limits), both from the new near-IR spectra and
from those of Natta et al. (2006), were then estimated from empirical
relations with the Pa
line we followed the procedures described by Natta et al. (2006). Accretion
luminosities (or upper limits), both from the new near-IR spectra and
from those of Natta et al. (2006), were then estimated from empirical
relations with the Pa![]() or Br
or Br![]() luminosities
(Natta et al. 2004;Calvet et al. 2004). They are listed in Col. 8 of
Table 2. Mass accretion rates (or upper
limits), listed in Col. 9 of the same table, were calculated from
luminosities
(Natta et al. 2004;Calvet et al. 2004). They are listed in Col. 8 of
Table 2. Mass accretion rates (or upper
limits), listed in Col. 9 of the same table, were calculated from
![]() and the photospheric parameters derived from the near-IR
photometry. They were therefore computed only for YSOs for which these
latter parameters are available, i.e. Class II and Class III objects
with complete 2MASS photometry. As a result, the new near-IR spectra
add only one accretion rate (for IRS 54/GY 378) and two upper limits
(for GY 253 and IRS 51/GY 315) to the values in Natta et al. (2006).
and the photospheric parameters derived from the near-IR
photometry. They were therefore computed only for YSOs for which these
latter parameters are available, i.e. Class II and Class III objects
with complete 2MASS photometry. As a result, the new near-IR spectra
add only one accretion rate (for IRS 54/GY 378) and two upper limits
(for GY 253 and IRS 51/GY 315) to the values in Natta et al. (2006).
Table 4: Results from the analysis of the Spitzer/IRS and DROXO datasets (cf. Sects. 3.1 and 3.2).
Given the fragmentary nature of the above described system parameters,
we strive to obtain a more complete and homogeneous set of estimates
by fitting the SEDs of our objects with star/disk/envelope models. The
details of the procedure, as well as the tests we performed to
ascertain its usefulness, are described in the Appendix. Table 3 lists, for each source, the quality of the fit
(the ![]() of the ``best-fit'' model) and the adopted values, with
uncertainties
of the ``best-fit'' model) and the adopted values, with
uncertainties![]() , for
the following stellar and circumstellar parameters: extinction (the
sum of interstellar and envelope extinction), stellar effective
temperature and mass, disk mass, disk and envelope accretion rates.
The last column indicates the evolutionary stage assigned following
the criteria given by Robitaille et al. (2007), and reported in the Appendix
(Sect. A.2), based on the disk and envelope accretion rates
and on the disk mass. These definitions are meant to reproduce in most
cases the classical classification based on the SED slope (i.e.
Class I, II, and III), which is often used to describe the
evolutionary status of YSOs. The stages, being based on physical
quantities, have however the advantage of not depending on the
inclination of the system with respect to the line of sight or on the
effective temperature of the central object.
, for
the following stellar and circumstellar parameters: extinction (the
sum of interstellar and envelope extinction), stellar effective
temperature and mass, disk mass, disk and envelope accretion rates.
The last column indicates the evolutionary stage assigned following
the criteria given by Robitaille et al. (2007), and reported in the Appendix
(Sect. A.2), based on the disk and envelope accretion rates
and on the disk mass. These definitions are meant to reproduce in most
cases the classical classification based on the SED slope (i.e.
Class I, II, and III), which is often used to describe the
evolutionary status of YSOs. The stages, being based on physical
quantities, have however the advantage of not depending on the
inclination of the system with respect to the line of sight or on the
effective temperature of the central object.
Comparing the evolutionary stages from the SED fits with the IR
classes derived from the ISOCAM photometry
(Tables 2 and 3) we find
agreement in 19 out of 27 cases![]() (6, 11 and 2 Class/Stage I, II, and
III objects, respectively): 2 Class II objects according to the
ISOCAM classification are reclassified as Stage I and one as
Stage III; 4 Class I and 1 Class III are reclassified as Stage II.
In the following, we will base our discussion on the evolutionary
stages defined according to the results of the SED fits. However, in
order to use a more familiar terminology, when referring to the
``stages'', we will improperly adopt the term ``Class''.
(6, 11 and 2 Class/Stage I, II, and
III objects, respectively): 2 Class II objects according to the
ISOCAM classification are reclassified as Stage I and one as
Stage III; 4 Class I and 1 Class III are reclassified as Stage II.
In the following, we will base our discussion on the evolutionary
stages defined according to the results of the SED fits. However, in
order to use a more familiar terminology, when referring to the
``stages'', we will improperly adopt the term ``Class''.
3 Analysis
We here describe the steps taken to derive X-ray and [Ne II]/[Ne III] luminosities from the XMM-Newton and the Spitzer IRS data, respectively.
3.1 X-ray luminosities
We discuss separately the X-ray luminosities of the 21 YSOs for which an analysis of the X-ray spectra from the DROXO observation was possible (cf. Sect. 2.2), and those of the remaining 7 objects for which we either make use of previous Chandra ACIS observations or we compute upper limits from the DROXO data. We will then discuss possible biases and uncertainties on the X-ray luminosities due to the high source absorption and to their intrinsic variability.
3.1.1 Spectral analysis of DROXO sources
For the 21 YSOs with usable DROXO data, the observed low-resolution X-ray spectra were fitted with simple emission models convolved with the detector response using XSPEC v.12.3.1 (Arnaud 1996) as described by Pillitteri et al. (2009). We analyzed the time-averaged spectra accumulated during times of low background, i.e. excluding the intense background flares due to solar soft protons. This is the same time filter used by Pillitteri et al. (2009) for source detection, as it maximized the sensitivity to faint sources. It is not, however, the same filter used by Pillitteri et al. (2009) for spectral analysis. This latter differs from source to source and was devised to maximize the S/N by including times of high background when the source is bright enough to contribute positively to the S/N. Although the resulting spectra have higher S/N than those based on the universal time filter we use here, the ensuing luminosities are not suitable for our purpose as they do not scale linearly with the time-averaged luminosities.
As done by Pillitteri et al. (2009), in many cases we fitted
simultaneously data from all three EPIC instruments. In other cases,
the combined fits were statistically unsatisfactory because of
cross-calibration issues![]() and we excluded one or two of the detectors. The choice of detectors
is the same as that of Pillitteri et al. (2009). In all cases, a model
of isothermal plasma emission (the APEC model in XSPEC) subject to
photoelectric absorption (WABS) from material in the line of sight is
found to be adequate. We adopted the plasma elemental abundances
derived by Maggio et al. (2007) for YSOs in the Orion Nebula Cluster (ONC).
In one case (EL29/GY214), the abundances of metals (all elements other
than H and He) had to be increased by a factor of 3.5, with respect to
the Maggio et al. (2007) values, in order to obtain a reasonable fit. The
spectra were fitted with a variety of initial parameters to avoid
ending up in a local minimum of the
and we excluded one or two of the detectors. The choice of detectors
is the same as that of Pillitteri et al. (2009). In all cases, a model
of isothermal plasma emission (the APEC model in XSPEC) subject to
photoelectric absorption (WABS) from material in the line of sight is
found to be adequate. We adopted the plasma elemental abundances
derived by Maggio et al. (2007) for YSOs in the Orion Nebula Cluster (ONC).
In one case (EL29/GY214), the abundances of metals (all elements other
than H and He) had to be increased by a factor of 3.5, with respect to
the Maggio et al. (2007) values, in order to obtain a reasonable fit. The
spectra were fitted with a variety of initial parameters to avoid
ending up in a local minimum of the ![]() space. The resulting fits
are all statistically reasonable, with a mean
space. The resulting fits
are all statistically reasonable, with a mean
![]() and a
maximum of 1.7. Results for the 21 usable DROXO sources (along with
X-ray luminosities or upper limits for the other 7 YSOs; see below),
are presented in Table 4, Cols. 6-9. For
each source we indicate the detector(s) used for the spectral
analysis, the
and a
maximum of 1.7. Results for the 21 usable DROXO sources (along with
X-ray luminosities or upper limits for the other 7 YSOs; see below),
are presented in Table 4, Cols. 6-9. For
each source we indicate the detector(s) used for the spectral
analysis, the ![]() and kT values from the spectral fits, and the
absorption corrected X-ray luminosity in the 0.3-10 keV band.
Statistical 90% confidence intervals for these quantities are also
given. For
and kT values from the spectral fits, and the
absorption corrected X-ray luminosity in the 0.3-10 keV band.
Statistical 90% confidence intervals for these quantities are also
given. For ![]() and kT these were obtained within XSPEC with the
error command, while for
and kT these were obtained within XSPEC with the
error command, while for ![]() they were propagated from
those on the plasma emission measures.
they were propagated from
those on the plasma emission measures.
3.1.2 Other objects
We then estimated fluxes, or upper limits, for the 7 YSOs without a
usable DROXO detection, marked in Table 4 by
footnotes in the ``Instr.'' column indicating the source of the quoted
![]() ,
kT, and
,
kT, and ![]() values. IRS42/GY252 was detected in
DROXO but, being contaminated by the wings of another bright source,
we prefer to use the luminosity obtained by Imanishi et al. (2001) from the
analysis of a Chandra ACIS spectrum, corrected for the different
distance assumptions and choice of energy bands. IRS37/GY244 was
also detected by Imanishi et al. (2001) but not in the DROXO data, possibly
because it lies close to the edge of the EPIC field and in the
PSF-wings of a brighter X-ray source. The X-ray luminosity given by
Imanishi et al. (2001) for IRS37/GY244 is, however, based on a poorly
constrained spectral fit and we, therefore, decided to estimate
values. IRS42/GY252 was detected in
DROXO but, being contaminated by the wings of another bright source,
we prefer to use the luminosity obtained by Imanishi et al. (2001) from the
analysis of a Chandra ACIS spectrum, corrected for the different
distance assumptions and choice of energy bands. IRS37/GY244 was
also detected by Imanishi et al. (2001) but not in the DROXO data, possibly
because it lies close to the edge of the EPIC field and in the
PSF-wings of a brighter X-ray source. The X-ray luminosity given by
Imanishi et al. (2001) for IRS37/GY244 is, however, based on a poorly
constrained spectral fit and we, therefore, decided to estimate ![]() from the ACIS count rate and a suitable conversion factor
(see below). The same method was adopted to estimate the
from the ACIS count rate and a suitable conversion factor
(see below). The same method was adopted to estimate the ![]() of IRS14/GY54 and WL16/GY182. These were detected as faint X-ray
sources by Flaccomio et al. (2003) in a re-analysis of the Chandra data
but no spectral analysis is possible due to the low photon statistics.
The remaining three objects, IRS48/GY304, WL11/GY229, and CRBR85, are
not detected in any X-ray dataset and we estimated upper limits to
their
of IRS14/GY54 and WL16/GY182. These were detected as faint X-ray
sources by Flaccomio et al. (2003) in a re-analysis of the Chandra data
but no spectral analysis is possible due to the low photon statistics.
The remaining three objects, IRS48/GY304, WL11/GY229, and CRBR85, are
not detected in any X-ray dataset and we estimated upper limits to
their ![]() from the upper limit to their XMM-Newton
(DROXO) count-rate.
from the upper limit to their XMM-Newton
(DROXO) count-rate.
Count-rate to luminosity conversion factors were thus employed for six
objects for which no reliable spectral anlaysis was possible, i.e.
three Chandra ACIS detections and three XMM-Newton upper
limits. The conversion factors were computed with the Portable,
Interactive Multi-Mission Simulator![]() (PIMMS) assuming an
isothermal plasma emission. This requires the assumption of a plasma
temperature, kT, and, more crucially, of an absorption column
density,
(PIMMS) assuming an
isothermal plasma emission. This requires the assumption of a plasma
temperature, kT, and, more crucially, of an absorption column
density, ![]() .
For the temperature we took kT = 3.4 keV, the
median of the kT values obtained from the X-ray spectral fits of the
DROXO detections in our sample. Absorption estimates were derived from
the AJ values in Table 2, when
available, and from the
.
For the temperature we took kT = 3.4 keV, the
median of the kT values obtained from the X-ray spectral fits of the
DROXO detections in our sample. Absorption estimates were derived from
the AJ values in Table 2, when
available, and from the ![]() values in
Table 3 in the remaining cases. AJ and
values in
Table 3 in the remaining cases. AJ and
![]() were converted to
were converted to ![]() following Vuong et al. (2003):
following Vuong et al. (2003):
![]() cm-2. To the three
cm-2. To the three ![]() estimates from the Chandra ACIS count-rates we assign a 90% uncertainty of 0.5 dex.
estimates from the Chandra ACIS count-rates we assign a 90% uncertainty of 0.5 dex.
3.1.3 Biases and uncertainties
Given the high absorption to which ![]() Ophiuchi members are
subject, we may wonder whether some or all of our X-ray luminosities
are biased by the fact that low temperature emission components may be
fully absorbed and therefore unaccounted for in the spectral fits. A
very soft X-ray emission like that of the evolved CTTS TW Hya
(e.g. Stelzer & Schmitt 2004), kT=0.2-0.3 keV, would indeed have remained
undetected in
Ophiuchi members are
subject, we may wonder whether some or all of our X-ray luminosities
are biased by the fact that low temperature emission components may be
fully absorbed and therefore unaccounted for in the spectral fits. A
very soft X-ray emission like that of the evolved CTTS TW Hya
(e.g. Stelzer & Schmitt 2004), kT=0.2-0.3 keV, would indeed have remained
undetected in ![]() Ophiuchi, as for a typical
Ophiuchi, as for a typical
![]() cm-2 the observed flux in the XMM-Newton band is reduced by a factor
cm-2 the observed flux in the XMM-Newton band is reduced by a factor ![]()
![]() ,
with
respect to the unabsorbed case. The X-ray spectrum of TW Hya is,
however, quite peculiar among YSOs. In the
,
with
respect to the unabsorbed case. The X-ray spectrum of TW Hya is,
however, quite peculiar among YSOs. In the ![]() 1 Myr old ONC, for
example, the Chandra Orion Ultradeep Project (COUP) observation
(Getman et al. 2005) indicates that, based on a sample of
1 Myr old ONC, for
example, the Chandra Orion Ultradeep Project (COUP) observation
(Getman et al. 2005) indicates that, based on a sample of ![]() 100 members
subject to little absorption (
100 members
subject to little absorption (
![]() cm-2) and
whose X-ray spectra are well fit by 2-T models, the high-temperature
component dominates the emission in most cases (80%) and, indeed, the
mean kT (weighted by the emission measures of the two components) is
>1.07 keV in 95% of the cases. We therefore argue that, if low
temperature components similar to those observed in the ONC should
remain indeed unobserved with our data, the resulting underestimation
of the X-ray luminosities would typically be less than a factor of
two.
cm-2) and
whose X-ray spectra are well fit by 2-T models, the high-temperature
component dominates the emission in most cases (80%) and, indeed, the
mean kT (weighted by the emission measures of the two components) is
>1.07 keV in 95% of the cases. We therefore argue that, if low
temperature components similar to those observed in the ONC should
remain indeed unobserved with our data, the resulting underestimation
of the X-ray luminosities would typically be less than a factor of
two.
Another source of uncertainty on the X-ray luminosities is their
intrinsic time variability. While a full study of YSO variability in
![]() Ophiuchi is beyond the scope of the present work, assessing its
effect is important when we correlate
Ophiuchi is beyond the scope of the present work, assessing its
effect is important when we correlate ![]() with other
quantities observed non-simultaneously with the X-ray observation.
Pillitteri et al. (2009) compare the average X-ray emission during the
DROXO observation with that detected during previous Chandra and
XMM-Newton observations of
with other
quantities observed non-simultaneously with the X-ray observation.
Pillitteri et al. (2009) compare the average X-ray emission during the
DROXO observation with that detected during previous Chandra and
XMM-Newton observations of ![]() Ophiuchi. The comparison
indicates that the activity levels, averaged over
Ophiuchi. The comparison
indicates that the activity levels, averaged over ![]() 1 day, which
is the typical length of the previous observations, usually vary by
less than a factor of 2 (1
1 day, which
is the typical length of the previous observations, usually vary by
less than a factor of 2 (1![]() )
over the timescale of years. The
variability within each X-ray observation, i.e. on the timescale of
hours, can however be much larger due to flares that can reach up to
)
over the timescale of years. The
variability within each X-ray observation, i.e. on the timescale of
hours, can however be much larger due to flares that can reach up to
![]() 100 times the quiescent X-ray luminosity. These large flares are
however not frequent. For the YSOs in the ONC, for example, an
analysis of the lightcurves in the COUP dataset along the lines of
Wolk et al. (2005) and Caramazza et al. (2007) indicates that the X-ray flux is above
the quiescent level
100 times the quiescent X-ray luminosity. These large flares are
however not frequent. For the YSOs in the ONC, for example, an
analysis of the lightcurves in the COUP dataset along the lines of
Wolk et al. (2005) and Caramazza et al. (2007) indicates that the X-ray flux is above
the quiescent level![]() by a factor of 2 or more for 10-15% of the time, and by a factor of 5 or more for
2-3% of the time. Making the simplifying assumption that the Spitzer IRS observations are much shorter than the timescale of the
X-ray variability, we can take these fractions as the fractions of
objects for which the Spitzer observations coincided with an
X-ray emission level above the characteristic level by more than the
specified factor. For the 28 objects in our sample, this implies 3-4 objects with a difference in
by a factor of 2 or more for 10-15% of the time, and by a factor of 5 or more for
2-3% of the time. Making the simplifying assumption that the Spitzer IRS observations are much shorter than the timescale of the
X-ray variability, we can take these fractions as the fractions of
objects for which the Spitzer observations coincided with an
X-ray emission level above the characteristic level by more than the
specified factor. For the 28 objects in our sample, this implies 3-4 objects with a difference in ![]() of a factor of >2 and
of a factor of >2 and ![]() 1 with a difference of a factor of >5.
1 with a difference of a factor of >5.
3.2 [Ne II] and [Ne III] line luminosities
The estimation of neon line luminosities is performed in two steps: the direct measurement of fluxes from the reduced IRS spectra and the correction for extinction.
3.2.1 Fluxes
We measured the [Ne II] and [Ne III] line fluxes,
![]() and
and
![]() ,
by integrating the spectra in the
,
by integrating the spectra in the
![]() -12.83
-12.83 ![]() m and
m and
![]() -15.57
-15.57 ![]() m intervals,
respectively. The underlying continuum was subtracted by fitting a
polynomial to two intervals on the left and right of the lines:
12.71-12.78
m intervals,
respectively. The underlying continuum was subtracted by fitting a
polynomial to two intervals on the left and right of the lines:
12.71-12.78 ![]() m and 12.84-12.91
m and 12.84-12.91 ![]() m for [Ne II] and
15.45-15.53
m for [Ne II] and
15.45-15.53 ![]() m and 15.58-15.65
m and 15.58-15.65 ![]() m for [Ne III]. The degree of
the polynomial ranged between 1 and 3 and the fit was repeated after
excluding datapoints that deviated more than 2
m for [Ne III]. The degree of
the polynomial ranged between 1 and 3 and the fit was repeated after
excluding datapoints that deviated more than 2![]() from a first
fit. The 1
from a first
fit. The 1![]() uncertainties on the fluxes,
uncertainties on the fluxes,
![]() and
and
![]() ,
were then estimated by propagating the
uncertainties on the individual spectral bins, taken as the maximum
between the formal uncertainties given by the reduction process and
the 1
,
were then estimated by propagating the
uncertainties on the individual spectral bins, taken as the maximum
between the formal uncertainties given by the reduction process and
the 1![]() dispersion of the continuum fit. The lines were
considered detected if the signal to noise ratio,
dispersion of the continuum fit. The lines were
considered detected if the signal to noise ratio,
![]() ,
was
>3. In the opposite case, upper limits were computed as
,
was
>3. In the opposite case, upper limits were computed as
![]() +3
+3 ![]() .
As indicated in
Sect. 2.1, four YSOs have spectra from two separate
observations: since the Ne lines are not detected in any of the
spectra of these four objects, we report the most stringent of the
upper limits and the continuum fluxes of the relative spectra.
.
As indicated in
Sect. 2.1, four YSOs have spectra from two separate
observations: since the Ne lines are not detected in any of the
spectra of these four objects, we report the most stringent of the
upper limits and the continuum fluxes of the relative spectra.
The [Ne II] line was detected in 10 YSOs, i.e. ![]() 36% of our
sample, while the [Ne III] line is detected only in one star,
WL5/GY246, interestingly the brightest in X-rays in our sample (Sect. 4.2) and likely a Class III object (see below).
Figure 1 shows the 10 detected [Ne II] lines and
the single detected [Ne III] line. Gaussian profiles centered at the
nominal line wavelengths and with normalizations from the measured
fluxes are superimposed on the observed spectra.
36% of our
sample, while the [Ne III] line is detected only in one star,
WL5/GY246, interestingly the brightest in X-rays in our sample (Sect. 4.2) and likely a Class III object (see below).
Figure 1 shows the 10 detected [Ne II] lines and
the single detected [Ne III] line. Gaussian profiles centered at the
nominal line wavelengths and with normalizations from the measured
fluxes are superimposed on the observed spectra.
One of our YSOs, IRS 51/GY 315, was also included in the study of
Lahuis et al. (2007) using c2d data and here we use the same spectrum. Our 3![]() upper limits on [Ne II] and [Ne III] fluxes are
upper limits on [Ne II] and [Ne III] fluxes are ![]() 20%
and
20%
and ![]() 50% higher than implied by the 1
50% higher than implied by the 1![]() upper limits of
Lahuis et al. (2007). We attribute the discrepancy to the differences between
the two measuring procedures.
upper limits of
Lahuis et al. (2007). We attribute the discrepancy to the differences between
the two measuring procedures.
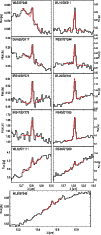 |
Figure 1:
Spitzer/IRS spectra in the [Ne II] 12.81 |
| Open with DEXTER | |
Table 5: Different estimates of the J-band extinction for the objects in our sample, and adopted values (cf. Sect. 3.2.2).
3.2.2 Extinction correction and luminosities
In order to correct the line (and continuum) fluxes for extinction, we
have chosen, for each of our YSO, a best-guess extinction (![]() )
from the up to three estimates at our disposal. The AJvalues from Table 2, estimated from the 2MASS
photometry, were adopted when available. We otherwise estimated
AJ from the
)
from the up to three estimates at our disposal. The AJvalues from Table 2, estimated from the 2MASS
photometry, were adopted when available. We otherwise estimated
AJ from the ![]() values given by the X-ray spectral
fits (Table 4), converted according to
Vuong et al. (2003) (
values given by the X-ray spectral
fits (Table 4), converted according to
Vuong et al. (2003) (
![]()
![]() ). In the
absence of the previous two estimates, we computed AJ from
the
). In the
absence of the previous two estimates, we computed AJ from
the ![]() values given by the SED model fits and listed in
Table 3:
AJ=0.282
values given by the SED model fits and listed in
Table 3:
AJ=0.282 ![]() (Rieke & Lebofsky 1985). We make an exception to this rule for WL12/GY111, for
which the
(Rieke & Lebofsky 1985). We make an exception to this rule for WL12/GY111, for
which the ![]() value is very uncertain and we prefer to use the
extinctions from the SED fit. Table 5 lists these
three estimates, along with uncertainties for the latter two, and the
adopted AJ value. For extinctions taken from
Table 2, we adopted a 1
value is very uncertain and we prefer to use the
extinctions from the SED fit. Table 5 lists these
three estimates, along with uncertainties for the latter two, and the
adopted AJ value. For extinctions taken from
Table 2, we adopted a 1![]() uncertainty
of 1 mag.
uncertainty
of 1 mag.
The choice of extinction-law, i.e., of the two ratios
A12.81/AJand
A15.55/AJ, for the [Ne II] and [Ne III] lines,
respectively, is critical for the derivation of unabsorbed line
fluxes. The extinction law at these wavelengths, in between two strong
silicates absorption features at 9.7 ![]() m and 18
m and 18 ![]() m, is not well
established and seems to depend significantly on the grain
characteristics (Weingartner & Draine 2001; Draine 2003). Chapman et al. (2009) have recently
established that, for stars in the
m, is not well
established and seems to depend significantly on the grain
characteristics (Weingartner & Draine 2001; Draine 2003). Chapman et al. (2009) have recently
established that, for stars in the ![]() Ophiuchi region with low
absorption (AK<0.5), the RV=3.1 extinction law computed by
Weingartner & Draine (2001) for a ``standard'' grain size distribution fits the
measurements between 1.25
Ophiuchi region with low
absorption (AK<0.5), the RV=3.1 extinction law computed by
Weingartner & Draine (2001) for a ``standard'' grain size distribution fits the
measurements between 1.25 ![]() m to 24
m to 24 ![]() m. The extinction law of
highly absorbed stars (AK>2), however, is better reproduced by the
RV=5.5 Weingartner & Draine (2001) extinction law, implying grain growth in the
dense parts of the cloud. Since, with one exception, the stars in our
sample are highly extinguished, we adopt the RV=5.5 extinction law
and specifically
A12.81/AJ=0.16 and
A15.55/AJ=0.13.
m. The extinction law of
highly absorbed stars (AK>2), however, is better reproduced by the
RV=5.5 Weingartner & Draine (2001) extinction law, implying grain growth in the
dense parts of the cloud. Since, with one exception, the stars in our
sample are highly extinguished, we adopt the RV=5.5 extinction law
and specifically
A12.81/AJ=0.16 and
A15.55/AJ=0.13.
With AJ ranging from 0.7 to 25 mag, the resulting correction
factors for the [Ne II] 12.81 ![]() m line fluxes range from
m line fluxes range from ![]() 1.1 to
1.1 to ![]() 39 (mean: 5.9). Note that the difference with respect
to the RV=3.1 extinction law is significant: had we adopted it
(
A12.81/AJ=0.097), the 12.81
39 (mean: 5.9). Note that the difference with respect
to the RV=3.1 extinction law is significant: had we adopted it
(
A12.81/AJ=0.097), the 12.81 ![]() m correction factor would have
ranged from 1.1 to 9.5 (mean 2.7)
m correction factor would have
ranged from 1.1 to 9.5 (mean 2.7)![]() .
.
[Ne II] and [Ne III] line luminosities were derived from the measured fluxes, assuming a distance of 120 pc. The resulting line luminosities and upper limits for the whole sample are listed in Table 4, along with absorption-corrected continuum flux densities at the nominal line wavelengths. The reported uncertainties reflect measurement errors as well as uncertainties in AJ, but neglect possible systematic uncertainties related to the extinction law.
We conclude this section with a cautionary note: the adopted extinction values refer to the central objects. The luminosity corrections are thus valid only if the bulk of the [Ne II] and [Ne III] lines originates in the proximity of the YSOs. This assumptions may be false for emission from shocks associated with jets and outflows.
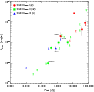 |
Figure 2:
[Ne II] 12.81 |
| Open with DEXTER | |
4 Results
4.1 The [Ne II] line
We detect [Ne II] ![]() m line emission in 10 out of the
28 YSOs observed with Spitzer/IRS within the DROXO field of view
(cf. Fig. 1). In one case, WL5/GY246, we also
detect the [Ne III]
m line emission in 10 out of the
28 YSOs observed with Spitzer/IRS within the DROXO field of view
(cf. Fig. 1). In one case, WL5/GY246, we also
detect the [Ne III] ![]() m line. All the [Ne II] detections
in
m line. All the [Ne II] detections
in ![]() Oph are X-ray sources: 9 are DROXO sources and the tenth,
IRS37/GY244, was detected in an earlier Chandra observation
(Imanishi et al. 2001, see Sect. 3.1.2). Conversely the line
is not detected in any of the three X-ray undetected objects.
Oph are X-ray sources: 9 are DROXO sources and the tenth,
IRS37/GY244, was detected in an earlier Chandra observation
(Imanishi et al. 2001, see Sect. 3.1.2). Conversely the line
is not detected in any of the three X-ray undetected objects.
We investigated possible relations between the [Ne II] line emission and other physical parameters of the systems. First, however, we discuss an important observational bias, namely the dependence of our line detection sensitivity on the continuum intensity. Figure 2 shows the relation between the [Ne II] line luminosity and the continuum flux density at the same wavelength. Both quantities are corrected for interstellar extinction and stars of different evolutionary classes are plotted with different symbols. The lower boundary of detections and upper limits clearly shows a positive correlation, most likely due to the expected anti-correlation between the detection sensitivity and the counting-statistic uncertainties (that increase with the continuum). The upper envelope, however, also shows a correlation, which is independent of this detection bias and whose physical origin is unclear. Figure 2 also indicates that Class I objects have higher continuum flux densities and [Ne II] line luminosities than Class II and Class III objects. This is not immediately interpretable in terms of the X-ray excitation mechanism discussed in the introduction.
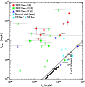 |
Figure 3:
[Ne II] luminosity vs. |
| Open with DEXTER | |
Figure 3 shows the scatter plot between the [Ne II]
line luminosity and ![]() in the 0.3-10 keV band
in the 0.3-10 keV band![]() . We also plot the six T-Tauri stars in the Pascucci et al. (2007)
sample (four [Ne II] detections and two upper limits) and two stars
(CS Cha and TW Hya) from Espaillat et al. (2007). Also shown are the
theoretical predictions by MGN 08, calculated, as a function of
. We also plot the six T-Tauri stars in the Pascucci et al. (2007)
sample (four [Ne II] detections and two upper limits) and two stars
(CS Cha and TW Hya) from Espaillat et al. (2007). Also shown are the
theoretical predictions by MGN 08, calculated, as a function of
![]() ,
assuming the D'Alessio et al. (1999) disk model (
,
assuming the D'Alessio et al. (1999) disk model (
![]() ,
,
![]() ,
,
![]() ,
,
![]() yr-1), and the predictions of GH 08 for their fiducial
model (model ``A'':
yr-1), and the predictions of GH 08 for their fiducial
model (model ``A'':
![]() ,
,
![]() ,
,
![]() ,
,
![]() yr-1,
yr-1,
![]() erg/s) and two variations: model ``B'' (with 100 times
lower dust opacity, taken to represent an evolved disk) and model
``D'' (with 10 times higher FUV flux).
erg/s) and two variations: model ``B'' (with 100 times
lower dust opacity, taken to represent an evolved disk) and model
``D'' (with 10 times higher FUV flux).
Three conclusions are apparent: i) no overall trend of increasing
[Ne II] line luminosity with ![]() is apparent; ii) two of the
10 measured [Ne II] luminosities, those of DoAr 25 and
WL 5/GY 246, as well as the 18 upper limits, are consistent with
predictions by current models for X-ray ionization of the disk; iii)
the remaining 8 measured [Ne II] luminosities are 1 to 3 orders of
magnitude brighter than predicted. With respect to this latter point,
it is important to note, however, that the authors of both
calculations stress that their models refer to objects with specific
star and disk parameters and are moreover affected by several
uncertainties, e.g. in the atomic physics, in the simplified disk
models that do not include holes, gaps, and rims, and in the current
lack of EUV photoexcitation. Our findings indeed confirm these
suspicions, and indicate that physical parameters other than
is apparent; ii) two of the
10 measured [Ne II] luminosities, those of DoAr 25 and
WL 5/GY 246, as well as the 18 upper limits, are consistent with
predictions by current models for X-ray ionization of the disk; iii)
the remaining 8 measured [Ne II] luminosities are 1 to 3 orders of
magnitude brighter than predicted. With respect to this latter point,
it is important to note, however, that the authors of both
calculations stress that their models refer to objects with specific
star and disk parameters and are moreover affected by several
uncertainties, e.g. in the atomic physics, in the simplified disk
models that do not include holes, gaps, and rims, and in the current
lack of EUV photoexcitation. Our findings indeed confirm these
suspicions, and indicate that physical parameters other than ![]() are likely to be important in determining the [Ne II] line
luminosity.
are likely to be important in determining the [Ne II] line
luminosity.
Rather than a connection with ![]() ,
Fig. 3
indeed suggests that the [Ne II] flux might be related to the
evolutionary state of the YSOs, Class I being the strongest and
Class III the faintest emitters. The position of TW Hya and of the
six Pascucci et al. (2007) ``transition disk''-systems, seems consistent with
this interpretation. CS Cha, also believed to host a transition disk,
has however a strong [Ne II] emission, in line with that of most of
the [Ne II] detections in our sample. Within our sample, the higher
[Ne II] luminosity of Class I objects with respect to Class II ones
is confirmed with significances ranging from 99.8% to 99.99% by the
five two-population tests for censored data implemented in the
ASURV package (Feigelson & Nelson 1985; Isobe & Feigelson 1990).
,
Fig. 3
indeed suggests that the [Ne II] flux might be related to the
evolutionary state of the YSOs, Class I being the strongest and
Class III the faintest emitters. The position of TW Hya and of the
six Pascucci et al. (2007) ``transition disk''-systems, seems consistent with
this interpretation. CS Cha, also believed to host a transition disk,
has however a strong [Ne II] emission, in line with that of most of
the [Ne II] detections in our sample. Within our sample, the higher
[Ne II] luminosity of Class I objects with respect to Class II ones
is confirmed with significances ranging from 99.8% to 99.99% by the
five two-population tests for censored data implemented in the
ASURV package (Feigelson & Nelson 1985; Isobe & Feigelson 1990).
 |
Figure 4:
[Ne II] luminosity vs. M* ( left panel) and
|
| Open with DEXTER | |
The overall lack of correlation with X-ray luminosity leads us to
investigate possible correlations of the [Ne II] emission with other
stellar and circumstellar parameters. Figure 4
shows the relations with disk mass accretion rate and with stellar
mass, both estimated from the SED fits. Also shown are the MGN 08 and
the GH 08 model predictions. The most fundamental of stellar
parameters, mass, does not seem to influence the [Ne II] luminosity.
At any given mass, Class I objects have significantly higher line
luminosities than Class II and Class III ones; this points toward a
role of parameters related to the YSO evolution, such as matter
inflows and outflows. The [Ne II] luminosity seems indeed to to
correlate with ![]() .
Statistical tests for censored data, the
Generalized Kendall's
.
Statistical tests for censored data, the
Generalized Kendall's ![]() and the Spearman's
and the Spearman's ![]() as implemented
in the ASURV package, confirm the existence of a correlation
with
as implemented
in the ASURV package, confirm the existence of a correlation
with ![]() 99.5% confidence. The stars from Pascucci et al. (2007) and
Espaillat et al. (2007), shown in Fig. 4 but not used for
the correlation tests, appear compatible with our sample. The
correlation with
99.5% confidence. The stars from Pascucci et al. (2007) and
Espaillat et al. (2007), shown in Fig. 4 but not used for
the correlation tests, appear compatible with our sample. The
correlation with ![]() may also explain the correlation of the
[Ne II] luminosity with the continuum flux at 12.81
may also explain the correlation of the
[Ne II] luminosity with the continuum flux at 12.81 ![]() m (Fig. 2), as this latter correlates strongly with
m (Fig. 2), as this latter correlates strongly with ![]() (not shown, confidence
(not shown, confidence ![]() 99.99%). The [Ne II] -
99.99%). The [Ne II] -
![]() correlation might also explain, at least in part, the
difference in the [Ne II] luminosity among the different evolutionary
classes, as Class I objects have statistically higher accretion
rates.
correlation might also explain, at least in part, the
difference in the [Ne II] luminosity among the different evolutionary
classes, as Class I objects have statistically higher accretion
rates.
As for the discrepancy with the X-ray excitation models, we note that
three out of five Class I [Ne II] detections have nominal accretion
rates that are higher than those used as inputs for both of the models
considered here. This might be the reason for their higher than
predicted line luminosities. The other Class I [Ne II] detections,
WL 20 and IRS 37, however, have ![]() estimates that, although
with large uncertainties, are similar to those assumed by the X-ray
ionization models and still their line luminosity is much higher than
predicted. It is also possible that the [Ne II]-
estimates that, although
with large uncertainties, are similar to those assumed by the X-ray
ionization models and still their line luminosity is much higher than
predicted. It is also possible that the [Ne II]-![]() correlation
simply results from Class I objects having brighter line emission due
to a mechanism unrelated to disk mass accretion. One good candidate
might be the defining characteristics of Class I objects, i.e. high
envelope accretion rates and/or their associated outflows. Indeed the
[Ne II] luminosity also shows a significant correlation, at the
correlation
simply results from Class I objects having brighter line emission due
to a mechanism unrelated to disk mass accretion. One good candidate
might be the defining characteristics of Class I objects, i.e. high
envelope accretion rates and/or their associated outflows. Indeed the
[Ne II] luminosity also shows a significant correlation, at the
![]() 99.9% level, with the
99.9% level, with the
![]() values derived from
the SED fits.
values derived from
the SED fits.
4.2 The [Ne III] line
A spectral feature at ![]() 15.55
15.55 ![]() m, likely associated with a
[Ne III] transition, is detected in only one star, WL 5. An
alternative identification for the observed feature might be a water
rotational transition at 15.57
m, likely associated with a
[Ne III] transition, is detected in only one star, WL 5. An
alternative identification for the observed feature might be a water
rotational transition at 15.57 ![]() m, as detected e.g. by
Carr & Najita (2008) and Salyk et al. (2008) in three CTTs. The line observed from
WL 5 is however well centered at 15.55
m, as detected e.g. by
Carr & Najita (2008) and Salyk et al. (2008) in three CTTs. The line observed from
WL 5 is however well centered at 15.55 ![]() m (cf.
Fig. 1) and the wavelength difference to the water
line is significant:
m (cf.
Fig. 1) and the wavelength difference to the water
line is significant: ![]() 2 spectral bins or about the FWHM spectral
resolution. Moreover, the many other water lines that are seen in the
spectra published by Carr & Najita (2008) and Salyk et al. (2008) are not visible
in the part of the WL 5 spectrum shown in Fig. 1,
with the exception of a likely H2O line at 15.67
2 spectral bins or about the FWHM spectral
resolution. Moreover, the many other water lines that are seen in the
spectra published by Carr & Najita (2008) and Salyk et al. (2008) are not visible
in the part of the WL 5 spectrum shown in Fig. 1,
with the exception of a likely H2O line at 15.67 ![]() m. We are
therefore confident in the identification of the line as [Ne III].
m. We are
therefore confident in the identification of the line as [Ne III].
WL 5 is a Class III object and, according to its F7 spectral type
(Greene & Meyer 1995), one of the most massive/hottest objects of the sample
of [Ne II] detections (see the Appendix for a detailed discussion of
its properties). For both neon lines, WL 5 has the lowest observed (i.e. absorbed) continuum flux among the stars in which
[Ne II] was detected, thus facilitating the detections of the lines.
The luminosities of both neon lines compare reasonably well with the
prediction of MGN 08 for the ![]() of the object
(
of the object
(
![]() erg s-1): the [Ne II] line is only 7%
fainter than predicted (well within 1
erg s-1): the [Ne II] line is only 7%
fainter than predicted (well within 1![]() )
and the [Ne III] line
is 70% brighter than predicted (within 2
)
and the [Ne III] line
is 70% brighter than predicted (within 2![]() ).
).
All the other stars with [Ne II] detection in our sample have [Ne III] upper limits that are significantly higher and therefore compatible with the predictions of MGN 08. If we assume that the line ratios predicted by MGN 08, rather than the luminosities, are correct and use the measured [Ne II] line luminosities to predict [Ne III] luminosities, we conclude that, for 8 out of 9 stars, our detection sensitivity for [Ne III] is too low by a factor of 2.4-8. For the remaining case, IRS 43/GY 265, the star in our sample with the brightest [Ne II] line, the measured upper limit is only 10% higher than the predicted [Ne III] flux.
5 Summary and discussion
We investigated the origin of the [Ne II] and [Ne III] fine
structure lines by studying a sample of 28 ![]() Ophiuchi members in
the field of view of the DROXO deep X-ray observation and with
available Spitzer IRS data. The [Ne II] 12.81
Ophiuchi members in
the field of view of the DROXO deep X-ray observation and with
available Spitzer IRS data. The [Ne II] 12.81 ![]() m and the
[Ne III] 15.55
m and the
[Ne III] 15.55 ![]() m lines were detected in ten and one YSOs,
respectively; absorption corrected line luminosities and upper limits
for non-detections were computed and compared with predictions of
X-ray disk ionization models. Finally, we explored empirical relations
between [Ne II] line luminosity and stellar and circumstellar
parameters estimated by fitting the SEDs of the objects with
star/disk/envelope models.
m lines were detected in ten and one YSOs,
respectively; absorption corrected line luminosities and upper limits
for non-detections were computed and compared with predictions of
X-ray disk ionization models. Finally, we explored empirical relations
between [Ne II] line luminosity and stellar and circumstellar
parameters estimated by fitting the SEDs of the objects with
star/disk/envelope models.
The luminosities of the 10 detected [Ne II] lines are, for the most
part, 1-3 dex higher than predicted by models of X-ray irradiated (and
ionized) circumstellar disks. Moreover, the [Ne II] luminosities do
not correlate with the X-ray luminosities. We conclude that, if these
lines are indeed produced by X-ray ionization, factors other than ![]() are also important for the line production. Published
models might still be valid: since they assume given star and disk
characteristics (or a few variations), it is possible that some of
these assumptions are critical and that they do not correspond to the
characteristics of most of our stars. Other excitation mechanisms
might, however, turn out to be more important than X-rays, such as
strong shocks resulting from the interaction of the stellar wind and
jets with circumstellar material (van Boekel et al. 2009; Hartmann & Raymond 1989; Hollenbach & McKee 1989).
are also important for the line production. Published
models might still be valid: since they assume given star and disk
characteristics (or a few variations), it is possible that some of
these assumptions are critical and that they do not correspond to the
characteristics of most of our stars. Other excitation mechanisms
might, however, turn out to be more important than X-rays, such as
strong shocks resulting from the interaction of the stellar wind and
jets with circumstellar material (van Boekel et al. 2009; Hartmann & Raymond 1989; Hollenbach & McKee 1989).
Interestingly, the [Ne II] luminosities of two of the objects in our
sample, DoAr 25 and WL 5/GY 246, match the theoretical prediction
for X-ray irradiated disks remarkably well. DoAr 25 is a Class II
object with a mass accretion rate similar to that assumed by the
models we have used for comparison. WL 5 is, based on its SED between 1 and 8 ![]() m, a Class III object, but we cannot exclude the
presence of a gas disk or a dust disk with a large inner hole. It
might be similar to the four stars with transitional disks studied by
Brown et al. (2007), for one of which, T Cha, the [Ne II] line was
detected by Lahuis et al. (2007). WL 5 is, moreover, together with Sz 102
(Lahuis et al. 2007), the second YSO for which a detection of the [Ne III]
line has been reported. As for the [Ne II] line, the luminosity of
the [Ne III] line of WL 5 is roughly consistent with theoretical
predictions for the X-ray irradiation mechanism. Also largely
consistent with this mechanism are the upper limits to the
luminosities of the undetected [Ne II] and [Ne III] lines.
m, a Class III object, but we cannot exclude the
presence of a gas disk or a dust disk with a large inner hole. It
might be similar to the four stars with transitional disks studied by
Brown et al. (2007), for one of which, T Cha, the [Ne II] line was
detected by Lahuis et al. (2007). WL 5 is, moreover, together with Sz 102
(Lahuis et al. 2007), the second YSO for which a detection of the [Ne III]
line has been reported. As for the [Ne II] line, the luminosity of
the [Ne III] line of WL 5 is roughly consistent with theoretical
predictions for the X-ray irradiation mechanism. Also largely
consistent with this mechanism are the upper limits to the
luminosities of the undetected [Ne II] and [Ne III] lines.
The [Ne II] 12.81 ![]() m line luminosity correlates with the
continuum flux at the same wavelength. While the lower envelope of the
relation may be explained by a sensitivity bias, the upper envelope
likely reflects a correlation with some physical characteristics to
which the continuum flux is related. The disk accretion rate, which we
have found to correlate with the continuum flux at 12.81
m line luminosity correlates with the
continuum flux at the same wavelength. While the lower envelope of the
relation may be explained by a sensitivity bias, the upper envelope
likely reflects a correlation with some physical characteristics to
which the continuum flux is related. The disk accretion rate, which we
have found to correlate with the continuum flux at 12.81 ![]() m, is
one candidate, and indeed the [Ne II] luminosity correlates with it.
A tentative physical explanation of the correlation might involve the
increased EUV flux produced in the accretion shock, provided that this
latter is able to reach and significantly ionize neon atoms above the
accretion disk. Alternatively, given the correlation generally found
between accretion and outflow rates, the correlation might result from
the [Ne II] emission being produced in outflow-related shocks, as
mentioned above. Finally, the statistical correlation might be
unphysical, and simply driven by the higher accretion rates of
Class I objects combined with their higher [Ne II] luminosities.
m, is
one candidate, and indeed the [Ne II] luminosity correlates with it.
A tentative physical explanation of the correlation might involve the
increased EUV flux produced in the accretion shock, provided that this
latter is able to reach and significantly ionize neon atoms above the
accretion disk. Alternatively, given the correlation generally found
between accretion and outflow rates, the correlation might result from
the [Ne II] emission being produced in outflow-related shocks, as
mentioned above. Finally, the statistical correlation might be
unphysical, and simply driven by the higher accretion rates of
Class I objects combined with their higher [Ne II] luminosities.
Indeed, Class I objects, i.e. those with significant envelope accretion, have significantly higher [Ne II] luminosities than Class II objects. We propose that the presence of a circumstellar envelope and/or envelope accretion and/or the strong associated outflows, i.e. the defining characteristics of Class I objects, plays a role in determining the line emission. Larger YSO samples and more sophisticated theoretical models are needed to pinpoint the production mechanism of these gas-tracing lines and to derive a consistent picture of the environment around YSOs at different evolutionary stages.
Acknowledgements
We acknowledge financial support by the Agenzia Spaziale Italiana. This work is based in part on observations made with the Spitzer Space Telescope and with XMM-Newton. Spitzer is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. XMM-Newton is an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. We thank the anonymous referee for numerous and insightful comments and suggestions.
References
- Alexander, R. D. 2008, MNRAS, 391, L64 [NASA ADS] (In the text)
- Allen, L. E., Myers, P. C., Di Francesco, et al. 2002, ApJ, 566, 993 [NASA ADS] [CrossRef]
- Andre, P., & Montmerle, T. 1994, ApJ, 420, 837 [NASA ADS] [CrossRef] (In the text)
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 (In the text)
- Bontemps, S., André, P., Kaas, A. A., et al. 2001, A&A, 372, 173 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Brandner, W., Sheppard, S., Zinnecker, H., et al. 2000, A&A, 364, L13 [NASA ADS]
- Brown, J. M., Blake, G. A., Dullemond, C. P., et al. 2007, ApJ, 664, L107 [NASA ADS] [CrossRef] (In the text)
- Calvet, N., Muzerolle, J., Briceño, C., et al. 2004, AJ, 128, 1294 [NASA ADS] [CrossRef] (In the text)
- Caramazza, M., Flaccomio, E., Micela, G., et al. 2007, ArXiv e-prints, 706 (In the text)
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] (In the text)
- Carr, J. S., & Najita, J. R. 2008, Science, 319, 1504 [NASA ADS] [CrossRef] (In the text)
- Cecchi-Pestellini, C., Ciaravella, A., & Micela, G. 2006, A&A, 458, L13 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chapman, N. L., Mundy, L. G., Lai, S.-P., & Evans, N. J. 2009, ApJ, 690, 496 [NASA ADS] [CrossRef] (In the text)
- D'Alessio, P., Canto, J., Calvet, N., & Lizano, S. 1998, ApJ, 500, 411 [NASA ADS] [CrossRef]
- D'Alessio, P., Calvet, N., Hartmann, L., Lizano, S., & Cantó, J. 1999, ApJ, 527, 893 [NASA ADS] [CrossRef] (In the text)
- D'Antona, F., & Mazzitelli, I. 1997, Mem. Soc. Astron. Ital., 68, 807 [NASA ADS] (In the text)
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef]
- Ercolano, B., Drake, J. J., Raymond, J. C., & Clarke, C. C. 2008, ApJ, 688, 398 [NASA ADS] [CrossRef]
- Espaillat, C., Calvet, N., D'Alessio, P., et al. 2007, ApJ, 664, L111 [NASA ADS] [CrossRef] (In the text)
- Evans, II, N. J., Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [NASA ADS] [CrossRef] (In the text)
- Feigelson, E. D., & Montmerle, T. 1999, ARA&A, 37, 363 [NASA ADS] [CrossRef] (In the text)
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef]
- Flaccomio, E., Micela, G., & Sciortino, S. 2003, A&A, 402, 277 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef]
- Getman, K. V., Flaccomio, E., Broos, P. S., et al. 2005, ApJS, 160, 319 [NASA ADS] [CrossRef] (In the text)
- Glassgold, A. E., Najita, J., & Igea, J. 1997, ApJ, 480, 344 [NASA ADS] [CrossRef]
- Glassgold, A. E., Najita, J., & Igea, J. 2004, ApJ, 615, 972 [NASA ADS] [CrossRef] (In the text)
- Glassgold, A. E., Najita, J. R., & Igea, J. 2007, ApJ, 656, 515 [NASA ADS] [CrossRef] (In the text)
- Gorti, U., & Hollenbach, D. 2008, ApJ, 683, 287 [NASA ADS] [CrossRef]
- Greene, T. P., & Meyer, M. R. 1995, ApJ, 450, 233 [NASA ADS] [CrossRef] (In the text)
- Hartmann, L., & Raymond, J. C. 1989, ApJ, 337, 903 [NASA ADS] [CrossRef]
- Herczeg, G. J., Najita, J. R., Hillenbrand, L. A., & Pascucci, I. 2007, ApJ, 670, 509 [NASA ADS] [CrossRef]
- Hollenbach, D., & McKee, C. F. 1989, ApJ, 342, 306 [NASA ADS] [CrossRef]
- Ilgner, M., & Nelson, R. P. 2006, A&A, 455, 731 [NASA ADS] [CrossRef] [EDP Sciences]
- Imanishi, K., Koyama, K., & Tsuboi, Y. 2001, ApJ, 557, 747 [NASA ADS] [CrossRef] (In the text)
- Isobe, T., & Feigelson, E. D. 1990, BAAS, 22, 917 [NASA ADS]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] (In the text)
- Lahuis, F., van Dishoeck, E. F., Blake, G. A., et al. 2007, ApJ, 665, 492 [NASA ADS] [CrossRef] (In the text)
- Lombardi, M., Lada, C., & Alves, J. 2008, ArXiv e-prints, 801 (In the text)
- Lorenzani, A., & Palla, F. 2001, in From Darkness to Light: Origin and Evolution of Young Stellar Clusters, ed. T. Montmerle, & P. André, ASP Conf. Ser., 243, 745 (In the text)
- Luhman, K. L., & Rieke, G. H. 1999, ApJ, 525, 440 [NASA ADS] [CrossRef] (In the text)
- Maggio, A., Flaccomio, E., Favata, F., et al. 2007, ApJ, 660, 1462 [NASA ADS] [CrossRef] (In the text)
- Meijerink, R., Glassgold, A. E., & Najita, J. R. 2008, ApJ, 676, 518 [NASA ADS] [CrossRef]
- Meyer, M. R., Calvet, N., & Hillenbrand, L. A. 1997, AJ, 114, 288 [NASA ADS] [CrossRef] (In the text)
- Najita, J., Carr, J. S., Glassgold, A. E., Shu, F. H., & Tokunaga, A. T. 1996, ApJ, 462, 919 [NASA ADS] [CrossRef] (In the text)
- Natta, A., Testi, L., Muzerolle, J., et al. 2004, A&A, 424, 603 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Natta, A., Testi, L., & Randich, S. 2006, A&A, 452, 245 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pascucci, I., Hollenbach, D., Najita, J., et al. 2007, ApJ, 663, 383 [NASA ADS] [CrossRef] (In the text)
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] (In the text)
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., Wood, K., & Denzmore, P. 2006, ApJS, 167, 256 [NASA ADS] [CrossRef] (In the text)
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., & Wood, K. 2007, ApJS, 169, 328 [NASA ADS] [CrossRef] (In the text)
- Salyk, C., Pontoppidan, K. M., Blake, G. A., et al. 2008, ApJ, 676, L49 [NASA ADS] [CrossRef] (In the text)
- Sciortino, S., Pillitteri, I., Damiani, F., et al. 2006, in The X-ray Universe 2005, ed. A. Wilson, ESA SP-604, 111 (In the text)
- Stanke, T., Smith, M. D., Gredel, R., & Khanzadyan, T. 2006, A&A, 447, 609 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stelzer, B., & Schmitt, J. H. M. M. 2004, A&A, 418, 687 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences]
- van Boekel, R., Güdel, M., Henning, T., Lahuis, F., & Pantin, E. 2009, A&A, 497, 137 [NASA ADS] [CrossRef] [EDP Sciences]
- Vuong, M. H., Montmerle, T., Grosso, N., et al. 2003, A&A, 408, 581 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef]
- Wilking, B. A.,
Gagné, M., & Allen, L. E. 2008, Star Formation in the
 Ophiuchi Molecular Cloud, ed. B. Reipurth, 351
(In the text)
Ophiuchi Molecular Cloud, ed. B. Reipurth, 351
(In the text) - Wolk, S. J., Harnden, Jr., F. R., Flaccomio, E., et al. 2005, ApJS, 160, 423 [NASA ADS] [CrossRef] (In the text)
- Yakubov, S. D. 1992, Sov.t Astron. Lett., 18, 311 [NASA ADS] (In the text)
Online Material
Appendix A: (Circum)Stellar parameters from SED fits
 |
Figure A.1:
Comparison between mass accretion rates from the literature
and those derived from SED fits for the sample of T-Tauri stars
considered in Robitaille et al. (2006). SED fits and determination of parameter
ranges were performed as for the |
| Open with DEXTER | |
In this appendix, we describe how we constrained some stellar and circumstellar parameters of the objects in our sample by comparing their SEDs with the theoretical models of Robitaille et al. (2006). These consist of a grid of 200 000 model SEDs that include contributions from the central star, the circumstellar disk, and the envelope, parametrized with 14 parameters. The models that best approximate the observed SEDs were found with the aid of the Web-based tool presented by Robitaille et al. (2007). As stated by Robitaille et al. (2007), and in accord with basic principles, this method does not allow the simultaneous determination of all 14 physical parameters, since the SEDs are often defined by less than 14 independent fluxes. However, depending on the available fluxes, some of the parameters can be constrained more narrowly than others. We are interested here, in particular, in obtaining the range of values compatible with the observed SEDs for: i) the extinction toward our objects; ii) their disk accretion rates.
A.1 The method and its validation
Our procedure follows closely that of Robitaille et al. (2007): from the Web
interface we obtain, for each object, a list of the 1000 models that
best approximate the observed SEDs, i.e. those with the smallest ![]() .
Our ``best guess'' parameter values and associated
confidence intervals are then derived by selecting a set of statistically reasonable models and computing the median and the
.
Our ``best guess'' parameter values and associated
confidence intervals are then derived by selecting a set of statistically reasonable models and computing the median and the
![]()
![]() quantiles of the parameter values for these models. The
statistically reasonable models were defined as those with reduced
quantiles of the parameter values for these models. The
statistically reasonable models were defined as those with reduced
![]() ,
where
,
where
![]() refers to
the best fit model, or if this condition results in less than 10 models, the 10 models with smallest
refers to
the best fit model, or if this condition results in less than 10 models, the 10 models with smallest ![]() .
Note that, because
the uncertainties on the observed SEDs are not well defined (see
below), and the parameter space is sampled only discretely by the
adopted grid of models, the statistical significance of the thus
derived confidence intervals cannot be easily assessed.
.
Note that, because
the uncertainties on the observed SEDs are not well defined (see
below), and the parameter space is sampled only discretely by the
adopted grid of models, the statistical significance of the thus
derived confidence intervals cannot be easily assessed.
A similar method![]() was tested by Robitaille et al. (2007) by considering a sample of
Taurus-Auriga objects for which stellar and circumstellar parameters
had been derived independently in the literature and comparing these
parameters with those obtained from fitting the SEDs, defined from the
optical to millimeter wavelengths. In the case of our heavily absorbed
was tested by Robitaille et al. (2007) by considering a sample of
Taurus-Auriga objects for which stellar and circumstellar parameters
had been derived independently in the literature and comparing these
parameters with those obtained from fitting the SEDs, defined from the
optical to millimeter wavelengths. In the case of our heavily absorbed
![]() Ophiuchi YSOs, the SEDs lack, with the exception of one star,
data in the optical bands, i.e. those more directly affected by the
accretion-shock emission. In order to test our ability to constrain
the accretion rates in the absence of optical information, we repeated
the SED fits of the Taurus-Auriga stars of Robitaille et al. (2007), using the
same datapoints to define the SEDs, and both including and excluding
the optical magnitudes. The results are shown in
Fig. A.1. Panel a), analogous to Fig. 2b in
Robitaille et al. (2007), compares the accretion rates derived from the SED fits,
including optical data, with independent values from the literature.
Panel b) compares the results of the SED fits without the optical
magnitudes with the literature data. The agreement between the two
quantities is acceptable and may actually be considered better than in
the former panel: the reduced
Ophiuchi YSOs, the SEDs lack, with the exception of one star,
data in the optical bands, i.e. those more directly affected by the
accretion-shock emission. In order to test our ability to constrain
the accretion rates in the absence of optical information, we repeated
the SED fits of the Taurus-Auriga stars of Robitaille et al. (2007), using the
same datapoints to define the SEDs, and both including and excluding
the optical magnitudes. The results are shown in
Fig. A.1. Panel a), analogous to Fig. 2b in
Robitaille et al. (2007), compares the accretion rates derived from the SED fits,
including optical data, with independent values from the literature.
Panel b) compares the results of the SED fits without the optical
magnitudes with the literature data. The agreement between the two
quantities is acceptable and may actually be considered better than in
the former panel: the reduced ![]() ,
computed from the identity
relation considering only uncertainties on
,
computed from the identity
relation considering only uncertainties on
![]() ,
is indeed
reduced from
,
is indeed
reduced from ![]() 12 to 1.7. This can in part be attributed to the
increased error bars; note, however, that the average of the unsigned
differences, abs(
12 to 1.7. This can in part be attributed to the
increased error bars; note, however, that the average of the unsigned
differences, abs(
![]() ), is almost
unchanged, 0.49 dex for panel a) and 0.48 dex for panel b).
Panel c) compares the
), is almost
unchanged, 0.49 dex for panel a) and 0.48 dex for panel b).
Panel c) compares the ![]() from the SED fits with and without
optical magnitudes, showing that the two sets of values agree within
uncertainties. We conclude that the SEDs defined from IR to
millimeter wavelengths are indeed sensitive to the accretion rate, at
least in the
from the SED fits with and without
optical magnitudes, showing that the two sets of values agree within
uncertainties. We conclude that the SEDs defined from IR to
millimeter wavelengths are indeed sensitive to the accretion rate, at
least in the ![]() range covered by the Taurus-Auriga sample:
log
range covered by the Taurus-Auriga sample:
log
![]() .
.
This is due to the effect of viscous heating affecting the disk
thermal structure. To exemplify this effect we plot in
Fig. A.2, as a function of accretion rate, the ratio
between the IRAC 3 band and the J-band flux, for the Robitaille et al. (2006)
models for stars with mass between 0.7 and 1.3 ![]() ,
age between 1 and 2 Myr (implying little or no circumstellar envelope), and low
disk inclination with respect to the line of sight (
,
age between 1 and 2 Myr (implying little or no circumstellar envelope), and low
disk inclination with respect to the line of sight (
![]() ).
We plot with different symbols models with disk inner radii in
different ranges, since the inner hole affects the flux at the IRAC 3
wavelength (5.8
).
We plot with different symbols models with disk inner radii in
different ranges, since the inner hole affects the flux at the IRAC 3
wavelength (5.8 ![]() m). A relation between the two quantities is
seen for models with moderate inner disk holes, apparently
characterized by different regimes in three different
m). A relation between the two quantities is
seen for models with moderate inner disk holes, apparently
characterized by different regimes in three different ![]() ranges:
ranges:
![]() ,
,
![]() ,
and
,
and
![]() .
The factor of
.
The factor of ![]() 2 scatter
around this relation may likely be attributed to model variations
within the specified parameter ranges and to the several other
unconstrained model parameters. Similar and even more pronounced
trends are apparent in analogous plots using fluxes in longer
wavelength IRAC and MIPS bands, with the expected difference that at
the longer wavelengths, emitted farther out in the disk, the size of
the inner hole has a much smaller effect. The three regimes in
Fig. A.2 can be understood as follows: i) for
large accretion rates,
2 scatter
around this relation may likely be attributed to model variations
within the specified parameter ranges and to the several other
unconstrained model parameters. Similar and even more pronounced
trends are apparent in analogous plots using fluxes in longer
wavelength IRAC and MIPS bands, with the expected difference that at
the longer wavelengths, emitted farther out in the disk, the size of
the inner hole has a much smaller effect. The three regimes in
Fig. A.2 can be understood as follows: i) for
large accretion rates,
![]() ,
the flux in
the IRAC band, emitted by the inner disk (R<1 AU), is significantly
affected by viscous accretion (D'Alessio et al. 1998,1999); ii) for
,
the flux in
the IRAC band, emitted by the inner disk (R<1 AU), is significantly
affected by viscous accretion (D'Alessio et al. 1998,1999); ii) for
![]() disk heating is
dominated by the stellar photospheric emission and, consequently, no
relation between the IRAC flux and
disk heating is
dominated by the stellar photospheric emission and, consequently, no
relation between the IRAC flux and ![]() is observed; iii) for
is observed; iii) for
![]() we again observe a direct
relation between the IRAC 3 flux and
we again observe a direct
relation between the IRAC 3 flux and ![]() ,
which we attribute to
the fact that these low accretion rates correspond, in the
Robitaille et al. (2006) model grid, to very low disk masses (
,
which we attribute to
the fact that these low accretion rates correspond, in the
Robitaille et al. (2006) model grid, to very low disk masses (
![]() for the
for the ![]() 1 solar mass stars
plotted in Fig. A.2). Since, in the model grid, disk
mass and accretion are directly correlated and such low mass disks are
optically thin (Robitaille et al. 2006), lower accretion rates imply lower disk
mass and lower emission in the IRAC band. The IRAC 3 flux vs.
1 solar mass stars
plotted in Fig. A.2). Since, in the model grid, disk
mass and accretion are directly correlated and such low mass disks are
optically thin (Robitaille et al. 2006), lower accretion rates imply lower disk
mass and lower emission in the IRAC band. The IRAC 3 flux vs.
![]() correlation in this regime does not therefore imply that
that the mid-IR SED carries direct information on disk
accretion.
correlation in this regime does not therefore imply that
that the mid-IR SED carries direct information on disk
accretion.
As a result of this discussion, in the derivation of accretion rates
for our ![]() Ophiuchi sample from the SED fits, we decided not to
use values below
Ophiuchi sample from the SED fits, we decided not to
use values below
![]() yr-1. In such cases we
instead conservatively assigned upper limits to
yr-1. In such cases we
instead conservatively assigned upper limits to ![]() equal to the
maximum between
equal to the
maximum between
![]() yr-1 and the upper end of
the
yr-1 and the upper end of
the ![]() confidence interval (see above).
confidence interval (see above).
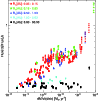 |
Figure A.2:
Scatter plot of the ratio between the flux in the IRAC 1
band over that in J, as a function of
disk accretion rate, according to the Robitaille et al. (2006) models for a solar
mass stars. Each point corresponds to one of the Robitaille et al. (2006) models
satisfying the following conditions: mass of the central object
between 0.7 and 1.3 |
| Open with DEXTER | |
A.2 The  Ophiuchi sample
Ophiuchi sample
We collected photometric measurements and uncertainties (when
available) for our ![]() Ophiuchi sample from several sources: J,
H, and
Ophiuchi sample from several sources: J,
H, and ![]() magnitudes (or upper limits) were taken for almost all
objects from 2 MASS
magnitudes (or upper limits) were taken for almost all
objects from 2 MASS![]() ; Spitzer IRAC (bands 1-4) and MIPS (bands 1 &
2) photometry was collected from the c2d database
; Spitzer IRAC (bands 1-4) and MIPS (bands 1 &
2) photometry was collected from the c2d database![]() (Evans et al. 2003); 1.2 mm
fluxes were collected from Stanke et al. (2006) and 1.3 mm fluxes from
Andre & Montmerle (1994)
(Evans et al. 2003); 1.2 mm
fluxes were collected from Stanke et al. (2006) and 1.3 mm fluxes from
Andre & Montmerle (1994)![]() . Optical
. Optical
![]() photometry for one object
with small absorption (DoAr 25) was taken from Yakubov (1992). Table A.1 lists all the photometric flux densities collected
from the literature.
photometry for one object
with small absorption (DoAr 25) was taken from Yakubov (1992). Table A.1 lists all the photometric flux densities collected
from the literature.
Finally, we complement the photometric data with flux densities from
the IRS spectra (cf. Sect. 2.1). We computed flux
densities between 10 and 18 ![]() m, at regular wavelength intervals
spaced by 0.5
m, at regular wavelength intervals
spaced by 0.5 ![]() m. Each flux density was taken as the average of the
spectral bins in 0.2
m. Each flux density was taken as the average of the
spectral bins in 0.2 ![]() m intervals centered at the nominal
wavelength. For the four stars with two IRS observations, we have
taken the average of the two spectra. (In three cases the
wavelength-averaged fluxes differ by less than 0.1 dex, while in one
case, EL29/GY214, the difference is 0.4 dex. In all cases we verified
that the results of the model fits did not change appreciably choosing
either of the two spectra). Table A.2 lists the
flux densities from the IRS spectra. As stated in
Sect. 2.1 our sky subtraction procedure does not
take into account diffuse nebular emission. In order to assess the
significance of diffuse emission on the object flux densities, we have
considered the IRS spectra of the 13 YSOs in our sample observed in
the context of the Spitzer legacy program From Molecular
Cores to Planet-Forming Disks (``c2d'', Evans et al. 2003). As with the
entire c2d sample, the reduced/sky-subtracted IRS spectra have been
analyzed (and made publicly available) by the c2d team, using a
sophisticated extraction and sky subtraction method based on the
modelling of the cross dispersion profiles (Lahuis et al. 2007). We have
compared the flux densities derived from the c2d-reduced spectra with
those derived from the same spectra reduced by us. We find the spectra
to be similar, with both the maximum and the wavelength-averaged
discrepancy decreasing with object intensity. The maximum discrepancy
falls below 10% for the 9 YSOs with c2d-reduced spectra that have an
average flux >0.5 Jy. Based on this comparison, and noting that the
c2d objects are representative of our sample in their position with
respect to nebulosity seen in IRAC and MIPS maps, we decided to use
the IRS-derived fluxes to define the SEDs of the 17 stars with average
IRS flux >0.5 Jy.
m intervals centered at the nominal
wavelength. For the four stars with two IRS observations, we have
taken the average of the two spectra. (In three cases the
wavelength-averaged fluxes differ by less than 0.1 dex, while in one
case, EL29/GY214, the difference is 0.4 dex. In all cases we verified
that the results of the model fits did not change appreciably choosing
either of the two spectra). Table A.2 lists the
flux densities from the IRS spectra. As stated in
Sect. 2.1 our sky subtraction procedure does not
take into account diffuse nebular emission. In order to assess the
significance of diffuse emission on the object flux densities, we have
considered the IRS spectra of the 13 YSOs in our sample observed in
the context of the Spitzer legacy program From Molecular
Cores to Planet-Forming Disks (``c2d'', Evans et al. 2003). As with the
entire c2d sample, the reduced/sky-subtracted IRS spectra have been
analyzed (and made publicly available) by the c2d team, using a
sophisticated extraction and sky subtraction method based on the
modelling of the cross dispersion profiles (Lahuis et al. 2007). We have
compared the flux densities derived from the c2d-reduced spectra with
those derived from the same spectra reduced by us. We find the spectra
to be similar, with both the maximum and the wavelength-averaged
discrepancy decreasing with object intensity. The maximum discrepancy
falls below 10% for the 9 YSOs with c2d-reduced spectra that have an
average flux >0.5 Jy. Based on this comparison, and noting that the
c2d objects are representative of our sample in their position with
respect to nebulosity seen in IRAC and MIPS maps, we decided to use
the IRS-derived fluxes to define the SEDs of the 17 stars with average
IRS flux >0.5 Jy.
As suggested by Robitaille et al. (2007), in order to account for systematic uncertainties, underestimation of the measurement errors, and intrinsic object variability over time, a lower limit of 25%, 10%, and 40% was imposed on the uncertainties of optical, NIR/MIR, and millimeter fluxes, respectively.
Figure A.3 exemplifies the ``fitting'' procedure
described in Sect. A.1 for three of our YSOs. It shows
the SEDs with the best fit models and the distributions of two fit
parameters, ![]() and
and
![]() ,
both for the 1000 models with lowest
,
both for the 1000 models with lowest ![]() and for the statistically reasonable
ones (cf. A.1). SEDs and best fit models for the 28 YSOs in our sample are shown in Fig. A.4.
and for the statistically reasonable
ones (cf. A.1). SEDs and best fit models for the 28 YSOs in our sample are shown in Fig. A.4.
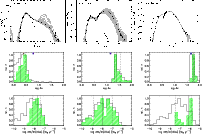 |
Figure A.3:
Examples of SED fits for three objects in our sample with
[Ne II] detections. From left to right: DoAr25/GY17, WL20/GY240, and
IRS44/GY269. The first is classified as Stage/Class II, the other two as
Stage/Class I. The upper row shows the SEDs and the best fit models as
produced by the Web interface provided by Robitaille et al. (2006). For the
datapoints, detections and upper limits are indicated by circles and
triangles, respectively. The lower two rows represent distributions of
two fit parameters, |
| Open with DEXTER | |
 |
Figure A.4: SEDs and best fit models, as produced by the Web interface provided by Robitaille et al. (2006), for the 28 YSOs in our sample. |
| Open with DEXTER | |
Following visual examination of the SED fits and of the distributions
of model parameters used to define the confidence intervals, we
decided to modify the input datapoints for two objects: for
IRS45/GY273 we excluded the 1.2 and 1.3 mm datapoints from
Stanke et al. (2006) and Andre & Montmerle (1994); including these
points significantly worsened the quality of the fit and had a
significant effect on the values of the parameters. The 1.2 mm flux
is >20 times higher than the 1.3 mm flux (an upper limit) and
can probably be attributed to an extended source that includes
our YSO. For GY289, a source with average IRS flux <0.5 Jy, we
decided to include the IRS datapoints because: i) they agree quite
well with the MIPS fluxes at similar wavelengths; ii) the quality of
the model fit is reasonable (
![]() )
and; iii) the
confidence intervals of the model parameters are narrower but
compatible with those from the fit performed without these points.
)
and; iii) the
confidence intervals of the model parameters are narrower but
compatible with those from the fit performed without these points.
For one object, WL5/GY246, we could not obtain a unique fit with the above procedure. The object was previously classified as a deeply absorbed Class III star with an F7 spectral type (Greene & Meyer 1995), and our SED was defined by J, H, K, Spitzer IRAC 1-4 and 1.2/1.3 mm fluxes. Fits both with and without the mm fluxes, likely contaminated by nearby sources (cf. Stanke et al. 2006; Andre & Montmerle 1994), consistently yield high envelope and/or disk accretion rates, typical of a Class I object, but having little effect on the NIR/MIR part of the SED due to the associated large inner disk radii. The NIR/MIR SED can however be fit equally well by purely photospheric ``Phoenix'' models, as suggested by the same Robitaille et al. (2007) web interface used to fit the star/disk/envelope models. We thus decided to assume that WL5/GY246 is a Class III object and to derive its extinction, effective temperature, and stellar mass using the J, H, and K photometry, the spectral type, and the calibrations tabulated by Kenyon & Hartmann (1995). Uncertainties were estimated from the assumed uncertainty on the spectral type, one subclass, and the range of values obtained by estimating the absorption from the J-H, H-K, and J-K colors.
Table 3, introduced in the main text (Sect. 2.3), lists the outcome of the SED-fit process: the
quality of the fit (the ![]() of the ``best-fit'' model), the
object extinction (the sum of interstellar and envelope extinction),
the stellar effective temperature and mass, the disk mass, the disk
and envelope accretion rates, the evolutionary Stage. The last
quantity was assigned following Robitaille et al. (2007). Stage I:
of the ``best-fit'' model), the
object extinction (the sum of interstellar and envelope extinction),
the stellar effective temperature and mass, the disk mass, the disk
and envelope accretion rates, the evolutionary Stage. The last
quantity was assigned following Robitaille et al. (2007). Stage I:
![]() ;
Stage II:
;
Stage II:
![]() and
and
![]() ;
Stage III:
;
Stage III:
![]() and
and
![]() .
As indicated in the main
text, in order to use a designation more familiar to researchers in
the field, we also refer to the ``Stages'' as ``Classes''.
.
As indicated in the main
text, in order to use a designation more familiar to researchers in
the field, we also refer to the ``Stages'' as ``Classes''.
Figures A.5 and A.6 compare the
extinction values (![]() )
and stellar
)
and stellar
![]() obtained
from the SED fits with the same parameters listed in
Table 2 for Class II and Class III stars.
Given the considerable uncertainties of both determinations, the SED
fits yield results similar to those obtained with the method of
Natta et al. (2006). A similar comparison with the accretion rates derived
from the Pa
obtained
from the SED fits with the same parameters listed in
Table 2 for Class II and Class III stars.
Given the considerable uncertainties of both determinations, the SED
fits yield results similar to those obtained with the method of
Natta et al. (2006). A similar comparison with the accretion rates derived
from the Pa![]() and Br
and Br![]() NIR line fluxes (in
Table 2) is less conclusive due to the large number
of upper limits and to the large uncertainties that affect the
spectroscopic measurements as well as the SED fits. Seven objects can
be used for the comparison, having accretion rate estimates or upper
limits from both methods. For only two stars, both methods yield
estimates: those for IRS 54 are in good agreement; for WL 16 the
spectroscopic estimate is 2.6 dex higher than the value from the SED
fits,
NIR line fluxes (in
Table 2) is less conclusive due to the large number
of upper limits and to the large uncertainties that affect the
spectroscopic measurements as well as the SED fits. Seven objects can
be used for the comparison, having accretion rate estimates or upper
limits from both methods. For only two stars, both methods yield
estimates: those for IRS 54 are in good agreement; for WL 16 the
spectroscopic estimate is 2.6 dex higher than the value from the SED
fits,
![]()
![]() yr-1. The discrepancy is
however reduced to 1.2 dex when comparing the result of the SED fit
with the Natta et al. (2006) value. Moreover, the derivation of
yr-1. The discrepancy is
however reduced to 1.2 dex when comparing the result of the SED fit
with the Natta et al. (2006) value. Moreover, the derivation of ![]() from the Pa
from the Pa![]() line with the method of Natta et al. (2006, see also Sect. 2.3# is better suited for cool stars and is
likely to yield inaccurate results for WL 16 (
line with the method of Natta et al. (2006, see also Sect. 2.3# is better suited for cool stars and is
likely to yield inaccurate results for WL 16 (
![]() K). An independent estimate by Najita et al. (1996) yielded
an upper limit compatible with the SED value:
K). An independent estimate by Najita et al. (1996) yielded
an upper limit compatible with the SED value:
![]()
![]() yr-1. Three other stars have
yr-1. Three other stars have
![]() estimates from the SED fits and upper limits from
Table 2: in two cases, IRS 51 and IRS 47,
the confidence intervals from the SED fits are consistent with the
upper limits; for DoAr 25/GY17, the only star with optical
magnitudes, the SED fit yields an accretion rate that is 1.6 dex
higher than the upper limit from the Pa
estimates from the SED fits and upper limits from
Table 2: in two cases, IRS 51 and IRS 47,
the confidence intervals from the SED fits are consistent with the
upper limits; for DoAr 25/GY17, the only star with optical
magnitudes, the SED fit yields an accretion rate that is 1.6 dex
higher than the upper limit from the Pa![]() line. Finally, for two
stars, WL 10 and WL 11, the spectroscopic estimates are 0.4 dex and
0.1 dex larger than the upper limits from the SED fits. The
discrepancy is however reduced to 0.24 dex for WL 10 and disappears
for WL 11 if the slightly larger
line. Finally, for two
stars, WL 10 and WL 11, the spectroscopic estimates are 0.4 dex and
0.1 dex larger than the upper limits from the SED fits. The
discrepancy is however reduced to 0.24 dex for WL 10 and disappears
for WL 11 if the slightly larger ![]() values from Natta et al. (2006)
are considered instead of those in Table 2.
values from Natta et al. (2006)
are considered instead of those in Table 2.
A.3 Summary
In this Appendix we have shown that the SED models of Robitaille et al. (2006), although undeniably approximate, can be useful to constrain parameters such as the line-of-sight absorption and the disk accretion rate, even in the absence of optical photometry. Although resulting uncertainties in these parameters are often large, the constraints are by and large compatible with independent determinations obtained with more direct methods.
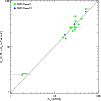 |
Figure A.5:
Comparison of the |
| Open with DEXTER | |
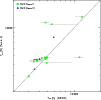 |
Figure A.6: Same as Fig. A.5 for the effective temperatures. |
| Open with DEXTER | |
Table A.1: Flux densities, in mJy, collected from the literature (cf. Sect. A.2) and used for the SED fits.
Table A.2: Flux densities, in Jy, obtained from the IRS spectra for the SED fits.
Footnotes
- ... DROXO
![[*]](/icons/foot_motif.png)
- Appendix A is only available in electronic form at http://www.aanda.org
- ...
rate
![[*]](/icons/foot_motif.png)
- Note, however, that the four [Ne II] detections of
Pascucci et al. (2007) span very small ranges of [Ne II] line and X-ray
luminosities, both
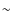 0.2 dex, comparable with uncertainties. The
same applies to
0.2 dex, comparable with uncertainties. The
same applies to 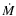 ,
for which the range is 0.5 dex.
,
for which the range is 0.5 dex.
- ...
pages
![[*]](/icons/foot_motif.png)
- http://ssc.spitzer.caltech.edu/postbcd/irs_reduction.html
- ... SPOT
![[*]](/icons/foot_motif.png)
- http://ssc.spitzer.caltech.edu/propkit/spot
- ...
background
![[*]](/icons/foot_motif.png)
- http://ssc.spitzer.caltech.edu/documents/background
- ... detectors
![[*]](/icons/foot_motif.png)
- The off-axis angle gives an indication of the quality of the point spread function, which is sharpest on the optical axis; the effective exposure times are normalized values taking into account the vignetting of the optical system and the detector efficiency at the source position.
- ...
uncertainties
![[*]](/icons/foot_motif.png)
- As noted in the Appendix, Sect. A.1, the statistical significance of uncertainties is not easily assessed; the plausibility of the uncertainties on disk mass accretion rates is, however, indicated by a comparison with independent estimates from the literaure for a control sample of stars in the Taurus-Aurigae region (cf. Fig. A.1).
- ... cases
![[*]](/icons/foot_motif.png)
- As described in the Appendix, we rejected the result of the SED fits for one of our 28 YSOs, WL5/GY246. We consider it as a Class III object, i.e. the same Class given by the ISOCAM photometry, and derive its parameters from the spectral type and NIR photometry.
- ... issues
![[*]](/icons/foot_motif.png)
- One or both of the following: i) the source falls on a gap between the CCDs in one of the detectors, and we are unable to properly account for the missing part of the PSF; ii) the source is intense and the statistical uncertainties per spectral bin are lower than the precision of the cross-calibration.
- ... Simulator
![[*]](/icons/foot_motif.png)
- http://heasarc.gsfc.nasa.gov/Tools/w3pimms.html
- ... level
![[*]](/icons/foot_motif.png)
- More precisely, the ``characteristic level'' as defined by Wolk et al. (2005) and Caramazza et al. (2007).
- ... (mean 2.7)
![[*]](/icons/foot_motif.png)
- The correction factors
computed from the two extinction laws differ significantly only for
high extinctions: for DoAr 25, AJ=0.7, the difference is
only
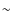 4%.
4%.
- ... band
![[*]](/icons/foot_motif.png)
- The
choice of energy band is not particularly important: had we
restricted
 to E>0.87 keV, i.e. to photons relevant for
the K-shell ionization of Ne, the points in Fig. 3
would have shifted downward by 0.05-0.15 dex depending on the plasma
temperature.
to E>0.87 keV, i.e. to photons relevant for
the K-shell ionization of Ne, the points in Fig. 3
would have shifted downward by 0.05-0.15 dex depending on the plasma
temperature.
- ... method
![[*]](/icons/foot_motif.png)
- Robitaille et al. (2007) took the confidence interval
for each parameter as the full range of values in the selected models,
and the ``best guess'' values as those of the model with minimum
 .
.
- ... 2 MASS
![[*]](/icons/foot_motif.png)
- The J-band flux of WL5/GY246 and the H-band flux of CRBR85 were taken from Allen et al. (2002) (converted from the HST bands); the J-band upper limit for CRBR85 was taken from Brandner et al. (2000).
- ... database
![[*]](/icons/foot_motif.png)
- Photometry extracted from the final (November 2007) c2d data delivery, selected according to the following conditions on quality flags: ``detection quality flag'' equal to ``A'', ``B'', or ``U''; ``image type'' equal to ``0'' for MIPS2 and different from ``-2'' and ``0'' for IRAC and MIPS1; ``flux quality'' flag equal to ``A'', ``B'', or empty.
- ...Andre & Montmerle (1994)
![[*]](/icons/foot_motif.png)
- Seven total fluxes from spatially resolved maps (Table 2 in Andre & Montmerle 1994), and 15 peak fluxes or upper limits (from Table 1 in the same work), converted to total flux with the factors suggested by the authors.
All Tables
Table 1: Observation parameters for the Spitzer/IRS and DROXO data.
Table 2: Stellar/circumstellar data for the objects in our sample (see Sect. 2.3).
Table 3: Parameters from SED fits(cf. Sect. A.2).
Table 4: Results from the analysis of the Spitzer/IRS and DROXO datasets (cf. Sects. 3.1 and 3.2).
Table 5: Different estimates of the J-band extinction for the objects in our sample, and adopted values (cf. Sect. 3.2.2).
Table A.1: Flux densities, in mJy, collected from the literature (cf. Sect. A.2) and used for the SED fits.
Table A.2: Flux densities, in Jy, obtained from the IRS spectra for the SED fits.
All Figures
 |
Figure 1:
Spitzer/IRS spectra in the [Ne II] 12.81 |
| Open with DEXTER | |
| In the text | |
 |
Figure 2:
[Ne II] 12.81 |
| Open with DEXTER | |
| In the text | |
 |
Figure 3:
[Ne II] luminosity vs. |
| Open with DEXTER | |
| In the text | |
 |
Figure 4:
[Ne II] luminosity vs. M* ( left panel) and
|
| Open with DEXTER | |
| In the text | |
 |
Figure A.1:
Comparison between mass accretion rates from the literature
and those derived from SED fits for the sample of T-Tauri stars
considered in Robitaille et al. (2006). SED fits and determination of parameter
ranges were performed as for the |
| Open with DEXTER | |
| In the text | |
 |
Figure A.2:
Scatter plot of the ratio between the flux in the IRAC 1
band over that in J, as a function of
disk accretion rate, according to the Robitaille et al. (2006) models for a solar
mass stars. Each point corresponds to one of the Robitaille et al. (2006) models
satisfying the following conditions: mass of the central object
between 0.7 and 1.3 |
| Open with DEXTER | |
| In the text | |
 |
Figure A.3:
Examples of SED fits for three objects in our sample with
[Ne II] detections. From left to right: DoAr25/GY17, WL20/GY240, and
IRS44/GY269. The first is classified as Stage/Class II, the other two as
Stage/Class I. The upper row shows the SEDs and the best fit models as
produced by the Web interface provided by Robitaille et al. (2006). For the
datapoints, detections and upper limits are indicated by circles and
triangles, respectively. The lower two rows represent distributions of
two fit parameters, |
| Open with DEXTER | |
| In the text | |
 |
Figure A.4: SEDs and best fit models, as produced by the Web interface provided by Robitaille et al. (2006), for the 28 YSOs in our sample. |
| Open with DEXTER | |
| In the text | |
 |
Figure A.5:
Comparison of the |
| Open with DEXTER | |
| In the text | |
 |
Figure A.6: Same as Fig. A.5 for the effective temperatures. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


