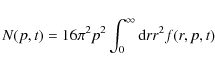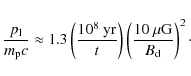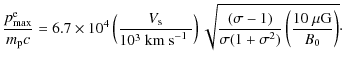Theory of cosmic ray and γ-ray production in the supernova remnant RX J0852.0-4622

E. G. Berezhko; G. Pühlhofer; H. J. Völk

doi:10.1051/0004-6361/200809473

Free Access

Issue		A&A Volume 505, Number 2, October II 2009


Page(s)		641 - 654
Section		Interstellar and circumstellar matter
DOI		https://doi.org/10.1051/0004-6361/200809473
Published online		28 July 2009

Theory of cosmic ray and 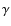$\gamma$ -ray production in the supernova remnant RX J0852.0-4622

E. G. Berezhko¹ - G. Pühlhofer^2, - H. J. Völk³

1 - Yu.G. Shafer Institute of Cosmophysical Research and Aeronomy, 31 Lenin Ave., 677980 Yakutsk, Russia
2 - Landessternwarte, Königstuhl, 69117 Heidelberg, Germany
3 - Max-Planck-Institut für Kernphysik, Postfach 103980, 69029 Heidelberg, Germany

Received 28 January 2008 / Accepted 23 June 2009

Abstract
Aims. The properties of the Galactic supernova remnant (SNR) RX J0852.0-4622 are theoretically analysed.
Methods. An explicitly time-dependent, nonlinear kinetic model of cosmic ray (CR) acceleration in SNRs is used to describe the properties of SNR RX J0852.0-4622, the accelerated CRs, and the nonthermal emission. The source is assumed to be at a distance of $\approx$ 1 kpc in the wind bubble of a massive progenitor star. An estimate of the thermal X-ray flux in this configuration is given.
Results. We find that the overall synchrotron spectrum of RX J0852.0-4622 as well as the filamentary structures in hard X-rays lead to an amplified magnetic field $B > 100 ~\mu$ G in the SNR interior. This implies that the leptonic very high energy (VHE) $\gamma$ -ray emission is suppressed, and that the VHE $\gamma$ -rays are hadronically dominated. The energy spectrum of protons produced over the lifetime of the remnant until now may well reach ``knee'' energies. The derived $\gamma$ -ray morphology is consistent with the HESS measurements. The amount of energy in energetic particles corresponds to about 35% of the hydrodynamic explosion energy. A remaining uncertainty concerns the thermal X-ray flux at 1 keV. A rough estimate, which is possibly not quite appropriate for the assumed wind bubble configuration, is found to be higher than the nonthermal flux at this energy.
Conclusions. It is concluded that this SNR expanding into the wind bubble of a massive star in a dense gas environment can be a hadronic $\gamma$ -ray source that is consistent with all existing multiwavelength constraints, except possibly the thermal X-ray emission.

Key words: ISM: cosmic rays - acceleration of particles - shock waves - supernovae: individual: SNR RX J0852.0-4622 - radiation mechanisms: non-thermal - gamma rays: theory

1 Introduction

RX J0852.0-4622 (also known as G266.2-1.9) is a shell-type supernova remnant (SNR) with a diameter of $2^{\circ}$ , located in the Galactic plane. The SNR was originally discovered in X-rays with the ROSAT satellite (Aschenbach 1998; Aschenbach et al. 1999). In projection along the line of sight, RX J0852.0-4622 is located entirely within the far larger Vela SNR and is only visible in hard X-rays, where the thermal radiation from the Vela SNR is no longer dominant. While nonthermal emission from the shell of RX J0852.0-4622 has been confirmed by several X-ray observatories (Slane et al. 2001; Iyudin et al. 2005; Bamba et al. 2005), a clear detection of the thermal X-ray emission from the shell or the interior has not yet been possible because of confusion with the Vela SNR. This implies that the thermal emission is very weak.

The radio emission of RX J0852.0-4622 is also weak. In fact the SNR radio shell was only identified (Duncan & Green 2000; Combi et al. 1999; Stupar et al. 2005) after its discovery in X-rays. Before that, only a bright radio spot was known as ``Vela Z'' (Milne 1968), which was usually identified with the Vela SNR. In addition, significant Galactic background variation over the size of the remnant cannot be excluded. The radio spectrum of RX J0852.0-4622 is therefore not well determined. Only for the northeastern rim a spectral index can be derived with moderate accuracy (Duncan & Green 2000).

The shell of RX J0852.0-4622 was also detected in very high energy (VHE) $\gamma$ -rays by the HESS collaboration (Aharonian et al. 2005,2007a), to have a $\gamma$ -ray flux at 1 TeV as high as that from the Crab Nebula. Emission from the northwestern rim had already been detected before by the CANGAROO experiment (Katagiri et al. 2005). The CANGAROO data have since been revised (Enomoto et al. 2006).

RX J0852.0-4622 is the second SNR after RX J1713.7-3946 (e.g. Aharonian et al. 2007b), where morphologically a SNR shell was unambiguously found to accelerate particles to TeV energies and beyond. As a third and fourth source of this character, the objects RC W86 (Hoppe & Lemoine-Goumard 2008; Aharonian et al. 2008) and SN 1006 (Naumann-Godo et al. 2009) have recently been detected. A few other TeV sources have been detected in the HESS Galactic plane survey that are spatially coincident with radio shell-type SNRs. So far, however, the data do not permit us to unambiguously identify the $\gamma$ -ray emission with the SNR shells, e.g., using morphological arguments. In several cases, the TeV emission might also be associated with X-ray emitting pulsar wind nebula candidates.

Despite the lack of precise information from radio data and the uncertainties in key astrophysical parameters, the prominence of RX J0852.0-4622 has therefore prompted us to model the acceleration of both electrons and protons together with their nonthermal emission in detail, applying explicitly time-dependent nonlinear kinetic theory. The theory couples particle acceleration on a kinetic level with the gas dynamical evolution of the system (Berezhko et al. 1996; Berezhko & Völk 1997,2000).

Compared to the other SNRs that were successfully described within the framework of this theory (e.g. Berezhko & Völk 2006; Berezhko 2008,2005), the present uncertainties regarding RX J0852.0-4622 are quite large. Such important astronomical parameters as the distance and age are not well known. It is not even clear, whether the source is in front or behind the Vela SNR. The latter object is generally considered to lie at a distance $d=250 \pm 30$ pc (Cha et al. 1999). A position behind the Vela SNR could correspond to a solution with d=1 kpc (Slane et al. 2001), whereas another solution could correspond to the earlier distance estimate of d=200 pc (Aschenbach 1998).

This prompted us originally to construct two quite different source scenarios, one in front, and the other behind the Vela SNR. They were intended to correspond to earlier distance estimates: a ``nearby'' solution with d=200 pc (Aschenbach 1998) in front of, and a ``distant'' solution with d=1 kpc (Slane et al. 2001) behind the Vela SNR. However, no ``nearby'' solution could be found that fulfilled all the observational constraints. Therefore, we abandoned the possibility of a small distance to RX J0852.0-4622 and assume here that the source is at a distance d=1 kpc.

In agreement with Slane et al. (2001) but with independent additional arguments, we assume that the observed nonthermal emission of RX J0852.0-4622 indicates that the SNR emerged from a core collapse explosion into the wind bubble of a massive progenitor star in a dense gas environment, possibly a molecular cloud. In this case, the major part of the swept-up volume has originally been occupied by the highly diluted bubble gas that also has a minimal thermal emissivity. At the current epoch, however, we assume that the SNR shock already propagates into the dense shell of ambient interstellar medium (ISM) that was originally compressed by the stellar wind. This also implies that the magnetic field upstream of the SNR shock is of interstellar origin.

We note here that this solution has a similar character as the solution suggested earlier for the object RX J1713.7-3946 (Berezhko & Völk 2006). In this sense, the two SNRs RX J0852.0-4622 and RX J1713.7-3946 can be considered as twins.

The hydrodynamic state of the system, i.e., the given linear radius for known angular radius and distance together with the present age and shock velocity, etc., is basically determined by the choice of mechanical explosion energy, ejected mass, and external density.

The lack of knowledge about the radio spectral shape makes it impossible to derive from the radio synchrotron observations - and as far as the magnetic field is concerned, from the combined radio and X-ray synchrotron spectral observations - the most relevant pair of physical parameters for the acceleration theory, namely the proton injection rate and the effective magnetic field strength (Berezhko et al. 2002; Berezhko 2008; Völk 2004; Berezhko 2005). Thus, even if we consider the circumstellar medium (CSM) structure to be given, it is impossible to predict directly the form of the overall synchrotron and the full VHE $\gamma$ -ray emission from theory.

The observed overall nonthermal spectral shape - including the VHE $\gamma$ -rays - and the small-scale filamentary structures in the nonthermal X-ray emission of RX J0852.0-4622 nevertheless provide evidence for effective nuclear cosmic ray (CR) acceleration, associated with considerable magnetic field amplification. This conclusion is possible because the overall nonthermal spectrum can be theoretically fitted with an appropriate proton injection rate, electron-to-proton ratio, and effective magnetic field strength (assumed to be uniform inside the shocked CSM cf. Berezhko & Völk 2004b).

The main result of this paper is that the resulting VHE $\gamma$ -ray flux is hadronically dominated. The well-known difference in the effectiveness of the basic radiation mechanisms then implies that the energy density of the nuclear component of the nonthermal charged-particle population in the SNR by far dominates that of the energetic electron component generated in the source. The energy in nonthermal particles at the present epoch amounts to $\sim$ 35 percent of the assumed total mechanical energy $E_{\rm sn}= 1.3\times 10^{51}$ erg, released in the explosion. Therefore, from the point of view of energetics, this solution for RX J0852.0-4622 more than fulfils the average requirement on a SNR source of the Galactic CRs. In this context, we also qualitatively discuss the question of the possible escape of the highest-energy particles, accelerated at an earlier phase of the SNR than the one we can observe at present.

In the next section, the theoretical model is described. Section 3 presents our assumptions about the values of the physical parameters inferred by the broadband data and physical considerations. It also contains a discussion of the thermal emission, even though it has not been possible to estimate it appropriately for the assumed wind bubble and shell configuration. The results for the gas dynamics, the particle acceleration coupling with it, the $\gamma$ -ray emission, and for the thermal X-ray emission are presented and discussed in Sect. 4. In Sect. 5, our conclusions are summarized.

2 Model

The theoretical model for the particle acceleration combined with the gas dynamics of the explosion was described earlier, for instance in an analysis of SNR RX J1713.7-3946 (see Berezhko & Völk 2006, and references therein).

In its fastest moving outer parts, the ejected mass $M_{\rm ej}$ initially has a power law distribution d $M_{\rm ej}$ /d $u\propto u^{2-k}$ in flow velocity u with 7<k<12 (Chevalier 1982; Jones et al. 1981). We choose k=8 (as in the case of SNR RX J1713.7-3946).

The interaction of the ejecta with the CSM creates a strong outward-propagating shock wave in the CSM at which particles are accelerated. Our nonlinear model is based on an explicitly time-dependent solution of the CR transport equations together with the gas dynamic equations in spherical symmetry. In particular, the theory takes into account the adiabatic energy losses of thermal and nonthermal particles in the SNR interior, the diffusion of nonthermal particles from the outer shock into that interior, and the backreaction of CRs on the shock structure and dynamics. This backreaction decelerates the thermal gas already in front of the shock and leads to a smooth shock precursor that reduces the Mach number of the subsequent collisionless plasma shock (the subshock), heating the inflowing gas.

However, nuclear particles are only effectively injected into the acceleration process at those parts of the moving shock surface, where the locally mean magnetic field vector is quasi-parallel to the shock normal. These regions are characterized by magnetic flux tubes within which the injection of moderately suprathermal particles proceeds.

In quasi-perpendicular shock regions, on the other hand, injection is instantaneously strongly suppressed or completely prohibited. In the extreme, there are then separated regions at the shock surface, where particle injection is permanently either allowed or prohibited. In addition no nuclear particles are then accelerated in the prohibited regions. An example of this extreme situation is SN 1006, where the X-ray emitting polar cap regions correspond to the quasi-parallel regions. In these allowed regions, diffusive shock acceleration strongly proceeds at the Bohm diffusion level (see below) as a result of the effective injection of low-energy particles. However, since Bohm diffusion is isotropic, the energetic particles can also cross field lines and thus possibly reach quasi-perpendicular regions of the shock where they can also accelerate. The extent to which this happens depends on the spatial scales that separate quasi-perpendicular regions from quasi-parallel regions. For a homogeneous external magnetic field, about 80% of the shock surface is quasi-perpendicular in the above sense, and therefore only a fraction $f_{{\rm re}} \approx 0.2$ of the shock accelerates efficiently (Völk et al. 2003). However, we argue in Sect. 3.1.4 that for a SNR, propagating into a stellar wind bubble with a radiatively cooling shell of high-density gas, the above spatial scales are probably so small that $f_{{\rm re}} \approx 1$ . This has substantial implications especially for the resulting thermal X-ray emission, because the observed VHE $\gamma$ -ray emission (which is by implication of hadronic origin) then requires a lower gas density.

For a given magnetic field strength, the electron injection rate in spherical symmetry is determined by the intensity of the observed overall synchrotron spectrum. For a given injection rate of nuclear particles and magnetic field strength, the ratio $K_{\rm ep}$ of the densities of nonthermal electrons to nuclear particle can then be calculated.

As a result of the streaming instability, the accelerating CRs very effectively excite large-amplitude magnetic fluctuations upstream of the SN shock (McKenzie & Völk 1982; Blandford & Ostriker 1978; Bell 1978). Since these fluctuations scatter CRs extremely strongly, we approximate the CR diffusion coefficient $\kappa (p)$ by its lower limit, corresponding to a scattering mean free path equal to the particle gyro radius. In this so-called Bohm limit, $\kappa (p)= [mc^3/(3eB)] (v/c)(p/mc)$ , where e and m are the particle charge and mass, v and p denote the particle velocity and momentum, respectively, B is the effective magnetic field strength (see below), and c is the speed of light. Regarding the nuclear particles with the highest energies, this Bohm limit may also imply an underestimate for $\kappa (p)$ for another reason, since for these particles the effective, amplified field has spatial scales that are smaller or equal to their gyro radius (Pelletier el al. 2006; Bell 2004). To this extent our assumption of Bohm diffusion in the amplified field yields an upper limit to the maximum energy of the nuclear particle (e.g. Zirakashvili & Ptuskin 2008). In addition, we assume that the interior effective magnetic field has a uniform strength after its MHD compression in the thermal subshock. Practically speaking we assume this uniformity over a spatial scale that is large compared to the thickness of the observed X-ray filaments (Berezhko & Völk 2004b). For a different point of view, we refer to Pohl et al. (2005).

Another important nonlinear effect of the strong excitation of magnetic fluctuations by the accelerating particles themselves is the heating of the thermal plasma in the shock precursor that is generated by the accelerating particles. Combined analytical and numerical efforts, using plasma theory to develop a nonlinear description of the magnetic field evolution (Lucek & Bell 2000; Pelletier el al. 2006; Bell & Lucek 2001; Bell 2004; Ptuskin & Zirakashvili 2003), concluded that a considerable amplification of the upstream magnetic field should occur in the acceleration process to what we call the effective magnetic field. The physical reason is that the beam of the efficiently accelerated nuclear CR component also excites in particular a non-resonant magnetic mode in addition to the well-known resonant Alfvén waves (Bell 2004). The latter have nevertheless been argued to contribute dominantly to the overall turbulent magnetic energy density in the shock precursor (Pelletier el al. 2006). However, the three-dimensional MHD simulations of the non-resonant instability by Bell (2004) and Zirakashvili et al. (2008) show that the nonlinear growth of the magnetic fluctuations is accompanied by the formation of internal shocks and correspondingly strong dissipation, which heats the thermal plasma. Analogous dissipation should occur in three dimensions for the wave modes of the resonant streaming instability. We approximate this physical process by assuming that the heat input into the thermal gas equals the (linear) growth of the turbulent field energy in the excited Alfvén waves in the already amplified effective field (see Völk et al. 2008; Berezhko 2008, for the correspondence of this approach to existing theory and experiment).

As already mentioned in the Introduction, without a reliable spectral index for the observed spatially-integrated radio synchrotron emission we choose the strength of the effective field as well as the nuclear injection rate $\eta$ , so as to optimally fit both the calculated synchrotron spectrum (from radio to X-ray energies) and the calculated VHE $\gamma$ -ray spectrum to the observations. Subsequently, this spectrally fitted magnetic field is compared with the field derived from the observed filamentary structure. The degree of agreement between these two field strengths is then used as a measure of the success and self-consistency of the model.

The filament-based magnetic field strength $B_{\rm d}$ downstream of the shock is determined by the observed width L of the X-ray filament - interpreted as the synchrotron cooling length behind the shock - by means of the relation

$\begin{displaymath}B_{\rm d}=[3m_{\rm e}^2c^4/(4er_0^2l_2^2)]^{1/3}(\sqrt{1+\delta^2}-\delta)^{-2/3}, \end{displaymath}$

(1)

where $\delta^2=0.12c/(r_0\nu)[V_{\rm s}/(\sigma c)]^2$ , $l_2\approx L/7$ is the radial width of the X-ray emissivity $q_{\nu}(\epsilon_{\nu},r)$ , $\epsilon_{\nu}$ is the X-ray energy, corresponding to the frequency $\nu$ , and r₀ denotes the classical electron radius (Berezhko & Völk 2004a). This field strength is clearly a lower limit.

Since we already used the observed amplitude of the VHE $\gamma$ -ray spectrum to determine $\eta$ , we do not predict this amplitude, as one could do using a detailed knowledge of the integrated synchrotron spectrum. The above consistency condition for the effective field still needs to be fulfilled for the solution to be acceptable.

We do not investigate only whether the chosen values for B and $\eta$ are consistent with the Chandra measurement of the X-ray filamentary structure (Bamba et al. 2005), but also the extent to which they are consistent with the semi-empirical relation (Berezhko & Völk 2006)

$\begin{displaymath}B_0^2/(8\pi P_{\rm c}) \approx 5\times 10^{-3}, \end{displaymath}$

(2)

which connects the upstream magnetic field pressure $B_0^2/(8\pi)$ in the shock precursor (i.e. upstream, but amplified by the CR instability) to the pressure $P_{\rm c}$ of the accelerated particles that drives the field amplification in the first place. Equation (2) holds for a number of SNRs that could be analysed with the aid of a well-known radio spectrum for these sources (Völk et al. 2005). The degree of fulfilment of this relation is an additional quality criterium for the model to judge its success in theoretically describing the TeV $\gamma$ -ray source. Equation (2), or a relation of a similar type (Bell & Lucek 2001), is also likely to hold for an individual object during its time evolution. However, to avoid the introduction of an additional theoretical parameter, we consider B₀ as a constant in time, equal to its present value, in our evaluation of the models for RX J0852.0-4622. We return to this point in Sect. 4.3.

In this specific form, the three theory ``parameters'' B, $\eta$ , and $K_{\rm ep}$ are determined quantitatively by comparison with observations at the present age of the source. Their time-dependence during the evolution of the SNR is disregarded in this paper.

The numerical solution of the dynamical equations at each instant of time yields the CR spectrum and the spatial distributions of CRs and thermal gas. This allows the calculation of the spectra of the expected fluxes of nonthermal emission produced by the accelerated CRs, the morphology of the emission, and the future evolution inasmuch as the same physical processes continue to work at later times.

In the following, we consider the wind bubble scenario for RX J0852.0-4622 in the general framework of this model.

3 Physical parameters of RX J0852.0-4622

Table 1: Key model parameters, and corresponding spectral, dynamical, and morphological values expected from the calculations.

In this section, we describe the physical parameters of the model. Section 3.1 provides an overview of the available broadband data. Section 3.2 describes the setup of the scenario. Because of the scarcity - and sometimes ambiguity - of the available data, we adopt some general arguments from the non-thermal particle emission not only to constrain the acceleration parameters but also the environmental parameter gas density and its spatial distribution. The values of all relevant physical parameters are given in Table 1.

3.1 Broadband data of RX J0852.0-4622

In the following we discuss a number of characteristics of the object, suggested by broadband data, in order to describe it in a detailed way.

3.1.1 Morphology of RX J0852.0-4622 in general

RX J0852.0-4622 is a shell-type SNR with a shell diameter of $2^{\circ}$ , as seen in hard X-rays (Slane et al. 2001; Aschenbach 1998; Aschenbach et al. 1999) and VHE $\gamma$ -rays (Aharonian et al. 2005,2007a). The radio continuum emission also correlates spatially well with the high energy emission (Duncan & Green 2000; Aharonian et al. 2007a; Stupar et al. 2005). This confirms the shell-type nature of the source, although confusion with the emission from the Vela SNR prevented its detection based on radio data alone.

In X-rays, a central diffuse source of $\sim$ $9' \times 14'$ extension is seen NW of the geometrical centre of the SNR (Slane et al. 2001; Becker et al. 2007; Becker & Aschenbach 2002). While Slane et al. (2001) argue that the hard spectrum of the source seen with ASCA hints at a Pulsar Wind Nebula (PWN), Becker et al. (2007) argue, based on XMM-Newton data, that the source is soft and reject a PWN nature. Hence, there is currently no agreement about whether RX J0852.0-4622 is a centre-filled, composite SNR or not. Spatially-integrated fluxes would only marginally be affected. There is however the possibility that this central PWN would slightly influence the VHE $\gamma$ -ray radial profile (see Aharonian et al. 2007a, and Fig. 7).

3.1.2 Central compact object and pulsar association

At the geometrical centre of the shell of RX J0852.0-4622, there is the X-ray point source CXOU J085201.4-461753 (Aschenbach et al. 1999; Pavlov et al. 2001; Mereghetti et al. 2002; Kargaltsev et al. 2002; Mereghetti 2001), a central compact object (CCO) similar to that detected in the centre of Cas A. CXOU J085201.4-461753 might be a neutron star, but the nature of the object and the possibly associated compact H $\alpha$ nebula (Pellizzoni et al. 2002) is still under debate (e.g. Reynoso et al. 2006; Mignani et al. 2007; Becker et al. 2007). No X-ray pulsations have been detected (Becker et al. 2007; Kargaltsev et al. 2002). The association of CXOU J085201.4-461753 with RX J0852.0-4622 is nevertheless suggestive and, if true, would allow conclusions to be drawn about the nature of the progenitor of RX J0852.0-4622. Since the scenario discussed in this paper implies a core collapse SN, it does not exclude an association of CXOU J085201.4-461753 with RX J0852.0-4622.

In the literature the possibility is also discussed that RX J0852.0-4622 is associated with PSR J0855-4644 (Redman & Meaburn 2005). This appears unlikely, however, given the implications of this association for the distance and age of RX J0852.0-4622 (Redman & Meaburn 2005).

3.1.3 Non-thermal X-rays

The soft X-ray emission from RX J0852.0-4622 is heavily confused by thermal emission from the Vela SNR. While the emission from the Vela SNR seems consistently constrained to two thermal components ( $T_{1,2} = 0.05~{\rm keV}, 1.2~{\rm keV}$ ) with an absorption column density of about $10^{20}~{\rm cm}^{-2}$ (Lu & Aschenbach 2000), the surface brightness and temperatures of these components are sufficiently variable to prevent a clean subtraction of the Vela SNR in the X-ray spectra of RX J0852.0-4622 (Slane et al. 2001; Iyudin et al. 2005; Aharonian et al. 2007a). In the spectra above $\sim$ $1~{\rm keV}$ , the non-thermal emission from RX J0852.0-4622 nevertheless clearly dominates. We adopt the common interpretation that this component is synchrotron emission from relativistic electrons and use two estimates of the total X-ray synchrotron flux from RX J0852.0-4622 in our modelling (see Figs. 3, 5). The first (lower) estimate was derived using the averaged power-law spectra derived from the three brightest shell components (Slane et al. 2001), which we scaled up to match the total flux measured with ROSAT in the soft X-ray band (Aschenbach 1998). The second (upper) estimate is a reanalysis of the ASCA data set presented in Aharonian et al. (2007a).

High-resolution imaging of this synchrotron X-ray component with XMM-Newton (Iyudin et al. 2007,2005) and especially with Chandra (Pannuti et al. 2004; Bamba et al. 2005) permits the derivation of synchrotron cooling times and therefore an estimate of the effective magnetic field (e.g. Berezhko & Völk 2004a; Bamba et al. 2005; Berezhko et al. 2003a). To test our model, we will compare the B-field derived in this manner to the field value that is required to fit the spatially integrated synchrotron data (see Sect. 4).

3.1.4 Thermal X-rays

The detection of thermal X-ray emission could help to constrain the gas density and/or its spatial distribution in the SNR. However, the interpretation of the X-ray spectra is impeded by the strong background emission from the Vela SNR, the latter being dominated by low-temperature (<1 keV) X-ray emission. After subtraction of this emission, the remaining emission (dominant at higher energies) was attributed to either gas at higher temperatures from RX J0852.0-4622 (Aschenbach et al. 1999), or to synchrotron emission plus a very small thermal contribution (Slane et al. 2001). The latter conclusion was basically taken over in the recent HESS paper (Aharonian et al. 2007a) which also contains a reanalysis of the ASCA data, although the X-ray line features exhibited in the spectrum below 2 keV might be associated with either RX J0852.0-4622 or the Vela SNR, or with both. Similarly, the residuals of the spectra for the ASCA data visible around 1 keV suggest that another component, which might originate from RX J0852.0-4622, is needed. The possible detection of a thermal emission component from RX J0852.0-4622 by Uchiyama (2008) must be mentioned here again.

These are complex possibilities. The calculation of the thermal emission for the concrete case of RX J0852.0-4622 is compounded by the wind-bubble plus swept-up-shell geometry. Standard methods for calculating the thermal emission from SNRs approximate the configuration either by a plane shock geometry or by a classical Sedov solution, and they neglect the existence of the accelerated particle component. Neither of these approximations is appropriate for the case of RX J0852.0-4622 in its present phase. The plane approximation disregards the adiabatic gas cooling in the interior and the overall dynamic evolution of the system. The classical Sedov solution implies a uniform circumstellar medium. In the extreme case, the radiatively cooled wind bubble shell is even denser - and therefore even thinner - than assumed in Sect. 3.2.2. and it might only be reached recently before the present epoch. Collisional electron heating then had little time to operate before now.

Another important aspect is the modification of the SNR shock by the accelerating CRs. For a SNR shock propagating into a uniform medium with a uniform magnetic field, this implies, as mentioned before, that the most of the shock surface corresponds to a quasi-perpendicular shock with a strongly reduced injection of nuclear particles (Völk et al. 2003). Suprathermal injection of ions is only possible in the quasi-parallel shock regions. If the spatial scales of the quasi-perpendicular regions are large enough, then the cross-field diffusion of the highest-energy particles, accelerated in the magnetic flux tubes delineating the neighboring quasi-parallel shock regions, does not reach deeply into these quasi-perpendicular regions. In the corresponding magnetic flux tubes, there are no nuclear particles to be accelerated, there is no magnetic field amplification, and the shock there remains unmodified. This means that in the quasi-perpendicular regions the shock dissipation and therefore the gas heating occurs in a locally unmodified shock with the overall shock speed, leading to a correspondingly high gas temperature and high thermal emission. In the case where a radiatively cooling shell of a wind bubble is the obstacle for the SNR expansion, the situation may differ. MHD instabilities and the radiative cooling of such a shell probably break it into many small regions with strongly varying field directions. Then the spatial scales separating the flux tubes that originate from quasi-perpendicular regions from those of quasi-parallel shock regions may become small enough for cross-field diffusion to also fill the quasi-perpendicular flux tubes with accelerating particles such that particle acceleration plus magnetic field amplification occur practically everywhere over the shock surface (Völk et al. 2008; Völk 2008). In this extreme case, this implies shock modification over the entire shock region and thus a reduced gas heating due to only subshock dissipation. The enhanced overall acceleration efficiency then also implies that there is a lower density of thermal gas for a given hadronic $\gamma$ -ray flux, and thus a lower thermal emission. The low swept-up mass in a low-density wind bubble in addition lowers the overall thermal emissivity compared to that of a classical Sedov remnant with the same upstream gas density at the shock at the present epoch.

In Sect. 4.4, a rough estimate of the resulting thermal X-ray emission is given, based on the emission from a classical Sedov solution in a uniform ambient medium. According to this estimate, the thermal emission of soft X-rays at 1 keV is larger than the corresponding nonthermal X-ray emission. However, the error in this estimate is not known and is likely to be quite large. Therefore, an uncertainty remains, which we cannot resolve at this point.

3.1.5 X-ray morphology absorption and relation to CO data

Absorption of soft X-rays by neutral hydrogen can be used to place constraints on the source distance. Slane et al. (2001) used CO data of the Vela Molecular Ridge (VMR) to reject a distance of RX J0852.0-4622 of more than 1-2 kpc, based on the lack of strong X-ray absorption variation that should have been detected across RX J0852.0-4622. This is broadly in agreement with the inference by Moriguchi et al. (2001) that there is an anticorrelation between X-ray emission and molecular gas traced in CO, especially with respect to the VMR at a distance of 1-2 kpc.

In the 2-10 keV band, which is not expected to exhibit absorption, an X-ray powerlaw spectrum can be derived. Assuming this powerlaw to continue down to 0.7 keV, Slane et al. (2001) derived an absorption column density of $(4.0 \pm 1.8) \times 10^{21}$ cm^-2 for RX J0852.0-4622. Since this column density is much larger than the one towards the Vela SNR, they concluded that RX J0852.0-4622 should be at a much larger distance than the Vela SNR.

3.1.6 Radio spectrum

We assume that the radio emission is caused by synchrotron radiation. There is no good radio spectrum available for the entire remnant. We use the differential flux values given by Duncan & Green (2000) at 2.42 GHz and 1.40 GHz, the errors of which represent the uncertainty of the background level. The spectral index between the two bands has quite a large error ( $\alpha = 0.4 \pm 0.5$ ), but for the north-western rim a higher quality spectrum ( $\alpha = 0.40 \pm 0.15$ ) could be derived. If this value is representative of the entire remnant, as Duncan & Green (2000) argue, then this index is somewhat harder than what expected for a modified SNR shock environment, although still compatible within a $2\sigma$ error range.

3.1.7 Gamma-ray and X-ray line emission from radioactive ⁴⁴Ti decay

The $^{44}{\rm Ti}$ production in a SN explosion depends on progenitor star mass and explosion-type, with a yield spanning two orders of magnitude (see, e.g. Renaud et al. 2006a, and references therein). Because of the short lifetime of $\sim$ 80 years (e.g. Wietfeldt et al. 1999), the mere detection of hard X-ray and $\gamma$ -ray de-excitation lines at 69.7, 78.4, and 1157 keV from the $^{44}{\rm Ti}$ radioactive decay products can be used to constrain significantly the SNR age. So far, however, these lines have only been detected unambiguously from Cassiopeia A (age presumably $\sim$ 330 years), with COMPTEL onboard CGRO (Iyudin et al. 1994), PDS onboard BeppoSAX (Vink et al. 2001), and the ISGRI imager onboard INTEGRAL (Renaud et al. 2006c).

For RX J0852.0-4622, the situation is unfortunately unresolved. From COMPTEL data, the detection of a $\gamma$ -ray line at $1163\pm16~{\rm keV}$ , consistent with the $^{44}{\rm Ti}$ $\gamma$ -ray decay line, was claimed and predominantly attributed to RX J0852.0-4622 (Iyudin et al. 1998; Aschenbach et al. 1999). Using this $^{44}{\rm Ti}$ line flux, and using a rather high shock velocity, Aschenbach et al. (1999) derived an age of $680\pm 100$ yrs, and a distance of 200 pc. Such $\gamma$ -ray data also suggest a core collapse SN event.

However, Schönfelder et al. (2000) pointed out that the significance of the COMPTEL $^{44}{\rm Ti}$ result is only marginal. And the COMPTEL result has so far been unable to be confirmed with the INTEGRAL instruments SPI and ISGRI. The SPI upper limit provides a poor constraint (von Kienlin et al. 2005). Under a point-source assumption, the ISGRI non-detection of the 78 keV line would conflict with the COMPTEL result (Renaud et al. 2006a). However, an extended-source analysis has yet to be performed (Renaud et al. 2006b).

Therefore, a nearby and rather recent event is not excluded by these specific observations, even though the arguments for this are rather weak.

3.2 Model parameters for a SN explosion at a 1 kpc distance

As discussed in the previous section, the main observational motivation for locating RX J0852.0-4622 at a distance of $\sim$ $1~{\rm kpc}$ is the much higher column density in neutral hydrogen derived from the X-ray spectrum of RX J0852.0-4622, compared to the values for Vela SNR.

3.2.1 Reasons for a wind bubble scenario

The lack (or low level) of thermal X-ray emission and the strong X-ray synchrotron flux already led Slane et al. (2001) to the conclusion that RX J0852.0-4622 could be evolving into a wind bubble. Similarly, Duncan & Green (2000) argue that the unusual radio properties of RX J0852.0-4622 (bipolar shell morphology, low surface brightness) could be explained if the SNR has so far evolved in a low-density region.

We can use the non-thermal X-ray plus $\gamma$ -ray emission from RX J0852.0-4622 to place these arguments for a wind bubble scenario on a more firm footing, anticipating for the moment that the VHE $\gamma$ -ray emission is indeed dominated by hadronic emission. As we see in Sect. 4, this latter conclusion follows because for the assumption of a significantly amplified magnetic field, it is possible to fit all the nonthermal spectra as well as the morphology in nonthermal X-rays and gamma-rays - and this amplified field does not exceed that derived from the observed X-ray filaments. This amplification is however possible only for the nonthermal pressure of the nuclear particles.

Arguments similar to those given below were used in Berezhko & Völk (2006) for the comparable case of SNR RX J1713.7-3946 to which we refer the reader.

To yield the observed nonthermal X-ray luminosity in the case of a uniform ISM, the shock speed should be sufficiently large, $V_s \ga 10^3$ km s^-1 (Berezhko & Völk 2004b). Given that the SNR should already be in the Sedov phase, the observed size $R_{\rm s} \sim 20~{\rm pc}$ , corresponding to a distance of 1 kpc, infers the age constraint $t_{\rm sn}\approx 0.4R_{\rm s}/V_{\rm s}\la 3\times 10^3$ yr. For a typical SN type Ia explosion energy $E_{\rm sn}=10^{51}$ erg and ejected mass of $1.4~M_{\odot}$ this would then imply a very low ISM number density $N_{\rm H}\la 10^{-2}$ cm^-3. On the other hand, the peak TeV $\gamma$ -ray luminosity, achieved during SNR evolution from a type Ia event, roughly scales as (Berezhko & Völk 1997)

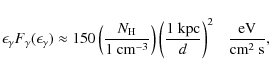$\begin{displaymath}\epsilon_{\gamma}F_{\gamma}(\epsilon_{\gamma})\approx 150 \le... ...{~kpc}}{d}\right)^2 ~~~\frac{\mbox{eV}}{\mbox{cm}^2~\mbox{s}}, \end{displaymath}$

(3)

for $f_{\rm re}= 1$ . Here $F_{\gamma}(\epsilon_{\gamma})$ is the integral flux of $\gamma$ -rays for energies greater than $\epsilon _{\gamma }$ . This expression indicates that for $N_{\rm H}<10^{-2}$ cm^-3, we expect to have an energy flux $\epsilon_{\gamma}F_{\gamma}(\epsilon_{\gamma})<1.5$ eV/(cm² s). This is an order of magnitude lower than the observed flux (see Sect. 4).

Therefore, the nonthermal observations make it clear that SNR RX J0852.0-4622 cannot correspond to a type Ia event, if the source distance is as large as d=1 kpc. As a consequence, we consider a core collapse SN event.

3.2.2 Wind bubble parameters

The progenitor stars of core collapse SNe that modify significantly the density of their environment are massive main-sequence stars with initial masses $M_{\rm i}>15~M_{\odot}$ which have intense winds, e.g. (Abbot 1982). During their evolution in the surrounding uniform ISM of gas number density $\rho_0=m_{\rm p} N_{\rm ISM}$ , they create on average a low-density bubble, surrounded by a shell of swept-up and compressed ISM of radius (Chevalier & Liang 1989; Weaver et al. 1977)

$\begin{displaymath}R_{\rm sh}=0.76( 0.5 \dot{M}V_{\rm w}^2 t_{\rm w}^3/\rho_0)^{1/5}, \end{displaymath}$

(4)

where $\dot{M}$ is the mass-loss rate of the progenitor star, $V_{\rm w}$ is the wind speed, and $t_{\rm w}$ is the duration of the wind phase. The values of these parameters are given in tabular form by Chevalier (1982) in terms of $M_{\rm i}$ .

To determine the SNR shock dynamics inside the shell, we model the gas number density distribution in both the bubble and the shell in the form (e.g. Berezhko & Völk 2006) as

$\begin{displaymath}N_{\rm g}=N_{\rm b}+(r/R_{\rm sh})^{3(\sigma_{\rm sh} -1)}N_{\rm sh}, \end{displaymath}$

(5)

where $N_{\rm sh}=\sigma_{\rm sh} N_{\rm ISM}$ is the peak number density in the shell, $N_{\rm b}$ is the gas number density inside the bubble, typically very small compared with the shell density, and $\sigma_{\rm sh} = N_{\rm sh}/N_{\rm ISM}$ is the shell compression ratio. We note that as a result of radiative cooling the compression ratio $\sigma_{\rm sh}$ can exceed the classical upper limit of 4. The possibility of a very thin wind bubble with $\sigma_{\rm sh}\gg 4$ was indicated in Sect. 3.1.4. above.

The mass of the bubble

$\begin{displaymath}M_{\rm b}=(4\pi R_{\rm sh}^3/3)m_{\rm p} N_{\rm b} \end{displaymath}$

(6)

is rather small, $M_{\rm b}< M_{\odot}$ , in the case of moderate progenitor masses $M_{\rm i}<20~M_{\odot}$ , whereas the shell mass

$\begin{displaymath}M_{\rm sh}=4\pi N_{\rm sh}m_{\rm p}\int_0^{R_{\rm sh}}{\rm d}... ...h})^{3(\sigma -1)} = (4\pi R_{\rm sh}^3/3)N_{\rm ISM}m_{\rm p} \end{displaymath}$

(7)

is many hundreds of solar masses. Therefore, during SNR shock propagation through the bubble, only a small fraction of its energy is given to gas of stellar origin. The main part of the explosion energy is deposited in the shell.

Here we use the gas number density distribution $N_{\rm g}(r)=\rho(r)/m_{\rm p}$ in the form of

$\begin{displaymath}N_{\rm g}=\{0.003+0.24[r/(17.5~\mbox{pc})]^{12}\}~~\mbox{cm}^{-3}, \end{displaymath}$

(8)

which fixes the gas density at the present shock radius and provides a consistent fit for all existing data for SNR RX J0852.0-4622. With Eq. (4), this relation also connects the external density $N_{\rm ISM}$ with the progenitor mass.

This distribution corresponds to a bubble with $\sigma_{\rm sh}=5$ and $28<R_{\rm sh}<32$ pc created by the wind of a main-sequence star of initial mass $15~M_{\odot}<M_{\rm i}<20~M_{\odot}$ in the surrounding ISM of hydrogen number density $11<N_{\rm ISM}<49$ cm^-3, respectively (Chevalier & Liang 1989). It implies that this bubble is located inside a region of dense gas.

3.2.3 Further parameters that determine the SN evolution and CR acceleration

We use the SNR parameters $E_{\rm sn}= 1.3\times 10^{51}$ erg, $M_{\rm ej}=3.5~M_{\odot}$ , and k=8, which, as shown below, provide a good fit to the observed SNR properties.

We also use an upstream effective magnetic field value B₀=20 $\mu$ G, which is required to provide the observed synchrotron flux in the radio and X-ray bands (see below). This value of B₀ is significantly higher than a merely MHD-compressed dense-gas magnetic field in the inner part of the shell, at densities $N_{\rm g} \leq 0.24~\mbox{cm}^{-3}$ .

4 Results and discussion

We discuss the physical characteristics of the wind bubble scenario in detail, and compare them with those inferred from observations.

The calculated dynamical characteristics of the SNR are shown in Fig. 1. From Fig. 1a, one can see that, for the assumed distance of 1 kpc, the calculation fits the observed SNR size $R_{\rm s}\approx 17.5$ pc at the age $t_{{\rm sn}} = 3745$ yr.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{09473fg1.eps} \end{figure}$

Figure 1:

Model parameters as a function of time: a) shock radius $R_{\rm s}$ and overall shock speed $V_{\rm s}$ ; b) total shock ( $\sigma$ ) and subshock ( $\sigma _{\rm s}$ ) compression ratios; c) ejecta ( $E_{\rm ej}$ ) and CR ( $E_{\rm c}$ ) energies in spherical symmetry. The vertical dotted line marks the current epoch of SNR evolution. The external gas density $N_{{\rm g}}=\rho _{{\rm g}} / m_{\rm p} = 1.4 N_{{\rm H}}$ is also shown in panel a).

Open with DEXTER

To reproduce the observed synchrotron and $\gamma$ -ray spectra (see below), we assume a proton injection rate $\eta=10^{-3}$ . This leads to a moderate nonlinear modification of the shock, which at the current age of $t_{{\rm sn}} = 3745$ yrs has a total compression ratio $\sigma \approx 5.2$ and a subshock compression ratio $\sigma_{\rm s} \approx 3.1$ (Fig. 1b). All parameters used and the resulting model properties are summarized in Table 1.

For its adopted density, the wind bubble contains only a small amount of gas $M_{{\rm b}}\approx 0.3~M_{\odot}$ . Therefore, the SN shock deposits only about 20% of the explosion energy during the initial 1000 years of propagation through the bubble, as seen in Fig. 1. However, until the current epoch, the SN shock has already swept up a considerable mass $M_{{\rm sw}}\approx 25~M_{\odot}$ . Therefore, the ejecta have transformed about 85% of their initial energy into gas and CR energy (Fig. 1c). The acceleration process is therefore characterised by a high efficiency based on the assumption of spherical symmetry: at the current time, about 35% of the explosion energy has been transferred to CRs, and the relative CR energy content $E_{\rm c}$ continues to increase to a maximum of about $0.55 E_{{\rm sn}}$ in the later phase (Fig. 1c), when particles begin to leave the source.

$\begin{figure} \par\includegraphics[width=9cm,clip]{09473fg2.eps} \end{figure}$	Figure 2: The overall (volume-integrated) CR spectrum as a function of particle momentum. Solid and dashed lines correspond to protons and electrons, respectively.
Open with DEXTER

Therefore, in absolute terms, the CRs inside SNR RX J0852.0-4622 already contain

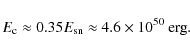$\begin{displaymath}E_{{\rm c}} \approx 0.35 E_{{\rm sn}} \approx 4.6 \times 10^{50}~{\rm erg}. \end{displaymath}$

(9)

The volume-integrated (or overall) CR spectrum

$\begin{displaymath}N(p,t)=16\pi^2p^2 \int_0^{\infty}{\rm d}r r^2 f(r,p,t) \end{displaymath}$

(10)

has, for the case of protons, an almost pure power-law form $N\propto p^{-\gamma}$ over a wide momentum range from $10^{-2}m_{\rm p}c$ up to the cutoff momentum $p_{\rm max}\approx 6\times 10^5m_{\rm p}c$ , corresponding to a cutoff energy of $\approx$ $5.6 \times 10^{14}$ eV (see Fig. 2). This value $p_{\rm max}$ is limited mainly by geometrical factors, such as the finite size and speed of the shock, its deceleration and the adiabatic cooling effect in the downstream region (Berezhko 1996). Because of the shock modification the power-law index slowly varies from $\gamma=2.4$ at $p~~\raisebox{0.2em}{$<$ }\!\!\!\!\! \raisebox{-0.25em}{$\sim$ }~~ m_{\rm p}c$ to $\gamma=1.9$ at $p\sim 100m_{\rm p}c$ . The shape of the overall electron spectrum $N_{\rm e}(p)$ deviates from that of the proton spectrum N(p) at high momenta $p>p_{\rm l}\approx 350m_{\rm p}c$ , as a result of the synchrotron losses in the downstream region with a magnetic field strength $B_{\rm d}\sim 100~\mu$ G, which is assumed to be uniform ( $B_{\rm d}=B_2=\sigma B_0$ ). Therefore, within the momentum range $p_{\rm l}<p< p_{\rm max}^{\rm e}$ , the electron spectrum is considerably steeper $N_{\rm e}\propto p^{-3}$ .

Specifically, the synchrotron losses become important for electron momenta greater than (Berezhko et al. 2002)

$\begin{displaymath}\frac{p_{\rm l}}{m_{\rm p}c} \approx 1.3 \left(\frac{10^8~\m... ...t}\right) \left(\frac{10~\mu\mbox{G}}{B_{\rm d}}\right)^2\cdot \end{displaymath}$

(11)

Substituting the SN age t=3745 yr into this expression, we have $p_{\rm l}\approx 350m_{\rm p}c$ , in agreement with the numerical result (see Fig. 2).

$\begin{figure} \par\includegraphics[width=16.5cm]{09473fg3.eps} \end{figure}$

Figure 3:

Calculated broadband spectral energy density of RX J0852.0-4622, as a function of photon energy $\epsilon _{\gamma }$ . In the $\gamma$ -ray region, the solid line shows the $\pi ^0$ -decay emission and the dashed line denotes the inverse Compton (IC) emission. Radio fluxes were obtained with the Parkes telescope (Duncan & Green 2000). For the X-ray synchrotron flux, a lower boundary is given by the sum of the ASCA fluxes from the brightest parts of the SNR, as given by Slane et al. (2001), scaled to match the total remnant's flux measured with ROSAT in the soft X-ray range (Aschenbach 1998). The upper boundary comes from a reanalysis of the total ASCA data from the remnant, as given in Aharonian et al. (2007a). TeV data are from CANGAROO (Enomoto et al. 2006) and HESS (Aharonian et al. 2007a).

Open with DEXTER

The maximum electron momentum can be roughly estimated by equating the synchrotron loss time with the acceleration time. This gives (e.g. Berezhko et al. 2002)

$\displaystyle \frac{p_{\rm max}^{\rm e}}{m_{\rm p}c} = 6.7\times 10^4 \left(\fr... ...(\sigma-1)}{\sigma (1+ \sigma^2)} \left(\frac{10~\mu\mbox{G}}{B_0}\right)}\cdot$

(12)

At the current epoch, $V_{\rm s}\approx 1316$ km s^-1, which leads to a maximum electron momentum $p_{\rm max}^{\rm e} \approx 10^4m_{\rm p}c$ , in agreement with the numerical results (Fig. 2).

As a result of the shock propagating through the wind shell (cf. Fig. 1), the SN shock speed decreases rather quickly during the period t>10³ yr. Therefore, during previous evolutionary phases, the shock has produced electron spectra with cutoff momenta $p_{\rm max}^{\rm e}$ larger than at the current epoch. Because of this, the spatially integrated electron spectrum has a relatively smooth cutoff (see Fig. 2). Together with the synchrotron cooling, this represents a good fit of the observed X-ray spectrum (see below).

The present-day parameters $B_{\rm d}= 104$ $\mu$ G and $K_{\rm ep}\approx 3\times10^{-4}$ provide good agreement between the calculated and the measured spectral energy distribution of the synchrotron emission in the radio to X-ray ranges at the present time (Fig. 3). The steepening of the electron spectrum at high energies due to synchrotron losses and the smooth cutoff of the overall electron spectrum together naturally yield a fit to the X-ray data with their soft spectrum. This smooth spectral behaviour is achieved in an assumed upstream field of 20 $\mu$ G, which leads to the above downstream field $B_{\rm d}$ .

Figure 3 also shows the calculated $\gamma$ -ray spectral energy distributions corresponding to $\pi ^0$ -decay, IC emission, and nonthermal Bremsstrahlung, together with the existing experimental data.

According to the calculation, the hadronic $\gamma$ -ray production exceeds the electron contribution by more than two orders of magnitude at all energies. These $\gamma$ -ray spectra are shown in detail in Fig. 4. For energies $\epsilon_{\gamma}=1{-}100$ GeV, the $\gamma$ -ray spectrum is close to d $F_{\gamma}$ /d $\epsilon_{\gamma}\propto \epsilon_{\gamma}^{-2}$ , hardening from $\epsilon_{\gamma}=0.1{-}1$ TeV, whereas starting from $\epsilon_{\gamma}\approx 1$ TeV, it has a smooth extended cutoff despite the comparatively far sharper cutoff of the proton energy spectrum, cf. Fig. 2.

$\begin{figure} \par\includegraphics[width=9cm,clip]{09473fg4.eps} \end{figure}$

Figure 4:

Calculated nonthermal Bremsstrahlung (NB, dash-dotted line), inverse Compton (IC, dashed line), and $\pi ^0$ -decay (solid line) $\gamma$ -ray spectral energy distributions as functions of photon energy $\epsilon _{\gamma }$ for the high-injection, high-field model. The observed HESS (Aharonian et al. 2007a) and CANGAROO (Enomoto et al. 2006) $\gamma$ -ray fluxes are shown as well.

Open with DEXTER

Note that the $\gamma$ -ray cutoff energy $\epsilon_{\gamma}^{\max}\approx 0.1p_{\rm max}c$ is sensitive to the magnetic field strength $B_{\rm d}$ , since the proton cutoff momentum has a dependence $p_{\rm max}\propto R_{\rm s}V_{\rm s}B_{\rm d}$ (Berezhko 1996). It is clearly seen from Fig. 4 that the calculated spectrum fits the HESS measurements in an acceptable way, at least up to $\approx$ 5 TeV. However, the four highest-energy points tend to lie below the theoretical curve. This can be the result of the escape of the highest-energy protons during the deceleration of the shock in the shell. (See Sect. 4.1 for further details.)

The hadronic dominance within the VHE $\gamma$ -ray emission that we predict here, could be investigated further in the near future by the Fermi instrument in the GeV region. Although at these comparatively low $\gamma$ -ray energies, the $\gamma$ -ray background from the diffuse Galactic $\gamma$ -rays is quite significant, especially for such a large, low-surface brightness source as RX J0852.0-4622 (Drury et al. 1994), Fermi should be able to detect the overall very high $\gamma$ -ray flux from RX J0852.0-4622. It is therefore to be expected that the Fermi instrument will confirm our prediction that the spatially-integrated $\gamma$ -ray spectral energy density at 1 GeV is only a factor of $\approx$ 1.5 lower than at 1 TeV cf. Fig. 4, as a result of the nonlinear modification of the acceleration process. If the nonlinear modification in the wind bubble is weaker than assumed here, then this difference in the spectral energy density between 1 GeV and 1 TeV should be even smaller.

$\begin{figure} \par\includegraphics[width=9cm,clip]{09473fg5.eps} \end{figure}$

Figure 5:

Calculated synchrotron emission flux as a function of frequency $\nu$ . The solid line corresponds to the high-injection, high-field model, the dashed line corresponds to a hypothetical very low injection, and therefore unmodified low-field model. Parkes radio data (Duncan & Green 2000) and ASCA X-ray data (Slane et al. 2001; Aharonian et al. 2007a) are shown (see also the caption of Fig. 3).

Open with DEXTER

In Fig. 5, we separately present the differential synchrotron spectrum, produced at the current epoch. For comparison, we also show a synchrotron spectrum, which would correspond to a hypothetical acceleration scenario in which the proton injection rate is taken to be so small ( $\eta=10^{-5}$ ) that the accelerated nuclear CRs do not produce any significant shock modification or magnetic field amplification; the value B₀=5 $\mu$ G is used in this case. There are two small but distinct differences between the synchrotron spectra that correspond to these two scenarios. The high-injection, high-field scenario leads to a steep differential radio frequency spectrum $S_{\nu}\propto \nu^{-\alpha}$ with power law index $\alpha\approx 0.7$ , whereas for the unmodified, low-field scenario $\alpha=0.5$ . Unfortunately, the low quality of the existing radio data does not allow us to differentiate between these two scenarios in the radio range, to conclude from the radio spectrum alone whether or not we are dealing in the case of RX J0852.0-4622 with efficient CR acceleration leading to a significant shock modification and magnetic field amplification. The essentially different behaviour of these two spectra at X-ray frequencies around $\nu = 10^{18}$ Hz demonstrates on the other hand that in the case of strong CR production and an amplified magnetic field $B_{\rm d}\approx 100$ $\mu$ G, the spectrum $S_{\nu}(\nu)$ naturally exhibits a smooth cutoff consistent with the experiment. In the simple, unmodified low-field case, the spectrum $S_{\nu}(\nu)$ has too sharp a cutoff to be consistent with the experiment.

It is noted that the X-ray flux represented in Figs. 3 and 5 comes from two different analyses of the X-ray flux (see also Sect. 3.1): the lower boundary was derived by summing up the ASCA fluxes from the brightest parts of the SNR (Slane et al. 2001) and scaling the result to match the total SNR's flux measured with ROSAT (Aschenbach 1998). The upper boundary - a factor of two higher - comes from a reanalysis of the total ASCA data from the remnant, as given in Aharonian et al. (2007a).

The properties of small-scale structures of RX J0852.0-4622 seen in X-rays furnish even stronger evidence that the magnetic field inside the SNR is indeed amplified considerably. As in the case of other young SNRs (e.g. SN 1006, Cassiopeia A, Tycho's SNR), Chandra shows very fine filamentary structures in nonthermal X-rays in the very outer part of the remnant. The thinnest filament detected by Bamba et al. (2005) has an angular thickness $\Delta \psi\approx 38''$ in the radial profile of the X-ray emission in the 2-10 keV range. To determine whether this type of structure is consistent with our theory, we present in Fig. 6 the projected radial profile

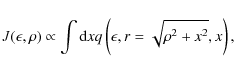$\begin{displaymath}J(\epsilon,\rho)\propto \int {\rm d}x q\left(\epsilon,r=\sqrt{\rho^2+x^2},x\right), \end{displaymath}$

(13)

calculated for the X-ray energy $\epsilon_{\nu}=1$ keV. The abscissa in Fig. 6 (and correspondingly also in Fig. 7) is scaled to the radius of the remnant, i.e., to 17.5 pc, as derived from the angular radius of the remnant of $\sim$ $1^{\circ}$ . Here $q(\epsilon, r)$ is the luminosity in the nonthermal emission with photon energy $\epsilon$ . The integration is performed along the line of sight. One can see that the theory predicts the peak of the emission just behind the shock front with a thickness $\Delta \rho/R_{\rm s}\approx 10^{-2}$ , which corresponds to an angular width $\Delta \psi\approx 36''$ . It corresponds reasonably well to the Chandra observation. At the same time Fig. 6 also shows that the unmodified low-field solution cannot explain the filament structure seen with Chandra.

$\begin{figure} \par\includegraphics[width=9cm,clip]{09473fg6.eps} \end{figure}$	Figure 6: The projected radial profile of the X-ray synchrotron emission for $\epsilon_{\rm \nu}=1~{\rm keV}$ . The abscissa is normalized to the shock radius and corresponds therefore to an angular scale. The solid line corresponds to the high-injection, high-field model, the dash-dotted line corresponds to a hypothetical low-injection, low-field model.
Open with DEXTER

For other young SNRs, it has already been demonstrated (Berezhko & Völk 2004a; Berezhko et al. 2003a) that the measured width of the projected radial profile of the nonthermal X-ray emission provides the possibility to determine the internal magnetic field strength according to Eq. (1).

Substituting into this equation $l_2=L/7=8.2\times 10^{16}$ cm, $\sigma=5.2$ , $V_{\rm s}=1316$ km s^-1, and $\nu =3\times 10^{17}$ Hz (i.e., X-ray energy $\epsilon_{\nu}\approx 1$ keV), we obtain $B_{\rm d} \approx 139$ $\mu$ G, which agrees within 30% with the value $B_{\rm d}= 104$ $\mu$ G used in our spectrum calculation. Such a difference in $B_{\rm d}$ corresponds to the uncertainty in the field determination in the other objects analysed until now.

The magnetic field amplification is driven by the gradient in the (nuclear) CR pressure upstream of the outer shock, and we can check whether RX J0852.0-4622 belongs to the class of objects that fulfil Eq. (2). In the present case of d=1 kpc, we find that $P_{\rm c}\approx 0.15\rho_0 V_{\rm s}^2$ , where $\rho_0=N_{\rm g}(R_{\rm s})m_{\rm p}$ is the ambient gas density at the current shock front position. Substituting $N_{\rm g}(R_{\rm s})=0.24$ cm^-3 and B₀=20 $\mu$ G, we have $B_0^2/(8\pi P_{\rm c}) \approx 6.5\times 10^{-3}$ , in rather good agreement with the average number in Eq. (2).

The line-of-sight integrated $\gamma$ -ray emission profile as a function of projected radius $\rho$ is calculated for $\epsilon_{\rm\gamma}=1$ TeV and is presented in Fig. 7. Because of the large radial gradient in the gas and CR distributions inside the SNR, the theoretically predicted three-dimensional radial emissivity profile of TeV-emission is concentrated within a thin shell of width $\Delta r\sim 0.01R_{\rm s}$ . As a result of the projection effect, the two-dimensional width is a factor of seven larger than the width of the three-dimensional profile, i.e., $\Delta \rho\approx 0.1R_{{\rm s}}$ (solid lines in Fig. 7). Since the HESS instrument in addition has a finite angular resolution, we also present as dashed lines in Fig. 7 the modified radial profile convolved with a Gaussian point spread function with a $\sigma_{\rho}=\Delta \rho = 0.06R_{\rm s}$ , corresponding to an angular resolution of $\sigma_{\psi} = 0.06^{\circ}$ .

$\begin{figure} \par\includegraphics[width=9cm]{09473fg7.eps} \end{figure}$

Figure 7:

The $\gamma$ -ray emissivities for the $\gamma$ -ray energy $\epsilon_{\gamma}=1~{\rm TeV}$ as a function of projected, normalized radial distance $\rho /R_{\rm s}$ . The calculated radial profile is represented by the solid line. Data points are from the Northern part of RX J0852.0-4622 as measured with HESS (Aharonian et al. 2007a), with an analysis point spread function of Gaussian width $0.06^\circ$ . The dashed line represents the calculated profile convolved with the same point spread function.

Open with DEXTER

Figure 7 shows that the expected radial profile of the TeV-emission, after taking into account the instrumental angular resolution, is much broader than the intrinsic projected profile and is characterised by a minimum-to-maximum intensity ratio $J^{\rm min}_{\gamma}/J^{\rm max}_{\gamma} \approx 0.35$ . The radial profile measured by HESS compares reasonably well with the theoretical prediction if we ignore the two data points in the central region. This might be justified because a central component (e.g. a PWN) cannot be fully excluded, as also argued in Aharonian et al. (2007a).

$\begin{figure} \par\includegraphics[width=9cm]{09473fg8.eps} \end{figure}$	Figure 8: The time dependence of the fluxes of the synchrotron emission at frequency $\nu=1~{\rm GHz}$ (dash-dotted line), synchrotron X-ray emission with energy $\epsilon_{\nu}=1~{\rm keV}$ (dashed line) and TeV-energy $\gamma$ -ray (solid line). The fluxes are normalised to their values F₀ at the current epoch.
Open with DEXTER

To illustrate the expected time evolution of the nonthermal emission, we show in Fig. 8 the fluxes of radio emission at the frequency $\nu=1$ GHz, and X-ray emission at the energy $\epsilon_{\nu}=1$ keV, as well as the TeV flux, all as a function of time. Since the CR energy content still increases, the radio emission increases during the subsequent centuries. However, because of the substantial shock deceleration, the nonthermal X-ray emission is expected to decrease with time at a rate of about 0.04%/yr. The TeV $\gamma$ -ray emission, on the other hand, will increase at a rate of 0.14%/yr because of the continuing increase in the ambient gas density. Nevertheless, a change of the order of one percent in 7 years is probably very difficult to measure. Therefore, we cannot place much practical weight on these expectations in terms of the secular variation in the nonthermal fluxes.

4.1 Escape

The decrease in the shock speed $V_{\rm s}$ during SNR evolution diminishes the maximum energy to which particles can be accelerated during any given phase. This has the well-known consequence that particles already accelerated to a higher maximum energy at earlier times can now begin to escape diffusively from the interior of the remnant, even without any change in the scattering mean free path, as predicted analytically (Berezhko & Krymsky 1988) and confirmed numerically (Berezhko et al. 1996).

Compared with this escape - which is relatively slow in our model because the diffusion of CR particles with momenta $p>p_{\rm m}(t)$ higher than the current cutoff momentum $p_{\rm m}(t)$ is still described by Bohm diffusion - the true CR escape is presumably much faster. Since the CRs with $p>p_{\rm m}(t)$ develop a much smaller spatial gradient than those with momenta $p<p_{\rm m}(t)$ (which are still efficiently accelerated by the shock), their production of chaotic magnetic fields whose scales are approximately equal to their gyroradii, decreases quickly with time. As a consequence, their diffusion coefficient increases considerably so that they leave the SNR much more rapidly than by means of Bohm diffusion, and these CRs then contribute less to the $\gamma$ -ray flux of the source than calculated above. The $\gamma$ -ray spectrum corresponding to the particles that remain confined in the SNR should therefore drop off faster with energy than given by the solid line in Fig. 4. However, the HESS data at the highest $\gamma$ -ray energies do not imply that this effect is very significant in the present case.

Secondly, the field amplification is probably stronger during earlier phases of the remnant evolution, when $\rho_0 V_{\rm s}^2$ is larger than at later phases (Bell & Lucek 2001). Our calculation has assumed that the effective field strength isconstant. Correcting for this, the overall nuclear particle spectrum released into the Interstellar Medium by SNRs presumably forms the Galactic CR spectrum up to an energy of 10¹⁷ eV (Berezhko & Völk 2007). That protons alone should be able to reach energies $\ga$ 10¹⁵ eV was shown for the case of a representative type Ia SN by Berezhko & Völk (2004b). This is likely to be true also for RX J0852.0-4622 and, by implication, also for its twin RX J1713.7-3946, even though their environmental conditions differ drastically from those of a type Ia SN.

We add here that the above maximum energies of energetic nuclei are calculated based on the assumption of Bohm diffusion. To this extent, they are upper limits, given the strength of the corresponding amplified magnetic field.

Except for special cases, one should therefore expect that escape sets in when the source becomes older. Ptuskin & Zirakashvili (2005,2003) in addition argued that at late times the damping of the scattering magnetic fluctuations should increase the scattering mean free path. The decrease in the effective field strength, on the one hand, and the scattering strength (by the deceleration of the shock and wave damping) on the other, go in the same direction to lower the cutoff energy of the accelerating population. The relative importance of these effects probably depends on the details of the source, in particular its evolutionary phase.

4.2 A rough estimate of the thermal X-ray emission

Using the results for the dynamical evolution of the system, one can also attempt to estimate the thermal X-ray emission. As argued in Sect. 3.1.4, this is only possible in an approximate way, even if the ejecta emission is disregarded with the argument that the ejected mass in the present phase is small compared to the swept-up mass. Looking at Fig. 1a, it can be seen that the SNR is well past the sweep-up phase and has entered a quasi-Sedov phase in the stellar wind shell, i.e., a roughly self-similar evolutionary phase, modified by strong particle acceleration relative to a purely gas dynamic evolution.

The approximation used is the following. The bubble case is compared with a SNR in a uniform medium in the classical Sedov phase without any CR acceleration, for four assumptions: (i) the total hydrodynamic explosion energy is the same in both cases; (ii) the downstream unmodified temperature $T_{\rm s}$ , determining the overall shock velocity and the thermal emission, is the same; (iii) the present gas density upstream of the shock is the same; and (iv) the two objects are at the same distance of 1 kpc. The results of Hamilton et al. (1983) for the thermal X-ray flux from a classical Sedov SNR are used, employing the emission measure of the bubble remnant instead of that of the classical Sedov remnant with the same four parameters as above. This means that the X-ray emissivity of the remnant is reduced by the ratio $R_{\rm em} =EM_{\rm b}/EM_{\rm S}$ of the emission measure $EM_{\rm b}$ for the bubble solution to the emission measure for the classical Sedov solution $EM_{\rm S}$ , which corresponds to a uniform ambient gas density $N_{{\rm g}}(R_{{\rm s}})$ .

The thermally relevant gas temperature in the presence of particle acceleration is the temperature $T_{\rm sub}$ downstream of the gas subshock. It corresponds to the temperature downstream of a shock that is nonlinearly modified by the internal energy and the pressure of the accelerated particles.

The CR-modified shock, i.e., the precursor-subshock system, is approximated by a plane parallel structure, which implies that the precursor size is small compared to the SNR shock radius. This is generally the case. Conservation of mass, momentum, and energy fluxes then permits in a straightforward way to calculate the ratio of the true downstream gas temperature $T_{\rm sub}$ and the downstream gas temperature $T_{\rm s}$ that would be obtained without particle acceleration

$\begin{displaymath}\frac{T_{\rm sub}}{T_{\rm s}}= \frac{[(\sigma_{\rm s} -1)(\gamma+1)+2](\gamma+1)^2} {4 \gamma (\gamma -1) \sigma^2}\cdot \end{displaymath}$

(14)

Here $\sigma$ and $\sigma _{\rm s}$ are the total and the subshock compression ratio, respectively, as given in Fig. 1. The specific heat ratio $\gamma$ for the nonrelativistic thermal gas may be taken as $\gamma = 5/3$ . For the present phase of RX J0852.0-4622 , i.e., $\sigma \approx 5.2$ and $\sigma_{\rm s} \approx 3.1$ , one then obtains $T_{\rm sub}\approx 0.45T_{\rm s}$ .

Hamilton et al. (1983) infer the gas temperature $T_{\rm s}$ to be

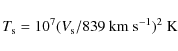$\begin{displaymath}T_{\rm s}=10^7(V_{\rm s}/839~ {\rm km~ s}^{-1})^2 ~{\rm K} \end{displaymath}$

(15)

in terms of the overall shock velocity $V_{\rm s}$ , assuming a highly ionized system. For RX J0852.0-4622 the latter quantity is given in our Fig. 1a. Using the present value $V_{\rm s}=1316$ km s^-1, the foregoing equations result in $T_{\rm s}\approx 2.5 \times 10^7$ K and $T_{\rm sub} \approx 1.1\times 10^7$ K, corresponding to a thermal energy of about 1 keV.

For the emission measure EM, we have $EM=\int_0^{R_{\rm s}}{\rm d}r r^2 N_{\rm g}^2(r)$ , if we disregard irrelevant numerical factors. To calculate $R_{\rm em}$ for the CR-modified shock, the overall shock is approximated by a shock in a thermal gas with an adiabatic index $\gamma_{\rm cr}$ , such that $(\gamma_{\rm cr} +1)/(\gamma_{\rm cr} -1) = \sigma$ , where $\sigma$ denotes, as before, the total compression ratio of the CR-modified shock. The corresponding solution for the gas dynamical quantities is approximated as being self-similar (cf. Sedov 1959). If the ambient density profile has a radial dependence in the form of a power law $N_{\rm g}(r)=N_0(r/R_0)^{\beta}$ , then the self-similar density distribution in the SNR, downstream of the shock, can be approximated by a power-law profile, with the same swept-up mass as the full solution. It has then the form $N_{\rm g}(r)=\sigma N_0(r/R_{\rm s})^{\beta'}$ with $\beta'= 3(\sigma -1)+ \beta\sigma$ , where $N_0=N_{\rm g}(R_{\rm s})$ . This density profile infers the emission measure $EM=N_0^2R_{\rm s}^3\sigma^2/(2\beta'+3)$ .

The classical gas dynamic Sedov solution for a SN explosion into a uniform medium has $\beta = 0$ and $\sigma = 4$ . Using the same values for N₀ for both density profiles leads to $R_{\rm s}\approx 12.51$ pc for the Sedov case and to $R_{\rm em} \approx 0.63$ for the bubble case $\beta=12$ and $\sigma=5.2$ . The swept-up mass in the Sedov case is $M_{\rm S} \approx 50.3~M_{\odot}$ .

Using the differential thermal X-ray model spectra dF/d $\epsilon\approx 10^{-4}$ photons/(keV cm² s) from Hamilton et al. (1983, see their Fig. 2# for their $\lg T_s=7.75$ and $\lg T_s=7.25$ , $\eta = N_{\rm H}^2 E_{\rm sn}=10^{49}$ erg cm^-6, scaling it according to dF/d $\epsilon\propto \eta$ with a factor of $\approx$ 3.8 for $\eta \approx 3.8\times 10^{49}$ erg cm^-6, multiplying it by the factor $\theta^2 [E_{\rm sn}/(10^{51}{\rm erg})]^{-1/2} \approx 0.65 \times 10^4$ , as required, where $\theta \approx 86$ arcmin for the angular size of the classical Sedov remnant corresponding to the above parameters (Hamilton et al. 1983), and multiplying it finally also by the factor $R_{\rm em}$ , results in a thermal spectral energy density $\epsilon^2$ dF/d $\epsilon \approx 1560$ eV cm^-2 s^-1 for $\epsilon =1$ keV.

This must be compared with the observed nonthermal X-ray energy flux at 1 keV (see Fig. 3) $\epsilon^2$ dF/d $\epsilon \approx 100$ eV cm^-2 s^-1. Therefore, at 1 keV, the thermal flux, calculated in this form, is higher than the nonthermal flux by a factor of about 16.

However, we note that the above X-ray energy flux has to be considered as a rough upper limit estimate because of the following reasons.

First of all, the SN shock into the bubble and shell interacts with a strongly rising gas density profile. For the estimate, the peak value of the gas density was however used.

In the case of a modified shock, the true gas temperature $T_{\rm sub}$ is at least by a factor of 2 lower than the temperature $T_{\rm s}$ used in our estimate. From a general point of view, the true thermal X-ray emission is expected to be lower because of the lower temperature. A rough correction can be made in the following way. The shock radius corresponding to the Sedov solution depends on the relevent parameters according to the relation $R_{\rm s}\propto (E_{SN}/(T_{\rm s} N_{\rm H}))^{1/3}$ . According to this relation, the shock with the same radius but with two times lower postshock temperature corresponds to a two times lower explosion energy. This shock is characterised by the parameter value $\eta \approx 1.9\times 10^{49}$ erg cm^-6 inferring a 1 keV thermal X-ray flux that is lower by a factor of two than the above consideration.

Third, as already mentioned, the calculation in Sect. 4 was performed for a rather moderate value of the injection rate, which leads to a moderate shock modification. Higher injection rates cannot be excluded by the present data, which can lead to a considerably higher shock modification with significantly lower gas energy and gas temperature. For a comparatively extreme position, we refer to the recent paper by Drury et al. (2008).

The fourth reason is that, for a fixed $\gamma$ -ray flux $F_{\gamma}\propto N_{\rm H} E_{SN}/d^2$ , the required gas number density scales as $N_{\rm H}\propto d^2$ with source distance d. Consequently, a decrease in d requires a decrease in the gas density. The thermal X-ray luminosity is quite sensitive to both the gas density and the total gas energy because roughly dF/d $\epsilon\propto N_{\rm H}^2 E_{SN}$ . A somewhat smaller distance than the value d=1 kpc, assumed here, cannot be excluded.

Finally, the bubble solution developed in this paper has quite a different temperature profile than any ``equivalent'' classical Sedov solution used to estimate the thermal emission. This arises from the approximate uniformity of the total pressure in the SNR interior, which roughly implies that $T_{\rm sub} \propto N_{\rm H}^{-1}$ . The density profiles are indeed quite different in both cases.

As a result, we believe that the uncertainties in the thermal X-ray emission are quite large. This situation also implies some systematic error in the overall model presented, although this can hardly change its key properties. In our opinion, the uncertainty in the thermal emission has to be resolved by future work that extends the efforts of Hamilton et al. (1983) to more general circumstellar density profiles and ejected masses for core-collapse supernovae.

5 Conclusions

We have argued that a solution behind the Vela SNR, involving the core collapse of a massive star in its own wind bubble, describes the available data reasonably well. The physical characteristics of this solution are very similar to those of the well-known SNR RX J1713.7-3946. In this sense, RX J0852.0-4622 and SNR RX J1713.7-3946 are twins.

The calculated $\gamma$ -ray spectrum has a smooth cutoff at higher energies. The presently observable lower limit to the magnetic field amplification - in terms of thin shock filaments in hard X-rays - is consistent with that deduced from a theoretical fit to the observed synchrotron spectra. If anything, the spectrally deduced field amplification is lower than the filament-deduced field amplification. Overall, the field amplification is also consistent with the semi-empirical relation Eq. (2) between the CR pressure $P_{\rm c}$ and the magnetic pressure, where $P_{\rm c}$ stems from the proton injection rate required to fit the observed $\gamma$ -ray emission. We conclude from these consistency arguments that the observational lack of a detailed radio synchrotron spectrum does not preclude the determination of a consistent amplified field.

The magnetic field amplification results in a significant depression in the density of ultra-high energy electrons and reduces the IC and NB contributions of these electrons to less than one percent of the $\pi ^0$ -decay $\gamma$ -ray emission.

A remaining uncertainty is connected with the thermal emission properties. For the wind bubble configuration this may indeed not be too critical, since gas heating should occur primarily at the subshock alone. In addition, the amount of swept-up mass is rather small compared to a classical Sedov remnant in a uniform circumstellar medium of equal present preshock density.

Apart from this uncertainty, the main result is the hadronic dominance in the $\gamma$ -ray emission spectrum. As a consequence of the nonlinear modification of the shock the spatially integrated $\gamma$ -ray spectral energy distribution at 1 GeV is predicted to be at most a factor 1.5 lower than at 1 TeV.

Acknowledgements

This work has been supported in part by the Russian Foundation for Basic Research (grants 06-02-96008, 07-02-0221). The authors thank V. S. Ptuskin and V. N. Zirakashvili and the anonymous referee for discussions on the thermal emission properties. E.G.B. acknowledges the hospitality of the Max-Planck-Institut für Kernphysik, where part of this work was carried out.

References

Abbott, D. C. 1982, ApJ, 263, 723 [NASA ADS] [CrossRef] (In the text)
Aharonian, F. A., Akhperjanian, A. G., Baze-Bachi, A. R., et al. (HESS Collaboration) 2005, A&A, 437, L7
Aharonian, F. A., Akhperjanian, A. G., Baze-Bachi, A. R., et al. (HESS Collaboration) 2007a, ApJ, 661, 236
Aharonian, F. A., Akhperjanian, A. G., Baze-Bachi, A. R., et al. (HESS Collaboration) 2007b, A&A, 464, 235 (In the text)
Aharonian, F. A., et al. (HESS Collaboration) 2008, A&A, [arXiv:0810.2689]
Aschenbach, B. 1998, Nature, 396, 141 [NASA ADS] [CrossRef]
Aschenbach, B., Iyudin, A. F., & Schönfelder, V. 1999, A&A, 350, 997 [NASA ADS]
Bamba, A., Yamazaki, R., & Hiraga, J. S. 2005, ApJ, 632, 294 [NASA ADS] [CrossRef]
Becker, W., & Aschenbach, B. 2002, Proc. of the 270, WE-Heraeus Seminar on Neutron Stars, Pulsars, and Supernova Remnants, ed. W. Becker, H. Lesch, & J. Trümper, MPE report 278, 64, available from ADS and [arXiv:astro-ph/0208492]
Becker, W., Hui, C. Y., Aschenbach, B., & Iyudin, A. F. 2007, A&A, submitted [arXiv:astro-ph/0607081]
Bell, A. R. 1978, MNRAS, 182, 147 [NASA ADS]
Bell, A. R. 2004, MNRAS, 327, 433
Bell, A. R., & Lucek, S. G. 2001, MNRAS, 321, 433 [NASA ADS] [CrossRef]
Berezhko, E. G. 1996, Astropart. Phys., 5, 367 [NASA ADS] [CrossRef] (In the text)
Berezhko, E. G. 2005, Adv. Space Res., 35, 1031 [NASA ADS] [CrossRef]
Berezhko, E. G. 2008, Adv. Space Res., 41, 429 [NASA ADS] [CrossRef]
Berezhko, E. G., & Krymsky, G. F. 1988, Soviet Phys.-Uspekhi, 12, 155 (In the text)
Berezhko, E. G., & Ksenofontov, L. T. 1999, JETPh, 89, 391 [NASA ADS] [CrossRef]
Berezhko, E. G., & Völk, H. J. 1997, Astropart. Phys., 7, 183 [NASA ADS] [CrossRef]
Berezhko, E. G., & Völk, H. J. 2000, A&A, 357, 183 [NASA ADS]
Berezhko, E. G., & Völk, H. J. 2004a, A&A, 419, L27 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Berezhko, E. G., & Völk, H. J. 2004b, A&A, 427, 525 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Berezhko, E. G., & Völk, H. J. 2006, A&A, 451,981
Berezhko, E. G., & Völk, H. J. 2007, ApJ, 661, L175 [NASA ADS] [CrossRef] (In the text)
Berezhko, E. G., Elshin, V. K., & Ksenofontov, L. T. 1996, JETPh, 82, 1 [NASA ADS]
Berezhko, E. G., Ksenofontov, L. T., & Völk, H. J. 2002, A&A, 395, 943 [NASA ADS] [CrossRef] [EDP Sciences]
Berezhko, E. G., Ksenofontov, L. T., & Völk, H. J. 2003a, A&A, 412, L11 [NASA ADS] [CrossRef] [EDP Sciences]
Berezhko, E. G., Pühlhofer, G., & Völk, H. J. 2003b, A&A, 400, 971 [NASA ADS] [CrossRef] [EDP Sciences]
Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [NASA ADS] [CrossRef]
Borkowski, K. J., Lyerly, W. J., & Reynolds, S. P. 2001, ApJ, 548, 820 [NASA ADS] [CrossRef]
Caraveo, P. A., De Luca, A., Mignani, R. P., & Bignami, G. F. 2001, ApJ, 561, 930 [NASA ADS] [CrossRef]
Cha, A. N., Sembach, K. R., & Danks, A. C. 1999, ApJ, 515, L25 [NASA ADS] [CrossRef] (In the text)
Chevalier, R. A. 1982, ApJ, 258, 790 [NASA ADS] [CrossRef]
Chevalier, R., & Liang, P. 1989, ApJ, 344, 332 [NASA ADS] [CrossRef]
Combi, J. A., Romero, G. E., & Benaglia, P. 1999, ApJ, 519, L177 [NASA ADS] [CrossRef]
Dodson, R., Legge, D., Reynolds, J. E., & McCulloch, P. M. 2003, ApJ, 596, 1137 [NASA ADS] [CrossRef]
Drury, L.O'C., Aharonian, F. A., & Völk, H. J. 1994, A&A, 287, 959 [NASA ADS] (In the text)
Drury, L.O'C., Aharonian, F. A., Malyshev, D., & Gabici, S. 2008, A&A, 496, 1 [NASA ADS] [CrossRef] (In the text)
Duncan, A. R., & Green, D. A. 2000, A&A, 364, 732 [NASA ADS]
Ellison, D. C., Baring, M. G., & Jones, F. C. 1995, ApJ, 453, 873 [NASA ADS] [CrossRef]
Enomoto, R., Tanimory, T., Naito, T., et al. 2002, Nature, 416, 823 [NASA ADS] [CrossRef]
Enomoto, R., Watanabe, S., Tanimori, T., et al. 2006, ApJ, 652, 1268 [NASA ADS] [CrossRef] (In the text)
Hamilton, A. J. S., & Sarazin, C. L. 1984, ApJ, 284, 601 [NASA ADS] [CrossRef]
Hamilton, A. J. S., Sarazin, C. L., & Chevalier, R. A. 1983, ApJS, 41, 115 [NASA ADS] [CrossRef] (In the text)
Hoppe, S., & Lemoine-Goumard, M. (HESS Collaboration) 2008, Proc. 30th ICRC, Merida, 2007, 2, 255, [arXiv:astro-ph/0709.4103]
Iyudin, A. F., Diehl, R., Bloemen, H., et al. 1994, A&A, 284, L1 [NASA ADS] (In the text)
Iyudin, A. F., Schönfelder, V., Bennett, K., et al. 1998, Nature, 396, 142 [NASA ADS] [CrossRef]
Iyudin, A. F., Aschenbach, B., Becker, W., et al. 2005, A&A, 429, 225 [NASA ADS] [CrossRef] [EDP Sciences]
Iyudin, A. F., Aschenbach, B., Burwitz, V., et al. 2007,[arXiv:astro-ph/0702404]
Jones, E. M., Smith, B. W., & Straka, W. C. 1981, ApJ, 249, 185 [NASA ADS] [CrossRef]
Kargaltsev, O., Pavlov, G. G., Sanwal, D., & Garmire, G. P. 2002, ApJ, 580, 1060 [NASA ADS] [CrossRef]
Katagiri, H., Enomoto, R., Ksenofontov, L. T., et al. (CANGAROO collaboration) 2005, ApJ, 619, L163 (In the text)
von Kienlin, A., et al., in Proc 5th INTEGRAL Science workshop, 2005, ESA SP-552 (Noordwijk: ESA), [arXiv:astro-ph/0407129] (In the text)
Lu, F. J., & Aschenbach, B. 2000, A&A, 362, 1083 [NASA ADS] (In the text)
Lucek, S. G., & Bell, A. R. 2000, MNRAS, 314, 65 [NASA ADS] [CrossRef]
Malkov, M. A., & Völk, H. J. 1995, A&A, 300, 605 [NASA ADS]
McKenzie, J. F., & Völk, H. J. 1982, A&A, 116, 191 [NASA ADS]
Mereghetti, S. 2001, ApJ, 548, L213 [NASA ADS] [CrossRef]
Mereghetti, S., Pellizzoni, A., & De Luca, A. 2002, in Neutron Stars in Supernova Remnants, ASP Conf. Ser., 271, ed. P. O. Slane, & B. M. Gaensler (San Francisco: ASP), 289, [arXiv:astro-ph/0112152]
Mignani, R. P., De Luca, A., Zaggia, S., et al. 2007, A&A, submitted [arXiv:astro-ph/0707.0937]
Milne, D. K. 1968, Australian J. Phys., 21, 201 [NASA ADS] (In the text)
Moriguchi, Y., Yamaguchi, N., Onshi, T., et al. 2001, Publ. Astron. Soc. Japan, 53, 1025 [NASA ADS] (In the text)
Naumann-Godo, M., et al. (HESS Collaboration) 2009, in High Energy Gamma-Ray Astronomy, ed. F. A. Aharonian, W. Hofmann, & F. M. Rieger, Melville, New York, AIP Conf. Proc., 1085, 304 (In the text)
Niemic, J., Pohl, M., Stroman, T., et al. 2008, ApJ, 684, 1174 [NASA ADS] [CrossRef]
Pastorello, A., Zampieri, L., Turatto, M., et al. 2004, MNRAS, 347, 74 [NASA ADS] [CrossRef]
Pavlov, G. G., Sanwal, D., Kiziltan, B., & Garmire, G. P. 2001, ApJ, 559, L131 [NASA ADS] [CrossRef]
Pannuti, T. G., Keohane, J. W., Allen, G. E., et al. 2004, in X-ray and Radio connections, ed. L. O. Sjouwerman, & K. K. Dyer, published electronically by NRAO, http://www.aoc.nrao.edu/events/xraydio, available also at ADS
Pelletier, G., Lemoine, M., & Marcowith, A. 2006, A&A, 453, 181 [NASA ADS] [CrossRef] [EDP Sciences]
Pellizzoni, A., Mereghetti, S., & De Luca, A. 2002, A&A, 393, L65 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Pohl, M., Yan, H., & Lazarian, A. 2005, ApJ, 626, L101 [NASA ADS] [CrossRef] (In the text)
Ptuskin, V. S., & Zirakashvili, V. N. 2003, A&A, 403, 1 [NASA ADS] [CrossRef] [EDP Sciences]
Ptuskin, V. S., & Zirakashvili, V. N. 2005, A&A, 429, 755 [NASA ADS] [CrossRef] [EDP Sciences]
Redman, M. P., & Meaburn, J. 2005, MNRAS, 356, 969 [NASA ADS] [CrossRef] (In the text)
Renaud, M., Vink, J., Decourchelle, A., et al. 2006a, New Astron. Rev., 50, 540 [NASA ADS] [CrossRef] (In the text)
Renaud, M., Gros, A., Lebrun, F., et al. 2006b, A&A, 456, 389 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Renaud, M., Vink, J., Decourchelle, A., et al. 2006c, ApJ., 647, 41 [NASA ADS] [CrossRef] (In the text)
Reynoso, E. M., Dubner, G., Giacani, E., et al. 2006, A&A, 449, 243 [NASA ADS] [CrossRef] [EDP Sciences]
Schönfelder, V., Bloemen, H., Collmar, W., et al. 2000, in AIP Conf. Ser., 510, 54 (In the text)
Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics, 4th Russian edition, translated by M. Holt, & M. Friedman (New York, NY: Academic Press Inc.), Chapt. IV (In the text)
Slane, P., Hughes, J. P., Edgar, R. J., et al. 2001, ApJ, 548, 814 [NASA ADS] [CrossRef]
Stupar, M., Filipovic, M. D., Jones, P. A., & Parker, Q. A. 2005, Adv. Space Res., 35, 1047 [NASA ADS] [CrossRef]
Uchiyama, Y. 2008, Invited talk at 37th COSPAR Scientific Assembly, Montreal, Canada, 3248 (In the text)
Vink, J., Laming, J. M., Kaastra, J. S., et al. 2001, ApJ, 560, L79 [NASA ADS] [CrossRef] (In the text)
Völk, H. J. 2004, Proc. 28th ICRC (Tsukuba), Invited Papers, 8, 29
Völk, H. J. 2008, Invited talk at 37th COSPAR Scientific Assembly Montreal, Canada, 3356
Völk, H. J., Berezhko, E. G., Ksenofontov, L. T., & Rowell, G. P. 2002, A&A, 396, 971
Völk, H. J., Berezhko, E. G., & Ksenofontov, L. T. 2003, A&A, 409, 563 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Völk, H. J., Berezhko, E. B., & Ksenofontov, L. T. 2005, A&A, 433, 229 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Völk, H. J., Berezhko, E. B., & Ksenofontov, L. T. 2008, A&A, 483, 529 [NASA ADS] [CrossRef] [EDP Sciences]
Weaver, R., McCray, R., Castor, J., et al. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef]
Wietfeldt, F. E., Schima, F. J., Coursey, B. M., & Hoppes, D. D. 1999, Phys. Rev. C, 59, 528 [NASA ADS] [CrossRef] (In the text)
Zirakashvili, V. N., & Ptuskin, V. S. 2008, ApJ, 678, 939 [NASA ADS] [CrossRef] (In the text)
Zirakashvili, V. N., Ptuskin, V. S., & Völk, H. J. 2008, ApJ, 678, 225 [NASA ADS] (In the text)

Footnotes

...ühlhofer^2,: Now at Institut für Astronomie und Astrophysik, Universität Tübingen, Sand 1, 72076 Tübingen, Germany.
... weak: Uchiyama (2008) has found that the X-ray emission from RX J0852.0-4622 might show a thermal component.
...(Cha et al. 1999): The distance to the Vela pulsar is estimated at 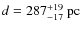$d=287^{+19}_{-17}~{\rm pc}$ (Dodson et al. 2003), see also Caraveo et al. (2001).
... gas: It is implicitly assumed here that any energy loss due to radiative gas cooling has no effect on the shock structure. Given the rather high internal temperature $T_{\rm sub}$ of the remnant at this stage (see Sect. 4.2), this appears to be a safe assumption.
... plasma: Particle-in-cell simulations by Niemiec et al. (2008) led these authors even to the extreme conclusion that the non-resonant instability amplitudes become never large as a result of the bulk acceleration of the thermal gas by the streaming CRs. We believe that in a quasi-steady shock configuration the CR current is being steadily driven through the upstream gas by the downstream overpressure, as implied above.
...(Völk et al. 2003): For earlier discussions of this question in a more general context, see Malkov & Völk (1995); Ellison et al. (1995).

All Tables

Table 1: Key model parameters, and corresponding spectral, dynamical, and morphological values expected from the calculations.

All Figures

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{09473fg1.eps} \end{figure}$	Figure 1: Model parameters as a function of time: a) shock radius $R_{\rm s}$ and overall shock speed $V_{\rm s}$ ; b) total shock ( $\sigma$ ) and subshock ( $\sigma _{\rm s}$ ) compression ratios; c) ejecta ( $E_{\rm ej}$ ) and CR ( $E_{\rm c}$ ) energies in spherical symmetry. The vertical dotted line marks the current epoch of SNR evolution. The external gas density $N_{{\rm g}}=\rho _{{\rm g}} / m_{\rm p} = 1.4 N_{{\rm H}}$ is also shown in panel a).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{09473fg2.eps} \end{figure}$	Figure 2: The overall (volume-integrated) CR spectrum as a function of particle momentum. Solid and dashed lines correspond to protons and electrons, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=16.5cm]{09473fg3.eps} \end{figure}$	Figure 3: Calculated broadband spectral energy density of RX J0852.0-4622, as a function of photon energy $\epsilon _{\gamma }$ . In the $\gamma$ -ray region, the solid line shows the $\pi ^0$ -decay emission and the dashed line denotes the inverse Compton (IC) emission. Radio fluxes were obtained with the Parkes telescope (Duncan & Green 2000). For the X-ray synchrotron flux, a lower boundary is given by the sum of the ASCA fluxes from the brightest parts of the SNR, as given by Slane et al. (2001), scaled to match the total remnant's flux measured with ROSAT in the soft X-ray range (Aschenbach 1998). The upper boundary comes from a reanalysis of the total ASCA data from the remnant, as given in Aharonian et al. (2007a). TeV data are from CANGAROO (Enomoto et al. 2006) and HESS (Aharonian et al. 2007a).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{09473fg4.eps} \end{figure}$	Figure 4: Calculated nonthermal Bremsstrahlung (NB, dash-dotted line), inverse Compton (IC, dashed line), and $\pi ^0$ -decay (solid line) $\gamma$ -ray spectral energy distributions as functions of photon energy $\epsilon _{\gamma }$ for the high-injection, high-field model. The observed HESS (Aharonian et al. 2007a) and CANGAROO (Enomoto et al. 2006) $\gamma$ -ray fluxes are shown as well.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{09473fg5.eps} \end{figure}$	Figure 5: Calculated synchrotron emission flux as a function of frequency $\nu$ . The solid line corresponds to the high-injection, high-field model, the dashed line corresponds to a hypothetical very low injection, and therefore unmodified low-field model. Parkes radio data (Duncan & Green 2000) and ASCA X-ray data (Slane et al. 2001; Aharonian et al. 2007a) are shown (see also the caption of Fig. 3).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{09473fg6.eps} \end{figure}$	Figure 6: The projected radial profile of the X-ray synchrotron emission for $\epsilon_{\rm \nu}=1~{\rm keV}$ . The abscissa is normalized to the shock radius and corresponds therefore to an angular scale. The solid line corresponds to the high-injection, high-field model, the dash-dotted line corresponds to a hypothetical low-injection, low-field model.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{09473fg7.eps} \end{figure}$	Figure 7: The $\gamma$ -ray emissivities for the $\gamma$ -ray energy $\epsilon_{\gamma}=1~{\rm TeV}$ as a function of projected, normalized radial distance $\rho /R_{\rm s}$ . The calculated radial profile is represented by the solid line. Data points are from the Northern part of RX J0852.0-4622 as measured with HESS (Aharonian et al. 2007a), with an analysis point spread function of Gaussian width $0.06^\circ$ . The dashed line represents the calculated profile convolved with the same point spread function.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{09473fg8.eps} \end{figure}$	Figure 8: The time dependence of the fluxes of the synchrotron emission at frequency $\nu=1~{\rm GHz}$ (dash-dotted line), synchrotron X-ray emission with energy $\epsilon_{\nu}=1~{\rm keV}$ (dashed line) and TeV-energy $\gamma$ -ray (solid line). The fluxes are normalised to their values F₀ at the current epoch.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

Theory of cosmic ray and -ray production in the supernova remnant RX J0852.0-4622

1 Introduction

2 Model

3 Physical parameters of RX J0852.0-4622

3.1 Broadband data of RX J0852.0-4622

3.1.1 Morphology of RX J0852.0-4622 in general

3.1.2 Central compact object and pulsar association

3.1.3 Non-thermal X-rays

3.1.4 Thermal X-rays

3.1.5 X-ray morphology absorption and relation to CO data

3.1.6 Radio spectrum

3.1.7 Gamma-ray and X-ray line emission from radioactive 44Ti decay

3.2 Model parameters for a SN explosion at a 1 kpc distance

3.2.1 Reasons for a wind bubble scenario

3.2.2 Wind bubble parameters

3.2.3 Further parameters that determine the SN evolution and CR acceleration

4 Results and discussion

4.1 Escape

4.2 A rough estimate of the thermal X-ray emission

5 Conclusions

References

Footnotes

All Tables

All Figures

Theory of cosmic ray and $\gamma$ -ray production in the supernova remnant RX J0852.0-4622

3.1.7 Gamma-ray and X-ray line emission from radioactive ⁴⁴Ti decay