Radio astrometry with chromatic AGN core positions

R. W. Porcas

doi:10.1051/0004-6361/200912846

Free Access

Issue		A&A Volume 505, Number 1, October I 2009


Page(s)		L1 - L4
Section		Letters
DOI		https://doi.org/10.1051/0004-6361/200912846
Published online		03 September 2009

LETTER TO THE EDITOR

Radio astrometry with chromatic AGN core positions

R. W. Porcas

Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany

Received 8 July 2009 / Accepted 25 August 2009

Abstract
Aims. The effect of frequency-dependent AGN core positions (``core-shifts'') on radio Very Long Baseline Interferometry (VLBI) global astrometry measurements is investigated.
Methods. The basic equations relating to VLBI astrometry are reviewed, including the effects of source structure. A power-law representation of core-shifts, based on both observations and theoretical considerations of jet conditions, is incorporated.
Results. It is shown that, in the presence of core-shifts, phase and group-delay astrometry measurements yield different positions. For a core displacement from the jet base parametrized by $\Delta$ x $(\lambda) = k\lambda^{\beta}$ , group delays measure a ``reduced'' core-shift of $(1-\beta)\Delta$ x $(\lambda)$ . For the astrophysically-significant case of $\beta = 1$ , group delays measure no shift at all, giving the position of the jet base. At 8.4 GHz an estimated typical offset between phase and group-delay positions of $\sim$ 170 $\mu$ as is smaller than the current $\sim$ 250 $\mu$ as precision of group-delay positions of the sources used to define the ICRF; however, this effect must be taken into account for future measurements planned with improved accuracy when comparing with optical positions of AGN to be obtained with the GAIA mission.

Key words: astrometry - reference systems - galaxies: jets - techniques: interferometric

1 Introduction

In astronomy the highest angular resolution achieved on a routine basis is provided by the technique of radio Very Long Baseline Interferometry (VLBI). Observations with intercontinental baselines can be used to image sources with sub-mas resolution, and astrometry with a precision $\sim$ 2 orders of magnitude smaller is possible. VLBI positions of a few hundred point-like extragalactic radio sources are used to define the International Celestial Reference Frame (ICRF; see Ma et al. 1998; Fey et al. 2004). Most radio sources are not points on this angular scale, however, and are far from circularly-symmetric, the emission rather arising from collimated jets of relativistic plasma. Furthermore, different regions of the emission have different spectral indices. The question as to what points these positions refer to is not just of academic interest. The ESA space mission GAIA (e.g. Lindgren et al. 2007), due for launch in 2011, will measure the positions of many AGN at optical wavelengths with precisions as good as 24 $\mu$ as. Furthermore, proposed improvements in VLBI instrumentation (Petrachenko 2006) hold promise for much improved VLBI global astrometric precision. Alignment of a GAIA-based optical reference frame with the ICRF will require a physical understanding of the location of the radio positions at this level.

1.1 Astrometry using interferometer phase

The high resolution of VLBI results from the fact that the visibility phase, $\phi$ , is sensitive to changes in the geometric path length difference in the two arms of an interferometer. For a baseline of length L this difference is $L~\cos{\theta}$ , where $\theta$ is the (instantaneous) angle between the source position, x, and the baseline direction in the sky. For a small position offset in the sky, $\Delta$ x, the component in the resolution direction (the direction of arc $\theta$ on the sky), $\Delta{x{'}}$ , gives rise to a change in path difference of $L~\sin{\theta}~\Delta{x{'}}$ resulting in an ``astrometric'' phase change

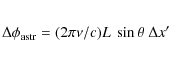
$\begin{eqnarray*}\Delta{\phi}_{\rm astr} = (2\pi\nu/c)L~\sin{\theta}~\Delta{x{'}} \end{eqnarray*}$

where $L~\sin{\theta}$ is the baseline length projected in the source direction, $\nu$ is the observing frequency and c is the speed of light. The resolution is characterised by the lobe (or fringe)-spacing, $\Omega_{\rm lobe} = c/({\nu}L~\sin{\theta})$ , the position change in the resolution direction which changes $\phi$ by one turn. For baseline lengths of several thousands of kilometers and observing frequencies above 5 GHz, $\Omega_{\rm lobe}$ can be less than 1 mas. Radio source images with resolutions (beam FWHM) ${\sim}0.4~\Omega_{\rm lobe}$ are made using VLBI arrays, and the separation between unresolved features in such images can be determined to a small fraction of the beamwidth. The relative position of two point sources close together on the sky can also be directly measured using the difference of their interferometer phases. For measurements with high signal-to-noise ratios the precision can be a small fraction of $\Omega_{\rm lobe}$ , $\sim$ a few $\mu$ as.

However, $\phi$ is only measured modulo $2\pi$ whereas the geometric path length difference, $L~\cos{\theta}$ , can be hundreds of millions of wavelengths. Furthermore, even with an accurate knowledge of instrumental phase and clock offsets, telescope positions and the orientation of the baseline in space, the signal propagation through the neutral troposphere and the ionosphere above the telescopes adds an unknown number of turns of phase, which varies on a short timescale. The additional path, A, through the troposphere ( $\sim$ 2 m at the zenith) is non-dispersive, adding an additional interferometer phase $\phi{_{\rm trop}}=(2\pi\nu/c)(A^B-A^A)$ where the superscripts A,B refer to the two telescopes. However, the path through the ionosphere, $I(\nu)$ , is dispersive, producing a phase advance at each telescope, and an interferometer phase change

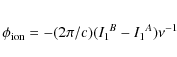
$\begin{eqnarray*}\phi_{\rm ion} = -(2\pi/c)(I_1{^B}-I_1{^A})\nu^{-1} \end{eqnarray*}$

where I₁ is the path at unit frequency. For close source pairs (whose atmospheric paths can be considered the same), these problems can be solved by observing both sources simultaneously, or by rapidly switching between them, enabling their relative phase to be tracked as the Earth rotates, and solving for the $2\pi$ phase ambiguities (Marcaide & Shapiro 1983). However, for very large source separations the relative phase between two sources cannot easily be used directly for relative astrometry.

1.2 Group-delay astrometry

Observations over a wide frequency band can solve the phase ambiguity problem by furnishing another variable; since $\phi$ varies linearly with frequency for non-dispersive (geometric and tropospheric) signal paths, the phase slope across the band - the group delay $\tau = (1/2\pi){\rm d}\phi/{\rm d}\nu$ - provides an unambiguous measure of the path length difference, $L\cos{\theta}/c$ , albeit with a reduced precision which depends on the bandwidth spanned. A small position offset results in an astrometric delay change

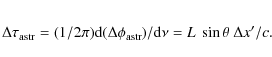
$\begin{eqnarray*}\Delta\tau_{\rm astr} = (1/2\pi){\rm d}(\Delta\phi_{\rm astr})/{\rm d}\nu = L~\sin{\theta}~\Delta{x}{'}/c. \end{eqnarray*}$

The dispersive ionospheric contribution produces a delay of

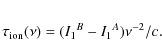
$\begin{eqnarray*}\tau_{\rm ion}(\nu) = (I_1{^B}-I_1{^A})\nu^{-2}/c. \end{eqnarray*}$

By observing simultaneously in two widely separated frequency bands $\nu_1, \nu_2$ , the delay difference between the bands can be used to estimate, and remove, the ionospheric contributions to the group delay measurement at the higher frequency $\nu _2$ .

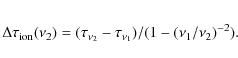
$\begin{eqnarray*}\Delta\tau_{\rm ion}(\nu_2) = (\tau_{{\nu}_2} - \tau_{{\nu}_1})/(1 - ({\nu}_1/{\nu}_2)^{-2}). \end{eqnarray*}$

Group delay astrometry measurements of compact radio sources (mostly Active Galactic Nuclei, AGN) are regularly carried out by the International VLBI Service (IVS) in 24-h observing runs, using a global network of telescopes observing at 2.3 and 8.4 GHz, and bandwidths spanning a few hundred MHz. After ionospheric delay correction, the 8.4 GHz group delays are analysed using a model for the tropospheric delay, producing fits for Earth rotation parameters, telescope coordinates and radio source positions. Such group delay positions of radio sources, and with quoted errors as small as 250 $\mu$ as, are used to define the ICRF to an accuracy of $\sim$ 30 $\mu$ as.

1.3 Astrometry with extended sources

The visibility phase of an extended source is conventionally divided into 2 terms: (a) that due to the path length difference to some reference position within the source, x₀; and (b) a source structure term, $\phi$ $_{\rm str}$ , which can be determined by evaluating the relevant component of the Fourier transform of a map of the source brightness distribution centred on x₀. Note that $\phi$ $_{\rm str}$ is generally a ``baseline-dependent'' quantity, which allows these 2 terms to be separated by self-calibration procedures when imaging sources with a VLBI array (Cotton 1979; Cornwell & Wilkinson 1981; Schwab & Cotton 1983). All the sources used for defining the ICRF exhibit a dominant compact feature - the ``core'' - which provides an obvious reference position within the structure. The difference of visibility phase between two extended sources can be used to determine the precise separation between their reference points by first imaging the sources, evaluating the structure phase terms and correcting their visibility phases (Marcaide & Shapiro 1983). Charlot (1990) has emphasised that this correction may also be necessary even when using group delays for astrometry, in those cases where ${\phi}_{\rm str}$ varies rapidly with resolution, giving rise to a baseline-dependent structure delay $(1/2\pi){\rm d}{\phi}_{\rm str}/{\rm d}\nu$ across the observing band. In principle, source structure corrections should be made separately at both 2.3 and 8.4 GHz when ionospheric corrections are made to group delays (Petrov 2007).

When sources are observed using a wide bandwidth, the change of source structure with frequency across the band needs to be taken into account. The technique of Multi-Frequency Synthesis (MFS) has been developed for astronomical imaging of extended sources, which uses wide (30%) bandwidths in order to fill in the range of resolutions covered by interferometer arrays (Conway et al. 1990; Sault & Wieringa 1994). The algorithms used for MFS are primarily concerned with producing a single-frequency image with high dynamic range, but they also estimate the spectral index distribution. Evaluating the source structure contribution to the wideband visibility function used for group-delay measurements in principle requires both of these components.

2 Frequency-dependent core-shifts

The sources used by the IVS for defining the ICRF are chosen to be largely point-like at both 2.3 and 8.4 GHz, making structural corrections apparently unimportant. However, due to opacity in the dominant, compact core component at the base of the relativistic jet, the position of the peak of radio emission is expected to be frequency-dependent (Blandford & Königl 1979; Königl 1981). Marcaide et al. (1985) discovered a shift of 700 $\mu$ as between the positions of the ``cores'' of the quasar 1038+528A measured at 2.3 and 8.4 GHz by comparing their separations from a feature in the nearby quasar 1038+528B. Using observations at additional frequencies, they described the position change with an ad hoc law, $k\lambda^{\beta}$ , with $0.7 < \beta < 2.0$ . In order to measure such ``core-shifts'' it is necessary to correctly register the images at different frequencies. This can be done by assuming that another feature of the structure has a frequency-independent position, by phase-reference imaging using another source with a frequency-independent position, by using the technique of frequency phase-referencing (Middelberg et al. 2005; Rioja et al. 2005) or by comparing the separations of multiple gravitationally-lensed images of a single source at different frequencies (Porcas & Patnaik 1995; Mittal et al. 2006).

Lobanov (1998) has suggested the application of such opacity effects to the study of the conditions within the central regions of AGNs. He measured a value $\beta = 1.04$ for the core of the quasar 3C 345, close to the value of 1 expected for synchrotron self-absorption in the regime of equipartition between jet particle and magnetic field energy densities. Kovalev et al. (2008) have investigated the prevalence of core-shifts in a sample of 29 sources for which a secondary (presumed achromatic) feature in the jet could be used as a position reference. They report a median core-shift of 440 $\mu$ as between 2.3 and 8.4 GHz, with a largest value of 1400 $\mu$ as. Although the sources used in these studies necessarily had jet components in addition to the compact, ``chromatic'' core, there is no reason to suppose that such core-shifts are absent even in sources which show little evidence of other structure. Thus one must assume that the sources used to define the ICRF (at 8.4 GHz) in fact have frequency-dependent positions. The measured values of core-shifts are typically smaller than the beamwidth of VLBI arrays used to image sources and this effect does not, therefore, easily lend itself to correction using the MFS techniques mentioned above.

2.1 Effect of core-shifts on astrometry measurements

Hitherto the effects of AGN core-shifts within the observing band on VLBI astrometric group delay measurements have not been widely considered. Here this effect is investigated. For simplicity the core is considered to be a point source at each frequency, whose position along a fixed direction depends on frequency. Following Marcaide et al. (1985) the shift, $\Delta$ x $(\lambda)$ , with respect to a reference position, x₀ (the jet base), is parametrized with a power-law, $\Delta$ x $(\lambda) = k\lambda^{\beta}$ which can be re-written as

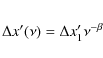
$\begin{eqnarray*}\Delta{x'}(\nu) =\Delta{x}_{1}'\nu^{-\beta} \end{eqnarray*}$

where $\Delta{x}_{1}{'}$ is the shift in the resolution direction at unit frequency. The astrometric phase term then becomes

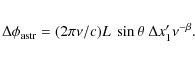
$\begin{eqnarray*}\Delta{\phi}_{\rm astr} = (2\pi\nu/c)L~\sin{\theta}~\Delta{x}_{1}'\nu^{-\beta}. \end{eqnarray*}$

Relative astrometry using interferometer phase measurements refers to the frequency-shifted core position or the average position of the core within that band. The astrometric contribution to the group delay, however, becomes

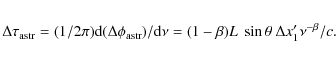
$\begin{eqnarray*}\Delta\tau_{\rm astr} = (1/2\pi){\rm d}(\Delta\phi_{\rm astr})/{\rm d}\nu = (1-\beta)L~\sin{\theta}~\Delta{x}_{1}'\nu^{-\beta}/c. \end{eqnarray*}$

Note that the astrometric correction from a group delay measurement responds to a ``reduced'' core-shift of $(1-\beta)\Delta{x}_{1}'\nu^{-\beta}$ . In the special case of $\beta = 1$ , the group delay measures no core-shift at all but gives a position corresponding to the jet base, x₀. In general, phase and group-delay positions will differ at any frequency by an amount $\beta\Delta{x}_{1}'\nu^{-\beta}$ .

The presence of core-shifts interacts with dual-frequency group-delay corrections for the ionospheric path. If not taken into account, the delay difference between measurements at two frequencies introduced by the core-shift,

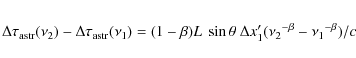
$\begin{eqnarray*}\Delta\tau_{\rm astr}(\nu_{2}) - \Delta\tau_{\rm astr}(\nu_{1})... ...in{\theta}~\Delta{x}_{1}'(\nu_2{^{-\beta}}- \nu_1{^{ -\beta}})/c \end{eqnarray*}$

will be incorporated as part of the ionospheric correction, $\Delta\tau_{\rm ion}(\nu_2)$ , resulting in a further (but typically smaller) shift $\Delta$ x $_{\rm ion}$ in the measured position at $\nu _2$ :

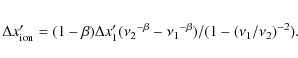
$\begin{eqnarray*}\Delta{x}_{\rm ion}' = (1-\beta)\Delta{x}_{1}'(\nu_2{^{-\beta}}-\nu_1{^{-\beta}})/(1 - ({\nu}_1/{\nu}_2)^{-2}). \end{eqnarray*}$

Of course, for the case of $\beta = 1$ , there is no measured core-shift and hence the ionospheric correction is properly applied.

3 Discussion

Table 1 compares values of core-shifts and group-delay measurements for various assumed values of $\beta$ for a source having a core-shift between 2.3 and 8.4 GHz of $440~\mu$ as, the median value found by Kovalev et al. (2008). For values of $\beta$ above 0.7 the typical shift from x₀ at 8.4 GHz is within the current quoted 250 $\mu$ as error for group-delay positions. For $\beta = 1$ the typical shift is 166 $\mu$ as. For a baseline length of 6000 km (such as that between Westford, Ma, USA and Wettzell, Germany) and an observing frequency of 8.4 GHz, $\Omega_{\rm lobe}$ is 1.2 mas. The shift produces an astrometric phase term $\Delta{\phi}_{\rm astr} = 49^\circ$ . For a fixed offset of 166 $\mu$ as the phase change across a 720 MHz band (as used for IVS observations) due to the changing resolution would amount to $4^\circ$ . However, the small shift in core position across the band of 14 $\mu$ as exactly cancels this change, resulting in a phase offset of $49^\circ$ at all frequencies and an astrometric group delay $\Delta\tau_{\rm astr} = 0$ . Note that, for $\beta > 1$ , the group delay position is on the opposite side of x₀ from the jet direction. For the (probably physically unlikely) case of $\beta = 2$ the effect of the core-shift on group delays is indistinguishable from that of the ionosphere, and ionosphere-corrected delays again refer to x₀, as in the case of $\beta = 1$ .

Table 1: Position shifts in $\mu$ as assuming various values of $\beta$ , for a source with measured core-shift between $\nu _1$ = 2.3 GHz and $\nu _2$ = 8.4 GHz of $440~\mu$ as, the median value found by Kovalev et al. (2008).

3.1 The ICRF

The ICRF is the current best realization of the Celestial Reference Frame, based on ionosphere-corrected, 8.4 GHz group-delay positions for several hundred radio sources. The sources are all compact and hopefully stable, resulting in consistent and repeatable positions when measured using the standard IVS observing bands. VLBI observations link the ICRF with the International Terrestial Reference Frame (ITRF) via group-delay positions of AGN cores in the sky and radio telescope positions on the Earth. Just as the mathematically well-defined, but sometimes physically inaccessible, positions of telescopes (the intersection of the azimuth and elevation axes) must be located with respect to the grid of geodetic monuments on the Earth, so too must ``mathematical'' group-delay positions of AGN cores be located with respect to radiating points in the sky at radio and other wavebands. The phenomenon of core-shifts complicates this procedure although, if $\beta = 1$ for most AGN cores, the relationship is less frequency-dependent than one would otherwise suppose, since all group delay positions at whatever frequency then refer to the same point.

Jacobs & Sovers (2008) have recently established a Celestial Reference Frame based on VLBI group-delay measurements at 8.4 and 32 GHz, where the 8.4 GHz measurements are used to make ionospheric delay corrections. Their frame is based on the positions of 318 compact radio sources. For sources in common with the ICRF, the weighted rms position differences are 241 $\mu$ as in RA cos(dec) and 290 $\mu$ as in declination. These differences are close to those one might expect from the measuring precisions alone. For the case of $\beta = 1$ , the group-delay positions at both frequencies measure the same position of the jet base, x₀. Note that the typical core-shift at 32 GHz is only 44 $\mu$ as, corresponding to the difference between phase and group-delay positions.

3.2 Phase-reference observations

VLBI phase-referencing is a technique whereby the visibility phase of one source (the calibrator) is subtracted from that of another (the target). It can be used either to remove unwanted instrumental and propagation phase terms from a weak target source visibility, and/or to measure the relative position between the target and calibrator. The technique has also been successfully used for spacecraft navigation. Calibrator sources and their positions are often chosen from those used to define the ICRF, or from the VLBA Calibrator Survey (VCS; Petrov et al. 2008, and references therein) for which similar precise ionosphere-corrected 8.4 GHz group-delay positions have been measured. As shown above, these positions do not, in general, refer to the core position at 8.4 GHz. Although this does not detract at all from the ability of phase-referencing to detect weak sources, it does require a reinterpretation of the derived position of the target, since this is measured with respect to the calibrator core position at the observing frequency, not its listed group-delay position. Knowledge of the calibrator core shift at the frequency of observation is hence necessary to locate the target in the ICRF.

Relative positions derived from VLBI phase measurements are more precise than positions determined using group-delays. Fomalont (2006) has suggested that more accurate ICRF positions might be obtained from 8.4 GHz relative phase measurements by first determining the relative positions of groups of sources within a radius of perhaps $20^\circ$ , and then ``stitching'' together many such groups to cover the whole sky. This may indeed be possible but one should note that the relative positions measured at 8.4 GHz between ICRF sources will not correspond to their relative positions measured using group-delays at 8.4 GHz.

Marti-Vidal et al. (2008) have used wide-field phase-differenced observations at 15.4 GHz, and an atmospheric model, to determine positions for 13 AGN cores in the S5 polar cap sample, with quoted precisions ranging from 14-200 $\mu$ as. They determined mean position corrections with respect to ICRF group-delay positions of 278 $\mu$ as in RA and 170 $\mu$ as in declination. Note that, for $\beta = 1$ , the group-delay positions refer to the jet base, whereas the 15.4 GHz interferometer phase positions refer to the 15.4 GHz core position, typically $\sim$ 93 $\mu$ as away.

3.3 VLBI2010

Within the program VLBI2010 the IVS community is planning a major upgrade in instrumentation for global geodetic and astrometric observing (Petrachenko 2006). Amongst other improvements it is planned to observe in 4 different frequency bands between 2 and 18 GHz, both to improve the group-delay resolution, and also to attempt the transition from group-delay to using the full precision of interferometer phase measurements. Hobiger et al. (2009) have considered schemes for solving the $2\pi$ phase ambiguities which arise in interpolating the interferometer phase between the bands, taking into account the need to solve for the dispersive ionospheric path and core-shifts in the different bands. Their simulations, however, which use phase and group-delay measurements from the 4 bands, assume fixed core-shifts in each of the bands and do not take account of the shift within the bands. In fact, for the case $\beta = 1$ , the core-shift has no effect on the group-delay measurements and adds just a constant phase offset at all 4 bands, which would make the interpolation problem in the presence of an unknown ionospheric path easier to solve. However, for unknown values of $\beta$ and $\Delta$ x₁ phase measurements in at least 3 frequency bands would be needed to determine these core-shift parameters.

4 Conclusions

It has been shown that the phenomenon of AGN frequency core-shifts, arising from opacity effects on the radio synchrotron emission at the base of relativistic jets, breaks the proportional relationship between interferometer phase and group-delay measurements in astrometry. The effect on the latter has been investigated using a simple model of a point-source core whose position down the jet has a power-law dependence on wavelength. This is no doubt an over-simplification as both the exponent $\beta$ and the jet angle may change with position along the jet (Lobanov 1998). Nevertheless, the results indicate that significant position differences arise at the sub-mas level between measurements using phase and group delays. These differences are comparable to the current precision of source positions derived from group delay measurements and used to establish the ICRF. However, they will assume a greater importance in the near future when improved radio-astronomical instrumentation, and the GAIA mission at optical wavelengths, produce positions with up to an order of magnitude better precision.

The core-shift coefficient, $\Delta{x}_{1}$ , and power-law exponent, $\beta$ , are governed by the precise physical conditions in the synchrotron-emitting jet. Blandford & Königl (1979) have shown that, for synchrotron self-absorption in an equi-partition regime, $\Delta{x}_{1}$ is proportional to (luminosity)^2/3, whereas $\beta$ can be expected to be $\sim$ 1. If this is indeed common, then group-delay measurements at any frequency refer to a fixed point at the base of the jet, perhaps close to the centre of optical emission. This is more simple than one might expect. Note that the process of delay fringe-fitting, used for most astronomical VLBI data analysis, determines delay (but not phase) residuals with respect to this position. An improved Celestial Reference Frame, based on interferometer phase measurements of core positions, would presumably align well with the present ICRF, since the offsets between the cores and the jet bases in the set of defining source will be randomly distributed in angle. The VLBI2010 project holds promise for such an advance in the coming years.

Acknowledgements

I thank Bill Petrachenko for discussions on the use of visibility phase in future VLBI2010 observing scenarios, and Andrei Lobanov for comments on the text.

References

Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] (In the text)
Charlot, P. 1990, AJ, 99, 1309 [NASA ADS] [CrossRef] (In the text)
Conway, J. E., Cornwell, T. J., & Wilkinson, P. N. 1990, MNRAS, 246, 490 [NASA ADS] (In the text)
Cornwell, T. J., & Wilkinson, P. N. 1981, MNRAS, 196, 1067 [NASA ADS] (In the text)
Cotton, W. D. 1979, AJ, 84, 1122 [NASA ADS] [CrossRef] (In the text)
Fomalont, E. 2006, Proc. 4th IVS General Meeting, ed. D. Behrend, & K. Baver, NASA/CP-2006-214140, 307 (In the text)
Fey, A. L., Ma, C., Arias, E. F., et al. 2004, AJ, 127, 3587 [NASA ADS] [CrossRef] (In the text)
Hobiger, T., Sekido, M., Koyama, Y., & Kondo, T. 2009, Adv. Space Res., 43, 187 [NASA ADS] [CrossRef] (In the text)
Jacobs, C., & Sovers, O. 2008, Proc. 5th IVS General Meeting, ed. A. Finkelstein, & D. Behrend, (St. Petersburg: Nauka), 284 (In the text)
Königl, A. 1981, ApJ, 243, 700 [NASA ADS] [CrossRef] (In the text)
Kovalev, Y. Y., Lobanov, A. P., Pushkarev, A. B., & Zensus, J. A. 2008, A&A, 483, 759 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Lindegren, L., Babusiaux, C., Bailer-Jones, C., et al. 2007, Proc. IAU Symp., 248, ed. J. Jin, I. Platais, & M. A. C. Perryman (Cambridge: CUP), 217 (In the text)
Lobanov, A. P. 1998, A&A, 330, 79 [NASA ADS] (In the text)
Ma, C., Arias, E. F., Eubanks, T. T., et al. 1998, AJ, 116, 516 [NASA ADS] [CrossRef] (In the text)
Marcaide, J. M., & Shapiro, I. I. 1983, AJ, 88, 1133 [NASA ADS] [CrossRef] (In the text)
Marcaide, J. M., Shapiro, I. I., Corey, B. E., et al. 1985, A&A, 142, 71 [NASA ADS] (In the text)
Marti-Vidal, I., Marcaide, J. M., Guirado, J. C., Perez-Torres, M. A., & Ros, E. 2008, A&A, 478, 267 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Middelberg, E., Roy, A. L., Walker, R. C., & Falcke, H. 2005, A&A, 433, 897 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Mittal, R., Porcas, R., Wucknitz, O., Biggs, A., & Browne, I. 2006, A&A, 447, 515 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Petrachenko, B. 2006, Proc. 4th IVS General Meeting, ed. D. Behrend, & K. Baver, NASA/CP-2006-214140, 67 (In the text)
Petrov, L. 2007, Proc. of the 18th European VLBI for Geodesy and Astrometry Working Meeting, ed. J. Böhm, A. Pany, & H. Schuh, Technische Universität Wien, 141 (In the text)
Petrov, L., Kovalev, Y. Y., Fomalont, E. B., & Gordon, D. 2008, ApJ, 136, 580 [NASA ADS] (In the text)
Porcas, R. W., & Patnaik, A. R. 1995, Proc. 10th Working Meeting on European VLBI for Geodesy and Astrometry, ed. R. Lanottte, & G. Bianco, Matera, 188 (In the text)
Rioja, M., Dodson, R., Porcas, R., Suda, H., & Colomer, F. 2005, Proc. 17th Working Meeting on European VLBI for Geodesy and Astrometry, ed. M. Vennebusch, & A. Nothnagel, Noto: INAF, 125 (In the text)
Sault, R. J., & Wieringa, M. H. 1994, A&AS, 108, 585 [NASA ADS] (In the text)
Schwab, F. R., & Cotton, W. D. 1983, AJ, 88, 688 [NASA ADS] [CrossRef] (In the text)

All Tables

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.