| Issue |
A&A
Volume 505, Number 1, October I 2009
|
|
|---|---|---|
| Page(s) | 83 - 96 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200912621 | |
| Published online | 24 July 2009 | |
The role of environment in the morphological transformation of galaxies in 9 rich intermediate redshift clusters
M. Huertas-Company1,2 - G. Foex3 - G. Soucail3 - R. Pelló3
1 - ESO, Alonso de Cordova 3107, Vitacura, Casilla 19001, Santiago 19, Chile
2 - LESIA - Paris Observatory, 5 place Jules Janssen, 92195 Meudon, France
3 - Laboratoire d'Astrophysique de Toulouse-Tarbes, CNRS and Université de Toulouse, 14 Av. E. Belin, 31400 Toulouse, France
Received 3 June 2009 / Accepted 16 July 2009
Abstract
Context. Rich clusters offer a unique laboratory for studying the effects of local environment on the morphological transformation of galaxies moving from the blue star-forming cloud to the red passive sequence. Due to the high-density, any environmental process should be more pronounced there compared to the field population.
Aims. Ideally, we would like to reconstruct the evolution of a single, hypothetical representative galaxy as it enters the cluster. For that purpose wide-field imaging is crucial to probe a wide range of densities and environments (from the core to the outskirts) and isolate this way, the different physical processes which are responsible of the migration from the blue-cloud to the red-sequence.
Methods. We analyze a sample of 9 massive clusters at 0.4<z<0.6 observed with MegaCam in 4 photometric bands (g,r,i,z) from the core to a radius of 5 Mpc (![]() 4000 galaxies). Galaxy cluster candidates are selected using photometric redshifts computed with HyperZ. Morphologies are estimated with GALSVM in two broad morphological types (early-type and late-type). We examine the morphological composition of the red-sequence and the blue-cloud and study the relations between galaxies and their environment through the morphology-density relations (
4000 galaxies). Galaxy cluster candidates are selected using photometric redshifts computed with HyperZ. Morphologies are estimated with GALSVM in two broad morphological types (early-type and late-type). We examine the morphological composition of the red-sequence and the blue-cloud and study the relations between galaxies and their environment through the morphology-density relations (![]() )
and the morphology-radius relation (T-R) in a mass limited sample (
)
and the morphology-radius relation (T-R) in a mass limited sample (
![]() ).
).
Results. We find that the red sequence is already in place at
![]() and it is mainly composed of very massive (
and it is mainly composed of very massive (
![]() )
early-type galaxies. These massive galaxies seem to be already formed when they enter the cluster, probably in infalling groups, since the fraction remains constant with the cluster radius. Their presence in the cluster center could be explained by a segregation effect reflecting an early assembly history. Any evolution that takes place in the galaxy cluster population occurs therefore at lower masses (
)
early-type galaxies. These massive galaxies seem to be already formed when they enter the cluster, probably in infalling groups, since the fraction remains constant with the cluster radius. Their presence in the cluster center could be explained by a segregation effect reflecting an early assembly history. Any evolution that takes place in the galaxy cluster population occurs therefore at lower masses (
![]() ). For these galaxies, the evolution, is mainly driven by galaxy-galaxy interactions in the outskirts as revealed by the
). For these galaxies, the evolution, is mainly driven by galaxy-galaxy interactions in the outskirts as revealed by the ![]() relation. Finally, the majority of less massive galaxies (
relation. Finally, the majority of less massive galaxies (
![]() )
are late-type galaxies at all locations, suggesting that they have not started the morphological transformation yet even if this low mass bin might be affected by incompleteness.
)
are late-type galaxies at all locations, suggesting that they have not started the morphological transformation yet even if this low mass bin might be affected by incompleteness.
Key words: galaxies: clusters: general - galaxies: evolution - galaxies: fundamental parameters - galaxies: high-redshift
1 Introduction
Studies of galaxy properties and their dependences on environment are key to understanding the mechanisms that are responsible for galaxy evolution since they constitute a natural test for cosmological theories of galaxy formation. Evidence has accumulated in recent years that environmental processes affect both the star formation and morphological characteristics of galaxies, the endpoint being the present-day morphology-density relation (Dressler 1980; Treu et al. 2003).
In particular, two fundamental observational results deal with the star formation history and the color-morphology distribution of field galaxies: a) the downsizing (e.g. Cowie et al. 1996; Bundy et al. 2005), i.e. a stronger and earlier decline of star formation in massive galaxies compared to a slower decrease of the star formation rate of the present blue/late-type galaxies; and b) the bimodality (e.g. Baldry et al. 2004; Strateva et al. 2001) of the galaxy distribution in the color-mass space, i.e. a marked segregation in color between the blue cloud (low mass, star-forming late-type galaxies) and the red-sequence (massive, red, passive early-type galaxies).
Therefore, the scenario which seems to emerge is that galaxies move from the blue population to the red-sequence at rates and cosmic epochs that depend very strongly on their mass and environment. However, the nature and timescale of the relevant mechanisms that lead this mass-dependent transition are still unclear. We need processes to quench the star formation above a mass threshold such as gas loss caused by AGN feedback and/or supernova feedback (e.g. Neistein et al. 2006; Di Matteo et al. 2005; Menci et al. 2006), consumption of all available gas in the wake of violent merging (e.g. Faber et al. 2007), ram-pressure stripping/harassment in clusters that turns off efficient cold gas accretion. A combination of these processes are normally required in semi-analytical models to ensure that quenching is efficient, permanent, and mass-dependent (De Lucia et al. 2006).
From that point of view, rich clusters offer a unique laboratory for studying the effects of local environment on the transition between the blue cloud and the red sequence (e.g. Poggianti et al. 2006). Their cores have the highest volume density of galaxies in the universe so that any environmental dependence of galaxy formation or evolution processes should be more pronounced there, when contrasted with studies of the field population. Ideally, we would like to make a significant step forward and reconstruct the complete evolution of a single, hypothetical representative galaxy as it enters the cluster potential and interacts with the ICM. How do star-formation and morphology evolve as a galaxy enters the cluster? How does it move form the blue-cloud to the red-sequence? To answer these questions it becomes necessary to assign timescales to the phenomena observed and to connect afterwards clusters at different redshifts into a temporal sequence. The various processes that can take place can be classified in three broad headings (see Treu et al. 2003 for a nice review):
- 1)
- galaxy-ICM interactions, which refers to the interaction of a cluster galaxy with the gaseous component of the cluster;
- 2)
- galaxy-cluster gravitational interactions, including tidal and related dynamical processes and;
- 3)
- smaller scale galaxy-galaxy interactions.
The main problem of HST imaging is however its small field of view, which makes it very time consuming to obtain a wide view of the cluster from the inner core to the outskirts. That is the main reason why most of these previous works focus on the inner 0.5 Mpc of several clusters which is lower than the virial radius (![]() 2 Mpc). However probing the outskirts of clusters is essential to discriminate between the different
processes that can induce morphological transformation of a galaxy entering the cluster. Treu et al. (2003) have shown indeed that depending on the analyzed zone it is possible to isolate
one process from another. Thanks to a wide survey on a single target, they were able to show
that the most likely processes responsible for the mild gradient in the morphological mix outside the virial radius are galaxy-galaxy interactions.
This later affirmation has been confirmed in more recent works. Using a volume-limited sample, Patel et al. (2009) argued that the evolution in the galaxies entering a cluster at
2 Mpc). However probing the outskirts of clusters is essential to discriminate between the different
processes that can induce morphological transformation of a galaxy entering the cluster. Treu et al. (2003) have shown indeed that depending on the analyzed zone it is possible to isolate
one process from another. Thanks to a wide survey on a single target, they were able to show
that the most likely processes responsible for the mild gradient in the morphological mix outside the virial radius are galaxy-galaxy interactions.
This later affirmation has been confirmed in more recent works. Using a volume-limited sample, Patel et al. (2009) argued that the evolution in the galaxies entering a cluster at
![]() is mainly driven by the local environment. In this last work, the authors also showed an interesting trend: the dependence of galaxy evolution in clusters with the stellar mass. They indeed identify the same downsizing effect as seen in the field (Cowie et al. 1996; Bundy et al. 2005), with massive galaxies having their star forming rate decline faster.
is mainly driven by the local environment. In this last work, the authors also showed an interesting trend: the dependence of galaxy evolution in clusters with the stellar mass. They indeed identify the same downsizing effect as seen in the field (Cowie et al. 1996; Bundy et al. 2005), with massive galaxies having their star forming rate decline faster.
At this point, it becomes interesting to have a wide view of a statistically representative sample of clusters at high redshift with robust stellar mass estimates to probe the physical mechanisms responsible of the mass-dependent transition from the blue-cloud to the red-sequence. MegaCam, the wide field imager installed at the Canada France Hawaii Telescope can probe in a single pointing a cluster at
![]() from the core to
from the core to ![]() 12 Mpc radius. Problems come now from angular resolution, since determining morphologies of galaxies from this ground-based images is not trivial. Huertas-Company et al. (2008) describes a method to estimate robust morphologies on poorly resolved data. In that work, the authors were able to prove that, when applied to seeing-limited data, the method can provide morphological information in two broad classes, with an accuracy close to that obtained with space data.
12 Mpc radius. Problems come now from angular resolution, since determining morphologies of galaxies from this ground-based images is not trivial. Huertas-Company et al. (2008) describes a method to estimate robust morphologies on poorly resolved data. In that work, the authors were able to prove that, when applied to seeing-limited data, the method can provide morphological information in two broad classes, with an accuracy close to that obtained with space data.
Table 1: Main properties of clusters in our sample.
In the present paper we use this method combined with accurate photometric redshift estimates in 9 rich clusters at intermediate redshifts (0.4<z<0.6). We show that we are able to isolate galaxy cluster members and to estimate the morphologies of ![]() 4000 galaxies with a fair degree of reliability. We then connect them to the cluster environment in three mass ranges to probe the mass-dependent transition from the blue-cloud to the red-sequence.
4000 galaxies with a fair degree of reliability. We then connect them to the cluster environment in three mass ranges to probe the mass-dependent transition from the blue-cloud to the red-sequence.
The paper is organized as follows: in Sect. 2 we introduce the observational data. In Sect. 3 we describe our method for selecting member galaxies based on photometric redshifts. We combine the photometric redshift estimate with the shape of the redshift probability function (P(z)) function to establish a robust criteria for selecting galaxies. The physical properties computed are described in Sect. 4. We specially focus on the morphology determination and on the accuracy quantification. We then describe and discuss our main results in Sect. 5.
Throughout the paper, we assume that the Hubble constant, the matter density, and the cosmological constant are H0=70 km s-1 Mpc-1,
![]() and
and
![]() respectively.
respectively.
2 Data description
The data used in this paper are part of an imaging survey of X-ray
clusters at intermediate redshift (
![]() ), undertaken to
study the mass distribution in these clusters and to compare the X-ray
distribution of the intra-cluster gas and the dark matter distribution
traced by weak lensing. The sample has been selected to be representative
of the rich cluster population at intermediate redshift and is part of the full and unbiased sample observed with XMM-Newton as part as a Large Programme (PI: Arnaud). As the main goal of the optical follow-up was to study in details the mass distribution by weak lensing techniques, only the
hottest and most massive clusters of the sample were selected. This
ended with a sub-sample of 10 clusters, 9 of which are studied in this
paper. The last one, RXJ1347.5-1145 was discarded because it was observed
in different conditions at CFHT and so would reduce the homogeneity of the
study. The 9 resulting clusters were observed with the wide-field imager
MegaCam installed at CFHT, and in 4 photometric bands (
g',r',i',z')
and with integration times of 1600 s, 7200 s, 1200 s and 1800 s respectively. We asked for a longer exposture time in r' because
these data are dedicated to the weak lensing measurement of the mass
distribution in the clusters, while the color information is restricted
to the study of the cluster population. We will therefore use r' band data for the morphological analysis as well (Sect. 4.1). The total field of view covered
by the mosaic is one square degree, with a pixel scale of 0.187
), undertaken to
study the mass distribution in these clusters and to compare the X-ray
distribution of the intra-cluster gas and the dark matter distribution
traced by weak lensing. The sample has been selected to be representative
of the rich cluster population at intermediate redshift and is part of the full and unbiased sample observed with XMM-Newton as part as a Large Programme (PI: Arnaud). As the main goal of the optical follow-up was to study in details the mass distribution by weak lensing techniques, only the
hottest and most massive clusters of the sample were selected. This
ended with a sub-sample of 10 clusters, 9 of which are studied in this
paper. The last one, RXJ1347.5-1145 was discarded because it was observed
in different conditions at CFHT and so would reduce the homogeneity of the
study. The 9 resulting clusters were observed with the wide-field imager
MegaCam installed at CFHT, and in 4 photometric bands (
g',r',i',z')
and with integration times of 1600 s, 7200 s, 1200 s and 1800 s respectively. We asked for a longer exposture time in r' because
these data are dedicated to the weak lensing measurement of the mass
distribution in the clusters, while the color information is restricted
to the study of the cluster population. We will therefore use r' band data for the morphological analysis as well (Sect. 4.1). The total field of view covered
by the mosaic is one square degree, with a pixel scale of 0.187
![]() (
(![]() 1.1 kpc at z=0.5). At the average cluster redshift (
1.1 kpc at z=0.5). At the average cluster redshift (![]() ), this corresponds to a radius up to
), this corresponds to a radius up to ![]() 12 Mpc, well above the virial radius (
12 Mpc, well above the virial radius (![]() 1-2 Mpc, see Table 1). Consequently,
the outskirts of the clusters as well as they global environment can
also be probed. The basic properties of the clusters are summarized in
Table 1 and more details can be found in Foex et al. (in preparation).
1-2 Mpc, see Table 1). Consequently,
the outskirts of the clusters as well as they global environment can
also be probed. The basic properties of the clusters are summarized in
Table 1 and more details can be found in Foex et al. (in preparation).
Data reduction was done in a standard way in the Terapix
center![]() or using the specific tools
developped by Terapix (astrometry, stacking and photometric
calibration). The photometric catalogs were built using
SEXTRACTOR (Bertin & Arnouts 1996) in dual mode for multi-color
photometry. As illustration, we show in Fig. 1,
a color composite image of one of the clusters. On average, the
image quality on the final r' images is
or using the specific tools
developped by Terapix (astrometry, stacking and photometric
calibration). The photometric catalogs were built using
SEXTRACTOR (Bertin & Arnouts 1996) in dual mode for multi-color
photometry. As illustration, we show in Fig. 1,
a color composite image of one of the clusters. On average, the
image quality on the final r' images is
![]() with
some variation from cluster to cluster. The completeness magnitude
of the photometric catalogues is about r'=25, g'=25, i'=24 and
z'=23.5. For the details of the photometric survey of these clusters,
we refer to Foex et al. (2009, in preparation). In this paper, we
restrict the analysis to objects with 18<r<23 lying at a radius lower
than 5 Mpc. As we will show in Sect. 4 this is
equivalent to a mass cut at
with
some variation from cluster to cluster. The completeness magnitude
of the photometric catalogues is about r'=25, g'=25, i'=24 and
z'=23.5. For the details of the photometric survey of these clusters,
we refer to Foex et al. (2009, in preparation). In this paper, we
restrict the analysis to objects with 18<r<23 lying at a radius lower
than 5 Mpc. As we will show in Sect. 4 this is
equivalent to a mass cut at
![]() .
The magnitude
cut is motivated by the reliability of the morphological classification
(Sect. 4.1) while the distance cut is done to reduce the field
contaminations (Sect. 3).
.
The magnitude
cut is motivated by the reliability of the morphological classification
(Sect. 4.1) while the distance cut is done to reduce the field
contaminations (Sect. 3).
![\begin{figure}
\par\includegraphics[width=15.9cm,clip]{12621fg1.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg29.png) |
Figure 1:
Color image of a
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12621fg2.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg33.png) |
Figure 2:
Spatial distributions of galaxies in the different clusters. Red circles indicate early-type objects and blue spiral symbols late-type galaxies. The symbol sizes code three different mass ranges; big:
|
| Open with DEXTER | |
3 Cluster member selection
The most unambiguous way to determine cluster membership is by means of accurate spectroscopic redshifts. Unfortunately, it is too time consuming to obtain high-sepctroscopic completeness,
even to relatively bright limits. He we adopt a method for membership determination based on photometric redshift estimates presented in Pello et al. (2009). Usually,
![]() -based methods for determining cluster membership are based on a simple cut in redshift, such that a galaxy is considered to be member if
-based methods for determining cluster membership are based on a simple cut in redshift, such that a galaxy is considered to be member if
![]() .
The problem of this kind of approach is that
.
The problem of this kind of approach is that
![]() can be as high as 0.3, producing high field
contaminations. As a matter of fact, the accuracy of photometric redshifts as a function of redshift strongly depends on the filter set and its ability to detect strong spectral features, such as the 4000
can be as high as 0.3, producing high field
contaminations. As a matter of fact, the accuracy of photometric redshifts as a function of redshift strongly depends on the filter set and its ability to detect strong spectral features, such as the 4000 ![]() break. In this case, the contiguous spectral coverage from g to z is well suited to derive good-quality photometric redshifts for galaxies between 0.2<z<1.2, i.e. within the redshift range of interest for our study. Galaxies below
break. In this case, the contiguous spectral coverage from g to z is well suited to derive good-quality photometric redshifts for galaxies between 0.2<z<1.2, i.e. within the redshift range of interest for our study. Galaxies below
![]() or beyond
or beyond
![]() will have poor-quality redshifts and broad redshift probability distributions. We therefore expect this population to contaminate the
will have poor-quality redshifts and broad redshift probability distributions. We therefore expect this population to contaminate the
![]() distribution in these regions (see Fig. 4). To reduce this contamination, we combine both the best-fit redshift and the information contained in the full redshift probability distribution P(z), by computing the integrated probability for the galaxy to be in the cluster (
distribution in these regions (see Fig. 4). To reduce this contamination, we combine both the best-fit redshift and the information contained in the full redshift probability distribution P(z), by computing the integrated probability for the galaxy to be in the cluster (
![]() ):
):
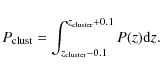 |
(1) |
Since the contaminating galaxies do not exhibit strong features within the griz spectral domain (i.e. their broad redshift-probability distributions avoid the cluster redshift), this selection criterion based on the probability distribution should remove most of them. By using a representative spectroscopic sample, which is available for MS0451.5-0305 (Ellingson et al. 1998) we can calibrate the threshold value
Figure 3 shows the evolution of the rejection of field galaxies as well as the completeness of the members selection for different values of
![]() and for different radii. We clearly see that increasing the probability threshold results in an increase of the fraction of rejected non-members while the fraction of cluster members progressively decreases. Since our main objective is to study the effects of the cluster environment on morphology and color we want to reduce the number of field contaminations. We therefore consider as galaxy cluster members all the objects which have
and for different radii. We clearly see that increasing the probability threshold results in an increase of the fraction of rejected non-members while the fraction of cluster members progressively decreases. Since our main objective is to study the effects of the cluster environment on morphology and color we want to reduce the number of field contaminations. We therefore consider as galaxy cluster members all the objects which have
![]() and
and
![]() .
As shown in Fig. 3, this ensures at least 80% completeness and
.
As shown in Fig. 3, this ensures at least 80% completeness and ![]() 80% rejections up to r<2 Mpc. Above this distance, the completeness is slightly lower (
80% rejections up to r<2 Mpc. Above this distance, the completeness is slightly lower (![]() 70%) but the rejection remains high. We establish the limit of 5 Mpc as the distance at which there is still a reasonable compromise between completeness and field contamination, well above the virial radius of the clusters. This results in a sample of 3861 galaxies distributed in the 9 clusters. We show in Fig. 2, the spatial distribution of galaxies in the 9 clusters.
70%) but the rejection remains high. We establish the limit of 5 Mpc as the distance at which there is still a reasonable compromise between completeness and field contamination, well above the virial radius of the clusters. This results in a sample of 3861 galaxies distributed in the 9 clusters. We show in Fig. 2, the spatial distribution of galaxies in the 9 clusters.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12621fg3.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg45.png) |
Figure 3: Galaxy cluster member selection accuracy for MS 0451.5-0305. The different panels show the results for different radii. Solid lines indicate the completeness and dashed lines the contaminations from non-members as a function of the probability threshold. The vertical dashed line shows the adopted probability threshold. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12621fg4.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg46.png) |
Figure 4: Photometric redshift distributions for all the clusters. Dashed vertical lines show the cluster spectroscopic redshift. |
| Open with DEXTER | |
4 Physical properties
4.1 Morphology
4.1.1 Method
We now discuss the morphological classification of the objects belonging to the cluster. Morphologies are determined in the r-band images using GALSVM![]() . GALSVM is a non-parametric N-dimensional code based on support vector machines (SVM) that uses a training set built from a local visually classified sample. (Huertas-Company et al. 2008). Basically we separate galaxies in two broad morphological types (late and early type). By late-type we mean spiral and irregular galaxies (S/I) and early-type galaxies include elliptical and lenticular types (E/S0).
. GALSVM is a non-parametric N-dimensional code based on support vector machines (SVM) that uses a training set built from a local visually classified sample. (Huertas-Company et al. 2008). Basically we separate galaxies in two broad morphological types (late and early type). By late-type we mean spiral and irregular galaxies (S/I) and early-type galaxies include elliptical and lenticular types (E/S0).
Broadly, the employed procedure can be summarized in 4 main steps (see Huertas-Company et al. 2008 for more details):
- 1.
- Build a training set: we select a nearby visually classified sample at wavelengths corresponding to the rest-frame of the high redshift sample to be analyzed to minimize morphological k-correction effects. In our case, we want to simulate r-band observations at
 .
We use therefore an SDSS local sample observed in the g band which roughly corresponds to the rest-frame wavelength. We then move the sample to the proper redshift and
image quality, assign a magnitude randomly selected in the magnitude range [19:23] with a distribution representative of the observed luminosity function and drop it in a real image to properly simulate the background noise.
.
We use therefore an SDSS local sample observed in the g band which roughly corresponds to the rest-frame wavelength. We then move the sample to the proper redshift and
image quality, assign a magnitude randomly selected in the magnitude range [19:23] with a distribution representative of the observed luminosity function and drop it in a real image to properly simulate the background noise.
- 2.
- Measure a set of morphological parameters on the sample. In this particular case, the classification is made in 7 dimensions, including: ellipticity, asymmetry, gini, concentration, M20 and smoothness. For more details on how these parameters are exactly computed please consult Huertas-Company et al. (2008).
- 3.
- Train a support vector based learning machine with a fraction of the simulated sample and use the other fraction to test and estimate errors.
- 4.
- Classify real data with the trained machine.
4.2 Accuracy of classifications: cross-checking with HST
One of the main challenges of the present work is performing a morphological classification on seeing-limited images. Until now, all the works involving morphological classifications of distant galaxy clusters have been based on HST imaging. We need consequently to carefully investigate the accuracy of our classification. Fortunately, two of our clusters have published data obtained with the space telescope. This is the case of MS 1621.5+2640 (Saintonge et al. 2005; Ellingson et al. 1997) and MS 0451.5-0305 (Ellingson et al. 1998; Moran et al. 2007). We therefore have a reference to calibrate our morphological classification on seeing-limited images.
MS 0451.5-0305
This cluster has available published results on 96 galaxies based on HST imaging which enables a second calibration of our classification. Moran et al. (2007) performed detailed visual morphological classifications using WFPC2 imaging. Figure 6 shows the comparison of our GALSVM-based classification with their results. Both classifications are in good agreement: a big fraction (
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12621fg5.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg48.png) |
Figure 5:
Stamps of the same galaxies seen by HST and MegaCam. The stamps size is 10'' |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12621fg6.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg49.png) |
Figure 6: Relation between the visual morphology computed in Moran et al. (2007) and the GALSVM type. Filled histograms show the fraction of GALSVM early-type objects and empty histograms the fraction of late-type galaxies. |
| Open with DEXTER | |
MS 1621.5+2640
Saintonge et al. (2005) performed an automated morphological classification based on model-fitting of 258 galaxies. They used the bulge fraction (B/T) as the main parameter to split objects into different morphological classes. In Table 2 we compare the probability of being early-type according to our classification and the bulge fraction of Saintonge et al. (2005) for the 59 galaxies identified as cluster members and within our selected magnitude range: a galaxy with a low bulge fraction should have also a low probability of begin elliptical. Of course the dispersion of the distribution is considerable but we have to keep in mind that we are not measuring the same parameters, so points do not necessarily have to lie on the unity slope line. Since we are only interested in splitting the galaxies into two rough morphological types, we have to look at the fraction of galaxies that are clearly miss-classified, if we consider the HST-based classification as a reference (which is not necessarily true since it is an automated classification as well). This includes objects which are clear disc-dominated galaxies (B/T<0.3) but have a probability of being early-type greater that 0.5 and vice-versa, galaxies with a bulge fraction bigger than 0.7 but low probabilities of being ellipticals. We find that the first represent 5 objects out of 41 early-type objects and the second one out of 18. We conclude then that our classification is robust and in good agreement with the HST one. Note however that we might be slightly over-estimating the fraction of elliptical galaxies if compared with HST studies as pointed out in the previous comparison. If we indeed consider galaxies with an intermediate bulge-fraction (i.e. 0.3 < B/T < 0.7), most of them (25/31) fall in the early-type class. It worth noticing here that despite of these differences with HST, this work presents 2 important advantages: first, the size of the sample (Table 2: Relation between the bulge fraction computed in Saintonge et al. (2005) and the probability of being early-type computed by GALSVM.
4.3 Stellar masses
Recent works have shown that the relations between galaxies and their environment in clusters strongly depend on the considered mass range (Patel et al. 2009; Holden et al. 2007). Holden et al. (2007) did not find, for example, any evolution on the early-type population with
M > 1010.6 solar masses, using a mass-limited sample. They suggested therefore that most of the morphological transformation which occurs from
![]() must affect the low mass galaxies. It appears therefore interesting to investigate the effect of stellar mass on the different analyzed trends in our sample. In this work, stellar masses are computed directly from the best-fitting model of the photometric redshift estimate using a Chabrier (2003) IMF. The mass estimate takes into account the age of the model as well as the star forming history. Even though we do not have NIR photometry, we consider our mass estimates reliable since at
must affect the low mass galaxies. It appears therefore interesting to investigate the effect of stellar mass on the different analyzed trends in our sample. In this work, stellar masses are computed directly from the best-fitting model of the photometric redshift estimate using a Chabrier (2003) IMF. The mass estimate takes into account the age of the model as well as the star forming history. Even though we do not have NIR photometry, we consider our mass estimates reliable since at
![]() the redder filters (i,z) are probing the SED around 5000 Å, (beyond the 4000 Å break) where the flux is mostly coming from evolved stellar populations.
the redder filters (i,z) are probing the SED around 5000 Å, (beyond the 4000 Å break) where the flux is mostly coming from evolved stellar populations.
Mass distributions for all the clusters are shown in Fig. 7. They are clearly bimodal for most of the clusters, with late-type galaxies dominating the low-mass regime (
![]() )
and the early-type ones dominating the high-mass one
)
and the early-type ones dominating the high-mass one
![]() ,
with of course some cluster-to-cluster variations. We try to estimate the mass completeness of our sample using the magnitude cut for the morphological classification (r' < 23), which is about 2 mag brighter than the magnitude limit of the catalogs. If we compare the mass function of the morphologically classified sample with that of the full sample up to the magnitude limit (r' = 25), we find that it is complete at the 50% level for a mass of
,
with of course some cluster-to-cluster variations. We try to estimate the mass completeness of our sample using the magnitude cut for the morphological classification (r' < 23), which is about 2 mag brighter than the magnitude limit of the catalogs. If we compare the mass function of the morphologically classified sample with that of the full sample up to the magnitude limit (r' = 25), we find that it is complete at the 50% level for a mass of
![]() (or
(or
![]() ). In the following, we will therefore divide the sample in three stellar mass bins:
). In the following, we will therefore divide the sample in three stellar mass bins:
![]() ,
,
![]() ,
,
![]() .
While the two last bins are not affected by incompleteness, the less massive one can be, specially for the early-type population which is mostly red and is therefore lost earlier in a magnitude limited survey. Nevertheless, we have decided to include this mass bin since some information can be extracted anyway. However, we are aware that this might introduce some biases when interpreting our results so we will properly point out and take into account this point when necessary in the following sections. Note also that a rough estimate of the apparent magnitude of a
.
While the two last bins are not affected by incompleteness, the less massive one can be, specially for the early-type population which is mostly red and is therefore lost earlier in a magnitude limited survey. Nevertheless, we have decided to include this mass bin since some information can be extracted anyway. However, we are aware that this might introduce some biases when interpreting our results so we will properly point out and take into account this point when necessary in the following sections. Note also that a rough estimate of the apparent magnitude of a ![]() galaxy at
galaxy at
![]() is
is
![]() so the magnitude limit for the morphological classification corresponds to a
so the magnitude limit for the morphological classification corresponds to a
![]() galaxy.
galaxy.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12621fg7.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg59.png) |
Figure 7: Stellar mass histograms for all the galaxies in the 9 clusters. Solid black lines show the histogram for all the galaxies while color lines show the histograms separated by morphological type (blue: late-type, red: early-type). |
| Open with DEXTER | |
4.4 Local density
The local density has been shown to play a key role in the evolution of galaxies, since the efficiency of the different mechanisms involved in such transformation often depends on the local density. To characterize it for all the galaxies in our sample we compute the local projected galaxy density, ![]() ,
at each galaxy location. We use the nth nearest neighbor definition, with n = 10, to compute
,
at each galaxy location. We use the nth nearest neighbor definition, with n = 10, to compute ![]() :
:
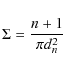 |
(2) |
where d n is the projected distance of the nth nearest neighbor. The value of n = 10 is commonly used in clusters since it is a good measure of the local over-density in this high density environments (Cooper et al. 2005). We include in the computation, all the cluster members selected with the method presented in Sect. 3. To avoid edge biases, we include galaxies a bit further of our 5 Mpc distance limit. We show in Fig. 8, the relationship between radius and local density. We clearly see that local density is not a well-defined function of radius, except in the central
5 Results and discussion
5.1 Composition of the red-sequence
Mass-color diagrams are a powerful tool to study the star-formation (SF) activity of galaxies. Galaxy distribution in this plane is bimodal, with passive red galaxies lying in a tight mass-color relation called the red-sequence (RS) and blue-star forming galaxies presenting a wider range of colors and masses and therefore lying in the so-called blue-cloud. This bimodality is usually analysed through the color-magnitude relation (e.g. Mei et al. 2009). The advantage of the
color-stellar mass relation is that it displays a less scattered relation, especially for the blue cloud. This is can be understood because there is a correlation between color and M/L ration
for late-type galaxies which is partly removed in a stellar mass-color relation and gives a narrower blue cloud (e.g. Patel et al. 2009).
In terms of galaxy evolution in dense environments, as galaxies enter in the cluster, we expect that their star-formation processes are
quenched by the different interaction effects. Galaxies move progressively
from the blue-cloud to the red-sequence, while suffering a morphological
transformation from late-types to earlier types. By looking at the composition of the red-sequence we can identify which galaxies have already suffered the transformation in clusters at
![]() and then try to isolate the processes responsible of this transformation. Nevertheless, this scheme is too simple to interpret all the diversity of galaxy morphologies and cannot explain the status of the ``red late-type galaxies'' or the ``blue early-type'' ones, but at least part of the bimodality is imprinted by evolution processes.
and then try to isolate the processes responsible of this transformation. Nevertheless, this scheme is too simple to interpret all the diversity of galaxy morphologies and cannot explain the status of the ``red late-type galaxies'' or the ``blue early-type'' ones, but at least part of the bimodality is imprinted by evolution processes.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12621fg8.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg62.png) |
Figure 8: Local density vs. radius for all the clusters in our sample. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12621fg9.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg63.png) |
Figure 9:
Stellar mass-color plots in the 2 central Mpc for all the 9 clusters in the sample. Early-type galaxies are shown with red filled circles and late-type with blue spiral symbols. Solid line indicate the best fit to the red-sequence and dashed lines 1.5 |
| Open with DEXTER | |
Figure 9 shows the g-r-stellar mass diagrams in the central 2 Mpc of all the clusters in our sample. We define whether a galaxy belongs or not to the red-sequence based on its deviation from the color-mass relation (CMR) shown in Fig. 9 (black solid line). The CMR is derived by performing an iterative fit to early-type galaxies with
![]() and rejecting the 2
and rejecting the 2![]() outliers of the best-fit at each iteration upon convergence. A galaxy is then said to belong to the red-sequence if it lies within the 2
outliers of the best-fit at each iteration upon convergence. A galaxy is then said to belong to the red-sequence if it lies within the 2![]() scatter of the non-rejected galaxies (dashed lines). It is worth noticing that despite of the fact that we see the same trends in all the clusters, we find that the CMR is not universal and that it is subjected to a cluster-to-cluster variance over the cluster population with different scatters and abundances. It is beyond the scope of this paper to analyze in details the shapes of the red-sequences but we are planning to do it in a coming paper. However, some interesting information can be extracted from these plots. First, they help checking the mass completeness limit of our sample and verifying that red objects (mostly early-type) are indeed lost earlier. As a matter of fact, above
scatter of the non-rejected galaxies (dashed lines). It is worth noticing that despite of the fact that we see the same trends in all the clusters, we find that the CMR is not universal and that it is subjected to a cluster-to-cluster variance over the cluster population with different scatters and abundances. It is beyond the scope of this paper to analyze in details the shapes of the red-sequences but we are planning to do it in a coming paper. However, some interesting information can be extracted from these plots. First, they help checking the mass completeness limit of our sample and verifying that red objects (mostly early-type) are indeed lost earlier. As a matter of fact, above
![]() we do clearly see the RS while below this mass, red galaxies start to become less abundant. This fact confirms that results obtained in the low mass bin (
we do clearly see the RS while below this mass, red galaxies start to become less abundant. This fact confirms that results obtained in the low mass bin (
![]() )
might be affected by incompleteness and should be analyzed carefully.
Second, it is possible to study the general composition of the red-sequence. If we first look at the morphological distributions, we clearly find out the expected trend, i.e. the majority of object lying in the RS are early-type objects (76%, Table 3). This result just confirms that as galaxies enter in the cluster and transform into elliptical galaxies, they progressively become redder and move to the red-sequence.
)
might be affected by incompleteness and should be analyzed carefully.
Second, it is possible to study the general composition of the red-sequence. If we first look at the morphological distributions, we clearly find out the expected trend, i.e. the majority of object lying in the RS are early-type objects (76%, Table 3). This result just confirms that as galaxies enter in the cluster and transform into elliptical galaxies, they progressively become redder and move to the red-sequence.
Furthermore, the majority of early-type objects lying the red sequence are massive objects (
![]() )
and as we progressively move into lower masses the number of galaxies of later morphological types becomes more important.
)
and as we progressively move into lower masses the number of galaxies of later morphological types becomes more important.
These tendancies with the stellar mass suggest that most of the evolution in these intermediate redshift clusters is affecting low mass galaxies (
![]() ), while the most massive galaxies seem to be well in place in the red-sequence. These results seem to be in agreement with De Lucia et al. (2007) who also found that, at intermediate redshift, luminous galaxies are already in place in the RS and evolve passively, while there is a deficit of faint red galaxies, suggesting that these galaxies are populating the RS from the blue cloud between
), while the most massive galaxies seem to be well in place in the red-sequence. These results seem to be in agreement with De Lucia et al. (2007) who also found that, at intermediate redshift, luminous galaxies are already in place in the RS and evolve passively, while there is a deficit of faint red galaxies, suggesting that these galaxies are populating the RS from the blue cloud between ![]() and today. Furthermore, semi-analytical models (e.g. Menci et al. 2008) also predict that at a cosmic time of
and today. Furthermore, semi-analytical models (e.g. Menci et al. 2008) also predict that at a cosmic time of
![]() Gyr (
Gyr (
![]() ), more than
), more than ![]() of the stellar mass finally assembled in red-sequence galaxies at
of the stellar mass finally assembled in red-sequence galaxies at ![]() is already in place.
is already in place.
Table 3: Composition of the red sequence in the 2 central MegaParsecs.
5.2 Radial trends
The morphologies of galaxies are correlated with distance from the cluster center in nearby clusters (e.g. Whitmore et al. 1993) and groups (e.g. Postman & Geller 1984) as well as at higher redshifts (e.g. van Dokkum et al. 2000; Abraham et al. 1996). An increase of the fraction of early-type galaxies towards the center is observed in all cases, but the detailed evolution of the morphology-radius relation from high redshift remains uncertain. Figure 10 shows the fractions of early and late-type galaxies at different radii for clusters in our sample. All the clusters present similar trends: as detected in previous works, we observe a correlation between morphology and distance, with elliptical galaxies representing about 80% of the galactic populations in the inner parts (d<0.5 Mpc) and decreasing at larger distances. More precisely, we see a steep decrease of the early-type fraction in the central Megaparsec which goes from ![]() 80% to
80% to ![]() 60% and then a mild decrease in the outer parts from
60% and then a mild decrease in the outer parts from ![]() 60% to
60% to ![]() 40% in agreement with previous HST-based works (e.g. Treu et al. 2003). These two different regimes are normally explained by different processes. While the explanation of the steep increase of the early-type fraction in the inner cores requires phenomena related to the cluster potential, such as tidal interaction or ram-pressure stripping which accelerate the morphological transformation, this is not the case in the outskirts. As a matter of fact, in the periphery, most of the galaxies have never been through the center and therefore are free from effects such as ram-pressure stripping. The mild decrease in the outskirts might be explained by a progressive quenching of the star formation (starvation, Balogh et al. 2000) or after a starburst phase (e.g. Poggianti et al. 1999).
40% in agreement with previous HST-based works (e.g. Treu et al. 2003). These two different regimes are normally explained by different processes. While the explanation of the steep increase of the early-type fraction in the inner cores requires phenomena related to the cluster potential, such as tidal interaction or ram-pressure stripping which accelerate the morphological transformation, this is not the case in the outskirts. As a matter of fact, in the periphery, most of the galaxies have never been through the center and therefore are free from effects such as ram-pressure stripping. The mild decrease in the outskirts might be explained by a progressive quenching of the star formation (starvation, Balogh et al. 2000) or after a starburst phase (e.g. Poggianti et al. 1999).
Another possibility is that the morphology radii relation is the consequence of a segregation effect: objects with different radii represent galaxies with different early assembly histories (through mergers) that keep a correlation between their history and the location in the cluster (e.g. Diaferio et al. 2001).
If this last scenario reveals to be true massive galaxies should have had their star formation activity decrease faster than less massive galaxies and therefore should be already predominantly early-type when they enter the cluster at
![]() .
Figure 11 shows the radial trends for different mass ranges, averaged for all the clusters in order to have better statistics. The fraction of massive galaxies (
.
Figure 11 shows the radial trends for different mass ranges, averaged for all the clusters in order to have better statistics. The fraction of massive galaxies (
![]() )
remains almost constant at all radii, indeed suggesting that these galaxies were formed before they entered the cluster, probably in infalling groups through galaxy-galaxy interactions and consequently experience small evolution. As a matter of fact, evidence that the source of the constituent galaxies of massive clusters are groups in the outskirts has also been seen in previous works (Dressler et al. 1997; Patel et al. 2009; Gonzalez et al. 2005; Moran et al. 2007). The presence of these galaxies in the cluster center can perhaps be explained by a segregation effect.
)
remains almost constant at all radii, indeed suggesting that these galaxies were formed before they entered the cluster, probably in infalling groups through galaxy-galaxy interactions and consequently experience small evolution. As a matter of fact, evidence that the source of the constituent galaxies of massive clusters are groups in the outskirts has also been seen in previous works (Dressler et al. 1997; Patel et al. 2009; Gonzalez et al. 2005; Moran et al. 2007). The presence of these galaxies in the cluster center can perhaps be explained by a segregation effect.
The general trend of a decrease of early-type galaxies with radius has to come therefore from lower mass galaxies, especially the intermediate mass range (
![]() ). Most of the evolution in the cluster galaxy population therefore seems to be occurring in this stellar mass range. On the contrary, for the
lowest mass bin in our sample (
). Most of the evolution in the cluster galaxy population therefore seems to be occurring in this stellar mass range. On the contrary, for the
lowest mass bin in our sample (
![]() ), the galaxy population is dominated by late-type galaxies as if they did not have time to evolve yet. Note that we do not consider the very central part of the cluster (d < 0.5 Mpc) because there are too few
low mass galaxies and numbers are not significant enough. We have to be however very cautious when analyzing this low mass bin, since as stated in Sect. 5.1, it might be strongly affected by incompleteness, leading to an under-estimate of the early-type population. As a mater of fact, since most of the galaxies lost in this mass bin are probably red early-type galaxies, the values measured should be considered as lower limits. In order to give a rough estimate of the maximum value, we considered that the 50% of galaxies are E/S0s and estimated how the fraction of these galaxies would rise at every position (see Fig. 11). We observe that, even if we loose half the early-type population at all distances, it would remain below the late-type population.
), the galaxy population is dominated by late-type galaxies as if they did not have time to evolve yet. Note that we do not consider the very central part of the cluster (d < 0.5 Mpc) because there are too few
low mass galaxies and numbers are not significant enough. We have to be however very cautious when analyzing this low mass bin, since as stated in Sect. 5.1, it might be strongly affected by incompleteness, leading to an under-estimate of the early-type population. As a mater of fact, since most of the galaxies lost in this mass bin are probably red early-type galaxies, the values measured should be considered as lower limits. In order to give a rough estimate of the maximum value, we considered that the 50% of galaxies are E/S0s and estimated how the fraction of these galaxies would rise at every position (see Fig. 11). We observe that, even if we loose half the early-type population at all distances, it would remain below the late-type population.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12621f11.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg71.png) |
Figure 10: Fraction of morphological types (r < 23) as a function of cluster radius. Red points: E/S0 galaxies, blue points: S/I galaxies. The total number of objects is shown in each plot. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12621f12.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg72.png) |
Figure 11: Morphological mixing as a function of the cluster radius, averaged for all the clusters in the sample and for different mass ranges. Filled circles are early-type galaxies and spiral symbols are late-type galaxies. The left panel shows the results for the whole sample. Notice that for the low mass bin ( top right) the two first points are not significative since there are too few objects. The total number of objects is shown in each plot. In the low mass bin, vertical arrows show an estimate of the possible effects of incompleteness (see text for details). |
| Open with DEXTER | |
5.3 Morphology-density relation
Figure 12 shows the ![]() relation for all the clusters in the sample. In all clusters, the fraction of early-type galaxies increases monotonically with local surface density, with some heterogeneity due to cluster-to-cluster variations. This relation
is not entirely correlated with the decrease of the early-type fraction with radius (the T-R relation) even if there are some similarities. In practice, we see that, beyond
relation for all the clusters in the sample. In all clusters, the fraction of early-type galaxies increases monotonically with local surface density, with some heterogeneity due to cluster-to-cluster variations. This relation
is not entirely correlated with the decrease of the early-type fraction with radius (the T-R relation) even if there are some similarities. In practice, we see that, beyond ![]() 1 Mpc, the correlation between radius and density (Fig. 8) is weaker with
a high dispersion in the number density so that we span more different environments.
1 Mpc, the correlation between radius and density (Fig. 8) is weaker with
a high dispersion in the number density so that we span more different environments.
Therefore, as shown in previous works, studying the properties of galaxies in the center (d<1 Mpc) and in the outskirts (d>2 Mpc) separately, helps separating different physical phenomena. While at the center, the effects of local environment (density) and cluster potential (distance to the center) are very well correlated, this is not the case in the outskirts. Consequently, differentiating the analysis of galaxy properties in the
outskirts with respect to radial distance R or local number density ![]() will tell us if
galaxies are entering the cluster in groups and evolving afterwards or if they are acquiring
the relation between morphology and environment/radius once they enter the cluster.
will tell us if
galaxies are entering the cluster in groups and evolving afterwards or if they are acquiring
the relation between morphology and environment/radius once they enter the cluster.
Figure 13 indeed shows the trend with density of the early-type fraction averaged over all the clusters for galaxies in the outer parts (d>2 Mpc) and in the central regions (d<1 Mpc). The fraction of early-type galaxies is systematically higher in all the environments in the center than in the outskirts. This rise of the global fraction of E/S0 objects reflects the fact that galaxies are experiencing a strong
morphological segregation in cluster centers. In the outskirts of the cluster, the global
morphological mixing is correlated with local density, i.e. the fraction of early-type
galaxies rises with increasing density and the ![]() relation is preserved. This seems to
indicate that morphological transformation of galaxies entering the cluster is strongly
influenced by the local environment and more precisely by interactions with galaxies in their
close surroundings. The correlation is also present in the cluster center, but with a higher fraction of E/S0 galaxies at all redshifts. Galaxies therefore continue evolving inside the cluster and migrating to the red-sequence but keeping a memory of their surroundings.
relation is preserved. This seems to
indicate that morphological transformation of galaxies entering the cluster is strongly
influenced by the local environment and more precisely by interactions with galaxies in their
close surroundings. The correlation is also present in the cluster center, but with a higher fraction of E/S0 galaxies at all redshifts. Galaxies therefore continue evolving inside the cluster and migrating to the red-sequence but keeping a memory of their surroundings.
Are all galaxies evolving at the same speed and independantly of their mass? In Fig. 14 the fractions of each morphological type for three stellar mass ranges in the center and in the outskirts of the cluster are shown. We detect different behaviors depending on the considered mass range. Massive galaxies
![]() are mostly elliptical (
are mostly elliptical (![]() 70%) in the cluster outskirts at all the environments. The fraction is slightly lower than the one measured in the cluster center (
70%) in the cluster outskirts at all the environments. The fraction is slightly lower than the one measured in the cluster center (![]() 80%) but remains high. This seems to indicate that an important fraction of galaxies in this mass range are already formed when they enter the cluster at
80%) but remains high. This seems to indicate that an important fraction of galaxies in this mass range are already formed when they enter the cluster at ![]() and
have already experienced morphological evolution in their local environment (tidal interactions and merging in groups, Bamford et al. 2009).
and
have already experienced morphological evolution in their local environment (tidal interactions and merging in groups, Bamford et al. 2009).
Intermediate mass objects (
![]() )
show a different trend. If we consider the cluster outskirts, we do see a relation between the morphological mixing and the local density: galaxies in the higher density bin (
)
show a different trend. If we consider the cluster outskirts, we do see a relation between the morphological mixing and the local density: galaxies in the higher density bin (
![]() )
are mostly early-type (
)
are mostly early-type (![]() 60%) while the fraction decreases to
60%) while the fraction decreases to ![]() 40% at lower densities. This population is therefore experiencing an evolution driven by the local environment when entering the cluster and dominates the general trend seen in the whole sample (Fig. 13). If we now look at the central regions, the correlation is almost absent and the fraction of early-type galaxies rises in all the density bins. This again suggests that this population is evolving as it moves to the cluster center but galaxies still preserve a memory of their location when they entered the cluster.
40% at lower densities. This population is therefore experiencing an evolution driven by the local environment when entering the cluster and dominates the general trend seen in the whole sample (Fig. 13). If we now look at the central regions, the correlation is almost absent and the fraction of early-type galaxies rises in all the density bins. This again suggests that this population is evolving as it moves to the cluster center but galaxies still preserve a memory of their location when they entered the cluster.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{12621f13.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg76.png) |
Figure 12: Morphology-density relation for all the clusters in the sample. Blue lines are late-type systems and red lines are early-type. The total number of objects is shown in each plot. |
| Open with DEXTER | |
If we consider now low massive galaxies (
![]() ), we again detect a different behavior. First, this population is dominated by late-type objects at almost all densities, even if we still measure a higher fraction of E/S0 galaxies at high densities, i.e. the cross-over between late-type and early-type systems occurs at higher density than for the more massive galaxies. It seems that morphological transformation is still going on even close to the cluster center (Holden et al. 2007). Once again, this result might be a consequence of incompleteness in this mass bin, which leads to an under-estimate of the red early-type population. As for Sect. 5.2 we show with vertical arrows in Fig. 14 how the fractions would increase if we consider that we loose 50% of the early-type population. Taking into account this effect reduces the trend, but there are still more late-type galaxies at all densities than than in the more massive bins.
), we again detect a different behavior. First, this population is dominated by late-type objects at almost all densities, even if we still measure a higher fraction of E/S0 galaxies at high densities, i.e. the cross-over between late-type and early-type systems occurs at higher density than for the more massive galaxies. It seems that morphological transformation is still going on even close to the cluster center (Holden et al. 2007). Once again, this result might be a consequence of incompleteness in this mass bin, which leads to an under-estimate of the red early-type population. As for Sect. 5.2 we show with vertical arrows in Fig. 14 how the fractions would increase if we consider that we loose 50% of the early-type population. Taking into account this effect reduces the trend, but there are still more late-type galaxies at all densities than than in the more massive bins.
Therefore, the transition from the blue-cloud to the red sequence is performed at different speeds mainly driven by the local environment: more massive galaxies drift to the red-sequence at earlier epochs. Massive galaxies have converted the gas into stars earlier probably because at high redshift their star formation was not effectively self-limited by feedback. Most of these galaxies are already massive, gas-poor and with an early-type morphology when they enter the cluster.
The transition for intermediate/low-mass galaxies is still going-on at ![]() and seems to be mainly driven by the local environment as stated by the correlation between morphology and density at all the cluster locations. Starbusts resulting from galaxy merging or starvation processes can be responsible of this transition: galaxy encounters can significantly accelerate the star formation and provoke the transition to the red-sequence. Semi-analytical models show however that this process is effective mainly for midsize galaxies which strike the best compromise between cross section and abundance (Maulbetsch et al. 2007). Galaxy interactions can also trigger the AGN phase. The AGN feedback can then contribute to suppress any residual star formation.
and seems to be mainly driven by the local environment as stated by the correlation between morphology and density at all the cluster locations. Starbusts resulting from galaxy merging or starvation processes can be responsible of this transition: galaxy encounters can significantly accelerate the star formation and provoke the transition to the red-sequence. Semi-analytical models show however that this process is effective mainly for midsize galaxies which strike the best compromise between cross section and abundance (Maulbetsch et al. 2007). Galaxy interactions can also trigger the AGN phase. The AGN feedback can then contribute to suppress any residual star formation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12621f14.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg78.png) |
Figure 13: Mean fractions of early-type (filled circles) and late-type (spiral symbols) galaxies as a function of local density in the cluster center ( top panels) and in the cluster outskirts ( bottom panels). The total number of objects is shown in each plot. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12621f15.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg79.png) |
Figure 14:
Mean fractions of early-type (filled circles) and late-type (spiral symbols) galaxies as a function of local density in the cluster center ( top panels) and in the cluster outskirts ( bottom panels) and for different mass ranges. Colors indicate three different mass ranges: red (
|
| Open with DEXTER | |
6 Summary and conclusions
We have presented a morphological study of a sample of galaxies in 9 X-ray luminous clusters at intermediate redshift (
![]() ). Wide field imaging provides information up to 5 Mpc from the cluster center, well above the virial radius and allows to explore the distant
outskirts of the clusters, where the local environment is dominant with respect to cluster
distance. Using photometric redshifts we are able to select cluster members with less than
20% of field contamination, thanks to a detailed comparison with spectroscopic redshifts
when available. Galaxies are then separated into two morphological classes with our automatic
galaxy classifier GALSVM, developped and validated by Huertas-Company et al. (2008).
Direct comparison with HST imaging of a sub-sample of galaxies in two independant clusters demonstrates that our method, based on ground-based data, is in agreement with HST results for more than 90% of the galaxies up to a magnitude limit r'=23. This magnitude cut which defines our working sample is about 1.5 mag. fainter that a
). Wide field imaging provides information up to 5 Mpc from the cluster center, well above the virial radius and allows to explore the distant
outskirts of the clusters, where the local environment is dominant with respect to cluster
distance. Using photometric redshifts we are able to select cluster members with less than
20% of field contamination, thanks to a detailed comparison with spectroscopic redshifts
when available. Galaxies are then separated into two morphological classes with our automatic
galaxy classifier GALSVM, developped and validated by Huertas-Company et al. (2008).
Direct comparison with HST imaging of a sub-sample of galaxies in two independant clusters demonstrates that our method, based on ground-based data, is in agreement with HST results for more than 90% of the galaxies up to a magnitude limit r'=23. This magnitude cut which defines our working sample is about 1.5 mag. fainter that a ![]() galaxy at
galaxy at
![]() and ensures multi-color photometric completeness. In addition, multi-color photometric information, available in 4 bands (
g', r', i' and z'), enables an estimate the stellar mass of the galaxies from their SED fitting. We estimate that our sample is 50% complete down to a
stellar mass of
and ensures multi-color photometric completeness. In addition, multi-color photometric information, available in 4 bands (
g', r', i' and z'), enables an estimate the stellar mass of the galaxies from their SED fitting. We estimate that our sample is 50% complete down to a
stellar mass of
![]() (or
(or
![]() .
All in all, our full galaxy sample contains 3861 galaxies inside 9 clusters.
.
All in all, our full galaxy sample contains 3861 galaxies inside 9 clusters.
The main results can be summarized as follows:
- In all clusters, we clearly identify the red sequence of early-type galaxies and we are able to build a stellar mass versus color sequence of galaxies. Both sequences are mostly populated with massive (
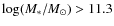 )
early-type galaxies. As found by previous studies, the galaxy red sequence is already formed at
)
early-type galaxies. As found by previous studies, the galaxy red sequence is already formed at
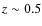 and early-type galaxies properties are already well in place (Patel et al. 2009). Physical processes which occur in dense environments have consequently a rapid and early influence of the
evolution of galaxy properties (harassment, ram pressure strippring, etc ...). They are very efficient in cluster centers and operate early in the cluster histories so that galaxies
evolve quickly towards gas poor massive early-type galaxies.
and early-type galaxies properties are already well in place (Patel et al. 2009). Physical processes which occur in dense environments have consequently a rapid and early influence of the
evolution of galaxy properties (harassment, ram pressure strippring, etc ...). They are very efficient in cluster centers and operate early in the cluster histories so that galaxies
evolve quickly towards gas poor massive early-type galaxies.
- The population of massive galaxies (
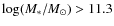 )
does not seem to have evolved significantly since
)
does not seem to have evolved significantly since
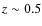 .
In fact, the fraction of early-type galaxies among this population is very high and remains almost constant (T-R relation), from the cluster center (
.
In fact, the fraction of early-type galaxies among this population is very high and remains almost constant (T-R relation), from the cluster center (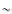 90%) to the outskirts (
90%) to the outskirts (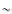 70% at the virial radius and above), suggesting that these galaxies experience no evolution. They were probably formed at higher redshifts
before entering the cluster in infalling groups and their location in the cluster center might be mostly explained by a segregation effect.
70% at the virial radius and above), suggesting that these galaxies experience no evolution. They were probably formed at higher redshifts
before entering the cluster in infalling groups and their location in the cluster center might be mostly explained by a segregation effect.
- When we consider the whole sample, the
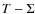 relation shows a clear correlation
between morphology and local density with early-type galaxies dominating the densest regions.
This was initially pointed out by (Dressler 1980) in the local universe and confirmed later
on more distant clusters (e.g. Postman et al. 2005).
The
relation shows a clear correlation
between morphology and local density with early-type galaxies dominating the densest regions.
This was initially pointed out by (Dressler 1980) in the local universe and confirmed later
on more distant clusters (e.g. Postman et al. 2005).
The 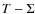 relation is also clearly detected in
the cluster outskirts, where cluster radius and local density are no longer correlated. It
seems therefore that the morphological evolution is mainly driven by the local environment
through galaxy-galaxy interactions (merging, starvation), independently of cluster
properties. Galaxies entering the cluster keep a memory of their surroundings and evolve
accordingly. They evolve however at different speeds, depending on the stellar mass.
relation is also clearly detected in
the cluster outskirts, where cluster radius and local density are no longer correlated. It
seems therefore that the morphological evolution is mainly driven by the local environment
through galaxy-galaxy interactions (merging, starvation), independently of cluster
properties. Galaxies entering the cluster keep a memory of their surroundings and evolve
accordingly. They evolve however at different speeds, depending on the stellar mass.
- Most of the evolution within clusters at
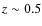 is taking place in galaxies with intermediate mass (
is taking place in galaxies with intermediate mass (
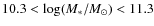 )
or even lower. These galaxies do show a
relation between the morphological mixing and the local density in both the center and the outskirts with differences between dense and loose global environments. In dense environments,
early-type galaxies are in place in a similar way as for the most massive ones, while in external areas, the
)
or even lower. These galaxies do show a
relation between the morphological mixing and the local density in both the center and the outskirts with differences between dense and loose global environments. In dense environments,
early-type galaxies are in place in a similar way as for the most massive ones, while in external areas, the 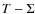 relation is similar to the one in the field. So the morphological dichotomy is prominent in structures representative of galaxy groups but in poorer environments, the morphological transformation from spiral-types to early-types has not produced significant changes in the galaxy distribution. Galaxies in this mass range are experiencing a migration from the blue-cloud to the red-sequence as they move into the cluster, mainly driven by interactions with their surroundings. The migration is accelerated when galaxies, within their local environment, cross the densest parts of the clusters in the central Mpc or so.
relation is similar to the one in the field. So the morphological dichotomy is prominent in structures representative of galaxy groups but in poorer environments, the morphological transformation from spiral-types to early-types has not produced significant changes in the galaxy distribution. Galaxies in this mass range are experiencing a migration from the blue-cloud to the red-sequence as they move into the cluster, mainly driven by interactions with their surroundings. The migration is accelerated when galaxies, within their local environment, cross the densest parts of the clusters in the central Mpc or so.
- Galaxies in the smallest mass bin (
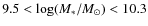 )
are basically late-type galaxies at all the clusters locations and environments (even if they present a trend with the local density), suggesting that they do no have started the morphological transformation at
)
are basically late-type galaxies at all the clusters locations and environments (even if they present a trend with the local density), suggesting that they do no have started the morphological transformation at 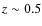 .
However, our conclusions are weaker for this population because the number of galaxies is small, especially in the cluster center and results can be affected by incompleteness specially in the early-type population. However, even considering that 50% of early-type galaxies are lost in this mass bin, this population seems to be dominated by late-type galaxies.
.
However, our conclusions are weaker for this population because the number of galaxies is small, especially in the cluster center and results can be affected by incompleteness specially in the early-type population. However, even considering that 50% of early-type galaxies are lost in this mass bin, this population seems to be dominated by late-type galaxies.
In order to better trace the general scheme of the morphological evolution of galaxies in different environments, two approaches are necessary. First, we wish to analyse in more details the dependence of these global tendancies with the general properties of the clusters themselves. This will be done in a future work as soon as the mass distribution of the clusters is available using weak lensing mass maps (work in progress, Foex et al. in preparation) and/or X-ray properties such as luminosity and temperature. Clusters of galaxies are not a fully homogeneous population and some of the evolution properties of their cluster members are attached to their intrinsic caracteristics (Poggianti et al. 2009). Second, it is also necessary to extend this approach to more distant clusters to connect clusters at different epochs and trace an evolutionary track. In order to better probe the stellar mass and the morphology traced by the old stellar population, near-infrared imaging is preferred (Huertas-Company et al. 2009).
Acknowledgements
We are grateful to C. Lidman and M. West for many interactions and helpful discussions. The authors want to thank as well the anonymous referee for useful comments which clearly helped to improve the paper. We also thank the Programme National de Cosmologie of the CNRS and ESO for financial support.
References
- Abraham, R. G., van den Bergh, S., Glazebrook, K., et al. 1996, ApJS, 107, 1 [NASA ADS] [CrossRef]
- Baldry, I. K., Glazebrook, K., Brinkmann, J., et al. 2004, ApJ, 600, 681 [NASA ADS] [CrossRef]
- Balogh, M. L., Navarro, J. F., & Morris, S. L. 2000, ApJ, 540, 113 [NASA ADS] [CrossRef] (In the text)
- Bamford, S. P., Nichol, R. C., Baldry, I. K., et al. 2009, MNRAS, 393, 1324 [NASA ADS] [CrossRef] (In the text)
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Böhringer, H., Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [NASA ADS] [CrossRef]
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] (In the text)
- Bundy, K., Ellis, R. S., & Conselice, C. J. 2005, ApJ, 625, 621 [NASA ADS] [CrossRef]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] (In the text)
- Cooper, M. C., Newman, J. A., Madgwick, D. S., et al. 2005, ApJ, 634, 833 [NASA ADS] [CrossRef] (In the text)
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [NASA ADS] [CrossRef]
- De Lucia, G., Springel, V., White, S. D. M., Croton, D., & Kauffmann, G. 2006, MNRAS, 366, 499 [NASA ADS] [CrossRef] (In the text)
- De Lucia, G., Poggianti, B. M., Aragón-Salamanca, A., et al. 2007, MNRAS, 374, 809 [NASA ADS] [CrossRef] (In the text)
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef]
- Diaferio, A., Kauffmann, G., Balogh, M. L., et al. 2001, MNRAS, 323, 999 [NASA ADS] [CrossRef] (In the text)
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef]
- Dressler, A., Oemler, A. J., Sparks, W. B., et al. 1994, ApJ, 435, L23 [NASA ADS] [CrossRef]
- Dressler, A., Oemler, A. J., Couch, W. J., et al. 1997, ApJ, 490, 577 [NASA ADS] [CrossRef]
- Ellingson, E., Yee, H. K. C., Abraham, R. G., et al. 1997, ApJS, 113, 1 [NASA ADS] [CrossRef]
- Ellingson, E., Yee, H. K. C., Abraham, R. G., Morris, S. L., & Carlberg, R. G. 1998, ApJS, 116, 247 [NASA ADS] [CrossRef] (In the text)
- Faber, S. M., Willmer, C. N. A., Wolf, C., et al. 2007, ApJ, 665, 265 [NASA ADS] [CrossRef] (In the text)
- Gonzalez, A. H., Tran, K.-V. H., Conbere, M. N., et al. 2005, ApJ, 624, L73 [NASA ADS] [CrossRef]
- Holden, B. P., Illingworth, G. D., Franx, M., et al. 2007, ApJ, 670, 190 [NASA ADS] [CrossRef]
- Huertas-Company, M., Rouan, D., Tasca, L., Soucail, G., & Le Fèvre, O. 2008, A&A, 478, 971 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Huertas-Company, M., Tasca, L., Rouan, D., et al. 2009, A&A, 497, 743 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Maulbetsch, C., Avila-Reese, V., Colín, P., et al. 2007, ApJ, 654, 53 [NASA ADS] [CrossRef] (In the text)
- Mei, S., Holden, B. P., Blakeslee, J. P., et al. 2009, ApJ, 690, 42 [NASA ADS] [CrossRef] (In the text)
- Menci, N., Fontana, A., Giallongo, E., Grazian, A., & Salimbeni, S. 2006, ApJ, 647, 753 [NASA ADS] [CrossRef]
- Menci, N., Rosati, P., Gobat, R., et al. 2008, ApJ, 685, 863 [NASA ADS] [CrossRef] (In the text)
- Moran, S. M., Ellis, R. S., Treu, T., et al. 2007, ApJ, 671, 1503 [NASA ADS] [CrossRef]
- Neistein, E., van den Bosch, F. C., & Dekel, A. 2006, MNRAS, 372, 933 [NASA ADS] [CrossRef]
- Patel, S. G., Kelson, D. D., Holden, B. P., et al. 2009, ApJ, 694, 1349 [NASA ADS] [CrossRef] (In the text)
- Pello, R., Rudnick, G., De Lucia, G., et al. 2009, A&A, accepted (In the text)
- Pickles, A. J. 1998, PASP, 110, 863 [NASA ADS] [CrossRef] (In the text)
- Poggianti, B. M., Smail, I., Dressler, A., et al. 1999, ApJ, 518, 576 [NASA ADS] [CrossRef] (In the text)
- Poggianti, B. M., von der Linden, A., De Lucia, G., et al. 2006, ApJ, 642, 188 [NASA ADS] [CrossRef] (In the text)
- Poggianti, B. M., Fasano, G., Bettoni, D., et al. 2009, ArXiv e-prints (In the text)
- Postman, M., & Geller, M. J. 1984, ApJ, 281, 95 [NASA ADS] [CrossRef] (In the text)
- Postman, M., Franx, M., Cross, N. J. G., et al. 2005, ApJ, 623, 721 [NASA ADS] [CrossRef] (In the text)
- Sadat, R., Blanchard, A., Kneib, J.-P., et al. 2004, A&A, 424, 1097 [NASA ADS] [CrossRef] [EDP Sciences]
- Saintonge, A., Schade, D., Ellingson, E., Yee, H. K. C., & Carlberg, R. G. 2005, ApJS, 157, 228 [NASA ADS] [CrossRef]
- Stanford, S. A., Eisenhardt, P. R. M., & Dickinson, M. 1995, ApJ, 450, 512 [NASA ADS] [CrossRef]
- Strateva, I., Ivezic, Z., Knapp, G. R., et al. 2001, AJ, 122, 1861 [NASA ADS] [CrossRef]
- Treu, T., Ellis, R. S., Kneib, J.-P., et al. 2003, ApJ, 591, 53 [NASA ADS] [CrossRef]
- van Dokkum, P. G., Franx, M., Fabricant, D., Illingworth, G. D., & Kelson, D. D. 2000, ApJ, 541, 95 [NASA ADS] [CrossRef]
- Whitmore, B. C., Gilmore, D. M., & Jones, C. 1993, ApJ, 407, 489 [NASA ADS] [CrossRef] (In the text)
Footnotes
All Tables
Table 1: Main properties of clusters in our sample.
Table 2: Relation between the bulge fraction computed in Saintonge et al. (2005) and the probability of being early-type computed by GALSVM.
Table 3: Composition of the red sequence in the 2 central MegaParsecs.
All Figures
![\begin{figure}
\par\includegraphics[width=15.9cm,clip]{12621fg1.eps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg29.png) |
Figure 1:
Color image of a
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12621fg2.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg33.png) |
Figure 2:
Spatial distributions of galaxies in the different clusters. Red circles indicate early-type objects and blue spiral symbols late-type galaxies. The symbol sizes code three different mass ranges; big:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12621fg3.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg45.png) |
Figure 3: Galaxy cluster member selection accuracy for MS 0451.5-0305. The different panels show the results for different radii. Solid lines indicate the completeness and dashed lines the contaminations from non-members as a function of the probability threshold. The vertical dashed line shows the adopted probability threshold. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12621fg4.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg46.png) |
Figure 4: Photometric redshift distributions for all the clusters. Dashed vertical lines show the cluster spectroscopic redshift. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12621fg5.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg48.png) |
Figure 5:
Stamps of the same galaxies seen by HST and MegaCam. The stamps size is 10'' |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12621fg6.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg49.png) |
Figure 6: Relation between the visual morphology computed in Moran et al. (2007) and the GALSVM type. Filled histograms show the fraction of GALSVM early-type objects and empty histograms the fraction of late-type galaxies. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12621fg7.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg59.png) |
Figure 7: Stellar mass histograms for all the galaxies in the 9 clusters. Solid black lines show the histogram for all the galaxies while color lines show the histograms separated by morphological type (blue: late-type, red: early-type). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12621fg8.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg62.png) |
Figure 8: Local density vs. radius for all the clusters in our sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12621fg9.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg63.png) |
Figure 9:
Stellar mass-color plots in the 2 central Mpc for all the 9 clusters in the sample. Early-type galaxies are shown with red filled circles and late-type with blue spiral symbols. Solid line indicate the best fit to the red-sequence and dashed lines 1.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12621f11.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg71.png) |
Figure 10: Fraction of morphological types (r < 23) as a function of cluster radius. Red points: E/S0 galaxies, blue points: S/I galaxies. The total number of objects is shown in each plot. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{12621f12.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg72.png) |
Figure 11: Morphological mixing as a function of the cluster radius, averaged for all the clusters in the sample and for different mass ranges. Filled circles are early-type galaxies and spiral symbols are late-type galaxies. The left panel shows the results for the whole sample. Notice that for the low mass bin ( top right) the two first points are not significative since there are too few objects. The total number of objects is shown in each plot. In the low mass bin, vertical arrows show an estimate of the possible effects of incompleteness (see text for details). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{12621f13.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg76.png) |
Figure 12: Morphology-density relation for all the clusters in the sample. Blue lines are late-type systems and red lines are early-type. The total number of objects is shown in each plot. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12621f14.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg78.png) |
Figure 13: Mean fractions of early-type (filled circles) and late-type (spiral symbols) galaxies as a function of local density in the cluster center ( top panels) and in the cluster outskirts ( bottom panels). The total number of objects is shown in each plot. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{12621f15.ps}
\end{figure}](/articles/aa/full_html/2009/37/aa12621-09/Timg79.png) |
Figure 14:
Mean fractions of early-type (filled circles) and late-type (spiral symbols) galaxies as a function of local density in the cluster center ( top panels) and in the cluster outskirts ( bottom panels) and for different mass ranges. Colors indicate three different mass ranges: red (
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


