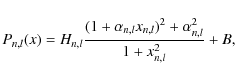The onset of solar cycle 24

D. Salabert; R. A. García; P. L. Pallé; S. J. Jiménez-Reyes

doi:10.1051/0004-6361/200912736

Free Access

Issue		A&A Volume 504, Number 1, September II 2009


Page(s)		L1 - L4
Section		Letters
DOI		https://doi.org/10.1051/0004-6361/200912736
Published online		18 August 2009

LETTER TO THE EDITOR

What global acoustic modes are telling us

D. Salabert^1,2 - R. A. García³ - P. L. Pallé^1,2 - S. J. Jiménez-Reyes^1,2

1 - Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
2 - Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
3 - Laboratoire AIM, CEA/DSM-CNRS, Université Paris 7 Diderot, IRFU/SAp, Centre de Saclay, 91191 Gif-sur-Yvette, France

Received 21 June 2009 / Accepted 23 July 2009

Abstract
We study the response of the low-degree, solar p-mode frequencies to the unusually extended minimum of solar surface activity since 2007. A total of 4768 days of observations collected by the space-based, Sun-as-a-star helioseismic GOLF instrument are analyzed. A multi-step iterative maximum-likelihood fitting method is applied to subseries of 365 days and 91.25 days to extract the p-mode parameters. Temporal variations in the l=0, 1, and 2 p-mode frequencies are then obtained from April 1996 to May 2009. While the p-mode frequency shifts are closely correlated with solar surface activity proxies during the past solar cycles, the frequency shifts of the l=0 and l=2 modes increase from the second half of 2007, when no significant surface activity is observable. On the other hand, the l=1 modes follow the general decreasing trend of solar surface activity. The different behaviors between the l=0 and l=2 modes and the l=1 modes may be interpreted as different geometrical responses to the spatial distribution of the solar magnetic field beneath the surface of the Sun. The analysis of the low-degree, solar p-mode frequency shifts indicates that the solar activity cycle 24 started in late 2007, despite the absence of activity on the solar surface.

Key words: methods: data analysis - Sun: helioseismology - Sun: activity

1 Introduction

The success of helioseismology is due to its capability to accurately measure the p-mode parameters of the solar eigenmode spectrum, which allow us to infer unique information about the internal structure and dynamics of the Sun from its surface all the way down to the core. It has contributed greatly to a clearer understanding of the Sun and provided insights into the complex solar magnetism, by means for instance of the variability of the characteristics of the p-mode spectrum.

Evidence of low-degree p-mode frequency changes with solar activity, first revealed by Woodard & Noyes (1985), were established by Pallé et al. (1989) with the analysis of helioseismic observations spanning the complete solar cycle 21 (1977-1988). Later on, Woodard & Libbrecht (1991) measured similar variations in intermediate and high angular-degree modes. As longer, higher quality, and continuous helioseismic observations became available, the solar p-mode frequencies proved to be very sensitive to the solar surface activity not only during solar cycle 23 (see for example, Jiménez-Reyes et al. 2004; Howe et al. 2002, and references therein) but also over the last three solar cycles (21, 22, and 23), spanning a period of thirty years (Chaplin et al. 2007), with high levels of correlation with solar surface activity proxies.

The frequency shifts have also been shown to be angular-degree dependent (Jiménez-Reyes et al. 2001), or rather mode-inertia dependent, but Howe et al. (2002) found that the latitudinal distribution of the frequency differences for high l modes shows close temporal and spatial correlation with the surface magnetic field distribution. A marginal but significant l dependence of the frequency shifts of the low-degree p modes has also been clearly identified (Chaplin et al. 2004; Jiménez-Reyes et al. 2004). The size of the shift also reflects differences in mode inertia. However, the change in inertia with l is small for low-degree modes, and the spatial distribution dominates as well.

The unusual long and deep solar activity minimum as well as the lack of a visible onset of the new cycle 24 motivated the present work to investigate the response of the low-degree p-mode frequencies to this extended minimum (2007 till present) as compared with the rest of cycle 23 (since 1996).

2 Data and analysis

2.1 Data sets

$\begin{figure} \par\includegraphics[angle=90,width=17cm]{12736fg1.eps} \end{figure}$

Figure 1:

Mean frequency shifts $\langle \delta\nu_{0,1,2} \rangle$ in $\mu$ Hz of the low-degree solar p modes extracted from the analysis of the 365-day (filled circles) and the 91.25-day (plus signs) GOLF spectra. The associated mean error bars are also represented. The corresponding 10.7-cm radio flux averaged over the same 91.25-day timespan is shown as a proxy of the solar surface activity (solid line).

Open with DEXTER

We analyzed observations collected by the space-based instrument Global Oscillations at Low Frequency (GOLF) instrument onboard the Solar and Heliospheric Observatory (SOHO) spacecraft. GOLF is a resonant scattering spectrophotometer measuring the Doppler wavelength shift - integrated over the solar surface - in the D₁ and D₂ Fraunhofer sodium lines at 589.6 and 589.0 nm, respectively (Gabriel et al. 1995). A total of 4768-day velocity time series (García et al. 2005) starting on 1996 April 11 were used (see calibration method in Jiménez-Reyes et al. 2003). Contiguous subseries of 365 and 91.25 days were produced with a four-time overlap. The series with a filling factor less than 60% for the 365-day series and 70% for the 91.25-day series were not used in the following analysis, resulting in a total of 49 and 197 non-independent time series of 365 days and 91.25 days, respectively. Thus, the averaged duty cycles for the 365-day and 91.25-day time series were 94.9% and 97.8%, respectively.

We also considered contemporaneous observations collected by the ground-based Mark-I instrument at the Observatorio del Teide (Brookes et al. 1978). Mark-I is also a resonant scattering spectrophotometer, but observes in the potassium Fraunhofer line at 769.9 nm. A total of 19 independent yearly time series of consecutive 108 days with the highest duty cycle (mean value 38%) were used.

2.2 Mode parameter extraction

The power spectrum of each 365-day and 91.25-day time series was fitted to yield estimates of the mode parameters. This fitting was performed by a multi-step iterative method (Salabert et al. 2007; Gelly et al. 2002). The asymmetric profile of Nigam & Kosovichev (1998) was used to describe each component, as

$\begin{displaymath}P_{n,l}(x) = H_{n,l} \frac{(1+\alpha_{n,l} x_{n,l})^2+\alpha_{n,l}^2}{1+ x_{n,l}^2} + B, \end{displaymath}$

(1)

where $x_{n,l} = 2(\nu-\nu_{n,l})/\Gamma_{n,l}$ , and $\nu_{n,l}$ , $\Gamma_{n,l}$ , and H_n,l represent the central frequency, the full-width-at-half-maximum (FWHM), and the power height of the spectral density, respectively, for a given mode (n,l). The peak asymmetry is described by the parameter $\alpha_{n,l}$ , while B represents an additive, constant background level in the fitted window. Because of their close proximity in frequency, modes are fitted in pairs (i.e., l=2 with 0, and l=3 with 1). While each mode parameter within a pair of modes are free, the peak asymmetry is set to be the same within pairs of modes. The mode parameters were extracted by maximizing a likelihood function following the $\chi^2$ with 2 degrees-of-freedom statistics of the power spectrum. The natural logarithms of the mode height, FWHM, and background noise were varied resulting in normal distributions. The formal uncertainties in each parameter were then derived from the inverse Hessian matrix. A similar analysis was applied to the Mark-I spectra.

2.3 Determination of the frequency shifts

The temporal variations in the p-mode frequencies were obtained by comparing each measured (l,n) frequency with the corresponding (l,n) averaged frequency over the entire set of analyzed spectra for the different datasets. The formal uncertainties returned by the fits were used as weights in the average computation. The frequency shifts thus obtained were then averaged over the frequency range 2000 $\mu$ Hz $\leq \nu \leq 3300~\mu$ Hz. We note that because of its lower signal-to-noise ratio, we did not use the l=3 modes in the following analysis. Linear regressions between the frequency shifts and solar surface activity proxies were performed. Mean values of daily measurements of the 10.7-cm radio flux and the Mount Wilson magnetic plage strength index (MPSI) were calculated over the same 365-day and 91.25-day subseries.

3 Results

$\begin{figure} \par\includegraphics[angle=90,width=17cm]{12736fg2.eps} \end{figure}$	Figure 2: Mean frequency shifts $\langle \delta\nu\rangle$ in $\mu$ Hz of the l=0, 1, and 2 solar p modes ( left to right panels) extracted from the analysis of the 365-day GOLF spectra. The associated mean error bars are also represented. The corresponding 10.7-cm radio flux averaged over the same 365-day timespan is shown as a proxy of the solar surface activity (dotted line).
Open with DEXTER

Table 1: Frequency shifts at each l per unit of change in solar proxy and correlations from the analysis of independent 91.25-day GOLF spectra.

Since the minimum of solar cycle 23 has lasted longer than predicted and no surface activity has been observed since the end of 2007, we expect that the frequency shifts would also exhibit an extended minimum. Figure 1 shows the temporal variation in the frequency shifts $\langle \delta\nu_{0,1,2} \rangle$ averaged over the modes l=0, 1, and 2 extracted from the analysis of both the 365-day and 91.25-day GOLF spectra. As already widely reported, the frequency shifts represented in Fig. 1 are well correlated with the solar surface activity over cycle 23 (1996-2007). However, as we can see in Fig. 1, the mean frequency shifts begin to increase from the second half of 2007 when no significant surface activity is observed. Excellent qualitative agreement was obtained with the Mark-I data, although more detailed work is in progress.

Figure 2 shows the dependence of the frequency shifts $\langle \delta\nu_l \rangle$ on the angular degree l with time, measured from the 365-day spectra. In Table 1, we present the frequency shifts at each l per unit of change in two global solar activity proxies, as well as the associated Pearson correlation coefficient, $r_{\rm p}$ , the Spearman rank correlation coefficient, $r_{\rm s}$ , and the two-sided significance of its deviation from zero, $P_{\rm s}$ . These values were obtained from the analysis of the 91.25-day spectra by using only independent points (43 for the period April 1996-June 2007, and 7 for the period June 2007-May 2009). We note that they correspond to one combination of independent series and that they are consistent within $1\sigma$ with any other of the chosen sets. Given the range of analyzed frequencies and the considered time spans, the amount of uncovered shifts over cycle 23 and their correlations are consistent within the uncertainties with Jiménez-Reyes et al. (2004) and Chaplin et al. (2004). The l=2 modes have larger variations compared to both the l=1 and l=0 modes.

Since the end of 2007, the frequency shifts of the l=1 modes have continued to slowly decrease, following the trend in the solar surface activity, while the l=0 and l=2 modes have exhibited a very different behavior of increasing frequency shifts, as expected if solar cycle 24 has already started to progress. The l=0 and 2 frequency shifts show a negative correlation with surface activity, while the l=1 frequency shifts are to some extent still correlated with surface activity (Table 1). We note that the significance of a null correlation is higher because of the far lower number of independent points (7 points) for the period June 2007-May 2009. To highlight this different behavior with l, Fig. 3 compares the frequency shifts of the l=0 and l=1 modes with those of the l=2 modes for the two periods April 1996-June 2007 and June 2007-May 2009, confirming the results shown on Fig. 2. While the modes have a similar behavior during cycle 23 and until the first half of 2007, the l=0 and 2 modes behave differently from to the l=1 modes, from June 2007 and onwards.

The different behaviors observed for the values of angular degree can be interpreted in terms of the spatial geometry of the modes measured with the GOLF instrument. Sun-as-a-star observations such as those made by the GOLF and Mark-I instruments are sensitive only to the modes with l+|m| even. This is because the solar rotation axis lies close to the plane of the sky from the observing point. The observed l=1 frequency is therefore a weighted measurement of the visible components ( l=1, |m|=1), while in the case of the l=2 mode, the fitted frequency corresponds to the weighted measurement of the zonal (l=2, m=0) and sectoral ( l=2, |m|=2) components (Jiménez-Reyes et al. 2004). The sectoral modes are more concentrated along the equator, while the zonal modes are most sensitive to the high latitudes. Thus, the l=2 modes seen by full-disk instruments are more sensitive to the high latitudes of the Sun. They have larger frequency variations than the l=0 modes, which are averaged across the entire visible solar disk, while the full-disk l=1 mode is more concentrated along the equator. The results presented here appear to indicate that the process responsible for the frequency shifts at high latitudes and related to the new solar cycle 24 started in late 2007.

4 Summary and discussion

$\begin{figure} \par\includegraphics[angle=90,width=18cm]{12736fg3.eps} \end{figure}$

Figure 3:

Relation of the mean frequency shifts (in $\mu$ Hz) between angular degree l for the periods April 1996-June 2007 (open circles) and June 2007-May 2009 (filled squares) from the analysis of the 91.25-day GOLF spectra (only independent points were used). Left panel: $\langle \delta\nu_{0} \rangle$ against $\langle \delta\nu_{2} \rangle$ . Right panel: $\langle \delta\nu_{1} \rangle$ against $\langle \delta\nu_{2} \rangle$ . The solid lines correspond to linear fits between the data, and the dashed lines represent the 1:1 correlation.

Open with DEXTER

While solar p-mode frequency shifts have been shown to be closely correlated with the solar surface activity during previous solar cycles (Chaplin et al. 2007; Jiménez-Reyes et al. 2004; Howe et al. 2002), it appears that during the unpredicted long minimum of cycle 23, the frequency shifts of the low-degree p modes have exhibited unexpected behavior. Since the second half of the year 2007, the frequency shifts have been observed to be uncorrelated with surface activity. While no significant surface activity was observed, the frequency shifts of the modes l=0 and 2 show significant increases, and those of the l=1 modes follow the extended minimum. The difference between the l=0 and 2 modes and the l=1 modes can be interpreted as a different response to the spatial distribution of the solar magnetic field. In Sun-as-a-star measurements such as the GOLF observations, the modes l=0 and 2 modes are more sensitive to the high latitudes than the l=1 modes. This behavior of the frequency shifts is indicative of variations in the magnetic flux at high latitudes related to the onset of solar cycle 24. This result qualitatively agrees with the measurements of the cosmogenic isotopes ¹⁰Be (Beer et al. 1998) and ¹⁴C (Stuiver & Braziunas 1989), which exhibit an 11-year periodic variation even during extremely low epochs of surface activity, such as the Maunder minimum.

To estimate in a simple manner when the minimum of cycle 23 occurred, we performed a second order polynomial fit to the mean frequency shifts (l=0 and 2) over the period 2006-2009. To do so, we used only independent points from the analysis of the 91.25-day series. Thus, we inferred that the minimum of solar cycle 23 must have occurred during the last quarter of 2007.

Predictions of the solar cycle properties, such as its strength and pattern, infer significantly different conclusions for cycle 24 (see e.g., Dikpati & Gilman 2006; Svalgaard et al. 2005). Most of these models are calibrated using solar observables, such as the sunspot number, that reflect changes in the solar surface. It is clear that there is a time delay between the emergence of magnetic fields located probably close to the tachocline and the appearance of activity on the surface. The physical conditions beneath the surface are thus modified during this process. Our findings show that the signatures of activity appear in the solar acoustic mode parameters before they become evident in other solar activity proxies, and therefore must be taken into account in the calibration of the solar dynamo models.

To study in more detail the spatial dependence of the frequency shifts during this peculiar solar minimum, this work will be extended to the analysis of the spatially-resolved observations from the Global Oscillation Network Group (GONG) and Michelson Doppler Imager (MDI) instruments, which allow the decomposition into individual m components. Jiménez-Reyes et al. (2004) previously showed that the values of the frequency shifts for l=0, 1, and 2 measured in MDI data scale to the corresponding spherical harmonic components of the observed line-of-sight surface magnetic field. The analysis of the variability in the other p-mode parameters during this extended minimum is also currently underway.

Acknowledgements

The authors thank O. L. Creevey for helpful discussions and useful comments on the manuscript. The GOLF instrument onboard SOHO is a cooperative effort of many individuals, to whom we are indebted. SOHO is a project of international collaboration between ESA and NASA. We thank all the members, past and present, of the helioseismology group at the IAC for doing Mark-I observations and maintenance. The use of Birmingham University resonant scattering spectrophotometer at Observatorio del Teide is also deeply acknowledged. The 10.7-cm radio flux data were obtained from the National Geophysical Data Center. This study includes data from the synoptic program at the 150-Foot Solar Tower of the Mt. Wilson Observatory. The Mt. Wilson 150-Foot Solar Tower is operated by UCLA, with funding from NASA, ONR and NSF, under agreement with the Mt. Wilson Institute. D. S. acknowledges the support of the grant PNAyA2007-62650 from the Spanish National Research Plan. This work was supported by the European Helio- and Asteroseismology Network (HELAS), a major international collaboration funded by the European Commission's FP6, and by the CNES/GOLF grant at the SAp/CEA-Saclay.

References

Beer, J., Tobias, S., & Weiss, N. 1998, Sol. Phys., 181, 237 [NASA ADS] [CrossRef] (In the text)
Brookes, J. R., Isaak, G. R., & van der Raay, H. B. 1978, MNRAS, 185, 1 [NASA ADS] (In the text)
Chaplin, W. J., Elsworth, Y., Isaak, G. R., Miller, B. A., & New, R. 2004, MNRAS, 352, 1102 [NASA ADS] [CrossRef]
Chaplin, W. J., Elsworth, Y., Miller, B. A., Verner, G. A., & New, R. 2007, ApJ, 659, 1749 [NASA ADS] [CrossRef] (In the text)
Dikpati, M., & Gilman, P. A. 2006, ApJ, 649, 498 [NASA ADS] [CrossRef]
Gabriel, A. H., Grec, G., Charra, J., et al. 1995, Sol. Phys., 162, 61 [NASA ADS] [CrossRef] (In the text)
García, R. A., Turck-Chièze, S., Boumier, P., et al. 2005, A&A, 442, 385 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Gelly, B., Lazrek, M., Grec, G., et al. 2002, A&A, 394, 285 [NASA ADS] [CrossRef] [EDP Sciences]
Howe, R., Komm, R. W., & Hill, F. 2002, ApJ, 580, 1172 [NASA ADS] [CrossRef]
Jiménez-Reyes, S. J., Corbard, T., Pallé, P. L., Roca Cortés, T., & Tomczyk, S. 2001, A&A, 379, 622 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Jiménez-Reyes, S. J., García, R. A., Jiménez, A., et al. 2003, ApJ, 595, 446 [NASA ADS] [CrossRef] (In the text)
Jiménez-Reyes, S. J., García, R. A., Chaplin, W. J., et al. 2004, ApJ, 610, L65 [NASA ADS] [CrossRef]
Nigam, R., & Kosovichev, A. G. 1998, ApJ, 505, L51 [NASA ADS] [CrossRef] (In the text)
Pallé, P. L., Régulo, C., & Roca Cortés, T. 1989, A&A, 224, 253 [NASA ADS] (In the text)
Salabert, D., Chaplin, W. J., Elsworth, Y., New, R., & Verner, G. A. 2007, A&A, 463, 1181 [NASA ADS] [CrossRef] [EDP Sciences]
Stuiver, M., & Braziunas, T. F. 1989, Nature, 338, 405 [NASA ADS] [CrossRef] (In the text)
Svalgaard, L., Cliver, E. W., & Kamide, Y. 2005, Geophys. Res. Lett., 32, 1104 [CrossRef]
Woodard, M. F., & Noyes, R. W. 1985, Nature, 318, 449 [NASA ADS] [CrossRef] (In the text)
Woodard, M. F., & Libbrecht, K. G. 1991, ApJ, 374, L61 [NASA ADS] [CrossRef] (In the text)

All Tables

Table 1: Frequency shifts at each l per unit of change in solar proxy and correlations from the analysis of independent 91.25-day GOLF spectra.

All Figures

$\begin{figure} \par\includegraphics[angle=90,width=17cm]{12736fg1.eps} \end{figure}$	Figure 1: Mean frequency shifts $\langle \delta\nu_{0,1,2} \rangle$ in $\mu$ Hz of the low-degree solar p modes extracted from the analysis of the 365-day (filled circles) and the 91.25-day (plus signs) GOLF spectra. The associated mean error bars are also represented. The corresponding 10.7-cm radio flux averaged over the same 91.25-day timespan is shown as a proxy of the solar surface activity (solid line).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=17cm]{12736fg2.eps} \end{figure}$	Figure 2: Mean frequency shifts $\langle \delta\nu\rangle$ in $\mu$ Hz of the l=0, 1, and 2 solar p modes ( left to right panels) extracted from the analysis of the 365-day GOLF spectra. The associated mean error bars are also represented. The corresponding 10.7-cm radio flux averaged over the same 365-day timespan is shown as a proxy of the solar surface activity (dotted line).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=90,width=18cm]{12736fg3.eps} \end{figure}$	Figure 3: Relation of the mean frequency shifts (in $\mu$ Hz) between angular degree l for the periods April 1996-June 2007 (open circles) and June 2007-May 2009 (filled squares) from the analysis of the 91.25-day GOLF spectra (only independent points were used). Left panel: $\langle \delta\nu_{0} \rangle$ against $\langle \delta\nu_{2} \rangle$ . Right panel: $\langle \delta\nu_{1} \rangle$ against $\langle \delta\nu_{2} \rangle$ . The solid lines correspond to linear fits between the data, and the dashed lines represent the 1:1 correlation.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.