| Issue |
A&A
Volume 503, Number 3, September I 2009
|
|
|---|---|---|
| Page(s) | L25 - L28 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/200912534 | |
| Published online | 11 August 2009 | |
LETTER TO THE EDITOR
Hinode/EIS observations of propagating low-frequency slow magnetoacoustic waves in fan-like coronal loops![[*]](/icons/foot_motif.png)
T. J. Wang1,2 - L. Ofman1,2 - J. M. Davila2 - J. T. Mariska3
1 - Department of Physics, Catholic University of America, 620 Michigan Avenue, Washington, DC 20064, USA
2 - NASA Goddard Space Flight Center, Code 671, Greenbelt, MD 20771, USA
3 - Space Science Division, Naval Research Laboratory, Washington, DC 20375, USA
Received 19 May 2009 / Accepted 28 July 2009
Abstract
Aims. We report the first observation of multiple-periodic propagating disturbances along a fan-like coronal structure simultaneously detected in both intensity and Doppler shift in the Fe XII 195 Å line with the EUV Imaging Spectrometer (EIS) onboard Hinode. A new application of coronal seismology is provided based on this observation.
Methods. We analyzed the EIS sit-and-stare mode observation of oscillations using the running difference and wavelet techniques.
Results. Two harmonics with periods of 12 and 25 min are detected. We measured the Doppler shift amplitude of 1-2 km s-1, the relative intensity amplitude of 3%-5% and the apparent propagation speed of 100-120 km s-1.
Conclusions. The amplitude relationship between intensity and Doppler shift oscillations provides convincing evidence that these propagating features are a manifestation of slow magnetoacoustic waves. Detection lengths (over which the waves are visible) of the 25 min wave are about 70-90 Mm, much longer than those of the 5 min wave previously detected by TRACE. This difference may be explained by the dependence of damping length on the wave period for thermal conduction. Based on a linear wave theory, we derive an inclination of the magnetic field to the line-of-sight about
![]() ,
a true propagation speed of
,
a true propagation speed of
![]() km s-1 and a temperature of
km s-1 and a temperature of
![]() MK near the loop's footpoint from our measurements.
MK near the loop's footpoint from our measurements.
Key words: Sun: atmosphere - Sun: corona - Sun: oscillations - Sun: UV radiation - waves
1 Introduction
Quasi-periodic propagating intensity disturbances in fanlike large coronal loops were first observed with SOHO/EIT 195 Å data (Berghmans & Clette 1999), and then were confirmed with TRACE 171 Å data (e.g. De Moortel et al. 2000). These disturbances with a propagation speed on the order of 150 km s-1 have been interpreted as slow magnetoacoustic waves (Nakariakov et al. 2000). Detection of these waves is important for our understanding of the energy balance in the outer solar atmosphere and also highly valuable for coronal seismology (e.g. reviews by Nakariakov & Verwichte 2005).
Many authors have found evidence of 3 min and 5 min oscillations propagating through the chromosphere and transition region into the lower corona (e.g. De Moortel et al. 2002; Marsh et al. 2003; Wang et al. 2009), supporting their origin in the photospheric p-modes by wave leakage (De Pontieu et al. 2005). In addition, there were also a few reports of similar propagating waves with long periods (10-15 min) observed in coronal loops by EIT (Berghmans & Clette 1999), TRACE (McIntosh et al. 2008), and STEREO/EUVI (Marsh et al. 2009), but their origin is still not clear. Long-period (10-30 min) oscillations were also observed in polar coronal holes (e.g. Banerjee et al. 2009).
In this study, we detect two long-period (12 and 25 min) harmonics in propagating slow magnetoacoustic waves in fanlike coronal loops with observations from the EUV Imaging Spectrometer (EIS) onboard Hinode. The EIS instrument with high sensitivity and spectral resolution (Culhane et al. 2007) can achieve relative Doppler-shift measurements with an accuracy of less than 1 km s-1 (Erdélyi & Taroyan 2008; van Doorsselaere et al. 2008; Mariska et al. 2008), providing us a good opportunity for detecting oscillations and waves in solar atmosphere.
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{12534fg1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg5.png) |
Figure 1:
a) The TRACE |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.5cm,height=6.3 cm,clip]{12534fg2.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg6.png) |
Figure 2:
The upwardly-propagating waves in coronal loops observed by Hinode/EIS. a) Time series of relative intensity along the slit in the Fe XII |
| Open with DEXTER | |
2 Observation
EIS has both imaging and spectroscopic capabilities. Its spectroscopic mode can operate in a rastering mode or a sit-and-stare mode. In the latter case, the 1'' or 2'' slit is placed at a fixed location on the Sun, and repeated exposures are obtained while the Hinode spacecraft tracks the solar rotation.
The observations were obtained on 2007 February 1 in AR 10940. An EIS spectroheliogram was taken from 00:12 to 01:22 UT with the 1'' slit and covering a
![]() region.
A sit-and-stare observation within the region was taken from 01:32 to 07:32 UT with the
region.
A sit-and-stare observation within the region was taken from 01:32 to 07:32 UT with the
![]() slit and an exposure time of 60 s. The data cover 17 spectral windows with a cadence of about 62 s.
This paper presents the result mainly for the Fe XII
slit and an exposure time of 60 s. The data cover 17 spectral windows with a cadence of about 62 s.
This paper presents the result mainly for the Fe XII ![]() 195 line. The raw data were first processed using the standard routine eis_prep in Solar Software (SSW). The Fe XII 195.12 Å line was then fitted with a single Gaussian profile, providing the total intensity, Doppler shift, and line width. The effect of a weak blended line, 195.18 Å (Young et al. 2009), is negligible since only relative Doppler shift variations are concerned in our study.
195 line. The raw data were first processed using the standard routine eis_prep in Solar Software (SSW). The Fe XII 195.12 Å line was then fitted with a single Gaussian profile, providing the total intensity, Doppler shift, and line width. The effect of a weak blended line, 195.18 Å (Young et al. 2009), is negligible since only relative Doppler shift variations are concerned in our study.
Hinode is known to have instrumental jitter in both the x and y directions. We estimated drifts of the pointing using the SSW routine eis_jitter from the satellite alignment data (Shimizu et al. 2007), and find that the displacements of the EIS pointing are within 3'' during the observation. For the sit-and-stare data analyzed below, the pointing drifts in the y-direction have been corrected. The drifts in the x-direction have little effect on our result since they are slow and orbit-related with an amplitude less than 2'' and a period of about 90 min.
3 Results
A part of TRACE 195 Å image recorded at 03:15 UT shows a typical fan-like set of diverging coronal loops, located at the northern edge of NOAA active region 10940 (Fig. 1a). The EIS spectroheliogram
taken at 00:12 UT only covers part of this structure (Fig. 1b). The slit used for the sit-and-stare observation is almost aligned along a loop. The Doppler shift map in EIS Fe XII ![]() 195
shows that the eastern part of footpoints of the fan-like loops is dominated by redshifts, while the western part of footpoints is dominated by blueshifts (Fig. 1c). The sit-and-stare mode observations
show weak blueshifts less than 7 km s-1 at a region of
y = 90''-120''.
195
shows that the eastern part of footpoints of the fan-like loops is dominated by redshifts, while the western part of footpoints is dominated by blueshifts (Fig. 1c). The sit-and-stare mode observations
show weak blueshifts less than 7 km s-1 at a region of
y = 90''-120''.
Time-distance maps in intensity and Doppler shift for the EIS
Fe XII line are shown in Fig. 2. To enhance weak propagating intensity disturbances, the time series of relative intensity were normalized to the background trend at each position along the slit by [
![]() ]/
]/
![]() (Fig. 2a), where
(Fig. 2a), where
![]() is the background trend at y = yi taken as a 20 min average smoothing of I(t,yi), while the 30 min
average smoothing gives almost no difference. The background trend was also subtracted from the time series of Doppler shift with a similar method (Fig. 2d). The upwardly propagating disturbances
can be seen in both intensity and Doppler shift as weak bright and dark bands with the positive gradient.
The propagating disturbances are slightly affected by a small bright point at
y = 130''-140''. The footpoint of the loop (at
y = 80''-100'') appears to be characterized by the relatively
high-frequency features, while the upper part is dominated by the relatively low-frequency features.
In other words, the lower frequency component appears to propagate over a longer distance than the
higher frequency one. These time-variable features can be enhanced in a running difference image,
which was created by subtracting from each frame a frame taken some exposures later. The middle and right panels of Fig. 2 show the 5 min and 10 min running difference images,
which clearly reveal the presence of multiple-period modes in the propagating disturbances.
The propagation velocity transverse to the line of sight is estimated as the gradient of
the lines outlining the evident slanting bands in the running difference images (see two examples shown
in Figs. 2b and 2e). For nine propagation features selected for intensity and Doppler
shift separately, we measured the projected propagation speed of
is the background trend at y = yi taken as a 20 min average smoothing of I(t,yi), while the 30 min
average smoothing gives almost no difference. The background trend was also subtracted from the time series of Doppler shift with a similar method (Fig. 2d). The upwardly propagating disturbances
can be seen in both intensity and Doppler shift as weak bright and dark bands with the positive gradient.
The propagating disturbances are slightly affected by a small bright point at
y = 130''-140''. The footpoint of the loop (at
y = 80''-100'') appears to be characterized by the relatively
high-frequency features, while the upper part is dominated by the relatively low-frequency features.
In other words, the lower frequency component appears to propagate over a longer distance than the
higher frequency one. These time-variable features can be enhanced in a running difference image,
which was created by subtracting from each frame a frame taken some exposures later. The middle and right panels of Fig. 2 show the 5 min and 10 min running difference images,
which clearly reveal the presence of multiple-period modes in the propagating disturbances.
The propagation velocity transverse to the line of sight is estimated as the gradient of
the lines outlining the evident slanting bands in the running difference images (see two examples shown
in Figs. 2b and 2e). For nine propagation features selected for intensity and Doppler
shift separately, we measured the projected propagation speed of
![]() km s-1
for intensity and
km s-1
for intensity and
![]() km s-1 for Doppler shift. In addition, we also examined the coordinated
TRACE data, but no corresponding propagating features are found in the constructed time-distance image
along the EIS slit (see Fig. A.1 online). This may come from the lower sensitivity of TRACE compared to EIS.
km s-1 for Doppler shift. In addition, we also examined the coordinated
TRACE data, but no corresponding propagating features are found in the constructed time-distance image
along the EIS slit (see Fig. A.1 online). This may come from the lower sensitivity of TRACE compared to EIS.
![\begin{figure}
\par\includegraphics[width=8cm, height=7cm]{12534fg3.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg13.png) |
Figure 3: Wavelet analysis for oscillation 1 at y =150 ''. a) Time profiles of Doppler shift and relative intensity. Here positive values for the Doppler shift represent the blueshifted emission. b) The wavelet power spectrum for Doppler shift. The dark color represents high power and the dotted contour encloses regions of greater than 99% confidence for a white-noise process. c) The global wavelet spectrum (solid line) and its 99% confidence level (dotted line). d) and e): The same as b) and c) but for relative intensity. |
| Open with DEXTER | |
The periods of the disturbances were investigated using a wavelet analysis method (Torrence & Compo 1998). The Morlet wavelet was chosen for the convolution of time series. The intensity and Doppler shift oscillations at three positions ( y = 150'', 110'', and 60''-65'', denoted as oscillations 1, 2, and 3) were selected for analysis. Oscillation 1 is located at the position of a loop with a projected distance of about 50 Mm away from the footpoint, near which oscillation 2 is measured. Oscillation 3 was selected for comparison, located at another loop intersecting the slit (Fig. 1a). The time profiles used for the analysis of oscillation 3 were obtained by averaging over six pixels along the slit because the oscillation region varied slightly in the y-direction during the observation. In practice, we first subtracted the background trend for both intensity and Doppler shift, which was obtained by temporally smoothing the series. Since oscillation 1 is dominated by the lower-frequency wave component, the background is taken as a 20 min average smoothing. To emphasize the shorter-frequency wave component in oscillations 2 and 3, the background is chosen as a 10 min average smoothing.
The evolution of detrended relative intensity and Doppler shift for three oscillations is shown in panels (a) of Figs. 3 and 4, and of Fig. A.2 (online only). There is a good in-phase relationship between the intensity and Doppler velocity, which is consistent with the signature as predicted by linear MHD wave theory for an upwardly propagating slow magnetoacoustic wave in coronal loops. The wavelet spectrum and the global wavelet spectrum are shown in panels (b)-(e) of Figs. 3 and 4, and of Fig. A.2 (online only). Cross-hatched regions in the wavelet spectrum indicate the ``cone of influence'', where edge effects become important due to the finite length of time series. The global wavelet spectrum is the average of the wavelet power over time at each oscillation period.
For oscillation 1 the wavelet spectra for both intensity and Doppler shift
shows strong power at the period in a range of 20-30 min over a duration of 6 cycles. From the global
wavelet spectra, the oscillation period for Doppler shift is measured to be 25.6![]() 6.3 min and the period for intensity is
6.3 min and the period for intensity is
![]() min. The uncertainties are taken as the half FWHM of the peak. The average maximum amplitude for Doppler shift is
min. The uncertainties are taken as the half FWHM of the peak. The average maximum amplitude for Doppler shift is
![]() km s-1and for relative intensity is (
km s-1and for relative intensity is (
![]() )%, where the errors are the standard deviation of
absolute peak values. As a comparison, we also examined the case with a subtraction of the 30 min smoothing background (see Fig. A.3 online), and find that the power
of the 26 min band shows almost no change, while the power of the 88 min band for Doppler shift rises
above the 99% confidence level, which is caused by the orbital effect.
)%, where the errors are the standard deviation of
absolute peak values. As a comparison, we also examined the case with a subtraction of the 30 min smoothing background (see Fig. A.3 online), and find that the power
of the 26 min band shows almost no change, while the power of the 88 min band for Doppler shift rises
above the 99% confidence level, which is caused by the orbital effect.
Oscillation 2 clearly shows that most of the wavelet power is concentrated within two period bands ranging from 8-16 min and from 20-30 min, indicating that the waves near the footpoint consist of multiple harmonic modes. The two periods are measured to be
![]() min and
min and
![]() min for Doppler shift, and
min for Doppler shift, and
![]() min
and
min
and
![]() min for intensity. The average maximum amplitude for Doppler shift is
min for intensity. The average maximum amplitude for Doppler shift is
![]() km s-1and for intensity is (
km s-1and for intensity is (
![]() )%. Oscillation 3 shows most of the wavelet powers for Doppler shift and intensity concentrated in a range of 8-14 min. The measurements of periods and amplitudes for
oscillations 1-3 are summarized in Table A.1 (online only).
)%. Oscillation 3 shows most of the wavelet powers for Doppler shift and intensity concentrated in a range of 8-14 min. The measurements of periods and amplitudes for
oscillations 1-3 are summarized in Table A.1 (online only).
![\begin{figure}
\par\includegraphics[width=8cm, height=6.5cm]{12534fg4.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg24.png) |
Figure 4: Wavelet analysis for oscillation 2 at y =110''. The annotations are same as in Fig. 3. |
| Open with DEXTER | |
We show a new application of coronal seismology based on interpreting our observation in terms of slow magnetoacoustic waves. Assuming that the coronal field, along which the waves propagate, has an inclination, ![]() ,
to the line of sight, we have
,
to the line of sight, we have
where
From Eqs. (1) and (2) we derive the inclination angle,
Note that Eq. (3) also holds in the condition with a steady flow in the loop. We take
4 Discussion
We have reported on the first observation of the multiple-period (12 and 25 min) propagating disturbances along a fan-like coronal structure in both intensity and Doppler shift in the Fe XII 195 Å line with Hinode/EIS. The phase and amplitude relationships between the intensity and Doppler shift oscillations provide convincing evidence that they are a propagating slow magnetoacoustic wave.
With high cadence (15 s) EIT 195 Å observations, Berghmans & Clette (1999) first detected the propagating intensity disturbances in fanlike coronal loops. They noticed that these disturbances are associated with recurrent footpoint brightenings, appearing as transient flows ejected periodically. In our case the propagating features are detected in both intensity and Doppler shift. The small Doppler shift amplitude of several km s-1 is consistent with the intensity amplitude as expected for a slow magnetoacoustic wave, thus, interpreting these oscillations in terms of propagating slow magnetosonic waves is more appropriate. In addition, the apparent propagation speed of the oscillations >100 km s-1 is an order of magnitude higher than any flow speeds detected in this region.
In our case the dominant oscillations have periods of about 25 min, much longer than those observed in the TRACE loops of around 5 min (De Moortel et al. 2002). It is not clear whythe longer periods reported here were not observed in TRACE loops. One reason for De Moortel et al. (2002) detecting only the 5 min oscillations could be attributed to the selection criterion they used, where a running difference technique with time lag of 90 s would eliminate the long-period components that may exist in some cases. De Pontieu et al. (2005) suggest that 5 min waves in coronal loops come from the leakage of p-modes through the chromosphere tunneled by highly inclined magnetic fields. However, the origin of 20-30 min waves is difficult to explain by such a mechanism because their period is much longer than the cutoff period of the slow magnetoacoustic waves in the chromosphere (Bel & Leroy 1977). Therefore, another explanation is required, e.g., possibly the coupling with the photospheric f-mode caused by local convective motions.
The detection length is defined as the distance along the loop over which the intensity disturbances can be observed. TRACE observations show that the waves are damped quickly with a detection length
typically in the range of 3-23 Mm (De Moortel et al. 2002). Theoretical and numerical studies show that
thermal conduction can play an important role in the quick damping of slow magnetosonic waves
in coronal loops (e.g. Ofman & Wang 2002; Klimchuk et al. 2004; De Moortel & Hood 2004). In our case the detection length is measured
to be about 69 Mm for intensity and about 87 Mm for Doppler velocity, much longer than
in the TRACE case. This difference may be explained by the dependence of the damping length on the
wavelength and the temperature of the ambient plasma (Klimchuk et al. 2004). Thus, the longer period waves
reported here have longer wavelength than in previous observations, resulting in weaker damping by
thermal conduction. In addition, the present loop appears cooler (![]() 0.7 MK as estimated in the
previous section) than previously observed loops (1.0-1.5 MK for TRACE loops).
0.7 MK as estimated in the
previous section) than previously observed loops (1.0-1.5 MK for TRACE loops).
Acknowledgements
Hinode is a Japanese mission developed and launched by ISAS/JAXA in partnership with NAOJ, NASA, and STFC (UK). Additional operation support is provided by ESA and NSC (Norway). The authors are grateful to Dr. Harry Warren for his planning of EIS observations. The work of L.O. and T.J.W. was supported by NRL grant N00173-06-1-G033. L.O. was also supported by NASA grant NNG06GI55G. The authors also thank the referee, Dr. Dipankar Banerjee, for his constructive comments and suggestions.
References
- Banerjee, D., Teriaca, L., Gupta, G. R., et al. 2009, A&A, 499, L29 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bel, N., & Leroy, B. 1977, A&A, 55, 239 [NASA ADS] (In the text)
- Berghmans, D., & Clette, F. 1999, Sol. Phys., 186, 207 [NASA ADS] [CrossRef] (In the text)
- Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 243, 19 [NASA ADS] [CrossRef] (In the text)
- De Moortel, I., & Hood, A. W. 2004, A&A, 415, 705 [NASA ADS] [CrossRef] [EDP Sciences]
- De Moortel, I., Ireland, J., & Walsh, R. W. 2000, A&A, 355, L23 [NASA ADS] (In the text)
- De Moortel, I., Ireland, J., Walsh, R. W., et al. 2002, Sol. Phys., 209, 61 [NASA ADS] [CrossRef]
- De Pontieu, B., Erdélyi, R., & De Moortel, I. 2005, ApJ, 624, L61 [NASA ADS] [CrossRef] (In the text)
- Erdélyi, R., & Taroyan, Y. 2008, A&A, 489, L49 [NASA ADS] [CrossRef] [EDP Sciences]
- Klimchuk, J. A., Tanner, S. E. M., & De Moortel, I. 2004, ApJ, 616, 1232 [NASA ADS] [CrossRef]
- Mariska, J. T., Warren, H. P., Ugarte-Urra, I., et al. 2008, PASJ, 59, S713
- Marsh, M. S., Walsh, R. W., De Moortel, I., et al. 2003, A&A, 404, L37 [NASA ADS] [CrossRef] [EDP Sciences]
- Marsh, M. S., Walsh, R. W., & Plunkett, S. 2009, ApJ, 697, 1674 [NASA ADS] [CrossRef] (In the text)
- McIntosh, S. W., De Pontieu, B., & Tomczyk, S. 2008, Sol. Phys., 252, 321 [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M., & Verwichte, E. 2005, Living Reviews in Solar Physics, 2, 3 [NASA ADS], http://www.livingreviews.org/lrsp-2005-3 (In the text)
- Nakariakov, V. M., Verwichte, E., Berghmans, D., et al. 2000, A&A, 362, 1151 [NASA ADS] (In the text)
- Ofman, L., & Wang, T. J. 2002, ApJ, 580, L85 [NASA ADS] [CrossRef]
- Shimizu, T., Katsukawa, Y., Matsuzaki, K., et al. 2007, PASJ, 59, 845 (In the text)
- Torrence, C., & Compo, G. P. 1998, Bull. Meteor. Soc., 79, 61 [CrossRef] (In the text)
- van Doorsselaere, T., Nakariakov, V. M., Young, P. R., et al. 2008, A&A, 487, L17 [NASA ADS] [CrossRef] [EDP Sciences]
- Wang, T. J., Ofman, L., & Davila, J. M. 2009, ApJ, 696, 1448 [NASA ADS] [CrossRef]
- Young, P. R., Watanabe, T., Hara, H., et al. 2009, A&A, 495, 587 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Online Material
Appendix A: Online materials
![\begin{figure}
\par\includegraphics[width=8cm]{12534fa1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg45.png) |
Figure A.1: Comparisons between EIS and TRACE observations. a) Constructed TRACE 195 Å time-distance image along the EIS slit. b) Same as a) but with the background subtraction, where the background is taken as the average over time at each position along the cut. c) The EIS Fe XII intensity time series. d) Same as c) but with the background subtraction. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12534fa2.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg46.png) |
Figure A.2: Wavelet analysis for oscillation 3 averaged over y = 60''-65''. The annotations are same as in Fig. 3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{12534fa3.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg47.png) |
Figure A.3: Wavelet analysis for oscillation 1 at y = 150'', which is the same as Fig. 3 but with a subtraction of the background taken as a 30 min average smoothing. |
| Open with DEXTER | |
Table A.1: Measurements of the oscillations in fanlike loops found in the EIS sit-and-stare data in the Fe XII (195 Å) linea.
Footnotes
- ... loops
![[*]](/icons/foot_motif.png)
- Appendix is only available in electronic form at http://www.aanda.org
All Tables
Table A.1: Measurements of the oscillations in fanlike loops found in the EIS sit-and-stare data in the Fe XII (195 Å) linea.
All Figures
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{12534fg1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg5.png) |
Figure 1:
a) The TRACE |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.5cm,height=6.3 cm,clip]{12534fg2.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg6.png) |
Figure 2:
The upwardly-propagating waves in coronal loops observed by Hinode/EIS. a) Time series of relative intensity along the slit in the Fe XII |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=7cm]{12534fg3.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg13.png) |
Figure 3: Wavelet analysis for oscillation 1 at y =150 ''. a) Time profiles of Doppler shift and relative intensity. Here positive values for the Doppler shift represent the blueshifted emission. b) The wavelet power spectrum for Doppler shift. The dark color represents high power and the dotted contour encloses regions of greater than 99% confidence for a white-noise process. c) The global wavelet spectrum (solid line) and its 99% confidence level (dotted line). d) and e): The same as b) and c) but for relative intensity. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=6.5cm]{12534fg4.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg24.png) |
Figure 4: Wavelet analysis for oscillation 2 at y =110''. The annotations are same as in Fig. 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{12534fa1.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg45.png) |
Figure A.1: Comparisons between EIS and TRACE observations. a) Constructed TRACE 195 Å time-distance image along the EIS slit. b) Same as a) but with the background subtraction, where the background is taken as the average over time at each position along the cut. c) The EIS Fe XII intensity time series. d) Same as c) but with the background subtraction. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12534fa2.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg46.png) |
Figure A.2: Wavelet analysis for oscillation 3 averaged over y = 60''-65''. The annotations are same as in Fig. 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{12534fa3.eps}
\end{figure}](/articles/aa/full_html/2009/33/aa12534-09/Timg47.png) |
Figure A.3: Wavelet analysis for oscillation 1 at y = 150'', which is the same as Fig. 3 but with a subtraction of the background taken as a 30 min average smoothing. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



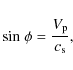
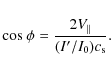
![\begin{displaymath}\phi={\rm tan}^{-1}\left[\frac{1}{2}V_{\rm p}\left(\frac{I^{\prime}/I_0}{V_{\parallel}}\right)\right].
\end{displaymath}](/articles/aa/full_html/2009/33/aa12534-09/img39.png)