EDP Sciences
Home All issues Volume 503 / No 3 (September I 2009) A&A, 503 3 (2009) 913-928 Full HTML
Free Access
Issue
A&A
Volume 503, Number 3, September I 2009
Page(s) 913 - 928
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/200911703
Published online 09 July 2009

Synthetic photometry for carbon rich giants

I. Hydrostatic dust-free models[*]

B. Aringer1,2,3 - L. Girardi2 - W. Nowotny1 - P. Marigo3 - M. T. Lederer1

1 - Department of Astronomy, University of Vienna, Türkenschanzstraße 17, 1180 Wien, Austria
2 - Osservatorio Astronomico di Padova - INAF, Vicolo dell'Osservatorio 5, 35122 Padova, Italy
3 - Dipartimento di Astronomia, Università di Padova, Vicolo dell'Osservatorio 2, 35122 Padova, Italy

Received 22 January 2009 / Accepted 5 April 2009

Abstract
Context. Carbon rich objects represent an important phase during the late stages of evolution of low and intermediate mass stars. They contribute significantly to the chemical enrichment and to the infrared light of galaxies. A proper description of their atmospheres is crucial for the determination of fundamental parameters such as effective temperature or mass loss rate.
Aims. We study the spectroscopic and photometric properties of carbon stars. In the first paper of this series we focus on objects that can be described by hydrostatic models neglecting dynamical phenomena like pulsation and mass loss. As a consequence, the reddening due to circumstellar dust is not included. Our results are collected in a database, which can be used in conjunction with stellar evolution and population synthesis calculations involving the AGB.
Methods. We have computed a grid of 746 spherically symmetric COMARCS atmospheres covering effective temperatures between 2400 and 4000 K, surface gravities from $\log({g}~[{\rm cm/s}^2]) = 0.0$ to -1.0, metallicities ranging from the solar value down to one tenth of it and C/O ratios in the interval between 1.05 and 5.0. Subsequently, we used these models to create synthetic low resolution spectra and photometric data for a large number of filter systems. The tables including the results are electronically available. First tests of the application on stellar evolution calculations are shown.
Results. We have selected some of the most commonly used colours in order to discuss their behaviour as a function of the stellar parameters. A comparison with measured data shows that down to 2800 K the agreement between predictions and observations of carbon stars is good and our results may be used to determine quantities like the effective temperature. Below this limit the synthetic colours are much too blue. The obvious reason for these problems is the neglect of circumstellar reddening and structural changes due to pulsation and mass loss.
Conclusions. The warmer carbon stars with weak pulsation can be successfully described by our hydrostatic models. In order to include also the cooler objects with intense variations, at least a proper treatment of the reddening caused by the dusty envelopes is needed. This will be the topic of the second paper of this series.

Key words: stars: late-type - stars: AGB and post-AGB - stars: atmospheres - infrared: stars - stars: carbon - Hertzsprung-Russell (HR) and C-M diagrams

1 Introduction

During the evolution of low to intermediate mass stars along the TP-AGB (thermal pulsing asymptotic giant Branch), material processed by the nuclear reactions in the He burning shell may be dredged up to the surface, changing the chemical abundances in the atmosphere. Especially, the amount of carbon will be increased significantly by this mechanism. If the particle density exceeds that of oxygen (the ratio of the particle densities $\rm C/O > 1$), the spectral appearance of the object becomes completely different. Instead of O-bearing molecules like TiO, VO, SiO, OH and H2O the opacities in the cool outer layers and the observed energy distributions are dominated by C2, CN, C3, HCN and C2H2 (e.g. Querci et al. 1974; Jørgensen et al. 2000; Loidl et al. 2001). This characterizes a classical carbon star.

Carbon stars are among the brightest stellar objects in resolved galaxies containing young and intermediate-age populations, especially in the near infrared. Moreover, they contribute significantly to the integrated spectra of such systems. These two facts become obvious in the Magellanic Clouds: in the LMC for instance, among the approximately 31000 AGB stars brighter than the tip of the RGB (Cioni & Habing 2003), there are about 11000 carbon rich objects (Blanco & McCarthy 1983). These sources alone contribute to roughly 20 percent of the integrated bolometric luminosity of LMC clusters with intermediate ages (Frogel et al. 1990, Fig. 16). Thus, the influence of C-type giants on the total flux emitted by galaxies is noticeable.

It is therefore very important that carbon stars are properly taken into account in models of galaxies. For this, two major ingredients are necessary. First, evolutionary tracks providing the distributions of luminosities, effective temperatures and surface compositions of the red giants as a function of age, initial mass and metallicity have to be available. Such calculations were presented for example in the work of Marigo & Girardi (2007). Secondly, one needs synthetic spectra including the circumstellar reddening by dust, which allow the conversion of the model quantities into observable properties of stars. The implementation of this can be found in Marigo et al. (2008).

The main goal of this work is to present a set of photometric data and low resolution energy distributions allowing such a conversion from stellar fundamental parameters into measurable quantities. Based on observational material, libraries of overall carbon star spectra have been published by Lançon & Wood (2000) and Lançon & Mouhcine (2002). However, they extend only up to 2.5 $\mu$m, neglecting the mid and far infrared. In addition, their coverage of stellar parameters is very limited. This applies also to the input data used by Marigo et al. (2008) which are based on the hydrostatic model atmospheres and synthetic spectra of Loidl et al. (2001). As an example, they only have included calculations for solar metallicity.

Loidl et al. (2001) and Jørgensen et al. (2000) have computed synthetic low and medium resolution spectra based on hydrostatic carbon star models and compared them to observations in the optical as well as in the near and mid infrared range. Their results were obtained using previous versions of COMA and the MARCS code (see Sect. 2.1). One of the most important differences to the work presented here is that they have completely neglected atomic line opacities, which causes flux deviations mainly at shorter wavelengths. In addition, there are also changes concerning the molecular input data. A comparison of the results based on our calculations to convert the isochrones of Marigo et al. (2008) to the 2MASS $M_{K_{\rm s}}$ versus $(J{-}K_{\rm s})$ diagram and the original ones obtained with the spectra from Loidl et al. (2001) is shown in Sect. 4.2.2 (Fig. 19).

It was demonstrated for example by Gautschy-Loidl et al. (2004), Loidl et al. (1999) or Nowotny et al. (2005a,b) that hydrostatic models do not reproduce the atmospheric structure and spectra of cool carbon stars with intense variations and mass loss. Such objects are dominated by their pulsation creating shock waves, the formation of dust and a strong wind giving rise to a circumstellar shell. Since all of these phenomena are time-dependent and coupled, they have to be described by comprehensive dynamical calculations, such as presented by Höfner et al. (2003) or Mattsson et al. (2008). The photometric properties of the corresponding models will be discussed in the next paper of this series. In the current work we focus on warmer objects with small pulsation amplitudes. Nevertheless, the reddening due to circumstellar dust, which causes the most important differences between the presented hydrostatic and dynamical atmospheres for the cool mass-losing carbon stars, may be simulated in connection with our data by using approximative approaches such as in Bressan et al. (1998) and Groenewegen (2006).

2 Model atmospheres and spectral synthesis

2.1 Hydrostatic models and opacities

In order to study the spectra and photometric properties of carbon stars, we have produced a grid of 746 spherically symmetric hydrostatic model atmospheres. They were computed with the COMARCS program which is based on the version of the MARCS code (Gustafsson et al. 1975, 2008) used in Jørgensen et al. (1992) and Aringer et al. (1997). In contrast to the previous approaches, COMARCS works with external opacity tables including the coefficients for a two-dimensional spline interpolation in pressure and temperature at the desired wavelengths. The applied method is an algorithm developed by Hardy (1971) with the implementation found in the book of Späth (1991). The frequency grid adopted for the opacity sampling in our calculations corresponds to the one used by Aringer et al. (1997). It consists of 5364 points. Such tables with spline coefficients for the different wavelengths are produced for each combination of microturbulence and chemical abundances to be investigated. This was done using the opacity generation code COMA (Copenhagen Opacities for Model Atmospheres).

The COMA program was originally developed to compute wavelength dependent absorption coefficients for dynamical model atmospheres of cool giants as they are used for example in the work of Höfner et al. (2003). In addition, it was adapted to determine weighted mean opacities for different applications like stellar evolution calculations (e.g. Cristallo et al. 2007; Lederer & Aringer 2009). Starting from a given temperature-pressure or temperature-density structure (table with values) the abundances of many important species are evaluated based on the equilibrium for ionisation and molecule formation. Thus, we assume chemical equilibrium except for the treatment of dust (and also some tests with results from non-equilibrium calculations). As a next step, the computed partial pressures of the neutral atoms, ions and molecules can be used to determine the continuous and line opacity at each selected frequency point (in LTE). Since the first version of COMA described by Aringer (2000), a considerable number of updates have been made including a more complete treatment of ionisation (Gorfer 2005), additional chemistry routines (Gibbs energy minimisation, Falkesgaard 2001), the addition of atomic transitions from the VALD database (Kupka et al. 2000) or the possibility to take the effect and opacity of dust into account (Nowotny et al. 2007). And, of course the number of incorporated molecules contributing to the total absorption has been increased significantly. The calculations presented here cover the following species: CO, CH, C2, SiO, CN, TiO, H2O, C2H2, HCN, C3, OH, VO, CO2, SO2, HF, HCl, FeH, CrH, ZrO and YO.

A table containing most of the line lists used and the corresponding references can be found in Cristallo et al. (2007). Four of the molecules included in our work do not appear in the mentioned collection of data: ZrO from Plez et al. (2003), YO from John Littleton (priv. comm.), FeH from Dulick et al. (2003) and CrH from Bauschlicher et al. (2001). The abundance of FeH originally was not computed in any of the chemical routines of COMA. Thus, we had to add the corresponding equilibrium constants to the program. They were determined using the partition function for FeH given by Dulick et al. (2003) and for the atomic contributors Fe and H by Irwin (1981). For some of the molecules already appearing in Cristallo et al. (2007) the line data changed: in the case of SO2 and HCl they have been updated from HITRAN 1996 to HITRAN 2004 (Rothman et al. 2005) which is here now also used for OH. The opacity of CO2 is calculated from HITEMP (Rothman et al. 1995) instead of HITRAN which results in a much larger number of transitions (1032269). Finally, the lines of HF are taken from the list of Tipping (priv. comm.) discussed in Uttenthaler et al. (2008). However, all of these changes do not have a significant effect on the atmospheric structures, since the molecules involved are only of minor importance for the overall absorption in the temperature range covered by the hydrostatic models. Also the uncertainties of the opacities from TiO and H2O, where the existing line lists show considerable differences in some spectral regions (see e.g. Aringer et al. 2008), do not influence our results. The partial pressures of these species always remain very low in a carbon rich environment - at least as long as one assumes chemical equilibrium.

 \begin{figure} \par\includegraphics[width=12cm,clip]{11703f01.eps}\end{figure} Figure 1:

Atmospheric structures of a sequence of COMARCS models with $\log({g}~[{\rm cm/s}^2]) = 0.0$, C/O = 1.4, $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 1.0$ and different values of $T_{\rm eff}$. The temperature is shown as a function of the gas pressure.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=12cm,clip]{11703f02.eps}\end{figure} Figure 2:

Atmospheric structures of a sequence of COMARCS models with C/O = 1.1, $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 1.0$and different values of $\log({g}~[{\rm cm/s}^2])$at $T_{\rm eff} = 2800~$K. In addition, the results for $\log({g}~[{\rm cm/s}^2]) = 0.0$at $T_{\rm eff} = 3200~$K have been included. The temperature is shown as a function of the gas pressure.
Open with DEXTER

The dominating molecules in our models of carbon stars are CO, C2, CN, C2H2, HCN and C3. Their contribution to the spectral absorption is shown in Sect. 3.2 (Fig. 4). Following the work of Loidl et al. (2001) and the suggestions in the SCAN database (Jørgensen 1997) we have scaled down the gf-values of the C2 lines taken from the original list of Querci et al. (1974) at wavelengths longer than 1.15 $\mu$m by a factor of up to 10 in most of the calculations. This has only a minor influence on the model structures, but it causes moderate changes of the spectral appearance in the region between 1.3 and 2.1 $\mu$m. Thus, we have also produced some reference spectra with unscaled C2 data. The corresponding effects on the photometric results will be discussed in more detail later in this work.

As in the original version of COMA, Doppler profiles including the thermal and the microturbulent contribution are assumed for the molecules. First, there exists almost no information on the damping constants of molecular transitions. In addition, especially for those species which dominate the overall opacity like C2H2 or HCN, and in all regions close to bandheads the wings of even the strongest lines will be much weaker than the Doppler cores of the many overlapping neighboring ones. The absorption of all atoms except for hydrogen where we interpolate in tabulated profiles is computed with full Voigt functions, adopting the damping constants listed in the VALD database.

2.2 Model parameters

The parameter range of the COMARCS atmospheres was chosen to include the typical effective temperatures, surface gravities and C/O ratios expected for carbon stars from synthetic evolution calculations as they are presented by Marigo & Girardi (2007) or Marigo et al. (2008). Sub-grids of models have been produced for the three metallicities $Z/Z_{\odot } = 1.0$, $Z/Z_{\odot} = 0.33$ and $Z/Z_{\odot} = 0.1$which covers the major populations in the Milky Way as well as in the Magellanic Clouds. All elements heavier than He were scaled with Z in the same way. Thus, we did not take into account any possible individual variations of the different species except for the carbon abundance. However, due to the combination of the fact that the opacities in cool giant atmospheres are dominated by a small number of molecules with the preferred formation of CO, the studied model structures and photometric indices will mainly depend on [C] and the ratio C/O. For the solar composition we adopted the values from Anders & Grevesse (1989) except for C, N and O where we took the data from Grevesse & Sauval (1994). This is in agreement with our previous work (e.g. Aringer et al. 1999) and results in a $Z_{\odot}$ of approximately 0.02.

All sub-grids were computed completely for objects with a mass of $M = 2.0~M_{\odot}$, which can be regarded as typical for many carbon stars. At constant effective temperature and surface gravity, this value determines the ratio of the atmospheric extension to the stellar radius and thus the overall spherical geometry. In order to investigate the influence of the mass we also produced a large number of models with $M = 1.0~M_{\odot}$. For solar metallicity, almost the complete grid of 2.0 $M_{\odot }$stars is covered by calculations for 1.0 $M_{\odot }$. Exceptions are some of the most extended atmospheres where it was more difficult to obtain converging hydrostatic solutions for 1.0 $M_{\odot }$ in several cases, as well as objects hotter than 3400 K which are not on the AGB (see later in this section). For the lower values of $Z/Z_{\odot }$, only a very small number of 1.0 $M_{\odot }$ models restricted to an effective temperature of 2600 K exists. This is not a big problem, since the sphericity corrections of the photometric indices in the near infrared always remain relatively small, as it can be concluded from Fig. 8 and the corresponding discussion of the results (Sect. 3.3.1). Uncertainties due to pulsation and mass loss or unknown abundances are much larger. In addition, some of the basic trends of the metal-poor models as a function of mass may also be deduced from the solar metallicity atmospheres, although one should keep in mind that the behaviour can sometimes be quite complex. Finally, for $T_{\rm eff} = 2800~$K, $\log({g}~[{\rm cm/s}^2]) = -0.70$, $Z/Z_{\odot } = 1.0$ and C/O = 1.1 we have computed objects with 3.0, 5.0, 10.0 and 99.0 $M_{\odot }$ in order to follow the convergence towards the plane parallel solution.

For solar metallicity, our grid contains C/O ratios of 1.05, 1.10, 1.40 and 2.00. Due to the much lower amount of oxygen, the situation is quite different for $Z/Z_{\odot} = 0.33$ and $Z/Z_{\odot} = 0.1$. In such stars, C/O values around 1.0 are expected to appear rarely, since they may already increase to much higher quantities after one 'third dredge up' event. On the other hand, for the more evolved carbon giants, ratios considerably larger than 2.0 can be reached (see Marigo & Girardi 2007). Thus, for $Z/Z_{\odot} = 0.33$ and $Z/Z_{\odot} = 0.1$ our grid includes models with C/O = 1.4, 2.0 and 5.0.

The temperatures covered by the sub-grid for solar metallicity range from 2400 to 4000 K with steps of 100 K. For $Z/Z_{\odot} = 0.33$ and $Z/Z_{\odot} = 0.1$ the lower limit was increased to 2600 K, as expected from stellar evolution calculations (e.g. Marigo et al. 2008). The region of AGB carbon stars extends only up to between 3200 and 3500 K, depending on the initial mass and chemical composition. Nevertheless, we also included hotter atmospheres, because the computations predict some objects with $\rm C/O > 1$having a higher temperature during their post-AGB phase. A typical sequence of models with different values of $T_{\rm eff}$ at constant surface gravity, mass and element abundances is shown in Fig. 1. In addition, the effect of changing $\log({g})$ is demonstrated in Fig. 2.

Models with $\log({g}~[{\rm cm/s}^2]) = 0.0$have been calculated for all combinations of effective temperature, metallicity and C/O ratio, except for some of the hotter atmospheres between 3500 and 3800 K with a high total carbon abundance ( $Z/Z_{\odot} = 0.33$ with C/O = 5.0 as well as $Z/Z_{\odot } = 1.0$ with C/O = 2.0) where we could not obtain a converging hydrostatic solution. This value of the surface gravity is also the general upper limit of our grid. It is obvious that for the cooler objects it corresponds to luminosities much lower than those expected for AGB stars. For example, at $T_{\rm eff} = 2600~$K and one solar mass, $\log({g}~[{\rm cm/s}^2]) = 0.0$results in only 1122 $L_{\odot}$, which is by a factor of 5 to 10 less than predicted for a typical carbon giant. However, since it was much easier to get converging solutions for the higher surface gravities, we always used this value of $\log({g})$ in order to iterate from one grid temperature to the next.

Table 1:   Lower limits of $\log({g})$ in the grid of atmospheric models for carbon stars. The upper limit is always $\log({g}~[{\rm cm/s}^2]) = 0.0$.

The lower limit for the surface gravity of our models depends on the effective temperature. It was chosen to cover the region of AGB carbon stars predicted by Marigo & Girardi (2007) and Marigo et al. (2008) and it is listed in Table 1. The smallest values of $\log({g}~[{\rm cm/s}^2]) = -1.0$appear for the coolest giants with $T_{\rm eff} \le 2700$ K, while they increase continuously, when the objects become warmer. In the range between 3500 and 4000 K we have only computed atmospheres with $\log({g}~[{\rm cm/s}^2]) = 0.0$and 2.0 $M_{\odot }$. As already mentioned before, most or all of these stars will not be on the AGB. The standard (maximum) step width in $\log({g}~[{\rm cm/s}^2])$ is 0.2 above and 0.1 below -0.6. However, due to difficulties concerning the convergence of the more extended models it had to be decreased in many cases by a factor of two to 0.1 or 0.05. These problems are also the reason why the lower limits given in Table 1 could by far not be reached with all combinations of metallicity, C/O ratio and mass. Especially in situations with a high carbon abundance ( $Z/Z_{\odot} = 0.33$with C/O = 5.0, $Z/Z_{\odot } = 1.0$with C/O = 2.0) and around 3000 K, it became harder (large number of iterations, highly dependent on initial conditions) or impossible to obtain hydrostatic solutions at decreased surface gravities. In addition, it turned out to be more difficult to calculate models with a lower mass (1.0 $M_{\odot }$).

A list of all computed COMARCS models and synthetic spectra including their parameters can be found in the bolometric correction tables which are available at http://stev.oapd.inaf.it/synphot/Cstars or also at the CDS.

For the microturbulent velocity we adopted a value of $\xi = 2.5$ km s-1, which is in agreement with our previous work (Aringer et al. 1997) and with high resolution observations of AGB stars (e.g. Smith & Lambert 1990; Lebzelter et al. 2008). Due to the fact that a large fraction of the opacity in cool carbon giants is generated by many weak overlapping lines, a change of $\xi$ does only have a small effect on the atmospheres and photometric results as long as it remains moderate (e.g. between 2.0 and 3.5 km s-1). The models were calculated in the range from $\rm\tau_{Rosseland} = 10^2$to 10-5 with a constant logarithmic step size of 0.1. Thus, each of the structures consists of 71 depth points. For a considerable number of atmospheres we had to exclude a few of the outermost layers in order to obtain converging solutions. The missing data were added subsequently by extrapolation. It was shown with several test computations that the structures produced by this method are usually close to the ones determined considering the full depth range. However, we never excluded more than 10 points (outer boundary of the calculation at $\rm\tau_{Rosseland} = 10^{-4}$), since this may easily result in larger errors, already visible in the calculated spectra (>1%).

2.3 Synthetic spectra

The described hydrostatic COMARCS atmospheres were used to compute synthetic opacity sampling spectra covering the range between 400 and 22500 cm-1(0.444 to 25.0 $\mu$m) with a resolution of R = 10 000. Based on the corresponding radial temperature-pressure structures we derived the necessary opacities in the different layers again with the COMA code. Except for the denser wavelength grid, this was done with the same settings as for the generation of the input data produced for the atmospheric models, ensuring a consistent treatment of the absorption, which is very important for obtaining realistic spectra (see Aringer 2005). The results of these opacity calculations are then processed by a spherical radiative transfer program developed for the work of Windsteig et al. (1997) that computes the desired stellar fluxes. This approach is not completely consistent with the models, since COMARCS uses a different set of routines. Nevertheless, for the atmospheric parameters and wavelength ranges studied here, the deviations between the low resolution opacity sampling spectra generated directly by COMARCS and the code from Windsteig et al. (1997) are negligible.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f03.eps}\end{figure} Figure 3:

Three spectra based on COMARCS models with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 1.0$and different values of $T_{\rm eff}$, C/O and $\log({g}~[{\rm cm/s}^2])$. The resolution is R = 200.
Open with DEXTER

Due to the statistical nature of the opacity sampling approach, only the average over a larger number of wavelength points (usually 20 to 100) gives a realistic representation of the observed stellar spectra. As a consequence, we reduced the resolution of our results to R = 200 by convolving them with a Gaussian function defined by the corresponding half width. No additional broadening caused for example by a macroturbulent velocity was assumed. Some of the emerging spectra are shown in Fig. 3 where the change of the overall shape as well as of individual features with effective temperature, surface gravity and C/O ratio can be seen. It should be noted that the actual sampling of the wavelength grid is with R = 2000 significantly higher than the real resolution, resulting in a relatively smooth appearance of the plotted energy distributions. These R = 200 data are electronically available as described in Sect. 3.2.

2.4 Synthetic photometry

Based on our theoretical results we have calculated synthetic bolometric corrections following the same formalism as described in Girardi et al. (2002, Eqs. (7) and (8)). For each of the different filters we first convolved the total transmission curve with the original opacity sampling spectra, integrating either the photon energy or the number of detected photons. The latter selection depends on the definition of the investigated photometric system, if amplifiers or counting devices are used. Then, the obtained magnitudes were scaled with respect to values corresponding to a reference intensity in order to assess the zero points. This quantity was determined from a convolution with the filter curve applied to a constant flux per unit wavelength (frequency) in the case of STmag (ABmag) systems or to a Vega ($\alpha$ Lyr) spectrum for Vegamag systems. The standard star data were taken from the work of Bohlin (2007). They are expected to be accurate to within about 2% in the optical and near infrared range. Most of the photometric systems are defined in a way that Vega has magnitudes close to zero in all filters with just small corrections representing the offsets found during observational campaigns such as, for example, the 2MASS survey.

We deal with about 25 photometric systems, most of which are listed in Table 2 of Marigo et al. (2008) together with their sources of transmission curves and reference magnitudes. In addition, we recently inserted information on the HST/WFC3 camera (Girardi et al. 2008), CFHT/Megacam (McLeod et al. 2000; Coupon et al. 2008), UT/DMC (Kuncarayakti et al. 2008) and the Washington+DDO51 (KPNO Mosaic, Geisler 1984, see also http://www.noao.edu/kpno/mosaic/filters) filters. Since the number of entries in our database is continuously growing, an updated overview may always be found at http://stev.oapd.inaf.it/cmd. Regarding the specific case of carbon star spectra, we already include most of the photometric systems in which these cool objects are more interesting for observation, such as Bessell JHK, 2MASS, UKIDSS, HST/NICMOS, OGLE, SDSS, AKARI and Spitzer.

3 Results of the modelling

3.1 Model structures

In Figs. 1 and 2 some typical examples for the hydrostatic models computed with COMARCS are presented. One can see how the temperature-pressure structure, which is of great importance for the spectral appearance, changes as a function of $T_{\rm eff}$ and $\log({g})$. It is obvious that the variation of these two parameters produces clear and uniform trends concerning the position and shape of the corresponding curves. For example, a decreased surface gravity will always result in an atmosphere extending to lower densities at the outer boundary, or with a growing value of $T_{\rm eff}$ the whole structure is shifted to warmer temperatures. Such a regular behaviour usually also appears for the other parameters, which are mass, metallicity and C/O ratio. Thus, in many situations it will be possible to determine atmospheres not included in the current grid by interpolation or even extrapolation. However, this has to be done with care, since uniform clear trends do not occur in all cases (see the discussion on the effect of mass in the spectra in the following section, Sect. 3.2).

3.2 Spectra

The complete grid of our final spectra with R = 200 can be obtained from http://stev.oapd.inaf.it/synphot/Cstars. The corresponding tables consist of three columns: wavelength [Å], continuum normalized flux and specific luminosity times frequency ( $\rm\nu \cdot {\it L}_{\nu}$[erg/s]). The second quantity is determined from the division of the result of a full radiative transfer calculation including all opacities by one where the atomic and molecular line absorption is completely neglected (only continuum opacities). This allows us to evaluate the apparent intensity of the different features. As an example for the data we present in Fig. 3 three spectra generated from models with similar luminosity, but varying effective temperature, surface gravity and C/O ratio. They cover the interval from 0.5 to 10 $\mu$m, which is only a part of the whole computed frequency range extending between 0.444 and 25 $\mu$m. As it has been mentioned in the previous section, the resolution is R = 200, while the sampling of the wavelength grid was chosen to be ten times higher.

 \begin{figure} \par\includegraphics[width=11.8cm,clip]{11703f04.eps} \end{figure} Figure 4:

Continuum normalized spectra for the most important molecular species based on a COMARCS model with $T_{\rm eff} = 2600~$K, $\log({g}~[{\rm cm/s}^2]) = -0.2$, $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 1.0$ and C/O = 1.10.
Open with DEXTER

In Fig. 4 we show spectra demonstrating the contribution of the most important molecules, which have been derived by including only the opacity of the corresponding species into the radiative transfer. Subsequently, the results were normalized to the continuum in the same way as described above. We divided them by the output of a calculation where the absorption generated by lines was completely neglected. All spectra are based on the same atmospheric model with $T_{\rm eff} = 2600~$K, $\log({g}~[{\rm cm/s}^2]) = -0.2$, $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 1.0$ and C/O = 1.10. It is obvious that molecular transitions block a large fraction of the radiation in the shown frequency interval. The opacity around and below 1 $\mu$m is dominated by the bands of C2 and CN, while at longer wavelengths C2H2 and HCN are the most important species. However, the intensity of the features generated by the latter polyatomic molecules decreases significantly for higher effective temperatures. On the other hand, the variation of the absorption produced by C2 and CN as a function of the stellar parameters is much less pronounced. In addition, the bands of C3 may become considerably stronger with growing C/O ratios.

 \begin{figure} \par\includegraphics[width=11.8cm,clip]{11703f05.eps} \end{figure} Figure 5:

Continuum normalized spectra based on COMARCS models with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 2.0$, C/O = 1.10 and different values of $\log({g}~[{\rm cm/s}^2])$. Two effective temperatures are compared: 2600 K and 3100 K.
Open with DEXTER

The behaviour of the molecular features depending on the stellar properties of carbon stars has already been used to determine parameters like effective temperature or C/O ratio by a comparison of calculated and observed results (e.g. Aoki et al. 1998, 1999; Jørgensen et al. 2000; Loidl et al. 2001). Since this work focuses mainly on the photometric characteristics, we will only discuss two selected examples of the spectroscopic changes, which are interesting for a possible interpolation or extrapolation based on our grid. More detailed studies involving the low resolution energy distributions will follow in the future.

The change of the line absorption with surface gravity is displayed in Fig. 5 where we show continuum normalized spectra for different values of $\log({g})$ emerging from cooler atmospheres with $T_{\rm eff} = 2600$ K and hotter ones with $T_{\rm eff} = 3100$ K. The models have solar metallicity and their C/O ratio is 1.10. As one would expect, the warmer object produces much weaker molecular features. Even at the low resolution of the final spectra the flux level of the continuum is almost reached at some places around 4 and 6 $\mu$m. This is not the case for the cooler atmosphere where the line absorption blocks in most regions more than 50% of the radiation. There exists also a general trend that the molecular features become slightly weaker at lower surface gravity, if the other parameters are not altered. This behaviour is expected for extended giants and caused by the larger dimensions of the corresponding objects creating stronger sphericity effects[*] at constant mass (Aringer et al. 1999). For both of the presented sequences the changes as a function of $\log({g})$ are reasonably linear. Since the variation with temperature is usually also quite regular, an interpolation concerning these two parameters should work well.

 \begin{figure} \par\includegraphics[width=12cm,clip]{11703f06.eps} \end{figure} Figure 6:

Continuum normalized spectra based on COMARCS models with $Z/Z_{\odot } = 1.0$, C/O = 1.40 and different values of $\log({g}~[{\rm cm/s}^2])$ and stellar mass (in $M_{\odot }$). Two effective temperatures are compared: 2600 K and 3100 K.
Open with DEXTER

However, in some cases the situation can be more complex. This is demonstrated in Fig. 6 where we investigate the combined effects of mass and surface gravity at 2600 and 3100 K. The spectra shown are again normalized with respect to the continuum and the corresponding models have solar metallicity and a C/O ratio of 1.40. At 2600 K we find a quite regular behaviour which also complies with the expectations concerning sphericity. As was discussed before (see Fig. 5) the intensity of the line absorption decreases for lower values of $\log({g})$. On the other hand, there is a shift due to mass which grows for declining surface gravities. The molecular features are in general deeper, if the objects become more massive. Both trends are in agreement with the predicted weakening of the line absorption due to sphericity effects. But at 3100 K the behaviour is rather different. It is obvious that for this temperature not all parts of the spectrum react in the same way to changes of surface gravity and mass. Especially the deep feature at 3 $\mu$m, produced mainly by HCN and C2H2, does not really follow the trends expected from spericity, since the intensity decreases a lot for more massive stars. A similar behaviour can be found for the wings of the broad 14 $\mu$m band, not shown in the plot. The absorption in the corresponding region is also caused by the two species HCN and C2H2. This demonstrates that due to the complex interaction of atmospheric structure, opacities and chemical equilibrium, simple predictions deduced from a single mechanism are not always possible. On the other hand, there are spectral ranges where we see also at 3100 K variations as a function of $\log({g})$ and mass, which agree very well with the expectations from sphericity (e.g. around 4 or 6 $\mu$m).

As will be discussed in the next section, the stellar mass has in general only a rather small influence on the investigated photometric properties. For the warmer stars with $T_{\rm eff} \ge 3000$ K the spectra below 2.5 $\mu$m also change only marginally as a function of $\log({g})$. Thus, the mentioned irregularities will usually not hamper a proper prediction and interpolation of the colours. The possible uncertainties due to circumstellar reddening by dust and structural variations caused by atmospheric dynamics, which are not considered in the presented models, are much larger, even in objects with relatively weak pulsations. The special behaviour of the 3 $\mu$m feature might affect the L band, since it partly overlaps with the corresponding filter curve.

3.3 Photometry

The synthetic photometry computed for the complete grid of our hydrostatic COMARCS models is available at http://stev.oapd.inaf.it/synphot/Cstars or also at the CDS. A detailed description of the corresponding data can be found in Sect. 2.4. The tables list the bolometric corrections (BC) as a function of the stellar parameters $T_{\rm eff}$, $\log({g}~[{\rm cm/s}^2])$, $M/M_{\odot}$, $Z/Z_{\odot }$ and C/O ratio for the different included filter magnitudes. We have prepared a separate file for each of the studied photometric systems.

The complete set of tables covers 36 photometric systems, each of them including several filters. This wealth of information may be exploited by the users of the database. Here, we restrict ourselves to certain typical examples. We have chosen some of the standard visual and near infrared filters as defined by Bessell (1990) and Bessell & Brett (1988), since they were applied for a large number of observations. The V, J, H and K magnitudes and colours appearing in the following discussions and figures are based on this photometric system (called the Bessell system in our work).

The observed colours of many carbon stars are severely affected by circumstellar (see the discussion in Sect. 4) and interstellar reddening. Since our results do not include these processes, they have to be applied a posteriori to the data.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f07.eps} \end{figure} Figure 7:

Predicted (J-H) colours as a function of effective temperature calculated from COMARCS models with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 2.0$, C/O = 1.10 and different values of $\log({g}~[{\rm cm/s}^2])$.
Open with DEXTER

3.3.1 The ( 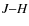$\textit {J}{-}\textit {H}$) colour

In Figs. 7, 8 and 9 we investigate the behaviour of the (J-H) colour as a function of the effective temperature. In the first of the plots we do this for the different values of $\log({g})$, selecting objects with solar metallicity and C/O = 1.10 as an example. As described in Sect. 2.2 (see Table 1), the range of available surface gravities decreases towards warmer atmospheres and above 3400 K only models with $\log({g}~[{\rm cm/s}^2]) = 0.0$have been included in our grid. It is obvious that the spread of the (J-H) colours has a significant minimum around 2900 K, where it becomes practically negligible. It grows quite rapidly, if the stars get cooler. As a consequence, the largest differences appear at the lowest temperature of 2400 K where the dispersion reaches more than 0.1 mag. Above 2900 K the spread also increases, but it remains always moderate or small, which is partly due to the limited $\log({g})$ range for the warmer atmospheres. Below 2900 K the more extended models are redder, while beyond this value they have bluer colours.

The value of 2900 K also corresponds to the point of reversion for the general trend as a function of temperature where (J-H) reaches a maximum. Towards warmer and cooler atmospheres the colours become bluer. This turnaround is caused by the behaviour of different molecular features situated in the region of the filters. In the J band the flux is affected mainly by C2 and CN, while the H band covers a considerable depression due to a mixture of C2, CN, CO, C2H2 and HCN. The temperature dependent intensity of the polyatomic species especially plays a key role for the colour reversion, which makes a determination of the stellar parameters difficult and ambiguous. However, the turnaround will usually not be visible in observations of real stars, since all cooler objects are severely reddened by dust.

The circumstellar reddening, which is discussed in more detail in the next section (Sect. 4.1) and in the second paper of this series, affects all photometric indices. It induces changes much larger than those caused by the molecular features. Thus, the ambiguity mentioned above plays only a minor role and for the coolest stars the determination of the parameters without a proper modelling of mass loss and dust opacities is impossible.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f08.eps} \end{figure} Figure 8:

Predicted differences in the (J-H) colours between objects with 1.0 and 2.0 $M_{\odot }$ as a function of effective temperature calculated from COMARCS models with $Z/Z_{\odot } = 1.0$, C/O = 1.10 and various values of $\rm log({g}~[{\rm cm/s}^2])$.
Open with DEXTER

In Fig. 8 we study the influence of the stellar mass on the (J-H) colour at various values of the surface gravity. The differences between 1.0 and 2.0 $M_{\odot }$are shown taking again solar metallicity and C/O = 1.10 as an example. As one would expect, the shifts grow in general for smaller values of $\log({g})$. In addition, they reach a maximum around 2700 K. Their behaviour as a function of temperature and surface gravity is not always completely regular, which is in agreement with the results from the synthetic spectra discussed in the previous section (see Fig. 6). A very good example is the differences at $\log({g}~[{\rm cm/s}^2]) = -1.0$. Nevertheless, the spread in (J-H) due to mass remains in most cases rather small ($\le$0.04 mag). Other effects, like changing the elemental abundances or adding a dust opacity, are much more important. The same is also true for the other colour indices investigated here.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f09.eps} \end{figure} Figure 9:

Predicted (J-H) colours as a function of effective temperature calculated from COMARCS models with $\log({g}~[{\rm cm/s}^2]) = 0.0$, $M/M_{\odot } = 2.0$and different values of $Z/Z_{\odot }$ (denoted as $Z/Z_{\rm sol}$ in the plot) and C/O.
Open with DEXTER

The temperature-dependent behaviour of (J-H) for different chemical compositions is shown in Fig. 9. The sequences of models in the plot represent various metallicities and C/O ratios assuming $\log({g}~[{\rm cm/s}^2]) = 0.0$ and $M/M_{\odot } = 2.0$. The latter two values have been chosen, since the corresponding COMARCS atmospheres exist for most of the possible combinations of the remaining parameters ( $T_{\rm eff}$, C/O, Z). It was already mentioned in the preceding discussion that the trend of (J-H) with temperature reverses at a certain point where the maximum of the index is reached. Towards cooler and warmer models the colours become bluer. In Fig. 9 one can see that this applies to all investigated chemical compositions. However, the maximum is shifted to higher temperatures, if the metallicity becomes lower. At $Z/Z_{\odot} = 0.33$it is situated around 3000 K and at $Z/Z_{\odot} = 0.1$around 3100 K.

There exists a clear trend that in all atmospheres cooler than about 3300 to 3400 K the (J-H) index becomes bluer towards larger C/O ratios, if the metallicity and the other stellar parameters are kept constant. The corresponding spread in the colour temperature relation for our grid reaches between 0.1 and 0.2 mag. The situation is quite different for models that are warmer than 3400 K. In those objects the value of C/O plays only a minor role. On the other hand, one can see in Fig. 9 that at higher temperatures the colours become redder, if the metallicity decreases. A multiplication of $Z/Z_{\odot }$by a factor of one third gives a positive shift of 0.04 to 0.05 mag in (J-H). At a constant C/O ratio, which introduces significant deviations below 3300 to 3400 K, this rule applies down to about 3000 K. Around 2700 to 2800 K the colour differences due to metallicity almost disappear. And for the cooler temperatures we find a reversion of the trend, because (J-H) slightly increases with growing $Z/Z_{\odot }$.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f10.eps} \end{figure} Figure 10:

Predicted (J-K) colours as a function of effective temperature calculated from COMARCS models with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 2.0$, C/O = 1.10 and different values of $\log({g}~[{\rm cm/s}^2])$.
Open with DEXTER
 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f11.eps} \end{figure} Figure 11:

Predicted (J-K) colours as a function of effective temperature calculated from COMARCS models with $\log({g}~[{\rm cm/s}^2]) = 0.0$, $M/M_{\odot } = 2.0$ and different values of $Z/Z_{\odot }$ (denoted as $Z/Z_{\rm sol}$ in the plot) and C/O.
Open with DEXTER

3.3.2 The ( 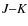$\textit {J}{-}\textit {K}$) colour

The behaviour of (J-K) as a function of the effective temperature is very interesting, since the corresponding relation has often been used to determine that stellar parameter from photometric observations. This may work quite well for the warmer objects, as one can see in Fig. 10 where we plot the colours of models with different values of $\log({g})$. Following the previous discussion on (J-H), we have taken COMARCS atmospheres with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 2.0$and C/O = 1.1 as an example. Above 2800 K the (J-K) index clearly decreases towards higher temperatures. The scatter in the almost linear relation, which is produced by the variation of the surface gravity in our grid, remains negligible. From Fig. 11, where we study the effect of different chemical compositions for $\log({g}~[{\rm cm/s}^2]) = 0.0$and $M/M_{\odot } = 2.0$, it is evident that down to 3000 K also changes of metallicity and C/O ratio do not create too large deviations. Nevertheless, similar to the case of (J-H), the trend with temperature reverses for the coolest models. As one can see in Figs. 10 and 11 the turnaround with the reddest (J-K) appears at 2800 K for $Z/Z_{\odot } = 1.0$and a value of C/O below 1.4. It shifts to 2900 or even further to 3000 K, if the metallicity decreases and the relative abundance of carbon becomes higher. The explanation for this reversion is similar to the one for the behaviour of (J-H) in the coolest atmospheres. The suppression of the flux in the K band due to molecular absorption of polyatomic species grows at lower temperatures much more than in the wavelength region where the J magnitude is determined. The K filter covers mainly features of CN and C2H2. However, the turnaround will usually also not become visible in populations of real stars, since the coolest objects show a severe reddening caused by circumstellar dust.

Looking at Fig. 10 it becomes obvious that significant shifts introduced by the variation of the surface gravity in our grid appear only below 2900 K. The corresponding spread in the colour temperature relation grows rapidly towards cooler models. At 2400 K the difference between atmospheres with $\log({g}~[{\rm cm/s}^2]) = -1.0$ and 0.0 reaches almost 0.2 mag. In general, the more extended objects are redder in (J-K). Figure 11 shows that below 3000 K the colour also depends on the chemical composition. It gets bluer if the metallicity decreases. For the coolest models a multiplication of $Z/Z_{\odot }$by a factor of one third reduces the index by approximately 0.05 to 0.06 mag. The C/O value also plays a role below 3000 K. As long as the ratio remains small, (J-K) decreases with higher relative carbon abundance. However, this trend saturates, and above C/O = 1.4 there are no noticeable differences. As already mentioned, we find that the shifts due to the chemical composition, which almost disappear between 3000 and 3200 K, never become large in the warmer models. In general, at the higher temperatures (J-K) turns slightly redder with an increasing C/O ratio, while the behaviour as a function of metallicity is not so regular and causes only minor deviations.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f12.eps} \end{figure} Figure 12:

Predicted (V-K) colours as a function of effective temperature calculated from COMARCS models with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 2.0$, C/O = 1.10 and different values of $\log({g}~[{\rm cm/s}^2])$.
Open with DEXTER

3.3.3 The ( 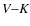$\protect\textit{V}{-}\textit{K}$) colour

As one can see in Figs. 12 and 13 the (V-K) index could be a quite good indicator of the effective temperature. The relative scatter due to variations of surface gravity and chemical abundances remains in most cases reasonably small (< $\rm0.2~mag \sim 100~K$). Furthermore, in contrast to (J-H) or (J-K), the overall relation that the colour becomes redder for cooler atmospheres is never reversed. It only saturates at the lowest temperatures where the application of hydrostatic dust-free models is not useful (see Sect. 4.1). Unfortunately, there are almost no simultaneous measurements of V and K magnitudes for individual carbon stars. In addition, this index will be severely affected by interstellar as well as circumstellar reddening.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f13.eps} \end{figure} Figure 13:

Predicted (V-K) colours as a function of effective temperature calculated from COMARCS models with $\log({g}~[{\rm cm/s}^2]) = 0.0$, $M/M_{\odot } = 2.0$and different values of $Z/Z_{\odot }$ (denoted as $Z/Z_{\rm sol}$ in the plot) and C/O.
Open with DEXTER

In general, atmospheres with a smaller surface gravity have redder (V-K) colours. In Fig. 12 we demonstrate this for the carbon stars from our grid with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 2.0$ and C/O = 1.10. One can see that significant shifts due to the different values of $\log({g})$ appear only below 2900 to 3000 K, and they increase towards the coolest temperatures where up to 0.5 mag may be reached. This applies also to the variations caused by changes of the chemical abundances. The behaviour of objects with $\log({g}~[{\rm cm/s}^2]) = 0.0$ and $M/M_{\odot } = 2.0$is shown in Fig. 13. The plot reveals that at lower temperatures, models with a higher C/O ratio and a decreased metallicity tend to produce bluer colours. Above 3000 K this trend reverses, but the corresponding relative differences do not become considerable.

4 Discussion

4.1 Comparison with observations

In the previous section we showed some examples representative of the results of our computations. Now, we compare them to observational data. We will restrict ourselves again to the Bessell photometric system (Bessell 1990; Bessell & Brett 1988). We start with the work of Bergeat et al. (2001), who established a calibration scheme for the effective temperature of galactic carbon stars by relating interferometric results to colours like (J-K), (H-K) or (V-K). The conversion of measured angular diameters into stellar parameters depends on estimates for the distance and functions describing the limb darkening of the investigated objects. Especially if one studies cooler AGB giants, both of these tasks may become quite problematic. The difficulties are mainly caused by the large extensions of the atmospheres, the diameters of which change considerably with wavelength due to molecular absorption and with time due to pulsation. These variations are often accompanied by complicated radial density structures and the formation of dust shells (e.g. Hofmann et al. 1998; Jacob & Scholz 2002; Aringer et al. 2008). Thus, the result will depend very much on the model applied to interpret the intensity profile of the observed star and the corresponding uncertainties. For such objects, even the theoretical choice of a diameter to define the effective temperature is rather arbitrary, since the range with an optical depth around one may become quite broad.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f14.eps} \end{figure} Figure 14:

The (J-K) colour as a function of the effective temperature is shown for COMARCS models with $Z/Z_{\odot } = 1.0$ and $M/M_{\odot } = 2.0$. Several typical sequences characterized by different values of $\log({g}~[{\rm cm/s}^2])$ and C/O are included. The theoretical results are compared to the data from Bergeat et al. (2001, Table 4) which have been derived from observations (stars).
Open with DEXTER

4.1.1 ( 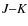$\textit {J}{-}\textit {K}$) versus effective temperature

In Fig. 14, where we show (J-K) as a function of the effective temperature, COMARCS models with solar metallicity are compared to the results of Bergeat et al. (2001). The sequences of atmospheres with different values of $\log({g})$ and C/O, which are included in the plot, were selected in order to represent approximately the spread introduced by the variation of these parameters (see Figs. 10 and 11). As one can see, the agreement between calculated and observed colours is quite good in the range from 3200 down to 2800 K. The only distinction is that the measured data show a much larger scatter than the synthetic ones. However, this may very well be due to uncertainties concerning the variability, the correction of the interstellar reddening or the determination of the linear diameters. Below 2800 K the colours predicted by the COMARCS models are systematically bluer than those taken from the observations. While the (J-K) value in the results of Bergeat et al. (2001) continues to increase towards the coolest stars, this trend reverses for our hydrostatic calculations. As a consequence, the difference between measured and synthetic data grows considerably at lower temperatures. Nevertheless, this behaviour is not completely unexpected. We have already mentioned that the cooler AGB giants are severely affected by pulsation, dust formation and mass loss, which cannot be described within the framework of hydrostatic models (e.g. Höfner et al. 2003). Due to circumstellar reddening and the development of very extended and complicated temperature density structures, these processes show a strong influence on the spectra and filter magnitudes of the stars (Gautschy-Loidl et al. 2004). The problem will be discussed in more detail in the second paper of this series where we present synthetic colours based on dynamical calculations taking the corresponding time dependent phenomena into account. It is mainly the opacity of amorphous carbon dust which changes the overall energy distribution of the objects. It causes the high (J-K) values appearing for the observed data in Fig. 14 and is not included in our COMARCS models[*] which seem to be appropriate down to about 2800 K. We want to emphasize again that below this point the conversion of measured angular diameters into effective temperatures also will be problematic.

In Fig. 14 one can see two of the observed stars situated at rather high temperatures above 3600 K (BL Ori, V4378 Sgr) which are far away from our COMARCS sequences. However, as Bergeat et al. (2001) already have noted they also do not fit into the relation defined by the other measured objects. It is possible that an error concerning the determination of the interferometric data or their interpretation occured. In reality the stars may be much cooler.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f15.eps} \end{figure} Figure 15:

The (H-K) colour as a function of the effective temperature is shown for COMARCS models with $Z/Z_{\odot } = 1.0$ and $M/M_{\odot } = 2.0$. Several typical sequences characterized by different values of $\log({g}~[{\rm cm/s}^2])$ and C/O are included. Results from calculations with a scaled C2 line list (dashed lines, open symbols) and with the unscaled original one (full lines, filled symbols) are compared to each other and to the data from Bergeat et al. (2001, Table 4) which have been derived from observations (stars).
Open with DEXTER

4.1.2 ( 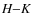$\textit {H}{-}\textit {K}$) versus effective temperature

In Fig. 15 we present a comparison of the observed colour temperature relation for carbon stars with COMARCS models, which is similar to the one in Fig. 14, but shows (H-K) instead of (J-K). The plot again includes sequences from our grid of hydrostatic atmospheres with solar metallicity and different values of $\log({g})$ and C/O (dashed lines, open symbols). It is obvious that the (H-K) indices produced by the calculations are systematically bluer than the measured ones. Apart from the deviations below 2800 K growing towards cooler temperatures, which already appeared for (J-K) and have been explained by the contribution of circumstellar dust and dynamical changes of the structures, there exists a shift of around 0.1 mag for all of the hotter objects. This problem is not restricted to the data of Bergeat et al. (2001), but occurs also in the two colour diagrams based on other observations (not shown here).

In order to find possible explanations for the differences between measured and predicted (H-K) values of the warmer stars, we investigated the influence of the scaling applied to the C2 absorption in our calculations. This has been proposed by Loidl et al. (2001) and is described in the section about model atmospheres and opacities (Sect. 2.1). We produced a few series of synthetic spectra and filter magnitudes using the original C2 list without any changes (full lines and filled symbols in Fig. 15). The relative effect of the scaling on (H-K) is much stronger than on the other Bessell colours discussed in our work. This can be explained by the fact that the corresponding variations reach a maximum in the H band and the comparatively small flux difference between H and K. From looking at Fig. 15 it becomes clear that the calculated (H-K) indices based on the original linelist are by 0.08 to 0.1 mag higher, if the temperature is kept constant. The consequence of the shift to redder colours is a much better agreement with the observations in the region above 2800 K, while below this limit we still see considerable deviations, growing towards cooler stars. Thus, the results for (H-K) with the unscaled C2opacity would confirm the ones derived from (J-K). This may be interpreted as an indication that it is preferable to use the original C2 data without any correction of the gf-values and to add approximately 0.1 mag to the (H-K) indices from our standard grid. However, since there is not much effect on the other colours, one should be careful drawing conclusions concerning the molecular absorption. Future work on the C2 opacities and spectral investigations can solve this problem.

 \begin{figure} \par\includegraphics[width=9cm,clip]{1170316b.eps}\vspace*{6mm} \par\includegraphics[width=9cm,clip]{1170316a.eps} \end{figure} Figure 16:

The (V-K) colour as a function of the effective temperature is shown for COMARCS models with $Z/Z_{\odot } = 1.0$ and $M/M_{\odot } = 2.0$. Several typical sequences characterized by different values of $\log({g}~[{\rm cm/s}^2])$ and C/O are included. The theoretical results are compared to the data from Bergeat et al. (2001) which have been derived from observations. In the upper panel we present the original (V-K) indices given by the authors (stars), while in the lower one we take the V variability of the objects into account. The ranges between the corresponding maxima and minima are shown as error bars. The V and K magnitudes used for the second plot were taken from various sources listed in the text. They do not include the values from Bergeat et al. (2001).
Open with DEXTER

4.1.3 ( 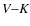$\protect\textit{V}{-}\textit{K}$) versus effective temperature

The last comparison of our solar metallicity COMARCS sequences with the results of Bergeat et al. (2001) is displayed in Fig. 16, where we show (V-K) as a function of the effective temperature. A plot based on the original photometric data as they were published by the authors can be seen in the upper panel. The obvious agreement between predicted and observed colours in all regions of the diagram is rather surprising, because from the preceding discussion one would expect deviations for the cooler stars, which are due to circumstellar reddening and dynamical changes of the atmospheric structures. The influence of dust on (V-K) should be much more pronounced than on the infrared indices like (H-K) or (J-K). However, Bergeat et al. (2001) have neglected the pulsation of the objects producing the strongest variability at shorter wavelengths, as in the V range. Since the measurements of the interferometric radii as well as of the V and K magnitudes have not all been done simultaneously, this may create some bias in the diagram.

In order to consider at least the V amplitude of the objects studied by Bergeat et al. (2001), we have determined the (V-K) values corresponding to the maxima and minima of the visual flux. The K magnitudes were assumed to remain constant. The colour ranges obtained with this approach are displayed in the lower panel of Fig. 16 (bars). In most cases we could take the necessary photometric data from the General Catalogue of Variable Stars (GCVS4, Samus et al. 2006, 2007). If the GCVS did not include the needed information, we estimated the interval covered by the V magnitudes using the AAVSO Light Curve Generator (http://www.aavso.org/data/lcg/). For a few of the objects we were not able to find any published measurements revealing the temporal behaviour of the fluxes in the V band (AB Gem, V4378 Sgr, DR Ser). Since all of them are Lb (irregular) variables, which normally show rather moderate photometric changes, we assumed the brightness listed in the General Catalog of Cool Galactic Carbon Stars (GCCCS, Stephenson 1989) as the mean value and an amplitude of 0.5 mag. The K magnitudes were taken from the 5th edition (Gezari et al. 2000) of the Catalog of Infrared Observations (Gezari et al. 1993), the Two Micron All Sky Survey (2MASS, Skrutskie et al. 2006), Whitelock et al. (2006) and Menzies et al. (2006). For the correction of the interstellar reddening we used the coefficients given by Bergeat et al. (2001).

If one compares the upper and the lower panel of Fig. 16, it becomes obvious that the original (V-K) data from Bergeat et al. (2001) are in most cases situated within the range of variability, but not in its centre. They are systematically shifted to bluer colours. The same is true for the values predicted from our COMARCS models, which cover the same regions of the diagram, as was mentioned before. All of this may be explained by the fact that the authors have used V measurements biased towards higher fluxes corresponding to phases of the pulsation where the circumstellar extinction caused by dust remains weak. However, also in the bottom panel of Fig. 16, a clear increase in the differences between synthetic and observed colours at lower temperatures is not visible. Such a behaviour contradicts the trend found for (J-K) and (H-K) as well as the expectations of stronger dynamical effects and higher mass loss rates in cooler objects. Nevertheless, since there are severe uncertainties concerning this diagram, one should be rather careful with any definite conclusions. First, we have neglected the variation of the K magnitudes and the angular diameters, which is most likely less pronounced than the change of the visual flux, but still quite considerable. In principle it would be desirable to use simultaneous measurements or at least temporal mean values of all involved quantities. Unfortunately, such data are not available at the moment. Secondly, the applied corrections of the interstellar reddening (Knapik & Bergeat 1997) may be problematic in the case of stars with intense pulsations, because they are based on assumptions concerning a characteristic energy distribution for the objects.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f17.eps} \end{figure} Figure 17:

The bolometric corrections for the K magnitude ( $\rm BC_{\it K}$) are shown as a function of the (J-K) colour. Several representative sequences of COMARCS atmospheres characterized by different values of $\log({g}~[{\rm cm/s}^2])$, $Z/Z_{\odot }$ (denoted as $Z/Z_{\rm sol}$ in the plot) and C/O are displayed. The models, which cover the effective temperature ranges given in the legend, have two solar masses. The minima of $\rm BC_{\it K}$ correspond always to the warmest object in each series. In addition, we have included the observed mean relations for galactic carbon stars from Bergeat et al. (2002, dashed line), Costa & Frogel (1996, full line) and Whitelock et al. (2006, dotdashed line).
Open with DEXTER

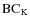
4.1.4 Bolometric correction $\rm BC_{K}$

In Fig. 17 we study the behaviour of the bolometric corrections for the K magnitude ( $\rm BC_{\it K}$) as a function of the (J-K) colour. We compare several effective temperature sequences of COMARCS atmospheres with observed mean relations for galactic carbon stars taken from the work of Bergeat et al. (2002), Costa & Frogel (1996) and Whitelock et al. (2006). The included model series correspond to different values of metallicity, C/O ratio and surface gravity. Since Costa & Frogel (1996) claim that their results may be used for LMC objects, we have also considered a set of calculations assuming $Z/Z_{\odot} = 0.33$.

From the hottest COMARCS atmospheres producing the smallest (J-K) indices and bolometric corrections down to about 2800 K, the agreement between predictions and observations is very good. In this range we see a clear relation that with decreasing effective temperature (J-K) becomes redder and $\rm BC_{\it K}$ larger. Nevertheless, at the cooler hydrostatic models the trend reverses for both quantities and there are deviations between the calculated positions in the diagram and the measured mean sequences, which grow progressively. As was discussed in the beginning of this section, the observed carbon stars also extend to much higher (J-K) values than the COMARCS atmospheres. The results of Whitelock et al. (2006), which are obviously focused on objects with considerable mass loss rates, have almost no overlap with the computed colours, since they only cover the interval down to (J-K) $\sim$ 1.5. In agreement with the work of Bergeat et al. (2002), they reveal that for the very red sources the bolometric corrections decrease again. In the relation published by Costa & Frogel (1996) such a behaviour does not appear. However, their results were mainly determined for bluer carbon stars and are only extrapolated towards larger (J-K) indices.

The most important conclusion from our plot of the bolometric corrections versus (J-K) colour in Fig. 17 is the confirmation of the scenario described in the beginning of this section. Down to about 2800 K the COMARCS models reproduce the observations quite well, while at cooler temperatures the spectral flux distributions of the real stars are dominated by circumstellar dust shells and dynamical changes of the atmospheric structure.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11703f18.eps} \end{figure} Figure 18:

Two colour diagram (I-K) versus (J-K) for several representative sequences of COMARCS atmospheres characterized by different values of $\log({g}~[{\rm cm/s}^2])$, $Z/Z_{\odot }$ (denoted as $Z/Z_{\rm sol}$ in the plot) and C/O. All models have two solar masses. The series start at $T_{\rm eff} = 2600~$K and range up to 4000 K for $\log({g}~[{\rm cm/s}^2]) = 0.0$, up to 3200 K for $\log({g}~[{\rm cm/s}^2]) = -0.4$ and up to 2900 K for $\log({g}~[{\rm cm/s}^2]) = -0.8$. The warmest objects correspond to the bluest colours. The data are compared to observations of LMC carbon stars published by Costa & Frogel (1996).
Open with DEXTER

4.1.5 Near infrared two colour diagram

Another confirmation of this scenario can be found in Fig. 18, where we show a two colour diagram with (I-K) versus (J-K). Several representative temperature sequences of subsolar metallicity COMARCS atmospheres are compared to the observations of LMC carbon stars published by Costa & Frogel (1996). Again, the included model series correspond to different values of $\log({g})$, $Z/Z_{\odot }$ and C/O. It is obvious that for the warmer objects having bluer colours the agreement between predicted and measured positions in the diagram can be regarded as good. On the other hand, as in Fig. 17, the observed data extend to much larger (I-K) or (J-K) indices than the calculations. They also do not show any signs of the reversion of the trend with temperature appearing for the COMARCS atmospheres below 2800 K. A similar behaviour confirming the discussed scenario can also be found in most of the other two colour diagrams combining different Bessell filters (not shown here).

Samples of distant carbon stars are often selected due to the red colours of these objects. A good example is the criterion of (J - K) > 1.4 (e.g. Cioni & Habing 2003). However, from the predicted and observed values in Fig. 18 it becomes clear that such a photometric choice will neglect many of the bluer sources with low mass loss rates.

4.2 Application of the data to stellar evolution

4.2.1 Defining an interpolation scheme

The models presented in this paper define a 5-dimensional grid in metallicity, effective temperature, surface gravity, C/O ratio and mass. Nevertheless, the latter has a quite small influence on the synthetic colours and bolometric corrections, as it is shown in Fig. 8. In addition, the atmospheres for many combinations of the other parameters have only been calculated with 2.0 $M_{\odot }$. A more extensive grid involving 1.0 $M_{\odot }$ computations exists only for solar metallicity. As a consequence, the effect of stellar mass may be treated as a correction to be applied a posteriori to the results, and we remain with a 4-dimensional interpolation to determine the desired photometric quantities.

For an object with a given value of Z, $T_{\rm eff}$, $\log({g})$ and C/O we first identify the metallicity interval (Z1,Z2) of the grid where it is located and compute the weighting factors for a linear interpolation in log(Z). Subsequently, we look for the proper temperature intervals $(T_{{\rm eff},1},T_{{\rm eff},2})$ at Z1 and Z2. These are not necessarily equal, since due to problems with the convergence of the more extended models and the different expected properties of carbon stars (see Sect. 2.2), the spacing and range of coverage with respect to a certain parameter may change as a function of the other stellar quantities. For example, at solar metallicity our calculations go down to 2400 K, while for $Z/Z_{\odot} = 0.33$and $Z/Z_{\odot} = 0.1$ the lower limit was increased to 2600 K following the predictions from synthetic AGB evolution. From each $T_{{\rm eff},1}$ and $T_{{\rm eff},2}$ we are then able to determine the weighting factors for a linear interpolation in $\log(T_{\rm eff})$. As a next step we use the same method for $\log({g})$ where the interval ( $\log({g})_1$, $\log({g})_2$) has to be defined for all combinations of Z1 and Z2 with $T_{{\rm eff},1}$ and $T_{{\rm eff},2}$. Finally, we include also the C/O ratio into this scheme. In the ideal case, when the investigated object is situated completely inside all limits, we remain with 16 final weighting factors computed from the product of the four individual contributions of the mentioned parameters which may then be applied to the colours or bolometric corrections of the corresponding grid points. Extrapolations are in general avoided by selecting the available maximum or minimum values. They were only allowed for the effective temperature with an amount of up to 100 K.

 \begin{figure} \par\includegraphics[width=8.5cm,clip]{11703f19.ps} \end{figure} Figure 19:

Selected isochrones from Marigo et al. (2008), focusing on the part of the 2MASS $M_{K_{\rm s}}$ versus $(J{-}K_{\rm s})$diagram that corresponds to the upper RGB (black lines) and TP-AGB phases. To avoid confusion in the figure the TP-AGB part covers only the quiescent stages, neglecting the thermal pulse cycle variations, and we do not show the final points in which stars cross back to the blue during their evolution to the post-AGB. The TP-AGB is marked either as oxygen rich (blue lines in the electronic version) or as carbon rich (red lines). Full lines are results obtained using the present database of transformations for carbon stars, whereas dashed lines are the ones from Marigo et al. (2008) based on spectra from Loidl et al. (2001). The effect of circumstellar dust is not considered. The ages ( $\rm log({\it t}~[yr])$) and metallicities of the isochrones are indicated in the plot.
Open with DEXTER

4.2.2 Theoretical isochrones

Interpolated bolometric corrections computed in this way can then be applied to theoretical TP-AGB models. Figure 19 illustrates the difference between the results based on our data to convert the isochrones of Marigo et al. (2008) to the 2MASS M $_{K_{\rm s}}$ versus $(J{-}K_{\rm s})$ diagram and the original ones obtained with the spectra taken from Loidl et al. (2001). The latter were only available for a few selected stellar parameters (mainly temperatures) and solar metallicity. We have chosen curves with $\rm log({\it t}~[yr]) = 8.5$ for $Z = Z_{\odot} = 0.019$, $\rm log({\it t}~[yr]) = 9.0$for $Z = 0.42~Z_{\odot} = 0.008$ and $\rm log({\it t}~[yr]) = 9.5$ for $Z = 0.053~Z_{\odot} = 0.001$, because the typical age range for the appearance of the carbon star branch changes with the chemical abundances. The effect of circumstellar dust has been neglected in the plot. As it was already mentioned it would shift the objects with mass loss to much redder colours.

The figure shows that at all metallicities the AGB C-stars are predicted to be distributed along a sort of tail redward of the location of the oxygen rich giants. This behaviour is largely due to lower effective temperatures caused by the opacity of carbonic molecules as has been described in Marigo (2002), Marigo et al. (2003) and Marigo & Girardi (2007). Applying the atmospheric models presented here to the determination of photometric properties results in some changes in the discussed colour magnitude diagram. Compared to the calculations based on the spectra of Loidl et al. (2001) the objects become bluer and in most cases brighter. As a consequence, especially at the two higher metallicities, the maximum $(J{-}K_{\rm s})$ value decreases by up to 0.15 mag. A part of the flux differences can be attributed to a variation of the photometric zero points caused by the more limited wavelength coverage of the data from Loidl et al. (2001). The bulk of the change is due to revised opacities and the much larger parameter range included in the current grid. As an example, Loidl et al. (2001) did not consider any atomic lines and only solar metallicity spectra were available for the conversion of the isochrones.

Observed carbon star red tails in systems like the Magellanic Clouds present the majority of giants extending more or less uniformly in the interval $1.2 \la (J{-}K_{\rm s}) \la 2.0$. The results shown in Fig. 19 do not reproduce the redder part of this distribution. As it has been discussed, this is mainly due to the neglect of the circumstellar dusty envelopes. Also, the effect of the pulsation on the atmospheric structure and colour excursions caused by thermal pulse cycles may play a role. Evaluating the impact of such phenomena remains beyond the scope of the present paper. Work is in progress to create a complete simulation of the Magellanic Cloud TP-AGB stars considering all the processes affecting their photometric properties.

The present database of bolometric corrections has already been incorporated into the interactive web interface http://stev.oapd.inaf.it/cmd which can be used to generate interpolated Marigo et al. (2008) isochrones and their derivatives in many photometric systems. The tables containing the BC values as well as the synthetic spectra are provided in the repository http://stev.oapd.inaf.it/synphot/Cstars. The reddening caused by circumstellar dust may currently be simulated in connection with our data by applying the approximative approaches from Bressan et al. (1998) and Groenewegen (2006). This is the same procedure as used for the results of Marigo et al. (2008).

5 Conclusions

We have produced a grid of hydrostatic COMARCS atmospheres covering effective temperatures between 2400 and 4000 K, surface gravities from $\log({g}~[{\rm cm/s}^2]) = 0.0$ to -1.0, metallicities ranging from the solar value down to one tenth of it and C/O ratios in the interval between 1.05 and 5.0. Based on these models we calculated synthetic low resolution spectra and bolometric corrections for a considerable number of standard photometric systems, which are publicly available on the web. As an example we have shown some of the Bessell colours as a function of the stellar parameters. It turned out that the mass, which represents in principle the sphericity of the atmospheres, usually has only a quite small effect on the overall energy distribution. On the other hand, as one would expect, the effective temperature is the most important quantity. Especially for the warmer carbon stars its determination based on photometric measurements may reveal rather reliable results, if one chooses the right colour indices and has at least a rough estimate of the other parameters. In addition, the effect of the interstellar reddening has to be taken into account, which represents the main source of uncertainties, at least for individual stars.

However, we have also demonstrated that our hydrostatic dust-free atmospheres fail to reproduce the redder and cooler carbon stars. The photometric properties based on the models from our grid were compared to several observed data sets involving effective temperatures obtained from interferometry, bolometric corrections and two colour diagrams. Most of these investigations confirm the same scenario. Down to about 2800 K the agreement between predicted and measured energy distributions is quite good, while below this limit the COMARCS atmospheres are much too blue. In some cases the photometric indices of the coolest models even decrease again due to the influence of molecular features. Such a behaviour definitely does not appear for the observed carbon stars, which always extend to considerably redder colours than any of the calculations. The main explanation for these differences is the neglect of the dusty circumstellar envelopes in the presented COMARCS atmospheres. But dynamical changes of the radial pressure temperature structure connected to pulsation and mass loss also play an important role.

Many time-dependent phenomena appearing in AGB stars, like the intense pulsation creating shock waves or dust formation driving heavy stellar winds, cannot be described within the framework of hydrostatic atmospheres in chemical equilibrium, as it has been demonstrated by a large number of models and observations (e.g. Aringer et al. 1999; Alvarez & Plez 1998; Loidl et al. 1999; Höfner et al. 2003). Thus, a forthcoming paper of this series will focus on the effect of dynamics and mass loss on the photometric properties of carbon rich giants. There we demonstrate that these processes offer a natural explanation for the very red colours seen in a large number of objects. The calculations will be based on models including pulsation and time-dependent dust formation as have been published by Höfner et al. (2003) or Mattsson et al. (2008).

For the warmer COMARCS models, which are in agreement with the observations, we found that the photometric changes as a function of the stellar parameters show in most cases clear and predictable trends. An exception is the dependence on mass, which corresponds to the effect of sphericity. However, as we have demonstrated, the latter plays only a minor role for the different colours. Thus, it is possible to interpolate between the photometric fluxes based on our grid, which allows us to connect the results to stellar evolution calculations. The effect of applying our bolometric corrections to the isochrones from Marigo et al. (2008) has been shown in this paper as a first test. For the moment we have neglected the influence of dynamical processes and the reddening caused by the dusty envelopes of the stars. The latter will be included in a more systematic study involving stellar evolution and population synthesis computations that will be presented in a forthcoming publication. It can already be taken into account in combination with our data by using approximative descriptions like the ones from Bressan et al. (1998) and Groenewegen (2006).

Acknowledgements
We acknowledge financial support from the University of Padova (Progetto di Ricerca di Ateneo CPDA052212). L.G. acknowledges support from PRIN INAF07 1.06.10.03. The work presented here was supported by the Austrian Science Fund (FWF) projects P19503-N16 and P18939-N16. B.A. acknowledges funding by the contract ASI-INAF I/016/07/0. M.T.L. has been supported by the Austrian Academy of Sciences (DOC programme) and acknowledges funding by the Austrian Sience Fund (FWF) project P-18171. We thank U. G. Jørgensen and R. Gautschy-Loidl for their support concerning the opacity data of C3 and C2H2. We acknowledge with thanks the variable star observations from the AAVSO International Database contributed by observers worldwide and used in this research. We thank A. Bressan and M. Groenewegen for their early interest in this work and for many useful suggestions.

References

Footnotes

... models[*]
Table of the photometry and spectra are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/503/913
... effects[*]
In extended giants absorption lines or bands will become weaker in a spherical atmosphere, since they are filled with emission components originating from the optically thin outer parts of the stellar disk (e.g. Aringer 2005).
... models[*]
An equilibrium description of the dust in a hydrostatic atmosphere results in much too high condensation degrees and opacities.

All Tables

Table 1:   Lower limits of $\log({g})$ in the grid of atmospheric models for carbon stars. The upper limit is always $\log({g}~[{\rm cm/s}^2]) = 0.0$.

All Figures

  \begin{figure} \par\includegraphics[width=12cm,clip]{11703f01.eps}\end{figure} Figure 1:

Atmospheric structures of a sequence of COMARCS models with $\log({g}~[{\rm cm/s}^2]) = 0.0$, C/O = 1.4, $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 1.0$ and different values of $T_{\rm eff}$. The temperature is shown as a function of the gas pressure.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{11703f02.eps}\end{figure} Figure 2:

Atmospheric structures of a sequence of COMARCS models with C/O = 1.1, $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 1.0$and different values of $\log({g}~[{\rm cm/s}^2])$at $T_{\rm eff} = 2800~$K. In addition, the results for $\log({g}~[{\rm cm/s}^2]) = 0.0$at $T_{\rm eff} = 3200~$K have been included. The temperature is shown as a function of the gas pressure.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f03.eps}\end{figure} Figure 3:

Three spectra based on COMARCS models with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 1.0$and different values of $T_{\rm eff}$, C/O and $\log({g}~[{\rm cm/s}^2])$. The resolution is R = 200.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=11.8cm,clip]{11703f04.eps} \end{figure} Figure 4:

Continuum normalized spectra for the most important molecular species based on a COMARCS model with $T_{\rm eff} = 2600~$K, $\log({g}~[{\rm cm/s}^2]) = -0.2$, $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 1.0$ and C/O = 1.10.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=11.8cm,clip]{11703f05.eps} \end{figure} Figure 5:

Continuum normalized spectra based on COMARCS models with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 2.0$, C/O = 1.10 and different values of $\log({g}~[{\rm cm/s}^2])$. Two effective temperatures are compared: 2600 K and 3100 K.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{11703f06.eps} \end{figure} Figure 6:

Continuum normalized spectra based on COMARCS models with $Z/Z_{\odot } = 1.0$, C/O = 1.40 and different values of $\log({g}~[{\rm cm/s}^2])$ and stellar mass (in $M_{\odot }$). Two effective temperatures are compared: 2600 K and 3100 K.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f07.eps} \end{figure} Figure 7:

Predicted (J-H) colours as a function of effective temperature calculated from COMARCS models with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 2.0$, C/O = 1.10 and different values of $\log({g}~[{\rm cm/s}^2])$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f08.eps} \end{figure} Figure 8:

Predicted differences in the (J-H) colours between objects with 1.0 and 2.0 $M_{\odot }$ as a function of effective temperature calculated from COMARCS models with $Z/Z_{\odot } = 1.0$, C/O = 1.10 and various values of $\rm log({g}~[{\rm cm/s}^2])$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f09.eps} \end{figure} Figure 9:

Predicted (J-H) colours as a function of effective temperature calculated from COMARCS models with $\log({g}~[{\rm cm/s}^2]) = 0.0$, $M/M_{\odot } = 2.0$and different values of $Z/Z_{\odot }$ (denoted as $Z/Z_{\rm sol}$ in the plot) and C/O.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f10.eps} \end{figure} Figure 10:

Predicted (J-K) colours as a function of effective temperature calculated from COMARCS models with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 2.0$, C/O = 1.10 and different values of $\log({g}~[{\rm cm/s}^2])$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f11.eps} \end{figure} Figure 11:

Predicted (J-K) colours as a function of effective temperature calculated from COMARCS models with $\log({g}~[{\rm cm/s}^2]) = 0.0$, $M/M_{\odot } = 2.0$ and different values of $Z/Z_{\odot }$ (denoted as $Z/Z_{\rm sol}$ in the plot) and C/O.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f12.eps} \end{figure} Figure 12:

Predicted (V-K) colours as a function of effective temperature calculated from COMARCS models with $Z/Z_{\odot } = 1.0$, $M/M_{\odot } = 2.0$, C/O = 1.10 and different values of $\log({g}~[{\rm cm/s}^2])$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f13.eps} \end{figure} Figure 13:

Predicted (V-K) colours as a function of effective temperature calculated from COMARCS models with $\log({g}~[{\rm cm/s}^2]) = 0.0$, $M/M_{\odot } = 2.0$and different values of $Z/Z_{\odot }$ (denoted as $Z/Z_{\rm sol}$ in the plot) and C/O.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f14.eps} \end{figure} Figure 14:

The (J-K) colour as a function of the effective temperature is shown for COMARCS models with $Z/Z_{\odot } = 1.0$ and $M/M_{\odot } = 2.0$. Several typical sequences characterized by different values of $\log({g}~[{\rm cm/s}^2])$ and C/O are included. The theoretical results are compared to the data from Bergeat et al. (2001, Table 4) which have been derived from observations (stars).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f15.eps} \end{figure} Figure 15:

The (H-K) colour as a function of the effective temperature is shown for COMARCS models with $Z/Z_{\odot } = 1.0$ and $M/M_{\odot } = 2.0$. Several typical sequences characterized by different values of $\log({g}~[{\rm cm/s}^2])$ and C/O are included. Results from calculations with a scaled C2 line list (dashed lines, open symbols) and with the unscaled original one (full lines, filled symbols) are compared to each other and to the data from Bergeat et al. (2001, Table 4) which have been derived from observations (stars).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{1170316b.eps}\vspace*{6mm} \par\includegraphics[width=9cm,clip]{1170316a.eps} \end{figure} Figure 16:

The (V-K) colour as a function of the effective temperature is shown for COMARCS models with $Z/Z_{\odot } = 1.0$ and $M/M_{\odot } = 2.0$. Several typical sequences characterized by different values of $\log({g}~[{\rm cm/s}^2])$ and C/O are included. The theoretical results are compared to the data from Bergeat et al. (2001) which have been derived from observations. In the upper panel we present the original (V-K) indices given by the authors (stars), while in the lower one we take the V variability of the objects into account. The ranges between the corresponding maxima and minima are shown as error bars. The V and K magnitudes used for the second plot were taken from various sources listed in the text. They do not include the values from Bergeat et al. (2001).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f17.eps} \end{figure} Figure 17:

The bolometric corrections for the K magnitude ( $\rm BC_{\it K}$) are shown as a function of the (J-K) colour. Several representative sequences of COMARCS atmospheres characterized by different values of $\log({g}~[{\rm cm/s}^2])$, $Z/Z_{\odot }$ (denoted as $Z/Z_{\rm sol}$ in the plot) and C/O are displayed. The models, which cover the effective temperature ranges given in the legend, have two solar masses. The minima of $\rm BC_{\it K}$ correspond always to the warmest object in each series. In addition, we have included the observed mean relations for galactic carbon stars from Bergeat et al. (2002, dashed line), Costa & Frogel (1996, full line) and Whitelock et al. (2006, dotdashed line).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11703f18.eps} \end{figure} Figure 18:

Two colour diagram (I-K) versus (J-K) for several representative sequences of COMARCS atmospheres characterized by different values of $\log({g}~[{\rm cm/s}^2])$, $Z/Z_{\odot }$ (denoted as $Z/Z_{\rm sol}$ in the plot) and C/O. All models have two solar masses. The series start at $T_{\rm eff} = 2600~$K and range up to 4000 K for $\log({g}~[{\rm cm/s}^2]) = 0.0$, up to 3200 K for $\log({g}~[{\rm cm/s}^2]) = -0.4$ and up to 2900 K for $\log({g}~[{\rm cm/s}^2]) = -0.8$. The warmest objects correspond to the bluest colours. The data are compared to observations of LMC carbon stars published by Costa & Frogel (1996).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{11703f19.ps} \end{figure} Figure 19:

Selected isochrones from Marigo et al. (2008), focusing on the part of the 2MASS $M_{K_{\rm s}}$ versus $(J{-}K_{\rm s})$diagram that corresponds to the upper RGB (black lines) and TP-AGB phases. To avoid confusion in the figure the TP-AGB part covers only the quiescent stages, neglecting the thermal pulse cycle variations, and we do not show the final points in which stars cross back to the blue during their evolution to the post-AGB. The TP-AGB is marked either as oxygen rich (blue lines in the electronic version) or as carbon rich (red lines). Full lines are results obtained using the present database of transformations for carbon stars, whereas dashed lines are the ones from Marigo et al. (2008) based on spectra from Loidl et al. (2001). The effect of circumstellar dust is not considered. The ages ( $\rm log({\it t}~[yr])$) and metallicities of the isochrones are indicated in the plot.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.