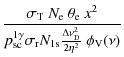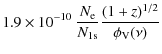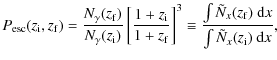| Issue |
A&A
Volume 503, Number 2, August IV 2009
|
|
|---|---|---|
| Page(s) | 345 - 355 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200912335 | |
| Published online | 02 July 2009 | |
Cosmological hydrogen recombination: influence of resonance and electron scattering
J. Chluba1,2 - R. A. Sunyaev1,3
1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching bei München, Germany
2 -
Canadian Institute for Theoretical Astrophysics, 60 St. George Street, Toronto, ON M5S 3H8, Canada
3 -
Space Research Institute, Russian Academy of Sciences, Profsoyuznaya 84/32, 117997 Moscow, Russia
Received 15 April 2009 / Accepted 23 April 2009
Abstract
In this paper we consider the effects of resonance and electron scattering on the escape of Lyman ![]() photons during cosmological hydrogen recombination. We pay particular attention to the influence of atomic recoil, Doppler boosting, and Doppler broadening using a Fokker-Planck approximation of the redistribution function describing the scattering of photons on the Lyman
photons during cosmological hydrogen recombination. We pay particular attention to the influence of atomic recoil, Doppler boosting, and Doppler broadening using a Fokker-Planck approximation of the redistribution function describing the scattering of photons on the Lyman ![]() resonance of moving hydrogen atoms. We extend the computations of our recent paper on the influence of the 3d/3s-1s two-photon channels on the dynamics of hydrogen recombination, simultaneously including the full time dependence of the problem, the thermodynamic corrections factor, leading to a frequency-dependent asymmetry between the emission and absorption profile, and the quantum-mechanical corrections related to the two-photon nature of the 3d/3s-1s emission and absorption process on the exact shape of the Lyman
resonance of moving hydrogen atoms. We extend the computations of our recent paper on the influence of the 3d/3s-1s two-photon channels on the dynamics of hydrogen recombination, simultaneously including the full time dependence of the problem, the thermodynamic corrections factor, leading to a frequency-dependent asymmetry between the emission and absorption profile, and the quantum-mechanical corrections related to the two-photon nature of the 3d/3s-1s emission and absorption process on the exact shape of the Lyman ![]() emission profile. We show here that, because of the redistribution of photons over frequency hydrogen recombination is sped up by
emission profile. We show here that, because of the redistribution of photons over frequency hydrogen recombination is sped up by
![]() at
at ![]() .
For the CMB temperature and polarization power spectra, this results in
.
For the CMB temperature and polarization power spectra, this results in
![]() at
at
![]() ,
which is in turn important for analyzing future CMB data in the context of the P LANCK Surveyor, S PT, and A CT. The main contribution to this correction comes from the atomic recoil effect (
,
which is in turn important for analyzing future CMB data in the context of the P LANCK Surveyor, S PT, and A CT. The main contribution to this correction comes from the atomic recoil effect (
![]() at
at ![]() ), while Doppler boosting and Doppler broadening partially cancel this correction, again slowing hydrogen recombination down by
), while Doppler boosting and Doppler broadening partially cancel this correction, again slowing hydrogen recombination down by
![]() at
at ![]() .
The influence of electron scattering close to the maximum of the Thomson visibility function at
.
The influence of electron scattering close to the maximum of the Thomson visibility function at
![]() can be neglected. We also give the cumulative results, in addition including the time-dependent correction, the thermodynamic factor, and the correct shape of the emission profile. This amounts to
can be neglected. We also give the cumulative results, in addition including the time-dependent correction, the thermodynamic factor, and the correct shape of the emission profile. This amounts to
![]() at
at
![]() and
and
![]() at
at
![]() .
.
Key words: cosmic microwave background - cosmological parameters - radiative transfer - cosmology: theory - scattering
1 Introduction
Motivated by the great experimental prospects with the P LANCK surveyor, S PT, and A CT, several independent groups (e.g. Dubrovich & Grachev 2005; Wong & Scott 2007; Chluba & Sunyaev 2006; Kholupenko & Ivanchik 2006; Switzer & Hirata 2008; Rubiño-Martín et al. 2006) have investigated details in the physics of cosmological recombination and their impact on the theoretical predictions for the cosmic microwave background (CMB) temperature and polarization power spectra. The declared goal for our theoretical understanding of the ionization history is the
![]() accuracy level (e.g. see Seljak et al. 2003; Hu et al. 1995) close to the maximum of the Thomson visibility function (Sunyaev & Zeldovich 1970) at
accuracy level (e.g. see Seljak et al. 2003; Hu et al. 1995) close to the maximum of the Thomson visibility function (Sunyaev & Zeldovich 1970) at
![]() (e.g. see Sunyaev & Chluba 2008; Fendt et al. 2009, for a more detailed overview of the different previously neglected physical processes that are important at this level of accuracy).
(e.g. see Sunyaev & Chluba 2008; Fendt et al. 2009, for a more detailed overview of the different previously neglected physical processes that are important at this level of accuracy).
This paper is a continuation of our recent work on cosmological recombination, in which we studied the effects of 3d-1s and 3s-1s two-photon processes on the dynamics of hydrogen recombination (Chluba & Sunyaev 2009a). Here we now wish to give the results for the changes in the Lyman ![]() escape probability and free electron fraction, while accounting for the effects of partial frequency redistribution related to the resonance scattering of moving neutral atoms and electron scattering during this epoch. In our previous work we neglected this aspect of the problem, although in the standard textbook formulation based on a Fokker-Planck expansion of the frequency redistribution function (Rybicki 2006), we obtained these results already some time ago. Here we explain the main results of these computations that we also partly used elsewhere (Chluba & Sunyaev 2008; Rubiño-Martín et al. 2008), and also refine our computations including the 3d-1s and 3s-1s two-photon corrections.
escape probability and free electron fraction, while accounting for the effects of partial frequency redistribution related to the resonance scattering of moving neutral atoms and electron scattering during this epoch. In our previous work we neglected this aspect of the problem, although in the standard textbook formulation based on a Fokker-Planck expansion of the frequency redistribution function (Rybicki 2006), we obtained these results already some time ago. Here we explain the main results of these computations that we also partly used elsewhere (Chluba & Sunyaev 2008; Rubiño-Martín et al. 2008), and also refine our computations including the 3d-1s and 3s-1s two-photon corrections.
It is well known (e.g. see Rybicki & dell'Antonio 1994) that, for the conditions in our Universe (practically no collisions), the frequency redistribution function for photons scattering off moving atoms is given by the so-called type-II redistribution as defined in Hummer (1962). The main physical processes accounted for in the Fokker-Planck expansion of this frequency redistribution function stem from (i) atomic recoil; (ii) Doppler boosting; and (iii) Doppler broadening. All three physical processes are also well-known in connection with the Kompaneets equation, which describes the repeated scattering of photons by free electrons.
Atomic recoil leads to a systematic drift of photons towards lower frequencies after each resonance scattering. This allows some additional photons to escape from the Lyman ![]() resonance, thereby speeding hydrogen recombination up, as already demonstrated by Grachev & Dubrovich (2008). We found very similar results for this process some time ago (e.g. see footnote 10 in Chluba & Sunyaev 2009b), which here we now present in detail and also refine simultaneously including additional corrections.
resonance, thereby speeding hydrogen recombination up, as already demonstrated by Grachev & Dubrovich (2008). We found very similar results for this process some time ago (e.g. see footnote 10 in Chluba & Sunyaev 2009b), which here we now present in detail and also refine simultaneously including additional corrections.
However, the effects of (ii) and (iii) were not taken into account in the analysis of Grachev & Dubrovich (2008). Like atomic recoil, Doppler boosting leads to a systematic motion of photons, but this time towards higher frequencies. Therefore it is expected to slow recombination down.
In contrast to this, Doppler broadening can lead to both an increase or a decrease in the escape probability depending on where the photon initially is emitted. As we explain here, if the photons are initially emitted in the vicinity of the Doppler core, line diffusion helps to bring some of them towards the red wing, before they actually die (mainly due to two-photon absorption to the third shell). Similarly, for photons emitted on the blue side of the resonance, line broadening allows some finite number of them to transverse the Doppler core. In the no-line-scattering approximation![]() , this would not be possible, so that the escape fraction is increased in both cases.
In contrast to this, for photons emitted on the red side of the resonance, the effect of Doppler broadening decreases the escape fraction, since even up to
, this would not be possible, so that the escape fraction is increased in both cases.
In contrast to this, for photons emitted on the red side of the resonance, the effect of Doppler broadening decreases the escape fraction, since even up to ![]() Doppler width below the line center, a significant fraction of the photons still returns close to the Doppler core, where they die efficiently. As we show here, the combination of Doppler boosting and Doppler broadening in total leads to an additional decrease in the escape probability as compared to the no-line-scattering approximation.
Doppler width below the line center, a significant fraction of the photons still returns close to the Doppler core, where they die efficiently. As we show here, the combination of Doppler boosting and Doppler broadening in total leads to an additional decrease in the escape probability as compared to the no-line-scattering approximation.
Very similar arguments apply for the expected correction due to electron scattering. However, there are some important differences: (i) electron scattering is expected to become less significant at lower redshifts, since the free electron fraction decreases with time; (ii) in contrast to resonance scattering for Lyman ![]() photons, the electron scattering cross section is achromatic; and (iii) due to the lower mass of the electron, the recoil effect is
photons, the electron scattering cross section is achromatic; and (iii) due to the lower mass of the electron, the recoil effect is
![]() stronger. Nevertheless, it turns out that during hydrogen recombination electron scattering can be neglected in the analysis of future CMB data. This is because of its much smaller cross section in comparison with line scattering and the decreasing number density of free electrons (see Sect. 2.2).
stronger. Nevertheless, it turns out that during hydrogen recombination electron scattering can be neglected in the analysis of future CMB data. This is because of its much smaller cross section in comparison with line scattering and the decreasing number density of free electrons (see Sect. 2.2).
We would like to mention that, while this paper was in preparation another investigation of this problem was carried out by Hirata & Forbes (2009). The results obtained in their work seem to be similar to those presented here.
2 Additions to the kinetic equation for the photons in the vicinity of the
Lyman
 resonance
resonance
Here we give the additional terms for the photon radiative transfer equation that are necessary for describing the effect of resonance and electron scattering in the Lyman ![]() escape problem during cosmological hydrogen recombination. We use the same notation as in Chluba & Sunyaev (2009b) and Chluba & Sunyaev (2009a), also introducing the dimensionless frequency variable
escape problem during cosmological hydrogen recombination. We use the same notation as in Chluba & Sunyaev (2009b) and Chluba & Sunyaev (2009a), also introducing the dimensionless frequency variable
![]() and photon distribution,
and photon distribution,
![]() ,
with
,
with
![]() ,
where
,
where ![]() is the physical specific intensity of the ambient radiation field.
The photon occupation number then is
is the physical specific intensity of the ambient radiation field.
The photon occupation number then is
![]() .
With this choice of variables, the redshifting of photons due to the Hubble expansion is automatically taken into account in x (for more details see Chluba & Sunyaev 2009b).
.
With this choice of variables, the redshifting of photons due to the Hubble expansion is automatically taken into account in x (for more details see Chluba & Sunyaev 2009b).
It is clear that Lyman-![]() line and electron scattering (both including the Doppler-broadening, recoil and induced scatterings) only lead to the redistribution of photons over frequency, but do not change the total number of photons in each event. Also a blackbody spectrum with
line and electron scattering (both including the Doppler-broadening, recoil and induced scatterings) only lead to the redistribution of photons over frequency, but do not change the total number of photons in each event. Also a blackbody spectrum with
![]() should not be altered by these processes. Within the Fokker-Planck formulation of the corresponding processes, these requirements are directly fulfilled.
should not be altered by these processes. Within the Fokker-Planck formulation of the corresponding processes, these requirements are directly fulfilled.
2.1 Lyman-
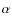 resonance scattering
resonance scattering
The contribution to the collision term due to redistribution of photon by resonance scattering off moving atoms can be written as (e.g. see Rybicki 2006)
where
As shown in Rybicki (2006), within a Fokker-Planck formulation for the case of Doppler redistribution, Eq. (1) can be cast in the form
where
It is important to note that Eq. (2) simultaneously includes the effects of line diffusion, atomic recoil![]() , and stimulated scattering
, and stimulated scattering![]() . In this formulation it therefore preserves a Planckian photon distribution
. In this formulation it therefore preserves a Planckian photon distribution
![]() with
with
![]() .
This can be easily verified when realizing that
.
This can be easily verified when realizing that
![]() .
Also one can easily verify that
.
Also one can easily verify that
![]() in the Fokker-Planck formulation.
in the Fokker-Planck formulation.
In Eq. (2) we also took into account that not every scattering leads to the reappearance of the photon, since per scattering the fraction
![]() of photons disappear into other channels, i.e. to higher levels and the continuum. Here
of photons disappear into other channels, i.e. to higher levels and the continuum. Here
![]() is the single scattering albedo that is equivalent to the one photon emission probability
is the single scattering albedo that is equivalent to the one photon emission probability
![]() in our formulation. However, since
in our formulation. However, since
![]() is always very close to unity (e.g. see Chluba & Sunyaev 2009a), one could also neglect this detail here.
is always very close to unity (e.g. see Chluba & Sunyaev 2009a), one could also neglect this detail here.
The corresponding term in the variables x and
![]() then reads as
then reads as
where we made the substitutions
2.2 Electron scattering
The contribution to the collision term due to scattering off free, non-relativistic electrons can be described with the Kompaneets-equation. Because of the similarity with Eq. (2) (see also Rybicki 2006) it is straightforward to obtain the corresponding terms for our set of variables:
where
One should mention that in the case of electron scattering the Fokker-Planck approximation for the frequency redistribution function may not be sufficient towards the end of hydrogen recombination (![]() ). However, the overall correction to the ionization history turns out to be very small close the maximum of the Thomson visibility function (e.g. see Fig. 8), so that no big difference is expected when more correctly using a scattering Kernel-approach (Sazonov & Sunyaev 2000; Syunyaev 1980), which accurately takes both the Doppler effect and electron recoil into account.
). However, the overall correction to the ionization history turns out to be very small close the maximum of the Thomson visibility function (e.g. see Fig. 8), so that no big difference is expected when more correctly using a scattering Kernel-approach (Sazonov & Sunyaev 2000; Syunyaev 1980), which accurately takes both the Doppler effect and electron recoil into account.
![\begin{figure}
\par\mbox{\includegraphics[width=0.9\columnwidth]{eps/12335fig01a...
...}
\includegraphics[width=0.885\columnwidth]{eps/12335fig01b.eps} }\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg70.png) |
Figure 1:
Time evolution of the photon distribution for single (narrow-line) injection at the line center. The death probability for a 3-shell hydrogen atom was used and electron scattering has been neglected. We use the time-variable
|
| Open with DEXTER | |
2.2.1 Relative importance of electron scattering
Since the line-profile
![]() is a strong function of frequency, resonance scattering is most important close to the Lyman
is a strong function of frequency, resonance scattering is most important close to the Lyman ![]() line center, while in the very distant wings, electron scattering is expected to dominate. Comparing the diffusion coefficients in frequency space for resonant and electron scattering,
line center, while in the very distant wings, electron scattering is expected to dominate. Comparing the diffusion coefficients in frequency space for resonant and electron scattering,
shows that at redshift
Because of the changes in
![]() the ratio (5) is a strong function of redshift. However, electron scattering is expected to influence the evolution of photons close to the line center significantly only at redshifts
the ratio (5) is a strong function of redshift. However, electron scattering is expected to influence the evolution of photons close to the line center significantly only at redshifts ![]() ,
i.e. well before the main epoch of hydrogen recombination. Therefore one expects that electron scattering has a low impact on the
development of the photons close to the center of the Lyman-
,
i.e. well before the main epoch of hydrogen recombination. Therefore one expects that electron scattering has a low impact on the
development of the photons close to the center of the Lyman-![]() transition, hence on the escape probability during hydrogen recombination.
transition, hence on the escape probability during hydrogen recombination.
3 Illustrative time-dependent solutions for different initial photon distributions
To illustrate the main physical effects related to resonance scattering and electron scattering, we numerically solved the radiative transfer equation, injecting a single narrow-line at different distances from the line center. For the computations we include the frequency redistribution of photons, redshifting, and real absorption using the normal ``1+1'' photon picture (see Chluba & Sunyaev 2009b). We neglect the effects due to two-photon corrections here. Furthermore, we assume that the solution for the electron number density and the 1s-population are given by the output of the R ECFAST code (Seager et al. 1999). A few words about the PDE-solver can be found in the Appendix A.
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]
{eps/12335fig02a.eps}\hsp...
...\hspace{5mm}
\includegraphics[width=8.5cm]
{eps/12335fig02d.eps} }\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg83.png) |
Figure 2:
Time evolution of the photon distribution for single (narrow-line) injection on the red side of the Lyman- |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{eps/12335fig03a.eps}\hspace{5mm}
\includegraphics[width=8.5cm]{eps/12335fig03b.eps} }\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg84.png) |
Figure 3:
Time evolution of the photon distribution for single (narrow-line) injection at
|
| Open with DEXTER | |
3.1 Time-dependent solutions
In Fig. 1 we present the results for single injection of photons at the Lyman-![]() line center. In practice we use a Gaussian initial photon distribution that is centered on the injection frequency
line center. In practice we use a Gaussian initial photon distribution that is centered on the injection frequency
![]() and has a width
and has a width
![]() .
Furthermore, we re-normalized by a convenient factor such that induced effects are negligible.
We started our computation at injection redshift
.
Furthermore, we re-normalized by a convenient factor such that induced effects are negligible.
We started our computation at injection redshift
![]() ,
i.e. close to the time where the maximum of the CMB spectral distortion due to the Lyman-
,
i.e. close to the time where the maximum of the CMB spectral distortion due to the Lyman-![]() transition appears (Rubiño-Martín et al. 2006). At this redshift, roughly 20% of all hydrogen atoms have already recombined,
and the death probability for a 3-shell hydrogen atom
transition appears (Rubiño-Martín et al. 2006). At this redshift, roughly 20% of all hydrogen atoms have already recombined,
and the death probability for a 3-shell hydrogen atom![]() is
is
![]() (see Fig. 1 in Chluba & Sunyaev 2009b).
(see Fig. 1 in Chluba & Sunyaev 2009b).
From Fig. 1 one can see that, after a short time, the initial photon distribution has broadened significantly, bringing photons to the wings of the Lyman-![]() transition. After
transition. After
![]() ,
the death of photons in the line center becomes important, owing to
,
the death of photons in the line center becomes important, owing to
![]() being so small.
The solution remains very symmetric until
being so small.
The solution remains very symmetric until
![]()
![]() 1010 and only then does redshifting due to the expansion of the Universe start to become important. (As we will see line-recoil only affects the photon distribution at the level of few percent in addition.) When the bulk of photons reaches a distance
1010 and only then does redshifting due to the expansion of the Universe start to become important. (As we will see line-recoil only affects the photon distribution at the level of few percent in addition.) When the bulk of photons reaches a distance
![]() ,
a sizable amount of them remains on the blue side of the Lyman-
,
a sizable amount of them remains on the blue side of the Lyman-![]() line, and the evolution starts to become dominated by redshifting and absorption only when the maximum of the photon distribution reaches
line, and the evolution starts to become dominated by redshifting and absorption only when the maximum of the photon distribution reaches
![]() ,
with very small changes because of frequency redistribution.
,
with very small changes because of frequency redistribution.
In Fig. 2 we present the results for single injection of photons at different distances to the line center. Again photons were injected at
![]() .
Focusing on the case
.
Focusing on the case
![]() ,
one can again observe the fast broadening of the initial photon distribution. However, now the characteristic time for line scattering has increased by a factor of
,
one can again observe the fast broadening of the initial photon distribution. However, now the characteristic time for line scattering has increased by a factor of
![]() because frequency redistribution already takes place in the wings of the Voigt-profile. It is important to note that, due to line scattering, photons strongly diffuse
back into the line center, thereby increasing the possibility of being absorbed. Also one can see that because of diffusion some photons even reach far into the blue side of the Lyman-
because frequency redistribution already takes place in the wings of the Voigt-profile. It is important to note that, due to line scattering, photons strongly diffuse
back into the line center, thereby increasing the possibility of being absorbed. Also one can see that because of diffusion some photons even reach far into the blue side of the Lyman-![]() resonance. Again only after the bulk of photons has reached a distance of
resonance. Again only after the bulk of photons has reached a distance of
![]() redshifting and absorption play the most important role in the evolution of the photon distribution.
redshifting and absorption play the most important role in the evolution of the photon distribution.
Looking at the other two cases, it becomes clear that, for injection at
![]() ,
a few photons still diffuse back to the line center, whereas for
,
a few photons still diffuse back to the line center, whereas for
![]() ,
practically all photons remain below
,
practically all photons remain below
![]() at all times. Comparing the maxima of the final photon distribution (at
at all times. Comparing the maxima of the final photon distribution (at
![]() )
for all the discussed cases shows that, as expected, the
efficiency of absorption decreases when increasing
)
for all the discussed cases shows that, as expected, the
efficiency of absorption decreases when increasing
![]() .
.
It is also interesting to look at cases of injecting photons on the blue side of the Lyman-resonance. In such cases all photons have to pass at least once through the resonance before they can escape, and one expects that many photons die during this passage. In Fig. 3 we show the results for single injection at
![]() .
At the beginning the evolution of the spectrum looks very similar (except for mirror-inversion) to the case of injection at
.
At the beginning the evolution of the spectrum looks very similar (except for mirror-inversion) to the case of injection at
![]() .
However, at late times one can see that there are significantly fewer photons reaching the red side of the Lyman-
.
However, at late times one can see that there are significantly fewer photons reaching the red side of the Lyman-![]() resonance. Indeed this amount is comparable to the case of injection directly at the center.
resonance. Indeed this amount is comparable to the case of injection directly at the center.
3.2 Escape probability for single narrow line injection
Given an initial photon distribution, one can compute the total number of photons that survive the evolution over a period of time for the given transfer problem. Here we assume that fresh photons appear only at time t=0. Comparing the total number of photons at the final stage with the initial number then yields the numerical escape or survival probability
for the given diffusion problem
where
The expansion of the Universe photons leads to a redshift towards lower frequencies. Neglecting any redistribution process, with time this will increase the distance of the initial photon distribution to the line center, thereby decreasing the probability of real line absorption. Assuming that the initial photon distribution is given by a ![]() -function then with Eq. (6), one obtains
-function then with Eq. (6), one obtains
for this case. Here
We now want to compare the differential escape probability Eq. (7) with the numerical results obtained when including the redistribution of photons over frequency. The results of the previous section suggest the following:
- (i)
- For photons injected close to the line center the diffusion due to
resonance scattering helps to bring photons towards the wings. In
comparison to the case with no-scattering, this should increase the escape
probability.
- (ii)
- At intermediate distances on the red side of the line center (
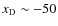 to -100 Doppler width), line diffusion brings some photons back to the Doppler core, so it should decrease the escape probability in comparison to the case without line scattering.
to -100 Doppler width), line diffusion brings some photons back to the Doppler core, so it should decrease the escape probability in comparison to the case without line scattering.
- (iii)
- Far in the red wing of the line (
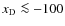 )
the escape fraction will depend mainly on the death probability and the expansion rate of the Universe. In this regime line scattering does lead to some line broadening, but should no longer affect the escape probability significantly.
)
the escape fraction will depend mainly on the death probability and the expansion rate of the Universe. In this regime line scattering does lead to some line broadening, but should no longer affect the escape probability significantly.
- (iv)
- The escape probability for injections on the blue side of the resonance nearly becomes independent of the initial distance to the line center and should be comparable to the one inside the Doppler core.
Since the absorption cross section in wings of the line scales like
![]() ,
even
beyond
,
even
beyond
![]() percent-level absorption can still occur, which should be taken into account when computing the total escape probability until redshift
percent-level absorption can still occur, which should be taken into account when computing the total escape probability until redshift
![]() .
However, the effect of resonance scattering becomes negligible at this distance from the line center (see below), and the time evolution can in principle be described fully analytically. For simplicity we neglected this additional complication and typically chose
.
However, the effect of resonance scattering becomes negligible at this distance from the line center (see below), and the time evolution can in principle be described fully analytically. For simplicity we neglected this additional complication and typically chose
![]() ,
which ensured that the remaining absorption only leads to modifications of
,
which ensured that the remaining absorption only leads to modifications of
![]() to the obtained escape probability. Up to this level of accuracy, the obtained curves presented in this section can
be considered as the frequency-dependent total escape probability until
to the obtained escape probability. Up to this level of accuracy, the obtained curves presented in this section can
be considered as the frequency-dependent total escape probability until
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig04a.eps}\par\includegraphics[width=8.5cm,clip]{eps/12335fig04b.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg117.png) |
Figure 4:
Escape probability,
|
| Open with DEXTER | |
In Fig. 4 we present some results for computations of the frequency-dependent escape probability,
![]() ,
for injection redshifts
,
for injection redshifts
![]() and 1300. For comparison we also give the corresponding escape probabilities,
and 1300. For comparison we also give the corresponding escape probabilities,
![]() ,
Eq. (7), for
,
Eq. (7), for
![]() -function injection when neglecting line scattering. At large distance (
-function injection when neglecting line scattering. At large distance (
![]() )
from the line center,
)
from the line center,
![]() practically coincides with
practically coincides with
![]() in all these cases. As mentioned above this behavior is expected since line scattering should not strongly affect the evolution of the line anymore. At intermediate distances from the line center, including line scattering indeed decreases the escape probability in comparison to the cases without scattering. Looking in detail at the dependence of
in all these cases. As mentioned above this behavior is expected since line scattering should not strongly affect the evolution of the line anymore. At intermediate distances from the line center, including line scattering indeed decreases the escape probability in comparison to the cases without scattering. Looking in detail at the dependence of
![]() close to the center of the line shows that the presumptions (i) and (iv) also hold. Our computations clearly show that there is a non-vanishing escape probability for photons from the blue side of the line, which is practically
zero
close to the center of the line shows that the presumptions (i) and (iv) also hold. Our computations clearly show that there is a non-vanishing escape probability for photons from the blue side of the line, which is practically
zero![]() in the case of pure absorption. This probability is nearly constant, extending even into the core of the line and down to
in the case of pure absorption. This probability is nearly constant, extending even into the core of the line and down to
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig05.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg124.png) |
Figure 5:
Frequency
|
| Open with DEXTER | |
To understand up to which distance to the line center the effect of resonance scattering is important, we compared the results for the escape probability including line scattering with the analytic no-scattering solution, asking the question at which distance in the red wing the
modification due to line scattering becomes ![]() percent. In Fig. 5 we summarize the results of this comparison. It is clear that at all redshifts of interest line-scattering is only important for
percent. In Fig. 5 we summarize the results of this comparison. It is clear that at all redshifts of interest line-scattering is only important for
![]()
![]() 102, but at the percent level may in principle be neglected below this frequency. We have already made use of this result in some earlier work (Chluba & Sunyaev 2008).
102, but at the percent level may in principle be neglected below this frequency. We have already made use of this result in some earlier work (Chluba & Sunyaev 2008).
3.2.1 Role of atomic-recoil
Every resonance scattering caused by atomic-recoil leads to a small shift in the photon energy towards lower frequencies. The strength of the recoil due to the frequency dependence of the scattering cross section is a strong function of photon energy, peaking close to the Lyman-![]() line center and dropping rather strongly in the damping wings. This is in stark contrast to electron recoil, for which the scattering cross section is practically independent of frequency.
line center and dropping rather strongly in the damping wings. This is in stark contrast to electron recoil, for which the scattering cross section is practically independent of frequency.
To understand the importance of the atomic recoil effect for the differential escape probability, we therefore performed several computations of the frequency-dependent escape probability for injection of photons at different distances from the line center, explicitly neglecting the effect of atomic recoil. In Fig. 6 we present the correction to the escape probability, which only stems from the atomic-recoil term. As expected, atomic recoil helps photons to escape in the whole range of frequencies. However, the decrease in the scattering cross-section makes the
corresponding correction very small at distances below
![]() to -150. Also the amplitude of the effect increases towards lower redshifts, simply because more hydrogen atoms have become neutral. The largest correction is coming from the line center and is practically constant over the whole Doppler core and the blue side of the resonance. We will see below that the total correction to the Lyman
to -150. Also the amplitude of the effect increases towards lower redshifts, simply because more hydrogen atoms have become neutral. The largest correction is coming from the line center and is practically constant over the whole Doppler core and the blue side of the resonance. We will see below that the total correction to the Lyman ![]() escape probability is very similar to the value obtained for injections close to the line center (see Sect. 4).
escape probability is very similar to the value obtained for injections close to the line center (see Sect. 4).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig06.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg126.png) |
Figure 6:
Relative difference in the escape probability for single (narrow line) injection at different distances from the line center when including the effect of atomic recoil. Here
|
| Open with DEXTER | |
3.2.2 Role of electron scattering
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig07.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg127.png) |
Figure 7:
Relative difference in the escape probability for single (narrow line) injection at different distances from the line center when including electron scattering. Here
|
| Open with DEXTER | |
In Fig. 7 we show the relative difference in the escape probability for single (narrow-line) injection at different distances from the line center when including electron scattering. As expected, electron scattering has an effect that is similar to the one of resonance scattering, helping photons to escape more efficiently from the line center, but bringing some photons from the wings back into the Doppler core, diminishing the probability of their survival. At higher injection redshift, the differences become larger, due to the
increase in the number of free electrons as compared to the number of neutral hydrogen atoms. At
![]() the relative difference becomes smaller than
the relative difference becomes smaller than
![]() in the full range of injection frequencies considered. Close to the maximum of the visibility function
in the full range of injection frequencies considered. Close to the maximum of the visibility function
![]() ,
one does not expect a large correction caused by electron scattering. In addition it is clear that the increase in the escape in the Doppler-core should be partially canceled by the decrease in the red wing. As we see in Sect. 4, the net effect of electron
scattering on the Lyman
,
one does not expect a large correction caused by electron scattering. In addition it is clear that the increase in the escape in the Doppler-core should be partially canceled by the decrease in the red wing. As we see in Sect. 4, the net effect of electron
scattering on the Lyman ![]() escape probability during hydrogen recombination is always
escape probability during hydrogen recombination is always ![]() at
at
![]() .
.
4 Changes in the Lyman
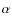 escape probability during hydrogen recombination
escape probability during hydrogen recombination
In this section we now present the results for the changes in the Lyman ![]() escape probability during hydrogen recombination. Our approach here is very similar to the one used in our earlier, semi-analytical works (Chluba & Sunyaev 2009b,a). Given the solution for the populations of the different hydrogen levels, we numerically solve the transfer equation for the Lyman
escape probability during hydrogen recombination. Our approach here is very similar to the one used in our earlier, semi-analytical works (Chluba & Sunyaev 2009b,a). Given the solution for the populations of the different hydrogen levels, we numerically solve the transfer equation for the Lyman ![]() problem obtaining the spectral distortion in the vicinity of the Lyman
problem obtaining the spectral distortion in the vicinity of the Lyman ![]() resonance at different redshifts. From this we can compute the effective escape probability by convolving this distortion with the corresponding Lyman
resonance at different redshifts. From this we can compute the effective escape probability by convolving this distortion with the corresponding Lyman ![]() absorption profile. We also follow a very similar approach in our previous computations of the radiative transfer problem during helium recombination, where some of the results obtained in that case have already been used in Rubiño-Martín et al. (2008).
absorption profile. We also follow a very similar approach in our previous computations of the radiative transfer problem during helium recombination, where some of the results obtained in that case have already been used in Rubiño-Martín et al. (2008).
We start by discussing the results in the standard ``1+1'' formulation (Sect. 4.1).
We then include the effect due to the thermodynamic correction factor ![]() (Sect. 4.2), which was introduced earlier (Chluba & Sunyaev 2009b,a) using the detailed balance argument. Finally we also include the corrections to the 3d-1s and 3s-1s two-photon emission profile (Sect. 4.3).
(Sect. 4.2), which was introduced earlier (Chluba & Sunyaev 2009b,a) using the detailed balance argument. Finally we also include the corrections to the 3d-1s and 3s-1s two-photon emission profile (Sect. 4.3).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig08.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg134.png) |
Figure 8:
Changes in the Lyman |
| Open with DEXTER | |
4.1 Results in the standard ``1 + 1'' photon formulation
In Fig. 8 we present the results for the escape probability using the standard ``1+1'' photon formulation. In this case the emission and absorption profile are given by the normal Voigt profile. We also include the full time dependence of the problem in the computations of the line emission rate and the absorption optical depth. In the no-scattering approximation (Chluba & Sunyaev 2009b) this leads to the dashed curve shown in Fig. 8.
As already mentioned by Chluba & Sunyaev (2009b), the standard ``1+1'' photon formulation has several discrepancies, leading to an unphysical self-feedback of Lyman ![]() photons at low redshifts (
photons at low redshifts (
![]() ). Nevertheless, one can study the influence of the redistribution of photons by resonance and electron scattering even in this approach, and as we see one obtains very similar results for the effect of resonance scattering in comparison with the more complete formulation using the two-photon picture (Sect. 4.3).
). Nevertheless, one can study the influence of the redistribution of photons by resonance and electron scattering even in this approach, and as we see one obtains very similar results for the effect of resonance scattering in comparison with the more complete formulation using the two-photon picture (Sect. 4.3).
In Fig. 8 we show the separate correction caused by atomic recoil (thin solid line). We obtained this curve by taking the difference in the escape probabilities for the case with all corrections due to line and electron scattering included and for the one in which line recoil was switched off. The importance of recoil increases towards lower redshifts, reaching the level of
![]() at
at ![]() .
If we look at the results presented in Fig. 6 for the case of single narrow line injection, we can even see that the total recoil correction seen in Fig. 8 is very close to the value obtained for line center injection. This is expected, since the largest contribution to the total value of the escape probability always comes from the Doppler core.
.
If we look at the results presented in Fig. 6 for the case of single narrow line injection, we can even see that the total recoil correction seen in Fig. 8 is very close to the value obtained for line center injection. This is expected, since the largest contribution to the total value of the escape probability always comes from the Doppler core.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig09.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg138.png) |
Figure 9:
Changes in the Lyman |
| Open with DEXTER | |
We can also see that the effect of electron scattering (dotted curve) is very small, leading to a correction ![]() at
at ![]() .
Close to the maximum of the Thomson visibility function, the effect of electron scattering is negligible. This curve was computed using the numerical results in which we switched off electron scattering and then compared it to the one where it was included.
.
Close to the maximum of the Thomson visibility function, the effect of electron scattering is negligible. This curve was computed using the numerical results in which we switched off electron scattering and then compared it to the one where it was included.
Finally, we also computed the contribution that can be attributed to the effect of Doppler boosting and Doppler broadening (dash-dotted curve). For this we computed the escape probability when neglecting electron scattering and atomic recoil, but only including the line diffusion term. We then took the difference to result obtained in the no-scattering approximation, as given earlier (Chluba & Sunyaev 2009b). One can see that the diffusion term results in a decrease in the escape probability at low redshifts. However, this decrease is about 3 times smaller than the increase in the escape probability caused by atomic recoil. Therefore the net effect because of resonance scattering is an increase in the escape probability, reaching
![]() at
at ![]() .
As explained in Sect. 3.2, this shows that the decrease in the red wing escape probability due to the return of photons towards the Doppler core by line diffusion is more important than the increase in the escape fraction from within the Doppler core caused by Doppler broadening.
.
As explained in Sect. 3.2, this shows that the decrease in the red wing escape probability due to the return of photons towards the Doppler core by line diffusion is more important than the increase in the escape fraction from within the Doppler core caused by Doppler broadening.
We would like to mention that the small variability in the diffusion contribution at ![]() is likely caused by some details in our numerical treatment. However, we expect that the corresponding result is converged at the
is likely caused by some details in our numerical treatment. However, we expect that the corresponding result is converged at the
![]() level of the correction, which is sufficient for our purposes here.
level of the correction, which is sufficient for our purposes here.
4.2 Effect of the thermodynamic corrections factor
If we now include the frequency-dependent asymmetry between the emission and absorption profile due to the thermodynamic correction factor that was introduced earlier (Chluba & Sunyaev 2009b,a), we obtain the results presented in Fig. 9. The dashed line again shows the correction in the no-scattering approximation (Chluba & Sunyaev 2009a). The main correction to the redistribution of photons over frequency again is because of the line recoil term (thin solid line). One can see that it is practically the same as in the previous case (see Fig. 8). Also the total correction due to electron scattering did not change very much. In both cases the difference was less than ![]() on the correction. However, the correction due to the line diffusion term seems to be slightly increased, suggesting a
on the correction. However, the correction due to the line diffusion term seems to be slightly increased, suggesting a ![]() induced correction to the correction that is not completely negligible.
induced correction to the correction that is not completely negligible.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig10.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg143.png) |
Figure 10:
Changes in the Lyman |
| Open with DEXTER | |
4.3 Corrections caused by the shape of the emission profile
Finally, we also ran the code including the correct shape of the 3d/3s-1s emission and absorption profile (Chluba & Sunyaev 2009a). The results of these computations are shown in Fig. 10. The dashed line again shows the correction in the no-scattering approximation (Chluba & Sunyaev 2009a). The dotted line in addition indicates the correction that was associated with the effect of the emission profile in the no-scattering approximation (Chluba & Sunyaev 2009a). We also computed the pure profile correction using the numerical results obtained when including the redistribution of photons to obtain the dash-dotted curve. As one can see the difference to the no redistribution case is very small. Therefore we did not compute the pure recoil correction, the line diffusion correction, or the correction due to electron scattering, since they should also be very similar to the contributions shown in Fig. 9.
5 Corrections to the ionization history
In this section we give the expected correction to the ionization history when including the processes discussed in this paper. For this we modified the R ECFAST code (Seager et al. 1999), so that we can load the pre-computed change in the Sobolev escape probability studied here.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig11.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg144.png) |
Figure 11:
Changes in the Lyman |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig12.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg145.png) |
Figure 12: Changes in the free electron fraction because of the different processes under discussion here. The dashed line shows the result obtained in the no-scattering approximation (Chluba & Sunyaev 2009a). |
| Open with DEXTER | |
In Fig. 11 we present the final curves for
![]() as obtained for the different processes discussed in this paper. In Fig. 12 we show the corresponding correction in the free electron fraction computed with the modified version of R ECFAST. The atomic recoil effect alone (thin solid line) leads to
as obtained for the different processes discussed in this paper. In Fig. 12 we show the corresponding correction in the free electron fraction computed with the modified version of R ECFAST. The atomic recoil effect alone (thin solid line) leads to
![]() at
at ![]() .
This is in very good agreement with the result of Grachev & Dubrovich (2008). We already quoted this result earlier (see footnote 10 in Chluba & Sunyaev 2009b); however, there we just estimated the change in the free electron fraction using our full numerical result for the recoil correction on the Lyman
.
This is in very good agreement with the result of Grachev & Dubrovich (2008). We already quoted this result earlier (see footnote 10 in Chluba & Sunyaev 2009b); however, there we just estimated the change in the free electron fraction using our full numerical result for the recoil correction on the Lyman ![]() escape probability, without running it through the R ECFAST code. By including electron scattering and all terms (line recoil and the diffusion term) for the redistribution of photons by the Lyman
escape probability, without running it through the R ECFAST code. By including electron scattering and all terms (line recoil and the diffusion term) for the redistribution of photons by the Lyman ![]() resonance, we obtain the dotted line. Here the total correction due to redistribution of photons only reaches
resonance, we obtain the dotted line. Here the total correction due to redistribution of photons only reaches
![]() at
at ![]() .
As we have seen in Sect. 4, this occurs because the diffusion term slows recombination down again, since photons from the red wing return close to the Doppler core, where they die efficiently again. Finally, the total correction including all the effects of photon redistribution and the correction for the time dependence, thermodynamic factor, and shape of the profile, which were discussed earlier (Chluba & Sunyaev 2009a), has a maximum of
.
As we have seen in Sect. 4, this occurs because the diffusion term slows recombination down again, since photons from the red wing return close to the Doppler core, where they die efficiently again. Finally, the total correction including all the effects of photon redistribution and the correction for the time dependence, thermodynamic factor, and shape of the profile, which were discussed earlier (Chluba & Sunyaev 2009a), has a maximum of
![]() at
at
![]() .
Here the main contribution is coming from the the time-dependent correction and thermodynamic factor as explained in Chluba & Sunyaev (2009a).
.
Here the main contribution is coming from the the time-dependent correction and thermodynamic factor as explained in Chluba & Sunyaev (2009a).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig13a.eps}\par\includegraphics[width=8.5cm,clip]{eps/12335fig13b.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg147.png) |
Figure 13: Changes in the CMB temperature and polarization power spectra. The upper panel shows the changes from the redistribution of photons by line and electron scattering alone. The lower panel shows the cumulative result in addition including the time-dependent correction, the thermodynamic factor, and the correction due to the shape of the emission profile, as discussed earlier (Chluba & Sunyaev 2009a). |
| Open with DEXTER | |
In Fig. 13 we finally show the changes in the CMB temperature and polarization power spectra. The corrections to
![]() related to the redistribution of photons over frequency alone (upper panel) results in changes to the TT and EE power spectra, with peak-to-peak amplitude
related to the redistribution of photons over frequency alone (upper panel) results in changes to the TT and EE power spectra, with peak-to-peak amplitude
![]() at
at
![]() .
When including the processes discussed in Chluba & Sunyaev (2009a) at
.
When including the processes discussed in Chluba & Sunyaev (2009a) at
![]() ,
we find a cumulative correction of
,
we find a cumulative correction of
![]() for the TT power spectrum and
for the TT power spectrum and
![]() for the EE power spectrum. It will be important to take these changes into account in the analysis of future CMB data.
for the EE power spectrum. It will be important to take these changes into account in the analysis of future CMB data.
6 Conclusions
We have considered the effect of frequency redistribution on the escape of Lyman ![]() photons during hydrogen recombination. We showed that line recoil speeds hydrogen recombination up by
photons during hydrogen recombination. We showed that line recoil speeds hydrogen recombination up by
![]() at
at ![]() .
On the other hand, the combined effect of Doppler boosting and Doppler broadening at different distances from the line center slows hydrogen recombination down by
.
On the other hand, the combined effect of Doppler boosting and Doppler broadening at different distances from the line center slows hydrogen recombination down by
![]() at
at ![]() .
As explained in Sect. 3, line diffusion (including both Doppler boosting and Doppler broadening) increases the escape fraction for photons that are emitted in the vicinity of the Doppler core in comparison with the value obtained in the no-scattering approximation. In particular some small fraction of photons that are emitted on the blue side of the resonance can still escape, since thanks to line diffusion, they pass through the Doppler core faster than dying there. On the other hand, for photons that are emitted at
.
As explained in Sect. 3, line diffusion (including both Doppler boosting and Doppler broadening) increases the escape fraction for photons that are emitted in the vicinity of the Doppler core in comparison with the value obtained in the no-scattering approximation. In particular some small fraction of photons that are emitted on the blue side of the resonance can still escape, since thanks to line diffusion, they pass through the Doppler core faster than dying there. On the other hand, for photons that are emitted at
![]() (i.e. in the red wing), it becomes harder to escape, since line diffusion brings some of these photons back close to the Doppler core, where they are absorbed efficiently. For photons that are emitted at
(i.e. in the red wing), it becomes harder to escape, since line diffusion brings some of these photons back close to the Doppler core, where they are absorbed efficiently. For photons that are emitted at
![]()
![]() 102, the redistribution over frequency can be neglected. We also showed that electron scattering has a minor effect on recombination dynamics at redshifts
102, the redistribution over frequency can be neglected. We also showed that electron scattering has a minor effect on recombination dynamics at redshifts ![]() .
In total the redistribution of photons over frequency speeds up hydrogen recombination by
.
In total the redistribution of photons over frequency speeds up hydrogen recombination by
![]() at
at ![]() (cf. Fig. 12). This results in changes to the CMB temperature and polarization power spectra (see Fig. 13 for details), which should be taken into account when analyzing future CMB data.
(cf. Fig. 12). This results in changes to the CMB temperature and polarization power spectra (see Fig. 13 for details), which should be taken into account when analyzing future CMB data.
In addition, we would like to mention that the cumulative changes (including the processes discussed in Chluba & Sunyaev 2009a and those of this work) in the Lyman ![]() photon escape probability will be essential for precise computations of the cosmological recombination spectrum (e.g. see Sunyaev & Chluba 2007, for review and references). Here it is interesting that the changes in the shape of the recombination lines connected with electrons passing through the Lyman
photon escape probability will be essential for precise computations of the cosmological recombination spectrum (e.g. see Sunyaev & Chluba 2007, for review and references). Here it is interesting that the changes in the shape of the recombination lines connected with electrons passing through the Lyman ![]() channel are expected to be
channel are expected to be
![]() at
at
![]() (in comparison to
(in comparison to ![]() for
for ![]() at
at
![]() ). Observing the cosmological recombination lines and looking at their exact shape would therefore provide a more direct and
). Observing the cosmological recombination lines and looking at their exact shape would therefore provide a more direct and
![]() times more sensitive probe for the physics of cosmological recombination than with the CMB temperature anisotropies.
times more sensitive probe for the physics of cosmological recombination than with the CMB temperature anisotropies.
Appendix A: Computational details
A.1 Solver for the differential equations
To solve the photon transfer equation we used the solver D03PPF from the N AG![]() -Library. It provides possibilities for extensive error control and adaptive remeshing. In particular, for computations with narrow initial spectra or low line scattering efficiency, this feature became very important. However, remeshing also leads to an additional loss of accuracy for long integrations and therefore has to be applied with caution.
-Library. It provides possibilities for extensive error control and adaptive remeshing. In particular, for computations with narrow initial spectra or low line scattering efficiency, this feature became very important. However, remeshing also leads to an additional loss of accuracy for long integrations and therefore has to be applied with caution.
Typically we used
![]() grid points for the representation of the photon distribution and required relative accuracies
grid points for the representation of the photon distribution and required relative accuracies
![]() .
We checked the convergence of the results by varying the accuracy requirements and number of grid points, and also by running several test problems for which analytic solutions exist.
.
We checked the convergence of the results by varying the accuracy requirements and number of grid points, and also by running several test problems for which analytic solutions exist.
References
- Basko, M. M. 1978, Z. Eksper. Teoretich. Fiz., 75, 1278 [NASA ADS]
- Basko, M. M. 1981, Astrophys., 17, 69 [NASA ADS] [CrossRef]
- Chluba, J., & Sunyaev, R. A. 2006, A&A, 446, 39 [NASA ADS] [CrossRef] [EDP Sciences]
- Chluba, J., & Sunyaev, R. A. 2008, A&A, 480, 629 [NASA ADS] [CrossRef] [EDP Sciences]
- Chluba, J., & Sunyaev, R. A. 2009a, A&A, submitted (In the text)
- Chluba, J., & Sunyaev, R. A. 2009b, A&A, 496, 619 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dubrovich, V. K., & Grachev, S. I. 2005, Astron. Lett., 31, 359 [NASA ADS] [CrossRef]
- Fendt, W. A., Chluba, J., Rubiño-Martín, J. A., & Wandelt, B. D. 2009, ApJS, 181, 627 [NASA ADS] [CrossRef]
- Grachev, S. I., & Dubrovich, V. K. 2008, Astron. Lett., 34, 439 [NASA ADS] [CrossRef] (In the text)
- Hirata, C. M., & Forbes, J. 2009, Phys. Rev. D, submitted (In the text)
- Hu, W., Scott, D., Sugiyama, N., & White, M. 1995, Phys. Rev. D, 52, 5498 [NASA ADS] [CrossRef]
- Hummer, D. G. 1962, MNRAS, 125, 21 [NASA ADS] (In the text)
- Jackson, J. D. 1998, Classical Electrodynamics, 3rd edn. (Wiley-VCH) (In the text)
- Kholupenko, E. E., & Ivanchik, A. V. 2006, Astron. Lett., 32, 795 [NASA ADS] [CrossRef]
- Lee, H.-W. 2005, MNRAS, 358, 1472 [NASA ADS] [CrossRef] (In the text)
- Rubiño-Martín, J. A., Chluba, J., & Sunyaev, R. A. 2006, MNRAS, 371, 1939 [NASA ADS] [CrossRef]
- Rubiño-Martín, J. A., Chluba, J., & Sunyaev, R. A. 2008, A&A, 485, 377 [NASA ADS] [CrossRef] [EDP Sciences]
- Rybicki, G. B. 2006, ApJ, 647, 709 [NASA ADS] [CrossRef] (In the text)
- Rybicki, G. B., & dell'Antonio, I. P. 1994, ApJ, 427, 603 [NASA ADS] [CrossRef] (In the text)
- Sazonov, S. Y., & Sunyaev, R. A. 2000, ApJ, 543, 28 [NASA ADS] [CrossRef]
- Seager, S., Sasselov, D. D., & Scott, D. 1999, ApJ, 523, L1 [NASA ADS] [CrossRef] (In the text)
- Seljak, U., Sugiyama, N., White, M., & Zaldarriaga, M. 2003, Phys. Rev. D, 68, 083507 [NASA ADS] [CrossRef]
- Sunyaev, R. A., & Chluba, J. 2007, Nuovo Cimento B Serie, 122, 919 [NASA ADS] (In the text)
- Sunyaev, R. A., & Chluba, J. 2008, in Frontiers of Astrophysics: A Celebration of NRAO's 50th Anniversary, ed. A. H. Bridle, J. J. Condon, & G. C. Hunt, ASP Conf. Ser., 395, 35
- Sunyaev, R. A., & Zeldovich, Y. B. 1970, Astrophys. Space Sci., 7, 3 [NASA ADS] (In the text)
- Switzer, E. R., & Hirata, C. M. 2008, Phys. Rev. D, 77, 083006 [NASA ADS] [CrossRef]
- Syunyaev, R. A. 1980, SvA Lett., 6, 213 [NASA ADS]
- Wong, W. Y., & Scott, D. 2007, MNRAS, 375, 1441 [NASA ADS] [CrossRef]
Footnotes
- ... approximation
![[*]](/icons/foot_motif.png)
- In this approximation, only true line emission and line absorption and redshifting of photons are included in the computation. The redistribution of photons over frequency is neglected.
- ... recoil
![[*]](/icons/foot_motif.png)
- This term was first introduced by Basko (1981,1978).
- ... scattering
![[*]](/icons/foot_motif.png)
- This term is not important for the escape of Lyman
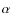 photons during hydrogen recombination.
photons during hydrogen recombination.
- ... atom
![[*]](/icons/foot_motif.png)
- The main contribution to the death of photons comes from the two-photon absorption to the 3d-state. By including more shells the death probability changes by less that 10% during hydrogen recombination. (Chluba & Sunyaev 2009a).
- ... depends
![[*]](/icons/foot_motif.png)
- For
simplicity we used
![$z_{\rm t}=z_{\rm i}[1+x_{\rm D, t}\Delta\nu_{\rm D}(z_{\rm
i})/\nu_{21}]$](/articles/aa/full_html/2009/32/aa12335-09/img110.png) .
.
- ...
zero
![[*]](/icons/foot_motif.png)
- There is a small difference close to the line center because we used
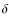 -function injection for the computation of
-function injection for the computation of
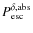 instead of the Gaussian that was used in the numerical computation. However, this will only make the transition
instead of the Gaussian that was used in the numerical computation. However, this will only make the transition
 less steep, without changing the main conclusion.
less steep, without changing the main conclusion.
- ... AG
![[*]](/icons/foot_motif.png)
- www.nag.co.uk
All Figures
![\begin{figure}
\par\mbox{\includegraphics[width=0.9\columnwidth]{eps/12335fig01a...
...}
\includegraphics[width=0.885\columnwidth]{eps/12335fig01b.eps} }\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg70.png) |
Figure 1:
Time evolution of the photon distribution for single (narrow-line) injection at the line center. The death probability for a 3-shell hydrogen atom was used and electron scattering has been neglected. We use the time-variable
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]
{eps/12335fig02a.eps}\hsp...
...\hspace{5mm}
\includegraphics[width=8.5cm]
{eps/12335fig02d.eps} }\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg83.png) |
Figure 2:
Time evolution of the photon distribution for single (narrow-line) injection on the red side of the Lyman- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{eps/12335fig03a.eps}\hspace{5mm}
\includegraphics[width=8.5cm]{eps/12335fig03b.eps} }\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg84.png) |
Figure 3:
Time evolution of the photon distribution for single (narrow-line) injection at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig04a.eps}\par\includegraphics[width=8.5cm,clip]{eps/12335fig04b.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg117.png) |
Figure 4:
Escape probability,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig05.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg124.png) |
Figure 5:
Frequency
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig06.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg126.png) |
Figure 6:
Relative difference in the escape probability for single (narrow line) injection at different distances from the line center when including the effect of atomic recoil. Here
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig07.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg127.png) |
Figure 7:
Relative difference in the escape probability for single (narrow line) injection at different distances from the line center when including electron scattering. Here
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig08.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg134.png) |
Figure 8:
Changes in the Lyman |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig09.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg138.png) |
Figure 9:
Changes in the Lyman |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig10.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg143.png) |
Figure 10:
Changes in the Lyman |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig11.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg144.png) |
Figure 11:
Changes in the Lyman |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig12.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg145.png) |
Figure 12: Changes in the free electron fraction because of the different processes under discussion here. The dashed line shows the result obtained in the no-scattering approximation (Chluba & Sunyaev 2009a). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{eps/12335fig13a.eps}\par\includegraphics[width=8.5cm,clip]{eps/12335fig13b.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa12335-09/Timg147.png) |
Figure 13: Changes in the CMB temperature and polarization power spectra. The upper panel shows the changes from the redistribution of photons by line and electron scattering alone. The lower panel shows the cumulative result in addition including the time-dependent correction, the thermodynamic factor, and the correction due to the shape of the emission profile, as discussed earlier (Chluba & Sunyaev 2009a). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\displaystyle %
\left.\mathcal{C}[N_{\nu}]\right\vert _{\rm r}
\approx
p^{1\gam...
...kT_{\rm e}}\frac{N_{\nu}}{\nu^2}\left(1+\frac{c^2 N_\nu}{2\nu^2}\right)\right],$](/articles/aa/full_html/2009/32/aa12335-09/img40.png)
![$\displaystyle %
\left.\mathcal{C}[\tilde{N}_x]\right\vert _{\rm r}
\approx
p^{1...
...~\frac{\tilde{N}_{x}}{x^2}\left(1+\frac{c^2 \tilde{N}_{x}}{2 x^2}\right)\right]$](/articles/aa/full_html/2009/32/aa12335-09/img58.png)
![$\displaystyle %
\left.\mathcal{C}[\tilde{N}_x]\right\vert _{\rm C}
= \sigma_{\r...
...\frac{\tilde{N}_{x}}{x^2}\left(1+\frac{c^2 \tilde{N}_{x}}{2 x^2}\right)\right],$](/articles/aa/full_html/2009/32/aa12335-09/img65.png)