| Issue |
A&A
Volume 503, Number 2, August IV 2009
|
|
|---|---|---|
| Page(s) | 357 - 371 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200911788 | |
| Published online | 22 June 2009 | |
Internal dynamics of Abell 1240: a galaxy cluster with symmetric double radio relics
R. Barrena1 - M. Girardi2,3 - W. Boschin2,4 - M. Dasí1,5
1 - Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, 38205 La Laguna (Tenerife), Canary Islands, Spain
2 -
Dipartimento di Astronomia of the Università degli Studi di Trieste, via Tiepolo 11, 34143 Trieste, Italy
3 -
INAF - Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
4 -
Fundación Galileo Galilei - INAF, Rambla José Ana Fernández Perez 7, 38712 Breña Baja (La Palma), Canary Islands, Spain
5 -
Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
Received 4 February 2009 / Accepted 12 May 2009
Abstract
Context. The mechanisms giving rise to diffuse radio emission in galaxy clusters, and in particular their connection with cluster mergers, are still debated.
Aims. We aim to obtain new insights into the internal dynamics of the cluster Abell 1240, which appears to contain two roughly symmetric radio relics, separated by ![]() 2
h70-1 Mpc.
2
h70-1 Mpc.
Methods. Our analysis is based mainly on redshift data for 145 galaxies mostly acquired at the Telescopio Nazionale Galileo and on new photometric data acquired at the Isaac Newton Telescope. We also use X-ray data from the Chandra archive and photometric data from the Sloan Digital Sky Survey (Data Release 7). We combine galaxy velocities and positions to select 89 cluster galaxies and analyze the internal dynamics of the Abell 1237 + Abell 1240 cluster complex, Abell 1237 being a close companion of Abell 1240 in its southern direction.
Results. We estimate similar redshifts for Abell 1237 and Abell 1240,
![]() and
and
![]() ,
respectively. For Abell 1237, we estimate a line-of-sight (LOS) velocity dispersion of
,
respectively. For Abell 1237, we estimate a line-of-sight (LOS) velocity dispersion of
![]() km s
km s![]() and a mass of
and a mass of ![]()
![]() .
For Abell 1240, we estimate a LOS
.
For Abell 1240, we estimate a LOS
![]() km s
km s![]() and a mass in the range
and a mass in the range
![]()
![]() ,
which takes account of its complex dynamics. Abell 1240 is shown to have a bimodal structure with two galaxy clumps roughly aligned along its N-S direction, the same as defined by the elongation of its X-ray surface brightness and the axis of symmetry of the relics. The two brightest galaxies of Abell 1240, associated with the northern and southern clumps, are separated by a LOS rest-frame velocity difference
,
which takes account of its complex dynamics. Abell 1240 is shown to have a bimodal structure with two galaxy clumps roughly aligned along its N-S direction, the same as defined by the elongation of its X-ray surface brightness and the axis of symmetry of the relics. The two brightest galaxies of Abell 1240, associated with the northern and southern clumps, are separated by a LOS rest-frame velocity difference
![]() km s
km s![]() and a projected distance
and a projected distance ![]() h70-1 Mpc. The two-body model agrees with the hypothesis that we are looking at a cluster merger that occurred largely in the plane of the sky, the two galaxy clumps being separated by a rest-frame velocity difference
h70-1 Mpc. The two-body model agrees with the hypothesis that we are looking at a cluster merger that occurred largely in the plane of the sky, the two galaxy clumps being separated by a rest-frame velocity difference
![]() km s
km s![]() at a time of 0.3 Gyr after the crossing core, while Abell 1237 is still infalling onto Abell 1240. Chandra archive data confirm the complex structure of Abell 1240 and allow us to estimate a global X-ray temperature of
at a time of 0.3 Gyr after the crossing core, while Abell 1237 is still infalling onto Abell 1240. Chandra archive data confirm the complex structure of Abell 1240 and allow us to estimate a global X-ray temperature of
![]() keV.
keV.
Conclusions. In agreement with the findings from radio data, our results for Abell 1240 strongly support the ``outgoing merger shocks'' model to explain the presence of the relics.
Key words: galaxies: clusters: individual: Abell 1240 - galaxies: clusters: individual: Abell 1237 - galaxies: clusters: general - galaxies: distances and redshifts
1 Introduction
Merging processes constitute an essential ingredient of the evolution of galaxy clusters (see Feretti et al. 2002, for a review). An interesting aspect of these phenomena is the possible connection of cluster mergers with the presence of extended, diffuse radio sources:
halos and relics. The synchrotron radio emission of these sources demonstrates the existence of large-scale cluster magnetic fields and of widespread relativistic particles. Cluster mergers have been suggested to provide the large amount of energy necessary for electron reacceleration up to relativistic energies and for magnetic field amplification (Feretti 1999, 2002; Sarazin 2002). Radio relics (``radio gischts'' as referred by Kempner
et al. 2003), which are polarized and elongated radio sources located in the cluster peripheral regions, seem to be directly associated with merger shocks (e.g., Ensslin et al. 1998; Roettiger et al. 1999; Ensslin & Gopal-Krishna 2001; Hoeft et al. 2004). Radio halos, unpolarized sources that permeate the cluster volume in a similar way to the X-ray emitting gas, are more likely to be associated with the turbulence following a cluster merger (Cassano & Brunetti 2005). However, the precise radio halos relic formation scenario is still debated since the diffuse radio sources are quite uncommon and one can study these phenomena only on the basis of sufficient statistics (few dozen clusters up to ![]() ,
e.g., Giovannini et al. 1999; see also Giovannini & Feretti 2002; Feretti 2005) and attempt a classification (e.g., Kempner et al. 2003; Ferrari et al. 2008).
,
e.g., Giovannini et al. 1999; see also Giovannini & Feretti 2002; Feretti 2005) and attempt a classification (e.g., Kempner et al. 2003; Ferrari et al. 2008).
There is growing evidence of the connection between diffuse radio emission and cluster merging, until up to now diffuse radio sources have been detected only in merging systems. In most of these
cases, the cluster dynamical state has been derived from X-ray observations (see Buote 2002; Feretti 2006, 2008, and refs. therein). Optical data are a powerful way of investigating the presence and the dynamics of cluster mergers (e.g., Girardi & Biviano 2002), too. The spatial and kinematical analysis of member galaxies allows us to detect and measure the amount of substructure, and to identify and analyze possible pre-merging clumps or merger remnants. This optical information is really complementary to X-ray information since galaxies and intracluster medium react on different timescales during a merger (see, e.g., numerical simulations by Roettiger et al. 1997). In this context, we are conducting an intensive observational and data analysis program to study the internal dynamics of clusters with diffuse radio emission by using member galaxies (Girardi et al. 2007, and refs. therein![]() ).
).
During our observational program, we conducted an intensive study
of the cluster Abell 1240 (hereafter A1240). A1240 is a very
rich, X-ray luminous, Abell cluster: Abell richness class =2 (Abell
et al. 1989);
![]() erg s-1 recovered from ROSAT data (David et al. 1999, correcting for our cluster redshift, see below). Optically, the cluster center is not dominated by any single
galaxy - it is classified as Bautz-Morgan class III (Abell et al.
1989).
erg s-1 recovered from ROSAT data (David et al. 1999, correcting for our cluster redshift, see below). Optically, the cluster center is not dominated by any single
galaxy - it is classified as Bautz-Morgan class III (Abell et al.
1989).
Kempner & Sarazin (2001) revealed the presence of two roughly
symmetric radio relics from the Westerbork Northern Sky Survey. They
appear on either side of the cluster center, north and south, at
distances of ![]() 6
6
![]() and 7
and 7
![]() .
Kempner & Sarazin also
noticed that A1240 has an elongated X-ray morphology (recovered
from ROSAT observations) consistent with a slightly asymmetric merger
with the apparent axis roughly aligned with the axis of symmetry of
the relics (see also Bonafede et al. 2009). The presence of
double relics was confirmed by deep VLA observations (Bonafede
et al. 2009, see Fig. 1). Very few other
clusters with double relics have been observed: Abell 3667 (Röttgering et al. 1997), Abell 3376 (Bagchi et al. 2006), Abell 2345 (Giovannini et al. 1999;
Bonafede et al. 2009), and RXCJ 1314.4-2515 (Feretti et al. 2005; Venturi et al. 2007). The relics of Abell 3667 were explained by the ``outgoing merger shocks'' model
(Roettiger et al. 1999). Observations of Abell 3376 agree with both the ``outgoing merger shocks'' and the ``accretion shock'' models (Bagchi et al. 2006). In the case of Abell 2345, the observations are difficult to reconcile with theoretical scenarios (Bonafede et al. 2009). Instead, more data are needed for RXCJ 1314.4-2515 (Feretti et al. 2005; and Venturi et al. 2007). As for A1240, the detailed analysis of its radio
properties agrees with the ``outgoing merger shocks'' model
(Bonafede et al. 2009), but the main global properties are
unknown and the internal cluster dynamics has never been studied.
.
Kempner & Sarazin also
noticed that A1240 has an elongated X-ray morphology (recovered
from ROSAT observations) consistent with a slightly asymmetric merger
with the apparent axis roughly aligned with the axis of symmetry of
the relics (see also Bonafede et al. 2009). The presence of
double relics was confirmed by deep VLA observations (Bonafede
et al. 2009, see Fig. 1). Very few other
clusters with double relics have been observed: Abell 3667 (Röttgering et al. 1997), Abell 3376 (Bagchi et al. 2006), Abell 2345 (Giovannini et al. 1999;
Bonafede et al. 2009), and RXCJ 1314.4-2515 (Feretti et al. 2005; Venturi et al. 2007). The relics of Abell 3667 were explained by the ``outgoing merger shocks'' model
(Roettiger et al. 1999). Observations of Abell 3376 agree with both the ``outgoing merger shocks'' and the ``accretion shock'' models (Bagchi et al. 2006). In the case of Abell 2345, the observations are difficult to reconcile with theoretical scenarios (Bonafede et al. 2009). Instead, more data are needed for RXCJ 1314.4-2515 (Feretti et al. 2005; and Venturi et al. 2007). As for A1240, the detailed analysis of its radio
properties agrees with the ``outgoing merger shocks'' model
(Bonafede et al. 2009), but the main global properties are
unknown and the internal cluster dynamics has never been studied.
Indeed, few spectroscopic data have been reported in the field of A1240 (see NED) and the value usually quoted in the literature for the cluster redshift (z=0.159; see, e.g., David et al. 1999) is given by Ebeling et al. (1996), on the basis of the 10th-ranked cluster galaxy. The true cluster redshift, as estimated in this paper, is instead z=0.195 Even poorer information is known for Abell 1237 (hereafter A1237), a close southern companion of A1240, of richness class =1 and Bautz-Morgan class III (Abell et al. 1989).
We performed spectroscopic and photometric observations of the A1237+A1240 complex with the Telescopio Nazionale Galileo (TNG) and the Isaac Newton Telescope (INT), respectively. Our present analysis is based mainly on our new optical data and X-ray Chandra archival data. We also use the few public redshifts and the photometric data available from the Sloan Digital Sky Survey (SDSS, Data Release 7). This paper is organized as follows. We present our new optical data and the cluster catalog in Sect. 2. We present our results about the cluster structure based on optical and X-ray data in Sects. 3 and 4, respectively. Finally, we briefly discuss our results and give our conclusions in Sects. 5 and 6.
![\begin{figure}
\par\includegraphics[width=17.95cm]{11788f1.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg45.png) |
Figure 1: INT R-band image of the cluster A1240 (North at the top and East to the left) with, superimposed, the contour levels of the Chandra archival image ID 4961 (thin contours; photons in the energy range 0.5-2 keV) and the contour levels of a VLA radio image at 1.4 GHz (thick contours; Bonafede et al. 2009). Arrows show the positions of the two radio relics. Boxes highlight the brightest galaxies of A1240: BCGN, BCGS, and BCGE (see text). |
| Open with DEXTER | |
Unless otherwise stated, we provide errors at the 68% confidence level (hereafter c.l.). Results with a c.l. below 90% are considered very poorly/no significant. The values of these c.l. are generally not explicitly listed throughout the paper.
Throughout this paper, we use H0=70 km s-1 Mpc-1 in a flat cosmology with
![]() and
and
![]() .
In the adopted cosmology, 1
.
In the adopted cosmology, 1
![]() corresponds
to
corresponds
to ![]() 194
h70-1 kpc
194
h70-1 kpc ![]() at the cluster redshift.
at the cluster redshift.
![\begin{figure}
\par\includegraphics[width=18cm]{11788f2.ps}\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg48.png) |
Figure 2: INT R-band image of the A1237+A1240 complex (North at the top and East to the left). Circles and annuli indicate cluster members of A1240 and A1237, respectively (see Table 1). Boxes indicate non-member galaxies. |
| Open with DEXTER | |
2 New data and galaxy catalog
Multi-object spectroscopic observations of A1240 were carried out at
the TNG telescope in December 2006 and December 2007. We used
DOLORES/MOS with the LR-B Grism 1, yielding a dispersion of 187 Å/mm. In December 2006, we used the old Loral CCD with a pixel size
of 15 ![]() m, while in December 2007 we used the new E2V CCD with a
pixel size of 13.5
m, while in December 2007 we used the new E2V CCD with a
pixel size of 13.5 ![]() m. Both the CCDs are matrices of
m. Both the CCDs are matrices of
![]() pixels. In total, we observed four MOS masks (2 in
2006 and 2 in 2007) for a total of 142 slits. We acquired three
exposures of 1800 s for each mask. Wavelength calibration was
performed using Helium-Argon lamps. Reduction of spectroscopic data
was carried out with the IRAF
pixels. In total, we observed four MOS masks (2 in
2006 and 2 in 2007) for a total of 142 slits. We acquired three
exposures of 1800 s for each mask. Wavelength calibration was
performed using Helium-Argon lamps. Reduction of spectroscopic data
was carried out with the IRAF![]() package.
package.
Radial velocities were determined using the cross-correlation
technique (Tonry & Davis 1979) implemented in the RVSAO
package (developed at the Smithsonian Astrophysical Observatory
Telescope Data Center). Each spectrum was correlated with six
templates for a variety of galaxy spectral types: E, S0, Sa, Sb, Sc,
and Ir (Kennicutt 1992). The template producing the highest value
of ![]() ,
i.e., the parameter given by RVSAO and related to the
signal-to-noise ratio of the correlation peak, was chosen. All spectra
and their best correlation functions were examined
visually to verify the redshift determination. In 4 cases (IDs 55, 61,
69, 129, 137; see Table 1), we took the EMSAO redshift
as a reliable estimate of the redshift. Our spectroscopic survey in
the field of A1240 consists of spectra for 118 galaxies with a median
nominal error on cz of 50 km s-1. The nominal errors given by the
cross-correlation are known to be smaller than the true errors (e.g.,
Malumuth et al. 1992; Bardelli et al. 1994; Ellingson
& Yee 1994; Quintana et al. 2000; Boschin et al. 2004). Double redshift determinations for four galaxies allowed us to estimate the true intrinsic errors. We compared the first and second determinations by computing the mean and the rms of the variable
,
i.e., the parameter given by RVSAO and related to the
signal-to-noise ratio of the correlation peak, was chosen. All spectra
and their best correlation functions were examined
visually to verify the redshift determination. In 4 cases (IDs 55, 61,
69, 129, 137; see Table 1), we took the EMSAO redshift
as a reliable estimate of the redshift. Our spectroscopic survey in
the field of A1240 consists of spectra for 118 galaxies with a median
nominal error on cz of 50 km s-1. The nominal errors given by the
cross-correlation are known to be smaller than the true errors (e.g.,
Malumuth et al. 1992; Bardelli et al. 1994; Ellingson
& Yee 1994; Quintana et al. 2000; Boschin et al. 2004). Double redshift determinations for four galaxies allowed us to estimate the true intrinsic errors. We compared the first and second determinations by computing the mean and the rms of the variable
![]() .
We obtained
.
We obtained ![]() with a rms of 2.8, which should be compared with the expected values of 0 and 1. The resulting mean shows that the two sets of measurements are consistent with having the same velocity zeropoint. According to the
with a rms of 2.8, which should be compared with the expected values of 0 and 1. The resulting mean shows that the two sets of measurements are consistent with having the same velocity zeropoint. According to the ![]() -test, the high value of the rms suggests that the errors are underestimated. Only when nominal errors are multiplied by a factor
-test, the high value of the rms suggests that the errors are underestimated. Only when nominal errors are multiplied by a factor ![]() 2 of the rms is in acceptable agreement with the value of 1. Therefore, hereafter we assume that true errors are larger than nominal cross-correlation errors by a factor of 2. For the four galaxies with two redshift estimates, we used the weighted mean of the two measurements and the corresponding errors.
2 of the rms is in acceptable agreement with the value of 1. Therefore, hereafter we assume that true errors are larger than nominal cross-correlation errors by a factor of 2. For the four galaxies with two redshift estimates, we used the weighted mean of the two measurements and the corresponding errors.
We also used 32 publically available redshift data taken from NED within
a box of
![]()
![]() from the cluster center. They come from the SDSS
(Data Release 7). Before matching the SDSS data with our catalog, we payed
particular attention to their compatibility. Five galaxies are in common
between SDSS and TNG data. For them we computed the mean and the rms of
the variable
from the cluster center. They come from the SDSS
(Data Release 7). Before matching the SDSS data with our catalog, we payed
particular attention to their compatibility. Five galaxies are in common
between SDSS and TNG data. For them we computed the mean and the rms of
the variable
![]() .
We obtained
.
We obtained
![]() and
and
![]() ,
to be compared
with the expected values of 0 and 1. The resulting mean shows that the
two sets of measurements are consistent with having the same velocity
zeropoint, and the value of rms is compatible with a value of 1
according to the
,
to be compared
with the expected values of 0 and 1. The resulting mean shows that the
two sets of measurements are consistent with having the same velocity
zeropoint, and the value of rms is compatible with a value of 1
according to the ![]() -test. Thus, we added the redshifts coming
from the literature. For the five galaxies in common we used the
weighted mean of the two redshift determinations and the corresponding
errors. We obtained a final catalog of 145 galaxies with measured
radial velocities.
-test. Thus, we added the redshifts coming
from the literature. For the five galaxies in common we used the
weighted mean of the two redshift determinations and the corresponding
errors. We obtained a final catalog of 145 galaxies with measured
radial velocities.
Our photometric observations were carried out with the Wide Field Camera
(WFC), mounted at the prime focus of the 2.5 m INT telescope. We observed
the A1237+A1240 complex with ![]() and
and ![]() in photometric
conditions. The R image was obtained in 2004 December 19 with a seeing
condition of 3.0
in photometric
conditions. The R image was obtained in 2004 December 19 with a seeing
condition of 3.0
![]() .
We acquired the B image in 2006 May 14 with a
seeing of about 1.1
.
We acquired the B image in 2006 May 14 with a
seeing of about 1.1
![]() .
.
The WFC consists of a four-CCD mosaic covering a
![]()
![]() field of view, with only a 20% marginally vignetted area. We acquired nine exposures of 720 s in
field of view, with only a 20% marginally vignetted area. We acquired nine exposures of 720 s in ![]() and 300 s in
and 300 s in ![]() Harris filters (a total of 6480 s and 2700 s in each band) developing a dithering
pattern of nine positions. This observing mode allowed us to create a ``supersky'' frame that was used to correct our images for fringing patterns (Gullixson 1992). In addition, the dithering helped us to clean cosmic rays and avoid gaps between the CCDs in the final images. The complete reduction process (including flat fielding, bias subtraction, and bad-column elimination) yielded a final coadded image where the variation in the sky was lower than 0.4% in the entire frame. Another effect associated with the wide field frames is the distortion of the field. To match the photometry of several filters, a good astrometric solution is needed to take into account these distortions. Using the imcoords IRAF tasks and taking as a reference the USNO B1.0
catalog, we were able to find an accurate astrometric solution (
Harris filters (a total of 6480 s and 2700 s in each band) developing a dithering
pattern of nine positions. This observing mode allowed us to create a ``supersky'' frame that was used to correct our images for fringing patterns (Gullixson 1992). In addition, the dithering helped us to clean cosmic rays and avoid gaps between the CCDs in the final images. The complete reduction process (including flat fielding, bias subtraction, and bad-column elimination) yielded a final coadded image where the variation in the sky was lower than 0.4% in the entire frame. Another effect associated with the wide field frames is the distortion of the field. To match the photometry of several filters, a good astrometric solution is needed to take into account these distortions. Using the imcoords IRAF tasks and taking as a reference the USNO B1.0
catalog, we were able to find an accurate astrometric solution (
![]()
![]() )
across the full frame. The photometric calibration was performed using Landolt standard fields obtained during the observation.
)
across the full frame. The photometric calibration was performed using Landolt standard fields obtained during the observation.
We finally identified galaxies in our ![]() and
and ![]() images and measured their magnitudes with the SExtractor package
(Bertin & Arnouts 1996) and AUTOMAG procedure. In a few cases
(e.g., close companion galaxies, galaxies close to defects of the CCD),
the standard SExtractor photometric procedure failed. In these cases,
we computed magnitudes by hand. This method consists of assuming a
galaxy profile of a typical elliptical galaxy and scaling it to the
maximum observed value. The integration of this profile gives us an
estimate of the magnitude. This method is similar to PSF photometry,
but assumes a galaxy profile that is more appropriate in this case.
images and measured their magnitudes with the SExtractor package
(Bertin & Arnouts 1996) and AUTOMAG procedure. In a few cases
(e.g., close companion galaxies, galaxies close to defects of the CCD),
the standard SExtractor photometric procedure failed. In these cases,
we computed magnitudes by hand. This method consists of assuming a
galaxy profile of a typical elliptical galaxy and scaling it to the
maximum observed value. The integration of this profile gives us an
estimate of the magnitude. This method is similar to PSF photometry,
but assumes a galaxy profile that is more appropriate in this case.
We transformed all magnitudes to the Johnson-Cousins system (Johnson & Morgan 1953; Cousins 1976). We used
![]() and
and ![]() as derived from the Harris filter
characterization
as derived from the Harris filter
characterization![]() and assuming a
and assuming a
![]() for E-type galaxies (Poggianti 1997). As a final step, we estimated and corrected the galactic extinction
for E-type galaxies (Poggianti 1997). As a final step, we estimated and corrected the galactic extinction
![]() ,
,
![]() from Burstein & Heiles's (1982) reddening maps. We estimated that our photometric sample is complete down to R=20.5 (22.0) and B=22.0 (23.0) for S/N=5 (3) within the observed field. We assigned magnitudes to all galaxies of our spectroscopic catalog. We measured redshifts for galaxies down to magnitude
from Burstein & Heiles's (1982) reddening maps. We estimated that our photometric sample is complete down to R=20.5 (22.0) and B=22.0 (23.0) for S/N=5 (3) within the observed field. We assigned magnitudes to all galaxies of our spectroscopic catalog. We measured redshifts for galaxies down to magnitude ![]() 20, but a high level of completeness is reached only for galaxies with magnitude R<19 (
20, but a high level of completeness is reached only for galaxies with magnitude R<19 (![]() 45% completeness).
45% completeness).
Table 1 provides our velocity catalog (see also
Fig. 2) which contains the following entries:
identification number of each galaxy, ID (Col. 1); right ascension
and declination, ![]() and
and ![]() (J2000, Col. 2); B and R
magnitudes (Cols. 3 and 4); heliocentric radial velocities,
(J2000, Col. 2); B and R
magnitudes (Cols. 3 and 4); heliocentric radial velocities,
![]() (Col. 5) with errors,
(Col. 5) with errors, ![]() (Col. 6); redshift source (Col. 7; T:TNG, S:SDSS); and member assignment (Col. 8; 1:A1240, 2:A1237, 0:background/foreground).
(Col. 6); redshift source (Col. 7; T:TNG, S:SDSS); and member assignment (Col. 8; 1:A1240, 2:A1237, 0:background/foreground).
Table 1: Velocity catalog of 145 spectroscopically measured galaxies in the field of the A1237+A1240 complex.
3 Analysis and results
3.1 Member selection
To select cluster members out of 145 galaxies with redshifts, we followed a two step procedure. First, we performed the 1D adaptive-kernel method (hereafter DEDICA, Pisani 1993, 1996; see also Fadda et al. 1996; Girardi et al. 1996). We searched for significant peaks in the velocity distribution at >99% c.l. This procedure detected A1237+A1240 as a peak at
![]() populated by 95 galaxies considered as candidate cluster members (see Fig. 3). Out of 50 non-members, 24 and 26 are foreground and background galaxies, respectively.
populated by 95 galaxies considered as candidate cluster members (see Fig. 3). Out of 50 non-members, 24 and 26 are foreground and background galaxies, respectively.
 |
Figure 3: Redshift galaxy distribution. The solid line histogram refers to the 95 galaxies assigned to the A1237+A1240 complex according to the DEDICA reconstruction method. |
| Open with DEXTER | |
All the galaxies assigned to the cluster peak were analyzed in the second
step, which uses the combination of position and velocity information,
the ``shifting gapper'' method by Fadda et al. (1996). This
procedure rejects galaxies that are too far in velocity from the main
body of galaxies within a fixed bin that varies it position from the
cluster center. The procedure is iterated until the number
of cluster members converges to a stable value. Following Fadda et al. (1996), we used a gap of 1000 km s![]() - in the cluster
rest-frame - and a bin of 0.6
h70-1 Mpc, or one large enough to include 15
galaxies.
- in the cluster
rest-frame - and a bin of 0.6
h70-1 Mpc, or one large enough to include 15
galaxies.
The choice of the center of A1240 was not obvious. No evident dominant
galaxy is present, but instead there are some luminous galaxies. In
particular, the two brightest ones, ID. 75 and ID. 56, lie in the
southern and northern region of A1240, respectively, and show
comparable luminosity (hereafter BCGS and BCGN). The third is
located in the eastern region, but is ![]() 0.5 R-magnitudes
fainter than BCGS and BCGN (ID. 111, hereafter BCGE). As the
cluster center, we hereafter assume the position of the centroid of
the X-ray emission recovered by David et al. (1999)
[
0.5 R-magnitudes
fainter than BCGS and BCGN (ID. 111, hereafter BCGE). As the
cluster center, we hereafter assume the position of the centroid of
the X-ray emission recovered by David et al. (1999)
[
![]() ,
,
![]() (J2000.0)] which lies between the two dominant
galaxies. After the ``shifting gapper'' procedure we obtain a sample
of 89 fiducial cluster members (see Fig. 4).
(J2000.0)] which lies between the two dominant
galaxies. After the ``shifting gapper'' procedure we obtain a sample
of 89 fiducial cluster members (see Fig. 4).
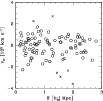 |
Figure 4: Rest-frame velocity vs. projected clustercentric distance for the 95 galaxies in the main peak (Fig. 3) showing galaxies detected as interlopers by our ``shifting gapper'' procedure (crosses). Circles indicate the 89 cluster members. |
| Open with DEXTER | |
We also compared with the results of alternative member selection
procedures. We applied the ``shifting gapper'' procedure adopting
as cluster center the brightest cluster galaxy (BCGS). We found a
cluster sample of 89 galaxies, 88 of which are in common with our
above sample. To analyze the effect of a fully alternative
selection procedure we also applied the classical 3-![]() clipping procedure by Yahil & Vidal (1977) to the entire sample of
145 galaxies after a very rough cut in velocity space,
i.e., rejecting galaxies with velocities differing by more than 8000 km s
clipping procedure by Yahil & Vidal (1977) to the entire sample of
145 galaxies after a very rough cut in velocity space,
i.e., rejecting galaxies with velocities differing by more than 8000 km s![]() from the mean velocity. This classical procedure leads to a
sample of 90 galaxies, 89 of which forms our adopted sample. In
conclusion, the sample of member galaxies that we adopt in this work is
quite unaffected by the member selection procedure.
from the mean velocity. This classical procedure leads to a
sample of 90 galaxies, 89 of which forms our adopted sample. In
conclusion, the sample of member galaxies that we adopt in this work is
quite unaffected by the member selection procedure.
The galaxy distribution analyzed by the 2D DEDICA method clearly shows the presence of a southern external clump (see Fig. 5, see also Sect. 3.7). Gal et al. (2003) recovered a cluster in the same position from the digitized Second Palomar Observatory Sky Survey. We identify this galaxy clump with A1237, which is likely to have a cluster redshift similar to that of A1240 (cf. the magnitudes of their 10th-ranked cluster galaxies, Abell et al. 1989). We note that the center reported by Abell et al. is quite imprecise and lies on the southern border of the galaxy concentration we detect.
![\begin{figure}
\par\includegraphics[width=6cm]{11788f5.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg85.png) |
Figure 5: Spatial distribution on the sky and relative isodensity contour map of cluster members (A1237+A1240), obtained with the DEDICA method. The positions of the brightest galaxies are indicated (BCGN, BCGS, BCGE for A1240 and BCG1 and BCG2 for A1237). The plot is centered on the cluster center defined in this paper as the X-ray center. The two relics are indicated in a schematic way. |
| Open with DEXTER | |
We used the 2D DEDICA results, i.e., the peaks detected in the 2D galaxy distribution, to assign galaxies to different subclumps. The 2D DEDICA algorithm detected nine peaks, four of which are more significant than the 99% c.l. The southern three peaks, only one of which is very significant, we assigned to A1237 (for a total of 27 members). The six northern peaks, three of which are very significant, we assigned to A1240 (for a total of 62 members). This assignment is shown in Fig. 6 - left panel.
As for A1240, the 2D DEDICA algorithm detected a clear bimodal structure (see Fig. 5) along the North-South direction. This bimodality is also shown in our analysis of photometric ``likely'' members in Sect. 3.7 and corresponds to the elongated hot gas distribution shown by the previous analyses of ROSAT data (David et al. 1999; Bonafede et al. 2009) and our analysis of Chandra data (see Sect. 4). Therefore, we decide to consider: a southern structure - hereafter A1240S - associated with the southern peak of A1240 (the most significant in the entire DEDICA analysis); a northern structure - hereafter a1240N - associated to the four northern peaks (two of which are very significant). In this way, we assigned 32 (27) members to A1240N (A1240S). A1240S and A1240N host the brightest and the second brightest galaxies, BCGS and BCGN, respectively. We considered three galaxies separately belonging to a minor, eastern peak (hereafter A1240E) since their assignation to A1240N or A1240S is not obvious. A1240E hosts the BCGE. The assignment of galaxies within A1240 is summarized as follows: we assigned to A1240S the galaxies belonging to the southern peak (detected with a >99.99% c.l.); to A1240N, the galaxies belonging to the four, northern peaks (two of which are detected with a >99.8% c.l.); and to A1240E the galaxies belonging to the eastern peak.
 |
Figure 6: Spatial distribution on the sky of 89 cluster members. Left panel: open symbols indicate cluster members. In particular, squares, circles, rotated squares, and triangles indicate A1240N, A1240S, A1240E and A1237. The crosses indicate emission-line galaxies. Right panel: the larger the symbol, the smaller is the radial velocity. The six close northern circles indicate the high velocity galaxies that we consider to be responsible for the apparent large global mean velocity of A1240N galaxies (see Sect. 3.4 and Fig. 10 in the following, too). |
| Open with DEXTER | |
3.2 The A1237+A1240 complex in velocity space
According to the 1D Kolmogorov-Smirnov test (hereafter 1DKS-test; see, e.g., Press et al 1992), there is no significant difference between the velocity distributions of A1237 and A1240 (see also Fig. 6 - right panel). This result inspired us to investigate the global velocity distribution of this merging structure.
We analyzed the velocity distribution of cluster galaxies (see
Fig. 7) using a few tests where the null hypothesis is
that the velocity distribution is a single Gaussian. We estimated three
shape estimators: the kurtosis, the skewness, and the scaled tail
index (see, e.g., Beers et al. 1991). According to the value
of the skewness (-0.379), the velocity distribution is marginally
asymmetric differing from a Gaussian at the ![]() c.l. (see
Table 2 of Bird & Beers 1993). We also analyze the presence
of ``weighted gaps'' in the velocity distribution. A weighted gap in
the space of the ordered velocities is defined as the difference
between two contiguous velocities, weighted by the location of these
velocities with respect to the middle of the data (Wainer & Schacht 1978; Beers et al. 1991). We detected a strongly significant gap (at the >99.9% c.l.) and five minor gaps (at the
c.l. (see
Table 2 of Bird & Beers 1993). We also analyze the presence
of ``weighted gaps'' in the velocity distribution. A weighted gap in
the space of the ordered velocities is defined as the difference
between two contiguous velocities, weighted by the location of these
velocities with respect to the middle of the data (Wainer & Schacht 1978; Beers et al. 1991). We detected a strongly significant gap (at the >99.9% c.l.) and five minor gaps (at the ![]() 98% c.l.), see Fig. 7 - lower panel. The most
important gap, which is very significant since it is located in the central
region of the velocity distribution, separates the cluster into two
subgroups of 37 and 52 galaxies. When comparing the 2D galaxy
distributions of these subgroups, we found no difference according to
a 2D Kolmogorov-Smirnov test (Fasano & Franceschini 1987).
98% c.l.), see Fig. 7 - lower panel. The most
important gap, which is very significant since it is located in the central
region of the velocity distribution, separates the cluster into two
subgroups of 37 and 52 galaxies. When comparing the 2D galaxy
distributions of these subgroups, we found no difference according to
a 2D Kolmogorov-Smirnov test (Fasano & Franceschini 1987).
 |
Figure 7: Upper panel: velocity histogram for the entire cluster sample (thin line), A1240 (solid line), and A1237 (dashed line). The velocities of the three brightest galaxies of A1240 are indicated (BCGN, BCGS, and BCGE), as well as the two brightest galaxies of A1237 (BCG1 and BCG2). Lower panel: stripe density plot where the arrows indicate the positions of the significant gaps. The main and minor weighted gaps are indicated by large and small arrows, respectively. |
| Open with DEXTER | |
We also performed the 2D and 3D Kaye's mixture model (KMM) test (as implemented by Ashman et al. 1994) and compared the results to check the effect of adding velocity information. The KMM algorithm fits a user-specified number of Gaussian distributions to a dataset and assesses the improvement of that fit over a single Gaussian and give an assignment of objects into groups. We used the A1237+A1240 galaxy assignment found by the 2D DEDICA analysis to determine the first guess when fitting two groups. The 2D KMM algorithm identifies a two-group partition, at the >99.9% c.l. according to the likelihood ratio test, leading to two groups of 66 and 23 galaxies. The addition of the velocity information to the KMM algorithm leads to the same group partition.
Finally, we combined galaxy velocity and position information to compute the ![]() -statistics devised by Dressler & Shectman (1988). This test is sensitive to spatially compact subsystems that have either an average velocity differing from the cluster mean, or a velocity dispersion that differs from the global value, or both. We found no evidence of substructure.
-statistics devised by Dressler & Shectman (1988). This test is sensitive to spatially compact subsystems that have either an average velocity differing from the cluster mean, or a velocity dispersion that differs from the global value, or both. We found no evidence of substructure.
We conclude that, although the velocity distribution shows evidence of a complex structure, A1237 and A1240 are so similar in velocity space that the velocity information is not useful in improving the galaxy assignment recovered from the 2D analysis (see Sect. 3.1).
3.3 Global kinematical properties
As for the entire cluster complex, by applying the biweight estimator to
the 89 members (Beers et al. 1990), we
computed a mean redshift of
![]() 0.0003, i.e.,
0.0003, i.e.,
![]() km s-1. We estimated the LOS velocity
dispersion,
km s-1. We estimated the LOS velocity
dispersion,
![]() ,
by using the biweight estimator and
applying the cosmological correction and the standard correction for
velocity errors (Danese et al. 1980). We obtain
,
by using the biweight estimator and
applying the cosmological correction and the standard correction for
velocity errors (Danese et al. 1980). We obtain
![]() km s-1, where the errors were estimated by a
bootstrap technique.
km s-1, where the errors were estimated by a
bootstrap technique.
The results obtained for the 62 members of A1240 are:
![]() ,
i.e.,
,
i.e.,
![]() km s
km s![]() ,
and
,
and
![]() km s-1. To evaluate the robustness of
km s-1. To evaluate the robustness of
![]() of A1240, we analyze the velocity dispersion profile
(Fig. 8). The integral profile is roughly flat in the
external cluster regions suggesting that the value of
of A1240, we analyze the velocity dispersion profile
(Fig. 8). The integral profile is roughly flat in the
external cluster regions suggesting that the value of
![]() for A1240 is quite robust. Figure 8 also shows that the
for A1240 is quite robust. Figure 8 also shows that the
![]() and
and
![]() profiles are not disturbed
by the presence of A1237. Table 2 lists the number of the
member galaxies
profiles are not disturbed
by the presence of A1237. Table 2 lists the number of the
member galaxies ![]() and the main kinematical properties of
A1237 and A1240. Figure 9 compares the
and the main kinematical properties of
A1237 and A1240. Figure 9 compares the
![]() and
and
![]() profiles of A1240 and A1237,
where for A1240 we show separately the results for A1240N and A1240S.
The value
profiles of A1240 and A1237,
where for A1240 we show separately the results for A1240N and A1240S.
The value
![]() of A1237 is similar to that of A1240S,
suggesting a continuity in the velocity field. However, the
value of
of A1237 is similar to that of A1240S,
suggesting a continuity in the velocity field. However, the
value of
![]() of A1237 is clearly lower than that of A1240S,
suggesting that A1237 is truly a less massive system.
of A1237 is clearly lower than that of A1240S,
suggesting that A1237 is truly a less massive system.
 |
Figure 8:
Upper panel: rest-frame velocity (in units of 103 km s-1) vs. projected clustercentric distance for the 89 cluster galaxies. Circles and squares indicate members of A1240 and A1237. Central and lower panels: integral profiles of mean LOS velocity (in units of 103 km s-1) and LOS velocity dispersion (in units of km s-1) for the 62 members of A1240 (dots with the |
| Open with DEXTER | |
Table 2: Global properties of galaxy systems.
 |
Figure 9: Upper panel: rest-frame velocity (in units of 103 km s-1) vs. projected clustercentric distance for the members of A1240N (squares), A1240S (circles) and A1237 (crosses). In this and other panels, the lower axis give the clustercentric distance of A1240N (A1240S) galaxies versus the negative (positive) axis from the A1240 center, while the upper axis give the clustercentric distance of A1237 galaxies from the A1237 center. The center of A1240 is defined as the X-ray center. The center of A1237 is defined as the position of the main peak in the 2D analysis. Central and lower panels: 68% error bands of integral profiles of LOS mean velocity (in units of 103 km s-1) and LOS velocity dispersion (in units of km s-1) for A1240N and A1240S (solid lines) and A1237 (dashed lines). The circles in the central panel indicate the positions and velocities of the two brightest galaxies of A1240 (BCGN and BCGS) and the two brightest galaxies of A1237 (BCG1 and BCG2). |
| Open with DEXTER | |
3.4 Internal structure of A1240
According to the 1DKS-test, there is no difference between the velocity distributions of A1240N and A1240S. The velocity distribution of A1240 shows signatures of non-Gaussianity similar to those of the entire cluster complex (e.g. a slight asymmetry and an important gap, see Fig. 7). As in the case of A1237 versus (hereafter vs.) A1240 case, we find that A1240N and A1240S are so similar in velocity space that the velocity information is not useful for improving the galaxy assignment. However, in contrast to the case of A1237 and A1240, A1240N and A1240S are spatially closer and probably strongly interacting (see Sect. 5). This implies that the galaxy assignment is be questionable and that we must devote more care in determining the individual kinematical properties of the two subclumps.
The value of global
![]() of A1240N is nominally
larger than that of A1240S, i.e.,
of A1240N is nominally
larger than that of A1240S, i.e.,
![]() km s
km s![]() and
and
![]() km s
km s![]() respectively, only at
a
respectively, only at
a ![]() 2
2![]() c.l. Looking at Fig. 9,
the two cores of A1240N and A1240S also seem to have similar
c.l. Looking at Fig. 9,
the two cores of A1240N and A1240S also seem to have similar
![]() :
this is shown in Fig. 10,
where we directly compare the profiles of A1240N and A1240S. The
large global
:
this is shown in Fig. 10,
where we directly compare the profiles of A1240N and A1240S. The
large global
![]() of A1240N is probably caused by a
few galaxies with high velocity with respect to mean cluster radial
velocity in the extreme northern cluster regions (see the six galaxies
shown as close circles in Fig. 6 - right panel; see also Fig. 10). The recent merger of two subclumps may indeed result in a plume, or arm, of outflying
galaxies detected in terms of their different velocity with respect to the cluster (see e.g., the case of Abell 3266; Quintana et al. 1996; and Flores et al. 2000). Because of these difficulties in detecting a quantitative difference between A1240N and A1240S, we decided to use the position and velocity of BCGN and BCGS as tracers of the two interacting clumps. Dominant galaxies trace the cluster substructures (Beers & Geller 1983) and are also good tracers of interacting subclumps during a cluster merger (e.g., Boschin et al. 2006; Barrena et al. 2007a; Boschin et al. 2009).
of A1240N is probably caused by a
few galaxies with high velocity with respect to mean cluster radial
velocity in the extreme northern cluster regions (see the six galaxies
shown as close circles in Fig. 6 - right panel; see also Fig. 10). The recent merger of two subclumps may indeed result in a plume, or arm, of outflying
galaxies detected in terms of their different velocity with respect to the cluster (see e.g., the case of Abell 3266; Quintana et al. 1996; and Flores et al. 2000). Because of these difficulties in detecting a quantitative difference between A1240N and A1240S, we decided to use the position and velocity of BCGN and BCGS as tracers of the two interacting clumps. Dominant galaxies trace the cluster substructures (Beers & Geller 1983) and are also good tracers of interacting subclumps during a cluster merger (e.g., Boschin et al. 2006; Barrena et al. 2007a; Boschin et al. 2009).
The nominal value of global
![]() of A1240N is smaller than
that of A1240S, the two values being
of A1240N is smaller than
that of A1240S, the two values being
![]() km s
km s![]() and
and
![]() km s
km s![]() ,
respectively. Using the
brightest galaxies as centers when comparing the respective
,
respectively. Using the
brightest galaxies as centers when comparing the respective
![]() profiles confirms this trend (see Fig. 10 - right lower
panel). Thus, although the nominal values of individual
profiles confirms this trend (see Fig. 10 - right lower
panel). Thus, although the nominal values of individual
![]() might
not be fully reliable, we decide to adopt them in describing A1240N
and A1240S. Table 2 summarizes the properties of A1240N
and A1240S.
might
not be fully reliable, we decide to adopt them in describing A1240N
and A1240S. Table 2 summarizes the properties of A1240N
and A1240S.
 |
Figure 10: Upper panels: error bands of integral profiles of LOS mean velocity for A1240N (dashed line) and A1240S (solid line). The distance is computed using as the center the position of the most important peak (on the left) and the position of the brightest cluster member (on the right). The horizontal lines indicate the velocities of BCGN and BCGS (dashed and solid lines, respectively). The close circles point out at which radius the six northern high velocity galaxies in A1240N are included to show their effect on the estimate of the mean velocity (see the text and Fig. 6, too). Lower panels: the same for integral profiles of the LOS velocity dispersion. |
| Open with DEXTER | |
3.5 Internal structure of A1237
As for A1237, it appears dominated by two bright galaxies, BCG1 and
BCG2 (IDs. 29 and 27, see Table 1) and the 2D DEDICA
algorithm shows the presence of one significant peak (at the >99% c.l.) and two minor peaks that are significant at the 97% and 89% c.l. (see the somewhat elongated structure of A1237 in
Fig. 5). Both the analysis of SDSS and our photometric data show that A1237 has only one clearly defined peak in the 2D galaxy distribution (see Sect. 3.7). This last result is based on a much larger sample, thus we conclude that we have no evidence of a complex structure in A1237. The velocity distribution shows evidence of a platykurtic behavior, but at a poorly significant
level (at the ![]() 95% c.l.).
95% c.l.).
3.6 Mass estimates
Under the usual assumptions (cluster sphericity, dynamical equilibrium
and galaxy distribution tracing the mass distribution), we can compute
global virial quantities. Following the prescriptions of Girardi &
Mezzetti (2001), the virial radius is
![]() h70-1 Mpc
h70-1 Mpc![]() (see their Eq. (1) after introducing the scaling
with H(z); see also Eq. (8) of Carlberg et al. 1997, for
R200) and the virial mass (Limber & Mathews 1960; see
also, e.g., Girardi et al. 1998) is:
(see their Eq. (1) after introducing the scaling
with H(z); see also Eq. (8) of Carlberg et al. 1997, for
R200) and the virial mass (Limber & Mathews 1960; see
also, e.g., Girardi et al. 1998) is:
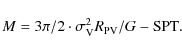 |
(2) |
The quantity SPT, the surface pressure term correction (The & White 1986), is assumed to be equal to 20% of the mass since this is the typical value recovered for the mass computed within the virial radius in the literature when the data of many clusters are combined together to improve the quality of the statistical analysis (Carlberg et al. 1997; Girardi et al. 1998). The quantity
After applying this procedure, we obtain a mass estimate of
![]()
![]()
![]() and
and
![]()
![]()
![]() .
.
When a cluster shows a strongly substructured appearance (e.g., a
bimodal structure), the use of the global
![]() to compute
the mass might be misleading (Girardi et al. 1997, and
refs. therein). The true mass could be overestimated or
underestimated depending on the viewing angle of the cluster
structure. When the two subclumps are aligned along the LOS, they
cannot be clearly distinguished in their projection on the sky, but
they can appear as two peaks (less or more overlapped, depending on
their relative velocity) in the redshift distribution: in this case
the mass estimated by the observed global
to compute
the mass might be misleading (Girardi et al. 1997, and
refs. therein). The true mass could be overestimated or
underestimated depending on the viewing angle of the cluster
structure. When the two subclumps are aligned along the LOS, they
cannot be clearly distinguished in their projection on the sky, but
they can appear as two peaks (less or more overlapped, depending on
their relative velocity) in the redshift distribution: in this case
the mass estimated by the observed global
![]() is
likely to be an overestimate of the true cluster mass (e.g.,
cf. Tables 7 and 8 of Girardi et al. 1998). When the two
subclumps are aligned along an axis parallel to the plane of sky,
they appear as two structures in their projection on the sky but
they cannot be distinguished in the redshift distribution (since
their relative velocity has no component along the LOS
direction). In this case the global velocity distribution is probably
related to the superimposed velocity distributions of the two clusters
and the observed global
is
likely to be an overestimate of the true cluster mass (e.g.,
cf. Tables 7 and 8 of Girardi et al. 1998). When the two
subclumps are aligned along an axis parallel to the plane of sky,
they appear as two structures in their projection on the sky but
they cannot be distinguished in the redshift distribution (since
their relative velocity has no component along the LOS
direction). In this case the global velocity distribution is probably
related to the superimposed velocity distributions of the two clusters
and the observed global
![]() does not accurately reflect
the existence of both the two subclumps.
does not accurately reflect
the existence of both the two subclumps.
The A1240N+A1240S system is comparable to the second case discussed
above: the two subclumps can be separated on the sky, but lie at a
similar z. Our analysis in Sect. 5 indeed shows that
the axis of the A1240N+A1240S system is probably roughly parallel to the
plane of sky. A more reliable mass estimate of A1240 might be
obtained by adding the mass estimates of the two subclumps, each mass
recovered from their respective
![]() (see
Table 2). We obtain a mass
(see
Table 2). We obtain a mass
![]()
![]() .
Another possible approach is to consider the future, virialized A1240
cluster and its global properties. Since the cluster virial mass
computed within the virial radius scales with
.
Another possible approach is to consider the future, virialized A1240
cluster and its global properties. Since the cluster virial mass
computed within the virial radius scales with
![]() ,
we expect that the
,
we expect that the
![]() of the virialized A1240
corresponds to
of the virialized A1240
corresponds to
![]() ,
i.e.,
,
i.e.,
![]() km s
km s![]() ,
which is larger than the LOS
,
which is larger than the LOS
![]() measured in observed data. This
corresponds to a mass of
measured in observed data. This
corresponds to a mass of
![]()
![]()
![]() in good agreement with the above estimate. In conclusion,
we estimated a mass in the range of
in good agreement with the above estimate. In conclusion,
we estimated a mass in the range of
![]()
![]() for
A1240, and a combined cluster mass of
for
A1240, and a combined cluster mass of
![]()
![]() .
.
3.7 Analysis of photometric data
The results of the 2D DEDICA method applied to the 89 cluster members are shown in Sect. 3.1. However, our spectroscopic data are affected by magnitude incompleteness and the field around the cluster is not covered in an homogeneous way. To overcome these limits, we used our photometric catalog.
We selected cluster member candidates on the basis of the B-R vs.
R relation, as already performed in some previous works of ours (e.g., Barrena et al. 2007b). To determine the relation, we fixed the slope according to López-Cruz et al. (2004, see their Fig. 3) and
applied the 2![]() -clipping fitting procedure to the cluster
members obtaining
-clipping fitting procedure to the cluster
members obtaining
![]() for the red sequence of
A1240 galaxies. Figure 11 shows B-R vs. R diagram for
galaxies with available spectroscopy and the fitted line.
for the red sequence of
A1240 galaxies. Figure 11 shows B-R vs. R diagram for
galaxies with available spectroscopy and the fitted line.
In our photometric catalog, we considered galaxies (objects with
SExtractor stellar index ![]() 0.9) lying within 0.25 mag of the
relation. Following Visvanathan & Sandage (1977), the width
of 0.25 mag corresponds approximately to 2
0.9) lying within 0.25 mag of the
relation. Following Visvanathan & Sandage (1977), the width
of 0.25 mag corresponds approximately to 2![]() around the
color-magnitude relation (see also Mazure et al. 1988, for
a classical application to the Coma cluster). The contour map for 370
probable cluster members with
around the
color-magnitude relation (see also Mazure et al. 1988, for
a classical application to the Coma cluster). The contour map for 370
probable cluster members with ![]() shows the bimodal structure of
A1240 and the presence of A1237, confirming the results of
Sect. 3.1 (see Fig. 12). Similar results were
obtained with different magnitude cut-offs (e.g.,
shows the bimodal structure of
A1240 and the presence of A1237, confirming the results of
Sect. 3.1 (see Fig. 12). Similar results were
obtained with different magnitude cut-offs (e.g., ![]() and
and ![]() ).
).
![\begin{figure}
\par\includegraphics[width=8cm]{11788f11.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg147.png) |
Figure 11:
B-R vs. R diagram for galaxies with available spectroscopy is shown by large circles and squares (members and non-members, respectively). Small points indicate galaxies found in our INT photometric sample, i.e., objects with a class star |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{11788f12.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg148.png) |
Figure 12:
Spatial distribution on the sky and relative isodensity contour map
of probable cluster members (applying the color-magnitude selection to the INT photometric catalog) with |
| Open with DEXTER | |
We also used public photometric data from the SDSS. In particular, we used r', i', and z' magnitudes, already corrected for Galactic extinction and consider galaxies within a radius of 30
![]() from the cluster center.
from the cluster center.
Following Boschin et al. (2008, see also Goto et al. 2002), from the SDSS photometric catalog we considered
galaxies (here objects with r' phototype parameter =3)
within ![]() 0.08 mag in value from the median values of
r'-i'=0.47 and
i'-z'=0.32 colors of the spectroscopically cluster members. The
value of 0.08 mag is two times the typical scatter reported by Goto et
al. (2002) for the corresponding color-magnitude relations
r'-i' vs. r' and i'-z' vs. r'. However, this
member selection does not seem enough conservative in the case of
A1240. Using our spectroscopic catalog, we notice that this
color-color selection recognizes as ``likely members'' 21 of the
56 non-member galaxies (compared to the 11 of 56 using the
color-magnitude selection). Therefore, we decided to use here a more
conservative selection, i.e., considering only galaxies lying within
0.08 mag in value from the median values of
r'-i'=0.47 and
i'-z'=0.32 colors of the spectroscopically cluster members. The
value of 0.08 mag is two times the typical scatter reported by Goto et
al. (2002) for the corresponding color-magnitude relations
r'-i' vs. r' and i'-z' vs. r'. However, this
member selection does not seem enough conservative in the case of
A1240. Using our spectroscopic catalog, we notice that this
color-color selection recognizes as ``likely members'' 21 of the
56 non-member galaxies (compared to the 11 of 56 using the
color-magnitude selection). Therefore, we decided to use here a more
conservative selection, i.e., considering only galaxies lying within
![]() 0.04 mag from the median values of r'-i' and i'-z'colors (see Fig. 13 with 272 galaxies for r'<20.8).
The galaxy distribution shows the N-S elongation of A1240 and the
presence of A1237. Another cluster is also shown at
0.04 mag from the median values of r'-i' and i'-z'colors (see Fig. 13 with 272 galaxies for r'<20.8).
The galaxy distribution shows the N-S elongation of A1240 and the
presence of A1237. Another cluster is also shown at ![]() 25
25
![]() south-east of A1240. This cluster was also detected by Gal et al. (2003) and Koester et al. (2007), who estimated a
photometric
south-east of A1240. This cluster was also detected by Gal et al. (2003) and Koester et al. (2007), who estimated a
photometric
![]() -0.19.
-0.19.
![\begin{figure}
\par\includegraphics[width=8cm]{11788f13.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg150.png) |
Figure 13:
Spatial distribution on the sky and relative isodensity contour map
of likely cluster members (applying the color-color selection to the SDSS photometric catalog) with
|
| Open with DEXTER | |
4 X-ray analysis of A1240
The X-ray analysis of A1240 was performed on the archival data of the Chandra ACIS-I observation 800407 (exposure ID #4961). The pointing has an exposure time of 52 ks. Data reduction was performed using the package CIAO![]() (Chandra Interactive Analysis of Observations) on chips I0, I1, I2, and I3 (field of view
(Chandra Interactive Analysis of Observations) on chips I0, I1, I2, and I3 (field of view ![]()
![]() ). First, we removed events from the level 2 event list with a status not equal to zero and with grades one, five, and seven. We then selected all events with energy between 0.3 and 10 keV. In addition, we cleaned bad offsets and examined the data, filtering out bad columns and removing data for when the count rate exceeded three standard deviations from the mean count rate per 3.3 s interval. We then cleaned the chips for flickering pixels, i.e., times where a pixel has events in two sequential 3.3 s intervals. The resulting exposure time for the reduced data was 51.3 ks.
). First, we removed events from the level 2 event list with a status not equal to zero and with grades one, five, and seven. We then selected all events with energy between 0.3 and 10 keV. In addition, we cleaned bad offsets and examined the data, filtering out bad columns and removing data for when the count rate exceeded three standard deviations from the mean count rate per 3.3 s interval. We then cleaned the chips for flickering pixels, i.e., times where a pixel has events in two sequential 3.3 s intervals. The resulting exposure time for the reduced data was 51.3 ks.
A quick look at the reduced image is sufficient ascertain approximately the morphology of the extended X-ray emission of A1240. However, the cluster was centered exactly on the ``cross'' of the gaps among the four chips. To obtain a more precise result, we had to correct the photon counts in the poorly exposed ACIS CCD gaps. First, we binned the reduced image. We then applied a soft smoothing and correct the photon counts by dividing by an exposure map. The result is an image from which we extracted the contour levels (soft photons in the energy range 0.5-2 keV) plotted in Fig. 1.
The complex X-ray morphology of A1240 is clearly evident. In particular,
the central X-ray emission is clearly elongated in the N-S direction,
i.e., in the same direction defined by the two galaxy clumps A1240N and
A1240S. Contour levels in Fig. 1 also areindicative of a
diffuse source ![]() 6
6
![]() SE of the cluster center. A visual inspection of
the INT R-band image shows that this structure does not relate to
any evident galaxy concentration. We suspect that it could be a distant
background galaxy group. Unfortunately, a more quantitative
morphological analysis is not trivial. The gaps in the
ACIS chips can in fact make the computation of the surface
brightness distribution quite difficult. The disturbed morphology of the ICM
is also inconsistent with our sphericaly symmetric assumption. These
factors together, unfortunately, make no possible a detailed X-ray analysis.
SE of the cluster center. A visual inspection of
the INT R-band image shows that this structure does not relate to
any evident galaxy concentration. We suspect that it could be a distant
background galaxy group. Unfortunately, a more quantitative
morphological analysis is not trivial. The gaps in the
ACIS chips can in fact make the computation of the surface
brightness distribution quite difficult. The disturbed morphology of the ICM
is also inconsistent with our sphericaly symmetric assumption. These
factors together, unfortunately, make no possible a detailed X-ray analysis.
 |
Figure 14:
|
| Open with DEXTER | |
As for the spectral properties of the cluster X-ray photons, we
compute a global estimate of the ICM temperature. The temperature is
computed from the X-ray spectrum of the cluster within a circular
aperture of ![]() 2.58
2.58
![]() radius (0.5 Mpc at the cluster
redshift; see Fig. 14) around the center of the four
ACIS chips. By fixing the absorbing Galactic hydrogen column density at
radius (0.5 Mpc at the cluster
redshift; see Fig. 14) around the center of the four
ACIS chips. By fixing the absorbing Galactic hydrogen column density at
![]() cm-2, as computed from the HI maps by Dickey
& Lockman (1990), we fit a Raymond-Smith (1977)
spectrum using the CIAO package Sherpa with a
cm-2, as computed from the HI maps by Dickey
& Lockman (1990), we fit a Raymond-Smith (1977)
spectrum using the CIAO package Sherpa with a ![]() statistics
and assuming a metal abundance of 0.3 in solar units. We found a best-fit
model temperature of
statistics
and assuming a metal abundance of 0.3 in solar units. We found a best-fit
model temperature of
![]() keV.
keV.
We then searched for temperature gradients by dividing the 0.5 Mpc radius circle into four quadrants (chosen in order to avoid the gaps among the chips), as shown in Fig. 14. As expected for a
merging cluster, there is some evidence that the ICM temperature is not homogeneous, with the Western quadrant (
![]() keV) being hotter than the Northern (
keV) being hotter than the Northern (
![]() keV), the Eastern (
keV), the Eastern (
![]() keV), and Southern (
keV), and Southern (
![]() keV) quadrants. More detailed temperature and metallicity maps would be very helpful for a more accurate measurement of the properties of the ICM, but the photon statistics is insufficient for this aim. In particular, we do not provide any estimate of the ICM temperature in the proximity of the two relics, where the X-ray surface brightness is too low to obtain any reliable measurement (see Fig. 14).
keV) quadrants. More detailed temperature and metallicity maps would be very helpful for a more accurate measurement of the properties of the ICM, but the photon statistics is insufficient for this aim. In particular, we do not provide any estimate of the ICM temperature in the proximity of the two relics, where the X-ray surface brightness is too low to obtain any reliable measurement (see Fig. 14).
5 Discussion of cluster structure
Optical and available X-ray data indicate that A1240 is a strongly substructured cluster, elongated in the N-S direction, the same direction as the axis of symmetry of the relics. We have also detect two clumps, separated by 1.2 h70-1 Mpc, in the galaxy distribution. These observational features suggest that we are observing a cluster that has just formed by the merging of two main subclumps. The difficulty in separating the two subclumps in velocity space and the small LOS velocity difference between the two BCGs suggest that the axis of the merger lies in the plane of the sky. The evidence of a very disturbed ICM distribution, somewhat displaced from the galaxy distribution, suggests that the merger is seen after the phase of the core passage, as shown by the results of the numerical simulation (e.g., Roettiger et al. 1997, their Figs. 7-14).
In terms of observational cluster structure, A1240 is similar to Abell
3667 (see Roettiger et al. 1999, and refs. therein), where the
optical and X-ray structures are elongated in a direction roughly
similar to that of the axis of symmetry of the two radio relics, which
are separated by ![]() 3-4
h70-1 Mpc. The two intervening galaxy subclumps
are separated by
3-4
h70-1 Mpc. The two intervening galaxy subclumps
are separated by ![]() 1
h70-1 Mpc
1
h70-1 Mpc![]() with a small LOS velocity difference
with a small LOS velocity difference
![]() 120 km s
120 km s![]() between the dominant galaxies. Basic observational
features of Abell 3667 can be explained by the ``outgoing merger
shocks'' model, where shocks provide sites of diffusive shock
acceleration of relativistic electrons causing the presence of the
radio sources (Roettiger et al. 1999).
between the dominant galaxies. Basic observational
features of Abell 3667 can be explained by the ``outgoing merger
shocks'' model, where shocks provide sites of diffusive shock
acceleration of relativistic electrons causing the presence of the
radio sources (Roettiger et al. 1999).
For A1240, we have detected two galaxy subclumps in the N-S direction, the same direction as the elongation of the X-ray surface brightness and the axis of symmetry of the two radio relics. The values of relevant parameters for the two-clump system, deduced from the BCGN and BCGS, are the relative LOS velocity in the rest-frame,
![]() km s
km s![]() ,
and the projected linear distance between the two clumps, D=1.2
h70-1 Mpc. The two roughly symmetric relics lie more externally, separated by a projected linear distance
,
and the projected linear distance between the two clumps, D=1.2
h70-1 Mpc. The two roughly symmetric relics lie more externally, separated by a projected linear distance ![]() 2
h70-1 Mpc
2
h70-1 Mpc![]() (Bonafede et al. 2009).
(Bonafede et al. 2009).
We now use the above parameters and the mass of the system computed to be in a range of
![]()
![]() to investigate the dynamics of A1240N and A1240S. In particular, we use different analytic approaches based on an energy integral formalism in the framework of locally flat spacetime and Newtonian gravity (e.g., Beers et al. 1982).
to investigate the dynamics of A1240N and A1240S. In particular, we use different analytic approaches based on an energy integral formalism in the framework of locally flat spacetime and Newtonian gravity (e.g., Beers et al. 1982).
First, we compute the Newtonian criterion for gravitational binding
that is stated in terms of the observables to be
![]() ,
where
,
where ![]() is the
projection angle between the plane of the sky and the line connecting
the centers of the two clumps. The thin curve in Fig. 15
separates the bound and unbound regions according to the Newtonian
criterion (above and below the curve, respectively). Considering the
lower (upper) limit to
is the
projection angle between the plane of the sky and the line connecting
the centers of the two clumps. The thin curve in Fig. 15
separates the bound and unbound regions according to the Newtonian
criterion (above and below the curve, respectively). Considering the
lower (upper) limit to
![]() ,
the N+S system is bound between
,
the N+S system is bound between
![]() and
and
![]() (
(
![]() and
and
![]() ); the
corresponding probability, computed by considering the solid angles
(i.e.,
); the
corresponding probability, computed by considering the solid angles
(i.e.,
![]() ), is 84%
(89%).
), is 84%
(89%).
 |
Figure 15:
System mass vs. projection angle for bound and unbound solutions
(thick solid and thick dashed curves, respectively) of
the two-body model applied to A1240N and A1240S subsystems. Labels
BI |
| Open with DEXTER | |
Then, we applied the analytical two-body model introduced by Beers et al. (1982) and Thompson (1982; see also Lubin et al. 1998, for a more recent application). This model assumes radial orbits for the clumps with no shear or net rotation of the system. According to the boundary conditions usually considered, the clumps are assumed to begin their evolution at time t0=0 with a separation d0=0, and are now moving apart or coming together for the first time in their history.
In the case of the A1240N+A1240S system, where the first core passage has probably already occurred, we assume that the time t0=0 with separation d0=0 is the time of their core crossing and that we are looking at the cluster a time t after. To obtain an estimate of t, we use the Mach number of the shock
![]() as inferred by Bonafede et al. (2009) from the radio spectral index. The Mach number is defined to be
as inferred by Bonafede et al. (2009) from the radio spectral index. The Mach number is defined to be
![]() ,
where
,
where
![]() is the velocity of the shock and
is the velocity of the shock and ![]() in the sound speed in the pre-shock gas (see e.g., Sarazin 2002, for a review). The value of
in the sound speed in the pre-shock gas (see e.g., Sarazin 2002, for a review). The value of ![]() ,
obtained from our estimate of
,
obtained from our estimate of ![]() ,
i.e.,
,
i.e.,
![]() km s-1, leads to a value of
km s-1, leads to a value of
![]() km s-1. Assuming the shock velocity to be a constant, the shock covered a
km s-1. Assuming the shock velocity to be a constant, the shock covered a ![]() 1
h70-1 Mpc
1
h70-1 Mpc![]() scale (i.e., the distance of the relics from the cluster center) in a time of
scale (i.e., the distance of the relics from the cluster center) in a time of ![]() 0.3 Gyr. We assume this time as our estimate of t. Although the velocity of the shock is not constant, studies based on numerical simulations show how the variation in
0.3 Gyr. We assume this time as our estimate of t. Although the velocity of the shock is not constant, studies based on numerical simulations show how the variation in
![]() is much smaller than the variation in the relative velocity of the subclumps identified with their dark matter components (see Fig. 4 of Springel & Farrar 2007; and Fig. 14 of Mastropietro & Burkert 2008), thus our rough estimate of t is acceptable as a first order approximation.
is much smaller than the variation in the relative velocity of the subclumps identified with their dark matter components (see Fig. 4 of Springel & Farrar 2007; and Fig. 14 of Mastropietro & Burkert 2008), thus our rough estimate of t is acceptable as a first order approximation.
The bimodal model solution gives the total system mass
![]() as a function of
as a function of ![]() (e.g., Gregory & Thompson 1984).
Figure 15 compares the bimodal-model solutions with the
observed mass of the system. The present solutions span the bound
outgoing solutions (i.e., expanding), BO; the bound incoming solutions
(i.e., collapsing), BI
(e.g., Gregory & Thompson 1984).
Figure 15 compares the bimodal-model solutions with the
observed mass of the system. The present solutions span the bound
outgoing solutions (i.e., expanding), BO; the bound incoming solutions
(i.e., collapsing), BI![]() and BI
and BI![]() ;
and the unbound
outgoing solutions, UO. For the incoming case, there are two solutions
because of the ambiguity in the projection angle
;
and the unbound
outgoing solutions, UO. For the incoming case, there are two solutions
because of the ambiguity in the projection angle ![]() .
Both the BO
and UO solutions are, in principle, consistent with the observed mass
range. However, the BO solution is the more likely solution, since the
probability associated with the BO solution is much higher than that
associated with the UO solution. We obtain that P(BO) and P(UO) are,
in fact,
.
Both the BO
and UO solutions are, in principle, consistent with the observed mass
range. However, the BO solution is the more likely solution, since the
probability associated with the BO solution is much higher than that
associated with the UO solution. We obtain that P(BO) and P(UO) are,
in fact, ![]() and
and ![]() ,
respectively, where these probabilities
are computed considering the solid angles (see above) and assuming
that the region of
,
respectively, where these probabilities
are computed considering the solid angles (see above) and assuming
that the region of
![]() values is equally probable for
individual solutions (see e.g., Barrena et al. 2007b). For
the projection angle, we assume a value of
values is equally probable for
individual solutions (see e.g., Barrena et al. 2007b). For
the projection angle, we assume a value of
![]()
![]() .
This small angle means that the true spatial distance
between A1240 subclumps is similar to the projected one while the
real, i.e. deprojected, velocity difference is
.
This small angle means that the true spatial distance
between A1240 subclumps is similar to the projected one while the
real, i.e. deprojected, velocity difference is
![]() km s-1, a quite reasonable value during cluster mergers (see,
e.g. Springel & Farrar 2007, and refs. therein). We note that
the relative velocity between galaxy clumps is smaller than the shock
velocity, i.e., the regime is not stationary, but this is expected
when comparing shock and collisionless components in numerical
simulations (Springel & Farrar 2007; Mastropietro & Burkert
2008). The merger of the A1240 clumps occurred main in the
plane of the sky, so it is very similar to the case of Abell 3667.
However, the case of A1240 is more complicated because of the presence
of A1237.
km s-1, a quite reasonable value during cluster mergers (see,
e.g. Springel & Farrar 2007, and refs. therein). We note that
the relative velocity between galaxy clumps is smaller than the shock
velocity, i.e., the regime is not stationary, but this is expected
when comparing shock and collisionless components in numerical
simulations (Springel & Farrar 2007; Mastropietro & Burkert
2008). The merger of the A1240 clumps occurred main in the
plane of the sky, so it is very similar to the case of Abell 3667.
However, the case of A1240 is more complicated because of the presence
of A1237.
We investigate the relative dynamics of A1237 and A1240 with the same
approach described above. The values of the relevant observable
quantities for the two-clump system are based on Table 2,
i.e. LOS
![]() km s
km s![]() and D=2.7
h70-1 Mpc. For the mass of the
system, we use the mass range computed in Sect. 3.6,
and D=2.7
h70-1 Mpc. For the mass of the
system, we use the mass range computed in Sect. 3.6,
![]()
![]() .
The Newtonian criterion for
gravitational binding leads to a system bound between
.
The Newtonian criterion for
gravitational binding leads to a system bound between
![]() and
and
![]() (
(
![]() and
and
![]() ); the corresponding
probability, computed by considering the solid angles (i.e.,
); the corresponding
probability, computed by considering the solid angles (i.e.,
![]() ), is
), is ![]() (
(![]() ).
).
In the case of A1237 and A1240, we have no evidence of a previous
merger since the gas distribution of A1240 (although very complex)
does not show any evidence of peculiar displacement in the direction of
A1237. We therefore assume that we are looking at A1237 and A1240
before their encounter. X-ray observations of A1237 would be
useful to confirm this hypothesis. Based on our assumption, we can use
the standard version of the analytical two-body model to study the
A1237+A1240 system, where the clumps are assumed to start their
evolution at time t0=0 with separation d0=0, and are moving
apart or coming together for the first time in their history. We
are looking at the system at the time of t=11.090 Gyr, i.e., the
age of the Universe at the system redshift. The solutions
consistent with the observed mass include the bound and
present incoming solution (i.e., collapsing), BI![]() and
BI
and
BI![]() ,
and the bound-outgoing solution, BO (see
Fig. 16). The associated probabilities are
,
and the bound-outgoing solution, BO (see
Fig. 16). The associated probabilities are ![]() ,
,
![]() ,
and
,
and ![]() ,
for BI
,
for BI![]() ,
BI
,
BI![]() ,
and BO,
respectively. The most probable solution is also the most
interesting one, since the BI
,
and BO,
respectively. The most probable solution is also the most
interesting one, since the BI![]() solution provides the same
value of
solution provides the same
value of
![]()
![]() already found for the A1240N+S
merger. In this case, the direction of the clump velocities
are consistent, too: at the present time, A1240N has already crossed
A1240S, now being in front of A1240S and moving outgoing; A1237 is
lying behind A1240 and is infalling almost along the same N-S
direction.
already found for the A1240N+S
merger. In this case, the direction of the clump velocities
are consistent, too: at the present time, A1240N has already crossed
A1240S, now being in front of A1240S and moving outgoing; A1237 is
lying behind A1240 and is infalling almost along the same N-S
direction.
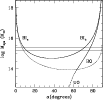 |
Figure 16: System mass vs. projection angle for bound and unbound solutions (solid and dashed curves, respectively) of the two-body model applied to A1237 and A1240 systems. |
| Open with DEXTER | |
6 Conclusions
Our results strongly support the conclusion of Bonafede et al. (2009), which was based on radio data, in favor of the ``outgoing merger shocks'' model for the double relics of A1240. We detect the intervening merging subclumps and recover an acceptable model for the internal cluster dynamics. Our results also suggest that we are looking at the cluster accretion along a large-scale structure filament.
Our analysis shows how powerful the study of the internal cluster dynamics is by analyzing the kinematics of cluster galaxies. Other insights into A1240 might be recovered by a clearer knowledge of galaxy properties, e.g., spectral signatures of past activity, which could be useful in determining the relevant timescales (see e.g., Ferrari et al. 2003; Boschin et al. 2004) and from deeper X-ray observations (see, e.g Vikhlinin et al. 2001, for the discovery of a ``cold front'' in Abell 3667). Finally, we point out that A1240, with its displacement between collisional (gas) and collisionless components (galaxies), is an excellent candidate for studying the properties of dark matter, in particular its collisional cross-section, as already performed for other merging clusters (Markevitch et al. 2004; Bradac et al. 2008).
Acknowledgements
We are in debt with Klaus Dolag for interesting discussions. We thank the anonymous referee for her/his useful suggestions. This publication is based on observations made on the island of La Palma with the Italian Telescopio Nazionale Galileo (TNG) and the Isaac Newton Telescope (INT). The TNG is operated by the Fundación Galileo Galilei - INAF (Istituto Nazionale di Astrofisica). The INT is operated by the Isaac Newton Group. Both telescopes are located in the Spanish Observatorio of the Roque de Los Muchachos of the Instituto de Astrofisica de Canarias.
This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
This research has made use of the galaxy catalog of the Sloan Digital Sky Survey (SDSS). Funding for the SDSS has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the U.S. Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. The SDSS Web site is http://www.sdss.org/.
The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Abell, G. O., Corwin, H. G. Jr., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] (In the text)
- Ashman, K. M., Bird, C. M., & Zepf, S. E. 1994, AJ, 108, 2348 [NASA ADS] [CrossRef] (In the text)
- Bagchi, J., Durret, F., Lima Neto, G. B., & Paul, S. 2006, Science, 314, 791 [NASA ADS] [CrossRef] (In the text)
- Bardelli, S., Zucca, E., Vettolani, G., et al. 1994, MNRAS, 267, 665 [NASA ADS] (In the text)
- Barrena, R., Boschin, W., Girardi, M., & Spolaor, M. 2007a, A&A, 467, 37 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Barrena, R., Boschin, W., Girardi, M., & Spolaor, M. 2007b, A&A, 469, 861 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Beers, T. C., & Geller, M. J. 1983, ApJ, 274, 491 [NASA ADS] [CrossRef] (In the text)
- Beers, T. C., Geller, M. J., & Huchra, J. P. 1982, ApJ, 257, 23 [NASA ADS] [CrossRef] (In the text)
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] (In the text)
- Beers, T. C., Forman, W., Huchra, J. P., Jones, C., & Gebhardt, K. 1991, AJ, 102, 1581 [NASA ADS] [CrossRef] (In the text)
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bird, C. M., & Beers, T. C. 1993, AJ, 105, 1596 [NASA ADS] [CrossRef] (In the text)
- Bonafede, A., Giovannini, G., Feretti, L., Govoni, F., & Murgia M. 2009, A&A, 494, 429 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Boschin, W., Girardi, M., Barrena, R., et al. 2004, A&A, 416, 839 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Boschin, W., Girardi, M., Spolaor, M., & Barrena, R. 2006, A&A, 449, 461 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Boschin, W., Barrena, R., Girardi, M., & Spolaor, M. 2008, A&A, 487, 33 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Boschin, W., Barrena, R., & Girardi, M. 2009, A&A, 495, 15 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bradac, M., Allen, S. W., Treu, T., et al. 2008, ApJ, 687, 959 [NASA ADS] [CrossRef] (In the text)
- Buote, D. A. 2002, in Merging Processes in Galaxy Clusters, Optical Analysis of Cluster Mergers, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.) (In the text)
- Burstein, D., & Heiles, C. 1982, AJ, 87, 1165 [NASA ADS] [CrossRef] (In the text)
- Carlberg, R. G., Yee, H. K. C., & Ellingson, E. 1997, ApJ, 478, 462 [NASA ADS] [CrossRef] (In the text)
- Cassano, R., & Brunetti, G. 2005, MNRAS, 357, 1313 [NASA ADS] [CrossRef] (In the text)
- Cousins, A. W. J. 1976, Mem. R. Astr. Soc, 81, 25 [NASA ADS] (In the text)
- Danese, L., De Zotti, C., & di Tullio, G. 1980, A&A, 82, 322 [NASA ADS] (In the text)
- David, L. P., Forman, W., & Jones, C. 1999, ApJ, 519, 533 [NASA ADS] [CrossRef] (In the text)
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] (In the text)
- Dressler, A., & Shectman, S. A. 1988, AJ, 95, 985 [NASA ADS] [CrossRef] (In the text)
- Ebeling, H., Voges, W., Böhringer, H., et al. 1996, MNRAS, 281, 799 [NASA ADS] (In the text)
- Ellingson, E., & Yee, H. K. C. 1994, ApJS, 92, 33 [NASA ADS] [CrossRef] (In the text)
- Ensslin, T. A., & Gopal-Krishna 2001, A&A, 366, 26 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ensslin, T. A., Biermann, P. L., Klein, U., & Kohle, S. 1998, A&A, 332, 395 [NASA ADS] (In the text)
- Fadda, D., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1996, ApJ, 473, 670 [NASA ADS] [CrossRef] (In the text)
- Fasano, G., & Franceschini, A. 1987, MNRAS, 225, 155 [NASA ADS] (In the text)
- Feretti, L. 1999, MPE Rep, 271 (In the text)
- Feretti, L. 2002, The Universe at Low Radio Frequencies, held 30 Nov.-4 Dec. 1999, Pune, India, ed. A. Pramesh Rao, G. Swarup, & Gopal-Krishna, Proc. IAU Symp., 199, 133 (In the text)
- Feretti, L. 2005, X-Ray and Radio Connections, ed. L. O. Sjouwerman, & K. K. Dyer, Published electronically by NRAO, http://www.aoc.nrao.edu/events/xraydio, held 3-6 February 2004 in Santa Fe, New Mexico, USA (In the text)
- Feretti, L. 2006, Proceedings of the XLIst Rencontres de Moriond, XXVIth Astrophysics Moriond Meeting: From dark halos to light, ed. L. Tresse, S. Maurogordato, & J. Tran Thanh Van, [arXiv:astro-ph/0612185] (In the text)
- Feretti, L. 2008, Mem. SAIt, 79, 176 [NASA ADS] (In the text)
- Feretti, L., Gioia I. M., & Giovannini G. 2002, Astrophysics and Space Science Library, 272, Merging Processes in Galaxy Clusters (The Netherlands: Kluwer Academic Publisher) (In the text)
- Feretti, L., Schuecker, P., Böehringer, H., Govoni, F., & Giovannini, G. 2005, A&A, 444, 157 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ferrari, C., Maurogordato, S., Cappi, A., & Benoist C. 2003, A&A, 399, 813 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ferrari, C., Govoni, F., Schindler, S., Bykov, A. M., & Rephaeli, Y. 2008, Space Sci. Rev., 134, 93 [NASA ADS] [CrossRef] (In the text)
- Flores, R. A., Quintana, H., & Way, M. J. 2000, ApJ, 532, 206 [NASA ADS] [CrossRef] (In the text)
- Gal, R. R., de Carvalho, R. R., Lopes, P. A. A., et al. 2003, AJ, 125, 2064 [NASA ADS] [CrossRef] (In the text)
- Giovannini, G., & Feretti, L. 2002, in Merging Processes in Galaxy Clusters, Diffuse Radio Sources and Cluster Mergers, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.) (In the text)
- Giovannini, G., Tordi, M., & Feretti, L. 1999, New Astron., 4, 141 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., & Mezzetti, M. 2001, ApJ, 548, 79 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., & Biviano, A. 2002, in Merging Processes in Galaxy Clusters, Optical Analysis of Cluster Mergers, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.) (In the text)
- Girardi, M., Biviano, A., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1995, ApJ, 438, 527 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., Fadda, D., Giuricin, G., et al. 1996, ApJ, 457, 61 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., Escalera, E., Fadda, D., et al. 1997, ApJ, 482, 11 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., Giuricin, G., Mardirossian, F., Mezzetti, M., & Boschin, W. 1998, ApJ, 505, 74 [NASA ADS] [CrossRef] (In the text)
- Girardi, M., Barrena, R., & Boschin, W. 2007, Contribution to Tracing Cosmic Evolution with Clusters of Galaxies: Six Years Later conference http://www.si.inaf.it/sesto2007/contributions/Girardi.pdf (In the text)
- Goto, T., Sekiguchi, M., Nichol, R. C., et al. 2002, AJ, 123, 1807 [NASA ADS] [CrossRef] (In the text)
- Gregory, S. A., & Thompson, L. A. 1984, ApJ, 286, 422 [NASA ADS] [CrossRef] (In the text)
- Gullixson, C. A. 1992, in Astronomical CCD Observing and Reduction techniques ed. S. B. Howell, ASP Conf. Ser., 23, 130 (In the text)
- Hoeft, M., Brüggen, M., & Yepes, G. 2004, MNRAS, 347, 389 [NASA ADS] [CrossRef] (In the text)
- Johnson, H. L., & Morgan, W. W. 1953, ApJ, 117, 313 [NASA ADS] [CrossRef] (In the text)
- Kempner, J. C., & Sarazin, C. L. 2001, ApJ, 548, 639 [NASA ADS] [CrossRef] (In the text)
- Kempner, J. C., Blanton, E. L., Clarke, T. E., et al. 2003, Proceedings of The Riddle of Cooling Flows in Galaxies and Clusters of Galaxies, ed. T. H. Reiprich, J. C. Kempner, & N. Soker, [arXiv:astro-ph/0310263] (In the text)
- Kennicutt, R. C. 1992, ApJS, 79, 225 [CrossRef] (In the text)
- Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 239 [NASA ADS] [CrossRef] (In the text)
- Limber, D. N., & Mathews, W. G. 1960, ApJ, 132, 286 [NASA ADS] [CrossRef] (In the text)
- López-Cruz, O., Barkhouse, W. A., & Yee, H. K. C. 2004, ApJ, 614, 679 [NASA ADS] [CrossRef] (In the text)
- Lubin, L. M., Postman, M., & Oke, J. B. 1998, AJ, 116, 643 [NASA ADS] [CrossRef] (In the text)
- Malumuth, E. M., Kriss, G. A., Dixon, W., Van Dyke, Ferguson, H. C., & Ritchie, C. 1992, AJ, 104, 495 [NASA ADS] [CrossRef] (In the text)
- Markevitch, M., Gonzalez, A. H., Clowe, D., et al. 2004, ApJ, 606, 819 [NASA ADS] [CrossRef] (In the text)
- Mastropietro, C., & Burkert, A. 2008, MNRAS, 389, 967 [NASA ADS] [CrossRef] (In the text)
- Mazure, A., Proust, D., Mathez, G., & Mellier, Y. 1988, A&AS, 76, 339 [NASA ADS] (In the text)
- Pisani, A. 1993, MNRAS, 265, 706 [NASA ADS] (In the text)
- Pisani, A. 1996, MNRAS, 278, 697 [NASA ADS] (In the text)
- Poggianti, B. M. 1997, A&AS, 122, 399 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, in Numerical Recipes, second edition (Cambridge University Press) (In the text)
- Quintana, H., Ramírez, A., & Way, M. J. 1996, AJ, 112, 360 [CrossRef] (In the text)
- Quintana, H., Carrasco, E. R., & Reisenegger, A. 2000, AJ, 120, 511 [NASA ADS] [CrossRef] (In the text)
- Raymond, J. C., & Smith, B. W. 1977, ApJS, 35, 419 [NASA ADS] [CrossRef] (In the text)
- Roettiger, K., Loken, C., & Burns, J. O. 1997, ApJS, 109, 307 [NASA ADS] [CrossRef] (In the text)
- Roettiger, K., Burns, J. O., & Stone, J. M. 1999, ApJ, 518, 603 [NASA ADS] [CrossRef] (In the text)
- Röttgering, H. J. A., Wieringa, M. H., Hunstead, R. W., & Ekers, R. D. 1997, MNRAS, 290, 577 [NASA ADS] (In the text)
- Sarazin, C. L. 2002, in Merging Processes in Galaxy Clusters, The Physics of Cluster Mergers, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.) (In the text)
- Springel, V., & Farrar, G. R. 2007, MNRAS, 380, 911 [NASA ADS] [CrossRef] (In the text)
- The, L. S., & White, S. D. M. 1986, AJ, 92, 1248 [NASA ADS] [CrossRef] (In the text)
- Thompson, L. A. 1982, in Early Evolution of the Universe and the Present Structure, ed. G.O. Abell, & G. Chincarini, (Dordrecht: Reidel), IAU Symp., 104 (In the text)
- Tonry, J., & Davis, M. 1979, ApJ, 84, 1511 [NASA ADS] (In the text)
- Venturi, T., Giacintucci, S., Brunetti, G., et al. 2007, A&A, 4363, 937 [NASA ADS] [CrossRef] (In the text)
- Vikhlinin, A., Markevitch, M., & Murray, S. S. 2001, ApJ, 551, 160 [NASA ADS] [CrossRef] (In the text)
- Visvanathan, N., & Sandage, A. 1977, ApJ, 216, 214 [NASA ADS] [CrossRef] (In the text)
- Wainer, H., & Schacht, S. 1978, Psychometrika, 43, 203 [CrossRef] (In the text)
Footnotes
- ... therein
![[*]](/icons/foot_motif.png)
- Please visit the web site of the DARC (Dynamical Analysis of Radio Clusters) project: http://adlibitum.oat.ts.astro.it/girardi/darc.
- ... IRAF
![[*]](/icons/foot_motif.png)
- IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.
- ...
characterization
![[*]](/icons/foot_motif.png)
- Taken from http://www.ast.cam.ac.uk/~wfcsur/technical/photom/colours/
- ... CIAO
![[*]](/icons/foot_motif.png)
- CIAO is freely available at http://asc.harvard.edu/ciao/
All Tables
Table 1: Velocity catalog of 145 spectroscopically measured galaxies in the field of the A1237+A1240 complex.
Table 2: Global properties of galaxy systems.
All Figures
![\begin{figure}
\par\includegraphics[width=17.95cm]{11788f1.ps}
\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg45.png) |
Figure 1: INT R-band image of the cluster A1240 (North at the top and East to the left) with, superimposed, the contour levels of the Chandra archival image ID 4961 (thin contours; photons in the energy range 0.5-2 keV) and the contour levels of a VLA radio image at 1.4 GHz (thick contours; Bonafede et al. 2009). Arrows show the positions of the two radio relics. Boxes highlight the brightest galaxies of A1240: BCGN, BCGS, and BCGE (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{11788f2.ps}\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg48.png) |
Figure 2: INT R-band image of the A1237+A1240 complex (North at the top and East to the left). Circles and annuli indicate cluster members of A1240 and A1237, respectively (see Table 1). Boxes indicate non-member galaxies. |
| Open with DEXTER | |
| In the text | |
 |
Figure 3: Redshift galaxy distribution. The solid line histogram refers to the 95 galaxies assigned to the A1237+A1240 complex according to the DEDICA reconstruction method. |
| Open with DEXTER | |
| In the text | |
 |
Figure 4: Rest-frame velocity vs. projected clustercentric distance for the 95 galaxies in the main peak (Fig. 3) showing galaxies detected as interlopers by our ``shifting gapper'' procedure (crosses). Circles indicate the 89 cluster members. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm]{11788f5.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg85.png) |
Figure 5: Spatial distribution on the sky and relative isodensity contour map of cluster members (A1237+A1240), obtained with the DEDICA method. The positions of the brightest galaxies are indicated (BCGN, BCGS, BCGE for A1240 and BCG1 and BCG2 for A1237). The plot is centered on the cluster center defined in this paper as the X-ray center. The two relics are indicated in a schematic way. |
| Open with DEXTER | |
| In the text | |
 |
Figure 6: Spatial distribution on the sky of 89 cluster members. Left panel: open symbols indicate cluster members. In particular, squares, circles, rotated squares, and triangles indicate A1240N, A1240S, A1240E and A1237. The crosses indicate emission-line galaxies. Right panel: the larger the symbol, the smaller is the radial velocity. The six close northern circles indicate the high velocity galaxies that we consider to be responsible for the apparent large global mean velocity of A1240N galaxies (see Sect. 3.4 and Fig. 10 in the following, too). |
| Open with DEXTER | |
| In the text | |
 |
Figure 7: Upper panel: velocity histogram for the entire cluster sample (thin line), A1240 (solid line), and A1237 (dashed line). The velocities of the three brightest galaxies of A1240 are indicated (BCGN, BCGS, and BCGE), as well as the two brightest galaxies of A1237 (BCG1 and BCG2). Lower panel: stripe density plot where the arrows indicate the positions of the significant gaps. The main and minor weighted gaps are indicated by large and small arrows, respectively. |
| Open with DEXTER | |
| In the text | |
 |
Figure 8:
Upper panel: rest-frame velocity (in units of 103 km s-1) vs. projected clustercentric distance for the 89 cluster galaxies. Circles and squares indicate members of A1240 and A1237. Central and lower panels: integral profiles of mean LOS velocity (in units of 103 km s-1) and LOS velocity dispersion (in units of km s-1) for the 62 members of A1240 (dots with the |
| Open with DEXTER | |
| In the text | |
 |
Figure 9: Upper panel: rest-frame velocity (in units of 103 km s-1) vs. projected clustercentric distance for the members of A1240N (squares), A1240S (circles) and A1237 (crosses). In this and other panels, the lower axis give the clustercentric distance of A1240N (A1240S) galaxies versus the negative (positive) axis from the A1240 center, while the upper axis give the clustercentric distance of A1237 galaxies from the A1237 center. The center of A1240 is defined as the X-ray center. The center of A1237 is defined as the position of the main peak in the 2D analysis. Central and lower panels: 68% error bands of integral profiles of LOS mean velocity (in units of 103 km s-1) and LOS velocity dispersion (in units of km s-1) for A1240N and A1240S (solid lines) and A1237 (dashed lines). The circles in the central panel indicate the positions and velocities of the two brightest galaxies of A1240 (BCGN and BCGS) and the two brightest galaxies of A1237 (BCG1 and BCG2). |
| Open with DEXTER | |
| In the text | |
 |
Figure 10: Upper panels: error bands of integral profiles of LOS mean velocity for A1240N (dashed line) and A1240S (solid line). The distance is computed using as the center the position of the most important peak (on the left) and the position of the brightest cluster member (on the right). The horizontal lines indicate the velocities of BCGN and BCGS (dashed and solid lines, respectively). The close circles point out at which radius the six northern high velocity galaxies in A1240N are included to show their effect on the estimate of the mean velocity (see the text and Fig. 6, too). Lower panels: the same for integral profiles of the LOS velocity dispersion. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11788f11.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg147.png) |
Figure 11:
B-R vs. R diagram for galaxies with available spectroscopy is shown by large circles and squares (members and non-members, respectively). Small points indicate galaxies found in our INT photometric sample, i.e., objects with a class star |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11788f12.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg148.png) |
Figure 12:
Spatial distribution on the sky and relative isodensity contour map
of probable cluster members (applying the color-magnitude selection to the INT photometric catalog) with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{11788f13.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11788-09/Timg150.png) |
Figure 13:
Spatial distribution on the sky and relative isodensity contour map
of likely cluster members (applying the color-color selection to the SDSS photometric catalog) with
|
| Open with DEXTER | |
| In the text | |
 |
Figure 14:
|
| Open with DEXTER | |
| In the text | |
 |
Figure 15:
System mass vs. projection angle for bound and unbound solutions
(thick solid and thick dashed curves, respectively) of
the two-body model applied to A1240N and A1240S subsystems. Labels
BI |
| Open with DEXTER | |
| In the text | |
 |
Figure 16: System mass vs. projection angle for bound and unbound solutions (solid and dashed curves, respectively) of the two-body model applied to A1237 and A1240 systems. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


