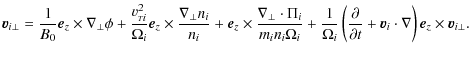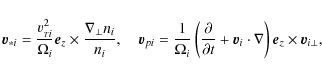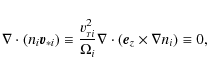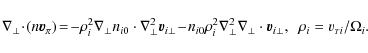EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 503 / No 2 (August IV 2009) A&A, 503 2 (2009) 591-593 Full HTML
Free Access
Issue
A&A
Volume 503, Number 2, August IV 2009
Page(s) 591 - 593
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200811356
Published online 15 July 2009

Diamagnetic current does not produce an instability in the solar corona

J. Vranjes - S. Poedts

Center for Plasma Astrophysics, and Leuven Mathematical Modeling and Computational Science Center (LMCC), Celestijnenlaan 200 B, 3001 Leuven, Belgium

Received 16 November 2008 / Accepted 12 June 2009

Abstract
Context. The solar atmosphere contains density irregularities of various sizes embedded in magnetic fields. In the case of a density gradient perpendicular to the magnetic field vector, the plasma supports drift waves that are usually growing as a result of the free energy stored in the density gradient.
Aims. Some basic features of the drift wave are discussed here and, in particular, the gyro-viscosity stress tensor effects and the properties of the diamagnetic drift. Also, the recently proposed ``new'' instability due to the diamagnetic drift is checked.
Methods. This analysis involves a calculation that considers some terms missing in previous calculations that have appeared in the literature.
Results. It is shown that the diamagnetic drift, which is essential for the recently proposed new physical phenomenon, cannot contribute to the flux in the continuity equation. Moreover, the part of the ion polarization drift contribution to the ion flux cancels out exactly with the contribution of the part of the stress tensor drift to the same flux.
Conclusions. Thus, the ion diamagnetic current does not produce an instability in the solar corona.

Key words: Sun: corona - waves - instabilities

1 Introduction

Observations in the past have provided ample evidence of numerous plasma density irregularities, filaments, and threads in the magnetically dominated solar atmosphere. The most recent Hinode observations (see e.g. De Pontieu et al. 2007) only confirm that the solar atmosphere is a highly structured and inhomogeneous system with grass-like density filaments of various sizes pervading the whole domain. Such density irregularities are, as a rule, associated with the magnetic field, thus creating a perfect environment for the drift wave. Clearly, the observable characteristic dimensions of the density irregularities are limited by the presently available spatial resolutions of the current instruments (presently a fraction of an arcsecond). However, even extremely short, meter-size scales cannot be excluded, especially in the solar corona Vranjes & Poedts 2008; hence, the density inhomogeneity scale lengths may have any values from the meter size up to thousands of kilometers in the case of coronal plumes.

In the past, the role of drift waves in the solar atmosphere has either been overlooked or greatly underestimated. This may be partly because the study of drift waves necessarily implies a multi-component fluid or kinetic description, contrary to the MHD (magnetohydrodynamics) model widely applied in solar physics, within which the drift wave can simply not be obtained. In fact, the drift mode is not only able to survive drastically different plasma characteristics such as the collisional-collisionless extremes in the lower and upper solar atmosphere, respectively, but in fact to benefit (grow) from each of them separately. As a result the term `universally growing mode' for the drift mode in the literature.

In collisional plasma, such as in the lower solar chromosphere, the mode grows thanks to electron collisions, and this can be studied within the framework of the fluid description. In collision-less plasma, such as in the solar corona, the mode grows due to the electron resonant effects, and this is a purely kinetic effect. All that is needed for the growth is simply the presence of density gradients perpendicular to the ambient magnetic field vector. A plasma flow along the magnetic field, with a density gradient in the perpendicular direction (shear plasma flow) can make the mode grow, as has been shown both within fluid Saleem et al. 2007 and kinetic theory Kaneko et al. 2003. The same holds for the case of a current directed along the magnetic field vector Goldston & Rutherford 1995 or in the case of a perpendicular electron or ion temperature gradient Goldston & Rutherford 1995,Weiland 2000, so numerous experimentally verified ways exist to make the mode unstable/growing (see also Vranjes $\&$ Poedts 2009). The purpose of the present work is to show, however, that the recently suggested additional instability triggering mechanism, the diamagnetic currents, cannot possibly make the mode growing.

2 Elements of the drift wave theory

Within the fluid description, the motion of ions and electrons is described by

$\displaystyle m_in_i\left[\frac{\partial \vec v_i}{\partial t} + (\vec v_i\cdot\nabla) \vec v_i\right]$ = $\displaystyle e n_i \left(-\nabla \phi + \vec v_i\times \vec B_0\right)$  
    $\displaystyle - \kappa T_i\nabla n_i - \nabla\cdot \Pi_i$ (1)

and

\begin{displaymath}0 = -e n_e \left(-\nabla \phi + \vec v_e\times \vec B_0\right) - \kappa T_e \nabla n_e, \end{displaymath} (2)

respectively. The shape of these equations reveals that we are dealing with electrostatic perturbations, the hot ion effects are included through the pressure and the gyro-viscosity stress tensor terms, and the lefthand side of the electron momentum equation is omitted, implying perturbations with phase speed and a perturbed velocity both far below the electron thermal velocity.

In certain parameter domains, the drift mode may become electromagnetic Vranjes $\&$ Poedts 2006, provided the plasma $\beta$ is large enough. This yields a coupling of the drift and the kinetic Alfvén wave. However, as shown by Vranjes & Poedts (2006), the Alfvén part of the mode is of no interest as it is always damped by the collisions, so it will not be discussed here. The usual gas viscosity is as a rule negligible even for a relatively high-density environment like the photosphere and chromosphere. More details are available in Vranjes $\&$ Poedts (2006).

The ion gyro-viscous components that we need here are given by Weiland 2000

\begin{eqnarray*}\Pi_{xy}&=&\Pi_{yx}=\frac{n_i \kappa T_i}{2 \Omega_i} \left(\fr... ...y}}{\partial x} + \frac{\partial v_{ix}}{\partial y}\right)\cdot \end{eqnarray*}


Here and below we have taken $\vec B_0= B_0 \vec e_z$, and $v_{{\scriptscriptstyle T}i}^2=\kappa T_i/m_i$.

The ion perpendicular velocity, obtained from Eq. (1), is described by the following recurrent formula

$\displaystyle \vec v_{i\bot}=\frac{1}{B_0} \vec e_z \times \nabla_{\perp}\phi +... ...al}{\partial t}+ \vec v_i \cdot \nabla \right) \vec e_z \times \vec v_{i \bot}.$     (3)

It can be calculated up to small terms of any order using the drift approximation $\vert\partial/\partial t\vert\ll \Omega_i$.

2.1 Gyro-viscosity effects and ``new instability'' driven by ion diamagnetic current

The ion gyro-viscosity is usually overlooked in the literature in studies within the framework of the multi-component plasma theory. For the solar plasma case, this may have particularly important consequences because the ion and electron temperatures are typically of the same order of magnitude, so that a cold ion approximation and the consequent neglect of the ion gyro-viscosity cannot be justified. In fact, such a neglect may even give rise to some artificial, unphysical results, as shown below.

As a matter of fact, it is a well known Weiland 2000,Vranjes $\&$ Poedts 2006, yet often disregarded fact, that a part of the ion gyro-viscosity stress tensor contributes to the cancellation of some terms in the ion continuity equations. This implies that, if the gyro-viscosity terms are omitted in the derivations, the resulting ion equations contain terms that cannot possibly be there. Moreover and unfortunately, these extra terms yield some false physical effects. A typical example of that type can be seen in the recent work Mecheri & Marsch 2008 where the discovery of a ``new instability'' of the drift wave was claimed as a result of such an erroneous calculation.

The above-mentioned cancellation of terms appears when Eq. (3) is substituted into the ion continuity equation $\partial n_i/\partial t+ \nabla_\bot\cdot (n_i v_{i\bot}) + \nabla_z\cdot(n_i v_{iz})=0$. The cancellation involves, respectively, the diamagnetic and polarization drifts from one side

\begin{displaymath}\vec v_{*i}=\frac{v_{{\scriptscriptstyle T} i}^2}{\Omega_i} \... ... \vec v_i \cdot \nabla\right) \vec e_z \times \vec v_{i \bot}, \end{displaymath} (4)

and the stress tensor drift term $\vec v_{\pi i}=\vec e_z \times \nabla_{\perp}\cdot \Pi_i/(m_i n_i \Omega_i)$ from the other.

From the first expression in Eq. (4), it is seen that, as long as the magnetic field is homogeneous, we have

\begin{displaymath}\nabla\cdot (n_i\vec v_{*i})\equiv \frac{v_{{\scriptscriptsty... ...^2}{\Omega_i} \nabla\cdot (\vec e_z\times \nabla n_i)\equiv 0, \end{displaymath} (5)

describing a well-known fundamental property Weiland 2000. Physically, this is because the diamagnetic drift is a fluid effect and not a particle drift, therefore it cannot contribute to the flux in the continuity equation. It appears due to the gyration of ion particles in the presence of a density gradient and without any macroscopic motion of the ion guiding center. As a result, this term does not contribute to the flux in the continuity equations. However, this term is essential in the mentioned work of Mecheri $\&$ Marsch where, because of an inappropriate linearization, it gives rise to the term (in their notation) $(\vec k \cdot \vec v_{dj}) n_{j1}$ (here, $v_{*i}\equiv v_{di}$) in the continuity equation (their Eq. (10)). It is exactly this term that provides the source of the current-driven instability discussed in the paper. We note, however, that, strictly speaking, the magnetic field in the work of Mecheri and Marsch is indeed inhomogeneous. Yet, precisely in this particular and essential term $(\vec k \cdot \vec v_{dj}) n_{j1}$, the magnetic field inhomogeneity is explicitly omitted as a higher order correction (cf. Eq. (13) and the related text in their work), and consequently, the condition (5) given above holds within the same approximation.

The mentioned cancellation of terms appears due to the convective derivative part

\begin{displaymath}(\vec v_i\cdot\nabla)\vec e_z\times \vec v_{i\bot} \end{displaymath} (6)

in the polarization drift $\vec v_{pi}$. The procedure is described in detail by Weiland (2000) and by Vranjes & Poedts (2006). Within the approximation of small gradients of the equilibrium quantities, the last $\vec v_{i\bot}$ in the convective derivative (6) contains only the leading-order perturbed drifts from Eq. (3). On the other hand, the first $\vec v_i$ in (6) can only be the equilibrium ion diamagnetic drift. This is then to be used in the term $\nabla_\bot\cdot(n_i \vec v_{pi})$ in the continuity equation.

On the other hand, the (gyro-viscosity) stress tensor drift term yields

\begin{displaymath}\nabla_{\perp}\!\cdot\!(n \vec v_\pi)\! =\!-\rho_i^2 \nabla_{... ...vec v_{i\bot}, ~~ \rho_i=v_{{\scriptscriptstyle T}i}/\Omega_i. \end{displaymath} (7)

Within the second-order small terms approximation, the first term on the righthand side in this expression cancels out exactly with the term $\nabla_{\perp}\cdot[n (\vec v_i\cdot\nabla)\vec e_z\times \vec v_{i\bot}]$, which is the contribution of the convective derivative (6) discussed above in the polarization drift.

We stress that the cancellation of terms is exact and valid for any plasma regardless of any specific parameters, and this includes the solar corona. Moreover, the analysis of drift waves obtained from this formal fluid theory can also be easily obtained by using the kinetic theory where the problem of the stress tensor is not an issue (cf., references Weiland 2000, and Vranjes $\&$ Poedts 2006).

However, if the derivation is performed incorrectly, e.g. by simply ignoring the stress tensor contribution, then the resulting equations contain some extra terms originating from the convective derivative in the ion polarization drift. For perturbations of the form $\sim $ $\exp(- {\rm i} \omega t + {\rm i} k_y y + {\rm i} k_z z)$ this implies terms like $\vec k \cdot \vec v_{*i}$, which in reality cancel out exactly. These extra terms are in fact explicitly seen throughout Mecheri $\&$ Marsch (2008), and are erroneously claimed to produce a ``new instability'' of the drift wave. We observe that the stress tensor contribution is included nowhere in the work of Mecheri $\&$ Marsch, so their equations contain extra terms originating both from the polarization drift and from condition (5) not being taken into account.

3 Summary

The importance of the drift wave in the solar atmosphere has been pointed out, and the most important mechanisms that make the mode grow are briefly mentioned. The diamagnetic drift (current) plays an essential role in the description of the drift wave. We have stressed that: (i) the diamagnetic drift is a fluid effect and not a particle drift, therefore it cannot contribute to the flux in the continuity equation; and (ii) a well-known cancellation exists of the part of the ion polarization drift contribution to the ion flux on the one hand and the contribution of the part of the stress tensor drift to the same flux, on the other. Therefore, to avoid artificial, unphysical results, great care is needed in studies dealing with hot ion effects as in the case of the solar corona. We have shown that the results presented in the work of Mecheri $\&$ Marsch are an artifact of some basic errors in the starting set of equations. Their equations indeed contain the terms that determine all the results obtained in the commented paper. However, those terms cancel out exactly due to Eq. (5) and due to the stress tensor effect. This cancellation is valid in general and independent of the physical system, and it must be taken into account in a proper model.

Acknowledgements
These results were obtained in the framework of the projects GOA/2009-009 (K.U.Leuven), G.0304.07 (FWO-Vlaanderen) and C 90347 (ESA Prodex 9). Financial support by the European Commission through the SOLAIRE Network (MTRN-CT-2006-035484) is gratefully acknowledged.

References

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.