| Issue |
A&A
Volume 503, Number 2, August IV 2009
|
|
|---|---|---|
| Page(s) | 309 - 322 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200811250 | |
| Published online | 15 June 2009 | |
Synchrotron self-Compton flaring of TeV blazars
II. Linear and nonlinear electron cooling
C. Röken - R. Schlickeiser
Institut für Theoretische Physik, Lehrstuhl IV: Weltraum- und Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
Received 29 October 2008 / Accepted 9 May 2009
Abstract
A theoretical radiation model for the flaring of TeV blazars is discussed here for the case of a nonlinear electron synchrotron cooling in these sources. We compute analytically the optically thick and thin synchrotron radiation intensities and photon density distributions in the emission knot as functions of frequency and time followed by the synchrotron self-Compton intensity and fluence in the optically thin frequency range using the Thomson approximation of the inverse Compton cross section. At all times and frequencies, the optically thin part of the synchrotron radiation process is shown to provide the dominant contribution to the synchrotron self-Compton quantities, while the optically thick part is always negligible. Afterwards, we compare the linear to the nonlinear synchrotron radiation cooling model using the data record of PKS 2155-304 on MJD 53944 favouring a linear cooling of the injected monoenergetic electrons. The good agreement of both the linear and the nonlinear cooling model with the data supports the relativistic pickup process operating in this source.
Additionally, we discuss the synchrotron self-Compton scattering, applying the full Klein-Nishina cross section to achieve the most accurate results for the synchrotron self-Compton intensity and fluence distributions.
Key words: radiation mechanisms: non-thermal - methods: analytical - galaxies: active
1 Introduction
A process describing the energy loss of ultra-relativistic electrons in cosmic-ray sources named inverse Compton scattering has been considered to be very likely responsible for the production of the high-energy radiation emitted by active galactic nuclei. In this process, low-energy photons are scattered to higher energies by relativistic electrons within the jets of these sources. There are several possible external and internal generators of the low-energy photon field, such as the accretion disc of the central black hole (Dermer et al. 1992; Dermer & Schlickeiser 1993), the broad-line region (Sikora et al. 1994), dust surrounding the active galactic nucleus (Blazejowski et al. 2000; Arbeiter et al. 2002) or synchrotron radiation produced in the jet itself. In this work, the process of interest is the inverse Compton scattering of internal synchrotron radiation called synchrotron self-Compton scattering (Maraschi et al. 1992).
Numerical models were applied in most of the studies of this process, e.g. Mastichiadis & Kirk (1997), Dermer et al. (1997), Chiaberge & Ghisellini (1999), Sokolov et al. (2004) and Böttcher (2007). Here, we investigate analytically the influence of a nonlinear electron synchrotron cooling on the synchrotron self-Compton process following the analysis of the flaring of TeV blazars due to the synchrotron self-Compton process for a linear synchrotron radiation cooling behaviour of the injected electrons (Schlickeiser & Röken 2008), where a ![]() -distribution approximation (Reynolds 1982; Dermer & Schlickeiser 1993) was used for the computation of the inverse Compton scattering rate
-distribution approximation (Reynolds 1982; Dermer & Schlickeiser 1993) was used for the computation of the inverse Compton scattering rate
![]() .
Most of the calculations of photon spectra modelling quantities have been based on such rather simple approximations. Therefore, we also determine the inverse Compton scattering rate, the synchrotron self-Compton intensities and fluences for the linear and nonlinear synchrotron photon densities and electron populations for the full Klein-Nishina cross section to obtain more general results (Appendix B).
.
Most of the calculations of photon spectra modelling quantities have been based on such rather simple approximations. Therefore, we also determine the inverse Compton scattering rate, the synchrotron self-Compton intensities and fluences for the linear and nonlinear synchrotron photon densities and electron populations for the full Klein-Nishina cross section to obtain more general results (Appendix B).
We assume that a flare of the emission knot occurs at the time t = t0 due to a uniform instantaneous injection of monoenergetic ultra-relativistic electrons. The emission knot itself moves with a relativistic bulk speed V with respect to an external observer. We model the emission knot as a spherical magnetised, fully ionised plasma cloud of radius R consisting of cold electrons and protons with a uniform density distribution and a randomly oriented large-scale time-dependent magnetic field B(t) that adjusts itself to the actual kinetic energy density of the radiating electrons in these sources, yielding the different nonlinear synchrotron radiation cooling behaviour. This magnetic field is most likely generated from the interaction of the relativistically moving knot with the surrounding ambient intergalactic and interstellar medium that is also responsible for the injection of the ultra-relativistic particles by the relativistic pickup process (Pohl & Schlickeiser 2000; Gerbig & Schlickeiser 2007; Stockem et al. 2007). The existence of a magnetic field is mandatory for the generation of synchrotron radiation and hence, the synchrotron self-Compton process.
In our analysis we assume that the synchrotron radiation losses of relativistic electrons
in a constant (linear case) or partition
(nonlinear) magnetic field dominate over synchrotron self-Compton losses which also imply nonlinear
electron energy losses (Schlickeiser 2009) because the energy density of the target synchrotron
photons is given by an energy integral over the radiating electron distribution function. Therefore, our analysis
applies to blazar sources where the observed low-energy synchrotron component in the spectral
energy distribution dominates over the high-energy synchrotron self-Compton component. Apart from the exceptional ![]() -ray flare in July 2006 (Aharonian et al. 2009a) this applies in particular to the powerful blazar PKS 2155-304
as the existing multifrequency campaigns of this source indicate (see Fig. 10 of Aharonian et al. 2005; Fig. 2 of Aharonian et al. 2009b), especially in low activity states. We therefore compare our results with the
high-energy observations from this source.
-ray flare in July 2006 (Aharonian et al. 2009a) this applies in particular to the powerful blazar PKS 2155-304
as the existing multifrequency campaigns of this source indicate (see Fig. 10 of Aharonian et al. 2005; Fig. 2 of Aharonian et al. 2009b), especially in low activity states. We therefore compare our results with the
high-energy observations from this source.
Before starting the analysis we explain our assumption that magnetic field partition is instantaneously
established as the electrons cool. Equipartition conditions are often invoked in astrophysical sources for convenience, as discussed e.g. in the review by Beck & Krause (2005). Observationally, for a variety of non-thermal sources
the equipartition concept is supported by magnetic field estimates such as e.g. the Coma cluster of galaxies
(Schlickeiser et al. 1987). From a theoretical point of view, there is no simple explanation of partition
but we will outline the basic arguments here. An upper limit on the magnetic field strength can be derived by applying Chandrasekhar's (1961, p. 583) general result, derived from the virial theorem, that for the existence of a stable equilibrium in the radiating source it is necessary that the total magnetic field energy of the system does not exceed
the system's gravitational potential energy. Such a magnetic field upper limit corresponds to lower limits
on the system's parallel and perpendicular plasma betas,
![]() and
and
![]() ,
respectively, as bi-Maxwellian plasma distributions with different temperatures along and perpendicular
to the magnetic field are the most likely distributions of cosmic plasmas. The solar wind plasma is
the only cosmic plasma where detailed in-situ satellite observations of plasma properties are available
(Bale 2008). Ten years of Wind/SWE data (Kasper et al. 2002) have demonstrated that the proton and electron
temperature anisotropies
,
respectively, as bi-Maxwellian plasma distributions with different temperatures along and perpendicular
to the magnetic field are the most likely distributions of cosmic plasmas. The solar wind plasma is
the only cosmic plasma where detailed in-situ satellite observations of plasma properties are available
(Bale 2008). Ten years of Wind/SWE data (Kasper et al. 2002) have demonstrated that the proton and electron
temperature anisotropies
![]() are bounded by ion cyclotron, mirror and
firehose instabilities (Hellinger et al. 2002) at large values of the parallel plasma
beta
are bounded by ion cyclotron, mirror and
firehose instabilities (Hellinger et al. 2002) at large values of the parallel plasma
beta
![]() .
In the parameter plane defined by the temperature anisotropy
.
In the parameter plane defined by the temperature anisotropy
![]() and the parallel plasma beta
and the parallel plasma beta
![]() ,
stable plasma configurations are
only possible within a rhomb-like configuration around
,
stable plasma configurations are
only possible within a rhomb-like configuration around
![]() ,
whose limits are
defined by the threshold conditions for these instabilities. If a plasma would start with parameter values outside this rhomb-like configuration, it immediately would generate fluctuations via the instabilities, which quickly relax the plasma distribution into the stable regime within the
rhomb-configuration. Similar anisotropic plasma distributions, such as relativistic kappa-distributions,
are to be expected during the pickup of interstellar particles by the interaction of the
relativistic jet in the case of blazars with the surrounding ambient interstellar or intergalactic
medium (Stockem et al. 2007). Such an interaction is a
prominent example of the relativistic collision of plasma shells with different properties
(temperature, density, composition etc.). Experimentally (Kapetanakos 1974; Tatarakis et al. 2003)
and from numerous particle-in-cell (PIC) simulations (e.g. Lee & Lampe 1973; Nishikawa et al. 2003; Silva et al. 2003; Frederiksen et al. 2004; Sakai et al. 2004; Jaroschek et al. 2005) such collisions of plasma shells
lead to the onset of linear Weibel-type plasma instabilities perpendicular to the
flow directions in both unmagnetised and slightly magnetised plasmas, and to the development of
anisotropic relativistic plasma distributions. The PIC simulations of electron-proton and electron-positron plasmas
demonstrate that these instabilities generate magnetic fields in the form of aperiodic fluctuations
at almost equipartition strength on the shortest plasma time scale. The aperiodic magnetic fluctuations
will scatter the initially beam-like interstellar particles by rapid pitch-angle scattering
in the rest frame of the jet, leading to an efficient pickup of nearly monoenergetic relativistic
electrons and protons (Schlickeiser et al. 2002). The superposition of the plasma shell particles and the
scattered interstellar particles results in a total plasma distribution with finite anisotropy
that then, as in the solar wind case, controls the magnetic field strength. Many details of the
complicating plasma processes leading to partition still have to be worked out, starting with studies
of the micro instabilities of relativistic anisotropic plasmas (e.g. Lazar et al. 2008).
,
whose limits are
defined by the threshold conditions for these instabilities. If a plasma would start with parameter values outside this rhomb-like configuration, it immediately would generate fluctuations via the instabilities, which quickly relax the plasma distribution into the stable regime within the
rhomb-configuration. Similar anisotropic plasma distributions, such as relativistic kappa-distributions,
are to be expected during the pickup of interstellar particles by the interaction of the
relativistic jet in the case of blazars with the surrounding ambient interstellar or intergalactic
medium (Stockem et al. 2007). Such an interaction is a
prominent example of the relativistic collision of plasma shells with different properties
(temperature, density, composition etc.). Experimentally (Kapetanakos 1974; Tatarakis et al. 2003)
and from numerous particle-in-cell (PIC) simulations (e.g. Lee & Lampe 1973; Nishikawa et al. 2003; Silva et al. 2003; Frederiksen et al. 2004; Sakai et al. 2004; Jaroschek et al. 2005) such collisions of plasma shells
lead to the onset of linear Weibel-type plasma instabilities perpendicular to the
flow directions in both unmagnetised and slightly magnetised plasmas, and to the development of
anisotropic relativistic plasma distributions. The PIC simulations of electron-proton and electron-positron plasmas
demonstrate that these instabilities generate magnetic fields in the form of aperiodic fluctuations
at almost equipartition strength on the shortest plasma time scale. The aperiodic magnetic fluctuations
will scatter the initially beam-like interstellar particles by rapid pitch-angle scattering
in the rest frame of the jet, leading to an efficient pickup of nearly monoenergetic relativistic
electrons and protons (Schlickeiser et al. 2002). The superposition of the plasma shell particles and the
scattered interstellar particles results in a total plasma distribution with finite anisotropy
that then, as in the solar wind case, controls the magnetic field strength. Many details of the
complicating plasma processes leading to partition still have to be worked out, starting with studies
of the micro instabilities of relativistic anisotropic plasmas (e.g. Lazar et al. 2008).
The paper is structured as follows: first we solve the partial differential equation for the time-dependent evolution of the volume-averaged relativistic electron population inside the radiation source assuming a nonlinear synchrotron radiation cooling of the electrons and provide the necessary intrinsic synchrotron radiation formulas (Sects. 2 and 3). Then we calculate the associated synchrotron radiation intensities (Sect. 4). In Sect. 5 the optically thin synchrotron self-Compton emission is determined using the Thomson limit of the Klein-Nishina cross section followed by the calculation of the nonlinear synchrotron self-Compton fluence distribution including a comparison of the linear to the nonlinear model by application to the data record of the PKS 2155-304 flare on MJD 53944 in Sect. 6. In Appendix B we compute the linear and nonlinear synchrotron self-Compton intensities and fluences using the full Klein-Nishina cross section and compare the approximate to the exact results.
2 Nonlinear electron synchrotron cooling
To begin with, we choose the appropriate reference frame for the calculations of all physical quantities for the nonlinear cooling process of relativistic electrons due to synchrotron radiation to be a coordinate system comoving with the radiation source.
Once ultra-relativistic electrons (
![]() )
enter the observed physical system with a large-scale magnetic field at the rate
)
enter the observed physical system with a large-scale magnetic field at the rate
![]() and at the time t = t0, here a jet-plasmoid of an active galactic nucleus, they compete with electron synchrotron energy losses. The time-dependent evolution of the competition process is mathematically described by a partial differential equation for the volume-averaged relativistic eletron population inside a radiating source first derived by Kardashev (1962)
and at the time t = t0, here a jet-plasmoid of an active galactic nucleus, they compete with electron synchrotron energy losses. The time-dependent evolution of the competition process is mathematically described by a partial differential equation for the volume-averaged relativistic eletron population inside a radiating source first derived by Kardashev (1962)
where
is the synchrotron energy loss rate depending on the magnetic field energy density UB. The function
In this work, we discuss as an illustrative, but physically justified example the case of one instantaneous monoenergetic injection of ultra-relativistic electrons
![]() with the injection strength q0. At all times we assume that the entering electrons are ultra-relativistic (
with the injection strength q0. At all times we assume that the entering electrons are ultra-relativistic (
![]() ), resulting in the relation
), resulting in the relation
![]() ,
implying
,
implying
![]() for the differential electron number densities. So we find for the energy integrated kinetic energy density of the relativistic electrons
for the differential electron number densities. So we find for the energy integrated kinetic energy density of the relativistic electrons
In the case of nonlinear cooling under the fixed partition condition
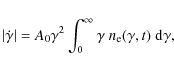 |
(4) |
where
with
where
3 Intrinsic synchrotron radiation formulas
An appropriate approximation for the pitch-angle averaged synchrotron power of a single electron in vacuum (Crusius & Schlickeiser 1986, 1988) reads
where
with a0 = 1.151, exhibiting a similar asymptotic behaviour as the function
In the nonlinear cooling case the gyrofrequency,
![]() ,
is a time-dependent function due to the imposed partition condition between the energy densities of the magnetic field and the relativistic electrons leading to a time-dependence of the magnetic field
,
is a time-dependent function due to the imposed partition condition between the energy densities of the magnetic field and the relativistic electrons leading to a time-dependence of the magnetic field
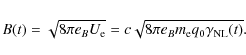 |
(9) |
Hence, we obtain for the gyrofrequency, using (6),
| (10) |
where
depending on the spontaneous synchrotron emission coefficient
and the synchrotron optical depth,
In a strict sense the approximations in (11) are valid only for the cases
4 Synchrotron radiation intensities
Inserting the nonlinear electron density distribution (5) into the synchrotron emissivities (12) and (13) and carrying out the ![]() -integrations, we obtain in terms of the normalised frequency
-integrations, we obtain in terms of the normalised frequency
![]()
and
where we used the characteristic frequency
for the characteristic values of the electron injection rate
4.1 Synchrotron intensity variation
Following the discussion of the intensity variations for fixed frequencies as a function of time for optically thin emission frequencies
![]() ,
performed by Schlickeiser & Lerche (2007), we calculate the light curves at optically thick emission frequencies to
,
performed by Schlickeiser & Lerche (2007), we calculate the light curves at optically thick emission frequencies to
where
4.2 Synchrotron photon density distribution
With the synchrotron intensities (A.6), (A.7) and the definition
![]() we obtain for the differential synchrotron photon number density
we obtain for the differential synchrotron photon number density
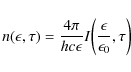 |
(18) |
for the case of optically thin energies
and for optically thick energies
where
5 Synchrotron self-Compton emission
The differential number density of Compton scattered synchrotron photons with the normalised scattered photon energy
![]() is given by
is given by
using the
Inserting the relativistic electron distribution (5) into Eq. (21) we obtain
Equation (22) then yields
Making use of the synchrotron photon number densities (19) and (20) we find for the synchrotron self-Compton intensity
and
respectively.
We introduce a strictly decreasing function to simplify the following expressions and relations
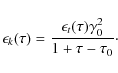 |
(27) |
For times
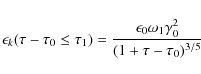 |
(28) |
and
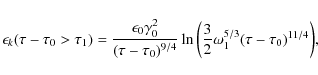 |
(29) |
using Eqs. (A.2) and (A.5).
6 Synchrotron self-Compton fluences
We discuss the synchrotron self-Compton fluence distribution described by the time-integrated synchrotron self-Compton intensity (22)
in two scattered photon energy ranges: for energies
6.1 High scattered photon energies
For energies
![]() only Eq. (26) contributes, so that
only Eq. (26) contributes, so that
Substituting
where
We obtain with the new variable
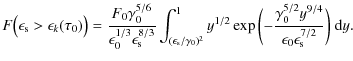 |
(34) |
Defining s = y9/4 and
For high scattered photon energies,
| = | 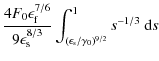 |
||
| = | ![$\displaystyle \frac{2 F_0 \epsilon_{\rm f}^{7/6}}{3 \epsilon_{\rm s}^{8/3}} \biggl( 1 - \biggl[ \frac{\epsilon_{\rm s}}{\gamma_0}\biggr]^3\biggr)\cdot$](/articles/aa/full_html/2009/32/aa11250-08/img128.png) |
(36) |
For scattered photon energies
| = |  |
||
| = | ![$\displaystyle \frac{4 F_0}{9 \epsilon_{\rm s}^{1/3} \epsilon_{\rm f}^{7/6}} \Ga...
...^{9/2}}, \biggl[\frac{\epsilon_{\rm f}}{\epsilon_{\rm s}} \biggr]^{7/2} \Biggr)$](/articles/aa/full_html/2009/32/aa11250-08/img133.png) |
(37) |
in terms of the generalised incomplete gamma function
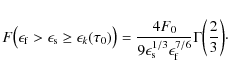 |
(38) |
6.2 Low scattered photon energies
For low scattered photon energies,
![]() ,
Eqs. (25) and (26) contribute to the spectral fluence. Starting with the scattered photon range
,
Eqs. (25) and (26) contribute to the spectral fluence. Starting with the scattered photon range
![]() we find, substituting as before
we find, substituting as before
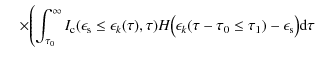 |
|||
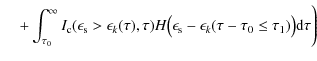 |
|||
![$\displaystyle \hspace*{4mm} = \frac{R \sigma_T I_0}{6 \pi A_0 \gamma_0^2} \Bigg...
...\frac{3 \epsilon_{\rm s} z^{9/4}}{2 \gamma_0^2 \epsilon_0}\biggr]^{-1} {\rm d}z$](/articles/aa/full_html/2009/32/aa11250-08/img143.png) |
|||
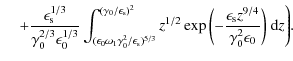 |
(39) |
The integrand of the first integral can be approximated within the domain of integration by
![\begin{displaymath}z^{3/2} \biggl[1 + \frac{3 \epsilon_{\rm s}}{2 \gamma_0^2 \epsilon_0} z^{9/4} \biggr]^{-1} \approx z^{3/2} .
\end{displaymath}](/articles/aa/full_html/2009/32/aa11250-08/img145.png) |
(40) |
Using this approximation and the previous substitutions we obtain for the fluence
![$\displaystyle F\bigl(\epsilon_k(\tau_1) \leq \epsilon_{\rm s} \leq \epsilon_k(\...
...frac{\epsilon_0 \omega_1 \gamma_0^2}{\epsilon_{\rm s}}\biggr]^{25/6} - 1\biggr)$](/articles/aa/full_html/2009/32/aa11250-08/img146.png) |
|||
![$\displaystyle \hspace*{4mm}+ \frac{4 \epsilon_0^{1/3} \gamma_0^{2/3}}{9 \epsilo...
...biggl[\frac{\epsilon_{\rm f}}{\epsilon_{\rm s}}\biggr]^{7/2}\biggr)\Biggr)\cdot$](/articles/aa/full_html/2009/32/aa11250-08/img147.png) |
(41) |
The dominant contribution to the fluence again represents synchrotron photons from the optically thin part of the synchrotron spectrum
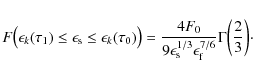 |
(42) |
For scattered photon energies
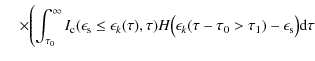 |
|||
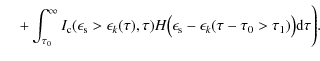 |
(43) |
Using the substitutions and approximations applied before we obtain
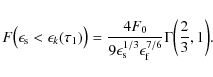 |
(44) |
Again the contribution representing the optically thick part of the spectrum is negligibly small compared to the contribution representing the optically thin part, demonstrating that the fluence distribution
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11250fg1.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg156.png) |
Figure 1: Time-averaged spectrum observed from PKS 2155-304 on MJD 53944. The dashed line represents the fit for the linear cooling case (Schlickeiser & Röken 2008), whereas the solid curve illustrates the fit for the nonlinear cooling case. |
| Open with DEXTER | |
6.3 AIC model selection test
Figure 1 shows the linear (dashed curve) and nonlinear (solid curve) fits to the time-averaged spectrum observed from PKS 2155-304 on MJD 53944 (Aharonian et al. 2007). For the generation of these fits we first had to transform the calculated fluence distributions from the comoving frame into the observer frame (asterisked quantities)
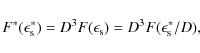 |
(45) |
followed by the construction of the linear model parametric function
(results from the linear synchrotron self-Compton fluence distribution in the
with
7 Summary and conclusions
Schlickeiser & Lerche (2007) developed a nonlinear model for the synchrotron radiation cooling of ultra-relativistic particles in powerful non-thermal radiation sources assuming a partition condition between the energy densities of the magnetic field and the relativistic electrons. Here, we used this model in order to calculate the synchrotron self-Compton process in flaring TeV blazars and compared it to the results obtained with the standard linear synchrotron cooling model. For simplicity we chose the case of instantaneously injected monoenergetic relativistic electrons as an example, although other injection scenarios, like the instantaneous injection of power-law distributed electrons (Schlickeiser & Lerche 2008), are also possible. After the nonlinear electron synchrotron cooling, the created synchrotron photons with non-relativistic energies are multiple Thomson scattered off the cooled electrons in the source (synchrotron self-Compton process).
We calculated the optically thin and thick synchrotron radiation intensities as well as the synchrotron photon density distributions in the emission knot as functions of frequency and time. These synchrotron photons serve as target photons in the synchrotron self-Compton process. Using the Thomson approximation of the inverse Compton cross section, we determined the synchrotron self-Compton intensity and fluence for the nonlinear electron cooling. It is shown that the optically thick synchrotron radiation component provides only a negligible contribution to the synchrotron self-Compton quantities at all frequencies and times, as in the linear cooling case. In Appendix B, we extended our calculations to the full Klein-Nishina cross section and obtained additional positive and negative, non-vanishing fluence contributions only in the high-energy regime
![]() of the scattered photons, e.g. generalised incomplete
of the scattered photons, e.g. generalised incomplete ![]() -functions or the new generalised dual hypergeometric functions. Surprisingly, for the special class of electron and synchrotron photon distributions used in this work, these contributions nearly cancel each other out on average, leaving only a small positive fluence contribution (see Figs. B.5 and B.6) which we expected to be due to the consideration of high energy photons in the scattering process. Because of the smallness of the new contribution it can be justified to model the photon spectra by applying the
-functions or the new generalised dual hypergeometric functions. Surprisingly, for the special class of electron and synchrotron photon distributions used in this work, these contributions nearly cancel each other out on average, leaving only a small positive fluence contribution (see Figs. B.5 and B.6) which we expected to be due to the consideration of high energy photons in the scattering process. Because of the smallness of the new contribution it can be justified to model the photon spectra by applying the ![]() -distribution approximation for the calculation of the differential inverse Compton scattering rate for electron and synchrotron densities of the form (B.15), (B.16) as well as (B.23) and (B.24).
-distribution approximation for the calculation of the differential inverse Compton scattering rate for electron and synchrotron densities of the form (B.15), (B.16) as well as (B.23) and (B.24).
Finally, we compared the linear to the nonlinear fluence distribution, fitting both to the observed TeV fluence spectrum of PKS 2155-304 on MJD 53944 and performed a statistical quality-of-fit test (AIC test). For this particular data record, we found the linear model to be more appropriate than the nonlinear. Actually, with the formalism we presented here, we cannot fit the entire spectral energy distribution because we neglect the synchrotron self-Compton component of energy losses and only discuss the synchrotron one. Therefore, Schlickeiser (2009) has shown that synchrotron self-Compton cooling is an alternative nonlinear cooling process that can be handled analytically as long as it operates in the Thomson limit. Nonetheless, the excellent agreement of both linear and nonlinear synchrotron self-Compton fluence spectra with the observation of the gamma-ray flare of PKS 2155-304 supports the injection scenario of monoenergetic electrons by the relativistic pickup process.
Acknowledgements
This work was partially supported by the German Ministry for Education and Research (BMBF) through Verbundforschung Astroteilchenphysik grant 05 CH5PC1/6 and the Deutsche Forschungsgemeinschaft through grant Schl 201/16-2.
Appendix A: Synchrotron optical depth and photon spectra
A.1 Optical depth
The synchrotron emission of ultra-relativistic electrons is optically thin for frequencies and times satisfying the condition
![]() and optically thick for
and optically thick for
![]() .
The transition occurs at the frequency
.
The transition occurs at the frequency
![]() defined by
defined by
![]() .
For
.
For
![]() (and its analytical continuation) the optical depth (15) reduces to
(and its analytical continuation) the optical depth (15) reduces to
as long as
In the domain
Substituting
with the proper transition frequency
In Fig. A.1, we present the time-dependence of the transition frequency. For small times
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg2.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg196.png) |
Figure A.1:
Normalised synchrotron transition frequency |
| Open with DEXTER | |
A.2 Synchrotron spectra
According to Eq. (11), the synchrotron intensity in the optically thick frequency domain
![]() is given by
is given by
where
In Fig. A.2, we show the intensity distribution as a function of the frequency
Applying the transition frequencies (A.2) and (A.5) we obtain for the transition intensity at normalised times
whereas at times
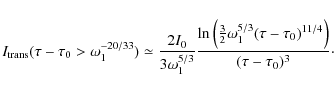 |
(A.10) |
At small times
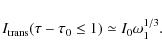 |
(A.11) |
The time-dependence of the transition intensity is presented in Fig. A.3.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg3.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg211.png) |
Figure A.2:
Synchrotron intensity distribution as a function of frequency |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg4.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg212.png) |
Figure A.3:
Synchrotron transition intensity
|
| Open with DEXTER | |
Appendix B: Synchrotron self-Compton scattering with the full Klein-Nishina cross section
B.1 The process of synchrotron self-Compton emission
The differential inverse Compton scattering rate
![]() in a coordinate system comoving with the radiation source (unprimed quantities) is given by (Dermer et al. 1992)
in a coordinate system comoving with the radiation source (unprimed quantities) is given by (Dermer et al. 1992)
where
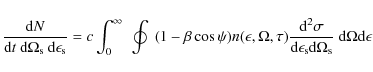 |
(B.2) |
with the normalised energy of an incoming photon
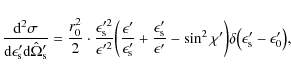 |
(B.3) |
where
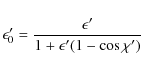 |
(B.4) |
and
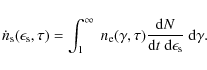 |
(B.5) |
Following the paper of Arbeiter et al. (2005) we can write
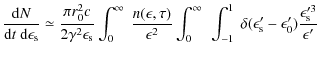 |
|||
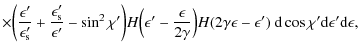 |
(B.6) |
where
where
In the following calculations of the synchrotron self-Compton intensities and fluences we disregard (B.8) and only use the dominant contribution (B.7) of the differential scattering rate for a single electron.
B.2 Linear and nonlinear synchrotron self-Compton intensities
Neglecting effects due to stimulated synchrotron self-Compton emission and absorption the synchrotron self-Compton intensity reads
where
Consequently, we have to distinguish between the three cases
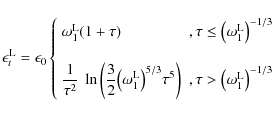 |
(B.11) |
and for the nonlinear electron cooling case
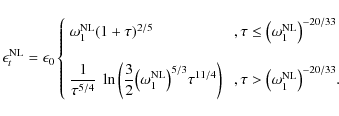 |
(B.12) |
Here, we discuss only the case
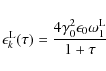 |
(B.13) |
and
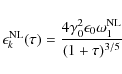 |
(B.14) |
with
B.2.1 Linear electron cooling
To compute the linear differential scattering rate we insert the linear differential electron density (Schlickeiser & Lerche 2007)
and the linear synchrotron photon density
into Eq. (B.10). Then we obtain
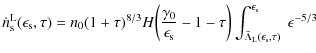 |
|||
![$\displaystyle \hspace*{4mm}\times {\rm e}^{- f(\tau) \epsilon} \biggl( \bigl(1 ...
...lon, \epsilon_{\rm s}, \tau) \bigl[ 1 + \epsilon_{\rm s} \epsilon \bigr] \Bigr)$](/articles/aa/full_html/2009/32/aa11250-08/img259.png) |
|||
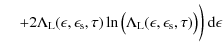 |
(B.17) |
with the constant
where
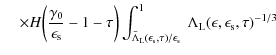 |
|||
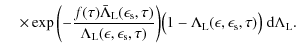 |
(B.19) |
Substituting
| |
= | 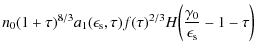 |
|
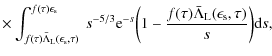 |
(B.20) |
which is solved by generalised incomplete Gamma functions
| |
= | 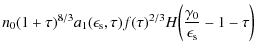 |
|
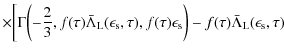 |
|||
![$\displaystyle \times \Gamma\biggl(- \frac{5}{3}, f(\tau) \bar \Lambda_{\rm L}(\epsilon_{\rm s}, \tau), f(\tau) \epsilon_{\rm s} \biggr) \biggr]$](/articles/aa/full_html/2009/32/aa11250-08/img279.png) |
|||
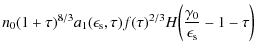 |
|||
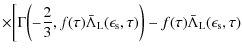 |
|||
![$\displaystyle \times \Gamma\biggl(- \frac{5}{3}, f(\tau) \bar \Lambda_{\rm L}(\epsilon_{\rm s}, \tau) \biggr) \biggr].$](/articles/aa/full_html/2009/32/aa11250-08/img282.png) |
(B.21) |
We, thus, find the linear synchrotron self-Compton intensity to be
where
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg5.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg289.png) |
Figure B.1:
Normalised linear synchrotron intensity
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg6.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg290.png) |
Figure B.2:
Normalised linear synchrotron light curve
|
| Open with DEXTER | |
B.2.2 Nonlinear electron cooling
With the nonlinear differential electron density (Schlickeiser & Lerche 2007)
and the nonlinear synchrotron photon density
the differential scattering rate reads
| |
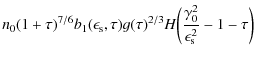 |
||
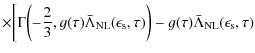 |
|||
![$\displaystyle \times \Gamma\biggl(- \frac{5}{3}, g(\tau) \bar \Lambda_{\rm NL}(\epsilon_{\rm s}, \tau) \biggr) \biggr],$](/articles/aa/full_html/2009/32/aa11250-08/img296.png) |
(B.25) |
where
In Figs. B.3 and B.4 we present the nonlinear synchrotron intensity (B.26) as a function of the energy
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{11250fg7.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg306.png) |
Figure B.3:
Normalised nonlinear synchrotron intensity
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{11250fg8.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg307.png) |
Figure B.4:
Normalised nonlinear synchrotron light curve
|
| Open with DEXTER | |
B.3 Linear and nonlinear synchrotron self-Compton fluences
By the time-integration of the synchrotron self-Compton intensity (B.9) we obtain the synchrotron self-Compton fluence distribution
Here, we only have to examine the range for high scattered photon energies
B.3.1 Linear electron cooling
With the linear synchrotron self-Compton intensity distribution (B.22) the synchrotron self-Compton fluence (B.27) reads for
![]()
| |
= |  |
|
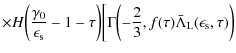 |
|||
![$\displaystyle - f(\tau) \bar \Lambda_{\rm L}(\epsilon_{\rm s}, \tau) \Gamma\big...
...au) \bar \Lambda_{\rm L}(\epsilon_{\rm s}, \tau) \biggr) \biggr]~ {\rm d}\tau ,$](/articles/aa/full_html/2009/32/aa11250-08/img316.png) |
(B.28) |
where
| |
= | 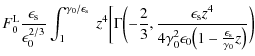 |
|
![$\displaystyle - \frac{\epsilon_{\rm s} z^4}{4 \gamma_0^2 \epsilon_0 \bigl( 1 - ...
...\bigl( 1 - \frac{\epsilon_{\rm s}}{\gamma_0} z\bigr)} \biggr) \biggr]~{\rm d}z.$](/articles/aa/full_html/2009/32/aa11250-08/img322.png) |
(B.29) |
Transforming
For scattered photon energies
| |
= | 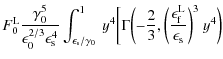 |
|
![$\displaystyle - \biggl(\frac{\epsilon_{\rm f}^{\rm L}}{\epsilon_{\rm s}}\biggr)...
...lon_{\rm f}^{\rm L}}{\epsilon_{\rm s}}\biggr)^3 ~ y^4 \biggr) \biggr]~{\rm d}y.$](/articles/aa/full_html/2009/32/aa11250-08/img330.png) |
(B.31) |
Partial integration leads to the solution
consisting of incomplete and generalised incomplete
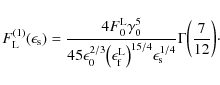 |
(B.33) |
For high scattered photon energies,
Because all integrals in the high-energy scattered photon range are finally of the form of the integral on the right-hand-side of (B.34), we solve this in detail to demonstrate the analytical methods used. For this purpose, the exponential function can be Taylor-expanded leading to
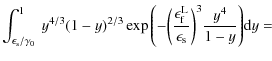 |
|||
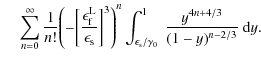 |
(B.35) |
The denominator of the integrand can be written as a generalised geometric series
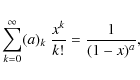 |
(B.36) |
where
![$\displaystyle \sum_{n = 0}^{\infty} \sum_{k = 0}^{\infty} \frac{(n - 2/3)_k}{n!...
...\biggr]^3\Biggr)^n \int_{\epsilon_{\rm s}/\gamma_0}^1 ~y^{4n+k+4/3}~ {\rm d}y =$](/articles/aa/full_html/2009/32/aa11250-08/img345.png) |
|||
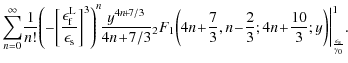 |
(B.37) |
The dominating contribution of the sum is of zeroth order, so that we obtain approximately
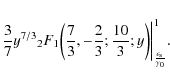 |
(B.38) |
The whole solution of the integral (B.34) reads
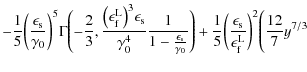 |
|||
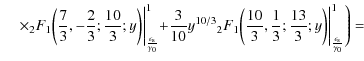 |
|||
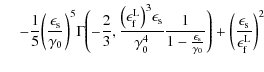 |
|||
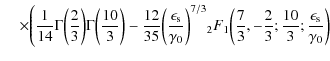 |
|||
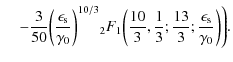 |
(B.39) |
The second integral of (B.30),
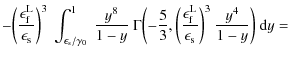 |
|||
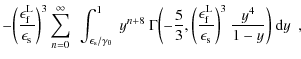 |
(B.40) |
yields the solution
For the first time, defining generalised dual hypergeometric functions
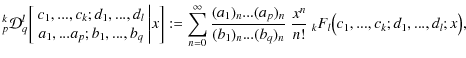 |
(B.42) |
the solution (B.41) can be written in a more compact form
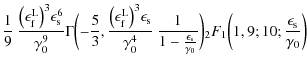 |
|||
![$\displaystyle - \biggl( \frac{\epsilon_{\rm s}}{\epsilon_{\rm f}^{\rm L}} \bigg...
...+ 7/3, -5/3; n + 10/3 \\ 1, 9, 7/3; 10, 10/3 \end{array} \biggl\vert y \biggr]$](/articles/aa/full_html/2009/32/aa11250-08/img360.png) |
|||
![$\displaystyle + \frac{1}{30} y^{10/3} ~
{^2_3}\mathcal{D}_2^1 \biggl[ \begin{ar...
...iggl\vert y \biggr]
\Biggr)\Biggl\vert^{1}_{\frac{\epsilon_{\rm s}}{\gamma_0}}.$](/articles/aa/full_html/2009/32/aa11250-08/img361.png) |
(B.43) |
The whole first fluence contribution (B.30) then reads
We obtain for the second term of
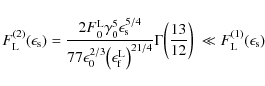 |
(B.45) |
and for
![\begin{eqnarray*}&& + \frac{6}{91} y^{13/3} ~
{^2_3}\mathcal{D}_2^1 \biggl[ \b...
...gr] \Biggl\vert^{1}_{\frac{\epsilon_{\rm s}}{\gamma_0}}
\Biggr),
\end{eqnarray*}](/articles/aa/full_html/2009/32/aa11250-08/img373.png)
where the total fluence is finally
B.3.2 Nonlinear electron cooling
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg9.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg375.png) |
Figure B.5:
Normalised linear fluence distributions for the full Klein-Nishina cross section (solid curve) and for the |
| Open with DEXTER | |
Using the nonlinear synchrotron self-Compton intensity (B.26), the nonlinear synchrotron self-Compton fluence reads for
![]()
| |
= | 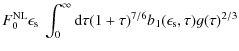 |
|
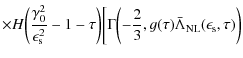 |
|||
![$\displaystyle - g(\tau) \bar \Lambda_{\rm NL}(\epsilon_{\rm s}, \tau) \Gamma\bi...
...c{5}{3}, g(\tau) \bar \Lambda_{\rm NL}(\epsilon_{\rm s}, \tau) \biggr) \biggr],$](/articles/aa/full_html/2009/32/aa11250-08/img380.png) |
(B.47) |
where
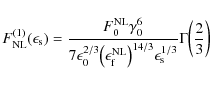 |
(B.48) |
and
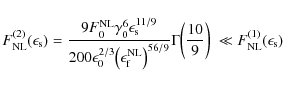 |
(B.49) |
as well as for
and
In Figs. B.5 and B.6, we show the linear,
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg10.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg404.png) |
Figure B.6:
Normalised nonlinear fluence distributions for the full Klein-Nishina cross section (solid curve) and for the |
| Open with DEXTER | |
![\begin{displaymath}F_{\rm L}^{\delta}(\epsilon_{\rm s}) = \frac{12}{7} F_0^{{\rm...
...\biggl( \frac{\epsilon_{\rm s}}{\gamma_0}\biggr)^{7/3} \Biggr]
\end{displaymath}](/articles/aa/full_html/2009/32/aa11250-08/img405.png) |
(B.52) |
and
![\begin{displaymath}F_{\rm NL}^{\delta}(\epsilon_{\rm s}) = \frac{2}{3} F_0^{NL, ...
...ggl( \frac{\epsilon_{\rm s}}{\gamma_0}\biggr)^{3} \Biggr]\cdot
\end{displaymath}](/articles/aa/full_html/2009/32/aa11250-08/img406.png) |
(B.53) |
Despite the different mathematical form of the full Klein-Nishina fluence distributions and the approximated fluence distributions in the high-energy regime, in both electron synchrotron cooling cases the plots look nearly identical, except for the expected, but small positive fluence contribution in the Klein-Nishina plots due to the consideration of high energy photons. This is caused by the almost cancellation of the significant positive and negative additional contributions of the full Klein-Nishina fluence distribution between each other.
References
- Abramowitz, M., & Stegun, I. S. 1972 (Washington: National Bureau of Standards) (In the text)
- Aharonian, F. A., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (H. E. S. S. Collaboration) 2005, A&A, 442, 895 (In the text)
- Aharonian, F. A., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (H. E. S. S. Collaboration) 2007, ApJ, 664, L71 (In the text)
- Aharonian, F. A., et al. (H. E. S. S. Collaboration) 2009, ApJ, in press [arXiv:0903.2924]
- Aharonian, F. A., Akhperjanian, A. G., Anton, G., et al. (H. E. S. S. Collaboration) 2009, ApJ, 696, L150
- Akaike, H. 1974, IEEE Transactions on Automatic control, 19, 716 [NASA ADS] [CrossRef] (In the text)
- Arbeiter, C., Pohl, M., & Schlickeiser, R. 2002, A&A, 386, 415 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Arbeiter, C. 2005, Dissertation, Ruhr-Universität Bochum (In the text)
- Arbeiter, C., Pohl, M., & Schlickeiser, R. 2005, ApJ, 627, 62 [NASA ADS] [CrossRef] (In the text)
- Bale, S. D. 2008, Talk given at the general meeting of the Center for Magnetic Self-Organisation www.cmso.info/cmsopdf/general_jul08/talks/bale.pdf (In the text)
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] (In the text)
- Blazejowski, M., Sikora, M., Moderski, R., & Madejski, G. M. 2000, ApJ, 545, 107 [NASA ADS] [CrossRef] (In the text)
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] (In the text)
- Böttcher, M. 2007, Astrophys. Space Sci., 309, 95 [NASA ADS] [CrossRef]
- Chandrasekhar, S. 1961, Hydrodynamic and Hydromagnetic Stability (Oxford: Dover Publ.) (In the text)
- Chiaberge, M., & Ghisellini, G. 1999, MNRAS, 306, 551 [NASA ADS] [CrossRef] (In the text)
- Crusius, A., & Schlickeiser, R. 1986, A&A, 164, L16 [NASA ADS] (In the text)
- Crusius, A., & Schlickeiser, R. 1988, A&A, 196, 327 [NASA ADS] (In the text)
- Dermer, C. D., & Schlickeiser, R. 1993, ApJ, 416, 458 [NASA ADS] [CrossRef] (In the text)
- Dermer, C. D., Schlickeiser, R., & Mastichiadis, A. 1992, A&A, 256, L27 [NASA ADS] (In the text)
- Dermer, C. D., Sturner, S. J., & Schlickeiser, R. 1997, ApJS, 109, 103 [NASA ADS] [CrossRef] (In the text)
- Frederiksen, J. T., Hededal, C. B., Haugbolle, T., & Nordlund, A. 2004, ApJ, 608, L13 [NASA ADS] [CrossRef] (In the text)
- Gerbig, D., & Schlickeiser, R. 2007, ApJ, 664, 750 [NASA ADS] [CrossRef] (In the text)
- Hellinger, P., Travnicek, P., & Matsumoto, H. 2002, Geophys. Res. Lett., 29, 87 [CrossRef] (In the text)
- Jaroschek, C., Lesch, H., & Treumann, R. 2005, ApJ, 618, 822 [NASA ADS] [CrossRef] (In the text)
- Jauch, J. M., & Rohrlich, F. 1976, The Theory of Photons and Electrons (Springer-Verlag) (In the text)
- Jones, F. C. 1968, Phys. Rev., 167, 1159 [NASA ADS] [CrossRef]
- Kapetanakos, C. A. 1974, Appl. Phys. Lett., 25, 484 [NASA ADS] [CrossRef] (In the text)
- Kardashev, N. S. 1962, SvA, AJ, 6, 317 (In the text)
- Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2002, Geophys. Res. Lett., 29, 20 [NASA ADS] [CrossRef] (In the text)
- Lazar, M., Schlickeiser, R., Poedts, S., & Tautz, R. C. 2008, MNRAS, 390, 168 [NASA ADS] [CrossRef] (In the text)
- Lee, R., & Lampe, M. 1973, Phys. Rev. Lett., 31, 1390 [NASA ADS] [CrossRef] (In the text)
- Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [NASA ADS] [CrossRef] (In the text)
- Mastichiadis, A., & Kirk, J. G. 1997, A&A, 320, 19 [NASA ADS] (In the text)
- Ng, J. S. T., & Noble, R. J. 2006, Phys. Rev. Lett., 96, 115006 [NASA ADS] [CrossRef]
- Nishikawa, K. I., Hardee, P., Richarson, G., et al. 2003, ApJ, 595, 555 [NASA ADS] [CrossRef] (In the text)
- Pohl, M., & Schlickeiser, R. 2000, A&A, 354, 395 [NASA ADS] (In the text)
- Reynolds, S. P. 1982, ApJ, 256, 38 [NASA ADS] [CrossRef] (In the text)
- Röken, C., & Schlickeiser, R. 2009, ApJ, published
- Sakai, J. I., Schlickeiser, R., & Sukla, P. K. 2004, Phys. Lett. A, 330, 384 [NASA ADS] [CrossRef] (In the text)
- Schlickeiser, R. 2003, A&A, 410, 397 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schlickeiser, R. 2009, MNRAS, submitted (In the text)
- Schlickeiser, R., & Lerche, I. 2007, A&A, 476, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schlickeiser, R., & Lerche, I. 2008, A&A, 485, 315 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schlickeiser, R., & Röken, C. 2008, A&A, 477, 701 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schlickeiser, R., Sievers, A., & Thiemann, H. 1987, A&A, 182, 21 [NASA ADS] (In the text)
- Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [NASA ADS] [CrossRef] (In the text)
- Silva, L. O., Fonseca, R. A., Tonge, J. W., et al. 2003, ApJ, 596, L121 [NASA ADS] [CrossRef] (In the text)
- Sokolov, A., Marscher, A. P., & McHardy, I. M. 2004, ApJ, 613, 725 [NASA ADS] [CrossRef] (In the text)
- Stockem, A., Lerche, I., & Schlickeiser, R. 2007, ApJ, 659, 419 [NASA ADS] [CrossRef] (In the text)
- Tatarakis, M., et al. 2003, Phys. Rev. Lett., 90, 175001 [NASA ADS] [CrossRef] (In the text)
All Figures
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11250fg1.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg156.png) |
Figure 1: Time-averaged spectrum observed from PKS 2155-304 on MJD 53944. The dashed line represents the fit for the linear cooling case (Schlickeiser & Röken 2008), whereas the solid curve illustrates the fit for the nonlinear cooling case. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg2.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg196.png) |
Figure A.1:
Normalised synchrotron transition frequency |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg3.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg211.png) |
Figure A.2:
Synchrotron intensity distribution as a function of frequency |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg4.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg212.png) |
Figure A.3:
Synchrotron transition intensity
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg5.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg289.png) |
Figure B.1:
Normalised linear synchrotron intensity
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg6.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg290.png) |
Figure B.2:
Normalised linear synchrotron light curve
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{11250fg7.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg306.png) |
Figure B.3:
Normalised nonlinear synchrotron intensity
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{11250fg8.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg307.png) |
Figure B.4:
Normalised nonlinear synchrotron light curve
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg9.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg375.png) |
Figure B.5:
Normalised linear fluence distributions for the full Klein-Nishina cross section (solid curve) and for the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{11250fg10.eps}
\end{figure}](/articles/aa/full_html/2009/32/aa11250-08/Timg404.png) |
Figure B.6:
Normalised nonlinear fluence distributions for the full Klein-Nishina cross section (solid curve) and for the |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



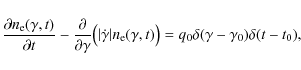
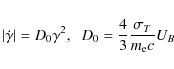
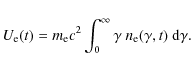
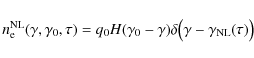
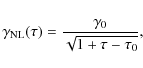
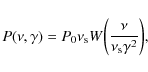
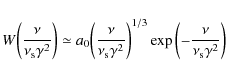
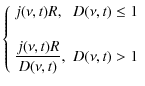
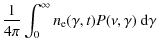
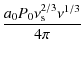
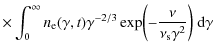
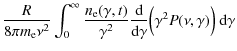
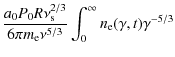
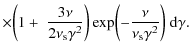
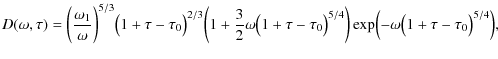
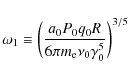
![$\displaystyle {I(\omega \leq \omega_t, \tau) \over I_0}{\omega^{5/3}_1 \over \o...
...2} \biggl[1 + \frac{3}{2} ~\omega (1 + \tau - \tau_0)^{5/4}\biggr] \biggr)^{-1}$](/articles/aa/full_html/2009/32/aa11250-08/img80.png)
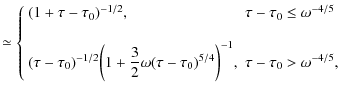
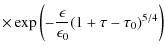
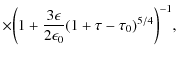
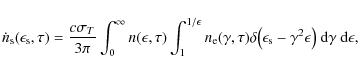
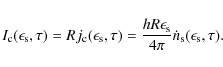
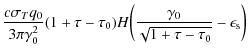
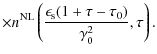
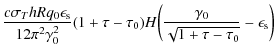
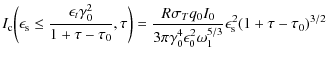
![$\displaystyle \hspace*{4mm}\times H\biggl({\gamma _0 \over \sqrt{1 + \tau - \ta...
...lon_{\rm s} \over \epsilon_0 \gamma _0^2}(1 + \tau - \tau_0)^{9/4} \biggr]^{-1}$](/articles/aa/full_html/2009/32/aa11250-08/img105.png)
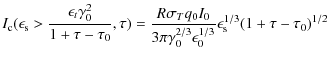
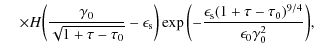
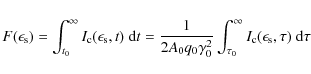
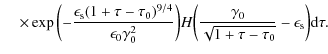
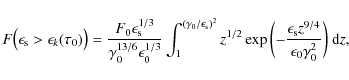
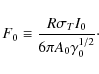
![$\displaystyle F\bigl(\epsilon_{\rm s} > \epsilon _k(\tau_0)\bigr) = \frac{4 F_0...
...[ \frac{\epsilon_{\rm f}}{\epsilon_{\rm s}}\biggr]^{7/2} s\biggr)} ~ {\rm d}s .$](/articles/aa/full_html/2009/32/aa11250-08/img124.png)
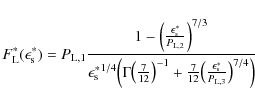
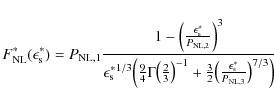
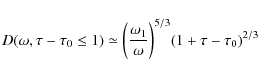
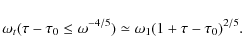
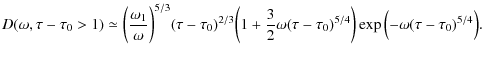
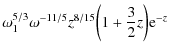
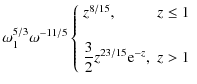
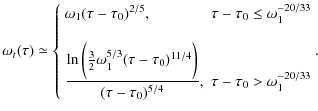
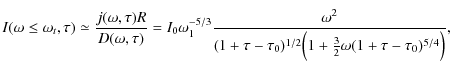
![$\displaystyle I_0 \omega^{-5/3}_1 {\omega^2_t\over (1 + \tau - \tau_0)^{1/2} \Bigl[1 + \frac{3}{2} \omega_t (1 + \tau - \tau_0)^{5/4} \Bigr]}\cdot$](/articles/aa/full_html/2009/32/aa11250-08/img205.png)
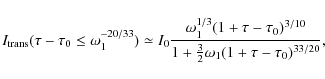
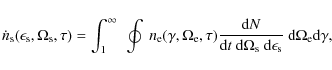
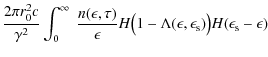
![$\displaystyle \times \biggl( \bigl(1 - \Lambda(\epsilon, \epsilon_{\rm s})\bigr...
...(\epsilon, \epsilon_{\rm s}) \bigl[ 1 + \epsilon_{\rm s} \epsilon \bigr] \Bigr)$](/articles/aa/full_html/2009/32/aa11250-08/img234.png)
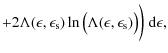
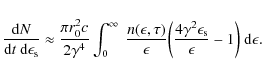
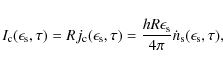
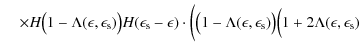
![$\displaystyle \hspace*{4mm} \times \bigl[ 1 + \epsilon_{\rm s} \epsilon \bigr] ...
...da(\epsilon, \epsilon_{\rm s}) \bigr)} \biggr) ~ {\rm d}\epsilon {\rm d}\gamma.$](/articles/aa/full_html/2009/32/aa11250-08/img244.png)
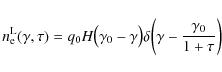
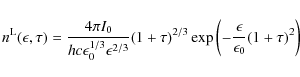
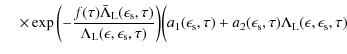
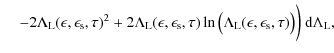
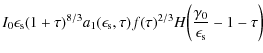
![$\displaystyle \times \Gamma\biggl(- \frac{5}{3}, f(\tau) \bar \Lambda_{\rm L}(\epsilon_{\rm s}, \tau) \biggr) \biggr],$](/articles/aa/full_html/2009/32/aa11250-08/img285.png)
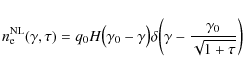
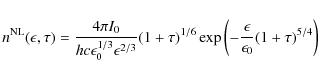
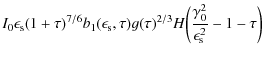
![$\displaystyle \times \Gamma\biggl(- \frac{5}{3}, g(\tau) \bar \Lambda_{\rm NL}(\epsilon_{\rm s}, \tau) \biggr) \biggr].$](/articles/aa/full_html/2009/32/aa11250-08/img302.png)
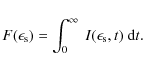
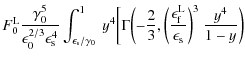
![$\displaystyle - \biggl(\frac{\epsilon_{\rm f}^{\rm L}}{\epsilon_{\rm s}}\biggr)...
...rm L}}{\epsilon_{\rm s}}\biggr)^3 ~ \frac{y^4}{1 - y} \biggr) \biggr]~{\rm d}y.$](/articles/aa/full_html/2009/32/aa11250-08/img326.png)
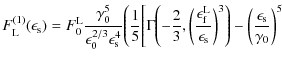
![$\displaystyle \hspace*{4mm} \times \Gamma\Biggl( - \frac{2}{3}, \frac{\bigl(\ep...
...ggl( \frac{\epsilon_{\rm f}^{\rm L}}{\epsilon_{\rm s}}\biggr)^3 \Biggr) \Biggr]$](/articles/aa/full_html/2009/32/aa11250-08/img332.png)
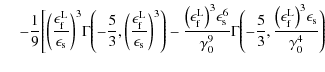
![$\displaystyle \hspace*{4mm}+ \biggl( \frac{\epsilon_{\rm s}}{\epsilon_{\rm f}^{...
...rac{\epsilon_{\rm f}^{\rm L}}{\epsilon_{\rm s}}\biggr)^3 \Biggr)\Biggr] \Biggr)$](/articles/aa/full_html/2009/32/aa11250-08/img334.png)
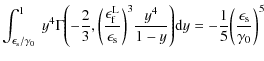
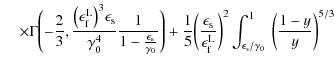
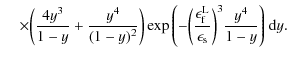
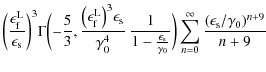
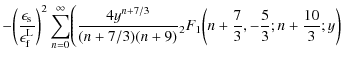
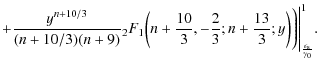
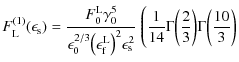
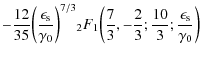
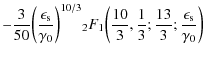
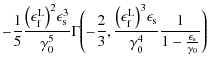
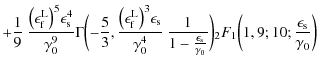
![$\displaystyle - \frac{4}{21} y^{7/3} ~
{^2_3}\mathcal{D}_2^1 \biggl[ \begin{arr...
...array} \biggl\vert y \biggr]\Biggl\vert^{1}_{\frac{\epsilon_{\rm s}}{\gamma_0}}$](/articles/aa/full_html/2009/32/aa11250-08/img367.png)
![$\displaystyle - \frac{1}{30} y^{10/3} ~
{^2_3}\mathcal{D}_2^1 \biggl[ \begin{ar...
...ggl\vert y \biggr] \Biggl\vert^{1}_{\frac{\epsilon_{\rm s}}{\gamma_0}}
\Biggr).$](/articles/aa/full_html/2009/32/aa11250-08/img368.png)
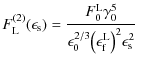
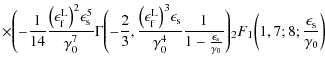
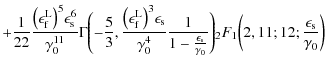
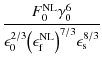
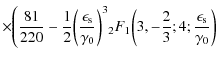
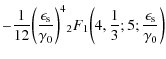
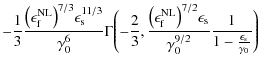
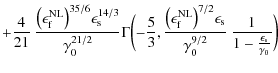
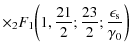
![$\displaystyle - \frac{2}{7} y^3 ~
{^2_3}\mathcal{D}_2^1 \biggl[ \begin{array}{c...
...array} \biggl\vert y \biggr]\Biggl\vert^{1}_{\frac{\epsilon_{\rm s}}{\gamma_0}}$](/articles/aa/full_html/2009/32/aa11250-08/img393.png)
![$\displaystyle - \frac{1}{21} y^4 ~
{^2_3}\mathcal{D}_2^1 \biggl[ \begin{array}{...
...iggl\vert y \biggr] \Biggl\vert^{1}_{\frac{\epsilon_{\rm s}}{\gamma_0}}
\Biggr)$](/articles/aa/full_html/2009/32/aa11250-08/img394.png)
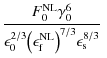
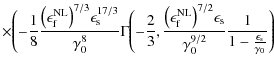
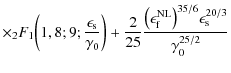
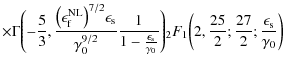
![$\displaystyle + \frac{9}{80} y^{5} ~
{^2_3}\mathcal{D}_2^1 \biggl[ \begin{array...
...array} \biggl\vert y \biggr]\Biggl\vert^{1}_{\frac{\epsilon_{\rm s}}{\gamma_0}}$](/articles/aa/full_html/2009/32/aa11250-08/img400.png)
![$\displaystyle + \frac{1}{48} y^{6} ~ {^2_3}\mathcal{D}_2^1 \biggl[ \begin{array...
...rray} \biggl\vert y \biggr] \Biggl\vert^{1}_{\frac{\epsilon_{\rm s}}{\gamma_0}}$](/articles/aa/full_html/2009/32/aa11250-08/img401.png)
![$\displaystyle - \frac{9}{125} y^{5} ~
{^2_3}\mathcal{D}_2^1 \biggl[ \begin{arra...
...array} \biggl\vert y \biggr]\Biggl\vert^{1}_{\frac{\epsilon_{\rm s}}{\gamma_0}}$](/articles/aa/full_html/2009/32/aa11250-08/img402.png)
![$\displaystyle - \frac{1}{75} y^6 ~ {^2_3}\mathcal{D}_2^1 \biggl[ \begin{array}{...
...ggl\vert y \biggr] \Biggl\vert^{1}_{\frac{\epsilon_{\rm s}}{\gamma_0}}
\Biggr).$](/articles/aa/full_html/2009/32/aa11250-08/img403.png)