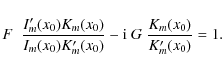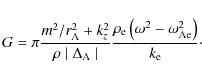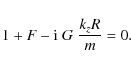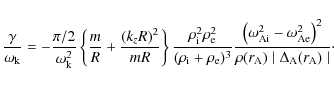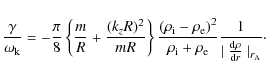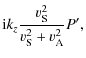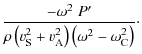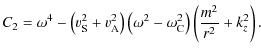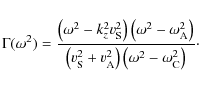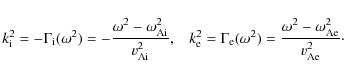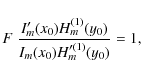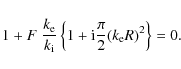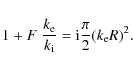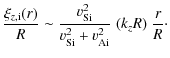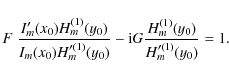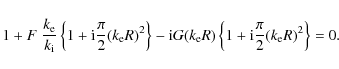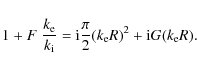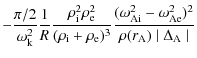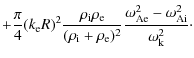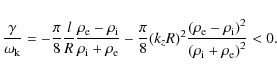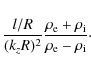| Issue |
A&A
Volume 503, Number 1, August III 2009
|
|
|---|---|---|
| Page(s) | 213 - 223 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912399 | |
| Published online | 22 June 2009 | |
On the nature of kink MHD waves in magnetic flux tubes
M. Goossens1 - J. Terradas1 - J.
Andries1,2,![]() -
I. Arregui3 -
J. L. Ballester3
-
I. Arregui3 -
J. L. Ballester3
1 - Centre Plasma Astrophysics and Leuven Mathematical Modeling and
Computational Science Center, Katholieke Universiteit Leuven, 3001 Leuven,
Belgium
2 -
Centre for Stellar and Planetary Astrophysics, Monash University, 3800
Victoria, Australia
3 -
Departament de Física, Universitat de les Illes Balears, Spain
Received 28 April 2009 / Accepted 4 June 2009
Abstract
Context. Magnetohydrodynamic (MHD) waves are often reported in the solar atmosphere and usually classified as slow, fast, or Alfvén. The possibility that these waves have mixed properties is often ignored.
Aims. The goal of this work is to study and determine the nature of MHD kink waves.
Methods. This is done by calculating the frequency, the damping rate and the eigenfunctions of MHD kink waves for three widely different MHD waves cases: a compressible pressure-less plasma, an incompressible plasma and a compressible plasma which allows for MHD radiation.
Results. In all three cases the frequency and the damping rate are for practical purposes the same as they differ at most by terms proportional to (kz R)2. In the magnetic flux tube the kink waves are in all three cases, to a high degree of accuracy incompressible waves with negligible pressure perturbations and with mainly horizontal motions. The main restoring force of kink waves in the magnetised flux tube is the magnetic tension force. The total pressure gradient force cannot be neglected except when the frequency of the kink wave is equal or slightly differs from the local Alfvén frequency, i.e. in the resonant layer.
Conclusions. Kink waves are very robust and do not care about the details of the MHD wave environment. The adjective fast is not the correct adjective to characterise kink waves. If an adjective is to be used it should be Alfvénic. However, it is better to realize that kink waves have mixed properties and cannot be put in one single box.
Key words: magnetohydrodynamics (MHD) - waves - Sun: magnetic fields
1 Introduction
The last decade has seen an avalanche of observations of magnetohydrodynamic (MHD) waves in the solar atmosphere. It is clear now that MHD waves are ubiquitous in the solar atmosphere. This has triggered new theoretical research for explaining and interpreting the observed properties. A special point of attention is whether these MHD waves are slow, fast or Alfvén waves. Apparently, a large fraction of the solar MHD waves community favours very clear cut divisions and does not seem to appreciate the possibility of MHD waves with mixed properties. The transverse oscillations observed in coronal loops (see for example Nakariakov et al. 1999; Aschwanden et al. 1999), often triggered by a nearby solar flare, are interpreted as fast kink MHD waves. A striking property of these transverse waves is their fast damping with damping times of the order of 3-5 periods. Resonant absorption is up to today the only damping mechanism that offers a consistent explanation of this rapid damping. Resonant absorption relies on the transfer of energy from a global MHD wave to local resonant Alfvén waves. If this mechanism is indeed operational then this means that the observed transverse oscillations have Alfvénic properties in at least part of the oscillating loop. The debate on the nature of MHD waves in the solar atmosphere has gained new momentum when several groups, e.g. De Pontieu et al. (2007), Okamoto et al. (2007), Tomczyk et al. (2007) reported the detection of Alfvén waves in HINODE observations. Van Doorsselaere et al. (2008) compared fast kink MHD waves to torsional Alfvén waves and concluded that the HINODE observations can be explained in terms of fast kink MHD waves.
This paper will not try to explain the HINODE observations. Its aim is to determine the nature of kink MHD waves on magnetic flux tubes. We have no doubt about the explanation of transverse oscillation of coronal loops in terms of kink MHD waves. MHD waves with their azimuthal wave number equal to 1, i.e. m=1, are the only motions that displace the axis of the loop and the loop as a whole. It is not clear to us on what arguments the use of the adjective fast is based. As far as we know there has not been any study of the forces that drive the kink waves in coronal loops. If these waves are fast, then the pressure gradient force should be, in general, the dominant force compared to the magnetic tension force. We have to admit that we also have used the adjective fast without a solid argument in favour of this classification. Our aim is to understand the spatial structure of the motions in the kink waves.
An MHD wave on an axi-symmetric 1-D cylindrical plasma equilibrium is
characterised by two wave numbers, the azimuthal wave number m, and the axial
wave number kz. In addition modes can have a different number of nodes in the
radial direction and this number can be used to further classify the modes.
Hence, an MHD eigenmode is characterised by three numbers. The azimuthal wave
number is an integer. The modes with m=0 are usually called sausage (slow and
fast) or torsional (Alfvén). The modes with m=1 are named kink and the
modes with ![]() are flute modes. The axial wave number kz can be
discretised as
are flute modes. The axial wave number kz can be
discretised as
![]() with L the length of the loop and
with L the length of the loop and
![]() Depending on the dimensions of the equilibrium model there can be
more than one radial eigenmode for a given couple (m, kz). In what follows we
shall study linear MHD waves that are superimposed on a flux tube in static
equilibrium with a straight and constant axial magnetic field. This equilibrium
model contains the essential physics of the problem and allows a relatively
straightforward mathematical analysis of the MHD waves. MHD waves have been
investigated in previous studies. However, these studies almost exclusively
focused on the frequencies of the MHD waves and in addition they were in most
cases restricted to real frequencies. For example, the paper by Edwin & Roberts (1983),
which is often referred to in the solar MHD wave community, is limited to real
frequencies and does not give any information on the eigenfunctions beyond the
fact that they can be expressed in terms of Bessel functions. Complex frequencies
were considered by Spruit (1982) and by Cally (1985). Cally (1985)
rightfully pointed out that essential physics is lost by restricting the analysis
to real frequencies. Spruit (1982) is an exception to the rule in that he
discussed the eigenfunctions. In short, the eigenfunctions of MHD waves are not
well documented even for uniform equilibrium states and definitely not for
non-uniform equilibrium states.
Depending on the dimensions of the equilibrium model there can be
more than one radial eigenmode for a given couple (m, kz). In what follows we
shall study linear MHD waves that are superimposed on a flux tube in static
equilibrium with a straight and constant axial magnetic field. This equilibrium
model contains the essential physics of the problem and allows a relatively
straightforward mathematical analysis of the MHD waves. MHD waves have been
investigated in previous studies. However, these studies almost exclusively
focused on the frequencies of the MHD waves and in addition they were in most
cases restricted to real frequencies. For example, the paper by Edwin & Roberts (1983),
which is often referred to in the solar MHD wave community, is limited to real
frequencies and does not give any information on the eigenfunctions beyond the
fact that they can be expressed in terms of Bessel functions. Complex frequencies
were considered by Spruit (1982) and by Cally (1985). Cally (1985)
rightfully pointed out that essential physics is lost by restricting the analysis
to real frequencies. Spruit (1982) is an exception to the rule in that he
discussed the eigenfunctions. In short, the eigenfunctions of MHD waves are not
well documented even for uniform equilibrium states and definitely not for
non-uniform equilibrium states.
In order to illustrate the nature of MHD kink waves we shall study them for three widely different MHD waves cases. The first case deals with compressible MHD waves of a pressureless plasma on a high density flux tube embedded in a low density magnetic plasma exterior. The assumption of a pressureless plasma removes the slow waves from the analysis and the velocity and displacement have no axial component. The density being higher in the flux tube than in the exterior means that according to common wisdom the MHD waves are propagating (body waves) in the flux tube and evanescent (surface wave) in the exterior. The second case deals with MHD waves of an incompressible plasma. The assumption of incompressibility removes the fast waves. The waves are evanescent (surface waves) both in the interior and exterior of the flux tube and this behaviour is independent of the density being higher or lower in the interior. In the third case we consider a situation where the compressible MHD waves are propagating in the exterior. In that case the MHD waves are damped by MHD radiation, but the kink MHD wave hardly feels this wave leakage.
2 Propagating kink MHD waves on dense pressureless flux tubes
2.1 Equations for MHD waves for a pressureless plasma cylinder
The equations for linear MHD waves on a 1-dimensional pressureless
cylinder with a straight field can be obtained from the more
general equations by e.g. Appert et al. (1974); Sakurai et al. (1991a);
Goossens et al. (1992), Goossens et al. (1995) by putting the local
speed of sound ![]() and the azimuthal component of the
equilibrium magnetic field
and the azimuthal component of the
equilibrium magnetic field
![]() equal to 0. The resulting
equations are (see e.g. Goossens 2008)
equal to 0. The resulting
equations are (see e.g. Goossens 2008)
![]() is the Lagrangian displacement and P' is the
Eulerian perturbation of total pressure. The coefficient functions
D and C2 in (1) are
is the Lagrangian displacement and P' is the
Eulerian perturbation of total pressure. The coefficient functions
D and C2 in (1) are
For completeness we have also listed the expression for the local cusp frequency
The nature of an MHD wave is determined by the competition of the
restoring forces which are the force due to the total (gas plus magnetic) pressure gradient and
the magnetic tension force. In ideal MHD we can obtain the
following expression for the Lorentz force, the magnetic tension
force ![]() and the magnetic pressure force
and the magnetic pressure force
![]() in
linear MHD waves on a background with a constant magnetic field
in
linear MHD waves on a background with a constant magnetic field
In a non-uniform plasma with
It is standard practice to rewrite the two first order ordinary
differential equations of (1) as a
second order ordinary differential equation for P':
where
2.2 Pressureless flux tubes with uniform density
For a uniform plasma we can rewrite (7) as
Here
Note that the quantities
which means that
This allows us to define radial wave numbers
Equation (9) can then be solved in terms of Bessel functions Jm(x) (
The prime denotes a derivative with respect to the argument x or y and
with the quantity F given by
being
The solution for the frequency is
and for the radial wave numbers
The right hand side of (18) is almost invariably called the square of the kink frequency and denoted as
The TT approximations to the eigenfunctions are
Note that when deriving (21) we have omitted terms of order (kz R)2 and higher unless the terms of order (kz R)2 are the first non-vanishing contribution to the expression under study. For example the expressions for
So far we have described the properties of modes that involve non-zero total
pressure (![]() ). However, if the medium is uniform the system of equations
given by (1) also allows pure incompressible Alfvén
waves. They are only driven by magnetic tension, their eigenfrequency is simply
). However, if the medium is uniform the system of equations
given by (1) also allows pure incompressible Alfvén
waves. They are only driven by magnetic tension, their eigenfrequency is simply
![]() and the total pressure, P', is equal to zero. To have such
modes the displacement has to satisfy
and the total pressure, P', is equal to zero. To have such
modes the displacement has to satisfy
![]() .
In
cylindrical coordinates this means that,
.
In
cylindrical coordinates this means that,
If we prescribe the radial dependence of one of the components of the displacement, we can easily calculate the other component from the previous equation. The case m=0 is a particular solution that represents torsional Alfvén waves (
2.3 Beyond the TT approximation for pressureless uniform flux tubes
The analytic expressions (21) (![]() )
have been obtained
in the limit
)
have been obtained
in the limit
![]() .
It is straightforward to solve the dispersion relation (15) and calculate the spatial solutions (14). This
allows us to determine how the analytical expressions are modified by effects due
to a finite radius. In Fig. 1 the eigenfunctions of three loops with
different radii are represented. It is clear that the spatial profile is well
described by the approximated solutions in the TT limit given by
Eqs. (21). The radial and azimuthal components are
constant inside the loop, the azimuthal component has the expected jump at r=R,
while the total pressure grows linearly with the radius. Increasing R results
in an increase of the total pressure, and thus compressibility, since this
magnitude is proportional to (kzR)2. Interestingly, for fat loops (see the
case R/L=0.1) the TT approximations of the eigenfunctions are still quite
valid. An analysis of the forces (not shown here) indicates that, even for thick
loops, the tension dominates over the magnetic pressure gradient.
.
It is straightforward to solve the dispersion relation (15) and calculate the spatial solutions (14). This
allows us to determine how the analytical expressions are modified by effects due
to a finite radius. In Fig. 1 the eigenfunctions of three loops with
different radii are represented. It is clear that the spatial profile is well
described by the approximated solutions in the TT limit given by
Eqs. (21). The radial and azimuthal components are
constant inside the loop, the azimuthal component has the expected jump at r=R,
while the total pressure grows linearly with the radius. Increasing R results
in an increase of the total pressure, and thus compressibility, since this
magnitude is proportional to (kzR)2. Interestingly, for fat loops (see the
case R/L=0.1) the TT approximations of the eigenfunctions are still quite
valid. An analysis of the forces (not shown here) indicates that, even for thick
loops, the tension dominates over the magnetic pressure gradient.
![\begin{figure}
\par\includegraphics[width=7.6cm]{12399f1a.eps}\vspace*{3mm}
\inc...
...99f1b.eps}\vspace*{3mm}
\includegraphics[width=7.6cm]{12399f1c.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12399-09/Timg113.png) |
Figure 1:
Radial dependence of the normalised eigenfunctions, |
| Open with DEXTER | |
2.4 Pressureless flux tubes with non-uniform density
In this subsection we remove the discontinuous variation of density from its
internal value
![]() to
to
![]() by a continuous
variation in a non-uniform layer
[R - l/2 , R + l/2]. A fully non-uniform
equilibrium state corresponds to l= 2 R. When the jump in
by a continuous
variation in a non-uniform layer
[R - l/2 , R + l/2]. A fully non-uniform
equilibrium state corresponds to l= 2 R. When the jump in
![]() is replaced by a continuous variation of
is replaced by a continuous variation of
![]() new physics is
introduced in the system. The continuous variation of
new physics is
introduced in the system. The continuous variation of
![]() has
the important effect that the kink MHD wave, which has its frequency in the
Alfvén continuum, interacts with local Alfvén continuum waves and gets
damped. This resonant damping is translated in a complex frequency (and complex
eigenfunction). In the present paper damped global eigenmodes that are coupled
to resonant Alfvén waves in a non-uniform equilibrium state shall be
computed by two methods. The first method is to use a numerical code that
integrates the resistive MHD equations in the whole volume of the equilibrium
state to determine a selected mode or part of the resistive spectrum of the
system (see for example Van Doorsselaere et al. 2004; Arregui et al. 2005; Terradas et al. 2006).
The second method was introduced by Tirry & Goossens (1996). It circumvents the
numerical integration of the non-ideal MHD equations and only requires numerical
integration (or closed analytical solutions) of the linear ideal MHD equations.
The method relies on the fact that dissipation is important only in a narrow
layer around the resonant point where the real part of the quasi-mode frequency
equals the local Alfvén frequency. This makes it possible to obtain
analytical solutions to simplified versions of the linear dissipative MHD
equations which accurately describe the linear motions in the dissipative layer
and in two overlap regions to the left and right of the dissipative layer. In
these overlap regions both ideal MHD and dissipative MHD are valid. Asymptotic
analysis of the analytical dissipative solutions allows to derive jump
conditions that can be used to connect the solutions to the left and right of
the dissipative layer. The jump conditions were derived by e.g.
Sakurai et al. (1991a), Goossens et al. (1992), Goossens et al. (1995) and
Goossens & Ruderman (1995) for the driven problem and by Tirry & Goossens (1996) for the
eigenvalue problem. A schematic overview of the various regions involved in this
method is shown in Fig. 1 of Stenuit et al. (1998). This method was used for
computing eigenmodes of various non-uniform plasma configurations by e.g.
Tirry et al. (1998b,a), Stenuit et al. (1999,1998),
Andries & Goossens (2001); Andries et al. (2000). A related method was used by Sakurai et al. (1991b)
and Stenuit et al. (1995) for the computation of resonant Alfvén waves in the
driven problem with a prescribed and real frequency and by Keppens et al. (1994)
for computing the multiple scattering and resonant absorption of p-modes by
fibril sunspots. Comparison with results of fully dissipative computations show
that the method is very accurate.
has
the important effect that the kink MHD wave, which has its frequency in the
Alfvén continuum, interacts with local Alfvén continuum waves and gets
damped. This resonant damping is translated in a complex frequency (and complex
eigenfunction). In the present paper damped global eigenmodes that are coupled
to resonant Alfvén waves in a non-uniform equilibrium state shall be
computed by two methods. The first method is to use a numerical code that
integrates the resistive MHD equations in the whole volume of the equilibrium
state to determine a selected mode or part of the resistive spectrum of the
system (see for example Van Doorsselaere et al. 2004; Arregui et al. 2005; Terradas et al. 2006).
The second method was introduced by Tirry & Goossens (1996). It circumvents the
numerical integration of the non-ideal MHD equations and only requires numerical
integration (or closed analytical solutions) of the linear ideal MHD equations.
The method relies on the fact that dissipation is important only in a narrow
layer around the resonant point where the real part of the quasi-mode frequency
equals the local Alfvén frequency. This makes it possible to obtain
analytical solutions to simplified versions of the linear dissipative MHD
equations which accurately describe the linear motions in the dissipative layer
and in two overlap regions to the left and right of the dissipative layer. In
these overlap regions both ideal MHD and dissipative MHD are valid. Asymptotic
analysis of the analytical dissipative solutions allows to derive jump
conditions that can be used to connect the solutions to the left and right of
the dissipative layer. The jump conditions were derived by e.g.
Sakurai et al. (1991a), Goossens et al. (1992), Goossens et al. (1995) and
Goossens & Ruderman (1995) for the driven problem and by Tirry & Goossens (1996) for the
eigenvalue problem. A schematic overview of the various regions involved in this
method is shown in Fig. 1 of Stenuit et al. (1998). This method was used for
computing eigenmodes of various non-uniform plasma configurations by e.g.
Tirry et al. (1998b,a), Stenuit et al. (1999,1998),
Andries & Goossens (2001); Andries et al. (2000). A related method was used by Sakurai et al. (1991b)
and Stenuit et al. (1995) for the computation of resonant Alfvén waves in the
driven problem with a prescribed and real frequency and by Keppens et al. (1994)
for computing the multiple scattering and resonant absorption of p-modes by
fibril sunspots. Comparison with results of fully dissipative computations show
that the method is very accurate.
A drastic variant of the method that avoids solving the non-ideal
MHD equations uses the so-called thin boundary (TB) approximation.
In this lazy version the ideal MHD equations are not solved in the
non-uniform plasma but the plasma is treated as if it were uniform
all the way up to the dissipative layer. This is definitely a very
strong assumption since the thickness of the dissipative layer is
measured by the quantity
![]() :
:
Here
where Rm is the magnetic Reynolds number (
In the TB approximation we need to add an additional term to the
dispersion relation which takes into account the jump in the radial
component across the resonant layer where the real part of the kink
eigenmode is equal to the local Alfvén frequency
![]() .
.
![]() is the resonant position which in the thin
boundary approximation
is the resonant position which in the thin
boundary approximation
![]() .
The jump in
.
The jump in ![]() is
is
The modified version of the ideal dispersion relation (15) is
F is given by (16) and G is defined as
G contains the effect of the resonance. When we combine the thin tube (TT) approximation with the thin boundary (TB) approximation, we can simplify the dispersion relation to
The zero order solution to (28), i.e. the solution when the effect of the resonance is not taken into account is of course (18). In order to take the effect of the resonance into account we write
and approximate
Equation (30) agrees with Eq. (77) of Goossens et al. (1992) when that equation is corrected for a typo as the factor
Equation (30) shows that the damping decrement depends
linearly on m. Since we are mainly interested in m=1 we shall
specialise to that value in the remainder of this subsection. If the
variation of
![]() is solely due to the variation of density
is solely due to the variation of density
![]() as is the case here since we have considered a constant
axial magnetic field, Eq. (30) can be
rewritten as
as is the case here since we have considered a constant
axial magnetic field, Eq. (30) can be
rewritten as
For a linear profile of density
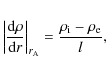
so that
In (32)
For a sinusoidal profile of density
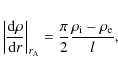
so that
Here the results agree with those obtained by Ruderman & Roberts (2002). At this point we like to stress that the TTTB approximation turns out to be remarkably accurate far beyond its domain of applicability. This is clearly illustrated in a recent analytical seismological study by Goossens et al. (2008) which complemented a fully numerical seismology investigation by Arregui et al. (2007).
The eigenfunctions in the thin dissipative layer can be described by
the functions ![]() and
and ![]() defined by
Goossens et al. (1995) for the driven problem and the functions
defined by
Goossens et al. (1995) for the driven problem and the functions
![]() and
and
![]() defined by Ruderman et al. (1995)
for the incompressible eigenvalue problem and by Tirry & Goossens (1996)
for the compressible eigenvalue problem. In the dissipative layer the
MHD kink waves are highly Alfvénic. This can be understood as follows.
From the analysis by Sakurai et al. (1991a), Goossens et al. (1995) and
Tirry & Goossens (1996) it follows that in the dissipative layer, the
Eulerian perturbation of total pressure P' is constant and that
defined by Ruderman et al. (1995)
for the incompressible eigenvalue problem and by Tirry & Goossens (1996)
for the compressible eigenvalue problem. In the dissipative layer the
MHD kink waves are highly Alfvénic. This can be understood as follows.
From the analysis by Sakurai et al. (1991a), Goossens et al. (1995) and
Tirry & Goossens (1996) it follows that in the dissipative layer, the
Eulerian perturbation of total pressure P' is constant and that
![]() .
We do not have to
worry about
.
We do not have to
worry about ![]() since it is zero for a pressureless plasma. In
addition
since it is zero for a pressureless plasma. In
addition
Here
where we have used
In the dissipative layer the magnetic tension force is far bigger than the pressure gradient force. Hence the MHD kink wave is highly Alfvénic in the dissipative layer.
2.5 Beyond the TTTB approximation for pressureless non-uniform flux tubes
In this subsection we go beyond the thin boundary approximation and we consider thick non-uniform layers with l/R = 0.2 and 0.4. The eigenfunctions are numerically calculated by solving the full set of linear, resistive MHD equations described in Terradas et al. (2006) and using the PDE2D code (Sewell 1995). Figure 2 displays the obtained results. It is clear that the two inhomogeneous solutions are almost identical to the homogeneous solution, except in the non-uniform layer, where large displacements are found. This is the location where the resonance takes place.
In Fig. 3 we see that both the radial and azimuthal components of the Lorentz force are dominated by magnetic tension. The magnitude of the magnetic tension and pressure is of the same order (with the tension about twice as important as the magnetic pressure force such as corresponds to a density contrast of 3) except in the inhomogeneous layer where the tension in the azimuthal direction is clearly dominant, reflecting the strong Alfvénic nature of the solution in the dissipative layer.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{12399f2a.eps}\vspace*{3mm}...
....eps}\vspace*{3mm}
\includegraphics[width=6.7cm,clip]{12399f2c.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12399-09/Timg153.png) |
Figure 2:
Radial dependence of the moduli of the eigenfunctions, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{12399f3a.eps}\vspace*{3mm}...
....eps}\vspace*{3mm}
\includegraphics[width=6.1cm,clip]{12399f3c.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12399-09/Timg154.png) |
Figure 3: Top panel: moduli of the radial forces. Middle panel: moduli of the azimuthal forces. Bottom panel: ratio of the modulus of the magnetic tension to the magnetic pressure gradient in the radial and the azimuthal direction. This case corresponds to the eigensolution displayed in Fig. 2 with l/R=0.4. The vertical dashed lines show the limits of the non-uniform layer. |
| Open with DEXTER | |
3 Incompressible MHD waves on flux tubes
3.1 Equations for incompressible MHD waves on a plasma cylinder
The equations for incompressible MHD waves can be found in
Goossens et al. (1992). Incompressibility means that we take the
limit
![]() and enforce
and enforce
![]() Note also that in the incompressible case
Note also that in the incompressible case
![]() .
The relevant equations are
.
The relevant equations are
As before we concentrate on solutions with
Here we do not need to worry about propagating and/or evanescent behaviour of the solutions and the local radial wave number. The solutions are always evanescent or surface waves and the local radial wave number is kz. Note that in our notation
3.2 Incompressible MHD waves on uniform flux tubes
For a uniform plasma we can rewrite (38) as
Equation (39) can then be solved in terms of Bessel functions Im(x) (x = kz r) in the internal part of the flux tube and Km(x) in the exterior region
Continuity of total pressure and the radial component of the Lagrangian displacement leads to the dispersion relation:
The incompressible version of F is
Now x0 = kz R. The dispersion relation (41) can be solved numerically. However, if we consider the TT approximation, the Bessel functions Im(x) and Km(x) in (41) are replaced with their first order asymptotic expansions, and the dispersion relation (41) is reduced to
The solution is again given by Eq. (18), i.e.
As before we have omitted terms of order (kz R)2 and higher unless the terms of order (kz R)2 are the first non-vanishing contribution to the expression under study. It is instructive to compare (44) with (21). The expressions for
3.3 Beyond the TT approximation for incompressible MHD waves on uniform flux tubes
As in the compressible case the analytic expressions (44) have
been obtained in the limit
![]() .
It is easy to solve the dispersion
relation (41) and determine the spatial
solutions (40). In Fig. 1 the eigenfunctions of
three loops with variable radii are represented with circles. Again it is clear
that the spatial profile is well described by the approximated solutions in the
TT limit given by Eqs. (44). As expected, the case with
R/L=0.1 shows the largest deviation from the TT approximation.
Figure 1 also allows us a direct comparison with the eigenfunctions in
the compressible approximation. As the ratio R/L decreases the eigenfunctions
of the compressible and incompressible cases tend to be the same, in agreement
with the analytical expressions given by (44) and (21).
We arrive to the same conclusion for the forces, even for
thick loops, the tension dominates over the magnetic pressure gradient.
.
It is easy to solve the dispersion
relation (41) and determine the spatial
solutions (40). In Fig. 1 the eigenfunctions of
three loops with variable radii are represented with circles. Again it is clear
that the spatial profile is well described by the approximated solutions in the
TT limit given by Eqs. (44). As expected, the case with
R/L=0.1 shows the largest deviation from the TT approximation.
Figure 1 also allows us a direct comparison with the eigenfunctions in
the compressible approximation. As the ratio R/L decreases the eigenfunctions
of the compressible and incompressible cases tend to be the same, in agreement
with the analytical expressions given by (44) and (21).
We arrive to the same conclusion for the forces, even for
thick loops, the tension dominates over the magnetic pressure gradient.
3.4 Incompressible MHD waves on non-uniform flux tubes
We again remove the discontinuous variation of density from its internal value
![]() to
to
![]() by a continuous variation in a non-uniform. By doing so,
we allow interaction of the global kink wave with local Alfvén/slow
continuum waves and the
discontinuous behaviour of
by a continuous variation in a non-uniform. By doing so,
we allow interaction of the global kink wave with local Alfvén/slow
continuum waves and the
discontinuous behaviour of
![]() and
and ![]() are replaced
by singular behaviour in ideal MHD and by large but finite values in
non-ideal MHD. In the thin boundary approximation we need to add an
additional term to the dispersion relation which takes into account the jump in
the radial component across the resonant layer where the real part of the kink
eigenmode is equal to the local Alfvén frequency. For the incompressible
case the jump in
are replaced
by singular behaviour in ideal MHD and by large but finite values in
non-ideal MHD. In the thin boundary approximation we need to add an
additional term to the dispersion relation which takes into account the jump in
the radial component across the resonant layer where the real part of the kink
eigenmode is equal to the local Alfvén frequency. For the incompressible
case the jump in ![]() is (see e.g. Goossens et al. 1992)
is (see e.g. Goossens et al. 1992)
In the incompressible limit
![]() and the
Alfvén resonance and slow resonance coincide. The jump in
and the
Alfvén resonance and slow resonance coincide. The jump in
![]() due to the Alfvén resonance is given in (25).
The jump in
due to the Alfvén resonance is given in (25).
The jump in ![]() due to the slow resonance is
due to the slow resonance is
For the incompressible limit
We see that Eq. (45) is the combination of the jump due to the Alfvén
resonance (25) and the jump due to the slow
resonance (47). The contribution to the jump in ![]() due to
the slow resonance is of order (kz R)2 compared to that of the
Alfvén resonance and can be neglected in our thin tube
approximation. Note that
due to
the slow resonance is of order (kz R)2 compared to that of the
Alfvén resonance and can be neglected in our thin tube
approximation. Note that
![]() so that
the slow resonance has its biggest effect for incompressible
plasmas. Even in that case it is unimportant compared to the
Alfvén resonance. This is in agreement with a result obtained
for MHD waves in prominences by Soler et al. (2009). For sentimental
reasons we shall keep the contribution due to the slow resonance.
so that
the slow resonance has its biggest effect for incompressible
plasmas. Even in that case it is unimportant compared to the
Alfvén resonance. This is in agreement with a result obtained
for MHD waves in prominences by Soler et al. (2009). For sentimental
reasons we shall keep the contribution due to the slow resonance.
The modified version of the ideal dispersion relation (41) is
F is given by (16) and G is defined as
When we combine the TT approximation with TB approximation, the dispersion relation is reduced to
The zero order solution to (50) without taking into account the effect of the resonance is of course (18). The effect of the resonance is contained in G. In order to take that effect into account we proceed as before
and approximate
If the variation of
From here on we shall specialise to m=1. For a linear profile of density
For a sinusoidal profile of density
For all practical purposes we can neglect the contribution proportional to (kz R)2 and conclude that the damping due to resonant absorption of the kink mode in an incompressible plasma is the same as that in a pressureless plasma (see Eqs. (32) and (33)). If we forget about differences proportional to (kz R)2 then the conclusion is that kink MHD waves in pressureless plasmas and incompressible plasmas are the same. In view of that conclusion it is difficult to understand why a kink mode can be called fast as fast waves are absent from incompressible plasmas.
The eigenfunctions in the thin dissipative layer can be described by
the functions
![]() and
and
![]() which were first
introduced by Ruderman et al. (1995) for non-stationary incompressible
resonant Alfvén waves in planar plasmas. The conclusion is the same
as in the previous section. The kink MHD waves are highly Alfvénic
in the dissipative layer.
which were first
introduced by Ruderman et al. (1995) for non-stationary incompressible
resonant Alfvén waves in planar plasmas. The conclusion is the same
as in the previous section. The kink MHD waves are highly Alfvénic
in the dissipative layer.
4 MHD kink waves in the presence of MHD radiation
4.1 Equations for compressible MHD waves on a non-zero beta plasma cylinder
So far we have seen that kink MHD waves in the thin
tube approximation do not care about propagating (body wave) or
evanescent (surface wave) behaviour in the internal part of the flux
tube. The behaviour in the exterior plasma was until now evanescent.
Here we take the next step and consider leakage of energy due to MHD
radiation. MHD radiation causes the frequencies to be complex even
in absence of resonant damping. MHD waves in the presence of MHD
radiation were studied for uniform flux tubes by Spruit (1982)
in the TT approximation and by Cally (1985,2003) for
arbitrary values of the radius. Stenuit et al. (1998) and
Stenuit et al. (1999) determined MHD waves undergoing resonant
absorption and/or leakage for photospheric flux tubes embedded in a
non-magnetic surrounding. Stenuit et al. (1999) pointed out which Hankel
function to use for leaky and non-leaky waves. We use the equations
for linear MHD waves on a 1-dimensional cylinder with a straight
field. Effects due to plasma pressure and compressibility are taken
into account. The equations are
The coefficient functions D and C2 are now
As before we rewrite the two first order differential equations of (56) as a second order ordinary differential equation for P':
where
We have solved the set of Eqs. (56) under general conditions allowing for non-zero plasma pressure and compressibility, see Cally (1985); Spruit (1982) for uniform plasmas and Goossens & Hollweg (1993) for nonuniform plasmas. Here we present the results for a pressureless plasma with
4.2 MHD waves on uniform flux tubes
For a uniform plasma without gas pressure we recover Eq. (9).
Now
![]() and
and
![]() and
and
![]() .
The radial wave numbers are now defined as (see
Eq. (13))
.
The radial wave numbers are now defined as (see
Eq. (13))
The solutions to Eq. (9) are now
The formulation with the Hankel functions is convenient as it enables us to distinguish between incoming and outgoing waves. With the classic convention that
Continuity of total pressure and the radial component of the
Lagrangian displacement leads to the dispersion relation:
where F is defined by (16). Now
When we neglect in a zeroth order approximation the effect of MHD radiation the solution to Eq. (63) is again Eq. (18) for the square of the frequency and Eq. (19) for the radial wave numbers.
We can rewrite Eq. (63) correct up to second order in
![]() as
as
The solution is
Equation (65) shows that in order for damping due to wave leakage to occur we need
The ratio of the force due to the pressure gradient to the magnetic tension force is here also given by Eq. (6).
The TT approximations to the eigenfunctions are again given by
Eqs. (21). If we allow
![]() then we find a non-zero
then we find a non-zero ![]() with
with
4.3 MHD radiating waves on non-uniform flux tubes
Once more we remove the discontinuous variation of
density. Now the jump in
![]() is given by (25), and the modified version of the
ideal dispersion relation (62) is
is given by (25), and the modified version of the
ideal dispersion relation (62) is
The TT approximation to this equation (for m=1) is
In the third term of the left hand side of the previous equation we can drop
The solution of (70) is
In case of a constant magnetic field so that the variation of the local Alfvén frequency is solely due to a variation of density (71) can be further simplified to
Equation (72) is derived for a linear variation of density. For a sinusoidal variation the factor
This clearly indicates that damping due to resonant absorption dominates over that due to MHD radiation (since
The remarkable result is that the frequency of the kink wave and its damping due to resonant absorption found for a compressible plasma with a non-zero plasma pressure differ by terms of order (kz R)2, even when we allow MHD radiation. If we neglect contributions proportional to (kz R)2 then the simple conclusion is that the frequency of the kink wave and its damping due to resonant absorption are the same in the three cases that we have considered.
Again, as in the two previous cases, the eigenfunctions in the thin dissipative
layer can be described by the functions
![]() and
and
![]() .
Again the conclusion is that kink MHD waves are highly Alfvénic in the
dissipative layer.
.
Again the conclusion is that kink MHD waves are highly Alfvénic in the
dissipative layer.
5 Conclusion
This paper has examined the nature of MHD kink waves. This was done by determining the frequency, the damping rate and in particular the eigenfunctions of MHD kink waves for three widely different MHD waves cases: a compressible pressureless plasma, an incompressible plasma and a compressible plasma which allows for MHD radiation. The overall conclusion is that kink waves are very robust and do not care about the details of the MHD wave environment. In all three cases the frequency and the damping rate are for practical purposes the same as they differ at most by terms proportional to (kz R)2. In the magnetic flux tube the kink waves are in all three cases, to a high degree of accuracy incompressible waves with negligible pressure perturbations and with mainly horizontal motions. The main restoring force of kink waves in the magnetised flux tube is the magnetic tension force. The gradient pressure force cannot be neglected except when the frequency of the kink wave is equal or slightly differs from the local Alfvén frequency, i.e. in the resonant layer. The adjective fast is not the correct adjective to characterisekink waves. If an adjective is to be used it should be Alfvénic. However, it is better to realize that kink waves have mixed properties and cannot be put in one single box.
Acknowledgements
This research was begun when M.G. was a visitor of the Solar Physics Group at the UIB. It is pleasure for M.G. to acknowledge the warm hospitality of the Solar Physics Group at the UIB and the support received from UIB. M.G. and J.T. also acknowledge support from K.U.Leuven via GOA/2009-009. J.A. was supported by an International Outgoing Marie Curie Fellowship within the 7th European Community Framework Programme. In addition, J.T., I.A. and J.L.B. acknowledge the funding provided under projects AYA2006-07637 (Spanish Ministerio de Educación y Ciencia) and PCTIB2005GC3-03 (Conselleria d'Economia, Hisenda i Innovació of the Government of the Balearic Islands).
References
- Andries, J., & Goossens, M. 2001, A&A, 368, 1083 [NASA ADS] [CrossRef] [EDP Sciences]
- Andries, J., Tirry, W. J., & Goossens, M. 2000, ApJ, 531, 561 [NASA ADS] [CrossRef]
- Appert, K., Gruber, K., & Vaclavik, J. 1974, Phys. Fluids, 17, 1471 [NASA ADS] [CrossRef] (In the text)
- Arregui, I., Van Doorsselaere, T., Andries, J., Goossens, M., & Kimpe, D. 2005, A&A, 441, 361 [NASA ADS] [CrossRef] [EDP Sciences]
- Arregui, I., Andries, J., Van Doorsselaere, T., Goossens, M., & Poedts, S. 2007, A&A, 463, 333 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef]
- Cally, P. S. 1985, Sol. Phys., 103, 277 [NASA ADS] [CrossRef] (In the text)
- Cally, P. S. 2003, Sol. Phys., 217, 95 [NASA ADS] [CrossRef]
- De Pontieu, B., McIntosh, S. W., Carlsson, M., et al. 2007, Science, 318, 1574 [NASA ADS] [CrossRef] (In the text)
- Edwin, P., & Roberts, B. R. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] (In the text)
- Goossens, M. 2008, Proc. IAU Symp., 247, 228 [NASA ADS] (In the text)
- Goossens, M., & Hollweg, J. V. 1993, Sol. Phys., 145, 19 [NASA ADS] [CrossRef] (In the text)
- Goossens, M., & Ruderman, M. S. 1995, Phys. Scr., T60, 171 [NASA ADS] [CrossRef] (In the text)
- Goossens, M., Hollweg, J. V., & Sakurai, T. 1992, Sol. Phys., 138, 233 [NASA ADS] [CrossRef] (In the text)
- Goossens, M., Ruderman, M. S., & Hollweg, J. V. 1995, Sol. Phys., 157, 75 [NASA ADS] [CrossRef] (In the text)
- Goossens, M., Arregui, I., Ballester, J. L., & Wang, T. J. 2008, A&A, 484, 851 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hollweg, J. V., & Yang, G. 1988, J. Geophys. Res., 93, 5423 [NASA ADS] [CrossRef] (In the text)
- Keppens, R., Bogdan., T. J., & Goossens, M. 1994, ApJ, 436, 372 [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M., Ofman, L., DeLuca, E. E., Roberts, B. R., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef]
- Okamoto, T. J., Tsuneta, S., Berger, T. E., et al. 2007, Science, 318, 1577 [NASA ADS] [CrossRef] (In the text)
- Ruderman, M. S., & Roberts, B. R. 2002, ApJ, 577, 475 [NASA ADS] [CrossRef] (In the text)
- Ruderman, M. S., Tirry, W., & Goossens, M. 1995, J. Plasma Phys., 54, 129 [NASA ADS] [CrossRef] (In the text)
- Sakurai, T., Goossens, M., & Hollweg, J. V. 1991a, Sol. Phys., 133, 227 [NASA ADS] [CrossRef] (In the text)
- Sakurai, T., Goossens, M., & Hollweg, J. V. 1991b, Sol. Phys., 133, 247 [NASA ADS] [CrossRef] (In the text)
- Sewell, G. 2005, The numerical Solution of Ordinary and Partial Differential Equations (Hoboken: Wiley & Sons) (In the text)
- Soler, R., Oliver, R., Ballester, J. L., & Goossens, M. 2009, ApJ, 695, L166 [NASA ADS] [CrossRef] (In the text)
- Spruit, H. 1982, Sol. Phys., 75, 3 [NASA ADS] [CrossRef] (In the text)
- Stenuit, H., Erdelyi, R., & Goossens, M. 1995, Sol. Phys., 161, 139 [NASA ADS] [CrossRef] (In the text)
- Stenuit, H., Keppens, R., & Goossens, M. 1998, A&A, 331, 392 [NASA ADS] (In the text)
- Stenuit, H., Tirry, W. J., Keppens, R., & Goossens, M. 1999, A&A, 342, 863 [NASA ADS]
- Terradas, J., Oliver, R., & Ballester, J. L. 2006, ApJ, 642, 533 [NASA ADS] [CrossRef]
- Terradas, J., Andries, J., Goossens, M., et al. 2008, ApJ, 687, L115 [NASA ADS] [CrossRef] (In the text)
- Tirry, W. J., & Goossens, M. 1996, ApJ, 471, 501 [NASA ADS] [CrossRef] (In the text)
- Tirry, W. J., Cadez, V. M., Erdelyi, R., & Goossens, M. 1998a, A&A, 332, 786 [NASA ADS]
- Tirry, W. J, Goossens, M., Pinter, B., Cadez, V., & VanLommel, P. 1998b, ApJ, 503, 422 [NASA ADS] [CrossRef]
- Tomczyk, et al. 2007, Science, 318, 1192 [NASA ADS] [CrossRef] (In the text)
- Van Doorsselaere, T., Andries, J., Poedts, D., & Goossens, M. 2004, ApJ, 606, 1223 [NASA ADS] [CrossRef]
- Van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2008, ApJ, 676, L73 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- Postdoctoral Fellow of the National Fund for Scientific Research-Flanders (Belgium) (F.W.O.-Vlaanderen).
All Figures
![\begin{figure}
\par\includegraphics[width=7.6cm]{12399f1a.eps}\vspace*{3mm}
\inc...
...99f1b.eps}\vspace*{3mm}
\includegraphics[width=7.6cm]{12399f1c.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12399-09/Timg113.png) |
Figure 1:
Radial dependence of the normalised eigenfunctions, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{12399f2a.eps}\vspace*{3mm}...
....eps}\vspace*{3mm}
\includegraphics[width=6.7cm,clip]{12399f2c.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12399-09/Timg153.png) |
Figure 2:
Radial dependence of the moduli of the eigenfunctions, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{12399f3a.eps}\vspace*{3mm}...
....eps}\vspace*{3mm}
\includegraphics[width=6.1cm,clip]{12399f3c.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa12399-09/Timg154.png) |
Figure 3: Top panel: moduli of the radial forces. Middle panel: moduli of the azimuthal forces. Bottom panel: ratio of the modulus of the magnetic tension to the magnetic pressure gradient in the radial and the azimuthal direction. This case corresponds to the eigensolution displayed in Fig. 2 with l/R=0.4. The vertical dashed lines show the limits of the non-uniform layer. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



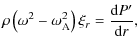
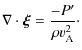
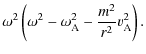
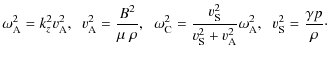
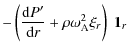
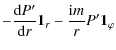
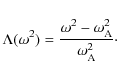
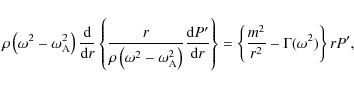
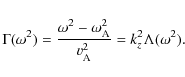
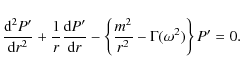
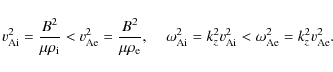
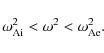
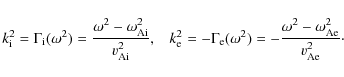
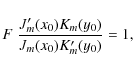
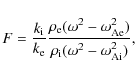
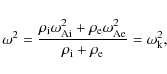
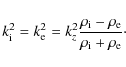
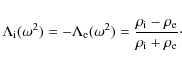
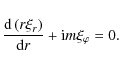
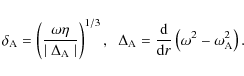
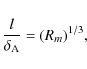
![\begin{displaymath}[\xi_r]= -{\rm i} \pi \frac{ m^2 / r_{\rm A}^2}{ \rho
\mid \Delta_{\rm A} \mid } P', \;\; [P']= 0.
\end{displaymath}](/articles/aa/full_html/2009/31/aa12399-09/img123.png)
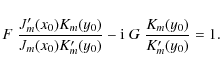
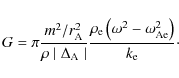
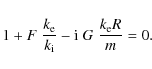
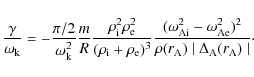
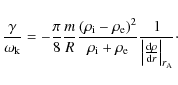
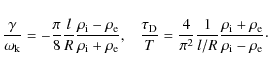
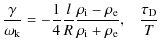 =
= 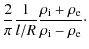
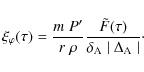
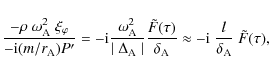
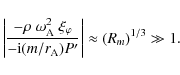
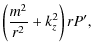
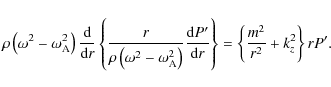
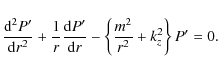
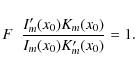
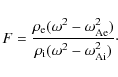
![$\displaystyle ~[\xi_r] = -{\rm i} \pi \frac{ m^2 / r_{\rm A}^2 + k_z^2} {
\rho \mid \Delta_{\rm A} \mid } \;\;P',$](/articles/aa/full_html/2009/31/aa12399-09/img189.png)
![$\displaystyle [\xi_r] = -{\rm i} \pi \frac{ k_z^2}{ \rho \mid \Delta_{\rm C} \mid}
\left \{ \frac{ v_{\rm S}^2}{ v_{\rm S}^2 + v_{\rm A}^2} \right \}^2 P',$](/articles/aa/full_html/2009/31/aa12399-09/img191.png)
![$\displaystyle [\xi_r] = -{\rm i} \pi \frac{ k_z^2}{ \rho \mid \Delta_{\rm C} \mid}
P',$](/articles/aa/full_html/2009/31/aa12399-09/img194.png)