| Issue |
A&A
Volume 502, Number 3, August II 2009
|
|
|---|---|---|
| Page(s) | 913 - 927 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200911857 | |
| Published online | 15 June 2009 | |
The puzzling dredge-up pattern in NGC 1978
M. T. Lederer1 - T. Lebzelter1 - S. Cristallo2 - O. Straniero2 - K. H. Hinkle3 - B. Aringer1,4
1 - University of Vienna, Department of Astronomy,
Türkenschanzstraße 17, 1180 Vienna, Austria
2 -
INAF, Osservatorio Astronomico di Collurania, 64100 Teramo, Italy
3 -
National Optical Astronomy Observatories![]() , PO Box 26732, Tucson, AZ 85726, USA
, PO Box 26732, Tucson, AZ 85726, USA
4 -
INAF, Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5, 35122 Padova, Italy
Received 16 February 2009 / Accepted 2 June 2009
Abstract
Context. Low-mass stars are element factories that efficiently release their products in the final stages of their evolution by means of stellar winds. Since they are large in number, they contribute significantly to the cosmic matter cycle. To assess this contribution quantitatively, it is crucial to obtain a detailed picture of the stellar interior, particularly with regard to nucleosynthesis and mixing mechanisms.
Aims. We seek to benchmark stellar evolutionary models of low-mass stars. In particular, we measure the surface abundance of 12C in thermally pulsing AGB stars with well-known mass and metallicity, which can be used to infer information about the onset and efficiency of the third dredge-up.
Methods. We recorded high-resolution near-infrared spectra of AGB stars in the LMC cluster NGC 1978. The sample comprised both oxygen-rich and carbon-rich stars, and is well-constrained in terms of the stellar mass, metallicity, and age. We derived the C/O and 12C/ 13C ratio from the target spectra by a comparison to synthetic spectra. Then, we compared the outcomes of stellar evolutionary models with our measurements.
Results. The M stars in NGC 1978 show values of C/O and 12C/ 13C that can best be explained with moderate extra-mixing on the RGB coupled to a moderate oxygen enhancement in the chemical composition. These oxygen-rich stars do not seem to have undergone third dredge-up episodes (yet). The C stars show carbon-to-oxygen and carbon isotopic ratios consistent with the occurrence of the third dredge-up. We did not find S stars in this cluster. None of the theoretical schemes that we considered was able to reproduce the observations appropriately. Instead, we discuss some non-standard scenarios to explain the puzzling abundance pattern in NGC 1978.
Key words: stars: abundances - stars: AGB and post-AGB - stars: evolution
1 Introduction
Modelling the final phases in the evolution of a low-mass star is a demanding task. The stellar interior is a site of rich nucleosynthesis, particularly when the star evolves on the asymptotic giant branch (AGB). The freshly synthesised elements are carried to the outer layers of the star by means of the third dredge-up (TDU, for a review see Busso et al. 1999). The onset and efficiency of this mixing mechanism depends on the mass and the metallicity of the star. Various stellar evolution models developed in the recent past (e.g. Straniero et al. 1997; Karakas & Lattanzio 2007; Straniero et al. 2006; Stancliffe et al. 2004; Herwig 2000) agree on the theoretical picture of the TDU, but details are still subject to discussions. It is thus important to test the models against observations and to derive constraints to improve our understanding of the involved phenomena and related problems. AGB stars are tracers of intermediate-age stellar populations, which can only be modelled accurately when the evolution of the constituents is known. Moreover, evolved low-mass stars undergo strong mass loss in the late stages of their evolution. They enrich the interstellar medium with the products of nuclear burning and thus, as they are large in number, play a significant role in the cosmic matter cycle.
The primary indicator of TDU is a carbon surface
enhancement. An originally oxygen-rich star can be transformed
into a carbon star by an efficient dredge-up of
12C to the surface. The criterion to distinguish
between an oxygen-rich and a carbon-rich chemistry is the number
ratio of carbon to oxygen atoms,
![]() .
During the
thermally pulsing (TP) AGB phase, while the
.
During the
thermally pulsing (TP) AGB phase, while the
![]() ratio is
constantly rising as a consequence of the TDU,
there are mechanisms that may counteract
the increase in the carbon isotopic ratio
12C/ 13C. The radiative gap between the
convective envelope and the hydrogen burning shell can be bridged
by a slow mixing mechanism
(cf. Nollett et al. 2003; Wasserburg et al. 1995). In this
way, 12C and isotopes of other elements are fed back
to nuclear processing. The physical origin of this
phenomenon is still not known, which is another argument to
establish observational data in order to benchmark theoretical
predictions.
ratio is
constantly rising as a consequence of the TDU,
there are mechanisms that may counteract
the increase in the carbon isotopic ratio
12C/ 13C. The radiative gap between the
convective envelope and the hydrogen burning shell can be bridged
by a slow mixing mechanism
(cf. Nollett et al. 2003; Wasserburg et al. 1995). In this
way, 12C and isotopes of other elements are fed back
to nuclear processing. The physical origin of this
phenomenon is still not known, which is another argument to
establish observational data in order to benchmark theoretical
predictions.
Measurements of the carbon abundance and the carbon isotopic ratio have been done for a few bright field AGB stars (Smith & Lambert 1990; Lambert et al. 1986; Harris et al. 1987). The direct comparison of the values inferred from field star observations to evolutionary models is complicated by the fact that luminosity and mass of those targets can be determined only inaccurately, while both quantities are crucial input parameters for the models. A strategy to circumvent this problem is to observe AGB stars in globular clusters (GC). They provide a rather homogeneous sample with respect to distance, age, mass, and metallicity. Admittedly, this simplistic picture is slowly disintegrating. There is evidence that globular clusters often harbour more than one population with abundance variations among the constituents (Piotto et al. 2007; Renzini 2008; Mackey & Broby Nielsen 2007). The parameters like mass and metallicity are, however, still much better constrained than for field stars. For our purpose, i.e. investigating the abundance variations due to the TDU, the old Milky Way globular clusters are not well suited. The AGB stars of the current generation have an envelope mass too low for TDU to occur, while more massive stars have evolved beyond the AGB phase. The intermediate-age globular clusters in the Large Magellanic Cloud (LMC) serve our needs better. We started with an investigation of the AGB stars in NGC 1846 (Lebzelter et al. 2008, henceforth Paper I) and indeed demonstrated the abundance variation along the AGB due to the TDU.
In this paper, we pursue this idea and study the AGB stars in the
LMC globular cluster NGC 1978, deriving
![]() and
12C/ 13C ratios. We give an overview of
previous studies of this cluster and our observations in
Sect. 2. Details about the data analysis are
given in Sect. 3. In
Sect. 3.4 we describe the
evolutionary models we use for a comparison to our
observational results. The results follow in
Sect. 4. We discuss our findings in
Sect. 5, giving scenarios on how to interpret
the puzzling case of NGC 1978 before we conclude in
Sect. 6.
and
12C/ 13C ratios. We give an overview of
previous studies of this cluster and our observations in
Sect. 2. Details about the data analysis are
given in Sect. 3. In
Sect. 3.4 we describe the
evolutionary models we use for a comparison to our
observational results. The results follow in
Sect. 4. We discuss our findings in
Sect. 5, giving scenarios on how to interpret
the puzzling case of NGC 1978 before we conclude in
Sect. 6.
2 Observations
2.1 The target cluster: NGC 1978
The globular cluster NGC 1978 is a member of the intermediate-age (
Mucciarelli et al. (2007a) derived the cluster age, distance
modulus, and turn-off mass by fitting isochrones to the cluster
colour-magnitude diagram (CMD). The resulting values are
![]() ,
(m-M)0=18.50 and
,
(m-M)0=18.50 and
![]() ,
respectively, for the best
fit found when using isochrones from the Pisa Evolutionary
Library (PEL, Castellani et al. 2003). When adopting other
isochrones with different overshooting prescriptions, the
parameters vary so that one could also derive a somewhat lower
turn-off mass (
,
respectively, for the best
fit found when using isochrones from the Pisa Evolutionary
Library (PEL, Castellani et al. 2003). When adopting other
isochrones with different overshooting prescriptions, the
parameters vary so that one could also derive a somewhat lower
turn-off mass (
![]() ), a lower
distance modulus (
(m-M)0=18.38), and a cluster age from 1.7 to
), a lower
distance modulus (
(m-M)0=18.38), and a cluster age from 1.7 to
![]() .
.
The various radial velocity measurements quoted in the literature
widely agree within the error bars, e.g.
Olszewski et al. (1991) and Schommer et al. (1992) derived
![]() whereas Ferraro et al. (2006) determined a mean heliocentric
velocity of NGC 1978 of
whereas Ferraro et al. (2006) determined a mean heliocentric
velocity of NGC 1978 of
![]() and
with a velocity dispersion
and
with a velocity dispersion
![]() .
.
NGC 1978 harbours a number of red giant stars (Lloyd Evans 1980) some of which are known to be carbon stars (Frogel et al. 1990). The easiest explanation for such an occurrence is that these C stars are AGB stars undergoing the third dredge-up or, alternatively, that they underwent mass accretion from an old AGB companion, which subsequently evolved into a white dwarf. More exotic explanations will be discussed in Sect. 5.2.
2.2 Spectroscopy
Table 1: NGC 1978 targets and log of observations (LE stands for Lloyd Evans 1980).
We recorded high-resolution near-infrared spectra of 12 AGB stars in the LMC globular cluster NGC 1978. Ten stars from our target list were already identified by Lloyd Evans (1980) as red giant stars (and are tagged LE in this work) but largely without information about the spectral type. Frogel et al. (1990) listed a number of AGB stars in NGC 1978, comprising also the stars from LE, and gave information about the spectral type, the cluster membership, and near-infrared photometry data. Based on this information, we selected ten targets that could be observed with the Phoenix spectrograph mounted at the Gemini South Telescope (Hinkle et al. 2003,1998) with reasonable exposure times. Additionally, we constructed a colour-magnitude diagram from Two Micron All Sky Survey (2MASS, Skrutskie et al. 2006) data and picked two more stars that, judging from their K magnitude and (J-K) colour index, are also located on the AGB of NGC 1978 (stars A and B). Details about the observation targets together with the observing log are given in Table 1. The distribution of all the targets within the cluster is illustrated in Fig. 1.
Our observing programme required observations at two
different wavelengths, one in the H band and one in the K band. For
this purpose, we utilised the Phoenix order sorting filters H6420
and K4220. However, poor weather conditions in the last of the 4 observing nights prohibited to record H-band spectra for the
targets LE2 and LE7. For the star LE9, we obtained spectra from
queue mode observations in the semester 2008A. The exact
wavelength settings are similar to the ones described in
Lebzelter et al. (2008), i.e. in the K band our spectra run
approximately from 23 580 to
![]() .
In the H band (
.
In the H band (
![]() ), the spectral region observed was shifted to
slightly higher wavelengths to cover a larger part of the CO 3-0
band head at
), the spectral region observed was shifted to
slightly higher wavelengths to cover a larger part of the CO 3-0
band head at
![]() .
The slit width was set to
.
The slit width was set to
![]() (the widest slit) which resulted
in a spectral resolution of
(the widest slit) which resulted
in a spectral resolution of
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm]{11857f01.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg39.png) |
Figure 1:
Distribution of observed targets in the cluster NGC 1978. The picture was acquired from the 2MASS catalogue using Aladin (Bonnarel et al. 2000). Numbers refer to the nomenclature of Lloyd Evans (1980). The additional targets A and B were chosen according to their position in the 2MASS colour-magnitude diagram. The stars A, 4, 5, 8, 9, and 10 possess an oxygen-rich atmosphere while B, 1, 2, 3, 6, and 7 are carbon stars. The cluster is elongated and its major axis stretches roughly from south-east to north-west. The displayed sky region is
|
| Open with DEXTER | |
The total integration time per target and wavelength setting
ranged between 20 (LE3) and 120 (LE9) minutes. For each target we observed
at two or three different positions along the slit. Each night, we also recorded a
spectrum of a hot star without intrinsic lines in the respective
wavelength regions in order to correct the spectra of our
programme stars for telluric lines. The resulting signal-to-noise
was from 50 to above 100 per resolution element (![]() 4 pixels).
See Table 1 for details.
4 pixels).
See Table 1 for details.
2.3 Data reduction
The data reduction procedure was carried out as described at length for example in Smith et al. (2002) and in the Phoenix data reduction IRAF tutorial
To correct the AGB star spectra for telluric lines, we acquired the
spectrum of an early type star without intrinsic lines. The
telluric absorption features were removed using the IRAF task
telluric in the K band. The H-band spectra are almost free of
telluric lines, they were, however, also processed in the same way
to remove the fringing. In the H band, we did the wavelength
calibration for a K-type radial velocity standard (HD 5457,
![]() ,
Wilson 1953)
recorded alongside with the programme stars. Using the Arcturus
atlas from Hinkle et al. (1995), we identified several
features (OH, Fe, Ti, Si lines) in the spectrum and derived a
dispersion solution. The relation was then applied to the
remaining spectra. This procedure allowed us to derive radial
velocities from the H-band spectra. For the K-band spectra we did
a direct calibration using the CO lines in the spectrum of an
M-type target. That solution was then also applied to the carbon-star spectra.
,
Wilson 1953)
recorded alongside with the programme stars. Using the Arcturus
atlas from Hinkle et al. (1995), we identified several
features (OH, Fe, Ti, Si lines) in the spectrum and derived a
dispersion solution. The relation was then applied to the
remaining spectra. This procedure allowed us to derive radial
velocities from the H-band spectra. For the K-band spectra we did
a direct calibration using the CO lines in the spectrum of an
M-type target. That solution was then also applied to the carbon-star spectra.
![\begin{figure}
\par\includegraphics[width=18cm]{11857f02.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg42.png) |
Figure 2:
Overview about observations: H-band spectra are shown on the left side, K-band spectra on the right. The spectra are ordered by increasing infrared colour
|
| Open with DEXTER | |
3 Data analysis
3.1 Contents of the observed wavelength ranges
The wavelength ranges were chosen such that from the H band spectra we could derive the stellar parameters and the C/O ratio. Subsequently, we inferred the carbon isotopic ratio 12C/ 13C from the K band. In practice, the parameters are tuned iteratively. The region in the H band is widely used in the literature (e.g. McSaveney et al. 2007; Yong et al. 2008; Smith et al. 2002) to derive oxygen abundances from the contained OH lines. From the relative change of those features in comparison to the band head from the 12C 16O 3-0 vibration transition, it is possible to determine the C/O ratio in the stellar atmosphere. A weak CN line and a few metal lines (Fe, Ti, Si) aid in the pinning down of the parameters, especially the effective temperature.
The K-band spectra comprise a number of CO lines from first
overtone (
![]() )
transitions. Beside features from the
main isotopomer 12C 16O, we also find
some 13C 16O lines in this region. We
derived the carbon isotopic ratio by fitting these lines. Apart
from the CO lines, there is also a single HF line blended with a
13CO feature.
)
transitions. Beside features from the
main isotopomer 12C 16O, we also find
some 13C 16O lines in this region. We
derived the carbon isotopic ratio by fitting these lines. Apart
from the CO lines, there is also a single HF line blended with a
13CO feature.
In Fig. 2, we give an overview about our observations. For the oxygen-rich stars, the key features in the H band are marked. In the K band, we indicate the position of the 13CO lines. The selection of the wavelength ranges was driven by the oxygen-rich case. From Fig. 2 it is obvious that the regions are not well suited for the analysis of carbon-star spectra. Both H- and K-band spectra are crowded with features from the CN and C2 molecules, occurring in addition to the CO lines. The polyatomic molecules C2H2, HCN, and also C3contribute to the opacity by means of many weak lines that form a pseudo-continuum (see Sect. 3.3.2). The major part is due to C2H2 absorption that increases with decreasing effective temperature. In the H band, the CO band head is strongly affected by neighbouring features. Generally speaking, there is not a single unblended line in the carbon-rich case. The situation in the K band, however, is not that bad. The 12CO lines are still visible, although blended with CN features, but there are only a few C2lines. The pseudo-continuum is essentially all due to C2H2, contributions from other molecules are negligible.
3.2 Synthetic spectra
We compare our observations with synthetic spectra based on model atmospheres that were calculated with the COMARCS code (details will be given in a forthcoming paper by Aringer et al. 2009). COMARCS is a modified version of the MARCS code (originating from Jørgensen et al. 1992; Gustafsson et al. 1975; recently extensively described by Gustafsson et al. 2008). In the model calculations, we deduced the temperature and, accordingly, pressure stratification assuming a spherical configuration in hydrostatic and local thermodynamic equilibrium (LTE). For stars showing only a small variability, LTE is a reasonable approximation. Possible deviations from LTE have a smaller influence on the abundance determination than large deviations from the hydrostatic equilibrium (see for example Johnson 1994 for a discussion of non-LTE effects in cool star atmospheres). In the evaluation of the chemical equilibrium, which is a consequence of LTE, we take all relevant opacity sources into account in both model calculation and spectral synthesis. In the oxygen-rich case H2O, TiO, CO, and CN are major opacity contributors, while HCN, C2H2, C2 (and others) are important in the carbon-rich case. The opacity coefficients utilised by COMARCS are calculated with the COMA code (Aringer et al. 2009; Aringer 2000). The atomic line data were taken from VALD (Kupka et al. 2000), an overview of the molecular line lists used with all the sources documented can be found in Lederer & Aringer (2009). Model atmospheres and synthetic spectra that were calculated following the method outlined above have been shown to describe the spectra of cool giant stars appropriately (e.g. Loidl et al. 2001; Aringer et al. 2002). We applied the same procedure successfully in Paper I for our analysis of the AGB stars in the LMC cluster NGC 1846.
From the parameters that determine an atmospheric model, we held
the mass and the metallicity constant. The respective values are
![]() and
and
![]() ,
and
were taken from the literature (see Sect. 1). In the model
calculations, the microturbulent velocity was set to
,
and
were taken from the literature (see Sect. 1). In the model
calculations, the microturbulent velocity was set to
![]() ,
which is in the range that is
found for atmospheres of low-mass giants
(e.g. Gautschy-Loidl et al. 2004; Aringer et al. 2002; Smith et al. 2002).
By varying the remaining parameters effective temperature
,
which is in the range that is
found for atmospheres of low-mass giants
(e.g. Gautschy-Loidl et al. 2004; Aringer et al. 2002; Smith et al. 2002).
By varying the remaining parameters effective temperature
![]() ,
logarithm of the surface gravity
,
logarithm of the surface gravity
![]() ,
and carbon-to-oxygen ratio (C/O),
we constructed a grid of model atmospheres and spectra. This was
done such that we cover the
,
and carbon-to-oxygen ratio (C/O),
we constructed a grid of model atmospheres and spectra. This was
done such that we cover the
![]() and
and ![]() range resulting from
colour-temperature relations and bolometric corrections
applied to our sample stars. The step
size in effective temperature was set to
range resulting from
colour-temperature relations and bolometric corrections
applied to our sample stars. The step
size in effective temperature was set to
![]() ,
whilst
the surface gravity was altered in steps of 0.25 on a
logarithmic scale, i.e. for
,
whilst
the surface gravity was altered in steps of 0.25 on a
logarithmic scale, i.e. for ![]() ,
ranging from 0.0 to +0.5. For some carbon stars in our sample we got
,
ranging from 0.0 to +0.5. For some carbon stars in our sample we got
![]() from the colour transformations and the adopted mass. The spectral
features used in the analysis show only a minor dependence on this
parameter thus we fixed
from the colour transformations and the adopted mass. The spectral
features used in the analysis show only a minor dependence on this
parameter thus we fixed
![]() in the analysis of the carbon
stars. In this way we also avoid convergence problems for the
atmospheric models.
in the analysis of the carbon
stars. In this way we also avoid convergence problems for the
atmospheric models.
The element composition is scaled solar
(Grevesse & Noels 1993), but we assumed an
oxygen over-abundance of
![]() motivated by the
results of our work on NGC 1846 (Paper I) and by the paper of
Hill et al. (2000). We altered the C/O ratio in steps
of 0.05 in the oxygen-rich case and 0.10 in the carbon-rich case.
This was done by changing the carbon abundance while leaving the
other abundances untouched.
motivated by the
results of our work on NGC 1846 (Paper I) and by the paper of
Hill et al. (2000). We altered the C/O ratio in steps
of 0.05 in the oxygen-rich case and 0.10 in the carbon-rich case.
This was done by changing the carbon abundance while leaving the
other abundances untouched.
The synthetic spectra cover a wavelength range of
![]() (
(
![]() )
in
the H band and of
)
in
the H band and of
![]() (
(
![]() )
in the K band. The spectra were
first calculated with a resolution of
)
in the K band. The spectra were
first calculated with a resolution of
![]() and then convolved with a
Gaussian
and then convolved with a
Gaussian![]() to match the resolution of our observed spectra
(R=50 000). By applying another convolution with a Gaussian
profile we took the macroturbulent velocity into account. To
determine the carbon isotopic ratio
12C/ 13C (which is about 89.9 in the
Sun according to Anders & Grevesse 1989), we altered this
parameter as well. The carbon isotopic ratio has virtually no
effect on the model structure and was consequently only considered
in the spectral synthesis calculations.
to match the resolution of our observed spectra
(R=50 000). By applying another convolution with a Gaussian
profile we took the macroturbulent velocity into account. To
determine the carbon isotopic ratio
12C/ 13C (which is about 89.9 in the
Sun according to Anders & Grevesse 1989), we altered this
parameter as well. The carbon isotopic ratio has virtually no
effect on the model structure and was consequently only considered
in the spectral synthesis calculations.
3.3 Determination of abundance ratios
We derive the effective temperature
For each target we fit the parameters in a two-step
process. The idea is to fit the spectral ranges at once rather
than tuning individual abundances (except for carbon) to fit
single spectral features. From the H band, we could in this way
constrain the stellar parameters (
![]() and
and ![]() )
and the C/O ratio. Variations in
)
and the C/O ratio. Variations in ![]() had the smallest effect
on the synthetic spectra. A small uncertainty in the stellar mass
or radius estimate has thus only a minor influence on the derived
abundance ratios. Using the parameters as obtained from the H band, we then calculated
K-band spectra with a varying
12C/ 13C ratio to determine this
parameter as well. The carbon isotopic ratio does not influence
the appearance of the H band spectrum significantly, as was
verified by test calculations.
had the smallest effect
on the synthetic spectra. A small uncertainty in the stellar mass
or radius estimate has thus only a minor influence on the derived
abundance ratios. Using the parameters as obtained from the H band, we then calculated
K-band spectra with a varying
12C/ 13C ratio to determine this
parameter as well. The carbon isotopic ratio does not influence
the appearance of the H band spectrum significantly, as was
verified by test calculations.
To match the shape of the spectral features we also had to assume
a macroturbulent velocity which reduces the effective resolution
of the spectra. This artificial broadening includes the
instrumental profile, but it is also used to imitate at least partly
the dynamical effects in the stellar atmosphere, which become
increasingly important for carbon stars. This is also why the
adopted values were generally lower for the
oxygen-rich targets: they were fitted by applying a macroturbulent
velocity of
![]() .
The carbon
stars displayed a stronger broadening of the features (cf.
Fig. 2). We needed values of
.
The carbon
stars displayed a stronger broadening of the features (cf.
Fig. 2). We needed values of
![]() and even
and even
![]() (LE6) to fit the spectra
(compare also de Laverny et al. 2006 who find comparable
values in their study). We consistently applied the same value for
the H and the K band.
(LE6) to fit the spectra
(compare also de Laverny et al. 2006 who find comparable
values in their study). We consistently applied the same value for
the H and the K band.
We tried to objectify the search for the best fit by applying a
least-square fitting method. Although we were in this way able to
narrow down the possible solutions to a few candidate spectra
quickly, the final decision about our best fit was done by visual
inspection. The reason is that spectral features with a false
strength or position (both due to imperfect line data)
in the synthetic spectrum, or spectral
regions with a high noise level dominate ![]() and confuse an
automatic minimisation algorithm. As the last step in the fitting
procedure is done by eye, we assign a formal error to the derived
parameters. In the case that the best fit parameters lie
in-between our grid values, we quote the arithmetic mean of the
candidate models as our fit result. The error bars were estimated
from the range of parameters of the model spectra that still gave
an acceptable fit.
and confuse an
automatic minimisation algorithm. As the last step in the fitting
procedure is done by eye, we assign a formal error to the derived
parameters. In the case that the best fit parameters lie
in-between our grid values, we quote the arithmetic mean of the
candidate models as our fit result. The error bars were estimated
from the range of parameters of the model spectra that still gave
an acceptable fit.
The formal errors for the
derived C/O and 12C/ 13C ratios
given in Table 3 compare well with
the uncertainties found by some basic error estimates, as will be shown
in the following. Therefore the quintessence of the discussion in
Sect. 5 is on a sound footing.
We consider typical uncertainties in the stellar
parameters and investigate the influence on the derived abundance
ratios. The correlations between the stellar parameters and possible systematic errors from the model syntheses have not been taken into account in the error analysis.
For the oxygen-rich case, we start from a baseline model with
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() .
Changes of
.
Changes of
![]() ,
,
![]() ,
and
,
and
![]() correspond to changes
in
correspond to changes
in
![]() of 0.02, 0.03, and 0.01, respectively
of 0.02, 0.03, and 0.01, respectively![]() .
Summed in quadrature this results in a typical total uncertainty of 0.04 for the C/O ratio of our M-type targets. The same exercise
for the carbon isotopic ratio results in
.
Summed in quadrature this results in a typical total uncertainty of 0.04 for the C/O ratio of our M-type targets. The same exercise
for the carbon isotopic ratio results in
![]() of 2, 2, and 3 (parameter dependence as above), and
thus a total uncertainty of 4. Concerning the carbon-rich case, we start from a carbon-rich model with parameters
of 2, 2, and 3 (parameter dependence as above), and
thus a total uncertainty of 4. Concerning the carbon-rich case, we start from a carbon-rich model with parameters
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and vary the parameters as described above. This leads to a total
and vary the parameters as described above. This leads to a total
![]() .
For the carbon isotopic ratio we find
.
For the carbon isotopic ratio we find
![]() .
.
A considerable part of our discussion will be concerned with the
12C/ 13C ratios of our targets.
Since the derived isotopic ratios depend on the
parameters of the 13CO lines (taken from the
list of Goorvitch & Chackerian 1994, see also Appendix A), we want to assess
possible systematic errors in the line strengths. In the case that
the predicted line strengths in the list are too large, one would
have to increase 12C/ 13C
(equivalent to a decrease of the 13C abundance) in
order to fit a 13CO feature compared with the case
where the predicted strengths are correct. The actual
12C/ 13C ratio would then be lower than the derived value.
For some oxygen-rich stars in our sample we get carbon isotopic ratios that
are close to the value of the CN cycle equilibrium (4-5). A
necessary further reduction is thus not very likely. If the
theoretical line strengths are too low, the above argument is
reversed. One would assume a lower
12C/ 13C ratio to fit the 13CO
features, which means that one would underestimate the actual isotopic
ratio. Since we, of course, use the same line list for the analysis of
both M and C stars, this would shift up the
12C/ 13C for all targets in
Figs. 7, 8, and 9.
Similar to a ![]() uncertainty,
the values for the carbon stars
would be stronger affected. Hence, underestimated
13CO line strengths would relax the necessity of
efficient additional mixing processes on the RGB as discussed
in Sect. 5.
uncertainty,
the values for the carbon stars
would be stronger affected. Hence, underestimated
13CO line strengths would relax the necessity of
efficient additional mixing processes on the RGB as discussed
in Sect. 5.
In the next section, we discuss M and C stars separately. The features contained in the spectra depend on the chemistry regime and some issues cannot be discussed in a general way.
3.3.1 M-type stars
In the search for a good fit we took advantage of the way features
react to parameter changes. An increasing temperature weakens all
features in the H band. The OH/Fe blend at approximately
![]() is a good temperature indicator. The two
neighbouring OH lines and the CO band head react less on
temperature changes.
The remaining lines show only a weak
dependence on
is a good temperature indicator. The two
neighbouring OH lines and the CO band head react less on
temperature changes.
The remaining lines show only a weak
dependence on
![]() .
The K band is largely insensitive
to temperature changes, only the 13CO lines show a
weak dependence on temperature which adds to the uncertainty in
determining the isotopic ratio. The only feature strongly reacting
when altering
.
The K band is largely insensitive
to temperature changes, only the 13CO lines show a
weak dependence on temperature which adds to the uncertainty in
determining the isotopic ratio. The only feature strongly reacting
when altering
![]() in the model calculations
is the blend including the HF line, its strength decreases when
the temperature is increased.
in the model calculations
is the blend including the HF line, its strength decreases when
the temperature is increased.
An increase in C/O enhances the strength of the CO band head and causes stronger CN lines, while the OH lines get slightly weaker, especially the feature blended with an Fe line. Lowering C/O decreases the strength of the CO features in the K band.
The CO band head is also sensitive to changes in ![]() ,
while
the other features practically are not.
Changes in the surface gravity also
affect the measured carbon isotopic ratios (see Sect. 3.3).
Two of the 13CO lines in the spectra of the oxygen-rich
stars are unblended ( 13CO 2-0 R18 and
13CO 2-0 R19). Blended 13CO features
were used to check the isotopic ratio derived from the clean
lines.
,
while
the other features practically are not.
Changes in the surface gravity also
affect the measured carbon isotopic ratios (see Sect. 3.3).
Two of the 13CO lines in the spectra of the oxygen-rich
stars are unblended ( 13CO 2-0 R18 and
13CO 2-0 R19). Blended 13CO features
were used to check the isotopic ratio derived from the clean
lines.
The continuum is well defined in the oxygen-rich case. We utilised the least-square method in the process of finding the best fit.
3.3.2 C-type stars
Several things make the fitting of carbon stars more difficult compared with the case of M-type stars. Foremost, the quality of the line data for the molecules appearing in the carbon-rich case hampers the qualitative analysis profoundly. For CN, C3, and C2H2 we used the SCAN database (Jørgensen 1997). The line positions in the computed CN list are not accurate enough for modelling high-resolution spectra. With the help of measured line positions for CN that were compiled by Davis et al. (2005), we were able to correct the wavelengths of the strongest lines. While the results were satisfying in the oxygen-rich case, in the carbon-star spectra many additional weak lines show up that could not be corrected. The case of C2 (we used the line data from Querci et al. 1974), producing a wealth of spectral features, is even more problematic: no observed reference line list is available for this molecule, so both line positions and strengths are subject to large uncertainties. We corrected the line list manually by removing strong features that did not appear in any of our observations. Several features were shifted to other wavelengths where it was evident from the observations that the lines are at the wrong position. Unlike for M stars, the H-band spectra of carbon stars are also affected by the carbon isotopic ratio. Lines from 13C 12C or 13C 14N are important in some blends, however, the quality of the line data for these features could not be assessed for the above described reasons.
The molecules C2H2 and C3 are incorporated into our
calculations via low-resolution opacity sampling data. The
absorption thus becomes manifest as a pseudo-continuum in the
spectra. A possible occurrence of strong lines or regions with
particularly low absorption cannot be reproduced with this
approach. The pseudo-continuum level reacts sensitively to
temperature changes. In general, an increase in
![]() reduces the feature strength. The relative changes of different
line strength can be used to constrain the temperature range.
The lower the temperature gets, the higher the contribution of
C2H2 and C3 becomes, whereas C2H2 dominates the
absorption. An increase in the C/O ratio has the same effect.
The implications for abundance determination of the ill-defined
continuum in carbon stars is discussed in detail in Paper I.
We want to stress here the consequences for the
reduces the feature strength. The relative changes of different
line strength can be used to constrain the temperature range.
The lower the temperature gets, the higher the contribution of
C2H2 and C3 becomes, whereas C2H2 dominates the
absorption. An increase in the C/O ratio has the same effect.
The implications for abundance determination of the ill-defined
continuum in carbon stars is discussed in detail in Paper I.
We want to stress here the consequences for the ![]() method.
The absorption in the pseudo-continuum varies with temperature requiring scaling of
the observed spectrum before a comparison. Due to this scaling the
value of
method.
The absorption in the pseudo-continuum varies with temperature requiring scaling of
the observed spectrum before a comparison. Due to this scaling the
value of ![]() changes in the same manner, so that model
spectra with lower effective temperatures (causing a lower flux
level due to an increased pseudo-continuum) always result in a
lower
changes in the same manner, so that model
spectra with lower effective temperatures (causing a lower flux
level due to an increased pseudo-continuum) always result in a
lower ![]() ,
pretending to fit the observations better. This is
of course an artificial effect, and thus we cannot rely on the
least-square method as objective criterion.
,
pretending to fit the observations better. This is
of course an artificial effect, and thus we cannot rely on the
least-square method as objective criterion.
A change in ![]() has only small effects on the carbon-star
spectra. A higher surface gravity produces a higher
pseudo-continuum in the K band.
In general
has only small effects on the carbon-star
spectra. A higher surface gravity produces a higher
pseudo-continuum in the K band.
In general ![]() only marginally affects the spectral lines.
However, in the determination of 12C/ 13C
the uncertainty in
only marginally affects the spectral lines.
However, in the determination of 12C/ 13C
the uncertainty in ![]() has to be taken into account.
In the K band, all
13CO lines are blended with other features. The
carbon isotopic ratio is already so high that the strengths of the
13CO lines have become rather insensitive to changes
in this parameter. As a consequence, even the small uncertainties
in
has to be taken into account.
In the K band, all
13CO lines are blended with other features. The
carbon isotopic ratio is already so high that the strengths of the
13CO lines have become rather insensitive to changes
in this parameter. As a consequence, even the small uncertainties
in ![]() correspond to large changes in the isotopic ratio,
which adds to the errors.
correspond to large changes in the isotopic ratio,
which adds to the errors.
Variations of the C/O ratio have the strongest impact on the H-band spectra when C/O is slightly above 1. The strength of the CO band head rapidly drops when C/O is increased to 1.3, approximately. Then a saturation sets in and the strength of the CO band head varies slowly with C/O. This behaviour and strong CN features sitting in the band head hamper an accurate C/O determination. The lines of C2 and CN increase in strength when C/O rises, both in the H and the K band. The CO lines in the K band decrease in strength for higher values of C/O. The changes are, however, small and do not allow for a determination of the C/O ratio from the K-band spectra alone.
Figure 3 is, as an example, a fit for the
star B, which is a carbon star. The star has an effective
temperature of about
![]() (see also
Table 3 for the other fit parameters). The
pseudo-continuum contribution is relatively weak, although there
are almost no line-free regions in both spectral bands. A number
of features is successfully reproduced by our models, the
deviations in other regions are most probably due to uncertain
line data.
(see also
Table 3 for the other fit parameters). The
pseudo-continuum contribution is relatively weak, although there
are almost no line-free regions in both spectral bands. A number
of features is successfully reproduced by our models, the
deviations in other regions are most probably due to uncertain
line data.
To measure the 12C/ 13C ratio in the carbon-star
spectra, we utilised the 13CO lines at 23 579.9,
23 590.2, and
![]() (the leftmost lines indicated in the
right panel of Fig. 2). In the vicinity of the other
13CO lines, there are obviously absorption features missing
in our synthetic spectra (see Fig. 3). We cannot rule
out that our analysis of a limited number of line blends could introduce
a systematic error in the inferred carbon isotopic ratios. Therefore, we
emphasise that it would be worthwhile to reassess the isotopic ratios in other
wavelength regions, particulary in the light of the discussion in
Sect. 5.
(the leftmost lines indicated in the
right panel of Fig. 2). In the vicinity of the other
13CO lines, there are obviously absorption features missing
in our synthetic spectra (see Fig. 3). We cannot rule
out that our analysis of a limited number of line blends could introduce
a systematic error in the inferred carbon isotopic ratios. Therefore, we
emphasise that it would be worthwhile to reassess the isotopic ratios in other
wavelength regions, particulary in the light of the discussion in
Sect. 5.
We also identified four low-excitation 12CO 2-0 lines
in the K band (see also Fig. 2).
According to Hinkle et al. (1982), low-excitation lines form
in the outer atmospheric layers, opposite to high-excitation lines
that show characteristics similar to second overtone transitions
(
![]() ). In all the carbon-star spectra, these lines could
not be fitted with our synthetic spectra. The calculations
underestimate the line strength, suggesting that the extended
atmospheres of luminous carbon stars are not well reproduced by
our hydrostatic models.
). In all the carbon-star spectra, these lines could
not be fitted with our synthetic spectra. The calculations
underestimate the line strength, suggesting that the extended
atmospheres of luminous carbon stars are not well reproduced by
our hydrostatic models.
![\begin{figure}
\par\includegraphics[width=18cm]{11857f03.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg89.png) |
Figure 3: Observation and fit of the carbon star B in NGC 1978. The fit parameters are given in Table 3. The relatively high effective temperature and low C/O ratio compared with the other carbon stars in our sample allowed a reasonable fit. Deviations can to a high fraction be ascribed to uncertain line data. The strong low-excitation CO lines in the K band are not reproduced by the models. See text for details. |
| Open with DEXTER | |
3.4 Stellar evolutionary models
The stellar evolutionary models presented in this paper have been computed with the FRANEC code (Chieffi et al. 1998). The release we are currently using is optimised to properly compute low-mass models during their AGB phase. Up-to-date input physics, such as low-temperature carbon-enhanced opacities, have been adopted (Lederer & Aringer 2009; Cristallo et al. 2007). Physical phenomena, such as hydrodynamical instabilities at radiative-convective interfaces and the mass-loss rate, have been properly taken into account (Cristallo et al. 2009; Straniero et al. 2006). The inclusion of an additional mixing mechanism taking place below the convective envelope (usually referred to as extra-mixing) during the RGB and the AGB phase was described in Paper I.
4 Results
4.1 Cluster membership
We derived the heliocentric radial velocity by cross-correlating
the H-band spectra with a template spectrum (using the IRAF task fxcor). Data for the star LE9 were taken in the semester 2008A,
and no radial velocity standard (K-type star) was recorded, so no
information could be deduced for this target. While the quality of
our LE8 data is too low to derive abundance ratios, it is still
adequate to measure the radial velocity (only with a
slightly larger error than for the other targets). The sample
shows a relatively homogeneous radial velocity distribution, the spread is
quite narrow, so we conclude that all our targets are actually
cluster members. The results are summarised in
Table 2. The value
![]() (with a velocity
dispersion of
(with a velocity
dispersion of
![]() )
we find is well
in line with earlier determinations (see Sect. 1). As a comparison,
Carrera et al. (2008) measured radial velocities in four fields with
different distances to the LMC centre. The mean values found
in the individual fields range from +278 to
)
we find is well
in line with earlier determinations (see Sect. 1). As a comparison,
Carrera et al. (2008) measured radial velocities in four fields with
different distances to the LMC centre. The mean values found
in the individual fields range from +278 to
![]() .
The velocity dispersion in the metallicity bin with
.
The velocity dispersion in the metallicity bin with
![]() is
is
![]() .
.
The errors for the carbon stars are systematically larger than for the oxygen-rich stars. This can easily be understood by looking at Fig. 2. The features in the C-rich case are usually broader and consequently the peak in the cross-correlation function (and thus the FWHM) is broader, too.
Table 2: Radial velocities of NGC 1978 targets
Table 3: Data and fit results for oxygen-rich (first group) and carbon-rich (second group) targets in NGC 1978.
4.2 Stellar parameters and abundance ratios
We summarise our fit results in Table 3. In the
first column, we list the star identifier (compare
Fig. 1), followed by the K magnitude and the
colour index (J-K) taken from the 2MASS database. In the next
two columns, we quote the effective temperature and luminosity
(rounded to
![]() )
resulting from the respective
colour calibrations and bolometric corrections (see
Sect. 3.3). The parameters resulting from our
fitting procedure (
)
resulting from the respective
colour calibrations and bolometric corrections (see
Sect. 3.3). The parameters resulting from our
fitting procedure (
![]() ,
,
![]() ,
,
![]() ,
C/O, 12C/ 13C) are listed in the
subsequent columns.
We note that none of our target stars is
a large amplitude variable, thus the influence of variability on
the stellar parameters can be safely ignored. A detailed
discussion of the small amplitude variability (
,
C/O, 12C/ 13C) are listed in the
subsequent columns.
We note that none of our target stars is
a large amplitude variable, thus the influence of variability on
the stellar parameters can be safely ignored. A detailed
discussion of the small amplitude variability (
![]() in R) will be given elsewhere (Wood & Lebzelter, in
preparation).
in R) will be given elsewhere (Wood & Lebzelter, in
preparation).
The derived effective temperatures are systematically higher than
the
![]() values inferred from the infrared colour
transformations (compare the resulting
values inferred from the infrared colour
transformations (compare the resulting
![]() to
to
![]() deduced from the fit in Table 3).
Better agreement between the two temperature
scales is found when we adopt a scaled solar oxygen abundance
rather than an over-abundance of
deduced from the fit in Table 3).
Better agreement between the two temperature
scales is found when we adopt a scaled solar oxygen abundance
rather than an over-abundance of
![]() ,
which was
our standard choice in the analysis (we refer to
Sects. 1 and 3.2 for details).
However, this is not too surprising since the colour-temperature
relations from Houdashelt et al. (2000) were derived from synthetic
spectra based on scaled solar abundances.
We want to mention that the results from
Smith et al. (2002, their Fig. 8) imply
,
which was
our standard choice in the analysis (we refer to
Sects. 1 and 3.2 for details).
However, this is not too surprising since the colour-temperature
relations from Houdashelt et al. (2000) were derived from synthetic
spectra based on scaled solar abundances.
We want to mention that the results from
Smith et al. (2002, their Fig. 8) imply
![]() for the LMC, contrary to our assumption.
Also, Mucciarelli et al. (2008) found that the other alpha element
abundances are roughly scaled solar
(
for the LMC, contrary to our assumption.
Also, Mucciarelli et al. (2008) found that the other alpha element
abundances are roughly scaled solar
(
![]() )
in NGC 1978.
However, in another recent work Goudfrooij et al. (2009)
derived
)
in NGC 1978.
However, in another recent work Goudfrooij et al. (2009)
derived
![]() for the LMC cluster NGC 1846.
Apart from the
influence on the temperature scale, a higher oxygen abundance
would shift the derived C/O ratios only to slightly higher
values (Fig. 4). The derived carbon isotopic
ratios are marginally affected by an oxygen over-abundance.
for the LMC cluster NGC 1846.
Apart from the
influence on the temperature scale, a higher oxygen abundance
would shift the derived C/O ratios only to slightly higher
values (Fig. 4). The derived carbon isotopic
ratios are marginally affected by an oxygen over-abundance.
We found that for the five oxygen-rich stars within our sample the
C/O ratio is varying little, the values range from 0.13 to 0.18 with a typical uncertainty of ![]() 0.05. The isotopic
ratios vary in the range between 9 and 16 with an uncertainty
ranging up to
0.05. The isotopic
ratios vary in the range between 9 and 16 with an uncertainty
ranging up to ![]() 4. Considering the error bars, all M stars
occupy more or less the same region in Fig. 5, where
we display the measured C/O and 12C/ 13C of
our sample stars.
No target is offset from the spot marking the abundance ratios
expected after the evolution on the first giant branch
(
4. Considering the error bars, all M stars
occupy more or less the same region in Fig. 5, where
we display the measured C/O and 12C/ 13C of
our sample stars.
No target is offset from the spot marking the abundance ratios
expected after the evolution on the first giant branch
(
![]() ,
12C/ 13C
,
12C/ 13C![]() 10). In other words, we
do not find conclusive signs of third dredge-up among the
oxygen-rich stars in the cluster. This is also consistent with the
results from Lloyd Evans (1983) who did not find S-type
stars in NGC 1978. The total number of our targets is small, so general statements
based on our results are rather weak due to the poor statistics.
However, the fact that we find oxygen-rich stars, in which the TDU
does not seem to be active, does not exclude that this phenomenon is
at work in other stars of the cluster.
10). In other words, we
do not find conclusive signs of third dredge-up among the
oxygen-rich stars in the cluster. This is also consistent with the
results from Lloyd Evans (1983) who did not find S-type
stars in NGC 1978. The total number of our targets is small, so general statements
based on our results are rather weak due to the poor statistics.
However, the fact that we find oxygen-rich stars, in which the TDU
does not seem to be active, does not exclude that this phenomenon is
at work in other stars of the cluster.
![\begin{figure}
\par\includegraphics[width=18cm]{11857f04.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg125.png) |
Figure 4:
Fit of the H band spectrum of the target LE5 adopting different oxygen abundances. A value of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{11857f05.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg127.png) |
Figure 5:
Measured abundances ratios C/O and 12C/ 13C for the targets in NGC 1978. Oxygen-rich targets appear to the left of the dotted line at
|
| Open with DEXTER | |
In fact, we also identify a sub-sample of
carbon-rich stars belonging to NGC 1978. Satisfactory fits could only
be achieved for the two hottest carbon stars (B and LE6) in our
sample. We also derived C/O and
12C/ 13C.
The error bars are larger than for the M stars, the reasons
for that are outlined in the previous sections.
For the two cool objects LE1 and LE3, we could
only derive lower limits for C/O and
12C/ 13C. For an
increasing carbon content, the features saturate, thus we cannot give a
reliable upper limit for C/O.
The C/O ratios that we found are in line with the
results obtained by other groups. Matsuura et al. (2005) adopted
![]() to explain molecular features in low-resolution spectra of LMC carbon stars.
Investigations of planetary nebulae in the LMC exhibit a range
of C/O ratios from
slightly above 1 up to even 5 (e.g. Stanghellini et al. 2005).
We are not aware of measurements of the carbon isotopic ratio
directly from carbon-rich AGB stars in the LMC
other than the ones presented here and in Paper I.
Reyniers et al. (2007) analysed the post-AGB object
MACHO 47.2496.8 (
to explain molecular features in low-resolution spectra of LMC carbon stars.
Investigations of planetary nebulae in the LMC exhibit a range
of C/O ratios from
slightly above 1 up to even 5 (e.g. Stanghellini et al. 2005).
We are not aware of measurements of the carbon isotopic ratio
directly from carbon-rich AGB stars in the LMC
other than the ones presented here and in Paper I.
Reyniers et al. (2007) analysed the post-AGB object
MACHO 47.2496.8 (
![]() )
in the LMC and derived
)
in the LMC and derived
![]() and
and
![]() .
A peculiar combination of
C/O and 12C/ 13C values even more extreme than those of
our carbon-rich targets was presented by de Laverny et al. (2006).
They found
.
A peculiar combination of
C/O and 12C/ 13C values even more extreme than those of
our carbon-rich targets was presented by de Laverny et al. (2006).
They found
![]() and
and
![]() for
BMB-B 30 (with
for
BMB-B 30 (with
![]() )
in the SMC.
)
in the SMC.
Qualitative estimates based on the K-band spectra of the targets
LE2 and LE7 suggest that those have an
effective temperature between the groups LE1-LE3 and B-LE6
(see Fig. 2). Except for the target
B, the difference between the derived effective temperature and
the
![]() value obtained from the colour transformation is not quite as
high as in the oxygen-rich case (about
value obtained from the colour transformation is not quite as
high as in the oxygen-rich case (about
![]() ). We
repeated the analysis for the star B with a scaled solar oxygen
abundance (as for LE5, Fig. 4) and also found
a lower
). We
repeated the analysis for the star B with a scaled solar oxygen
abundance (as for LE5, Fig. 4) and also found
a lower
![]() ,
whereas the C/O ratio remained basically
unchanged. Almost all spectral features in the carbon-rich case react
sensitively to temperature changes, therefore
,
whereas the C/O ratio remained basically
unchanged. Almost all spectral features in the carbon-rich case react
sensitively to temperature changes, therefore
![]() can
be better defined than the C/O ratio. A remarkable result is that
- opposite to our findings for NGC 1846 (Paper I) - we do not
find a saturation level for the carbon isotopic ratio. This
indicates that extra-mixing is not at work in NGC 1978.
can
be better defined than the C/O ratio. A remarkable result is that
- opposite to our findings for NGC 1846 (Paper I) - we do not
find a saturation level for the carbon isotopic ratio. This
indicates that extra-mixing is not at work in NGC 1978.
![\begin{figure}
\par\includegraphics[width=8.8cm]{11857f06.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg135.png) |
Figure 6:
Colour-magnitude diagram based on 2MASS data for NGC 1978 (complete within a radius of
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{11857f07.eps}\includegraphics[width=8.5cm]{11857f08.eps} }\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg136.png) |
Figure 7: Comparison between observational data and theoretical models. 12C/ 13C isotopic ratios vs. C/O ratios are reported. In the left panel we report the range of O-rich stars only, while in the right panel the whole sample has been considered. The star symbols with error bars indicate our observations. The red dotted, the blue dashed, and the green long-dashed curves in the left panel are partly covered by other tracks in the plot. The symbols in the left panel mark the end point of the tracks after the RGB phase. In the right panel, the symbols indicate the values attained during the interpulse phases, which are on the order of 103 times longer than the TDU episodes. See text for details. |
| Open with DEXTER | |
In Fig. 6 we show a CMD of NGC 1978 (see
Sect. 5 for a discussion of the photometric errors).
We do not plot the bolometric magnitudes on the
ordinate because of the inconsistent bolometric corrections
applied to the targets.
The CMD contains all targets that lie within a radius of
![]() with respect to the cluster centre (cf. Fig. 1).
Data points with superimposed symbols refer to stars contained in our sample.
The oxygen-rich stars (empty squares) seem to form a
sequence with a C/O ratio increasing with luminosity which might
hint at a mild dredge-up. However, this could be misleading, as we have
to take the error bars quoted in Table 3 into
account. Moreover, the isotopic ratios do not appear in an ordered
sequence. The carbon stars (red triangles) are brighter in K and have
significantly redder colours. For the stars LE1 and LE3, having
the highest (J-K) values, the indicated numbers refer to lower
limits for the abundance ratios. The two carbon stars
with the lowest K magnitude are
LE2 and LE7 which were excluded from our analysis. Both have
luminosities comparable to the brightest oxygen-rich
stars. A possible explanation is that these stars are in a
post-flash dip phase (Iben & Renzini 1983), displacing them
about 1 magnitude down from the average luminosity in this
evolutionary stage in the CMD (see also the discussion in
Paper I).
with respect to the cluster centre (cf. Fig. 1).
Data points with superimposed symbols refer to stars contained in our sample.
The oxygen-rich stars (empty squares) seem to form a
sequence with a C/O ratio increasing with luminosity which might
hint at a mild dredge-up. However, this could be misleading, as we have
to take the error bars quoted in Table 3 into
account. Moreover, the isotopic ratios do not appear in an ordered
sequence. The carbon stars (red triangles) are brighter in K and have
significantly redder colours. For the stars LE1 and LE3, having
the highest (J-K) values, the indicated numbers refer to lower
limits for the abundance ratios. The two carbon stars
with the lowest K magnitude are
LE2 and LE7 which were excluded from our analysis. Both have
luminosities comparable to the brightest oxygen-rich
stars. A possible explanation is that these stars are in a
post-flash dip phase (Iben & Renzini 1983), displacing them
about 1 magnitude down from the average luminosity in this
evolutionary stage in the CMD (see also the discussion in
Paper I).
5 Discussion
We seek to explain the following observed features of NGC 1978:
- 1.
- the cluster harbours carbon stars;
- 2.
- the M stars do not show conclusive signs of third dredge-up;
- 3.
- there is no saturation of the carbon isotopic ratio.
The first point in the list is a clear indication of ongoing TDU in the cluster. The second point may at first seem to contrast this statement, while low number statistics could resolve this apparent contradiction: the lifetime of a thermally pulsing AGB star is short, so in a sample of a few stars we do not necessarily have to find a star with an enhanced carbon abundance. This possibly explains the large gap between the M and the C stars in terms of C/O (see Fig. 5). An alternative scenario where the TDU is so efficient that the star becomes carbon-rich after a single dredge-up episode occurs only at much lower metallicity (e.g. Herwig et al. 2000).
Let us put aside the C/O error bars for a moment and speculate
about the group of M stars. The 2MASS data come with uncertainties
in K of lower than 0.05, except for LE10 where the error is 0.076![]() In any case, the luminosity sequence
that the stars form is conserved. The star LE9 is the faintest at K, with mK=12.3,
in the sample and also the star with the lowest C/O ratio.
Cioni et al. (2000) identify the RGB tip in the LMC at
In any case, the luminosity sequence
that the stars form is conserved. The star LE9 is the faintest at K, with mK=12.3,
in the sample and also the star with the lowest C/O ratio.
Cioni et al. (2000) identify the RGB tip in the LMC at
![]() .
According to this value, LE9 could as
well be an RGB star or located at the early-AGB. The targets LE5
and LE10 are possibly at the very beginning of the thermally
pulsing asymptotic giant branch (TP-AGB) star phase. The case of
LE4 and, in particular, A is more difficult. Comparing these stars
with those of similar luminosity in the sample of NGC 1846, we
note that the latter are classified as S stars and present C/O ratios of 0.4 or even higher. The C/O ratio we find for the star
A (0.23) is slightly higher than the average of the other stars,
perhaps compatible with just one (the first) TDU episode.
The bolometric magnitude of A also roughly corresponds to the
limit we found for the onset of the TDU in NGC 1846 (
.
According to this value, LE9 could as
well be an RGB star or located at the early-AGB. The targets LE5
and LE10 are possibly at the very beginning of the thermally
pulsing asymptotic giant branch (TP-AGB) star phase. The case of
LE4 and, in particular, A is more difficult. Comparing these stars
with those of similar luminosity in the sample of NGC 1846, we
note that the latter are classified as S stars and present C/O ratios of 0.4 or even higher. The C/O ratio we find for the star
A (0.23) is slightly higher than the average of the other stars,
perhaps compatible with just one (the first) TDU episode.
The bolometric magnitude of A also roughly corresponds to the
limit we found for the onset of the TDU in NGC 1846 (
![]() ).
).
5.1 Stellar evolutionary models
In this section we present theoretical tracks computed with the FRANEC code, and we compare them with observations. In the left panel of Fig. 7, we report the evolution of the 12C/ 13C versus C/O curves from the pre-main sequence up to the early-AGB phase in the region where the M stars of NGC 1978 lie. In practice, the end point of each curve (marked by a symbol in the left panel of Fig. 7) represents the value attained at the tip of the RGB phase, which is conserved up to the onset of the first thermal pulse. In the right panel, instead, we extend the axes to also include the C-rich stars. We plot the whole AGB evolutionary tracks and mark the values attained after each TDU episode.
We firstly concentrate on the O-rich stars of our sample. We carry
on our analysis under the assumption that these stars have not
experienced TDU, because they still are at the beginning of the
TP-AGB phase or because they arrived on the AGB with a too small
envelope mass. In this case, their initial surface composition
has been modified by the occurrence of the First Dredge-up
(FDU) only and, eventually, by an additional slow mixing operating
below the convective envelope during the RGB phase (the so called
extra-mixing, see e.g. Denissenkov & Pinsonneault 2008; Nollett et al. 2003; Charbonnel & Zahn 2007). Our reference model (ST, dash-dotted magenta curve) has an initial mass
![]() with Z=0.006, corresponding to
with Z=0.006, corresponding to
![]() .
We assume an
initial solar-scaled composition, which implies
.
We assume an
initial solar-scaled composition, which implies
![]() and
and
![]() .
After the FDU, the surface
values attain
.
After the FDU, the surface
values attain
![]() and
and
![]() .
This is due to the fact that the
convective envelope penetrates into regions where partial
hydrogen-burning occurred before. No extra-mixing has been included
in the ST case.
The values so obtained clearly disagree with the M stars observations,
which show an average
.
This is due to the fact that the
convective envelope penetrates into regions where partial
hydrogen-burning occurred before. No extra-mixing has been included
in the ST case.
The values so obtained clearly disagree with the M stars observations,
which show an average
![]() and an average
and an average
![]() .
Thus, we explored the
possibility of an occurrence of extra-mixing on the RGB.
.
Thus, we explored the
possibility of an occurrence of extra-mixing on the RGB.
This hypothesis is supported by the bulk of observations of RGB stars in the
galactic field, as well as in open and globular
clusters (see e.g. Gratton et al. 2000).
These observations show that this additional mixing occurs in low-mass stars (
![]() )
during the first ascent along the Red Giant Branch.
Moreover, Eggleton et al. (2008) identified a mixing mechanism driven
by a molecular weight inversion (
)
during the first ascent along the Red Giant Branch.
Moreover, Eggleton et al. (2008) identified a mixing mechanism driven
by a molecular weight inversion (![]() -mixing) in three-dimensional
stellar models that must operate in all low-mass stars while they are on the RGB.
The operation of this RGB
extra-mixing is also required to explain the relatively low
12C/ 13C ratios in the M stars of NGC 1846 (Paper I).
-mixing) in three-dimensional
stellar models that must operate in all low-mass stars while they are on the RGB.
The operation of this RGB
extra-mixing is also required to explain the relatively low
12C/ 13C ratios in the M stars of NGC 1846 (Paper I).
As in Paper I, we include this additional mixing right
after the RGB luminosity bump. The extension of the zone in which
this additional mixing takes place is fixed by prescribing the
maximum temperature the material is exposed to
(
![]() ). The circulation rate is tuned by setting the
mixing velocity to a value that is a small fraction (cf. Paper I)
of the typical convective velocities in the envelope of an RGB star. As discussed in
Paper I, the carbon isotopic ratio largely depends on
). The circulation rate is tuned by setting the
mixing velocity to a value that is a small fraction (cf. Paper I)
of the typical convective velocities in the envelope of an RGB star. As discussed in
Paper I, the carbon isotopic ratio largely depends on
![]() .
In Fig. 7
we report two models, characterised by
.
In Fig. 7
we report two models, characterised by
![]() K (red dotted curve) and
K (red dotted curve) and
![]() K (blue short-dashed curve). In the
first case, the final 12C/ 13C ratio decreases, reaching a
value in good agreement with those observed in the M stars of NGC 1978. Notwithstanding, the C/O ratio remains unaltered and higher
than the observed one. An increase of
K (blue short-dashed curve). In the
first case, the final 12C/ 13C ratio decreases, reaching a
value in good agreement with those observed in the M stars of NGC 1978. Notwithstanding, the C/O ratio remains unaltered and higher
than the observed one. An increase of
![]() up to
up to
![]() K leads to a lower C/O ratio of about 0.21, which is in
better agreement with the observations. However, the corresponding
12C/ 13C ratio is 5, which is definitely
lower than the average value (11). Note that only LE5 shows such a
low value (
K leads to a lower C/O ratio of about 0.21, which is in
better agreement with the observations. However, the corresponding
12C/ 13C ratio is 5, which is definitely
lower than the average value (11). Note that only LE5 shows such a
low value (
![]() ).
).
Then, we explored the possible effect of an oxygen
enhancement (see the discussion in Sect. 2.1). The
black solid line in Fig. 7 represents a model similar to
the ST case, but with
![]() .
As for the ST case, the effects
of the FDU are clearly recognisable. An additional model, as
obtained by including an RGB extra-mixing
(
.
As for the ST case, the effects
of the FDU are clearly recognisable. An additional model, as
obtained by including an RGB extra-mixing
(
![]() K) is also reported (green line).
The final surface composition of this model (
K) is also reported (green line).
The final surface composition of this model (
![]() and
and
![]() )
is close to the average values of the
observed sample (
)
is close to the average values of the
observed sample (
![]() and
and
![]() ). Thus, a first
conclusion is that moderate RGB extra-mixing
(
). Thus, a first
conclusion is that moderate RGB extra-mixing
(
![]() K) coupled to
moderate oxygen enhancement appears to nicely reproduce the
observed average composition of the M stars in NGC 1978. The same
conclusion has been reached in the case of NGC 1846 (Paper I).
K) coupled to
moderate oxygen enhancement appears to nicely reproduce the
observed average composition of the M stars in NGC 1978. The same
conclusion has been reached in the case of NGC 1846 (Paper I).
What are the implications of this scenario when applied to the whole observational sample (O-rich and C-rich stars)? We carry on our analysis assuming that the carbon stars are intrinsic, i.e. that their surface composition, in particular the high C/O and carbon isotopic ratios, is the result of nucleosynthesis and mixing processes occurring during the thermally pulsing AGB evolution.
In the right panel of Fig. 7 we report
the same models as shown in the left panel.
None of the theoretical tracks can simultaneously reproduce the abundance
ratios of the M and C stars. The high values of the C-star
carbon isotopic ratio can only be reproduced by the oxygen-enhanced
model with no RGB extra-mixing. All the other models predict too low
12C/ 13C ratios. The situation appears even more peculiar when compared
with the case of NGC 1846, for which we found C stars with higher values
of C/O, but with
![]() between 60 and 70, so that an AGB
extra-mixing (in addition to the RGB extra-mixing) was invoked to
reproduce the observations. The vast difference between the two
clusters is illustrated in Fig. 8. In the left panel,
data for NGC 1978 are compared with three models computed under
different assumptions for the RGB and the AGB extra-mixing,
namely no extra-mixing (black-solid line), moderate RGB
extra-mixing only (green-long-dashed line), and moderate AGB
extra-mixing only (blue-dashed line). All the three models have
between 60 and 70, so that an AGB
extra-mixing (in addition to the RGB extra-mixing) was invoked to
reproduce the observations. The vast difference between the two
clusters is illustrated in Fig. 8. In the left panel,
data for NGC 1978 are compared with three models computed under
different assumptions for the RGB and the AGB extra-mixing,
namely no extra-mixing (black-solid line), moderate RGB
extra-mixing only (green-long-dashed line), and moderate AGB
extra-mixing only (blue-dashed line). All the three models have
![]() and
and
![]() .
In the right panel, data for NGC 1846
are compared with similar models. In this case, the mass is
.
In the right panel, data for NGC 1846
are compared with similar models. In this case, the mass is
![]() and
the red-dashed line refers to a model with both RGB
and AGB extra-mixing (see Paper I for more details on models
with AGB extra-mixing). In summary, the high carbon isotopic
ratio observed for the C stars of NGC 1978
(
and
the red-dashed line refers to a model with both RGB
and AGB extra-mixing (see Paper I for more details on models
with AGB extra-mixing). In summary, the high carbon isotopic
ratio observed for the C stars of NGC 1978
(
![]() )
rules out both
RGB and AGB extra-mixing, which are instead required to reproduce
the evolutionary sequence of M, S, and C stars in NGC 1846.
)
rules out both
RGB and AGB extra-mixing, which are instead required to reproduce
the evolutionary sequence of M, S, and C stars in NGC 1846.
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{11857f09.eps}\hspace*{3mm}
\includegraphics[width=8.5cm]{11857f10.eps} }
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg162.png) |
Figure 8: Comparison between observational data and theoretical models. 12C/ 13C isotopic ratios vs. C/O ratios are reported. In the left panel, we report observational data of the cluster NGC 1978, accompanied by selected theoretical tracks. As a comparison, in the right panel, we report the fitting curve for another LMC cluster (NGC 1846). The symbols along the tracks indicate the values attained during the interpulse phases (see also Fig. 7). The star symbols with error bars indicate our observations. See text for details. |
| Open with DEXTER | |
5.2 Alternative scenarios
In the previous section, we did not identify a theoretical scenario that satisfactorily reproduces the whole set of stars belonging to NGC 1978 (including both the O-rich and the C-rich sub-sample). Moreover, the intermediate-age LMC cluster NGC 1846, which we investigated in Paper I, presents a totally different abundance pattern, which cannot be ascribed to the same theoretical scenario. The lack of S stars is an additional peculiarity of NGC 1978. So far, our arguments have been based on the assumption that the stars in our sample possess the same initial composition, mass, and age so that they form an evolutionary sequence, in which the variations of the surface composition are due to intrinsic processes only. In this section, we speculate about possible alternative scenarios, namely:
- 1.
- the existence of two stellar populations having different ages;
- 2.
- the existence of rejuvenated stars;
- 3.
- the activation of additional mixing at the base of the convective zones generated by a thermal pulse.
The scenario of a single age stellar population does not
exclude the existence of rejuvenated stars. Merging, coalescence,
or mass accretion processes are often invoked to explain the Blue
Stragglers observed in many GCs. Actually, a non-negligible number
of stars lie above the turn-off and the sub-giant branch in the
colour-magnitude diagram of NGC 1978
(Mucciarelli et al. 2007a), although we cannot exclude that those
are field stars or the result of unresolved pairs.
If the product of one of the above mentioned
processes is a star with a mass larger than ![]() ,
or if the
rejuvenating process leaves the envelope composition enriched with
heavy elements, the efficiency of the RGB extra-mixing is
significantly reduced (Charbonnel & Zahn 2007).
Such a scenario might explain the high carbon isotopic ratio of
the C stars, but the lack of S stars remains a mystery
,
or if the
rejuvenating process leaves the envelope composition enriched with
heavy elements, the efficiency of the RGB extra-mixing is
significantly reduced (Charbonnel & Zahn 2007).
Such a scenario might explain the high carbon isotopic ratio of
the C stars, but the lack of S stars remains a mystery![]() .
Moreover, even if we do not have a detailed statistics of the
number of binary systems in NGC 1978
.
Moreover, even if we do not have a detailed statistics of the
number of binary systems in NGC 1978![]() , it seems unlikely that two merger
events occur nearly simultaneously to produce the stars B and LE6,
for instance.
, it seems unlikely that two merger
events occur nearly simultaneously to produce the stars B and LE6,
for instance.
![\begin{figure}
\par\includegraphics[width=8.8cm]{11857f11.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg168.png) |
Figure 9: 12C/ 13C isotopic ratio vs. C/O ratio for a series of models including an overshoot at the base of convective zone generated by the TPs. The extension (in fraction of the pressure scale height) of the overshoot zone is indicated in the legend. |
| Open with DEXTER | |
The last alternative scenario we have investigated regards
the possible modification of the efficiency of the mixing
processes taking place during the AGB phase,
which is responsible for the
increase of 12C and 16O in the envelope. A deeper TDU
would increase both the carbon isotopic ratio and the C/O ratio, thus leaving
the slope of the curves in the right panel of
Fig. 7 unaltered.
In this scenario, the possibility of producing S stars
as a consequence of the TDU is reduced, since the transition to
the C-star stage is more rapid. We recall that
the TDU depth basically depends on the strength of the thermal
pulses: stronger TPs push outward the external layers more easily, therefore
inducing deeper dredge-up episodes. In turn, the strength of a
thermal pulse depends on many physical and chemical properties, such as
the core and the envelope mass, or the CNO content in the envelope
(Straniero et al. 2003). On the other hand, an increase of the
primary oxygen that is dredged up might limit the increase of the C/O at the surface and steepen the 12C/ 13C-C/O
relation. The fraction of oxygen produced by the
![]() reaction increases toward
the centre. Therefore, an additional mixing process, as due to a
ballistic overshoot or to non-standard mechanisms (such as
rotation or magnetic kick), that moves primary O (and C) from the deep
interior to the He-rich inter-shell, may indirectly explain the
high carbon isotopic ratio of the carbon stars in NGC 1978.
To shed light on this possibility, we computed some additional
models, in which we applied an artificial overshoot at the base of
the convective zone generated by the TPs. The initial mass adopted
in the models is
reaction increases toward
the centre. Therefore, an additional mixing process, as due to a
ballistic overshoot or to non-standard mechanisms (such as
rotation or magnetic kick), that moves primary O (and C) from the deep
interior to the He-rich inter-shell, may indirectly explain the
high carbon isotopic ratio of the carbon stars in NGC 1978.
To shed light on this possibility, we computed some additional
models, in which we applied an artificial overshoot at the base of
the convective zone generated by the TPs. The initial mass adopted
in the models is
![]() ,
and the initial composition is
oxygen-enhanced (+0.2 dex). A moderate RGB extra-mixing
(
,
and the initial composition is
oxygen-enhanced (+0.2 dex). A moderate RGB extra-mixing
(
![]() K, corresponding to
the case of the green long-dashed line in Fig. 7) has
been included. We parametrise the additional mixing by limiting the
extension of the overshoot layer to a fraction of the pressure scale
height of the most internal convective mesh point.
In Fig. 9, we report the resulting
12C/ 13C isotopic ratios as a function of C/O.
K, corresponding to
the case of the green long-dashed line in Fig. 7) has
been included. We parametrise the additional mixing by limiting the
extension of the overshoot layer to a fraction of the pressure scale
height of the most internal convective mesh point.
In Fig. 9, we report the resulting
12C/ 13C isotopic ratios as a function of C/O.
Even if these models apparently provide a simultaneous
reproduction of the composition of both M and C stars, we have to
stress the theoretical and observational evidence against
such a process. At the He-flash peak, the inner border of the
convective zone already reaches the layer where the temperature attains its
maximum value. Below this point, due to the neutrino energy loss, the
temperature (and the entropy) decreases, so that the deceleration
due to the buoyancy is quite strong. Herwig et al. (2006) showed that
even if the pressure and the entropy barrier at the base of the
convective shell generated by a TP is stiff, convective plumes can
penetrate into the underlying radiative layers due to
g-mode oscillations. These structures reach down to about
![]() cm below the formal convective border (see their Fig. 24),
and develop mean vertical velocities that are about 1000 times lower
than the average convective velocities.
The extension of this penetration has the same order of
magnitude as the overshoot zone in our models, namely
cm below the formal convective border (see their Fig. 24),
and develop mean vertical velocities that are about 1000 times lower
than the average convective velocities.
The extension of this penetration has the same order of
magnitude as the overshoot zone in our models, namely
![]() cm,
cm,
![]() cm, and
cm, and
![]() cm, for 0.25
cm, for 0.25 ![]() ,
0.35
,
0.35 ![]() ,
and 0.5
,
and 0.5
![]() ,
respectively (these are mean values). However, if in our 1D models the whole
mass of the spherical overshoot region is
efficiently mixed, the amount of mass contained in the
penetrating plumes of the 3D model is certainly lower. In
addition, the result of the 3D model may be affected by the
assumed boundary conditions. As was stressed by Herwig et al. (2006), their
models ignore
,
respectively (these are mean values). However, if in our 1D models the whole
mass of the spherical overshoot region is
efficiently mixed, the amount of mass contained in the
penetrating plumes of the 3D model is certainly lower. In
addition, the result of the 3D model may be affected by the
assumed boundary conditions. As was stressed by Herwig et al. (2006), their
models ignore ![]() -gradients, which increase the
stability and reduce mixing across the formal convective boundaries.
Moreover, they found that the amplitude of the gravity waves depends both on
the resolution adopted in the simulation and on the choice of the heating rate.
-gradients, which increase the
stability and reduce mixing across the formal convective boundaries.
Moreover, they found that the amplitude of the gravity waves depends both on
the resolution adopted in the simulation and on the choice of the heating rate.
On the other hand, the bulk of the C stars in the Milky Way as well
as those in NGC 1846 have 12C/ 13C ratios in the range
from 40 to 70,
and only in a few cases up to 100 (Lambert et al. 1986). This occurrence leads us to the conclusion
that such an overshoot is supposedly an uncommon process.
Note that the occurrence of an overshoot below the convective zone
generated by a TP causes considerable changes of the physical
conditions in the He-rich inter-shell. In particular, higher
temperatures develop at the pulse peak and, therefore, the
![]() reaction rate becomes an important neutron source, even in low-mass AGB stars.
In such a case, the resulting s-process nucleosynthesis would
be characterised by an overproduction of neutron-rich isotopes. For
instance, the expected isotopic compositions of strontium, zirconium,
molybdenum, and barium would substantially differ from those
measured in pre-solar SiC grains, which were produced in the
cool circumstellar envelope of a past generation of C stars
(see Lugaro et al. 2003). Additionally, calculated element
abundances ratios such as Rb/Sr would not match
observations obtained from carbon stars
(see Abia et al. 2001).
For these reasons, if the
overshoot from the base of the convective zone
generated by TPs is non-negligible, it should be a rare event.
reaction rate becomes an important neutron source, even in low-mass AGB stars.
In such a case, the resulting s-process nucleosynthesis would
be characterised by an overproduction of neutron-rich isotopes. For
instance, the expected isotopic compositions of strontium, zirconium,
molybdenum, and barium would substantially differ from those
measured in pre-solar SiC grains, which were produced in the
cool circumstellar envelope of a past generation of C stars
(see Lugaro et al. 2003). Additionally, calculated element
abundances ratios such as Rb/Sr would not match
observations obtained from carbon stars
(see Abia et al. 2001).
For these reasons, if the
overshoot from the base of the convective zone
generated by TPs is non-negligible, it should be a rare event.
In summary, a clear and coherent picture of the AGB stars in the cluster NGC 1978 within the more general context of low-mass AGB stellar evolution and nucleosynthesis cannot be easily achieved. Once again, we stress the uniqueness of the C star sample of NGC 1978 with respect to other LMC clusters.
6 Conclusions
In this paper, we presented a sample of AGB stars belonging to the LMC cluster NGC 1978. Where it was possible, we derived the C/O and the 12C/ 13C ratios. The spectroscopic data reveal the presence of two sub-samples, one whereWe did not find a theoretical scheme that is able to satisfactorily reproduce the chemical abundance pattern in NGC 1978. By claiming the existence of a non-standard mixing mechanism, we postulated some possible solutions. However, we are aware that too many ad hoc assumptions make our analysis objectionable, taking into account that some of them are strongly limited by observational constraints. In particular, a more consistent picture of all the additional mixing mechanisms, which are active during the RGB and the AGB phase, is required. We also discussed the scenario of multiple stellar populations and rejuvenated stars, and highlighted the differences to the abundance pattern in the cluster NGC 1846.
Narrower constraints for stellar evolutionary models could be derived from atmospheric models including a set of accurate molecular line data, especially in the case of carbon stars. Additionally, the more evolved a star is (thus having a higher luminosity and C/O ratio), the more dynamic effects influence the spectral appearance. From the observational point of view, improvements could be achieved by means of the choice of the observed wavelength regions, some of which are less crowded with molecular lines. Moreover a comparison between low-resolution data and high-resolution data should be explored further (cf. Wahlin et al. 2006). If low-resolution data deliver robust C/O ratios (and stellar parameters), the isotopic ratios could be derived in the high-resolution spectra more accurately.
In conclusion, we affirm that there is much room for improvement. As a first step, we are currently acquiring new data to increase our statistics by studying more AGB stars in other LMC globular clusters. In this way, we could shed light on the puzzling abundance pattern that we found in NGC 1978.
Acknowledgements
MTL and TL acknowledge funding by the Austrian Science Fund FWF (projects P-18171 and P-20046). MTL has been supported by the Austrian Academy of Sciences (DOC programme). OS and SC have been supported by the MIUR Italian Grant Program PRIN 2006. BA acknowledges funding by the Austrian Science Fund FWF (project P-19503). BA acknowledges funding by the contract ASI-INAF I/016/07/0. Based on observations obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the Science and Technology Facilities Council (United Kingdom), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), Ministério da Ciência e Tecnologia (Brazil) and Ministerio de Ciencia, Tecnología e Innovación Productiva (Argentina). The observations were obtained with the Phoenix infrared spectrograph, which was developed and is operated by the National Optical Astronomy Observatory. The spectra were obtained as part of the programs GS-2006B-C-6 and GS-2008A-Q-65. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
Appendix A: Changes to the CO line list
To match the positions of the CO lines in the recorded K-band spectra, we had to modify some transition frequencies as given in the list of Goorvitch (1994)![]() . The wavenumbers were taken from the Infrared Atlas of the Arcturus Spectrum (Hinkle et al. 1995). The changes are documented in Table A.1. The given quantities are the old and new transition frequency (
. The wavenumbers were taken from the Infrared Atlas of the Arcturus Spectrum (Hinkle et al. 1995). The changes are documented in Table A.1. The given quantities are the old and new transition frequency (![]() ), the lower state term energy
), the lower state term energy ![]() ,
the logarithm of the gf-value (
,
the logarithm of the gf-value (![]() ), the lower and upper state vibrational quantum numbers (
), the lower and upper state vibrational quantum numbers (![]() and
and ![]() ), the lower state angular momentum number (
), the lower state angular momentum number (![]() ), and the isotope identification.
), and the isotope identification.
Table A.1: Modified line positions of CO lines in the K band.
At a later point in the analysis, we compared the corrections of the line positions to the CO data given by Chandra et al. (1996). The wavenumbers from the Arcturus atlas are in good agreement with their transition frequencies. The differences are less than 0.04 cm-1 for the 1-3 vibration transitions and less than 0.01 cm-1 for the other lines. However, we did not use the Chandra et al. (1996) data, because the line strengths of the 12CO 3-0 band head in the H band from this list are severely underestimated and therefore unusable for the analysis.
References
- Abia, C., Busso, M., Gallino, R., et al. 2001, ApJ, 559, 1117 [NASA ADS] [CrossRef] (In the text)
- Alcaíno, G., Liller, W., Alvarado, F., et al. 1999, A&AS, 135, 103 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [NASA ADS] [CrossRef] (In the text)
- Aringer, B. 2000, Ph.D. Thesis, University of Vienna
- Aringer, B., Girardi, L., Nowotny, W., Marigo, P., & Lederer, M. T. 2009, A&A in press, [ArXiv:0905.4415] (In the text)
- Aringer, B., Kerschbaum, F., & Jørgensen, U. G. 2002, A&A, 395, 915 [NASA ADS] [CrossRef] [EDP Sciences]
- Bessell, M. S., Wood, P. R., & Evans, T. L. 1983, MNRAS, 202, 59 [NASA ADS] (In the text)
- Bonnarel, F., Fernique, P., Bienaymé, O., et al. 2000, A&AS, 143, 33 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [NASA ADS] [CrossRef] (In the text)
- Carpenter, J. M. 2001, AJ, 121, 2851 [NASA ADS] [CrossRef] (In the text)
- Carrera, R., Gallart, C., Hardy, E., Aparicio, A., & Zinn, R. 2008, AJ, 135, 836 [NASA ADS] [CrossRef] (In the text)
- Castellani, V., Degl'Innocenti, S., Marconi, M., Prada Moroni, P. G., & Sestito, P. 2003, A&A, 404, 645 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chandra, S., Maheshwari, V. U., & Sharma, A. K. 1996, A&AS, 117, 557 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Charbonnel, C., & Zahn, J.-P. 2007, A&A, 467, L15 [NASA ADS] [CrossRef] [EDP Sciences]
- Chieffi, A., Limongi, M., & Straniero, O. 1998, ApJ, 502, 737 [NASA ADS] [CrossRef] (In the text)
- Chiosi, E., & Vallenari, A. 2007, A&A, 466, 165 [NASA ADS] [CrossRef] [EDP Sciences]
- Cioni, M.-R. L., van der Marel, R. P., Loup, C., & Habing, H. J. 2000, A&A, 359, 601 [NASA ADS] (In the text)
- Cole, A. A., Tolstoy, E., Gallagher, III, J. S., & Smecker-Hane, T. A. 2005, AJ, 129, 1465 [NASA ADS] [CrossRef] (In the text)
- Cristallo, S., Straniero, O., Lederer, M. T., & Aringer, B. 2007, ApJ, 667, 489 [NASA ADS] [CrossRef]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, in press, [ArXiv:0902.0243]
- Davis, S., Wallace, L., Brault, J., & Engleman, R. 2005, The CN spectrum from the infrared to the ultraviolet (NSO Technical Report) (In the text)
- de Laverny, P., Abia, C., Domínguez, I., et al. 2006, A&A, 446, 1107 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Denissenkov, P. A., & Pinsonneault, M. 2008, ApJ, 684, 626 [NASA ADS] [CrossRef]
- Eggleton, P. P., Dearborn, D. S. P., & Lattanzio, J. C. 2008, ApJ, 677, 581 [NASA ADS] [CrossRef] (In the text)
- Ferraro, F. R., Mucciarelli, A., Carretta, E., & Origlia, L. 2006, ApJ, 645, L33 [NASA ADS] [CrossRef] (In the text)
- Fischer, P., Welch, D. L., & Mateo, M. 1992, AJ, 104, 1086 [NASA ADS] [CrossRef] (In the text)
- Frogel, J. A., Mould, J., & Blanco, V. M. 1990, ApJ, 352, 96 [NASA ADS] [CrossRef] (In the text)
- Gautschy-Loidl, R., Höfner, S., Jørgensen, U. G., & Hron, J. 2004, A&A, 422, 289 [NASA ADS] [CrossRef] [EDP Sciences]
- Girardi, L., Chiosi, C., Bertelli, G., & Bressan, A. 1995, A&A, 298, 87 [NASA ADS] (In the text)
- Goorvitch, D. 1994, ApJS, 95, 535 [NASA ADS] [CrossRef] (In the text)
- Goorvitch, D., & Chackerian, Jr., C. 1994, ApJS, 91, 483 [NASA ADS] [CrossRef] (In the text)
- Goudfrooij, P., Puzia, T. H., Kozhurina-Platais, V., & Chandar, R. 2009, AJ, 137, 4988 [NASA ADS] [CrossRef] (In the text)
- Gratton, R. G., Carretta, E., Matteucci, F., & Sneden, C. 2000, A&A, 358, 671 [NASA ADS] (In the text)
- Grevesse, N., & Noels, A. 1993, Phys. Scri. Vol. T, 47, 133 [NASA ADS] [CrossRef] (In the text)
- Grocholski, A. J., Sarajedini, A., Olsen, K. A. G., Tiede, G. P., & Mancone, C. L. 2007, AJ, 134, 680 [NASA ADS] [CrossRef] (In the text)
- Gustafsson, B., Bell, R. A., Eriksson, K., & Nordlund, A. 1975, A&A, 42, 407 [NASA ADS]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Harris, M. J., Lambert, D. L., Hinkle, K. H., Gustafsson, B., & Eriksson, K. 1987, ApJ, 316, 294 [NASA ADS] [CrossRef]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS]
- Herwig, F., Blöcker, T., & Driebe, T. 2000, Mem. Soc. Astron. Ital., 71, 745 [NASA ADS] (In the text)
- Herwig, F., Freytag, B., Hueckstaedt, R. M., & Timmes, F. X. 2006, ApJ, 642, 1057 [NASA ADS] [CrossRef] (In the text)
- Hill, V., François, P., Spite, M., Primas, F., & Spite, F. 2000, A&A, 364, L19 [NASA ADS] (In the text)
- Hinkle, K., Wallace, L., & Livingston, W. C. 1995, Infrared atlas of the Arcturus spectrum, 0.9-5.3 microns (San Francisco, Calif.: Astronomical Society of the Pacific) (In the text)
- Hinkle, K. H., Hall, D. N. B., & Ridgway, S. T. 1982, ApJ, 252, 697 [NASA ADS] [CrossRef] (In the text)
- Hinkle, K. H., Cuberly, R. W., Gaughan, N. A., et al. 1998, in Infrared Astronomical Instrumentation, Presented at the Society of Photo-Optical Instrumentation Engineers (SPIE) Conference, ed. A. M. Fowler, Proc. SPIE, 3354, 810
- Hinkle, K. H., Blum, R. D., Joyce, R. R., et al. 2003, in 4834, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, ed. P. Guhathakurta, 353
- Houdashelt, M. L., Bell, R. A., Sweigart, A. V., & Wing, R. F. 2000, AJ, 119, 1424 [NASA ADS] [CrossRef] (In the text)
- Iben, Jr., I., & Renzini, A. 1983, ARA&A, 21, 271 [NASA ADS] [CrossRef] (In the text)
- Johnson, H. B. 1994, in Lecture Notes in Physics, Molecules in the Stellar Environment (Berlin: Springer Verlag), ed. U. G. Jorgensen, IAU Coll., 146, 234 (In the text)
- Jørgensen, U. G. 1997, ed. E. F. van Dishoeck, IAU Symp., 178, 441 (In the text)
- Jørgensen, U. G., Johnson, H. R., & Nordlund, A. 1992, A&A, 261, 263 [NASA ADS]
- Karakas, A., & Lattanzio, J. C. 2007, PASA, 24, 103 [NASA ADS]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, BaltA, 9, 590 [NASA ADS] (In the text)
- Lambert, D. L., Gustafsson, B., Eriksson, K., & Hinkle, K. H. 1986, ApJS, 62, 373 [NASA ADS] [CrossRef]
- Lebzelter, T., Lederer, M. T., Cristallo, S., et al. 2008, A&A, 486, 511 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lederer, M. T., & Aringer, B. 2009, A&A, 494, 403 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lloyd Evans, T. 1980, MNRAS, 193, 87 [NASA ADS] (In the text)
- Lloyd Evans, T. 1983, MNRAS, 204, 985 [NASA ADS] (In the text)
- Loidl, R., Lançon, A., & Jørgensen, U. G. 2001, A&A, 371, 1065 [NASA ADS] [CrossRef] [EDP Sciences]
- Lugaro, M., Davis, A. M., Gallino, R., et al. 2003, ApJ, 593, 486 [NASA ADS] [CrossRef] (In the text)
- Mackey, A. D., & Broby Nielsen, P. 2007, MNRAS, 379, 151 [NASA ADS] [CrossRef]
- Matsuura, M., Zijlstra, A. A., van Loon, J. T., et al. 2005, A&A, 434, 691 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- McSaveney, J. A., Wood, P. R., Scholz, M., Lattanzio, J. C., & Hinkle, K. H. 2007, MNRAS, 378, 1089 [NASA ADS] [CrossRef]
- Mucciarelli, A., Carretta, E., Origlia, L., & Ferraro, F. R. 2008, AJ, 136, 375 [NASA ADS] [CrossRef] (In the text)
- Mucciarelli, A., Ferraro, F. R., Origlia, L., & Fusi Pecci, F. 2007a, AJ, 133,2053 (In the text)
- Mucciarelli, A., Origlia, L., & Ferraro, F. R. 2007b, AJ, 134, 1813 [NASA ADS] [CrossRef]
- Nollett, K. M., Busso, M., & Wasserburg, G. J. 2003, ApJ, 582, 1036 [NASA ADS] [CrossRef]
- Olszewski, E. W., Schommer, R. A., Suntzeff, N. B., & Harris, H. C. 1991, AJ, 101, 515 [NASA ADS] [CrossRef] (In the text)
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef]
- Querci, F., Querci, M., & Tsuji, T. 1974, A&A, 31, 265 [NASA ADS] (In the text)
- Renzini, A. 2008, MNRAS, 391, 354 [NASA ADS] [CrossRef]
- Reyniers, M., Abia, C., van Winckel, H., et al. 2007, A&A, 461, 641 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schommer, R. A., Suntzeff, N. B., Olszewski, E. W., & Harris, H. C. 1992, AJ, 103, 447 [NASA ADS] [CrossRef] (In the text)
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] (In the text)
- Smith, V. V., & Lambert, D. L. 1990, ApJS, 72, 387 [NASA ADS] [CrossRef]
- Smith, V. V., Hinkle, K. H., Cunha, K., et al. 2002, AJ, 124, 3241 [NASA ADS] [CrossRef] (In the text)
- Stancliffe, R. J., Tout, C. A., & Pols, O. R. 2004, MNRAS, 352, 984 [NASA ADS] [CrossRef]
- Stanghellini, L., Shaw, R. A., & Gilmore, D. 2005, ApJ, 622, 294 [NASA ADS] [CrossRef] (In the text)
- Straniero, O., Chieffi, A., Limongi, M., et al. 1997, ApJ, 478, 332 [NASA ADS] [CrossRef]
- Straniero, O., Domínguez, I., Cristallo, R., & Gallino, R. 2003, PASA, 20, 389 [NASA ADS] (In the text)
- Straniero, O., Gallino, R., & Cristallo, S. 2006, Nucl. Phys. A, 777, 311 [NASA ADS] [CrossRef]
- van den Bergh, S. 2008, AJ, 135, 1731 [NASA ADS] [CrossRef] (In the text)
- Wahlin, R., Eriksson, K., Gustafsson, B., et al. 2006, Mem. Soc. Astron. It., 77, 955 [NASA ADS] (In the text)
- Wasserburg, G. J., Boothroyd, A. I., & Sackmann, I.-J. 1995, ApJ, 447, L37 [NASA ADS] [CrossRef]
- Wilson, R. E. 1953, General catalogue of stellar radial velocities (Washington: Carnegie Institution of Washington) (In the text)
- Wood, P. R., Bessell, M. S., & Fox, M. W. 1983, ApJ, 272, 99 [NASA ADS] [CrossRef] (In the text)
- Yong, D., Meléndez, J., Cunha, K., et al. 2008, ApJ, 689, 1020 [NASA ADS] [CrossRef]
Footnotes
- ... Observatories
![[*]](/icons/foot_motif.png)
- Operated by the Association of Universities for Research in Astronomy, under cooperative agreement with the National Science Foundation.
- ...
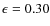
![[*]](/icons/foot_motif.png)
- The flattening of a
globular cluster is defined as
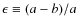 ,
where ais the major axis and b is the minor axis of the cluster.
,
where ais the major axis and b is the minor axis of the cluster.
- ... tutorial
![[*]](/icons/foot_motif.png)
- Available at http://www.noao.edu/usgp/phoenix/. IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.
- ...
Gaussian
![[*]](/icons/foot_motif.png)
- The Gaussian has the functional form
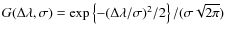 ,
whereby
,
whereby
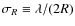 to reduce the effective resolution to a
given R, or
to reduce the effective resolution to a
given R, or
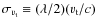 to account for
the macroturbulent velocity
to account for
the macroturbulent velocity  .
.
- ... respectively
![[*]](/icons/foot_motif.png)
- Note
that we also include changes of the macroturbulent velocity in the error analysis.
The equivalent width of a spectral line is unaffected by
 ,
but in
the spectrum synthesis method uncertainties in this parameter influence the
derived abundances.
,
but in
the spectrum synthesis method uncertainties in this parameter influence the
derived abundances.
- ... is 0.076
![[*]](/icons/foot_motif.png)
- The errors for (J-K) are higher, ranging up to and being even greater than 0.1. This could also affect the differences between the effective temperature scales discussed in Sect. 4.
- ... mystery
![[*]](/icons/foot_motif.png)
- Note that our sample contains almost all AGB stars in this cluster (see Fig. 6).
- ... NGC 1978
![[*]](/icons/foot_motif.png)
- Estimated binary fractions in other LMC and SMC clusters range from 10 (NGC 1783, Mucciarelli et al. 2007b)
to
 30 per cent (Chiosi & Vallenari 2007).
30 per cent (Chiosi & Vallenari 2007).
- ...Goorvitch (1994)
![[*]](/icons/foot_motif.png)
- Available at the CDS: http://vizier.cfa.harvard.edu/viz-bin/VizieR?-source=J/ApJS/95/535.
All Tables
Table 1: NGC 1978 targets and log of observations (LE stands for Lloyd Evans 1980).
Table 2: Radial velocities of NGC 1978 targets
Table 3: Data and fit results for oxygen-rich (first group) and carbon-rich (second group) targets in NGC 1978.
Table A.1: Modified line positions of CO lines in the K band.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm]{11857f01.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg39.png) |
Figure 1:
Distribution of observed targets in the cluster NGC 1978. The picture was acquired from the 2MASS catalogue using Aladin (Bonnarel et al. 2000). Numbers refer to the nomenclature of Lloyd Evans (1980). The additional targets A and B were chosen according to their position in the 2MASS colour-magnitude diagram. The stars A, 4, 5, 8, 9, and 10 possess an oxygen-rich atmosphere while B, 1, 2, 3, 6, and 7 are carbon stars. The cluster is elongated and its major axis stretches roughly from south-east to north-west. The displayed sky region is
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{11857f02.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg42.png) |
Figure 2:
Overview about observations: H-band spectra are shown on the left side, K-band spectra on the right. The spectra are ordered by increasing infrared colour
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{11857f03.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg89.png) |
Figure 3: Observation and fit of the carbon star B in NGC 1978. The fit parameters are given in Table 3. The relatively high effective temperature and low C/O ratio compared with the other carbon stars in our sample allowed a reasonable fit. Deviations can to a high fraction be ascribed to uncertain line data. The strong low-excitation CO lines in the K band are not reproduced by the models. See text for details. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{11857f04.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg125.png) |
Figure 4:
Fit of the H band spectrum of the target LE5 adopting different oxygen abundances. A value of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{11857f05.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg127.png) |
Figure 5:
Measured abundances ratios C/O and 12C/ 13C for the targets in NGC 1978. Oxygen-rich targets appear to the left of the dotted line at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{11857f06.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg135.png) |
Figure 6:
Colour-magnitude diagram based on 2MASS data for NGC 1978 (complete within a radius of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{11857f07.eps}\includegraphics[width=8.5cm]{11857f08.eps} }\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg136.png) |
Figure 7: Comparison between observational data and theoretical models. 12C/ 13C isotopic ratios vs. C/O ratios are reported. In the left panel we report the range of O-rich stars only, while in the right panel the whole sample has been considered. The star symbols with error bars indicate our observations. The red dotted, the blue dashed, and the green long-dashed curves in the left panel are partly covered by other tracks in the plot. The symbols in the left panel mark the end point of the tracks after the RGB phase. In the right panel, the symbols indicate the values attained during the interpulse phases, which are on the order of 103 times longer than the TDU episodes. See text for details. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{11857f09.eps}\hspace*{3mm}
\includegraphics[width=8.5cm]{11857f10.eps} }
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg162.png) |
Figure 8: Comparison between observational data and theoretical models. 12C/ 13C isotopic ratios vs. C/O ratios are reported. In the left panel, we report observational data of the cluster NGC 1978, accompanied by selected theoretical tracks. As a comparison, in the right panel, we report the fitting curve for another LMC cluster (NGC 1846). The symbols along the tracks indicate the values attained during the interpulse phases (see also Fig. 7). The star symbols with error bars indicate our observations. See text for details. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{11857f11.eps}
\end{figure}](/articles/aa/full_html/2009/30/aa11857-09/Timg168.png) |
Figure 9: 12C/ 13C isotopic ratio vs. C/O ratio for a series of models including an overshoot at the base of convective zone generated by the TPs. The extension (in fraction of the pressure scale height) of the overshoot zone is indicated in the legend. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


