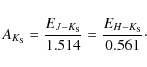EDP Sciences
Home All issues Volume 502 / No 2 (August I 2009) A&A, 502 2 (2009) 559-567 Full HTML
Free Access
Issue
A&A
Volume 502, Number 2, August I 2009
Page(s) 559 - 567
Section Galactic structure, stellar clusters, and populations
DOI https://doi.org/10.1051/0004-6361/200911853
Published online 27 May 2009

The stellar population of the star-forming region G61.48+0.09[*]

A. Marín-Franch1 - A. Herrero1,2 - A. Lenorzer1 - F. Najarro3 - S. Ramirez1 - A. Font-Ribera1 - D. Figer4

1 - Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
2 - Departamento de Astrofisica, Universidad de La Laguna, Spain
3 - Departamento de Astrofisica Molecular e Infrarroja, IEM, CSIC, Madrid, Spain
4 - Rochester Institute of Technology, Rochester, NY, USA

Received 16 February 2009 / Accepted 21 April 2009

Abstract
Context. We present the results of a near-infrared photometric and spectroscopic study of the star-forming region G61.48+0.09.
Aims. The purpose of this study is to characterize the stellar content of the cluster and to determine its distance, extinction, age, and mass.
Methods. The stellar population was studied by using color-magnitude diagrams to select twenty promising cluster members, for which follow-up spectroscopy was done. The observed spectra allowed a spectral classification of the stars.
Results. Two stars have emission lines, twelve are G-type stars, and six are late-O or early-B stars.
Conclusions. The cluster's extinction varies from $A_{K_{\rm S}} = 0.9$ to $A_{K_{\rm S}} = 2.6$, (or $A_{V} \sim 8$ to $A_{V} \sim 23$). G61.48+0.09 is a star-forming region located at $2.5\pm0.4$ kpc. The cluster is younger than 10 Myr and has a minimum stellar mass of $1.5\pm 0.5 \times 10 ^{3}$ $M_\odot$. However, the actual total mass of the cluster remains undetermined, as we cannot see its whole stellar content.

Key words: stars: early-type - Galaxy: structure - infrared: stars - stars: Hertzprung-Russel (HR) and C-M diagrams - Galaxy: open clusters and associations: andividual: G61.48+0.09

1 Introduction

The exploration of the Milky Way is experiencing a strong boost thanks to recent infrared surveys, such as 2MASS (Skrutskie et al. 2006) and GLIMPSE (Benjamin et al. 2003), frequently combined with data from other wavelength ranges, such as radio or $\gamma$-rays. A strong effort is being dedicated to the discovery of new stellar clusters containing massive stars (Arches, Quintuplet, Figer et al. 1999; RSGC1; 2006) or to deeper study of already known stellar clusters and cluster candidates, resulting sometimes in their identification as massive stellar clusters (Cyg OB2, Knödlseder 2000; Westerlund1, Clark & Negueruela 2002). The search has been strongly enabled by new catalogs of stellar cluster candidates: Bica et al. (2003), Dutra et al. (2003), Mercer et al. (2005) and Froebrich (2007). This remarkable effort is leading us towards re-evaluating our ideas about the Milky Way star-forming activity (see i.e. Figer 2008).

Hanson & Popescu (2008) review recent advances and predict that more clusters will be discovered or identified. Recent examples, Messineo 1 (Messineo et al. 2008) and DBS2003-179 (Borissova et al. 2008), seem to confirm this prediction. Unlike earlier results, both clusters are moderate in their masses (about 2000 and 7000 $M_\odot$), which indicates that we are discovering representatives of probably a large number of intermediate-mass stellar clusters. This is consistent with what we could expect, because the luminosity function of clusters in spiral galaxies follows a declining power law with exponent $\alpha= -2$(Larsen 2002), which for clusters of similar age can be translated into the same law for the mass function. Because they are massive and numerous, these clusters may play a substantial role in the star formation history of the Milky Way and other galaxies.

This is the first paper in our MASGOMAS (MAssive Stars in Galactic Obscured MAssive clusterS) project, a study of massive star cluster candidates in the Milky Way, which is being carried out using LIRIS at WHT. Our idea is to select known clusters or cluster candidates from the literature that could turn out to be massive clusters, to observe them photometrically, and to perform a spectroscopic follow-up of the most promising ones. In this paper we present a photometric and spectroscopic study of the stellar population of G61.48+0.09, a cluster that has got recent attention Puga et al. (2004) and whose distance is a matter of debate (see below).

 \begin{figure} \par\includegraphics[width=14cm]{11853f1.eps} \end{figure} Figure 1:

Near- ($K_{\rm S}$, LIRIS@WHT) and mid- (3.6 $\mu $m, GLIMPSE) infrared images of the star-forming region G61.48+0.09. The grey contours correspond to the Garay et al. (1998) continuum emission at 8.3 GHz. The positions of stars L1 and L2 are also marked.

Table 1:   Imaging/spectroscopic observations details.

G61.48+0.09 is a complex star-forming region located in the direction of the Cygnus arm. Figure 1 shows near- (left panel) and a mid- (right panel) infrared images of the G61.48+0.09 region. Continuum emission contour levels at 8.3 GHz (Garay et al. 1998) are also shown. As seen in the right panel of this figure, the G61.48+0.09 region consists of some bright stars surrounded by an HII region, Sh2-88, composed of two subregions, B1 (westwards) and B2 (eastwards; Deharveng et al. 2000). The central part is a triplet of stars. Although the region has been extensively studied by different authors, no spectroscopy of their stars exists. In their polarimetric study of the region, Puga et al. (2004) present a detailed review of previous radio and near-IR photometric work. From their polarimetric study and the energetics balance, they conclude (as did Deharveng et al. 2000) that the main ionizing source of this region is probably still hidden behind obscuring clouds of natal material. A strong source in the L' band, identified as L1, and a fainter L-source identified as L2, are proposed as possible main ionizing sources. L1 and L2 locations have also been marked in Fig. 1. In the right panel, L1 can clearly be seen as a bright object in the center of the HII subregion Sh2-88B2.

The distance to G61.48+0.09 is somewhat controversial. The first determination was a kinematic distance derived by Reifenstein et al. (1970), who used the Schmidt (1965) model of the Galaxy to arrive at the two possible distances of 2.0 and 7.5 kpc. Since then, many authors have made new determinations obtaining different values, but always in rough agreement with one of the 2 values obtained by Reifenstein. Churchwell et al. (1990) give a distance of 5.4 kpc based on ammonia observations combined with the identification of the region with CO observations from Solomon et al. (1987), who use different techniques to distinguish close and far distances in the list of giant molecular clouds from Sanders et al. (1986). A comparison of different determinations may be found in Deharveng et al. (2000), who adopt the short distance of 2.5 kpc, as most authors do. Nevertheless, the distance from Churchwell et al. (1990) has very recently been adopted by Zhu et al. (2008) in their study of Galactic clusters. Of course, many derived global properties of G61.48+0.09, e.g., total stellar mass or energetic content, may strongly depend on the adopted distance.

We present new NIR photometric data and, for the first time, NIR spectroscopy of stars in the cluster region. Section 2 presents the observations and data reduction. In Sect. 3 we present the results of the photometric (3.1) and spectroscopic (3.2) analysis. Section 4 presents the discussion of these results and in Sect. 5 we present our conclusions.

2 Observations and data reduction

This study is based on broad-band imaging and on spectroscopic observations with LIRIS, a near-IR imager/spectrograph mounted at the Cassegrain focus of the 4.2 m William Herschel Telescope (La Palma). Table 1 gives a summary of the observation details.

2.1 Photometry

LIRIS is equipped with a Hawaii $1024 \times 1024$ HgCdTe array detector, with a spatial scale of 0.25  $\hbox{$^{\prime\prime}$ }\rm pixel^{-1}$, providing a field of view of 4.27 $\hbox{$^\prime$ }$ on each side. Broad-band imaging observations were performed using the J, H, and $K_{\rm S}$ filters. A standard dithering mode (8-point pattern) was used to optimize cosmic rays/bad pixels rejection and sky computation. Two different fields have been observed: the target field, centered on the G61.48+0.09 region, and a control field located $\sim$8 $\hbox{$^\prime$ }$ west of the target field. Figure 2 shows a DSS-2-infrared survey image in which both target (a) and control (b) fields have been marked. It can be seen that there is a lack of stars around the G61.48+0.09 field if compared to the control filed. This suggests that there is a cloud associated to the G61.48+0.09 region that is responsible for the increased extinction of the background field stars. The data were reduced using the FATBOY (Eikenberry et al. 2006; Warner et al. 2009) and LIRIS-QL image reduction packages following standard NIR reduction procedures. The average seeing during the imaging observations of the G61.48+0.09 region was $\sim$0.6 $\hbox{$^{\prime\prime}$ }$. In the left panel of Fig. 1, the resulting G61.48+0.09 image in the $K_{\rm S}$-band is shown.

DAOPHOT II, ALLSTAR, and ALLFRAME (Stetson et al. 1994) were then used to obtain the instrumental photometry of the stars. The photometric lists of the observed targets were cleaned of non-stellar objects and poorly measured stars on the basis of the SHARP and PSF fitting $\sigma $ parameters provided by ALLFRAME. Only stars with |SHARP| < 0.25 and $\sigma < 0.1$ have been considered. The photometric calibration was based on the 2MASS photometry. Figure 3 shows the 2MASS color-magnitude diagram (CMD) of the target field. For the calibration, a set of isolated, unsaturated stars for which good photometry exists in both 2MASS and our images was selected. These stars have been marked in Fig. 3 with open circles. They span a wide range of magnitudes ( $13 > K_{\rm S} > 9$ mag) and colors ( $0 < (J-K_{\rm S}) < 5$). After we compared their instrumental photometry with the 2MASS catalog, a calibration equation (which includes a color term) was derived for the J, H, and $K_{\rm S}$ filters. Figure 4 shows the photometric calibration results for our target field. Left panels show the photometric transformation from instrumental (INSTR) to calibrated 2MASS magnitudes. Central panels show the difference between the calibrated photometry and the 2MASS photometry. It can be seen that this difference is less than 0.05 mag for most of the selected stars. The right hand panels show the PSF fitting $\sigma $ parameter provided by ALLFRAME. This calibration procedure was repeated for the control field. Finally, as the few stars brighter than $K_{\rm S}\sim10$ appear saturated in our data, their magnitudes were obtained directly from the 2MASS catalog.

It is worth mentioning that the 2MASS photometry for most of the stars brighter than $K_{\rm S} \sim 11$ and redder than $(J-K_{\rm S}) \sim 3$ is strongly affected by the molecular cloud. For those stars, the 2MASS catalog adds the emission of dense cloud clumps to the star photometry, making the star artificially brighter and redder. In fact, some of the 2MASS detections in this region of the CMD are not real stars, but molecular cloud clumps instead. This effect is due to the limited 2MASS spatial resolution. For this reason, it is not possible to increase the number of stars with $(J-K_{\rm S})> \sim 4-5$ used for the photometric calibration. The calibrated photometry is then less reliable for stars with $(J-K_{\rm S}) > 5$. But, as it will be shown in Sects. 3 and 4, these stars are background late type stars that have not been used for the cluster description, with the exception of a YSO. As a conclusion, this lack of highly reddened stars in the photometric calibration does not affect cluster results significantly.

2.2 Spectroscopy

We obtained medium-resolution HK- and K-band spectra with WHT/LIRIS in multi-object (MOS) and long-slit (LS) spectroscopic modes. The slit width was 0.8 $\hbox{$^{\prime\prime}$ }$, allowing a spectral resolution of $\lambda / \Delta \lambda \sim 945$ and 2500 in the HK- and K-band spectra, respectively. We observed in a standard nodding pattern ABBA with individual exposure times of 20, 40, and 120 s (HK) and 120 s (K). Table 1 lists the details of the spectroscopic observations, and Fig. 5 shows a false color-composition image of the G61.48+0.09 field marked with the position of the spectroscopically observed stars (see Sect. 3.2).

The observations were reduced by first scaling the B fields to their corresponding A fields using the quotient of medians as scaling factors. This step crudely corrects for average sky variations between frames with long integration times. We then subtracted B frames from A frames, and A frames from B frames before applying flatfield correction. The AB and BA frames were shifted in the spatial direction so that all positive continuum traces coincide before all frames were combined into a master frame. We then extracted the spectra from the master frame. The spectra were correlated with that of the standard star to yield wavelength solutions accounting for distortions of high orders. This solution was then applied to the spectra before division by the spectrum of the standard star from which the stellar features had been removed.

 \begin{figure} \par\includegraphics[width=9cm]{11853f5.eps} \end{figure} Figure 5:

False color composition image of the central part of the G61.48+0.09 field. The position of the spectroscopically observed stars is shown. The early-type stars (see Table 2) have been marked with circles, and the rest with squares.

3 Results

3.1 Color-magnitude diagrams

The CMDs of the target and control fields can provide valuable information about the G61.48+0.09 region's extinction, distance, and stellar content. Figure 6 shows the CMDs corresponding to the G61.48+0.09 region (a) and the control field (b).

The position of a star on the CMD is determined from its absolute magnitude, intrinsic color, distance and extinction. When comparing target and control fields CMDs, the first major difference that can be observed is the absence of the red-clump strip in the target field, while this feature can be clearly seen in the control one. The red-clump strip is the CMD trace that is populated by red-clump stars located at different distances. López-Corredoira et al. (2002) developed a method to use red-clump stars as a distance indicator. In essence, this method uses a K2III star as representative red-clump star and, assuming an extinction law, computes the expected position of this star in the CMD when located at different distances. Comparing the former with the observed red-clump strip, the distance of red-clump stars can be estimated.

In this paper we adopt the Cox (2000) absolute V-magnitude and Ducati et al. (2001) IR colors for a K2III star. Figure 6 shows the expected position of a K2III star as a function of its distance. The Rieke et al. (1989) extinction law and R=3.09 (Rieke & Lebofsky 1985) were assumed. That the red-clump strip is not seen in the G61.48+0.09 region shows that the cluster, in particular its associated cloud, is adding extinction to the background red-clump stars. This indicates that the cluster is located between these red-clump stars and the Sun. In other words, an upper limit to the distance can be established by comparing the target and control CMDs. As a result, it can be concluded that the G61.48+0.09 region is located at a distance less than $\sim$4 kpc. This rough estimation depends on the assumed intrinsic colors and magnitudes of a K2III star, as well as on the assumed extinction law.

 \begin{figure} \par\includegraphics[width=9cm]{11853f6.eps} \end{figure} Figure 6:

Color-magnitude diagrams of the target (a) and control (b) fields. The black solid line shows the expected position of a K2III star as a function of its distance. To construct the K2III sequence, data for MV have been taken from Cox (2000) and IR intrinsic colors from Ducati et al. (2001). Grey lines represent a fraction of an 11.2 Gyr and solar metallicity isochrone, located at different distances. The Pietrinferni et al. (2004) stellar evolution library and the Castelli & Kurucz (2003) bolometric correction library were used to generate the isochrones, and the Rieke et al. (1989) extinction law and R=3.09 (Rieke & Lebofsky 1985) were assumed.

On the other hand, the local main sequence (MS) can be clearly seen in both CMDs, although for magnitudes fainter than $K_{\rm S} \sim 14$, it appears more affected by extinction in the target field than in the control one. This additional extinction stems from the presence of the star-forming region G61.48+0.09. At this point, a simplistic approximation can be done. Binney et al. (2000) find the age of the solar neighborhood to be $11.2\pm0.75$ Gyr. If we assume that the solar neighborhood is composed mainly of stars with this age and solar metallicity, then a suitable isochrone can be over-plotted in Fig. 6. In this context, a portion of an 11.2 Gyr and solar metallicity isochrone, located at different distances has been overplotted. The IAC-star (Aparicio & Gallart 2004) synthetic CMD program was used to compute the isochrone. Pietrinferni et al. (2004) stellar evolution library and Castelli & Kurucz (2003) bolometric correction library were considered, together with the Rieke et al. (1989) extinction law. When comparing these isochrones with the CMDs, it can be observed that the main difference between the target and control MSs starts at a distance of $\sim$2.5 kpc. That is, local MS stars located at a distance shorter than $\sim$2.5 kpc are not affected by the presence of the star-forming region G61.48+0.09, but more distant MS stars have an increased extinction when compared to the control field.

As a result, this simple argument leads to a distance estimation of $\sim$2.5 kpc for the star-forming region G61.48+0.09. In Sect. 4, a more precise distance determination of G61.48+0.09 is derived based on the spectroscopic analysis combined with photometric information, but it is interesting how this photometric analysis is able to provide a first approximation. Kinematical studies are compatible with distances of 2.0 and 6.5 kpc, so this photometric analysis points towards G61.48+0.09 located at a distance closer to the lower value.

It is worth mentioning that no trace of a cluster MS is found in the G61.48+0.09 region's CMD. As shown later, this cluster is affected by a high differential reddening, which explains the absence of a cluster MS. This differential reddening is shifting every cluster member in a different way along the reddening vector, so the cluster MS is highly blurred.

3.2 Spectral classification

The G61.48+0.09 region's CMD was used to select promising cluster members, for which follow up spectroscopy was done. The selection was made based on the location of these stars in the CMD and their position in the cluster. In other words, the LS and MOS candidate list was made based on photometric and spatial information. This selection actually depends on the field morphology, since it was mainly observed with multiobject spectroscopy.

The observed spectra are presented in Fig. 7. Two objects are classified as emission-line objects, twelve turned out to be red objects, mainly G-type stars, and six turned out to be OB stars, from O9 to B3-B5. For the classification, the catalogs of Hanson & Conti (1996), Hanson et al. (1998), and Wallace & Hinkle (1997) and the relation between spectral type and equivalent width of the CO band head given in Davies et al. (2007) were used. The more recent atlas of Hanson et al. (2005) or the high-resolution atlas of Wallace & Hinkle (1996) were not used, because their resolutions ($R\sim8000$) are much higher than ours.

Cool stars were first classified in spectral type using the Wallace & Hinkle (1997) catalog. To this aim, the CO band and the features around 2.265 $\mu $m (Ca/Sc/Ti), 2.207 (Na/Sc/V) and 2.09 (CN) were used as primary indicators. Typical uncertainties (estimated from independent determinations by two of us) are $\pm$1 spectral subclass. After determining the spectral type, we determined the luminosity class using the spectral type-EW(CO) relation in Davies et al. (2007). This is illustrated in Fig. 8 where we show the EW of the CO band head in our stars and Davies relationship. The CO EW was determined in the same way as indicated in Davies et al. (2007): we measured the EW between 2.294 and 2.304 $\mu $m and adopted the average level between 2.288 and 2.293 $\mu $m for the continuum. Errors were estimated from the local continuum rms.

 \begin{figure} \par\includegraphics[width=16cm]{11853f7.ps} \end{figure} Figure 7:

H and K spectra of observed stars in the G61.48+0.09 star-forming region.

 \begin{figure} \par\includegraphics[width=8cm]{11853f8.ps} \end{figure} Figure 8:

EW of the CO band head versus spectral type. Dotted line is the relation for supergiants presented by Davies et al. (2007) and the dashed line is the corresponding relation for giants by the same authors.

 \begin{figure} \par\includegraphics[width=8.2cm]{11853f9.eps} \end{figure} Figure 9:

Color-color diagrams of the G61.48+0.09 region (target field). Open and filled circles represents the late and early type stars, respectively, listed in Table 2. The solid line indicates the direction of the reddening vector for a B2V star, while the dotted lines corresponds to a G6III. Ducati et al. (2001) IR intrinsic colors and the Rieke et al. (1989) extinction law have been adopted.

We see that the K and M stars fit the giant calibration clearly. The situation is less clear for the G stars, but their positions in the CMD indicate that they are not brighter than the blue stars in the sample. Therefore, they cannot be red-yellow supergiants. This same argument can be applied to stars $\char93 18$ and $\char93 26$, for which we could not get the spectra of the CO band (because of the usual displacement of the spectra when the slits are displaced from the mask's central line), and for star $\char93 17$ (F-type), where the CO-band is not visible. Additionally, we note that from the observed spectrum, star $\char93 17$ could be a main sequence object, but then it would be too bright when corrected for reddening (except if it has a particularly strong differential obscuration). The spectra, magnitudes, and CO band-head equivalent widths are thus compatible with all stars of type later than A, because they are yellow or red giants.

Early type spectra were classified using the Hanson & Conti (1996) and Hanson et al. (1998) atlases. The main indicator used was the presence of HeI lines at 1.701 and 2.113. They are present in all stars we classified as early-type stars, except in star $\char93 22$. According to Hanson & Conti (1996) and Hanson et al. (1998), these lines begin to disappear around B3/B5 in dwarfs. For supergiants, the HeI 1.70 line is present for all spectral types and the HeI 2.113 dissappears around B8/B9. The behavior of the Br series as compared with the other early-type stars points to a classification as B3/B5, probably of luminosity class V. Stars $\char93 4$, $\char93 5$, and $\char93 22$ were thus classified as B1, B2, and B3-B5, respectively. Star $\char93 12$ shows also a trace of HeII 2.189 and was classified as O9.

Table 2:   Spectroscopically observed stars in G61.48+0.09.

We tried to derive the luminosity class for the early types directly from their spectra, but the low resolution in the H-band and the uncertainties in the reduction of the Br$_\gamma$ line in the K band prevented us from using the broadening of the H lines for the classification. We also tried to use the ratio of the Br11/HeI 1.701 $\mu $m. This is difficult for star $\char93 12$, as we are in the region of lower sensitivity for this indicator. Stars $\char93 4$ and $\char93 5$ have values favoring luminosity class V, while star $\char93 22$ is clearly of luminosity class V according to this ratio.

However, we can still use an indirect argument to assign a luminosity class to star $\char93 12$. The stars $\char93 8$ and $\char93 6$ are red giants and have very large extinctions. This indicates that they are behind the group of early-type stars. Therefore, they limit the possible distance to star $\char93 12$ and, consequently, its absolute magnitude, which then correspond to luminosity class V stars. The same argument can be applied to the rest of the stars in the cluster. Moreover, this conclusion is consistent with our previous analysis of the CMD (see Sect. 3.1). If the early type stars were supergiants, then the derived cluster distance would be 7-8 kpc. This is not consistent with Fig. 6, where the CMD of the target field does not show the red clump strip for distances between 3 and 7 kpc.

If the early-type stars were just giants, the result would still be inconsistent. Star $\char93 22$, and most probably also stars $\char93 4$ and $\char93 5$, are dwarfs. Assuming that stars $\char93 12$ and $\char93 2$ (that is classified as B0V below) are giants would result in two different distances for the two groups. Stars $\char93 22$, $\char93 4$, and $\char93 5$ are located at a distance of $\sim$2.5 kpc, while stars $\char93 12$ and $\char93 2$ would be at 3.5 kpc. This argument leads us to a luminosity class V for all the early-type stars.

The spectra of stars $\char93 1$, $\char93 2$, $\char93 3$, and $\char93 14$ show strong emission lines. The first three are in the central part of the cluster and were observed using a long slit that included all three stars. Unfortunately, the nebular emission in that region is very strong and highly spatially variable, so that at our low resolution their spectra are contaminated by emission lines, particularly in Br$_\gamma$. A similar problem arises with star $\char93 14$ in the B1 subregion, which was observed in the MOS mask. We cannot separate the nebular and stellar lines.

Star $\char93 3$ displays a spectrum that resembles that of star $\char93 22$ (i.e., without any clear He features) except for the emission in the Bracket series. We classify it as a B3-B5 star contaminated by the strong nebular emission.

Stars $\char93 2$ shows a weak absorption at HeI 1.701 and a weak Br11 line, without any trace of HeII absorption, which at this resolution is consistent with an O9 or B0 spectral type. This is also consistent with the K-band spectrum showing no absorption features, with a moderate emission in Br$_\gamma$ and HeI 2.059 and with the analysis of Puga et al. (2004), who estimate a B0V spectral type for this star. In our CMD this star falls between stars $\char93 12$ and $\char93 4$ that we classify as O9V and B1V. Therefore we classify star $\char93 2$ as B0V.

Star $\char93 1$ (star $\char93 82$ of Deharveng et al. 2000; and Puga et al. 2004) is the outstanding red object at the center of the cluster, and it could be its main ionization source. In such a case, its spectrum would correspond to that of an early O dwarf. However, we find no trace of HeII lines or CIII/NIII/OIII emission at 2.116, indicating that the spectral type is later than O7.5. At the same time, we see no CO absorption, so the star has to be of mid-F type or earlier. If the extinction law towards the object is normal, then the spectrum and the observed K magnitude would be compatible with an early F supergiant, but then the star should be much redder in the color-color diagram. Therefore we conclude that the object has a spectral type between early-A and late-O. We cannot make a better classification, but we note that the K-band spectrum resembles that of the YSO object in G118.796+1.030 presented by Bik et al. (2005), so we classify it as YSO. This is consistent with the strong reddening present in this star and with the difficulties pointed out by Puga et al. to fit its SED. This classification, however, indicates that this is not the main ionization source of the cluster, which is probably one of the hidden sources (see Puga et al. 2004, for a more detailed discussion).

Star $\char93 14$ is quite similar to star $\char93 1$ in the K-band, but with a stronger and broader emission in the Br$_\gamma$ line, as well as in the Bracket series in the H-band. We classify it as Be because we cannot identify further features. Stars $\char93 1$ and $\char93 14$ have very high (J-Ks) colors. For star $\char93 14$ this is not a problem, because it still falls within our calibration star's range. Star $\char93 1$ falls beyond this limit, but we note that star $\char93 6$, which falls in the same region, has infrared colors that are consistent with its spectral classification and a very high reddening. We thus think that the colors of star $\char93 1$ are reliable. The color excesses are consistent with disks around star $\char93 14$ (Gehrz et al. 1974) and star $\char93 1$ (Jiang et al. 2008).

The derived spectral types and some cross-correlations with previous works can be found in Table 2.

4 Discussion

The spectral classification of the early OB stars found, along with their photometry, allows determination of various cluster parameters, such as its extinction, distance, age, and mass.

4.1 Extinction, distance, and age

Once the spectral type and luminosity class of a star is derived, its intrinsic color and absolute magnitude is known. The extinction of this star can be derived by comparing them with its apparent color and magnitude. Assuming the Rieke et al. (1989) extinction law with R=3.09 (Rieke & Lebofsky 1985), the extinction, $A_{K_{\rm S}}$, of a star can be determined using the equation:

\begin{displaymath} A_{K_{\rm S}} = {{E_{J-K_{\rm S}}} \over {1.514}} = {{E_{H-K_{\rm S}}} \over {0.561}}\cdot \end{displaymath} (1)

Because the intrinsic colors of the cluster stars are known from their spectral classification, $A_{K_{\rm S}}$ can be derived from the color-color diagram. Figure 9 shows these diagrams for the stars in the G61.48+0.09 target region. The reddening vector from the expected intrinsic colors of a B2V and G9III star was computed assuming the extinction law of Rieke et al. (1989). The stars classified in Sect. 3.2 as early (O9V-B5V) and late (G3III-M3III) type stars, respectively, are marked. It can be seen how the assumed extinction law reproduces the slope in the color-color diagram very well for both the early and late type stars. This suggests that the extinction law assumed for the dense molecular cloud is not very different from the one in the interstellar medium. We also see that the early-type stars are affected by a strong differential reddening. The most reddened early-type star ($\char93 $12) is actually far from what we would identify as the center of the cluster (centered at star $\char93 $2). This is an indication that the cluster is still sweeping out the original molecular material. Besides, stars $\char93 $1(YSO) and $\char93 $14 (Be) present high infrared excess.

We adopted the Cox (2000) absolute V-magnitude and Ducati et al. (2001) IR colors for the early type stars except for star $\char93 12$ (O9V), for which Martins et al. (2005) observational scale colors were adopted. The value of $A_{K_{\rm S}}$ was obtained for each star using Eq. (1), and the mean of the two results is considered as the final $A_{K_{\rm S}}$. Table 3 lists the $A_{K_{\rm S}}$ results in Col. (1). It can be seen that the analyzed stars' extinctions vary from $A_{K_{\rm S}} = 0.9$, or $A_{V} \sim 8$, to $A_{K_{\rm S}} = 2.6$, or $A_{V} \sim 23$. That is, the extinction is highly variable across the G61.48+0.09 star-forming region.

 \begin{figure} \par\includegraphics[width=9cm]{11853f10.eps} \end{figure} Figure 10:

Calibrated color-magnitude diagram of the G61.48+0.09 star-forming region. The spectroscopically observed stars have been marked with filled circles. Filled triangles show the position of the reddening corrected early type stars, that is, they show the reddening corrected cluster main sequence. Open triangles show the reddening corrected position of the late type stars. The solid line shows the zero-age main sequence located at a distance of 2.5 kpc. Vertical dashed lines show the intrinsic color interval of the late type stars with spectral types between G0III and M3III.

Once the extinction of the individual stars is known, their distances can be derived by comparing their apparent and absolute magnitudes. Column 2 in Table 3 lists the derived distances for the six cluster stars. The mean obtained distance is 2.5 kpc. The uncertainty associated to the distance determination has several contributions. On one hand, any uncertainty in the photometry of the stars, in their assumed intrinsic colors and absolute magnitudes, has an effect on the distance result. On the other hand, the dominant source of error comes from the extinction. As mentioned before, the Rieke et al. (1989) extinction law with R=3.09 (Rieke & Lebofsky 1985) was adopted. The interstellar extinction law could be different in dense molecular clouds. For example, Breger et al. (1981) found an anomalous extinction law in Orion, and Chini (1981) found it in the Ophiuchus dark cloud, so the interstellar extinction law for the cluster stars could be different from the adopted one, although not much according to Fig. 9. If that is the case, any differences between the adopted and real extinction laws would affect the derived distance. For this reason, we consider the sigma of these individual distances as the final uncertainty; that is, we adopt $2.5\pm0.4$ kpc as the distance of the cluster. This distance, 2.5 kpc, is fully compatible with the shorter distance derived in previous kinematical studies and with the analysis of the CMD from previous section.

Figure 10 shows the calibrated CMD obtained for the star-forming region G61.48+0.09. The spectroscopically observed stars are marked (as above). In this CMD we can see the local MS formed by slightly reddened field stars while cluster stars are expected to have larger reddening. This figure also shows the reddening corrected position of the spectroscopically observed stars. Solid lines show the zero-age MS located at a distance of 2.5 kpc. Vertical dashed lines show the color interval of the late type stars with spectral types between G0III and M3III.

Only an upper limit can be established with the present data for the cluster's age. The earliest star found in this cluster is an O9V. If we assume that all stars in the cluster were formed at the same time, and we adopt the calibration of stellar parameters given by Martins et al. (2005) and the evolutionary models from Schaller et al. (1992), then we can conclude that the cluster must be younger than $\sim$10 Myr. For older ages this O9V star would have evolved into a giant. This is consistent with the lack of red supergiants in the cluster, which need slightly less than 10 Myr to develop from 25 $M_\odot$ stars in the Schaller et al. (1992) models (including rotation in the evolutionary models does not change this conclusion).

4.2 Mass

We estimated the stellar cluster mass of G61.48+0.09 assuming a Salpeter IMF. Likewise, we also assumed that the mass interval for O9V stars, the earliest type we found, is 15.6-18.8 $M_\odot$ (from the observational scale in Martins et al. 2005). With these assumptions, the estimated mass contained in stars for G61.48+0.09 is $1.5\pm 0.5 \times 10 ^{3}$ $M_\odot$, where the error has been estimated from our adopted uncertainty of $\pm$1 spectral subtype. This error is larger than the one derived from changing the spectral type-stellar mass relationship, but other important sources may contribute to enlarge the uncertainty and make our estimation a lower limit.

Table 3:   Derived extinctions and distances for the cluster stars.

The first one comes from the slope of the IMF. We assumed a Salpeter form, which agrees with most determinations for clusters in the mass range we investigated in G61.48+0.09 (Massey 2003). Evidence of anomalous, flatter IMFs are found only in more massive clusters (Figer 2005). Therefore we consider the Salpeter form adequate for G61.48+0.09.

The second one comes from the possible presence of other early-type stars. We have seen in Sect. 3.1 that the CMD stellar population above stars $\char93 $2 and $\char93 12$ is consistent with the nearby field population, which is also confirmed by the classification of star $\char93 8$ as a M2 III star. Therefore we do not expect any contribution by these stars to the early spectral type population of G61.48+0.09. More difficult is the possible contribution of star $\char93 $1. If the strong IR excess comes from to a disk around a young star, then its mass is probably not higher than 20 $M_\odot$ (Cesaroni et al. 2006). Assuming a second object of the same mass as star $\char93 12$, we would obtain a cluster mass of 2900 $M_\odot$ (again with a Salpeter IMF).

The final uncertainty would come from the lack of an evident stellar ionizing source. The ionizing fluxes derived by Puga et al. (2004) cannot be fitted by stars $\char93 1$ and $\char93 2$ (Puga et al. stars 82 and 83) at the spectral types and luminosity classes we have assigned them. Therefore, we have to look for another ionizing source, which presumably would have earlier spectral type and higher mass. Puga et al. (2004) propose the source they identify in the $L^\prime$-band as L1. Inspection of the Spitzer archive does not help, since the region is saturated at the long wavelengths. Therefore, we emphasize that the mass we derive for the cluster is a lower limit.

Table 4:   Summary of cluster properties.

5 Conclusions

This study of the stellar population of G61.48+0.09 is part of our larger study of massive star-cluster candidates in the Milky Way that is being carried out using LIRIS at the WHT. New near-IR photometric data and, for the first time, near-IR spectroscopy of stars in the cluster region have been presented.

From the study of the color-magnitude diagram and the spectroscopic analysis, we concluded that G61.48+0.09 is a star-forming region located at $2.5\pm0.4$ kpc, in agreement with authors that have chosen the short distance scale (see Deharveng et al. 2000). The cluster is younger than 10 Myr and we obtained a stellar mass of $1.5\times 10^{3}$ $M_\odot$, although with large uncertainty, as we could not see the whole stellar content of G61.48+0.09. In particular, our classification of observed spectral types cannot account for the ionizing fluxes derived by Puga et al. (2004), and it is unlikely that any of the stars observed in the near IR can be the ionizing source. Table 4 lists a summary of all cluster properties.

Acknowledgements

We thank E. Puga for her careful reading of the manuscript and useful comments. A.M.F. would like to thank C. Warner, A. Gonzalez, and the FLAMINGOS-2 team for providing access to the prerelease version of the FATBOY pipeline. S.R. was supported by the MAEC-AECID scholarship. Part of this work was supported by the Science and Technology Ministry of the Kingdom of Spain (grants AYA2007-67456-C02-01/02 and AYA2008-06166-C03-01/02 and Consolider-Ingenio 2010 Program CSD 2006-00070 ) and by NASA under award NNG 05-GC37G, through the Long-Term Space Astrophysics program. The William Herschel Telescope is operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias.

References

Online Material

 \begin{figure} \par\includegraphics[width=15cm]{11853f2.eps} \end{figure} Figure 2:

Wide field DSS-2-infrared survey image of the G61.48+0.09 star-forming region. The squares represent the observed target a) and control b) fields of view.

 \begin{figure} \par\includegraphics[width=15cm]{11853f3.eps} \end{figure} Figure 3:

2MASS CMD of the target field. The stars used for the photometric calibration are marked with open circles.

 \begin{figure} \par\includegraphics[width=15cm]{11853f4.eps} \end{figure} Figure 4:

Photometric calibration in the J-, H-, and $K_{\rm S}$-bands for the G61.48+0.09 field. Left panels show the photometric calibration from instrumental (INSTR) to the calibrated magnitudes (2MASS). Central panels show the difference between the calibrated photometry and the 2MASS photometry. Right panels show the PSF fitting $\sigma $ parameter provided by ALLFRAME.


Footnotes

... G61.48+0.09[*]
Figures 2-4, are only available in electronic form at http://www.aanda.org

All Tables

Table 1:   Imaging/spectroscopic observations details.

Table 2:   Spectroscopically observed stars in G61.48+0.09.

Table 3:   Derived extinctions and distances for the cluster stars.

Table 4:   Summary of cluster properties.

All Figures

  \begin{figure} \par\includegraphics[width=14cm]{11853f1.eps} \end{figure} Figure 1:

Near- ($K_{\rm S}$, LIRIS@WHT) and mid- (3.6 $\mu $m, GLIMPSE) infrared images of the star-forming region G61.48+0.09. The grey contours correspond to the Garay et al. (1998) continuum emission at 8.3 GHz. The positions of stars L1 and L2 are also marked.
In the text

  \begin{figure} \par\includegraphics[width=9cm]{11853f5.eps} \end{figure} Figure 5:

False color composition image of the central part of the G61.48+0.09 field. The position of the spectroscopically observed stars is shown. The early-type stars (see Table 2) have been marked with circles, and the rest with squares.
In the text

  \begin{figure} \par\includegraphics[width=9cm]{11853f6.eps} \end{figure} Figure 6:

Color-magnitude diagrams of the target (a) and control (b) fields. The black solid line shows the expected position of a K2III star as a function of its distance. To construct the K2III sequence, data for MV have been taken from Cox (2000) and IR intrinsic colors from Ducati et al. (2001). Grey lines represent a fraction of an 11.2 Gyr and solar metallicity isochrone, located at different distances. The Pietrinferni et al. (2004) stellar evolution library and the Castelli & Kurucz (2003) bolometric correction library were used to generate the isochrones, and the Rieke et al. (1989) extinction law and R=3.09 (Rieke & Lebofsky 1985) were assumed.

In the text

  \begin{figure} \par\includegraphics[width=16cm]{11853f7.ps} \end{figure} Figure 7:

H and K spectra of observed stars in the G61.48+0.09 star-forming region.
In the text

  \begin{figure} \par\includegraphics[width=8cm]{11853f8.ps} \end{figure} Figure 8:

EW of the CO band head versus spectral type. Dotted line is the relation for supergiants presented by Davies et al. (2007) and the dashed line is the corresponding relation for giants by the same authors.

In the text

  \begin{figure} \par\includegraphics[width=8.2cm]{11853f9.eps} \end{figure} Figure 9:

Color-color diagrams of the G61.48+0.09 region (target field). Open and filled circles represents the late and early type stars, respectively, listed in Table 2. The solid line indicates the direction of the reddening vector for a B2V star, while the dotted lines corresponds to a G6III. Ducati et al. (2001) IR intrinsic colors and the Rieke et al. (1989) extinction law have been adopted.
In the text

  \begin{figure} \par\includegraphics[width=9cm]{11853f10.eps} \end{figure} Figure 10:

Calibrated color-magnitude diagram of the G61.48+0.09 star-forming region. The spectroscopically observed stars have been marked with filled circles. Filled triangles show the position of the reddening corrected early type stars, that is, they show the reddening corrected cluster main sequence. Open triangles show the reddening corrected position of the late type stars. The solid line shows the zero-age main sequence located at a distance of 2.5 kpc. Vertical dashed lines show the intrinsic color interval of the late type stars with spectral types between G0III and M3III.
In the text

  \begin{figure} \par\includegraphics[width=15cm]{11853f2.eps} \end{figure} Figure 2:

Wide field DSS-2-infrared survey image of the G61.48+0.09 star-forming region. The squares represent the observed target a) and control b) fields of view.
In the text

  \begin{figure} \par\includegraphics[width=15cm]{11853f3.eps} \end{figure} Figure 3:

2MASS CMD of the target field. The stars used for the photometric calibration are marked with open circles.
In the text

  \begin{figure} \par\includegraphics[width=15cm]{11853f4.eps} \end{figure} Figure 4:

Photometric calibration in the J-, H-, and $K_{\rm S}$-bands for the G61.48+0.09 field. Left panels show the photometric calibration from instrumental (INSTR) to the calibrated magnitudes (2MASS). Central panels show the difference between the calibrated photometry and the 2MASS photometry. Right panels show the PSF fitting $\sigma $ parameter provided by ALLFRAME.
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.