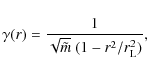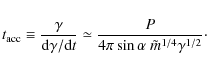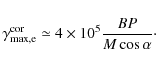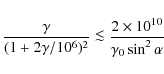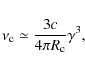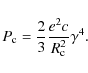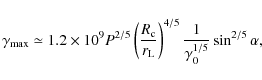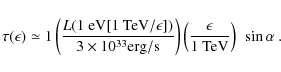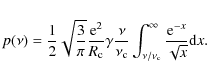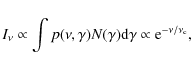| Issue |
A&A
Volume 502, Number 1, July IV 2009
|
|
|---|---|---|
| Page(s) | 15 - 20 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200912101 | |
| Published online | 27 May 2009 | |
On particle acceleration and very high energy
 -ray emission in Crab-like pulsars
-ray emission in Crab-like pulsars
Z. Osmanov1 - F. M. Rieger2,3
1 - E. Kharadze Georgian National Astrophysical Observatory, Ilia Chavchavadze State University,
Kazbegi str. 2a, 0106 Tbilisi, Georgia
2 - Max-Planck-Institut für Kernphysik,
Saupfercheckweg 1, 69117 Heidelberg, Germany
3 - European Associated Laboratory for Gamma-Ray Astronomy,
jointly supported by CNRS and MPG, Germany
Received 18 March 2009 / Accepted 18 May 2009
Abstract
Context. The origin of very energetic charged particles and the production of very high-energy (VHE) gamma-ray emission remains still a challenging issue in modern pulsar physics.
Aims. By applying a toy model, we explore the acceleration of co-rotating charged particles close to the light surface in a plasma-rich pulsar magnetosphere and study their interactions with magnetic and photon fields under conditions appropriate for Crab-type pulsars.
Methods. Centrifugal acceleration of particles in a monopol-like magnetic field geometry is analyzed and the efficiency constraints, imposed by corotation, inverse Compton interactions and curvature radiation reaction are determined. We derive expressions for the maximum particle energy and provide estimates for the corresponding high-energy curvature and inverse Compton power outputs.
Results. It is shown that for Crab-like pulsars, electron Lorentz factor up to
![]() can be achieved, allowing inverse Compton (Klein-Nishina) up-scattering of thermal photons to TeV energies with a maximum luminosity output of
can be achieved, allowing inverse Compton (Klein-Nishina) up-scattering of thermal photons to TeV energies with a maximum luminosity output of ![]() 1031 erg/s. Curvature radiation, on the other hand, will result in a strong GeV emission output of up to
1031 erg/s. Curvature radiation, on the other hand, will result in a strong GeV emission output of up to ![]() (1034-1035) erg/s, quasi-exponentially decreasing towards higher energies for photon energies below
(1034-1035) erg/s, quasi-exponentially decreasing towards higher energies for photon energies below ![]() 50 GeV.
50 GeV.
Conclusions. Accordingly to the results presented only young pulsars are expected to be sites of detectable VHE ![]() -ray emission.
-ray emission.
Key words: stars: pulsars: general - acceleration of particles - radiation mechanisms: non-thermal
1 Introduction
One of the fundamental problems in pulsar physics is related to the
origin of the observed non-thermal emission. While it seems evident
that efficient particle acceleration and emission processes must be
operating in a pulsar's rotating magnetosphere, current theoretical
approaches differ widely in their assumptions about the localization
of the relevant zones: According to standard polar cap models, for
example, charged particles are uprooted from the neutron star's
surface by strong electrostatic fields (Ruderman & Sutherland 1975). Still close to
the star, these particles are then assumed to be efficiently
accelerated along open field lines in parallel electric fields
induced by space-charge-limited flow (Michel 1991), field-line
curvature (Arons 1983) and/or inertial frame dragging effects
(Muslimov & Tsygan 1992). In most cases, the parallel electric field component
is shorted out at some altitude by the onset of electron-positron
pair cascades in strong magnetic fields (one-photon pair
production), either initiated by curvature (Daugherty & Harding 1982) or Inverse
Compton radiation (Dermer & Sturner 1994). Outer gap models, on the other hand,
assume that primary particles are efficiently accelerated in vacuum
gaps in the outer magnetosphere, inducing pair cascades through
![]() -pair production (Cheng et al. 1986; Chiang & Romani 1994; Hirotani 2007). In
all these approaches the maximum attainable particle energy is
either limited by the gap size or radiation reaction. In
conventional polar cap models, for example, a critical issue has
always been the question whether particles can indeed gain enough
energy inside the gap to account for the observed non-thermal
radiation from
-pair production (Cheng et al. 1986; Chiang & Romani 1994; Hirotani 2007). In
all these approaches the maximum attainable particle energy is
either limited by the gap size or radiation reaction. In
conventional polar cap models, for example, a critical issue has
always been the question whether particles can indeed gain enough
energy inside the gap to account for the observed non-thermal
radiation from ![]() -ray pulsars. Several scenarios have been
proposed to enlarge the gap zone and consequently increase the
corresponding energy output (e.g., Usov & Shabad 1985; Arons & Scharlemann 1979; Muslimov & Tsygan 1992), yet
-ray pulsars. Several scenarios have been
proposed to enlarge the gap zone and consequently increase the
corresponding energy output (e.g., Usov & Shabad 1985; Arons & Scharlemann 1979; Muslimov & Tsygan 1992), yet
![]() -ray emission from Crab-like pulsars still proves
challenging to account for. The efficiency of particle acceleration
along magnetic field lines has also been studied more recently based
on numerical solutions of the structure of a stationary,
axisymmetric and force-free magnetosphere of an aligned pulsar
(Contopoulos et al. 1999). According to the results obtained, the relativistic
magnetospheric outflow is not accelerated efficiently enough to
account for the production of high energy gamma-rays. In some
respects, this result may not come unexpected as the magnetic field
configuration is restricted to be force-free, thus preventing
efficient acceleration. In a rather different approach, Beskin & Rafikov (2000)
analyzed the acceleration of a (stationary) two-component,
electron-positron outflow in a monopole magnetic field configuration
for high (Michel) magnetization parameters
-ray emission from Crab-like pulsars still proves
challenging to account for. The efficiency of particle acceleration
along magnetic field lines has also been studied more recently based
on numerical solutions of the structure of a stationary,
axisymmetric and force-free magnetosphere of an aligned pulsar
(Contopoulos et al. 1999). According to the results obtained, the relativistic
magnetospheric outflow is not accelerated efficiently enough to
account for the production of high energy gamma-rays. In some
respects, this result may not come unexpected as the magnetic field
configuration is restricted to be force-free, thus preventing
efficient acceleration. In a rather different approach, Beskin & Rafikov (2000)
analyzed the acceleration of a (stationary) two-component,
electron-positron outflow in a monopole magnetic field configuration
for high (Michel) magnetization parameters
![]() ,
indicating the ability of the field to sling particles to
high velocities. Here,
,
indicating the ability of the field to sling particles to
high velocities. Here, ![]() is the electron density, B the
induction of the magnetic field, c is the speed of light and
e and
is the electron density, B the
induction of the magnetic field, c is the speed of light and
e and ![]() are electron's charge and the rest mass respectively.
Considering plasma dynamics close to the force-free regime
(first-order correction), they showed that for small longitudinal
currents very high Lorentz factors can be achieved, with almost all
of the electromagnetic energy being converted into the kinetic
energy of particles (
are electron's charge and the rest mass respectively.
Considering plasma dynamics close to the force-free regime
(first-order correction), they showed that for small longitudinal
currents very high Lorentz factors can be achieved, with almost all
of the electromagnetic energy being converted into the kinetic
energy of particles (
![]() )
in a thin layer
close to the light cylinder surface.
)
in a thin layer
close to the light cylinder surface.
In the present contribution we consider another acceleration mechanism that may help to overcome the energy problem arising in some polar cap-type models. To this end, we explore the acceleration of co-rotating charged particles in an idealized monopole-like magnetic field region close to the light surface where the parallel electric field component is effectively screened out, but where inertial (centrifugal) effects become important in describing the plasma dynamics. This follows earlier suggestions by Gold (1968; 1969) about efficient particle acceleration close the light cylinder in a co-rotating neutron star magnetosphere (see also Ruderman 1972). A detailed analysis of centrifugal acceleration along rotating straight field lines in the test particle limit has been presented by Machabeli & Rogava (1994), showing that due to the relativistic mass increment the radial acceleration of a particle changes sign, similar to results obtained for particle motion close to a Schwarzschild black hole (Abramowicz & Prasanna 1990). Based on this, the plasma motion in pulsar magnetospheres has been analyzed and equations describing the behavior of a co-rotating plasma stream have been derived (e.g., Chedia et al. 1996; Machabeli et al. 2005). More recently, the generalization to curved field lines (e.g., Archimedes spiral, where a particle may asymptotically reach the force-free regime) has been examined and the consequences of radiation reaction analyzed (Rogava et al. 2003; Dalakishvili et al. 2007). Independently, applications of centrifugal particle acceleration to milli-second pulsars were considered and curvature radiation effects discussed in Gangadhara (1996) (see also Thomas & Gangadhara 2007, for a recent generalization). In a wider context, the efficiency of centrifugal particle acceleration was studied for Active Galactic Nuclei (AGN) (Gangadhara & Lesch 1997; Rieger & Mannheim 2000; Osmanov et al. 2007), based on scenarios where AGN jets originate as centrifugally-driven outflows (Blandford & Payne 1982).
In the present paper, we analyze the efficiency of centrifugal acceleration for Crab-like pulsars, taking constraints imposed by co-rotation, inverse Compton interactions and curvature radiation into account. The paper is arranged as follows: In Sect. 2 the radial particle motion due to centrifugal acceleration effects is described and co-rotation constraints discussed. In Sect. 3 we examine possible radiative feedbacks on the process of acceleration for typical millisecond pulsars, considering some major limiting processes: inverse Compton scattering, curvature radiation and pair creation. In Sect. 4 the relevance of our results is shortly discussed in the context of recent observational evidence.
2 Centrifugal acceleration of particles
2.1 A simplified approach
We consider an idealized, single-particle approach, where in the local frame of reference, each particle is only subject to the action of the centrifugal force and gains energy while moving outward along the magnetic field. The field configuration is supposed to be almost straight, at least inside the co-rotation zone. This seems a reasonable assumption to make as efficient particle acceleration is expected to take place on characteristic length scales much smaller than the light cylinder radius. When applied to open field lines, our results are thus not expected to be very sensitive to further magnetospheric details. Ifand its Lorentz factor can be expressed as
where
Obviously, for a particle approaching the light surface, the acceleration timescale decreases with
2.2 Co-rotation constraints
Suppose that the co-rotation zone extends outwards from the neutron
star up to the vicinity of the the light surface (Gold 1968, 1969). Because
of strong synchrotron losses, electrons will quickly lose their relativistic
perpendicular energy, i.e. on a timescale which for most pitch angles ![]() is much smaller than the transit time
is much smaller than the transit time
![]() to
their ground Landau state, so that they may be approximately described as
moving one-dimensionally along the field lines. Yet, even if one neglects
radiation reaction (e.g., curvature losses, see below) co-rotation will only
be possible as long as the kinetic energy density of the electrons
to
their ground Landau state, so that they may be approximately described as
moving one-dimensionally along the field lines. Yet, even if one neglects
radiation reaction (e.g., curvature losses, see below) co-rotation will only
be possible as long as the kinetic energy density of the electrons
![]() does not exceed the energy density in the field
does not exceed the energy density in the field ![]() (Alfvén corotation condition). For a number density
(Alfvén corotation condition). For a number density
![]() ,
where M denotes the multiplicity (number of secondaries to number of
primaries) and
,
where M denotes the multiplicity (number of secondaries to number of
primaries) and
![]() [particles cm-3] the classical Goldreich-Julian number
density close to the star, the co-rotation condition implies an upper
limit for achievable electron Lorentz factors of
[particles cm-3] the classical Goldreich-Julian number
density close to the star, the co-rotation condition implies an upper
limit for achievable electron Lorentz factors of
For a Crab-type pulsar with
The onset of a pair production front in polar cap models, close to the neutron star, is usually expected to result in a multiplicity
3 Emission constraints
In realistic astrophysical environments, radiation reaction will impose
additional constraints on the efficiency of any particle acceleration process.
For pulsars, important limitations could arise through inverse Compton
scattering with ambient soft photons field or synchro-curvature losses
along curved particle trajectories. Pair production (i.e., one-photon or
photon-photon) on the other hand, could possibly lead to a suppression
of detectable high energy ![]() -rays.
-rays.
3.1 Inverse compton interactions
Thermal radiation as well as synchrotron radiation by secondary electrons could in principle lead to a non-negligible target photon field for Inverse Compton (IC) interactions and thereby limit achievable electron energies.
3.1.1 Inverse Compton with thermal photons
It has often been assumed that IC interactions with thermal photons
from the neutron star surface are generally negligible far away from
the surface because (i) the photon density decreases with distance
r; and (ii) charges and photon are traveling in almost the same
direction, so that (anisotropic) inverse Compton losses become
exceedingly small (e.g., Morini 1981). While the first consideration
is certainly true, the latter may not necessarily be the case. In
fact, if electrons are co-rotating with the plasma, their main
velocity component close to the light cylinder is expected to be in
the azimuthal direction, implying a preferred interaction angle of
almost 90 degree, so that IC interactions with thermal photon field
may possibly become relevant for milli-second pulsars. Although
pulsars are born at very high temperatures
![]() K, their
surface temperatures quickly cool down to
K, their
surface temperatures quickly cool down to ![]()
![]() K by
various neutrino emission processes and thermal emission of photons
(e.g., Tsuruta et al. 2002; Yakovlev & Pethick 2004). Standard (modified UCRA, plasma
neutrino and photon cooling) models predict a surface temperature
above 106 K for pulsars with ages
K by
various neutrino emission processes and thermal emission of photons
(e.g., Tsuruta et al. 2002; Yakovlev & Pethick 2004). Standard (modified UCRA, plasma
neutrino and photon cooling) models predict a surface temperature
above 106 K for pulsars with ages
![]() yr (neutrino cooling stage), and below 105 K for pulsars
exceeding 106.7 yr (photon cooling stage). Using the standard
cooling curve, one can employ an approximate phenomenological
description for the temperature-age dependence given by
(Zhang & Harding 2000)
yr (neutrino cooling stage), and below 105 K for pulsars
exceeding 106.7 yr (photon cooling stage). Using the standard
cooling curve, one can employ an approximate phenomenological
description for the temperature-age dependence given by
(Zhang & Harding 2000)
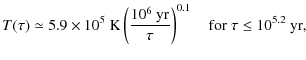 |
(6) | ||
 |
(7) |
Hence, for a Crab-type pulsar (
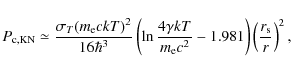 |
(8) |
where
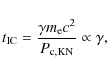 |
(9) |
which to first order is proportional to
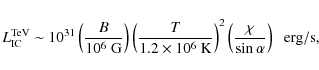 |
(10) |
where
3.1.2 Inverse Compton with infrared photons
Secondary synchrotron emission could possibly lead to a non-negligible
photon field in the infrared-optical regime where IC interactions may occur
in the Thomson regime. For the Crab pulsar, the (isotropic, phase-averaged)
near infrared-optical luminosity is of order
![]() erg/s,
turning significantly downward for lower frequencies (e.g., Middleditch et al. 1983;
Eikenberry et al. 1997; Sollerman 2003). This suggests a photon energy density close to the
light surface of order
erg/s,
turning significantly downward for lower frequencies (e.g., Middleditch et al. 1983;
Eikenberry et al. 1997; Sollerman 2003). This suggests a photon energy density close to the
light surface of order
![]() erg/cm3, comparable to the thermal one. Approximating
the single particle (non-resonant, quasi-isotropic) Compton power by
erg/cm3, comparable to the thermal one. Approximating
the single particle (non-resonant, quasi-isotropic) Compton power by
![]() ,
where
,
where
![]() ,
the characteristic IC cooling timescale
close to
,
the characteristic IC cooling timescale
close to ![]() then becomes
then becomes
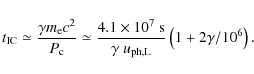 |
(11) |
Comparing acceleration, occurring on
and verifies that IC interactions with the infrared-optical photon field will not impose a severe constraint on the maximum achievable Lorentz factor. IC up-scattering by electrons with
3.2 Curvature radiation
Approaching the light surface, field line bending may no longer be
negligible so that a particle may efficiently lose energy due to curvature
radiation. In analogy to synchrotron radiation, curvature radiation can
be described as emission from relativistic charged particles moving
around the arc of a circle, chosen such that the actual acceleration
corresponds to the centripetal one (e.g., Ochelkov & Usov 1980). The critical
frequency where most of the radiation is emitted is given by
which for, e.g.,
The characteristic cooling timescale
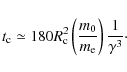 |
(15) |
To find the maximum electron Lorentz factor attainable in the presence of curvature radiation, we can again balance
indicating that for a Crab-type pulsar (P=0.033 s,
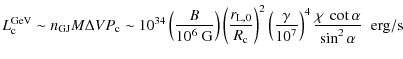 |
(17) |
using
3.3 Pair creation and
 -absorption
-absorption
In the magnetosphere of a pulsar, pair creation via magnetic photon
absorption (
| (18) |
For a Crab-type pulsar (
Apart from one-photon pair production, energetic photons may also
undergo photon-photon interactions (
![]() )
with background soft photons of energy
)
with background soft photons of energy
![]() (e.g., Chiang & Romani 1994).
Let us thus consider the following cases:
(e.g., Chiang & Romani 1994).
Let us thus consider the following cases:
(1) In the case of TeV photons, the threshold condition requires the
presence of soft photons with energies
![]() eV or larger. The
cross-section for
eV or larger. The
cross-section for
![]() -pair production has a sharp
maximum of
-pair production has a sharp
maximum of ![]()
![]() at
at
![]() ,
so that the optical
depth can be approximated by
,
so that the optical
depth can be approximated by
![]() where
where
![]() is the corresponding luminosity at which the peak occurs and
is the corresponding luminosity at which the peak occurs and
![]() the path length. For a characteristic (observed
pulsed Crab) photon field of
the path length. For a characteristic (observed
pulsed Crab) photon field of
![]() erg/s (e.g., Eikenberry et al. 1997; Sollerman 2003) this
would result in
erg/s (e.g., Eikenberry et al. 1997; Sollerman 2003) this
would result in
noting that
(2) The situation could be somewhat different for the GeV curvature photons. In this case
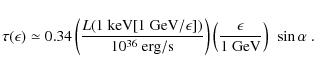 |
(20) |
To first order, the soft X-ray flux of the Crab follows
4 Conclusions
Based on our idealized model analysis above, the efficiency of particle acceleration close to the light surface is essentially limited by curvature radiation reaction or the Alfvén corotation condition.
We have studied the implications for conditions applicable to
Crab-type pulsars, assuming a plasma-rich environment with pair
density exceeding the primary Goldreich-Julian (close to the star)
one by
![]() .
In this case, electron Lorentz factors up to
.
In this case, electron Lorentz factors up to
![]() appear possible. Synchro-curvature
radiation could then lead to a relatively strong (averaged) power
output of
appear possible. Synchro-curvature
radiation could then lead to a relatively strong (averaged) power
output of ![]() (1034-1035) erg/s at
(1034-1035) erg/s at ![]() 2 GeV that would
be consistent with, e.g., EGRET observations of the Crab
(Kuiper et al. 2001). The emissivity of curvature radiation can be
described by
2 GeV that would
be consistent with, e.g., EGRET observations of the Crab
(Kuiper et al. 2001). The emissivity of curvature radiation can be
described by
For a power law-type distribution of particles, for example,
so that in the case of the Crab the curvature output might be expected to decay quasi-exponentially for energies above
For older pulsars (e.g., ![]() s) and
s) and ![]() ,
co-rotation usually
imposes the strongest constraint, so that achievable maximum Lorentz
factors are typically limited to
,
co-rotation usually
imposes the strongest constraint, so that achievable maximum Lorentz
factors are typically limited to ![]() (104-105). Although curvature
radiation may then peak in the optical-UV (up to
(104-105). Although curvature
radiation may then peak in the optical-UV (up to ![]() 10 eV) and
inverse Compton (Thomson) scattering of curvature or thermal photons
could result in very high energy emission up to
10 eV) and
inverse Compton (Thomson) scattering of curvature or thermal photons
could result in very high energy emission up to ![]() 50 GeV, their
associated power is negligible due to the small electron Lorentz factors
and the substantially reduced target photon energy density. Hence,
within the approach considered only young pulsars (
50 GeV, their
associated power is negligible due to the small electron Lorentz factors
and the substantially reduced target photon energy density. Hence,
within the approach considered only young pulsars (![]() s)
might be expected to produce detectable high energy gamma-ray
emission.
s)
might be expected to produce detectable high energy gamma-ray
emission.
The proposed scenario could in principle work for a variety of angles, so that the resultant emission needs not necessarily to be strongly pulsed. Note that for most circumstances, the major condition limiting the Lorentz factors of electrons results from co-rotation. Yet, for large inclination angles, curvature radiation reaction can become dominant over co-rotation, cf. Eqs. (4) and (16) and see Fig. 1 for illustration.
The analysis presented is based on a number of idealizations, which we plan to remedy in future studies. This particularly involves the assumptions of, e.g., quasi-straight field lines and a single particle approach in which plasma effects are neglected. On the other hand, one of the strengths of the present concept is its ability to explicitly take inertial effects into account and so to allow to estimate the size and extent of the VHE regions in young pulsars.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{fig1.eps}}
\end{figure}](/articles/aa/full_html/2009/28/aa12101-09/Timg146.png) |
Figure 1:
Maximum Lorentz factors versus the inclination angle:
|
| Open with DEXTER | |
Acknowledgements
Discussions with Felix Aharonian, George Machabeli and Vasily Beskin are gratefully acknowledged. Z.O. acknowledges the hospitality of the Max-Plank Institute for Nuclear Physics (Heidelberg, Germany) during his short term visits. The study of Z.O. was partially supported by the Georgian National Science Foundation grant GNSF/ST06/4-096.
References
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS Collaboration) 2007, A&A, 466, 543 (In the text)
- Abramowicz, M. A., & Prasanna, A. R. 1990, MNRAS, 245, 729 [NASA ADS] (In the text)
- Albert J., Aliu, E., Anderhub, H., et al. (MAGIC Collaboration) 2008, ApJ, 674, 1037 (In the text)
- Aliu, E., et al. (MAGIC Collaboration) 2008, Science, 322, 1224 (In the text)
- Arons, J. 1983, ApJ 266, 215 (In the text)
- Arons, J., & Scharlemann, E. T. 1979, ApJ, 231, 854 [NASA ADS] [CrossRef] (In the text)
- Beskin, V. S., Gurevich, A. V., & Istomin, Ya. N. 1983, Sov. Phys. JETP, 58, 235
- Beskin, V. S., & Rafikov, R. R. 2000, MNRAS, 313, 433 [NASA ADS] [CrossRef] (In the text)
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 (In the text)
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] (In the text)
- Cheng, K. S., Ho, C., & Ruderman, M. A. 1986, ApJ, 300, 500 [NASA ADS] [CrossRef] (In the text)
- Chedia, O. V., Kahniashvili, T. A., Machabeli, G. Z., & Nanobashvili, I. S. 1996, Ap&SS, 239, 57 [NASA ADS] [CrossRef] (In the text)
- Chiang, J., & Romani, R. W. 1994, ApJ, 436, 754 [NASA ADS] [CrossRef] (In the text)
- Contopoulos, I., Kazanas, D., & Fendt, C. 1999, ApJ, 511, 351 [NASA ADS] [CrossRef] (In the text)
- Crusius-Wätzel, A. R., Kunzl, T., Lesch, H., et al. 2001, ApJ, 546, 401 [NASA ADS] [CrossRef] (In the text)
- Dalakishvili, G. T., Rogava, A. D., & Berezhiani, V. I. 2007, Phys. Rev. D, 76, 045003 [NASA ADS] [CrossRef] (In the text)
- Daugherty, J. K., & Harding, A. K. 1982, ApJ, 252, 337 [NASA ADS] [CrossRef] (In the text)
- Daugherty, J. K., & Harding, A. K. 1983, ApJ 273, 761 (In the text)
- Dermer, C. D., & Sturner, S. J. 1994, ApJ, 420, L75 [NASA ADS] [CrossRef] (In the text)
- Eikenberry, S. S., Fazio, G. G., Ransom, S. M., et al. 1997, ApJ 477, 465 (In the text)
- Erber, T. 1966, Rev. Mod. Phys., 38, 626 [NASA ADS] [CrossRef] (In the text)
- Gangadhara, R. T. 1996, A&A, 314, 853 [NASA ADS] (In the text)
- Gangadhara, R. T., & Lesch, H. 1997, A&A, 323, L45 [NASA ADS] (In the text)
- Gold, T. 1968, Nature, 218, 731 [NASA ADS] [CrossRef] (In the text)
- Gold, T. 1969, Nature, 221, 25 [NASA ADS] [CrossRef] (In the text)
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef]
- Hirotani, K. 2007, ApJ 662, 1173 (In the text)
- Kuiper, L., Hermsen, W., Cusumano, G., et al. 2001, A&A, 378, 918 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lessard, R. W., Bond, I. H., Bradbury, S. M., et al. (Whipple Collaboration) 2000, ApJ, 531, 942 (In the text)
- Lyne, A. G., & Graham-Smith, F. 2006, Pulsar Astronomy (3rd ed.) (Cambridge Univ. Press)
- Machabeli, G. Z., & Rogava, A. D. 1994, Phys. Rev. A, 50, 98 [NASA ADS] [CrossRef] (In the text)
- Machabeli, G. Z., Osmanov, Z. N., & Mahajan, S. M. 2005, Physics of Plasmas 12, 062901 (In the text)
- Massaro, E., Cusumano, G., Litterio, M., & Mineo, T. 2000, A&A, 361, 695 [NASA ADS] (In the text)
- Massaro, E., Campana, R., Cusumano, G., Mineo, T., et al. 2006, A&A, 459, 859 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Melrose, D. B. 1998, Proc. of APPTC'97 (Toki, Japan), ed. Y. Tomita, et al., 96 (In the text)
- Michel, F. C. 1991, Theory of Neutron Star Magnetospheres (Univ. of Chicago Press) (In the text)
- Middleditch, J., Pennypacker, C., & Burns, M. S. 1983, ApJ, 273, 261 [NASA ADS] [CrossRef] (In the text)
- Morini, M. 1981, Ap&SS, 79, 203 [NASA ADS] [CrossRef] (In the text)
- Muslimov, A. G., & Tsygan, A. I. 1992, MNRAS, 255, 61 [NASA ADS] (In the text)
- Ochelkov, Yu. P., & Usov, V. V. 1980, Ap&SS, 69, 439 [NASA ADS] [CrossRef] (In the text)
- Osmanov, Z., Rogava, A. S., & Bodo, G. 2007, A&A, 470, 395 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pacini, F., & Salvat, M. 1983, ApJ, 274, 369 [NASA ADS] [CrossRef] (In the text)
- Possenti, A., Cerutti, R., Colpi, M., & Mereghetti, S. 2002, A&A, 387, 993 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rieger, F. M., & Mannheim, K. 2000, A&A, 353, 473 [NASA ADS] (In the text)
- Rogava, A. D., Dalakishvili, G., & Osmanov, Z. 2003, Gen. Rel. and Grav., 35, 1133 [NASA ADS] [CrossRef] (In the text)
- Ruderman, A., & Sutherland, P. G. 1975, ApJ, 196, 51 [NASA ADS] [CrossRef] (In the text)
- Ruderman, M. 1972, ARA&A 10, 427 (In the text)
- Shearer, A., & Golden, A. 2001, ApJ, 547, 967 [NASA ADS] [CrossRef] (In the text)
- Sollerman, J. 2003, A&A, 406, 639 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tsai, W.-Y., & Erber, T. 1974, Phys. Rev. D, 10, 492 [NASA ADS] [CrossRef] (In the text)
- Thomas, R. M. C., & Gangadhara, R. T. 2007, A&A, 467, 911 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tsuruta, S., Teter, M. A., Takatsuka, T., Tatsumi, T., & Tamagaki, R. 2002, ApJ, 571, L143 [NASA ADS] [CrossRef] (In the text)
- Usov, V. V., & Shabad, A. 1985, Ap&SS, 117, 309 [NASA ADS] [CrossRef] (In the text)
- Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] (In the text)
- Zhang, B., & Harding, A. K. 2000, ApJ, 532, 1150 [NASA ADS] [CrossRef] (In the text)
All Figures
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[angle=0]{fig1.eps}}
\end{figure}](/articles/aa/full_html/2009/28/aa12101-09/Timg146.png) |
Figure 1:
Maximum Lorentz factors versus the inclination angle:
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}
\frac{{\rm d}^2r}{{\rm d}t^2}=\frac{\Omega_{\rm e}^2r}{1-\Om...
...\rm e}^2r^2-2
\left(\frac{{\rm d}r}{{\rm d}t}\right)^2\right],
\end{displaymath}](/articles/aa/full_html/2009/28/aa12101-09/img20.png)