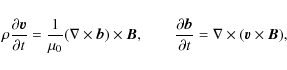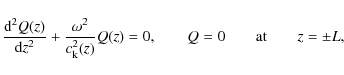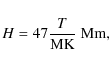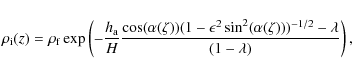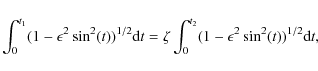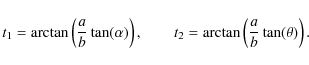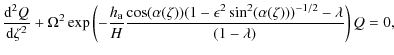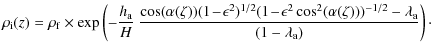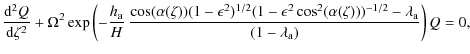EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 502 / No 1 (July IV 2009) A&A, 502 1 (2009) 315-323 Full HTML
Free Access
Issue
A&A
Volume 502, Number 1, July IV 2009
Page(s) 315 - 323
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200811405
Published online 16 April 2009

The effect of elliptic shape on the period ratio P1/P2 of emerging coronal loops

R. J. Morton - R. Erdélyi

Solar Physics and Space Plasma Research Centre (SP2RC), University of Sheffield, Hicks Building, Hounsfield Road, Sheffield S3 7RH, UK

Received 24 November 2008 / Accepted 28 March 2009

Abstract
Aims. We determine the effect of an elliptical shape on the period ratio for the standing transversal oscillations of a longitudinally stratified coronal loop throughout its emergence from the low solar atmosphere into the ubiquitously magnetised corona.
Methods. Under the assumption that elliptical curvature has a negligible effect on eigenfrequencies, the equation that describes the projection of a density profile onto a magnetic flux tube with elliptical shape is obtained in a gravitationally stratified atmosphere. The effect of the elliptical shape on the period ratio of the fundamental mode to the first harmonic ( P1/P2) at various stages of emergence is determined, assuming that the oscillation periods are much shorter than the characteristic time scale of loop emergence.
Results. We find that there are two separate cases of elliptical shape that occur, the minor ellipse and the major ellipse. It is then shown how the period ratio  P1/P2 is dependent upon the ellipticity ($\epsilon $), the parameter characterising the stage of emergence ($\lambda $) and the density scale height (H). Ellipticity is found to make an important contribution to  P1/P2 for the minor ellipse when compared to its counterpart of standing oscillations of stratified loops with semi-circle or circle-arc shape. The major ellipse was found to have a lesser effect on the period ratio of standing oscillations. We also find the value of  P1/P2 is dependent upon the stage of emergence of the loop, where the greatest contribution from emergence to the ratio of  P1/P2 is when the loop is almost fully emerged. The important implication for magneto-seismological interpretations of the observations of oscillating coronal loops is that measurements of ellipticity and stage of emergence should supplement observations of oscillation periods and should be considered when applying observed frequencies of the fundamental mode and first harmonic to determine the diagnostic properties of these oscillating loops, e.g. the density scale height or strength of magnetic field. Neglecting the determination of ellipticity and stage of emergence may result in a $35\%$ error in estimating density scale height.

Key words: magnetohydrodynamics (MHD) - plasmas - Sun: corona - waves

1 Introduction

In recent years it has been possible to study the plasma fine structure of the complex and dynamic magnetised solar atmosphere due to the relatively high-resolution imaging and spectroscopic data obtained from the Solar and Heliospheric Observatory (SOHO), the Transitional Region and Coronal Explorer (TRACE) and Hinode. Various magnetohydrodynamic (MHD) waves (e.g. longitudinal, transverse) have been observed and identified within a variety of open (e.g. sunspots, pores, plumes) and closed (e.g. prominences, coronal loops) magnetic structures (see Banerjee et al. 2007; Nakariakov & Verwichte 2005 for the latest reviews of observational results with plenty of further references therein). The study of these magnetic oscillations, in order to derive information on the diagnostic properties of the plasma, is known as solar magneto-seismology and the methodology was first suggested by Uchida (1970) and Roberts et al. (1984) who initially used the term of coronal seismology for specific coronal applications. The field has rapidly developed and the method of magneto-seismology is now an integral acquisition tool for developing our understanding of the large range of dynamical events that are detected in the solar atmosphere, often with applications to the problem of coronal heating (Erdélyi 2006a,2008,2006b; Taroyan 2008).

 \begin{figure} \par\mbox{\subfigure[Elliptically curved magnetic flux tube]{\inc... ...tube]{\includegraphics[width=2.7in, height=1.5in]{1405fig2.eps} }}\end{figure} Figure 1:

a) Sketch showing the equilibrium state of an elliptically curved, magnetic flux tube with plasma density  $\rho _{\rm i}(z')$, magnetic field of strength  $\vec{B}_{\rm i}$ embedded in plasma with density  $\rho _{\rm e}(z')$ of strength  $\vec{B}_{\rm e}$. b) Sketch showing the equilibrium state of a straight, cylindrical magnetic flux tube onto which the elliptical density profile is projected. The straight cylinder has radius R, length 2L, plasma density  $\rho _{\rm i}(z)$, magnetic field of strength  $\vec{B}_{\rm i}$ and is embedded in a plasma with density  $\rho _{\rm e}(z)$ of strength  $\vec{B}_{\rm e}$.
Open with DEXTER

Measured properties of the MHD oscillations (such as period, spatial distribution of velocity and/or amplitudes, damping rate) may be inverted to retrieve information about otherwise unmeasurable or hardly measurable solar atmospheric parameters (e.g. gravitational or magnetic stratification, structuring, loop expansion, cross-sectional shape, loop geometry, wave leakage, magnetic twist, loop curvature). The basic theoretical model of oscillations in coronal loops, put forward in a seminal paper by Edwin & Roberts (1983), was an ideal and linear MHD theory of a straight and homogenous cylindrical magnetic flux tube. However, SOHO, TRACE and Hinode observations clearly show that the properties of oscillations of various solar magnetic loops can be significantly different from those predicted by the homogenous cylindrical tube model. The source of these differences is thought to be due to various geometric and physical (often second-order) effects, as listed above (e.g. stratification, expansion, structuring, shape, wave leakage, variable background on the time scale of oscillations, cross section geometry, etc. to name a few).

It is clear there are a number of effects to be considered when interpreting solar flux tube wave or oscillation observations using the tools of magneto-seismology. However, there are at least two key measurable quantities that one can use for the magneto-seismology theory: period (or frequency) ratio  P1/P2 of the fundamental mode to the first harmonic of oscillations (i.e. temporal seismology) and amplitude distribution of oscillations along the flux tube (i.e. spatio-seismology). For a review on magneto-seismology of kink oscillations see Ruderman & Erdélyi (2009).

Erdélyi & Verth (2007); Verth et al. (2007) found that the spatial position along the loop of the maximum amplitude of the first harmonic of the standing fast kink mode varies when the loop is stratified (referred to as anti-node shift). The predicted anti-node shifts calculated in Verth et al. (2007), are between 600 to 6000 km depending on the density profile used. At present there has been no observation yet of the anti-node shift due to the low spatial resolution of current observational instruments.

The period ratio was first measured by Verwichte et al. (2004), who observed two values in different loops, P1/P2=1.81 $\pm$ 0.25 and 1.64 $\pm$ 0.23. These values are in contrast to the theoretically derived value for the period ratio using the uniform tube model, where  $P_{1}/P_{2}\equiv2$. The systematic deviation between the theoretical and observed values is a serious inspiration to refine modelling efforts, just like such ``discrepancies'' were the driving impetus for helioseismology (see, e.g. Erdélyi 2006a,b). Andries et al. (2005a,b) and Goossens et al. (2006) suggested that the ratio of the periods of the fundamental mode to the first harmonic, P1/P2, could be used as a tool to determine the density scale height in the corona. For a specific review on the application of the period ratio as a tool for coronal seismology see Andries et al. (2009).

To the best of our knowledge, stratification (Andries et al. 2005b; McEwan et al. 2006) and loop expansion due to a non-constant magnetic field (Verth 2007; Verth & Erdélyi 2008; Ruderman et al. 2008) so far seem to be the main causes of the most dominant deviation between the measured and theoretically predicted periods of oscillations. However, magnetic structuring and gravitational stratification are, in a sense, in competition with each other, since their effect on the period ratio of  P1/P2 is opposite, i.e. the tube expansion parameter discussed by Verth & Erdélyi (2008) increases the period ratio ( P1/P2>2), while the longitudinal stratification causes the period ratio to decrease ( P1/P2<2). This raises the question: what physical effect(s) or perhaps loop properties are then responsible for the deviation of the measured period ratio from those predicted by magneto-seismology? Could the answer be linked to loop geometry, e.g. curvature, shape, cross-section, stage of emergence, etc.?

There have been a number of other investigations into how the different geometries of coronal loops affect MHD oscillations. Dymova & Ruderman (2006) investigated the dependence of  P1/P2 on circular shape loop geometry for a longitudinally stratified loop. This idea was underpinned by the first impression of oscillating coronal loops appearing to have circular shape. They modeled the loop as an arc of a circle with curvature radius  $r_{\rm curv}$ with the center at a distance l from the photosphere. It was found that the shape of the loop, determined by the parameter $\lambda=l/r_{\rm curv}$, had a marked effect on the ratio  P1/P2. They concluded that in order to determine the scale height from the observed values of  P1/P2, a more precise knowledge of the loop shape is needed.

Investigations of elliptical cross-sectional geometry of loops in cold plasma by Ruderman (2003) and in a finite plasma-$\beta$ by Erdélyi & Morton (2009), has shown that magnetic loops can support additional transverse modes compared to the cylindrical model. However, it is shown in Erdélyi & Morton (2009) that the period ratio is practically unaffected by the ellipticity of the loop cross-section. In spite of the high spatial and temporal resolution of the current cohort of instrumentation, this latter theory has yet to be put to the test. We can conclude that curvature and cross-section are less dominant parameters for temporal magneto-seismology in coronal applications, so we shall ignore their geometric properties in what follows.

In this paper we investigate the effect of loop shape on the period ratio  P1/P2 by examining loops which deviate from a circular shape. Here we analyse the standing oscillations of loops with an elliptical shape. Further to this, we also investigate how  P1/P2 is influenced by the different consecutive stages of emergence of an elliptical loop. It is assumed that the characteristic time of emergence is much greater than the period of loop oscillations. This assumption is verified observationally as the loop emergence takes place on day-scale, while transverse oscillations are reported with periods in the sub-hour domain. The projection of an exponential density profile on to a loop with an elliptical shape is calculated and the Sturm-Liouville equation describing a stratified magnetic flux tube (Dymova & Ruderman 2005; Erdélyi & Verth 2007) is solved numerically. The effect on the period ratio  P1/P2 is then calculated for different values of ellipticity at various stages of emergence. The magnitude of the effect of ellipticity is then compared with the circle-arc model (Dymova & Ruderman 2006). Beside the theoretical justification given above, in this particular aspect, recent progress by Aschwanden et al. (2008) in 3D reconstruction of loops using the Solar TErrestrial RElations Observatory (STEREO), has provided new and interesting information on the loop geometry. It was found that the majority of the loops studied were in fact non-circular in shape, with a deviation from circularity up to $30\%$.

2 Modelling of coronal loop geometry

In this paper we consider a thin coronal loop with a circular cross-section which has elliptical shape as shown in Fig. 1a. The effects of circular curvature on the eigenfrequencies of transverse oscillations have been investigated and found to be of the order $\delta^2=(R/2L)^2$, where R is the radius of the loop cross-section and 2L is the loop length (Terradas et al. 2006; Van Doorsselaere et al. 2004. Note, caution should be exercised as there is a flaw in the derivation in Van Doorsselaere et al. 2004). It was noted by Terradas et al. (2006) that one of the main differences between the straight and curved cylindrical magnetic flux tubes was that curvature introduces preferential directions of oscillations. The introduction of a curved shape on the cylindrical tube changes the problem from 1-dimensional to 2-dimensional. For example, two distinct kink modes can occur in a curved loop, polarised along the vertical (z' axis in Fig. 1a) and along the horizontal axis (x' axis in Fig. 1a). The periods of these two kink modes are similar to each other and to the period of the kink mode found in the model of a straight magnetic tube of Edwin & Roberts (1983). Most importantly, in the context of this study, in the thin tube limit ($R \ll 2L$) the difference between these modes is negligible, so a straight tube approximation can be used when studying curved loops. Dymova & Ruderman (2006) applied this ``straightening'' approximation to study the effects of circular shape on the transverse oscillations of longitudinally stratified loops.

A study of oscillations in a magnetic tube with semi-elliptical shape is possible using a variation of the toroidal coordinate system. However, the model appears to have no analytic solution due to the dependence of the equilibrium quantities on all the spatial coordinates. Since Díaz (2006) found that the effects of curvature on oscillations of an elliptically curved magnetic slab are negligible, this may suggest that one would find similar results for a semi-elliptical magnetic tube. In this paper, we progress under the assumption that the effect of elliptical curvature is negligible in the thin tube approximation and leave a study, analytic or numerical, of the semi-elliptical loop till a later date.

Consider a straight magnetic flux tube with a cross-section of radius R and length 2L which is embedded in a magnetic environment (see Fig. 1b). The magnetic field inside and outside the tube is uniform, with the internal (external) magnetic field of the form $\vec{B}_{{\rm i}}=B_{{\rm i}}\hat{\vec{z}}$ ( $\vec{B}_{{\rm e}}=B_{{\rm e}}\hat{\vec{z}}$). Here, $\hat{\vec{z}}$ is the unit vector in the z-direction and we assume $B_{{\rm i}}\approx B_{{\rm e}}$. The plasma inside and outside the tube is an ideal and cold plasma (i.e. $\beta=0$, where $\beta$ is the plasma beta defined by $\beta=2\mu_0p/B^2$). The cold plasma approximation is valid in the corona because the characteristic value of $\beta\sim 0.01$. Linear perturbations about the equilibrium for a cold plasma are described by the linear, ideal MHD equations

\begin{displaymath}% \rho\frac{\partial \vec{v}}{\partial t} = \frac{1}{\mu_{0}}... ...l \vec{b}}{\partial t} = \nabla \times(\vec{v}\times \vec{B}), \end{displaymath} (1)


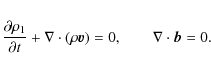
\begin{eqnarray*}\frac{\partial\rho_{1}}{\partial t}+\nabla\cdot(\rho\vec{v})=0,\qquad \nabla\cdot\vec{b}=0. \end{eqnarray*}


Here $\rho$ is the equilibrium density, $\rho_{1}$ is the density perturbation, $\vec{v}$ is the velocity perturbation, $\vec{B}$ is the equilibrium magnetic field, $\vec{b}$ is the perturbation of the magnetic field and $\mu_{0}$ is the magnetic permeability of free space. The densities are considered to be functions of longitudinal coordinates only, where, $\rho=\rho_{\rm i}(z)$ inside the tube and $\rho=\rho_{\rm e}(z)$ outside the tube. We assume that there is uniform stratification, such that $\rho_{\rm e}(z)/\rho_{\rm i}(z)=\chi<1$.

It was shown in Dymova & Ruderman (2005) and Erdélyi & Verth (2007), for the first order approximation with respect to the parameter $\delta=R/2L$ where $R \ll 2L$ (thin tube approximation), that the solutions to Eqs. (1) for the squared frequencies of the kink tube oscillations are the eigenvalues of the Sturm-Liouville problem

\begin{displaymath}% \frac{{\rm d}^2Q(z)}{{\rm d}z^2}+\frac{\omega^2}{c^2_{\rm k}(z)}Q(z)=0, \qquad Q=0 \qquad \mbox{at} \qquad z=\pm L, \end{displaymath} (2)

where

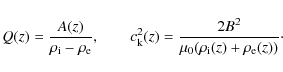\begin{displaymath}% Q(z)=\frac{A(z)}{\rho_{\rm i}-\rho_{\rm e}}, \qquad c^2_{\r... ...(z)=\frac{2B^2}{\mu_{0}(\rho_{\rm i}(z)+\rho_{\rm e}(z))}\cdot \end{displaymath} (3)

Here A(z) is the magnetic pressure perturbation and  $c_{\rm k}(z)$ is the kink speed as function of z. The boundary condition $Q(\pm L)=0$ is valid because footpoints of coronal loops are fixed in the lower solar atmosphere where the densities are orders of magnitude greater than in the corona. This condition is known as line-tying and implies $\vec{v}(\pm L)=0$, then from Eq. (1) one can find the magnetic pressure perturbation, $P=Bb/2\mu_{0}$, at $z\pm L$ is also zero. It then follows that variable Q also satisfies these boundary conditions.

A comment by Dymova & Ruderman (2006), concerning the radial dependence of density, should also be repeated. From equilibrium conditions, it can be shown that the dependence of density perpendicular to the magnetic field can be chosen arbitrarily. However, we need to consider the density variation in the radial direction as a discontinuous jump between definite magnetic surfaces. A continuous density profile would cause the oscillations of the coronal loop to experience resonant damping (see, e.g. Ruderman & Roberts 2002), however this is well beyond the scope of the current study.

3 Elliptically shaped loops with plasma density exponentially decreasing with height

Now consider a coronal loop with a plasma density that is exponentially decreasing with height, i.e.

\begin{displaymath}% \rho(h)=\rho_{\rm f}\exp(-h/H), \end{displaymath} (4)

where $\rho_{\rm f}$ is the density at the loop footpoints, h is the height of an element in the atmosphere measured from the photosphere and H is the density scale height. The stratification profile Eq. (4) can then be projected onto the geometry of a given loop, i.e. the elliptically shaped loop here. However, there are two possible loop geometries when considering an elliptical shape. The first is when the minor axis of the ellipse is in the vertical direction (see Fig. 2). This shall be referred to as the minor elliptical loop. The other possibility is that the major axis of the ellipse is in the vertical direction (see Fig. 7a). This shall be referred to as the major elliptical loop. First, the effect of ellipticity on the ratio  P1/P2 for various values  $h_{\rm a}/H$ shall be discussed for both of these cases, where $h_{\rm a}$ is the height of the loop apex above the photosphere. A discussion of the effect of loop emergence on transverse oscillations will follow.

In order to allow us to make a direct prediction of observables, it is necessary that the values of $h_{\rm a}/H$ used reflect the possible range of values available in the corona. A relationship between temperature and hydrostatic scale height for plasma in hydrostatic equilibrium is given by (e.g. Aschwanden 2004),

\begin{displaymath}% H=47\frac{T}{{\rm MK}} \;{\rm Mm}, \end{displaymath} (5)

where MK = 106 K. For hot coronal loops with $T\approx 2$ $\times$ 106 K, the hydrostatic scale height $H\approx94$ Mm. For a semi-circular loop with a typical length (i.e. 2L=120 Mm) the ratio of $h_{\rm a}/H\sim0.41$. There have also been observations of cool coronal loops (see, e.g. Testa et al. 2002) with temperatures of $T\approx 2$ $\times$ 105 K, giving $H\sim9.4$ Mm and $h_{\rm a}/H\sim4.06$. Therefore, in this paper the typical values of  $h_{\rm a}/H$ will be taken from 0 to 4.

 \begin{figure} \par\includegraphics[width=9cm,clip]{1405fig3.eps} \end{figure} Figure 2:

Sketch showing a partially emerged loop with minor elliptical shape. The geometry of the shape is described by the arc of an ellipse with a minor half-axis of length b and a major half-axis of length a, the height of the loop apex the photosphere $h_{\rm a}$, and the distance of the center of the ellipse below the photosphere $l=b-h_{\rm a}$.
Open with DEXTER

Table 1:   Approximate values of ellipticity derived for the STEREO loops observed by Aschwanden et al. (2008).

 \begin{figure} \par\mbox{\subfigure[Early stage emergence ($\lambda=1/2$ )]{\inc... ...} \subfigure[]{\includegraphics[width=5.8cm,clip]{1405fg4d.eps} }}\end{figure} Figure 3:

a)- c) The ratio of the periods of the fundamental mode to the first harmonic, P1/P2, as a function of density stratification parameter, $h_{\rm a}/H$. The period ratio  P1/P2 is shown for a number of values of ellipticity ($\epsilon $) at various stages of emergence ($\lambda $). The solid line in each plot is the analogous circle-arc case, i.e.  $\epsilon =0$. d) The ratio of the periods of the fundamental mode to the first harmonic, P1/P2, as a function of ellipticity for $\lambda =0$, i.e. the semi-ellipse.
Open with DEXTER

Recent observations using STEREO (Aschwanden et al. 2008), have provided an insight to the extent of the ellipticity of loops in the corona. Seven loops were reconstructed in three-dimensions and a circle, with radius  $r_{\rm fit}$, was fitted through the loop footpoints and the loop top above the midpoint. The maximum ( $R_{{\rm max}}$) and minimum radii ( $R_{{\rm min}}$) of the loops, measured from the center of the fitted circle, were determined (see Table 1 for observed values). The ratio of these radii ( $R_{{\rm max}}, R_{{\rm min}}$) to the radius of the fitted circle was taken to define the circularity of loops, i.e. $C_{{\rm max,min}}=R_{{\rm max,min}}/r_{{\rm fit}}$. The largest value obtained was $\sup{\{C_{{\rm max}}\}=1.30}$ (loop No. 7), a $30\%$ departure from circularity. Although this is not a strict measure of ellipticity, it clearly shows the departure of the loops from the circular shape. Taking e.g. $R_{{\rm max}}=a$ and $R_{{\rm min}}=b$ from loop 7, we obtain a rough estimate for the ellipticity of $\epsilon=0.74$. The other estimated values of ellipticity range between 0.5-0.76 for the loops 1-7 and the values are shown in Table 1. Caution should be taken with these values as the fitting procedure for the circle does not take into account the inclination of the loop apex from the vertical axis. This means  $R_{{\rm max}}$ and  $R_{{\rm min}}$, in some cases, are larger and smaller, respectively, than the actual maximum and minimum radius. The estimate of the ellipticity is then larger than the actual value. Nonetheless, taking these estimates from the observations into account, we conjecture that loops with large ellipticities would probably be rare within the corona. A typical value of ellipticity that is considered here for the minor elliptical loop is $\epsilon=0.6$. For a loop of total length approximately 120 Mm, the length of the minor half-axis would be $b\sim 24$ Mm and major half-axis $a\sim 31$ Mm for this value of ellipticity.

3.1 Minor elliptical loop

Consider a loop with elliptical shape with a given state of emergence as shown in Fig. 2. There are a number of parameters that characterise the problem and should be central in a quantitative description of standing oscillations in the prescribed geometry. One parameter describes the state of emergence of the loop, denoted by

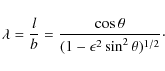\begin{displaymath}% \lambda=\frac{l}{b}=\frac{\cos\theta}{(1-\epsilon^2\sin^2\theta)^{1/2}}\cdot \end{displaymath} (6)

Here l is the distance of the loop center from the photosphere, b is the length of the minor half-axis of the ellipse and $\theta$ is the angle between the minor axis and the line joining the center of the ellipse to the loop foot-point. Positive values of l, hence positive $\lambda $, refer to the center of the elliptical loop sitting below the photosphere (early stage emergence) and negative l (negative $\lambda $) for the center above the photosphere (late stage emergence). A value of l=0 ($\lambda =0$) corresponds to a loop having a semi-elliptical shape. The ellipticity of the loop also needs to be considered, where the ellipticity is defined by

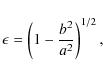\begin{displaymath}% \epsilon=\left(1-\frac{b^2}{a^2}\right)^{1/2}, \end{displaymath} (7)

where a is the length of the major half-axis. A value of $\epsilon =0$ corresponds to a circular shape and $\epsilon=1$ is essentially a straight tube. The last parameter is  $h_{\rm a}/H$.

The projection of the exponential density profile, Eq. (4), on to the minor elliptical loop gives,

\begin{displaymath}% \rho_{\rm i}(z)=\rho_{\rm f}\exp\left(-\frac{h_{\rm a}}{H}\... ...n^2\sin^2(\alpha(\zeta)))^{-1/2}-\lambda}{(1-\lambda)}\right), \end{displaymath} (8)

where $\zeta=z/L$ and $\alpha(\zeta)$ is the angle between the minor axis and a plasma element located at a distance z along the loop (see Fig. 2). The value of the function  $\alpha(\zeta)$ can be found through the computation of the ellipse arc length, i.e. using the equation

\begin{displaymath}% \int^{t_{1}}_{0}(1-\epsilon^2\sin^2(t))^{1/2}{\rm d}t=\zeta\int^{t_{2}}_{0}(1-\epsilon^2\sin^2(t))^{1/2}{\rm d}t, \end{displaymath} (9)

where t1, t2 are parametric angles related to the polar angles $\alpha$ and $\theta$ by

\begin{displaymath}% t_{1}=\arctan\left(\frac{a}{b}\tan(\alpha)\right), \qquad t_{2}=\arctan\left(\frac{a}{b}\tan(\theta)\right). \end{displaymath} (10)

The integrals in Eq. (9) are known as incomplete elliptic integrals of the second kind. It is well known that the elliptic integrals in Eq. (9) cannot be expressed in terms of elementary functions, however, various approximations of the integrals do exist (see, e.g. Kennedy 1954). The substitution of Eqs. (8) in to (2) gives


$\displaystyle \frac{{\rm d}^2Q}{{\rm d}\zeta^2}+ \Omega^2\exp\left(-\frac{h_{\r... ...)) (1-\epsilon^2\sin^2(\alpha(\zeta)))^{-1/2}-\lambda}{(1-\lambda)}\right) Q=0,$     (11)

where $\Omega=\omega L/c_{{\rm kf}}$ and $c_{{\rm kf}}=2B^2/\mu_{0}\rho_{\rm f}(1+\chi)$ is the kink speed at the footpoints. The boundary conditions for Eq. (11) are now Q=0 at $\zeta=\pm 1$. If the ellipticity of the loop is zero, then Eq. (9) reduces to $\alpha=\zeta\theta$ and Eq. (11) reduces to

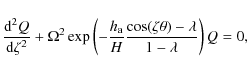\begin{displaymath}% \frac{{\rm d}^2Q}{{\rm d}\zeta^2}+\Omega^2\exp\left(-\frac{... ... a}}{H}\frac{\cos(\zeta\theta)-\lambda}{1-\lambda}\right) Q=0, \end{displaymath} (12)

which is the equation found by Dymova & Ruderman (2006) for the circular loop. Further to this, in the limit $H\rightarrow \infty$ (i.e. uniform loop), then Eq. (11) is reduced to

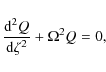\begin{displaymath}% \frac{{\rm d}^2Q}{{\rm d}\zeta^2}+\Omega^2Q=0, \end{displaymath} (13)

which is the equation for a straight magnetic flux tube with a homogenous density profile, the eigenvalue solution to which is

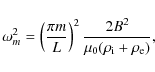\begin{displaymath}% \omega^2_{m}= \left(\frac{\pi m}{L}\right)^2\frac{2B^2}{\mu_{0}(\rho_{\rm i}+\rho_{\rm e})}, \end{displaymath} (14)

where m is the mode number.

 \begin{figure} \par\mbox{\subfigure[$h_{\rm a}/H=1.0$ ]{\includegraphics[width=5... ...rm a}/H=3.0$ ]{\includegraphics[width=5.4cm,clip]{1405fg5c.eps} }}\end{figure} Figure 4:

Showing the value of P1/P2 as a function of the loop shape parameter, $\lambda $, at various values of  $h_{\rm a}/H$ for the elliptically shaped loop.
Open with DEXTER

 \begin{figure} \par\mbox{\subfigure[Early stage emergence ($\lambda=1/2$ )]{\inc... ...ambda=-1/2$ )]{\includegraphics[width=4.9cm,clip]{1405fg6c.eps} }}\end{figure} Figure 5:

Shown is the percentage difference between the values of  P1/P2 when comparing the minor elliptical and the circle-arc geometries for a range of  $h_{\rm a}/H$ at different stages of emergence.
Open with DEXTER

In order to progress in solving Eq. (11), we proceed by solving the equation numerically using the shooting method (see, e.g. Zwillinger 1989). This involves selecting an initial value for $\Omega$ and then solving Eq. (11). $\Omega$ is then adjusted till the boundary conditions are satisfied.

In Figs. 3a-c, the ratio of P1/P2 is plotted against the ratio of the height of the loop apex above the photosphere to the scale height ( $h_{\rm a}/H$). The different panels show the period ratio of a coronal loop at various stages of emergence, where we assume the characteristic time for emergence is much greater than the period of an oscillation within the loop. Figure 3a shows  P1/P2 for a loop at an early stage of emergence ( $\lambda =1/2$), Fig. 3b is a half emerged loop ($\lambda =0$), i.e. the semi-ellipse, and Fig. 3c is a loop at a late stage of emergence ( $\lambda =-1/2$). It is clear from Fig. 3 that the ratio of  P1/P2 for the elliptical loop is dependent upon the level of stratification ( $h_{\rm a}/H$) and ellipticity ($\epsilon $). Although perhaps not immediately obvious, the ratio  P1/P2 is also dependent on the stage of emergence ($\lambda $). The effect of the ellipticity, for small values of  $h_{\rm a}/H$, is to increase the value of  P1/P2 in comparison to the circle arc model. This is due to the loop apex becoming flatter as the ellipticity increases, hence the density along the loop takes on a profile more similar to that of the linear profile suggested by Erdélyi & Verth (2007) and reduces the amount of stratification. Further to this, it can be seen in Fig. 3c that as  $h_{\rm a}/H$ increases, P1/P2 for the elliptical loops tends to the values obtained for the circle-arc model. This also occurs for the $\lambda=0,1/2$ cases, however, it is not so easily seen. Also in Fig. 3c the value of  P1/P2 for the elliptical loops can be seen to decrease below the circle arc model. The reason for this is because when the value of  $h_{\rm a}/H$ becomes sufficiently large, P1/P2 reaches an almost constant value for all further values of  $h_{\rm a}/H$ and hence, is almost independent of  $h_{\rm a}/H$. For the circle arc model this happens at a lower value of  $h_{\rm a}/H$ than for the elliptic model. The value of  P1/P2 for the elliptic model then continues to decrease for increasing  $h_{\rm a}/H$, while P1/P2 stays almost constant for the circle arc model. We can conclude from this that the effect produced by the shape of the loop on  P1/P2 is limited by the scale height, for small enough values of H there is a maximum effect from loop shape. Further, the effect of the elliptical shape on  P1/P2 is felt at smaller values of scale heights than the circle-arc model.

The effect of ellipticity is shown explicitly in Fig. 3d, where  P1/P2 is plotted against the ellipticity for different arbitrarily fixed though observationally typical values of  $h_{\rm a}/H$. As  $\epsilon\rightarrow1$, the value of  P1/P2 tends to 2 for all values of  $h_{\rm a}/H$. This is expected because as the ellipticity tends to high values, the length of the minor axis is much less than the major axis (i.e. $b \ll a$). The coronal loop could then be approximated by a straight tube lying horizontally along the surface of the photosphere. The tube would then have an almost homogenous density profile hence the ratio of  P1/P2 tends to the value obtained for the homogenous tube, i.e. 2.

The effect of emergence, quantised by $\lambda $, on loop oscillations is emphasised in Fig. 4. For $\epsilon =0$ (circular-arc) the effect of $\lambda $ on  P1/P2 is almost linear, with the value of  P1/P2 decreasing as the loop emerges. Increasing the ellipticity causes the effect of $\lambda $ to have a parabolic profile which has minimum effect on the period ratio around $\lambda =0$. This suggests that the degree of stratification in the loop decreases as the loop starts to emerge ( $1>\lambda>0$), and once it is half emerged ($\lambda =0$) the degree of stratification starts to increases as the loop enters the late stage of emergence ( $0>\lambda>-1$). It is also clear from Fig. 4 that during an early stage of emergence, the circular shaped loop has greater degree of stratification than the elliptic shape. This is expected as the elliptically shaped loop is flatter at the loop apex. However, during the later stages of emergence, the stratification of the elliptically shaped loop becomes greater. This happens at smaller values of $\lambda $ for decreasing values of scale height (increasing values of  $h_{\rm a}/H$).

Let us now study how the modelling of a loop with an elliptic shape compares to modelling a loop with a circular shape in regards to the ratio of the periods of the fundamental and first harmonic oscillations. The relative percentage difference of the period ratio between the circle-arc and elliptical models is plotted in Fig. 5. It can be seen clearly here that the effect of ellipticity compared to the circle-arc model is not constant for different values of  $h_{\rm a}/H$. There is a maximum value for the difference between the elliptical and circle-arc model, occurring at different values of  $h_{\rm a}/H$ for the various values of $\lambda $. The observations of multimode oscillations by, e.g. Van Doorsselaere et al. (2008), have a measurement error of approximately $3\%$, and it is seen in Fig. 5 that the percentage difference between the circle-arc and elliptical models can be greater than this error. The ellipticity of the coronal loop should then be measured and determined when trying to deduce the density scale height from multimode oscillations.

From the observations of transverse oscillations by Van Doorsselaere et al. (2008), we can obtain estimates of the density scale height. Van Doorsselaere et al. (2008) calculated a density scale height of 109 Mm, a value which is almost twice that of the expected hydrostatic value. This estimate was debated when loop expansion was also taken into account e.g. Ruderman et al. (2008) and Verth et al. (2008). Ruderman et al. (2008) estimated the scale height for a range of values of tube expansion ($\Gamma $) and found the estimated the values of scale height were smaller than estimates without expansion, e.g. for $\Gamma=1.3$ the estimated scale height is $H\sim63$ Mm, and for $\Gamma=1.5$ the scale height is $H\sim49$ Mm. We now consider how the elliptical shape of the loop combined with loop expansion effects the estimated value of scale height. The result for the Van Doorsselaere et al. (2008) observations with two different values of $\Gamma $ are shown in Fig. 6 (labeled vD). Note that values in Fig. 6 are calculated for $h_{\rm a}$ held constant, this means that as $\epsilon $ changes so does the length of the loop. The ellipticity can be seen to have a salient effect on the estimation of the scale height, e.g. for $\epsilon=0.3$ and $\Gamma=1.3$ the scale height estimate is $H\sim59$ Mm, while for $\epsilon=0.7$ ( $\Gamma=1.3$) $H\sim40$ Mm. This latter example shows there could be up to a factor of 1/3 uncertainty in obtaining the scale height. In Verth et al. (2008), a value of  P1/P2=1.54 was observed and the loop under observation had a measured $\Gamma\sim2.05$. Assuming a semi-circular loop, the scale height was calculated as H=7.65 Mm. The estimates of scale height with the inclusion of ellipticity is shown in Fig. 6 (labeled VEJ). The ellipticity now produces an uncertainty of factor 1/4 in the density scale height, which is about 2 Mm. Either way, whichever measurement is correct, we can conclude that the elliptical shape has a profound importance in determining the scale height from the period ratio of oscillating loops.

 \begin{figure} \par\includegraphics[width=7.5cm,clip]{1405fig7.eps} \end{figure} Figure 6:

The calculated values of density scale height, taking into account elliptical loop shape, using the observations of Van Doorsselaere et al. (2008) with corrections due to tube expansion ($\Gamma $) according to Verth et al. (2008), labeled vD, and observations of Verth et al. (2008), labeled VEJ.
Open with DEXTER

3.2 Major elliptical loop

Consider a loop with elliptical geometry as shown in Fig. 7a. The stage of emergence is now denoted by  $\lambda_{\rm a}$, where

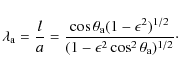\begin{displaymath}% \lambda_{\rm a}=\frac{l}{a}=\frac{\cos\theta_{\rm a}(1-\epsilon^2)^{1/2}}{(1-\epsilon^2\cos^2\theta_{\rm a})^{1/2}}\cdot \end{displaymath} (15)

Here $\theta_{\rm a}$ is the angle between the major axis and the line joining the center of the ellipse to the loop foot-point. As with $\lambda $ for the minor ellipse, $\lambda_{\rm a}>0$ when the loop is in the early stage emergence and $\lambda_{\rm a}<0$ in the late stage emergence. The projection on the major elliptical loop of Eq. (4) gives,
$\displaystyle % \rho_{\rm i}(z)=\rho_{\rm f}\times\exp\left(-\frac{h_{\rm a}}{H... ...\cos^2(\alpha(\zeta)))^{-1/2}-\lambda_{\rm a}}{(1-\lambda_{\rm a})}\right)\cdot$     (16)

The function $\alpha(\zeta)$ can now found from

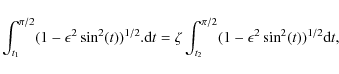\begin{displaymath}% \int^{\pi/2}_{t_{1}}(1-\epsilon^2\sin^2(t))^{1/2}.{\rm d}t=\zeta\int^{\pi/2}_{t_{2}}(1-\epsilon^2\sin^2(t))^{1/2}{\rm d}t, \end{displaymath} (17)

where t1 is given in Eq. (10) and

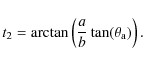\begin{displaymath}% t_{2}=\arctan\left(\frac{a}{b}\tan(\theta_{\rm a})\right). \end{displaymath} (18)

The substitution of Eqs. (16) into (2) gives


$\displaystyle % \frac{{\rm d}^2Q}{{\rm d}\zeta^2}+\Omega^2\exp\left(-\frac{h_{\... ...\cos^2(\alpha(\zeta)))^{-1/2}-\lambda_{\rm a}}{(1-\lambda_{\rm a})}\right) Q=0,$     (19)

where $\Omega$ is the same as before.

As with Eq. (11), (19) has no analytical solution. Solving numerically, the ratio of periods  P1/P2 is plotted against  $h_{\rm a}/H$ in Fig. 7b. It can be concluded from Fig. 7b that the major elliptical loop has a much smaller effect on the period ratio of  P1/P2 than the minor elliptical loop. The major elliptical loop also causes the value of  P1/P2 to decrease compared to the circle arc model. This is a qualitatively different result from the model of oscillating minor elliptical loops. For values of $\epsilon\leq0.95$ there is a very small deviation from the semi-circular loop. A value of $\epsilon=0.95$ for a loop of typical length 120 Mm would have $a\approx40$ Mm and $b \approx12$ Mm, and for $\epsilon=0.99$, $a\approx40$ Mm and $b \approx6$ Mm. As mentioned earlier, we conjecture that such a strong ellipticity, i.e.  $\epsilon>0.9$, would probably be unlikely in coronal loops. For the early and late stages of emergence (e.g.  $\lambda_{\rm a}=0.5$, -0.5) a similar feature is found as the semi-emerged ellipse, i.e. only at large values of ellipticity do we see appreciable difference from the circle-arc case in the period ratio of standing oscillations.

 \begin{figure} \par\mbox{\subfigure[Major ellipse]{\includegraphics[width=4.2cm,... ...\lambda=0$ )]{\includegraphics[width=7.1cm,clip]{1405fg8b.eps} } }\end{figure} Figure 7:

a) Sketch showing the a loop with major elliptical shape. The shape is described by the arc of an ellipse with a minor half-axis of length b and a major half-axis of length a, the height of the loop apex above the photosphere, $h_{\rm a}$, and the distance of the center of the ellipse below the photosphere, l. b) The ratio of theperiods of the fundamental mode to the first harmonic, P1/P2, as a function of density stratification parameter, $h_{\rm a}/H$. The solid line is the analogous circle-arc case.
Open with DEXTER

4 Conclusions

In this paper we investigated the period ratio of transverse oscillations of a coronal loop with an elliptical shape, at various stages of its emergence from the sub-photosphere into the solar corona. The effect of curvature of the loop on eigenfrequencies of standing oscillations was neglected and we concentrated on the influence of the loop shape and the state of emergence. This paper generalises earlier studies, e.g. Andries et al. (2005a) and Dymova & Ruderman (2006), who investigated the effect of a circular loop shape on the parameter  P1/P2 (the period ratio of the fundamental mode to the first harmonic of standing oscillations).

In order to model an oscillating coronal loop with an elliptical shape embedded in a gravitationally stratified solar plasma, an exponential density profile was projected onto an elliptical shape determining the loop and the parameters found to characterise the geometry were the ellipticity ($\epsilon $), the ratio of loop height above the photosphere to the scale height ( $h_{\rm a}/H$) and the measure of the stage of emergence ($\lambda $). We considered two types of elliptical loop that can occur, the minor elliptical loop where minor axis of the ellipse is the vertical axis of the loop (see Fig. 2), and the major elliptical loop where major axis of the ellipse is the vertical axis of the loop (see Fig. 7a).

Numerical solutions of the Sturm-Liouville problem, as shown by Eq. (2), were found for both minor and major elliptical loops, and the relationship between  P1/P2, $h_{\rm a}/H$, $\epsilon $ and $\lambda $ was shown in detail.

We found that for the minor ellipse, a situation that occurs most plausibly under coronal conditions, increasing ellipticity increases the value of the ratio  P1/P2 compared to the circular arc model for all values of $\lambda $. It was also discovered that as  $h_{\rm a}/H$ reaches a large enough value, the value of  P1/P2 becomes almost independent of  $h_{\rm a}/H$. This implies that loop shape has a limited effect on longitudinal stratification and P1/P2 under circumstances only when $h_{\rm a}/H \gg 1$. The effect of the elliptical shape on P1/P2 was found to be felt at larger values of  $h_{\rm a}/H$ than the circle arc model (see, e.g Fig. 3c).

The difference between the period ratio P1/P2 of standing kink oscillations of loops with elliptical and circular shapes was demonstrated in Fig. 5, and it shows that the percentage difference can reach ${\sim}6$%. This means the effect of ellipticity on standing oscillations could be measured even by the current cohort of high-resolution instrumentation. Further to this, Fig. 4 also indicates that P1/P2 is strongly effected by the value of $\lambda $ (stage of emergence of the loop), with the strength of the effect increasing as $\lambda\rightarrow -1$ and the scale height ( $h_{\rm a}/H$) increases. It can easily be calculated that a loop which is in a late stage of emergence (i.e. $\lambda\rightarrow -1$) can show a deviation of up to 10% in P1/P2 from that of the semi-emerged loop ($\lambda =0$). Not including the stage of emergence could lead to an error of up to $30\%$ upon estimating the density scale height. For a coronal loop of typical length (100 Mm) embedded in a gravitationally stratified atmosphere this could mean an error of around 6 Mm when estimating the scale height.

The major ellipse, however, is found to have a less pronounced effect on P1/P2 compared to the circle arc case. Only at high values of ellipticity ( $\epsilon>0.95$) is the difference between the frequency ratio of the major ellipse and circle arc models noticeable. As discussed in Sect. 3.1, there is observational evidence that loops will not have such a high degree of ellipticity and the greatest value of ellipticity estimated for the seven loops observed by Aschwanden et al. (2008) provides initial evidence for this claim.

The present error bars on measurements of multimode oscillations are approximately 3% (private communication with authors of Verth et al. 2008). The difference between the minor ellipse and circle arc surpassed this for reasonable values of ellipticity, e.g. those derived from STEREO observations. Therefore, the ellipticity of the loop is an important parameter along with the stage of emergence and should be taken into account when using observational data from multimode oscillations to estimate the density scale height and ultimately determining the solar magnetic field by the technique of magneto-seismology.

Acknowledgements
The authors thank M. Ruderman and G. Verth for a number of useful discussions. R.E. acknowledges M. Kéray for patient encouragement. The authors are also grateful to NSF, Hungary (OTKA, Ref. No. K67746) and the Science and Technology Facilities Council (STFC), UK for the financial support they received.

References

All Tables

Table 1:   Approximate values of ellipticity derived for the STEREO loops observed by Aschwanden et al. (2008).

All Figures

  \begin{figure} \par\mbox{\subfigure[Elliptically curved magnetic flux tube]{\inc... ...tube]{\includegraphics[width=2.7in, height=1.5in]{1405fig2.eps} }}\end{figure} Figure 1:

a) Sketch showing the equilibrium state of an elliptically curved, magnetic flux tube with plasma density  $\rho _{\rm i}(z')$, magnetic field of strength  $\vec{B}_{\rm i}$ embedded in plasma with density  $\rho _{\rm e}(z')$ of strength  $\vec{B}_{\rm e}$. b) Sketch showing the equilibrium state of a straight, cylindrical magnetic flux tube onto which the elliptical density profile is projected. The straight cylinder has radius R, length 2L, plasma density  $\rho _{\rm i}(z)$, magnetic field of strength  $\vec{B}_{\rm i}$ and is embedded in a plasma with density  $\rho _{\rm e}(z)$ of strength  $\vec{B}_{\rm e}$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{1405fig3.eps} \end{figure} Figure 2:

Sketch showing a partially emerged loop with minor elliptical shape. The geometry of the shape is described by the arc of an ellipse with a minor half-axis of length b and a major half-axis of length a, the height of the loop apex the photosphere $h_{\rm a}$, and the distance of the center of the ellipse below the photosphere $l=b-h_{\rm a}$.
Open with DEXTER
In the text

  \begin{figure} \par\mbox{\subfigure[Early stage emergence ($\lambda=1/2$ )]{\inc... ...} \subfigure[]{\includegraphics[width=5.8cm,clip]{1405fg4d.eps} }}\end{figure} Figure 3:

a)- c) The ratio of the periods of the fundamental mode to the first harmonic, P1/P2, as a function of density stratification parameter, $h_{\rm a}/H$. The period ratio  P1/P2 is shown for a number of values of ellipticity ($\epsilon $) at various stages of emergence ($\lambda $). The solid line in each plot is the analogous circle-arc case, i.e.  $\epsilon =0$. d) The ratio of the periods of the fundamental mode to the first harmonic, P1/P2, as a function of ellipticity for $\lambda =0$, i.e. the semi-ellipse.
Open with DEXTER
In the text

  \begin{figure} \par\mbox{\subfigure[$h_{\rm a}/H=1.0$ ]{\includegraphics[width=5... ...rm a}/H=3.0$ ]{\includegraphics[width=5.4cm,clip]{1405fg5c.eps} }}\end{figure} Figure 4:

Showing the value of P1/P2 as a function of the loop shape parameter, $\lambda $, at various values of  $h_{\rm a}/H$ for the elliptically shaped loop.
Open with DEXTER
In the text

  \begin{figure} \par\mbox{\subfigure[Early stage emergence ($\lambda=1/2$ )]{\inc... ...ambda=-1/2$ )]{\includegraphics[width=4.9cm,clip]{1405fg6c.eps} }}\end{figure} Figure 5:

Shown is the percentage difference between the values of  P1/P2 when comparing the minor elliptical and the circle-arc geometries for a range of  $h_{\rm a}/H$ at different stages of emergence.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{1405fig7.eps} \end{figure} Figure 6:

The calculated values of density scale height, taking into account elliptical loop shape, using the observations of Van Doorsselaere et al. (2008) with corrections due to tube expansion ($\Gamma $) according to Verth et al. (2008), labeled vD, and observations of Verth et al. (2008), labeled VEJ.
Open with DEXTER
In the text

  \begin{figure} \par\mbox{\subfigure[Major ellipse]{\includegraphics[width=4.2cm,... ...\lambda=0$ )]{\includegraphics[width=7.1cm,clip]{1405fg8b.eps} } }\end{figure} Figure 7:

a) Sketch showing the a loop with major elliptical shape. The shape is described by the arc of an ellipse with a minor half-axis of length b and a major half-axis of length a, the height of the loop apex above the photosphere, $h_{\rm a}$, and the distance of the center of the ellipse below the photosphere, l. b) The ratio of theperiods of the fundamental mode to the first harmonic, P1/P2, as a function of density stratification parameter, $h_{\rm a}/H$. The solid line is the analogous circle-arc case.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.