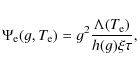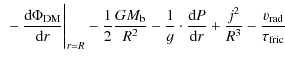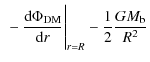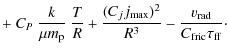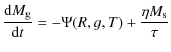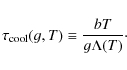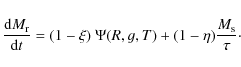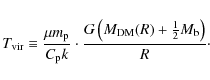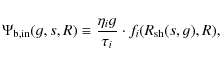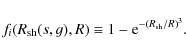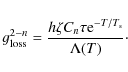| Issue |
A&A
Volume 502, Number 1, July IV 2009
|
|
|---|---|---|
| Page(s) | 45 - 59 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200810259 | |
| Published online | 15 June 2009 | |
Starbursts in isolated galaxies
I. The influence of stellar birth function and IMF
Ch. Theis1,4 - J. Köppen2,3,4
1 - Institute of Astronomy, University of Vienna,
Türkenschanzstr. 17, 1180 Vienna, Austria
2 -
Observatoire Astronomique de Strasbourg, 11 rue de
l'Université, 67000 Strasbourg, France
3 -
International Space University, Parc d'Innovation,
1, rue Jean-Dominique Cassini,
67400 Illkirch-Graffenstaden, France
4 -
Institut für Theoretische Physik und Astrophysik,
Universität Kiel, 24098 Kiel, Germany
Received 26 May 2008 / Accepted 22 April 2009
Abstract
Context. Starbursts and substantial variations in the star formation histories are a common phenomenon in galaxies. Although predominantly found in interacting galaxies, they also occur in isolated galaxies.
Aims. We study the stability properties of isolated star-forming dwarf galaxies with the aim of identifying starburst modes. The impact of the stellar birth function, i.e. a spontaneous and an induced star formation mode, the initial mass function (IMF), the stellar feedback and the interstellar medium (ISM) model on the galactic star formation history are investigated. We especially focus on dynamically driven starbursts induced by stellar feedback.
Methods. We apply a one-zone model for a star-gas system coupled by both mass and energy transfer. Additionally, we extend the network for active dynamical evolution. This allows for a coupling between the dynamical state of the galaxy and its internal properties, such as star formation activity or the thermal state of the ISM.
Results. While the influence of the dynamics on the total star formation rate is strong, especially with nonlinear stellar birth functions, the coupling of the internal properties (gas temperature) on the dynamics is rather limited, because radiative cooling keeps the gas temperature well below the virial temperature. Because of short cooling and feedback timescales, the star formation rate is close to the equilibrium star formation rates. Quasi-periodic starbursts occur, because star formation follows the variations in the gas density induced by decaying virial oscillations. This behaviour is quite insensitive to the nature and the details of the stellar birth description, viz. whether spontaneous or induced star formation is considered or the IMF is varied. A second type of burst is found as an instability operating when the cooling may drop at very low densities with increasing temperature, in regimes beyond 104 K.
Conclusions. Bursts of star formation occur during transitory phases, when dynamical equilibrium is established. Then they are quasi-periodic on the dynamical timescale. Because of short heating and cooling timescales, the star formation rate follows the equilibrium star formation rate corresponding to the actual gas density.
Key words: galaxies: evolution - galaxies: starburst - ISM: general
1 Introduction
Variations in the star formation rate (SFR) in dwarf galaxies have been deduced from several observations like direct measurements of individual star formation histories (Dohm-Palmer et al. 2002), a large variation in the specific SFR, or short gas depletion times (Gallagher & Hunter 1984). Especially interesting is the group of isolated starburst galaxies, because no external triggers can be invoked for their high activity. Van Zee (2001) studied a large sample of isolated dwarf irregular galaxies. For the majority of these galaxies, she found a fairly constant SFR over the past 10 Gyr indicating that they reached a quasi-equilibrium state burning on a long gas depletion time of about 20 Gyr. However, a small fraction of her sample shows high star formation activity that is strongly concentrated in the central region and/or characterised by small radial scale lengths, i.e. enhanced gas densities. Already Gallagher & Hunter (1984) stressed that the observation of starburst dIrrs implies a mechanism to organise large-scale star formation which cannot operate all the time due to fast consumption of fuel. On the other hand, the instability leading to an episodic SFR should only work in a small parameter range, because most of the isolated dIrrs seem to evolve in a highly self-regulated manner.
The first theoretical models dealing with star formation variations in galaxies were based on closed-box models. For reasonable models of the interstellar medium (ISM) it turned out that stellar feedback is very effective in suppressing instabilities of the ISM (e.g. Ikeuchi & Tomita 1983; Scalo & Struck-Marcell 1986). These models only allow for a burst-like behaviour when a long time-delay (of the order of 108 yrs) between star formation and stellar feedback is introduced. Recently Quillen & Bland-Hawthorn (2008) emphasised the importance of such a long time-delay of the feedback for creating episodic star formation in Milky Way type galaxies. The drawback of these models is the long time-delay that exceeds the short feedback timescales related to massive star formation by far. The latter are a few Myr at most (if not quasi-instantaneously when taking stellar winds into account). It is not clear what has kept the ISM from experiencing feedback by stars for such a long time.
Köppen et al. (1995, hereafter KTH95) investigated a simple numerical model motivated by full chemodynamical simulations. They show that the effective SFR is almost independent of the detailed recipe for the stellar birth function, provided a negative feedback due to the thermal state of the ISM is considered in the stellar birth function. This also holds for a multi-phase ISM (Köppen et al. 1998). All these box models suffer, however, from neglecting galactic dynamics. Additionally, they are designed for small galactic regions of a few 100 pc. As a result, coherence between different unstable regions and global starbursts could not be modelled.
Recently, several attempts have been made to study the evolution of isolated dwarf galaxies by taking full stellar and gas dynamics, as well as star formation and stellar feedback, into account (e.g. Hensler et al. 2004; Pelupessy et al. 2004, 2005). Though these calculations differ in many details, they agree in producing large-scale star formation variations on dynamical timescales in some of their models. This indicates the crucial role dynamics plays for episodic starburst behaviour.
Starbursts are often associated with galaxy interactions. E.g. most of the ultraluminous infrared galaxies are interpreted as the result of galaxy interactions or mergers (e.g. Sanders & Mirabel 1996). It is interesting that the response of galaxies to interaction-induced perturbations is not unique or simple. Di Matteo et al. (2007) present a subset of merger events created in a numerical survey of galaxy collisions. Their Figs. 8 and 9 show a variety of reaction patterns of the SFR after the first closest approach, ranging from strong starbursts to almost no enhancement in the star formation activity. Another example for dwarf galaxy interactions is presented in Bekki (2008). Despite this model-to-model variation, statistics of large galaxy-pair samples show a clear correlation between interactions and star formation activity. For example using 12 500 galaxy pairs from the SDSS survey Nikolic et al. (2004) find an enhanced star formation rate for projected separations below 50 kpc and an anti-correlation between the projected separation and the star formation rate (for more details, cf. to the review by Struck 2006).
A major disadvantage of the simulations - either for isolated or interacting galaxies - is their complexity. This prevents a detailed investigation of the parameter space and sometimes also hides the key physical mechanisms. Instead of analysing dwarf galaxies by such detailed and complex models, we study here a set of equations that is as simple as possible and that incorporates the main generic features of the complex numerical simulations. The advantage is a (semi-)analytical treatment and a more direct physical interpretation of the implemented physics. Moreover, extended parameter studies can be carried out much more easily with our set of equations than with the full numerical modelling.
This paper introduces an extended version of the analytical models of KTH95 that allows us to deal with the dynamical evolution of a galaxy. By this, the evolution of the star formation
activity not only depends on the internal properties of the ISM, but also on the dynamical state of the galaxy. As an application of our analytical model, the star formation activity for dwarf galaxies in the mass regime of a few
![]() is studied.
is studied.
In this paper we investigate the influence on the star formation by studying a generalized stellar birth function (composed of a spontaneous star formation mode with negative thermal feedback and an induced star formation mode), the initial stellar mass function, and the stellar feedback.
This paper is organised as follows. In Sect. 2 we introduce our set of equations. A reference model and the result of parameter variations are presented in Sect. 3. Section 4 contains a discussion of the results.
2 The numerical model
2.1 The non-dynamical closed box model
Motivated by the complex and computationally expensive chemo-dynamical calculations of Theis et al. (1992) (also used in the simulations for dwarf galaxies by Hensler et al. 2004), KTH95 analysed a set of closed-box models that was designed to be as simple as possible, but still keeps the main qualitative features of the chemo-dynamical network (e.g. feedback processes). These simplified equations describe the temporal evolution of the density of short-lived massive stars (s), of gas (g), and of the internal energy (e) of the gas:
The gas is consumed by star formation denoted by a stellar birth function
The last equation deals with the energy budget of the ISM gas. Its internal energy is characterised by its temperature T. Assuming a turbulence-driven ISM it receives heating mainly by massive stars (e.g. Ly-continuum radiation or type II supernovae). The conversion factor h can be constant, if all the energy is absorbed, or it may depend on gas density, e.g. for radiative heating in an optically thin gas. The main dissipative process of the gas is radiative cooling. The energy loss scales with g2, where the proportionality factor
![]() is the classical cooling function.
is the classical cooling function.
The set of equations is closed by a generalized Schmidt-like stellar birth function
This function corresponds to spontaneous star formation. (An induced star formation mode will be discussed later in Sect. 3.3.) Different to the classical Schmidt-law we allow for a (negative) thermal feedback
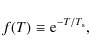 |
(5) |
which reduces the star formation efficiency in case of high gas temperatures
In case of radiative cooling, thermal equilibrium is quickly established due to short heating and cooling timescales (KTH95). As a result the effective SFR
![]() (which allows for a
stationary solution of Eqs. (2) and (3)) is independent of the adopted stellar birth function
(which allows for a
stationary solution of Eqs. (2) and (3)) is independent of the adopted stellar birth function
where
2.2 Including the dynamics
We extend our closed-box model for dynamical evolution by considering a volume with characteristic radius R (e.g. the half-mass radius) of the baryonic system of the galaxy. The equation of motion - motivated by the corresponding equation for a thin gaseous shell - is given by
The first two terms in (7) describe the gravity, i.e. the contribution of the dark matter potential and the self-gravity of the baryons with the total mass
From the (half-mass) volume
![]() of the system and the mass of each component the densities can be derived, e.g. the gas density reads
of the system and the mass of each component the densities can be derived, e.g. the gas density reads
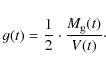 |
(8) |
Integrating Eqs. (1)-(3) over volume yields the equations for the total masses of the gas, the massive stars, and the total internal energy
The total SFR
The temperature is related to the internal energy E by
![]() .
The factor 1/2 stems from the assumption that R is the half-mass radius. The last term in Eq. (11) denotes the
.
The factor 1/2 stems from the assumption that R is the half-mass radius. The last term in Eq. (11) denotes the
![]() work. The pressure P is given by
P = 2/3 E/V = 2/3 b g T. In case
of radiative dissipation, the corresponding timescale
work. The pressure P is given by
P = 2/3 E/V = 2/3 b g T. In case
of radiative dissipation, the corresponding timescale
![]() is defined as
is defined as
Dissipation by radiative cooling is included by a cooling function combined from Dalgarno & McCray (1972) for
For the dark matter halo, we apply the universal halo suggested by Burkert (1995) for dwarf galaxies. The scale radius r0 of the Burkert halo was set to 8 kpc. For a baryonic mass of
![]()
![]()
![]() and
and
![]() kpc the initial baryonic mass fraction is about 10%.
kpc the initial baryonic mass fraction is about 10%.
The constants CP, Cj, and
![]() are adjusted to a 3d-SPH simulation of a collapsing gas sphere in a given static dark matter halo potential. The simulations were done with the SPH part of the code described in Harfst et al. (2006). Two sets of constants were derived: set 1 (CP=1.91, Cj=0.15,
are adjusted to a 3d-SPH simulation of a collapsing gas sphere in a given static dark matter halo potential. The simulations were done with the SPH part of the code described in Harfst et al. (2006). Two sets of constants were derived: set 1 (CP=1.91, Cj=0.15,
![]() )
gives a good fit to the early evolution, whereas set 2
(CP=1.97, Cj=0.11,
)
gives a good fit to the early evolution, whereas set 2
(CP=1.97, Cj=0.11,
![]() )
describes the late evolution (Fig. 1). The main freedom in the choice of parameters comes from the damping behaviour that is covered by a variation of a factor of 2 in the constant
)
describes the late evolution (Fig. 1). The main freedom in the choice of parameters comes from the damping behaviour that is covered by a variation of a factor of 2 in the constant
![]() ,
i.e. in the frictional timescale. When minimising the deviations over all periods the best fit was reached by CP=1.74, Cj=0.13,
,
i.e. in the frictional timescale. When minimising the deviations over all periods the best fit was reached by CP=1.74, Cj=0.13,
![]() .
If not stated differently, we apply these values.
.
If not stated differently, we apply these values.
The Eqs. (7)-(12) yield a closed set of equations including a first approximation for the dynamical evolution. We solve the differential equations using a fourth-order Runge-Kutta integrator with adaptive timestep (Press et al. 1992). The integration accuracy is set to 10-10 (or better). For convenience we also consider an equation for the mass ![]() of the long-lived low-mass stars and the stellar remnants
of the long-lived low-mass stars and the stellar remnants
The formation of the low-mass stars is described by the first term and the production of stellar remnants by the second term in Eq. (13). We neglect the gas return by long-lived low-mass stars. This approximation is appropriate for gas-rich systems. Therefore, our models cannot provide a realistic evolution of the gas mass, if the gas fraction is smaller than a few percent. From Eqs. (9) and (10) we get the solution
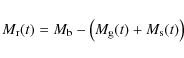 |
(14) |
describing mass conservation, and
A more accurate treatment would include mass return of low-mass stars by planetary nebulae and type Ia supernovae. This would imply the numerically rather expensive computation of the instantaneous mass transfer rates from the details of the past star formation history for the spectrum of stellar masses. For our purpose of studying the general features of galaxy evolution with a simplified dynamics, such an elaborate approach would not be such an advantage that it would justify the computational effort.
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f1a.eps} \includegraphics[angle=270,width=8.5cm,clip]{10259f1b.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg69.png) |
Figure 1: Temporal evolution of the half-mass radius in a 3D-SPH simulation of a collapsing gas sphere in a dark matter halo and the result for the simple equation of motion (7). Shown are models fitting the early stage well (with CP=1.91, Cj=0.15, Cf=2.06, left) or the late stage (with CP=1.97, Cj=0.11, Cf=0.88, right). |
| Open with DEXTER | |
2.3 Units
For our calculations we used the following units: 1 ![]() ,
1 pc, and 1 Myr. If not stated differently, parameters and results are given in these units or the corresponding derived units, e.g. mass densities in
,
1 pc, and 1 Myr. If not stated differently, parameters and results are given in these units or the corresponding derived units, e.g. mass densities in
![]() .
.
3 Results
Table 1: Properties of the numerical models.
3.1 The reference model
![\begin{figure}
\par\includegraphics[angle=270,width=16cm,clip]{10259f2.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg77.png) |
Figure 2:
Initial temporal evolution of a model with a baryonic mass of 2 |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{10259f3.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg78.png) |
Figure 3: Same as Fig. 2, but for 5 Gyr of evolution. |
| Open with DEXTER | |
As a first example we present a model with a total baryonic mass of 2 ![]()
![]() starting at a radius of
starting at a radius of
![]() .
The stellar birth function
.
The stellar birth function
![]() is parametrised by a Schmidt-exponent of n=1.5 and a constant
C1.5=0.06. Additionally, a feedback term with
is parametrised by a Schmidt-exponent of n=1.5 and a constant
C1.5=0.06. Additionally, a feedback term with
![]() is considered. The initial temperature is set to
is considered. The initial temperature is set to
![]() close to the system's virial temperature
close to the system's virial temperature
This definition is motivated by Eq. (7) assuming force equilibrium between thermal pressure at a temperature
Figure 2 shows the early evolution: Due to strong cooling, the gas temperature drops almost immediately to values near
![]() bringing the system far out of virial equilibrium. In the ongoing collapse, the density increases. Cooling and density enhancement continue, until star formation becomes more prominent after about 100 Myr. The first stars reinject energy to the ISM
leading to the quasi-equilibrium stage known from the box models of KTH95. Different to them, the density increases because of the continuing collapse: the temperature evolves on the line of equilibrium temperatures characteristic of the densities set by the dynamical state of the system. Though the star formation and, by this, the stellar energy injection grow, too, the feedback cannot prevent further collapse, because cooling is still too efficient to allow the gas to reach the virial temperature. The collapse proceeds until
bringing the system far out of virial equilibrium. In the ongoing collapse, the density increases. Cooling and density enhancement continue, until star formation becomes more prominent after about 100 Myr. The first stars reinject energy to the ISM
leading to the quasi-equilibrium stage known from the box models of KTH95. Different to them, the density increases because of the continuing collapse: the temperature evolves on the line of equilibrium temperatures characteristic of the densities set by the dynamical state of the system. Though the star formation and, by this, the stellar energy injection grow, too, the feedback cannot prevent further collapse, because cooling is still too efficient to allow the gas to reach the virial temperature. The collapse proceeds until
![]() ,
when the angular momentum conservation in (7) becomes dominant and the system expands again. By this, the first starburst episode comes to an end and the cooling rate drops. The gas is quickly heated to
,
when the angular momentum conservation in (7) becomes dominant and the system expands again. By this, the first starburst episode comes to an end and the cooling rate drops. The gas is quickly heated to
![]() ;
however, the gas never reaches the virial temperature thanks to the large
increase of the cooling rate at temperatures beyond
;
however, the gas never reaches the virial temperature thanks to the large
increase of the cooling rate at temperatures beyond
![]() .
The next star formation cycle starts when the gas is collapsing again.
.
The next star formation cycle starts when the gas is collapsing again.
The longterm evolution of this model shows that the previously discussed bursts are just transitory phenomena caused by the initial departure from dynamical equilibrium (Fig. 3). The oscillations are almost completely damped after 2 Gyr. However, only the first two or three peaks in the SFR are enough strong to be characterised as a starburst by standard definitions. Later on no bursts are found. Such behaviour, i.e. only an initial burst, was found in almost all models.
Two general properties of our models can already be seen in the reference model. First, despite the coupling of stars and gas in the dynamical equation, Eq. (7), the dynamics do (almost) not care about the star formation and the related stellar feedback. This is caused by the very efficient cooling resulting in gas temperatures well below the virial temperature. Second, the SFR is strongly modulated by the dynamics. Exceptions to both rules exist, but these are either singular or in physically uninteresting regimes (and beyond the validity of our model equations).
3.2 Influence of stellar birth function
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10259f4.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg89.png) |
Figure 4: Temporal evolution of the SFR for models with different exponent in the stellar birth function: n=1 (model DN1, filled circles), n=1.1 (DN2, dot-dashed), n=1.5(DN3, solid), n=2 (DN4, open squares) and n=2.5 (DN5, dashed). The normalisation constant Cn is kept constant at 0.007. No negative thermal feedback term is included in the stellar birth function. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=15.95cm,clip]{10259f5.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg90.png) |
Figure 5: Temporal evolution of model DN1 characterised by a linear Schmidt law ( n=1, C1=0.007), but without a negative thermal feedback term in the stellar birth function. For further details see Fig. 2. |
| Open with DEXTER | |
![\begin{figure}\includegraphics[angle=270,width=15.95cm,clip]{10259f6.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg91.png) |
Figure 6: Temporal evolution of model DN2 characterised by a Schmidt law ( n=1.1, Cn=0.007), but without a negative thermal feedback term in the stellar birth function. For further details see Fig. 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=16cm,clip]{10259f7.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg92.png) |
Figure 7: Temporal evolution of model DN4 characterized by a Schmidt law ( n=2, Cn=0.007), but without a negative thermal feedback term in the stellar birth function. For further details see Fig. 2. |
| Open with DEXTER | |
In this section we address the influence of the stellar birth function and its parametrization according to Eq. (4). In a first series of models (DN1 to DN5), we varied the exponent n in the stellar birth function fixing the constant Cn to 0.007. We also neglected the negative thermal feedback; i.e., we consider the limit
![]() .
This represents the classical Schmidt-law for which the stellar birth function only depends on density, but not on the temperature of the gas.
.
This represents the classical Schmidt-law for which the stellar birth function only depends on density, but not on the temperature of the gas.
The Schmidt exponent.
Figure 4 shows the temporal evolution of the SFR for different exponents n. With increasing n, the SFR becomes increasingly sensitive to the density variations. The peaks of the SFR are fairly similar compared to the large SFR variations, whereas the amount of available fuel varies strongly with n as a time integration of the SFR shows: for the linear Schmidt law, it takes 200 Myr to convert 50% of the gas into stars, whereas for n=1.5 this takes about 1.4 Gyr. With increasing nonlinearity of the stellar birth function
A linear Schmidt law (n=1) with no thermal feedback term in the stellar birth function
represents a singular case with respect to the SFR ![]() .
For n=1, the SFR is proportional to the total gas mass, but independent on the gas density:
.
For n=1, the SFR is proportional to the total gas mass, but independent on the gas density:
![]() .
This leads to an exponential decay of the gas mass, irrespective of the dynamical state of the system: the virial oscillations do not show up in the exponentially decaying SFR or the
amount of massive stars (Fig. 5, left panels).
.
This leads to an exponential decay of the gas mass, irrespective of the dynamical state of the system: the virial oscillations do not show up in the exponentially decaying SFR or the
amount of massive stars (Fig. 5, left panels).
During the early evolution, the gas temperature is always close to 104 K (Fig. 5, lower right panel). The high temperatures are a result of stellar heating. Because of a lack of negative thermal feedback in model DN1, the temperature does not regulate the stellar birth function. Only the strong rise in the cooling function beyond 104 K prevents the gas from reaching higher temperatures. On the other hand, the temperatures are too low in the early stage to become dynamically important as a comparison with the virial temperatures shows (lower right panel in Fig. 5). This lack of star formation induced feedback to the dynamics has already been found in the reference model. Thus, for the linear Schmidt law, both the dynamics and the star formation history are practically decoupled.
The normalisation constant.
In a next step we study the influence of the constant Cn in the stellar birth function. For a quadratic Schmidt law we varied Cn by two orders of magnitude. Initially, the difference in the normalisation constant is directly reflected in the enhanced SFR of model DN6 (Fig. 8). The enhanced SFR leads to a stronger stellar feedback for model DN6. By this, the mean radius increases by about 50% and the period of the variations is accordingly longer compared to model DN4. The oscillations are more strongly damped and already after about 500 Myr the mean SFR is lower for the model with the larger star formation constant. The latter is a direct consequence of the lack of fuel after the first strong starburst for model DN6.
The negative thermal feedback.
So far, we have neglected the thermal feedback
Reducing ![]() to 104 K (model DT2) brings
to 104 K (model DT2) brings ![]() closer to the actual temperatures of the ISM mainly set by the strong rise in the cooling function. Variations in the temperature influence the stellar birth function much more strongly than in model DT1. This can be seen in the
reduced overall SFR, which shows a modulated exponential decay. Setting
closer to the actual temperatures of the ISM mainly set by the strong rise in the cooling function. Variations in the temperature influence the stellar birth function much more strongly than in model DT1. This can be seen in the
reduced overall SFR, which shows a modulated exponential decay. Setting ![]() to 102 or 103 K makes the density variations and its impact on the temperature by cooling to the
dominant factor for the global SFR. The oscillation periods are then given by the dynamical timescale and the star formation reaches a quasi-equilibrium state when the virial
oscillations have been decayed.
to 102 or 103 K makes the density variations and its impact on the temperature by cooling to the
dominant factor for the global SFR. The oscillation periods are then given by the dynamical timescale and the star formation reaches a quasi-equilibrium state when the virial
oscillations have been decayed.
It is also interesting to consider the long-term evolution of model DT2 (
![]() ,
Fig. 10): after about 6 Gyr of self-regulated quasi-equilibrium evolution, the SFR enters an oscillating period over the next 3 Gyr. Then again the evolution becomes rather stable. This variation of the SFR is directly caused by the temperature fluctuations between about 1.4
,
Fig. 10): after about 6 Gyr of self-regulated quasi-equilibrium evolution, the SFR enters an oscillating period over the next 3 Gyr. Then again the evolution becomes rather stable. This variation of the SFR is directly caused by the temperature fluctuations between about 1.4 ![]()
![]() and 8
and 8 ![]()
![]() as the upper two panels
in Fig. 10 show. Since
as the upper two panels
in Fig. 10 show. Since ![]() amounts to
amounts to
![]() ,
the feedback term varies by about a factor of 103. A comparison of the radial variations and the temperature
variations shows that the fluctations are not caused by the dynamical evolution (Fig. 10, lower panel): the radial oscillations are too small in amplitude and are not in phase with the temperature variations.
,
the feedback term varies by about a factor of 103. A comparison of the radial variations and the temperature
variations shows that the fluctations are not caused by the dynamical evolution (Fig. 10, lower panel): the radial oscillations are too small in amplitude and are not in phase with the temperature variations.
Though e.g. the temperature variations are too large to allow for a complete explanation by linear perturbation theory, a linear stability analysis might give a first clue to the existence of this unstable regime. Since the dynamical evolution is unimportant here, we can apply the results of the stability analysis for the nondynamical set of Eqs. (1)-(3) given in KTH95: a necessary condition for stability is that Eq. (28) of KTH95 holds. In the limit of low gas densities, we can rewrite this stability criterion as
This is the case, if the logarithmic slope
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f8.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg102.png) |
Figure 8: Temporal evolution of the SFR for the models DN4 and DN6 both characterized by a quadratic Schmidt law with different normalisation constants: Cn=0.007 (DN4) and Cn=0.7 (DN6). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f9.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg105.png) |
Figure 9:
Temporal evolution of the SFR for models with a linear Schmidt law (n=1) and a negative thermal feedback term with different values of the temperature parameter |
| Open with DEXTER | |
Assuming that the logarithmic slope of the cooling function is close to one, instability can only occur if the cooling timescale is longer than the mean stellar lifetime ![]() of the massive stars. In the early stages when the gas density is high, the instability criterion will not be met due to the high efficiency of cooling. However, in the late stages when most gas is consumed (or lost), the
cooling timescale becomes long even for temperatures above 104 K.
of the massive stars. In the early stages when the gas density is high, the instability criterion will not be met due to the high efficiency of cooling. However, in the late stages when most gas is consumed (or lost), the
cooling timescale becomes long even for temperatures above 104 K.
For a metallicity of 1/10 ![]() ,
the cooling curve according to Böhringer & Hensler has a first region of negative slope between 1.5
,
the cooling curve according to Böhringer & Hensler has a first region of negative slope between 1.5 ![]() 104 K and 4
104 K and 4 ![]() 104 K. Therefore, the evolution becomes unstable once the equilibrium temperature rises to 1.5
104 K. Therefore, the evolution becomes unstable once the equilibrium temperature rises to 1.5 ![]() 104 K. The next unstable region caused by He line emission exists for equilibrium temperatures close to
105 K. However, in model DT2 this regime is not reached within the first 10 Gyr.
104 K. The next unstable region caused by He line emission exists for equilibrium temperatures close to
105 K. However, in model DT2 this regime is not reached within the first 10 Gyr.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10259f10.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg108.png) |
Figure 10:
Late temporal evolution of the gas temperature ( upper and
lower panel, solid line), the SFR ( middle panel) and the mean radius of the system ( lower panel, dashed line) for the model with a linear Schmidt law (n=1) and a negative thermal
feedback term with |
| Open with DEXTER | |
3.3 Influence of positive stellar feedback
The star formation recipe discussed in Sect. 3.2 corresponds to a spontaneous star formation mode with a negative stellar feedback. However, there might also be positive stellar feedback (see e.g. the stochastically self-propagating star formation models (SSPSF) by Gerola & Seiden 1978). A model often discussed is the SN-induced star formation (e.g. Ehlerová et al. 1997; Hosokawa & Inutsuka 2005,2006): the basic idea is that expanding SN-shells sweep up the ambient ISM in a thin, very dense shell. Such shells cool very efficiently which results in fragmentation and subsequent star formation.
To investigate the influence of an induced star formation mode, we extend our stellar birth function to
which allows for both a spontaneous star formation mode and an induced star formation mode. For the spontaneous star formation mode
where fi denotes the fraction of a galaxy covered by SN shells, i.e. g fi is the maximum amount of gas undergoing SN shell-induced star formation. A fraction
In the case of low star formation activity, only a small fraction of the galactic volume is affected by induced star formation, whereas for high star formation activity most of the gas mass might be swept up. The related star formation timescale
Figure 11 displays the SFR for different combinations of the star formation modes. In case of a low temperature
![]() K, the overall SFR is dominated by the induced star formation (ISF) mode (upper panel of Fig. 11) as the agreement between model DI1 (ISF only mode) and the model DI2 (combined star formation modes) demonstrates. This is caused by the high temperatures of about 104 K created by the massive stars formed by induced star formation. Due to negative thermal feedback the spontaneous star formation is almost completely suppressed. This suppression can, of course, not take place in a purely spontaneous star formation model (model A). In that case, the amplitudes of the density driven SFR variations increase because of the temperature dependent variations in the feedback term. The dominance of the dynamical evolution is reflected in the almost identical periods of the SFR in all models. The slightly longer
periods for the models DI1 and DI2 (which include induced star formation) stem from the larger equilibrium radii leading to a longer free-fall time.
K, the overall SFR is dominated by the induced star formation (ISF) mode (upper panel of Fig. 11) as the agreement between model DI1 (ISF only mode) and the model DI2 (combined star formation modes) demonstrates. This is caused by the high temperatures of about 104 K created by the massive stars formed by induced star formation. Due to negative thermal feedback the spontaneous star formation is almost completely suppressed. This suppression can, of course, not take place in a purely spontaneous star formation model (model A). In that case, the amplitudes of the density driven SFR variations increase because of the temperature dependent variations in the feedback term. The dominance of the dynamical evolution is reflected in the almost identical periods of the SFR in all models. The slightly longer
periods for the models DI1 and DI2 (which include induced star formation) stem from the larger equilibrium radii leading to a longer free-fall time.
To have a substantial contribution from the spontaneous star formation mode in a stellar birth function including induced star formation, the high efficiency of the thermal feedback has to be reduced. This can be realized by an increase in the feedback temperature scale ![]() close
to or above the actual gas temperature. Model DI3 has a
close
to or above the actual gas temperature. Model DI3 has a ![]() of 104 K: models using either of the two star formation modes (induced SF, spontaneous SF) or both of them become then comparable in star formation amplitudes, peak values and the overall production rate of stars (Fig. 11, lower panel). Still, the SFR is dominated by the dynamically driven oscillations. It is interesting to note that after 1 Gyr the combined SFR (model DI3) becomes smaller than both single-mode models (DI1 and A2).
of 104 K: models using either of the two star formation modes (induced SF, spontaneous SF) or both of them become then comparable in star formation amplitudes, peak values and the overall production rate of stars (Fig. 11, lower panel). Still, the SFR is dominated by the dynamically driven oscillations. It is interesting to note that after 1 Gyr the combined SFR (model DI3) becomes smaller than both single-mode models (DI1 and A2).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10259f11.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg118.png) |
Figure 11:
Temporal evolution of the SFR for models with different stellar birth modes: induced star formation only (dashed line, DI1), spontaneous star formation only (solid line; |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f12.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg119.png) |
Figure 12: Temporal evolution of the relative contribution of the spontaneous (solid) and the induced (dot-dashed) star formation mode to the total mass converted into stars for model DI3. For comparison the combined SFR is also shown (plus). |
| Open with DEXTER | |
The relative fraction of the spontaneous and the induced star formation mode in the combined model DI3 with respect to the total number of stars formed is shown in Fig. 12: at the very beginning the spontaneous star formation exceeds the induced star formation. However, with an increasing overall SFR the induced star formation begins to dominate and the spontaneous star formation drops to 30%. The contribution of the induced star formation drops already before reaching the first peak of the SFR: this is caused by the dynamics, i.e. the increase in the gas density during the collapse of the system and the subsequent enhanced spontaneous star formation. The temperature of the gas remains almost constant close to 104 K during this evolution. After a Hubble time about 62% of the stars are produced by induced star formation.
It is remarkable that adding induced star formation does not (necessarily) result in a quick consumption of all available gas. For our fiducial model, roughly half of the stars are formed in one of the two star formation modes. Though this fraction can be varied by e.g. amplifying the thermal feedback term of the spontaneous star formation mode or changing the efficiency factor ![]() of the induced star formation, none of the star formation modes leads to a
completely different behaviour of the system: still the overall star formation rate is controlled by the global dynamics.
of the induced star formation, none of the star formation modes leads to a
completely different behaviour of the system: still the overall star formation rate is controlled by the global dynamics.
3.4 Influence of the IMF
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10259f13.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg120.png) |
Figure 13:
Temporal evolution of the SFR for the reference model A (solid), models DX1 and DX2 with a constant IMF-derived fraction |
| Open with DEXTER | |
Constant IMF.
A variation in the stellar initial mass function will mainly affect the mass fraction
Variable IMF.
Recently, Weidner & Kroupa (2005) suggested a variable IMF that depends on the global star formation activity of the galaxy. Their main idea is that relations exist between the global galactic SFR and the maximum mass of the molecular clouds as well as between the cloud mass and the maximum mass of the most massive stars in star formation regions. By this, the global SFR affects the IMF for massive stars which are responsible for the main heating and the metal production.
To investigate such a scenario we modified our equations by introducing an efficiency factor
![]() for the production of massive stars; i.e., we replaced
for the production of massive stars; i.e., we replaced ![]() by
by
![]() .
The efficiency factor was given by a simple fitting formula adopted from the analysis of Köppen et al. (2006):
.
The efficiency factor was given by a simple fitting formula adopted from the analysis of Köppen et al. (2006):
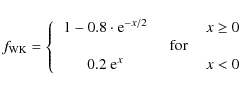 |
(20) |
with
We considered two cases for the energy feedback. In the first case we assumed that the feedback is given by type II supernovae (model DWK1). In that case the heating coefficient corresponding to the energy input per supernova has to be multiplied by the number of massive stars. The number of massive stars, however, depends mainly on the lower mass limit of the mass range of massive stars, and not on the upper mass region that is mainly affected by a Weidner-Kroupa type IMF. A detailed calculation shows that the conversion factor between the number of massive stars and their mass varies only by a factor of 2 when changing the SFR from
![]() to
to
![]() .
In our model DWK1 we neglect this small variation and keep the energy equation.
.
In our model DWK1 we neglect this small variation and keep the energy equation.
In the second case, we assume that the heating is mainly done via radiation (model DWK2). Then, the heating coefficient h becomes a function of the SFR, because of the strong dependence
of the stellar radiative energy input on the upper stellar masses caused by the mass-luminosity relation. A detailed calculation shows that the corresponding efficiency factor is similar to the one for the mass fraction. Therefore, we use for simplicity the same factor
![]() ,
i.e. h is replaced by
,
i.e. h is replaced by
![]() in Eq. (11) (or Eq. (3), respectively).
in Eq. (11) (or Eq. (3), respectively).
Figure 13 shows the evolution of both models. The difference between models with and without a variable IMF are marginal in both, amplitude and timing. Compared to the reference model A, the Weidner-Kroupa-type IMF models have a slightly enhanced SFR. This enhancement is necessary to balance the deficit in the stellar feedback caused by the reduced number of massive stars in the Weidner-Kroupa-type IMF models.
In general the qualitative evolution of the models is not affected by the shown IMF variations, either if we change the mass fraction ![]() assuming a stationary IMF or if we apply the temporal variable star formation-dependent IMF suggested by Weidner & Kroupa (2005). The main reason is the very efficient self-regulation.
assuming a stationary IMF or if we apply the temporal variable star formation-dependent IMF suggested by Weidner & Kroupa (2005). The main reason is the very efficient self-regulation.
4 Discussion
4.1 Timescales
Basically four physically distinct timescales are involved in our description: the heating and cooling timescales,
![]() and
and
![]() ,
the dynamical timescale
,
the dynamical timescale
![]() and the gas consumption (or star formation) timescale
and the gas consumption (or star formation) timescale
![]() .
KTH95 already has shown that
.
KTH95 already has shown that
![]() is usually longer than the timescales governing the energetics of the ISM. This also holds in case of a multiphase ISM model (Köppen et al. 1998), where
the timescale for the additional equilibrium between evaporation and condensation of the gas clouds is well separated from the other two, leaving them unperturbed. Therefore, we expect that inclusion
of a multiphase ISM model would not alter the basic behaviour of our system.
is usually longer than the timescales governing the energetics of the ISM. This also holds in case of a multiphase ISM model (Köppen et al. 1998), where
the timescale for the additional equilibrium between evaporation and condensation of the gas clouds is well separated from the other two, leaving them unperturbed. Therefore, we expect that inclusion
of a multiphase ISM model would not alter the basic behaviour of our system.
For typical mean gas densities the dynamical timescale exceeds also the cooling and heating time (though it is less than the gas consumption time). Therefore, the system almost instantaneously adjusts to the equilibrium state given by the actual gas density. Provided the temperature remains in a regime with a positive slope of the cooling function, the system is then stable. This holds e.g. for temperatures below 104 K, (which is practically the temperature regime for high and moderate gas densities). Thus, the radial oscillations are only initial transient virial oscillations acting on a dynamical timescale.
This behaviour turned out to be rather robust against variations in model parameters like stellar heating, gas mass, initial spatial extension, stellar birth function (with the exception of a linear stellar birth function resulting in an exponentially decaying SFR). Also different IMF parametrizations or even a variable IMF (like the integrated galactic IMF suggested by Weidner & Kroupa 2005) do not change the behaviour of the system qualitatively provided the feedback mechanisms are not cutoff.
4.2 Generic behaviour
Our calculations show that the evolution of the coupled star-gas system is dominated by the dynamical state of the system. Due to the short heating and cooling timescales, the ISM relaxes quickly. Thus, the system's behaviour is governed by the dynamical equation Eq. (7), which has the structural form
with coefficients Ai that are positive for physically sensible descriptions. For simplicity we only consider the self-gravity term here. With a proper choice of the time unit, A4 can be set to unity.
For
![]() there exist equilibrium positions, where the forces cancel out
there exist equilibrium positions, where the forces cancel out
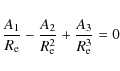 |
(23) |
or
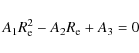 |
(24) |
with the formal solution
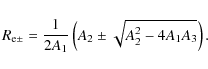 |
(25) |
If A22 > 4 A1 A3, two real equilibrium radii exist. Note that for A1 = 0 (i.e. a gas temperature well below the virial temperature) one simply has a single solution
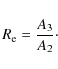 |
(26) |
The analysis of the local stability of these equilibrium points (via the linearized equations) of the Jacobi matrix
 |
(27) | ||
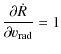 |
(28) | ||
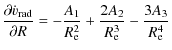 |
(29) | ||
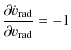 |
(30) |
with
| (31) | |||
| (32) | |||
| (33) |
shows if equilibrium solutions exist ( A22 > 4 A1 A3) that
The consequences of this general structure are shown by a few representative trajectories in the phase space. In Fig. 14 we depict these already for the complete system of our equations. One notes that if the initial conditions are close enough to the attracting focus, the system performs damped nonlinear oscillations before settling in the equilibrium. If the initial radius or the initial speed is too large, there will be a collapse, followed by an expansion. This takes the system to the vicinity of the saddle point, whence the expansion continues without bounds.
If one looks more closely at the behaviour in the equilibrium state (shown in the inset in Fig. 14), one finds that the equilibrium radius does not stay constant, but always increases, more or less rapidly depending on the coefficients Ai. The reason is that the coefficient A1 of the pressure term in the full set of equations depends on the gas temperature. When the system reaches the (dynamical) equilibrium, the gas continues to be consumed by star formation. The cooling of the gas therefore slows down, and the gas temperature increases slowly, giving rise to a slow expansion that contributes to the decrease in the gas density. This rise in temperature causes an increase in the equilibrium radius, which the system simply follows. This leads to the slow drift seen in the inset of Fig. 14.
In Fig. 15 we plot a trajectory in the radius-temperature plane. One notes that the oscillations in radius and temperature go with a nearly constant phase lag, but once the oscillations have damped out, a steady secular increase in both radius and temperature takes over (cf. to inset in Fig. 15).
4.3 Heating-cooling equilibrium at low gas densities
The equilibrium between heating and cooling plays a crucial role for the overall evolution of our system. Cooling is very efficient for typical galactic mean densities, thereby compensating for the
stellar heating processes. However, when the gas density drops, the heating by stars (
![]() )
can overcome the cooling (
)
can overcome the cooling (
![]() ), so the gas quickly heats up (here we assume a linear stellar birth function). Once
temperatures become higher than the virial temperature, the gaseous system expands and a mass loss occurs even without any dramatic event like a starburst. The critical density
), so the gas quickly heats up (here we assume a linear stellar birth function). Once
temperatures become higher than the virial temperature, the gaseous system expands and a mass loss occurs even without any dramatic event like a starburst. The critical density
![]() for gas loss can be estimated from the balance between heating and cooling from Eq. (3) with
for gas loss can be estimated from the balance between heating and cooling from Eq. (3) with
![]()
For the values of model DN1 (linear Schmidt law), we get
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f14.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg159.png) |
Figure 14:
Evolution of the reference model A (solid) and the model DT5 (quadratic Schmidt law with feedback term,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f15.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg160.png) |
Figure 15: Evolution of the reference model A in the R-T plane. The inset shows a blow-up near the equilibrium position reached after the initial oscillations. In the inset linear temperature values are used. |
| Open with DEXTER | |
It is interesting to note that no critical density exists for a quadratic Schmidt law. If n is higher than 2, the system would even run into a cooling catastrophe. In the case of optically thin heating, h in Eq. (34) has to be replaced by
![]() .
Thus, the critical exponent for a cooling catastrophe already becomes n=1. This means that, for all reasonable stellar birth functions, the gas cools down below a critical density. In that case other heating mechanisms providing a steady energy source independent of the amount of massive stars (hence, the SFR and the gas density) might become significant.
.
Thus, the critical exponent for a cooling catastrophe already becomes n=1. This means that, for all reasonable stellar birth functions, the gas cools down below a critical density. In that case other heating mechanisms providing a steady energy source independent of the amount of massive stars (hence, the SFR and the gas density) might become significant.
4.4 Are the dynamics influenced by stellar feedback?
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f16.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg162.png) |
Figure 16: Temporal evolution of the mean radius of model DN1 (solid) and the same model, but neglecting the pressure term in the dynamical equation Eq. (7) (dashed). |
| Open with DEXTER | |
In this paragraph we discuss the impact of stellar feedback on the dynamical evolution. The latter is described by Eq. (7) which contains a pressure gradient term:
![]() .
Stellar feedback can influence the dynamical evolution via this term by heating. Practically speaking, this happens when the pressure term is close to or exceeds the gravitational acceleration terms (the first two terms in Eq. (7)), i.e. when the gas temperature is close to the virial temperature or higher. However, in case of the evolutionary stages shown in this paper the gas temperatures are always of the order 104 K or below, whereas the virial temperature is at least a few 105 K. Physically, the low gas temperatures are
caused by the steep rise in the cooling function beyond 104 K (cf. e.g. Fig. 1 in Böhringer & Hensler 1989). For typical gas densities, unrealistically high heating rates are required to reach (and keep) temperatures beyond 104 K.
.
Stellar feedback can influence the dynamical evolution via this term by heating. Practically speaking, this happens when the pressure term is close to or exceeds the gravitational acceleration terms (the first two terms in Eq. (7)), i.e. when the gas temperature is close to the virial temperature or higher. However, in case of the evolutionary stages shown in this paper the gas temperatures are always of the order 104 K or below, whereas the virial temperature is at least a few 105 K. Physically, the low gas temperatures are
caused by the steep rise in the cooling function beyond 104 K (cf. e.g. Fig. 1 in Böhringer & Hensler 1989). For typical gas densities, unrealistically high heating rates are required to reach (and keep) temperatures beyond 104 K.
Therefore, the dynamics are almost unaffected by the thermal state of the gas. This is nicely illustrated in Fig. 16 where the mean radius of model DN1 is compared with a model neglecting the pressure term of Eq. (7): no substantial difference between both models is discernible. Small differences develop at maximum compression when the gravitational terms and the angular momentum almost cancel. For this short moment, the small pressure-gradient term contributes recognisably. It acts as a reduction of the gravity, e.g. like a density reduction, which results in slightly longer periods.
The situation only changes when either the gas temperature rises or the virial temperature decreases. The latter can happen for systems of lower mass, e.g., for compact systems like globular clusters (no DM,
![]() )
or more extended systems like dSph galaxies, when the virial temperatures drop down to a few 104 K (we will discuss this in a forthcoming paper). Alternatively, the gas temperature might be heated to a few 105 K. Practically speaking, this is
only the case where the criterion for run-away heating, Eq. (34), is fulfilled, i.e. when the gas density drops below a critical value due to gas consumption. The actual critical values, however, are too low, to be practically relevant within the limits of our model.
)
or more extended systems like dSph galaxies, when the virial temperatures drop down to a few 104 K (we will discuss this in a forthcoming paper). Alternatively, the gas temperature might be heated to a few 105 K. Practically speaking, this is
only the case where the criterion for run-away heating, Eq. (34), is fulfilled, i.e. when the gas density drops below a critical value due to gas consumption. The actual critical values, however, are too low, to be practically relevant within the limits of our model.
The physical reason for the general insensitivity of the dynamics to the thermal feedback induced by stars is the steep rise in the cooling function near 104 K. As long as radiative cooling is the main agent of energy dissipation and as long as the gas temperature is kept below 104 K, thermal feedback will only affect the dynamics of systems with a virial temperature near 104 K. However, for short periods (especially at early stages), the gas temperature might reach or exceed temperatures of 105 K briefly affecting the dynamics of systems with virial temperatures of that order.
However, thermal pressure (and therefore classical cooling) does not need to be the main agent counter acting gravity. If the system is composed of sufficiently compact objects, their velocity dispersion will provide a kinetic pressure, e.g., in case of a cloud system, the internal temperature of the clouds is irrelevant for their overall dynamics, which is driven by the velocity dispersion. In that case, inelastic cloud-cloud collisions provide the relevant energy dissipation mechanism. Different from radiative cooling, there is no steep increase in the cloud-cloud ``cooling'' function and the arguments preventing a strong mutual coupling between dynamics, star formation, and stellar feedback are not applicable. Additionally, the timescale for energy dissipation due to cloud-cloud collisions is much longer than the radiative cooling timescales, which also might allow for more of a variety of responses by the system. We will discuss the related aspects in a future paper.
4.5 Comparison with ``full'' dwarf galaxy simulations
How do our simple models compare with detailed numerical simulations? Though important, it is a difficult question. At the moment there are only a small number of sophisticated simulations available. They differ by many aspects between themselves and from our calculations: e.g. with respect to the implemented physics, the numerical methods or the initial conditions and the general physical set-up. Unfortunately, a standard test for dwarf galaxy evolution/physics does not exist.
With all these differences in mind a detailed comparison is not meaningful, but a qualitative comparison should shed light on the applicability of our ansatz; e.g., Pelupessy et al. (2004, hereafter PWI04) model the evolution of a rotating disk-like dwarf galaxy embedded in a dark matter halo. They apply a sophisticated ISM model including heating, cooling and an ionisation/recombination scheme. Their SFR develops a quasi-periodic behaviour with a period of about twice the dynamical time for (weak) bursts. PWI04 interpret this behaviour as the result of a kick that drives the gas out of the disk and the subsequent fallback of the gas initiating the next star formation episode. This concept is very similar to our adopted coupling between feedback and dynamics, though we are investigating a spherical system.
The overall star formation peaks in PWI04 are much smaller than in our calculations (by one order for a fiducial model including a feedback term). This might be caused by the different initial set-ups, because the spherical configuration we study allows for a much deeper collapse than a rotationally supported disk. As a result, the density and, thus, the star formation variations are much higher in our case than for PWI04. For comparison, the full 1d chemo-dynamical models of Hensler et al. (2004, afterwards HTG04) model spherical galaxies (but without dark matter) and they exhibit SFR comparable to ours. Similar to our calculations, the models by HTG04 show a strong trend toward self-regulation that has also been found in the 3D chemo-dynamical N-body-SPH models of Berczik et al. (2002) including dark matter. The PWI04 models exhibit no strong starbursts as the moderate variation in their star formation rates shows (Figs. 4 and 6 in PWI04). In contrast to them we were looking for strong variations that are rarer, but that exist (van Zee 2001).
Another interesting example of SFR variability is the SPH simulation of Struck (2005, hereafter S05), who investigated the evolution of a disk galaxy of about 2 ![]()
![]() .
The gaseous component in this simulation was subject to star formation, stellar feedback (by SNII) and dissipation (radiative cooling). S05 finds a strongly variable star formation with two modes: local, off-centre gas concentrations can lead to local, ``premature'' bursts preventing the system from a global starburst. The result is an incoherent star formation pattern with an irregular, mildly variable SFR. Sometimes, however, large-scale motions coherently funnel matter into the central region where a strong starburst is then ignited (cf. Figs. 1 and A1 in S05). The related timescale is about twice the free-fall timescale of a particle at 2-3 kpc above the plane. This burst mode corresponds physically to the oscillatory ``breathing'' mode seen in our calculations, though the masses of the models differ by one order of magnitude. Similarly, the burst duration (about 10 Myr) is comparable to the burst duration in our models. On the other hand, our simple model is unable to resolve purely local effects leading to incoherent star formation modes.
.
The gaseous component in this simulation was subject to star formation, stellar feedback (by SNII) and dissipation (radiative cooling). S05 finds a strongly variable star formation with two modes: local, off-centre gas concentrations can lead to local, ``premature'' bursts preventing the system from a global starburst. The result is an incoherent star formation pattern with an irregular, mildly variable SFR. Sometimes, however, large-scale motions coherently funnel matter into the central region where a strong starburst is then ignited (cf. Figs. 1 and A1 in S05). The related timescale is about twice the free-fall timescale of a particle at 2-3 kpc above the plane. This burst mode corresponds physically to the oscillatory ``breathing'' mode seen in our calculations, though the masses of the models differ by one order of magnitude. Similarly, the burst duration (about 10 Myr) is comparable to the burst duration in our models. On the other hand, our simple model is unable to resolve purely local effects leading to incoherent star formation modes.
Though a detailed comparison between our simple model and the different complex numerical simulations is unreasonable because of differences in implemented physics and in initial conditions, the qualitative agreement is obvious: the bursts essentially stem from the oscillations of the global dynamics. The gas simply has to follow them, so the starbursts could appear in any system. The tight coupling between the large-scale dynamics and the occurrence of global (strong) starbursts is corroborated in all the different studies, by this motivating and strengthening our ansatz.
4.6 A speculation about bursts in interacting galaxies...
By definition our model refers to isolated systems. However, the initial conditions leading to a collapse of the system could also stem from galaxy interactions. Therefore, one might speculate about the possible implications for interacting galaxies.
An important result of our simulations is the strong coupling of the SFR to the dynamics (with the discussed exception of linear Schmidt law without feedback term). To create a starburst, the gas density must be strongly enhanced, otherwise the self-regulation prevents large SFR variations. The availability of large amounts of gas alone is not sufficient for a starburst as the example of poststarburst E+A galaxies with a large amount of HI gas demonstrated (Buyle et al. 2006).
For interacting galaxies, one might speculate that only those perturbations leading to structural rearrangements, e.g. a substantial inflow of gas or a merger, end up in a starburst. Whether galaxies produce sufficient density enhancements, hence a starburst, depends not only on the existence of a proper perturbation (like an interaction or an internal bar) but also on the internal dynamical stability of the involved galaxies. This might explain the wide variety of star formation responses found in simulations of interacting galaxies (e.g. in Di Matteo et al. 2007).
4.7 Simplifications of the model
Describing galaxy evolution by a few equations always requires simplifications. Here we want to comment on a few simplifications (or neglections).
Dynamics.
The dynamics of the system is summarily described by a mean radius and its temporal change. A decomposition into several structural components (like a disk-bulge-halo structure) is beyond the limits of this model. Moreover, density gradients or even an asphericity are not considered. An extension of our simple model might be possible. However, with respect to structure formation, we think that the related physics are too complex to be condensed reliably into another ``simple'' equation.Implicitly we also assumed that the dynamics of the different baryonic components can be modelled by the same mean radius. This need not to be true, of course. Strictly speaking this is only valid when the dynamics of stars and gas is either subject to the same acceleration terms (e.g. similar pressure/velocity dispersion terms) and/or when the self-gravity of the stars is not important for the dynamical evolution of the gas. The latter is the case in gas-rich galaxies or in dark-matter-dominated potentials (when the self-gravity term remains unimportant). Since we are interested here in starburst galaxies that are mainly gas-rich dwarf galaxies, the restriction to gas-dominated stages seems reasonable. The dynamical equations can be easily extended to several distinct components, if required.
ISM description.
In our approach we adopted a single ISM phase. An extension to a multi-phase ISM model like in Köppen et al. (1998) would be possible and is envisaged. However, we do not expect significant changes, because the timescales related to the additional multi-phase ISM processes (like condensation, evaporation) are separated well from the other timescales: they are much longer than the dominant heating and cooling processes, so that thermal equilibrium is established rapidly and independently of the fractional ratio of clouds and intercloud gas. On the other hand, evaporation and condensation of clouds occur much faster than the gas consumption due to star formation. Thus, we expect that the system would again break down in a hierarchy of well-separated equilibria, and the related equilibrium SFR would thus still be governed by the equilibrium temperature in the cloud phase.
A new effect that arises for a clumpy ISM is another energy dissipation process. In the case of a diffuse ISM, dissipation is mainly driven by radiative cooling; however, in case of a system composed of molecular clouds, inelastic cloud collisions provide a ``cooling'' mechanism dissipating the kinetic energy related to the motion of the clouds. Though the scaling of this dissipation process is identical to radiative cooling (i.e.
![]() ), the related timescales differ strongly. In general, cloud-cloud collisions operate on a much longer timescale than radiative cooling or even the dynamics. Thus, the dynamical evolution of a cloud system might operate not only on a dynamical timescale, but also on a dissipational timescale which then directly affects the SFR. We will discuss the implications in a forthcoming paper in detail.
), the related timescales differ strongly. In general, cloud-cloud collisions operate on a much longer timescale than radiative cooling or even the dynamics. Thus, the dynamical evolution of a cloud system might operate not only on a dynamical timescale, but also on a dissipational timescale which then directly affects the SFR. We will discuss the implications in a forthcoming paper in detail.
Heating.
For the heating we only considered massive stars and instantaneous feedback. Though massive stars are considered to be a major source of ISM heating, e.g. with respect to turbulence, other sources might be interesting, too. For example, type I supernovae provide a nonlocal and a non-instantaneous energy source. Especially, the delayed energy feedback might be an important energy source after star formation has ceased. Similarly, the energy injected by an AGN might be an important energy source, too.
5 Summary and conclusions
We investigated the evolution of star-forming dwarf galaxies by means of an extended one-zone model. In contrast to previous one-zone models, the dynamics of the galaxy has been taken into account by an additional equation of motion for the mean radius of the galaxy. Comparison with SPH models shows that this rather approximate treatment is reasonable and provides a sensible description. This approach allows for a coupling between the dynamical state of the galaxy and its internal properties, such as star formation activity and the thermal state of the interstellar gas. Here we focussed especially on the conditions under which starburst episodes could occur in isolated galaxies.
We find that the seemingly complicated system of equations for the numerous physical variables (radius, radial speed, gas mass, star mass, thermal energy) breaks down into quite a clearly separated system for the internal conditions of the galaxy and the dynamical aspects that evolve more slowly. Thus, star formation and other internal processes are strongly governed by the dynamical state. In particular, the total SFR follows the evolution of the volume directly, if it depends nonlinearly on the local gas density. On the other hand, the dynamics are only very weakly influenced by the internal state, because the gas temperature remains well below virial temperature, primarily because of the strong rise of the radiative cooling function near 104 K. The consequence is that the evolution of the dynamical state of the galaxy remains fairly robust against changes and details in the internal condition, specifically the details of the prescriptions for star formation. We also expect that the inclusion of a multiphase description of the ISM would not upset this characteristic.
The evolution of the total SFR is thus dominated by the damped virial oscillations that cause enhancements of the SFR whenever the galaxy is in a more compressed state. This main type of quasi-periodic starbursts is related to the dynamical timescale of the system. Typically, the star formation variations follow the variations in the gas density induced by decaying virial oscillations. Because of the short heating and cooling timescales the established SFR remains close to the equilibrium SFR determined by the current mean gas density. Modifications in the adopted star formation modes, i.e. assuming both spontaneous and induced star formation/positive feedback, give qualitatively similar results. Induced star formation neither leads to a fundamentally different response nor causes a global conflagration. Variations in the IMF or introduction of a time-variable IMF similarly do not change that picture. In all cases, the variations in the SFR can be appreciable, amounting to peak values up to 10 times the average value.
A second type of burst occurs for low gas densities and temperatures beyond 104 K. This mode is not related to the dynamical evolution, but an instability operating when the cooling function drops with increasing temperature. The latter works for some temperature regimes (related to H and He line emission) above 104 K, which can only be reached when there is a very low gas density.
Since the first type of bursts is governed by the evolution of the dynamical state of the galaxy, it also seems plausible to discuss the results of our simplified models for isolated galaxies in other contexts, too. Virial oscillations following structural changes induced by galaxy interactions would also lead to an enhancement of the SFR, thus providing an additional mechanism that shapes starbursts. Alternatively, if an interaction does not result in a substantial mass redistribution, self-regulation might prevent a starburst.
Acknowledgements
We thank Jay Gallagher, Simone Recchi, and Shu-ichiro Inutsuka for stimulating discussions on starbursts and induced star formation. We are very grateful to the referee, Curt Struck, for detailed and fruitful comments that greatly improved the paper. C.T. is grateful to the Observatoire de Strasbourg for hospitality and support within the visitor programme.
References
- Bekki, K. 2008, MNRAS, 338, L10 [NASA ADS] (In the text)
- Berczik, P., Hensler, G., Theis, Ch., & Spurzem, R. 2002, Ap&SS, 281, 297 [NASA ADS] [CrossRef] (In the text)
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton Univ. Press)
- Blitz, L., & Rosolowsky, E. 2004, ApJ, 612, L29 [NASA ADS] [CrossRef]
- Böhringer, H., & Hensler, G. 1989, A&A, 215, 147 [NASA ADS] (In the text)
- Burkert, A. 1995, ApJ, 447, L25 [NASA ADS] [CrossRef] (In the text)
- Buyle, P., Michielsen, D., De Rijcke, S., et al. 2006, ApJ, 649, 163 [NASA ADS] [CrossRef] (In the text)
- Dalgarno, A., & McCray, R. A. 1972, ARA&A, 10, 375 [NASA ADS] [CrossRef] (In the text)
- Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2007, A&A, 468, 61 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dohm-Palmer, R. C., Skillman, E., Mateo, M., et al. 2002, AJ, 123, 813 [NASA ADS] [CrossRef] (In the text)
- Ehlerová, S., Palous, J., Theis, Ch., & Hensler, G. 1997, A&A, 328, 121 [NASA ADS] (In the text)
- Gallagher, J. S., & Hunter, D. 1984, ARA&A, 22, 37 [NASA ADS] (In the text)
- Gerola, H., & Seiden, P. E. 1978, ApJ, 223, 129 [NASA ADS] [CrossRef] (In the text)
- Greggio, L., Marconi, G., Tosi, M., & Focardi, P. 1993, AJ, 105, 894 [NASA ADS] [CrossRef]
- Harfst, S., Theis, Ch., & Hensler, G. 2006, A&A, 449, 509 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hensler, G., Theis, Ch., & Gallagher, J. 2004, A&A, 426, 25 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hosokawa, T., & Inutsuka, S. 2005, ApJ, 623, 917 [NASA ADS] [CrossRef] (In the text)
- Hosokawa, T., & Inutsuka, S. 2006, ApJ, 646, 240 [NASA ADS] [CrossRef]
- Ikeuchi, S., & Tomita, H. 1983, PASJ, 35, 77 [NASA ADS] (In the text)
- Köppen, J., Theis, Ch., & Hensler, G. 1995, A&A, 296, 99 [NASA ADS], KTH95 (In the text)
- Köppen, J., Theis, Ch., & Hensler, G. 1998, A&A, 331, 524 [NASA ADS] (In the text)
- Köppen, J., Weidner, C., & Kroupa, P. 2007, MNRAS, 375, 673 [NASA ADS] [CrossRef] (In the text)
- Nikolic, B., Cullen, H., & Alexander, P. 2004, MNRAS, 355, 874 [NASA ADS] [CrossRef] (In the text)
- Pelupessy, F. I., van der Werf, P. P., & Icke, V. 2004, A&A, 422, 55 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes (Cambridge: Cambridge University Press) (In the text)
- Quillen, A. C., & Bland-Hawthorn, J. 2008, MNRAS, 386, 2227 [NASA ADS] [CrossRef] (In the text)
- Samland, M., Hensler, G., & Theis, Ch. 1997, ApJ, 476, 544 [NASA ADS] [CrossRef]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] (In the text)
- Scalo, J., & Struck-Marcell, C. 1986, ApJ, 301, 77 [NASA ADS] [CrossRef] (In the text)
- Struck, C. 2005, in Proc. of Starbursts: From 30 Doradus to Lyman Break Galaxies, Cambridge, UK, ed. R. de Grijs, & R. M. Gonzalez-Delgado, Ap&SS, 329, 163 (In the text)
- Struck, C. 2006, in Astrophysics Update 2, ed. J. Mason, 115 (In the text)
- Theis, Ch., & Hensler, G. 1993, A&A, 280, 85 [NASA ADS]
- Theis, Ch., Burkert, A., & Hensler, G. 1992, A&A, 265, 465 [NASA ADS] (In the text)
- Weidner, C., & Kroupa, P. 2005, ApJ, 625, 754 [NASA ADS] [CrossRef] (In the text)
- van Zee, L. 2001, AJ, 121, 2003 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ...T
![[*]](/icons/foot_motif.png)
- Because the thermal state of all gas components is summarised in a single temperature T, this temperature is a ``typical'' temperature of the gas characterising the thermal energy or pressure of the ISM. This notion is rather similar e.g. to the notion of the external pressure in Blitz & Rosolowsky (2004).
- ... temperatures
![[*]](/icons/foot_motif.png)
- A negative temperature
 corresponds to a positive feedback. However, it is related to the gas temperature (velocity dispersion) alone. Therefore, we used a physically better motivated ansatz for positive stellar feedback in Sect. 3.3.
corresponds to a positive feedback. However, it is related to the gas temperature (velocity dispersion) alone. Therefore, we used a physically better motivated ansatz for positive stellar feedback in Sect. 3.3.
All Tables
Table 1: Properties of the numerical models.
All Figures
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f1a.eps} \includegraphics[angle=270,width=8.5cm,clip]{10259f1b.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg69.png) |
Figure 1: Temporal evolution of the half-mass radius in a 3D-SPH simulation of a collapsing gas sphere in a dark matter halo and the result for the simple equation of motion (7). Shown are models fitting the early stage well (with CP=1.91, Cj=0.15, Cf=2.06, left) or the late stage (with CP=1.97, Cj=0.11, Cf=0.88, right). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=16cm,clip]{10259f2.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg77.png) |
Figure 2:
Initial temporal evolution of a model with a baryonic mass of 2 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\includegraphics[angle=270,width=16cm,clip]{10259f3.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg78.png) |
Figure 3: Same as Fig. 2, but for 5 Gyr of evolution. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10259f4.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg89.png) |
Figure 4: Temporal evolution of the SFR for models with different exponent in the stellar birth function: n=1 (model DN1, filled circles), n=1.1 (DN2, dot-dashed), n=1.5(DN3, solid), n=2 (DN4, open squares) and n=2.5 (DN5, dashed). The normalisation constant Cn is kept constant at 0.007. No negative thermal feedback term is included in the stellar birth function. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=15.95cm,clip]{10259f5.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg90.png) |
Figure 5: Temporal evolution of model DN1 characterised by a linear Schmidt law ( n=1, C1=0.007), but without a negative thermal feedback term in the stellar birth function. For further details see Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}\includegraphics[angle=270,width=15.95cm,clip]{10259f6.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg91.png) |
Figure 6: Temporal evolution of model DN2 characterised by a Schmidt law ( n=1.1, Cn=0.007), but without a negative thermal feedback term in the stellar birth function. For further details see Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=16cm,clip]{10259f7.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg92.png) |
Figure 7: Temporal evolution of model DN4 characterized by a Schmidt law ( n=2, Cn=0.007), but without a negative thermal feedback term in the stellar birth function. For further details see Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f8.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg102.png) |
Figure 8: Temporal evolution of the SFR for the models DN4 and DN6 both characterized by a quadratic Schmidt law with different normalisation constants: Cn=0.007 (DN4) and Cn=0.7 (DN6). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f9.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg105.png) |
Figure 9:
Temporal evolution of the SFR for models with a linear Schmidt law (n=1) and a negative thermal feedback term with different values of the temperature parameter |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10259f10.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg108.png) |
Figure 10:
Late temporal evolution of the gas temperature ( upper and
lower panel, solid line), the SFR ( middle panel) and the mean radius of the system ( lower panel, dashed line) for the model with a linear Schmidt law (n=1) and a negative thermal
feedback term with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10259f11.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg118.png) |
Figure 11:
Temporal evolution of the SFR for models with different stellar birth modes: induced star formation only (dashed line, DI1), spontaneous star formation only (solid line; |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f12.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg119.png) |
Figure 12: Temporal evolution of the relative contribution of the spontaneous (solid) and the induced (dot-dashed) star formation mode to the total mass converted into stars for model DI3. For comparison the combined SFR is also shown (plus). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10259f13.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg120.png) |
Figure 13:
Temporal evolution of the SFR for the reference model A (solid), models DX1 and DX2 with a constant IMF-derived fraction |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f14.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg159.png) |
Figure 14:
Evolution of the reference model A (solid) and the model DT5 (quadratic Schmidt law with feedback term,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f15.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg160.png) |
Figure 15: Evolution of the reference model A in the R-T plane. The inset shows a blow-up near the equilibrium position reached after the initial oscillations. In the inset linear temperature values are used. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10259f16.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10259-08/Timg162.png) |
Figure 16: Temporal evolution of the mean radius of model DN1 (solid) and the same model, but neglecting the pressure term in the dynamical equation Eq. (7) (dashed). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.