EDP Sciences
Home All issues Volume 501 / No 3 (July III 2009) A&A, 501 3 (2009) 865-877 Full HTML
Free Access
Issue
A&A
Volume 501, Number 3, July III 2009
Page(s) 865 - 877
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/200811570
Published online 13 May 2009

A comprehensive study of large-scale structures in the GOODS-SOUTH field up to 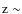${\rm z} \sim $ 2.5

S. Salimbeni1,2 - M. Castellano3,2 - L. Pentericci2 - D. Trevese3 - F. Fiore2 - A. Grazian2 - A. Fontana2 - E. Giallongo2 - K. Boutsia2 - S. Cristiani4 - C. De Santis5,6 - S. Gallozzi2 - N. Menci2 - M. Nonino4 - D. Paris2 - P. Santini2 - E. Vanzella4

1 - Department of Astronomy, University of Massachusetts, 710 North Pleasant Street, Amherst, MA 01003, USA
2 - INAF - Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monteporzio (RM), Italy
3 - Dipartimento di Fisica, Universitá di Roma ``La Sapienza'', P.le A. Moro 2, 00185 Roma, Italy
4 - INAF - Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy
5 - Dip. di Fisica, Universitá Tor Vergata, via della Ricerca Scientifica 1, 00133 Roma, Italy
6 - INFN-Roma Tor Vergata, via della Ricerca Scientifica 1, 00133 Roma, Italy

Received 22 December 2008 / Accepted 21 March 2009

Abstract
Aims. The aim of the present paper is to identify and study the properties and galactic content of groups and clusters in the GOODS-South field up to $z\sim 2.5$, and to analyse the physical properties of galaxies as a continuous function of environmental density up to high redshift.
Methods. We used the deep ( $z_{850}\sim 26$), multi-wavelength GOODS-MUSIC catalogue, which has a 15% of spectroscopic redshifts and accurate photometric redshifts for the remaining fraction. On these data, we applied a (2+1)D algorithm, previously developed by our group, that provides an adaptive estimate of the 3D density field. We supported our analysis with simulations to evaluate the purity and the completeness of the cluster catalogue produced by our algorithm.
Results. We find several high-density peaks embedded in larger structures in the redshift range 0.4-2.5. From the analysis of their physical properties (mass profile, M200, $\sigma_v$, $L_{\rm X}$, U-B vs. B diagram), we find that most of them are groups of galaxies, while two are poor clusters with masses a few times $10^{14}~M_\odot$. For these two clusters we find from the Chandra 2Ms data an X-ray emission significantly lower than expected from their optical properties, suggesting that the two clusters are either not virialised or are gas poor. We find that the slope of the colour magnitude relation, for these groups and clusters, is constant at least up to $z\sim 1$. We also analyse the dependence on environment of galaxy colours, luminosities, stellar masses, ages, and star formations. We find that galaxies in high-density regions are, on average, more luminous and massive than field galaxies up to $z \sim 2$. The fraction of red galaxies increases with luminosity and with density up to $z\sim 1.2$. At higher z this dependence on density disappears. The variation of galaxy properties as a function of redshift and density suggests that a significant change occurs at $z \sim 1.5$-2.

Key words: galaxies: distances and redshifts - galaxies: evolution - galaxies: high-redshift - galaxies: clusters: general - galaxies: fundamental parameters - cosmology: large-scale structure of Universe

1 Introduction

The study of galaxy clusters and of the variation of galaxy properties as a function of the environment are fundamental tools for understanding the formation and evolution of the large-scale structures and of the different galaxy populations, observed both in the local and in the high-redshift Universe. The effects of the environment on galaxy evolution have been studied at progressively higher redshifts through analysis of single clusters (e.g. Rettura et al. 2008; Tran et al. 2005; Mei et al. 2006; Nakata et al. 2005; Menci et al. 2008; Treu et al. 2003), as well as studying the variation of galaxy colours, morphologies, and other physical parameters as a function of projected or 3-dimensional density (e.g. Cooper et al. 2007; Cucciati et al. 2006; Dressler et al. 1997; Blanton et al. 2005; Elbaz et al. 2007). Moreover, the analysis of cluster properties at different wavelengths provides interesting insights into the matter content and evolutionary histories of these structures (Popesso et al. 2007; Lubin et al. 2004; Rasmussen et al. 2006).

A variety of survey techniques have proved effective at finding galaxy clusters up to $z\sim 1$ and beyond. The X-ray selected samples at $z \ge 1$ probe the most massive and dynamically relaxed systems (e.g., Maughan et al. 2004; Bremer et al. 2006; Lidman et al. 2008; Stanford et al. 2006). Large-area multicolour surveys, such as the red-sequence survey (e.g. Gladders & Yee 2005), have collected samples of systems in a range of evolutionary stages. The mid-IR cameras on board the Spitzer and Akari satellites has extended the range and power of multicolour surveys, producing confirmed and candidate clusters up to $z \sim 1.7$(Goto et al. 2008; Stanford et al. 2005; Eisenhardt et al. 2008). However, most of the previous techniques present some difficulties in the range 1.5< z <2.5, where we expect to observe the formation of the red sequence and the first hints of colour segregation (Cucciati et al. 2006; Kodama et al. 2007). Searching for extended X-ray sources becomes progressively more difficult at great distances, because the surface brightness of the X-ray emission fades as (1+z)4. The sensitivity of surveys exploiting the Sunyaev-Zeldovich (SZ) effect is, at present, insufficient at detecting any known clusters at z > 1 (Carlstrom et al. 2002; Staniszewski et al. 2008). Finally, detecting of galaxy overdensities in surveys using two-dimensional algorithms either requires additional a priori assumptions on galaxy luminosity function (LF), as in the Matched Filter algorithm (Postman et al. 1996), or relies on the presence of a red sequence (Gladders & Yee 2000). Biases produced by these assumptions can hardly be evaluated at high redshift.

In this context, photometric redshifts obtained from deep multi-band surveys for large samples of galaxies, though with relatively low accuracy if compared to spectroscopic redshifts, can be exploited to detect and study distant structures. In the past few years, several authors (e.g. Mazure et al. 2007; Zatloukal et al. 2007; Eisenhardt et al. 2008; Botzler et al. 2004; van Breukelen et al. 2006; Scoville et al. 2007) have developed or extended known algorithms to take the greater redshift uncertainties into account. We have developed a new algorithm that uses an adaptive estimate of the 3D density field, as described in detail in Trevese et al. (2007). This method combines galaxy angular positions and precise photometric redshifts to estimate the galaxy number density and to detect galaxy over-densities in three dimensions also at z>1, as described in Sect. 3.

Our first application to the K20 survey (Cimatti et al. 2002) detected two clusters at $z\sim 0.7$ and $z\sim 1$ (Trevese et al. 2007), previously identified through spectroscopy (Gilli et al. 2003; Adami et al. 2005). We then applied the algorithm to the much larger GOODS-South field, and in Castellano et al. (2007), elsewhere C07, we reported our initial results, i.e. the discovery of a forming cluster of galaxies at $z\sim 1.6$.

In this paper we present the application of the algorithm to the entire GOODS-South area ($\sim $ $143~{\rm arcmin}^2$), using the GOODS-MUSIC catalogue (Grazian et al. 2006a) up to $z\sim 2.5$, to give a comprehensive description of the large-scale structures in this field, with a detailed analysis of the physical properties of each high-density peak. We also study the physical properties of galaxies as a function of environmental density up to redshift 2.5, higher than previous similar studies (e.g., Cooper et al. 2007; Cucciati et al. 2006).

To validate our technique, we analysed the completeness and purity of our cluster detection algorithm, up to $z\sim 2.5$, through its application to a set of numerically simulated galaxy catalogues. Besides allowing an assessment of the physical reality of the structures found in the GOODS field, this analysis provides the starting point to test the reliability of the algorithm in view of our plan to apply it to photometric surveys of similar depth but covering much larger areas.

The paper is organised as follows. In Sect. 2, we describe the basic features of our dataset. In Sect. 3, we summarise the basic features of the (2+1)D algorithm used in our analysis, and compare it with other methods based on photometric redshifts. In Sect. 4, we show the results of the application of our method to simulated data. In Sect. 5, we present the catalogue of the structures detected and the derived physical properties. In Sect. 6, we study the colour-magnitude diagrams of the detected structures. In Sect. 7, we analyse the physical properties of galaxies as a continuous function of environmental density.

All the magnitudes used in the present paper are in the AB system, if not otherwise declared. We adopt a cosmology with $\Omega_\Lambda=0.7$, $\Omega_{\rm M}=0.3$, and $H_0=70~{\rm km~s}^{-1}~{\rm Mpc}^{-1}$.

2 The GOODS-MUSIC catalogue

We used the multicolour GOODS-MUSIC catalogue (GOODS MUlticolour Southern Infrared Catalogue; Grazian et al. 2006a). This catalogue comprises information in 14 bands (from U band to $8~\mu{\rm m}$) over an area of about 143.2  ${\rm arcmin}^2$. We used the z850-selected sample ( $z_{850}\sim 26$), which contains 9862 galaxies (after excluding AGNs and galactic stars). About 15% of the galaxies in the sample have spectroscopic redshift, and for the other galaxies we used photometric redshifts obtained from a standard $\chi^2$ minimisation over a large set of spectral models (see e.g., Fontana et al. 2000). The accuracy of the photometric redshift is very good, with an rms of 0.03 for the $\Delta z/(1+z)$ distribution up to redshift z=2. For a detailed description of the catalogue, we refer to Grazian et al. (2006a).

The method we applied to estimate the rest-frame magnitudes and the other physical parameters (M, SFR, age) is described in previous papers (e.g., Fontana et al. 2006). Briefly, we used a $\chi^2$ minimisation analysis, comparing the observed SED of each galaxy to synthetic templates, and the redshift is fixed during the fitting process to the spectroscopic or photometric redshift derived in Grazian et al. (2006a). The set of templates is computed with standard spectral synthesis models (Bruzual & Charlot 2003), chosen to broadly encompass the variety of star formation histories, metallicities, and extinctions of real galaxies. For each model of this grid, we computed the expected magnitudes in our filter set and found the best-fitting template. From the best-fitting template, we obtained, for each galaxy, the physical parameters that we used in the analysis. Clearly, the physical properties are subject to uncertainties and biases related to the synthetic libraries used to fit the galaxy SEDs; however, as shown in Fontana et al. (2006), the extension of the SEDs to mid-IR wavelengths with IRAC tends to reduce the uncertainties on the derived stellar masses. For a detailed analysis of the uncertainties on the physical properties we refer to our previous papers (Fontana et al. 2006; Grazian et al. 2007). In the present work we also used of the 2Ms X-ray observation of the Chandra Deep Field South presented by Luo et al. (2008) and of the catalogue of VLA radio sources (1.4 GHz) on the CDFS compiled by Miller et al. (2008).

3 The (2+1)D algorithm for the density estimation

To estimate a three-dimensional density, we developed a method that combines the angular position with the photometric redshift of each object. The algorithm is described in detail in Trevese et al. (2007). Here we outline its main features and, in the next section, we present the simulations used to estimate its reliability.

The procedure is designed to automatically take the probability into account that a galaxy in our survey is physically associated to a given overdensity. This is obtained by computing the galaxy densities in volumes whose shape is proportional to positional uncertainties in each dimension ($\alpha$, $\delta$, and z).

First, we divided the volume of the survey in cells whose extension in different directions ( $\Delta\alpha, \Delta \delta, \Delta z$) depends on the relevant positional accuracy and thus are elongated in the radial direction. We chose the cell sizes small enough to keep an acceptable spatial resolution, while avoiding a useless increase in the computing time. We adopted $\Delta z =0.025$(radial direction) and $\Delta \alpha = \Delta\delta \sim 2.4$ arcsec in transverse direction, the latter value corresponds to $\sim $30, 40 and 60 kpc (comoving), respectively at $z\sim 0.7$, $\sim $1.0 and $\sim $2.0.

Table 1:   Completeness and purity.

For each cell in space we then counted neighbouring objects in volumes that are progressively increased in each direction by steps of one cell, thus keeping the symmetry imposed by the different intrinsic resolution. When a number n of objects is reached, we assigned a comoving density $\rho = n/ V_n$ to the cell, where Vn is the comoving volume that includes the n-nearest neighbours. Clusters would be better characterised by their proper density since they have already decoupled from the Hubble flow; however, we notice that the average uncertainty on photometric redshifts, which grows with redshift as (1+z), forces us to measure densities in volumes that are orders of magnitude larger than the real volume of a cluster, even at low-z. Thus we decided to measure comoving densities, which have the further advantage of giving a redshift-independent density scale for the background. We fixed n = 15 as a trade off between spatial resolution and signal-to-noise ratio. Indeed, through the simulation described in Sect. 4, we verified that a lower n would greatly raise the high-frequency noise in the density maps, thus increasing the contamination from false detections in the cluster sample, even at low redshift (``purity'' parameter in Table 1). In the density estimation, we assigned a weight w(z) to each detected galaxy at redshift z, to take into account the increase in limiting absolute magnitude with increasing redshift for a given apparent magnitude limit. We chose w(z)=1/s(z), where s(z) is the fraction of objects detected with respect to a reference redshift $z_{\rm c}$ below which we detected all objects brighter than the relevant $M_{\rm c} \equiv M_{\rm lim}(z_{\rm c})$:

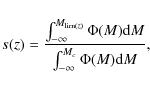\begin{displaymath}s(z)=\frac{\int^{M_{{\rm lim}(z)}}_{-\infty}\Phi(M){\rm d}M}{\int^{M_c}_{-\infty}\Phi(M){\rm d}M}, \end{displaymath} (1)

where $\Phi(M)$ is the redshift-dependent galaxy luminosity function computed with the same GOODS-MUSIC catalogue (Salimbeni et al. 2008), $M_{\rm lim}(z)$ is the absolute magnitude limit at the given redshift z, corresponding to the apparent magnitude limit $m_{\rm lim}$ of the survey, which depends on the position (see Grazian et al. 2006a). We used this correction to obtain a density scale independent of redshift, at least to a first approximation. In computing $M_{\rm lim}(z)$, we used K - and evolutionary - corrections for each object computed with the same best-fit SEDs used to derive the stellar masses, the rest-frame magnitudes, and the other physical properties.

We applied this algorithm to data from the GOODS-MUSIC catalogue, in a redshift range from $z\sim0.4$ to $z\sim 2.5$, where we have sufficient statistics. We performed this analysis by selecting galaxies brighter than MB=-18 up to redshift 1.8 and brighter than MB=-19 at higher redshift, to minimise the completeness correction described above, keeping the average weight w(z) below 1.6 in all cases.

Using this comoving density estimate we analysed the field in two complementary ways. First, we detected and studied galaxy overdensities, i.e. clusters or groups (see Sect. 5), defined as connected 3-dimensional regions with density exceeding a fixed threshold and a minimum number of members chosen according to the results of the simulations (Sect. 4). In particular, we isolated the structures as the regions having $\rho>\bar{\rho}+4 \sigma$ on our density maps and at least 5 members. We then considered as part of each structure the spatially connected region (in RA, Dec, and redshift) around each peak, with an environmental density of >$2\sigma$ above the average and at least 15 member galaxies. To avoid spurious connections between different structures at the same redshift, we considered regions within an Abell radius from the peak. The galaxies located in this region are associated with each structure. We then studied the variation of galaxy properties as a function of environmental density (Sect. 7), associating the comoving density at its position to each galaxy in the sample.

3.1 Comparison with other methods based on photometric redshifts

As mentioned in the introduction, other methods based on photometric redshifts have been developed for the detection of cosmic structures. Here we present the main differences between our algorithm and those that appeared most recently in the literature. However, a more detailed comparison is beyond the scope of the present work, since it would require extensive simulations and/or the application of the different methods to the same datasets.

A similar three-dimensional approach has been proposed by Zatloukal et al. (2007). They select cluster candidates detecting excess density in the 3D galaxy distribution reconstructed from the photometric redshift probability distributions p(z) of each object. However, at variance with our method, they do not adopt any redshift-dependent correction for their estimated density, since they analyse only a narrow redshift range. As we outlined in the previous section, such correction is needed to provide a redshift independent density scale in a deep sample such as the GOODS-MUSIC.

Botzler et al. (2004) expanded the well-known friends-of-friends (FoF) algorithm (Huchra & Geller 1982), to take photometric redshift uncertainties into account. This method links groups of individual galaxies if their redshift difference and angular distances are below fixed thresholds. These thresholds depend on the photometric redshift uncertainties, which are greater than the average physical distance between galaxies and also greater than the velocity dispersion of rich clusters. This could induce the problem of structures percolating through excessively large volumes. They dealt with this issue dividing the catalogue in redshift slices. Instead of comparing the distance between galaxy pairs, as done in an FoF approach, we used the statistical information of how many galaxies are in the neighbourhood of a given point to estimate a physical density. This approach can avoid the percolation problem more effectively, since it identifies structures from the 4$\sigma$ density peaks whose extension is limited by the fixed threshold in density.

Several authors, e.g. Scoville et al. (2007), Mazure et al. (2007), Eisenhardt et al. (2008), and van Breukelen et al. (2006) have estimated the surface density in redshift slices, each with different methods: the first two use adaptive smoothing of galaxy counts, Eisenhardt et al. (2008) analyse a density map convolved with a wavelet kernel, while the last author adopts FoF and Voronoi tessellation (Marinoni et al. 2002). At variance with these, we preferred to adopt an adaptive 3D density estimate to consider, automatically, distances in all directions and the relevant positional accuracies at the same time. This approach requires longer computational times, but allows for an increased resolution in high-density regions where the chosen number of objects is found in a smaller volume with respect to field and void regions. As a consequence it also avoids all peculiar ``border'' effects given by the limits of the redshift slices, and there is also no need to adopt additional criteria to decide whether an overdensity, present in two contiguous 2D density maps in similar angular positions, represents the same group or not (as done for example by Mazure et al. 2007). This clearly also depends on the ability of the algorithm to separate aligned structures (for a more detailed discussion of this see Sect. 4).

Finally, another important difference with respect to previous methods is in the way we use the photometric redshift: some authors use best-fit values of photometric redshift, e.g. Mazure et al. (2007), while Scoville et al. (2007), van Breukelen et al. (2006), Zatloukal et al. (2007), and Eisenhardt et al. (2008) consider the full probability distribution function (PDF) to take redshift uncertainties into account. As discussed by Scoville et al. (2007), this last method could tend to detect structures formed by early type galaxies, since they have smaller photometric redshift uncertainty, thanks to their stronger Balmer break, when this feature is well-sampled in the observed bands. We are less biased in this respect, since we considered the photometric redshift uncertainty in a conservative way, choosing only the maximum redshift range where we count neighbour galaxies to associate with each cell. We took this range as $\pm 2\cdot \sigma_z$ around the redshift of each cell, where $\sigma_z=0.03 \cdot (1+z)$(Grazian et al. 2006a) is the average accuracy of the photometric redshift in the range we analyse.

4 Simulations

We estimated the reliability of our cluster detection algorithm by testing it on a series of mock catalogues designed to reproduce the characteristics of the GOODS survey. These mock catalogues are composed by a given number of groups and clusters superimposed on a random (Poissonian) field. While this is a rather simplistic representation of a survey, it allows us to evaluate some basic features of our algorithm, without the use of N-body simulations. We expanded the previous simulations presented in Trevese et al. (2007), using a larger number of mock catalogues and adopting a more consistent treatment of the survey completeness. For each redshift, we calculated the limiting absolute B magnitude for the two populations of ``red'' and ``blue'' galaxies, defined from the minima in the U-V vs. B distribution in Salimbeni et al. (2008), using the average type-dependent K- and evolutionary corrections calculated from the best-fit SED of the objects in the real catalogue. We then generated an ``observed'' mock catalogue of field galaxies randomly distributed over an area equal to that of the GOODS-South survey. At each redshift, the number of objects in the catalogue is obtained from the integral of the rest frame B band luminosity function $\Phi(M_B,z)$ derived in Salimbeni et al. (2008), up to the limiting absolute MB(z) magnitude computed as described above.

Finally, we created different mock catalogues superimposing a number of structures on the random fields. Given the relatively small comoving volume sampled by the survey, we expect to find only groups and small clusters with a total mass $M\sim \ 10^{13}$- $10^{14}~M_\odot$ and a number of members corresponding to the lowest Abell richness classes (Girardi et al. 1998a). To check that the performance of the algorithm does not change appreciably with a varying number of real overdensities of this kind, we performed three different subset of simulations. Each subset is based on the analysis of 10 mock catalogues, with a number of groups equal to the number of $M> 10^{13}~M_{\odot}$, $M>2 \times 10^{13}~M_{\odot}$, and $M>3 \times 10^{13}~M_{\odot}$ DM haloes, obtained by integrating the Press $\&$ Schechter function (Press & Schechter 1974) over the comoving volume sampled by the survey. Their positions in real space are chosen randomly. Cluster galaxies follow a King-like spatial distribution $n(r) \propto [1+(r/r_{\rm c})^2]^{-3/2}$ (see Sarazin 1988) with a typical core radius $r_{\rm c} = 0.25$ Mpc.

To consider the uncertainty on photometric redshifts, to each cluster we assigned galaxy a random redshift extracted from a Gaussian distribution centred on the cluster redshift $z_{\rm cl}$ and having a dispersion $\sigma_z = 0.03 \cdot (1+z_{\rm cl})$. We neglected the cluster real velocity dispersion, which is much smaller than the $z_{\rm phot}$ uncertainty. We analysed the simulations in the same way as the real catalogue, i.e. calculating galaxy volume density considering objects with $M_B \leq -18$ at z< 1.8 and objects with $M_B \leq -19$ at $z \geq 1.8$.

We have evaluated the completeness of the sample of detected clusters (fraction of real clusters detected) and its purity (fraction of detected structures corresponding to real ones) at different redshifts (see Table 1). We also present the number of unresolved pairs (a detected structure corresponding to two real ones) and the number of double identifications (a unique real structure separated into two detected ones).

Table 2:   Average distances of detected peaks from real centres.

Our aim is to study the properties of individual structures and not, for example, to perform group number counts for cosmological purposes. For this reason, we prefered to choose conservative selection criteria in order to maximise the purity of our sample, while still keeping the completeness high. We isolated the structures as described in Sect. 3, and we considered as significant only those overdensities with at least 5 members in the $4\sigma$ region and 15 members in the $2\sigma$ region.

A structure in the input catalogue is identified if its centre is within $\Delta r=0.5$ Mpc projected distance, and within $\Delta z=0.1$, from the centre of a detected structure, for the low-redshift sample and $\Delta r=0.8$ Mpc, $\Delta z=0.2$ at high z (to account for the increased uncertainties in redshift and position). The results are reported in Table 1. We can see that the chosen thresholds and selection criteria allow for a high purity ($\sim $$100 \%$) at z <1.8, still detecting about the 80% of the real structures. At z >1.8, given the greatly reduced fraction of observed galaxies, the noise is higher, and these criteria turn out to be very conservative (therefore the completeness is low) but are necessary to keep a low number of false detections (purity $\sim 75$-$80 \%$). Table 2 shows the average distance between the centres of the real structures and the centres of their detected counterparts. The density peaks allow the positions of real groups to be identified with good accuracy.

We also evaluated the ability of the algorithm to separate real structures that are very close both in redshift and angular position. In Table 3 we present, for different intracluster distances, the density level at which couples of real groups appear as separated peaks. Both at low and high redshift it is not possible to separate structures whose centres are closer than 1.0 Mpc on the plane of the sky and 2$\sigma_z$ in redshift. For larger separations, it is possible to separate the groups using higher thresholds (5 or 6 $\sigma$ above the average $\rho$).

5 A catalogue of the detected overdensities in the GOODS-South field

Table 3:   Separation threshold for aligned groups.

 \begin{figure} \par\includegraphics[width=8.8cm,clip]{1570fig1.ps} \end{figure} Figure 1:

Upper panel: photometric redshift distribution of our sample (continuous line). Vertical lines mark the redshifts of the detected structures. Lower panel: redshift distribution of spectroscopically selected AGNs in the GOODS-South field (continuous line); the dashed-line histogram is the distribution of the AGNs associated with the overdensity peaks in Table 4.
Open with DEXTER

An inspection of the 3-D density map shows some complex high-density structures distributed over the entire GOODS field. In particular, we found diffuse overdensities at $z\sim 0.7$, at $z\sim 1$, at $z\sim 1.6$, and at $z\sim 2.3$. Some of these have already been partially described (Gilli et al. 2003; Adami et al. 2005; Vanzella et al. 2005; Castellano et al. 2007; Trevese et al. 2007; Díaz-Sánchez et al. 2007). Figure 1 shows the position of these overdensities over the photometric redshift distributions of our sample.These overdensities are also traced by the distribution of the spectroscopically confirmed AGNs in our catalogue, as shown in the lower panel of Fig. 1. (These objects are not included in the sample used for the density estimation.) This link between large-scale structures and AGN distribution was already noted, at lower redshift, in the CDFS (Gilli et al. 2003), in the E-CDFS (Silverman et al. 2008) and in the CDFN (Barger et al. 2003).

 \begin{figure} \par\includegraphics[width=17cm,clip]{1570fig2.ps} \end{figure} Figure 2:

Density isosurfaces for structures at $z\sim 0.7$ a), at $z\sim 0.95$ b), $z\sim 1.05$ c) and at $z\sim 2.3$ d) (average, average $+2\sigma $, average $+3\sigma $ to average $+10 \sigma $) superimposed on the ACS z850 band image of the GOODS-South field. Yellow crosses indicate the density peak of each structure, the number is the ID of the structure in Table 4. For the analogous picture regarding the cluster ID = 9 at $z\sim 1.6$ see Castellano et al. (2007). Other overdensities present did not pass our selection criteria described in Sect. 4.
Open with DEXTER

Within these large-scale overdensities, we identified the structures with the procedure described in Sect. 4. Using an analysis with a $5\sigma$ threshold, we found that two structures identified with $\rho>\bar{\rho}+4 \sigma$, at $z\sim 0.7$, and $z\sim 1$, are the sum of two different structures, so we used a $5\sigma$ threshold to separate these peaks. We then associated the galaxies belonging to the region of overlap between the two structures to the less distant peak.

Overall, we found four structures at $z\sim 0.7$, four structures at $z\sim 1$, one at $z\sim 1.6$ (see also C07) and three structures at $z\sim 2.3$. The density isosurfaces of the structures at $z\sim 0.7$, at $z\sim 0.96$, $z\sim 1.05$, and at $z\sim 2.3$ are shown in Fig. 2, superimposed on the ACS z850 band image of the GOODS-South. The analogous image for the overdensity at $z\sim 1.6$ is showen in Castellano et al. (2007). In the figure, we indicate the peak position of the identified structures. Other overdensities present did not pass our selection criteria described in Sect. 4.

All the structures are presented in Table 4, where we list the following properties:

Column 1: ID number.
Columns 2-4: the position of the density peak (redshift, RA, and Dec) obtained with our 3-D photometric analysis.
Column 5: the number of the objects associated with each structure as defined above. This number gives a hint on the richness of the structure; however, it should not be used to compare structures at different redshifts because of the different magnitude intervals sampled.
Column 6: the average number of field objects present in a volume equal to that associated to the structure, at the relevant redshift. We calculated this number by integrating the evolutive LFs obtained by Salimbeni et al. (2008). In particular, we integrated the LF up to an absolute limiting magnitude calculated using the average K - and evolutionary corrections - and z850 limiting observed magnitude as done in Sect. 4. In this way we take the selection effects into account given by the magnitude cut in our catalogue, as a function of redshift.
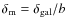
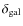Columns 7, 8: the M200 and r200 (assuming bias factors 1 and 2). The mass M200 is defined as the mass inside the radius corresponding to a density contrast $\delta_{\rm m}=\delta_{\rm gal}/b$$\sim $ 200 (Carlberg et al. 1997), where b is the bias factor. To estimate the 3D galaxy density contrast $\delta_{\rm gal}$, we count the objects in the photometric redshift range occupied by the structure as a function of the cluster-centric radius. We then perform a statistical subtraction of the background/foreground field galaxies, using an area at least 2.5 Mpc (comoving) away from the centre of every cluster in the relevant redshift interval. Finally, the density contrast is computed assuming spherical symmetry of the structure. 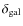The mass inside a volume V of density contrast $\delta_{\rm gal}$ is determined by adapting to our case the method used for spectroscopic data at higher z by Steidel et al. (1998):

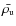\begin{displaymath} M=\bar{\rho_{\rm u}} \cdot V \cdot (1+\delta_{\rm m}), \end{displaymath} (2)

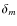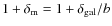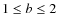in which $\bar{\rho_{\rm u}}$ is the average density of the Universe and $\delta_{m}$ is the total mass density contrast related to the galaxy number density contrast through a bias factor: $1+\delta_{\rm m}=1+\delta_{\rm gal}/b$. We assume a bias factor b in the range $1\le b \le 2$ (see Arnouts et al. 1999).
Column 9: the level of the density peak, measured in number of 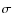$\sigma$ above the average volume density.
We then searched the available spectroscopic public data (Vanzella et al. 2005,2008; Szokoly et al. 2004; Le Fèvre et al. 2004; Wolf et al. 2001; Vanzella et al. 2006; Mignoli et al. 2005) to check whether any of the members of the structures have spectroscopic redshifts, to estimate their location and the velocity dispersion when the statistics are sufficient. Spectroscopic galaxies are considered members of a structure if their redshift was within $4500~{\rm km}~{\rm s}^{-1}$ (i.e. three times the velocity dispersion of a rich cluster) from the mode of its redshift distribution. From these data, we estimated the average redshift of the structure and the velocity dispersion using the biweight estimators, computed with the Rostat package (Beers et al. 1990), with $68\%$ confidence uncertainties obtained from a Jackknife analysis.

In Table 5 we present a value for the X-ray count rate in the band 0.3-4 kev, the corresponding flux (in the interval 0.5-2 keV) and the rest-frame luminosity (0.1-2.4 keV), from the Chandra 2Ms exposure (Luo et al. 2008). We measured the count rates in a square of side of $\sim $ $30 \hbox{$^{\prime\prime}$ }$, centred on the position of the peak of each structure. For the count-rate to flux conversion we assumed as spectrum a Raymond-Smith model (Raymond & Smith 1977) with T = 1 keV and 3 keV and metallicity of 0.2 $Z_\odot$.

Table 4:   Overdensities in the GOODS-South field.

Table 5:   X-ray observations.

5.1 Structures at z 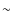$\sim $ 0.7

At redshift $z\sim 0.67$ we isolated three high density peaks (ID = 1, 2 and 3) that are part of a large scale structure already noted, as a whole, by Gilli et al. (2003).

For the structure with ID = 1, we estimated the redshift from the available 6 spectroscopic data. We found an average redshift of $0.665~\pm~0.001$ and a velocity dispersion of $446~\pm~180~{\rm km}~{\rm s}^{-1}$. Assuming that the cluster is virialised, we estimated $r_{\rm vir}=0.8$ Mpc and $M_{\rm vir}=1.0 \times 10^{14}~M_\odot$, using the relations in Girardi et al. (1998b). This estimate is also based on the assumption that there are no infalling galaxies and that the surface term (e.g. Carlberg et al. 1996) is negligible. Considering the uncertainties, also due to the small number of spectroscopic galaxies, $M_{\rm vir}$ is fairly consistent with the M200 estimated from the galaxy density contrast (0.9- $3 \times 10^{14}~M_\odot$).

We also derived the upper limits on the X-ray luminosities for this structure, which is close to 0.2- $0.3 \times 10^{43}~{\rm erg}~{\rm s}^{-1}$. All the properties presented are consistent with the structure being a galaxy group/small cluster (Bahcall 1999).

The structures with ID = 2, 3 have upper limits on their X-ray luminosities of the order of 0.2- $0.3 \times 10^{43}~{\rm erg}~{\rm s}^{-1}$, and their masses $M_{200}\sim 0.2$- $0.5 \times 10^{14}~M_\odot$. These X-ray luminosities and masses are all typical of galaxy groups/small clusters (Bahcall 1999). Each of these structures contains a spectroscopically confirmed galaxy detected in the VLA 1.4 GHz survey (Miller et al. 2008).

At a slightly higher redshift ($z\sim 0.7$), we identified a high density peak (ID = 4) embedded in another large-scale structure that was already known in the literature (Gilli et al. 2003; Adami et al. 2005; Trevese et al. 2007). In our previous paper (Trevese et al. 2007), we identified this structure applying our algorithm to the data from the K20 catalogue, and classified it as an Abell 0 cluster.

In this new analysis we found that this structure is symmetric and has a regular mass profile. It has 92 associated objects ( MB(AB)<-18) and two AGNs. From the density contrast we obtained an r200=1.7-2.4 Mpc and a total mass of M200=0.9- $3.0 \times 10^{14}~M_{\odot}$ for bias factor b=2-1. From the 36 galaxies with spectroscopic redshifts, we estimated a redshift location of $0.734~\pm~0.001$ and a velocity dispersion of $634~\pm~107~{\rm km}~{\rm s}^{-1}$. We derived a virial radius $r_{\rm vir}=1.3$ Mpc, and a virial mass $M_{\rm vir}=3.2 \times 10^{14}~M_\odot$, in good agreement with M200. The 3 sigma upper limit for the X-ray luminosity in the interval 0.1-2.4 keV is very low ( $L_{\rm X} =0.19$- $0.44 \times 10^{43}~{\rm erg}~{\rm s}^{-1}$). The area we considered does not include the X-ray source 173 of Luo et al. (2008), which like Gilli et al. (2003), we associated to the halo of the brightest cluster galaxy (ID $_{\rm GOODS-MUSIC} = 9792$). Alternatively, Adami et al. (2005) associate the bolometric luminosity ( $L_{\rm X}=0.11 \times 10^{43}~{\rm erg}~{\rm s}^{-1}$) of the X-ray source 173 to the thermal emission of the intra-cluster medium (ICM). From this value they deduce a galaxy velocity dispersion around 200- $300~{\rm km}~{\rm s}^{-1}$. This value apparently contrasts with the $\sigma_v$ estimated from the spectroscopic redshifts. We also associated the object 236 detected in the VLA 1.4 GHz survey to the galaxy ID $_{\rm GOODS-MUSIC}~=~9792$. It has an integrated emission of $517.5~\pm~13.1~\mu$Jy (Miller et al. 2008).

From this analysis we can conclude that our two independent mass estimates (M200 and $M_{\rm vir}$) are consistent with this structure being a virialised poor cluster. However, the X-ray emission is significantly lower than what is expected from its optical properties, as is shown from the comparison in Fig. 3 with the $M_{200}-L_{\rm X}$ relations found by Reiprich & Böhringer (2002) and by Rykoff et al. (2008).

 \begin{figure} \par\includegraphics[width=8.8cm,clip]{1570fig3.ps} \end{figure} Figure 3:

$L_{\rm X}$ vs. M200 for the clusters in Table 5. The horizontal error bar is calculated considering a bias factor in the range $1\le b \le 2$, while the vertical error bars are computed varying the gas temperature between T = 1 keV and T = 3 keV as discussed in the main body. The clusters at $z\sim 0.7$ and $z\sim 1.6$ are indicated by red points and error bars. The M200-$L_{\rm X}$ relations found by Reiprich & Böhringer (2002) and by Rykoff et al. (2008) are indicated by a black and green line, respectively.
Open with DEXTER

5.2 Structures at z $\sim $ 1

At redshift $\sim $1 we found four structures (ID = 5, 6, 7, and 8).

The structure with ID = 5 at $z\sim 0.96$ has 32 member galaxies. This structure can be associated to the extended X-ray source number 183 in the catalogue by Luo et al. (2008) derived from the 2MS Chandra observation. This extended X-ray source had not been associated to any structure so far. From the count rate in the interval 0.3-4 keV ( S/N = 11.3) we estimated a luminosity $L_{\rm X}=0.86$- $2.36 \times 10^{43}~{\rm erg}~{\rm s}^{-1}$ (in the interval 0.1-2.4 keV). For the structures with ID = 6, 7 we estimated $r_{200}\sim 1.2$-1.8 Mpc and a total mass of M200=0.4- $1.1 \times 10^{14}~M_{\odot}$. The 3 sigma upper limits for their X-ray luminosity are all slightly below $10^{43}~{\rm erg}~{\rm s}^{-1}$, consistent with their M200 masses.

The structure with ID = 8 at $z\sim 1.06$ has 38 associated galaxies and an AGN spectroscopically confirmed. We derived a precise redshift location of $z~=~1.0974~\pm~0.0015 $ and a velocity dispersion of $446~\pm~143~{\rm km}~{\rm s}^{-1}$, from 6 galaxies with spectroscopic redshift. From these galaxies we also obtained $M_{\rm vir}=0.8 \times 10^{14}~M_\odot$ and $r_{\rm vir}=0.8$ Mpc. We estimated r200=1.1-1.3 Mpc, and M200=0.2- $0.5 \times 10^{14}~M_\odot$, which are compatible values with a group of such $M_{\rm vir}$ and $r_{\rm vir}$. This structure was already found with different methods by Adami et al. (2005), using a FoF algorithm on spectroscopic data from the VIMOS VLT survey (structure 15 in their Table 4), and by Díaz-Sánchez et al. (2007) studying the extremely red objects on GOODS-South. (They call this structure GCL J0332.2-2752.) Their redshift positions and the velocity dispersions are consistent with those obtained in the present analysis. The 3 sigma upper limit for the X-ray luminosity is around $10^{43}~{\rm erg}~{\rm s}^{-1}$, consistent with the estimated M200 mass.

Considering their properties, these four structures can be classified as groups of galaxies. Consistent results for the structure with ID = 6 were obtained in Trevese et al. (2007).

5.3 Structures at high z

At redshift $z\sim 1.6$, we found a compact structure that corresponds to a forming cluster, as already discussed in detail by C07 (see also Kurk et al. 2008). We found a regular mass profile for this structure, and we estimated an r200=2.1-2.9 Mpc, and a M200=2.0- $4.9 \times 10^{14}~M_\odot$. This structure has 50 members, including 3 spectroscopic redshifts, and a confirmed AGN from the GOODS-MUSIC catalogue. We added three other spectroscopic redshifts from the GMASS sample (Cimatti et al. 2008). From these 6 redshifts we estimated a velocity dispersion of $482~\pm~217~{\rm km}^{-1}{\rm s}$, and derived an $M_{\rm vir}=1.4 \times 10^{14}~M_\odot$ and $r_{\rm vir}=1.46$ Mpc. This estimate is consistent with the value in Table 4. We derived an upper limit to the X-ray luminosity of 0.83- $3.67 \times 10^{43}~{\rm erg}~{\rm s}^{-1}$ (0.1-2.4 KeV), lower than expected from the velocity dispersion and the estimated M200 (see Fig. 3).

At $z\sim 2.2$ we found a diffuse overdensity, similar to those at lower redshift, embedding three structures. We associate 20, 23, and 19 galaxies to these structures. We estimated an $r_{200}\sim 1.3$-2 Mpc and a mass of $M_{200}\sim 0.6$- $1.6 \times 10^{14}~M_\odot$ for all these structures. These structures appear to be comparable to those at $\sim $0.7 and $\sim $1.6, and they could be forming clusters.

6 Colour-magnitude diagrams

 \begin{figure} \par\includegraphics[width=8.8cm,clip]{1570fig4.ps} \end{figure} Figure 4:

Rest-frame colour-magnitude relations (U-B vs. MB) for each structure at $z\sim 0.7$. Squares indicate passively evolving galaxies selected as $age/\tau \ge 4$, and the circles are galaxies with $age/\tau < 4$. Filled points indicate galaxies with spectroscopic redshift. The continuous lines are the fit to the red sequence of all the combined structures. The dotted lines are the uncertainties at 1-sigma obtained with a Jackknife analysis.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=8.8cm,clip]{1570fig5.ps} \end{figure} Figure 5:

Same as Fig. 4. Panel a) structures at $z\sim 0.7$; panel b) structures at $z\sim 1$; panel c) structure at $z\sim 1.6$ ; panel d) structures at $z\sim 2.2$. The two dashed lines in each of the two last bins of redshift are the red sequences estimated at $z\sim 0.7$ (shallower slope) and $\sim $1 (steeper slope).
Open with DEXTER

We studied the colour-magnitude diagrams (U-B vs. MB) for all the structures, as shown in Figs. 4 and 5. To estimate the slope of the red-sequence, we defined its members as passively evolving galaxies according to the physical criterion $age/\tau \ge 4$, where the age and $\tau$ (the star formation e-folding time) we are inferred for each galaxy from the SED fitting (Sect. 2). This quantity is, in practice, the inverse of the Scalo parameter (Scalo 1986), and a ratio of 4 was chosen to distinguish galaxies having prevalently evolved stellar populations from galaxies with recent episodes of star formation. Indeed, an $age/\tau=4$ corresponds to a residual 2% of the initial SFR for an exponential star formation history, as adopted in this paper. Grazian et al. (2006b) shows that this value can be used to effectively separate star-forming galaxies from the passively evolving population (see Grazian et al. 2006b, also for the discussion on the uncertainty associated to this parameter). Passively evolving galaxies are indicated in figures as filled squares.

 \begin{figure} \par\includegraphics[angle=-90,width=16cm,clip]{1570fig6.ps} \end{figure} Figure 6:

Fraction of red (filled circles) and blue galaxies (filled triangles) at decreasing rest frame B magnitudes ( from top to bottom) in four contiguous intervals of increasing redshift ( from left to right). Vertical error bars indicate the Poissonian uncertainty in each bin. The shaded areas are obtained by smoothing the red (blue) fraction with an adaptive sliding box. The horizontal errorbars indicate the range of density covered by the 5-95% of the total sample.
Open with DEXTER

Figure 4 shows the colour-magnitude diagrams for the four structures between z=0.66 and z=0.71. The cluster at $z\sim 0.71$ (Panel d) shows a well-defined red sequence, while the three structures at $z\sim 0.66$ have fewer passively evolving galaxies. Therefore, to increase our statistics, we estimated the colour-magnitude slope combining all the four structures in the interval 0.66<z<0.71 (see Panel a in Fig. 5). We obtained a value $-0.023\pm 0.006$ for the slope. The resulting colour-magnitude relation is plotted in all panels in Fig. 4 and in panel a in Fig. 5 as a continuous line. The dotted lines constrain the error at 1-sigma obtained with a Jackknife analysis. It is possible to see in Fig. 4 that this average colour-magnitude relation is roughly consistent with the position in the (U-B) vs. B diagram of the galaxies belonging to each single structure. We therefore applied the same method at higher redshift, i.e. we estimated the slope of the red sequence by combining the different structures at the same redshift.

Panel b of Fig. 5 shows the colour-magnitude diagram for the structures at $z\sim 1$. We found a slope of $-0.03\pm 0.01$.

Panel c in Fig. 5 shows the colour-magnitude diagram for the structure at $z\sim 1.6$. In this case we have galaxies distributed on less than a magnitude range, which is insufficient to estimate the slope of the ``red sequence''. However, if we plot the two sequences obtained at lower redshift, we can see that the few passively evolving galaxies are consistent with them.

Finally, at redshift $\sim $2, we only have 4 passive objects from the combination of 3 structures and there is no evidence of a well-defined red sequence. We note that the colours of these objects are generally bluer than the colour of the relations found at lower redshifts.

The values of the slopes of the structures at redshift $\sim $0.7 and $\sim $1 are consistent with those of previous determinations (e.g. Blakeslee et al. 2003; Trevese et al. 2007; Homeier et al. 2006). We confirm that the observations indicate no evolution up to redshift $\sim $1. This would imply that the mass-metallicity relation that produces the red sequence (Kodama et al. 1998) remains practically constant up to, at least, $z\sim 1$.

7 Galaxy properties as a function of the environment

To each object in the sample we associated the comoving density at its position, and we studied galaxy properties as a continuous function of the environmental density.

7.1 Galaxy populations: bimodality

We studied the variation in the fraction of red and blue galaxies as a function of the environmental density. To separate red and blue galaxies we used the minimum in the bimodal galaxy distribution in the (U-V) vs. B colour-magnitude diagram, derived by Salimbeni et al. (2008). Figure 6 shows the fraction of red and blue galaxies for different rest frame Bmagnitudes in four redshift intervals. In general, for every environment, we found that, at fixed luminosity, the red fraction increases with decreasing redshift, and, at fixed redshift, it increases at increasing B luminosity. We also found that for z<1.2the red fraction increases with density for every luminosity, while this effect is absent at higher redshift.

Our results extend to higher redshift those obtained by Cucciati et al. (2006) on the VVDS survey, with a shallower spectroscopic sample that reaches $z \sim 1.5$. We found that at z>1.2 even the highest luminosity galaxies are blue, star-forming objects, similar to the results in Cucciati et al. (2006), although our colour selection is slightly different, since we select two complementary samples in colour, while they select two extreme red and blue populations ( $(u^*-g')\ge 1.1$ and $(u^*-g')\le 0.55 )$). Our results also agree with the analysis of the DEEP2 survey by Cooper et al. (2007) in the redshift range 0.4<z<1.35. They find a weak correlation between red fraction and density at $z\sim 1.2$. We see that at z>1.2 this correlation disappears, indicating that the change probably occurs in the critical range 1.5<z<2.0, at least in the environments probed by our sample. However, we note that, given the relatively small area covered, we do not probe very high-density regions (i.e. rich clusters), at variance with wide, low-redshift surveys. When rich clusters are considered (e.g. Balogh et al. 2004), a stronger variation with environment in the colours of faint galaxies is seen. In any case, the disappearance at z>1.2 of the variation in the red fraction in the density range probed by our sample indicates that a relevant change in galaxy properties takes place at $z \sim 1.5$-2.

7.2 Galaxy physical properties in high and low density environments

 \begin{figure} \par\includegraphics[width=9cm,clip]{1570fig7.ps} \end{figure} Figure 7:

Galaxy stellar mass distribution in four redshift intervals. Shaded red histograms represent galaxies associated with the density peaks and empty black histograms represent galaxies in the low-density regions, as described in the text. In each panel the average value of $\log(M)$ for the two distributions are indicated by arrows of the same colour. The K-S probability is reported in each panel. Vertical lines indicate the mass limit at the median redshift of the bin ( $\log(M)=9.0$ at $z \sim 0.6$, $\log(M)=9.6$ at $z\sim 1$, $\log(M)=10.5$ at $z\sim 1.6$, and $\log(M) =11.1$ at $z \sim 2.15$).
Open with DEXTER

 \begin{figure} \par\includegraphics[width=9cm,clip]{1570fig8.ps} \end{figure} Figure 8:

Top: as in Fig. 7 but for the ages of galaxies. The average value of the age for the two distributions are indicated by arrows. Bottom: as in Fig. 7 but for SFR of galaxies. The average values of the $\log({\it SFR})$ for the two distributions are indicated by arrows.
Open with DEXTER

We then studied the distribution of physical parameters and photometric properties for galaxies in high-density environments, and compare it to field galaxies. The first sample is defined as the combination of the data from structures with similar redshifts (``group galaxies'' hereafter). The field galaxies are defined as those with an associated $\rho$ lower than the median density (0.0126 for z<1.8 and 0.0085 for z>1.8) of the entire sample (``field galaxies'' hereafter). We quantified the differences in the distributions of the galaxy physical properties, i.e. mass, age, star formation rate, through the probability $P_{\rm KS}$ of the two samples, obtained as described above, using a Kolmgorov-Smirnov test. We rejected the hypothesis that two samples are drawn from the same distribution if $P_{\rm KS}< 5 \times 10^{-2}$.

Figure 7 shows the distribution of the galaxy total stellar mass in high and low density regions, in the same four contiguous redshift intervals used before. The galaxies in a high-density environment have a distribution that generally peaks at higher masses with respect to ``field'' galaxies. For the mass distribution, we found a significant difference in all but the last redshift bin as shown from the $P_{\rm KS}$. It is important to point out here that the shape of the distributions at low masses could depend on the luminosity selection. In fact, a magnitude-limited sample does not have a well-defined limit in stellar mass. This effect depends on the range of M/L ratio spanned by galaxies with different colours, e. g. as shown in Fontana et al. (2006) in our sample, at $z\sim 1$, M/LKextends from 0.9, for redder objects, to 0.046, for bluer objects. If a colour segregation is present as a function of the environment, it could bias the distribution favouring the observation of lower mass galaxies in less dense regions, where the fraction of blue galaxies is higher. Although, as shown in Fig. 6, we did not find strong colour segregation, especially at z>1, we also carried out a more conservative analysis here. We considered only the range of masses above the completeness mass limit obtained from the maximal M/Lz850 for a passively evolving system ( $\log(M)>9.0$ at $z \sim 0.6$, $\log(M)> 9.6$ at $z\sim 1$, $\log(M)> 10.5$ at $z\sim 1.6$, and $\log(M) > 11.1$ at $z \sim 2.15$). Considering galaxies above these mass limits we found that the masses of ``group'' galaxies are still higher than those of ``field'' galaxies for the lower bin in redshift ( $P_{\rm KS}=9.7 \times 10^{-4}$). At z > 1.2, however, it is not possible to give a conclusive result because of the low statistic caused by this mass cut.

Analogous results are found from the analysis of the luminosity distribution of ``field'' and ``group'' galaxies. In particular, we found that the distribution of galaxies in ``groups'' have on average brighter MIrest-frame magnitudes at all redshifts. The results are also similar for the other rest frame bands, implying that galaxies in high-density environments have, on average, greater bolometric luminosity than do field galaxies.

Finally, we studied the age and SFR distributions for ``group'' and ``field'' galaxies (see Fig. 8). Only at low redshift does there appear to be a significant difference (respectively $P_{\rm KS}=3.0 \times 10^{-2}$ and $P_{\rm KS}=6.7 \times 10^{-3}$, see Fig. 8). The two age distributions show a similar shape for young galaxies, but ``group'' galaxies have a higher fraction of old galaxies. As also shown by the difference in the average ages for the two samples, the ``group'' galaxies are older than the field ones. At higher redshifts, the two distributions do not show any significative differences. Indeed, at higher redshifts, any possible difference in the age of the two galaxy populations is probably less than the uncertainty on the ages. Analogously, star-forming galaxies have a similar distribution for ``group'' and ``field'' samples, but the ``group'' sample has a higher faction of galaxies with low star formation as also shown by the different values of the average SFR.

8 Summary and conclusions

We applied a (2+1)D algorithm on the GOODS-MUSIC catalogue to identify structures in this area. This algorithm combines galaxy angular positions and precise photometric redshifts to give an adaptive estimate of the 3D density field effectively also at z>1and in a wide area. In this way we obtained a density map from redshift 0.4 up to 2.5, and we isolated the higher density regions. To identify density peaks we chose a conservative selection criterion (at least five galaxies in connected regions of $\rho>\bar{\rho}+4 \sigma$) in order to maximise the purity of our sample.

We built mock catalogues simulating the GOODS-South field. Applying our density thresholds and selection criteria to these catalogues, we found a purity near 100% (with less than 15-20% of lost structures) up to redshift 1.8, and $\sim $75-80% at higher redshift. In the higher redshift range, the criterion is very conservative, to keep a low number of false detections, therefore the completeness is low (<40%). From the simulations we also evaluated the ability of the algorithm in separating real structures that are very close both in redshift and angular position. Both at low and high redshift it is not possible to separate structures whose centres are closer than 1.0 Mpc on the plane of the sky and $2 \sigma_z$ in redshift. For larger separations it is possible to distinguish the groups, but by using higher thresholds (5 or 6$\sigma$above the average).

We found large-scale overdensities at different redshifts ($\sim $0.6, $\sim $1, $\sim $1.61 and $\sim $2.2), which are well traced by the AGN distribution, suggesting that the environment on large scales ($\sim $10 Mpc) has an influence on AGN evolution (Silverman et al. 2008). We isolated several groups and small clusters embedded in these large-scale structures. Most of the structures at $z\sim 0.7$ and $\sim $1 have properties of groups of galaxies: their masses are of the order of M200= 0.2- $0.8 \times 10^{14}~M_\odot$, and their X-ray luminosities are slightly below $10^{43}~{\rm erg}~{\rm s}^{-1}$, consistent with the expectations of the M200-$L_{\rm X}$ relations. The structure at z=0.71 and those at z>1.6seem to be more massive, and in particular the structures with ID = 4, and 9 can be classified as poor clusters. It is interesting to note that both these structures are significantly X-ray underluminous, as is evident by a comparison with the M200-$L_{\rm X}$ relations found by Reiprich & Böhringer (2002) and by Rykoff et al. (2008, Fig. 3). This is not surprising since several authors have observed that optically selected structures have an X-ray emission lower than what is expected from the observations of X-ray selected groups and clusters. This effect has been observed at low redshift in small groups (Rasmussen et al. 2006), in Abell clusters (Popesso et al. 2007), and in clusters at 0.6<z<1.1(Lubin et al. 2004). These results may be explained by the optically selected structures still being in the process of formation or the result of the alignment of two substructures along the line of sight, although it cannot be excluded that they contain less intracluster gas than expected, because of the effect of strong galactic feedback (Rasmussen et al. 2006). If these structures are virialised, as is probable in the case of the massive structure at z=0.71(ID = 4), this may indicate that they contain less intracluster gas than expected. It is worth investigating this issue in future deep surveys, since it would have interesting implications for the evolution of the baryonic content of these structures.

We then studied the colour magnitude diagrams (U-B vs. MB) for all the structures. We defined the members of the red sequence according to the physical criterion $age/\tau \ge 4$, which should select passively evolving galaxies with little residual star formation. We confirmed no evolution of the red sequence slope up to redshift $\sim $1. This implies that the mass-metallicity relation that produces the slope of the red sequence remains constant up to $z\sim 1$.

We then studied the variation in the fraction of red and blue galaxies as a function of the environmental density. We found that, at fixed redshift, the red fraction increases at increasing B luminosity, while, at fixed luminosity, it increases with decreasing redshift. We found that the increment of the red fraction at growing density disappears at z>1.2.

We also studied galaxy properties in different environments. We found that the galaxies in high-density environments have higher masses with respect to ``field galaxies'', in qualitative agreement with a downsizing scenario. The mass distributions show a significant difference in all but the last redshift bin. Similarly, the galaxies in groups have on average brighter rest-frame magnitudes, and there are a greater number of bright galaxies in groups at all redshifts compared to field galaxies. Finally, the age and SFR distributions for the two subsamples appear different only at low redshifts where ``group galaxies'' are generally older and less star forming than ``field'' ones.

From the analysis of the environmental dependence of galaxy colours and mass as a function of redshift, and from the absence of any well-defined red sequence at high redshift, we can argue that a critical period in which some basic characteristics of galaxy populations are established is that between $z \sim 1.5$ and $z \sim 2$.

Acknowledgements

We thank the anonymous referee for his/her helpful comments. S.S. acknowledges support from the UMASS Department of Astronomy through a postdoctoral fellowship.

References

 

All Tables

Table 1:   Completeness and purity.

Table 2:   Average distances of detected peaks from real centres.

Table 3:   Separation threshold for aligned groups.

Table 4:   Overdensities in the GOODS-South field.

Table 5:   X-ray observations.

All Figures

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1570fig1.ps} \end{figure} Figure 1:

Upper panel: photometric redshift distribution of our sample (continuous line). Vertical lines mark the redshifts of the detected structures. Lower panel: redshift distribution of spectroscopically selected AGNs in the GOODS-South field (continuous line); the dashed-line histogram is the distribution of the AGNs associated with the overdensity peaks in Table 4.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{1570fig2.ps} \end{figure} Figure 2:

Density isosurfaces for structures at $z\sim 0.7$ a), at $z\sim 0.95$ b), $z\sim 1.05$ c) and at $z\sim 2.3$ d) (average, average $+2\sigma $, average $+3\sigma $ to average $+10 \sigma $) superimposed on the ACS z850 band image of the GOODS-South field. Yellow crosses indicate the density peak of each structure, the number is the ID of the structure in Table 4. For the analogous picture regarding the cluster ID = 9 at $z\sim 1.6$ see Castellano et al. (2007). Other overdensities present did not pass our selection criteria described in Sect. 4.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1570fig3.ps} \end{figure} Figure 3:

$L_{\rm X}$ vs. M200 for the clusters in Table 5. The horizontal error bar is calculated considering a bias factor in the range $1\le b \le 2$, while the vertical error bars are computed varying the gas temperature between T = 1 keV and T = 3 keV as discussed in the main body. The clusters at $z\sim 0.7$ and $z\sim 1.6$ are indicated by red points and error bars. The M200-$L_{\rm X}$ relations found by Reiprich & Böhringer (2002) and by Rykoff et al. (2008) are indicated by a black and green line, respectively.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1570fig4.ps} \end{figure} Figure 4:

Rest-frame colour-magnitude relations (U-B vs. MB) for each structure at $z\sim 0.7$. Squares indicate passively evolving galaxies selected as $age/\tau \ge 4$, and the circles are galaxies with $age/\tau < 4$. Filled points indicate galaxies with spectroscopic redshift. The continuous lines are the fit to the red sequence of all the combined structures. The dotted lines are the uncertainties at 1-sigma obtained with a Jackknife analysis.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1570fig5.ps} \end{figure} Figure 5:

Same as Fig. 4. Panel a) structures at $z\sim 0.7$; panel b) structures at $z\sim 1$; panel c) structure at $z\sim 1.6$ ; panel d) structures at $z\sim 2.2$. The two dashed lines in each of the two last bins of redshift are the red sequences estimated at $z\sim 0.7$ (shallower slope) and $\sim $1 (steeper slope).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=-90,width=16cm,clip]{1570fig6.ps} \end{figure} Figure 6:

Fraction of red (filled circles) and blue galaxies (filled triangles) at decreasing rest frame B magnitudes ( from top to bottom) in four contiguous intervals of increasing redshift ( from left to right). Vertical error bars indicate the Poissonian uncertainty in each bin. The shaded areas are obtained by smoothing the red (blue) fraction with an adaptive sliding box. The horizontal errorbars indicate the range of density covered by the 5-95% of the total sample.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{1570fig7.ps} \end{figure} Figure 7:

Galaxy stellar mass distribution in four redshift intervals. Shaded red histograms represent galaxies associated with the density peaks and empty black histograms represent galaxies in the low-density regions, as described in the text. In each panel the average value of $\log(M)$ for the two distributions are indicated by arrows of the same colour. The K-S probability is reported in each panel. Vertical lines indicate the mass limit at the median redshift of the bin ( $\log(M)=9.0$ at $z \sim 0.6$, $\log(M)=9.6$ at $z\sim 1$, $\log(M)=10.5$ at $z\sim 1.6$, and $\log(M) =11.1$ at $z \sim 2.15$).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{1570fig8.ps} \end{figure} Figure 8:

Top: as in Fig. 7 but for the ages of galaxies. The average value of the age for the two distributions are indicated by arrows. Bottom: as in Fig. 7 but for SFR of galaxies. The average values of the $\log({\it SFR})$ for the two distributions are indicated by arrows.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.