| Issue |
A&A
Volume 501, Number 2, July II 2009
|
|
|---|---|---|
| Page(s) | 519 - 530 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200810610 | |
| Published online | 29 April 2009 | |
First stars XII. Abundances in extremely metal-poor turnoff stars, and comparison with the giants![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
P. Bonifacio1,2,3 - M. Spite2 - R. Cayrel2 - V. Hill2,4 - F. Spite2 - P. François2 - B. Plez5,6 - H.-G. Ludwig1,2 - E. Caffau2 - P. Molaro2,3 - E. Depagne7 - J. Andersen8,9 - B. Barbuy10 - T. C. Beers11 - B. Nordström8 - F. Primas12
1 - CIFIST Marie Curie Excellence Team
2 -
GEPI, Observatoire de Paris, CNRS, Université Paris Diderot; Place Jules Janssen 92190 Meudon, France
3 -
Istituto Nazionale di Astrofisica - Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
4 -
Laboratoire Cassiopée UMR 6202, Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte d'Azur, France
5 -
GRAAL, Université de Montpellier II, 34095 Montpellier Cedex 05, France
6 -
Department of Physics and Astronomy, Uppsala Astronomical Observatory, Box 515, 751 20 Uppsala, Sweden
7 -
Las Cumbres Observatory, Goleta, CA 93117, USA
8 -
The Niels Bohr Institute, Astronomy Group, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
9 -
Nordic Optical Telescope, Apartado 474, 38700 Santa Cruz de La Palma, Spain
10 -
IAG, Universidade de Sao Paulo, Depto. de Astronomia, Rua do Matao 1226, Sao Paulo 05508-900, Brazil
11 -
Department of Physics & Astronomy, CSCE: Center for the Study of Cosmic Evolution, and JINA: Joint Institute for Nuclear Astrophysics, Michigan State University, East Lansing, MI 48824, USA
12 -
European Southern Observatory, Karl Schwarzschild-Str. 2, 85749 Garching bei München, Germany
Received 15 July 2008 / Accepted 15 March 2009
Abstract
Context. The detailed chemical abundances of extremely metal-poor (EMP) stars are key guides to understanding the early chemical evolution of the Galaxy. Most existing data, however, treat giant stars that may have experienced internal mixing later.
Aims. We aim to compare the results for giants with new, accurate abundances for all observable elements in 18 EMP turnoff stars.
Methods. VLT/UVES spectra at
![]() and
and ![]() 130 per pixel (
130 per pixel (
![]() 330-1000 nm) are analysed with OSMARCS model atmospheres and the TURBOSPECTRUM code to derive abundances for C, Mg, Si, Ca, Sc, Ti, Cr, Mn, Co, Ni, Zn, Sr, and Ba.
330-1000 nm) are analysed with OSMARCS model atmospheres and the TURBOSPECTRUM code to derive abundances for C, Mg, Si, Ca, Sc, Ti, Cr, Mn, Co, Ni, Zn, Sr, and Ba.
Results. For Ca, Ni, Sr, and Ba, we find excellent consistency with our earlier sample of EMP giants, at all metallicities. However, our abundances of C, Sc, Ti, Cr, Mn and Co are ![]() 0.2 dex larger than in giants of similar metallicity. Mg and Si abundances are
0.2 dex larger than in giants of similar metallicity. Mg and Si abundances are ![]() 0.2 dex lower (the giant [Mg/Fe] values are slightly revised), while Zn is again
0.2 dex lower (the giant [Mg/Fe] values are slightly revised), while Zn is again ![]() 0.4 dex higher than in giants of similar [Fe/H] (6 stars only).
0.4 dex higher than in giants of similar [Fe/H] (6 stars only).
Conclusions. For C, the dwarf/giant discrepancy could possibly have an astrophysical cause, but for the other elements it must arise from shortcomings in the analysis. Approximate computations of granulation (3D) effects yield smaller corrections for giants than for dwarfs, but suggest that this is an unlikely explanation, except perhaps for C, Cr, and Mn. NLTE computations for Na and Al provide consistent abundances between dwarfs and giants, unlike the LTE results, and would be highly desirable for the other discrepant elements as well. Meanwhile, we recommend using the giant abundances as reference data for Galactic chemical evolution models.
Key words: Galaxy: abundances - Galaxy: halo - Galaxy: evolution - stars: abundances - stars: population II - stars: supernovae: general
1 Introduction
The surface composition of a cool star is a good diagnostic of the chemical composition of the gas from which it formed, if mixing with material processed inside the star itself has not occurred. Cool, long-lived stars have thus been extensively used to study the early chemical evolution of our Galaxy (and, by implication, other galaxies as well). The trends in abundance ratios that have been established over the past 30 years provide strong constraints on the early chemical evolution of the Milky Way (see Cayrel 1996, 2006, for classic and recent reviews of the topic).
Our own programme, ``First Stars'', is a comprehensive spectroscopic study of extremely metal-poor (EMP) stars to obtain precise information on the chemical composition of the early ISM and the yields of the first generation(s) of supernovae, conducted with the VLT and UVES spectrograph. The target stars were selected from the medium-resolution follow-up (Beers et al., in preparation; Allende Prieto et al. 2000) of the HK objective-prism survey (Beers et al. 1985,1992; Beers 1999), initiated by George Preston and Steve Shectman and later substantially extended and followed up by Beers as part of many collaborations, including the present one.
Several papers have presented our results on the giant stars, which lend themselves to the study of many elements: Hill et al. (2002 - First Stars I), Depagne et al. (2002 - First Stars II), François et al. (2003 - First Stars III), Cayrel et al. (2004 - First Stars V), Spite et al. (2005 - First Stars VI), François et al. (2007 - First Stars VIII), and Spite et al. (2006 - First Stars IX). In these papers, we found that the mixing with layers affected by nuclear burning caused some giants to have altered abundances with respect to their initial chemical composition. All the stars have undergone the first dredge-up, so their abundances of Li, C, and N are under suspicion. However, our detailed analysis (First Stars VI and IX) showed that the surface abundances of the less luminous giants (those below the ``bump'' in the luminosity function) are not significantly affected by mixing.
It is therefore expected that the less luminous giants and dwarfs should display the same abundances, provided that the surface composition of the latter has not been changed by atmospheric phenomena, such as diffusion. Comparing abundance ratios in dwarfs and giants can therefore, in principle, yield insight into the degree of mixing in giants and diffusion in dwarfs, as well as which element ratios are reliable guides to the composition of the early ISM in the Galaxy.
So far, only a few of our papers have discussed results for EMP dwarfs: Sivarani et al. (2004 - First Stars IV, 2006 - First Stars X), Bonifacio et al. (2007 - First Stars VII), and González Hernández et al. (2008 - First Stars XI). First Stars VII focused on the Li abundance, but also discussed the model parameters and [Fe/H] of the dwarf sample in considerable detail. Here we discuss the abundances from C to Ba in the same stars and compare the results for dwarfs and giants.
2 Observations and reduction
The sample of stars and the observational data are the same as discussed in Paper VII (Bonifacio et al. 2007). The observations were performed with the ESO VLT and the high-resolution spectrograph UVES (Dekker et al. 2000) at a resolution of R = 45 000 and typical S/N per pixel of ![]() 130 on the coadded spectra (average 5 pixels per resolution element). The spectra were reduced using the UVES context within MIDAS (Ballester et al. 2000); see Paper V for details. The region of the Mg I b triplet in our spectra is shown in Fig. 1 (see also Fig. 1 of Paper VII, which shows the Li line in the same stars). Equivalent widths were measured on the coadded spectra. For those few stars, for which spectra with different resolutions (different slit-width or image slicer used) were available, we separately coadded the spectra with the same resolution and then averaged the equivalent widths.
130 on the coadded spectra (average 5 pixels per resolution element). The spectra were reduced using the UVES context within MIDAS (Ballester et al. 2000); see Paper V for details. The region of the Mg I b triplet in our spectra is shown in Fig. 1 (see also Fig. 1 of Paper VII, which shows the Li line in the same stars). Equivalent widths were measured on the coadded spectra. For those few stars, for which spectra with different resolutions (different slit-width or image slicer used) were available, we separately coadded the spectra with the same resolution and then averaged the equivalent widths.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10610f1.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg13.png) |
Figure 1: The region of the Mg I b triplet in the programme stars. [Fe/H] is shown to the left of each spectrum. In these EMP stars, the triplet lines have no damping wings. |
| Open with DEXTER | |
3 Determination of atmospheric parameters
We carried out a classical 1D LTE analysis using OSMARCS models (see, e.g., Gustafsson et al. 1975, 2003, 2008). Estimates of
![]() were derived from the wings of H
were derived from the wings of H![]() ;
log g estimates were obtained by considering the ionisation equilibrium of iron.
Microturbulent velocities were fixed by requiring no trend in [Fe I/H] with equivalent width. Details are given in ``First Stars VII'', together with an extensive discussion of the effective temperature scale. In that paper we established that our H
;
log g estimates were obtained by considering the ionisation equilibrium of iron.
Microturbulent velocities were fixed by requiring no trend in [Fe I/H] with equivalent width. Details are given in ``First Stars VII'', together with an extensive discussion of the effective temperature scale. In that paper we established that our H![]() based temperatures satisfy the iron excitation equilibrium and are also in good agreement with the Alonso et al. (1996) colour-temperature calibration, which we used for the giant stars (Cayrel et al. 2004)
The adopted parameters are listed in Table 1.
based temperatures satisfy the iron excitation equilibrium and are also in good agreement with the Alonso et al. (1996) colour-temperature calibration, which we used for the giant stars (Cayrel et al. 2004)
The adopted parameters are listed in Table 1.
Table 1: Adopted model atmosphere parameters.
The parameters of the subgiant star BS 16076-006 require a comment, because the Balmer line broadening in this star increases from H![]() towards the higher members of the Balmer series. Our adopted
towards the higher members of the Balmer series. Our adopted
![]() (5199 K) is derived from the wings of H
(5199 K) is derived from the wings of H![]() ,
but the wings of H
,
but the wings of H![]() correspond to a much higher effective temperature, of the order of 5900 K. All values of
correspond to a much higher effective temperature, of the order of 5900 K. All values of
![]() derived from colours are also consistently higher than derived from the H
derived from colours are also consistently higher than derived from the H![]() profile, confirming this peculiarity. This star was also analysed from medium-resolution ESI - Keck spectra
(R = 7000) by Lai et al. (2004), who adopted a
profile, confirming this peculiarity. This star was also analysed from medium-resolution ESI - Keck spectra
(R = 7000) by Lai et al. (2004), who adopted a
![]() = 5458 K, based on photometry.
This
= 5458 K, based on photometry.
This
![]() is compatible with the profile of H
is compatible with the profile of H![]() ,
but too low to reproduce the profile of H
,
but too low to reproduce the profile of H![]() .
The cause of this peculiar behaviour (e.g. a binary companion or chromospheric activity) needs further investigation, but the three radial velocities derived from our two
spectra and the one of Lai et al. (2004) show no evidence of variation. None of our results depends critically on the abundances of this star, however. Our UVES spectra show that
CS 29527-015 is a double-lined binary. These two stars are omitted in Fig. 1.
.
The cause of this peculiar behaviour (e.g. a binary companion or chromospheric activity) needs further investigation, but the three radial velocities derived from our two
spectra and the one of Lai et al. (2004) show no evidence of variation. None of our results depends critically on the abundances of this star, however. Our UVES spectra show that
CS 29527-015 is a double-lined binary. These two stars are omitted in Fig. 1.
4 Abundance determination
The abundance analysis was performed using the LTE spectral line analysis code turbospectrum (Alvarez & Plez 1998). The abundances of the different elements have been determined mainly from the equivalent widths of unblended lines. Synthetic spectra have been used to determine abundances from the molecular bands, and also from atomic lines in cases when the lines were severely blended, affected by hyperfine structure, or were strong enough to show significant damping wings (see Sect. 6.1). The abundances of C and the ![]() elements (as well as for Sc) are listed in Table 2, those of the heavier (neutron-capture) elements are listed in Table 3.
elements (as well as for Sc) are listed in Table 2, those of the heavier (neutron-capture) elements are listed in Table 3.
Abundance uncertainties are discussed in detail in Cayrel et al. (2004) and Bonifacio et al. (2007). For a given temperature, the ionisation equilibrium provides an estimate of the
gravity with an internal precision of about 0.1 dex in log g, and the microturbulent velocity can be constrained within about 0.2
![]() .
The largest uncertainty comes from the temperature determination, which is uncertain by
.
The largest uncertainty comes from the temperature determination, which is uncertain by ![]() 100 K.
100 K.
The total error estimate is not the quadratic sum of the various sources of uncertainty, because the covariance terms are important. As an illustration of the total expected uncertainty we have computed the abundances of CS 29177-009 with different models. Model A has the nominal temperature 6260 K, gravity (log g = 4.5), and microturbulent velocity (![]() = 1.3
= 1.3
![]() ), while Models B and C differ in log g and
), while Models B and C differ in log g and ![]() by 1
by 1![]() .
Model D has a temperature 100 K lower and the same log g and
.
Model D has a temperature 100 K lower and the same log g and ![]() ,
while in Model E we have determined the ``best'' values of log g and
,
while in Model E we have determined the ``best'' values of log g and ![]() corresponding to the lower temperature. The detailed results of these computations are given in Table 4.
corresponding to the lower temperature. The detailed results of these computations are given in Table 4.
5 C, N, O abundances
5.1 Carbon
The carbon abundance was determined by spectrum synthesis of the
![]() band of CH (the G band). Wavelengths of the CH lines are from Luque & Crosley (1999); transition energies are from the list of Jørgensen et al. (1996); isotopic shifts were computed using the best set of available molecular constants. The strongest lines of
band of CH (the G band). Wavelengths of the CH lines are from Luque & Crosley (1999); transition energies are from the list of Jørgensen et al. (1996); isotopic shifts were computed using the best set of available molecular constants. The strongest lines of
![]() at 423 nm are invisible in all of our stars, so the
at 423 nm are invisible in all of our stars, so the
![]() ratio could not be measured. In computing the total C abundance, we have therefore assumed a solar
ratio could not be measured. In computing the total C abundance, we have therefore assumed a solar
![]() ratio.
ratio.
In Fig. 2 we present the measured [C/Fe] values in our dwarf stars and compare them to values for our unmixed giants from Paper V. In this figure we have omitted the mixed giants, located above the bump, since we have shown (First Stars VI and IX) that the abundances of C and N in the atmospheres of these stars are strongly affected by mixing and thus are not good diagnostics of their initial chemical compositions.
The mean [C/Fe] value for the turnoff stars is
![]()
![]() 0.10 (s.d.), but
0.10 (s.d.), but
![]()
![]() 0.16 (s.d.) for the giants. Thus, we find a moderately significant difference between the C abundances in the giants and the turnoff stars (Fig. 2). We discuss the possible causes of this discrepancy in Sect. 11.
The mean [C/Fe] has been computed excluding the binary turnoff star CS 29527-015, which
appears to be quite carbon-rich (Fig. 2).
0.16 (s.d.) for the giants. Thus, we find a moderately significant difference between the C abundances in the giants and the turnoff stars (Fig. 2). We discuss the possible causes of this discrepancy in Sect. 11.
The mean [C/Fe] has been computed excluding the binary turnoff star CS 29527-015, which
appears to be quite carbon-rich (Fig. 2).
5.2 Nitrogen
Generally, the NH (and CN) bands are not visible in the spectra of EMP turnoff stars (the stars are too hot), so N abundances can only be measured in strongly N-enhanced stars (First Stars X). The subgiant BS 16076-006 exhibits a weak NH band, however, and we find [N/Fe] = +0.29 for this star, when taking the correction of -0.4 dex derived in Paper VI into account.
Figure 3 shows the measured [N/Fe] ratios for our sample of ``unmixed'' giants (Paper VI). BS 16076-006 agrees with (and thus supports) the high [N/Fe] values found in the giants at the lowest metallicities.
Table 2:
Abundance ratios for C and the ![]() elements (the subgiant BS16076-06 is shown separately).
elements (the subgiant BS16076-06 is shown separately).
Table 3: Abundance ratios for the iron-peak and neutron-capture elements.
5.3 Oxygen
We have not been able to measure O abundances for any of our dwarf stars. The [O I] line at 630.03 nm, which we used for giants, is too weak, as is the permitted O I triplet at 770 nm, given the S/N we achieve in this spectral region. Only for the dwarf binary system CS 22876-032 have we been able to measure O abundances, using the OH lines in the UV (Gonzàlez Hernàndez et al. 2008; Paper XII), and these are compatible with the O abundances measured in giants.
Our spectra of the dwarfs discussed in the present paper do not cover the OH lines in the UV. The success in the case of CS 22876-032 suggests that these lines probably offer the only option for measuring O abundances in EMP dwarfs.
6 The
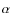 elements: Mg, Si, Ca, Ti
elements: Mg, Si, Ca, Ti
Figure 4 presents the observed [![]() /Fe] ratios in our EMP dwarf and giant samples. A priori, we expect to find the same mean abundance for these elements in dwarfs and in giants, and this is what we see for Ca. However, the mean [Mg/Fe] and [Si/Fe] ratios are
/Fe] ratios in our EMP dwarf and giant samples. A priori, we expect to find the same mean abundance for these elements in dwarfs and in giants, and this is what we see for Ca. However, the mean [Mg/Fe] and [Si/Fe] ratios are ![]() 0.2 and 0.3 dex lower in the EMP dwarfs than in the giants, while the mean abundance of [Ti/Fe] ratio
is higher in the dwarfs by about 0.2 dex. What are the possible causes of these differences?
0.2 and 0.3 dex lower in the EMP dwarfs than in the giants, while the mean abundance of [Ti/Fe] ratio
is higher in the dwarfs by about 0.2 dex. What are the possible causes of these differences?
Table 4: Abundance uncertainties linked to stellar parameters.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f2.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg30.png) |
Figure 2: [C/Fe] ratios in our turnoff stars (black dots) and unmixed giants (open circles). The grey triangle shows the subgiant BS 16076-006. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f3.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg31.png) |
Figure 3: [N/Fe] in our sample of unmixed giants. The triangle at [Fe/H] = -3.81 shows the subgiant BS 16076-006. |
| Open with DEXTER | |
6.1 Magnesium
In Fig. 4, the Mg abundance for the giant stars has been derived from a full fit to the profiles of the Mg lines, in contrast to the results given by Cayrel et al. (2004, Paper V). The equivalent widths of the Mg lines are often quite large (
![]() ), and in Paper V we underestimated the equivalent widths of these lines by neglecting the wings. For the most Mg-poor stars in our sample, the lines are weak and the difference negligible, but
it is quite significant in most of our stars, with a mean systematic difference of about 0.15 dex. In the dwarfs, the abundance has been derived from profile fits to the strongest lines (the lines at
), and in Paper V we underestimated the equivalent widths of these lines by neglecting the wings. For the most Mg-poor stars in our sample, the lines are weak and the difference negligible, but
it is quite significant in most of our stars, with a mean systematic difference of about 0.15 dex. In the dwarfs, the abundance has been derived from profile fits to the strongest lines (the lines at ![]() 383 nm, which are also located in the wings of a Balmer line), and from equivalent widths for the weak lines.
383 nm, which are also located in the wings of a Balmer line), and from equivalent widths for the weak lines.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f4a.ps}\par\includegr...
...ip]{10610f4c.ps}\par\includegraphics[width=8.5cm,clip]{10610f4d.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg33.png) |
Figure 4: [Mg/Fe], [Si/Fe], [Ca/Fe], and [Ti/Fe] in our programme stars. Symbols as in Fig. 2. |
| Open with DEXTER | |
6.2 Silicon
In the cool giants, the Si abundance is derived from a line at 410.3 nm. This line (multiplet 2) is located in the wing of H![]() ,
and the hydrogen line has been included in the computations. There is another line at 390.6 nm (multiplet 3), but in giants this line is severely blended by CH lines. In turnoff stars the line at 410.3 nm is invisible, but the CH lines are weak enough that the line at 390.6 nm can be used. Thus, in the end, only a single Si line (but not the
same one) could be used in both dwarfs and giants, but a systematic error in the log gf of these lines could explain the observed difference. Both lines are in fact measured in the subgiant star BS 16076-006 and yield consistent Si abundances, but given the uncertain atmospheric
parameters of this star (see 3), a systematic error in log gf cannot be ruled out. Our new [Si/Fe] ratios are in good agreement with the value found from the same Si line by Cohen (2004), also for EMP turnoff stars.
,
and the hydrogen line has been included in the computations. There is another line at 390.6 nm (multiplet 3), but in giants this line is severely blended by CH lines. In turnoff stars the line at 410.3 nm is invisible, but the CH lines are weak enough that the line at 390.6 nm can be used. Thus, in the end, only a single Si line (but not the
same one) could be used in both dwarfs and giants, but a systematic error in the log gf of these lines could explain the observed difference. Both lines are in fact measured in the subgiant star BS 16076-006 and yield consistent Si abundances, but given the uncertain atmospheric
parameters of this star (see 3), a systematic error in log gf cannot be ruled out. Our new [Si/Fe] ratios are in good agreement with the value found from the same Si line by Cohen (2004), also for EMP turnoff stars.
6.3 Titanium
The Ti I lines are very weak in turnoff stars, so the Ti abundance can only be determined from the Ti II lines. About 15 Ti II lines could be used, and the internal error of the mean is very small
(less than 0.1 dex). Figure 4 clearly shows higher [Ti/Fe] ratios in the dwarfs than in the giants (
![]() dex). Even if we use exactly the same lines in the giants as in the dwarfs, we observe the same effect; thus, an error in
log gf values cannot explain the difference. On the other hand, to reduce the derived [Ti/Fe] by 0.2 dex (keeping the same temperature) would require changing log g in the turnoff stars by about 1 dex, which is
incompatible with the ionisation equilibrium of the iron lines.
dex). Even if we use exactly the same lines in the giants as in the dwarfs, we observe the same effect; thus, an error in
log gf values cannot explain the difference. On the other hand, to reduce the derived [Ti/Fe] by 0.2 dex (keeping the same temperature) would require changing log g in the turnoff stars by about 1 dex, which is
incompatible with the ionisation equilibrium of the iron lines.
7 The light odd-Z metals: Na, Al, K, and Sc
7.1 Sodium and aluminium
In both dwarf and giant EMP stars, Na and Al abundances can only be derived from the resonance lines, which are very sensitive to NLTE effects (Cayrel et al. 2004). The Na and Al abundances in our two stellar samples have been derived using the NLTE line formation theory by Andrievsky et al. (2007, 2008) for Na and Al, respectively. When NLTE effects
are taken into account, the [Na/Fe] and [Al/Fe] abundance ratios are found to be constant and equal in the dwarfs and giants in the interval
![]() ([Na/Fe] = -0.2 and [Al/Fe] =
-0.1). This can be appreciated visually by looking at Fig. 7 of Andrievski et al. (2007) and Fig. 3 of Andrievski et al. (2008).
([Na/Fe] = -0.2 and [Al/Fe] =
-0.1). This can be appreciated visually by looking at Fig. 7 of Andrievski et al. (2007) and Fig. 3 of Andrievski et al. (2008).
7.2 Potassium and scandium
The K lines are very weak in our EMP turnoff stars, and [K/Fe] could not be determined. The Sc abundance in the dwarf stars was measured from the Sc II line at 424.6 nm. In giants, 7 Sc lines could be used, and the scatter in the abundances from individual lines is very small (below 0.1 dex). There is a systematic difference of about 0.2 dex between the Sc abundances in the giants and the dwarfs (Fig. 5).
8 Iron-peak elements
8.1 Chromium, cobalt, and nickel
Figure 6 shows the [Cr/Fe], [Co/Fe], and [Ni/Fe] ratios for our dwarf and giant samples. There is rather good agreement for Ni, but [Cr/Fe] and [Co/Fe] are about 0.2 dex higher in the dwarfs than in the giants. Recently Lai et al. (2008) have measured the chromium abundance in a sample of giants and turnoff stars in the same range of metallicity. The same shift appears between their giants and turnoff stars (Fig. 7).
Lai et al. also found an offset between the abundances derived from Cr I and Cr II. Cr II can only be measured in giants, and only a single Cr II line (
![]() )
appears at the edge of our blue spectra, but the same offset as observed by Lai et al. is clearly visible in our data (Fig. 8).
)
appears at the edge of our blue spectra, but the same offset as observed by Lai et al. is clearly visible in our data (Fig. 8).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f5.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg37.png) |
Figure 5: [Sc/Fe] in the programme stars. Symbols as in Fig. 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f6a.ps}\par\includegr...
...ip]{10610f6b.ps}\par\includegraphics[width=8.5cm,clip]{10610f6c.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg38.png) |
Figure 6: [Cr/Fe], [Mn/Fe], [Co/Fe], and [Ni/Fe] in the programme stars. Symbols as in Fig. 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f7.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg39.png) |
Figure 7: [Cr/Fe] in our stars (circles) compared to those of Lai et al. (2008, triangles). Filled symbols: turnoff stars; open symbols: giants. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f8.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg40.png) |
Figure 8: [Cr/Fe] in our stars from Cr I lines (open circles: giants, filled circles: turnoff stars), and from the single Cr II line (crosses; giants only). The large offset cannot be explained by measurement errors. |
| Open with DEXTER | |
The discrepancy between Cr I and Cr II, and between giants and turnoff stars, may point to non-LTE effects. The main Cr I lines are resonance lines. Unfortunately no precise structure model for the Cr atom exists, so it is not possible to explore this hypothesis at present. If significant NLTE effects were confirmed, the most reliable abundances should be those from the Cr II line, suggesting that
![]() at low metallicity.
at low metallicity.
Nissen & Schuster (1997) found a close correlation between the abundances of Na and Ni in the interval
![]() .
To explain this correlation, it has been suggested that the production of
.
To explain this correlation, it has been suggested that the production of
![]() during an SN II event depends on the neutron excess, which itself mainly depends on the amount of
during an SN II event depends on the neutron excess, which itself mainly depends on the amount of
![]() produced during hydrostatic carbon burning. However, this correlation is not observed in our sample (Fig. 9). In fact, [Ni/Fe] and [Na/Fe] have the same mean value in turnoff stars as in unmixed giants ([Ni/Fe] = 0.0 and [Na/Fe] = -0.2). [Na/Fe] is higher in several of the mixed giants, but this is due to mixing with the H-burning shell in layers that are deep enough to bring products of the Ne-Na cycle to the surface (see Andrievsky et al. 2007).
produced during hydrostatic carbon burning. However, this correlation is not observed in our sample (Fig. 9). In fact, [Ni/Fe] and [Na/Fe] have the same mean value in turnoff stars as in unmixed giants ([Ni/Fe] = 0.0 and [Na/Fe] = -0.2). [Na/Fe] is higher in several of the mixed giants, but this is due to mixing with the H-burning shell in layers that are deep enough to bring products of the Ne-Na cycle to the surface (see Andrievsky et al. 2007).
8.2 Manganese
The Mn abundances have been derived by fitting synthetic spectra to the observations, taking the hyperfine structure of the lines into account. We noted in Paper V that, in the giant stars, Mn abundances determined from the resonance lines were lower than those from the lines of higher excitation potential by about 0.4 dex. At this stage, we prefer the abundances from the high-excitation lines, because the resonance lines are more susceptible to non-LTE effects. However, only the resonance triplet is detected in the five most metal-poor giants, so for these stars the Mn abundance was determined from the triplet and corrected by the adopted 0.4 dex offset.
For most of the turnoff stars analysed here, again only the resonance triplet can be detected. In Fig. 10a the Mn abundances from these lines have been systematically increased by 0.4 dex, while in Fig. 10b [Mn/Fe] is derived from the resonance triplet profiles in all the stars and plotted without any correction. In both cases we find a systematic abundance difference of about 0.2 dex between the giants and the dwarfs.
8.3 Zinc
Zinc cannot be unambiguously assigned to the iron-peak category, since it may be formed by ![]() -rich freeze-out and neutron capture, as well as by burning in nuclear statistical equilibrium. In our sample, the only usable line is the strongest Zn I line of Mult. 2, at
481 nm. The line is very weak in all our stars, and we only consider it reliably detected and provide a measurement when the equivalent width is over 0.35 pm. Thus, Table 3 gives only six measurements and eleven upper limits; for two stars, the spectrum was affected by a defect, and it is not even possible to provide an upper limit.
-rich freeze-out and neutron capture, as well as by burning in nuclear statistical equilibrium. In our sample, the only usable line is the strongest Zn I line of Mult. 2, at
481 nm. The line is very weak in all our stars, and we only consider it reliably detected and provide a measurement when the equivalent width is over 0.35 pm. Thus, Table 3 gives only six measurements and eleven upper limits; for two stars, the spectrum was affected by a defect, and it is not even possible to provide an upper limit.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f9.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg44.png) |
Figure 9:
[Ni/Fe] vs. [Na/Fe] in dwarfs and giants; symbols as in Fig. 2. The dashed line shows the correlation found by Nissen & Schuster (1997) for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f10a.ps}\par\includegraphics[width=8.5cm,clip]{10610f10b.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg45.png) |
Figure 10:
[Mn/Fe] ratios for our dwarf and giant stars. In panel a), [Mn/Fe] in most of the giant stars is determined only from lines with excitation potential >2 eV (open squares). In the turnoff stars (black dots) and the five most metal-poor giants (open circles), only the resonance triplet of Mn is usable; [Mn/Fe] is then derived from these lines, corrected by +0.4 dex (see text). In panel b), [Mn/Fe] is determined from the resonance lines for all stars (giants and dwarfs), without any correction. In both cases, the mean [Mn/Fe] ratio is offset by |
| Open with DEXTER | |
Figure 11 shows [Zn/Fe] versus [Fe/H]; upper limits are shown as downward arrows and the giant stars from Cayrel et al. (2004) as open circles. The upper limits are consistent with the trend defined by the giant stars, but the six actual measurements appear to define a similar trend, shifted upwards by about 0.4 dex. This could be another example of the dwarf/giant discrepancy found for some other elements.
Since the majority of our [Zn/Fe] data are upper limits, we used survival statistics to analyse them. The giant stars with [Fe/H] ![]() -3.0 show a constant level of [Zn/Fe] = +0.199
-3.0 show a constant level of [Zn/Fe] = +0.199 ![]() 0.080. We selected the dwarf stars in the same metallicity range and used asurv Rev 1.2
0.080. We selected the dwarf stars in the same metallicity range and used asurv Rev 1.2![]() (Lavalley et al. 1992) to compute the Kaplan-Meier statistics, as described in Feigelson & Nelson (1985). The mean is +0.491
(Lavalley et al. 1992) to compute the Kaplan-Meier statistics, as described in Feigelson & Nelson (1985). The mean is +0.491 ![]() 0.055; since the lowest point is an upper limit, it was changed to a detection to compute the Kaplan-Meier statistics, which implies that this mean value is biased. The comparison of the two mean values for giants and dwarfs suggests that they are only marginally consistent: the 75th percentile of the [Zn/Fe] values for dwarfs (+0.223) corresponds to the mean value for giants. Changing the upper limits to
0.055; since the lowest point is an upper limit, it was changed to a detection to compute the Kaplan-Meier statistics, which implies that this mean value is biased. The comparison of the two mean values for giants and dwarfs suggests that they are only marginally consistent: the 75th percentile of the [Zn/Fe] values for dwarfs (+0.223) corresponds to the mean value for giants. Changing the upper limits to ![]() or
or ![]() would push the mean value for dwarfs even higher, thus making the values of dwarfs and giants even more inconsistent.
would push the mean value for dwarfs even higher, thus making the values of dwarfs and giants even more inconsistent.
We used the generalised version of Kendall's ![]() (Brown et al. 1974), as described in Isobe et al. (1986), to check that there is support for a correlation between [Fe/H] and [Zn/Fe] for the dwarf stars. The sample is composed of 6 detections and 11 upper limits. The probability of correlation is 91.3%, so there is a hint of a correlation, but no conclusive evidence.
(Brown et al. 1974), as described in Isobe et al. (1986), to check that there is support for a correlation between [Fe/H] and [Zn/Fe] for the dwarf stars. The sample is composed of 6 detections and 11 upper limits. The probability of correlation is 91.3%, so there is a hint of a correlation, but no conclusive evidence.
For Zn it appears unlikely that the giant/dwarf discrepancy is due to NLTE effects. Takeda et al. (2005) computed NLTE corrections for the Zn I line at 481 nm; the corrections are
small and negative for metal-poor giants, positive for metal-poor TO stars. Thus, if we applied these corrections to our sample, the discrepancy would increase from 0.2 to ![]() dex.
dex.
It is surprising that several stars display upper limits that are lower than the [Zn/Fe] ratios found in other stars of similar metallicity, suggesting a real cosmic scatter in the Zn abundance. It is interesting to note that, while for giant stars Lai et al. (2008) are in good agreement with our determinations, the two dwarf stars for which they have Zn measurements appear to be in line with the measurements of giants. This may give further support to the idea of a cosmic scatter of Zn abundances or to the existence of a Zn-rich population.
However, it should be kept in mind that the available Zn lines are all very weak (detections are about 0.4 pm, upper limits 0.1-0.2 pm), and the data should not be overinterpreted. We have, perhaps somewhat naïvely placed the upper limit at the measured value for all stars
below our chosen threshold. Had we decided to put the upper limit at ![]() above the measured EW, all the upper limits would move up among the measurements or beyond, and there would be no hint of any scatter in the Zn abundance. From the point of view of survival statistics, that the standard deviation from the mean is small, compared to observational errors, does not support the
presence of a real dispersion. The question of a scatter in Zn abundance in EMP dwarf stars clearly needs further study, if possible based on different lines.
above the measured EW, all the upper limits would move up among the measurements or beyond, and there would be no hint of any scatter in the Zn abundance. From the point of view of survival statistics, that the standard deviation from the mean is small, compared to observational errors, does not support the
presence of a real dispersion. The question of a scatter in Zn abundance in EMP dwarf stars clearly needs further study, if possible based on different lines.
9 Neutron-capture elements
Very few neutron-capture elements can be measured in turnoff stars, because their lines are generally very weak. We could, however, measure Sr abundances from the blue resonance line of Sr II, and sometimes also Ba abundances from the Ba II line at 455.4 nm. The Ba line is generally weak (about 0.5 pm) and located at the very end of the blue spectrum, where the noise is higher. As Fig. 12 shows, we find good agreement between dwarfs and giants, although the star-to-star scatter is very large, as has already been observed for the giant stars. In Fig. 13 we show the [Sr/Ba] ratio as a function of [Ba/H]. As already noticed in Paper VIII (Fig. 15), the scatter in this plane is greatly reduced. The dwarf stars appear to behave exactly in the same way as giants.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f11.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg51.png) |
Figure 11: [Zn/Fe] ratios in dwarf stars (this paper; filled circles) and in giants (Paper V; open circles). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f12a.ps}\par\includegraphics[width=8.5cm,clip]{10610f12b.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg52.png) |
Figure 12: [Sr/Fe] and [Ba/Fe] ratios in our dwarf and giant stars; symbols as in Fig. 2. The vertical scale is not the same as in the other figures. |
| Open with DEXTER | |
We have recently studied the Ba abundance in dwarfs and giants taking non-LTE effects into account (Andrievsky et al. 2009), but after correcting for NLTE the general behaviour of this element remains the same.
| |
Figure 13: [Sr/Ba] as a function of [Ba/H] in our dwarf (dots) and giant stars (open circles; data from Paper VIII). |
| Open with DEXTER | |
10 Comparison with other investigations.
Several other groups have now published detailed analyses of EMP stars similar to our own, and it is interesting to compare their results to ours. We focus on the results of the 0Z project (Cohen et al. 2004,2008) and Lai et al. (2008). The details of the comparison are provided in Appendices A-C. The final conclusion of this comparison is that there is excellent agreement between the three groups, and the small differences can be understood in terms of differences in the adopted atmospheric parameters, model atmospheres, or line selection. The MARCS model atmospheres used by us agree with the ATLAS non-overshooting models adopted by Lai et al. (2008), and both yield abundances that are about 0.1 dex lower than the ATLAS overshooting models adopted by the 0Z project.
11 Discussion
For most elements, the overall abundance trends defined by dwarfs and giants show good agreement. For example, [Ti/Fe] is constant at low metallicity in both giants and dwarfs, and [Mn/Fe] decreases with metallicity in both giants and dwarfs.
However, some elements show systematic shifts in [X/Fe] between turnoff stars and giants of the same metallicity. Generally,
![]() dex, except for Mg and Si, which show a negative shift. Also, [Cr/Fe] appears to be flat in the dwarfs, but displays a significant slope for the giants. It is difficult to explain these shifts
by systematic errors in the models (error in temperature or in gravity) because the effects on the abundance of all the elements are very similar (see Table 4), so the ratios [X/Fe] are
only slightly affected.
dex, except for Mg and Si, which show a negative shift. Also, [Cr/Fe] appears to be flat in the dwarfs, but displays a significant slope for the giants. It is difficult to explain these shifts
by systematic errors in the models (error in temperature or in gravity) because the effects on the abundance of all the elements are very similar (see Table 4), so the ratios [X/Fe] are
only slightly affected.
These differences are rather puzzling because, except for C, N, and possibly Na, the chemical composition of the giant stars should have been unaltered ever since the star formed, so one would expect that the abundances in giants would match those in dwarfs at any given metallicity. The discrepancy we find is most likely due to shortcomings in our analysis, but we do not know whether we should trust the derived results for giants or for dwarfs (or perhaps neither!).
In the following we discuss the two main simplifications of standard model atmospheres, the neglect of effects of granulation (``3D effects'' for short) and deviations from local thermodynamic equilibrium (NLTE) as possible causes of the observed discrepancies.
11.1 Granulation (3D) effects
It is well known that hydrodynamical simulations (``3D models'') predict much cooler temperatures in the outer layers of metal-poor stars than 1D models (Asplund et al. 1999; Collet et al. 2007; Caffau & Ludwig 2007; González Hernández et al. 2008, Paper XI). The effect is more pronounced for dwarfs than for giants. The species most affected by this difference are clearly those that predominantly reside in such cool layers, most notably the diatomic molecules such as CH and NH. Since one of the most striking differences between dwarfs and giants is in fact the C abundance, which we derive from CH lines, we decided to investigate the effects of granulation in more detail.
To accomplish this, we used the two
![]() (Freytag et al. 2002; Wedemeyer et al. 2004) 3D models described in Paper XI (
(Freytag et al. 2002; Wedemeyer et al. 2004) 3D models described in Paper XI (
![]() /log g/[Fe/H]: 6550/4.50/-3.0 and
5920/4.50/-3.0). Unfortunately, we do not yet have any fully relaxed models for giant stars, so we decided to use a representative snapshot of a 3D simulation of a giant close to relaxation (
/log g/[Fe/H]: 6550/4.50/-3.0 and
5920/4.50/-3.0). Unfortunately, we do not yet have any fully relaxed models for giant stars, so we decided to use a representative snapshot of a 3D simulation of a giant close to relaxation (
![]() /log g/[Fe/H]: 4880/2.00/-3.0).
/log g/[Fe/H]: 4880/2.00/-3.0).
Table 6 lists the mean 3D corrections as defined by Caffau & Ludwig (2007) for the three models described above. The sense of the correction is always 3D-1D. Approximating the 3D correction for the G-band as the average for just 4 lines is admittedly somewhat crude, but should provide a reliable order-of-magnitude estimate for the effect.
Table 5: Lines used to test the granulation effects.
For the C abundance, the effect is quite prominent for dwarfs. The magnitude of the correction is such that, if applied, the discrepancy in [C/Fe] between dwarfs and giants would be somewhat reduced (from 0.27 dex to 0.13 dex), but with the opposite sign, the dwarfs now showing a slightly lower C abundance. Given the crudeness of our 3D computations, we cannot claim with certainty that 3D effects will explain the discrepancy. To the extent that our order-of-magnitude estimates are reliable, it is possible that more accurate computations with a larger set of parameters, encompassing the full range of our dwarf and giant stars, would yield [C/Fe] ![]() 0.2 for both dwarfs and giants.
0.2 for both dwarfs and giants.
For the giant model, our computed correction for C is a factor of two smaller than the results of Collet et al. (2007). Also, for Fe, our corrections are considerably smaller than found by Collet et al., especially for the resonance line.
The issue clearly requires further investigation, which we will undertake when we have several fully relaxed 3D models of giants. A detailed discussion is therefore premature. At present it is unclear whether the different results we find come from some fundamental difference between the 3D codes:
![]() (Freytag et al. 2002; Wedemeyer et al. 2004) in our case, and the Stein & Nordlund (1998) code in the case of Collet et al. (2007), or simply from the choice of a MARCS model as the 1D reference by Collet et al. (2007).
(Freytag et al. 2002; Wedemeyer et al. 2004) in our case, and the Stein & Nordlund (1998) code in the case of Collet et al. (2007), or simply from the choice of a MARCS model as the 1D reference by Collet et al. (2007).
We performed spectrum synthesis computations, using
Linfor3D![]() to estimate 3D corrections for a few selected lines, listed in Table 5. This is not meant to substitute for a full 3D investigation of the sample, but should indicate whether the differences found between giants and dwarfs might vanish if suitable 3D models were used.
to estimate 3D corrections for a few selected lines, listed in Table 5. This is not meant to substitute for a full 3D investigation of the sample, but should indicate whether the differences found between giants and dwarfs might vanish if suitable 3D models were used.
For Si, Co, and Zn the predicted corrections are the same for giants and dwarfs, so the discrepancy for these elements should not come from granulation effects. For Sc and Ti, however, the differences go in the direction of increasing the discrepancy between dwarfs and giants.
For Mn and Cr, the difference in correction between dwarfs and giants is such as to exactly cancel the discrepancies. We caution, however, that the corrections listed in Table 6 are the average of those for the resonance and high excitation lines. The difference in correction between the two lines is smaller for the giant model (0.1 dex for Cr, 0.3 dex for Mn) than for the dwarf models (0.4-0.5 dex for Cr, 0.7 dex for Mn). This difference is still somewhat problematic, however, in the sense that, while the 1D analysis achieved a good excitation equilibrium for Cr, an analysis based on the 3D atmospheres does not. This suggests that the temperature scale appropriate for 3D models may in fact be different from those adopted in this paper and by Cayrel et al. (2004). As mentioned above, a 1D analysis implies an Mn abundance about 0.4 dex lower for the resonance lines than for the high-excitation lines, and the 3D corrections for Mn increase this difference, up to 1.1 dex.
Table 6: Mean 3D corrections for selected elements.
It is unlikely that using 3D models will bring the abundances in giants and dwarfs into agreement for all elements, although it may be possible for a few (most likely C, Cr, and Mn). However, a full re-analysis based on 3D models, including a redetermination of the atmospheric parameters, is needed before reaching a firm conclusion on this point. For the time being, since the predicted 3D corrections are always smaller for our giant model than for the dwarf models, we consider the 1D abundances for giants to be more reliable than for the dwarfs.
11.2 Deviations from local thermodynamic equilibrium.
The analysis in this paper and in Cayrel et al. (2004) is based on the assumption of local thermodynamic equilibrium (LTE), both in the computation of the model atmospheres and in the line transfer computations. For Na and Al, results based on NLTE line transfer computations have been presented in Andrievsky et al. (2007,2008). For both elements, the LTE computations implied a discrepancy between dwarfs and giants, while the NLTE computations provided consistent abundances between the two sets of stars. In the case of Na, the NLTE corrections are not very different for dwarfs or giant models for lines of a given equivalent width, but the correction depends strongly on the equivalent width. The giant stars, which are cooler, have larger equivalent widths and larger NLTE corrections. In this case the LTE abundances of dwarfs are to be considered more reliable than those of giants.
The result cannot be generalised, however, so detailed NLTE computations should be carried out for all the elements for which we find a discrepancy between dwarfs and giants. Also, from the point of view of departures from NLTE, one cannot a priori expect that the departures are larger for the stronger lines (i.e. for giants), although this is often the case.
Accordingly, except for the two elements Na and Al for which we already have NLTE computations, we cannot at present say whether accounting for NLTE effects could remove the discrepancy between dwarfs and giants. Computations of the NLTE abundance of Mg are under way.
11.3 Could the dwarf/giant discrepancy be real?
For C, the difference in [C/Fe] between dwarfs and giants might represent the effect of the first dredge-up, which could be responsible for a decrease in the C abundance due to a first mixing with the H-burning layer, where C is transformed into N. For the other elements we see no possible nucleosynthetic origin for the dwarf/giant discrepancy.
Another possibility is that the abundances in EMP turnoff stars are seriously affected by diffusion (see e.g. Korn et al. 2007; Lind et al. 2008). From Table 2 of Lind et al. (2008) one can deduce the following variations in abundance ratios between TO stars and RGB stars in the globular cluster NGC 6397:
![]()
![]() 0.17,
0.17,
![]()
![]() 0.13,
0.13,
![]()
![]() 0.12. Only for [Ti/Fe] is a variation marginally detected, which happens to be the same order of magnitude and sign as the giant/dwarf discrepancy observed by us.
0.12. Only for [Ti/Fe] is a variation marginally detected, which happens to be the same order of magnitude and sign as the giant/dwarf discrepancy observed by us.
Although a role of diffusion cannot be ruled out, the evidence in favour is, at best, very weak. Confirmation of the results of Korn et al. (2007) and Lind et al. (2008) by an
independent analysis would be useful, especially in view of the fact that previous investigations of the same cluster (Castilho et al. 2000; Gratton et al. 2001) gave different
results. As we pointed out in Paper VII, the adoption of a higher effective temperature for the turn-off stars of this cluster, as done by Bonifacio et al. (2002), would largely cancel the abundance differences between TO and RGB. Even if the results for NGC 6397 were confirmed, it is not obvious that they would apply to the field stars analysed in the present paper. Unlike the stars in a globular cluster, these stars are not necessarily strictly coeval, and their metallicities range from ![]() 0.7 to
0.7 to ![]() 1.7 dex below that of NGC 6397.
1.7 dex below that of NGC 6397.
11.4 Do the giant and dwarf samples belong to the same population?
It could be argued that the observed giant and turnoff samples might belong to different populations, since the giants would, on average, be more distant than the turnoff stars. To test this, we have compared the radial velocities of the two samples. It would have been preferable to compare the space velocities, but the distances and proper motions of the giants are generally very uncertain. Barycentric radial velocities for the turnoff stars are given in Bonifacio et al. (2007). For the giants they are given in Table 7; they are based on the yellow spectra centered at 573nm with laboratory and measured wavelengths of numerous Fe I lines (Nave et al. 1994). The wavelengths for the telluric lines for the zero points have been taken from Jacquinet-Husson et al. (2005). Velocity errors should be below 0.3 km s-1, more than adequate for the present purpose (see also Hill et al. 2002).
Since all the programme stars (except for a few of the giants) have been selected from the HK survey (Beers et al. 1985,1992; Beers 1999), which is kinematically unbiased, their radial velocities should be an unbiased estimate of the kinematic properties of the population. Thus, if the stars were indeed drawn from different populations, we would expect their radial-velocity distributions to differ. The mean radial velocities and standard deviations are -12 and 141
![]() for the giants, -32
for the giants, -32
![]() and 159
and 159
![]() for the turnoff stars, respectively. A Kolmogorov-Smirnov test shows only a 10-15% probability that the two samples have not been drawn from the same parent population. Thus, the radial-velocity data support the assumption that the dwarfs and giants belong to the same population.
for the turnoff stars, respectively. A Kolmogorov-Smirnov test shows only a 10-15% probability that the two samples have not been drawn from the same parent population. Thus, the radial-velocity data support the assumption that the dwarfs and giants belong to the same population.
12 Conclusions
We have determined abundances of C, Mg, Si, Ca, Sc, Ti, Cr, Mn, Co, Ni, Zn, Sr, and Ba for a sample of 18 EMP turnoff stars, which complements the sample of giants discussed by Cayrel et al. (2004). For the subgiant BS 16076-006, it was also possible to determine the N abundance.
For Ca, Ni, Sr, and Ba we find excellent consistency between the abundances in dwarfs and giants at any given metallicity. For the other elements we find abundances for the dwarfs that are about 0.2 dex larger than for giants, except for Mg and Si, for which the abundance in dwarfs is about 0.2 dex lower than in the giants, and Zn, for which the abundances in dwarfs are about 0.4 dex higher than in the giants.
The only element for which such a discrepancy could have an astrophysical explanation is C. In fact, if the first dredge-up were capable of bringing into the atmosphere material that had undergone CN processing, one would expect to find lower C abundance in giants than in dwarfs. Such an effect is not predicted by standard models of stellar evolution and would require some extra-mixing mechanism. For all the other elements which display a discrepancy between dwarfs and giants we are unable to find any plausible astrophysical explanation. We conclude that the discrepancies arise from shortcomings in our analysis, probably also for C, but certainly for all other elements for which discrepancies are found.
We have made an approximate assessment of the effects of granulation and conclude that they are unlikely to explain the discrepancies, except perhaps for C, Mn, and Cr. In any case, the 3D corrections appear to be smaller for giants than for dwarfs, which suggests that the 1D abundances of giants are preferable as reference data for studies of the chemical evolution of the Galaxy.
The other obvious shortcoming in our analysis is the assumption of local thermodynamic equilibrium. Detailed NLTE line transfer computations for our sample of stars exist for Na and Al (Andrievsky et al. 2007,2008), and for these two elements they in fact remove the dwarf/giant discrepancy implied by the LTE analysis. Computations for Mg are in progress, and it seems that the agreement between giants and dwarfs is at least improved. This result cannot be generalised to other elements, and it is not clear whether NLTE computations might remove any of the other discrepancies. Clearly, NLTE computations for other key elements are urgently needed.
For readers who wish to use our data for comparison with Galactic evolution models we suggest that, for elements for which a dwarf/giant discrepancy exists, the abundances in giants are to be preferred. We plan to publish an updated table of all the abundances in the First Stars programme in a final paper of the series. For the time being, we direct the reader who wants the most updated abundances of the First Stars giants to the following papers: for Li, C, N, and O, Spite et al. (2005, First Stars VI; 2006, First Stars IX); for Na, Andrievsky et al. (2007); for Mg to the NLTE abundances in Fig. 4 of the present paper (to be published in full soon); for Al, Andrievsky et al. (2008); for K, Ca, Sc, Ti, Mn, Fe, Co, Ni, Zn, Cayrel et al. (2004); for Cr, the Cr II abundances given in Fig. 8 should be preferred; for Ba Andrievsky et al. (2009); for all the other elements heavier than Zn, François et al. (2007, First Stars VIII).
The reasons for recommending the use of abundances in giants are threefold: 1) granulation effects are weaker for giants than for dwarfs; 2) giants have lower effective temperatures and stronger lines, so their abundances are better determined from the observational point of view; and 3) the atmospheres of giants stars are well mixed by convection and should be immune to chemical anomalies driven by diffusion. One should, however, bear in mind that future NLTE analyses of our data could imply substantial revision of the abundances in both giants and dwarfs.
Acknowledgements
We thank the ESO staff for assistance during all the runs of our Large Programme. R.C., P.F., V.H., B.P., F.S. and M.S. thank the PNPS and the PNG for their support. P.B., H.G.L. and E.C. acknowledge support from EU contract MEXT-CT-2004-014265 (CIFIST). T.C.B. acknowledges partial funding for this work from grants AST 00-98508, AST 00-98549, AST 04-06784, AST 07-07776, as well as from grant PHY 02-16783: Physics Frontiers Center/Joint Institute for Nuclear Astrophysics (JINA), all from the US National Science Foundation. B.N. and J.A. thank the Carlsberg Foundation and the Swedish and Danish Natural Science Research Councils for partial financial support of this work. We acknowledge use of the supercomputing centre CINECA, which has granted us time to compute part of the hydrodynamical models used in this investigation, through the INAF-CINECA agreement 2006, 2007.
References
- Allende Prieto, C., Rebolo, R., López, R. J. G., et al. 2000, AJ, 120, 1516 [NASA ADS] [CrossRef] (In the text)
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] (In the text)
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] (In the text)
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2007, A&A, 464, 1081 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2008, A&A, 481, 481 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2009, A&A, 494, 1083 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Asplund, M., & García Pérez, A. E. 2001, A&A, 372, 601 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Asplund, M., Nordlund, Å., Trampedach, R., & Stein, R. F. 1999, A&A, 346, L17 [NASA ADS] (In the text)
- Asplund, M., Grevesse, N., Sauval, A. J., Allende Prieto, C., & Kiselman, D. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ballester, P., Modigliani, A., Boitiquin, O., et al. 2000, ESO Messenger, 101, 31 [NASA ADS] (In the text)
- Beers, T. C. 1999, Ap&SS, 265, 547 [NASA ADS] [CrossRef] (In the text)
- Beers, T. C., Preston, G. W., & Shectman, S. A. 1985, AJ, 90, 2089 [NASA ADS] [CrossRef] (In the text)
- Beers, T. C., Preston, G. W., & Shectman, S. A. 1992, AJ, 103, 1987 [NASA ADS] [CrossRef]
- Boesgaard, A. M., King, J. R., Deliyannis, C. P., & Vogt, S. S. 1999, AJ, 117, 492 [NASA ADS] [CrossRef] (In the text)
- Bonifacio, P., Pasquini, L., Spite, F., et al. 2002, A&A, 390, 91 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bonifacio, P., Molaro, P., Sivarani, T., et al. 2007, A&A, 462, 851 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars VII) (In the text)
- Brown, B. J. Jr., Hollander, M., & Korwar, R. M. 1974, Nonparametric Tests of Independence for Censored Data, with Applications to Heart Transplant Studies, from Reliability and Biometry, ed. F. Proschan, & R. J. Serfling (Philadelphia: SIAM), 327 (In the text)
- Caffau, E., & Ludwig, H.-G. 2007, A&A, 467, L11 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2008, A&A, 488, 1031 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997a, A&A, 324, 432 [NASA ADS] (In the text)
- Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997b, A&A, 318, 841 [NASA ADS]
- Castelli, F., & Kurucz, R. L. 2003, in IAU Symp., ed. N. Piskunov, W. W. Weiss, & D. F. Gray, 20P (In the text)
- Castilho, B. V., Pasquini, L., Allen, D. M., Barbuy, B., & Molaro, P. 2000, A&A, 361, 92 [NASA ADS] (In the text)
- Cayrel, R. 1996, A&A Rev., 7, 217 [NASA ADS] (In the text)
- Cayrel, R. 2006, Reports on Progress in Physics, 69, 2823 [NASA ADS] [CrossRef] (In the text)
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars V) (In the text)
- Cohen, J. G., Christlieb, N., McWilliam, A., et al. 2004, ApJ, 612, 1107 [NASA ADS] [CrossRef] (In the text)
- Cohen, J. G., Christlieb, N., McWilliam, A., et al. 2008, ApJ, 672, 320 [NASA ADS] [CrossRef]
- Collet, R., Asplund, M., & Trampedach, R. 2007, A&A, 469, 687 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dekker, H., D'Odorico, S., Kaufer, A., et al. 2000, in Optical and IR Telescopes Instrumentation and Detectors, ed. I. Masanori, & A. F. Morwood, Proc. SPIE, 4008, 534 (In the text)
- Delahaye, F., & Pinsonneault, M. H. 2006, ApJ, 649, 529 [NASA ADS] [CrossRef] (In the text)
- Depagne, E., Hill, V., Spite, M., et al. 2002, A&A, 390, 187 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars II) (In the text)
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] (In the text)
- François, P., Depagne, E., Hill, V., et al. 2003, A&A, 403, 1105 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars III) (In the text)
- François, P., Depagne, E., Hill, V., et al. 2007, A&A, 476, 935 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars VIII) (In the text)
- Freytag, B., Steffen, M., & Dorch, B. 2002, Astron. Nachr., 323, 213 [NASA ADS] [CrossRef] (In the text)
- Goldman, A., & Gillis, J. R. 1981,J. Quant. Spec. Radiat. Transf., 25, 111 (In the text)
- González Hernández, J., Bonifacio, P., Ludwig, H.-G., et al. 2008, A&A, 480, 233 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars XI) (In the text)
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gustafsson, B., Bell, R. A., Eriksson, K., & Nordlund, Å. 1975, A&A, 42, 407 [NASA ADS] (In the text)
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2003, in Stellar Atmosphere Modeling, ed. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 331 (In the text)
- Gustafsson, B., Edvardsson, B., Eriksson, K., Graae-Jørgensen, U., Nordlund, Å., & Plez, B. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hill, V., Plez, B., Cayrel, C., et al. 2002, A&A, 387, 560 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars I) (In the text)
- Isobe, T., Feigelson, E. D., & Nelson, P. I. 1986, ApJ, 306, 490 [NASA ADS] [CrossRef] (In the text)
- Israelian, G., Rebolo, R., García López, R. J., et al. 2001, ApJ, 551, 833 [NASA ADS] [CrossRef] (In the text)
- Jacquinet-Husson, N., Scott, N.-A., Chédin, A., et al. 2005, JRSRT, 95, 429 [NASA ADS] (In the text)
- Jørgensen, U. G., Larsson, M., Iwamae, A., & Yu, B. 1996, A&A, 315, 204 [NASA ADS] (In the text)
- Korn, A., Grundahl, F., Richard, O., et al. 2007, ApJ, 671, 402 [NASA ADS] [CrossRef] (In the text)
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory), 13
- Lai, D. K., Bolte, M., Johnson, J. A., & Lucatello, S. 2004, AJ, 128, 2402 [NASA ADS] [CrossRef] (In the text)
- Lai, D. K., Bolte, M., Johnson, J., et al. 2008, ApJ, 681, 1524 [NASA ADS] [CrossRef] (In the text)
- Lind, K., Korn, A. J., Barklem, P. S., & Grundahl, F. 2008, A&A, 490, 777 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lavalley, M. P., Isobe, T., & Feigelson, E. D. 1992, BAAS, 24, 839 [NASA ADS] (In the text)
- Luque, J., & Crosley, D. R. 1999, SRI International report MP, 99-099 (In the text)
- Meléndez, J., Shchukina, N. G., Vasiljeva, I. E., & Ramirez, I. 2006, ApJ, 642, 1082 [NASA ADS] [CrossRef]
- Molaro, P., Bonifacio, P., & Primas, F. 1995, Mem. Soc. Astron. Ital., 66, 323 [NASA ADS] (In the text)
- Nave, G., Johansson, S., Learner, R. C. M., Thorne, A. P., & Brault, J. W. 1994, ApJS, 94, 221 [NASA ADS] [CrossRef] (In the text)
- Nissen, P. E., & Schuster, W. J. 1997, A&A, 326, 751 [NASA ADS] (In the text)
- Meynet, G., & Maeder, A. 2002, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences]
- Palacios, A., Charbonnel, C. Talon, S., & Siess, L. 2006 [arXiv:astro-ph/0602389]
- Plez, B., Hill, V., Cayrel, R., et al. 2004, ApJ, 617, L.119
- Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. Ital. Suppl., 5, 93 (In the text)
- Sivarani, T., Bonifacio, P., Molaro, P., et al. 2004, A&A, 413, 1073 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars IV) (In the text)
- Sivarani, T., Beers, T. C., Bonifacio, P., et al. 2006, A&A, 459, 125 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars X) (In the text)
- Sneden, C. A. 1973, Ph.D. Thesis (In the text)
- Sneden, C. 1974, ApJ, 189, 493 [NASA ADS] [CrossRef] (In the text)
- Sneden, C. 2007, http://verdi.as.utexas.edu/moog.html
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars VI) (In the text)
- Spite, M., Cayrel, R., Hill, V., et al. 2006, A&A, 455, 291 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars IX) (In the text)
- Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [NASA ADS] [CrossRef] (In the text)
- Takeda, Y., Hashimoto, O., Taguchi, H., et al. 2005, PASJ, 57, 751 [NASA ADS] (In the text)
- Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G., & Holweger, H. 2004, A&A, 414, 1121 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Online Material
Appendix A: Comparison with the 0Z project
The 0Z project (Cohen et al. 2004,2008) has produced a data set similar to that of the ``First Stars'' project, it is therefore of some interest to verify how these data sets compare. Cohen et al. (2004) analysed a set of dwarf stars that is directly comparable to those analysed in the present paper. The spectra were acquired with the HIRES spectrograph at the Keck I Telescope, at a resolution only slightly lower than our UVES-VLT data (34 000 rather than 45 000), and the S/N ratios are comparable. The equivalent widths were measured using an automatic code that fits Gaussians, therefore the general philosphy of EW measurement does not
differ from ours. In fact Cohen et al. (2008) observed two giant stars measured by Cayrel et al. (2004), and the equivalent widths compare very well (see Figs. 13 and 14 of Cohen et al. 2008, and related text). The two projects differ in the method used to fix the atmospheric parameters: we use the wings of H![]() for dwarf stars, while the 0Z project relies on photometry to derive
for dwarf stars, while the 0Z project relies on photometry to derive
![]() .
For surface gravity we use the iron ionisation equilibrium, while the 0Z project relies on theoretical isochrones.
.
For surface gravity we use the iron ionisation equilibrium, while the 0Z project relies on theoretical isochrones.
We have also investigated the gf values used by the two projects, and they are very similar, because the use of one or the other set would imply differences in the derived abundances smaller or equal to 0.02 dex. Thus, part of the differences will depend on the different adopted atmospheric parameters. There is no dwarf star in common between the two groups; thus it is not straightforward to compare the results of the two projects.
For the analysis the two projects use different model atmospheres and different line formation codes. We use MARCS model atmospheres and turbospectrum, while the 0Z project uses ATLAS models interpolated in the grid of Kurucz (1993), with the overshooting option switched on, and the MOOG code (Sneden 1973,1974,2007). As we show below, the difference in choice of line formation code is relatively unimportant, implying differences in the abundances of a few hundredths of dex; on the other hand, the choice of ATLAS overshooting models implies abundances that are higher by about 0.1 dex for all the models. Such behaviour has already been noticed by Molaro et al. (1995) for Li, but we show here that it is indeed true for all species.
In Table A.1 we list the abundances for the star HE 0508-1555 derived by using the equivalent widths of Cohen et al. (2004) and their atmospheric parameters (
![]() = 6365, log g = 4.4 and a microturbulent velocity of 1.6
= 6365, log g = 4.4 and a microturbulent velocity of 1.6
![]() )
with three different models: a MARCS model interpolated in our grid, an ATLAS model computed without overshooting, and an ATLAS model computed with overshooting. For all the models we assumed [M/H] = -3.0. Our ATLAS models are somewhat different from those of the Kurucz (1993) used by the 0Z project. In the first place we used the ``NEW'' opacity distribution functions (Castelli & Kurucz 2003) computed with 1
)
with three different models: a MARCS model interpolated in our grid, an ATLAS model computed without overshooting, and an ATLAS model computed with overshooting. For all the models we assumed [M/H] = -3.0. Our ATLAS models are somewhat different from those of the Kurucz (1993) used by the 0Z project. In the first place we used the ``NEW'' opacity distribution functions (Castelli & Kurucz 2003) computed with 1
![]() microturbulence. In the second place we used the Linux version of ATLAS (Sbordone et al. 2004). In all cases the line formation code used was turbospectrum. In the last two columns of Table A.1 we provide the abundances of Cohen et al. (2004), for the reader's convenience.
microturbulence. In the second place we used the Linux version of ATLAS (Sbordone et al. 2004). In all cases the line formation code used was turbospectrum. In the last two columns of Table A.1 we provide the abundances of Cohen et al. (2004), for the reader's convenience.
Inspection of Table A.1 immediately suggests that both the difference in ATLAS versions and the different line formation codes used are immaterial, since the abundances we find for almost all elements are within 0.04 dex of those of Cohen et al. (2004). The two exceptions are Al and Si. For Al there is a good reason for the discrepancy: both Al I lines used are affected by the neighbouring Balmer lines. In our analysis we used spectrum synthesis to derive the abundances. Instead, MOOG can take the absorption due to the Balmer lines into account, either using the opacit switch to introduce a fudge factor on the continuum opacity or using the strong keyword to read strong lines to be considered.
Table A.1: Abundances for HE 0508-1555 for different model atmospheres.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA1.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg63.png) |
Figure A.1:
Temperature structure for three models with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA2.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg64.png) |
Figure A.2:
Temperature structure of the deepest layers of three models with
|
| Open with DEXTER | |
For Si the difference between our result with the ATLAS overshooting model and the published value of Cohen et al. (2004) is 0.08 dex. This abundance is based on a single line of about 10 pm of EW, therefore clearly saturated. The precise value of the damping constants used for this line and the way the different codes use them may have an impact.
Another inference which can be drawn from Table A.1 is that MARCS models and ATLAS non-overshooting models provide results which are quite similar. This is not the case for the ATLAS overshooting models, which imply abundances which are higher by about 0.1 dex for all elements. The reason for this behaviour may be understood by looking at the temperature structure of the different models. In Fig. A.1 we compare the temperature structures of our MARCS model (solid line), the ATLAS non-overshooting model (dashed-dotted line) and the ATLAS overshooting model (dashed line). The temperature structure of the ATLAS non-overshooting and of the MARCS model are quite similar. In fact, the only difference is for the deepest layers and is driven by the different choices made for the mixing length.
In Fig. A.2 we show the temperature structure of the deeper layers of our MARCS model together with two ATLAS non-overshooting models with different values of
![]() 1.25 and 1.00. The ATLAS model with
1.25 and 1.00. The ATLAS model with
![]() = 1.00 is closer to the MARCS model, up to
= 1.00 is closer to the MARCS model, up to
![]() ,
but then becomes hotter than the MARCS model. In general it is impossible to chose
,
but then becomes hotter than the MARCS model. In general it is impossible to chose
![]() such that a MARCS and an ATLAS model have exactly the same structure in depth, due to the different formulations
of the mixing-length therory in the two codes. Such differences in the very deepest layers have very little influence on a typical abundance analysis. In fact, only the lines that form in these very deep layers are affected, i.e. very weak lines of 0.1 pm or smaller, and the wings of H
such that a MARCS and an ATLAS model have exactly the same structure in depth, due to the different formulations
of the mixing-length therory in the two codes. Such differences in the very deepest layers have very little influence on a typical abundance analysis. In fact, only the lines that form in these very deep layers are affected, i.e. very weak lines of 0.1 pm or smaller, and the wings of H![]() and higher members of the Balmer series.
and higher members of the Balmer series.
In general we can conclude that MARCS and ATLAS non-overshooting models are very similar, and an abundance analysis based on the two models will yield abundances that are consistent within a few
hundredths of dex. The situation is dramatically different when we consider the ATLAS overshooting models. Such models present a temperature structure that is very different from both ATLAS
non-overshooting and MARCS models in the region
![]() where the majority of lines used in abundance analysis are formed.
where the majority of lines used in abundance analysis are formed.
Castelli et al. (1997a,1997b) extensively investigated the effects of the approximate overshooting present in ATLAS and concluded that the no-overshooting models are capable of reproducing a larger set of observables, thus discouraging the use of overshooting models. To these considerations we may add that, having investigated the mean temperature structures of
![]() 3D hydrodynamical models, we never saw the typical ``bump'' in the temperature structure seen in ATLAS overshooting models. The real effect of the overshooting is the over-cooling of the outer layers with respect to what is predicted in radiative equilibrium models (Asplund et al. 1999; Collet et al. 2007; Caffau & Ludwig 2007; González Hernández et al. 2008, Paper XI). This is a further reason to avoid the use of the ATLAS overshooting models.
3D hydrodynamical models, we never saw the typical ``bump'' in the temperature structure seen in ATLAS overshooting models. The real effect of the overshooting is the over-cooling of the outer layers with respect to what is predicted in radiative equilibrium models (Asplund et al. 1999; Collet et al. 2007; Caffau & Ludwig 2007; González Hernández et al. 2008, Paper XI). This is a further reason to avoid the use of the ATLAS overshooting models.
It can be appreciated that the differences due to different models largely cancel out when considering abundance ratios, such as [Mg/Fe], rather than abundances relative to hydrogen. For example, [Mg/H] is -2.04 for the ATLAS non-overshooting model, but -1.90 for the ATLAS overshooting one; however, [Mg/Fe] is 0.50 in the first case and 0.51 in the second case.
A difference in the average [Mg/Fe] is found between us and the 0Z project, of the order of 0.2 dex (the 0Z project being higher), both if we consider only dwarf stars, only giants, or the full samples. Such an offset is roughly compatible with a ![]() error on each side, but perhaps a little disturbing. Only a 0.01 dex difference is due to the different adopted solar abundances. The use of different models and different atmospheric parameters should largely cancel out when considering a ratio such as [Mg/Fe]. Largely does not mean totally, however: Table C.1 shows a 0.06 dex difference in [Mg/Fe] for BS 16467-062, depending on the adopted atmospheric parameters.
error on each side, but perhaps a little disturbing. Only a 0.01 dex difference is due to the different adopted solar abundances. The use of different models and different atmospheric parameters should largely cancel out when considering a ratio such as [Mg/Fe]. Largely does not mean totally, however: Table C.1 shows a 0.06 dex difference in [Mg/Fe] for BS 16467-062, depending on the adopted atmospheric parameters.
Table 10 of Cohen et al. (2004) is also illuminating by showing how the average [Mg/Fe] changes if one considers the mean computed from the abundances derived from a single line of Mg I. Of the five Mg I lines used by Cohen et al. (2004), three tend to give systematically higher abundances, while two give systematically lower abundances. The final result depends on the set of adopted lines. This issue requires further investigation in the light of the study of deviations from thermodynamic equilibrium for the Mg I lines. Our abundance ratios agree with those provided by the 0Z project, within the stated errors.
At the end of this exercise we concluded that our measurements and those of the 0Z Team are highly consistent. Differences in the published abundances can be traced back to the different atmospheric parameters adopted, the different treatments of convection in the adopted model atmospheres (approximate overshooting versus no overshooting), and for some elements to the particular choice of lines.
Appendix B: Details of the comparison with Lai et al. (2008)
Lai et al. (2008) also analysed a set of stars that is comparable to that of the First Stars project with respect to metallicity. Their sample is also extracted from the HK survey and comprises both dwarfs and giants. Their method of determinng atmospheric parameters is similar to that of the 0Z project, photometric temperatures from the V-K colour and gravities derived from isochrones. They observe the giant star BS 16467-062, also observed by us (Paper V) and in the 0Z project (Cohen et al. 2008) and, not surprisingly, derive atmospheric parameters very close to those of Cohen et al. This allows a very tight comparison of the analysis by the three groups, which we defer to Sect. C.
Lai et al. use the same spectrum synthesis code as ours and also use ATLAS 9 non-overshooting models which, as discussed in Sect. A, are very similar to our MARCS models. It is therefore to be expected that the abundance ratios determined by the two groups are quite similar. In Fig. B.1 we compare the [Mg/Fe] ratios of the First Stars project with those of Lai et al. The overall agreement is satisfactory.
In Fig. B.2 we compare the [O/Fe] ratios of the First Stars project (only giants) with those of Lai et al. The figure seems to indicate good agreement; however we believe that this agreement is in fact fortuitous, as our oxygen abundances were based on the 630 nm [OI] line, while those of Lai et al. have been derived from one OH line of the UV
![]() electronic system around 318.5 nm (although the precise line used is not specified). These OH lines are known to provide very high [O/Fe] ratios when analysed with 1D model atmospheres (e.g. Boesgaard et al. 1999; Israelian et al. 2001). Asplund & García Pérez (2001) explained this behaviour as overcooling of the outer layers of the stars, caused by the overshooting of the convective elements and not properly described by 1D model atmospheres. Our own hdyrodynamical computations (González Hernández et al. 2008, Paper XI) confirm this interpretation. In view of this fact it is, at first sight, surprising to find that Lai et al. determine rather low [O/Fe] ratios from the OH lines. Closer inspection of their analysis reveals, however, that this is mainly driven by their adopted gf values for these lines.
electronic system around 318.5 nm (although the precise line used is not specified). These OH lines are known to provide very high [O/Fe] ratios when analysed with 1D model atmospheres (e.g. Boesgaard et al. 1999; Israelian et al. 2001). Asplund & García Pérez (2001) explained this behaviour as overcooling of the outer layers of the stars, caused by the overshooting of the convective elements and not properly described by 1D model atmospheres. Our own hdyrodynamical computations (González Hernández et al. 2008, Paper XI) confirm this interpretation. In view of this fact it is, at first sight, surprising to find that Lai et al. determine rather low [O/Fe] ratios from the OH lines. Closer inspection of their analysis reveals, however, that this is mainly driven by their adopted gf values for these lines.
In Fig. B.3 we show a portion of the spectrum of CS 31085-024, used by Lai et al., which we downloaded from the Keck Observatory Archive![]() compared with two synthetic spectra computed using an ATLAS 9 model with the atmospheric parameters adopted by Lai et al. and two different OH line lists. In the first case, we adopted the gf values for the OH lines of the (0-0) vibrational band of the
compared with two synthetic spectra computed using an ATLAS 9 model with the atmospheric parameters adopted by Lai et al. and two different OH line lists. In the first case, we adopted the gf values for the OH lines of the (0-0) vibrational band of the
![]() electronic system computed from the lifetimes calculated by Goldman & Gillis (1981), which we used in Paper IX. In the second case, we used the lines computed by Kurucz. This second list is far richer, since it includes lines from other
vibrational bands and not only the (0-0) band. However, even from this limited portion of the spectrum it can be appreciated that the Kurucz gf values are higher than those derived from the Goldman & Gillis (1981) lifetimes; use of the latter gf values would lead to considerably larger OH abundances.
electronic system computed from the lifetimes calculated by Goldman & Gillis (1981), which we used in Paper IX. In the second case, we used the lines computed by Kurucz. This second list is far richer, since it includes lines from other
vibrational bands and not only the (0-0) band. However, even from this limited portion of the spectrum it can be appreciated that the Kurucz gf values are higher than those derived from the Goldman & Gillis (1981) lifetimes; use of the latter gf values would lead to considerably larger OH abundances.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA3.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg69.png) |
Figure B.1: Comparison of the [Mg/Fe] ratios of the First Stars project and those of Lai et al. (2008). Our data are shown as circles, while those of Lai et al. as triangles. Open symbols correspond to giant stars, while filled symbols indicate dwarfs. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA4.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg70.png) |
Figure B.2:
Comparison of the [O/Fe] ratios of the First Stars project and those of Lai et al. (2008). Symbols as in Fig. B.1. Our oxygen abundances are derived from the 630 nm [OI] line, while those of Lai et al. from one UV OH line of the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA5.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg71.png) |
Figure B.3:
HIRES-Keck spectrum of the dwarf star CS 31085-024. The data is the same used by Lai et al. (2008), downloaded from the Keck Observatory Archive (http://www2.keck.hawaii.edu/koa/public/koa.php). Overlain on the spectrum are two synthetic spectra, computed with SYNTHE, from an ATLAS 9 model with
|
| Open with DEXTER | |
For this reason we believe that the oxygen abundances in the stars of the Lai et al. sample should be reinvestigated using a different set of gf values and hydrodynamical model atmospheres. It is likely that the 3D corrections for the giant stars (the majority of the Lai et al. sample with oxygen measurements) are smaller than those for dwarf stars (see Paper XI), since the overcooling is far less extreme in giants than in dwarfs. It is however unlikely that the effect is negligible.
We disagree with the statement by Lai et al., who discard the use of 3D models for the analysis of the OH lines since ``these models seem to overpredict the solar oxygen abundance derived from helioseismology (Delahaye & Pinsonneault 2006)''. In the first place the oxygen abundance in the Sun is not derived from OH UV lines; in the second place, it is now clear that the low solar oxygen abundances that have been claimed in the past (Asplund et al. 2004) are not due to the use of 3D hydrodynamical models, but to low measured EWs and extreme assumptions on the role of collisions with H atoms in the NLTE computations (see Caffau et al. 2008, for a discussion and a new measurement of the solar oxygen abundance). In our view the use of 3D hydrodynamical models is necessary for a reliable analysis of OH lines in metal-poor stars.
The [Cr/Fe] ratios were compared in Fig. 7 and we see that the picture that emerges is very consistent between the two analyses, including the dwarf-giant discrepancy discussed in Sect. 8.1. In agreement with us, Lai et al. note that, when Cr II lines are measurable, the [Cr II/Fe] ratio remains close to zero, suggesting that the decrease in [Cr/Fe] with decreasing metallicity, seen when Cr I lines are used, is probably an artifact due to deviations from LTE.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA6.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg72.png) |
Figure B.4: Comparison of the [Zn/Fe] ratios of the First Stars project and those of Lai et al. (2008). Symbols as in Fig. B.1. |
| Open with DEXTER | |
Finally in Fig. B.4 we compare the [Zn/Fe] ratios with those of Lai et al. (2008). They measured Zn in only two dwarfs, slightly more metal-rich than ours and the Zn abundances for these two are in line with what was derived from the giants. We note that the gf value adopted by Lai et al. is 0.04 dex lower than adopted by us.
Appendix C: Comparison for BS 16467-062
The giant star BS 16467-062 was observed independently by all three groups, ourselves (Cayrel et al. 2004, Paper V), the 0Z project (Cohen et al. 2008), and Lai et al. (2008). The last two groups used HIRES@Keck, while we used UVES@VLT.
In their Appendix B, Cohen et al. (2008) make a detailed comparison between the analysis of giant stars analysed by us and their own analysis. They conclude that the same star analysed by
the two groups will show a difference of 0.3 dex in [Fe/H]. This is based on their analysis
of the giant star BS 16467-062. We wish to explain how this difference arises. We used the EWs of Cohen et al. (2008) for this star and their gf values to redetermine the abundances using four models: a MARCS model and two ATLAS models (overshooting and non-overshooting) for
![]() = 5365 K
= 5365 K ![]() = 2.95, which are the parameters of Cohen et al. (2008) and the MARCS model with
= 2.95, which are the parameters of Cohen et al. (2008) and the MARCS model with
![]() = 5200 K,
= 5200 K, ![]() = 2.50, which was used in Cayrel et al. (2004, Paper V). The results are shown in Table C.1. We omit the results from the ATLAS non-overshooting model,
since they are identical to those obtained from the MARCS model. This could be expected by looking at Fig. C.1 in which the temperature structures of the two models are compared.
= 2.50, which was used in Cayrel et al. (2004, Paper V). The results are shown in Table C.1. We omit the results from the ATLAS non-overshooting model,
since they are identical to those obtained from the MARCS model. This could be expected by looking at Fig. C.1 in which the temperature structures of the two models are compared.
The differences in the abundances between the MARCS model with the parameters of Paper V and those
from an ATLAS overshooting model with the higher
![]() and
and ![]() of Cohen et al. (2008)
may indeed be as large as 0.3 dex. However, it is important to understand that this difference
stems from two distinct factors: on the one hand, the change in
of Cohen et al. (2008)
may indeed be as large as 0.3 dex. However, it is important to understand that this difference
stems from two distinct factors: on the one hand, the change in
![]() and
and ![]() ,
as each species displays a slightly different sensitivity to these; on the other hand, the use of approximate overshooting in the models of Cohen et al. (2008). The two effects are comparable.
,
as each species displays a slightly different sensitivity to these; on the other hand, the use of approximate overshooting in the models of Cohen et al. (2008). The two effects are comparable.
Table C.1: Abundances for BS 16467-062 different model atmospheres and the EWs of Cohen et al. (2008).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA7.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg73.png) |
Figure C.1:
Temperature structure for three models with
|
| Open with DEXTER | |
The difference in the abundances obtained from the two different MARCS models allow an estimate
of the sensitivity of the various abundances to the model parameters. The difference between the MARCS and ATLAS overshooting model allow to see the effect of the approximate overshooting.
We confirm that [Fe/H] for this star is 0.3 dex higher using the parameters of Cohen et al. (2008) and an ATLAS overshooting model, relative to what is derived using the parameters of Paper V and a MARCS model (or an ATLAS non-overshooting model). However, 0.17 dex of this difference arises from the different choices in
![]() and
and ![]() ,
and 0.13 dex comes about from the use of the approximate overshooting.
,
and 0.13 dex comes about from the use of the approximate overshooting.
Having understood these differences, we may conclude that there is excellent agreement between the two analyses. With our MARCS model and atmospheric parameters, but the EWs and gf values of Cohen et al. (2008), [Fe/H] for this star is -3.80, which compares very well with -3.77 given in Paper V. Note also that, when using MARCS models (or ATLAS non-overshooting models), our atmospheric parameters achieve a slightly better iron ionisation equilibrium (0.03 dex) than the parameters chosen by Cohen et al. (2008, 0.06 dex). However, since both these differences are much smaller than the line-to-line scatter, it is impossible to chose which set of parameters is better by just looking at the iron ionisation equilibrium. As noted above, most of these differences tend to cancel out when considering abundance ratios.
Iron is the element for which the largest number of lines is measured and, in this respect, its abundance is more robust. For other elements the difference between the values published in Paper V and an analysis by the 0Z Team may also reflect the different choice of lines. For instance for BS 16467-062, Cohen et al. (2008) measure 4 Mg I lines, while in Paper V we measured 8 lines, but used only 7 to derive the mean Mg abundance. The Mg lines in BS 16467-062 are all weak; thus, the re-measurement of the Mg abundance using line profile fitting (see Sect. 6.1) confirms the abundances provided in Paper V.
Table C.2: Abundances for BS 16467-062 for different atmospheric parameters and the EWs of Lai et al. (2008).
We discarded Mg I 416.7271 nm because the abundance derived from this line strongly deviates from those derived from the other lines. The line is rather weak (0.75 pm as measured in our data or 0.68 pm as measured by Cohen et al. 2008), but even for these very weak lines, the measurements are highly consistent. Thus the mean Mg abundance from our 7 lines is, as given in Paper V, 3.97, with a rather small scatter of 0.09 dex. On the other hand, the mean Mg abundance from the four lines measured by Cohen et al.(2008), including Mg I 416.7271 nm, and using the atmospheric parameters and model of Paper V, is 4.15 with a rather large scatter of 0.33 dex. The mean Mg abundance for these four lines from our measurements is 4.12 with a scatter of 0.38 dex. Finally if we take the measurements of Cohen et al.(2008) and discard the Mg I 416.7271 nm line, we obtain 3.99 with a scatter of 0.11, highly consistent with our published value in Paper V.
The three groups (First Stars, 0Z project, Lai et al.) have used different atmospheric parameters for this star, and the sensitivity of abundances to these is detailed in all three papers. In order to make a stringent comparison between the results of the three groups it is advisable to derive abundances from each set of EWs and gf values for a same model atmosphere and with the same spectrum synthesis code. We did so in Table C.3 where we used the MARCS model used in Paper V to rederive all the abundances. We compared the atomic species in common, excluding Al, for which both we and Lai et al. have used spectrum synthesis.
Table C.3:
Abundances for BS 16467-062 from Paper V and the same model but EWs from Cohen et al. (2008), Lai et al. (2008).
Inspection of Table C.3 immediately reveals that, with very few exceptions, the abundances
of the First Stars project rely on more lines than those of the other teams. This is particularly striking for iron, for which we use 130 Fe II lines compared to 55 of Cohen et al. and 52 of Lai et al. A similar situation is found for Ti, where we use 11 Ti I and 23 Ti II lines while Cohen et al. use 2 and 14, respectively, and Lai et al. 1 and 9. This probably reflects that the First Stars spectra have a larger total wavelength coverage and a more uniformly high S/N ratio across the spectra. This in part stems from UVES, as a two-arm spectrograph, covering roughly a 30% wider spectral range in a single exposure than HIRES, and
in part to the large amount of telescope time invested in the First Stars project. Once the Mg I line at 416.7 nm has been removed from the set of Cohen et al., the Mg abundance appears to be in remarkably good agreement, in spite of the much larger number of lines used by the First Stars team.
That the actual choice of lines does make a difference is obvious if we look at the Ca abundances. There is a difference of 0.23 dex in the Ca abundance derived in Paper V and that of Cohen et al. (2008). Of the three lines measured by Cohen et al. (2008), we have only two. The mean Ca abundance for these two lines is 2.81 with a 0.05 dex deviation, the discrepancy is reduced to 0.1 dex, totally consistent with the observational errors. We measured all four Ca lines used by Lai et al. (2008), and the mean of these four lines is close to the abundance given in Table C.3. However, Ca I 443.5 nm appears to be discrepant by 0.39 dex with respect to the mean of the
other three lines, which is 2.86, only 0.08 dex higher than the value of Lai et al. and fully consistent with observational errors. It is then clear that, for the species for which a limited number of lines is available, the actual choice of lines can make a difference.
Another noticeable difference is for Si. All three groups have determined the Si abundance from a single Si line; however, the other two teams have used the Si I 390.6 nm line, while we
used the 410.3 nm line since the other line is heavily contaminated by CH lines in the spectra
of giant stars. On the other hand, the EWs for the 390.6 nm line agree well among the three investigations (9.18 pm for us, 9.34 pm for Cohen et al. 2008; and 9.06 nm for Lai et al. 2008); thus the Si abundance derived from this line agrees well among the three investigations.
It is reassuring that for iron, for which all three groups have measured many lines, the results are fully consistent. The conclusion of these comparisons is that the results of the three teams are consistent, once the different choice of atmospheric parameters and models has been factored out.
Some caution must be exercised for the species that are represented by few lines, where the actual choice of lines can make a difference, especially if differential NLTE effects are present.
Table 1:
Adopted model atmosphere parameters.
Table 2:
Abundance ratios for C and the Table 3:
Abundance ratios for the iron-peak and neutron-capture elements.
Table 4:
Abundance uncertainties linked to stellar parameters.
Table 5:
Lines used to test the granulation effects.
Table 6:
Mean 3D corrections for selected elements.
Table A.1:
Abundances for HE 0508-1555 for different model atmospheres.
Table C.1:
Abundances for BS 16467-062 different model atmospheres and the EWs of Cohen et al. (2008).
Table C.2:
Abundances for BS 16467-062 for different atmospheric parameters and the EWs of Lai et al. (2008).
Table C.3:
Abundances for BS 16467-062 from Paper V and the same model but EWs from Cohen et al. (2008), Lai et al. (2008).
The region of the Mg I b triplet in the programme stars. [Fe/H] is shown to the left of each spectrum. In these EMP stars, the triplet lines have no damping wings.
[C/Fe] ratios in our turnoff stars (black dots) and unmixed giants (open circles). The grey triangle shows the subgiant BS 16076-006.
Footnotes
![]()
![]()
![]()
![]()
![]()
![]()
All Tables
![]() elements (the subgiant BS16076-06 is shown separately).
elements (the subgiant BS16076-06 is shown separately).
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10610f1.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg13.png)
Figure 1:
Open with DEXTER In the text
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f2.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg30.png)
Figure 2:
Open with DEXTER In the text
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f3.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg31.png) |
Figure 3: [N/Fe] in our sample of unmixed giants. The triangle at [Fe/H] = -3.81 shows the subgiant BS 16076-006. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f4a.ps}\par\includegr...
...ip]{10610f4c.ps}\par\includegraphics[width=8.5cm,clip]{10610f4d.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg33.png) |
Figure 4: [Mg/Fe], [Si/Fe], [Ca/Fe], and [Ti/Fe] in our programme stars. Symbols as in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f5.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg37.png) |
Figure 5: [Sc/Fe] in the programme stars. Symbols as in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f6a.ps}\par\includegr...
...ip]{10610f6b.ps}\par\includegraphics[width=8.5cm,clip]{10610f6c.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg38.png) |
Figure 6: [Cr/Fe], [Mn/Fe], [Co/Fe], and [Ni/Fe] in the programme stars. Symbols as in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f7.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg39.png) |
Figure 7: [Cr/Fe] in our stars (circles) compared to those of Lai et al. (2008, triangles). Filled symbols: turnoff stars; open symbols: giants. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f8.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg40.png) |
Figure 8: [Cr/Fe] in our stars from Cr I lines (open circles: giants, filled circles: turnoff stars), and from the single Cr II line (crosses; giants only). The large offset cannot be explained by measurement errors. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f9.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg44.png) |
Figure 9:
[Ni/Fe] vs. [Na/Fe] in dwarfs and giants; symbols as in Fig. 2. The dashed line shows the correlation found by Nissen & Schuster (1997) for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f10a.ps}\par\includegraphics[width=8.5cm,clip]{10610f10b.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg45.png) |
Figure 10:
[Mn/Fe] ratios for our dwarf and giant stars. In panel a), [Mn/Fe] in most of the giant stars is determined only from lines with excitation potential >2 eV (open squares). In the turnoff stars (black dots) and the five most metal-poor giants (open circles), only the resonance triplet of Mn is usable; [Mn/Fe] is then derived from these lines, corrected by +0.4 dex (see text). In panel b), [Mn/Fe] is determined from the resonance lines for all stars (giants and dwarfs), without any correction. In both cases, the mean [Mn/Fe] ratio is offset by |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f11.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg51.png) |
Figure 11: [Zn/Fe] ratios in dwarf stars (this paper; filled circles) and in giants (Paper V; open circles). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10610f12a.ps}\par\includegraphics[width=8.5cm,clip]{10610f12b.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg52.png) |
Figure 12: [Sr/Fe] and [Ba/Fe] ratios in our dwarf and giant stars; symbols as in Fig. 2. The vertical scale is not the same as in the other figures. |
| Open with DEXTER | |
| In the text | |
| |
Figure 13: [Sr/Ba] as a function of [Ba/H] in our dwarf (dots) and giant stars (open circles; data from Paper VIII). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA1.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg63.png) |
Figure A.1:
Temperature structure for three models with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA2.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg64.png) |
Figure A.2:
Temperature structure of the deepest layers of three models with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA3.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg69.png) |
Figure B.1: Comparison of the [Mg/Fe] ratios of the First Stars project and those of Lai et al. (2008). Our data are shown as circles, while those of Lai et al. as triangles. Open symbols correspond to giant stars, while filled symbols indicate dwarfs. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA4.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg70.png) |
Figure B.2:
Comparison of the [O/Fe] ratios of the First Stars project and those of Lai et al. (2008). Symbols as in Fig. B.1. Our oxygen abundances are derived from the 630 nm [OI] line, while those of Lai et al. from one UV OH line of the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA5.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg71.png) |
Figure B.3:
HIRES-Keck spectrum of the dwarf star CS 31085-024. The data is the same used by Lai et al. (2008), downloaded from the Keck Observatory Archive (http://www2.keck.hawaii.edu/koa/public/koa.php). Overlain on the spectrum are two synthetic spectra, computed with SYNTHE, from an ATLAS 9 model with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA6.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg72.png) |
Figure B.4: Comparison of the [Zn/Fe] ratios of the First Stars project and those of Lai et al. (2008). Symbols as in Fig. B.1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10610fA7.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10610-08/Timg73.png) |
Figure C.1:
Temperature structure for three models with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


