| Issue |
A&A
Volume 501, Number 2, July II 2009
|
|
|---|---|---|
| Page(s) | 437 - 443 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200810563 | |
| Published online | 13 May 2009 | |
A surviving disk from a galaxy collision at z = 0.4
Y. Yang1 - F. Hammer1 - H. Flores1 - M. Puech2,1 - M. Rodrigues1
1 - GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 5 Place Jules Janssen, Meudon, France
2 -
ESO, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
Received 10 July 2008 / Accepted 1 April 2009
Abstract
Context. Spiral galaxies dominate the local galaxy population. Disks are known to be fragile to collisions. Thus it is worthwhile to probe under what conditions a disk can possibly survive such interactions.
Aims. We present a detailed morpho-kinematic study of a massive galaxy with two nuclei, J033210.76-274234.6, at z=0.4.
Methods. The morphological analysis reveals that the object consists of two bulges and a massive disk, as well as a faint blue ring. Combining the kinematics with morphology we propose a near-center collision model for the object.
Results. We find that the massive disk is likely to have survived the collision of galaxies with an initial mass ratio of ![]() 4:1. The N-body/Smoothed Particle Hydrodynamics (SPH) simulations show that the collision possibly is a polar collision with a very small pericentric distance of
4:1. The N-body/Smoothed Particle Hydrodynamics (SPH) simulations show that the collision possibly is a polar collision with a very small pericentric distance of ![]() 1 kpc, and that the remnant of the main galaxy will be dominated by a disk. The results support the disk survival hypothesis.
1 kpc, and that the remnant of the main galaxy will be dominated by a disk. The results support the disk survival hypothesis.
Conclusions. The survival of the disk is related to the polar collision with an extremely small pericentric distance. With the help of N-body/SPH simulations we find that the probability of disk survival is quite large regardless of whether the two galaxies merge or not.
Key words: galaxies: formation - galaxies: evolution - galaxies: kinematics and dynamics - galaxies: interactions
1 Introduction
In the local universe, most of the intermediate-mass galaxies are spiral galaxies (Nakamura et al. 2004) that have experienced a violent merging stage over the last 8 Gyr (Rawat et al. 2008; Bundy et al. 2004; Le Fèvre et al. 2000). How the local spirals have been formed is still a matter of debate. Hammer et al. (2005) propose a scenario of ``disk-rebuilding'' based on the remarkable coincidence of the evolution of the merger rate, morphology and fraction of actively star-forming galaxies. In such a scenario, a significant fraction of galaxies experienced their last major merger during the last 8 Gyr, then, by accretion of gas and debris, the disks were formed around the merger remnants.
As a prediction of hierarchical models of structure formation (White & Rees 1978), galaxy-galaxy mergers or interactions have been an essential recipe to interpret the formation and evolution of galaxies (Springel 2000; Barnes & Hernquist 1992). Earlier numerical simulations predicted that the remnants of major mergers of disk galaxies (with mass ratios smaller than ![]() 4:1) are likely to be elliptical galaxies (e.g., Hernquist 1992; Barnes & Hernquist 1992; Barnes 1988), implying that the disks of the progenitors are easily destroyed in major mergers. The simulations by Barnes (2002) suggest that gas disks may be rebuilt after major mergers from the orbital angular momentum. Similar results are shown by recent simulations of gas-rich encounters (Hopkins et al. 2008; Springel & Hernquist 2005; Robertson et al. 2006). While minor mergers are less violent than major ones, the effect of minor mergers in re-shaping progenitors is significant, even with large mass ratios of 10:1 (Toth & Ostriker 1992). By the accretion of satellite galaxies, a thin disk will become thicker due to the dynamical heating by the satellite in-fall. Although the disks of spiral galaxies may survive minor mergers, their properties, such as the shape, star-formation and the bulge-to-disk ratio, are evolving towards the early type spirals (Walker et al. 1996).
4:1) are likely to be elliptical galaxies (e.g., Hernquist 1992; Barnes & Hernquist 1992; Barnes 1988), implying that the disks of the progenitors are easily destroyed in major mergers. The simulations by Barnes (2002) suggest that gas disks may be rebuilt after major mergers from the orbital angular momentum. Similar results are shown by recent simulations of gas-rich encounters (Hopkins et al. 2008; Springel & Hernquist 2005; Robertson et al. 2006). While minor mergers are less violent than major ones, the effect of minor mergers in re-shaping progenitors is significant, even with large mass ratios of 10:1 (Toth & Ostriker 1992). By the accretion of satellite galaxies, a thin disk will become thicker due to the dynamical heating by the satellite in-fall. Although the disks of spiral galaxies may survive minor mergers, their properties, such as the shape, star-formation and the bulge-to-disk ratio, are evolving towards the early type spirals (Walker et al. 1996).
One interesting galaxy interaction is head-on collision which may cause the formation of the ring in disk galaxies, so called ``collisional'' ring galaxies (Lynds & Toomre 1976). In this case, the satellite galaxy impacts close to the center of the host galaxy, and passes through the disk. Then a ring will be formed and propagate in the disk outwards due to the density wave. Simulations show that in most of the collisional ring galaxies, disks are severely affected (Appleton & Struck-Marcell 1996; Athanassoula et al. 1997). Therefore it is worthwhile to explore whether a disk will survive the collision, and under what conditions, such as mass ratio and orbital parameters.
We present a morphology and kinematics study of J033210.76-274234.6 which is possibly an indication of such a surviving disk. This paper is organized as follows: in Sect. 2 we describe the data we have obtained for the object; in Sect. 3, the analysis of morphology
is presented. In Sect. 4, we develop a dynamical model together with N-body/SPH simulations in order to explain the observations. We discuss the results and give our
conclusions in Sect. 5. Throughout the paper, we adopt the Concordance cosmological parameters of H0 = 70 km s-1 Mpc-1,
![]() and
and
![]() .
.
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[height=6.5cm]{0563fg1a.ps}\hspace{3mm}\includegraphics[height=6.5cm]{0563fg1b.ps}\end{tabular}
\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg5.png) |
Figure 1: Left: the three-color image composed from the B, V, z bands. The image has a size of 30 kpc. Right: B-z color map of the object. The regions with a signal-to-noise ratio greater than 3 are shown. The circles A, B indicate core-A and core-B, respectively. The radii of the two circles are equivalent to the effective radii of the two cores. These two panels have identical scale and orientation. |
| Open with DEXTER | |
2 Data
The object J033210.76-274234.6 (z = 0.41686) is located in the G OODS
(The Great Observatories Origins Deep Survey, Giavalisco et al. 2004). The public data of G OODSavailable for the detailed studies of its colors and morphology. We chose the data release 1.0 from G OODS Cutout Service![]() and obtained the images in 4 bands: F435W, F606W, F775W, F850LP, namely B, V, i, z. The drizzled HST/ACS images have a pixel scale of
and obtained the images in 4 bands: F435W, F606W, F775W, F850LP, namely B, V, i, z. The drizzled HST/ACS images have a pixel scale of
![]() ,
corresponding to 0.165 kpc/pixel at the target redshift. In Table 1 we list the photometric properties of the object.
,
corresponding to 0.165 kpc/pixel at the target redshift. In Table 1 we list the photometric properties of the object.
With the -GIRAFFE multi-object integral-field spectrograph at VLT (see Flores et al. 2006), the spatially-resolved kinematics of this object has been recovered by observing the [O II] doublet emission (Yang et al. 2008). The object was selected early into the sample of emission line galaxies (Yang et al. 2008). From the high quality FORS2 spectroscopic observation at VLT (Rodrigues et al. 2008), it is discovered to be a rather quiescent galaxy with weak [O II] EMISSION (AT 2 Å). DUE TO THE BRIGHTNESS OF THE OBJECT (V(AB) = 19.9) WE ARE ABLE TO RECOVER ITS KINEMATICS WITH G IRAFFE AT VLT.
3 Analysis
3.1 General properties
In Fig. 1, we show a three-color image and a B-z color map of the object. The color of the three-color image is slightly enhanced to see the structures more easily. Two bright nuclei can be easily recognized. We have plotted two circles in the B-z color map to indicate the core positions and the sizes at effective radius that are derived from the morphology analysis (see Sect. 3.2). The left core (hereafter core-A) has a color as red as the elliptical galaxies at redshift 0.4 (see Fig. 8 of Neichel et al. 2008). The right core (hereafter core-B) is slightly bluer than core-A, and its color is similar to that of an S0 galaxy. In addition, we detect several blue clumps surrounding the object center. Since it resembles a ring, we refer to it as the ``blue ring'' hereafter. It is detected in the B-band which corresponds to the U-band at rest frame. This suggests that star formation has been triggered in the ring.
Table 1: Properties of the target J033210.76-274234.6.
![\begin{figure}
\par\includegraphics[width=7.5cm]{0563fg2a.ps}\includegraphics[width=7.5cm]{0563fg2b.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg17.png) |
Figure 2: Left: light profile decomposition along the core axis of z-band. Right: the V-band residual image (slightly smoothed) of morphology decomposition. The blue annulus indicates the ring region. The other two green regions indicate the tail-like structure and the faint structure, respectively. The plume structures and the central light-deficiency are marked by arrows as well. |
| Open with DEXTER | |
3.2 Morphological analysis
G ALFIT (Peng et al. 2002) is used to perform a two-dimensional profile decomposition in order to study the intrinsic luminosity distribution. The technical details of the decomposition have been discussed in Neichel et al. (2008) and Rawat et al. (2007). We chose the Sérsic profile to model each component. The key parameter is the Sérsic index n, which gives the classical bulge profile of the de Vaucouleurs law when n=4, and the exponential disk when n=1.
We first investigated the light profile of the z-band. We initially defined a model of two Sérsic profiles that are centered at the two nuclei respectively. G ALFIT gives a best fit with
![]() of 1.88. The significant residuals imply the existence of an additional component. We then added the third component of Sérsic to the model. We obtain an optimized solution of
of 1.88. The significant residuals imply the existence of an additional component. We then added the third component of Sérsic to the model. We obtain an optimized solution of
![]() = 1.26 with n=5.67, 4.61, 0.48 for core-A, core-B and the third component, respectively. The two nuclei are bulges since their n is approximately 4. The third component resembles the disk shape of lower n. We have tried a four-component model which gave no improvement. Alternatively, we tried to fix the disk center to any of the cores, but no reasonable solutions were found. It is known that the Sérsic index is coupled to the effective radius
(Trujillo et al. 2001; Peng et al. 2002). Thus we fixed the index n to the classical values: n=4 for bulges and n=1 for the disk-like component. We obtained a reasonable fit with a
= 1.26 with n=5.67, 4.61, 0.48 for core-A, core-B and the third component, respectively. The two nuclei are bulges since their n is approximately 4. The third component resembles the disk shape of lower n. We have tried a four-component model which gave no improvement. Alternatively, we tried to fix the disk center to any of the cores, but no reasonable solutions were found. It is known that the Sérsic index is coupled to the effective radius
(Trujillo et al. 2001; Peng et al. 2002). Thus we fixed the index n to the classical values: n=4 for bulges and n=1 for the disk-like component. We obtained a reasonable fit with a
![]() of 1.34. Although the
of 1.34. Although the ![]() of the free-n fit is smaller than that of the fixed-n fit, it does not significantly improve the modeling. So we adopt the fixed-n model hereafter. We performed fixed-n fitting to the other three bands (i.e., B, V, i). The
findings are similar to what we find in the z-band. As a result, we have successfully recovered the main components of the object, i.e., the two bulges and the large disk centered between the two. The parameters of each component in z-band and the error estimation by G ALFIT are listed in Table 1.
of the free-n fit is smaller than that of the fixed-n fit, it does not significantly improve the modeling. So we adopt the fixed-n model hereafter. We performed fixed-n fitting to the other three bands (i.e., B, V, i). The
findings are similar to what we find in the z-band. As a result, we have successfully recovered the main components of the object, i.e., the two bulges and the large disk centered between the two. The parameters of each component in z-band and the error estimation by G ALFIT are listed in Table 1.
The left panel of Fig. 2 illustrates the results of the morphological decomposition. We show the light profile along the core axis which is defined to be the line across the centers of the two bulges. The profile of each seeing-convolved model component as well as the sum of them are plotted separately in Fig. 2 with different symbols. The light profile at |r|>5 kpc is close to a straight line, which is strongly indicative of the existence and the significance of the disk. The center of the disk is found to be located between the two nuclei (close to core-A), and no significant structures, e.g., arms, are found in the disk. Note that in the residual maps of all the bands, we find several structures (see V-band for example, the right panel in Fig. 2), including a shell-like structure following the blue ring, plume-like structures that are associated with core-A, a tail-like structure and a faint structures. These residuals indicate a recent galactic interaction in the object.
![\begin{figure}
\par\includegraphics[width=13.1cm,clip]{0563fig3.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg20.png) |
Figure 3:
Panel a), a 3D sketch of our target based on the morphological decomposition. The disk is represented by a gray plane. The two bulges are indicated by different
colors, red for core-A and orange for core-B. The blue ring is shown as well in blue. Two black dashed lines indicate the major axes of the ring and the disk, respectively. The black star between
the two bulges represents the center of the disk. The blue star (white star if in a black-white version) above the core-A indicates the center of the ring. The rotated grid in gray dotted lines indicates the G IRAFFE IFU elements (see panels b) and c)). The red and the blue
boxes (white boxes if in a black-white version) highlight the maximal and the minimal velocities
observed by G IRAFFE IFU. The green dashed box indicates the position and the coverage of the
FORS2 slit. Panels b) and c), the spatially-resolved kinematics, i.e., the velocity field and the velocity dispersion, respectively. The dashed-line grids indicate the spatial
resolution elements of IFU. The kinematics maps have been rotated to be aligned with the object
orientation. Panel d) shows the simulated image which is constructed using the projected star density (in yellow-green or in gray if in a black-white version) with the gas superposed in blue (in white if in a black-white version). Panels e) and f) show the simulated gas kinematics: VF- and |
| Open with DEXTER | |
4 Dynamical model
4.1 Analysis
The detection of a ring suggests that an almost central collision took place between two progenitors. The morphological analysis shows a very strong indication that the disk of the main progenitor was relatively little affected by this interaction, as weak perturbations are detected in the residuals. Below, with the help of N-body/SPH (e.g., Monaghan 1992) simulations, we construct a model for this collision in order to test whether the main progenitor disk may have survived the interaction.
With the spatially-resolved kinematics from G IRAFFE, the slit kinematics from FORS2, and the morphological decomposition, we are able to develop a dynamical model to interpret the interaction occurring in the object. The mass of each component is crucial to construct the model. We have obtained the stellar mass of the system from Puech et al. (2008) and listed it in Table 1. We estimate the stellar mass of each component according to their z-band light fraction (see Table 1), under the assumption that the luminosity in z-band (corresponding to R-band at rest frame) is approximately proportional to the stellar mass.
The panel (a) of Fig. 3 shows a 3D sketch of the object based on the morphological parameters that are derived from the decomposition. The disk is nearly face-on with an inclination of ![]() .
The two bulges have a projected distance of 2.15 kpc. The blue ring with an inclination of
.
The two bulges have a projected distance of 2.15 kpc. The blue ring with an inclination of ![]() is also shown in the figure. The ring has a radius of 7.18 kpc. The two plumes (Fig. 2) may be the tidal relics of the core collision, because they have a
red color similar to core-A which is marginally affected by the global low extinction AV = 0.2 (see Table 1). Moreover, we find that the center of core-B in B-band is slightly shifted from the centers in the other bands by 0.06'' (
is also shown in the figure. The ring has a radius of 7.18 kpc. The two plumes (Fig. 2) may be the tidal relics of the core collision, because they have a
red color similar to core-A which is marginally affected by the global low extinction AV = 0.2 (see Table 1). Moreover, we find that the center of core-B in B-band is slightly shifted from the centers in the other bands by 0.06'' (![]() kpc). This shift may
account for the asymmetric color distribution of core-B (see B-z map Fig. 1).
kpc). This shift may
account for the asymmetric color distribution of core-B (see B-z map Fig. 1).
What are the progenitors? The detection of the giant disk is robust. This disk does not seem to be severely affected by the collision. We refer to the galaxy associated with this disk as the main galaxy. We have noticed that the B-z color of the disk is 2.94 which is in agreement with the color of S0 galaxies at this redshift (see Fig. 8 of Neichel et al. 2008). From its location, brightness and color, core-A is likely to be the bulge of the main galaxy. If we take core-B as the bulge of the main galaxy, resulting in a bulge-to-total light ratio of B/T ![]() 0.17, then we would expect a bluer disk such as that of Sbc type galaxies.
0.17, then we would expect a bluer disk such as that of Sbc type galaxies.
The inclination of the blue ring is quite high compared to that of the detected disk. This suggests that the blue ring probably does not lie in the plane of the disk. It implies that another disk existed before the collision, and this disk had been disrupted during the collision and formed the ring. From the morphology decomposition, we have estimated the bulge mass of the two progenitors: for the main galaxy, the bulge represents 27% of the total mass of the system, and for the intruder, the bulge is 13%. It is difficult to estimate the exact mass ratios of the progenitors, since the intruder's disk was disrupted. However, we can estimate the limits.
We have observed the star-forming activities, i.e., the blue ring, which suggests that a significant fraction of gas preexisted in the intruder disk. First, let us assume the intruder is an Sa galaxy
with B/T of 0.3 which is a typical value for Sa galaxies. With this assumption, we arrive at a mass ratio of ![]() 1:1 between the progenitors. This seems not to be the case that we have observed. Otherwise we would have seen two rings with similar strength. Thus, the intruder could be an S0 galaxy with B/T ranging from 0.5 to 0.8. We assume a mean B/T value of 0.65 for the intruder, which gives a mass ratio of 4:1 for the progenitors. Even if we take B/T=0.8, the mass ratio only increases to 5:1 which could be the upper limit of the mass ratio. We adopt a mass ratio of 4:1 in the following discussion, implying a major merger is supposed.
1:1 between the progenitors. This seems not to be the case that we have observed. Otherwise we would have seen two rings with similar strength. Thus, the intruder could be an S0 galaxy with B/T ranging from 0.5 to 0.8. We assume a mean B/T value of 0.65 for the intruder, which gives a mass ratio of 4:1 for the progenitors. Even if we take B/T=0.8, the mass ratio only increases to 5:1 which could be the upper limit of the mass ratio. We adopt a mass ratio of 4:1 in the following discussion, implying a major merger is supposed.
| |
Figure 4: The velocity curve of the object, which is derived from the FORS2 slit observation. The coverage of slit is shown in the panel a) of Fig. 3 in a green dashed-line box. |
| Open with DEXTER | |
We obtained FORS2 slit observations of the object from Rodrigues et al. (2008), see Fig. 3 for the slit coverage. Using the absorption lines Ca II H, K, we are able to recover a velocity curve covering the central 7.2 kpc region (see Fig. 4), which suggests a disk dominated by rotation. With the maximal ![]() of 269 km s-1, the rotation velocity is estimated to be 360 km s-1 after correcting for disk inclination. With the mass ratio of 4:1, we can derive the stellar mass of the main galaxy to be 2.2
of 269 km s-1, the rotation velocity is estimated to be 360 km s-1 after correcting for disk inclination. With the mass ratio of 4:1, we can derive the stellar mass of the main galaxy to be 2.2 ![]()
![]() (80% of the total). We find that this galaxy is well in agreement with the stellar mass Tully-Fisher relation by Puech et al. (2007) and with the
(80% of the total). We find that this galaxy is well in agreement with the stellar mass Tully-Fisher relation by Puech et al. (2007) and with the
![]() relation by Hammer et al. (2007).
relation by Hammer et al. (2007).
The right panel of Fig. 3 shows the G IRAFFE 2D velocity field (VF) and velocity dispersion (![]() )
map. Since the maps are derived from the [O II] emission, the kinematics tracks the large-scale motion of the gas. The dynamical axis, which is defined as the line connecting the minimum and maximal velocity, is misaligned with the major axis of the ring. This suggests that the motion of gas is not a simple rotation pattern, and that another motion is
superposed on it. The velocity gradient follows the ring. The above facts are easily explained by the superposition of a disk rotation and an expanding velocity field related to the ring.
We estimate the expanding velocity of the ring to be 180
)
map. Since the maps are derived from the [O II] emission, the kinematics tracks the large-scale motion of the gas. The dynamical axis, which is defined as the line connecting the minimum and maximal velocity, is misaligned with the major axis of the ring. This suggests that the motion of gas is not a simple rotation pattern, and that another motion is
superposed on it. The velocity gradient follows the ring. The above facts are easily explained by the superposition of a disk rotation and an expanding velocity field related to the ring.
We estimate the expanding velocity of the ring to be 180 ![]() 70 km s-1 by taking into
account the geometric projection and several G IRAFFE measurements around the ring. This suggests the elapsed time after the impact to be 39 Myr by taking the ring radius of 7.18 kpc.
70 km s-1 by taking into
account the geometric projection and several G IRAFFE measurements around the ring. This suggests the elapsed time after the impact to be 39 Myr by taking the ring radius of 7.18 kpc.
4.2 N-body/SPH simulation
With the geometrical parameters and mass ratios derived above, we have constructed N-body/SPH simulations to demonstrate the formation of the blue ring and to test the disk survival hypothesis. We used the N-body/SPH software called ``Z ENO'' developed by Barnes![]() (e.g., Barnes & Hernquist 1992). Galaxy models are created following Barnes (2002,1988). With Z ENO, we take G = 1. The mass ratio between two the galaxies is set to be 4:1. Using the same fraction of halo and baryonic matter as in
Barnes (2002), the total mass of the system was set to 3.25 mass units. With the stellar mass of the system, 2.75
(e.g., Barnes & Hernquist 1992). Galaxy models are created following Barnes (2002,1988). With Z ENO, we take G = 1. The mass ratio between two the galaxies is set to be 4:1. Using the same fraction of halo and baryonic matter as in
Barnes (2002), the total mass of the system was set to 3.25 mass units. With the stellar mass of the system, 2.75 ![]()
![]() ,
we obtain the mass unit of simulation as 4.4
,
we obtain the mass unit of simulation as 4.4 ![]()
![]() .
Then we chose the length scale 38.6 kpc, resulting in the velocity unit of 221 km s-1 and the time unit of 176 Myr. For the main progenitor, we adopted
B/T=0.34, scale a length of 5.27 kpc and a scale height of 2.5 kpc; while for the intruder, B/T=0.65, the scale length of 3.0 kpc, and the scale height of 0.5 kpc was used. We assume 5% of gas distributed in the intruder disk, and no gas in the main galaxy. The gas has the same properties as in Barnes (2002), and the SPH calculation follows the isothermal equation of state.
Our simulations include
.
Then we chose the length scale 38.6 kpc, resulting in the velocity unit of 221 km s-1 and the time unit of 176 Myr. For the main progenitor, we adopted
B/T=0.34, scale a length of 5.27 kpc and a scale height of 2.5 kpc; while for the intruder, B/T=0.65, the scale length of 3.0 kpc, and the scale height of 0.5 kpc was used. We assume 5% of gas distributed in the intruder disk, and no gas in the main galaxy. The gas has the same properties as in Barnes (2002), and the SPH calculation follows the isothermal equation of state.
Our simulations include
![]() particles. The gas fraction in our system is very low. Therefore, we chose a small mass resolution for the SPH calculation in order to have a reasonable number of particles to trace the gas motion. We designed a polar collision that follows a parabolic orbit with a pericentric separation of
particles. The gas fraction in our system is very low. Therefore, we chose a small mass resolution for the SPH calculation in order to have a reasonable number of particles to trace the gas motion. We designed a polar collision that follows a parabolic orbit with a pericentric separation of ![]() 0.76 kpc. The fine-tuning of orbital parameters
0.76 kpc. The fine-tuning of orbital parameters![]() is necessary to closely match the morphology and the gas kinematics.
is necessary to closely match the morphology and the gas kinematics.
![\begin{figure}
\par\mbox{\includegraphics[width=6cm]{0563fg5a.ps}\hspace{1cm}\in...
...
\mbox{\hspace*{3.1cm}($a$ ) \hspace{6cm} ($b$ )\hspace*{3.1cm}}\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg30.png) |
Figure 5: Panel a), the simulated image for the intruder only, with gas superposed in blue. The arrow indicates the star distribution possibly corresponding to the observed tail-like structure. Panel b), the simulated image for the main galaxy only. A weak but broad ring can be recognized. Due to the superposition of the bulge, the left part of the ring shape is hidden. The cross indicates the center of the disk. See Sect. 4.2 for more details. |
| Open with DEXTER | |
This simulation matches both the morphology and the kinematics that we observed, as well as some detailed features. Below, we list those of features that are matched by the simulation. The strongest constraints are the ACS morphology and the G IRAFFE kinematics.
- 1.
- In Fig. 3d, we show a simulated image
![[*]](/icons/foot_motif.png) that is constructed using the projected star density with the gas superposed in blue. The observed blue ring is defined by rest-frame U-band clumps which indicate the star-burst regions. Thus the blue ring traces the gas. In the simulation, a gas ring begins to form after the first passage, and evolves over 35 Myr to match the observation. Note that the gas ring in the simulation has a slightly larger size than the observed blue ring in order to match the G IRAFFE kinematics. On the other hand, this is expected since the stellar evolution is found to be behind the expanding density wave (Appleton & Struck-Marcell 1996).
that is constructed using the projected star density with the gas superposed in blue. The observed blue ring is defined by rest-frame U-band clumps which indicate the star-burst regions. Thus the blue ring traces the gas. In the simulation, a gas ring begins to form after the first passage, and evolves over 35 Myr to match the observation. Note that the gas ring in the simulation has a slightly larger size than the observed blue ring in order to match the G IRAFFE kinematics. On the other hand, this is expected since the stellar evolution is found to be behind the expanding density wave (Appleton & Struck-Marcell 1996).
- 2.
- The kinematics of the object from G IRAFFE is derived from the [O II] doublet emission that is coming from the ionized gas. In Figs. 3e, f, we show kinematics of gas from the simulation. Geometrically and quantitatively, the simulated gas kinematics is in good agreement with the observations, i.e., the dynamical axis of the velocity field and the peak of the velocity dispersion.
- 3.
- In Fig. 1, there is slight distortion of the morphology in the left part of the ring, close to the edge of the ring. This distortion also can be seen in the B-z color map. In the simulated image, we find the same feature. The distortion is due to the superposition of the two galaxies.
- 4.
- Both the three-color image of Fig. 1 and the residual image of Fig. 2 show a tail-like feature. From the simulation we find that it is likely to be
the tidal tail created by the collision. In Fig. 5a, we compare the gas and the stellar component of the intruder galaxy. We notice that the stars move further than the gas, marked by the an arrow in the figure. Their relative position resembles the blue ring and the tail-like structure in the observation. The simulation does not show an exact tail structure. Nevertheless, the star dynamics has been demonstrated reasonably well.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0563fig6.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg31.png)
Figure 6: Panel a), the observed radial profile (solid line). The dashed line indicates the slope of the thin-disk component. At the radii from 5 to 10 kpc, we clearly have a thick-disk component which corresponds to the ring that has been formed in the disk of main galaxy. Panel b), the radial profile derived from the simulation. Clearly we have a thin- and a thick-disk component. The appearance of the thick-disk component is related to the formation of the ring. For comparison, the radial profile of the main progenitor is plotted with a dashed line.
Open with DEXTER - 5.
- Our target J033210.76-274234.6 is a strong galactic collision. We have estimated that the mass ratio of progenitors is not larger than 5:1, and adopted 4:1 in the modeling. The intruder penetrated the center of the main galaxy. A ring in the main galaxy is expected to be observed, as we have seen in the simulation (see Fig. 5b). Although we cannot see the ring directly, we have found two robust observational clues, combined with the simulation, to prove its existence. In Fig. 6, we compared the observed radial profile
with the simulated one. Both of them exhibit two disk components: a thick disk and a more extended thin disk. Note that for the observation, the thin disk is only detected in the radial profile.
Hence, from the simulation, we can conclude that the thick-disk component is caused by the formation of the ring. This leads to the realization that the disk we have seen in the three-color figure is actually the ring that has formed in the main galaxy. The second piece of evidence is from the residual image (see Fig. 2) where we have marked a light-deficient region in the central part. It is naturally explained when a disk with a ring is fitted and a disk profile subtracted. Therefore, the ring in the main galaxy has been observed. However, due to the superposition of the two bright bulges and the broadness of the ring, the shape of the ring is hidden. The broadness of the ring is linked to the thickness of the main disk, which has been investigated and proved by our simulations.
- 6.
- In the previous section, we mentioned that the center of core-B in the B band is slightly shifted from other bands, resulting in the asymmetric color distribution of core-B (see Fig. 1). In the simulation, we have observed that, after the first passage, part of the perturbed gas is falling back to the center of the intruder. The falling gas may cause the star-forming activities which could explain the color shift of core-B. Note that, from the simulation, we find that the maximum velocity in the VF map is also caused by the infalling gas.
- 7.
- The morphology decomposition reveals that the bulge of the main progenitor, core-A, has been shifted from the center of the disk. This is also confirmed by the simulation. In Fig. 5b, the bulge of the main galaxy is clearly shifted with respect to the center of the disk. The movement of the central bulge is due to the very close core interaction.
- 8.
- From the FORS2 slit spectrum, we have a constraint for the collision speed. We measured the velocity difference between the [O II] emission and Ca II H, K absorption lines,
finding 210
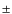 50 km s-1. Note that by measuring the absorption lines we are actually measuring the mean velocity of the two bright bulges when considering seeing effects. Using the simulation, we mimicked the slit observation and measured the mean velocity of star particles and of gas particles, respectively. We find a velocity difference of 270
50 km s-1. Note that by measuring the absorption lines we are actually measuring the mean velocity of the two bright bulges when considering seeing effects. Using the simulation, we mimicked the slit observation and measured the mean velocity of star particles and of gas particles, respectively. We find a velocity difference of 270 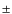 60 km s-1
which is consistent with the value from the observation.
60 km s-1
which is consistent with the value from the observation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0563fig7.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg32.png) |
Figure 7: The radial profiles of the remnants in the unbound case, panel a) for the remnant of the intruder, b) for the remnant of the main galaxy. The dashed lines in both figures indicate the disk components. Clearly, the remnant of the main progenitor is dominated by the disk. |
| Open with DEXTER | |
| |
Figure 8: Left: the face-on view of the merger remnants. The image has a size of 103 kpc. Right: the radial profile of the merger remnant. The disk component is indicated by a dashed line. |
| Open with DEXTER | |
5 Discussion and conclusion
Morpho-kinematics analysis reveals that J033210.76-274234.6 is dominated by a massive
disk. The spatially-resolved kinematics appears to be the superposition of the rotation and the expanding velocity field from the blue ring. We propose a near-center collision model which
explains all the observations. Consequently, we conclude that the disk of the main galaxy has survived the galaxy collision. Using the N-body/SPH simulations, we have successfully reproduced the ACS morphology and the G IRAFFE kinematics, as well as some details. We also explored the remnants of the collision. We find that this is a rare polar collision with a very small (![]() 1 kpc) pericentric separation, and that regardless of whether the two galaxies merge or not,
the remnant of the main galaxy is dominated by the disk component. The results support the disk survival hypothesis. The survival of the main disk is related to the exceptional collision with an extremely small pericentric distance and a polar orbit.
1 kpc) pericentric separation, and that regardless of whether the two galaxies merge or not,
the remnant of the main galaxy is dominated by the disk component. The results support the disk survival hypothesis. The survival of the main disk is related to the exceptional collision with an extremely small pericentric distance and a polar orbit.
Acknowledgements
We would like to thank the referee for the constructive comments, Isaura Fuentes-Carrera, Benoit Neichel and Sebastien Peirani for the helpful discussions. We are grateful to Albrecht Rüdiger for helping us in the writing of the paper. Especially, we would like to thank Joshua E. Barnes for his help with the simulations.
References
- Appleton, P. N., & Struck-Marcell, C. 1996, Fundamentals of Cosmic Physics, 16, 111 [NASA ADS]
- Athanassoula, E., Puerari, I., & Bosma, A. 1997, MNRAS, 286, 284 [NASA ADS]
- Barnes, J. E. 1988, ApJ, 331, 699 [NASA ADS] [CrossRef]
- Barnes, J. E., & Hernquist, L. 1992, ARA&A, 30, 705 [NASA ADS] [CrossRef]
- Barnes, J. E. 2002, MNRAS, 333, 481 [NASA ADS] [CrossRef] (In the text)
- Bundy, K., Fukugita, M., Ellis, R. S., Kodama, T., & Conselice, C. J. 2004, ApJ, 601, L123 [CrossRef]
- Flores, H., Hammer, F., Puech, M., Amram, P., & Balkowski, C. 2006, A&A, 455, 107 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] (In the text)
- Hammer, F., Flores, H., Elbaz, D., et al. 2005, A&A, 430, 115 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hammer, F., Puech, M., Chemin, L., Flores, H., & Lehnert, M. D. 2007, ApJ, 662, 322 [NASA ADS] [CrossRef] (In the text)
- Hernquist, L. 1992, ApJ, 400, 460 [NASA ADS] [CrossRef]
- Hopkins, P. F., Cox, T. J., Younger, J. D., & Hernquist, L. 2008 [arXiv:0806.1739]
- Le Fèvre, O., Abraham, R., Lilly, S. J., et al. 2000, MNRAS, 311, 565 [NASA ADS] [CrossRef]
- Lynds, R., & Toomre, A. 1976, ApJ, 209, 382 [NASA ADS] [CrossRef] (In the text)
- Monaghan, J. J. 1992, ARA&A, 30, 543 [NASA ADS] [CrossRef] (In the text)
- Nakamura, O., Fukugita, M., Brinkmann, J., & Schneider, D. P. 2004, AJ, 127, 2511 [NASA ADS] [CrossRef] (In the text)
- Neichel, B., Hammer, F., Puech, M., et al. 2008, A&A, 484, 159 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] (In the text)
- Puech, M., Hammer, F., Lehnert, M. D., & Flores, H. 2007, A&A, 466, 83 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Puech, M., Flores, H., Hammer, F., et al. 2008, A&A, 484, 173 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rodrigues, M., Hammer, F., Flores, H., et al. 2008, A&A, 492, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rawat, A., Kembhavi, A. K., Hammer, F., Flores, H., & Barway, S. 2007, A&A, 469, 483 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rawat, A., Hammer, F., Kembhavi, A. K., & Flores, H. 2008, ApJ, 681, 1089 [NASA ADS] [CrossRef]
- Robertson, B., Bullock, J. S., Cox, T. J., et al. 2006, ApJ, 645, 986 [NASA ADS] [CrossRef]
- Springel, V. 2000, MNRAS, 312, 859 [NASA ADS] [CrossRef]
- Springel, V., & Hernquist, L. 2005, ApJ, 622, L9 [NASA ADS] [CrossRef]
- Trujillo, I., Graham, A. W., & Caon, N. 2001, MNRAS, 326, 869 [NASA ADS] [CrossRef]
- Toth, G., & Ostriker, J. P. 1992, ApJ, 389, 5 [NASA ADS] [CrossRef] (In the text)
- Walker, I. R., Mihos, J. C., & Hernquist, L. 1996, ApJ, 460, 121 [NASA ADS] [CrossRef] (In the text)
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] (In the text)
- Yang, Y., Flores, H., Hammer, F., et al. 2008, A&A, 477, 789 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Footnotes
- ... Service
![[*]](/icons/foot_motif.png)
- http://archive.stsci.edu/eidol.php
- ... Barnes
![[*]](/icons/foot_motif.png)
- http://www.ifa.hawaii.edu/~barnes/software.html
- ... parameters
![[*]](/icons/foot_motif.png)
- In the Z ENO system, the exact parameters we adopted for the current model are, at t=-0.12 from the first passage, deltar=0,0,0.5 deltav=-0.56,0.38,-3.5, the orientation of intruder thetax=35 thetay=-25 thetaz=0 and the orientation of the main galaxy thetax=18 thetay=18 thetaz=55
- ... image
![[*]](/icons/foot_motif.png)
- 1) All the simulated images in this paper are created using the projected density of particles directly. Thus the gas component is over-represented by a factor of 50 times due to the large number of gas particles. 2) All the simulated images, except Fig. 8, have been scaled to the same physical size as Fig. 1.
All Tables
Table 1: Properties of the target J033210.76-274234.6.
All Figures
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[height=6.5cm]{0563fg1a.ps}\hspace{3mm}\includegraphics[height=6.5cm]{0563fg1b.ps}\end{tabular}
\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg5.png) |
Figure 1: Left: the three-color image composed from the B, V, z bands. The image has a size of 30 kpc. Right: B-z color map of the object. The regions with a signal-to-noise ratio greater than 3 are shown. The circles A, B indicate core-A and core-B, respectively. The radii of the two circles are equivalent to the effective radii of the two cores. These two panels have identical scale and orientation. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm]{0563fg2a.ps}\includegraphics[width=7.5cm]{0563fg2b.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg17.png) |
Figure 2: Left: light profile decomposition along the core axis of z-band. Right: the V-band residual image (slightly smoothed) of morphology decomposition. The blue annulus indicates the ring region. The other two green regions indicate the tail-like structure and the faint structure, respectively. The plume structures and the central light-deficiency are marked by arrows as well. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.1cm,clip]{0563fig3.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg20.png) |
Figure 3:
Panel a), a 3D sketch of our target based on the morphological decomposition. The disk is represented by a gray plane. The two bulges are indicated by different
colors, red for core-A and orange for core-B. The blue ring is shown as well in blue. Two black dashed lines indicate the major axes of the ring and the disk, respectively. The black star between
the two bulges represents the center of the disk. The blue star (white star if in a black-white version) above the core-A indicates the center of the ring. The rotated grid in gray dotted lines indicates the G IRAFFE IFU elements (see panels b) and c)). The red and the blue
boxes (white boxes if in a black-white version) highlight the maximal and the minimal velocities
observed by G IRAFFE IFU. The green dashed box indicates the position and the coverage of the
FORS2 slit. Panels b) and c), the spatially-resolved kinematics, i.e., the velocity field and the velocity dispersion, respectively. The dashed-line grids indicate the spatial
resolution elements of IFU. The kinematics maps have been rotated to be aligned with the object
orientation. Panel d) shows the simulated image which is constructed using the projected star density (in yellow-green or in gray if in a black-white version) with the gas superposed in blue (in white if in a black-white version). Panels e) and f) show the simulated gas kinematics: VF- and |
| Open with DEXTER | |
| In the text | |
| |
Figure 4: The velocity curve of the object, which is derived from the FORS2 slit observation. The coverage of slit is shown in the panel a) of Fig. 3 in a green dashed-line box. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm]{0563fg5a.ps}\hspace{1cm}\in...
...
\mbox{\hspace*{3.1cm}($a$ ) \hspace{6cm} ($b$ )\hspace*{3.1cm}}\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg30.png) |
Figure 5: Panel a), the simulated image for the intruder only, with gas superposed in blue. The arrow indicates the star distribution possibly corresponding to the observed tail-like structure. Panel b), the simulated image for the main galaxy only. A weak but broad ring can be recognized. Due to the superposition of the bulge, the left part of the ring shape is hidden. The cross indicates the center of the disk. See Sect. 4.2 for more details. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0563fig6.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg31.png) |
Figure 6: Panel a), the observed radial profile (solid line). The dashed line indicates the slope of the thin-disk component. At the radii from 5 to 10 kpc, we clearly have a thick-disk component which corresponds to the ring that has been formed in the disk of main galaxy. Panel b), the radial profile derived from the simulation. Clearly we have a thin- and a thick-disk component. The appearance of the thick-disk component is related to the formation of the ring. For comparison, the radial profile of the main progenitor is plotted with a dashed line. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0563fig7.ps}
\end{figure}](/articles/aa/full_html/2009/26/aa10563-08/Timg32.png) |
Figure 7: The radial profiles of the remnants in the unbound case, panel a) for the remnant of the intruder, b) for the remnant of the main galaxy. The dashed lines in both figures indicate the disk components. Clearly, the remnant of the main progenitor is dominated by the disk. |
| Open with DEXTER | |
| In the text | |
| |
Figure 8: Left: the face-on view of the merger remnants. The image has a size of 103 kpc. Right: the radial profile of the merger remnant. The disk component is indicated by a dashed line. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


