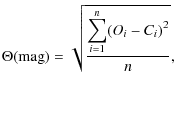| Issue |
A&A
Volume 501, Number 2, July II 2009
|
|
|---|---|---|
| Page(s) | 769 - 776 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200809877 | |
| Published online | 13 May 2009 | |
New binary asteroid 809 Lundia
I. Photometry and modelling
A. Kryszczynska1
- F. Colas2 - P. Descamps2 - P. Bartczak1 - M. Polinska1
- T. Kwiatkowski1 - J. Lecacheux3 - R. Hirsch1 - M. Fagas1 - K. Kaminski1 - T. Micha![]() owski1 - A. Marciniak1
owski1 - A. Marciniak1
1 - Astronomical Observatory, Adam Mickiewicz University,
S![]() oneczna 36, 60-286 Poznan, Poland
oneczna 36, 60-286 Poznan, Poland
2 - Institut de Mécanique Céleste et Calcul des Ephemerides,
Observatoire de Paris, UMR8028 CNRS, 77 Av. Denfert Rochereau, 75014 Paris, France
3 - Observatoire de Paris-Meudon, 5 place Jules Janssen, 92195 Meudon, France
Received 31 March 2008 / Accepted 23 February 2009
Abstract
CCD photometry of 809 Lundia obtained between September 2005 and January 2006 at Borowiec and Pic du Midi Observatories demonstrates that this object is a synchronous binary system with an orbital period of 15.418 ![]() 0.001 h. In this paper, we present the results of photometric observations of Lundia from two oppositions in 2005/2006 and 2007, as well as the first modelling of the system. For simplicity we assumed a fluid-like nature for each component with a modified Roche model and a triaxial ellipsoid shape in kinematic models. Our models provided similar results. Poles of the orbit in ecliptic coordinates are
0.001 h. In this paper, we present the results of photometric observations of Lundia from two oppositions in 2005/2006 and 2007, as well as the first modelling of the system. For simplicity we assumed a fluid-like nature for each component with a modified Roche model and a triaxial ellipsoid shape in kinematic models. Our models provided similar results. Poles of the orbit in ecliptic coordinates are
![]()
![]()
![]() ,
,
![]()
![]()
![]() (modified Roche) or
(modified Roche) or
![]()
![]()
![]() ,
,
![]()
![]()
![]() (kinematic). Triaxial ellipsoid shape solutions and a separation between components of 15.8 km are given after taking an equivalent diameter of 9.1 km from H = 11.8 mag and assuming an albedo of 0.4. The orbital period of the Lundia system obtained from modelling is the same as from the lightcurve analysis i.e., 15.418
(kinematic). Triaxial ellipsoid shape solutions and a separation between components of 15.8 km are given after taking an equivalent diameter of 9.1 km from H = 11.8 mag and assuming an albedo of 0.4. The orbital period of the Lundia system obtained from modelling is the same as from the lightcurve analysis i.e., 15.418 ![]() 0.001 h. The bulk density of both components is 1.64 or 1.71
0.001 h. The bulk density of both components is 1.64 or 1.71 ![]() 0.01
0.01
![]() .
The double system of Lundia probably originates from the fission process of a single body that could have been spun up by the YORP effect. The predicted lightcurves for future oppositions are also presented.
.
The double system of Lundia probably originates from the fission process of a single body that could have been spun up by the YORP effect. The predicted lightcurves for future oppositions are also presented.
Key words: planets and satellites: formation - minor planets, asteroids - techniques: photometric
1 Introduction
809 Lundia was discovered by Wolf at Heidelberg in August 1915 and named after the city and Observatory of Lund (Sweden). The parameters of the orbit of Lundia allow us to classify this object using hierarchical clustering method (HCM) to the Flora dynamical family, although it is not a member of the Flora/Ariadne family according to the wavelet analysis method (WAM) (Zappala et al. 1995).
The old Flora family was detected by Mothe-Diniz et al. (2005) as the nominal Baptistina family plus a lot of small clumps and background asteroids that eventually merge together at a different cutoff. However, they also merge with the Vesta family. In this classification, Lundia belongs to the background of the Baptistina and Vesta families.
Its spectra at visible wavelengths observed on 26 and 27 May 2001 allows us to identify Lundia as a V-type object outside the Vesta dynamical family (Florczak et al. 2002). Carruba et al. (2005) investigated the possibility of the migration of 809 Lundia and 956 Elisa from the Vesta family to their current positions by the interplay of the Yarkovsky effect and nonlinear secular resonances. However, they assumed single bodies. We now know that Lundia is a binary system, but we do not know how Yarkovsky/YORP effects or resonances influence binaries in the main belt. The effect called BYORP (Binary YORP) was studied by Cuk & Burns (2005) for NEAs synchronous binaries, showing that thermal radiation can affect orbits of synchronous asteroidal satelites. Vokrouhlicky et al. (2005) studied the possibility of detection of the-long term Yarkovsky perturbation in the relative motion of two components of binary system and concluded that it is detectable for the well-studied systems. However, their studies also concentrated on binary NEAs.
In this paper, we present CCD photometry of 809 Lundia and a description of observing techniques and data reduction. The modelling of the system using two different methods is also presented. In the second paper, we present the results of spectroscopic observations of the Lundia system.
2 Photometric observations
Table 1: Aspect data.
809 Lundia was observed within an ongoing program of observations of the Flora region. In this paper, we present lightcurves from 22 nights from two oppositions in 2005/2006 and 2007 at
Borowiec and Pic du Midi observatories. The aspect data for Lundia are listed in Table 1, the individual columns of which provide dates of observations with respect to the middle of the lightcurve, the asteroid's distances to the Sun (r) and the Earth (![]() )
in AU, phase angle (
)
in AU, phase angle (![]() ), ecliptic longitude (
), ecliptic longitude (![]() )
and latitude (
)
and latitude (![]() )
for J2000.0, and the observatory, i.e., Bor for Borowiec, and Pic for Pic du Midi.
)
for J2000.0, and the observatory, i.e., Bor for Borowiec, and Pic for Pic du Midi.
First photometric data were obtained on Sept. 18. 2005, almost two months before opposition on November 5.8, showing a deep minimum in the lightcurve and suggesting that this object could be a binary system. We continued observations of Lundia on 9 consecutive nights using our 0.4 m
telescope equipped with KAF 400 CCD and clear filter, finally obtaining a typical lightcurve of a synchronous binary asteroid (Kryszczynska et al. 2005), similar to 90 Antiope (Hansen et al. 1997; Micha![]() owski et al. 2002, 2004b; Descamps et al. 2007a), 854 Frostia, 1089 Tama, 1313 Berna, 4492 Debussy (Behrend et al. 2006), and Trojan asteroid 617 Patroclus (Marchis et al. 2006). All CCD frames from Borowiec were reduced with the CCLR STARLINK package. Corrections for bias,
dark current, and flat-fielding were applied and aperture photometry was used to measure the instrumental brightness of the asteroid, and the comparison and check star. Details concerning instrument and reduction procedure were described by Micha
owski et al. 2002, 2004b; Descamps et al. 2007a), 854 Frostia, 1089 Tama, 1313 Berna, 4492 Debussy (Behrend et al. 2006), and Trojan asteroid 617 Patroclus (Marchis et al. 2006). All CCD frames from Borowiec were reduced with the CCLR STARLINK package. Corrections for bias,
dark current, and flat-fielding were applied and aperture photometry was used to measure the instrumental brightness of the asteroid, and the comparison and check star. Details concerning instrument and reduction procedure were described by Micha![]() owski et al. (2004a). The composite lightcurve of Lundia from September 2005 is presented in Fig. 1. The vertical shift in each lightcurve was completed by minimizing the dispersion in the data points. The lightcurve of total amplitude 1.1 mag consists of two components. The first component due to the rotation of nonspherical bodies has an amplitude of 0.35 mag, and the second component caused by mutual eclipses has an amplitude of 0.75 mag. Lightcurve minima repeats every half of the period, which was estimated to be 15.4 h.
owski et al. (2004a). The composite lightcurve of Lundia from September 2005 is presented in Fig. 1. The vertical shift in each lightcurve was completed by minimizing the dispersion in the data points. The lightcurve of total amplitude 1.1 mag consists of two components. The first component due to the rotation of nonspherical bodies has an amplitude of 0.35 mag, and the second component caused by mutual eclipses has an amplitude of 0.75 mag. Lightcurve minima repeats every half of the period, which was estimated to be 15.4 h.
Photometric observations of Lundia were continued in Borowiec during 7 nights in October 2005. The composite lightcurve from October data is presented in Fig. 2 and has a total amplitude of 1.0 mag, i.e., 0.7 mag for the eclipsing, and 0.3 mag for the rotational component.
From the second part of November 2005, Lundia was observed at the 1.05 m telescope equipped with V, R, and I filters and THX 7863 CCD camera at Pic du Midi Observatory. After the bias and flat-field correction with the ASTROL package (developed at IMCCE) the asteroid brightness was measured with the PHOTOM aperture photometry programme included in the CCLR STARLINK package. The composite lightcurve from 2 nights in November 2005 is presented in Fig. 3 and shows a total amplitude of 1.0 mag, 0.65 mag for the eclipsing and 0.35 mag for the rotational components. This lightcurve has a feature visible close to the maximum of brightness (around 0.45 phase of rotation). It is not caused by a star in the field of view and seems to be real but we are unable to determine its origin.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{9877f1.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg24.png) |
Figure 1: Composite lightcurve of 809 Lundia from September 2005 data, zero phase corrected for light-time. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.5cm,clip]{9877f2.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg25.png) |
Figure 2: Composite lightcurve of 809 Lundia from October 2005 data, zero phase corrected for light-time. |
| Open with DEXTER | |
Unfortunately, the lightcurve from December 2005 presented in Fig. 4 is incomplete. Despite this, we see eclipses of 0.75 mag depth and a part of a rotational component that is of 0.3 mag amplitude.
Surprisingly, the lightcurve obtained in January 2006 (Fig. 5) when Lundia was almost 3 months after opposition has much smaller total amplitude of about 0.5 mag. Unfortunately it is incomplete because of the short observing window. However, we can see that the eclipsing component has an amplitude of only 0.25 mag suggesting significant change of the vieving geometry. We note that Figs. 1 to 5 have identical scales. Since the observing dataset was obtained over more than a 4-month period, we are able to confirm that Lundia is a synchronous binary system with the orbital as well as rotational periods of 15.418 ![]() 0.001 h.
0.001 h.
Lundia was also observed in its next oposition in December 2006 and January 2007 at Pic du Midi. No eclipses were visible in the lightcurve of 0.2 mag total amplitude (Fig. 6).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{9877f3.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg26.png) |
Figure 3: Composite lightcurve of 809 Lundia from November 2005 data, zero phase corrected for light-time. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{9877f4.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg27.png) |
Figure 4: Composite lightcurve of 809 Lundia from December 2005 data, zero phase corrected for light-time. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[angle=-90,width=8.5cm,clip]{9877f5.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg28.png) |
Figure 5: Composite lightcurve of 809 Lundia from January 2006 data, zero phase corrected for light-time. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[angle=-90,width=8.5cm,clip]{9877f6.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg29.png) |
Figure 6: Composite lightcurve of 809 Lundia from December 2006 and January 2007 data, zero phase corrected for light-time. |
| Open with DEXTER | |
3 Modelling
The effective diameter D=9.1 km of Lundia was calculated from its absolute magnitude H=11.8 mag by assuming an albedo
![]() equal to that of Vesta using the standard formula D=1329
equal to that of Vesta using the standard formula D=1329 ![]() 10(-H/5)
10(-H/5) ![]()
![]() (Pravec & Harris 2007, and references therein). However, both values H and
(Pravec & Harris 2007, and references therein). However, both values H and ![]() are the source of inaccuracies. The standard error for MPC H value
are the source of inaccuracies. The standard error for MPC H value ![]() mag implies that the effective diameter of Lundia is in range
mag implies that the effective diameter of Lundia is in range
![]() .
In addition the geometric albedo
.
In addition the geometric albedo ![]() has a large uncertainty. With the knowledge that Lundia is a V-type object, we can assume Vesta-like albedo. However, a Vesta albedo may differ by about 20% between the darkest and brightest areas of the surface of Vesta as suggested by Binzel et al. (1997) using HST data, and Drummond et al. (1998) using a ground-based adaptive optics system. Therefore, depending on which part of Vesta was observed, the albedo might differ significantly from the IRAS result of
has a large uncertainty. With the knowledge that Lundia is a V-type object, we can assume Vesta-like albedo. However, a Vesta albedo may differ by about 20% between the darkest and brightest areas of the surface of Vesta as suggested by Binzel et al. (1997) using HST data, and Drummond et al. (1998) using a ground-based adaptive optics system. Therefore, depending on which part of Vesta was observed, the albedo might differ significantly from the IRAS result of
![]() .
Tedesco (1989) reported that the average geometric albedo of Vesta is
.
Tedesco (1989) reported that the average geometric albedo of Vesta is
![]() .
Assuming that the albedo of Lundia is consistent with the value 0.4
.
Assuming that the albedo of Lundia is consistent with the value 0.4 ![]() 20%, the resulting range of possible effective diameters of Lundia increases to
20%, the resulting range of possible effective diameters of Lundia increases to
![]() .
An albedo of
.
An albedo of
![]() was adopted in modelling another V-type binary asteroid 3782 Celle (Ryan et al. 2004).
was adopted in modelling another V-type binary asteroid 3782 Celle (Ryan et al. 2004).
Thus, the resulting triaxial ellipsoid shape solutions in the modelling presented below as well as the separation between the components are only indiactive because they depend on the adopted equivalent diameter of Lundia of 9.1 km.
3.1 Modified Roche ellipsoids
In 1849, Edouard Roche tackled the problem of bodies in hydrostatic equilibrium orbiting each other synchronously along a circular, Keplerian path. As a result, mutual gravitational interactions exerted on these fluid bodies deform them into ellipsoids, called Roche ellipsoids, elongated along the line joining their centers (see Chandrasekhar 1969, for an extensive review). In the present case, the photometric evidence that the system is doubly synchronized with nearly equisized components suggests that the binary system of 809 Lundia could be dealt with initially as a Roche system. This approach was already adopted successfully for the system of 90 Antiope (Descamps et al. 2007a). The shapes and mutual separation of these ellipsoids depend on only two parameters, the size ratio q and the dimensionless rotation rate
![]() ,
where
,
where ![]() is the angular rotation rate,
is the angular rotation rate, ![]() is the bulk density assumed to be equal for the two components, and G is the gravitational constant.
is the bulk density assumed to be equal for the two components, and G is the gravitational constant.
![\begin{figure}
\includegraphics[width=12.5cm,clip]{9877f7.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg42.png) |
Figure 7:
Apparent aspect of the double system 809 Lundia at the times of observations. The orbit of the secondary, considered to be smaller component is shown. Phase ( |
| Open with DEXTER | |
Apart from the classical formulation of the Roche solutions (Leone et al. 1984), we introduced a correcting factor ![]() applied to either of the axis ratios
applied to either of the axis ratios ![]() and
and ![]() ,
with
,
with
![]() ,
of both Roche triaxial ellipsoids. Thereby,
,
of both Roche triaxial ellipsoids. Thereby, ![]() enhances artificially the flattening of the Roche solutions. In the classical Roche problem, the axis ratios
enhances artificially the flattening of the Roche solutions. In the classical Roche problem, the axis ratios
![]() and
and ![]() of an ellipsoid with semi-major axis a>b>c, which is the equilibrium shape of a primary body orbiting a spherical secondary, obeys the following equations:
of an ellipsoid with semi-major axis a>b>c, which is the equilibrium shape of a primary body orbiting a spherical secondary, obeys the following equations:
where q is the mass ratio of the primary to the secondary. The quantities A1, A2, and A3 are defined by (Chandrasekhar 1969):
The shape of the secondary component, defined by its axis ratios (
which in its simplest form becomes
In the modified Roche formalism, we assumed that the semi-major axis a (and a') is conserved robustly during the transformation. Consequently, the new volumes of the bodies were
where D is the new separation involved in the modified Roche solution. Equating Eqs. (4) and (5) we obtained
Thereby, for the sake of physical consistency of our modified Roche solution, the mutual separation of the ellipsoids (radius of the circular orbit), which is provided by the exact Roche solution, should be shortened by a factor
Synthetic lightcurves were computed from the knowledge of the modified Roche solutions, which were approximated by polyhedral models. The calculation of the incidence and emission angles of each facet was performed to estimate the retrieved flux by an Earth-observer by adding the contribution of each facet. Mutual shadowing between components was taken into account insofar as the phase angle was quite large at the times of observation, making the eclipse event one of the major photometric effects. As shown in Fig. 7, the umbra cast by a component upon another plays a critical role in the formation of the rotational lightcurve. The empirical Minnaert scattering law (Minnaert 1941) was used to describe the way surfaces reflect the solar light in any direction. It was assumed that the surfaces of both bodies are of the same physical nature, i.e., their grain density, albedo, and scattering properties are similar. Before going any further in the reduction of the observations, we had to determine the effect of each parameter (![]() ,
,
![]() ,
q, k) on the morphology of the resulting lightcurve. Figure 8 is devoted to this goal. The lightcurves were computed for an arbitrary date, in November 2005 for the effect of
,
q, k) on the morphology of the resulting lightcurve. Figure 8 is devoted to this goal. The lightcurves were computed for an arbitrary date, in November 2005 for the effect of ![]() ,
,
![]() and k, and in January 2006 for the effect of the mass ratio q. From Fig. 8a, we could infer that the normalized spin rate
and k, and in January 2006 for the effect of the mass ratio q. From Fig. 8a, we could infer that the normalized spin rate ![]() is the only Roche parameter governing the duration of an event. The main photometric effect of the correcting factor
is the only Roche parameter governing the duration of an event. The main photometric effect of the correcting factor ![]() was to enhance the slope of the flux variation, or the amplitude, outside the event. The specific contribution of mass ratio q was the magnitude differential between the minima provided that no mutual shadowing occured in the
involved event. This was precisely the case for the observation on January 2006. Lastly, the Minnaert limb-darkening parameter k was of little effect and initially taken to be 0.55, which is typical of atmosphereless dark bodies. These results were used to a great extent
as guidelines for the fitting procedure. We defined a goodness-of-fit criterion
was to enhance the slope of the flux variation, or the amplitude, outside the event. The specific contribution of mass ratio q was the magnitude differential between the minima provided that no mutual shadowing occured in the
involved event. This was precisely the case for the observation on January 2006. Lastly, the Minnaert limb-darkening parameter k was of little effect and initially taken to be 0.55, which is typical of atmosphereless dark bodies. These results were used to a great extent
as guidelines for the fitting procedure. We defined a goodness-of-fit criterion ![]() by:
by:
where n is the data number, Oi and Ci are observed and calculated magnitudes.
![\begin{figure}
\includegraphics[width=8.6cm,clip]{9877f8.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg62.png) |
Figure 8:
Effect of Roche parameters ( |
| Open with DEXTER | |
In a first step, the size ratio q could be kept fixed, equal to unity. The orbital angular velocity ![]() was derived independently from the lightcurve (see Sect. 2) so that the only remaining free parameters of the problem were the normalized spin rate
was derived independently from the lightcurve (see Sect. 2) so that the only remaining free parameters of the problem were the normalized spin rate ![]() ,
or equivalently the bulk density
,
or equivalently the bulk density ![]() ,
the correcting factor
,
the correcting factor ![]() ,
and the two coordinates of the rotation pole. In our model, the orbital plane was considered to be merged with the equatorial plane of either component. The spin vector was derived from an iterative procedure based on the estimation of the epoch corresponding to a nearly perfect edge-on aspect of the system. This method was described carefuly in Descamps et al. (2007b). In the present case, we initially guessed that this epoch was around September-December 2005, given the high magnitude drops recorded in the lightcurves during this period of time. From this condition, we derived an admissible set of pole solutions (Fig. 9). The most suitable was the one minimizing
,
and the two coordinates of the rotation pole. In our model, the orbital plane was considered to be merged with the equatorial plane of either component. The spin vector was derived from an iterative procedure based on the estimation of the epoch corresponding to a nearly perfect edge-on aspect of the system. This method was described carefuly in Descamps et al. (2007b). In the present case, we initially guessed that this epoch was around September-December 2005, given the high magnitude drops recorded in the lightcurves during this period of time. From this condition, we derived an admissible set of pole solutions (Fig. 9). The most suitable was the one minimizing ![]() .
Once we had derived an approximate pole solution, we could almost independently derive the values of
.
Once we had derived an approximate pole solution, we could almost independently derive the values of ![]() and
and ![]() .
At this stage we had an initial global solution with which we could constrain the mass ratio q from the observation of January 2006. The second step consisted of fitting the observed lightcurves with synthetic lightcurves by varying all parameters over a regular grid in the vicinity of the initial solution. The goodness-of-fit criterion was used to determine the best-fit solution given in Table 2. Figure 10 displays the corresponding fitted lightcurves. The classical
.
At this stage we had an initial global solution with which we could constrain the mass ratio q from the observation of January 2006. The second step consisted of fitting the observed lightcurves with synthetic lightcurves by varying all parameters over a regular grid in the vicinity of the initial solution. The goodness-of-fit criterion was used to determine the best-fit solution given in Table 2. Figure 10 displays the corresponding fitted lightcurves. The classical
![]() pole ambiguity was overcome owing to the strong phase effects, which allowed us to
decide between the symmetric pole solutions (Fig. 11). The spin axis was thus determined by its J2000 ecliptic coordinates
pole ambiguity was overcome owing to the strong phase effects, which allowed us to
decide between the symmetric pole solutions (Fig. 11). The spin axis was thus determined by its J2000 ecliptic coordinates
![]()
![]()
![]() ,
,
![]()
![]()
![]() .
From the value of
.
From the value of ![]() and assuming that the system had relaxed to Roche equilibrium,
it is straightforward to infer the bulk density
and assuming that the system had relaxed to Roche equilibrium,
it is straightforward to infer the bulk density ![]()
![]()
![]() .
We note that this density has been derived regardless of the mutual separation and absolute sizes of the components. It is not a measured density but a model density. It is noteworthy to point out that we found a unique solution for the correcting factor
.
We note that this density has been derived regardless of the mutual separation and absolute sizes of the components. It is not a measured density but a model density. It is noteworthy to point out that we found a unique solution for the correcting factor ![]()
![]() 0.02 that is not too far from the exact Roche solution (
0.02 that is not too far from the exact Roche solution (![]() ). In other words, it means that the real geometrical figures only differ from the hydrostatic equilibrium figures by less than 12%. The value of a axis in A component is assumed in the fitting process and depends on the adopted albedo of Lundia of 0.4, and after assuming an equivalent diameter of 9.1 km. The resulting triaxial-shape solutions are given in Table 3.
). In other words, it means that the real geometrical figures only differ from the hydrostatic equilibrium figures by less than 12%. The value of a axis in A component is assumed in the fitting process and depends on the adopted albedo of Lundia of 0.4, and after assuming an equivalent diameter of 9.1 km. The resulting triaxial-shape solutions are given in Table 3.
![\begin{figure}
\includegraphics[width=8cm,clip]{9877f9.eps} \end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg70.png) |
Figure 9: Admissible pole solutions for Lundia in equatorial J2000.0 coordinates. |
| Open with DEXTER | |
Table 2: Roche solution for the system of 809 Lundia.
![\begin{figure}
\includegraphics[width=15cm,clip]{9877f10.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg71.png) |
Figure 10: Synthetic composite lightcurves for each model of Lundia: modified Roche model (plain curves) and kinematic model (dashed curves). |
| Open with DEXTER | |
3.2 Kinematic model
Asuming that the system consists of two triaxial ellipsoids, we were able to determine the parameters of 809 Lundia and simulate the observed lightcurves presented in Fig. 10. The radius of the orbit was calculated form Kepler's third law. The system's orbital coordinates were calculated from their Keplerian elements, while the positions of the Earth and Sun were calculated according to equations given in Somma (1988). The determination of the brightness of the components was based on a ray-tracing method (method implemented from computer graphics) with a Lommel-Seeliger light-scatternig law. Using the genetic-algorithm-based fitting procedure PIKAIA developed by
Charbonneau (1995), we derived the best-fit solution to our model. In this method, the only value assumed at the beginning of the calculations was the semimajor axis a of the main body. This value could be estimated from Lundia's absolute magnitude and the assumption of a Vesta-like albedo.
The final parameters b, c, and a', b', c', density of the components, period of rotation, and coordinates of the spin axis of the system were fitted. The goodness-of-fit criterion ![]() was defined by Eq. (7). As in the case of modified Roche ellipsoids the sizes of the components depended on the adopted albedo of Lundia. The final spin axis of the system in J2000 ecliptic coordinates is
was defined by Eq. (7). As in the case of modified Roche ellipsoids the sizes of the components depended on the adopted albedo of Lundia. The final spin axis of the system in J2000 ecliptic coordinates is
![]() or
or ![]() ,
,
![]() .
Symmetric solutions with
.
Symmetric solutions with
![]() have the same probability. All parameters of the Lundia system
are summarized in Table 3.
have the same probability. All parameters of the Lundia system
are summarized in Table 3.
![\begin{figure}
\includegraphics[width=9cm,clip]{9877f11.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg75.png) |
Figure 11:
Effects of the pole solution. The pole I is given by its J2000 ecliptic coordinates
|
| Open with DEXTER | |
Table 3: Best-fit solutions of the two methods the system of 809 Lundia based on the fit of photometric observations made in 2005-2006 and 2006-2007 (see Fig. 9).
4 Future observations
Observing geometries and dates for the forthcoming oppositions of Lundia are listed in Table 4. Both models are capable of predicting lightcurves in future oppositions, examples being presented in Fig. 11. In July 2008 and January 2010, we expect to observe close to pole-on orientations of the Lundia system and measure lightcurves without eclipses/occultation events. Partial lightcurves obtained in May 2008 (during revision of this manuscript) were of small amplitude of about 0.2 mag., despite a 24 deg phase angle, and are compatible with the obtained pole solution.
Absolute photometry in 2010 should improve significantly the measurement of the equivalent diameter as well as diameters of the components. However, lightcurves obtained during oppositions when mutual occulatations/eclipses in the system are invisible have almost no influence on the results of the modelling and the parameters of the system.
Deep eclipses in the Lundia system are expected in May 2011 when viewing geometry will differ by ![]() from the 2005 opposition. Comparison of the observed and future ecliptic longitudes of the Earth in the reference frame of the asteroid is presented in Fig. 12. These values differ by
from the 2005 opposition. Comparison of the observed and future ecliptic longitudes of the Earth in the reference frame of the asteroid is presented in Fig. 12. These values differ by ![]() from the longitudes given in Tables 1 and 4.
from the longitudes given in Tables 1 and 4.
Table 4: Geometries of future observations of 809 Lundia.
5 Discussion
To paraphrase the title of a paper written more than twenty years ago ``Do we observe light curves of binary asteroids?'' (Cellino et al. 1985), despite the ability of our present model of Lundia to explain the photometric observations, are we really observing light curves of a binary asteroid? From a photometric point of view, a synchronous system behaves like a highly-elongated single rigid body. In this paper, the authors already addressed the issue of binarity by considering the morphology of the observed lightcurves. They concluded that such a statement cannot be assessed by analyzing lightcurves only. However, they considered some individual cases in which only one lightcurve was taken at opposition. In the problem of lightcurve convex inversion, Kaasalainen et al. (1992) proved a uniqueness theorem provided that photometric observations were made available from different viewing and illumination geometries. This theorem is valid for a single body and cannot be easily extended to synchronous systems, although but conspicuous features in the lightcurves of Lundia, such as the sudden variation in the slope whenever an event starts or ends, appear to support the idea that two bodies are present. The reliability of this idea is also supported by there being a unique slightly-modified Roche-solution for the interpretation of the lightcurves collected for a wide variety of aspects and phase angles.
![\begin{figure}
\includegraphics[width=8cm,clip]{9877f12.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg77.png) |
Figure 12: Kinematic ( top) and modified Roche ( bottom) models of Lundia. Shape parameters are given in Table 2. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=13.5cm,clip]{9877f13.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg78.png) |
Figure 13: Predicted lightcurves in the future observations of 809 Lundia. |
| Open with DEXTER | |
The synthetic lightcurves produced by the two solutions were superimposed on the observations in Fig. 10. Overall, the modified Roche solution provides the best-fit solution of the lightcurves in the sense of minimization of the goodness-of-fit criterion ![]() ,
which is on average on the order of 0.03 mag against 0.05 mag for the kinematic model. Both geometric solutions are displayed in Fig. 11. However, despite significant discrepancies in the shape of the ellipsoidal components, the global physical characteristics inferred from both solutions - a secondary to primary mass ratio of
,
which is on average on the order of 0.03 mag against 0.05 mag for the kinematic model. Both geometric solutions are displayed in Fig. 11. However, despite significant discrepancies in the shape of the ellipsoidal components, the global physical characteristics inferred from both solutions - a secondary to primary mass ratio of ![]() and a bulk density of
and a bulk density of
![]() (see Table 3) - are quite similar.
(see Table 3) - are quite similar.
809 Lundia was recently identified as a V-type asteroid outside Vesta dynamical family (Florczak et al. 2002). The spectroscopic link between 4 Vesta and the HED meteorites now seems to be accepted. We know that HED meteorites have bulk density of
![]() (Britt & Consolmagno 2004; McCausland & Flemming 2006). Thus, we may infer the macroscopic porosity of
(Britt & Consolmagno 2004; McCausland & Flemming 2006). Thus, we may infer the macroscopic porosity of ![]() that is typical of loosely consolidated bodies (Britt et al. 2002).
that is typical of loosely consolidated bodies (Britt et al. 2002).
The internal structure of asteroids is presently unclear. The outcomes of asteroid collisional evolution could be gravitational aggregates reaccreted from fragments of a parent body that was collisionaly disrupted or collisional shards that were never completely disrupted (Cheng 2009).
The parent body of Lundia could have been spun up by the YORP effect (see Bottke et al. 2006, and references therein). Vokrouhlicky et al. (2003) showed convincingly that YORP changed the spin rates and orientations of members of the Koronis family as large as 40 km in diameter by as much as ![]() 1 cycle per day per billion years. Since the rate of change of the spin rate from YORP is inversely proportional to the square of the asteroid size, and also to the inverse-square of the heliocentric distance, a main-belt asteroid of only 9 km in diameter can be spun up to instability in only
1 cycle per day per billion years. Since the rate of change of the spin rate from YORP is inversely proportional to the square of the asteroid size, and also to the inverse-square of the heliocentric distance, a main-belt asteroid of only 9 km in diameter can be spun up to instability in only ![]() 7 million years. Thus, the YORP effect is powerful enough to spin up small asteroids to fission or mass shedding in a much shorter time than their lifetimes (Pravec & Harris 2007).
7 million years. Thus, the YORP effect is powerful enough to spin up small asteroids to fission or mass shedding in a much shorter time than their lifetimes (Pravec & Harris 2007).
![\begin{figure}
\includegraphics[width=6.5cm,clip]{9877f14.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg84.png) |
Figure 14: Comparison of the ecliptic longitudes of the Earth in the reference frame of the asteroid: already observed (dark circles) and in the future oppositions (bright circles). |
| Open with DEXTER | |
The double system of Lundia may likely have originated from a fission process of a single parent body that is initiated for all doubly synchronous systems with congruent components (Descamps & Marchis 2008).
Acknowledgements
A part of this work was supported by the Polish Grant 1 P03D 008 26, The reduction of CCD data from Borowiec Observatory and aperture photometry of the Pic du Midi data were performed with the CCLR STARLINK package.
References
- Behrend, R., Bernasconi, L., Roy, R., et al. 2004, A&A, 446, 1177 [NASA ADS] [CrossRef]
- Binzel, R. P., Gaffey, M. J., Thomas, P. C., et al. 1997, Icarus, 128, 95 [NASA ADS] [CrossRef] (In the text)
- Bottke, W. F., Vokrouhlicky, D., Rubincam, D. P., & Broz, D. P. 2002, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: Univ. Arizona Press), 395
- Bottke, W. F., Vokrouhlicky, D., Rubincam, D. P., & Nesvorny, D. 2006, Annu. Rev. Earth Planet. Sci., 34, 157 [NASA ADS] [CrossRef] (In the text)
- Britt, D. T., & Consolmagno, G. J. 2004, 35th Lunar and Planetary Science Conference, League City, Texas, abst. 2108 (In the text)
- Britt, D. T., Yeomans, D., Housen, K., & Consolmagno, G. J. 2002, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: Univ. Arizona Press), 103 (In the text)
- Carruba, V., Mitchenko, T. A., Roig, F., Ferraz-Mello, S., & Nesvorny, D. 2005, A&A, 441, 819 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cellino, A., Pannunzio, R., Zappala, V., et al. 1985, A&A, 144, 355 [NASA ADS] (In the text)
- Chandrasekhar, S. 1969, Ellipsoidal figures of equilibrium (New Haven: Yale Univ. Press) (In the text)
- Charbonneau, P. 1995, ApJS, 101, 309 [NASA ADS] [CrossRef] (In the text)
- Cheng, A. F., The Hayabusa Team 2009, Planet. Space Sci., in press
- Cuk, M., & Burns, J. A. 2005, Icarus, 176, 418 [NASA ADS] [CrossRef] (In the text)
- Descamps, P., & Marchis, F. 2008, Icarus, 193, 74 [NASA ADS] [CrossRef] (In the text)
- Descamps, P., Marchis, F., Michalowski, T., et al. 2007a, Icarus, 187, 482 [NASA ADS] [CrossRef] (In the text)
- Descamps, P., Marchis, F., Michalowski, T., et al. 2007b, Icarus, 189, 362 [NASA ADS] [CrossRef] (In the text)
- Drummond, J. D., Fugate, R. Q., Christou, C., & Hege, E. K. 1998, Icarus, 132, 80 [NASA ADS] [CrossRef] (In the text)
- Florczak, M., Lazzaro, D., & Duffard, R. 2002, Icarus, 159, 178 [NASA ADS] [CrossRef] (In the text)
- Hansen, A. T., Arentoft, T., & Lang, K. 1997, Minor Planet Bull., 24, 17 [NASA ADS] (In the text)
- Kaasalainen, M., Lamberg, L., Lumme, K., & Bowell, T. 1992, A&A, 259, 318 [NASA ADS] (In the text)
- Kryszczynska, A., Kwiatkowski, T., Polinska, M., et al. 2005, CBET, 229 (In the text)
- Leone, G., Farinella, P., Paolicchi, P., & Zappala, V. 1984, A&A, 140, 265 [NASA ADS] (In the text)
- Marchis, F., Hestroffer, D., Descamps, P., et al. 2006, Nature, 439, 565 [NASA ADS] [CrossRef] (In the text)
- McCausland, P. J. A., & Flemming, R. L. 2006, 37th Lunar and Planetary Science Conference, League City, Texas, abst. 1574 (In the text)
- Michaowski, T., Colas, F., Kwiatkowski, T., et al. 2002, A&A, 396, 293 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Michaowski, T., Kwiatkowski, T., Kaasalainen, M., et al. 2004a, A&A, 416, 353 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Michaowski, T., Bartczak, P., Velichko, F. P., et al. 2004b, A&A, 423, 1159 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Minnaert, M. 1941, ApJ, 93, 403 [NASA ADS] [CrossRef] (In the text)
- Mothe-Diniz, T., Roig, F., & Carvano, J. M. 2005, Icarus, 174, 54 [NASA ADS] [CrossRef] (In the text)
- Pravec, P., & Harris, A. W. 2007, Icarus, 190, 250 [NASA ADS] [CrossRef] (In the text)
- Roche, E. 1849, Mémoire sur la figure d'une masse fluide, soumise l'attraction d'un point éloigné, Acad. Montpellier, 1, 243 (In the text)
- Rubincam, D. P. 2000, Icarus, 148, 2 [NASA ADS] [CrossRef]
- Ryan, W. H., Ryan, E. V., & Martinez, C. T. 2004, Planet. Space Sci., 52, 1093 [NASA ADS] [CrossRef] (In the text)
- Somma, M. 1988, Cel. Mech., 41, 389 [NASA ADS] [CrossRef] (In the text)
- Tedesco, E. F. 1989, in Asteroids II, ed. R. P. Binzel, T. Gehrels, & M. S. Matthews, 1090 (In the text)
- Vokrouhlicky, D., Nesvorny, D., & Bottke, W. F. 2003, Nature, 425, 147 [NASA ADS] [CrossRef] (In the text)
- Vokrouhlicky, D., Capek, D., Chesley, S. R., & Ostro, S. J. 2005, Icarus, 179, 128 [NASA ADS] [CrossRef] (In the text)
- Zappala, V., Bendjoya, P., Cellino, A., et al. 1995, Icarus, 116, 291 [NASA ADS] [CrossRef] (In the text)
All Tables
Table 1: Aspect data.
Table 2: Roche solution for the system of 809 Lundia.
Table 3: Best-fit solutions of the two methods the system of 809 Lundia based on the fit of photometric observations made in 2005-2006 and 2006-2007 (see Fig. 9).
Table 4: Geometries of future observations of 809 Lundia.
All Figures
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{9877f1.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg24.png) |
Figure 1: Composite lightcurve of 809 Lundia from September 2005 data, zero phase corrected for light-time. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.5cm,clip]{9877f2.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg25.png) |
Figure 2: Composite lightcurve of 809 Lundia from October 2005 data, zero phase corrected for light-time. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{9877f3.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg26.png) |
Figure 3: Composite lightcurve of 809 Lundia from November 2005 data, zero phase corrected for light-time. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{9877f4.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg27.png) |
Figure 4: Composite lightcurve of 809 Lundia from December 2005 data, zero phase corrected for light-time. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[angle=-90,width=8.5cm,clip]{9877f5.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg28.png) |
Figure 5: Composite lightcurve of 809 Lundia from January 2006 data, zero phase corrected for light-time. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[angle=-90,width=8.5cm,clip]{9877f6.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg29.png) |
Figure 6: Composite lightcurve of 809 Lundia from December 2006 and January 2007 data, zero phase corrected for light-time. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=12.5cm,clip]{9877f7.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg42.png) |
Figure 7:
Apparent aspect of the double system 809 Lundia at the times of observations. The orbit of the secondary, considered to be smaller component is shown. Phase ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.6cm,clip]{9877f8.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg62.png) |
Figure 8:
Effect of Roche parameters ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8cm,clip]{9877f9.eps} \end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg70.png) |
Figure 9: Admissible pole solutions for Lundia in equatorial J2000.0 coordinates. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=15cm,clip]{9877f10.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg71.png) |
Figure 10: Synthetic composite lightcurves for each model of Lundia: modified Roche model (plain curves) and kinematic model (dashed curves). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=9cm,clip]{9877f11.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg75.png) |
Figure 11:
Effects of the pole solution. The pole I is given by its J2000 ecliptic coordinates
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8cm,clip]{9877f12.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg77.png) |
Figure 12: Kinematic ( top) and modified Roche ( bottom) models of Lundia. Shape parameters are given in Table 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=13.5cm,clip]{9877f13.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg78.png) |
Figure 13: Predicted lightcurves in the future observations of 809 Lundia. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=6.5cm,clip]{9877f14.eps}
\end{figure}](/articles/aa/full_html/2009/26/aa09877-08/Timg84.png) |
Figure 14: Comparison of the ecliptic longitudes of the Earth in the reference frame of the asteroid: already observed (dark circles) and in the future oppositions (bright circles). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



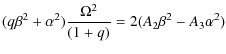
![$\displaystyle \left [ (3 + q) + \alpha^{2} \right ] \frac{\Omega^{2}}{(1+q)} = 2 (A_{1} - A_{3}\alpha^{2}),$](/articles/aa/full_html/2009/26/aa09877-08/img48.png)