| Issue |
A&A
Volume 501, Number 1, July I 2009
|
|
|---|---|---|
| Page(s) | 349 - 357 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200911752 | |
| Published online | 29 April 2009 | |
Composition of KBO (50000) Quaoar![[*]](/icons/foot_motif.png)
C. Morea Dalle Ore1,3 - M. A. Barucci2 - J. P. Emery4 - D. P. Cruikshank1 - L. V. Dalle Ore1 - F. Merlin5 - A. Alvarez-Candal2 - C. de Bergh2 - D. E. Trilling8 - D. Perna2,6,7 - S. Fornasier2 - R. M. E. Mastrapa1,3 - E. Dotto6
1 - NASA Ames Research Center, Mail Stop 245-6, Moffett Field, CA 94035, USA
2 - LESIA, Observatoire de Paris, 92195 Meudon Pricipal Cedex, France
3 - SETI Institute, 515 N. Whisman Rd., Mountain View, CA 94043 CA, USA
4 - Earth and Planetary Sciences Dept, University of Tennessee, Knoxville, TN 37996, USA
5 - Department of Astronomy, University of Maryland, College Park, MD 20742, USA
6 - INAF, Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monteporzio Catone, Roma, Italy
7 - Università di Roma Tor Vergata, via della Ricerca Scientifica 1, 00133
Roma, Italy
8 - Department of Physics and Astronomy, Northern Arizona University, Flagstaff, AZ 86011, USA
Received 30 January 2009 / Accepted 7 April 2009
Abstract
Aims. The objective of this work is to investigate the physical properties of objects beyond Neptune - the new frontiers of the Solar System - and in particular to study the surface composition of (50 000) Quaoar, a classical Transneptunian (or Kuiper Belt) object. Because of its distance from the Sun, Quaoar is expected to have preserved, to a degree, its original composition. Our goals are to determine to what degree this is true and to shed light on the chemical evolution of this icy body.
Methods. We present new near-infrared (3.6 and 4.5 ![]() m) photometric data obtained with the Spitzer Space Telescope. These data complement high resolution, low signal-to-noise spectroscopic and photometric data obtained in the visible and near-infrared (0.4-2.3
m) photometric data obtained with the Spitzer Space Telescope. These data complement high resolution, low signal-to-noise spectroscopic and photometric data obtained in the visible and near-infrared (0.4-2.3 ![]() m) at VLT-ESO and provide an excellent set of constraints in the model calculation process. We perform spectral modeling of the entire wavelength range - from 0.3 to 4.5
m) at VLT-ESO and provide an excellent set of constraints in the model calculation process. We perform spectral modeling of the entire wavelength range - from 0.3 to 4.5 ![]() m by means of a code based on the Shkuratov radiative transfer formulation of the slab model. We also attempt to determine the temperature of H2O ice making use of the crystalline feature at 1.65
m by means of a code based on the Shkuratov radiative transfer formulation of the slab model. We also attempt to determine the temperature of H2O ice making use of the crystalline feature at 1.65 ![]() m.
m.
Results. We present a model confirming previous results regarding the presence of crystalline H2O and CH4 ice, as well as C2H6 and organic materials, on the surface of this distant icy body. We attempt a measurement of the temperature and find that stronger constraints on the composition are needed to obtain a precise determination.
Conclusions. Model fits indicate that N2 may be a significant component, along with a component that is bright at
![]() m, which we suggest at this time could be amorphous H2O ice in tiny grains or thin grain coatings. Irradiated crystalline H2O could be the source of small-grained amorphous H2O ice. The albedo and composition of Quaoar, in particular the presence of N2, if confirmed, make this TNO quite similar to Triton and Pluto.
m, which we suggest at this time could be amorphous H2O ice in tiny grains or thin grain coatings. Irradiated crystalline H2O could be the source of small-grained amorphous H2O ice. The albedo and composition of Quaoar, in particular the presence of N2, if confirmed, make this TNO quite similar to Triton and Pluto.
Key words: techniques: spectroscopic - Kuiper Belt
1 Introduction
(50 000) Quaoar, discovered in 2002, is a classical Transneptunian (or Kuiper Belt) object. It orbits the Sun with a nearly circular orbit (e=0.039) that has a rather low inclination to the ecliptic (
Quaoar is one of the largest Transneptunian objects ever discovered.
First estimates of its diameter were based on direct size measurements with the Hubble Space Telescope by Brown & Trujillo (2004), who found its diameter to be
![]() km.
More recent data using thermal infrared photometric measurements with the Spitzer Space Telescope have led to an estimated diameter of 840 (+200, -190) km (Stansberry et al. 2008). The surface of Quaoar is intermediate in albedo with respect to other TNOs, with a visible geometric albedo of about 0.2 (Stansberry et al. 2008). In addition, it has been found that Quaoar is a very red object (spectral slope in the visible: around 28% per 100 nm; Marchi et al. 2003; Alvarez-Candal et al. 2008; Fornasier et al. 2004) and has been classified as an RR object in the Barucci taxonomic system (DeMeo et al. 2009).
The R-band polarimetric observations of Quaoar for solar phase angles in the 0.25-1.23 degree range indicate a nearly constant, relatively weak negative polarization (Bagnulo et al. 2006). As discussed by Bagnulo et al. (2008), this polarimetric behavior resembles more that of Eris and Pluto than of smaller objects. Photometric observations in the R band carried out at the same time by Bagnulo et al. (2006) show a linear phase curve. Rabinowitz et al. (2007) have published a more complete study of the phase curve of Quaoar with measurements in the B, V and I bands, and more data points in each band, and show that the phase curve is significantly wavelength dependent. The rotation period of Quaoar is approximately 17.68 h, showing a double-peaked lightcurve (Ortiz et al. 2003). Quaoar has one known satellite (at about 0.35
km.
More recent data using thermal infrared photometric measurements with the Spitzer Space Telescope have led to an estimated diameter of 840 (+200, -190) km (Stansberry et al. 2008). The surface of Quaoar is intermediate in albedo with respect to other TNOs, with a visible geometric albedo of about 0.2 (Stansberry et al. 2008). In addition, it has been found that Quaoar is a very red object (spectral slope in the visible: around 28% per 100 nm; Marchi et al. 2003; Alvarez-Candal et al. 2008; Fornasier et al. 2004) and has been classified as an RR object in the Barucci taxonomic system (DeMeo et al. 2009).
The R-band polarimetric observations of Quaoar for solar phase angles in the 0.25-1.23 degree range indicate a nearly constant, relatively weak negative polarization (Bagnulo et al. 2006). As discussed by Bagnulo et al. (2008), this polarimetric behavior resembles more that of Eris and Pluto than of smaller objects. Photometric observations in the R band carried out at the same time by Bagnulo et al. (2006) show a linear phase curve. Rabinowitz et al. (2007) have published a more complete study of the phase curve of Quaoar with measurements in the B, V and I bands, and more data points in each band, and show that the phase curve is significantly wavelength dependent. The rotation period of Quaoar is approximately 17.68 h, showing a double-peaked lightcurve (Ortiz et al. 2003). Quaoar has one known satellite (at about 0.35
![]() from Quaoar at discovery) with brightness in R about 6 mag fainter than the primary (Brown & Suer 2007).
from Quaoar at discovery) with brightness in R about 6 mag fainter than the primary (Brown & Suer 2007).
The first spectroscopic observations of Quaoar were made in the visible range using the ESO-NNT
(Marchi et al. 2003). They did not reveal any spectral bands, only a very red spectral slope.
The first near-IR spectroscopic observations of Quaoar were obtained with the Subaru telescope
(Jewitt & Luu 2004). They showed very clearly the presence of crystalline H2O ice at the
surface of this large TNO. There was also an indication of a very weak absorption band at 2.2 ![]() m,
with similarities to that observed on Charon at the same wavelength. The band on Quaoar was tentatively
assigned to ammonia hydrate (as for Charon). To explain the presence of crystalline H2O ice and
possibly of ammonia hydrate on the surface of this body, Jewitt & Luu (2004) concluded that resurfacing mechanisms must exist on Quaoar, probably indicating cryovolcanism.
We also note that Cook et al. (2007), who retrieved several unpublished spectra of Quaoar obtained at the Subaru telescope at different times, found that the band at 2.2
m,
with similarities to that observed on Charon at the same wavelength. The band on Quaoar was tentatively
assigned to ammonia hydrate (as for Charon). To explain the presence of crystalline H2O ice and
possibly of ammonia hydrate on the surface of this body, Jewitt & Luu (2004) concluded that resurfacing mechanisms must exist on Quaoar, probably indicating cryovolcanism.
We also note that Cook et al. (2007), who retrieved several unpublished spectra of Quaoar obtained at the Subaru telescope at different times, found that the band at 2.2 ![]() m, although always present, does not always appear at the same wavelength position. They proposed the presence of different hydration states for the ammonia hydrate, varying with surface location.
m, although always present, does not always appear at the same wavelength position. They proposed the presence of different hydration states for the ammonia hydrate, varying with surface location.
Table 1: Observing circumstances of (50000) Quaoar.
More recent observations by Schaller & Brown (2007b) with the Keck telescope confirmed the presence of a weak band at 2.2 ![]() m, but it was instead assigned to CH4 ice, as CH4 also fits stronger absorption bands at longer wavelengths (around 2.32 and 2.38
m, but it was instead assigned to CH4 ice, as CH4 also fits stronger absorption bands at longer wavelengths (around 2.32 and 2.38 ![]() m). Furthermore, slight remaining differences between the observed spectra and modeled spectra that included H2O ice and CH4 ice were best explained by the presence of ethane, another hydrocarbon ice, that is a likely by-product of CH4 irradiation (Baratta et al. 2003). The detection of small amounts of CH4 on Quaoar is not too surprising. Indeed, Schaller & Brown (2007a) have shown that, given its size and distance from the Sun, Quaoar could have retained at
least some of the very volatile species like CH4, N2 or CO that are observed on the surface of Pluto and other TNOs larger than Quaoar.
m). Furthermore, slight remaining differences between the observed spectra and modeled spectra that included H2O ice and CH4 ice were best explained by the presence of ethane, another hydrocarbon ice, that is a likely by-product of CH4 irradiation (Baratta et al. 2003). The detection of small amounts of CH4 on Quaoar is not too surprising. Indeed, Schaller & Brown (2007a) have shown that, given its size and distance from the Sun, Quaoar could have retained at
least some of the very volatile species like CH4, N2 or CO that are observed on the surface of Pluto and other TNOs larger than Quaoar.
In the course of a Large Programme at ESO-VLT (P.I. M.A. Barucci) we have obtained for this KBO
visible and near-infrared photometry (DeMeo et al. 2009) and nearly simultaneous spectra in the visible (from 0.4 to 0.85 ![]() m) and near-IR (J, H, and K bands). In this paper we have combined the visible (Alvarez-Cantal et al. 2008) and SINFONI H+K spectrum (Guilbert et al. 2009) with a J spectrum obtained the same night at ESO-VLT with the ISAAC instrument, as well as with broad-band photometric
data at 3.6 and 4.5
m) and near-IR (J, H, and K bands). In this paper we have combined the visible (Alvarez-Cantal et al. 2008) and SINFONI H+K spectrum (Guilbert et al. 2009) with a J spectrum obtained the same night at ESO-VLT with the ISAAC instrument, as well as with broad-band photometric
data at 3.6 and 4.5 ![]() m obtained at a different time with the Spitzer Space Telescope.
Based on this extended set of data, we present a new interpretation of the surface composition of Quaoar.
m obtained at a different time with the Spitzer Space Telescope.
Based on this extended set of data, we present a new interpretation of the surface composition of Quaoar.
2 Observational data
The data reported herein are a combination of spectroscopic and photometric data obtained in the visible and near-infrared (0.4-2.3
2.1 VLT-ESO data
The VLT data were collected during the night of 15 July 2007 in service mode using three different
instruments: FORS1, visible photometry and spectroscopy; ISAAC,
![]() photometry and J
spectroscopy; and SINFONI H+K spectroscopy. All three instruments were working simultaneously at UT1, UT2 and UT4 telescopes at Cerro Paranal (ESO, Chile).
photometry and J
spectroscopy; and SINFONI H+K spectroscopy. All three instruments were working simultaneously at UT1, UT2 and UT4 telescopes at Cerro Paranal (ESO, Chile).
2.1.1 Spectroscopy
The visible observations, covering the 0.4-0.94 ![]() m wavelength range, were acquired by Alvarez-Candal et al. (2008) with a spectral resolution of about 200. All the details of observations and reduction strategies are reported in Alvarez-Candal et al. (2008).
m wavelength range, were acquired by Alvarez-Candal et al. (2008) with a spectral resolution of about 200. All the details of observations and reduction strategies are reported in Alvarez-Candal et al. (2008).
J-band spectroscopy in the range 1.1-1.4 ![]() m, presented here for the first time, was performed using ISAAC in the short wavelength mode with a spectral resolution of about 500. The object was nodded between positions A and B along the 1
m, presented here for the first time, was performed using ISAAC in the short wavelength mode with a spectral resolution of about 500. The object was nodded between positions A and B along the 1
![]() wide slit for a total exposure time of 20 min (10 exposures of DIT = 120 s). The A and B images, taken 10
wide slit for a total exposure time of 20 min (10 exposures of DIT = 120 s). The A and B images, taken 10
![]() apart, were subtracted and combined using MIDAS following the procedure described by Barucci et al. (2002). The reflectance spectrum of the target object was obtained by dividing the spectrum of the observed object by the spectrum of the solar analog HD 147284 observed at airmass within a few percent from that of Quaoar. This J spectrum was
smoothed using a median filter to reach a spectral resolution of about 100, in order to improve
the signal-to-noise ratio.
apart, were subtracted and combined using MIDAS following the procedure described by Barucci et al. (2002). The reflectance spectrum of the target object was obtained by dividing the spectrum of the observed object by the spectrum of the solar analog HD 147284 observed at airmass within a few percent from that of Quaoar. This J spectrum was
smoothed using a median filter to reach a spectral resolution of about 100, in order to improve
the signal-to-noise ratio.
The H- and K-band spectroscopy (Guilbert et al. 2009) was obtained using SINFONI,
a near-infrared integral field spectrometer, installed on UT4-``Yepun'' ESO-VLT.
For these observations the H+K grating was used yielding a spectral resolution of about 1500 over the 1.45-2.45 ![]() m range. A median filtering technique was applied in order to remove bad pixels and residual spikes. See Guilbert et al. (2009) for all details on observations and data reduction. The spectrum was smoothed to a resolution of about 250.
m range. A median filtering technique was applied in order to remove bad pixels and residual spikes. See Guilbert et al. (2009) for all details on observations and data reduction. The spectrum was smoothed to a resolution of about 250.
Since different spectral ranges were covered with different instruments and setups, we adjusted the flux scale of each spectrum using the photometric colors obtained almost-simultaneously (DeMeo et al. 2009) and listed in Table 2.
2.1.2 Combining the data
To combine the different spectral ranges we use the photometric data reported in Table 2. First we normalize to unity the visible spectra at the effective wavelength of the V filter. Then we rescale the R, J, H, and K colors (Table 2) using
![\begin{displaymath}R_{\lambda_{\rm e}}=10^{-0.4[(M_{\lambda_{\rm e}}-V)-(M_{\lambda_{\rm e}}-V)_{\odot}]}
\end{displaymath}](/articles/aa/full_html/2009/25/aa11752-09/img12.png)
where
The obtained reflectances
![]() are used to re-normalize the other spectral ranges by means of a weighted mean, where the weights are given by the different transmission channels of the ISAAC filters J, H and
are used to re-normalize the other spectral ranges by means of a weighted mean, where the weights are given by the different transmission channels of the ISAAC filters J, H and ![]() (
(
![]() ). The re-normalized spectrum is then given by
). The re-normalized spectrum is then given by
![\begin{displaymath}F_{\lambda}^n=\bigg[\bigg(\frac{\sum_{i}T_{i}F_{i}}{\sum_{i}T_{i}}\bigg)^{-1} R_{\lambda_{\rm e}}\bigg] F_{\lambda}
\end{displaymath}](/articles/aa/full_html/2009/25/aa11752-09/img20.png)
where
Table 2: Photometric observations of (50 000) Quaoar from DeMeo et al. (2009).
| |
Figure 1:
Datasets adopted in the modeling process. The reflectance was normalized to 1.0 at 0.55 |
| Open with DEXTER | |
2.2 Spitzer data
The ground-based reflectance data have been complemented and extended to longer wavelengths with
broadband photometric measurements from the InfraRed Array Camera (IRAC) on the Spitzer Space Telescope (Werner et al. 2004; Fazio et al. 2004). Two observations separated by 3.25 days (4.4 rotations for
17.6788 h period) each detected Quaoar at both 3.6 and 4.5 ![]() m (
m (
![]() and 0.87
and 0.87 ![]() m, respectively).
Between the two dates, Quaoar moved
m, respectively).
Between the two dates, Quaoar moved ![]() 1
1![]() within the 5.2
within the 5.2![]() FOV of IRAC, enabling accurate subtraction of background flux. Each observation consisted of a 16 point dither pattern of 100 s frames for the 4.5
FOV of IRAC, enabling accurate subtraction of background flux. Each observation consisted of a 16 point dither pattern of 100 s frames for the 4.5 ![]() m channel followed immediately by a 16 point dither pattern of 100 s frames for the 3.6
m channel followed immediately by a 16 point dither pattern of 100 s frames for the 3.6 ![]() m channel. During the original cryogenic mission, IRAC imaged the same FOV at 5.8
m channel. During the original cryogenic mission, IRAC imaged the same FOV at 5.8 ![]() m simultaneously with the 3.6
m simultaneously with the 3.6 ![]() m channel and at 8.0
m channel and at 8.0 ![]() m simultaneously with the 4.5
m simultaneously with the 4.5 ![]() m channel. Quaoar was not detected in either of the two longer wavelength channels.
m channel. Quaoar was not detected in either of the two longer wavelength channels.
The images have all been processed with the IRAC automated data pipeline (version 14.0), which includes
steps such as dark subtraction, flat fielding, and flux calibration (see data handbook at
ssc.spitzer.caltech.edu/irac/dh/). We average the 16 calibrated frames from each observation
(omitting outliers) to calculate a background frame for the other date. This background frame is
subtracted from each data frame and corrections (supplied by the Spitzer Science Center) for
variation in pixel solid angle and array location dependent photometric variations are applied.
Aperture photometry is performed using 2 and 3 pixel radius apertures and aperture corrections
published in the IRAC data handbook. We calculate color corrections assuming a solar spectral
slope through the IRAC channels (Smith & Gottlieb 1974). Final fluxes are the average of all sixteen
frames (omitting outliers), and the 1-sigma uncertainties take into account photon counting statistics,
variation among the 16 dithered frames, and variation among the different aperture measurements (Table 3).
We also list magnitudes calculated from the measured fluxes using zero
magnitude fluxes derived from data in Reach et al. (2005) (and posted at
http://ssc.spitzer.caltech.edu/irac/calib/).
The geometric albedo in each channel is calculated from
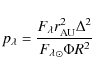
where
We use the measured light curve (Ortiz et al. 2003; Rabinowitz et al.
2007) to calculate the rotational phases of the various observations
used herein. Thirouin et al. (2009, in preparation) have reanalyzed the
data of Ortiz et al. (2003), confirming the rotation period of
![]() h (J. Ortiz, personal communication). We find that the
Spitzer thermal (MIPS) observations used by Stansberry et al. (2008) to
estimate the size of Quaoar are perfectly phased with the ground-based
data (within
h (J. Ortiz, personal communication). We find that the
Spitzer thermal (MIPS) observations used by Stansberry et al. (2008) to
estimate the size of Quaoar are perfectly phased with the ground-based
data (within ![]() 9
9![]() in longitude). The first IRAC date falls
in longitude). The first IRAC date falls ![]() 30
30![]() in longitude away (falling on the brightest part of the light curve),
whereas the second IRAC date is nearly perfectly 180
in longitude away (falling on the brightest part of the light curve),
whereas the second IRAC date is nearly perfectly 180![]() away from the
ground-based/MIPS rotational phase. Using this information, we
corrected the measured IRAC fluxes to the rotational phase of the
ground-based and MIPS observations. Lightcurve-corrected IRAC albedos
were then rederived as outlined above. Uncertainties in brightness from
propagating the rotational phase have been folded into the final albedo
uncertainties. While the best lightcurve solution predicts a
double-peaked lightcurve (with one maximum
away from the
ground-based/MIPS rotational phase. Using this information, we
corrected the measured IRAC fluxes to the rotational phase of the
ground-based and MIPS observations. Lightcurve-corrected IRAC albedos
were then rederived as outlined above. Uncertainties in brightness from
propagating the rotational phase have been folded into the final albedo
uncertainties. While the best lightcurve solution predicts a
double-peaked lightcurve (with one maximum ![]() 0.02 mag brighter than the
other), there is a small chance that the lightcurve is single-peaked.
In this case, the second IRAC date would fall on the same rotational
phase as the ground-based and MIPS observations, and the first IRAC data
would be
0.02 mag brighter than the
other), there is a small chance that the lightcurve is single-peaked.
In this case, the second IRAC date would fall on the same rotational
phase as the ground-based and MIPS observations, and the first IRAC data
would be ![]() 30
30![]() away.
away.
Table 3: Measured fluxes and albedos from IRAC.
3 Data analysis
3.1 Initial constraints and modeling strategy
The best and most straightforward way to identify surface materials spectroscopically is by detection of diagnostic absorption bands. Constraints on the presence of other materials necessarily rely on more subtle effects on the spectrum. With a spectrum as rich as that of Quaoar, we can be quite confident of the presence of several materials and have a good idea of others to consider prior to beginning the spectral modeling.
H2O is clearly present as indicated by its distinctive bands at 1.5 and 2.0 ![]() m (Jewitt & Luu 2004; Schaller & Brown 2007b). Furthermore, the distinctive 1.65
m (Jewitt & Luu 2004; Schaller & Brown 2007b). Furthermore, the distinctive 1.65 ![]() m feature reveals that at least a significant portion of the H2O is in the crystalline phase. This feature also provides a tool to determine the temperature of the ice on the surface of Quaoar. Several smaller absorption features (at 1.72, 2.32, and 2.38
m feature reveals that at least a significant portion of the H2O is in the crystalline phase. This feature also provides a tool to determine the temperature of the ice on the surface of Quaoar. Several smaller absorption features (at 1.72, 2.32, and 2.38 ![]() m) point strongly to the presence of CH4 ice, as described by Schaller & Brown (2007b).
m) point strongly to the presence of CH4 ice, as described by Schaller & Brown (2007b).
Several other materials are also hinted at, though less securely than H2O and CH4. The steep
red slope from the visible through ![]() 1.3
1.3 ![]() m is strongly suggestive of complex organic material. No other plausible material has yet been identified that can explain such steep spectral slopes (Cruikshank et al. 2005, and references therein). The slight difference in albedo at the second IRAC band (4.6
m is strongly suggestive of complex organic material. No other plausible material has yet been identified that can explain such steep spectral slopes (Cruikshank et al. 2005, and references therein). The slight difference in albedo at the second IRAC band (4.6 ![]() m) between the two observations is suggestive of a possible variation in composition. The fact that the variation is present mostly in the second band is a
constraint to the identification of the material that might be varying. Schaller & Brown (2007b) have reported the possible presence of ethane or other light hydrocarbons on the basis of weak features visible between 2.3 and 2.35
m) between the two observations is suggestive of a possible variation in composition. The fact that the variation is present mostly in the second band is a
constraint to the identification of the material that might be varying. Schaller & Brown (2007b) have reported the possible presence of ethane or other light hydrocarbons on the basis of weak features visible between 2.3 and 2.35 ![]() m, and Jewitt & Luu (2004) suggested the presence of NH4OH to explain a weak 2.2
m, and Jewitt & Luu (2004) suggested the presence of NH4OH to explain a weak 2.2 ![]() m feature. The goal of the present work is to test, via reflectance spectral modeling, which of the aforementioned materials are indeed present on the surface of Quaoar and to establish the relative amounts of the
main components contributing to the spectral albedo. To achieve this goal we compile a list of candidate components and test in a quantitative way which materials affect the spectrum significantly in terms of feature matching, continuum level and overall fit.
m feature. The goal of the present work is to test, via reflectance spectral modeling, which of the aforementioned materials are indeed present on the surface of Quaoar and to establish the relative amounts of the
main components contributing to the spectral albedo. To achieve this goal we compile a list of candidate components and test in a quantitative way which materials affect the spectrum significantly in terms of feature matching, continuum level and overall fit.
3.2 Albedo determination
The overall albedo of a spectrum is an important constraint in developing spectral models. This is particularly important when considering components that lack discrete absorption features in the wavelength range being studied. According to Stansberry et al. (2008) Quaoar is a fairly bright object with visual albedo of 19.9% (+13.17%-7.04%) determined by Spitzer/MIPS measurements of thermal emission from Quaoar at 24 and 70
3.3 Modeling
3.3.1 Adopted code
The geometric albedo of Quaoar at every wavelength is calculated by means of a code based on the Shkuratov (1999) radiative transfer formulation of the slab model. Shkuratov differs from Hapke's (1981) approach in the treatment of the phase function (which is calculated rather than assigned as an explicit parameter as in Hapke) (see Poulet et al 2002, for a comparison of the theories) as well as in the number of free input parameters. Shkuratov's formulation, as well as Hapke's, allows mixing of materials in a variety of ways that include molecular as well as intimate mixtures. Molecular mixtures consist of inclusions in a medium (usually ice) of contaminant particles. In this case, optical constants for the contaminated material are calculated by means of the effective medium theory (Shkuratov 1999). Intimate mixtures are the common salt and pepper mixtures.
Required input parameters are the relative amounts, grain size and optical constants of the selected components. In the case of Quaoar, the fact that the adopted wavelength range is quite extensive increases the number of constraints and contributes to limiting the number of multiple solutions.
Optical constants (real and imaginary indices of refraction, covering the same wavelengths as the observations), are available for only a limited number of materials and can be a limiting factor when modeling the surface of Quaoar and other Solar System bodies. The determination of optical constants from laboratory spectral data is often challenging and can result in substantial uncertainties, particularly in regions of the spectrum where absorption is very weak (Mastrapa et al. 2008). Table 4 lists the materials that we adopted for the modeling of Quaoar and the sources of the optical constants. We refer to each individual paper for an assessment of the uncertainty in the optical constants of each component.
3.3.2 Impact of individual materials on the spectrum
Each selected component plays an important role in the overall spectrum or parts of it. In some cases, such as for H2O, the effect is obvious and consists of the presence of discrete absorption bands, in others either the fundamental spectral bands fall outside the observed spectral range or the material has a featureless spectrum. In the latter case, the effect on the whole spectrum or on large parts of it can be quite subtle.
![\begin{figure}
\par\includegraphics[angle=90,width=9cm]{1752Fig2.eps} \end{figure}](/articles/aa/full_html/2009/25/aa11752-09/Timg43.png) |
Figure 2:
Geometric albedo of ices calculated with Shkuratov's method for
different grain sizes (smaller grains produce shallower lines).
Dots at the Spitzer wavelengths correspond to the position of ``synthetic Spitzer bands''
calculated integrating the models over the Spitzer filters wavelength ranges. The N2 spectrum represents the hexagonal |
| Open with DEXTER | |
Many of the materials that are likely to exist on KBO surfaces have stronger absorptions in the 3 to 5 ![]() m range than at shorter wavelengths, as shown in Fig. 2. This has also been observed on the surfaces of Pluto and Charon (Olkin et al. 2007; and Protopapa et al. 2008), even though, unlike the Quaoar case, on Pluto the 3.6
m range than at shorter wavelengths, as shown in Fig. 2. This has also been observed on the surfaces of Pluto and Charon (Olkin et al. 2007; and Protopapa et al. 2008), even though, unlike the Quaoar case, on Pluto the 3.6 ![]() m band is significantly lower than the 4.5
m band is significantly lower than the 4.5 ![]() m band. The Spitzer measurements are aimed at searching for these strong absorptions.
m band. The Spitzer measurements are aimed at searching for these strong absorptions.
When CH4, for example, is predominant in the mixture its effect is recognizable not only at 2.3 ![]() m where its bands can be detected, but also at the Spitzer wavelengths: the first IRAC band will be lower than the second because of the significant absorption at 3.3
m where its bands can be detected, but also at the Spitzer wavelengths: the first IRAC band will be lower than the second because of the significant absorption at 3.3 ![]() m (see Fig. 2). N2 on the other hand, is almost featureless in the visible and near-IR part of the spectrum, with the exception of its relatively weak band at 2.15
m (see Fig. 2). N2 on the other hand, is almost featureless in the visible and near-IR part of the spectrum, with the exception of its relatively weak band at 2.15 ![]() m. The stronger band of N2 at 4.3
m. The stronger band of N2 at 4.3 ![]() m can lower the second IRAC band (4.5
m can lower the second IRAC band (4.5 ![]() m) relative to the first (3.6
m) relative to the first (3.6 ![]() m). In the case of Quaoar, N2 could be either in its cubic
m). In the case of Quaoar, N2 could be either in its cubic ![]() -phase (stable for T<36 K) or in its hexagonal
-phase (stable for T<36 K) or in its hexagonal ![]() -phase, which is stable for
-phase, which is stable for
![]() K, introducing bands of different strength and possibly affecting the IRAC bands a different amount.
K, introducing bands of different strength and possibly affecting the IRAC bands a different amount.
Crystalline H2O ice is extremely absorbing at the Spitzer wavelengths darkening the albedo significantly, but amorphous H2O ice is less absorbing at 3.6 ![]() m, setting it apart from its
symmetrical counterpart. Triton tholin, a complex organic material, brightens the albedo at the Spitzer wavelengths and imparts a significant red slope in the visual part of the spectrum. Some minerals, such as pyroxenes, also have a relatively high albedo in the IR part of the spectrum.
m, setting it apart from its
symmetrical counterpart. Triton tholin, a complex organic material, brightens the albedo at the Spitzer wavelengths and imparts a significant red slope in the visual part of the spectrum. Some minerals, such as pyroxenes, also have a relatively high albedo in the IR part of the spectrum.
When these spectral behaviors of ices and Quaoar constraints are kept into account the outline of a set of materials that are likely to play an important role starts taking shape. In the case of Quaoar we find that the main contributors to the overall albedo and shape of the spectrum are CH4, N2, and H2O mixed intimately with tholins. The modeling of the red slope in the visible part of the spectrum indicates that CH4 and H2O ice are also mixed molecularly with tholins.
A few further materials were tested, at different stages of the modeling process, to determine whether a better fit could be achieved, particularly in the mid-IR part of the spectrum. These materials include minerals (olivine, pyroxene, NaCl) as well as alternative reddening materials (polyHCN) and ices (NH3). They were originally chosen as they are fairly bright in the region of the Spitzer bands or because, in the case of NH3, we were testing for irradiation products of CH4 and N2 (Moore & Hudson 2003; Piscitelli et al. 1988). They were ultimately abandoned in favor of the components that are part of the final model as their behavior did not reflect the observation requirements. NaCl was the only one that provided as good a fit as the H2O in very small grains, but wasn't adopted as the very limited inventory of Cl in the Solar System makes it an unlikely candidate.
Grain sizes were initially estimated based on the strength of the visible features, for those materials such as CH4 and H2O, that have bands in the observed wavelength range. The grain sizes of the components whose bands are not observable were estimated to be comparable in size to the grains of the components with observed bands. N2 is the exception as this ice requires very long path lengths to produce detectable absorptions, and our initial guess reflected commonly detected grain sizes for it.
The list of candidate materials, tentative grain sizes and relative amounts is used as input to an automatic routine that runs the code and compares the model to the observed data (calculating the rms of the differences). The ``amoeba'' routine performs multidimensional minimization of the rms, using the downhill simplex method of Nelder and Mead (1965). Local minima can be avoided by starting the process in different places in the parameter space. The routine also allows ``weights'' for different parts of the spectrum. The weights were varied between 1 and 0. The weights are taken into account when the rms is computed allowing us to control to which segment of the spectrum the fit should be tuned up. This tactic allows an extensive exploration of the parameter space, producing thousands of models. We find that when equal weight is given to the entire wavelength range the overall fit is poorer. Consequently, in the automatic procedure to model Quaoar, we chose to give all weight to the spectral part of the data, as the amount of information per segment of spectrum is higher than in the photometric bands.
3.3.3 Best model
Our best model consists of an intimate mixture of crystalline and amorphous H2O, CH4, N2, and C2H6 ice with triton and titan tholin. Both crystalline H2O and CH4 ice are contaminated molecularly by triton and titan tholin as well. Details of the best fit (shown in Fig. 3) are listed in Table 4.
Table 4: Best fitting model, model without N2, model with 10% N2.
Fitting the overall shape of the albedo distribution on Quaoar turned out to be a challenging enterprise, mostly due to the overall fairly high albedo. While its visual albedo is only intermediate, Quaoar's steep red slope makes its near-IR and IRAC albedo levels high, comparable to that of Sedna. The relative heights of the two Spitzer bands complicate the problem even more.
Using a mix of crystalline H2O and CH4 ices with reddening materials yields a satisfactory fit up to 2.5 ![]() m, but causes the model to be too dark at the wavelength of the Spitzer IRAC bands by about 40%. The low computed albedo at the Spitzer wavelengths is due to the relatively large amount of crystalline H2O ice present in the mixture. H2O ice reflectance, as shown in Fig. 2, is low at those wavelengths. The other materials, triton and titan tholin, as well as N2 and CH4 ice, are brighter, but not enough to completely counterbalance the effect of H2O ice. Furthermore, CH4 makes the first IRAC band lower than the second
in contrast with the observations. Several attempts at raising the albedo in this
region using a variety of materials have resulted in poor fits for the shorter wavelength data.
m, but causes the model to be too dark at the wavelength of the Spitzer IRAC bands by about 40%. The low computed albedo at the Spitzer wavelengths is due to the relatively large amount of crystalline H2O ice present in the mixture. H2O ice reflectance, as shown in Fig. 2, is low at those wavelengths. The other materials, triton and titan tholin, as well as N2 and CH4 ice, are brighter, but not enough to completely counterbalance the effect of H2O ice. Furthermore, CH4 makes the first IRAC band lower than the second
in contrast with the observations. Several attempts at raising the albedo in this
region using a variety of materials have resulted in poor fits for the shorter wavelength data.
In our quest to find a material that reflects very efficiently at the Spitzer wavelengths we
experimented with amorphous H2O - brighter than crystalline H2O ice in this region -
in extremely small grains (
![]() ): the fit is shown in Fig. 3 as the solid line and is our best fitting model. The broken line shows the same fit calculated with no amorphous H2O ice as a comparison. It is evident that the amorphous H2O ice increases the albedo at the wavelengths of the second Spitzer band improving the fit by about 20% at 4.5
): the fit is shown in Fig. 3 as the solid line and is our best fitting model. The broken line shows the same fit calculated with no amorphous H2O ice as a comparison. It is evident that the amorphous H2O ice increases the albedo at the wavelengths of the second Spitzer band improving the fit by about 20% at 4.5 ![]() m. The grain size of the amorphous H2O ice in the best model shown in the figure is slightly larger than 1.0
m. The grain size of the amorphous H2O ice in the best model shown in the figure is slightly larger than 1.0 ![]() m. Unfortunately, a grain size
m. Unfortunately, a grain size ![]()
![]() is not physically
acceptable for a component in an intimate mixture, as in this case the theory does not accommodate
diffractive behavior of the tiny particles. However, the result shown in Fig. 3 confirms the need for a very bright material. Broadening our search, we find that CO, like amorphous H2O in tiny grains, can also be used as a placeholder as it has a high reflectivity across the observed wavelength range. When substituted in the model CO yields as good a fit as amorphous H2O in tiny grains. The CO fundamental at 4.68
is not physically
acceptable for a component in an intimate mixture, as in this case the theory does not accommodate
diffractive behavior of the tiny particles. However, the result shown in Fig. 3 confirms the need for a very bright material. Broadening our search, we find that CO, like amorphous H2O in tiny grains, can also be used as a placeholder as it has a high reflectivity across the observed wavelength range. When substituted in the model CO yields as good a fit as amorphous H2O in tiny grains. The CO fundamental at 4.68 ![]() m falls within the second IRAC band, but is so narrow that its overall effect on that band is small. The overtone at 2.35
m falls within the second IRAC band, but is so narrow that its overall effect on that band is small. The overtone at 2.35 ![]() m is also narrow and falls in the middle of the complex bands of CH4, so it is difficult to discern in the current data. CO has been detected on Pluto and Triton, and is a plausible component of Quaoar.
Nevertheless, when CO is included in the model in place of amorphous H2O the fit does not improve significantly, leading us to conclude that CO, even though a possible component, is not the final solution to the problem of finding the ingredient that has a high albedo at the IRAC wavelengths.
m is also narrow and falls in the middle of the complex bands of CH4, so it is difficult to discern in the current data. CO has been detected on Pluto and Triton, and is a plausible component of Quaoar.
Nevertheless, when CO is included in the model in place of amorphous H2O the fit does not improve significantly, leading us to conclude that CO, even though a possible component, is not the final solution to the problem of finding the ingredient that has a high albedo at the IRAC wavelengths.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{1752Fig3.eps} \end{figure}](/articles/aa/full_html/2009/25/aa11752-09/Timg49.png) |
Figure 3: Best fitting model (solid line) compared to a model computed with the same components except amorphous H2O (broken line). Open diamonds show the model convolved to the Spitzer filter response functions. Open triangles mark the first Spitzer exposure, open squares indicate the position of the second. The model shows how amorphous H2O increases the albedo in the Spitzer wavelength region. The observations were scaled to Stansberry et al. (2008) visual geometric albedo. |
| Open with DEXTER | |
A scenario that should be considered is where the mixture of amorphous H2O and other components
is no longer a coarse-particle, intimate mixture. If the surface of Quaoar were covered with grains
of crystalline H2O ice mixed coarsely with CH4, N2, ethane ice and organic materials,
and these grains were in turn covered with a very thin (![]()
![]() )
layer of amorphous H2O ice, this layer would effectively change the absorption and refractive properties of the underlying particles, and possibly yield a more reflective material (Shkuratov 1999; Starukhina & Shkuratov 1996). More calculations will be necessary to test this hypothesis.
)
layer of amorphous H2O ice, this layer would effectively change the absorption and refractive properties of the underlying particles, and possibly yield a more reflective material (Shkuratov 1999; Starukhina & Shkuratov 1996). More calculations will be necessary to test this hypothesis.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{1752Fig4.eps}\end{figure}](/articles/aa/full_html/2009/25/aa11752-09/Timg50.png) |
Figure 4: A comparison of models with different amounts of N2 in their composition. The solid thin line shows the best model comprising 20% N2, the broken line shows the same model computed with no N2. Open diamonds show the model convolved to the Spitzer filter response functions. Open triangles mark the first Spitzer exposure, open squares indicate the position of the second. |
| Open with DEXTER | |
Even with fine-grained amorphous H2O, the model runs well below the measured albedo at 3.6 ![]() m. Since we know from the rotation lightcurve that the first of the Spitzer IRAC exposures overlaps the ground data (only
m. Since we know from the rotation lightcurve that the first of the Spitzer IRAC exposures overlaps the ground data (only ![]() 30
30![]() of separation in longitude) we can rule out the possibility of different terrains being sampled. Therefore, we are left with
two possibilities for explaining this poor fit. The first lies with the optical constants that can have significant uncertainty, particularly in regions of increased transparency, where they are highly sensitive to the choice of baseline (e.g., Mastrapa et al. 2008). The
of separation in longitude) we can rule out the possibility of different terrains being sampled. Therefore, we are left with
two possibilities for explaining this poor fit. The first lies with the optical constants that can have significant uncertainty, particularly in regions of increased transparency, where they are highly sensitive to the choice of baseline (e.g., Mastrapa et al. 2008). The ![]() 3.4-3.8
3.4-3.8 ![]() m is a relatively transparent region in H2O ice: a large error associated with the optical constants in this region is expected and could be the culprit of the problem.
Another possible explanation for the misfit at 3.6
m is a relatively transparent region in H2O ice: a large error associated with the optical constants in this region is expected and could be the culprit of the problem.
Another possible explanation for the misfit at 3.6 ![]() m is that there is still some component of the surface composition that we are missing.
m is that there is still some component of the surface composition that we are missing.
We have included N2 in our Quaoar model, a component that has not been detected on Quaoar before. N2 ice contributes to the model in two ways: it improves the fit at 2.149 ![]() m (Fig. 5) and it contributes to increasing the level of the albedo in the first Spitzer band at 3.6
m (Fig. 5) and it contributes to increasing the level of the albedo in the first Spitzer band at 3.6 ![]() m (Fig. 4). In fact, when the amount of N2 increases amorphous H2O in small grains, the very bright component of the mixture, decreases to compensate, as shown in Table 4. Because the bands of N2 ice are intrinsically weak, this
material could be present in relatively large amounts (although less than on Triton and Pluto)
and escape direct spectroscopic detection. However, from fitting the shape of the right wing of the
2
m (Fig. 4). In fact, when the amount of N2 increases amorphous H2O in small grains, the very bright component of the mixture, decreases to compensate, as shown in Table 4. Because the bands of N2 ice are intrinsically weak, this
material could be present in relatively large amounts (although less than on Triton and Pluto)
and escape direct spectroscopic detection. However, from fitting the shape of the right wing of the
2 ![]() m H2O feature (Fig. 5) we find that a model including 20% N2 (using
hexagonal
m H2O feature (Fig. 5) we find that a model including 20% N2 (using
hexagonal ![]() -phase optical constants) yields a good fit, and therefore suggests that N2 may
be a significant component on Quaoar, although its spectral absorption band is not fully resolved.
-phase optical constants) yields a good fit, and therefore suggests that N2 may
be a significant component on Quaoar, although its spectral absorption band is not fully resolved.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{1752Fig5.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11752-09/Timg51.png) |
Figure 5:
Best fit (solid line) and fit without N2. The fit at 2.149 |
| Open with DEXTER | |
Table 4 compares the best model (incorporating 20% N2), to a model with 10% and no N2 respectively to show how changing the amount of N2 affects the other components. The first row shows the rms error of each model when compared to the data. The following two rows show the amount of the materials specified mixed as inclusions in CH4, the third line the amount mixed as inclusions in crystalline H2O ice. Their grain size is not listed as in this kind of
mixture it is assumed to be ![]()
![]() .
The remaining materials listed in the table,
with grain sizes in parenthesis, are mixed intimately. The temperatures of H2O (amorphous and crystalline), CH4 and N2 ices are also listed after the name of the component.
.
The remaining materials listed in the table,
with grain sizes in parenthesis, are mixed intimately. The temperatures of H2O (amorphous and crystalline), CH4 and N2 ices are also listed after the name of the component.
It is difficult to assign an error estimate to the models as many of the parameters that enter in
the calculation are not very well known and we do not have any evaluation of their uncertainty or, as in the case of the optical constans, the error can be extremely large and misleading. While the quality of fit of the preferred models is in fact sensitive to these parameters, once they have been selected the models are quite sensitive to the choice of abundance, grain size and mixing geometry of the components. In fact, when looking at Table 4, it is possible to calibrate the uncertainty of each component abundance and grain size in the models: while the amount
of N2 varies by as much as 20% the remaining components have to compensate. As already noted it is the H2O in small grains that absorbs most of the change (by 11%), probably because of its lack of strong features that would otherwise constrain its abundance. The second component to change significantly (by 6%) is crystalline H2O ice, compensating the larger amount by choosing a smaller grain size and allowing an equally good fit of the 1.5 and 2 ![]() m bands. The remaining components vary by 1% at the most, indicating that the solution is fairly stable (as indicated also by the nearly constant rms among the different fits) and giving us a rough estimate of their error.
m bands. The remaining components vary by 1% at the most, indicating that the solution is fairly stable (as indicated also by the nearly constant rms among the different fits) and giving us a rough estimate of their error.
Following up on previous work suggesting that C2H6 and NH4OH might be present on the surface of Quaoar (Schaller & Brown 2007b; and Jewitt & Luu 2004) we experimented introducing each among the main components in our best fitting model. Optical constants for NH4OH (3% concentration of NH3, 80 K temperature) were provided by Roush and were the same used by Bauer et al. (2002) in their study of Miranda's surface composition. NH4OH has two bands in the IR part of the spectrum: at 2.0 and 2.2 ![]() m. While the 2.0
m. While the 2.0 ![]() m band overlaps with H2O ice, the second NH4OH band overlaps with one of the CH4 bands at
2.2
m band overlaps with H2O ice, the second NH4OH band overlaps with one of the CH4 bands at
2.2 ![]() m. Other bands confirm the presence of CH4, preventing us from validating the NH4OH detection. As far as C2H6 is concerned, a small amount of this component improves our best fit to the small absorption at
m. Other bands confirm the presence of CH4, preventing us from validating the NH4OH detection. As far as C2H6 is concerned, a small amount of this component improves our best fit to the small absorption at ![]() 2.27
2.27 ![]() m as shown in Fig. 6. The feature is hardly a detection as it is weak and close to the edge of the spectral data, however it is well matched by the synthetic spectrum. C2H6 has another, stronger band at
m as shown in Fig. 6. The feature is hardly a detection as it is weak and close to the edge of the spectral data, however it is well matched by the synthetic spectrum. C2H6 has another, stronger band at ![]() 2.32
2.32 ![]() m which falls very close to the edge of the spectrum where the noise level of the data is higher. When looking closely at this region of the spectrum the overall level of the absorption centered at
m which falls very close to the edge of the spectrum where the noise level of the data is higher. When looking closely at this region of the spectrum the overall level of the absorption centered at ![]() 2.325
2.325 ![]() m appears to be offset higher than the model.
This could indicate a slight overestimate of the CH4 abundance in the model. However, concerning C2H6, the pattern of the individual features in the
m appears to be offset higher than the model.
This could indicate a slight overestimate of the CH4 abundance in the model. However, concerning C2H6, the pattern of the individual features in the ![]() 2.325
2.325 ![]() m observed band shows the first of the three components at
m observed band shows the first of the three components at ![]() 2.318
2.318 ![]() m, even though affected by a noise spike, to be indeed the strongest, as expected in the presence of C2H6. Based on this subtle, but supporting evidence, we confirm Schaller & Brown's (2007b) original suggestion until better spectral data for this wavelength region becomes available.
m, even though affected by a noise spike, to be indeed the strongest, as expected in the presence of C2H6. Based on this subtle, but supporting evidence, we confirm Schaller & Brown's (2007b) original suggestion until better spectral data for this wavelength region becomes available.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{1752Fig6.eps}\end{figure}](/articles/aa/full_html/2009/25/aa11752-09/Timg52.png) |
Figure 6:
Detail of the best fit (solid line), a fit without C2H6 (dashed), and a fit with NH4OH in place of C2H6 (dotted). There is some evidence for C2H6 as shown by the fit to the 2.275 |
| Open with DEXTER | |
3.4 H2O ice temperature determination
Grundy & Schmitt (1998) showed that one of the most striking changes in the behavior of the crystalline H2O ice spectrum with temperature is the wavelength shift at 1.65 ![]() m. The shift is accompanied by temperature sensitive changes in the relative strength of the 1.65-
m. The shift is accompanied by temperature sensitive changes in the relative strength of the 1.65-![]() m band with respect to the adjacent H2O band absorption maximum at 1.50
m band with respect to the adjacent H2O band absorption maximum at 1.50 ![]() m. We apply the same technique described by Merlin et al. (2007) in their analysis of 2003 EL61 to determine the central position of the band in the spectrum of Quaoar. We find the minimum of the band at
m. We apply the same technique described by Merlin et al. (2007) in their analysis of 2003 EL61 to determine the central position of the band in the spectrum of Quaoar. We find the minimum of the band at
![]() m corresponding to an estimated upper limit for the crystalline H2O ice temperature of 30 K, where the error in wavelength includes both the uncertainty due to the calibration of the instrument and that of the measurement technique. The inferred temperature is lower than the Stefan Boltzmann value (40 K for a V albedo of 20%) possibly highlighting a problem in the assumptions. Indeed, because of the coincidence in wavelength of the 1.65-
m corresponding to an estimated upper limit for the crystalline H2O ice temperature of 30 K, where the error in wavelength includes both the uncertainty due to the calibration of the instrument and that of the measurement technique. The inferred temperature is lower than the Stefan Boltzmann value (40 K for a V albedo of 20%) possibly highlighting a problem in the assumptions. Indeed, because of the coincidence in wavelength of the 1.65-![]() m H2O band with a band of CH4, a shift in the observed absorption band may be caused by the presence of CH4, thus confusing the temperature effect in the H2O band.
m H2O band with a band of CH4, a shift in the observed absorption band may be caused by the presence of CH4, thus confusing the temperature effect in the H2O band.
To test to what degree CH4 contamination could be responsible for the shift in wavelength we calculate models with H2O, CH4, and C2H6 in proportions similar to the relative amounts present on Quaoar. We find that the shift in the band position as a function of composition is only a fraction of the measured shift. To further understand the nature of the shift in the observed 1.65 ![]() m band we compute models using two sets of optical constants for H2O ice at 40 K
- Mastrapa & Sandford (2008) and Grundy & Schmitt (1998) respectively - for which we know that the crystalline ice is in both its cubic and hexagonal phase for the former and purely hexagonal for the latter. The shifts in wavelengths for the corresponding synthetic spectra brace the shift of the observations pointing to the fact that Quaoar's crystalline H2O ice could be present in both cubic and hexagonal form. High resolution and high signal-to-noise spectral data in the Spitzer wavelength range might be required to obtain a firmer determination of Quaoar's surface composition and in turn the ability to discern to what degree the shift in wavelength is due to composition or to other factors related to its temperature and history.
m band we compute models using two sets of optical constants for H2O ice at 40 K
- Mastrapa & Sandford (2008) and Grundy & Schmitt (1998) respectively - for which we know that the crystalline ice is in both its cubic and hexagonal phase for the former and purely hexagonal for the latter. The shifts in wavelengths for the corresponding synthetic spectra brace the shift of the observations pointing to the fact that Quaoar's crystalline H2O ice could be present in both cubic and hexagonal form. High resolution and high signal-to-noise spectral data in the Spitzer wavelength range might be required to obtain a firmer determination of Quaoar's surface composition and in turn the ability to discern to what degree the shift in wavelength is due to composition or to other factors related to its temperature and history.
4 Conclusions
We present high signal-to-noise and high spectral resolution VLT data in conjunction with Spitzer data for Quaoar, a Transneptunian (Kuiper Belt) object. The spectral data cover the visual to near-infrared range while the Spitzer Space Telescope IRAC data consist of two photometric bands at 3.6 and 4.5 ![]() m. This extended wavelength range provides a large set of constraints when modeling the surface composition of this object, narrowing down the number of possible solutions.
m. This extended wavelength range provides a large set of constraints when modeling the surface composition of this object, narrowing down the number of possible solutions.
The overall high albedo of Quaoar is already an indication of the expected importance of ices on the surface of this TNO. Indeed, we confirm that the overall albedo shape and albedo levels can be fit by a combination of CH4 and H2O ice (already detected by Schaller & Brown 2007b) mixed both molecularly and intimately with tholins. Traces of ethane (also predicted by Schaller & Brown 2007b) are also indicated by the model fits. In addition, model fits suggest that N2 may be a significant component which, if verified, would make this TNO even more similar to Triton and Pluto. However, in contrast to Pluto and Triton which have spectra dominated by CH4, Quaoar's spectrum is dominated by H2O ice. The much reduced ability of Quaoar to retain very volatile species compared to Pluto and Triton (Schaller & Brown 2007a) could have led to a very different evolution with time of the surface volatiles, with the less volatile H2O ice being much more apparent.
Our data and models do not confirm the presence of NH4OH as a significant contributor to the observed spectrum. As already discussed by Schaller & Brown (2007b), this lessens the need to call for cryovolcanism to explain Quaoar's surface composition.
Our attempt at measuring the temperature of H2O ice on the surface of Quaoar based on the 1.65 ![]() m crystalline ice feature yields an estimate of 30 K. This lower than expected value highlights the difficulty to obtain a firm measurement due to the presence of CH4 mixed with H2O ice as well as to the possibility that crystalline ice might be present in both cubic and hexagonal phase on the surface of this KBO. A firmer determination of the composition will be necessary to make a more precise determination of the temperature and history of Quaoar.
m crystalline ice feature yields an estimate of 30 K. This lower than expected value highlights the difficulty to obtain a firm measurement due to the presence of CH4 mixed with H2O ice as well as to the possibility that crystalline ice might be present in both cubic and hexagonal phase on the surface of this KBO. A firmer determination of the composition will be necessary to make a more precise determination of the temperature and history of Quaoar.
Even our best-fit spectral model underestimates the albedo at the Spitzer wavelengths where
crystalline H2O ice is instead very absorbing. We find that a highly reflective material is required to fit the Spitzer data. We experiment with CO, which only partially fulfills this demand and can be used only as a placeholder as none of its features have been detected in the observed wavelength range. As an alternative, amorphous H2O in grains ![]()
![]() could also satisfy this need if the mixing was not between coarse particles as intimate mixtures assume, but as a very thin layer of amorphous H2O ice on top of the coarse mixture of the other components. in this case, the amorphous ice could be the result of irradiation of crystalline ice and represent a process that is part of the constant cycle of transformation of H2O ice on the surface of this (and some other) distant icy bodies (e.g. Mastrapa & Brown 2006). However, it remains to be seen if it would be compatible with the presence of the irradiated carbon-containing species that are advocated to account for the red color of Quaoar. Additional irradiation experiments on ices, particularly on ices with impurities, and spectral models that are appropriate for very fine grain sizes and thin coatings or layers will further test this scenario.
could also satisfy this need if the mixing was not between coarse particles as intimate mixtures assume, but as a very thin layer of amorphous H2O ice on top of the coarse mixture of the other components. in this case, the amorphous ice could be the result of irradiation of crystalline ice and represent a process that is part of the constant cycle of transformation of H2O ice on the surface of this (and some other) distant icy bodies (e.g. Mastrapa & Brown 2006). However, it remains to be seen if it would be compatible with the presence of the irradiated carbon-containing species that are advocated to account for the red color of Quaoar. Additional irradiation experiments on ices, particularly on ices with impurities, and spectral models that are appropriate for very fine grain sizes and thin coatings or layers will further test this scenario.
Acknowledgements
C.M.D.O. would like to thank Dr. Ted Roush for many helpful conversations as well as help in the everlasting search for optical constants and Dr. Ludmilla Kolokolova for advice with modeling codes. This work is based [in part] on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by NASA through an award issued by JPL/Caltech (program 20769).
References
- Alvarez-Candal, A., Fornasier, S., Barucci, M. A., et al. 2008, A&A, 487, 741 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bagnulo, S., Boehnhardt, H., Muinonen, K., et al. 2006, A&A, 450, 1239 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bagnulo, S., Belskaya, I., Muinonen, K., et al. 2008, A&A, 491, L33 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Baratta, G. A., Domingo, M., Ferini, G., et al. 2003, Nucl. Instrum. Methods Phys. Res. B, 209, 283 [NASA ADS] [CrossRef] (In the text)
- Barucci, M. A., Boehnhardt, H., Dotto, E., et al. 2002, A&A, 392, 335 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bauer, J. M., Roush, T. L., Geballe, T. R., et al. 2002, Icarus, 158, 178 [NASA ADS] [CrossRef] (In the text)
- Brown, M. E., & Suer, T.-A. 2007, IAU Circ., 8812, 1 [NASA ADS] (In the text)
- Brown, M. E., & Trujillo, C. A. 2004, AJ, 127, 2413 [NASA ADS] [CrossRef] (In the text)
- Cook, J. C., Desch, S. J., & Roush, T. L. 2007, BAAS, 38, 510 [NASA ADS] (In the text)
- Cruikshank, D. P., Imanaka, H., & Dalle Ore, C. M. 2005, Adv. Space Res., 36, 178 [NASA ADS] [CrossRef] (In the text)
- Delsanti, A. C., Hainaut, O., Jourdeuil, E., et al. 2004, A&A, 417, 1145 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- DeMeo, F. E., Fornasier, S., Barucci, M. A., et al. 2009, A&A, 493, 283 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] (In the text)
- Fornasier, S., Doressoundiram, A., Tozzi, G. P., et al. 2004, A&A, 421, 353 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Green, J. R., Brown, R. H., Cruikshank, D. P., et al. 1991, BAAS, 23, 1208 [NASA ADS]
- Grundy, W. M., & Schmitt, B. 1998, J. Geophys. Res., 103, 25809 [NASA ADS] [CrossRef] (In the text)
- Grundy, W. M., Schmitt, B., & Quirico, E. 2002, Icarus, 155, 486 [NASA ADS] [CrossRef]
- Guilbert, A., Alvarez-Candal, A., Merlin, F., et al. 2009, Icarus, 201, 272 [NASA ADS] [CrossRef] (In the text)
- Hapke, B. 1981, J. Geophys. Res., 86, 3039 [NASA ADS] [CrossRef] (In the text)
- Hudgins, D. M., Sandford, S. A., Allamandola, L. J., et al. 1993, ApJS, 86, 713 [NASA ADS] [CrossRef]
- Imanaka, H., Khare, B. N., McKay, C. P., et al. 2005, BAAS, 37, 772 [NASA ADS]
- Jewitt, D. C., & Luu, J. 2004, Nature, 432, 731 [CrossRef] (In the text)
- Khare, B. N., Sagan, C., Heinrich, M., et al. 1994, BAAS, 26, 1176 [NASA ADS]
- Marchi, S., Lazzarin, M., Magrin, S., et al. 2003, A&A, 408, L17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mastrapa, R. M. E., Bernstein, M. P., Sandford, S. A., et al. 2008, Icarus, 197, 307 [NASA ADS] [CrossRef] (In the text)
- Mastrapa, R. M. E., & Brown, R. H. 2006, Icarus, 183, 207 [NASA ADS] [CrossRef] (In the text)
- Mastrapa, R. M. E., & Sandford, S. A. 2008, AAS/Division for Planetary Sciences Meeting Abstracts, 40, #54.03 (In the text)
- Merlin, F., Guilbert, A., Dumas, C., et al. 2007, A&A, 466, 1185 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Moore, M. H., & Hudson, R. L. 2003, Icarus, 161, 486 [NASA ADS] [CrossRef] (In the text)
- Nelder, J., & Mead, R. 1965, Computer Journal, 7, 308 (In the text)
- Olkin, C. B., Young, E. F., Young, L. A., et al. 2007, AJ, 133, 420 [NASA ADS] [CrossRef] (In the text)
- Ortiz, J. L., Gutiérrez, P. J., Sota, A., et al. 2003, A&A, 409, L13 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Piscitelli, J. R., Cruikshank, D. P., & Bell, J. F. 1988, Icarus, 76, 118 [NASA ADS] [CrossRef] (In the text)
- Poulet, F., Cuzzi, J. N., Cruikshank, D. P., et al. 2003, Icarus, 160, 313 [NASA ADS] [CrossRef] (In the text)
- Protopapa, S., Boehnhardt, H., Herbst, T. M., et al. 2008, A&A, 490, 365 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rabinowitz, D. L., Schaefer, B. E., & Tourtellotte, S. W. 2007, AJ, 133, 26 [NASA ADS] [CrossRef] (In the text)
- Reach, W. T., Megeath, S. T., Cohen, M., et al. 2005, PASP, 117, 978 [NASA ADS] [CrossRef] (In the text)
- Schaller, E. L., & Brown, M. E. 2007a, ApJ, 659, L61 [NASA ADS] [CrossRef] (In the text)
- Schaller, E. L., & Brown, M. E. 2007b, ApJ, 670, L49 [NASA ADS] [CrossRef] (In the text)
- Shkuratov, Y., Starukhina, L., Hoffmann, H., et al. 1999, Icarus, 137, 235 [NASA ADS] [CrossRef] (In the text)
- Smith, E. V. P., & Gottlieb, D. M. 1974, Space Sci. Rev., 16, 771 [NASA ADS] (In the text)
- Stansberry, J., Grundy, W., Brown, M., et al. 2008, in Solar System Beyond Neptune, ed. M. A. Barucci et al. (Univ. of Arizona Press), 161 (In the text)
- Starukhina, L. V., & Shkuratov, Y. G. 1996, Solar System Research, 30, 299 [NASA ADS] (In the text)
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... Quaoar
![[*]](/icons/foot_motif.png)
- Based on observations at the VLT Observatory Cerro Paranal of European Southern Observatory, ESO, Chile, in the framework of program 178.C-0036.
All Tables
Table 1: Observing circumstances of (50000) Quaoar.
Table 2: Photometric observations of (50 000) Quaoar from DeMeo et al. (2009).
Table 3: Measured fluxes and albedos from IRAC.
Table 4: Best fitting model, model without N2, model with 10% N2.
All Figures
| |
Figure 1:
Datasets adopted in the modeling process. The reflectance was normalized to 1.0 at 0.55 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=9cm]{1752Fig2.eps} \end{figure}](/articles/aa/full_html/2009/25/aa11752-09/Timg43.png) |
Figure 2:
Geometric albedo of ices calculated with Shkuratov's method for
different grain sizes (smaller grains produce shallower lines).
Dots at the Spitzer wavelengths correspond to the position of ``synthetic Spitzer bands''
calculated integrating the models over the Spitzer filters wavelength ranges. The N2 spectrum represents the hexagonal |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{1752Fig3.eps} \end{figure}](/articles/aa/full_html/2009/25/aa11752-09/Timg49.png) |
Figure 3: Best fitting model (solid line) compared to a model computed with the same components except amorphous H2O (broken line). Open diamonds show the model convolved to the Spitzer filter response functions. Open triangles mark the first Spitzer exposure, open squares indicate the position of the second. The model shows how amorphous H2O increases the albedo in the Spitzer wavelength region. The observations were scaled to Stansberry et al. (2008) visual geometric albedo. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{1752Fig4.eps}\end{figure}](/articles/aa/full_html/2009/25/aa11752-09/Timg50.png) |
Figure 4: A comparison of models with different amounts of N2 in their composition. The solid thin line shows the best model comprising 20% N2, the broken line shows the same model computed with no N2. Open diamonds show the model convolved to the Spitzer filter response functions. Open triangles mark the first Spitzer exposure, open squares indicate the position of the second. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{1752Fig5.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa11752-09/Timg51.png) |
Figure 5:
Best fit (solid line) and fit without N2. The fit at 2.149 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{1752Fig6.eps}\end{figure}](/articles/aa/full_html/2009/25/aa11752-09/Timg52.png) |
Figure 6:
Detail of the best fit (solid line), a fit without C2H6 (dashed), and a fit with NH4OH in place of C2H6 (dotted). There is some evidence for C2H6 as shown by the fit to the 2.275 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


