| Issue |
A&A
Volume 501, Number 1, July I 2009
|
|
|---|---|---|
| Page(s) | 29 - 47 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200809840 | |
| Published online | 05 May 2009 | |
Pre-recombinational energy release and narrow features in the CMB spectrum
J. Chluba1 - R. A. Sunyaev1,2
1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching bei München, Germany
2 - Space Research Institute, Russian Academy of Sciences, Profsoyuznaya 84/32, 117997 Moscow, Russia
Received 25 March 2008 / Accepted 27 February 2009
Abstract
Energy release in the early Universe (
![]() )
should produce a broad spectral distortion of the cosmic microwave background (CMB) radiation field, which can be characterized as y-type distortion when the injection process started at redshifts
)
should produce a broad spectral distortion of the cosmic microwave background (CMB) radiation field, which can be characterized as y-type distortion when the injection process started at redshifts
![]() .
Here we demonstrate that if energy was released before the beginning of cosmological hydrogen recombination (
.
Here we demonstrate that if energy was released before the beginning of cosmological hydrogen recombination (
![]() ), closed loops of bound-bound and free-bound transitions in H I
and He II lead to the appearance of (i) characteristic multiple narrow spectral features at dm and cm wavelengths; and (ii) a prominent sub-millimeter feature consisting of absorption and
emission parts in the far Wien tail of CMB spectrum. The additional spectral features are generated in the pre-recombinational epoch of H I (
), closed loops of bound-bound and free-bound transitions in H I
and He II lead to the appearance of (i) characteristic multiple narrow spectral features at dm and cm wavelengths; and (ii) a prominent sub-millimeter feature consisting of absorption and
emission parts in the far Wien tail of CMB spectrum. The additional spectral features are generated in the pre-recombinational epoch of H I (![]() )
and He II (
)
and He II (![]() ), and therefore differ from those arising due to normal cosmological recombination in the undisturbed
CMB blackbody radiation field. We present the results of numerical computations including 25 atomic
shells for both H I and He II, and discuss the contributions of several individual transitions in detail. As examples, we consider the case of instantaneous energy
release (e.g., due to phase transitions), and exponential energy release (e.g., because of long-lived decaying particles). Our computations show that because of possible pre-recombinational
atomic transitions the variability in the CMB spectral distortion increases when comparing with the distortions arising in the normal recombination epoch. The amplitude of the spectral features, both at low and high frequencies, directly depends on the value of the y-parameter, which describes the intrinsic CMB spectral distortion resulting from the energy release. The time-dependence of the injection process also plays an important role, for example leading to non-trivial shifts in the quasi-periodic pattern at low frequencies along the frequency axis. The existence of these narrow spectral features would provide an unique way to separate y-distortions caused by pre-recombinational (
), and therefore differ from those arising due to normal cosmological recombination in the undisturbed
CMB blackbody radiation field. We present the results of numerical computations including 25 atomic
shells for both H I and He II, and discuss the contributions of several individual transitions in detail. As examples, we consider the case of instantaneous energy
release (e.g., due to phase transitions), and exponential energy release (e.g., because of long-lived decaying particles). Our computations show that because of possible pre-recombinational
atomic transitions the variability in the CMB spectral distortion increases when comparing with the distortions arising in the normal recombination epoch. The amplitude of the spectral features, both at low and high frequencies, directly depends on the value of the y-parameter, which describes the intrinsic CMB spectral distortion resulting from the energy release. The time-dependence of the injection process also plays an important role, for example leading to non-trivial shifts in the quasi-periodic pattern at low frequencies along the frequency axis. The existence of these narrow spectral features would provide an unique way to separate y-distortions caused by pre-recombinational (
![]() ) energy release from those arising in the post-recombinational era at redshifts
) energy release from those arising in the post-recombinational era at redshifts ![]() .
.
Key words: atomic processes - radiation mechanisms: general - cosmic microwave background - early Universe - cosmology: theory
1 Introduction
Measurements completed using data acquired with the C OBE/F IRAS instrument have proven that the spectrum of the cosmic microwave background (CMB) is close to being a perfect blackbody (Fixsen et al. 1996) of thermodynamic temperature T0=2.725 ![]() 0.001 K (Fixsen & Mather 2002; Mather et al. 1999). However, from the theoretical point of view, deviations of the CMB spectrum from that of a pure blackbody are not only possible but even inevitable if, for example, energy was released in the early Universe (e.g., due to viscous damping of acoustic waves, or annihilation or decay of particles). For very early energy release (
0.001 K (Fixsen & Mather 2002; Mather et al. 1999). However, from the theoretical point of view, deviations of the CMB spectrum from that of a pure blackbody are not only possible but even inevitable if, for example, energy was released in the early Universe (e.g., due to viscous damping of acoustic waves, or annihilation or decay of particles). For very early energy release (
![]() ), the resulting spectral distortion can be characterized as a Bose-Einstein
), the resulting spectral distortion can be characterized as a Bose-Einstein ![]() -type distortion (Sunyaev & Zeldovich 1970b; Illarionov & Syunyaev 1975b,a), while for energy release at low redshifts (
-type distortion (Sunyaev & Zeldovich 1970b; Illarionov & Syunyaev 1975b,a), while for energy release at low redshifts (
![]() ), the distortion is close to being a y-type distortion (Zeldovich & Sunyaev 1969).
), the distortion is close to being a y-type distortion (Zeldovich & Sunyaev 1969).
The most robust observational limits to these types of distortions are
![]() and
and
![]() (Fixsen et al. 1996). Due to rapid technological developments, improvements in these limits by a factor of
(Fixsen et al. 1996). Due to rapid technological developments, improvements in these limits by a factor of ![]() in principle may have been possible already several years ago (Fixsen & Mather 2002), and some efforts are being made to determine the absolute value of the CMB brightness temperature at low frequencies using the balloon-borne experiment A RCADE (Kogut et al. 2004; Fixsen et al. 2009; Kogut et al. 2006). However, today even a factor of
in principle may have been possible already several years ago (Fixsen & Mather 2002), and some efforts are being made to determine the absolute value of the CMB brightness temperature at low frequencies using the balloon-borne experiment A RCADE (Kogut et al. 2004; Fixsen et al. 2009; Kogut et al. 2006). However, today even a factor of
![]() is probably within reach for absolute measurement of the CMB spectrum (Mather 2007), in principle bringing us down to
is probably within reach for absolute measurement of the CMB spectrum (Mather 2007), in principle bringing us down to
![]() .
.
Also in the post-recombinational epoch (![]() ), y-type spectral distortions caused by different physical mechanisms should be produced. As an example, when performing measurements of the average CMB spectrum (e.g., with wide-angle horns or as achieved by C OBE/F IRAS),
all clusters of galaxies, hosting hot intergalactic gas, due to the thermal SZ-effect (Sunyaev & Zeldovich 1972b), should contribute to the integrated value of the observed y-parameter.
Similarly, supernova remnants at high redshifts (Oh et al. 2003), or shock waves arising due to large-scale structure formation (Miniati et al. 2000; Sunyaev & Zeldovich 1972a; Cen & Ostriker 1999) should lead to a
contribution to the overall y-parameter. For its possible value today, we only have the upper limit determined by C OBE/F IRAS and lower limits derived by estimating the total contribution of all clusters in the Universe (Markevitch et al. 1991; da Silva et al. 2000; Roncarelli et al. 2007). These lower limits exceed
), y-type spectral distortions caused by different physical mechanisms should be produced. As an example, when performing measurements of the average CMB spectrum (e.g., with wide-angle horns or as achieved by C OBE/F IRAS),
all clusters of galaxies, hosting hot intergalactic gas, due to the thermal SZ-effect (Sunyaev & Zeldovich 1972b), should contribute to the integrated value of the observed y-parameter.
Similarly, supernova remnants at high redshifts (Oh et al. 2003), or shock waves arising due to large-scale structure formation (Miniati et al. 2000; Sunyaev & Zeldovich 1972a; Cen & Ostriker 1999) should lead to a
contribution to the overall y-parameter. For its possible value today, we only have the upper limit determined by C OBE/F IRAS and lower limits derived by estimating the total contribution of all clusters in the Universe (Markevitch et al. 1991; da Silva et al. 2000; Roncarelli et al. 2007). These lower limits exceed
![]() ,
and it is possible that the contributions to the total value of y because of early energy release are comparable to or exceed those coming from the low redshift Universe.
,
and it is possible that the contributions to the total value of y because of early energy release are comparable to or exceed those coming from the low redshift Universe.
Several detailed analytical and numerical studies for various energy injection histories and mechanisms can be found in the literature (e.g., Burigana & Salvaterra 2003; Chluba & Sunyaev 2004; Daly 1991; Zeldovich et al. 1972; Hu et al. 1994; Hu & Silk 1993a; Sunyaev & Zeldovich 1970c; Salvaterra & Burigana 2002; Hu & Silk 1993b; Chan et al. 1975; Sunyaev & Zeldovich 1970b; Illarionov & Syunyaev 1975b; Danese & de Zotti 1982; Illarionov & Syunyaev 1975a; Ostriker & Thompson 1987; Burigana et al. 1995,1991b,a; Zeldovich & Sunyaev 1969; Sunyaev & Zeldovich 1970a). Two important conclusions can be drawn from these all studies: (i) the arising spectral distortions are always very broad and practically featureless; and (ii) due to the absence of narrow spectral features, distinguishing between the different injection histories is extremely difficult. This implies that if one would find a y-type spectral distortion in the average CMB spectrum, then it is practically impossible to determine whether the energy injection occurred just before, during, or after the epoch of cosmological recombination. Furthermore, these measurement require an absolute calibration and cross-calibration of the instrument, like for C OBE/F IRAS.
In this paper, we show that the pre-recombinational emission within the bound-bound and free-bound transition of atomic hydrogen and helium should leave multiple narrow features
(
![]() )
in the CMB spectrum, that might become observable at cm, dm, and sub-mm wavelengths (see Sect. 5). As for example discussed in Sunyaev & Chluba (2007), such kind of measurement could be performed differentially in frequency, without the requirement of an absolute calibration. This could in principle open a way to directly distinguish between pre- and post-recombinational y-distortions and even shed light on the
time-dependence of the energy injection process. We also find that the pre-recombinational emission produces a broad continuum spectrum, which close to the maximum of the CMB blackbody contributes very little but can reach
)
in the CMB spectrum, that might become observable at cm, dm, and sub-mm wavelengths (see Sect. 5). As for example discussed in Sunyaev & Chluba (2007), such kind of measurement could be performed differentially in frequency, without the requirement of an absolute calibration. This could in principle open a way to directly distinguish between pre- and post-recombinational y-distortions and even shed light on the
time-dependence of the energy injection process. We also find that the pre-recombinational emission produces a broad continuum spectrum, which close to the maximum of the CMB blackbody contributes very little but can reach
![]() of the intrinsic y-distortion at low frequencies (
of the intrinsic y-distortion at low frequencies (![]() GHz). Although this continuum has a different spectral behavior from that of a y-distortion, observationally the narrow spectral features are possibly more interesting, since it should be easier to extract them by employing a differential observing strategy.
GHz). Although this continuum has a different spectral behavior from that of a y-distortion, observationally the narrow spectral features are possibly more interesting, since it should be easier to extract them by employing a differential observing strategy.
How does this work? At redshifts well before the epoch of
![]() -recombination (
-recombination (
![]() ), the total number of CMB photons is unaffected by atomic transitions if the intrinsic CMB spectrum is represented by a pure blackbody. This is because the atomic emission and absorption processes balance each other in full thermodynamic equilibrium.
However, at lower redshifts (
), the total number of CMB photons is unaffected by atomic transitions if the intrinsic CMB spectrum is represented by a pure blackbody. This is because the atomic emission and absorption processes balance each other in full thermodynamic equilibrium.
However, at lower redshifts (
![]() ), due to the expansion of the Universe, the medium became sufficiently cold to allow the formation of neutral atoms. The transition to the neutral state is associated with the release of several additional photons per baryon (e.g.,
), due to the expansion of the Universe, the medium became sufficiently cold to allow the formation of neutral atoms. The transition to the neutral state is associated with the release of several additional photons per baryon (e.g., ![]() photons per
hydrogen atom, Chluba & Sunyaev 2006), even within a pure blackbody, ambient, CMB radiation field.
Refining early estimates (Dubrovich & Stolyarov 1997; Dubrovich 1975; Dubrovich & Stolyarov 1995; Zeldovich et al. 1968; Peebles 1968), the spectral distortions arising during hydrogen recombination (
photons per
hydrogen atom, Chluba & Sunyaev 2006), even within a pure blackbody, ambient, CMB radiation field.
Refining early estimates (Dubrovich & Stolyarov 1997; Dubrovich 1975; Dubrovich & Stolyarov 1995; Zeldovich et al. 1968; Peebles 1968), the spectral distortions arising during hydrogen recombination (
![]() ),
),
![]() -recombination (
-recombination (
![]() ), and
), and
![]() -recombination (
-recombination (
![]() )
within a pure blackbody ambient radiation field have been computed in detail (Chluba et al. 2007a; Chluba & Sunyaev 2006; Rubiño-Martín et al. 2006,2008). It was also emphasized that measuring these distortions in principle may open another independent way to determine the temperature of the CMB monopole, the specific entropy of the Universe, and the primordial helium abundance, well before the first appearance of stars
(e.g., Sunyaev & Chluba 2007,2008; Chluba & Sunyaev 2008b).
)
within a pure blackbody ambient radiation field have been computed in detail (Chluba et al. 2007a; Chluba & Sunyaev 2006; Rubiño-Martín et al. 2006,2008). It was also emphasized that measuring these distortions in principle may open another independent way to determine the temperature of the CMB monopole, the specific entropy of the Universe, and the primordial helium abundance, well before the first appearance of stars
(e.g., Sunyaev & Chluba 2007,2008; Chluba & Sunyaev 2008b).
However, the intrinsic CMB spectrum deviates from a pure blackbody (e.g., due to early energy injection, as explained above), then full equilibrium is perturbed, and the small imbalance
between emission and absorption in atomic transitions can lead to a net change in the number of photons, even prior to the epoch of recombination, in particular owing to loops starting and ending in the continuum (Lyubarsky & Sunyaev 1983). These loops attempt to diminish the maximal spectral distortions and produce several new photons per absorbed one. In this paper, we attempt to demonstrate how the cosmological recombination spectrum is affected by an intrinsic y-type CMB spectral distortion. We investigate the cases of single instantaneous energy injection (e.g., due to phase transitions) and for exponential energy injection (e.g., because of long-lived
decaying particles). There is no principle difficulty in performing the calculations for more
general injection histories, also including ![]() -type distortions, if necessary. However, this still requires a slightly more detailed study, which will be left for a future paper.
-type distortions, if necessary. However, this still requires a slightly more detailed study, which will be left for a future paper.
We also estimate the corrections due to free-free absorption and electron scattering. At observing frequency ![]() GHz, the free-free process is not important for y-distortions appearing at redshifts
GHz, the free-free process is not important for y-distortions appearing at redshifts ![]() .
However, the broadening caused by electron scattering must be taken into account for features appearing at redshifts
.
However, the broadening caused by electron scattering must be taken into account for features appearing at redshifts ![]() .
The recoil effect is mainly important for the Lyman-series features, but can otherwise be neglected. We also checked the effect of intrinsic y- and
.
The recoil effect is mainly important for the Lyman-series features, but can otherwise be neglected. We also checked the effect of intrinsic y- and ![]() -distortions on the CMB temperature and polarization power spectra but found no significant effect for the current upper limits
-distortions on the CMB temperature and polarization power spectra but found no significant effect for the current upper limits
![]() and
and
![]() imposed by C OBE/F IRAS (Fixsen et al. 1996).
imposed by C OBE/F IRAS (Fixsen et al. 1996).
In Sect. 2, we provide a short overview of the thermalization of CMB spectral distortions after early energy release, and provide formulae that we used in our computations to describe y-type distortions. In Sect. 3, we present explicit expressions for the net bound-bound and free-bound rates in a distorted ambient radiation field. We then derive some estimates of the expected contributions to the pre-recombinational signals coming from primordial helium in Sect. 4. Our main results are presented in Sect. 5, where we discuss a few simple cases (Sects. 5.1 and 5.2) to gain some level of understanding. We support our numerical computations by several analytic considerations in Sect. 5.1.1 and Appendix B. In Sect. 5.3, we then discuss the results for our 25 shell computations of hydrogen and He II. First we consider the dependence of the spectral distortions on the value of y (Sect. 5.3.1), where Figs. 5 and 6 play the main role. Then in Sects. 5.3.2 and 5.3.3, we investigate the dependence of the spectral distortions on the injection redshift and history, where we are particularly interested in changes in the low frequency variability of the signal (see Figs. 9 and 11). We present our conclusions in Sect. 6.
2 CMB spectral distortions after energy release
After any energy release in the Universe, the thermodynamic equilibrium between matter and radiation will in general be perturbed, and in particular, the distribution of photons will deviate from that of a pure blackbody. The combined action of Compton scattering, double Compton emission![]() (Lightman 1981; Pozdniakov et al. 1983; Thorne 1981, Chluba et al. 2007b), and bremsstrahlung
will attempt to restore full equilibrium, but, depending on the injection redshift, may not fully succeed. Using the approximate formulae given in Burigana et al. (1991b) and Hu & Silk (1993a), for the parameters within the concordance cosmological model (Bennett et al. 2003; Spergel et al. 2003), one can distinguish between the following cases for the residual CMB spectral distortions arising from a single energy injection,
(Lightman 1981; Pozdniakov et al. 1983; Thorne 1981, Chluba et al. 2007b), and bremsstrahlung
will attempt to restore full equilibrium, but, depending on the injection redshift, may not fully succeed. Using the approximate formulae given in Burigana et al. (1991b) and Hu & Silk (1993a), for the parameters within the concordance cosmological model (Bennett et al. 2003; Spergel et al. 2003), one can distinguish between the following cases for the residual CMB spectral distortions arising from a single energy injection,
![]() ,
at heating redshift
,
at heating redshift ![]() :
:
- (I)
-
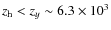 :
compton scattering is unable to establish full kinetic equilibrium of the photon distribution with the electrons. Photon-producing processes (mainly bremsstrahlung) can only restore a Planckian spectrum at very low frequencies. Heating results in a Compton y-distortion (Zeldovich & Sunyaev 1969) at high frequencies, as in the case of the thermal SZ effect, for y-parameter
:
compton scattering is unable to establish full kinetic equilibrium of the photon distribution with the electrons. Photon-producing processes (mainly bremsstrahlung) can only restore a Planckian spectrum at very low frequencies. Heating results in a Compton y-distortion (Zeldovich & Sunyaev 1969) at high frequencies, as in the case of the thermal SZ effect, for y-parameter
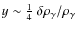 .
.
- (II)
-
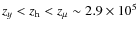 :
compton scattering can establish partial kinetic equilibrium of the photon distribution with the electrons. Photons produced at low frequencies (mainly by bremsstrahlung) diminish the spectral distortion close to their initial
frequency, but cannot strongly upscatter. The deviations from a blackbody represent a mixture of a y-distortion and a
:
compton scattering can establish partial kinetic equilibrium of the photon distribution with the electrons. Photons produced at low frequencies (mainly by bremsstrahlung) diminish the spectral distortion close to their initial
frequency, but cannot strongly upscatter. The deviations from a blackbody represent a mixture of a y-distortion and a  -distortion.
-distortion.
- (III)
-
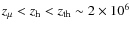 :
compton scattering can establish full kinetic equilibrium between the photon distribution and the electrons after a very short time. Low-frequency photons (mainly by double Compton emission) upscatter and slowly reduce the spectral distortion at high frequencies. The deviations from a blackbody can be described by a Bose-Einstein
distribution with a frequency-dependent chemical potential, which is constant at high and vanishes at low frequencies.
:
compton scattering can establish full kinetic equilibrium between the photon distribution and the electrons after a very short time. Low-frequency photons (mainly by double Compton emission) upscatter and slowly reduce the spectral distortion at high frequencies. The deviations from a blackbody can be described by a Bose-Einstein
distribution with a frequency-dependent chemical potential, which is constant at high and vanishes at low frequencies.
- (IV)
-
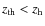 :
both Compton scattering and photon production processes are extremely efficient, restoring practically any spectral distortion caused by heating, eventually producing a pure blackbody spectrum with slightly higher temperature
:
both Compton scattering and photon production processes are extremely efficient, restoring practically any spectral distortion caused by heating, eventually producing a pure blackbody spectrum with slightly higher temperature
 than before the energy release.
than before the energy release.
2.1 Compton y-distortion
For energy release at low redshifts, the Compton process is no longer
able to establish full kinetic equilibrium between the CMB photons and electrons.
If the temperature of the radiation is lower than the temperature of the
electrons, photons are upscattered. For photons initially distributed
according to a blackbody spectrum of temperature
![]() ,
the efficiency of
this process is determined by the Compton y-parameter,
,
the efficiency of
this process is determined by the Compton y-parameter,
where
where
For computational reasons, it is convenient to introduce the frequency-dependent chemical potential produced by a y-distortion, which can be obtained with
where
2.1.1 Compton y-distortion from decaying particles
If all the energy is released at a single redshift,
![]() ,
then after a very short time a y-type distortion forms, where the y-parameter is approximately given by
,
then after a very short time a y-type distortion forms, where the y-parameter is approximately given by
![]() .
.
However, when the energy release is caused by decaying unstable particles of sufficiently long lifetimes, ![]() ,
then the CMB spectral distortion accumulates as a function of redshift. In this case, the fractional energy-injection rate is given by
,
then the CMB spectral distortion accumulates as a function of redshift. In this case, the fractional energy-injection rate is given by
![]() ,
so that the time-dependent y-parameter can be computed as
,
so that the time-dependent y-parameter can be computed as
where
3 Atomic transitions in a distorted ambient CMB radiation field
3.1 Bound-bound transitions
Using the occupation number of photons,
![]() ,
with frequency-dependent chemical potential
,
with frequency-dependent chemical potential ![]() ,
one can express the net rate connecting two bound atomic states i and j in the convenient form
,
one can express the net rate connecting two bound atomic states i and j in the convenient form
where pij is the Sobolev-escape probability (e.g., see Seager et al. 2000), Aij is the Einstein-A-coefficient of the transition
3.2 Free-bound transitions
For the free-bound transitions from the continuum to the bound atomic states i, one has
where
where
4 Expected contributions from helium
The number of helium nuclei is only ![]() of the number of hydrogen atoms in the Universe. Compared to the radiation released by hydrogen, one therefore naively expects a small addition of photons due to atomic transitions in helium. However, at a given frequency the photons due to He II have been released at redshifts about Z2=4 times higher than for hydrogen, when both the number density of particles and the temperature of the medium was higher. The expansion of the Universe then was also faster. As we show below, these circumstances make the contributions from helium comparable to those from hydrogen, where He II plays a far more important role than He I.
of the number of hydrogen atoms in the Universe. Compared to the radiation released by hydrogen, one therefore naively expects a small addition of photons due to atomic transitions in helium. However, at a given frequency the photons due to He II have been released at redshifts about Z2=4 times higher than for hydrogen, when both the number density of particles and the temperature of the medium was higher. The expansion of the Universe then was also faster. As we show below, these circumstances make the contributions from helium comparable to those from hydrogen, where He II plays a far more important role than He I.
4.1 Contributions due to He II
The speed at which atomic loops can be passed through is determined by the effective recombination rate to a given level i, since the bound-bound rates are always much faster. To estimate the contributions to the CMB spectral distortion by He II, we compute the change in the population of level i due to direct recombinations to that level over a very short time interval
![]() ,
i.e.
,
i.e.
![]() .
Since we consider the pre-recombinational epoch of helium, everything is completely ionized, so that
.
Since we consider the pre-recombinational epoch of helium, everything is completely ionized, so that
![]() .
.
Because all the bound-bound transition rates in He II are a factor of 16 higher than for hydrogen, the relative importance of the different channels to lower states should remain the same as in hydrogen![]() . Therefore, one can assume that the relative number of
photons, fij, emitted in the transition
. Therefore, one can assume that the relative number of
photons, fij, emitted in the transition
![]() per additional electron on the level i is similar to that for hydrogen at a factor of 4 lower redshift, i.e.,
per additional electron on the level i is similar to that for hydrogen at a factor of 4 lower redshift, i.e.,
![]() .
.
If we want to know how many of the emitted photons are observed in a fixed frequency interval ![]() today (
today (
![]() ), we must also consider that at higher redshift the expansion of the Universe is faster. Hence, the redshifting of photons by a given interval
), we must also consider that at higher redshift the expansion of the Universe is faster. Hence, the redshifting of photons by a given interval
![]() is accomplished in a shorter time interval. For a given transition, these are related by
is accomplished in a shorter time interval. For a given transition, these are related by
![]() ,
where
,
where ![]() is the transition frequency and
is the transition frequency and
![]() the redshift of emission. Here it is important that
the redshift of emission. Here it is important that
![]() .
Then the change in the number of photons produced by emission in the transition
.
Then the change in the number of photons produced by emission in the transition
![]() today should be proportional to
today should be proportional to
where
For hydrogenic atoms with charge Z the recombination rate (including stimulated recombination) within the ambient CMB blackbody, scales as (Kaplan & Pikelner 1970)
where
This estimate shows that prior to the epoch of
![]() recombination the release of photons by helium should be by a factor of
recombination the release of photons by helium should be by a factor of ![]() higher than hydrogen at about 4 times lower redshift! Therefore, one expects that at a given frequency in the Rayleigh-Jeans part of the CMB blackbody, the pre-recombinational emission originating in He II is already comparable to the contributions from hydrogen. As we show below (see Sect. 5.3.1), this is in good agreement with the results of our numerical calculations.
higher than hydrogen at about 4 times lower redshift! Therefore, one expects that at a given frequency in the Rayleigh-Jeans part of the CMB blackbody, the pre-recombinational emission originating in He II is already comparable to the contributions from hydrogen. As we show below (see Sect. 5.3.1), this is in good agreement with the results of our numerical calculations.
4.2 Contributions due to He I
In the case of neutral helium, the highly excited levels are basically hydrogenic. Therefore, one does not expect any amplification of the emission within loops prior to its recombination epoch.
Furthermore, the total period during which neutral helium can contribute significantly is limited to the redshift range starting at the end of
![]() recombination, say
recombination, say
![]() .
Therefore, neutral helium is typically inactive over a wide range of redshifts.
.
Therefore, neutral helium is typically inactive over a wide range of redshifts.
Still there could be some interesting features appearing in connection with the fine-structure transitions, which even within the standard computations lead to strong negative features in the He I recombination spectrum (Rubiño-Martín et al. 2008). The spectrum of neutral helium, especially at high frequencies, is also more complicated than for hydrogenic atoms, so that some non-trivial features might arise. We leave this problem to future work, and focus on the contributions of hydrogen and He II.
5 Results for intrinsic y-type CMB distortions
Here we discuss the results for the changes in the recombination spectra of hydrogen and He II for different values of the y-parameter. We use a modified version of the code developed for computations of the standard recombination spectrum (Chluba et al. 2007a; Rubiño-Martín et al. 2006), and numerically solve the pre-recombinational problem in the presence of an intrinsic y-distortion. Some of the computational details and the formulation of this problem can be found in Appendix A.
5.1 The 2 shell atom
To understand the properties of the numerical solution and also to check the correctness of our computations, we first considered the problem including only a small number of
shells. If we take 2 shells into account, we deal with only a few atomic transitions, namely the Lyman- and Balmer-continuum, and the Lyman-![]() line. In addition, one expects that during the recombination epoch of the considered atomic species (here H I or He II) the
2s-1s-two-photon decay channel will also contribute, but very little before that time.
line. In addition, one expects that during the recombination epoch of the considered atomic species (here H I or He II) the
2s-1s-two-photon decay channel will also contribute, but very little before that time.
In Fig. 1, we show the spectral distortion,
![]() ,
including 2 shells in our computations for different transitions as a function of redshift
,
including 2 shells in our computations for different transitions as a function of redshift![]() . It was assumed that energy was released in a single injection at
zi=50 000, producing y=10-5. All shown curves were computed using the
. It was assumed that energy was released in a single injection at
zi=50 000, producing y=10-5. All shown curves were computed using the ![]() -function approximation for the line-profiles (Kholupenko et al. 2005; Rubiño-Martín et al. 2006; Wong et al. 2006), in which the distortion is given by
-function approximation for the line-profiles (Kholupenko et al. 2005; Rubiño-Martín et al. 2006; Wong et al. 2006), in which the distortion is given by
![]() ,
where
,
where
![]() is the net rate of the transition
is the net rate of the transition
![]() .
This approximation is insufficient when one is interested in computing the true spectral distortions in frequency space, since for the free-bound contribution the recombinational lines are very broad (e.g., see Chluba & Sunyaev 2006). In addition, one should include the line-broadening due to electron scattering as explained in Appendix A.4 and the correct mapping from
.
This approximation is insufficient when one is interested in computing the true spectral distortions in frequency space, since for the free-bound contribution the recombinational lines are very broad (e.g., see Chluba & Sunyaev 2006). In addition, one should include the line-broadening due to electron scattering as explained in Appendix A.4 and the correct mapping from
![]() .
.
We note that in the ![]() -function approximation for the line profiles one has
-function approximation for the line profiles one has
![]() ,
where f(z) depends only on redshift and not on the considered transition. Therefore, considering
,
where f(z) depends only on redshift and not on the considered transition. Therefore, considering
![]() is a convenient way of studying the redshift dependence of the net rates between different levels.
is a convenient way of studying the redshift dependence of the net rates between different levels.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f1a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{eps/9840f1b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg129.png) |
Figure 1:
Spectral distortion,
|
| Open with DEXTER | |
Looking at Fig. 1, one can see that prior to the recombination epoch of the considered species one can find pre-recombinational emission and absorption in the Lyman- and
Balmer-continuum, and the Lyman-![]() line, which would be completely absent for y=0. As expected, during the pre-recombinational epochs the 2s-1s-two-photon transition is not important. This is because the 2s-1s transition is simply unable to compete with the
line, which would be completely absent for y=0. As expected, during the pre-recombinational epochs the 2s-1s-two-photon transition is not important. This is because the 2s-1s transition is simply unable to compete with the
![]() times faster Lyman-
times faster Lyman-![]() transition while the latter remains optically thin.
transition while the latter remains optically thin.
Summing the spectral distortions caused by the continua, one finds cancellation of the redshift-dependent emission at a level close to our numerical accuracy (relative accuracy
![]() for the spectrum). This is expected because of electron number conservation: in the pre-recombinational epoch the overall ionization state of the plasma is not affected significantly by the small deviations of the background radiation from full equilibrium. Therefore, all electrons
that enter an atomic species will leave it again, in general via another route to the continuum.
This implies that
for the spectrum). This is expected because of electron number conservation: in the pre-recombinational epoch the overall ionization state of the plasma is not affected significantly by the small deviations of the background radiation from full equilibrium. Therefore, all electrons
that enter an atomic species will leave it again, in general via another route to the continuum.
This implies that
![]() ,
which is a general property of the solution in the pre-recombinational epoch. This can also be concluded from Fig. 1, since in the
,
which is a general property of the solution in the pre-recombinational epoch. This can also be concluded from Fig. 1, since in the ![]() -function representation the Balmer-continuum line prior to the recombination epoch cancels the Lyman-continuum line at each redshift.
-function representation the Balmer-continuum line prior to the recombination epoch cancels the Lyman-continuum line at each redshift.
If we look at the Lyman- and Balmer-continuum in the case of hydrogen, we can see that at redshifts
![]() ,
electrons enter by the Lyman-continuum, and leave by the Balmer-continuum, while
in the redshift range
,
electrons enter by the Lyman-continuum, and leave by the Balmer-continuum, while
in the redshift range
![]() the opposite is true (see Sect. 5.1.1 for a detailed explanation). As expected, for
the opposite is true (see Sect. 5.1.1 for a detailed explanation). As expected, for ![]() the Lyman-
the Lyman-![]() transition exactly follows the Balmer-continuum, since every electron that enters the 2p-state and then reaches the ground level, also must pass through the Lyman-
transition exactly follows the Balmer-continuum, since every electron that enters the 2p-state and then reaches the ground level, also must pass through the Lyman-![]() transition. Using the analytic solution for the Lyman-
transition. Using the analytic solution for the Lyman-![]() line given in the
Appendix B, we find excellent agreement with the numerical results until the true recombination epoch is entered at
line given in the
Appendix B, we find excellent agreement with the numerical results until the true recombination epoch is entered at ![]() .
.
In the case of He II for the considered range of redshifts, the pre-recombinational emission (![]() )
is always generated in the loop
)
is always generated in the loop
![]() .
We again find excellent agreement with the analytic solution for the Lyman-
.
We again find excellent agreement with the analytic solution for the Lyman-![]() line. We note that for He II the total emission in the pre-recombinational epoch is much higher than in the recombination epoch at
line. We note that for He II the total emission in the pre-recombinational epoch is much higher than in the recombination epoch at
![]() (see discussion in
Sect. 4). The height of the maximum is even comparable to the H I Lyman-
(see discussion in
Sect. 4). The height of the maximum is even comparable to the H I Lyman-![]() line.
line.
As one can see in Fig. 1, at high redshift all transitions become weaker. This because the rest-frame frequencies of all lines are in the Rayleigh-Jeans part of the CMB spectrum, where the effective chemical potential of the y-distortion (see Sect. 2.1) decreases as![]()
![]() .
This implies that at higher redshift all transitions are more and more within a pure blackbody ambient radiation field. On the other hand, the effective chemical potential increases towards lower redshift, so that also the strength of the transitions increases. However, at
.
This implies that at higher redshift all transitions are more and more within a pure blackbody ambient radiation field. On the other hand, the effective chemical potential increases towards lower redshift, so that also the strength of the transitions increases. However, at ![]() in the case of hydrogen, and
in the case of hydrogen, and
![]() for He II, the escape probability in the Lyman-continuum (see Appendix A.1 and Eq. (B.3) for quantitative estimates) begins to decrease significantly, so that the pre-recombinational transitions cease. For a 2-shell atom this is because, the only loop that can operate is via the Lyman-continuum. The maximum in the pre-recombinational Lyman-
for He II, the escape probability in the Lyman-continuum (see Appendix A.1 and Eq. (B.3) for quantitative estimates) begins to decrease significantly, so that the pre-recombinational transitions cease. For a 2-shell atom this is because, the only loop that can operate is via the Lyman-continuum. The maximum in the pre-recombinational Lyman-![]() line forms because of this rather sharp transition to the optically thick region of the
Lyman-continuum (see also Sect. 5.1.1 for more details).
line forms because of this rather sharp transition to the optically thick region of the
Lyman-continuum (see also Sect. 5.1.1 for more details).
5.1.1 Analytic description of the pre-recombinational Lyman- line
line
One can understand the behavior of the numerical solution for the spectral distortions in more detail using our analytic description of the Lyman-![]() line given in Appendix B.
line given in Appendix B.
In Fig. 2, we show the comparison of different analytic approximations with the full numerical result. The curves labeled ``analytic Ia'' (dotted line) and ``analytic Ib'' (boxes) are both based on the formulae in Eqs. (B.2) and (B.7). In their derivation, we assumed that the population of the 2p-state evolves under quasi-stationary conditions, where the free electron fraction and proton number density are given by the R ECFAST-solution. For the approximation ``analytic Ia'', we did not include the escape probabilities in the H I Lyman-![]() line and H I Lyman-continuum, while the approximation ``analytic Ib'' also includes the escape probabilities described in Appendix B.1.1. A comparison of these curves indicates that for the shape of the distortion at
line and H I Lyman-continuum, while the approximation ``analytic Ib'' also includes the escape probabilities described in Appendix B.1.1. A comparison of these curves indicates that for the shape of the distortion at ![]() ,
the escape probabilities are very important. However, although at this redshift the Sobolev optical depth in the H I Lyman-
,
the escape probabilities are very important. However, although at this redshift the Sobolev optical depth in the H I Lyman-![]() line is roughly a factor of 14 higher than the optical depth in the H I Lyman-continuum, the derivation of
Eq. (B.8) shows that the H I Lyman-
line is roughly a factor of 14 higher than the optical depth in the H I Lyman-continuum, the derivation of
Eq. (B.8) shows that the H I Lyman-![]() escape probability plays only a secondary role in the pre-recombinational era.
escape probability plays only a secondary role in the pre-recombinational era.
Given the formulae in Appendix B.1.2, the spectral distortion can be written in the form
![]() .
The factor F(z) describes the normalization of the line (see Eq. (B.8)), also including the effect of the escape probabilities in the H I Lyman-
.
The factor F(z) describes the normalization of the line (see Eq. (B.8)), also including the effect of the escape probabilities in the H I Lyman-![]() line and continuum. One does not expect a strong change in the line shape when using simple equilibrium values in its evaluation. For simplicity, we assume below that F is given by Eq. (B.10), which should be accurate to a level of
line and continuum. One does not expect a strong change in the line shape when using simple equilibrium values in its evaluation. For simplicity, we assume below that F is given by Eq. (B.10), which should be accurate to a level of
![]() for the considered redshift range.
for the considered redshift range.
The term, ![]() ,
which is related to the imbalance of emission and absorption, should allow us to understand when and why the Lyman-
,
which is related to the imbalance of emission and absorption, should allow us to understand when and why the Lyman-![]() line becomes negative. In the most radical approximation (see Appendix B.1.2 for details), one can use
line becomes negative. In the most radical approximation (see Appendix B.1.2 for details), one can use
![]() ,
as derived in Eq. (B.14b), so that we obtain the curve labeled ``analytic II''. One can clearly see that this approximation represents the global behavior, but fails to explain the Lyman-
,
as derived in Eq. (B.14b), so that we obtain the curve labeled ``analytic II''. One can clearly see that this approximation represents the global behavior, but fails to explain the Lyman-![]() absorption at
absorption at
![]() .
For this approximation, the Lyman-
.
For this approximation, the Lyman-![]() line should always be in emission, even at high redshift, since
with
line should always be in emission, even at high redshift, since
with
![]() in the limit of small x, we have
in the limit of small x, we have
![]() .
This approximation indicates that to lowest order the main reason for emission in the Lyman-
.
This approximation indicates that to lowest order the main reason for emission in the Lyman-![]() line is the deviation of the effective chemical potential from zero at the Lyman-
line is the deviation of the effective chemical potential from zero at the Lyman-![]() resonance, and the Lyman- and Balmer-continuum frequency.
resonance, and the Lyman- and Balmer-continuum frequency.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f2.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg150.png) |
Figure 2:
Analytic representation of the pre-recombinational H I Lyman- |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f3a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{eps/9840f3b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg151.png) |
Figure 3:
Spectral distortion,
|
| Open with DEXTER | |
If we also account for the higher order terms of the line imbalance ![]() according to Eq. (B.16a), then we obtain the curve labeled ``analytic III'', which is close to the full solution and also reproduces its high redshift behavior, starting at a slightly higher
redshift (
according to Eq. (B.16a), then we obtain the curve labeled ``analytic III'', which is close to the full solution and also reproduces its high redshift behavior, starting at a slightly higher
redshift (
![]() instead of
instead of
![]() ). This is mainly caused by the approximations in the integrals (B.15) over the photoionization cross-sections (in particular M-1). However, if one evaluates these integrals more accurately, one does not recover the full solution exactly, since the free-bound Gaunt-factors are neglected; only when these factors are included and we evaluate the factor F correctly can we again obtain the full numerical result.
). This is mainly caused by the approximations in the integrals (B.15) over the photoionization cross-sections (in particular M-1). However, if one evaluates these integrals more accurately, one does not recover the full solution exactly, since the free-bound Gaunt-factors are neglected; only when these factors are included and we evaluate the factor F correctly can we again obtain the full numerical result.
5.2 The 3-shell atom
If one considers 3 shells, the situation becomes more complicated, since more loops connecting to the continuum are possible. Looking at Fig. 3, again we find that the sum over all
transition in the continua vanishes at redshifts prior to the true recombination epoch of the considered species. At ![]() in the case of hydrogen and
in the case of hydrogen and
![]() for He II, the escape probability in the Lyman-continuum becomes small. For 2 shells, this stopped the pre-recombinational emission until the true recombination epoch of the considered atomic species was entered (see Fig. 1). However, for 3 shells electrons can leave the 1s-level via the
Lyman-
for He II, the escape probability in the Lyman-continuum becomes small. For 2 shells, this stopped the pre-recombinational emission until the true recombination epoch of the considered atomic species was entered (see Fig. 1). However, for 3 shells electrons can leave the 1s-level via the
Lyman-![]() transition, and reach the continuum through the Balmer-continuum. For both hydrogen and He II, one can also see that the emission in the Lyman-
transition, and reach the continuum through the Balmer-continuum. For both hydrogen and He II, one can also see that the emission in the Lyman-![]() line stops completely when the Lyman-continuum is fully blocked. In this situation, only the loop
line stops completely when the Lyman-continuum is fully blocked. In this situation, only the loop
![]() via the Balmer-continuum operates. Only when the main recombinational epoch of the considered species is entered, is the Lyman-
via the Balmer-continuum operates. Only when the main recombinational epoch of the considered species is entered, is the Lyman-![]() line reactivated.
line reactivated.
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{eps/9840f4a.eps}\hspace*{3mm}
\includegraphics[width=4.3cm,clip]{eps/9840f4b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg156.png) |
Figure 4: Sketch of the main atomic loops for hydrogen and He II when including 3 shells. The left panel shows the loops for transitions that are terminating in the Lyman-continuum. The right panel shows the case, when the Lyman-continuum is completely blocked, and unbalanced transitions are terminating in the Balmer-continuum instead. |
| Open with DEXTER | |
In Fig. 4, we sketch the main atomic loops in hydrogen and He II when including 3 shells. For y=10-5, in the case of hydrogen the illustrated Lyman-continuum loops work in the redshift range
![]() ,
while the Balmer-continuum loop works for
,
while the Balmer-continuum loop works for
![]() .
In the case of He II, one finds that
.
In the case of He II, one finds that
![]() and
and
![]() for the Lyman- and Balmer-continuum loops, respectively. It is clear that in every closed loop, one energetic photons is destroyed and at least two photons are generated at lower frequencies. Including more shells will open the possibility of generating more photons per loop, simply because electrons can enter through highly excited levels and then preferentially cascade to the lowest shells via several intermediate levels, leaving the atomic species taking the fastest available route back to the continuum. We discuss this situation below in more detail (see
Sect. 5.3.1).
for the Lyman- and Balmer-continuum loops, respectively. It is clear that in every closed loop, one energetic photons is destroyed and at least two photons are generated at lower frequencies. Including more shells will open the possibility of generating more photons per loop, simply because electrons can enter through highly excited levels and then preferentially cascade to the lowest shells via several intermediate levels, leaving the atomic species taking the fastest available route back to the continuum. We discuss this situation below in more detail (see
Sect. 5.3.1).
Figures 1 and 3 both show that the pre-recombinational lines are emitted in a typical redshift range
![]() ,
while the signals from the considered recombinational epoch are released within
,
while the signals from the considered recombinational epoch are released within
![]() .
For the pre-recombinational signal, the expected line-width is
.
For the pre-recombinational signal, the expected line-width is
![]() .
However, the overlap of several lines, especially at frequencies where emission and absorption features nearly coincide, and the asymmetry of the pre-recombinational line profiles, still leads to more narrow spectral features with
.
However, the overlap of several lines, especially at frequencies where emission and absorption features nearly coincide, and the asymmetry of the pre-recombinational line profiles, still leads to more narrow spectral features with
![]() (see Sect. 5.3, Fig. 6).
(see Sect. 5.3, Fig. 6).
We also note that in all cases the true recombination epoch is not affected significantly by the small y-distortion in the ambient photon field. There the deviations from Saha-equilibrium because of the recombination dynamics dominate over those directly related to the spectral distortion, and in particular the changes in the ionization history are tiny.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f5a.eps}\includegr...
...eps/9840f5e.eps}\includegraphics[width=8.8cm,clip]{eps/9840f5f.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg164.png) |
Figure 5:
Contributions to the H I ( left panels) and He II ( right panels) recombination spectrum for different values of the initial y-parameter. Energy injection was assumed to occur at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f6a.eps}\includegr...
...eps/9840f6e.eps}\includegraphics[width=8.8cm,clip]{eps/9840f6f.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg165.png) |
Figure 6: Main contributions to the H I ( left panels) and He II ( right panels) spectral distortion at different frequencies for energy injection at zi=40 000 and y=10-5. We have also marked those peaks coming (mainly) from the recombination epoch (``rec'') and from the pre-recombination epoch (``pre'') of the considered atomic species. Note that the 2s-1s-two-photon decay contribution is not shown, since it does not lead to any significant pre-recombinational signal. |
| Open with DEXTER | |
5.3 The 25-shell atom
In this section, we discuss the results for our 25-shell computations. Given the large amount of transitions, it is more efficient to look directly at the spectral distortion as a function of frequency. However, following the approach of Sect. 5.1, we checked that the basic properties of the first few lines and continua as a function of redshift qualitatively do not change in comparison to the previous cases. In particular, only the Lyman- and Balmer-continuum become strongly negative, again for similar redshift ranges as for 2 or 3 shells. In overall absorption, the other continua (n>2) play no important role, although about 10% of all loops do end there (see Sect. 5.3.1 for more details).
We note that for the spectral distortion now the impact of electron scattering must be considered and the free-bound contribution must be computed using the full differential, photoionization cross-section (see Appendix A.4).
5.3.1 Dependence of the distortion on the value of y
In Fig. 5, we show the contributions to the recombination spectrum for different values of the initial y-parameter. In addition, Fig. 6 shows some of the main contributions to the total hydrogen and He II spectral distortion in more detail.
Bound-bound transitions
Focusing first on the contributions of bound-bound transitions, one can see that the standard recombination signal due to hydrogen is not strongly affected when y=10-7, whereas the helium signal already changed notably. Increasing the value of y in both cases leads to an increase in the overall amplitude of the distortion at low frequencies, and a large rise in the emission and variability at
![]() GHz. For H I at low frequencies, the level of the signal increased roughly by a factor of 5 when increasing the value of y from 0 to 10-5, while for He II the increase is about a factor of 40. This indicates that in the pre-recombinational epoch He II indeed behaves in a way similar to hydrogen, but with an amplification
GHz. For H I at low frequencies, the level of the signal increased roughly by a factor of 5 when increasing the value of y from 0 to 10-5, while for He II the increase is about a factor of 40. This indicates that in the pre-recombinational epoch He II indeed behaves in a way similar to hydrogen, but with an amplification
![]() (see Sect. 4).
(see Sect. 4).
At high frequencies, a strong emission-absorption feature appears in the range
![]() GHz, which is completely absent for y=0. For y=10-5 from peak to peak, this feature exceeds the normal Lyman-
GHz, which is completely absent for y=0. For y=10-5 from peak to peak, this feature exceeds the normal Lyman-![]() distortion (close to
distortion (close to
![]() GHz for H I
and
GHz for H I
and
![]() GHz for He II) by a factor of
GHz for He II) by a factor of ![]() for H I, and about 30 for He II. The absorption part is caused mainly by the pre-recombinational Lyman-
for H I, and about 30 for He II. The absorption part is caused mainly by the pre-recombinational Lyman-![]() ,
-
,
-![]() ,
and -
,
and -![]() transitions, while the emission part is dominated by the pre-recombinational emission in the Lyman-
transitions, while the emission part is dominated by the pre-recombinational emission in the Lyman-![]() line (also see Fig. 6 for more detail).
line (also see Fig. 6 for more detail).
We note that in the case of He II most of the recombinational Lyman-![]() emission (
emission (
![]() GHz) is completely wiped out by the pre-recombinational absorption in the higher Lyman-series, while for H I only a small part of the Lyman-
GHz) is completely wiped out by the pre-recombinational absorption in the higher Lyman-series, while for H I only a small part of the Lyman-![]() low frequency wing is affected. This is possible only because the pre-recombinational emission in the He II Lyman-series is so strongly enhanced, compared to the signal produced during the recombinational epoch.
low frequency wing is affected. This is possible only because the pre-recombinational emission in the He II Lyman-series is so strongly enhanced, compared to the signal produced during the recombinational epoch.
Free-bound transitions
Considering the free-bound contributions, one can again see that the hydrogen signal changes much less with increasing value of y than in the case of He II. In both cases, the variability in the free-bound signal decreases at low frequencies, while at high frequencies a strong and broad
absorption feature appears, which is mainly due to the Lyman-continuum. For y=10-5, this absorption feature even completely erases the Balmer-continuum contribution appearing during the true recombination epoch of the considered species. It is 2 times stronger than the H I Lyman-![]() line from the recombination epoch, and in the case of He II it exceeds the normal He II Lyman-
line from the recombination epoch, and in the case of He II it exceeds the normal He II Lyman-![]() line by more than one order of magnitude.
line by more than one order of magnitude.
However, apart from the absorption feature at high frequencies the free-bound contribution becomes practically featureless when reaching y=10-5. This is because of the strong overlap of different lines from the high redshift part, since the characteristic width of the recombinational emission increases as
![]() (see middle panels in
Fig. 5). In addition, the photons are released in a broader range of redshifts (see Sects. 5.1 and 5.2), leading to a decrease in the contrast between the spectral features from the recombinational epoch.
(see middle panels in
Fig. 5). In addition, the photons are released in a broader range of redshifts (see Sects. 5.1 and 5.2), leading to a decrease in the contrast between the spectral features from the recombinational epoch.
Total distortion
In the total spectra (see lower panels in Fig. 5), one can also clearly see a strong absorption feature at high frequencies, which is mainly associated with the Lyman-continuum and Lyman-series for n>2 (see Fig. 6 also). For y=10-5, in the case of hydrogen it exceeds the Lyman-![]() line from recombination (
line from recombination (
![]() GHz) by a factor of
GHz) by a factor of ![]() at
at
![]() GHz, while for He II it is even stronger by a factor of
GHz, while for He II it is even stronger by a factor of ![]() ,
reaching
,
reaching
![]() of the corresponding hydrogen feature. Checking the level
of emission at low frequencies, as expected (see Sect. 4), one can find that He II indeed contributes about 2/3 to the total level of emission.
of the corresponding hydrogen feature. Checking the level
of emission at low frequencies, as expected (see Sect. 4), one can find that He II indeed contributes about 2/3 to the total level of emission.
As illustrated in the upper panels of Fig. 6, the emission-absorption feature at high frequencies is caused by the overlap between the pre-recombinational Lyman-![]() line (emission) and the combination of the higher pre-recombinational Lyman-series and Lyman-continuum (absorption). At intermediate frequencies (middle panels), the main spectral features are due to the Balmer-
line (emission) and the combination of the higher pre-recombinational Lyman-series and Lyman-continuum (absorption). At intermediate frequencies (middle panels), the main spectral features are due to the Balmer-![]() ,
the pre-recombinational Balmer-series from n>3, and the Paschen-
,
the pre-recombinational Balmer-series from n>3, and the Paschen-![]() transition, with some additional broad contributions to the overall amplitude of the bump originating in higher continua.
transition, with some additional broad contributions to the overall amplitude of the bump originating in higher continua.
The lower panels of Fig. 6 show, as an example, the separate contributions to the bound-bound series for the 10th shell. One can notice that for hydrogen the recombinational and pre-recombinational emission are of similar amplitude, while for He II the pre-recombinational signal is more than one order of magnitude stronger (see Sect. 4 for an explanation). In both cases, the pre-recombinational emission is much broader than the recombinational signal, again mainly due to the time-dependence of the photon emission process (see Sects. 5.1 and 5.2), but to some extent also because of electron scattering.
Number of additional photons and loops
Using the free-bound spectrum, one can also estimate the effective number of loops![]() ,
,
![]() ,
involved in the production of all photons seen as additional CMB spectral distortion. The easiest way to compute this number is to consider the free-bound spectrum of each level using the
,
involved in the production of all photons seen as additional CMB spectral distortion. The easiest way to compute this number is to consider the free-bound spectrum of each level using the ![]() -function approximation. In
this way, one avoids the overlap between the emission and absorption contributions at different redshifts, which would lead to a small underestimation of
-function approximation. In
this way, one avoids the overlap between the emission and absorption contributions at different redshifts, which would lead to a small underestimation of
![]() .
In the case of full equilibrium, one should find that
.
In the case of full equilibrium, one should find that
![]() .
.
By computing the number of photons that can be seen as overall free-bound emission, one obtains the number of times an electron has entered an uncompensated loop via the considered level. On the other hand, by computing the number of photons that can be seen as overall bound-free absorption, one can determine the number of times that an uncompensated transition ended at that level. By evaluating the sum over the number of photons that can be seen as overall free-bound emission from all levels, one should find
![]() photons per nucleus. Similarly, the total number of photons absorbed in all bound-free transitions should be
photons per nucleus. Similarly, the total number of photons absorbed in all bound-free transitions should be
![]() photons per nucleus. The difference of
photons per nucleus. The difference of
![]() per nucleus is due the fact that at the end of the recombinational epoch of each atomic species
practically all electrons have been captured, without returning to the continuum afterwards.
In a similar way, one can also identify the partial contribution of each continuum.
per nucleus is due the fact that at the end of the recombinational epoch of each atomic species
practically all electrons have been captured, without returning to the continuum afterwards.
In a similar way, one can also identify the partial contribution of each continuum.
In Table 1, we provide a few examples, comparing also with the number of photons emitted for y=0. One can see that the effective number of loops per nucleus varies roughly in proportion to the values of y, i.e.,
![]()
![]() [y/10-5] and
[y/10-5] and
![]()
![]() [y/10-5]. If one considers a lower injection redshift, the proportionality constant should decrease, since the loops will be active over a shorter period. When also including more shells,
[y/10-5]. If one considers a lower injection redshift, the proportionality constant should decrease, since the loops will be active over a shorter period. When also including more shells,
![]() should increase because there are more channels through which the electrons can enter the atoms. Furthermore, the effective number of loops per nucleus is about one order of magnitude larger for He II than for hydrogen. As explained in Sect. 4, this is caused by the amplification of transitions for hydrogenic helium at high redshift.
should increase because there are more channels through which the electrons can enter the atoms. Furthermore, the effective number of loops per nucleus is about one order of magnitude larger for He II than for hydrogen. As explained in Sect. 4, this is caused by the amplification of transitions for hydrogenic helium at high redshift.
When comparing with the number of photons absorbed in the Lyman-continuum, one can also see that in practically all shown cases
![]() of all loops should end there. By computing this more carefully for hydrogen assuming y=10-5, we found that
of all loops should end there. By computing this more carefully for hydrogen assuming y=10-5, we found that
![]() of the pre-recombinational loops end in the Lyman-continuum, about
of the pre-recombinational loops end in the Lyman-continuum, about ![]() in the Balmer-continuum,
in the Balmer-continuum,
![]() in the Paschen-continuum, and the remaining
in the Paschen-continuum, and the remaining
![]() is distributed more or less evenly over all the other continua, with no strong drop toward higher shells. For helium, we found similar numbers.
is distributed more or less evenly over all the other continua, with no strong drop toward higher shells. For helium, we found similar numbers.
Table 1:
Approximate number of photons and loops per nucleus of the considered species for
![]() and different values of y.
and different values of y.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f7a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{eps/9840f7b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg196.png) |
Figure 7: H I ( upper panel) and He II ( lower panel) recombination spectra for different energy injection redshifts. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f8a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{eps/9840f8b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg197.png) |
Figure 8: Total H I + He II recombination spectra for different energy injection redshifts. The upper panel shows details of the spectrum at low, the lower at high frequencies. |
| Open with DEXTER | |
If we considered the total number of photons per nucleus emitted in the bound-bound transitions and subtracted the number of photons emitted for y=0, we were able to estimate the loop-efficiency,
![]() ,
or number of bound-bound photons generated per loop prior to the recombination epoch. For hydrogen, one finds
,
or number of bound-bound photons generated per loop prior to the recombination epoch. For hydrogen, one finds
![]() ,
while for He II one has
,
while for He II one has
![]() .
Similarly, one obtains a loop efficiency of
.
Similarly, one obtains a loop efficiency of
![]() for both the H I and He II Lyman-
for both the H I and He II Lyman-![]() lines. As expected these numbers are rather independent of the value of y, since they should reflect an atomic property. They should also be rather independent of the injection redshift, which mainly affects the total number of loops and thereby the total number of emitted photons. However, the loop efficiency should still increase when including more shells in the computation.
lines. As expected these numbers are rather independent of the value of y, since they should reflect an atomic property. They should also be rather independent of the injection redshift, which mainly affects the total number of loops and thereby the total number of emitted photons. However, the loop efficiency should still increase when including more shells in the computation.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f9a.eps}\includegr...
...eps/9840f9c.eps}\includegraphics[width=8.8cm,clip]{eps/9840f9d.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg202.png) |
Figure 9:
Comparison of the variable component in the H I + He II bound-bound and free-bound recombination spectra for single energy injection at different redshifts. In all cases the computations were performed including 25 shells and y=10-5. The blue dashed curve in all panel shows the variability in the normal H I + He II recombination spectrum (equivalent to energy injection below |
| Open with DEXTER | |
5.3.2 Dependence of the distortion on the redshift of energy injection
To understand how the pre-recombinational emission depends on the redshift at which the energy was released, in Fig. 7 we show a compilation of different cases for the total H I and He II signal. In Fig. 8, we also present the sum of both in more detail.
Features at high frequencies
For all shown cases, the absolute changes in the curves are strongest at high frequencies (
![]() GHz). One can also identify a rather broad bump at
GHz). One can also identify a rather broad bump at
![]() ,
followed by an emission-absorption feature in the frequency range
,
followed by an emission-absorption feature in the frequency range
![]() .
In particular the strength and position of this emission-absorption feature depends strongly on the redshift of energy injection.
.
In particular the strength and position of this emission-absorption feature depends strongly on the redshift of energy injection.
For the broad high-frequency signature, it is more important that the variability itself varies, rather than the overall amplitude increases. For example, in the frequency range
![]() ,
the normal recombinational signal has
,
the normal recombinational signal has ![]() spectral features, while for injection at
spectral features, while for injection at
![]() approximately 4 features are visible, which in this case only come from hydrogen because at
approximately 4 features are visible, which in this case only come from hydrogen because at
![]() He II is already completely recombined. We also note that neutral helium should add some signal, which was not included here. Nevertheless, we expect that this contribution is not strongly amplified as in the case of He II (see Sect. 4), and hence should not increase the total signal by more than
He II is already completely recombined. We also note that neutral helium should add some signal, which was not included here. Nevertheless, we expect that this contribution is not strongly amplified as in the case of He II (see Sect. 4), and hence should not increase the total signal by more than ![]() .
.
Variability at low frequencies
Focusing on the spectral distortions at low frequencies, the overall level of the distortion in general increases for higher redshifts of energy release. However, there is also some change in the variability of the spectral distortions. To study this variability in more detail, in each case we performed a smooth spline fit of the total H I + He II recombination spectrum and then subtracted this curve from the total spectrum. The remaining modulation of the CMB intensity was then converted into variations in the CMB brightness temperature using the relation
![]() ,
where
,
where ![]() is the blackbody intensity at temperature T0=2.725 K.
is the blackbody intensity at temperature T0=2.725 K.
Figure 9 shows the results of this procedure in several cases. It is most striking that the amplitude of the variable component decreases with increasing energy injection redshift. This can be understood as follows: we have seen in Sects. 5.1 and 5.2 that for very early energy injection most of the pre-recombinational emission is expected to be produced at
![]() for hydrogen, and
for hydrogen, and
![]() for helium,
(i.e., the redshifts at which the Lyman-continuum of the considered atomic species becomes optically thick) with a typical line-width
for helium,
(i.e., the redshifts at which the Lyman-continuum of the considered atomic species becomes optically thick) with a typical line-width
![]() .
In this case, the total variability of the signal is mainly due to the non-trivial superposition of many broad neighboring spectral features.
Most importantly, little variability will be added by the high redshift wing of the pre-recombinational lines and in particular the beginning of the injection process. This is because (i) at high z the emission is much smaller (cf. Figs. 1 and 3); and (ii) electron scattering broadens lines significantly, smoothing any broad feature even more (see Appendix A.4).
.
In this case, the total variability of the signal is mainly due to the non-trivial superposition of many broad neighboring spectral features.
Most importantly, little variability will be added by the high redshift wing of the pre-recombinational lines and in particular the beginning of the injection process. This is because (i) at high z the emission is much smaller (cf. Figs. 1 and 3); and (ii) electron scattering broadens lines significantly, smoothing any broad feature even more (see Appendix A.4).
On the other hand, when the energy injection occurs at lower redshift, this increases the variability of the signal because (i) electron scattering in the case of single momentary energy release does not smooth the step-like feature due to the beginning of the injection process as strongly; and (ii) the total emission amplitude and hence the step-like feature increases (see Figs. 1 and 3). When the injection occurs close to the redshift at which the Lyman-continuum is optically thick (see Sect. 5.1), i.e., where the pre-recombinational emission has an extremum, this should produce a strong increase in the variability. On the other hand, for energy injection well before this epoch the atomic transitions produce an increase in the overall amplitude of the distortions rather than the variability.
This can also be seen in Fig. 9, where for zi=4000 the variable component is
![]() times larger than the normal recombinational signal with a peak-to-peak amplitude of
times larger than the normal recombinational signal with a peak-to-peak amplitude of
![]() nK instead of
nK instead of
![]() nK at frequencies around
nK at frequencies around ![]() GHz. Even for
GHz. Even for
![]() ,
the amplitude of the variable component is still 1.5-2 times larger than in the case of standard recombination, but it practically does not change anymore when going to higher injection redshifts. For
,
the amplitude of the variable component is still 1.5-2 times larger than in the case of standard recombination, but it practically does not change anymore when going to higher injection redshifts. For
![]() ,
one expects a similarly strong increase in the variability as for
,
one expects a similarly strong increase in the variability as for
![]() ,
but this time due to He II. In addition to the change in amplitude of the variable component, in all cases the signal is shifted with respect to the normal recombinational signal. These shifts should also make it easier to distinguish between the spectral signatures from pre-recombinational energy release and those produced by normal recombination.
,
but this time due to He II. In addition to the change in amplitude of the variable component, in all cases the signal is shifted with respect to the normal recombinational signal. These shifts should also make it easier to distinguish between the spectral signatures from pre-recombinational energy release and those produced by normal recombination.
It is important to mention that the total amplitude of the variable component should still increase when more shells are included in the computation. As shown in Chluba et al. (2007a), for y=0 in particular the overall level of recombinational emission at low frequencies depends strongly on the
completeness of the atomic model. Similarly, the variability in the recombination spectrum changes.
This is illustrated in Fig. 10, where we compare the variability in the H I + He II recombination spectrum for 25 shells (y=0), with that obtained in our 100-shell computations (Chluba et al. 2007a; Rubiño-Martín et al. 2008). As one can see, at low frequencies (
![]() GHz) the amplitude of the variable component increases by more than a factor of 2 when 100 shells are included, reaching a peak-to-peak amplitude of
GHz) the amplitude of the variable component increases by more than a factor of 2 when 100 shells are included, reaching a peak-to-peak amplitude of ![]() nK. This is due to the fact that for a more complete atomic model additional electrons are able to pass through a particular transition between highly excited states.
nK. This is due to the fact that for a more complete atomic model additional electrons are able to pass through a particular transition between highly excited states.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f10.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg221.png) |
Figure 10:
Comparison of the variable component in the standard (y=0)
H I + He II bound-bound and free-bound recombination spectrum for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f11a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{eps/9840f11b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg222.png) |
Figure 11: Comparison of the variable component in the H I + He II bound-bound and free-bound recombination spectra for single energy injection (black solid curves) and energy injection due to long-lived decaying particles with different lifetimes (red dashed-dotted curves). In all cases the computations were performed including 25 shells and a maximal y-parameter y=10-5. |
| Open with DEXTER | |
5.3.3 Dependence of the distortion on the energy injection history
Until now we have only considered cases of single momentary energy injection. However, physically this may not be very realistic, since most of the possible injection mechanisms release energy over a broader range of redshifts. The discussion in Sect. 5.3.2 has also shown that for single injection a large part of the variability can be attributed to the onset of the energy release. Therefore it is important to investigate the potential signatures of other injection mechanisms.
For the signals under discussion, long-lived, decaying particles are the most interesting. In Sect. 2.1.1, we have given some simplified analytic description of this problem.
In Fig. 11, we show the variable component for the CMB spectral distortion due to the presence of hydrogen and He II at low frequencies, for both single injection and energy release from long-lived decaying particles. For
![]() ,
it is clear that the variability is significantly smaller than in the case of single energy injection. This is because the onset of the atomic transitions is much more gradual than in the case of single injection. However, one should mention that for energy injection due to decaying particles the effective y-parameter at z=4000 remains only
,
it is clear that the variability is significantly smaller than in the case of single energy injection. This is because the onset of the atomic transitions is much more gradual than in the case of single injection. However, one should mention that for energy injection due to decaying particles the effective y-parameter at z=4000 remains only ![]() of its maximal value, so that the level of variability cannot be compared directly with the case of single energy injection. Nevertheless, the structure of the variable component still depends non-trivially on the effective decay redshift, so that one in principle should be able to distinguish between the different injection scenarios.
of its maximal value, so that the level of variability cannot be compared directly with the case of single energy injection. Nevertheless, the structure of the variable component still depends non-trivially on the effective decay redshift, so that one in principle should be able to distinguish between the different injection scenarios.
Similarly, one could consider the case of annihilating particles. However, here energy is effectively released at higher redshift![]() and also over a much broader redshift interval. In this case, one has to follow the evolution in the CMB spectrum caused by this heating mechanism from an initial
and also over a much broader redshift interval. In this case, one has to follow the evolution in the CMB spectrum caused by this heating mechanism from an initial ![]() -type distortion to a partial y-type distortion in more detail. One can also expect that the redistribution of photons via electron scattering will become much more important (see Appendix A.4), and that the free-free process will strongly alter the number of photons emitted via atomic transitions (see Appendix A.5). In addition, collisional processes may become significant, in particular those leading to transitions among different bound-bound levels, or to the continuum, since they are not associated with the emission of photons.
This problem will be considered in a future work.
-type distortion to a partial y-type distortion in more detail. One can also expect that the redistribution of photons via electron scattering will become much more important (see Appendix A.4), and that the free-free process will strongly alter the number of photons emitted via atomic transitions (see Appendix A.5). In addition, collisional processes may become significant, in particular those leading to transitions among different bound-bound levels, or to the continuum, since they are not associated with the emission of photons.
This problem will be considered in a future work.
6 Discussion and conclusions
In the previous sections, we have shown in detail how intrinsic y-type CMB spectral distortions modify the radiation released by atomic transitions in primordial hydrogen and He II at high redshift. We presented the results of numerical computations including 25 atomic shells for both H I and He II, and discussed the contributions of several individual transitions in detail (e.g., see Fig. 6), by also taking the broadening of lines due to electron scattering into account. As examples, we investigated the case of instantaneous energy release (Sect. 5.3.2) and exponential energy release (Sect. 5.3.3) due to long-lived, decaying particles, separately.
Our computations indecated that several additional photons are released during the pre-recombinational epoch, which in terms of number can strongly exceed those from the recombinational epoch (see Sect. 5.3.1). The number of loops per nucleus scales roughly in proportion to the values of y, i.e.,
![]()
![]() [y/10-5] and
[y/10-5] and
![]()
![]() [y/10-5] for hydrogen and He II, respectively, where about 3 photons per loop are effectively emitted in the bound-bound transition.
[y/10-5] for hydrogen and He II, respectively, where about 3 photons per loop are effectively emitted in the bound-bound transition.
Because of the non-trivial overlap of broad neighboring pre-recombinational lines (from bound-bound and free-bound transitions), rather narrow (
![]() )
spectral features appear on top of a broad continuum, which both in shape and amplitude depend on the time-dependence of the energy injection process and the value of the intrinsic y-type CMB distortion. At high frequencies (
)
spectral features appear on top of a broad continuum, which both in shape and amplitude depend on the time-dependence of the energy injection process and the value of the intrinsic y-type CMB distortion. At high frequencies (
![]() GHz), an emission-absorption feature forms, which is completely absent for y=0, and is mainly due to the superposition of pre-recombinational emission in the
Lyman-
GHz), an emission-absorption feature forms, which is completely absent for y=0, and is mainly due to the superposition of pre-recombinational emission in the
Lyman-![]() line, and the higher Lyman-series and Lyman continuum.
line, and the higher Lyman-series and Lyman continuum.
Looking at Fig. 12, it becomes clear that this absorption feature (close to
![]() GHz) in all shown cases even exceeds the intrinsic y-distortion. For y=10-5, it even reaches
GHz) in all shown cases even exceeds the intrinsic y-distortion. For y=10-5, it even reaches
![]() of the CMB blackbody intensity. Unfortunately, it appears in the far Wien-tail of the CMB spectrum, where the cosmic infrared forming galaxies is dominant (Lagache et al. 2005; Fixsen et al. 1998). Still one may hope to be able to extract such spectral features in the future.
of the CMB blackbody intensity. Unfortunately, it appears in the far Wien-tail of the CMB spectrum, where the cosmic infrared forming galaxies is dominant (Lagache et al. 2005; Fixsen et al. 1998). Still one may hope to be able to extract such spectral features in the future.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f12.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg226.png) |
Figure 12:
Spectral distortions relative to the CMB blackbody spectrum, |
| Open with DEXTER | |
One should emphasize that all the discussed additional pre-recombinational spectral distortions are in general small in comparison to the intrinsic y-distortion. As Fig. 12 shows, the amplitude of the additional distortions is typically well below 1% of the CMB y-distortion. However, at low frequencies (![]() GHz) the additional
distortions should reach
GHz) the additional
distortions should reach
![]() of the intrinsic y-distortion, and at even lower frequency may also exceed it. But in this context, it is more important that due to the processes discussed here new narrow spectral features appear, of an unique variability (e.g. see Fig. 9), even stronger than that of the recombinational lines from standard recombination (y=0). This variability is very hard to mimic by any astrophysical foreground or
systematic problem with the instruments. As emphasized earlier for the cosmological recombination spectrum (Sunyaev & Chluba 2007,2008), this may allow us to measure them differentially, also making use of the fact that the same signal is coming from practically all directions on the sky.
For intrinsic y-distortions, direct differential measurements are much harder, since its spectrum is so broad. Furthermore, as pointed out in the introduction, by measuring the narrow spectral features under discussion one could in principle distinguish between pre- and post-recombinational energy release, an observation that cannot be easily achieved by measuring directly the average y-distortion of the CMB.
of the intrinsic y-distortion, and at even lower frequency may also exceed it. But in this context, it is more important that due to the processes discussed here new narrow spectral features appear, of an unique variability (e.g. see Fig. 9), even stronger than that of the recombinational lines from standard recombination (y=0). This variability is very hard to mimic by any astrophysical foreground or
systematic problem with the instruments. As emphasized earlier for the cosmological recombination spectrum (Sunyaev & Chluba 2007,2008), this may allow us to measure them differentially, also making use of the fact that the same signal is coming from practically all directions on the sky.
For intrinsic y-distortions, direct differential measurements are much harder, since its spectrum is so broad. Furthermore, as pointed out in the introduction, by measuring the narrow spectral features under discussion one could in principle distinguish between pre- and post-recombinational energy release, an observation that cannot be easily achieved by measuring directly the average y-distortion of the CMB.
We also note that in addition to the average y-parameter one could include possible knowledge on the angular dependence of the CMB spectrum. The y-distortion from resolved SZ-clusters is a trivial example and their signals can certainly be removed. However, the contributions from the warm-hot-interstellar-medium should be more uniform and should vary at very different angular scales. The presence of halos of annihilating (
![]() )
or decaying (
)
or decaying (
![]() )
dark matter at high redshifts (
)
dark matter at high redshifts (![]() )
will also lead to a slowly varying, angular-dependent, post-recombinational y-distortion. Because of their different dependencies on the dark matter number density
)
will also lead to a slowly varying, angular-dependent, post-recombinational y-distortion. Because of their different dependencies on the dark matter number density
![]() ,
these contributions will influence different angular scales at different redshifts. This angular dependence in principle would provide another way to separate pre- and post-recombinational energy release. However, one should also consider that the pre-recombinational energy release may not be uniform, since for example, phase transitions in different parts of the Universe occur at different redshifts. This makes the problem more involved and a detailed analysis of this possibility is beyond the scope of this paper.
,
these contributions will influence different angular scales at different redshifts. This angular dependence in principle would provide another way to separate pre- and post-recombinational energy release. However, one should also consider that the pre-recombinational energy release may not be uniform, since for example, phase transitions in different parts of the Universe occur at different redshifts. This makes the problem more involved and a detailed analysis of this possibility is beyond the scope of this paper.
We have also pointed out that there is no principle difficulty in computing the spectral distortions due to pre-recombinational atomic transitions in H I and He II for more general energy injection histories, if required. In particular very early injection, involving ![]() -type distortions, may be interesting, since stimulated emission could strongly amplify the
emission at low frequencies and hence the total number of emitted photons per atom. However, to treat this problem one has to follow the detailed evolution in the CMB spectral distortion produced by the injection process (see e.g. Hu & Silk 1993a). The effect of electron scattering on
the distortions caused by the pre-recombinational atomic transitions, in particular because of the recoil effect, must also be treated more rigorously. Simple estimates also show (see Appendix A.5) that at low frequencies the modifications due to free-free absorption becomes significant. Furthermore, one must account for collisional processes, since they should become important at very high redshift, even for shells with low n.
-type distortions, may be interesting, since stimulated emission could strongly amplify the
emission at low frequencies and hence the total number of emitted photons per atom. However, to treat this problem one has to follow the detailed evolution in the CMB spectral distortion produced by the injection process (see e.g. Hu & Silk 1993a). The effect of electron scattering on
the distortions caused by the pre-recombinational atomic transitions, in particular because of the recoil effect, must also be treated more rigorously. Simple estimates also show (see Appendix A.5) that at low frequencies the modifications due to free-free absorption becomes significant. Furthermore, one must account for collisional processes, since they should become important at very high redshift, even for shells with low n.
An additional difficulty arises because at both very low and very high frequencies, the back-reaction of the pre-recombinational distortion on the ambient radiation field may not be negligible (see Fig. 12). This may also affect the details of the results presented
here, although our main conclusions should not change. The inter-species feedback and reprocessing of photons (e.g.
![]() and
and
![]() )
may also produce some differences, close to the beginning of the pre-recombinational epochs of each atomic species. Furthermore, for more accurate predictions of the positions of the narrow features one should account for the background-induced, stimulated electron-scattering, which was discussed by Chluba & Sunyaev (2008a). We defer all of these problems to another paper.
)
may also produce some differences, close to the beginning of the pre-recombinational epochs of each atomic species. Furthermore, for more accurate predictions of the positions of the narrow features one should account for the background-induced, stimulated electron-scattering, which was discussed by Chluba & Sunyaev (2008a). We defer all of these problems to another paper.
Acknowledgements
The authors wish to thank J. A. Rubiño-Martín for useful discussions. We also wish to thank the referee for his comments and suggestions. In addition, we are grateful for discussions on experimental possibilities with J. E. Carlstrom, D. J. Fixsen, A. Kogut, L. Page, M. Pospieszalski, A. Readhead, E. J. Wollack and especially J. C. Mather. We would also like to thank J. Carlstrom and J. Ostriker for their comments and interest in the problem, and C. Thompson for additional discussion on superconducting strings. Also RS is very glad that he had the chance to work with Y. E Lyubarsky on the early ideas related to this problem.
Appendix A: Computational details
In this section, we outline the most important changes that had to be made to our multi-level code (Chluba et al. 2007a) to allow for an intrinsic y-type CMB spectral distortion. We also mention several approximations that can be used to ease the numerical integration of the coupled system of rate equations for the different populations of electrons in the energy levels of hydrogen and helium.
A.1 Formulation of the problem
Details about the formulation of the cosmological recombination problem for a pure blackbody CMB radiation field are given in Seager et al. (2000), Rubiño-Martín et al. (2006), and references therein. We shall use the same notation as in Rubiño-Martín et al. (2006). The main difference with respect to the standard recombination computation is caused by the possibility of a non-blackbody ambient radiation field, which affects the net bound-bound and free-bound rates as explained in Sect. 3. The temperature of the electrons in general is also no longer equal to the effective temperature of the photons, as we discuss below (see Sect. A.3). Since we consider only small intrinsic spectral distortions, all the modification to the solution for the level populations are rather small, and most of the differences will appear only as pre-recombinational emission due to atomic transitions, but with practically no net effect on the ionization history.
One additional modification is related to the Lyman-continuum. As was realized earlier (Peebles 1968; Zeldovich et al. 1968), during the recombination epochs photons cannot escape from the Lyman-continuum. However, at high redshift the number of neutral atoms is very small, so the
Lyman-continuum becomes optically thin. To include the escape of photons in the Lyman-continuum, we follow the analytic description of Chluba & Sunyaev (2007), in which an approximation of the escape probability in the Lyman-continuum was given by
with
A.2 High redshift solution
At high redshift, well before the true recombination epoch of the considered atomic species, one can simplify the problem by realizing that the ionization degree does not change significantly. Although the inclusion of intrinsic CMB spectral distortion produces some small changes in the populations with respect to the Saha values, the total number of electrons captured by protons and helium nuclei is tiny compared to the total number of free electrons. Therefore, one can neglect the evolution equation for the electrons, until the true recombination epoch is entered. For H I, we used this simplification until
![]() ,
while for He II we follow the full system below
,
while for He II we follow the full system below
![]() .
Before we simply used the R ECFAST-solution for
.
Before we simply used the R ECFAST-solution for ![]() (Seager et al. 1999,2000). In several different cases, we checked that these settings do not affect the spectra.
(Seager et al. 1999,2000). In several different cases, we checked that these settings do not affect the spectra.
Furthermore, we note that at high redshift for n>2 we used the variable
![]() instead of Ni, since
instead of Ni, since
![]() becomes so small. Here
becomes so small. Here
![]() is the expected population of level i in Boltzmann-equilibrium relative to the 2s-level. We then changed back to the variable Ni at sufficiently low redshifts.
is the expected population of level i in Boltzmann-equilibrium relative to the 2s-level. We then changed back to the variable Ni at sufficiently low redshifts.
A.3 Recombination and photoionization rates
The computation of the photoionization and recombination rates for many levels is rather time-consuming. In an earlier version of our code (Chluba et al. 2007a), we tabulated the recombination rates for all levels before the actual computation and used detailed balance to infer the photoionization rates. This treatment is possible as long as the photon and electron temperature do not depart significantly from each other, and when the background spectrum is given by a blackbody.
Here we now generalize this procedure accounting for the small difference between the electron and photon temperatures, in particular at low redshift (![]() ), and allowing for non-blackbody ambient photon distributions.
), and allowing for non-blackbody ambient photon distributions.
At high redshift (![]() ), the electron temperature is always equal to the Compton equilibrium temperature (Zeldovich & Sunyaev 1969):
), the electron temperature is always equal to the Compton equilibrium temperature (Zeldovich & Sunyaev 1969):
within the given ambient radiation field. Because of the extremely high specific entropy of the Universe (there are
At redshifts below
![]() ,
we solve for the electron temperature accounting for the non-blackbody ambient radiation field. In this case, the photon temperature inside the term due to the Compton interaction must be replaced by
,
we solve for the electron temperature accounting for the non-blackbody ambient radiation field. In this case, the photon temperature inside the term due to the Compton interaction must be replaced by
![]() as given by Eq. (A.2), such that the temperature evolution equation reads
as given by Eq. (A.2), such that the temperature evolution equation reads
where
Since for small intrinsic CMB spectral distortions, the correction to the solution for the temperature of the electrons is rather small, it is always possible to use the standard R ECFAST solution for ![]() as a reference. Tabulating both the photoionization and recombination rates, and their first derivatives with respect to the ratio of the electron to photon temperature
as a reference. Tabulating both the photoionization and recombination rates, and their first derivatives with respect to the ratio of the electron to photon temperature
![]() ,
it is possible to approximate the exact rates to high accuracy using first-order Taylor polynomials. To save memory, we only consider all these rates in some range of redshifts around the current point in the evolution and then update them from time to time. At high redshift, we typically used 200 points per decade in logarithmic spacing. At low redshift (
,
it is possible to approximate the exact rates to high accuracy using first-order Taylor polynomials. To save memory, we only consider all these rates in some range of redshifts around the current point in the evolution and then update them from time to time. At high redshift, we typically used 200 points per decade in logarithmic spacing. At low redshift (![]() ), we use 2 points per
), we use 2 points per
![]() .
Another improvement can be achieved by rescaling the reference solution for
.
Another improvement can be achieved by rescaling the reference solution for ![]() with the true solution whenever the tabulated rates are updated.
With these settings, we found excellent agreement with the full computation but at significantly lower computational cost.
with the true solution whenever the tabulated rates are updated.
With these settings, we found excellent agreement with the full computation but at significantly lower computational cost.
A.4 Inclusion of electron scattering
As mentioned by Dubrovich & Stolyarov (1997) and shown in more detail by Rubiño-Martín et al. (2008), the broadening due to the scattering of photons by free electrons must be included in the computation of the He II recombination spectrum. Similarly, one has to account for this effect, when computing the spectral distortions arising from higher redshifts. Here we only consider redshifts
![]() ,
and hence the electron scattering Compton-y-parameter
,
and hence the electron scattering Compton-y-parameter![]()
is lower than
Regarding the line-shifts caused by the recoil effect, one finds that they are not very important, since even for the H I Lyman-continuum one has
![]() at
at
![]() .
Although for the He II Lyman-continuum the shifts due to the recoil-effect is a factor of four higher, we shall not include it in our results. One therefore expects that at frequencies
.
Although for the He II Lyman-continuum the shifts due to the recoil-effect is a factor of four higher, we shall not include it in our results. One therefore expects that at frequencies
![]() GHz the presented distortions may still be modified due to this process, but we will consider this problem in a future paper.
GHz the presented distortions may still be modified due to this process, but we will consider this problem in a future paper.
For the bound-bound spectrum we follow the procedure described in Rubiño-Martín et al. (2008), where the resulting spectral distortion at observing frequency ![]() for one particular transition is given by
(see also Zeldovich & Sunyaev 1969)
for one particular transition is given by
(see also Zeldovich & Sunyaev 1969)
Here
For the spectral distortion resulting from the free-bound transitions, one in addition has to include the frequency-dependence of the photoionization cross-section. We shall neglect the line broadening because of electron scattering for the moment. Then, following Chluba & Sunyaev (2006) and using the definitions of Sect. 3.2, in the optically thin limit the spectral distortion of the CMB at observing frequency ![]() due to direct recombinations to level i is given by
due to direct recombinations to level i is given by
where
To include the broadening because of scattering by electrons, one has to
solve the 2-dimensional integral
where
In the numerical evaluation of these integrals, it is advisable to use knowledge about the integrand, since otherwise they may converge very slowly.
A.5 Estimate regarding the free-free process
The free-free optical depth,
![]() ,
is given by
,
is given by
Here
where
Using the condition
![]() ,
one can estimate the frequency
,
one can estimate the frequency
![]() below which one expects free-free absorption to become important. Since at
below which one expects free-free absorption to become important. Since at ![]() ,
all the atoms are ionized, the number density of free electrons is given by
,
all the atoms are ionized, the number density of free electrons is given by
![]() .
Here we used
.
Here we used
![]() as the present-day baryon number density. For
as the present-day baryon number density. For
![]() ,
one then finds that
,
one then finds that
![]() ,
where
,
where
![]() is the redshift of emission. Here we are only interested in photons that can be observed at
is the redshift of emission. Here we are only interested in photons that can be observed at ![]() ,
i.e.,
,
i.e., ![]() GHz today. At this frequency
GHz today. At this frequency
![]() for
for
![]() .
Below this redshift one can neglect the free-free process in the computation of the bound-bound and free-bound spectra. However, a more complete treatment will be presented in a future paper.
.
Below this redshift one can neglect the free-free process in the computation of the bound-bound and free-bound spectra. However, a more complete treatment will be presented in a future paper.
Assuming that
![]() ,
one finds that
,
one finds that
![]() for
for ![]() .
This justifies the approximations made above, since the contributions to the free-free optical depth coming from
.
This justifies the approximations made above, since the contributions to the free-free optical depth coming from ![]() are not very large.
are not very large.
Appendix B: Analytic solution
B.1 The 2-shell atom
Including only 2 shells, one can analytically derive the solution for the Lyman-![]() line under quasi-stationary evolution of the populations. For this, we need to determine the net radiative rate,
line under quasi-stationary evolution of the populations. For this, we need to determine the net radiative rate,
![]() ,
for w=3 and
,
for w=3 and
![]() .
The ratio
.
The ratio
![]() is determined directly by the given ambient radiation field including the spectral distortion. Since the distortions are assumed to be small, we can use
is determined directly by the given ambient radiation field including the spectral distortion. Since the distortions are assumed to be small, we can use
![]() for the term in front of the brackets. Here
for the term in front of the brackets. Here
![]() and
and
![]() are equilibrium values for the photon occupation number and the 2p-population, respectively. Therefore, we only have to determine the ratio
are equilibrium values for the photon occupation number and the 2p-population, respectively. Therefore, we only have to determine the ratio
![]() to compute the Lyman-
to compute the Lyman-![]() line intensity
analytically.
line intensity
analytically.
We shall first consider the situation for hydrogen at high redshift (
![]() ). There the escape probability in the H I Lyman-
). There the escape probability in the H I Lyman-![]() line and the H I Lyman-continuum are
close to unity. Therefore, the 2s-1s-two-photon transition does not play any important role in defining the number density of atoms in the ground state. Furthermore, one can assume that the 2s-population is always in Saha-equilibrium with the continuum, and hence
line and the H I Lyman-continuum are
close to unity. Therefore, the 2s-1s-two-photon transition does not play any important role in defining the number density of atoms in the ground state. Furthermore, one can assume that the 2s-population is always in Saha-equilibrium with the continuum, and hence
![]() where even
where even
![]() ,
since the total fraction of neutral atoms is tiny.
,
since the total fraction of neutral atoms is tiny.
For the 1s- and 2p-states, the rate equations read
| (B.1a) | |||
| (B.1b) |
where we have substituted
With the appropriate replacements of terms, the same expression can be used to compute the He II Lyman-
B.1.1 Including the Lyman- and continuum escape
and continuum escape
To include the escape probability in the Lyman-![]() line, P21, and the Lyman-continuum,
line, P21, and the Lyman-continuum,
![]() ,
one should simply replace
,
one should simply replace
![]() ,
,
![]() and
and
![]() ,
where the escape probabilities can be computed using equilibrium values for
,
where the escape probabilities can be computed using equilibrium values for
![]() and
and
![]() .
As long as the 2s-1s-two-photon transition can be neglected, this yields an accurate approximation for the Lyman-
.
As long as the 2s-1s-two-photon transition can be neglected, this yields an accurate approximation for the Lyman-![]() line (cf. Sects. 5.1).
line (cf. Sects. 5.1).
Around the region where the Lyman-continuum becomes optically thick (
![]() for H I and
for H I and
![]() for He II), for simple estimates one can use
for He II), for simple estimates one can use
where
B.1.2 More approximate behavior
To understand the solution for the H I Lyman-![]() line, we now turn to the corresponding intensity as a function of redshift (e.g. Rubiño-Martín et al. 2006). This yields
line, we now turn to the corresponding intensity as a function of redshift (e.g. Rubiño-Martín et al. 2006). This yields
Using the approximation (B.2) for
With this, one then has
Here we used
First factor
We can now simplify the expression in Eq. (B.7) when realizing that
except for the term inside brackets, in the case of small intrinsic CMB
spectral distortions, one can just use equilibrium values.
At high redshifts one has
![]() .
Furthermore
.
Furthermore
![]() and
and
![]() .
To high accuracy, one also finds
.
To high accuracy, one also finds
![]() and
and
![]() ,
so that
,
so that
Here we have also included the escape probabilities in the Lyman-
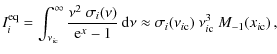 |
(B.9a) |
and we have assumed that
We checked the scaling of F numerically and found that
to within
Second factor
Using the definitions of
![]() and
and ![]() as given in Sects. 3.1 and 3.2, one finds directly
as given in Sects. 3.1 and 3.2, one finds directly
![]() with
with
Here
for the average of some function
In full thermodynamic equilibrium, one has
![]() ,
a property that can be verified using Eq. (B.11) with
,
a property that can be verified using Eq. (B.11) with ![]() and
and ![]() ,
since then
,
since then
![]() .
Therefore, we can write
.
Therefore, we can write
![]() .
Using
.
Using
![]() for small
intrinsic CMB distortions (i.e.
for small
intrinsic CMB distortions (i.e.
![]() ), one finds
), one finds
where
To lowest order, Eq. (B.14b) shows that the main reason for the emission in the Lyman-
If we again use the Kramers-approximation for the photoionization cross-section,
![]() ,
looking at Eq. (3) for
,
looking at Eq. (3) for ![]() in the case of a small y-type distortion, one can write
in the case of a small y-type distortion, one can write
where
It is important to mention that this is still a rather rough approximation, since by already applying the Kramers-formula to the photoionization cross-section, we have introduced some significant simplification. However, this approximation may be useful for simple estimates.
Appendix C: Some integrals
C.1 Integrals Mi
In the evaluation of the recombination and photoionization rates, integrals of the form
![]() appear. Below we now discuss those of importance to us here.
appear. Below we now discuss those of importance to us here.
C.1.1 Integral M-1
For i=-1, one can write
where
Since
![]() ,
it is clear that at
,
it is clear that at
![]() both Lyman- and Balmer-continuum are still in the exponential tail of the CMB blackbody. In the redshift range
both Lyman- and Balmer-continuum are still in the exponential tail of the CMB blackbody. In the redshift range
![]() ,
the Lyman-continuum is still in the exponential tail of the CMB, while the Balmer-continuum is already in the Rayleigh-Jeans part of the spectrum. Only at
,
the Lyman-continuum is still in the exponential tail of the CMB, while the Balmer-continuum is already in the Rayleigh-Jeans part of the spectrum. Only at
![]() can one use the low frequency expansion of Eq. (B.1.2) in both cases. However, to within
can one use the low frequency expansion of Eq. (B.1.2) in both cases. However, to within ![]() one may also apply Eq. (C.1a) to the entire range.
one may also apply Eq. (C.1a) to the entire range.
C.1.2 Integral M0
For i=0, one can write
which for
C.2 Integral S
In the evaluation of the recombination and photoionization rates, one also encounters
![]() .
The first part of this integral,
.
The first part of this integral,
![]() ,
can be directly taken yielding
,
can be directly taken yielding
![]() .
Introducing the polylogarithm
.
Introducing the polylogarithm
![]() and realizing
and realizing
![]() =
=
![]() ,
one can find
,
one can find
The given approximations are accurate to
References
- Bennett, C. L., Halpern, M., Hinshaw, G., et al. 2003, ApJS, 148, 1 [NASA ADS] [CrossRef]
- Burigana, C., & Salvaterra, R. 2003, MNRAS, 342, 543 [NASA ADS] [CrossRef]
- Burigana, C., Danese, L., & de Zotti, G. 1991a, ApJ, 379, 1 [NASA ADS] [CrossRef]
- Burigana, C., Danese, L., & de Zotti, G. 1991b, A&A, 246, 49 [NASA ADS]
- Burigana, C., de Zotti, G., & Danese, L. 1995, A&A, 303, 323 [NASA ADS]
- Cen, R., & Ostriker, J. P. 1999, ApJ, 514, 1 [NASA ADS] [CrossRef]
- Chan, K. L., Grant, C., & Jones, B. J. T. 1975, ApJ, 195, 1 [NASA ADS] [CrossRef]
- Chluba, J., & Sunyaev, R. A. 2004, A&A, 424, 389 [NASA ADS] [CrossRef] [EDP Sciences]
- Chluba, J., & Sunyaev, R. A. 2006, A&A, 458, L29 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chluba, J., & Sunyaev, R. A. 2007, A&A, 475, 109 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chluba, J., & Sunyaev, R. A. 2008a, A&A, 488, 861 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chluba, J., & Sunyaev, R. A. 2008b, A&A, 478, L27 [NASA ADS] [CrossRef] [EDP Sciences]
- Chluba, J., Rubiño-Martín, J. A., & Sunyaev, R. A. 2007a, MNRAS, 374, 1310 [NASA ADS] [CrossRef]
- Chluba, J., Sazonov, S. Y., & Sunyaev, R. A. 2007b, A&A, 468, 785 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- da Silva, A. C., Barbosa, D., Liddle, A. R., & Thomas, P. A. 2000, MNRAS, 317, 37 [NASA ADS] [CrossRef]
- Daly, R. A. 1991, ApJ, 371, 14 [NASA ADS] [CrossRef]
- Danese, L., & de Zotti, G. 1982, A&A, 107, 39 [NASA ADS]
- Dubrovich, V. K. 1975, SvA Lett., 1, 196 [NASA ADS]
- Dubrovich, V. K., & Stolyarov, V. A. 1995, A&A, 302, 635 [NASA ADS]
- Dubrovich, V. K., & Stolyarov, V. A. 1997, Astron. Lett., 23, 565 [NASA ADS]
- Fixsen, D. J., & Mather, J. C. 2002, ApJ, 581, 817 [NASA ADS] [CrossRef]
- Fixsen, D. J., Cheng, E. S., Gales, J. M., et al. 1996, ApJ, 473, 576 [NASA ADS] [CrossRef] (In the text)
- Fixsen, D. J., Dwek, E., Mather, J. C., Bennett, C. L., & Shafer, R. A. 1998, ApJ, 508, 123 [NASA ADS] [CrossRef]
- Fixsen, D. J., Kogut, A., Levin, S., et al. 2009, ArXiv e-prints
- Hu, W., & Silk, J. 1993a, Phys. Rev. D, 48, 485 [NASA ADS] [CrossRef]
- Hu, W., & Silk, J. 1993b, Phys. Rev. Lett., 70, 2661 [NASA ADS] [CrossRef]
- Hu, W., Scott, D., & Silk, J. 1994, ApJ, 430, L5 [NASA ADS] [CrossRef]
- Illarionov, A. F., & Syunyaev, R. A. 1975a, SvA, 18, 413 [NASA ADS]
- Illarionov, A. F., & Syunyaev, R. A. 1975b, SvA, 18, 691 [NASA ADS]
- Kaplan, S. A., & Pikelner, S. B. 1970, The interstellar medium (Cambridge: Harvard University Press) (In the text)
- Kholupenko, E. E., Ivanchik, A. V., & Varshalovich, D. A. 2005, Gravitation and Cosmology, 11, 161 [NASA ADS]
- Kogut, A., Fixsen, D. J., Levin, S., et al. 2004, ApJS, 154, 493 [NASA ADS] [CrossRef]
- Kogut, A., Fixsen, D., Fixsen, S., et al. 2006, New Astron. Rev., 50, 925 [NASA ADS] [CrossRef]
- Lagache, G., Puget, J.-L., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef]
- Lightman, A. P. 1981, ApJ, 244, 392 [NASA ADS] [CrossRef]
- Lyubarsky, Y. E., & Sunyaev, R. A. 1983, A&A, 123, 171 [NASA ADS] (In the text)
- Markevitch, M., Blumenthal, G. R., Forman, W., Jones, C., & Sunyaev, R. A. 1991, ApJ, 378, L33 [NASA ADS] [CrossRef]
- Mather, J. 2007, Nuovo Cimento B Serie, 122, 1315 [NASA ADS] (In the text)
- Mather, J. C., Fixsen, D. J., Shafer, R. A., Mosier, C., & Wilkinson, D. T. 1999, ApJ, 512, 511 [NASA ADS] [CrossRef]
- McDonald, P., Scherrer, R. J., & Walker, T. P. 2001, Phys. Rev. D, 63, 023001 [NASA ADS] [CrossRef]
- Miniati, F., Ryu, D., Kang, H., et al. 2000, ApJ, 542, 608 [NASA ADS] [CrossRef]
- Oh, S. P., Cooray, A., & Kamionkowski, M. 2003, MNRAS, 342, L20 [NASA ADS] [CrossRef] (In the text)
- Ostriker, J. P., & Thompson, C. 1987, ApJ, 323, L97 [NASA ADS] [CrossRef]
- Peebles, P. J. E. 1968, ApJ, 153, 1 [NASA ADS] [CrossRef]
- Pozdniakov, L. A., Sobol, I. M., & Syunyaev, R. A. 1983, Astrophys. Space Phys. Rev., 2, 189 [NASA ADS]
- Roncarelli, M., Moscardini, L., Borgani, S., & Dolag, K. 2007, MNRAS, 378, 1259 [NASA ADS] [CrossRef]
- Rubiño-Martín, J. A., Chluba, J., & Sunyaev, R. A. 2006, MNRAS, 371, 1939 [NASA ADS] [CrossRef]
- Rubiño-Martín, J. A., Chluba, J., & Sunyaev, R. A. 2008, A&A, 485, 377 [NASA ADS] [CrossRef] [EDP Sciences]
- Salvaterra, R., & Burigana, C. 2002, MNRAS, 336, 592 [NASA ADS] [CrossRef]
- Seager, S., Sasselov, D. D., & Scott, D. 1999, ApJ, 523, L1 [NASA ADS] [CrossRef]
- Seager, S., Sasselov, D. D., & Scott, D. 2000, ApJS, 128, 407 [NASA ADS] [CrossRef] (In the text)
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef]
- Sunyaev, R. A., & Zeldovich, Y. B. 1970a, Ap&SS, 7, 3 [NASA ADS]
- Sunyaev, R. A., & Zeldovich, Y. B. 1970b, Ap&SS, 7, 20 [NASA ADS]
- Sunyaev, R. A., & Zeldovich, Y. B. 1970c, Comments Astrophys. Space Phys., 2, 66 [NASA ADS]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972a, A&A, 20, 189 [NASA ADS]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972b, Comments Astrophys. Space Phys., 4, 173 [NASA ADS] (In the text)
- Sunyaev, R. A., & Zeldovich, I. B. 1980, ARA&A, 18, 537 [NASA ADS] [CrossRef]
- Sunyaev, R. A., & Chluba, J. 2007, Nuovo Cimento B Serie, 122, 919 [NASA ADS] (In the text)
- Sunyaev, R. A., & Chluba, J. 2008, in Frontiers of Astrophysics: A Celebration of NRAO's 50th Anniversary, ed. A. H. Bridle, J. J. Condon, & G. C. Hunt, ASP Conf. Ser., 395, 35
- Thorne, K. S. 1981, MNRAS, 194, 439 [NASA ADS]
- Wong, W. Y., Seager, S., & Scott, D. 2006, MNRAS, 367, 1666 [NASA ADS] [CrossRef]
- Zeldovich, Y. B., & Sunyaev, R. A. 1969, Ap&SS, 4, 301 [NASA ADS] [CrossRef] (In the text)
- Zeldovich, Y. B., Kurt, V. G., & Syunyaev, R. A. 1968, Zh. Eksper. Teoretich. Fiz., 55, 278 [NASA ADS]
- Zeldovich, Y. B., Illarionov, A. F., & Syunyaev, R. A. 1972, Sov. J. Exp. Theor. Phys., 35, 643 [NASA ADS]
Footnotes
- ... emission
![[*]](/icons/foot_motif.png)
- Because of the huge excess in the number of photons to baryons (
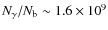 ), the double Compton process is the dominant source of new photons at redshifts
), the double Compton process is the dominant source of new photons at redshifts
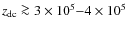 ,
while at
,
while at
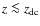 bremsstrahlung is more important.
bremsstrahlung is more important.
- ... hydrogen
![[*]](/icons/foot_motif.png)
- Even the factors due to stimulated emission in the ambient blackbody radiation field are the same!
- ... redshift
![[*]](/icons/foot_motif.png)
- This is a convenient representation of the spectrum, when one is interested in the time-dependence of the photon release, rather than the observed spectral distortion in frequency space. To obtain the latter, in the
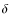 -function approximation for the line-profile one simply has to plot the presented curves as a function of
-function approximation for the line-profile one simply has to plot the presented curves as a function of
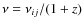 ,
where
,
where  is the rest-frame frequency of the considered transition.
is the rest-frame frequency of the considered transition.
- ... as
![[*]](/icons/foot_motif.png)
- Or more correctly
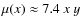 if one also takes into account the difference in the photon and electron temperature
if one also takes into account the difference in the photon and electron temperature
![$T_{\rm e}\approx T_{\gamma}[1+5.4~y]$](/articles/aa/full_html/2009/25/aa09840-08/img139.png) (see Appendix A.1).
(see Appendix A.1).
- ... loops
![[*]](/icons/foot_motif.png)
- This number can be non-integer, since in general only a fraction of all electrons that are captured by the nuclei really run through uncompensated loops during the pre-recombinational epoch.
- ... redshift
![[*]](/icons/foot_motif.png)
- This conclusion depends also on the temperature/energy dependence of the annihilation cross-section. We assumed s-wave annihilation (e.g. see McDonald et al. 2001).
- ...Compton-y-parameter
![[*]](/icons/foot_motif.png)
- Note that
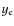 differs from y as defined in Eq. (1), since it describes the redistribution of some photon over frequency because of electron scattering rather than the global energy exchange with the ambient blackbody radiation field.
differs from y as defined in Eq. (1), since it describes the redistribution of some photon over frequency because of electron scattering rather than the global energy exchange with the ambient blackbody radiation field.
- ... with
![[*]](/icons/foot_motif.png)
- Note that even if one (more correctly) uses
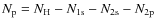 in Eq. (B.1), the solution for
in Eq. (B.1), the solution for  does not change.
does not change.
All Tables
Table 1:
Approximate number of photons and loops per nucleus of the considered species for
![]() and different values of y.
and different values of y.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f1a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{eps/9840f1b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg129.png) |
Figure 1:
Spectral distortion,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f2.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg150.png) |
Figure 2:
Analytic representation of the pre-recombinational H I Lyman- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f3a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{eps/9840f3b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg151.png) |
Figure 3:
Spectral distortion,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{eps/9840f4a.eps}\hspace*{3mm}
\includegraphics[width=4.3cm,clip]{eps/9840f4b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg156.png) |
Figure 4: Sketch of the main atomic loops for hydrogen and He II when including 3 shells. The left panel shows the loops for transitions that are terminating in the Lyman-continuum. The right panel shows the case, when the Lyman-continuum is completely blocked, and unbalanced transitions are terminating in the Balmer-continuum instead. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f5a.eps}\includegr...
...eps/9840f5e.eps}\includegraphics[width=8.8cm,clip]{eps/9840f5f.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg164.png) |
Figure 5:
Contributions to the H I ( left panels) and He II ( right panels) recombination spectrum for different values of the initial y-parameter. Energy injection was assumed to occur at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f6a.eps}\includegr...
...eps/9840f6e.eps}\includegraphics[width=8.8cm,clip]{eps/9840f6f.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg165.png) |
Figure 6: Main contributions to the H I ( left panels) and He II ( right panels) spectral distortion at different frequencies for energy injection at zi=40 000 and y=10-5. We have also marked those peaks coming (mainly) from the recombination epoch (``rec'') and from the pre-recombination epoch (``pre'') of the considered atomic species. Note that the 2s-1s-two-photon decay contribution is not shown, since it does not lead to any significant pre-recombinational signal. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f7a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{eps/9840f7b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg196.png) |
Figure 7: H I ( upper panel) and He II ( lower panel) recombination spectra for different energy injection redshifts. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f8a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{eps/9840f8b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg197.png) |
Figure 8: Total H I + He II recombination spectra for different energy injection redshifts. The upper panel shows details of the spectrum at low, the lower at high frequencies. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f9a.eps}\includegr...
...eps/9840f9c.eps}\includegraphics[width=8.8cm,clip]{eps/9840f9d.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg202.png) |
Figure 9:
Comparison of the variable component in the H I + He II bound-bound and free-bound recombination spectra for single energy injection at different redshifts. In all cases the computations were performed including 25 shells and y=10-5. The blue dashed curve in all panel shows the variability in the normal H I + He II recombination spectrum (equivalent to energy injection below |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f10.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg221.png) |
Figure 10:
Comparison of the variable component in the standard (y=0)
H I + He II bound-bound and free-bound recombination spectrum for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f11a.eps}\vspace*{3mm}
\includegraphics[width=8.8cm,clip]{eps/9840f11b.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg222.png) |
Figure 11: Comparison of the variable component in the H I + He II bound-bound and free-bound recombination spectra for single energy injection (black solid curves) and energy injection due to long-lived decaying particles with different lifetimes (red dashed-dotted curves). In all cases the computations were performed including 25 shells and a maximal y-parameter y=10-5. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{eps/9840f12.eps}
\end{figure}](/articles/aa/full_html/2009/25/aa09840-08/Timg226.png) |
Figure 12:
Spectral distortions relative to the CMB blackbody spectrum, |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



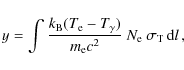
![\begin{displaymath}%
\Delta n_{\gamma} =y~\frac{x~{\rm e}^{x}}{({\rm e}^{x}-1)^2}\left[x~\frac{{\rm e}^{x}+1}{{\rm e}^{x}-1}-4\right]\,,
\end{displaymath}](/articles/aa/full_html/2009/25/aa09840-08/img61.png)
![\begin{displaymath}%
\mu(x) = \ln\left(\frac{1+n_\gamma}{n_\gamma}\right)-x
\sta...
...}
-y~x~\left[x~\frac{{\rm e}^{x}+1}{{\rm e}^{x}-1}-4\right]\,,
\end{displaymath}](/articles/aa/full_html/2009/25/aa09840-08/img63.png)
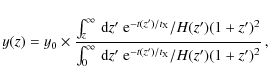
![\begin{displaymath}%
\Delta R_{ij}=p_{ij}~\frac{A_{ij}~N_i~{\rm e}^{x_{ij}+\mu_{...
...i}{g_j}~\frac{N_j}{N_i}~{\rm e}^{-[x_{ij}+\mu_{ij}]}\right]\,,
\end{displaymath}](/articles/aa/full_html/2009/25/aa09840-08/img82.png)
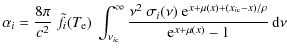

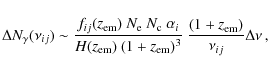
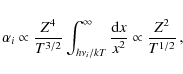
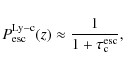

![\begin{displaymath}%
\frac{\displaystyle\partial T_{\rm e}}{\displaystyle\partia...
... e}}
~[T_{\rm e}-T_{\rm e}^{\rm eq}]+\frac{2T_{\rm e}}{1+z}\,,
\end{displaymath}](/articles/aa/full_html/2009/25/aa09840-08/img248.png)
![\begin{displaymath}%
{y_{\rm e}}(z)=\!\!\int_0^z\!\!\frac{kT_{\rm e}}{m_{\rm e}c...
... T}}{H(z')(1+z')}{\,\rm d}z'\approx4.8 \times 10^{-11}~[1+z]^2
\end{displaymath}](/articles/aa/full_html/2009/25/aa09840-08/img253.png)
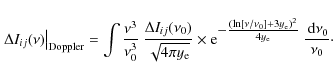
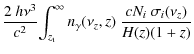
![$\displaystyle \times~ \left[ \frac{N_{\rm e}~N_{\rm p}}{N_{i}} \tilde{f}_i(T_{\rm e})~{\rm e}^{x_z+\mu(x_z)+[x_{i\rm c}-x_z]/\rho} -1 \right]\! {\rm d} z,$](/articles/aa/full_html/2009/25/aa09840-08/img269.png)
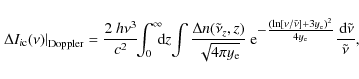
![$\displaystyle \times ~\left[\!
\frac{N_{\rm e}~N_{\rm p}}{N_{i}} \tilde{f}_i(T_{\rm e})~{\rm e}^{x+\mu(x)+[x_{i\rm c}-x]/\rho} -1\!
\right].$](/articles/aa/full_html/2009/25/aa09840-08/img280.png)
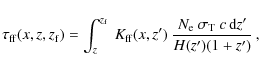
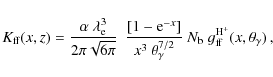
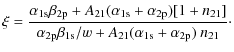
![$\displaystyle \tau^{\rm esc}_{\rm Ly-c} \approx
\left \{ \begin{array}{ll}
7.2 ...
...m e}^{x_{\rm 1s}}~[1+z]^{7/2} &\;\; {\rm for\; He {\sc ii}}
\end{array} \right.$](/articles/aa/full_html/2009/25/aa09840-08/img326.png)
![$\displaystyle \tau^{\rm esc}_{\rm Ly_\alpha} \approx
\left \{ \begin{array}{ll}...
... x_{\rm 1s}/4}]~[1+z]^{5/2} &\;\; {\rm for\; He {\sc ii}}\,,
\end{array}\right.$](/articles/aa/full_html/2009/25/aa09840-08/img327.png)
![$\displaystyle %
\Delta I_\nu=\frac{h~c}{4\pi}~\frac{\Delta R_{\rm Ly_\alpha}(z)...
...c{h~c}{4\pi}~\frac{A_{21}(1+n_{21})~N_{\rm 2p}[1-\xi\Lambda]}{H(z)[1+z]^3}\cdot$](/articles/aa/full_html/2009/25/aa09840-08/img329.png)
![$\displaystyle \times ~
\left[1-w~\frac{\alpha_{\rm 1s}\beta_{\rm 2p}}{\alpha_{\rm 2p}\beta_{\rm 1s}}~{\rm e}^{-(x_{21}+\mu_{21})}\right]\cdot$](/articles/aa/full_html/2009/25/aa09840-08/img334.png)
![$\displaystyle \frac{h~c}{4\pi}~\frac{3~N_{\rm e}~N_{\rm H}}{H(z)[1+z]^3} ~
\fra...
...m esc}_{\rm Ly-c}} \propto
\frac{(1+z)^{1/2}}{4+\tau^{\rm esc}_{\rm Ly-c}}\cdot$](/articles/aa/full_html/2009/25/aa09840-08/img343.png)
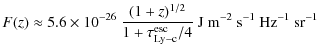
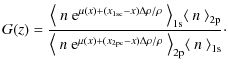
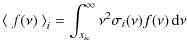
![$\displaystyle %
\Delta G \approx \frac{{\left<~ n_{\rm pl}~[\mu-\mu^{\rho}_{\rm...
...^\rho_{\rm 2p}] ~\right>_{\rm 2p}}}
{{\left<~ n_{\rm pl} ~\right>_{\rm 2p}}}\,,$](/articles/aa/full_html/2009/25/aa09840-08/img362.png)
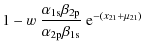
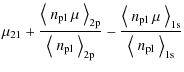
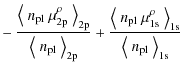
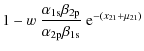
![$\displaystyle \qquad\quad\quad + ~y~x_{21}\left[ 9.4-x_{21}~\frac{{\rm e}^{x_{21}}+1}{{\rm e}^{x_{21}}-1} \right]\cdot$](/articles/aa/full_html/2009/25/aa09840-08/img374.png)
![$\displaystyle %
\int_{{x_{i\rm c}}}^\infty \frac{{\,\rm d}x}{x[{\rm e}^{x}-1]}$](/articles/aa/full_html/2009/25/aa09840-08/img376.png)
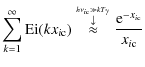
![$\displaystyle \frac{1}{{x_{i\rm c}}}\left[\!1-\frac{11-6\gamma}{12}~{x_{i\rm c}}-\frac{x^2_{i\rm c}}{12}+\frac{{x_{i\rm c}}}{2}\ln({x_{i\rm c}})\!\right]\!\!\,,$](/articles/aa/full_html/2009/25/aa09840-08/img379.png)
![$\displaystyle \int_{x_{i\rm c}}^\infty {\,\rm d}x/[{\rm e}^x-1]=\sum_{k=1}^\inf...
...c}}^\infty
{\rm e}^{-kx}{\,\rm d}x=\sum_{k=1}^\infty {\rm e}^{-k{x_{i\rm c}}}/k$](/articles/aa/full_html/2009/25/aa09840-08/img389.png)
![$\displaystyle \sum_{k=1}^{m\approx 5} \frac{2k-1}{k^2}\left[1+k~{x_{i\rm c}}\right]~{\rm e}^{-k{x_{i\rm c}}}$](/articles/aa/full_html/2009/25/aa09840-08/img405.png)
