Electron-impact excitation of Ar2+

J. M. Munoz Burgos; S. D. Loch; C. P. Ballance; R. F. Boivin

doi:10.1051/0004-6361/200911743

Home

All issues

Volume 500 / No 3 (June IV 2009)

A&A, 500 3 (2009) 1253-1261

Full HTML

Free Access

Issue		A&A Volume 500, Number 3, June IV 2009


Page(s)		1253 - 1261
Section		Atomic, molecular, and nuclear data
DOI		https://doi.org/10.1051/0004-6361/200911743
Published online		16 April 2009

Electron-impact excitation of Ar²⁺

J. M. Munoz Burgos - S. D. Loch - C. P. Ballance - R. F. Boivin

Department of Physics, Auburn University, Auburn, AL 36849, USA

Received 28 January 2009 / Accepted 12 March 2009

Abstract
Context. Emission from Ar III is seen in planetary nebulae, in H II regions, and from laboratory plasmas. The analysis of such spectra requires accurate electron impact excitation data.
Aims. The aim of this work is to improve the electron impact excitation data available for Ar²⁺, for application in studies of planetary nebulae and laboratory plasma spectra. The effects of the new data on diagnostic line ratios are also studied.
Methods. Electron-impact excitation collision strengths have been calculated using the R-Matrix Intermediate-Coupling Frame-Transformation method and the R-Matrix Breit-Pauli method. Excitation cross sections are calculated between all levels of the configurations 3s²3p⁴, 3s3p⁵, 3p⁶, 3p⁵3d, and 3s²3p³nl (3d $\le$ nl $\le$ 5s). Maxwellian effective collision strengths are generated from the collision strength data.
Results. Good agreement is found in the collision strengths calculated using the two R-Matrix methods. The collision strengths are compared with literature values for transitions within the 3s²3p⁴ configuration. The new data has a small effect on $T_{\rm e}$ values obtained from the $I(\lambda 7135~\AA + \lambda 7751~\AA)/ I(\lambda 5192~\AA)$ line ratio, and a larger effect on the $N_{\rm e}$ values obtained from the $I(\lambda 7135~\AA)/I(\lambda 9~\mu {\rm m})$ line ratio. The final effective collision strength data is archived online.

Key words: atomic data - atomic processes - ISM: planetary nebulae: general

1 Introduction

Argon is an important species for TOKAMAK studies, being used as a gas to radiatively cool the divertor and as a potential means of mitigating plasma disruptions (Whyte et al. 2002). In particular, Ar III lines have been shown to provide useful spectral diagnostics for astrophysical studies (Keenan & McCann 1990; Keenan & Conlon 1993). The 3s²3p⁴(¹D₂) $\rightarrow$ 3s²3p⁴(³P_1,2) and 3s²3p⁴(¹S₀) $\rightarrow$ 3s²3p⁴(¹D₂) transitions of Ar III emit strongly in planetary nebulae (Aller & Keyes 1987; Perez-Montero et al. 2007), and the 3s²3p⁴(³P₁) $\rightarrow$ 3s²3p⁴(³P₂) transition is seen in H II regions (Pipher et al. 1984). Transitions within the first 5 levels of Ar²⁺ have been shown to be very useful as spectral diagnostics. The ratio of $I(\lambda 7135~\AA + \lambda 7751~\AA)/ I(\lambda 5192~\AA)$ has been shown to be a good indicator of electron temperature (DeRobertis et al. 1987; Keenan & McCann 1990), and the ratio $I(\lambda 7135~\AA)/I(\lambda 9~\mu {\rm m})$ is density sensitive in the range 10²-10⁸ (cm^-3) (Keenan & Conlon 1993).

There has been much recent interest in improving the atomic data available for the low ion stages of argon, in particular for the excitation data that is required to model collision dominated plasmas. R-Matrix with pseudostates electron-impact excitation data was recently calculated for neutral argon (Ballance & Griffin 2008) and Ar⁺ (Griffin et al. 2007). Madison et al. (2004) calculated electron-impact excitation from the 3p⁵3d states of neutral argon using an R-Matrix method and two first order distorted-wave methods. For Ar²⁺, Johnson & Kingston (1990)calculated excitations within the configuration 3s²3p⁴ and 3s3p⁵ of Ar²⁺ using the R-Matrix method. Their results were generated in LS coupling and transformed to level-resolution using the JAJOM (Saraph 1978) method. Later Galavis et al. (1995) also used the R-Matrix method to calculate level-resolved excitations within the 3s²3p⁴ configuration as part of the IRON project. They used a large configuration-interaction calculation to get the atomic structure, followed by a smaller collision calculation. Burgess et al. (1997) pointed out that the 3s²3p⁴(¹D) $\rightarrow$ 3s²3p⁴(¹S) quadrupole effective collision strength of Galavis et al. (1995) did not appear to go to the expected high energy Born limit point. Galavis et al. (1998) then found that including more partial waves in the calculation for this transition increased the collision strength at higher energies, making it trend closer to the expected limit point. Neither the Johnson & Kingston (1990) or the Galavis et al. (1995) calculations include n=4 states in their target configurations.

On the experimental side, Boffard et al. (2007) measured optical emission cross sections for excitation from the ground state of neutral Ar to excited states. Jung et al. (2007) measured excitation cross sections for excitation of the metastable levels of neutral Ar to the 3p⁵5p configuration. Strinic et al. (2007) measured excitation coefficients for Ar⁺. To the best of our knowledge there are no experimental measurements of excitation cross sections for Ar²⁺.

The aim of this work is to use the R-Matrix method to calculate electron-impact excitation of Ar²⁺, including excitation up to the 5s subshell. This should improve upon the previous R-Matrix calculations for the first nine levels of this ion by including more resonance channels. It will also provide accurate atomic data for the excited configurations, which have not been calculated before using the R-Matrix method. With increased computational resources, R-Matrix calculations have developed from relatively small LS-coupled calculations, to large calculations involving hundreds of levels. Initially, level-resolved calculations were done by transforming LS calculations using the JAJOM (Saraph 1978) method, however this was found to contain potential problems, see Griffin et al. (1998), so the intermediate-coupling frame-transformation method (ICFT) was introduced by Griffin et al. (1998). Level-resolved Breit-Pauli calculations also became feasible because of large scale parallelization of the codes and were found to produce very similar results to the ICFT method, see Griffin et al. (1998). The ICFT method is computationally less demanding as it requires the diagonalization of LS-resolved Hamiltonians rather than LSJ-resolved Hamiltonians. As a large number of levels are involved in our calculation, resulting in thousands of transitions, we use the ICFT calculation as a consistency check on our Breit-Pauli calculation. We also note that fully relativistic Dirac R-Matrix calculations are also now possible for systems involving hundred of levels, see for example Ballance & Griffin (2008). We do not expect fully relativistic effects to be important for Ar²⁺.

Coupling to the target continuum was found to be large for neutral argon excitation data, decreasing the collision strength by up to a factor of two above the ionization threshold, see Ballance & Griffin (2008). The effect was found to be smaller, but still significant for Ar⁺, Griffin et al. (2007) found up to 30% decrease in collision strength above the ionization threshold. We expect the effect to be small for Ar²⁺, thus a non-pseudostate R-Matrix calculation should be sufficient. However, we examined our collision strength data above the ionization threshold for evidence of an artificial rise in the collision strength due to continuum coupling effects being omitted.

We will present results from three R-Matrix calculations. We will first compare an ICFT and Breit-Pauli calculation as a check on our results. Then we will show results from a Breit-Pauli calculation with the first 9 level energies shifted to NIST (2008) energy values. This last calculation will then be compared with literature values, and the effect of the new data on diagnostic line ratios will be discussed.

In the next section we will describe the theoretical methods used. Section 3 will then show the results of the comparison between the different theoretical methods and Sect. 4 will present our conclusions.

2 Theory

2.1 Atomic structure calculation and optimization

We use the AUTOSTRUCTURE (Badnell 1986) code, a many body Breit-Pauli structure package, to calculate the structure of the target used in our collision calculations. The graphical interface to AUTOSTRUCTURE, GASP (Graphical Autostructure Package, http://vanadium.rollins.edu/GASP/GASP.html) was used to run the AUTOSTRUCTURE code. We have included the following configurations in our calculation: 3s²3p⁴, 3s3p⁵, 3p⁶, 3p⁵3d and 3s²3p³nl (3d $\leqslant$ nl $\leqslant$ 5s). We found a significant improvement in the first 9 energy levels by including the 3p⁵3d configuration. The average percentage difference within the first 9 energy levels and those from NIST (2008) was 11.16% excluding the 3p⁵3d configuration, and 4.83% by including it in our structure. The same configurations were used in our scattering calculation.

Our structure was optimized by using a singular value decomposition (Golub & Van Loan 1989) method to give best agreement with selected NIST (2008) values for the level energies and line strengths. The orbitals were determined by using a Thomas-Fermi-Dirac-Amaldi (TFDA) statistical potential. To optimize our structure we make use of scale factors for the wavefunctions in each orbital. These scale factors, or $\lambda$ s, enable us to adjust the radial extent of the wavefunctions for each orbital. These small adjustments allow some fine tuning of the atomic structure and the associated line strengths.

We developed a code (LAMDA) to optimize our atomic structure by varying the $\lambda$ scale factors. This is similar to the approach of Bautista (2008). In order to monitor and compare the quality of our atomic structure, we make use of the NIST table quantities. The selected quantities that we wish to reproduce are the NIST energy (levels or terms) $Ei_{\rm nist}$ , and either the line strengths $Sij_{\rm nist}$ , the collision strengths $fij_{\rm nist}$ , or Einstein coefficients $Aij_{\rm nist}$ . In our modeling we prefer to use line strengths due to their greater independence of energies. Some of the NIST line strengths $Sij_{\rm nist}$ have a big uncertainty listed on the tables, therefore our code is able to chose the ones that have a small listed error, in this case we chose line strengths with less than 10% error. We optimized on the 114 NIST energy levels that were also in our structure calculation. Since the energies and line strengths depend upon the scale factors ( $\lambda$ s), we linearize both and approximate the relation between our chosen NIST quantities and our modeled values as $E_{\rm nist}~{\approx}~E_{\rm model} (\lambda) + \frac{\partial E}{\partial \lambda}\delta\lambda$ , and $S_{\rm nist}~{\approx}~S_{\rm model}(\lambda) + \frac{\partial S}{\partial \lambda}\delta\lambda$ .

To include both of these different quantities in our optimization we normalize both of them with their respective NIST values, therefore

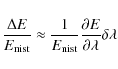$\begin{displaymath}\frac{\Delta E}{E_{\rm nist}}~{\approx}~\frac{1}{E_{\rm nist}} \frac{\partial E}{\partial \lambda} \delta\lambda \end{displaymath}$

(1)

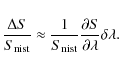$\begin{displaymath}\frac{\Delta S}{S_{\rm nist}}~{\approx}~\frac{1}{S_{\rm nist}}\frac{\partial S}{\partial \lambda} \delta\lambda. \end{displaymath}$

(2)

This way we get our complete model for any n number of energies, any m number of line strengths, and l number of scale factors as

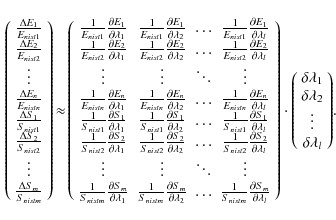$\begin{displaymath}{\bf } \left( \begin{array}{c} \frac{\Delta E_1}{E_{nist ... ..._2 \\ \vdots \\ \delta\lambda_l \end{array} \right)\!. \end{displaymath}$

(3)

We rewrite the model in vector notation as ${\bf\Delta {\vec P}}~{\approx}~{\bf M} \cdot {\delta \lambda}$ where we have defined ${\bf\Delta {\vec P}}$ as the normalized vector for the difference of quantities, ${\bf M}$ as the normalized Jacobian matrix, and ${\delta\lambda}$ as the correction scale factors vector. We write the solution of the vector of the correction of the scale factors as ${\delta\lambda}~{\approx}~{\bf M^{-1}} \cdot {\bf\Delta {\vec P}}$ . Having the correction for the scale factors we use them to get the new scale factors $\boldmath {\lambda}_{\rm new} = \boldmath {\lambda}_{\rm old} + {\delta\lambda}$ . With these new scale factors we recompute our model and compare it again with the NIST selected quantities. We rerun the whole process again until we are satisfied with the results. To measure the success of the optimization we compare the initial and final values for the least square $\chi^2$ which is given by $\chi^2 = \Delta P_1^2 + \Delta P_2^2 + \ldots + \Delta P_{N+M}^2$ . To get the inverse of the normalized $(n+m) \times l$ Jacobian matrix ${\bf M}$ which may not be square $(n+m) \neq l$ , and it may be singular. We decompose the matrix by using Singular Value Decomposition (Golub & Van Loan 1989). We express ${\bf M}$ as

$\begin{displaymath}{\bf M} = {\bf U} \cdot {\bf S} \cdot {\bf V^T} \end{displaymath}$

(4)

Where ${\bf U}$ is a $(n+m) \times (n+m)$ unitary matrix, ${\bf S}$ is a $(n+m) \times l$ diagonal matrix with nonnegative real numbers on the diagonal, and ${\bf V^T}$ denotes the conjugate transpose of ${\bf V}$ , an $l \times l$ unitary matrix. These matrices have the following properties

the columns of ${\bf V}$ form a set of orthonormal input or analyzing basis vector directions for ${\bf M}$ ;
the columns of ${\bf U}$ form a set orthonormal output basis vector directions for ${\bf M}$ ;
the matrix ${\bf S}$ contains the singular values, which can be thought of as scalar gain controls by which each corresponding input is multiplied to give a corresponding output.

Therefore the ``inverse'', or pseudoinverse, is given by

$\begin{displaymath}{\bf M^{-1}}~{\approx}~{\bf V} \cdot {\bf S^{-1}} \cdot {\bf U^T}. \end{displaymath}$

(5)

The matrix ${\bf S}$ is a diagonal matrix that contains K singular values. The number K determines the rank of the matrix, and the singular values are ordered in descending value $S_1 > S_2 > \ldots > S_K$ . The K rank of the matrix represents the number of ``dimensions''. The difficulty is to select the p number of singular values that we need to compute the pseudoinverse where $p \le K$ . Since we need to compute the vector of the scale factor corrections $\boldmath {\delta\lambda}$ we choose to put some physical constraints in order not to affect the different atomic orbitals by too much while we optimize others. Therefore we choose a range of values for the total scale factors given by

$\begin{displaymath}0.8 \le {\boldmath {\lambda}}_{\rm new} = {\boldmath {\lambda}}_{\rm old} + {\boldmath {\delta\lambda}} \le 1.2. \end{displaymath}$

(6)

With this restriction in place we select the p number of singular values to compute the singular values inverse matrix ${\bf S^{-1}}$ . There is not a specific method to know how many p singular values we need to compute the inverse of the singular values matrix. We use the number of singular values we need to meet condition (6). If condition (6) is not met, we multiply the Jacobian matrix by a certain factor greater than one and then compute the corrections again. If condition (6) still goes unmet, we again multiply the Jacobian matrix by a greater factor and recompute the optimization. The reason we multiply the Jacobian matrix by a factor greater than one is to increase the value of its derivatives, thereby reducing the size of the corrections for the scale factors $\boldmath {\delta\lambda}$ and to satisfy condition (6).

We obtained good results from the optimization process with a $\chi^2 = 4.13$ before the optimization and a $\chi^2 = 0.33$ after the optimization. That represents an improvement of 92.01% in our $\chi^2$ value. We found that this optimization method gave us better results than AUTOSTRUCTURE's default optimization of minimization of energies which gives a $\chi^2 = 2.07$ . We also found better average percentage difference within the first 9 energy levels and those from NIST. AUTOSTRUCTURE's default optimization gives a 20.03% difference while our optimization method gives 4.83%.

2.2 The R-Matrix method

The scattering calculation was performed with our set of parallel R-Matrix programs (Mitnik et al. 2003; Ballance & Griffin 2004), which are extensively modified versions of the serial RMATRIX I programs of Berrington et al. (1995). The method is based on partitioning the configuration space in to two regions by a sphere of radius a centered on the target nucleus. In the internal region $r \le a$ electron exchange and correlation between the scattered electron and the the N-electron target atom or ion are important and the (N+1)-electron collision complex behaves in a similar way to a bound state. In the external region r > a electron exchange between the scattered electron and the target can be neglected if the radius a is chosen so that the charge distribution of the target is contained within the sphere. Outside the R-Matrix box, the total wavefunction for a given LS symmetry is expanded in basis states given by:

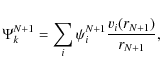$\begin{displaymath}\Psi^{N+1}_k = \sum_i \psi^{N+1}_i {v_i(r_{N+1})\over r_{N+1}}, \end{displaymath}$

(7)

where v_i(r) are radial continuum functions obtained by solution of radial asymptotic coupled differential equations. The inner and outer solutions are matched at the edge of the R-Matrix box to extract collision strengths.

In this paper we have employed both the Breit-Pauli and ICFT (Intermediate Coupling Frame Transformation) R-Matrix methods for electron-impact excitation (Griffin et al. 1998). The original impetus for the ICFT approach was to reduce the time consuming diagonalisation of each large Breit-Pauli Hamiltonian. In the ICFT method, as each partial wave includes only the mass-velocity and Darwin corrections to the LS $\Pi$ N+1 Hamiltonian and omits the spin-orbit interaction; this greatly reduces the size of each symmetric matrix to be diagonalised. In the outer region, the resulting LS-coupled scattering S- or K-matrices are transformed to jK coupling by means of an algebraic transformation to provide level-to-level excitation cross sections. This transformation involves TCC's (Term Coupling Coefficients) which are calculated from a Breit-Pauli structure calculation (including spin-orbit interaction), to express the eigenvectors for the resulting levels as linear combinations of the multi-configuration mixed terms. The coefficients of this expansion are the TCCs. With the implementation of a parallel versions of our codes, and for the scale of calculations described in this paper, both methods would take a similar amount of time, however the ICFT approach remains better suited for small memory serial machines and/or small parallel clusters as calculations increase in size. The consistency of results between ICFT and Breit-Pauli calculations reported later in this paper should provide a lower bound on the error we would expect in the subsequent collisional-radiative modeling. Effective collision strengths are generated from our R-Matrix collision strength data via convolution with a Maxwellian electron distribution.

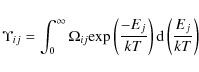$\begin{displaymath}\Upsilon_{ij} = \int_0^{\infty} \Omega_{ij} {\rm exp}\left(\frac{-E_j}{kT}\right){\rm d}\left(\frac{E_j}{kT}\right) \end{displaymath}$

(8)

where E_j is the energy of the outgoing electron and $\Omega_{ij}$ is the collision strength between i and j. We will make use of Burgess-Tully plots (Burgess et al. 1997) to show effective collision strengths from threshold to the infinite energy point on a single plot. For the type-2 transition that we will consider, this involves the following transformations:

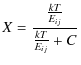$\displaystyle X = \frac{\frac{kT}{E_{ij}}}{\frac{kT}{E_{ij}} + C}$			(9)
$\displaystyle Y = \Upsilon_{ij}$			(10)

where E_ij is the energy of the transition i to j, and C is an arbitrary constant. We will use a C-value of 5.0 to compare with the Burgess-Tully results shown in Galavis et al. (1998).

2.3 Collisional radiative model

We use the ADAS (http://www.adas.ac.uk) suite of codes for our population and emission modeling. These codes are based on collisional-radiative theory, first developed by Bates et al. (1962) and later generalized by Summers & Hooper (1983). The method aims to encompass both the low density coronal and high density local thermodynamic equilibrium description of an ion and to track the shifting balance between radiative and collisional processes. The ion consists of a set of levels with radiative and collisional couplings. Ionization and recombination to and from metastables of the next ionization stage (i.e. the plus ion stage) are included. The time dependence of the population (N_i) of an arbitrary level i in ion stage +z is given by

$\displaystyle \frac{{\rm d}N_i}{{\rm d}t}$	=	$\displaystyle \displaystyle\sum_{\sigma}n_{\rm e}N_{\sigma}^{z+1} (\alpha_i^{\r... ...d}+n_{\rm e}\alpha_i^3) +\displaystyle\sum_{j<i}N_jn_{\rm e}q^{\rm e}_{j \to i}$
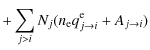		$\displaystyle +\displaystyle\sum_{j>i}N_j(n_{\rm e}q^{\rm e}_{j \to i}+A_{j \to i})$
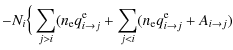		$\displaystyle -N_i \Big\{\displaystyle\sum_{j>i}(n_{\rm e}q^{\rm e}_{i \to j} +\displaystyle\sum_{j<i}(n_{\rm e}q^{\rm e}_{i \to j}+A_{i \to j})$
		$\displaystyle +\displaystyle\sum_{\sigma}(n_{\rm e}S_{i \to \sigma}+A^{\rm a}_{i \to \sigma}) \Big\}$	(11)

where $n_{\rm e}$ is the free electron density. A is the usual Einstein coefficients, $A^{\rm a}$ is the Auger rate, and $q^{\rm e}$ is the electron collisional excitation/de-excitation rate. $\alpha^{\rm r}$ , $\alpha^{\rm d}$ and $\alpha^3$ denote radiative, dielectronic and three-body recombination, respectively. $\sigma$ denotes the ground and metastable indices of the z+1 ion stage. It can be shown that we can reduce the equation to a more compact form.

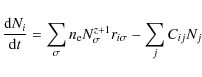$\begin{displaymath}\frac{{\rm d}N_i}{{\rm d}t} = \displaystyle\sum_{\sigma}n_{\rm e}N_{\sigma}^{z+1} r_{i\sigma}-\displaystyle\sum_{j}C_{ij}N_j \end{displaymath}$

(12)

with a populating term for $i \ne j$

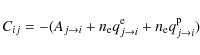$\begin{displaymath}C_{ij}=-(A_{j \to i}+n_{\rm e}q^{\rm e}_{j \to i}+n_{\rm e}q^{\rm p}_{j \to i}) \end{displaymath}$

(13)

a loss term

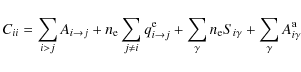$\begin{displaymath}C_{ii}=\displaystyle\sum_{i>j}A_{i \to j} +n_{\rm e}\display... ...e}S_{i\gamma} +\displaystyle\sum_{\gamma}A^{\rm a}_{i\gamma} \end{displaymath}$

(14)

and a composite recombination coefficient $r_{i\sigma}=\alpha^{\rm r}_i+ \alpha^{\rm d}_i+N_e\alpha^3_i$ . Setting the time dependence of the excited states to zero allows the population of the excited levels to be determined as functions of the ground and metastable populations of the Z ion stage ( $N_{\rho}$ ) and of the Z+1 ion stage ( $N_{\sigma}^{Z+1}$ )

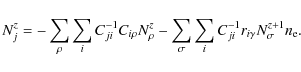$\begin{displaymath}N^z_j=-\displaystyle\sum_{\rho}\displaystyle\sum_{i}C^{-1}_{j... ...yle\sum_{i}C^{-1}_{ji} r_{i\gamma}N^{z+1}_{\sigma}n_{\rm e}. \end{displaymath}$

(15)

A spectral line intensity ratio for a homogeneous plasma is evaluated via

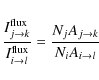$\begin{displaymath}\frac{I_{j \rightarrow k}^{\rm flux}}{I_{i \rightarrow l}^{\r... ...} = \frac{N_j A_{j \rightarrow k}}{N_i A_{i \rightarrow l}} \end{displaymath}$

(16)

and an energy intensity ratio is given by

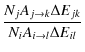$\displaystyle \frac{I_{j \rightarrow k}^{\rm energy}}{I_{i \rightarrow l}^{\rm energy}}$	=	$\displaystyle \frac{N_j A_{j \rightarrow k} \Delta E_{jk}}{N_i A_{i \rightarrow l} \Delta E_{il}}$
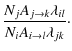	=	$\displaystyle \frac{N_j A_{j \rightarrow k} \lambda_{il}} {N_i A_{i \rightarrow l} \lambda_{jk}}\cdot$	(17)

When comparing with spectral line ratios observed from planetary nebulae we will use this latter equation, since the observations will be of the energy absorbed at a given wavelength.

3 Results

Our results can be split into three main areas: structure, collisional data and emission modeling.

3.1 Structure

Our final optimized structure consisted of configurations 3s²3p⁴, 3s3p⁵, 3p⁶, 3p⁵3d, and 3s²3p³nl (3d $\le$ nl $\le$ 5s), giving a total of 186 levels. Our optimized lambda parameters, obtained using our singular value decomposition code, are given in Table 1. Our structure was optimized using NIST energy levels and line strengths. The level energies from our structure calculation are given in Table 2. We show results for the first 29 levels, the remaining energies can be found in the archived datafile (see http://www-cfadc.phy.ornl.gov/data_and_codes). The average percentage error between our calculated energies and the NIST energies is 3.46%. The largest error is for the 3s²3p⁴(¹D₂) level. Because of the diagnostic importance of the transitions within the 3p⁴ configuration, we will shift to NIST values all the energies associated with the 3p⁴ and 3s3p⁵ configurations. This will be described in the next section.

Table 1: Final $\lambda$ values for the 1s-5s orbitals.

Table 2: Energies in Rydbergs for the lowest 29 levels of Ar²⁺.

As a further check on our structure, we present a selection of our calculated radiative rates in Table 3, we show our calculated radiative rates compared with NIST (2008) values and the calculations of Mendoza & Zeippen (1983). The average percentage difference between the NIST Einstein A coefficients and ours is 65.36%. We note that for most of the transitions the NIST uncertainty estimates on the Einstein A coefficients are 25% or $\geq$ 50%, our Einstein A coefficients are in general within the NIST uncertainty estimates. In the dataset we use for our emission modeling the Einstein A coefficients for transitions within the 3s²3p⁴ configuration will be replaced by the calculated values of Mendoza & Zeippen (1983). This will allow us to make a direct comparison with previous modeling results from the literature, highlighting the differences due to the excitation data only. However, our final archived dataset will contain our calculated Einstein A coefficients.

3.2 Scattering calculations

The orbitals used in our R-Matrix calculations were generated from the AUTOSTRUCTURE (Badnell 1986) code using the optimized $\lambda$ parameters from Table 1. Our exchange calculation included partial waves from L=0 to L=14 (J=0.5 to J=11.5 for the Breit-Pauli calculation). The non-exchange calculation went from L=10 up to L=40 (J=12.5 to J=37.5). The contributions from higher partial waves were then calculated for dipole transitions using the method originally described by Burgess (1970) and for the non-dipole transitions assuming a geometric series in L, using energy ratios, with special procedures for handling transitions between nearly degenerate terms. Using AUTOSTRUCTURE (Badnell 1986), we also calculated infinite energy Bethe/Born limits, allowing us to extend the effective collision strengths and rate coefficients to temperature ranges above the highest calculated collision strength. In our outer region calculations, we used 80 000 energy mesh points over the resonance region (up to 6 Ryd) and 500 energy mesh points for the higher energies (6 Ryd to 12 Ryd).

Table 3: Comparisons of selected radiative rates for transitions in Ar²⁺.

It has been shown by Griffin et al. (1998) that an ICFT calculation would produce the same results as a Breit-Pauli calculation. As a check on our calculation we performed an ICFT and a Breit-Pauli calculation using the same set of radial orbitals for both. Figure 1 shows the ICFT and Breit-Pauli collision strength for the 3s²3p⁴(¹P₂) $\rightarrow$ 3s²3p⁴(¹D₂) transition. Although small differences can be seen, the two calculations are clearly very close to each other.

This level of agreement was typical for the collision strengths calculated. The 186 levels in our Ar²⁺ calculation give rise to 17 205 transitions. We used the scatterplot method of Witthoeft et al. (2007) to compare the Maxwellian effective collision strengths for all of the transitions at one time. This method takes the ratio of effective collision strengths for all transitions for a given temperature and plots this ratio against one of the effective collision strengths. Thus a ratio of one would indicate the datasets are the same. This method also allows one to see the strength of the transitions that are in disagreement. We chose an electron temperature of 1.55 eV as one typical of planetary nebula and low enough to strongly sample the resonance region of the collision strengths. Of the 17 205 transitions, 82% of the ICFT effective collision strengths are within 10% of the Breit-Pauli values. 94% of the ICFT effective collision strengths are within 20% of the Breit-Pauli values and 98% are within 40%. Of the transitions that show a difference, they are in general for weaker transitions involving highly excited levels with effective collision strengths that are extremely sensitive to the resonance contributions on top of a weak background. These transitions are not likely to make a difference in population modeling. For example, the transitions within the 3p⁴ configuration are within 4% of each other. Population modeling using the ICFT and Breit-Pauli datasets produces essentially the same excited populations for all cases we investigated. For the final data set we used the Breit-Pauli results.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1743fig1.eps} \end{figure}$	Figure 1: Comparison of the ICFT and Breit-Pauli collision strengths for the 3s²3p⁴(³P₂) $\rightarrow$ 3s²3p⁴(¹D₂) transition. The dashed line shows the ICFT results and the solid line shows the Breit-Pauli results.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{1743fig2.eps} \end{figure}$	Figure 2: Scatter plot showing the ratio of effective collision strengths at Te = 1.55 eV between two Breit-Pauli R-Matrix calculations. One had 40 000 energy mesh point in the resonance region, the other had 80 000 energy mesh points in the resonance region. We show the ratio of effective collision strength vs. the effective collision strength of the 40 000 energy mesh calculation.
Open with DEXTER

To provide the most accurate data for modeling, a Breit-Pauli calculation was then done with shifts to NIST energies for the first 9 energy levels, due to their importance in spectral line diagnostics. To test the convergence of our energy mesh over the resonance region we performed a series of calculations using different meshes, namely 10 000, 20 000, 40 000 and 80 000 mesh points in the resonance region. We calculated Maxwellian averaged effective collision strengths for each of these meshes and compared the files. Figure 2 shows a scatterplot comparison of our Breit-Pauli calculation using 40 000 and 80 000 mesh points in the resonance region. Of the 17 205 transitions, most are converged, with a few outliers. There was a progression of convergence as the mesh was increased. For example, comparing calculations with 20 000 and 40 000 energy mesh points in the resonance region we found that 93.4% of the transitions were converged to within 2% of each other. Comparing the 20 000 and 40 000 energy mesh point calculations, 96.4% of the transitions were converged to within 2% of each other. Finally, comparing the 40 000 and 80 000 energy mesh point calculations, 98.4% of the transitions were converged to within 2% of each other, with 95.5% being within 1%. Thus, we believe that our 80 000 enegy mesh point calculation is converged.

$\begin{figure} \par\includegraphics[width=8.3cm,clip]{1743fig3.eps} \end{figure}$

Figure 3:

Comparison of selected Breit-Pauli collision strengths (with energy shifts included for the first 9 energy levels) with Johnson & Kingston (1990). Plot a) shows the 3p⁴(³P₂) $\rightarrow$ 3p⁴(³P₀) transition. Plot b) shows the 3p⁴(³P) $\rightarrow$ 3p⁴(¹D) transition, where the level-resolved Breit-Pauli collision strengths have been summed to give the term-resolved collision strength. Plot c) shows the 3p⁴(³P) $\rightarrow$ 3p⁴(¹S) transition, where the level-resolved Breit-Pauli collision strengths have been summed to give the term-resolved collision strength. Plot d) shows the 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀) transition. In all plots the solid line shows the Breit-Pauli results and the dot-dashed line shows the Results of Johnson & Kingston (1990).

Open with DEXTER

Of the previous R-Matrix calculations, we can compare with the collision strengths from Johnson & Kingston (1990), see Fig. 3 for a comparison of a selection of transitions. There are clear differences in the resonance positions and heights, with the background collision strengths being in good agreement. The differences in the resonance contributions may be due to the well known problems with the JAJOM method (Griffin et al. 1998) that was used by Johnson & Kingston (1990) to transform the LS results to LSJ resolution.

We can compare our effective collision strength results with the IRON project data of (Galavis et al. 1995), and with the tabulated values of Johnson & Kingston (1990). Figure 4 shows the comparison for a selection of transitions. Table 4 shows our calculated effective collision strengths for transitions between the 3s²3p⁴ levels. At the highest temperatures, our effective collision strengths are consistently higher than the previous calculations. Since we have a similar background cross-section, the differences are due to the extra resonance channels included in our calculation, and to a lesser extent differences in our top-up procedures. Most transitions show differences at low temperatures where sensitivity to the low energy resonance contribution is strongest. This is particularly true for the transitions 3p⁴(³P₂) $\rightarrow$ 3p⁴(¹S₀) and 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀), shown in Fig. 4e and f). In both cases our effective collision strengths are smaller than previous calculations at the lowest temperatures. This is most likely due to the contributions from near threshold resonances. For example, the 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀) transition has contribution due to a reported 3s3p⁵(³P)3d(²P) resonance that occurs at the excitation threshold in the previous R-Matrix calculations of Johnson & Kingston (1990). Galavis et al. (1995) also point out the large contribution from a near threshold resonance in their calculation of this transition. The near threshold resonance in the 3p⁴(³P) $\rightarrow$ 3p⁴(¹S) transition is likely to be due to the same resonance. We do not see this near threshold resonance in our calculations for either of these transitions. As will be seen later, these two transitions are key for spectral diagnostics. Thus, we performed a smaller R-Matrix calculation, using the same configurations as Johnson & Kingston (1990). In this calculation we do see a near threshold resonance in the 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀) transition, as seen in previous work. We identified the resonances as belonging to the J=3/2 partial wave. Investigation of the eigenphase sum shows that this broad resonance belongs to the 3s3p⁵3d configuration, and is shifted to lower energy in our larger Breit-Pauli calculation. Thus it does not contribute to our collision strength. Our resonance position should be more accurate, due to the larger number of configurations in our structure calculation. However, this resonance is very close to the excitation threshold and is clearly sensitive to configuration interaction effects. Experimental measurements of this collision strength would be very useful.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1743fig4.eps} \end{figure}$

Figure 4:

Comparison of selected Breit-Pauli effective collision strengths (with energy shifts included for the first 9 energy levels) with Johnson & Kingston (1990) and with Galavis et al. (1995,1998). Plot a) shows the 3p⁴(³P₂) $\rightarrow$ 3p⁴(³P₁) transition. Plot b) shows the 3p⁴(³P₂) $\rightarrow$ 3p⁴(³P₀) transition. Plot c) shows the 3p⁴(³P₁) $\rightarrow$ 3p⁴(³P₀) transition. Plot d) shows the 3p⁴(³P₂) $\rightarrow$ 3p⁴(¹D₂) transition. Plot e) shows the 3p⁴(³P₂) $\rightarrow$ 3p⁴(¹S₀) transition. Plot f) shows the 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀) transition. In all plots the solid line shows the Breit-Pauli R-Matrix results, the dashed line shows the results of Galavis et al. (1995) and the dot-dashed line shows the results of Johnson & Kingston (1990). In plot f) the double-dot dashed line shows the results of Galavis et al. (1998).

Open with DEXTER

Table 4: Effective collision strengths for transitions between the 3s²3p⁴ levels.

At higher temperatures for the 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀) transition we verify the findings of Burgess et al. (1997), and Galavis et al. (1998) that contributions from higher partial waves are required for the effective collision strength to tend to the right limit point. We plot our results for this transition in a Burgess-Tully plot in Fig. 5 to highlight the high energy behaviour. Our results go to a limit point of 1.72, close to the value of 1.68 expected by Burgess et al. (1997). As pointed out by Galavis et al. (1998), the rise in slope of the Burgess-Tully plot towards the limit point does not happen until relatively close to the limit point.

$\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{1743fig5.eps} \end{figure}$

Figure 5:

Burgess Tully plot of effective collision strength vs. reduced temperature (X). Results are shown for transition 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀). In the reduced temperature scale zero corresponds to the value at threshold and one corresponds to the value at the infinite energy point. The solid line shows the results from our Breit-Pauli R-Matrix calculation, the dashed line shows the results from the R-Matrix calculation of Galavis et al. (1995) and the double-dot dashed line shows the results of Galavis et al. (1998) where more partial waves were included compared to their previous calculation. The solid square shows the limit point of Burgess et al. (1997).

Open with DEXTER

3.3 Emission modeling

Our Breit-Pauli atomic dataset was used to model commonly observed forbidden transitions of Ar III. Our modeling data consists of the Breit-Pauli excitation data, including shifts to NIST energies for the first 9 levels. Our dipole Einstein A coefficients were evaluated in our R-Matrix calculation. Our non-dipole Einstein A coefficients came from an AUTOSTRUCTURE calculation. For the purpose of the modeling work in this paper we use the same Einstein A coefficients for transitions within the 3p⁴ configuration as those of Mendoza & Zeippen (1983). These were the Einstein A coefficients used in previous emission models using R-Matrix data from Keenan & McCann (1990), and Keenan & Conlon (1993). Using the same Einstein A coefficients will allow us to highlight differences in emission modeling due to the excitation collision data. The final set of data that is available online will include our computed Einstein A coefficients for all the transitions. We first consider the temperature sensitive energy intensity ratio

R₁	=	$\displaystyle I^{\rm energy}(\lambda 7135~{\rm\AA} + \lambda 7751~{\rm\AA})/I^{\rm energy} (\lambda 5192~{\rm\AA})$
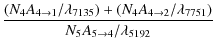	=	$\displaystyle \frac{(N_4 A_{4 \rightarrow 1}/\lambda_{7135}) + (N_4 A_{4 \rightarrow 2}/\lambda_{7751})}{N_5 A_{5 \rightarrow 4}/ \lambda_{5192}}$	(18)

where the numbers in the subscripts of N and A denote the index numbers of the energy levels involved in the transitions. The ratio is insensitive to electron density up to $N_{\rm e} \sim 1 \times 10^5$ (cm^-3). Our results are shown in Fig. 6. We also calculated this ratio using the data of Johnson & Kingston (1990) and the data of (Galavis et al. 1995), where we used Einstein A coefficients from Mendoza & Zeippen (1983) for the radiative rates. We note that the ratio we calculate for the Johnson & Kingston (1990) data is equivalent to that shown by Keenan & McCann (1990). Our R₁ ratio is close to that obtained from the two previous R-Matrix calculations. The excited populations are coronal at low densities and are only sensitive to excitation rate coefficients from the ground to the 3p⁴(¹S₀) level, excitation from the ground to 3p⁴(¹D₂) level, and radiative decay from the 3p⁴(¹S₀) and 3p⁴(¹D₂) levels. Since we use the same Einstein A coefficients in all of our calculations, the differences in our ratio are primarily because our effective collision strength for 3p⁴(³P₂) $\rightarrow$ 3p⁴(¹S₀) is smaller than archived data, due to differences in low energy resonance contributions. Our new R-Matrix data does not make a large difference to the temperatures diagnosed from measured line ratios. Our diagnosed temperatures are within 10% of those diagnosed using the older R-Matrix datasets.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1743fig6.eps} \end{figure}$

Figure 6:

R₁ line ratio as a function of electron temperature. The results are calculated at $N_{\rm e} = 1 \times 10^{3}$ (cm^-3), though the results are insensitive to electron density up to $N_{\rm e} = 1 \times 10^{5}$ (cm^-3). The solid line shows the results using the new R-Matrix Breit-Pauli collision data. The dot-dashed line show the results using the data of Johnson & Kingston (1990) and the dashed line shows the results using the data of Galavis et al. (1995).

Open with DEXTER

Our results for the density sensitive energy intensity ratio

R₂	=	$\displaystyle I^{\rm energy}(\lambda 7135~{\rm\AA})/I^{\rm energy}(\lambda 9~{\rm\mu m})$
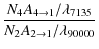	=	$\displaystyle \frac{N_4 A_{4 \rightarrow 1}/\lambda_{7135}}{N_2 A_{2 \rightarrow 1}/\lambda_{90000}}$	(19)

is shown in Fig. 7. We again compare with calculations using the data of Johnson & Kingston (1990) and the data of Galavis et al. (1995). The modeling using the Johnson and Kingston data is equivalent to the ratio shown in Keenan & Conlon (1993). For each temperature one can see that all the R₂ ratios go from their coronal value at low densities to their local thermodynamic equilibrium value by $N_{\rm e} \sim 1 \times 10^8$ (cm^-3). Our ratios are consistently lower than those from the previous R-Matrix calculations. This is primarily due to our collisional excitation rate from the ground to the 3p⁴(¹S₀) being smaller than those from the previous calculations. Our new data makes a significant difference to electron densities diagnosed using the above line ratio. For example, the line ratio for planetary nebula NGC 6572 shown in Keenan & Conlon (1993) is 0.23 and is for an electron temperature of 10 000 K. The new R-Matrix data gives a value of log₁₀ $(N_{\rm e}) = 4.98$ ( $N_{\rm e} = 9.46 \times 10^{4}$ cm^-3) compared with the value given by Keenan & Conlon using the data of Johnson & Kingston (1990) of log₁₀ $(N_{\rm e}) = 4.7 (N_{\rm e} = 5.0 \times 10^{4}$ cm^-3). We found that cascades from higher levels do not affect either the R₁ or R₂ line ratios. Measurement of the excitation cross sections for these forbidden transitions of Ar²⁺ would be very useful, especially measurements that could determine if there is a near threshold resonance in the 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀) and 3p⁴(³P) $\rightarrow$ 3p⁴(¹S) transitions. Our R-Matrix data also includes excitations up to excited configurations. We do not show any modeling results for transitions involving these configurations. We expect this data to be of high quality and intend to use the data to model Ar III spectra in the future. Our final dataset is archived online at the Oak Ridge atomic data center (http://www-cfadc.phy.ornl.gov/data_and_codes) and in the ADAS database (http://www.adas.ac.uk). Tables 2, 3, and 4 are also available in electronic form at the CDS.

$\begin{figure} \par\includegraphics[width=9cm,clip]{1743fig7.eps} \end{figure}$

Figure 7:

R₂ line ratio as a function of electron density. The results are calculated for a range of electron temperatures, namely 5000, 8000, 10 000, 15 000, 20 000 and 30 000 K. The lowest line ratio is the 5000 K results, with the higher ratios showing the progressively higher temperature results. The solid line shows the results using the new R-Matrix Breit-Pauli collision data. The dot-dashed line show the results using the data of Johnson & Kingston (1990) and the dashed line shows the results using the data of Galavis et al. (1995).

Open with DEXTER

4 Conclusions

The results of a 186 level R-Matrix calculations are presented for Ar²⁺.

1.: The results from an ICFT calculation are shown to be close to those from a Breit-Pauli calculation. Our final R-Matrix calculation consists of a Breit-Pauli calculation with the first 9 levels shifted to NIST energies.
2.: We compare the results of this calculation with literature values for transitions within the 3p⁴ configuration, finding differences at low temperatures due to low energy resonance contributions.
3.: We calculate one temperature sensitive and one density sensitive line ratio, finding that our new data does not make a significant differences to the temperature diagnostic, but does have a sizeable affect on the density diagnostic, compared to values calculated using previous R-Matrix data.
4.: Our final effective collision strengths are now available on the Oak Ridge National Laboratory Atomic Data Web (http://www-cfadc.phy.ornl.gov/data_and_codes) and in the ADAS (http://www.adas.ac.uk) database. The data presented at Tables 2, 3, and 4 is also available in electronic form at the CDS.

Acknowledgements

This work was supported by US DoE grant DE-FG02-99ER54367 to Rollins College and US DoE grants DE-FG05-96-ER54348 and DE-FG02-01ER54633 to Auburn University. Most of the computational work was carried out at the National Energy Research Scientific Computing Center in Oakland, California, and at the Alabama Supercomputer in Huntsville, Alabama.

References

Aller, L. H., & Keyes, C. D. 1987, ApJS, 65, 405 [NASA ADS] [CrossRef] (In the text)
Badnell, N. R. 1986, J. Phys. B, 19, 3827 [NASA ADS] [CrossRef] (In the text)
Badnell, N. R., Pindzola, M. S., Bray, I., & Griffin, D. C. 1998, J. Phys. B, 31, 911 [NASA ADS] [CrossRef]
Ballance, C. P., & Griffin, D. C. 2004, J. Phys. B, 37, 2943 [NASA ADS] [CrossRef] (In the text)
Ballance, C. P., & Griffin, D. C. 2008, J. Phys. B. 41, 065201 (In the text)
Ballance, C. P., & Griffin, D. C. 2008, J. Phys. B, 41, 195205 [NASA ADS] [CrossRef] (In the text)
Bates, D. R., Kingston, A. E., & McWhirter, R. W. P. 1962, Proc. Royal Soc. London, 267, 297 [NASA ADS] (In the text)
Bautista, M. A. 2008, J. Phys. B: At. Mol. Opt. Phys, 41, 65701 [CrossRef] (In the text)
Berrington, K. A., Eissner, W. B., & Norrington, P. H. 1995, Comput. Phys. Commun., 92, 290 [NASA ADS] [CrossRef] (In the text)
Boffard, J. B., Chiaro, B., Lin, C. C., & Weber, T. 2007, Atomic Data and Nuclear Data Tables, 93, 831 [NASA ADS] [CrossRef] (In the text)
Burgess, A. 1970, J. Phys. B, 7, L364 [CrossRef] (In the text)
Burgess, A., Chidichimo, M. C., & Tully, J. A. 1997, J. Phys. B, 30, 33 [NASA ADS] [CrossRef] (In the text)
De Robertis, M. M., Dufour, R. J., & Hunt, R. W. 1987, J. Roy. Astron. Soc. Can., 81, 195 [NASA ADS] (In the text)
Galavis, M. E., Mendoza, C., & Zeippen, C. J. 1995, A&AS, 111, 347 [NASA ADS] (In the text)
Galavis, M. E., Mendoza, C., & Zeippen, C. J. 1998, A&AS, 133, 245 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Golub, G. H., & Van Loan, C.F. 1989, Matrix Computations, 2nd edn. (Baltimore: Johns Hopkins University Press), 8.3, Chap. 12 (In the text)
Griffin, D. C., Badnell, N. R., & Pindzola, M. S. 1998, J. Phys. B, 31, 3713 [NASA ADS] [CrossRef] (In the text)
Griffin, D. C., Ballance, C. P., Loch, S. D., & Pindzola, M. S. 2007, J. Phys. B, 40, 4537 [NASA ADS] [CrossRef] (In the text)
Johnson, C. T., & Kingston, A.E. 1990, J. Phys. B, 23, 3393 [NASA ADS] [CrossRef] (In the text)
Jung, R. O., Boffard, J. B., Anderson, L. W., & Lin, C. C. 2007, Phys. Rev. Lett., 75, 052707 [NASA ADS] (In the text)
Keenan, F. P., & McCann, S. M. 1990, J. Phys. B, 23, L423 [NASA ADS] [CrossRef] (In the text)
Keenan, F. P., & Conlon, E. S. 1993, ApJ, 410, 426 [NASA ADS] [CrossRef] (In the text)
Madison, D. H., Dasgupta, A., Bartschat, K., & Vaid, D. 2004, J. Phys. B, 37, 1073 [NASA ADS] [CrossRef] (In the text)
Mendoza, C., & Zeippen, C. J. 1983, MNRAS, 202, 981 [NASA ADS] (In the text)
Mitnik, D. M., Griffin, D. C., Ballance, C. P., & Badnell, N. R. 2003, J. Phys. B, 36, 717 [NASA ADS] [CrossRef] (In the text)
Perez-Montero, E., Hagele, G. F., Contini, T., & Diaz, A. I. 2007, MNRAS, 381, 125 [NASA ADS] [CrossRef] (In the text)
Pipher, J. L., Helfer, H. L., Herter, T., et al. 1984, ApJ, 285, 174 [NASA ADS] [CrossRef] (In the text)
Ralchenko, Yu., Kramida, A. E., Reader, J., & NIST ASD Team. 2008, NIST Atomic Spectra Database, version 3.1.5, http://physics.nist.gov/asd3, National Institute of Standards and Technology, Gaithersburg, MD (In the text)
Saraph, H. E. 1978, Comput. Phys. Commun., 15, 247 [NASA ADS] [CrossRef] (In the text)
Strinic, A. I., Malovic, G. N., Petrovic, Z. L., & Sadeghi, N. 2007, Plasma, 75, 052707 (In the text)
Summer, H. P., & Hooper, M. 1983, Plasma Physics, 25, 1311 [NASA ADS] [CrossRef] (In the text)
Whyte, D. G., Jernigan, T. C., Humphreys, D. A., et al. 2002, Phys. Rev. Lett., 89, 055001 [NASA ADS] [CrossRef] (In the text)
Witthoeft, M. C., Whiteford, A. D., & Badnell, N. R. 2007, J. Phys. B, 40, 2969 [NASA ADS] [CrossRef] (In the text)

Footnotes

... online: Tables 2-4 are also available in electronic form at the CDS viaanonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/500/1253

All Tables

Table 1: Final $\lambda$ values for the 1s-5s orbitals.

Table 2: Energies in Rydbergs for the lowest 29 levels of Ar²⁺.

Table 3: Comparisons of selected radiative rates for transitions in Ar²⁺.

Table 4: Effective collision strengths for transitions between the 3s²3p⁴ levels.

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{1743fig1.eps} \end{figure}$	Figure 1: Comparison of the ICFT and Breit-Pauli collision strengths for the 3s²3p⁴(³P₂) $\rightarrow$ 3s²3p⁴(¹D₂) transition. The dashed line shows the ICFT results and the solid line shows the Breit-Pauli results.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{1743fig2.eps} \end{figure}$	Figure 2: Scatter plot showing the ratio of effective collision strengths at Te = 1.55 eV between two Breit-Pauli R-Matrix calculations. One had 40 000 energy mesh point in the resonance region, the other had 80 000 energy mesh points in the resonance region. We show the ratio of effective collision strength vs. the effective collision strength of the 40 000 energy mesh calculation.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.3cm,clip]{1743fig3.eps} \end{figure}$	Figure 3: Comparison of selected Breit-Pauli collision strengths (with energy shifts included for the first 9 energy levels) with Johnson & Kingston (1990). Plot a) shows the 3p⁴(³P₂) $\rightarrow$ 3p⁴(³P₀) transition. Plot b) shows the 3p⁴(³P) $\rightarrow$ 3p⁴(¹D) transition, where the level-resolved Breit-Pauli collision strengths have been summed to give the term-resolved collision strength. Plot c) shows the 3p⁴(³P) $\rightarrow$ 3p⁴(¹S) transition, where the level-resolved Breit-Pauli collision strengths have been summed to give the term-resolved collision strength. Plot d) shows the 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀) transition. In all plots the solid line shows the Breit-Pauli results and the dot-dashed line shows the Results of Johnson & Kingston (1990).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{1743fig4.eps} \end{figure}$	Figure 4: Comparison of selected Breit-Pauli effective collision strengths (with energy shifts included for the first 9 energy levels) with Johnson & Kingston (1990) and with Galavis et al. (1995,1998). Plot a) shows the 3p⁴(³P₂) $\rightarrow$ 3p⁴(³P₁) transition. Plot b) shows the 3p⁴(³P₂) $\rightarrow$ 3p⁴(³P₀) transition. Plot c) shows the 3p⁴(³P₁) $\rightarrow$ 3p⁴(³P₀) transition. Plot d) shows the 3p⁴(³P₂) $\rightarrow$ 3p⁴(¹D₂) transition. Plot e) shows the 3p⁴(³P₂) $\rightarrow$ 3p⁴(¹S₀) transition. Plot f) shows the 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀) transition. In all plots the solid line shows the Breit-Pauli R-Matrix results, the dashed line shows the results of Galavis et al. (1995) and the dot-dashed line shows the results of Johnson & Kingston (1990). In plot f) the double-dot dashed line shows the results of Galavis et al. (1998).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=9cm,clip]{1743fig5.eps} \end{figure}$	Figure 5: Burgess Tully plot of effective collision strength vs. reduced temperature (X). Results are shown for transition 3p⁴(¹D₂) $\rightarrow$ 3p⁴(¹S₀). In the reduced temperature scale zero corresponds to the value at threshold and one corresponds to the value at the infinite energy point. The solid line shows the results from our Breit-Pauli R-Matrix calculation, the dashed line shows the results from the R-Matrix calculation of Galavis et al. (1995) and the double-dot dashed line shows the results of Galavis et al. (1998) where more partial waves were included compared to their previous calculation. The solid square shows the limit point of Burgess et al. (1997).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{1743fig6.eps} \end{figure}$	Figure 6: R₁ line ratio as a function of electron temperature. The results are calculated at $N_{\rm e} = 1 \times 10^{3}$ (cm^-3), though the results are insensitive to electron density up to $N_{\rm e} = 1 \times 10^{5}$ (cm^-3). The solid line shows the results using the new R-Matrix Breit-Pauli collision data. The dot-dashed line show the results using the data of Johnson & Kingston (1990) and the dashed line shows the results using the data of Galavis et al. (1995).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{1743fig7.eps} \end{figure}$	Figure 7: R₂ line ratio as a function of electron density. The results are calculated for a range of electron temperatures, namely 5000, 8000, 10 000, 15 000, 20 000 and 30 000 K. The lowest line ratio is the 5000 K results, with the higher ratios showing the progressively higher temperature results. The solid line shows the results using the new R-Matrix Breit-Pauli collision data. The dot-dashed line show the results using the data of Johnson & Kingston (1990) and the dashed line shows the results using the data of Galavis et al. (1995).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.