| Issue |
A&A
Volume 500, Number 1, June II 2009
The first 40 years
|
|
|---|---|---|
| Page(s) | 213 - 214 | |
| DOI | https://doi.org/10.1051/0004-6361/200912155 | |
| Published online | 15 June 2009 | |
Special issue
COMMENTARY ON: PACZYNSKI B. AND WIITA P. J., 1980, A&A, 88, 23
The Paczynski-Wiita potential. A step-by-step ``derivation''
M. A. Abramowicz
1 - Dept. Physics, Göteborg Univ., 412-96 Göteborg, Sweden
2 - Copernicus Astronomical Ctr., Bartycka 18, 00-716 Warszawa, Poland
Paczynski realized that a properly chosen gravitational potential may accurately model (in a ``pseudo Newtonian'' theory) general relativistic effects that determine the motion of matter near a nonrotating black hole. Paczynski's choice, known today as the ``Paczynski-Wiita potential'', proved to be very practical. It was used by numerous researchers in the black-hole accretion theory and became a standard tool in relativistic astrophysics. The model is an example of Paczynski's admired ability to invent simple ideas that were brilliant, deep, and useful ``out of nowhere''. Paczynski has intuitively guessed the form of the potential. However, it could be also derived by a step-by-step formal procedure. I show the derivation here that is based on a standard definition of the relativistic ``effective potential'' in the Schwarzschild spacetime. The relativistic effective potential may be uniquely divided into its ``gravitational'' and ``centrifugal'' part. The gravitational part only differs from the Paczynski-Wiita potential by a constant.
Abramowicz et al. (1978), working in Paczynski's research group in Warsaw, found a practical mathematical scheme to construct fully relativistic models of thick accretion disks, known today as ``Polish doughnuts''. The models displayed several astrophysically interesting features, among them seriously super-Eddington luminosities, long and narrow funnels that could collimate jets, and a self-crossing ``Roche lobe'' equipotential. The scheme developed in Warsaw was suitable for both analytic and numerical calculations.
Some properties of the thick disks were obviously
connected to the strong-field effects of general relativity. Our leader,
Bohdan Paczynski, who was not familiar with the technicalities
of general relativity, asked me to find a Newtonian way to describe
these effects. I was rather unhappy about Paczynski's request,
because initially I wrongly imagined that the only method adequate for
the task should be the post-Newtonian scheme. It uses tedious, long, and
boring expansions. I was desperately working, producing
longer and longer formulae, when one day Paczynski came to my
office, and said ``Stop working on that. I found the solution.''
And he showed me his solution - a Newtonian![]() potential,
potential,
where r is the spherical radius, M the mass of the black hole, and
This was a brilliant display of the qualities of Paczynski's mind:
he just guessed the right, simple, and powerful solution
to the problem. His solution immediately proved to be very
practical. Shortly afterwards, Paczynski & Wiita (1980) used
(1) to numerically calculate
the models of thick disks. The models differed from those calculated
with the full strength of general relativity by only
a few percent. Later, this opened a flood gate when numerous
authors used the Paczynski-Wiita potential in their
calculations of black-hole accretion flows.
The potential is so remarkably successful that some researchers
use it even outside its obvious limits of applicability:
(a) for rotating black holes, which is wrong because
(1) does not include the
Lense-Thirring effect; and (b) for self-gravitating fluids, which is wrong because
![]() .
.
Why is the Newtonian Paczynski-Wiita potential (1) such an accurate model of the strong relativistic effects? Should this be considered a fortunate, unexpected coincidence, or could one ``derive'' the potential from the first principles of Einstein's general relativity? I remember discussing this question briefly with Thibault Damour in late 1970. Although we were convinced that the ``effective potential approach'' should provide such a derivation, we had not completed the relevant calculations. I summarize them here.
In Newtonian theory, let E be energy, L angular momentum,
![]() gravitational potential, and V radial velocity.
The orbital motion is often described in terms of the effective
potential
gravitational potential, and V radial velocity.
The orbital motion is often described in terms of the effective
potential
![]() ,
,
circular orbits located at the effective potential extrema,
or in terms of the gravitational potential
Let us consider almost circular motion of particles on the
Expansion of the lefthand side yields V2/2. One also defines
This brings Eq. (6) into a form identical with the Newtonian formula (3). Thus, the Newtonian condition (4) for the vanishing derivative of the effective potential may be applied to the relativistic effective potential (7), which gives
Because at the equatorial plane
Comparing Newton's Eq. (5) with Einstein's Eq. (9), we see that the gravitational potential in both equations has to have the same Paczynski-Wiita form (1). In deriving Eq. (9) we used
Thus, the Keplerian angular momentum derived (in the Schwarzschild spacetime) according to Einstein's theory, and derived with the Paczynski-Wiita potential, are both given by the same formula
In Newton's theory the angular momentum L and angular velocity
Nowak & Wagoner (1991) found that the potential given by a fitting formula
reproduces the angular velocity
Semerák & Karas (1999) discuss the Newtonian potential suitable for modeling the gravity of the Kerr black hole, including the Lense-Thirring effect, and Stuchlík & Kovár (2008) for the Schwarzschild-de Sitter spacetime.
Neither these four potentials nor a few other potentials
introduced by some other authors have become popular. Nowadays many more
astrophysicists know Einstein's general relativity than in the late 1970s, but quotations of Paczynski-Wiita potential show no sign of declining![]() .
.
Velocities of matter calculated with the Paczynski-Wiita potential
could exceed the light speed. This creates a serious problem
when one calculates the observed appearance of matter (e.g. spectra)
by the method of ray tracing. Abramowicz et al. (1996) found a
solution to this problem by showing how to incorporate the effects of
special relativity into the Paczynski-Wiita scheme. One should
interpret the ``true'' physical velocities
in terms of the calculated ones by
![]() .
Here V(...) denotes each of the three
components of the velocity, i.e.
.
Here V(...) denotes each of the three
components of the velocity, i.e.
![]() .
.
The Paczynski-Wiita potential (1) accurately models general relativistic effects in the Newtonian theory that determines the motion of matter near a nonrotating black hole. The Paczynski-Wiita potential is neither an approximation of relativistic gravity nor a fitting formula. Instead, it is a unique (``pseudo'') Newtonian model of the gravity of a nonrotating black hole. It reproduces exactly:
- the location of the marginally stable orbit
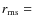 ISCO,
ISCO,
- the location of the marginally bound orbit
 ,
,
- the form of the Keplerian angular momentum L(r).
Acknowledgements
I acknowledge support from the Polish Ministry of Science grant N203 0093/1466 and Swedish Research Council grant VR Dnr 621-2006-3288.
References
- Abramowicz, M. A., Jaroszynski, M., & Sikora, M. 1978, A&A, 63, 221 [NASA ADS]
- Abramowicz, M. A., Beloborodov, A. M., Chen, X.-M., & Igumenshchev, I. V. 1996, A&A, 313, 334 [NASA ADS] (In the text)
- Kluzniak, W., & Lee, W. H. 2002, MNRAS, 335, L29 [NASA ADS] [CrossRef] (In the text)
- Nowak, M. A., & Wagoner, R. V. 1991, ApJ, 378, 656 [NASA ADS] [CrossRef] (In the text)
- Paczynski, B., & Wiita, P. J. 1980, A&A, 88, 23 [NASA ADS] (In the text)
- Semerák, O., & Karas, V. 1999, A&A, 343, 325 [NASA ADS] (In the text)
- Stuchlík, Z., & Kovár, J. 2008, Int. J. Mod. Phys. D, 17, 2089 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... Newtonian
![[*]](/icons/foot_motif.png)
- It is often called ``pseudo Newtonian'' to stress that it does not obey the Poisson equation. However, when the external gravity is fixed (as in the black-hole accretion theory), ``pseudo Newtonian'' is practically equivalent to ``Newtonian''. This is why I am using both terms here.
- ... declining
![[*]](/icons/foot_motif.png)
- Number of quotes in years 2000-2008, according to ADS: 21, 40, 32, 37, 45, 39, 30, 37, 46.
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



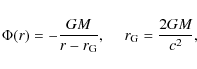
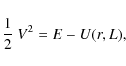
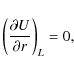
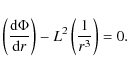
![\begin{displaymath}
\frac{1}{2}\ln(1 + V^2) = \ln (u_t) +
\frac{1}{2}\ln \left[ g^{tt} +
L^2~g^{\phi\phi}\right].
\end{displaymath}](/articles/aa/full_html/2009/22/aa12155-09/img18.png)
![\begin{displaymath}
U(r, L) \equiv -\frac{1}{2} \ln \left[ g^{tt} +
L^2~g^{\phi\phi}\right].
\end{displaymath}](/articles/aa/full_html/2009/22/aa12155-09/img20.png)
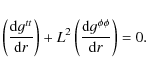
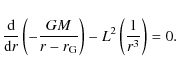
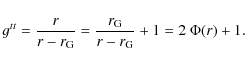
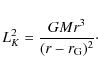
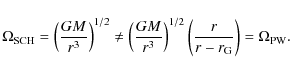
![\begin{displaymath}
\Phi_{\rm NW} = -\left(\frac{GM}{r}\right)\left[ 1 - 3\frac{GM}{r~c^2} +
12\left(\frac{GM}{r~c^2}\right)^2\right]
\end{displaymath}](/articles/aa/full_html/2009/22/aa12155-09/img31.png)
![\begin{displaymath}
\Phi_{\rm KL} = \left(\frac{GM}{3r_{\rm G}}\right)\left[1
- {\rm e}^{3r_{\rm G}/r} \right].
\end{displaymath}](/articles/aa/full_html/2009/22/aa12155-09/img35.png)