| Issue |
A&A
Volume 499, Number 3, June I 2009
|
|
|---|---|---|
| Page(s) | 851 - 863 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200911653 | |
| Published online | 08 April 2009 | |
A self-consistent empirical model atmosphere, abundance
and stratification analysis of
the benchmark roAp star  Circini
Circini![[*]](/icons/foot_motif.png)
O. Kochukhov1 - D. Shulyak2 - T. Ryabchikova2,3
1 - Department of Physics and Astronomy, Uppsala University, Box 515, 751 20 Uppsala, Sweden
2 -
Institute of Astronomy, Vienna University, Turkenschanzstrasse 17, 1180 Vienna, Austria
3 -
Institute of Astronomy, Russian Academy of Science, Pyatnitskaya 48, 119017 Moscow, Russia
Received 13 January 2009 / Accepted 15 March 2009
Abstract
Context. Chemically peculiar (CP) stars are unique natural laboratories for the investigation of the microscopic diffusion processes of chemical elements. The element segregation under the influence of gravity and radiation pressure leads to the appearance of strong abundance gradients in the atmospheres of CP stars. Consequently, the atmospheric temperature-pressure structure of these objects could deviate significantly from the atmospheres of normal stars with homogeneous abundances.
Aims. In this study we performed a self-consistent, empirical model atmosphere study of the brightest rapidly oscillating Ap star ![]() Cir. We account for chemical stratification in the model atmosphere calculations and assess the importance of non-uniform vertical element distribution on the model structure, energy distribution and hydrogen line profiles.
Cir. We account for chemical stratification in the model atmosphere calculations and assess the importance of non-uniform vertical element distribution on the model structure, energy distribution and hydrogen line profiles.
Methods. For the chemical stratification analysis we use the DDAFIT minimization tool in combination with a magnetic spectrum synthesis code. The model atmospheres with inhomogeneous vertical distributions of elements are calculated with the LLMODELS stellar model atmosphere code.
Results. Based on an iterative procedure of the chemical abundance analysis of 52 ions of 35 elements, stratification modeling of 4 elements (Si, Ca, Cr and Fe) and subsequent re-calculations of the atmospheric structure, we derived a new model atmosphere of ![]() Cir which is consistent with the inferred atmospheric chemistry of the star. We find
Cir which is consistent with the inferred atmospheric chemistry of the star. We find
![]() K,
K,
![]() ,
and demonstrate that chemical stratification has a noticeable impact on the model structure and modifies the formation of the hydrogen Balmer lines. At the same time, the energy distribution appears to be less sensitive to the presence of large abundance gradients.
,
and demonstrate that chemical stratification has a noticeable impact on the model structure and modifies the formation of the hydrogen Balmer lines. At the same time, the energy distribution appears to be less sensitive to the presence of large abundance gradients.
Conclusions. Our spectroscopically determined
![]() of
of ![]() Cir agrees with the fundamental effective temperature of this star. This shows that temperatures inferred in detailed spectroscopic analyses of cool magnetic CP stars are not affected by a large systematic bias.
Cir agrees with the fundamental effective temperature of this star. This shows that temperatures inferred in detailed spectroscopic analyses of cool magnetic CP stars are not affected by a large systematic bias.
Key words: stars: abundances - stars: atmospheres - stars: chemically peculiar - stars: individual: ![]() Circini
Circini
1 Introduction
Atmospheres of certain chemically peculiar (CP) B-F type stars are dynamically stable against strong convective and turbulent motion. In combination with strong, large-scale magnetic fields and slow rotation, this provides an ideal condition for microscopic particle diffusion (Michaud 1970). The overall, conspicuously non-solar, chemical signature of the CP-star atmospheres is determined by an interplay between the effects of gravitational settling and radiative levitation of chemical species. Due to rapid variation of thermodynamic properties in the outer stellar envelope, radiative diffusion is also able to produce a vertical element separation within the line-forming atmospheric region of certain CP stars. The resulting picture of chemical stratification depends upon the effective temperature and magnetic field strength of the star (Ryabchikova 2008). However, the light and iron-peak elements generally follow a simple step-like behaviour with a large (relative to solar) element underabundance in the upper atmosphere and an overabundance in the lower photospheric layers (see, for example, Kochukhov et al. 2006; Ryabchikova et al. 2005,2002; Bagnulo et al. 2001). A qualitatively similar chemical stratification is predicted by some available theoretical diffusion calculations (Babel 1992; LeBlanc et al. 2009; LeBlanc & Monin 2004). At the same time, rare-earth elements (REE) show a completely opposite picture with a large overabundance occurring in the superficial atmospheric layers and normal concentration or underabundance in the continuum forming regions (Mashonkina et al. 2008,2005).
Due to large abundance anomalies and chemical gradients, the atmospheric structure of CP stars can deviate significantly from that of the normal B-F stars with similar fundamental parameters and homogeneous atmospheres. For example, the presence of core-wing anomaly in the Balmer line profiles of cool Ap stars indicates that their temperature structure is most likely different from normal stars (Cowley et al. 2001; Kochukhov et al. 2002). If unaccounted for, these effects may lead to significant systematic errors in the determination of the stellar atmosphere and fundamental parameters.
In spite of recent advances in the theoretical treatment of chemical stratification in stellar atmospheres (Alecian & Stift 2007; LeBlanc et al. 2009; LeBlanc & Monin 2004; Hui-Bon-Hoa et al. 2000), existing models cannot be applied for the routine analysis of CP-star atmospheres due to their complexity, uncertainties in the description of relevant physical processes, incomplete atomic data, and occasional lack of self-consistency between the model atmosphere structure and vertical abundance profiles. Instead, empirical stratification studies, which derive element distributions from the observed line profiles, typically employ model atmospheres computed with the assumption of a homogeneous element distribution. This leads to an inconsistency between the inferred stratification and the adopted atmospheric temperature-pressure structure.
The aim of the present paper is to explore a new, alternative approach to the problem of understanding the interplay between non-solar, inhomogeneous chemistry and the atmospheric structure of CP stars. Similar to previous empirical stratification studies, we use high-quality spectroscopic observations to obtain the average chemical composition, vertical distribution of some of the most important elements, and place constraints on the stellar parameters. Then as a second step we include individual abundances as well as chemical stratification in the model atmosphere calculation with our LLMODELS code (Shulyak et al. 2004). This two-stage procedure is repeated until convergence is achieved, providing us with a self-consistent model atmosphere and reliable stellar parameters inferred from best available observations.
We selected the bright (V=3.2), cool magnetic Ap star ![]() Circini (HD 128898, HR 5463, HIP 71908) for our investigation. This star is the brightest of about 40 currently known rapidly
oscillating Ap (roAp) stars and is one of the most promising objects for detailed asteroseismic investigation. It pulsates in several non-radial oscillation modes (Kurtz et al. 1994) and was recently
observed photometrically by the WIRE satellite (Bruntt 2007). The time-resolved spectroscopic
observations of pulsations in
Circini (HD 128898, HR 5463, HIP 71908) for our investigation. This star is the brightest of about 40 currently known rapidly
oscillating Ap (roAp) stars and is one of the most promising objects for detailed asteroseismic investigation. It pulsates in several non-radial oscillation modes (Kurtz et al. 1994) and was recently
observed photometrically by the WIRE satellite (Bruntt 2007). The time-resolved spectroscopic
observations of pulsations in ![]() Cir (Kochukhov et al. 2007; Ryabchikova et al. 2007) allowed us to probe the vertical mode
cross-section and study the dynamics of the outer atmospheric layers enriched in REEs. These studies infer a very different pulsation behaviour of the lines of iron-peak and rare-earth elements, which yields an independent confirmation of the validity of the chemical stratification picture outlined above. The ongoing seismic studies of
Cir (Kochukhov et al. 2007; Ryabchikova et al. 2007) allowed us to probe the vertical mode
cross-section and study the dynamics of the outer atmospheric layers enriched in REEs. These studies infer a very different pulsation behaviour of the lines of iron-peak and rare-earth elements, which yields an independent confirmation of the validity of the chemical stratification picture outlined above. The ongoing seismic studies of ![]() Cir require reliable fundamental parameters and detailed
knowledge of the stellar atmospheric structure.
Cir require reliable fundamental parameters and detailed
knowledge of the stellar atmospheric structure.
A model atmosphere study of ![]() Cir may benefit from a rich collection of photometric,
spectrophotometric, and high-resolution spectroscopic data collected for this star over several
decades. In particular, the availability of the observed UV and optical spectral energy
distribution calibrated in absolute units is very valuable for testing theoretical models with
chemical stratification included. The absence of such data leaves a significant uncertainty in the parameter determinations of magnetic CP stars
(see, for example, Shulyak et al. 2009,2008).
Furthermore, the angular diameter of
Cir may benefit from a rich collection of photometric,
spectrophotometric, and high-resolution spectroscopic data collected for this star over several
decades. In particular, the availability of the observed UV and optical spectral energy
distribution calibrated in absolute units is very valuable for testing theoretical models with
chemical stratification included. The absence of such data leaves a significant uncertainty in the parameter determinations of magnetic CP stars
(see, for example, Shulyak et al. 2009,2008).
Furthermore, the angular diameter of ![]() Cir was recently measured interferometrically
by Bruntt et al. (2008, hereafter BNC08). This allowed a direct determination of the stellar radius for the first time for
any magnetic Ap star. The effective temperature subsequently could be inferred
from the bolometric flux,
almost independently of the model atmosphere techniques (however, still
using theoretically calculated flux for the IR region
due to the lack of spectrophotometric observations). Thus,
Cir was recently measured interferometrically
by Bruntt et al. (2008, hereafter BNC08). This allowed a direct determination of the stellar radius for the first time for
any magnetic Ap star. The effective temperature subsequently could be inferred
from the bolometric flux,
almost independently of the model atmosphere techniques (however, still
using theoretically calculated flux for the IR region
due to the lack of spectrophotometric observations). Thus, ![]() Cir is a unique benchmark cool Ap star
and an extremely useful object for the verification and calibration of various photometric and spectroscopic
techniques of deriving basic
stellar properties. The
Cir is a unique benchmark cool Ap star
and an extremely useful object for the verification and calibration of various photometric and spectroscopic
techniques of deriving basic
stellar properties. The
![]() K found by BNC08 is lower than all previous photometric and
spectroscopic temperature estimates, which span a range of 600 K. This new fundamental temperature
of
K found by BNC08 is lower than all previous photometric and
spectroscopic temperature estimates, which span a range of 600 K. This new fundamental temperature
of ![]() Cir differs significantly from
Cir differs significantly from
![]() K suggested for this star in the
earlier model atmosphere analysis (Kupka et al. 1996), raising doubts about the 150-200 K
K suggested for this star in the
earlier model atmosphere analysis (Kupka et al. 1996), raising doubts about the 150-200 K
![]() accuracy often claimed in the studies of cool Ap stars.
accuracy often claimed in the studies of cool Ap stars.
The chemical composition of the atmosphere of ![]() Cir was first studied by Kupka et al. (1996). Based on new
fundamental values of the atmospheric parameters, BNC08 redetermined abundances for a number of chemical elements using models with solar metallicity and with individual abundances. However, they did not carry out a stratification analysis but assumed a chemically-homogeneous atmosphere both for the line formation and for model atmosphere calculation. On the other hand, Ryabchikova et al. (2008) presented an analysis of the Ca stratification in
Cir was first studied by Kupka et al. (1996). Based on new
fundamental values of the atmospheric parameters, BNC08 redetermined abundances for a number of chemical elements using models with solar metallicity and with individual abundances. However, they did not carry out a stratification analysis but assumed a chemically-homogeneous atmosphere both for the line formation and for model atmosphere calculation. On the other hand, Ryabchikova et al. (2008) presented an analysis of the Ca stratification in ![]() Cir based on the model parameters from Kupka et al. (1996) and neglecting the influence of chemical gradients on the model structure.
Cir based on the model parameters from Kupka et al. (1996) and neglecting the influence of chemical gradients on the model structure.
In this paper we determine abundances and reconstruct the stratification of the most important elements in the atmosphere of ![]() Cir. We then explore the effect of this non-solar, inhomogeneous atmospheric chemistry on the derivation of stellar parameters. Since the non-uniform element distribution
changes the model temperature-pressure structure, we implement an iterative procedure of the
stratification and abundance analysis with the subsequent re-calculation of the model atmosphere
and re-determination of stellar parameters.
Cir. We then explore the effect of this non-solar, inhomogeneous atmospheric chemistry on the derivation of stellar parameters. Since the non-uniform element distribution
changes the model temperature-pressure structure, we implement an iterative procedure of the
stratification and abundance analysis with the subsequent re-calculation of the model atmosphere
and re-determination of stellar parameters.
This paper is organized as follows. In the next section we give an overview of observational data. Then, in Sect. 3 we describe the general methods of chemical abundance and stratification analysis, model atmosphere calculation and atomic line data used. In Sect. 4 the results of the stratification modeling are presented and the influence of chemical gradients on various observed stellar characteristics is discussed. The summary of our investigation and discussion of our results in the context of other recent studies of cool Ap stars are presented in Sect. 5.
2 Observations
For the abundance and stratification analysis we used the spectrum of ![]() Cir obtained with the UVES
instrument (Dekker et al. 2000) at the ESO VLT. The observations were carried out in two dichroic modes,
using a 0.5
Cir obtained with the UVES
instrument (Dekker et al. 2000) at the ESO VLT. The observations were carried out in two dichroic modes,
using a 0.5
![]() slit for a spectral resolution of 80 000. The spectra cover the full wavelength region of 3040-10 400 Å except for a few small gaps. Reduction of the UVES spectra was performed with the automatic pipeline (Ballester et al. 2000). The reduction process was described in more detail by Kochukhov et al. (2006) and Ryabchikova et al. (2008).
slit for a spectral resolution of 80 000. The spectra cover the full wavelength region of 3040-10 400 Å except for a few small gaps. Reduction of the UVES spectra was performed with the automatic pipeline (Ballester et al. 2000). The reduction process was described in more detail by Kochukhov et al. (2006) and Ryabchikova et al. (2008).
The observed ultraviolet spectral energy distribution of ![]() Cir was obtained from the IUE Newly Extracted Spectra (INES) archive
Cir was obtained from the IUE Newly Extracted Spectra (INES) archive![]() . We used the average of rebinned, high-dispersion spectra, recorded with a large aperture in the 1150-3100 Å wavelength window. For the spectral interval 3200-7500 Å we used low-resolution energy distributions of
. We used the average of rebinned, high-dispersion spectra, recorded with a large aperture in the 1150-3100 Å wavelength window. For the spectral interval 3200-7500 Å we used low-resolution energy distributions of ![]() Cir from the catalogues by Burnashev (1985) and Alekseeva et al. (1996). These data are calibrated in absolute flux and show a systematic difference of 5-10% below
Cir from the catalogues by Burnashev (1985) and Alekseeva et al. (1996). These data are calibrated in absolute flux and show a systematic difference of 5-10% below
![]() Å. The agreement is better than 5% for the longer wavelengths.
Å. The agreement is better than 5% for the longer wavelengths.
The spectrophotometry of ![]() Cir was complemented with the broad-band photometric measurements in the
UBVRI (Johnson et al. 1966) and JHKLM (Groote & Kaufmann 1983) systems. Stellar magnitudes were converted to absolute
flux units with the help of calibrations by Bessell et al. (1998) and Engels et al. (1981), respectively.
Cir was complemented with the broad-band photometric measurements in the
UBVRI (Johnson et al. 1966) and JHKLM (Groote & Kaufmann 1983) systems. Stellar magnitudes were converted to absolute
flux units with the help of calibrations by Bessell et al. (1998) and Engels et al. (1981), respectively.
Table 1:
List of Si, Cr, and Fe spectral lines used for stratification calculations. Columns give the ion identification, central wavelength, excitation potential, oscillator strength (![]() )
and the Stark damping constant (
)
and the Stark damping constant (
![]() )
for T=10 000 K. The last column gives reference for the adopted oscillator strength.
)
for T=10 000 K. The last column gives reference for the adopted oscillator strength.
In addition to using the low-resolution spectral energy distribution as well as metal and hydrogen line profiles in the UVES spectra, we compared predictions of our theoretical models with the Strömgren and Geneva photometric parameters of ![]() Cir. The observed Geneva colors were obtained from the catalogue by Rufener (1988). For the Strömgren photometry, numerous measurements listed for
Cir. The observed Geneva colors were obtained from the catalogue by Rufener (1988). For the Strömgren photometry, numerous measurements listed for ![]() Cir in the SIMBAD database
Cir in the SIMBAD database![]() yield average parameters
yield average parameters
![]() ,
,
![]() ,
,
![]() ,
and H
,
and H
![]() .
.
3 Methods
3.1 Abundance and stratification analysis
The classical abundance analysis in the approximation of a chemically-homogeneous atmosphere was carried out with the help of the equivalent width technique. We used the WIDTH9 code (Kurucz 1993), modified by Tsymbal (see Ryabchikova et al. 2002), to estimate abundances of 35 elements for a given model atmosphere. In few cases of blended lines or lines affected by the hyperfine structure (hfs) theoretical line profiles calculations were performed with
the magnetic spectrum synthesis code SYNTHMAG (Kochukhov 2007), assuming a homogeneous radial field structure with the magnetic field modulus of
![]() = 2.0 kG. This value corresponds to the upper limit of the field strength in
= 2.0 kG. This value corresponds to the upper limit of the field strength in ![]() Cir estimated by Kupka et al. (1996) and BNC08. We also tried
Cir estimated by Kupka et al. (1996) and BNC08. We also tried
![]() = 1.0 kG and found no significant effect on the results of abundance or stratification analysis.
= 1.0 kG and found no significant effect on the results of abundance or stratification analysis.
Since it is not possible to account for the Zeeman splitting and polarized radiative transfer in the WIDTH9 code, we used a pseudo-microturbulence to mimic the magnetic intensification effects (see Kupka et al. 1996). This approach is appropriate for the equivalent width analysis of magnetic stars with
![]()
![]() 3 kG. The pseudo-microturbulence
parameter of
3 kG. The pseudo-microturbulence
parameter of
![]() =
= ![]() km s-1 was estimated by matching profiles of the Fe I and Fe II lines computed with the full treatment of polarized radiative transfer and zero microturbulence by a non-magnetic spectrum synthesis calculation. Since
km s-1 was estimated by matching profiles of the Fe I and Fe II lines computed with the full treatment of polarized radiative transfer and zero microturbulence by a non-magnetic spectrum synthesis calculation. Since ![]() Cir has an inhomogeneous surface abundance structure (Kochukhov & Ryabchikova 2001; BNC08) and a non-uniform surface magnetic field distribution, results of the abundance analysis and the formal
Cir has an inhomogeneous surface abundance structure (Kochukhov & Ryabchikova 2001; BNC08) and a non-uniform surface magnetic field distribution, results of the abundance analysis and the formal
![]() value may slightly change with the rotation phase. However, the spectral and magnetic variation of this star over its 4.46
value may slightly change with the rotation phase. However, the spectral and magnetic variation of this star over its 4.46![]() rotation period are minor compared to other cool Ap stars (e.g., Kochukhov et al. 2004), which excludes a large influence of the horizontal inhomogeneities on the results of our analysis.
rotation period are minor compared to other cool Ap stars (e.g., Kochukhov et al. 2004), which excludes a large influence of the horizontal inhomogeneities on the results of our analysis.
Stratification modeling was performed for Si, Ca, Cr, and Fe. These elements have a sufficient number of lines in the observed wavelength region and are able to influence the model structure and flux distribution by altering the line blanketing. For these four stratified elements we adopted the step-function approximation of the vertical abundance distribution (Ryabchikova et al. 2005,2008). The vertical abundance profile was described by four parameters: chemical abundance in the upper atmosphere, abundance in deep layers, the position of the abundance jump and the width of the transition region where chemical abundance changes between the two values. All four parameters were optimized simultaneously with the IDL-based DDAFIT least-squares fitting procedure (Kochukhov 2007). This code adjusts the vertical abundance distribution of a given element to achieve the best fit to a set of observed spectral line profiles. In these calculations we used the SYNTHMAG code and adopted
![]() = 12.5 km s-1.
= 12.5 km s-1.
We note that the assumption of constant abundances in the upper atmosphere and in the lower photospheric layers is related to the lack of spectral lines sensitive to the abundance changes in these atmospheric regions. Due to substantial rotation of ![]() Cir our choice of lines for the stratification analysis is limited to
absorption features probing a certain line-forming region, which does not extend over the entire atmosphere. In particular, we cannot probe layers with
Cir our choice of lines for the stratification analysis is limited to
absorption features probing a certain line-forming region, which does not extend over the entire atmosphere. In particular, we cannot probe layers with
![]() .
The cores of strong lines could potentially
provide us with the information about stratification in the uppermost layers, but such lines are not available for the majority of elements. We estimated that robust determination of stratification using the lines available in the spectrum of
.
The cores of strong lines could potentially
provide us with the information about stratification in the uppermost layers, but such lines are not available for the majority of elements. We estimated that robust determination of stratification using the lines available in the spectrum of ![]() Cir is possible for the
Cir is possible for the
![]() region. Outside this
range of optical depths, an unconstrained solution of the vertical inversion problem is non-unique due to the ill-conditioned nature of the problem (Kochukhov et al. 2006). Thus, to overcome this difficulty, we force chemical abundance to a constant value in these layers.
region. Outside this
range of optical depths, an unconstrained solution of the vertical inversion problem is non-unique due to the ill-conditioned nature of the problem (Kochukhov et al. 2006). Thus, to overcome this difficulty, we force chemical abundance to a constant value in these layers.
3.2 Atomic line data
Atomic data for the abundance calculations were extracted from the recently updated VALD database (Piskunov et al. 1995; Kupka et al. 1999, see also http://vald.inasan.ru/~vald/ and references therein). For Tb III and Dy III transition probabilities were kindly provided by Ryabtsev (private communication). These calculations are based on the extended analysis of the energy level structure. For several ions (Mn I,II, Co I, Eu II, Ho II) with substantial hfs splitting we included this effect in the abundance calculations. The corresponding hfs constants were taken from Kurucz (2008) for Mn I, from Holt et al. (1999) for Mn II, from Pickering (1996) for Co I, from Lawler et al. (2001) for Eu II, and from Lawler et al. (2004) for Ho II.
Stratification analysis of Si, Ca, Cr, and Fe requires accurate and homogeneous line parameters for these elements. For Ca we used the same lines as in Ryabchikova et al. (2008). The line list for other elements is given in Table 1. The transition probabilities were improved by fitting the solar flux spectrum for a few Si I lines and one Fe I line. For Si II lines the Stark constants are taken from Wilke (2003), while for all other lines they are taken from Kurucz database (Kurucz 2008).
3.3 Model atmosphere calculations
Our model atmosphere calculations are based on the version 8.6 of the 1-D, LTE model atmosphere code LLMODELS (Shulyak et al. 2004). This program treats the bound-bound opacity by direct, line-by-line spectrum synthesis and is able to account for the effects of individual non-solar abundance and inhomogeneous vertical distribution of elements. Chemical abundances and stratification are provided as input parameters for the LLMODELS code and kept constant in the model atmosphere calculation process.
For all model atmosphere calculations in this paper we used a 72-layer vertical grid with equidistant spacing in the
![]() range between -7 and 2. The frequency-dependent quantities were calculated between 50 Å and 100 000 Å with a constant wavelength step of 0.1 Å. The VALD database was used as the main
source of the atomic data for computation of the line absorption coefficients. As it was shown by Kochukhov et al. (2005) and Khan & Shulyak (2006), magnetic fields with a strength of 1-3 kG expected for
range between -7 and 2. The frequency-dependent quantities were calculated between 50 Å and 100 000 Å with a constant wavelength step of 0.1 Å. The VALD database was used as the main
source of the atomic data for computation of the line absorption coefficients. As it was shown by Kochukhov et al. (2005) and Khan & Shulyak (2006), magnetic fields with a strength of 1-3 kG expected for ![]() Cir could be safely neglected in the model atmosphere calculations. Consequently, we ignored the effects of Zeeman splitting and polarized radiative transfer on the atmospheric structure. However, we used a pseudo-microturbulent velocity of 1 km s-1 to qualitatively treat magnetic intensification and for consistency with the abundance analysis.
Cir could be safely neglected in the model atmosphere calculations. Consequently, we ignored the effects of Zeeman splitting and polarized radiative transfer on the atmospheric structure. However, we used a pseudo-microturbulent velocity of 1 km s-1 to qualitatively treat magnetic intensification and for consistency with the abundance analysis.
The studies by Mashonkina et al. (2008,2005) demonstrated that the line formation of rare-earth elements Pr and Nd can strongly deviate from the local thermodynamic equilibrium. These elements are overabundant in the atmospheres of CP
stars by several dex compared to the solar atmosphere and have rich spectra dominated by the lines of the first and second ions. The doubly ionized lines of Pr, Nd, and of some other REEs are unusually strong due to combined effect of
stratification of these elements and departures from LTE. Therefore, a NLTE stratification treatment of REEs is essential for detailed spectrum synthesis and also for realistic estimate of their contribution to the line opacity in the model atmosphere calculations. However, a NLTE analysis is beyond the scope of this paper and currently could
not be coupled to a model calculation. The large
![]() of
of ![]() Cir compared to other cool Ap stars also makes it difficult to model stratification of REEs since some useful weak lines are not accessible for measurement. Therefore,
we followed Shulyak et al. (2009) in using a simplified treatment of the REE absorption. One can approximately reproduce the observed relative line strengths of the Pr, Nd, Dy, and Tb ions by using abundance derived from the second ions and
reducing the oscillator strengths for the singly ionized REE lines. The adopted reduction factor of 1.5 dex is close to the mean difference between concentrations of singly and doubly ionized REEs estimated in our classical abundance analysis of
Cir compared to other cool Ap stars also makes it difficult to model stratification of REEs since some useful weak lines are not accessible for measurement. Therefore,
we followed Shulyak et al. (2009) in using a simplified treatment of the REE absorption. One can approximately reproduce the observed relative line strengths of the Pr, Nd, Dy, and Tb ions by using abundance derived from the second ions and
reducing the oscillator strengths for the singly ionized REE lines. The adopted reduction factor of 1.5 dex is close to the mean difference between concentrations of singly and doubly ionized REEs estimated in our classical abundance analysis of ![]() Cir. With this scaling procedure the Pr, Nd, Dy, and Tb ionization equilibria are conserved in the model
atmosphere calculations while the line strength roughly matches the observed one for both ionization stages.
Cir. With this scaling procedure the Pr, Nd, Dy, and Tb ionization equilibria are conserved in the model
atmosphere calculations while the line strength roughly matches the observed one for both ionization stages.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11653f1.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg36.png) |
Figure 1: Comparison of the observed Fe line profiles (symbols) and calculations for the final stratified abundance distribution (solid line) and for the best-fit homogeneous abundance of Fe (dashed line). |
| Open with DEXTER | |
3.4 Self-consistent atmospheric modeling
Previous chemical stratification studies used high-resolution observations of CP stars to perform average abundance determination and to restore vertical abundance profiles for a few chemical elements. Generally, this analysis is performed by interpreting observed profiles of spectral lines with different strength, excitation potential, and ionization degree for a given element. However, the shapes and strengths of the line profiles predicted by theoretical models may also indirectly depend on the vertical distribution of chemical elements through the influence of line opacities, modified by peculiar abundances and chemical stratification, on the temperature-pressure structure of the model atmosphere. Thus, the stratification and abundance analyses are linked to the model atmosphere calculation. The extent of the feedback of stratification and non-solar chemical composition on the model structure cannot be estimated a priori. Consequently, one has to apply an iterative procedure of stratification and abundance analysis followed by re-calculation of the model atmosphere structure. For the present analysis of ![]() Cir this procedure included the following main steps:
Cir this procedure included the following main steps:
- 1.
- calculation of a model atmosphere grid using mean abundances derived in previous studies;
- 2.
- determination of
 and
and 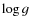 with the help of spectrophotometry, Balmer line profiles and broad-band colors;
with the help of spectrophotometry, Balmer line profiles and broad-band colors;
- 3.
- determination of the average abundances and chemical stratification using high-resolution spectra;
- 4.
- calculation of a new model atmosphere grid, taking into account individual abundances and stratification found in the previous step;
- 5.
- repeating the entire process starting from step 2 until convergence is achieved.
The final self-consistent, chemically-stratified model atmosphere is expected to reproduce
simultaneously the observed photometry, energy distribution, hydrogen line profiles and metallic line spectra. The method of self-consistent analysis of a cool Ap-star atmosphere applied here is similar to the procedure described by Shulyak et al. (2009) for the roAp star HD 24712. However, in practice robust re-determination of the atmospheric parameters is not possible for the latter star due to the lack of observational data. In contrast, ![]() Cir lends
itself to a thorough study of the interplay between atmospheric chemistry and stellar parameters.
Cir lends
itself to a thorough study of the interplay between atmospheric chemistry and stellar parameters.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11653f2.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg39.png) |
Figure 2: Same as in Fig. 1 but for Si. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11653f3.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg40.png) |
Figure 3: Same as in Fig. 1 but for Ca. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11653f4.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg41.png) |
Figure 4: Same as in Fig. 1 but for Cr. |
| Open with DEXTER | |
4 Results
4.1 Chemical abundance pattern
We started our analysis calculating model atmospheres for ![]() Cir with the homogeneously distributed
abundances taken from BNC08 and supplemented where necessary by the abundances from Kupka et al. (1996). Then the iterative procedure of stratification analysis was performed following the scheme outlined in Sect. 3.4. For each iteration we re-calculated atmospheric abundances of all available elements and vertical stratification profiles of Si, Ca, Cr, and Fe. In total, four such iterations of the abundance
analysis and model atmosphere calculations were necessary to obtain a converged solution. At each iteration an adjustment of
Cir with the homogeneously distributed
abundances taken from BNC08 and supplemented where necessary by the abundances from Kupka et al. (1996). Then the iterative procedure of stratification analysis was performed following the scheme outlined in Sect. 3.4. For each iteration we re-calculated atmospheric abundances of all available elements and vertical stratification profiles of Si, Ca, Cr, and Fe. In total, four such iterations of the abundance
analysis and model atmosphere calculations were necessary to obtain a converged solution. At each iteration an adjustment of
![]() by
by ![]() 200 K was required to fit the observed spectral energy distribution and the hydrogen line profiles. The final model atmosphere parameters inferred for
200 K was required to fit the observed spectral energy distribution and the hydrogen line profiles. The final model atmosphere parameters inferred for ![]() Cir are
Cir are
![]() K and
K and
![]() .
.
A comparison of the observed and calculated profiles of 17 Fe I and 14 Fe II lines used for stratification analysis is presented in Fig. 1. These synthetic spectra were computed with the vertical abundance distribution and atmospheric model obtained at the last iteration. Similar plots for Si, Ca, and Cr are provided in Figs. 2-4.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11653f5.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg42.png) |
Figure 5:
Vertical distribution of Si, Ca, Cr, and Fe abundance in the atmosphere of |
| Open with DEXTER | |
The variation of the stratification profiles of chemical elements during the iterative process is illustrated in Fig. 5. Neither the number of spectral lines used for the stratification analysis with DDAFIT nor their atomic parameters were modified during the iteration procedure and, thus, all the changes in the stratification profiles from one iteration to another are entirely due to changes of the model structure and a small adjustment of
![]() .
In general, the difference between the shape of the stratification profiles obtained on the first and last iterations is relatively small for all considered elements. The positions of the abundance jumps did not change much, although their amplitudes increased noticeably for Si and Ca. On the other hand, a large change of the
stratification parameters occurred at the second iteration, after stratified abundances were introduced in the model atmosphere calculation for the first time. For this iteration we also had to adopt a 50 K lower effective temperature compared to
.
In general, the difference between the shape of the stratification profiles obtained on the first and last iterations is relatively small for all considered elements. The positions of the abundance jumps did not change much, although their amplitudes increased noticeably for Si and Ca. On the other hand, a large change of the
stratification parameters occurred at the second iteration, after stratified abundances were introduced in the model atmosphere calculation for the first time. For this iteration we also had to adopt a 50 K lower effective temperature compared to
![]() K, which provided the best description of hydrogen lines and spectral energy distribution for other iterations.
K, which provided the best description of hydrogen lines and spectral energy distribution for other iterations.
For all four elements we obtained a familiar picture of a step-like decrease of abundance with height. A slight distortion of abundance profiles in deeper layers apparent in Fig. 5 is caused by a non-linear mapping from the column mass scale employed for vertical inversion to the standard optical depth used in the figure. For Cr and Fe the transition region is narrow and is located between
![]() and 0.0. It is centered at
and 0.0. It is centered at
![]() and is more extended for Si and Ca. All studied elements show a large
overabundance with respect to the sun in deep layers and significantly (Si, Ca) or marginally (Cr, Fe) sub-solar element concentrations in the upper atmosphere. The formal error of the stratification parameters ranges from 0.4-0.8 dex for Ca and Si to 0.05-0.15 dex for Fe and Cr, with the upper atmospheric abundance being more uncertain. At the same time, the position of abundance jump was determined with the precision of better than 0.1 dex in the
and is more extended for Si and Ca. All studied elements show a large
overabundance with respect to the sun in deep layers and significantly (Si, Ca) or marginally (Cr, Fe) sub-solar element concentrations in the upper atmosphere. The formal error of the stratification parameters ranges from 0.4-0.8 dex for Ca and Si to 0.05-0.15 dex for Fe and Cr, with the upper atmospheric abundance being more uncertain. At the same time, the position of abundance jump was determined with the precision of better than 0.1 dex in the
![]() scale for all four elements.
scale for all four elements.
Table 2 summarizes the final mean abundances derived after the fourth iteration of the model atmosphere calculations. Element concentrations are reported for 52 ions of 35 elements. For completeness we also included mean abundances of the stratified elements. Our abundance estimates are compared with those reported by Kupka et al. (1996) and BNC08 and with the solar abundances compiled by Asplund et al. (2005). We find that ![]() Cir has a moderate CNO deficiency, almost solar Ca to Fe abundances and an overabundance of Cr by
Cir has a moderate CNO deficiency, almost solar Ca to Fe abundances and an overabundance of Cr by ![]() 0.8 dex. The same overabundance is obtained for Co when hfs effects are taken into account. Ni exhibits a 0.8 dex deficiency. In general, our mean abundance results agree well with those by BNC08
except for C, S, Fe, Y II, Zr, and Ba. For the latter the difference in the adopted microturbulence parameter might be the reason for the discrepancy. BNC08 determined abundances for three out of 14 REE elements with stable isotopes, while we succeeded in estimating abundances for 12 REE species. For 6 REEs (Ce, Pr, Nd,
Tb, Dy, Er) abundances were obtained from the lines of the first and second ions separately. Although
0.8 dex. The same overabundance is obtained for Co when hfs effects are taken into account. Ni exhibits a 0.8 dex deficiency. In general, our mean abundance results agree well with those by BNC08
except for C, S, Fe, Y II, Zr, and Ba. For the latter the difference in the adopted microturbulence parameter might be the reason for the discrepancy. BNC08 determined abundances for three out of 14 REE elements with stable isotopes, while we succeeded in estimating abundances for 12 REE species. For 6 REEs (Ce, Pr, Nd,
Tb, Dy, Er) abundances were obtained from the lines of the first and second ions separately. Although ![]() Cir has a moderate REE enhancement of 0.7-1.6 dex according to the results obtained using the first ions, the REE anomaly typical for roAp stars (Ryabchikova et al. 2004) is clearly observed for all 6 REEs where abundances were obtained from the lines of two ionization
stages. This anomaly is
Cir has a moderate REE enhancement of 0.7-1.6 dex according to the results obtained using the first ions, the REE anomaly typical for roAp stars (Ryabchikova et al. 2004) is clearly observed for all 6 REEs where abundances were obtained from the lines of two ionization
stages. This anomaly is ![]() 1.7-1.8 dex for Ce, Pr, Nd, and Tb and increases to 2.3 dex for Dy
and Er. This ionization imbalance is an indication of the accumulation of the REEs in the upper atmospheric layers (Mashonkina et al. 2008,2005). Its effect on the model atmosphere calculations was investigated in detail by Shulyak et al. (2009).
1.7-1.8 dex for Ce, Pr, Nd, and Tb and increases to 2.3 dex for Dy
and Er. This ionization imbalance is an indication of the accumulation of the REEs in the upper atmospheric layers (Mashonkina et al. 2008,2005). Its effect on the model atmosphere calculations was investigated in detail by Shulyak et al. (2009).
Table 2:
Abundances in the atmosphere of ![]() Cir with the error estimates based on n measured lines. Abundances derived in our study are compared with those reported by Kupka et al. (1996) and BNC08. The solar abundances are from Asplund et al. (2005).
Cir with the error estimates based on n measured lines. Abundances derived in our study are compared with those reported by Kupka et al. (1996) and BNC08. The solar abundances are from Asplund et al. (2005).
The fourth column in Table 2 gives abundances and standard deviations obtained with the WIDTH9 code from n spectral lines neglecting hfs effects, while in the next column one finds abundances calculated with SYNTHMAG taking hfs effects into account. The largest hfs effect is evident for Ho II lines, where the final abundance decreases by about an order of magnitude. The hfs effect on Eu II lines is the smallest one and does not exceed 0.25 dex. The detailed treatment of the hyperfine splitting of the
Co I lines increases both the discrepancy with Co II and the standard deviation compared to the
WIDTH9 analysis. This could be a signature of Co stratification in the atmosphere of ![]() Cir. Separate hfs analysis of the three moderately strong lines in the 3500-3600 Å region (
Cir. Separate hfs analysis of the three moderately strong lines in the 3500-3600 Å region (![]() = 40-82 mÅ) and five weak to medium strength lines in the 5300-5400 Å region (
= 40-82 mÅ) and five weak to medium strength lines in the 5300-5400 Å region (![]() = 13-42 mÅ) gives
= 13-42 mÅ) gives
![]() and
and
![]() ,
respectively. This indicates possible Co
accumulation in deep layers of the stellar atmosphere. The absence of hfs constants for Co II lines does not allow us to carry out a formal Co stratification analysis. In addition, our abundance analysis shows that Sr might be strongly stratified in the atmosphere of
,
respectively. This indicates possible Co
accumulation in deep layers of the stellar atmosphere. The absence of hfs constants for Co II lines does not allow us to carry out a formal Co stratification analysis. In addition, our abundance analysis shows that Sr might be strongly stratified in the atmosphere of ![]() Cir similar to other Ap stars like, for example, HD 133792 (Kochukhov et al. 2006). However, the lack of a significant number of suitable unblended lines again prevented detailed stratification analysis for this element.
Cir similar to other Ap stars like, for example, HD 133792 (Kochukhov et al. 2006). However, the lack of a significant number of suitable unblended lines again prevented detailed stratification analysis for this element.
![\begin{figure}
\par\includegraphics[height=18cm,angle=90,clip]{11653f6.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg102.png) |
Figure 6:
Comparison between the observed (symbols) and theoretical (lines) spectral energy distribution of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=13cm,angle=90]{11653f7.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg103.png) |
Figure 7:
Theoretical spectral energy distributions for the model atmosphere parameters
|
| Open with DEXTER | |
4.2 Spectral energy distribution and photometry
We used the observed spectral energy distribution of ![]() Cir as the main effective temperature
indicator. Previous attempts to model the spectrophotometry of magnetic Ap stars
(Lipski & Stepien 2008; Adelman & Rayle 2000) could utilize only the information about the shape of the energy
distribution because observations were often given in relative flux units. Furthermore, the stellar angular diameters were generally unknown for Ap stars and had to be treated as free parameters.
For
Cir as the main effective temperature
indicator. Previous attempts to model the spectrophotometry of magnetic Ap stars
(Lipski & Stepien 2008; Adelman & Rayle 2000) could utilize only the information about the shape of the energy
distribution because observations were often given in relative flux units. Furthermore, the stellar angular diameters were generally unknown for Ap stars and had to be treated as free parameters.
For ![]() Cir we are in a favourable position to obtain a very precise estimate of the model atmosphere parameters from the observed stellar flux thanks to the
recent direct, interferometric determination of the angular diameter,
Cir we are in a favourable position to obtain a very precise estimate of the model atmosphere parameters from the observed stellar flux thanks to the
recent direct, interferometric determination of the angular diameter,
![]() mas (BNC08). Figure 6 presents a comparison of the photometric and
spectrophotometric measurements of
mas (BNC08). Figure 6 presents a comparison of the photometric and
spectrophotometric measurements of ![]() Cir, discussed in detail in Sect. 2, with the
theoretical flux distribution computed for the models with individual abundance and
stratification included. We find that observations are best fitted by the model with
Cir, discussed in detail in Sect. 2, with the
theoretical flux distribution computed for the models with individual abundance and
stratification included. We find that observations are best fitted by the model with
![]() K. The uncertainty of this effective temperature estimate, related to
fitting ambiguities and discrepancy between the two spectrophotometric scans available for
K. The uncertainty of this effective temperature estimate, related to
fitting ambiguities and discrepancy between the two spectrophotometric scans available for
![]() Cir, does not exceed 50 K. At the same time, a
Cir, does not exceed 50 K. At the same time, a
![]() error due to the angular diameter uncertainty is estimated to be 120 K. Thus, our analysis of the spectral energy distribution yields an
effective temperature with an overall accuracy of about 130 K.
error due to the angular diameter uncertainty is estimated to be 120 K. Thus, our analysis of the spectral energy distribution yields an
effective temperature with an overall accuracy of about 130 K.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{11653f8.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg105.png) |
Figure 8:
Dependence of the synthetic Strömgren (left panel) and Geneva
(right panel) photometric parameters on the
|
| Open with DEXTER | |
Following BNC08, we adopted
![]() for the modeling of the observed flux of
for the modeling of the observed flux of ![]() Cir. Changes of the surface gravity by 0.1-0.2 dex lead to a negligible modification of the theoretical spectral energy distribution and do not alter results of the
Cir. Changes of the surface gravity by 0.1-0.2 dex lead to a negligible modification of the theoretical spectral energy distribution and do not alter results of the
![]() determination.
determination.
In the case of ![]() Cir, spectrophotometry is not very sensitive to the adopted atmospheric
chemical composition and stratification. In Fig. 7
we compare LLMODELS fluxes calculated for our self-consistent, chemically-stratified model atmosphere and for the models adopting homogeneous solar abundance and the chemical composition published
by BNC08. All three models predict similar flux distributions, although
calculations with the non-solar abundances exhibit a more substantial redistribution of flux
from the UV region to the optical and IR. The chemically-stratified model predicts a
marginally lower flux for
Cir, spectrophotometry is not very sensitive to the adopted atmospheric
chemical composition and stratification. In Fig. 7
we compare LLMODELS fluxes calculated for our self-consistent, chemically-stratified model atmosphere and for the models adopting homogeneous solar abundance and the chemical composition published
by BNC08. All three models predict similar flux distributions, although
calculations with the non-solar abundances exhibit a more substantial redistribution of flux
from the UV region to the optical and IR. The chemically-stratified model predicts a
marginally lower flux for
![]() nm compared to the model with homogeneous
individual abundances.
nm compared to the model with homogeneous
individual abundances.
Observations in the Strömgren and Geneva photometric systems are often used for
determination of the atmospheric parameters of magnetic CP stars (Netopil et al. 2008; Hauck & North 1993).
Therefore, we examined the agreement of the photometric parameters of ![]() Cir predicted by our
self-consistent stratification models with the observed photometric properties of this star.
For stars with a temperature close to that of
Cir predicted by our
self-consistent stratification models with the observed photometric properties of this star.
For stars with a temperature close to that of ![]() Cir, the b-y and H
Cir, the b-y and H![]() parameters of the
Strömgren photometry can be used as
parameters of the
Strömgren photometry can be used as
![]() indicators, while c1 is mainly sensitive to the
surface gravity (Moon & Dworetsky 1985; Napiwotzki et al. 1993). For the Geneva photometry, the effective temperature
calibrations are usually based upon the B2-G and B2-V1 indices and gravity can be determined with the help of the reddening-free d-parameter (Hauck & North 1993; Kunzli et al. 1997). Figure 8 presents
these
indicators, while c1 is mainly sensitive to the
surface gravity (Moon & Dworetsky 1985; Napiwotzki et al. 1993). For the Geneva photometry, the effective temperature
calibrations are usually based upon the B2-G and B2-V1 indices and gravity can be determined with the help of the reddening-free d-parameter (Hauck & North 1993; Kunzli et al. 1997). Figure 8 presents
these
![]() and
and ![]() indicators for the entire model atmosphere grid computed with the
final abundances and chemical stratification. The observed range of the Strömgren
photometric observations of
indicators for the entire model atmosphere grid computed with the
final abundances and chemical stratification. The observed range of the Strömgren
photometric observations of ![]() Cir is indicated by the horizontal lines. Uncertainties of the
Geneva photometric parameters are calculated taking into account an observational error of
0.004 mag (Rufener 1988).
Cir is indicated by the horizontal lines. Uncertainties of the
Geneva photometric parameters are calculated taking into account an observational error of
0.004 mag (Rufener 1988).
Generally, Fig. 8 shows an excellent agreement between the observed and
synthetic b-y, B2-G, and B2-V1 indices for
![]() K estimated from
the spectrophotometry. The H
K estimated from
the spectrophotometry. The H![]() parameter indicates a somewhat lower
parameter indicates a somewhat lower
![]() on average, but it is still consistent with our model predictions if the scatter of photometric
measurements is taken into account. A direct spectroscopic comparison between the observed and computed hydrogen line profiles presented below provides a more robust method to estimate
on average, but it is still consistent with our model predictions if the scatter of photometric
measurements is taken into account. A direct spectroscopic comparison between the observed and computed hydrogen line profiles presented below provides a more robust method to estimate
![]() from the Balmer lines. The observed c1 index suggests
from the Balmer lines. The observed c1 index suggests
![]() while
while
![]() fits the observed Geneva d-parameter. Neither estimate
contradicts
fits the observed Geneva d-parameter. Neither estimate
contradicts
![]() determined by BNC08 with stellar
evolutionary models.
determined by BNC08 with stellar
evolutionary models.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11653f9.eps} %\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg111.png) |
Figure 9:
Comparison of the observed and theoretical H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11653f10.eps} %\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg112.png) |
Figure 10:
Comparison of the observed and theoretical H |
| Open with DEXTER | |
4.3 Hydrogen lines
Due to its relatively low temperature, the hydrogen line profiles of ![]() Cir are mostly
sensitive to
Cir are mostly
sensitive to
![]() .
Thus, we have used the H
.
Thus, we have used the H![]() and H
and H![]() lines to verify the effective
temperature of
lines to verify the effective
temperature of ![]() Cir determined from the stellar flux distribution. The comparison between the
observed hydrogen lines and the SYNTHMAG calculations for the final chemically-stratified
models is illustrated in Fig. 9. An effective temperature of
Cir determined from the stellar flux distribution. The comparison between the
observed hydrogen lines and the SYNTHMAG calculations for the final chemically-stratified
models is illustrated in Fig. 9. An effective temperature of
![]() K
yields the best fit to the H
K
yields the best fit to the H![]() and H
and H![]() profiles. The error takes into account
the fitting uncertainty and
profiles. The error takes into account
the fitting uncertainty and ![]() 1% ambiguity of the continuum normalization in the regions
around broad hydrogen line wings.
1% ambiguity of the continuum normalization in the regions
around broad hydrogen line wings.
Unlike the spectral energy distribution, hydrogen lines are significantly modified when
chemical stratification is included in the model atmosphere calculations.
Figure 10
shows that theoretical Balmer line profiles become
systematically weaker for the models which neglect chemical stratification. Consequently, the
stellar effective temperature will be overestimated by 200 K if such models are used
for fitting the hydrogen line wings. This interesting result is explained in
Fig. 11, which shows temperature as a function of continuum optical depth for models with
the same atmospheric parameters but different chemical compositions. The calculations with
homogeneous individual abundance do not deviate strongly from the solar-composition
model. On the other hand, the presence of a large Cr, Si, and Fe overabundance in deep
photospheric layers of the chemically-stratified model leads to a significant backwarming
effect, corresponding to a temperature increase by 200-400 K for
![]() .
The
strengthening of the hydrogen line wings reflects this change in the model atmosphere
structure.
.
The
strengthening of the hydrogen line wings reflects this change in the model atmosphere
structure.
5 Conclusions and discussion
An empirical investigation of the vertical distribution of chemical elements in the atmospheres of CP stars is of great importance for testing predictions of the microscopic particle diffusion theory. Such investigations yield stratification profiles for different chemical elements that could be directly compared with the diffusion calculations.
In this paper we determined empirical vertical distributions of Si, Ca, Cr, and Fe in the atmosphere of the brightest rapidly oscillating Ap star ![]() Cir. Stratification analysis was
complemented with the most detailed study of average abundances ever conducted for
Cir. Stratification analysis was
complemented with the most detailed study of average abundances ever conducted for ![]() Cir.
Unlike many previous empirical stratification studies of magnetic CP stars, we made an effort
to attain a self-consistency between the inferred chemical properties of the stellar
atmosphere and its temperature-pressure structure. This was achieved by using an iterative
procedure of deriving stratification and mean abundances from the observed high-resolution
spectra and subsequent recomputing of the model atmosphere structure.
Cir.
Unlike many previous empirical stratification studies of magnetic CP stars, we made an effort
to attain a self-consistency between the inferred chemical properties of the stellar
atmosphere and its temperature-pressure structure. This was achieved by using an iterative
procedure of deriving stratification and mean abundances from the observed high-resolution
spectra and subsequent recomputing of the model atmosphere structure.
Despite a significant improvement of this stellar atmosphere modeling methodology
compared to previous studies of cool Ap stars, the analysis presented in this paper has
several limitations, stemming from its empirical character. The lines available in the
spectra of ![]() Cir can be used to establish stratification of only four chemical elements and
do not allow us to explore stratification outside the optical depth range of approximately
Cir can be used to establish stratification of only four chemical elements and
do not allow us to explore stratification outside the optical depth range of approximately
![]() to +0.5. Furthermore, observations do not allow us to resolve possible variation of chemical stratification profiles over the stellar surface, which might be present due to magnetic field effects. Potential NLTE effects are also neglected.
to +0.5. Furthermore, observations do not allow us to resolve possible variation of chemical stratification profiles over the stellar surface, which might be present due to magnetic field effects. Potential NLTE effects are also neglected.
The availability of the photometric measurements in different systems, spectrophotometric
scans, hydrogen line profiles and, uniquely for ![]() Cir, direct interferometric measurement of
the angular diameter allowed us to derive accurate atmospheric parameters and test the
influence of non-solar, inhomogeneous abundances on fitting different types of observations.
Cir, direct interferometric measurement of
the angular diameter allowed us to derive accurate atmospheric parameters and test the
influence of non-solar, inhomogeneous abundances on fitting different types of observations.
The final atmospheric parameters of ![]() Cir were found to be
Cir were found to be
![]() K and
K and
![]() .
Together with the chemical stratification and mean abundances derived in
our study, these parameters reproduce all photometric, spectrophotometric, and spectroscopic
constraints available for
.
Together with the chemical stratification and mean abundances derived in
our study, these parameters reproduce all photometric, spectrophotometric, and spectroscopic
constraints available for ![]() Cir. Our atmospheric parameters are in excellent agreement with
Cir. Our atmospheric parameters are in excellent agreement with
![]() K,
K,
![]() determined by BNC08 from the
angular diameter measurement, bolometric flux and stellar structure calculations.
This is an indication that modern model atmosphere analyses of cool Ap stars are trustworthy and are not affected by significant systematic biases.
determined by BNC08 from the
angular diameter measurement, bolometric flux and stellar structure calculations.
This is an indication that modern model atmosphere analyses of cool Ap stars are trustworthy and are not affected by significant systematic biases.
The vertical distribution of chemical elements in the atmosphere of ![]() Cir was found to be
similar to the abundance profiles inferred for other cool Ap stars. All four elements
analysed for
Cir was found to be
similar to the abundance profiles inferred for other cool Ap stars. All four elements
analysed for ![]() Cir exhibit a large overabundance in the lower atmospheric layers and a solar
or subsolar abundance above
Cir exhibit a large overabundance in the lower atmospheric layers and a solar
or subsolar abundance above
![]() .
We found that the stratification
profiles of chemical elements derived using a model atmosphere computed with homogeneous
abundances could slightly differ from those obtained using a self-consistent analysis.
However, in general, these changes do not alter significantly the overall energy balance in
the stellar atmosphere.
.
We found that the stratification
profiles of chemical elements derived using a model atmosphere computed with homogeneous
abundances could slightly differ from those obtained using a self-consistent analysis.
However, in general, these changes do not alter significantly the overall energy balance in
the stellar atmosphere.
For the atmospheric parameters of ![]() Cir, chemical stratification has a minor
influence on the spectral energy distribution in comparison to chemically-homogeneous models.
Thus, interpretation of the spectrophotometric scans will not be significantly in error if
stratification is ignored. A similar result was obtained in our study of another cool Ap star
HD 24712 (
Cir, chemical stratification has a minor
influence on the spectral energy distribution in comparison to chemically-homogeneous models.
Thus, interpretation of the spectrophotometric scans will not be significantly in error if
stratification is ignored. A similar result was obtained in our study of another cool Ap star
HD 24712 (
![]() K,
K,
![]() Shulyak et al. 2009). We caution, however, that the
validity of this finding should not be extended outside the
Shulyak et al. 2009). We caution, however, that the
validity of this finding should not be extended outside the
![]() -8000 K range
addressed in our investigations. Hotter Ap stars might have a different abundance
stratification that makes a larger impact on the atmospheric structure and
stellar parameter determination.
-8000 K range
addressed in our investigations. Hotter Ap stars might have a different abundance
stratification that makes a larger impact on the atmospheric structure and
stellar parameter determination.
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{11653f11.eps} %\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg120.png) |
Figure 11:
Temperature as a function of standard optical depth,
|
| Open with DEXTER | |
On the other hand, we found that the backwarming effect introduced by concentration of
iron-peak elements in the lower atmospheric layers of the chemically-stratified model leads
to significant strengthening of the hydrogen line wings. The corresponding reduction of
![]() inferred from the Balmer lines amounts to
inferred from the Balmer lines amounts to ![]() 200 K. In the case of
200 K. In the case of ![]() Cir, only
chemically-stratified models are able to reproduce the H
Cir, only
chemically-stratified models are able to reproduce the H![]() and H
and H![]() profiles with a
profiles with a
![]() consistent with the photometric and spectrophotometric observations.
consistent with the photometric and spectrophotometric observations.
The effective temperature determined in our study is significantly lower than
![]() K
found in the previous spectroscopic analysis of
K
found in the previous spectroscopic analysis of ![]() Cir (Kupka et al. 1996). The origin of this discrepancy
is twofold. On the one hand, Kupka et al. (1996) analysed the star using standard model atmospheres, which
neglected a non-solar chemical composition and element stratification. This led to an overestimation
of
Cir (Kupka et al. 1996). The origin of this discrepancy
is twofold. On the one hand, Kupka et al. (1996) analysed the star using standard model atmospheres, which
neglected a non-solar chemical composition and element stratification. This led to an overestimation
of
![]() obtained with the help of photometric techniques and hydrogen line wing fitting. On the
other hand, the final
obtained with the help of photometric techniques and hydrogen line wing fitting. On the
other hand, the final
![]() was obtained by Kupka et al. (1996) by reducing abundance scatter for a set
of Fe I and Fe II lines, assuming a homogeneous distribution of this element with
height which seemed to be a reasonable approximation at that time. We now know that this assumption
is incorrect and that, due to their different formation heights, the Fe lines of different
excitation potentials and ionization degree give different apparent abundance due to stratification
effects in cool Ap stars. In this situation the criterium of minimum abundance scatter does not
allow one to recover the true stellar parameters.
was obtained by Kupka et al. (1996) by reducing abundance scatter for a set
of Fe I and Fe II lines, assuming a homogeneous distribution of this element with
height which seemed to be a reasonable approximation at that time. We now know that this assumption
is incorrect and that, due to their different formation heights, the Fe lines of different
excitation potentials and ionization degree give different apparent abundance due to stratification
effects in cool Ap stars. In this situation the criterium of minimum abundance scatter does not
allow one to recover the true stellar parameters.
Using the fundamental
![]() and a luminosity of
and a luminosity of
![]() estimated from the
Hipparcos parallax, BNC08 determined a stellar mass,
estimated from the
Hipparcos parallax, BNC08 determined a stellar mass,
![]() ,
with
the help of stellar structure models. We confirmed this result using Padova evolutionary tracks
(Girardi et al. 2000). Adopting our spectroscopic
,
with
the help of stellar structure models. We confirmed this result using Padova evolutionary tracks
(Girardi et al. 2000). Adopting our spectroscopic
![]() and the same luminosity as in
BNC08, we found
and the same luminosity as in
BNC08, we found
![]() for the Z=0.019 grids. The small formal
uncertainty of the stellar mass is unrealistic given the lack of knowledge about the overall metal
content of
for the Z=0.019 grids. The small formal
uncertainty of the stellar mass is unrealistic given the lack of knowledge about the overall metal
content of ![]() Cir. For example, assuming Z=0.008, which is closer to the recent determination of the
solar atmospheric metallicity (Asplund et al. 2005), yields a mass of
Cir. For example, assuming Z=0.008, which is closer to the recent determination of the
solar atmospheric metallicity (Asplund et al. 2005), yields a mass of
![]() .
For both
metallicities the stellar radius predicted by the Padova models is in excellent agreement with the
value of
.
For both
metallicities the stellar radius predicted by the Padova models is in excellent agreement with the
value of
![]() determined by BNC08. The Z=0.008-0.019
metallicity interval represents a reasonable estimate of the range of the bulk metal content of
nearby field stars (Bagnulo et al. 2006). Unknown initial helium abundance and variation in the treatment of
convection in stellar structure calculations may introduce additional uncertainties in the mass
determination for late-A stars (Cunha et al. 2003). Thus, despite availability of precise estimates of
the atmospheric parameters, radius and luminosity, we can only conclude that the mass of
determined by BNC08. The Z=0.008-0.019
metallicity interval represents a reasonable estimate of the range of the bulk metal content of
nearby field stars (Bagnulo et al. 2006). Unknown initial helium abundance and variation in the treatment of
convection in stellar structure calculations may introduce additional uncertainties in the mass
determination for late-A stars (Cunha et al. 2003). Thus, despite availability of precise estimates of
the atmospheric parameters, radius and luminosity, we can only conclude that the mass of ![]() Cir is
likely to be in the range of about 1.5
Cir is
likely to be in the range of about 1.5 ![]() to 1.7
to 1.7 ![]() .
.
In the light of new, reliable determination of the atmospheric and fundamental parameters of ![]() Cir,
one can use this star to test photometric temperature calibrations of cool Ap stars. These
calibrations were recently summarized and improved by Netopil et al. (2008). For magnetic Ap stars with
Cir,
one can use this star to test photometric temperature calibrations of cool Ap stars. These
calibrations were recently summarized and improved by Netopil et al. (2008). For magnetic Ap stars with
![]() K they provided a new B-V calibration and recommended using the B2-G calibration
by Hauck & North (1982) and the
K they provided a new B-V calibration and recommended using the B2-G calibration
by Hauck & North (1982) and the ![]() calibration by Napiwotzki et al. (1993) for the Geneva and Strömgren
photometric systems, respectively. Application of these photometric temperature calibrations gives
calibration by Napiwotzki et al. (1993) for the Geneva and Strömgren
photometric systems, respectively. Application of these photometric temperature calibrations gives
![]() K,
K,
![]() (Geneva) = 7678 K, and
(Geneva) = 7678 K, and
![]() (Strömgren) = 7692 K. In
comparison, an earlier Strömgren photometry calibration by Moon & Dworetsky (1985) yields
(Strömgren) = 7692 K. In
comparison, an earlier Strömgren photometry calibration by Moon & Dworetsky (1985) yields
![]() K.
Thus, all calibrations overestimate effective temperature of
K.
Thus, all calibrations overestimate effective temperature of ![]() Cir by 200-450 K while performing
much better for other cool Ap stars (Netopil et al. 2008). An unusually high abundance of Fe in the
atmosphere of
Cir by 200-450 K while performing
much better for other cool Ap stars (Netopil et al. 2008). An unusually high abundance of Fe in the
atmosphere of ![]() Cir compared to other cool magnetic Ap stars with
Cir compared to other cool magnetic Ap stars with
![]() K (Ryabchikova 2005) might
be the reason for deviating photometric behaviour of this star.
K (Ryabchikova 2005) might
be the reason for deviating photometric behaviour of this star.
A large difference in the mean iron-peak element abundances of ![]() Cir and of HD 24712, which we
analysed using a similar self-consistent model atmosphere technique (Shulyak et al. 2009), explains the
different influence of stratified abundances on the model structure of the two stars. Both Fe and Cr
are significantly more abundant in
Cir and of HD 24712, which we
analysed using a similar self-consistent model atmosphere technique (Shulyak et al. 2009), explains the
different influence of stratified abundances on the model structure of the two stars. Both Fe and Cr
are significantly more abundant in ![]() Cir. Consequently, their stratification changes the atmospheric
structure to a much greater extent than for HD 24712 in spite of the qualitatively similar
stratification profiles inferred for the two stars.
Cir. Consequently, their stratification changes the atmospheric
structure to a much greater extent than for HD 24712 in spite of the qualitatively similar
stratification profiles inferred for the two stars.
Some of the properties of ![]() Cir might be connected to the special aspect angle from which this star
is visible from Earth. The presence of narrow line profiles for the 4.46
Cir might be connected to the special aspect angle from which this star
is visible from Earth. The presence of narrow line profiles for the 4.46![]() rotation period
of
rotation period
of ![]() Cir indicates a relatively low inclination angle (
Cir indicates a relatively low inclination angle (
![]() ). The restricted visible
part of the stellar surface might not be representative of the whole star if, for example, it is
covered by predominantly horizontal magnetic fields and by spots of enhanced iron-peak element
abundance. Precise spectroscopic and polarization observations of
). The restricted visible
part of the stellar surface might not be representative of the whole star if, for example, it is
covered by predominantly horizontal magnetic fields and by spots of enhanced iron-peak element
abundance. Precise spectroscopic and polarization observations of ![]() Cir over the entire rotation
cycle are required to investigate the surface magnetic and abundance geometry.
Cir over the entire rotation
cycle are required to investigate the surface magnetic and abundance geometry.
Acknowledgements
This work was supported by FWF Lise Meitner grant Nr. M998-N16 (DS), FWF P17890-N2 (TR), RFBR 08-02-00469-a and Presidium RAS Programme ``Origin and evolution of stars and galaxies'' to TR.
References
- Adelman, S. J., & Rayle, K. E. 2000, A&A, 355, 308 [NASA ADS]
- Alecian, G., & Stift, M. J. 2007, A&A, 475, 659 [NASA ADS] [CrossRef] [EDP Sciences]
- Alekseeva, G. A., Arkharov, A. A., Galkin, V. D., et al. 1996, Baltic Astron., 5, 603 [NASA ADS] (In the text)
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes III, F. N. Bash, ASP Conf. Ser., 336, 25 (In the text)
- Babel, J. 1992, A&A, 263, 232 [NASA ADS]
- Bagnulo, S., Wade, G. A., Donati, J.-F., et al. 2001, A&A, 369, 889 [NASA ADS] [CrossRef] [EDP Sciences]
- Bagnulo, S., Landstreet, J. D., Mason, E., et al. 2006, A&A, 450, 777 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ballester, P., Modigliani, A., Bitquin, O., et al. 2000, Messenger, 101, 31 [NASA ADS] (In the text)
- Bard, A., & Kock, M. 1994, A&A, 282, 1014 [NASA ADS]
- Berry, H. G., Bromander, J., Curtis, L. J., & Buchta, R. 1971, Phys. Scr, 3, 125 [NASA ADS] [CrossRef]
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] (In the text)
- Bruntt, H. 2007, CoAst, 150, 326 [NASA ADS] (In the text)
- Bruntt, H., North, J. R., Cunha, M., et al. 2008, MNRAS, 386, 2039 [NASA ADS] [CrossRef] (In the text)
- Burnashev, V. I. 1985, Abastumanskaya Astrofiz. Obs., Byull., 59, 83 (In the text)
- Cowley, C. R., Hubrig, S., Ryabchikova, T. A., et al. 2001, A&A, 367, 939 [NASA ADS] [CrossRef] [EDP Sciences]
- Cunha, M. S., Fernandes, J. M. M. B., & Monteiro, M. J. P. F. G. 2003, MNRAS, 343, 831 [NASA ADS] [CrossRef] (In the text)
- Dekker, H., D'Odorico, S., Kayfer, A., Delabre, B., & Kotzlowski, H. 2000, Proc. SPIE, 4008, 534 [NASA ADS] (In the text)
- Engels, D., Sherwood, W. A., Wamsteker, W., & Schultz, G. V. 1981, A&AS, 45, 5 [NASA ADS] (In the text)
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Groote, D., & Kaufmann, J. P. 1983, A&AS, 53, 91 [NASA ADS] (In the text)
- Hauck, B., & North, P. 1982, A&A, 114, 23 [NASA ADS] (In the text)
- Hauck, B., & North, P. 1993, A&A, 269, 403 [NASA ADS]
- Holt, R. A., Scholl, T. J., & Rosner, S. D. 1999, MNRAS, 306, 107 [NASA ADS] [CrossRef] (In the text)
- Hui-Bon-Hoa, A., LeBlanc, F., & Hauschildt, P. H. 2000, ApJ, 535, L43 [CrossRef]
- Johnson, H. L., Iriarte, B., Mitchell, R. I., & Wisniewskj, W. Z. 1966, Comm. Lunar Plan. Lab., 4, 99 [NASA ADS] (In the text)
- Khan, S., & Shulyak, D. 2006, A&A, 448, 1153 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kochukhov, O. 2007, in Physics of Magnetic Stars, ed. D. O. Kudryavtsev, I. I. Romanyuk, Nizhnij Arkhyz., 109 (In the text)
- Kochukhov, O., & Ryabchikova, T. 2001, A&A, 377, L22 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kochukhov, O., Bagnulo, S., & Barklem, P. S. 2002, ApJ, 578, L75 [NASA ADS] [CrossRef]
- Kochukhov, O., Drake, N. A., Piskunov, N., & de la Reza, R. 2004, A&A, 424, 935 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kochukhov, O., Khan, S., & Shulyak, D. 2005, A&A, 433, 671 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kochukhov, O., Tsymbal, V., Ryabchikova, T., Makaganyk, V., & Bagnulo, S. 2006, A&A, 460, 831 [NASA ADS] [CrossRef] [EDP Sciences]
- Kochukhov, O., Ryabchikova, T., Weiss, W. W., et al. 2007, MNRAS, 376, 651 [NASA ADS] [CrossRef]
- Kunzli, M., North, P., Kurucz, R. L., & Nicolet, B. 1997, A&AS, 122, 51 [NASA ADS] [CrossRef] [EDP Sciences]
- Kupka, F., Ryabchikova, T. A., Weiss, W. W., et al. 1996, A&A, 308, 886 [NASA ADS] (In the text)
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences]
- Kurtz, D. W., Sullivan, D. J., Martinez, P., & Tripe, P. 1994, MNRAS, 270, 674 [NASA ADS] (In the text)
- Kurucz, R. L. 1993, Kurucz CD-ROM 13, Cambridge, SAO (In the text)
- Kurucz, R. L. 2008, http://cfaku5.cfa.harvard.edu/ATOMS (In the text)
- Lawler, J. E., Wickliffe, M. E., Den Hartog, E. A., & Sneden, C. 2001, ApJ, 563, 1075 [NASA ADS] [CrossRef] (In the text)
- Lawler, J. E., Sneden, C., & Cowan, J. J. 2004, ApJ, 604, 850 [NASA ADS] [CrossRef] (In the text)
- LeBlanc, F., & Monin, D. 2004, in the A-Star Puzzle, ed. J. Zverko, J. Ziznovsky, S. J. Adelman, & W. W. Weiss (Cambridge University Press), IAU Symp., 224, 193
- LeBlanc, F., Monin, D., Hui-Bon-Hoa, A., & Hauschildt, P. H. 2009, A&A, 495, 937 [NASA ADS] [CrossRef] [EDP Sciences]
- Lipski, ., & Stepien, K. 2008, MNRAS, 385, 481 [NASA ADS] [CrossRef]
- Martin, G. A., Fuhr, J. R., & Wiese, W. L. 1988, J. Phys. Chem. Ref. Data, 17, Suppl.3
- Mashonkina, L., Ryabchikova, T., & Ryabtsev, A. 2005, A&A, 441, 309 [NASA ADS] [CrossRef] [EDP Sciences]
- Mashonkina, L., Ryabchikova, T., Ryabtsev, A., & Kildiyarova, R. 2008, A&A, 495, 297 [NASA ADS] [CrossRef]
- Michaud, G. 1970, ApJ, 160, 641 [NASA ADS] [CrossRef] (In the text)
- Moon, T. T., & Dworetsky, M. M. 1985, MNRAS, 217, 305 [NASA ADS]
- Napiwotzki, R., Schoenberner, D., & Wenske, V. 1993, A&A, 268, 653 [NASA ADS]
- Netopil, M., Paunzen, E., Maitzen, H. M., North, P., & Hubrig, S. 2008, A&A, 491, 545 [NASA ADS] [CrossRef] [EDP Sciences]
- O'Brian, T. R., Wicklife, M. E., Lawler, J. E., Whaling, W., & Brault, J. W. 1991, JOSA, B8, 1185 [NASA ADS]
- Pickering, J. C. 1996, ApJS, 107, 811 [NASA ADS] [CrossRef] (In the text)
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS]
- Raassen, A. J. J., & Uylings, P. H. M. 1998, A&A, 340, 300 [NASA ADS]
- Ralchenko, Yu., Kramida, A. E., & Reader, J., and NIST ASD Team 2008, NIST Atomic Spectra Database (version 3.1.5), National Institute of Standards and Technology, Gaithersburg, MD
- Ryabchikova, T. 2005, Astron. Lett., 31, 388 [NASA ADS] [CrossRef] (In the text)
- Ryabchikova, T. 2008, CoSka, 38, 257 [NASA ADS] (In the text)
- Ryabchikova, T., Piskunov, N., Kochukhov, O. et al. 2002, A&A, 384, 545 [NASA ADS] [CrossRef] [EDP Sciences]
- Ryabchikova, T., Nesvacil, N., Weiss, W. W., et al. 2004, A&A, 423, 705 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ryabchikova, T., Leone, F., & Kochukhov, O. 2005, A&A, 438, 973 [NASA ADS] [CrossRef] [EDP Sciences]
- Ryabchikova, T., Sachkov, M., Kochukhov, O., & Lyashko, D. 2007, A&A, 473, 907 [NASA ADS] [CrossRef] [EDP Sciences]
- Ryabchikova, T., Kochukhov, O., & Bagnulo S. 2008, A&A, 480, 811 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rufener F. 1988, Catalogue of Stars Measured in the Geneva Observatory Photometric System, Geneva Observatory (In the text)
- Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz Ch., & Weiss, W. W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Shulyak, D., Kochukhov, O., & Khan, S. 2008, A&A, 487, 689 [NASA ADS] [CrossRef] [EDP Sciences]
- Shulyak, D., Ryabchikova, T., Mashonkina, L., & Kochukhov, O. 2009, A&A, submitted
- Schulz-Gulde, E. 1969, J. Quant. Spec. Radiat. Transf., 9, 13 [NASA ADS] [CrossRef]
- Wilke, R. 2003, Ph.D. Thesis, Heinrich-Heine-Universität, Düsseldorf (In the text)
Footnotes
- ...
 Circini
Circini![[*]](/icons/foot_motif.png)
- Based on observations collected at the European Southern Observatory, Paranal, Chile (ESO program 68.D-0254).
- ... archive
![[*]](/icons/foot_motif.png)
- http://sdc.laeff.inta.es/ines/index2.html
- ... database
![[*]](/icons/foot_motif.png)
- http://simbad.u-strasbg.fr/simbad/
All Tables
Table 1:
List of Si, Cr, and Fe spectral lines used for stratification calculations. Columns give the ion identification, central wavelength, excitation potential, oscillator strength (![]() )
and the Stark damping constant (
)
and the Stark damping constant (
![]() )
for T=10 000 K. The last column gives reference for the adopted oscillator strength.
)
for T=10 000 K. The last column gives reference for the adopted oscillator strength.
Table 2:
Abundances in the atmosphere of ![]() Cir with the error estimates based on n measured lines. Abundances derived in our study are compared with those reported by Kupka et al. (1996) and BNC08. The solar abundances are from Asplund et al. (2005).
Cir with the error estimates based on n measured lines. Abundances derived in our study are compared with those reported by Kupka et al. (1996) and BNC08. The solar abundances are from Asplund et al. (2005).
All Figures
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11653f1.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg36.png) |
Figure 1: Comparison of the observed Fe line profiles (symbols) and calculations for the final stratified abundance distribution (solid line) and for the best-fit homogeneous abundance of Fe (dashed line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11653f2.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg39.png) |
Figure 2: Same as in Fig. 1 but for Si. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11653f3.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg40.png) |
Figure 3: Same as in Fig. 1 but for Ca. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{11653f4.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg41.png) |
Figure 4: Same as in Fig. 1 but for Cr. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11653f5.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg42.png) |
Figure 5:
Vertical distribution of Si, Ca, Cr, and Fe abundance in the atmosphere of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=18cm,angle=90,clip]{11653f6.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg102.png) |
Figure 6:
Comparison between the observed (symbols) and theoretical (lines) spectral energy distribution of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=13cm,angle=90]{11653f7.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg103.png) |
Figure 7:
Theoretical spectral energy distributions for the model atmosphere parameters
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{11653f8.eps}
\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg105.png) |
Figure 8:
Dependence of the synthetic Strömgren (left panel) and Geneva
(right panel) photometric parameters on the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11653f9.eps} %\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg111.png) |
Figure 9:
Comparison of the observed and theoretical H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11653f10.eps} %\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg112.png) |
Figure 10:
Comparison of the observed and theoretical H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{11653f11.eps} %\end{figure}](/articles/aa/full_html/2009/21/aa11653-09/Timg120.png) |
Figure 11:
Temperature as a function of standard optical depth,
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


