EDP Sciences
Home All issues Volume 499 / No 3 (June I 2009) A&A, 499 3 (2009) 879-890 Full HTML
Free Access
Issue
A&A
Volume 499, Number 3, June I 2009
Page(s) 879 - 890
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/200911623
Published online 29 April 2009

Model atmospheres of chemically peculiar stars

Self-consistent empirical stratified model of HD 24712

D. Shulyak1 - T. Ryabchikova1,2 - L. Mashonkina2 - O. Kochukhov3

1 - Institute of Astronomy, Vienna University, Turkenschanzstrasse 17, 1180 Vienna, Austria
2 - Institute of Astronomy, Russian Academy of Science, Pyatnitskaya 48, 119017 Moscow, Russia
3 - Department of Astronomy and Space Physics, Uppsala University, Box 515, 751 20 Uppsala, Sweden

Received 7 January 2009 / Accepted 19 March 2009

Abstract
Context. High-resolution spectra of some chemically peculiar stars clearly demonstrate the presence of strong abundance gradients in their atmospheres. However, these inhomogeneities are usually ignored in the standard scheme of model atmosphere calculations, breaking the consistency between model structure and spectroscopically derived abundance pattern.
Aims. In this paper we present the first empirical self-consistent stellar atmosphere model of the roAp star HD 24712  with stratification of chemical elements included, and which is derived directly from the observed profiles of spectral lines without time-consuming simulations of physical mechanisms responsible for these anomalies.
Methods. We used the LLmodels  stellar model atmosphere code and DDAFIT  minimization tool for analysis of chemical element stratification and construction of a self-consistent atmospheric model. Empirical determination of Pr and Nd stratification in the atmosphere of HD 24712  is based on NLTE line formation for Pr II/III  and Nd II/III with the use of the DETAIL code.
Results. Based on an iterative procedure of stratification analysis and subsequent re-calculation of model atmosphere structure, we constructed a self-consistent model of HD 24712, i.e. the model whose temperature-pressure structure is consistent with the results of the stratification analysis. It is shown that stratification of chemical elements leads to considerable changes in model structure compared to the non-stratified homogeneous case. We find that accumulation of rare earth elements (REE) allows for the inverse temperature gradient to be present in the upper atmosphere of the star with a maximum temperature increase of about 600 K.

Key words: stars: chemically peculiar - stars: atmospheres - stars: individual: HD 24712

1 Introduction

Atmospheres of chemically peculiar (CP) stars have an inhomogeneous distribution of chemical elements. These inhomogeneities are frequently seen as abundance spots on stellar surfaces (see, for example, Kochukhov et al. 2004a,b; Lueftinger et al. 2003) and as clouds of chemical elements concentrated at certain depths along the stellar radii (Ryabchikova et al. 2005,2006,2002). Several tools have been developed and successfully applied to the analysis of element distributions based on a detailed analysis of observed line profiles. The horizontal element distribution is investigated using the rotational modulation of spectral lines: as a star rotates, the abundance spots on its surface should appear as variation of line profiles of respective elements observed at different rotational phases of the star. The automatic procedure of finding the spot position and abundance values via the comparison of observed and calculated spectra is performed via Doppler Imaging techniques first introduced by Goncharsky et al. (1982) and further developed by Piskunov & Wehlau (1990 see also Kochukhov et al. 2004b). The vertical distribution of chemical elements is modeled assuming the stratification profiles of chemical elements to be represented by a simple step-function with two different abundances in the upper and lower atmosphere as was suggested in Babel (1992), or, as recently shown by Kochukhov et al. (2006), applying the regularized minimization algorithm. The results of these analyses show that strong abundance gradients do exist in atmospheres of CP stars with accumulation of various chemical elements at different atmospheric layers.

From a theoretical point of view, the appearance of inhomogeneous element distribution with high abundance gradients in atmospheres of CP stars is explained by microscopic radiative diffusion processes: the atmospheres of these stars are believed to be dynamically stable enough for radiative levitation and gravitational settling to control the distribution of chemical elements (Michaud 1970).

These abundance inhomogeneities may have a rather strong influence on model atmosphere structure via modification of opacity and emissivity coefficients and thus the modeling of element distributions in stellar atmospheres should, in principle, include the simulation of these diffusion processes in every step of the model atmosphere calculation. Such models were successfully developed and improved in resent years (see, for example, Alecian & Stift 2007; Hui-Bon-Hoa et al. 2000), however, the sensitivity of modeled element distributions to the input physics (that is frequently poorly understood), the absence of accurate atomic data for some elements, and high computational expense do not allow implementation of these models for detailed modeling of theoretical line profiles and their comparison with high-resolution observations: although the theoretical stratification is able to predict some observed characteristics of CP stars, it is still not applied for the quantitative interpretations of modern high-resolution spectroscopic observations.

A necessary ingredient in the analysis of element stratification is the computation of synthetic spectra and their subsequent comparison with observations: a set of such computations is needed to construct the stratification profile of a given element that ensures a best fit between theoretical and observed line profiles. These empirical investigations of element stratification in stellar atmospheres are very important to understand the physical conditions in atmospheres of CP stars and, ideally, should provide the test ground for recent theoretical calculations. The only methodological difficulty in empirical analysis is that in almost all cases the synthetic spectrum is computed using standard model atmospheres, i.e. model atmosphere that were computed under the assumption of homogeneous element distribution.

To avoid this inconsistency we made an attempt to implement an iterative procedure of vertical stratification analysis with the subsequent re-calculation of model atmosphere structure. This procedure is applied to the cool roAp star HD 24712  for which the stratification of Si, Ca, Cr, Fe, Sr, Ba, Pr, and Nd is derived. Stratification analysis of Pr and Nd is based on non-local thermodynamic equilibrium (NLTE) line formation for Pr II/III  and Nd II/III. Using this approach we examine how the stratification profiles of different elements are changing compared to the case when only the non-stratified model is applied and what the overall effect is of inhomogeneous element distribution on the model atmosphere structure.

In the next section we give an overview of observations used. Then, in Sect. 3 we describe the general methods and atomic line data used for the analysis of element stratification. In Sect. 4 we present the results of the stratification analysis and its effect on model atmosphere structure and some observed parameters of the star. The main conclusions are summarized in Sect. 5

2 Observations

We used an average spectrum of HD 24712  obtained on November 10/11, 2004, with the HARPS (High Accuracy Radial velocity Planet Searcher) spectrometer at the 3.6-m telescope at ESO, La Silla. The details of the reduction procedure are given in Ryabchikova et al. (2007). In total 92 spectra were taken with 60 s exposure time, signal to noise ratio S/N = 120, and R = 120 000 resolving power. These spectra cover a spectral region from 3850 Å to 6730 Å. After averaging, the final S/N = 1000 was reached. HARPS spectra were obtained at the phase 0.867 close to magnetic maximum (Ryabchikova et al. 2007). Photometric color-indices were taken from the SIMBAD electronic database[*] with the additional Strömgren photometry from Martinez (1993), peculiar index a from Vogt et al. (1998), and Geneva colors from Burki et al. (1999). We also used UV spectroscopic observations extracted from the IUE data archive[*].

3 Methods

3.1 Stratification analysis

To analyse the stratification of chemical elements in the atmosphere of HD 24712 we applied a step-function approximation as performed in DDAFIT - an automatic procedure to determine vertical abundance gradients (Kochukhov 2007) that was successfully used in a number of studies (e.g. Ryabchikova et al. 2005,2008,2006). In this routine, the vertical abundance distribution of an element is described by four parameters: chemical abundance in the upper atmosphere, abundance in deep layers, the position of the abundance jump and the width of the transition region where the chemical abundance changes between the two values. All four parameters can be optimized simultaneously with the least-squares fitting procedure and based on observations of an unlimited number of spectral regions. DDAFIT  also allows a stratification analysis with the magnetically split lines. For HD 24712  we assumed a purely radial magnetic field with the modulus $\langle B \rangle$ = 3.1 kG (Ryabchikova et al. 2007). The spectral synthesis was performed using the SYNTHMAG  code (Kochukhov 2007) which represents an improved version of the program developed by Piskunov (1999).

For Pr and Nd, we performed a NLTE stratification analysis as described in Mashonkina et al. (2009) and Mashonkina et al. (2005) using a trial-and-error method and the observed equivalent widths of the lines of the first and second ions.

3.2 NLTE calculations

The present investigation of Pr II/III  and Nd II/III  is based on the NLTE methods treated in our earlier studies (Mashonkina et al. 2009,2005), where atomic data and the problems of line formation were considered in detail. Briefly, comprehensive model atoms of praseodymium and neodymium include the measured and the predicted energy levels, in total, 6708 levels of Pr II  and Pr III and 2258 levels of Nd II  and Nd III. The coupled radiative transfer and statistical equilibrium equations were solved using a revised version of the DETAIL program (Butler & Giddings 1985) based on the accelerated lambda iteration, which follows the efficient method described by Rybicki & Hummer (1991,1992).

As shown for Nd by Mashonkina et al. (2005) and for Pr by Mashonkina et al. (2009), the main non-LTE effect for their first ions in the model atmosphere representing the atmosphere of HD 24712  is overionization caused by a super-thermal radiation of non-local origin close to the thresholds of the low-excitation levels. The departures from LTE for the lines of the first and the second ions are of the opposite sign and they are significant if the element is concentrated in the uppermost atmospheric layers where collisions are inefficient in establishing thermodynamic equilibrium. For the Pr and Nd distribution in the atmosphere of HD 24712  determined by Mashonkina et al. (2009) and Mashonkina et al. (2005), the NLTE abundance corrections, $\Delta\epsilon_{\rm NLTE}= \epsilon_{\rm NLTE}-\epsilon_{\rm LTE}$, are positive for the lines of Pr II  and Nd II  and are between 1.0 dex and 1.4 dex, while $\Delta\epsilon_{\rm NLTE}$ is negative for the lines of Pr III  and Nd III  and ranges between -0.3 dex and -0.7 dex.

We performed NLTE calculations for H I using the method described in Mashonkina et al. (2008). The model atom includes levels with principal quantum numbers up to n=19. For the model atmospheres investigated in this study, the ground state keeps its thermodynamic equilibrium level populations throughout the atmosphere. In the layers where the core-to-wing transition is formed, namely between $\log \tau_{5000} \simeq -1.2$ and $\log \tau_{5000} \simeq -2.2$, the n = 2 level is closely coupled to the ground state, while departures from LTE for the n = 3 level are controlled by H$\alpha $  which serves as the pumping transition resulting in an overpopulation of the upper level. For H$\alpha $, NLTE leads to weakening of the core-to-wing transition compared to the LTE case.

3.3 Model atmospheres

To perform the model atmosphere calculations we used the recent version of the LLmodels  (Shulyak et al. 2004) stellar model atmosphere code (version 8.6). LLmodels  is 1-D, hydrostatic, plane-parallel LTE code which accounts for the effects of individual and stratified abundances. The stratification of chemical elements is an input parameter for the LLmodels  code and thus does not change during the model atmosphere calculation process. This allow us to explore the changes in model structure due to stratification that were extracted directly from observations without modeling the processes that could be responsible for the observed inhomogeneities.

The following calculation settings were used for each model atmosphere calculation: the atmosphere of a star is discretized into 120 layers between $\log\tau_{\rm 5000}=-8$ and 2 with a non-equidistant spacing, i.e. with the higher point density in the regions of steep abundance gradients to ensure accurate integration of radiation field properties and solution of other model equations. The frequency-dependent quantities are calculated with a variable wavelength step: 0.1 between 500 Å  and 20 000 Å, and 0.5 Å  between 20 000 Å  and 70 000 Å. The VALD database (Piskunov et al. 1995; Kupka et al. 1999) was used as a source of atomic line data for the computation of the line absorption coefficient.

Table 1:   A list of spectral lines used for the stratification calculations.

The use of the LTE assumption in atmosphere modeling results from the following consideration. The opacity in the atmosphere of HD 24712  is mostly contributed by neutral hydrogen. Our NLTE calculations for H I showed no significant deviations from thermodynamic equilibrium populations for the n=1 level throughout the atmosphere and for the n=2 level below $\log \tau_{\rm 5000} = -3$. The departures from LTE are found to be larger for the hotter atmosphere of Vega, however, self-consistent NLTE modelling of Hauschildt et al. (1999) leads to only 200-300 K changes in T distribution compared to the LTE model in the layers between $\log \tau_{\rm 5000} = -1$ and $\log \tau_{\rm 5000} = -6$. The NLTE effect on the atmospheric structure of HD 24712  is expected to be smaller. Another important opacity contributor is the iron group elements. The iron and chromium among them are concentrated in deep atmospheric layers of HD 24712, below $\log \tau_{\rm 5000} = -2$ (see Fig. 3), where the departures from LTE are expected to be small. This is confirmed by our NLTE calculations for Ca whose distribution in the atmosphere is similar to that of the iron group elements (Fig. 3). We used the NLTE method for Ca I/II described by Mashonkina et al. (2007). We do not know the distribution of light elements, C, N, and O, however, according to Khan & Shulyak (2006) these elements do not introduce noticeable changes in model structure and emergent flux. The influence of the departures from LTE for two rare-earth elements, Pr and Nd, on the atmospheric structure of HD 24712  is simulated in the present paper.

Finally, the magnetic field with an intensity less than 5 kG has a marginal impact on the model temperature-pressure structure (Kochukhov et al. 2005; Khan & Shulyak 2006). Thus, we ignored the effects of polarized radiative transfer and Zeeman splitting in all model atmosphere calculations presented in this study.

 \begin{figure} \par\includegraphics[width=9cm,clip]{figures/1623f1.eps}\end{figure} Figure 1:

Fe abundance distribution derived with the homogeneous model atmosphere and the range of the optical depth formation of Fe I and Fe II lines from Table 1 calculated with a homogeneous Fe abundance $\log({\rm Fe}/N_{\rm total})=-5.10$.
Open with DEXTER

3.4 Atomic line data for stratification analysis

As was emphasized in Ryabchikova et al. (2003) the vertical abundance stratification manifests itself as the inability to fit the core and wings of strong lines with developed Stark wings (Ca II K, Si II, Mg II lines, etc.) with the same abundance or the inability to describe the low and high-excitation lines of the same ion with a chemically homogeneous atmosphere. This means that the choice of a proper set of spectral lines is crucial for an element stratification study. Ideally, it should be a set of lines originating levels with a large range of excitation energies and from different ions, thus probing a substantial part of the stellar atmosphere. In chemically peculiar stars as cool as HD 24712  we are faced with severe blending by numerous lines of the rare-earth elements, therefore the strongest lines with developed wings (for example, the Fe I $\lambda$ 4045.8 Å  line) are not able to be used. Also, Fe II lines with the an upper level excitation potential at 10 eV and higher are not visible any longer. The blue spectral region is more crowded by the REE lines than the red one and the preferential working spectral region is 5000-6800 ÅÅ. Table 1 gives a list of Si, Ca, Cr, Fe, Sr, Ba lines used in LTE stratification analysis routines together with the atomic parameters and the references. For NLTE stratification analysis we used the same lines as given in Mashonkina et al. (2009,2005).

The ability of the chosen set of spectral lines to probe different atmospheric layers is illustrated in Fig. 1. The iron stratification derived with the initial model (see Sect. 4) is shown together with the ranges of Fe line depth formation calculated on a $\log\tau_{\rm 5000}$ scale. The latter were calculated with the contribution function to the emergent line radiation following Achmad et al. (1991). Figure 2 illustrates a fit of the calculated to the observed Fe Line profiles for homogeneous and stratified atmospheres. For Si, Ca, Cr, Sr, and Ba the corresponding plots are shown in Figs. 7-10.

3.5 Self-consistent models with empirical stratification

Using the methods of stratification analysis described above one could restore the element distribution profile of any chemical element for which accurate atomic line data exist. However, we should remember that the empirical analysis of chemical element stratification is based on model atmosphere techniques, and thus the temperature-pressure structure of the model atmosphere itself depends upon the stratification, which has to be found. Therefore, the calculation of the model atmosphere and the stratification (abundances) analysis are linked and thus an iterative procedure should be used in this case. In general, this procedure can be divided into several steps:

1.
calculation of the so-called first approximation, simplified model, that could be any standard model atmosphere with the atmospheric parameters close to those of the star to be analysed;
2.
determination of stratification of chemical elements based on spectroscopic analysis of individual spectral lines;
3.
calculation of an improved model atmosphere taking into account an stratification found in the previous step;
4.
comparison of the modeled energy distribution (or/and photometric colors) and hydrogen line profiles with observed ones and re-adjustment of model input parameters ( 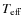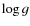$T_{\rm eff}$, $\log g$) if needed to fit observations. At this step several calculations of the model atmosphere with fixed stratification but different model parameters may be required;
5.
repeating the overall process starting from step 2 until stratification profiles of chemical elements and model parameters are not converged.
This procedure ensures the consistency between the model atmosphere structure and abundances used for the calculation of synthetic line profiles and the interpretation of observed data.

 \begin{figure} \par\includegraphics[width=18cm,clip]{figures/1623f2.eps}\end{figure} Figure 2:

A comparison between the observed Fe line profiles and calculations with the stratified abundance distribution (full line) and with the homogeneous ( $\log({\rm Fe}/N_{\rm total})=-5.10$) abundances (dashed line).
Open with DEXTER

4 Results

4.1 Construction of model atmosphere

In the present analysis we started from a chemically homogeneous model atmosphere with the parameters $T_{\rm eff}=7250$ K and $\log g=4.3$ and the abundances taken from Ryabchikova et al. (1997) (Model 1). These mean abundances were derived based on the observations close to magnetic maximum, and they provide a satisfactory fit to HARPS observations. Table 2 shows abundances of the elements which were not passed through the subsequent stratification analysis. For the rest of chemical elements the solar composition (Asplund et al. 2005) was assumed.

Based on this model the stratification of Fe, Ba, Ca, Sr, Cr, Si, Pr, and Nd was derived and is displayed in the top panel of Fig. 3.

 \begin{figure} \par\includegraphics[width=9cm,clip]{figures/1623f3a.eps}\par\includegraphics[width=9cm,clip]{figures/1623f3b.eps}\end{figure} Figure 3:

Stratification of eight elements in the atmosphere of HD 24712  derived using the homogeneous first-approximation model (Model 1, top panel) and using the final model with scaled REE opacity (Model 5, bottom panel).
Open with DEXTER
It is seen that the stratification of the majority of elements shows element underabundance in surface layers and overabundance in layers around the star's photosphere ( $\log\tau_{\rm 5000}\approx[-1,0]$). On the contrary, the distribution of Pr and Nd shows an inverse picture with a strong overabundance (up to 5 dex) in surface layers. This kind of element distribution, i.e. the difference between distribution of REEs compared to other elements, seems to be a common characteristic of the atmospheres of Ap stars (Ryabchikova et al. 2002).

The stratification shown in Fig. 3 (top panel) was then applied to the calculation of a new model atmosphere. Again, the individual values of the abundances of some other elements used for calculation were taken from Table 2.

Table 2:   Abundances of individual elements.

The stratification of REE elements and its implementation in model atmosphere computation deserve a more detailed description. Numerical calculations showed that the REE element stratification has a strong influence on the model atmosphere structure leading to the appearance of an inverse temperature gradient in the upper atmospheric region. This is illustrated in Fig. 4, where the models with the same atmospheric parameters and input line list were computed with and without stratification of chemical elements (solid and dotted lines respectively). It is seen that the heating of the stratified atmosphere starts at $\log \tau_{\rm 5000} = -3$ going outwards to the stellar surface and reaches its maximum of about 800 K around $\log\tau_{\rm 5000}=-4$ compared to the homogeneous abundance model. This temperature increase is caused by the presence of REE stratification and, as seen from Fig. 3, is directly related to the position of the abundance jumps of Pr and Nd. No other elements considered in our computations are responsible for such an effect. Indeed, the strong overabundance of Pr and Nd by 4-5 dex relative to their solar values and their rich spectra presented in the current version of the VALD database make the absorption coefficient very high at frequencies of REE transitions. The latter are generally located at the spectral region where the star with $T_{\rm eff}=7250$ K radiates most of its energy, dominating the total radiative energy balance, and thus allowing for the heating of atmospheric layers with high REE opacity.

The appearance of an inverse temperature gradient clearly shows that the REE elements no longer trace elements in atmospheres of Ap stars if their stratification is as strong (or comparably strong) as in the atmosphere of HD 24712. This immediately implies that not only synthetic line profiles, but also model atmospheres with REE stratification must be computed based on NLTE line formation for REEs. Unfortunately, this cannot be done with the current version of LLmodels. Nevertheless, to simulate NLTE effects of Pr and Nd in model atmosphere calculations we used the following approach. Mashonkina et al. (2005) and Mashonkina et al. (2009) found that, for the stratified distribution of Nd and Pr, the NLTE abundance corrections are positive for the lines of the first ions at a level of one order of magnitude and negative for the lines of the second ions at a level of $\simeq$0.5 dex. Thus, to account for the REE stratification in the LTE model atmosphere code, we scale the $\log(gf)$  values of Pr II and Nd II lines by -1.5 dex while taking abundances derived using second ions for model atmosphere calculation. This procedure was applied to all the Pr II and Nd II lines that are presented in the master line list used for model atmosphere calculations. Then, using this new line list, we recomputed the model atmosphere and re-derived the stratification of chemical elements. At each iteration Pr and Nd stratifications were recalculated based on NLTE line formation for Pr II/III  and Nd II/III. The best fit to the hydrogen H$\alpha $  line profile (wings) and photometric color indices required the decrease of effective gravity down to $\log g=4.1$ (mainly to $c_{\rm 1}$ index). No further changes were detected in the observed parameters and this gravity was considered as the final one. The model and stratification calculations converge after the second iteration (Model 4).

 \begin{figure} \par\includegraphics[width=9cm,clip]{figures/1623f4.eps}\end{figure} Figure 4:

Effect of Pr and Nd stratification on model temperature structure. Solid line - t7250g4.3 model calculated with homogeneous abundances; dotted line - t7250g4.3 model calculated with stratified abundances shown in Fig. 3; dashed and dash-dotted lines - t7250g4.1 models calculated with stratified abundances and scaled Pr II,III and Nd II,III $\log(gf)$ values.
Open with DEXTER

Except Pr and Nd, other REE elements can also be non-uniformly distributed in the atmosphere of HD 24712  and can also exhibit deviations from LTE. Among them, only the most abundant elements may play a noticeable role in the modification of atmospheric structure. At present, we do know either the distributions of these elements, or the magnitude of their NLTE effects. Preliminary abundance results for Ce and Sm show that the REE anomaly - the discrepancy between abundances inferred from the lines of a singly- and doubly-ionized element - reaches approximately the same magnitude as for Pr and Nd. Supposing that the Ce (which has the highest number of available lines in VALD  among other REE elements) has the same vertical distribution as Nd, we estimated its effect on atmospheric structure. We found that neglecting Ce stratification we underestimate the size of the temperature jump by no more than $\sim$200 K.

Decreasing the $\log(gf)$ values of Pr II and Nd II lines could, in principle, simulate the NLTE line opacity of these elements, however the second ions are also affected by NLTE effects that bring as much as 0.5 dex difference between LTE and NLTE abundances derived using second ion spectra. This forced us to compute another model where the $\log(gf)$ values of both first and second ions are changed by -1 dex and 0.5 dex respectively (Model 5). This model provides slightly higher temperature increases in superficial layers compared to the model where $\log(gf)$ values of only first ions were changed (see Fig. 4). It is seen that the simulation of NLTE REE opacity tends to decrease the amplitude of the temperature jump almost by a factor of two. However, independently of how to scale the REE opacity, the overall picture remains the same, illustrating the heating of surface layers in the region of strong Pr and Nd overabundance.

Table 3:   Observed and calculated photometric parameters of HD 24712.

We also tested the influence of Pr II and Nd II bound-free opacity on model structure and energy distribution. To simplify the computations we assumed three characteristic energy levels with excitation energies of 2 eV, 3 eV, and 4 eV for both ions. These levels further consist of 50 atomic states each with the statistical weight g=7. Such an approximation is based on the fact that both ions have essentially the same structure of states with the very close ionization potentials. The NLTE level populations were taken directly from the DETAIL code and then incorporated in LLmodels. For all the levels, the photoionization cross-sections were calculated using the hydrogenic approximation. It appeared that the effect of the Pr II and Nd II bound-free opacity becomes visible only if the abundances of these elements are increased by +6 dex for the stratified model where REEs are already in strong overabundance in surface layers. Even so, the cumulative effect on the temperature distribution was never higher than tens of K. We thus concluded that REE bound-free opacity can be ignored in the model atmosphere computations.

The bottom panel of Fig. 3 shows the stratification derived with Model 5. One can note that the stratification of REEs shows a more steep abundance jump in this case which is probably a result of more the refined set of optical depths around the REE jump implemented in the last iteration compared to the initial model and the first iteration. This is also the reason why the inverse temperature gradient shown in Fig. 4 is more steep for the model calculated with Model 5 stratification than for the model with stratification derived in Model 4. A few remarks concerning Sr and Ba stratification calculations should be made. Although we formally obtain Ba stratification, it is not significant because the difference between $\chi^2$ for line profile fits with uniform and stratified models does not exceed 15-16%, while $\chi^2$ differs by 5-10 times in the case of real stratification. Therefore uniform Ba distribution in the atmosphere of HD 24712 or at least in the layers where the studied Ba II lines are formed is more probable. For the Sr distribution we used five lines with the three weakest lines of Sr I. Strontium distribution is mainly based on strong Sr II lines, in particular, on resonance Sr II $\lambda$ 4215.5 Å. The wings of Sr II lines that probe abundance in the deeper atmospheric layers are blended, which obviously leads to larger formal computing errors of stratification parameter determination and, hence, to a worse $\chi^2$. To check the reliability of Sr stratification we recalculated it using Sr lines observed at a slightly different magnetic phase of 0.944 (see UVES time-series observations in Ryabchikova et al. 2007). Within the formal errors of the DDAFIT  procedure, strontium abundance profiles coincide below $\log \tau_{\rm 5000} = -2$ where practically all considered Sr lines are formed. They differ above $\log \tau_{\rm 5000} = -2$, where the only core of the Sr II $\lambda$ 4215.5 Å line is formed. The poor fit of this line in the transition region between the line core and the line wings indicates that a more complex shape of the abundance profile than a simple step-function is required to describe the observed line profile, similar to the Ap star HD 133792 (Kochukhov et al. 2006). Strontium stratification derived for HD 24712 is not spurious, but the shape of the Sr abundance profile may differ from that derived in the present study. The other elements that demonstrated strong changes during iterative stratification analysis are Si and Ca. Both elements show an increase of the abundance jump amplitude in the final stratification with strong underabundance in surface layers and with practically the same abundance near photospheric layers. The jump itself becomes steeper. It may be caused by the change in temperature and electron density structure of the atmosphere above $\log \tau_{\rm 5000} = -3$, where the central parts of the strongest Ca I $\lambda$ 4227 and Si II  $\lambda\lambda$ 6347,6371 are formed. However, the formal errors of Si and Ca abundances in the upper atmospheric layers derived in the DDAFIT  procedure are rather high, up to 1.5 dex, hence a 2.5 dex difference for the initial and final Ca distributions may be considered as within the $3\sigma$ limit.

The changes in element distributions between the two cases shown in Figs. 3 are purely due to the changes in model atmosphere structure. Thus we can conclude that the recalculation of the model atmosphere structure could be very important for the quantitative stratification analysis. For some elements, the stratification derived with models computed under the assumption of homogeneous elements distribution can be considered only as a first approximation.

Finally, in Table 3 we compare theoretical and observed photometric color-indices of HD 24712. The calculations are presented for two models with $T_{\rm eff}=7250$ K, $\log g=4.3$ (homogeneous and stratified abundances) and for three models with $T_{\rm eff}=7250$ K, $\log g=4.1$ but with different assumptions about Pr and Nd opacity. The theoretical colors were calculated with the modified computer codes taken from Kurucz (1993a). One can see that the color indices of the Strömgren system as well as U-B and V-B indices of the Geneva system are better represented by stratified models. In contrast, the last two Geneva indices given in Table 3 are better described by a homogeneous abundance model. However, these differences are not very large and we can conclude that, generally, the two final models calculated with the complex stratification shown in Fig. 3 (bottom panel) and scaled REE opacity demonstrates a good agreement with the observations. The Strömgren photometry taken from Martinez (1993), which is not available in electronic format, introduces additional uncertainties. In particular, index b-y of Martinez (1993) is better represented by a homogeneous model. Furthermore, the difference of 0.027 mag between the two observations for $c_{\rm 1}$ index (see Table 3) does not allow us to distinguish between homogeneous and stratified models. On the other hand, the observation of $c_{\rm 1}$ taken from Hauck & Mermilliod (1998) agrees nicely with predictions by the model with the scaled Pr II,III and Nd II,III opacity. The difference of 0.007 mag between models computed under two assumptions about the scaling of REE opacity (last two models in Table 3) is within the error bars of observations, but deviates significantly from $c_{\rm 1}$ calculated without REE scaling. Our calculations demonstrate that taking stratification effects into account we obtain lower surface gravities than follows from the calibrations based on homogeneous models. The strong impact of simulated NLTE effects of Pr and Nd on the $c_{\rm 1}$ value, temperature distribution, and colors demonstrates the need for more precise model atmosphere computations with accurate treatment of Pr, Nd, and possibly other REE line formations. Our choice of $\log g$ for the final model could also change as more advanced NLTE model atmospheres are employed. Moreover, the strong variability in the $c_{\rm 1}$ index with a peak-to-peak amplitude of 0.086 mag (Wollf & Morrison 1973) is likely to be responsible for the difference between the value of Martinez (1993) and the average value given by Hauck & Mermilliod (1998). Thus, at present it is difficult to say something more definite about the $\log g$ value of the star and we restrict ourselves to $\log g=4.1$.

As it was stated above, for the opacity calculation in model atmospheres we used REE data extracted from the VALD  database. However, for the NLTE calculations with the DETAIL  code it was necessary to have more extensive line lists for accurate calculations of radiative rates for each single atomic state. These detailed line lists for Pr II and Nd II/III were produced at the Institute of Spectroscopy (ISAN, Russia), and are described in Mashonkina et al. (2009,2005). Note that the ISAN data already contains Pr and Nd parameters from VALD thus providing only an additional number of predicted lines. For example, while VALD provides information about 508 Pr II, 1279 Nd II, and 55 Nd III lines, ISAN theoretical computations extended them up to 103428, 1172579, and 6858 lines respectively. However, this great increase in line numbers lead to only marginal changes in model temperature distribution. This allowed us to conclude that the radiative equilibrium balance in the atmosphere of HD 24712 is controlled by the strongest REE lines that are presented in VALD. The only noticeable changes were detected for the $c_{\rm 1}$ (increased by 0.012 mag) and $m_{\rm 1}$ index (decreased by 0.008 mag).

 \begin{figure} \par\includegraphics[width=9cm,clip]{figures/1623f5.eps}\end{figure} Figure 5:

Observed and calculated H$\alpha $  line profiles. Thick full line - HARPS observations; dotted line - model with $T_{\rm eff}=7250$ K, $\log g=4.3$ and with homogeneous element distribution; full line - model with $T_{\rm eff}=7250$ K, $\log g=4.3$ and with stratification shown in 3 ( top panel); dashed line - model with $T_{\rm eff}=7250$ K, $\log g=4.1$ and with final iteration shown in 3 ( bottom panel). Bottom panel shows the zoomed part of the figure in the top panel around the core of the line.
Open with DEXTER

 \begin{figure} \par\includegraphics*[angle=90,width=17cm,clip]{figures/1623f6.eps}\end{figure} Figure 6:

Calculated and observed energy distributions of HD 24712. Solid line - t7250g4.1 model calculated with stratified abundances shown in Fig. 3 ( bottom panel) and Pr II,III and Nd II,III $\log(gf)$ values changed by -1 dex and +0.5 dex respectively.
Open with DEXTER
 \begin{figure} \par\includegraphics[width=12cm,clip]{figures/1623f7.eps}\end{figure} Figure 7:

A comparison between the observed Si  line profiles and calculations with the stratified abundance distribution (full line) and with the homogeneous ( $\log(Si/N_{\rm total})=-4.50$) abundances (dashed line).
Open with DEXTER

 \begin{figure} \par\includegraphics[width=15cm,clip]{figures/1623f8.eps}\end{figure} Figure 8:

A comparison between the observed Ca  line profiles and calculations with the stratified abundance distribution (full line) and with the homogeneous ( $\log({\rm Ca}/N_{\rm total})=-5.80$) abundances (dashed line).
Open with DEXTER
 \begin{figure} \par\includegraphics[width=15cm,clip]{figures/1623f9.eps}\end{figure} Figure 9:

A comparison between the observed Cr  line profiles and calculations with the stratified abundance distribution (full line) and with the homogeneous ( $\log({\rm Cr}/N_{\rm total})=-5.80$) abundances (dashed line).
Open with DEXTER
 \begin{figure} \par\mbox{\includegraphics[height=9cm,clip]{figures/1623f10a.eps}\hspace{1cm} \includegraphics[height=9cm,clip]{figures/1623f10b.eps} } \end{figure} Figure 10:

A comparison between the observed Sr ( left panel) and Ba ( right panel) line profiles and calculations with the stratified abundance distribution (full line) and with the homogeneous ( $\log({\rm Sr}/N_{\rm total})=-8.00$, $\log({\rm Ba}/N_{\rm total})=-9.00$) abundances (dashed line).
Open with DEXTER

Figure 6 demonstrates the observed and predicted energy distributions of HD 24712. Observational data is represented by a combination of the IUE low-resolution flux and photometric measurements converted to absolute flux units. The theoretical fluxes are calculated with the last model from Table 3. Note that all the models from Table 3 represent observations well enough, and the only way to choose the best one would be the comparison of UV fluxes blueward of $\lambda=2000$ Å  where stratified models predict significant flux excess (almost one order of magnitude at maximum) compared to the homogeneous abundance model, but this does not play an unimportant role in the total energy balance in the atmosphere due to the relatively cool effective temperature of the star. Although the IUE observations tend to be closer to the theoretical stratified fluxes in this region, it is difficult to make a clear decision because of the large error bars in observations (see IUE data archive).

Fitting of the spectral energy distribution of HD 24712 calibrated in physical flux units allows us to derive the angular diameter of the star, $\theta=0.335\pm0.005$ mas. Combined with the revised Hipparcos parallax of $\pi=20.32\pm0.39$ mas (van Leeuwen 2007), this yields a new determination of the stellar radius, $R=1.772\pm0.043~R_{\odot}$.

4.2 Effect of REE stratification

It was shown above that the accumulation of Pr and Nd leads to the appearance of an inverse temperature gradient with a temperature jump of about 600 K compared to the non-stratified model. However, this temperature jump is located in upper atmospheric layers and has no influence on the wings of the H$\alpha $  line, as it is shown in Fig. 5. Thus, even in the case of strong stratification of REE elements, the determination of atmospheric stellar parameters by fitting the wings of hydrogen lines could be performed with the model not taking the stratification of REE into account.

However, LTE calculations show that the core of the H$\alpha $  line is influenced strongly by the stratification of Pr and Nd (bottom panel of Fig. 5). One could see that none of the H$\alpha $  profiles computed under the assumption of LTE line formation could fit the transition region between the line core and wing, that is commonly called the core-to-wing anomaly (CWA) and is frequently observed in spectra of Ap stars. Kochukhov et al. (2002) tried to explain this anomaly by the existence of the temperature bump in the upper atmospheric layers above $\log\tau_{\rm 5000}\approx-1$. What is interesting is that the heating of atmospheric layers due to REE stratification produces the same sharp transition between the line wings and core, but the central intensity of theoretical spectra are much shallower than that with a homogeneous abundance model which still provides the best fit. However, all stratification effects disappear when NLTE hydrogen lines formation is applied, which 'washes out' all stratification effects.

From Figs. 2 and 3 of Kochukhov et al. (2002) it is seen that in order to explain the core-to-wing anomaly of hydrogen Balmer lines, the temperature jump should be located between $\log\tau_{\rm 5000}\approx-3$ and -2. In our calculations the temperature gradient starts higher in the stellar atmosphere at $\log\tau_{\rm 5000}\approx-3$. The position of the temperature gradient caused by REE stratification depends on the details of NLTE line formation, but it is practically impossible to shift the REE jump position in HD 24712  downward by more than 0.3-0.5 dex on a $\log\tau_{\rm 5000}$ scale (Mashonkina et al. 2009).

REE stratification is not the only reason for inverse temperature gradients in the Ap star atmosphere. Alecian & Stift (2007) and LeBlanc et al. (2009) calculated element stratification in the atmospheres with a magnetic field and showed that the horizontal magnetic field changes the abundance distribution. Instead of a step-like shape which is obtained in diffusion calculations in non-magnetic atmospheres or in the presence of a predominantly vertical component of the field, one finds an abundance minimum and then an increase of element abundance in the uppermost atmospheric layers. These abundance increase might lead to the corresponding temperature increase started at $\log \tau_{\rm 5000} = -1$(see Fig. 5 of LeBlanc et al. 2009). In a simple step function approximation used in the present stratification analysis as well as in most other similar studies (Wade et al. 2001; Ryabchikova et al. 2005,2008,2006), we cannot probe an increase of element abundance in the uppermost atmospheric layers. However, relatively good fitting of the observed line profiles in many stars with different strengths of the magnetic field obtained with a step-like abundance distribution of Si, Ca, Cr, Fe - the main contributors to line opacities - supports the absence of a significant increase of element abundance immediately following the abundance jump. This is further corroborated by the vertical inverse problem solution for the Ap star HD 133792 (Kochukhov et al. 2006), where the authors were able to derive an element distribution without an a priori assumption about the shape of this distribution. One should note, however, that this method currently can be applied only to non-magnetic or weakly magnetic atmospheres. Additionally, in atmospheric diffusion calculations the stratification is generally obtained assuming that all the forces acting on a given plasma volume are in stationary equilibrium (total diffusion velocity is zero). Regarding real stars this is not necessarily the case and element stratification at a given moment could be different (see Alecian & Stift 2007).

Thus, to explain most of the observed peculiarities in cool Ap stars we need to implement the full NLTE treatment of REE elements in model atmosphere calculations and not the rough simulation presented in this study. The accumulation of other elements could also be responsible for CWA and more detailed investigation is needed to explore this effect.

5 Conclusions

The spectroscopic investigation of element stratification is the only method for testing modern predictions of particle diffusion theory in atmospheres of star where this mechanism is sufficient to produce detectable abundance gradients. It provides us with stratification profiles of different chemical elements that could be compared with recent self-consistent diffusion models. However, in most of the stratification analysis routines the standard stellar model atmospheres are used where homogeneous abundances are assumed.

To circumvent this difficulty we made an attempt to construct an empirical self-consistent model atmosphere where the stratification of chemical elements is derived directly from observed spectra and then treated in a model atmosphere code. This iterative procedure was applied to a cool CP star, HD 24712. Below we summarise the main results of this investigation:

  • The accumulation of Pr and Nd in the upper atmosphere has an impact on the temperature structure of the atmosphere. The strong overabundance of these elements leads to an appearance of an inverse temperature gradient with a maximum temperature increase of up to 600-800 K compared to a homogeneous abundance model.
  • For HD 24712  we find that the effect of element stratification has a minor influence on the observed energy distribution. The lack of good quality observations in the UV region (where the effect of stratification is more pronounced) does not allow us at present to carry out more precise investigations. The changes in temperature structure due to the stratification of Pr and Nd do not affect the wings of hydrogen lines and thus can be ignored in routine procedures to determine atmospheric stellar parameters.
  • Due to their high overabundance and important role in overall temperature balance, REE elements can no longer be considered as trace elements in the standard scheme of NLTE calculations. This implies that, to achieve a better consistency in the modelling of REE stratification, the model atmosphere should account for REE NLTE effects as well.
  • For HD 24712  we find no critical changes in the shape and amplitude of stratification profiles of chemical elements when recalculating the atmospheric temperature-pressure structure. Most of the changes are comparable with the error bars of the minimization procedure used.

Acknowledgements
This work was supported by following funding projects: FWF Lise Meitner grant Nr. M998-N16 (DS), FWF P17890-N2 (TR), RFBR 08-02-00469-a and Presidium RAS Programme ``Origin and evolution of stars and galaxies'' (T.R. and L.M.). We also acknowledge the use of electronic databases (VALD, SIMBAD, NASA's ADS).

References

Footnotes

... database[*]
http://simbad.u-strasbg.fr/simbad/
... archive[*]
http://ines.ts.astro.it/
... database[*]
http://cfaku5.cfa.harvard.edu/ATOMS

All Tables

Table 1:   A list of spectral lines used for the stratification calculations.

Table 2:   Abundances of individual elements.

Table 3:   Observed and calculated photometric parameters of HD 24712.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{figures/1623f1.eps}\end{figure} Figure 1:

Fe abundance distribution derived with the homogeneous model atmosphere and the range of the optical depth formation of Fe I and Fe II lines from Table 1 calculated with a homogeneous Fe abundance $\log({\rm Fe}/N_{\rm total})=-5.10$.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=18cm,clip]{figures/1623f2.eps}\end{figure} Figure 2:

A comparison between the observed Fe line profiles and calculations with the stratified abundance distribution (full line) and with the homogeneous ( $\log({\rm Fe}/N_{\rm total})=-5.10$) abundances (dashed line).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{figures/1623f3a.eps}\par\includegraphics[width=9cm,clip]{figures/1623f3b.eps}\end{figure} Figure 3:

Stratification of eight elements in the atmosphere of HD 24712  derived using the homogeneous first-approximation model (Model 1, top panel) and using the final model with scaled REE opacity (Model 5, bottom panel).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{figures/1623f4.eps}\end{figure} Figure 4:

Effect of Pr and Nd stratification on model temperature structure. Solid line - t7250g4.3 model calculated with homogeneous abundances; dotted line - t7250g4.3 model calculated with stratified abundances shown in Fig. 3; dashed and dash-dotted lines - t7250g4.1 models calculated with stratified abundances and scaled Pr II,III and Nd II,III $\log(gf)$ values.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{figures/1623f5.eps}\end{figure} Figure 5:

Observed and calculated H$\alpha $  line profiles. Thick full line - HARPS observations; dotted line - model with $T_{\rm eff}=7250$ K, $\log g=4.3$ and with homogeneous element distribution; full line - model with $T_{\rm eff}=7250$ K, $\log g=4.3$ and with stratification shown in 3 ( top panel); dashed line - model with $T_{\rm eff}=7250$ K, $\log g=4.1$ and with final iteration shown in 3 ( bottom panel). Bottom panel shows the zoomed part of the figure in the top panel around the core of the line.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics*[angle=90,width=17cm,clip]{figures/1623f6.eps}\end{figure} Figure 6:

Calculated and observed energy distributions of HD 24712. Solid line - t7250g4.1 model calculated with stratified abundances shown in Fig. 3 ( bottom panel) and Pr II,III and Nd II,III $\log(gf)$ values changed by -1 dex and +0.5 dex respectively.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{figures/1623f7.eps}\end{figure} Figure 7:

A comparison between the observed Si  line profiles and calculations with the stratified abundance distribution (full line) and with the homogeneous ( $\log(Si/N_{\rm total})=-4.50$) abundances (dashed line).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm,clip]{figures/1623f8.eps}\end{figure} Figure 8:

A comparison between the observed Ca  line profiles and calculations with the stratified abundance distribution (full line) and with the homogeneous ( $\log({\rm Ca}/N_{\rm total})=-5.80$) abundances (dashed line).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15cm,clip]{figures/1623f9.eps}\end{figure} Figure 9:

A comparison between the observed Cr  line profiles and calculations with the stratified abundance distribution (full line) and with the homogeneous ( $\log({\rm Cr}/N_{\rm total})=-5.80$) abundances (dashed line).
Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[height=9cm,clip]{figures/1623f10a.eps}\hspace{1cm} \includegraphics[height=9cm,clip]{figures/1623f10b.eps} } \end{figure} Figure 10:

A comparison between the observed Sr ( left panel) and Ba ( right panel) line profiles and calculations with the stratified abundance distribution (full line) and with the homogeneous ( $\log({\rm Sr}/N_{\rm total})=-8.00$, $\log({\rm Ba}/N_{\rm total})=-9.00$) abundances (dashed line).
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.