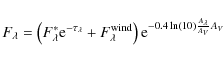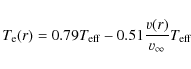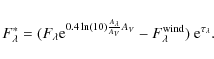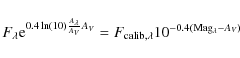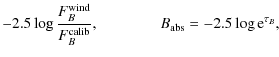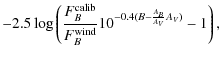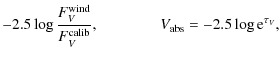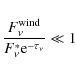| Issue |
A&A
Volume 499, Number 1, May III 2009
|
|
|---|---|---|
| Page(s) | 291 - 299 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200810319 | |
| Published online | 01 April 2009 | |
Parameters of galactic early B supergiants
The influence of the wind on the interstellar extinction determination
M. Kraus1 - M. Borges Fernandes2,3 - J. Kubát1
1 - Astronomický ústav, Akademie ved Ceské republiky, Fricova 298, 251 65 Ondrejov, Czech Republic
2 -
UMR 6525 H. Fizeau, Univ. Nice Sophia Antipolis, CNRS, Observatoire de
la Côte d'Azur, Av. Copernic, 06130 Grasse, France
3 -
Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium
Received 3 June 2008 / Accepted 16 February 2009
Abstract
Context. The interstellar extinction, E(B-V), of OB supergiants is usually derived from the observed color index, (B-V), in comparison with the intrinsic one. This method works properly only if the stellar wind does not influence the optical continuum emission. Over the past years, many OB supergiants have been found to have wind-velocity distributions with rather high ![]() values; i.e., their winds are only slowly accelerating, resulting in relative density enhancements within the wind-continuum forming region. It has been found that these kinds of winds might indeed influence the total continuum emission even at optical wavelengths.
values; i.e., their winds are only slowly accelerating, resulting in relative density enhancements within the wind-continuum forming region. It has been found that these kinds of winds might indeed influence the total continuum emission even at optical wavelengths.
Aims. We investigate the influence of the wind on the observed color indices of OB supergiants, in order to distinguish between interstellar and circumstellar extinction contributions.
Methods. We first tested the influence of the wind on the UBV band fluxes of a model O supergiant star with artificial winds of different ![]() values and a fixed interstellar extinction value. From the UBV magnitudes of these systems, the apparent interstellar extinction was then derived by calculating the values of E(B-V), from the (B-V) as well as from the (U-B) color index. Then we turned to a sample of galactic early-type B supergiants for which the stellar and wind parameters are known. All except one of these stars have
values and a fixed interstellar extinction value. From the UBV magnitudes of these systems, the apparent interstellar extinction was then derived by calculating the values of E(B-V), from the (B-V) as well as from the (U-B) color index. Then we turned to a sample of galactic early-type B supergiants for which the stellar and wind parameters are known. All except one of these stars have ![]() values higher than 1.0, which makes this set the most suitable one for our investigation. We calculated each star's wind contribution to the BV band fluxes. The observed magnitudes were corrected for the wind contributions, and the interstellar extinctions were derived and compared with those derived purely from the (B-V) color index.
values higher than 1.0, which makes this set the most suitable one for our investigation. We calculated each star's wind contribution to the BV band fluxes. The observed magnitudes were corrected for the wind contributions, and the interstellar extinctions were derived and compared with those derived purely from the (B-V) color index.
Results. From our model supergiant, we find that with increasing ![]() the wind starts to influence the observable color indices. The wavelength dependence of the wind contribution is thereby different from that of the interstellar extinction contribution. Thus, the interstellar extinction values derived from the two color indices of our reddened star plus wind systems disagree. This effect is stronger for higher
the wind starts to influence the observable color indices. The wavelength dependence of the wind contribution is thereby different from that of the interstellar extinction contribution. Thus, the interstellar extinction values derived from the two color indices of our reddened star plus wind systems disagree. This effect is stronger for higher ![]() .
In addition, E(B-V) derived from the (B-V) color index always overestimates the real interstellar extinction. This trend is also found for the investigated B supergiant sample. Consequently, the luminosities of these stars are systematically overestimated. Our wind model always computes lower limits to the real wind contributions. This means that the real interstellar extinction values, hence the stellar luminosities of the studied B supergiant sample, might well be lower.
.
In addition, E(B-V) derived from the (B-V) color index always overestimates the real interstellar extinction. This trend is also found for the investigated B supergiant sample. Consequently, the luminosities of these stars are systematically overestimated. Our wind model always computes lower limits to the real wind contributions. This means that the real interstellar extinction values, hence the stellar luminosities of the studied B supergiant sample, might well be lower.
Key words: stars: early-type - stars: fundamental parameters - supergiants - stars: winds, outflows
1 Introduction
The interstellar extinction is one of the most important astrophysical parameters. It is often derived from the observed color index of stars, usually from B-V, in comparison with the intrinsic color index, if the spectral type of the star is known. This method is reliable, as long as no additional component (like a wind or disk) adds to the total observable flux in the B and V bands. For typical OB supergiants with their winds of only moderate mass-loss rates, this was thought to be the case.
In the past few years, a lot of effort has been made to determine the
stellar and wind parameters of OB supergiants within and beyond the Milky Way
with high accuracy. It thereby turned out that many B-type supergiant
stars seem to have wind velocity distributions with rather high ![]() values,
extending up to about 3.5 (see e.g.
Evans et al. 2004; Trundle et al. 2004; Trundle & Lennon
2005; Crowther et al. 2006).
values,
extending up to about 3.5 (see e.g.
Evans et al. 2004; Trundle et al. 2004; Trundle & Lennon
2005; Crowther et al. 2006).
Waters & Lamers (1984) were the first to investigate the
influence of the wind velocity distribution on the total continuum emission
in more detail. They found that a high ![]() can lead to an enhanced emission.
These studies were, however, restricted to the radio and infrared ranges,
where the thermal wind in form of free-free and free-bound emission is known to
play the dominant role. Recently, Kraus et al. (2008a,b)
have shown that, for OB supergiants with high
can lead to an enhanced emission.
These studies were, however, restricted to the radio and infrared ranges,
where the thermal wind in form of free-free and free-bound emission is known to
play the dominant role. Recently, Kraus et al. (2008a,b)
have shown that, for OB supergiants with high ![]() values, the wind emission
can influence the total continuum even at optical wavelengths. This occurs
because, for
values, the wind emission
can influence the total continuum even at optical wavelengths. This occurs
because, for
![]() ,
the density within the innermost
,
the density within the innermost ![]() 2 R* is strongly enhanced, compared to a wind with
2 R* is strongly enhanced, compared to a wind with
![]() .
This
wind region of enhanced density coincides exactly with the formation
region of the optical wind continuum. Any density enhancement close to the star
will, therefore, immediately result in an enhanced thermal wind emission at
optical wavelengths.
.
This
wind region of enhanced density coincides exactly with the formation
region of the optical wind continuum. Any density enhancement close to the star
will, therefore, immediately result in an enhanced thermal wind emission at
optical wavelengths.
These new findings of the wind influence at optical wavelengths thus raise the
question of whether the wind can contaminate the observable UBV band fluxes
further such that the interstellar extinction values derived from
the color indices are influenced as well. Such an influence has recently
been found for the low-luminosity supergiant star AzV 172, for which the
interstellar extinction, hence the stellar luminosity, turned out to
be overestimated if the circumstellar extinction due to the wind is not
properly taken into account (Kraus et al. 2008c). This paper therefore
aims to provide a detailed investigation of the wind influence
on the UBV band fluxes and consequently on the observable color indices
of OB supergiants having winds with especially high ![]() values.
values.
The structure of the paper is as follows. We first investigate the influence of
the wind (for varying mass-loss and ![]() parameters) to the observable UBV
band fluxes and, therefore, to the apparent interstellar extinction that
results from the comparison of the observed to the intrinsic color indices
(Sect. 2). Then, we present our sample of early B supergiant stars
in Sect. 3. In Sect. 4 we describe our calculations of
the interstellar extinction taking the wind contributions into account. The
resulting extinction values are further compared to those received purely from
the observed (B-V) color index.
In Sect. 5 we discuss the wind contribution and its importance,
as well as the reliability of our simplified wind calculations. Other
consequences of the revised interstellar extinction values are mentioned and
discussed. Our results are summarized in Sect. 6.
parameters) to the observable UBV
band fluxes and, therefore, to the apparent interstellar extinction that
results from the comparison of the observed to the intrinsic color indices
(Sect. 2). Then, we present our sample of early B supergiant stars
in Sect. 3. In Sect. 4 we describe our calculations of
the interstellar extinction taking the wind contributions into account. The
resulting extinction values are further compared to those received purely from
the observed (B-V) color index.
In Sect. 5 we discuss the wind contribution and its importance,
as well as the reliability of our simplified wind calculations. Other
consequences of the revised interstellar extinction values are mentioned and
discussed. Our results are summarized in Sect. 6.
2 Interstellar and circumstellar extinction
To study the influence of winds with high ![]() values on the observable
color indices, we first calculated the emission of a model star at UBV
wavelengths and determine its intrinsic color indices (U-B)0 and (B-V)0.
This is done by using the code of Kubát (2003, and references
therein), which is suitable for the computation of non-LTE
spherically-symmetric model atmospheres in hydrostatic and radiative
equilibrium. The stellar continuum emission of a hydrogen plus helium
atmosphere is calculated by adopting the following set of stellar parameters,
which approximately corresponds to an O7 supergiant, based on the calibration
of Martins et al. (2005):
values on the observable
color indices, we first calculated the emission of a model star at UBV
wavelengths and determine its intrinsic color indices (U-B)0 and (B-V)0.
This is done by using the code of Kubát (2003, and references
therein), which is suitable for the computation of non-LTE
spherically-symmetric model atmospheres in hydrostatic and radiative
equilibrium. The stellar continuum emission of a hydrogen plus helium
atmosphere is calculated by adopting the following set of stellar parameters,
which approximately corresponds to an O7 supergiant, based on the calibration
of Martins et al. (2005):
![]() K,
K,
![]() ,
,
![]() ,
and
,
and
![]() .
In
addition, the star is placed to an arbitrary distance of 1 kpc.
.
In
addition, the star is placed to an arbitrary distance of 1 kpc.
With this set of parameters, we computed the stellar flux at the wavelengths
of the UBV bands, converted them into magnitudes based on the calibration
fluxes of Bessell (1979) for a zero magnitude star, and derived
the intrinsic color indices. For our model supergiant, we thus find
| (U-B)0 = -1.063, | (1) | ||
| (B-V)0 = -0.263. | (2) |
The stellar fluxes are then distance-diluted and reddened with an arbitrary interstellar extinction value of AV = 0.62, corresponding to E(B-V) = 0.20 for R = AV / E(B-V) = 3.1. The observable reddened fluxes are given by
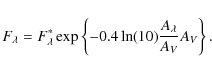 |
(3) |
The parameters
| (U-B) = -0.908, | (4) | ||
| (B-V) = -0.063. | (5) |
From these, the interstellar extinction value E(B-V) can be derived from either the (U-B) or the (B-V) color indices, via
The former relation is taken from Leitherer & Wolf (1984). Both relations give identical values for E(B-V), which agree with the input value.
![\begin{figure}
\includegraphics[width=9cm]{0319fig1.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg18.png) |
Figure 1:
Brightening of the UBV photometric data due to the presence of
high density winds. The dotted lines represent wind models with fixed
|
| Open with DEXTER | |
Next, we included the stellar wind. The star plus wind system was calculated
using the model of Kraus et al. (2008a), which treats the system in the
core-halo approximation. This means that we can calculate the observable
flux at any wavelength via
where
To investigate the influence of the wind to the total continuum emission, we
first neglected any interstellar extinction, but calculate the UBV band
fluxes for winds with (i) fixed value of
![]() and mass-loss rates
ranging from 5 to
and mass-loss rates
ranging from 5 to
![]() yr-1 and (ii) fixed
mass-loss rate of
yr-1 and (ii) fixed
mass-loss rate of
![]() yr-1 and
yr-1 and ![]() values
ranging from 1.0 to 3.0. We further fixed the terminal velocity at
values
ranging from 1.0 to 3.0. We further fixed the terminal velocity at
![]() km s-1, and we kept the electron temperature at a
constant value of
km s-1, and we kept the electron temperature at a
constant value of
![]() K. This is a reasonable assumption as
shown and discussed in Kraus et al. (2008a). The resulting fluxes from the
star plus wind systems are converted into magnitudes, which are then compared
to the intrinsic (i.e. pure) stellar magnitudes. This comparison is shown for
the set of wind models in Fig. 1, where we plot the difference
between the intrinsic stellar magnitudes and the magnitudes of the star with
wind systems obtained in the three photometric bands.
K. This is a reasonable assumption as
shown and discussed in Kraus et al. (2008a). The resulting fluxes from the
star plus wind systems are converted into magnitudes, which are then compared
to the intrinsic (i.e. pure) stellar magnitudes. This comparison is shown for
the set of wind models in Fig. 1, where we plot the difference
between the intrinsic stellar magnitudes and the magnitudes of the star with
wind systems obtained in the three photometric bands.
![\begin{figure}
\includegraphics[width=9cm]{0319fig2.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg26.png) |
Figure 2:
Density distribution in the wind continuum forming regions, i.e.,
within 2 R*, for winds with different |
| Open with DEXTER | |
Obviously, as soon as a wind is included, the star brightens in all bands,
with the strongest effect in the U and V bands, while the B band is only
marginally affected. Also obvious is that a ![]() value of 3.0 has a
much stronger effect than an increase in mass-loss rate (hence in wind
density) by a factor of 3. This can be understood by inspecting the density
distribution in the winds with different
value of 3.0 has a
much stronger effect than an increase in mass-loss rate (hence in wind
density) by a factor of 3. This can be understood by inspecting the density
distribution in the winds with different ![]() values (Fig. 2).
As shown by Kraus et al. (2008a), the optical continuum of the
wind is generated within the innermost 2 R*. In this region, the wind
with
values (Fig. 2).
As shown by Kraus et al. (2008a), the optical continuum of the
wind is generated within the innermost 2 R*. In this region, the wind
with
![]() remains at much higher densities due to the slow wind
acceleration (top panel of Fig. 2). The difference to the wind
with
remains at much higher densities due to the slow wind
acceleration (top panel of Fig. 2). The difference to the wind
with
![]() exceeds a factor of 8 at a distance of about
exceeds a factor of 8 at a distance of about
![]() and is still almost 4 times higher at 2 R* (bottom panel of
Fig. 2). This huge difference in density causes the strong wind
contribution to the optical continuum, especially in the U and V bands,
resulting in modified observable colors of the star, even in the absence of any
interstellar extinction. Another consequence of the wind, which is also
visible in Fig. 1 and which will be confirmed and
discussed further in Sect. 5.3 below, is the apparent higher stellar
luminosity, which results from the V band flux as long as no correction of
the photometric data, accounting for the wind contamination, is taken into
account.
and is still almost 4 times higher at 2 R* (bottom panel of
Fig. 2). This huge difference in density causes the strong wind
contribution to the optical continuum, especially in the U and V bands,
resulting in modified observable colors of the star, even in the absence of any
interstellar extinction. Another consequence of the wind, which is also
visible in Fig. 1 and which will be confirmed and
discussed further in Sect. 5.3 below, is the apparent higher stellar
luminosity, which results from the V band flux as long as no correction of
the photometric data, accounting for the wind contamination, is taken into
account.
Next, we included the interstellar extinction, which we fixed at
AV = 0.62,
i.e., at
E(B-V) = 0.20. We first calculated a reference wind model adopting
![]() ,
and a mass-loss rate of
,
and a mass-loss rate of
![]() yr-1.
The reddened and distance diluted fluxes, calculated with Eq. (8)
and converted into magnitudes, deliver as observable color indices for this
star plus wind system values of
(U-B) = -0.914 and
(B-V) = -0.059. If these
values are then used to derive the interstellar extinction from the two
relations (6) and (7), we find
E(B-V) = 0.194 from the
former and
E(B-V) = 0.204 from the latter. These two values, though still in
fairly good agreement, already show that, even for stars with winds of moderate
mass-loss rates and with a
yr-1.
The reddened and distance diluted fluxes, calculated with Eq. (8)
and converted into magnitudes, deliver as observable color indices for this
star plus wind system values of
(U-B) = -0.914 and
(B-V) = -0.059. If these
values are then used to derive the interstellar extinction from the two
relations (6) and (7), we find
E(B-V) = 0.194 from the
former and
E(B-V) = 0.204 from the latter. These two values, though still in
fairly good agreement, already show that, even for stars with winds of moderate
mass-loss rates and with a ![]() value of 1.0, the wind starts to
influence the total emission at the UBV bands.
value of 1.0, the wind starts to
influence the total emission at the UBV bands.
![\begin{figure}
\includegraphics[width=9cm]{0319fg3a.eps}\par\includegraphics[width=9cm]{0319fg3b.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg30.png) |
Figure 3:
Apparent interstellar extinction value of a star plus wind system,
resulting from different (increasing) mass-loss rates ( top) or different
|
| Open with DEXTER | |
Table 1: Sample of galactic early B supergiants from Crowther et al. (2006).
We next consider the influence of increasing mass-loss rate for a fixed ![]() value of 1.0, as well as the influence of increasing
value of 1.0, as well as the influence of increasing ![]() for a fixed
mass-loss rate. In both cases, the input interstellar extinction value is fixed
at
E(B-V) = 0.2. The results are shown in Fig. 3 where we plot the
extinction values derived either from (U-B) or from (B-V) (from the
Eqs. (6) and (7), respectively) as a function of mass-loss
rate (top panel) or as a function of
for a fixed
mass-loss rate. In both cases, the input interstellar extinction value is fixed
at
E(B-V) = 0.2. The results are shown in Fig. 3 where we plot the
extinction values derived either from (U-B) or from (B-V) (from the
Eqs. (6) and (7), respectively) as a function of mass-loss
rate (top panel) or as a function of ![]() (bottom panel).
From this figure we can draw some important conclusions:
(bottom panel).
From this figure we can draw some important conclusions:
- the wind serves as an additional extinction source
![[*]](/icons/foot_motif.png) and influences the individual bands differently (see Fig. 1).
This means that the resulting color index of a star depends not only on the
interstellar extinction, but also on the wind contamination, the latter having
a different wavelength dependence than the former;
and influences the individual bands differently (see Fig. 1).
This means that the resulting color index of a star depends not only on the
interstellar extinction, but also on the wind contamination, the latter having
a different wavelength dependence than the former;
- whether the observed magnitudes suffer from some circumstellar extinction caused by a strong wind can easily be tested by inspecting at least two color indices, e.g. B-V and U-B as shown here. If they deliver different values for the interstellar extinction, then circumstellar extinction due to the wind plays a non-negligible role;
- in the case of a non-negligible wind emission, the B-V color index always overestimates the real interstellar extinction value.
In the following we, therefore, investigate the wind influence on the color index B-V of a well-studied sample of galactic early-B type supergiants, with the aim of deriving their interstellar exinction parameters again by taking the wind influence at the B and V bands into account.
3 The B supergiant sample
We make use of a sample of galactic early-B type supergiants investigated by
Crowther et al. (2006, in the following referred to as CLW).
Their detailed spectral analysis revealed the complete set of stellar and wind
parameters, and interestingly, they found for all (except one) stars of
their sample ![]() values higher than 1.0. Their sample is therefore ideal
to study the influence of the wind emission at optical wavelengths (i.e.
especially at the photometric bands B and V) of early B supergiants with
slowly accelerating winds, i.e. winds with high
values higher than 1.0. Their sample is therefore ideal
to study the influence of the wind emission at optical wavelengths (i.e.
especially at the photometric bands B and V) of early B supergiants with
slowly accelerating winds, i.e. winds with high ![]() values.
values.
The sample B supergiants are listed in Table 1.
Given are the star number and name, the
spectral type and luminosity class, the V and B band magnitudes, and the
distance modulus with references. The effective temperature, surface gravity,
mass-loss rates, and ![]() values have been derived by CLW, and the terminal
velocities by Howarth et al. (1997). These values will be used
as fixed input into our model calculations. The stellar radii listed in
Table 1 have also been derived by CLW. Since we cannot a priori
adopt that these radii will not change when accounting for the stellar wind
contamination of the photometric data, we use them only in the first step
of the wind calculation as the lower boundary of the wind zone.
values have been derived by CLW, and the terminal
velocities by Howarth et al. (1997). These values will be used
as fixed input into our model calculations. The stellar radii listed in
Table 1 have also been derived by CLW. Since we cannot a priori
adopt that these radii will not change when accounting for the stellar wind
contamination of the photometric data, we use them only in the first step
of the wind calculation as the lower boundary of the wind zone.
The effective temperature as given by CLW is independent of reddening. We
therefore consider the CLW values given in Table 1 as reasonable.
The effective temperature is used further to constrain the electron temperature
in the wind. The electron temperature distribution in line-driven winds
of early-type stars can be written in the form
as shown by Bunn & Drew (1992). The generation region of the optical wind continuum is in the close vicinity to the stellar surface, i.e. within less than 2 R*. The extent of this region is largely independent of the value of
4 Results
In this section we first derive an expression for the color index (B* - V*) for the radiation emerging from the star based on observed quantities and the knowledge of the interstellar and wind contributions. From a comparison with intrinsic color indices, we then compute the interstellar extinction values towards the stars in our sample.
To calculate the interstellar extinction, AV, for the supergiant sample we
make use of Eq. (8). This equation can be rewritten to solve for the
stellar flux, delivering
The first term in parentheses is the observed, extinction-corrected flux, which results from the observed magnitude, Mag
where
with the following definitions:
Here,
Since the interstellar extinction AV that appears in the relations
Eqs. (15) and (17) is not known a priori, Eqs. (12)
and (13) form a coupled set of two equations for three independent
variables,
B*, V*, and AV. This system of equations is hence
underdetermined and cannot be solved without further constraints. On the
other hand, we can make use of the fact that
must be valid, i.e., the (B* - V*) color index, calculated by our analysis, must agree with the intrinsic (B - V)0 color index of a star with the same spectral type and luminosity class. With this additional constrain, the problem is reduced to one single equation with only one unknown parameter, i.e., the interstellar extinction AV, which can be solved easily. For calculating the (B* - V*) color index we do not need our (rather simple) stellar atmosphere code, which only treats H and He. Instead, this color index follows purely from the set of Eqs. (12) to (17).
To solve Eq. (18), we need to specify the intrinsic color index for each of our sample stars. Since we assume that the effective temperatures listed in Table 1 are correct because they have been derived with a reddening-independent method, the spectral types of the sample stars are fixed (see Table 1), and, following CLW, we apply the intrinsic color indices from the tables of Schmidt-Kaler (1982).
The wind emission is calculated as described in Sect. 2, i.e. we
adopt the wind as unclumped, spherically symmetric, and isothermal. Under
these assumptions, the wind emission,
![]() ,
is only a function of the
electron temperature and density distribution,
,
is only a function of the
electron temperature and density distribution,
![]() .
For our
supergiant sample with effective temperatures in the range
.
For our
supergiant sample with effective temperatures in the range
![]() K, it is reasonable to assume that hydrogen is fully
ionized and helium is singly ionized, while we neglect the contribution of the
metals as free electron donators; i.e., the electron density used is a lower
limit. With a helium abundance of about 10%, the number density of free
electrons in the wind becomes
K, it is reasonable to assume that hydrogen is fully
ionized and helium is singly ionized, while we neglect the contribution of the
metals as free electron donators; i.e., the electron density used is a lower
limit. With a helium abundance of about 10%, the number density of free
electrons in the wind becomes
![]() .
The
number density of hydrogen,
.
The
number density of hydrogen,
![]() ,
thereby follows from the equation
of mass continuity that is proportional to the ratio of mass-loss rate over
wind velocity distribution. With the knowledge of the mass-loss rate,
,
thereby follows from the equation
of mass continuity that is proportional to the ratio of mass-loss rate over
wind velocity distribution. With the knowledge of the mass-loss rate,
![]() ,
and wind velocity distribution given by
,
and wind velocity distribution given by
![]() and
and ![]() for each star (Table 1), we can then compute the electron density
distribution in the wind.
for each star (Table 1), we can then compute the electron density
distribution in the wind.
Besides the density distribution, the inner edge of the wind, determined by the stellar radius, plays a crucial role in defining the lower boundary for the wind calculations. Since the wind continuum at optical wavelengths is generated within the innermost 2 R*, a change in stellar radius will influence the total wind emission directly.
Since we do not know whether the stellar parameters derived by CLW, such as the radii, will change as a result of the wind influence, we use their values as listed in Table 1 as first-guess input parameters for the wind calculations. The interstellar extinction and stellar radius for each star thus has to be calculated iteratively:
- 1.
- the stellar radius,
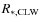 ,
as derived by CLW is used as
an input parameter;
,
as derived by CLW is used as
an input parameter;
- 2.
- with the stellar radius and wind parameters fixed, we next calculate
the wind emission,
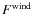 ,
in the B and V bands, as well as the
wind optical depths
,
in the B and V bands, as well as the
wind optical depths 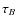 and
and 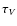 ,
needed to calculate the
set of Eqs. (14) and (16);
,
needed to calculate the
set of Eqs. (14) and (16);
- 3.
- the interstellar extinction AV then follows from solving Eq. (18), and the pure (i.e. interstellar and circumstellar extinction corrected) stellar B* and V* band magnitudes can be calculated from Eqs. (12) and (13), respectively;
- 4.
- the stellar radius can be calculated in terms of the radius derived by
CLW. Since we are dealing with two different bands, we obtain two radii given
by
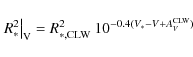
(19)
from the V band flux, and
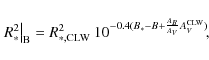
(20)
from the B band flux. Of course, these two radii must be identical. In these relations, B and V are the observed magnitudes, and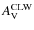 is the interstellar extinction as derived by CLW, based on the intrinsic
colors from Schmidt-Kaler (1982);
is the interstellar extinction as derived by CLW, based on the intrinsic
colors from Schmidt-Kaler (1982);
- 5.
- our newly derived stellar radius is then compared with the input radius. If they do not agree, the new radius is chosen as input radius, and the calculations are repeated from step 2 on, until output and input radii agree with an accuracy of better than 0.01 %.
![\begin{figure}
\includegraphics[width=8.5cm]{0319fig4.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg82.png) |
Figure 4:
Difference in interstellar extinction of the supergiant sample
calculated from the observed (B-V) color index (labeled AV)
compared to the value after taking the wind influence into account (labeled
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.5cm]{0319fig5.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg84.png) |
Figure 5:
Final results for the stellar radii (except for the star HD 152236
with
|
| Open with DEXTER | |
Also included in Fig. 4 are the error bars, which have been calculated based on the consideration of two main sources of errors: (i) the calibration fluxes from Bessell (1979) for a zero magnitude star, and (ii) the choice of the intrinsic color indices from Schmidt-Kaler (1982). A revision of the zero magnitude for the absolute flux calibration had been suggested by Mégessier (1995), and a new set of zero magnitude calibration fluxes has been calculated, e.g., by Colina et al. (1996). Compared to the old Bessell fluxes, the differences are rather small, with about 3% for the B band and less than 2% in the V band. Nevertheless, we adopted this new set of zero magnitude calibration fluxes to estimate the resulting errors in our calculated AVvalues. We further tested the influence of the chosen set of intrinsic color indices. As mentioned by CLW, their calculations resulted in intrinsic color indices that turned out to be about 0.02 mag more negative than the Schmidt-Kaler values. Our calculations show that, since we are plotting the differences in AV, these values are hardly influenced by the possible errors implemented due to differences in the intrinsic color indices.
The iteration also delivers new results for the stellar radii. These are shown in Fig. 5, where we plot in the top panel the stellar radii resulting from either the B or V band fluxes. They show excellent agreement. When comparing our stellar radii with those of CLW (Fig. 5, bottom panel), it is obvious that we find smaller (or about equal) stellar radii for all supergiants in the sample. The differences in radii can reach up to 6%, where the error bars shown are calculated based on the errors in AV.
5 Discussion
5.1 Wind contribution and importance
The deviations in AV found from our analysis spread from 0.001 mag to 0.02 mag (see Fig. 4). Of course, a deviation of only 0.001 mag cannot be detected easily from the observed colors, since it is within the error bars. Deviations greater than 0.005 mag, however, are considered as meaningful. For those stars, we would argue that the wind shows a non-negligible influence on the (B-V) color index.
The deviation in AV is highest for the stars # 1, 18, and 22. Inspection
of their parameters in Table 1 shows that # 18 is the one with
![]() ,
and # 22 with
,
and # 22 with
![]() ,
i.e., these are the stars with
the highest
,
i.e., these are the stars with
the highest ![]() value in the sample. For star # 1 we see that it has a
rather high mass-loss rate. It is therefore not surprising that the
overestimation in AV is found to be highest for these three targets.
value in the sample. For star # 1 we see that it has a
rather high mass-loss rate. It is therefore not surprising that the
overestimation in AV is found to be highest for these three targets.
On the other hand, there are a few targets with almost no deviation in AV(i.e. a deviation of less than 0.005 mag). These are the stars with lowest
![]() values (stars # 14 and 10 with
values (stars # 14 and 10 with
![]() and 1.2, respectively),
as well as some stars with rather low mass-loss rates. But before we can draw
any conclusion from this behavior, we need to have a closer look at the wind
influence.
and 1.2, respectively),
as well as some stars with rather low mass-loss rates. But before we can draw
any conclusion from this behavior, we need to have a closer look at the wind
influence.
A quantitative representation of the wind influence is displayed in Fig. 6. The top panel shows the ratio of the gain in wind emission at the B and V bands over the loss of stellar emission due to the wind extinction. For all stars, and therefore almost independent of the individual stellar and wind parameters, this ratio is found to be about two. This means that the wind emits about twice as much as it absorbs from the stellar light, adding some net amount to the total emission (opposite than the effect of interstellar extinction). In addition, the ratio is always higher in the V band. The wind thus has a stronger influence in the form of net emission in the V band than in the B band, and this difference in wind influence at the two different wavelengths even increases with decreasing effective temperature of the star (i.e. for the stars with higher numbers).
![\begin{figure}
\includegraphics[width=8.5cm]{0319fig6.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg86.png) |
Figure 6: Top panel: ratio of gain in thermal wind emission over the loss in stellar flux due to the extinction by the wind zone. Bottom panel: ratio of the wind continuum emission compared to the stellar continuum emission. |
| Open with DEXTER | |
Whether this wind emission will have observable consequences also depends
on the continuum strength of the underlying star. If the wind is negligible,
then
should be valid. We calculate this ratio for each target of our sample and plot it in the lower panel of Fig. 6. This ratio is found to spread over several orders of magnitude. Obviously, stars # 14 and 25 show the least wind influence, while stars # 1 and 18 display the strongest influence, in agreement with their least and strongest deviations in AV. For the rest of the sample, the situation is not as clear.
But obviously, a high mass-loss rate or a high ![]() value alone is no
guarantee of a strong wind influence. The situation is more complicated since,
on the one hand, other parameters like the stellar radius, the wind terminal
velocity, as well as the electron temperature, influence the density
distribution in the wind-forming region and the wind emission. On the other
hand, the strength of the stellar continuum, which is determined by the
effective temperature, stellar radius, and surface gravity also plays a
non-negligible role (see bottom panel of Fig. 6).
value alone is no
guarantee of a strong wind influence. The situation is more complicated since,
on the one hand, other parameters like the stellar radius, the wind terminal
velocity, as well as the electron temperature, influence the density
distribution in the wind-forming region and the wind emission. On the other
hand, the strength of the stellar continuum, which is determined by the
effective temperature, stellar radius, and surface gravity also plays a
non-negligible role (see bottom panel of Fig. 6).
Our research cannot provide a recipe for which parameter configuration the wind starts to influence the total continuum emission, but we would like to draw attention to its possible (and sometimes rather strong) influence. Whether or not the wind really influences the total continuum has to be checked for each star individually.
5.2 Reliability of the wind calculations
The wind calculations were performed with the code of Kraus et al. (2008a). As has been listed already in Sect. 2, this code makes use of several assumptions and simplifications, to keep the computations as simple as possible. However, all these assumptions and simplifications are such that the computed wind emission is a lower limit. This means that, in reality, the influence of the wind on the photometric data will be even more pronounced than predicted with our model. Consequently, the deviations in AV will be greater, and the resulting stellar radii will be even smaller than those found from our simple calculations. Of course, we cannot quantify the effect. This is only possible with an exact calculation of the emission of the star plus wind system. However, we expect the effects to be noticeable.
![\begin{figure}
\includegraphics[width=8.5cm]{0319fig7.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg88.png) |
Figure 7: Location of the supergiant sample in the HR diagram. Shown are our upper limits in luminosities, derived by taking the wind as an extinction source into account, compared to the luminosities determined by CLW. Evolutionary tracks are from Schaller et al. (1992) for non-rotating stars at solar metallicity. |
| Open with DEXTER | |
5.3 Consequences of the wind influence
Besides the overestimation of the interstellar extinction values, the neglect of the wind's influence on the observable continuum emission has further consequences for the set of stellar parameters.
First of all, we found that the stellar radii are smaller. Even though this is an effect of only a few percent, it nevertheless influences other parameters like, e.g., the stellar luminosity. In Sect. 2 we mentioned that a star with a high-density wind appears brighter in the V band (see Fig. 1), so that the real stellar luminosity will be overestimated. With the effective temperatures of the target stars from Table 1 and our revised stellar radii, we calculate the resulting stellar luminosities, which consequently are all lower than the values of CLW. The highest deviation with about 10% is thereby found for the star # 1. Even though it is known that the wind strengths tend to increase with luminosities, we do not find any correlation between the amount of luminosity reduction for the sample stars and their luminosities. The reason for this is that the wind influence is not a simple function of the wind strength, but depends on many different stellar and wind parameters, as discussed earlier. Therefore, we cannot make any predictions about its possible influence, but a detailed calculation is necessary for every individual star, checking for the possible wind contamination and hence the expected reduction in luminosity.
The positions of the stars with their revised (i.e. lower) luminosities are shown in Fig. 7. The shift in luminosity (which is likewise a downwards correction of the stellar masses when compared to the evolutionary tracks of Schaller et al. 1992) is quite obvious, and might even increase. Our derived luminosities must therefore be considered as upper limits. The neglect of the wind's influence on the optical continuum thus not only leads to an overestimation of the interstellar extinction, but also to an overestimation of the stellar luminosities and masses.
5.4 Clumped winds
Recent results from both observational and theoretical investigations of hot star winds suggest that the winds might be clumped (e.g., Crowther et al. 2002; Hillier et al. 2003; Bouret et al. 2003, 2005). As a consequence of such wind clumping, the mass-loss rates of the stars might be overestimated by about a factor of 3. The mass-loss rates provided by CLW for the OB supergiant sample studied here have been derived under the assumption of smooth rather than clumped winds. Consequently, they might well be lower, resulting in lower wind densities for the sample stars.
A detailed study of the influence of wind clumping is beyond the scope of this
paper, since it is not known whether the winds of the stars in our sample are
indeed clumped. In a recent study, Kraus et al. (2008b) investigated
the influence of wind clumping on the total continuum emission of hot stars
with high ![]() winds. Using the filling factor approach introduced by
Hillier et al. (2003), they found that the emission of clumped winds
is slightly reduced compared to unclumped winds. Nevertheless, the winds still
contaminate the optical continuum emission. The influence on the total
continuum emission when clumping is taken into account will thus be weaker, but
the wind contamination will nevertheless be present, even though in a milder
form.
winds. Using the filling factor approach introduced by
Hillier et al. (2003), they found that the emission of clumped winds
is slightly reduced compared to unclumped winds. Nevertheless, the winds still
contaminate the optical continuum emission. The influence on the total
continuum emission when clumping is taken into account will thus be weaker, but
the wind contamination will nevertheless be present, even though in a milder
form.
However, whether the winds of the studied galactic OB supergiant sample
are indeed clumped or whether the high ![]() values found by CLW have
a completely different cause, needs to be studied in more detail.
values found by CLW have
a completely different cause, needs to be studied in more detail.
6 Conclusions
We investigated the influence of winds with high ![]() values on the
observed photometric fluxes. We focused especially on the problem of proper
interstellar extinction derivation from the observed (B-V) color index.
For this, we first calculated the wind emission and absorption for a model
star plus wind system, increasing the mass-loss rate and the
values on the
observed photometric fluxes. We focused especially on the problem of proper
interstellar extinction derivation from the observed (B-V) color index.
For this, we first calculated the wind emission and absorption for a model
star plus wind system, increasing the mass-loss rate and the ![]() parameter.
We found that the wind influences the emission at the individual photometric
bands differently, i.e. with a different wavelength dependence than the
interstellar extinction does; consequently, any wind contribution might
be easily checked by looking at least at two different color indices.
We also found that the interstellar extinction derived from the observed
(B-V) color index is always overestimated.
parameter.
We found that the wind influences the emission at the individual photometric
bands differently, i.e. with a different wavelength dependence than the
interstellar extinction does; consequently, any wind contribution might
be easily checked by looking at least at two different color indices.
We also found that the interstellar extinction derived from the observed
(B-V) color index is always overestimated.
We then investigated a sample of galactic early-B type supergiants that has
previously been studied in great detail by Crowther et al. (2006).
This sample was ideal for our purposes, because for all except one star,
Crowther et al. (2006) derived ![]() parameters
considerably greater than unity. From their
parameters
considerably greater than unity. From their ![]() parameters and mass-loss
rates, we calculated the wind contribution to the B and V band fluxes
for all target stars and derived the interstellar extinction values again.
We found that, for all stars in the sample, the interstellar extinction is
overestimated when it is derived purely from the observed (B-V) color index,
without taking the wind's influence into account.
parameters and mass-loss
rates, we calculated the wind contribution to the B and V band fluxes
for all target stars and derived the interstellar extinction values again.
We found that, for all stars in the sample, the interstellar extinction is
overestimated when it is derived purely from the observed (B-V) color index,
without taking the wind's influence into account.
Another consequence of our analysis is that we could derive smaller stellar radii, hence lower luminosities and masses for all stars of the supergiant sample. This raises the question of whether the luminosities for all supergiant stars have to be corrected downwards. Even though the absolute values found from our analysis do not exceed about 10%, we want to stress that our wind calculations are only suitable to determine the lower limits of the wind emission. The real downward corrections in stellar luminosities and masses might therefore be higher.
Acknowledgements
We thank our anonymous referees for many constructive suggestions on the original manuscript. M.K. acknowledges financial support from GA AV CR grant number KJB300030701, and J.K. and M.K. from GA CR number 205/08/0003. M.B.F. acknowledges financial support from the Belgian Federal Science Policy Office (Research Fellowship for non-EU Postdocs) and from the Centre National de la Recherche Scientifique (CNRS).
References
- Baume, G., Vázquez, R. A., & Feinstein, A. 1999, A&AS, 137, 233 [NASA ADS] [CrossRef] [EDP Sciences]
- Baume, G., Vázquez, R. A., Carraro, G., & Feinstein, A. 2003, A&A, 402, 549 [NASA ADS] [CrossRef] [EDP Sciences]
- Bessell, M. S. 1979, PASP, 91, 589 [NASA ADS] [CrossRef] (In the text)
- Blaha, C., & Humphreys, R. M. 1989, AJ, 98, 1598 [NASA ADS] [CrossRef]
- Bouret, J.-C., Lanz, T., Hillier, D. J., et al. 2003, ApJ, 595, 1182 [NASA ADS] [CrossRef] (In the text)
- Bouret, J.-C., Lanz, T., & Hillier, D. J. 2005, A&A, 438, 301 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Brown, A. G. A., de Geus, E. J., & de Zeeuw, P. T. 1994, A&A, 289, 101 [NASA ADS]
- Bunn, J. C., & Drew, J. E. 1992, MNRAS, 255, 449 [NASA ADS] (In the text)
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] (In the text)
- Colina, L., Bohlin, R., & Castelli, F. 1996, Instrument Science Report CAL/SCS-008 (In the text)
- Crowther, P. A., Hillier, D. J., Evans, C. J., et al. 2002, ApJ, 579, 774 [NASA ADS] [CrossRef] (In the text)
- Crowther, P. A., Lennon, D. J., & Walborn, N. R. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] (CLW) (In the text)
- Evans, C. J., Crowther, P. A., Fullerton, A. W., & Hillier, D. J. 2004, ApJ, 610, 1021 [NASA ADS] [CrossRef] (In the text)
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] (In the text)
- Fitzpatrick, E. L., & Massa, D. 2005, AJ, 130, 1127 [NASA ADS] [CrossRef] (In the text)
- Garmany, C. D., & Stencel, R. E. 1992, A&AS, 94, 211 [NASA ADS]
- Hillier, D. J., Lanz, T., Heap, S. R., et al. 2003, ApJ, 588, 1039 [NASA ADS] [CrossRef] (In the text)
- Howarth, I. D., Siebert, K. W., Hussain, G. H. J., & Prinja, R. K. 1997, MNRAS, 284, 265 [NASA ADS] (In the text)
- Humphreys, R. M. 1978, ApJS, 38, 309 [NASA ADS] [CrossRef]
- Kraus, M., Kubát, J., & Krticka, J. 2008a, A&A, 481, 499 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kraus, M., Kubát, J., & Krticka, J. 2008b, in Clumping in Hot Star Winds, ed. W.-R. Hamann, A. Feldmeier, & L. Oskinova (Potsdam: Univ.-Verl.), 51 (In the text)
- Kraus, M., Borges Fernandes, M., Kubát, J., & de Araújo, F. X. 2008c, A&A, 487, 697 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kubát, J. 2003, in Modelling of Stellar Atmospheres, ed. N. Piskunov, W. W. Weiss, & D. F. Gray (San Francisco: ASP), IAU Symp., 210, A8 (In the text)
- Leitherer, C., & Wolf, B. 1984, A&A, 132, 151 [NASA ADS] (In the text)
- Markova, N., & Puls, J. 2008, A&A, 478, 823 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mathis, J. S. 1990, ARA&A, 28, 37 [NASA ADS] [CrossRef] (In the text)
- Mégessier, C. 1995, A&A, 296, 771 [NASA ADS] (In the text)
- Mokiem, M. R., de Koter, A., Vink, J. S., et al. 2007, A&A, 473, 603 [NASA ADS] [CrossRef] [EDP Sciences]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [NASA ADS] (In the text)
- Schmidt-Kaler, Th. 1982, in Landolt-Börnstein, New Series, Group IV, Vol. 2b, ed. K. Schaifers, & H. H. Voigt (Berlin: Springer), 1 (In the text)
- Trundle, C., & Lennon, D. J. 2005, A&A, 434, 677 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Trundle, C., Lennon, D. J., Puls, J., & Dufton, P. L. 2004, A&A, 417, 217 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Waters, L. B. F. M., & Lamers, H. J. G. L. M. 1984, A&AS, 57, 327 [NASA ADS] (In the text)
Footnotes
- ... source
![[*]](/icons/foot_motif.png)
- We call it extinction, even though the emission of the wind itself, which adds to the stellar flux, is much stronger than the amount of extinction the star light experiences when passing through the wind zone (see Kraus et al. 2008a).
All Tables
Table 1: Sample of galactic early B supergiants from Crowther et al. (2006).
All Figures
![\begin{figure}
\includegraphics[width=9cm]{0319fig1.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg18.png) |
Figure 1:
Brightening of the UBV photometric data due to the presence of
high density winds. The dotted lines represent wind models with fixed
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=9cm]{0319fig2.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg26.png) |
Figure 2:
Density distribution in the wind continuum forming regions, i.e.,
within 2 R*, for winds with different |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=9cm]{0319fg3a.eps}\par\includegraphics[width=9cm]{0319fg3b.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg30.png) |
Figure 3:
Apparent interstellar extinction value of a star plus wind system,
resulting from different (increasing) mass-loss rates ( top) or different
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.5cm]{0319fig4.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg82.png) |
Figure 4:
Difference in interstellar extinction of the supergiant sample
calculated from the observed (B-V) color index (labeled AV)
compared to the value after taking the wind influence into account (labeled
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.5cm]{0319fig5.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg84.png) |
Figure 5:
Final results for the stellar radii (except for the star HD 152236
with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.5cm]{0319fig6.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg86.png) |
Figure 6: Top panel: ratio of gain in thermal wind emission over the loss in stellar flux due to the extinction by the wind zone. Bottom panel: ratio of the wind continuum emission compared to the stellar continuum emission. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.5cm]{0319fig7.eps}\end{figure}](/articles/aa/full_html/2009/19/aa10319-08/Timg88.png) |
Figure 7: Location of the supergiant sample in the HR diagram. Shown are our upper limits in luminosities, derived by taking the wind as an extinction source into account, compared to the luminosities determined by CLW. Evolutionary tracks are from Schaller et al. (1992) for non-rotating stars at solar metallicity. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.