| Issue |
A&A
Volume 498, Number 2, May I 2009
|
|
|---|---|---|
| Page(s) | 543 - 550 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200811591 | |
| Published online | 05 March 2009 | |
Observational constraints on the magnetic field of RR Lyrae stars
K. Kolenberg1 - S. Bagnulo2
1 - Institut fuer Astronomie, Universitaet Wien, Tuerkenschanzstrasse 17,
1018 Wien, Austria
2 - Armagh Observatory, College Hill, Armagh BT61 9DG, UK
Received 23 December 2008 / Accepted 30 January 2009
Abstract
Context. A high percentage of the astrophysically important RR Lyrae stars show a periodic amplitude and/or phase modulation of their pulsation cycles. More than a century after its discovery, this ``Blazhko effect'' still lacks acceptable theoretical understanding. In one of the plausible models for explaining the phenomenon, the modulation is caused by the effects of a magnetic field. So far, the available observational data have not allowed us to either support nor rule out the presence of a magnetic field in RR Lyrae stars.
Aims. We intend to determine whether RR Lyrae stars are generally characterized by the presence of a magnetic field organized on a large scale.
Methods. With the help of the FORS1 instrument at the ESO VLT we performed a spectropolarimetric survey of 17 relatively bright southern RR Lyrae stars, both Blazhko stars and non-modulated stars, and determined their mean longitudinal magnetic field with a typical error bar <30 G.
Results. All our measurements of the mean longitudinal magnetic field resulted in null detections within 3![]() .
From our data we can set an upper limit for the strength of the dipole component of the magnetic fields of RR Lyrae stars to
.
From our data we can set an upper limit for the strength of the dipole component of the magnetic fields of RR Lyrae stars to ![]() 130 G. Because of the limitations intrinsic to the diagnostic technique, we cannot exclude the presence of higher order multipolar components.
130 G. Because of the limitations intrinsic to the diagnostic technique, we cannot exclude the presence of higher order multipolar components.
Conclusions. The outcome of this survey clarifies that the Blazhko modulation in the pulsation of RR Lyrae stars is not correlated with the presence of a strong, quasi-dipolar magnetic field.
Key words: stars: variables: RR Lyr - stars: magnetic fields - techniques: polarimetric - techniques: spectroscopic - stars: oscillations - stars: horizontal-branch
1 Introduction
Investigations of the pulsating RR Lyrae stars contribute to almost every branch of modern astronomy. These stars serve as standard candles to fix the cosmological distance scale and are often considered to be prototypes of purely radial pulsation. With mean periods of about half a day and brightness variations of about one magnitude, RR Lyrae stars pulsate in the radial fundamental mode (type RRab), the radial first overtone (type RRc), and both of these radial modes simultaneously (type RRd). However, additional cycles occur in many RR Lyrae stars. A considerable fraction of RR Lyrae stars (20-30% of Galactic RRab and 5% of RRc stars; Moskalik & Poretti 2003), or even higher numbers (about 50% according to the outcome of the Konkoly Blazhko survey - Jurcsik, private communication), shows a periodic amplitude/phase modulation on timescales of typically tens to hundreds of times the pulsation period. This phenomenon is denoted Blazhko effect (Blazhko 1907). More than a century after its discovery, the Blazhko effect remains a mystery. The most commonly stated hypotheses to explain the phenomenon invoke intrinsic effects, such as resonance, a magnetic field, or variable turbulent convection.Table 1: Our sample of RR Lyrae stars for the spectropolarimetry and the magnetic A star for comparison.
In the resonance models the modulation is caused by a (nonlinear) resonance between the
radial fundamental mode and a nonradial mode, most likely a dipole
![]() mode (Dziembowski & Mizerski 2004; Van Hoolst et al. 1998; Cox 1993). Like the
oblique pulsator model for roAp stars (Kurtz 1982), the magnetic models suppose
that Blazhko stars have a magnetic field inclined to the stellar
rotation axis (Cousens 1983; Shibahashi & Takata 1995). The magnetic field, assumed to be a dipole field, deforms the radial mode leading to an additional quadrupole
component
mode (Dziembowski & Mizerski 2004; Van Hoolst et al. 1998; Cox 1993). Like the
oblique pulsator model for roAp stars (Kurtz 1982), the magnetic models suppose
that Blazhko stars have a magnetic field inclined to the stellar
rotation axis (Cousens 1983; Shibahashi & Takata 1995). The magnetic field, assumed to be a dipole field, deforms the radial mode leading to an additional quadrupole
component
![]() ,
for which the symmetry axis coincides with the
magnetic axis. With the star's rotation, our view of the pulsation
components changes, causing the observed amplitude modulation. According to this model,
a magnetic dipole field with a strength of about 1 kG is needed for the
amplitude modulation to be observable (Shibahashi & Takata 1995).
Both the resonance and the magnetic models involve nonradial pulsation components,
of which the presence in RR Lyrae stars still remains to be proven (Kolenberg 2002; Chadid et al. 1999).
An alternative scenario has recently been proposed by Stothers (2006).
This model is based on purely radial pulsation and involves
a cyclic variation of turbulent convection
in the hydrogen and helium ionization zones of Blazhko stars. According to Stothers (2006),
the variation of the turbulent convection could be caused by a transient magnetic field in the star (turbulent dynamo mechanism).
The expected strength of such a field is not mentioned, and it would be harder to detect than a large-scale dipole field.
,
for which the symmetry axis coincides with the
magnetic axis. With the star's rotation, our view of the pulsation
components changes, causing the observed amplitude modulation. According to this model,
a magnetic dipole field with a strength of about 1 kG is needed for the
amplitude modulation to be observable (Shibahashi & Takata 1995).
Both the resonance and the magnetic models involve nonradial pulsation components,
of which the presence in RR Lyrae stars still remains to be proven (Kolenberg 2002; Chadid et al. 1999).
An alternative scenario has recently been proposed by Stothers (2006).
This model is based on purely radial pulsation and involves
a cyclic variation of turbulent convection
in the hydrogen and helium ionization zones of Blazhko stars. According to Stothers (2006),
the variation of the turbulent convection could be caused by a transient magnetic field in the star (turbulent dynamo mechanism).
The expected strength of such a field is not mentioned, and it would be harder to detect than a large-scale dipole field.
Photometric observations often hint at a much more complex scenario for Blazhko stars than a modulation with one single period. The prototype RR Lyr shows a longer cycle of about 4 years, beside its primary 0.567 d pulsation period, and its 40 d Blazhko period (which has decreased over the past decades - see Kolenberg et al. 2006). At the end of this cycle, the Blazhko effect suddenly weakens in strength and reappears with a change in the Blazhko phase (Detre & Szeidl 1973). Szeidl (1976) also reports stronger and weaker 4-year cycles in the Blazhko effect of RR Lyr. Other well-studied stars also reveal such longer cycles: about 3540 d in XZ Cyg (LaCluyzé et al. 2004), about 7200 d in XZ Dra (Jurcsik et al. 2002), and between 2000 and 3000 d in RV UMa (Kovacs 1995). In addition, extensive analyses of old and new photometry (same references as above) show that these well-studied stars exhibit coincident changes of both the primary pulsation period and the Blazhko period. Some Blazhko stars are also known to have two modulation periods, such as XZ Cyg (LaCluyzé et al. 2004) and UZ UMa (Sodor et al. 2006). These photometric observations clash with the models requiring the Blazhko period to be exactly equal or directly proportional to the rotation period of the star, such as the latest version of the magnetic model (Shibahashi 2000). However, long-term cyclic changes could still be interpreted in terms of the magnetic rotator-pulsator model, by explaining the observed phenomena with changes of the global magnetic field structure and/or strength.
From the observational point of view, the question whether RR Lyrae
stars are magnetic is still a matter of debate. Until recently, high-precision
spectropolarimetric measurements of RR Lyrae stars were hampered by
the brightness requirements of the technique.
RR Lyr, the prototype of the class, is by far the brightest
with
V=7.2-8.2, and it is the only object of its
kind that has been the target of spectropolarimetric observations, the
outcome of which is contradictory. Babcock (1958) and
Romanov et al. (1987) reported a
variable magnetic field in RR Lyr with a strength up to 1.5 kG.
Preston (1967) and Chadid et al. (2004) reported null detections. The
last group of authors obtained magnetic field measurements of RR Lyr with the
MuSiCoS spectropolarimeter attached to the 2 m telescope at Pic du
Midi (France) from 1999-2002. Having covered various phases in the
pulsation and the Blazhko cycle, they concluded from their data
(
![]() G) that RR Lyr is a bona fide non-magnetic
star.
G) that RR Lyr is a bona fide non-magnetic
star.
Though no significant dipole field was detected in RR Lyr by Chadid et al. (2004), there is the need for a more exhaustive test of the magnetic field hypothesis to explain the Blazhko phenomenon, which can be performed through a survey of a sample of RR Lyrae stars. To fully strengthen or disprove the hypothesis of a magnetic field being the driving force behind the Blazhko effect, we have a strong case by also checking non-modulated stars. A crucial test of the magnetic models for the Blazhko effect would be to investigate the presence of magnetic fields in a sample of RR Lyrae stars with different pulsational properties. Thanks to the highly efficient instrument FORS1 attached to VLT unit Kueyen, numerous RR Lyrae stars have now come within reach for spectropolarimetry. This paper presents the first survey of magnetic fields in a sample of RR Lyrae stars.
In Sect. 2 we discuss the targets, the observations and their reduction. The determination of the mean longitudinal magnetic field is described in Sect. 3. The outcome of our survey, in terms of the constraints on the magnetic field and the implications for the models for the Blazhko effect, is discussed in Sect. 4, and concluding remarks are given in Sect. 5.
2 Observations and data reduction
2.1 Target selection
We performed a high precision (The magnetic field strength may vary over the pulsation cycle and the Blazhko cycle, as was reported by Romanov et al. (1987). Based on the times of maxima given in the GEOS RR Lyrae database (http://rr-lyr.ast.obs-mip.fr/dbrr/), which contains also recent TAROT observations (LeBorgne et al. 2008, and references therein), and from our own data (Kolenberg et al. 2008,2007), we were able to determine the pulsation phases of our observed stars with a precision of 0.02. For the determination of the Blazhko phases, in contrast, we generally (except for SS For) could not rely on published accurate Blazhko ephemerides. In order to determine the Blazhko ephemerides for the observed stars, we used the parameters published by Wils & Sódor (2005) to fit the available data of the stars, ASAS data as well as our own measurements (if available). Monte Carlo simulations were used to determine the error on the Blazhko period. From the available photometric data we then extrapolated the Blazhko phase at the time of our FORS1 measurements. The error on the phase determination is dominated by the contribution of the error on the Blazhko period multiplied by the number of Blazhko cycles elapsed from the time of photometric measurements and of magnetic measurements. For all stars of our sample, the error in the determination of the Blazhko phase turned to be substantially higher than for pulsation phase. For some stars, those for which the photometric data were taken a few years prior to the FORS1 measurements, the uncertainty on the Blazhko phase turned out to be higher than 0.5, in which case our phase estimate is nearly meaningless.
Having 2.5 nights of observing time at our disposal in visitor mode, we optimized the observing strategy (number of different targets, slit width and exposure time) to get the most stringent constraints on the magnetic field (see Sect. 4.2).
2.2 Spectropolarimetry with FORS1
Observations were obtained in visitor mode during nights 2008-11-10 to 2008-11-13 with the Focal Reducer/Low Dispersion Spectrograph FORS1 (Appenzeller et al. 1998) of the ESO Very Large Telescope (VLT). We used grism 1200 B, which covers the spectral range of
The instrument was used in spectropolarimetric mode. Circular
polarization measurements were performed after insterting a
quarter-wave plate (at set position angles) and a Wollaston prism into
the parallel section of the instrument's optical path. For each star, we
obtained eight exposures with the position angle of the quarter-wave
plate set at
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Such a high number of
exposures was necessary to obtain a very high signal-to-noise ratio
(SNR) without saturating the CCD. Setting the retarder waveplate at
two different position angles allowed us to minimize the contributions
of spurious (instrumental) polarization (e.g. Semel et al. 1993).
The signal-to-noise ratio cumulated over both beams and all retarder
waveplate positions, estimated in the wavelength range 4475-4525 Å,
was between 1800 and 3000 per Å, allowing us to reach a typical
error bar of 0.05 % in the
.
Such a high number of
exposures was necessary to obtain a very high signal-to-noise ratio
(SNR) without saturating the CCD. Setting the retarder waveplate at
two different position angles allowed us to minimize the contributions
of spurious (instrumental) polarization (e.g. Semel et al. 1993).
The signal-to-noise ratio cumulated over both beams and all retarder
waveplate positions, estimated in the wavelength range 4475-4525 Å,
was between 1800 and 3000 per Å, allowing us to reach a typical
error bar of 0.05 % in the
![]() (the ratio
between Stokes V and Stokes I) profile in a 1 Å spectral bin.
(the ratio
between Stokes V and Stokes I) profile in a 1 Å spectral bin.
Data were reduced using standard IRAF routines and a dedicated FORTRAN
code. All the science frames were bias subtracted using a master bias
obtained from a series of five frames taken the morning after the
observations. No flat fielding procedure was applied to the data.
Spectrum extraction was performed by collapsing a 60 pixel
(=
![]() )
wide strip centred about the traced central peak. The
extraction parameters were obtained from the first exposure of each
series, and then adopted for all the remaining exposures, so as to
minimize the effects of a different sensitivity of the CCD between the
pixel regions illuminated by the two beams split by the Wollaston. Sky
subtraction was performed selecting symmetric regions on the left and
right side of each spectrum (typically between pixel 30 and 35 from
the central peak), and fitting those with a Chebyshev polynomial.
Owing to the limited size of the CCD region illuminated by each
beam split by the Wollaston prism, it was not possible to calculate
the sky contribution using a wider region. In fact,
since our targets are relatively bright, sky subtraction is not
a critical step, and could even have been skipped without significantly
affecting the final results.
)
wide strip centred about the traced central peak. The
extraction parameters were obtained from the first exposure of each
series, and then adopted for all the remaining exposures, so as to
minimize the effects of a different sensitivity of the CCD between the
pixel regions illuminated by the two beams split by the Wollaston. Sky
subtraction was performed selecting symmetric regions on the left and
right side of each spectrum (typically between pixel 30 and 35 from
the central peak), and fitting those with a Chebyshev polynomial.
Owing to the limited size of the CCD region illuminated by each
beam split by the Wollaston prism, it was not possible to calculate
the sky contribution using a wider region. In fact,
since our targets are relatively bright, sky subtraction is not
a critical step, and could even have been skipped without significantly
affecting the final results.
Wavelength calibration was based on one arc frame obtained the morning
after the observations, and typically led to a rms scatter of ![]() 0.02 pixels. Fine-tuning of wavelength calibration based on
night sky lines could not be performed, therefore the accuracy of the
absolute wavelength calibration is restricted by instrument flexures,
which are expected to be less than 1 pixel up to a zenith distance of
60
0.02 pixels. Fine-tuning of wavelength calibration based on
night sky lines could not be performed, therefore the accuracy of the
absolute wavelength calibration is restricted by instrument flexures,
which are expected to be less than 1 pixel up to a zenith distance of
60![]() (see FORS1/2 User Manual).
(see FORS1/2 User Manual).
The final products of data reduction are the
![]() profiles (the ratio
between Stokes V and Stokes I), together with their error bars,
calculated as explained in Bagnulo et al. (2006), i.e., combining all
eight exposures filtered using a
profiles (the ratio
between Stokes V and Stokes I), together with their error bars,
calculated as explained in Bagnulo et al. (2006), i.e., combining all
eight exposures filtered using a ![]() -clipping algorithm. In
addition, we obtained the so-called ``null profiles'',
-clipping algorithm. In
addition, we obtained the so-called ``null profiles'',
![]() profiles (Donati et al. 1997), which are expected to be distributed around
0 with the same FWHM that characterizes the
profiles (Donati et al. 1997), which are expected to be distributed around
0 with the same FWHM that characterizes the
![]() profiles. A deviation
from 0 of the
profiles. A deviation
from 0 of the
![]() profile exceeding 3
profile exceeding 3![]() would prompt for a
re-inspection of the data and data reduction quality, and for a search
for potential causes of spurious polarization, such as, e.g., those
due to spectral variability during the exposures.
would prompt for a
re-inspection of the data and data reduction quality, and for a search
for potential causes of spurious polarization, such as, e.g., those
due to spectral variability during the exposures.
It is well known that in RR Lyrae envelopes, especially those of RRab type stars, strong acoustic waves occur, and shock waves are produced at certain pulsational phases (Preston, et al. 1965; Chadid et al. 2008, and references therein for recent observations). The gas dynamics associated with these waves in the line forming region, as well as the existence of the preheating zones ahead of the shock fronts and the cooling zones behind them, can strongly affect the shape of the spectral lines in RR Lyrae stars, resulting in line asymmetry, additional broadening, line profile doubling, and emission components. These distortion effects are particularly present during the rise to maximum light, around the phase of minimum radius.
As pointed out by Wade et al. (2002) and Chadid et al. (2004), the rapid
changes in the line profiles of both the Balmer and the metallic lines
may lead to spurious polarization signals in high-resolution
spectropolarimetric data. However, it is reasonable to assume that
this problem is less critical with the technique based on
low-resolution spectra adopted in this work. Indeed, at a spectral
resolution of 1400 or 2800, as was obtained with FORS1 for this study,
most metal lines are not resolved, let alone their variations. Most of
our observations were obtained outside of the phase range in which the
stars are on the steep rising branch of their light curve (typically
the pulsation phase interval
![]() ). For the few stars in
our sample of which we obtained spectra close to the shock phase, we
could not see any effects on the spectra, in particular no spikes show
up in the null profiles, as we would expect if the resolved line profiles were
significantly changing during the observing time.
). For the few stars in
our sample of which we obtained spectra close to the shock phase, we
could not see any effects on the spectra, in particular no spikes show
up in the null profiles, as we would expect if the resolved line profiles were
significantly changing during the observing time.
3 Determinations of the mean longitudinal magnetic field
Our determinations of the mean longitudinal fieldwhere
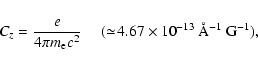 |
(2) |
where e is the electron charge,
A least-squares technique was used to derive the longitudinal field
via Eq. (1), by minimizing the expression
where, for each spectral point i, yi = (V/I)i,
![\begin{figure}
\par\includegraphics[angle=270,width=15cm,clip]{1591fig1.eps}\end{figure}](/articles/aa/full_html/2009/17/aa11591-08/Timg27.gif) |
Figure 1:
Spectropolarimetric observations of the magnetic star HD 94669 (left
panels) and two program RR Lyrae stars (MT Tel, middle panels, and
SS For, right panel). The top panels show the spectral region around
H |
| Open with DEXTER | |
Note that Eq. (1) is strictly correct under the so-called
weak field approximation, which, e.g., in the atmosphere of main
sequence A-type stars, is valid for field strengths ![]() 1 kG for
metal lines, and up to
1 kG for
metal lines, and up to ![]() 10 kG for H lines.
10 kG for H lines.
Using low resolution spectra such as those obtained in this work, it
would make sense to hypothesize that only broad H Balmer lines could
be used to determine the magnetic field, since most metal lines are
not resolved in the spectra. However, Bagnulo et al. (2002) and
Bagnulo et al. (2006) have shown that Eq. (1) may also be applied
to spectral regions with non resolved metal lines, leading to
results consistent to the
![]() determinations obtained on H Balmer
lines in the weak field regime. We checked that with our spectra the
determinations obtained on H Balmer
lines in the weak field regime. We checked that with our spectra the
![]() determination obtained from metal lines only are consistent,
within the error bars, with the
determination obtained from metal lines only are consistent,
within the error bars, with the
![]() values obtained from Balmer lines
only. For Balmer lines we adopted an effective Landé factor of 1
(Casini & Landi Degl'Innocenti 1994); for metal lines, following Chadid et al. (2004), we
used an effective Landé factor of 1.38. Finally, we applied the
least-square technique to the full spectrum, i.e., using both metal
and Balmer lines. This method allowed us to bring the
values obtained from Balmer lines
only. For Balmer lines we adopted an effective Landé factor of 1
(Casini & Landi Degl'Innocenti 1994); for metal lines, following Chadid et al. (2004), we
used an effective Landé factor of 1.38. Finally, we applied the
least-square technique to the full spectrum, i.e., using both metal
and Balmer lines. This method allowed us to bring the
![]() error bars
down to a typical level of 20-30 G.
error bars
down to a typical level of 20-30 G.
Similarly to the application by Bagnulo et al. (2006), the
![]() values were
determined using the
values were
determined using the
![]() profile obtained from the combinations of
all exposures. For the purpose of checking our results, we also calculated
the average of the
profile obtained from the combinations of
all exposures. For the purpose of checking our results, we also calculated
the average of the
![]() values obtained from individual pairs of
exposures for each star, always finding results consistent with the
values obtained from individual pairs of
exposures for each star, always finding results consistent with the
![]() value
obtained from the combined
value
obtained from the combined
![]() and I profiles.
and I profiles.
Since FORS1 is not equipped with circular polarization filters that
allow one to routinely check the correct alignment of the
polarimetric optics, and no standard stars for circular polarization
are available, we decided to perform a health check by
observing the well known magnetic Ap star HD 94660 (=KQ Vel=HIC 53379) during
our observing run. Two consecutive series of eight observations were
obtained, one with a 0.5
![]() slit width, and one with a
1.0
slit width, and one with a
1.0
![]() slit width, using the same strategy adopted for the
program stars. HD 94660 presents a roughly constant longitudinal
magnetic field, and the measured value of
slit width, using the same strategy adopted for the
program stars. HD 94660 presents a roughly constant longitudinal
magnetic field, and the measured value of ![]() -1960 G (from Balmer
lines only) is in reasonably good agreement with previous observations
(see, e.g., Fig. 3 of Bagnulo et al. 2006, the new observation presented in this paper
would be located at phase 0.96).
-1960 G (from Balmer
lines only) is in reasonably good agreement with previous observations
(see, e.g., Fig. 3 of Bagnulo et al. 2006, the new observation presented in this paper
would be located at phase 0.96).
Figure 1 shows our observations of stellar spectra in
circular polarization, and their interpretation in terms of magnetic
field for HD 94660, a known magnetic star, and two representative RR
Lyrae stars: MT Tel, an RRc star, and SS For, an RRab Blazhko star.
Note that the hotter RRc star clearly has less metal lines in its
spectrum than the RRab star. The bottom panels show the best fits to
the full spectrum obtained through minimizing the ![]() of
Eq. (3). Whereas a clear slope is observed in the
case of HD 94660, corresponding to the mean longitudinal magnetic
field
of
Eq. (3). Whereas a clear slope is observed in the
case of HD 94660, corresponding to the mean longitudinal magnetic
field
![]() , for the RR Lyrae stars the best fit results are consistent
with a curve with no significant slope.
, for the RR Lyrae stars the best fit results are consistent
with a curve with no significant slope.
The results of our survey are reported in
Table 2. Inspection of this table show that in
all cases our
![]() measurements are, within 3
measurements are, within 3![]() ,
fully consistent with a null
detection of the mean longitudinal magnetic field. In other words, for the 17 stars
in our sample and the 20 measurements taken, we obtained no field that
differed from zero exceeding the 3
,
fully consistent with a null
detection of the mean longitudinal magnetic field. In other words, for the 17 stars
in our sample and the 20 measurements taken, we obtained no field that
differed from zero exceeding the 3 ![]() significance level. In
fact, 14 of our 20 measurements were null detections within a
1
significance level. In
fact, 14 of our 20 measurements were null detections within a
1![]() significance level. A histogram reflecting our measurements
is given in Fig. 2.
significance level. A histogram reflecting our measurements
is given in Fig. 2.
Table 2: Determination of the mean longitudinal magnetic field of 17 RR Lyrae stars.
4 Discussion
4.1 The magnetic model challenged
The presence of a strong dipole magnetic field is a key ingredient for the model proposed by Shibahashi & Takata (1995) and Shibahashi (2000). Assuming that RR Lyrae stars have fairly strong dipole fields, Shibahashi (2000) showed that the radial mode in RR Lyrae stars would be deformed by the Lorenz force to have additional quadrupole (
Our sample of stars consisted of RR Lyrae stars with different pulsational properties: RRab, RRc stars, and modulated stars of both types. In none of these stars a field exceeding a significance level of ![]() was detected.
was detected.
For the magnetic field to have the effects described by Shibahashi & Takata (1995) and Shibahashi (2000), the presence of a dipole field with a strength of the order of 1 kG was assumed. In the following section we discuss what constraints our measurements set to the magnetic field strength and morphology of our sample of stars.
4.2 Constraints on the magnetic field
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1591fig2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa11591-08/Timg33.gif) |
Figure 2:
Distribution of the
|
| Open with DEXTER | |
We consider a magnetic configuration produced either by a dipole, or
by a (non-linear) quadrupole, or by the superposition of both.
The model is assumed to be centered, i.e. the elementary multipoles
that produce the magnetic configuration at the stellar surface are
located at the star's center. The dipole field
![]() can be characterized by the
dipole field strength
can be characterized by the
dipole field strength
![]() at the pole, plus the direction of a unit
vector
at the pole, plus the direction of a unit
vector ![]() ;
the quadrupole field
;
the quadrupole field
![]() can be characterized by the
quadupole field strength
can be characterized by the
quadupole field strength
![]() ,
plus the directions of two unit vectors
,
plus the directions of two unit vectors
![]() and
and ![]() .
The geometric configuration of a dipole
plus quadrupole magnetic field is illustrated in Fig. 1 of
Landolfi et al. (1998). Denoting by R* the star's radius, the magnetic
field vector at a given point
.
The geometric configuration of a dipole
plus quadrupole magnetic field is illustrated in Fig. 1 of
Landolfi et al. (1998). Denoting by R* the star's radius, the magnetic
field vector at a given point ![]() of the stellar surface is
given, respectively, by
of the stellar surface is
given, respectively, by
Note that while the quantity
Assuming a limb-darkening law of the form
| (5) |
where
where
Even a quick glance at the results in Table 2 tells us that, if a dipole field is present, its strength must be small, much smaller than the 1 kG field that the magnetic model (Shibahashi 2000) requires to be responsible for the Blazhko effect. Based on our measurements, it is possible to obtain more precise constraints on the magnetic field of our program stars.
Let us consider the case of a pure dipolar field. We assume that all
stars of our sample have the same dipolar strength, and that the
magnetic axis is randomly oriented with respect to the line of sight.
The probability ![]() for the tilt angle of the
field
for the tilt angle of the
field ![]() to be in the range
to be in the range
![]() is proportional to
is proportional to
![]() .
A simple application of Bayesian
statistics allows us to evaluate the probability
.
A simple application of Bayesian
statistics allows us to evaluate the probability
![]() that all the observed
stars of our sample are characterized by a dipolar field strength
higher than a certain threshold value
that all the observed
stars of our sample are characterized by a dipolar field strength
higher than a certain threshold value
![]() :
:
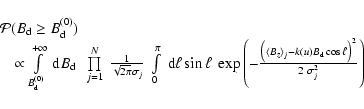 |
(7) |
where the product runs on the N=17 observed stars (for the
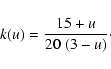 |
(8) |
Using a limb-darkening coefficient u=0.62, derived from Diaz-Cordoves et al. (1995; see also Kolenberg 2002), we obtain that if the RR Lyrae stars of our sample are all characterized by the same dipolar strength, with magnetic axis randomly oriented about the line of sight, then there is a 95% probability that their dipolar strength is
Equation (6) shows that, for the limb-darkening
coefficient of u=0.62, the contribution of the quadrupolar component
to the mean longitudinal magnetic field is always ![]() % the
contribution due to the dipolar component (assuming
% the
contribution due to the dipolar component (assuming
![]() =
=
![]() ). For a
linear quadrupole, i.e., with
). For a
linear quadrupole, i.e., with
![]() ,
we always have
,
we always have
![]() and
and
![]() ,
and our observations
rule out a quadrupolar field strength
,
and our observations
rule out a quadrupolar field strength
![]() 250 G at the 95% confidence level. If we consider the special case where
250 G at the 95% confidence level. If we consider the special case where
![]() and
and
![]() (for which
(for which
![]() ), we obtain the value
), we obtain the value
![]() = 1.9 kG as an upper limit to the quadrupole strength.
= 1.9 kG as an upper limit to the quadrupole strength.
Therefore, determinations of the mean longitudinal field as obtained in this work set fairly loose constraints on the magnetic field strength for morphologies of higher order than the dipole field.
4.3 Variability over pulsation cycle and Blazhko cycle
![\begin{figure}
\includegraphics[width=9cm,clip]{1591fig3.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa11591-08/Timg72.gif) |
Figure 3: Absolute value of the mean longitudinal field versus pulsation phase. Different symbols were used for different types of RR Lyrae stars. Data points for stars observed more than once are denoted with filled symbols. |
| Open with DEXTER | |
For two of the stars in our sample, CS Eri (RRc) and SS For (RRab-BL), we obtained more than one
measurement at different phases in their pulsation cycle. No clear variation with the pulsation phase
exceeding the error bars could be derived for these stars.
We observed SS For at 3 different phases: one at maximum
light, a second one approaching minimum light, and a third one on the
rising branch of the light variation. From the last spectrum a higher absolute
![]() was derived, but also
a higher error bar, which can be attributed to the lower signal-to-noise ratio of the spectrum.
SS For shows quintuplets in its
pulsation spectrum (Kolenberg et al. 2008) which, according to the magnetic model (Shibahashi 2000) are associated with the
effects of a magnetic field (see also Sect. 4.1), and hence was one
of our prime targets for investigating the presence of a magnetic
field.
was derived, but also
a higher error bar, which can be attributed to the lower signal-to-noise ratio of the spectrum.
SS For shows quintuplets in its
pulsation spectrum (Kolenberg et al. 2008) which, according to the magnetic model (Shibahashi 2000) are associated with the
effects of a magnetic field (see also Sect. 4.1), and hence was one
of our prime targets for investigating the presence of a magnetic
field.
Romanov et al. (1987) also reported a variation of their derived mean longitudinal magnetic field values over the Blazhko cycle of RR Lyr.
Chadid et al. (2004), in contrast, with 27 measurements of the same star, detected no significant changes at different Blazhko phases.
Within the allocated telescope time we were not able to follow one Blazhko star at different Blazhko phases. Only for some stars in our sample the Blazhko phase could be determined with a reasonable accuracy. However, we can safely say that the 11 Blazhko stars
in our sample were recorded at random Blazhko phases, and for all of them we obtained a mean longitudinal magnetic field consistent with a null detection within ![]() .
As discussed in Sect. 4.2, this implies low values for the magnetic dipole field.
.
As discussed in Sect. 4.2, this implies low values for the magnetic dipole field.
Our observations significantly enlarge the sample of spectropolarimetric measurements of RR Lyrae stars and follow the line of results obtained by Preston (1967) and Chadid et al. (2004). The latter authors declared RR Lyr to be a bona fide non-magnetic star on the basis of high-resolution spectropolarimetric data obtained over a 4-year time span.
Now why did earlier measurements of the magnetic field in specifically RR Lyr, the brightest star of the class, lead to reported values of the longitudinal magnetic field strength as high as about 1.5 kG (Romanov et al. 1987; Babcock 1958), while more recent observations contradict this?
Chadid et al. (2004) addressed this question in the necessary detail (in their Sect. 3.1), pointing at the limitations of the use of photographic plates resulting in underestimated error bars, and the distortions of the spectral lines caused by shock waves in certain pulsation phases (see also Wade et al. 2002). The measurement with by far the highest
![]() detection by Romanov et al. (1987) was recorded at the phase of the main shock in the star (
detection by Romanov et al. (1987) was recorded at the phase of the main shock in the star (![]() ). This may have led to spurious polarization signals. We also note two limiting factors of those earlier measurements: i) a quite low reciprocal dispersion (9 Å/mm) of their plate material, which is possibly not sufficient to perform high accuracy splitting measurements of the spectral lines observed in opposite polarization; ii) the employment of the Nasmyth focus station for the polarimeter: the oblique reflection from the tertiary mirror is prone to introduce a spurious polarization signal. This problem is much less critical at the Cassegrain focus, which was used instead for both the MuSiCoS observations obtained by Chadid et al. (2004), and the FORS1 measurements presented in this work. We therefore suggest that the magnetic field in RR Lyr was significantly overestimated in the earlier studies.
). This may have led to spurious polarization signals. We also note two limiting factors of those earlier measurements: i) a quite low reciprocal dispersion (9 Å/mm) of their plate material, which is possibly not sufficient to perform high accuracy splitting measurements of the spectral lines observed in opposite polarization; ii) the employment of the Nasmyth focus station for the polarimeter: the oblique reflection from the tertiary mirror is prone to introduce a spurious polarization signal. This problem is much less critical at the Cassegrain focus, which was used instead for both the MuSiCoS observations obtained by Chadid et al. (2004), and the FORS1 measurements presented in this work. We therefore suggest that the magnetic field in RR Lyr was significantly overestimated in the earlier studies.
5 Conclusion
The results of our survey of magnetic fields in RR Lyrae stars reveal a serious challenge to the magnetic models for explaining the Blazhko effect. For a sample consisting of 17 RR Lyrae stars with different pulsational properties, no substantial dipole magnetic field, as required by the magnetic model (Shibahashi 2000), was detected. We determined an upper limit for the strength of the dipole field in the stars of our sample at 130 G with a 95% confidence level. Our result implies that the Blazhko modulation in the pulsation of RR Lyrae stars is not correlated with the presence of a strong, quasi-dipolar magnetic field. For morphologies of higher order than the dipole field, however, our determinations of the mean longitudinal field as obtained in this work only set fairly loose constraints on the magnetic field strength. More complex magnetic field morphologies may be detected with high-resolution spectropolarimetric data.
Acknowledgements
This paper is based on observations made with ESO Telescopes at the La Silla-Paranal Observatory under program ID 082.D-0342. K.K. is supported by the Austrian Fonds zur Förderung der wissenschaftlichen Forschung, project number P19962-N16 and T359-N16. SB thanks D. J. Asher for very useful discussions. We thank the referee for constructive comments. The research has made use of the SIMBAD astronomical database (http://simbad.u-strasbg.fr/) and the GEOS RR Lyrae database (http://dbrr.ast.obs-mip.fr/).
References
- Appenzeller, I., Fricke, K., Furtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] (In the text)
- Babcock, H. W. 1958, ApJS, 3, 141 [NASA ADS] [CrossRef] (In the text)
- Bagnulo, S., Landi Degl'Innocenti, M., & Landi Degl'Innocenti, E. 1996, A&A, 308, 115 [NASA ADS] (In the text)
- Bagnulo, S., Szeifert, T., Wade, G. A., Landstreet, J. D., & Mathys, G. 2002, A&A, 389, 191 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bagnulo, S., Landstreet, J. D., Mason, E., et al. 2006, A&A, 450, 777 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Blazhko, S. N. 1907, Astron. Nachr., 175, 325 [NASA ADS] [CrossRef] (In the text)
- Casini, R., & Landi Degl'Innocenti, E. 1994, A&A, 291, 668 [NASA ADS] (In the text)
- Chadid, M., Kolenberg, K., Aerts, C., & Gillet, D. 1999, A&A, 352, 201 [NASA ADS]
- Chadid, M., Wade, G. A., Shorlin, S. L. S., & Landstreet, J. D. 2004, A&A, 413, 1087 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chadid, M., Vernin, J., & Gillet, D. 2008, A&A, 491, 537 [NASA ADS] [CrossRef] [EDP Sciences]
- Cox, A. N. 1993, Proc. IAU Coll., 139, 409 [NASA ADS]
- Cousens, A. 1983, MNRAS, 203, 1171 [NASA ADS]
- Diaz-Cordoves, J., Claret, A., & Gimenez, A. 1995, A&AS, 110, 329 [NASA ADS] (In the text)
- Detre L., & Szeidl, B. 1973, Proc. IAU Coll., 21, 11 [NASA ADS] (In the text)
- Donati, J.-F., Semel, M., Carter, B. D., et al. 1997, MNRAS, 291, 658 [NASA ADS] (In the text)
- Dziembowski, W. A., & Mizerski, T. 2004, Acta Astron., 54, 363 [NASA ADS] [CrossRef]
- Jurcsik J., Benko, J. M., & Szeidl, B. 2002, A&A, 390, 133 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jurcsik J., Sódor, Á., & Hurta, Zs. 2008, MNRAS, 391, 164 [NASA ADS] [CrossRef] (In the text)
- Jurcsik, J., et al., CoAst, 159, submitted
- Kholopov, P. N., Samus, N. N., Frolov, M. S., et al. 1999, Combined General Catalog of Variable Stars (Kholopov, 1988) (In the text)
- Kolenberg, K. 2002, Ph.D. Thesis, University of Leuven
- Kolenberg, K., et al. 2003, ASP, 305, 167 [NASA ADS] (In the text)
- Kolenberg, K., Smith, H. A., Gazeas, K. D., et al. 2006, A&A, 459, 588 [NASA ADS] [CrossRef] (In the text)
- Kolenberg, K., Guggenberger, E., & Medupe, T. 2007, CoAst, 150, 381 [NASA ADS]
- Kolenberg, K., Guggenberger, E., Medupe, T., et al. 2008, MNRAS, in press [arXiv:0812.2065]
- Kovacs, G. 1995, A&A, 295, 693 [NASA ADS] (In the text)
- Kurtz, D. W. 1982, MNRAS, 200, 807 [NASA ADS] (In the text)
- LaCluyzé, A., Smith, H. A., Gill, E.-M., et al. 2004, AJ, 127, 1653 [NASA ADS] [CrossRef] (In the text)
- Landolfi, M., Bagnulo, S., & Landi Degl'Innocenti, M. 1998, A&A, 338, 111 [NASA ADS] (In the text)
- Le Borgne, J. F., Klotz, A., & Boer, M. 2008, IBVS, 5823 (In the text)
- Moskalik, P., & Poretti, E. 2003, A&A, 398, 213 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Preston, G. W. 1967, in The Magnetic and Related Stars, ed. R. C. Cameron, 26 (In the text)
- Preston, G. W., Smak, J., & Paczynski, B. 1965, ApJS, 12, 99 [NASA ADS] [CrossRef]
- Romanov, Yu. S., Udovichenko, S. N., & Frolov, M. S. 1987, Sov. Astr. Lett., 13, 29 [NASA ADS] (In the text)
- Semel, M., Donati, J. F., & Rees, D. E. 1993, A&A, 278, 231 [NASA ADS] (In the text)
- Shibahashi, H. 2006, ASP Conf. Ser., 203, 299 [NASA ADS] (In the text)
- Shibahashi, H.,& Takata, M. 1995, ASP Conf., Ser., 83, 42
- Sódor, Á. 2006, Astron.Nachr., 88, 789
- Sódor, Á., Vida, K., Jurcsik, J., et al. 2006, IBVS, 5705 (In the text)
- Stothers, R. B. 2006, ApJ, 652, 643 [NASA ADS] [CrossRef] (In the text)
- Szeidl, B. 1976, Proc. IAU Coll., 29, 133 [NASA ADS] (In the text)
- Van Hoolst, T., Dziembowski, W. A., & Kawaler, S. D. 1998, MNRAS 297, 536
- Wade, G. A., Chadid, M., Shorlin, S. L. S., Bagnulo, S., & Weiss, W. W. 2002, A&A, 396, L17 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wils, P., & Sódor, Á. 2005, IBVS, 5655 (In the text)
All Tables
Table 1: Our sample of RR Lyrae stars for the spectropolarimetry and the magnetic A star for comparison.
Table 2: Determination of the mean longitudinal magnetic field of 17 RR Lyrae stars.
All Figures
![\begin{figure}
\par\includegraphics[angle=270,width=15cm,clip]{1591fig1.eps}\end{figure}](/articles/aa/full_html/2009/17/aa11591-08/Timg27.gif) |
Figure 1:
Spectropolarimetric observations of the magnetic star HD 94669 (left
panels) and two program RR Lyrae stars (MT Tel, middle panels, and
SS For, right panel). The top panels show the spectral region around
H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1591fig2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa11591-08/Timg33.gif) |
Figure 2:
Distribution of the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=9cm,clip]{1591fig3.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa11591-08/Timg72.gif) |
Figure 3: Absolute value of the mean longitudinal field versus pulsation phase. Different symbols were used for different types of RR Lyrae stars. Data points for stars observed more than once are denoted with filled symbols. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



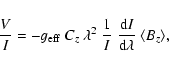
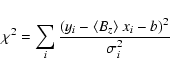
![$\displaystyle -\frac{\ensuremath{B_{\rm d}} }{2}
\left[~\vec{u}-3~\frac{\vec{u}\cdot\vec{r}}{R_*^2}\;\vec{r}~\right]$](/articles/aa/full_html/2009/17/aa11591-08/img43.gif)
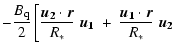
![$\displaystyle \left.+\left(\frac{\vec{u_1}\cdot\vec{u_2}}{R_*}-5~\frac{(\vec{u_1}\cdot\vec{r})(\vec{u_2}\cdot\vec{r})}{R_*^3} \right)\vec{r}~\right].$](/articles/aa/full_html/2009/17/aa11591-08/img46.gif)