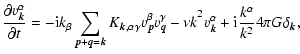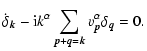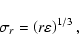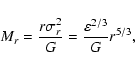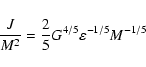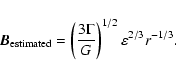EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 498 / No 2 (May I 2009) A&A, 498 2 (2009) 357-359 Full HTML
Free Access
Issue
A&A
Volume 498, Number 2, May I 2009
Page(s) 357 - 359
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/200810687
Published online 05 March 2009

Cosmic dark turbulence
(Research Note)

A. Nakamichi1 - M. Morikawa2

1 - Gunma Astronomical Observatory, 6860-86 Nakayama, Takayama Agatsuma, Gunma 377-0702, Japan
2 - Department of Physics, Ochanomizu University, 2-1-1 Otsuka, Bunkyo, Tokyo 112-8610, Japan

Received 27 July 2008 / Accepted 28 January 2009

Abstract
We aim for a consistent understanding of various scaling relations reported for self-gravitating systems, based on the proposal that the collisionless dark matter fluid turns into a turbulent state, i.e. dark turbulence, after crossing the caustic surface in the non-linear stage. Kolmogorov scaling laws with a constant energy flow per mass of $0.3~\rm cm^2/s^3$ are suggested from observations.

Key words: cosmology: theory - gravitation - turbulence - cosmology: dark matter - cosmology: observations - hydrodynamics

1 Introduction

We briefly report a possible origin of angular momentum as well as various scaling relations in self-gravitating systems (SGS) in the universe.

A typical mechanism of angular momentum acquisition for galaxies is tidal torquing (see for example Schaefer 2008), in which a system of mass Macquires most of its angular momentum $J\propto t_{{\rm TA}}^{1/3}M^{5/3}$(Sugerman et al. 2000) through tidal interaction before the turnaround time $t_{{\rm TA}}$.

On the other hand, we explore the fully nonlinear stage after the shell-crossing time, just after $t_{{\rm TA}}$. Although the amount of angular momentum is mostly acquired before $t_{{\rm TA}}$, a strongly interacting nonlinear period after that should remove the previous correlations. We assume that the collisionless dark matter (DM) fluid turns into a turbulent state, i.e. cosmic dark turbulence (CDT), after the shell-crossing time when multi-streaming initiates (Buchert 1999). The shell crossing and the initiation of turbulence are actually redshift dependent, which is quantitatively described in chapter 3 in Yoshisato et al. (2003). The scale range of the turbulent region, identified as the scale where shell crossing has already taken place at a given redshift, extends in time and is about 10 Mpc and smaller at present.

Universal scaling relations associated with this turbulence may be relevant to explain several scaling relations such as the scaling relations in the velocity dispersion (Sanders & McGaugh 2002), in M/L ratio (Bahcall et al. 2000), in the power spectrum of density fluctuations (Sanchez & Cole 2007), in cosmic magnetic fields, as well as in angular momentum. The purpose of this study is to consider all of these scaling relations from a simple principle.

2 Fluid description for self-gravitating systems and the Kolmogorov law

A set of Jeans equations for SGS and the Poisson equation becomes


    $\displaystyle \frac{\partial \rho }{\partial t}+\vec{\nabla}\cdot \left( \rho \vec{v}\right) =0,$  
    $\displaystyle \frac{\partial \vec{v}}{\partial t}+(\vec{v}\cdot \vec{\nabla})\vec{v}+\vec{\nabla}\Phi =0,$  
    $\displaystyle \vec{\nabla}^{2}\Phi =4\pi G\rho ,$ (1)

where $\vec{v}\left( \vec{x},t\right) $ is the velocity, p is the pressure, $\rho $ is the mass density. The Fourier transform of Eq. (1) becomes
    $\displaystyle \frac{\partial v_{\vec{k}}^{\alpha }}{\partial t}=-{\rm i}k_{\bet... ...v_{\vec{k}}^{\alpha }+{\rm i}\frac{k^{\alpha }}{k^{2}}4\pi G\delta _{\vec{k}} ,$  
    $\displaystyle \dot{\delta}_{\vec{k}}-{\rm i}k^{\alpha }\sum\limits_{\vec{p}+\vec{q}=\vec{k}}v{_{\vec{p}}^{\alpha }\delta _{\vec{q}}}={0.}$ (2)

Where ${K_{\vec{k}\mathbf{,}\alpha \gamma }=\delta }_{\alpha \gamma }-k_{\alpha }k_{\gamma }/k^{2},$ $v^{\alpha }\left( \vec{x} ,t\right) $ = $\int {\rm d}^{3}k\left( 2\pi \right) ^{-3}$ e $^{\rm i\vec{k}\vec{x}}$ $v{_{\vec{k}}^{\alpha }}\left( t\right) {,\ }\sum\limits_{\vec{p}+\vec{q}=\vec{k}}=$ $\int {\rm d}^{3}p{\rm d}^{3}q$ $\delta ^{3}\left( \vec{p}+\vec{q}-\vec{k}\right) ,\ \delta _{\vec{k}}\left( t\right) $ = $\int {\rm d}^{3}x{\rm e}^{\rm i\vec{k}\vec{x}}\rho \left( \vec{x},t\right)$, and a possible effective viscosity $\nu $ due to the dynamical friction. The Poisson equation is used for the above expression for the source term. We now look for the scaling solution, supposing the velocity $v_{\vec{k}}^{\alpha }$ and the density fluctuations $\delta _{\vec{k}}$ scale as $v_{\vec{k}}^{\alpha }\rightarrow \lambda ^{\mu }v_{\vec{k}}^{\alpha }$ and $\delta _{\vec{k}}\rightarrow \lambda ^{\nu }\delta _{\vec{k}}$ under the scaling transformation $\vec{k}\rightarrow \lambda \vec{k}\mathbf{,}$ or $\vec{x}\rightarrow \lambda ^{-1}\vec{x}$.

We assume the energy flow is a constant d $E\left( \vec{x}\right) /{\rm d}t= \varepsilon $, which is essential to characterize turbulence. We then have the scaling $\partial v_{\vec{k}}^{\alpha }/\partial t\rightarrow \lambda ^{4+2\mu }\partial v_{\vec{k}}^{\alpha }/\partial t$ in the inertial regime, i.e. the viscosity term does not dominate as in the collisionless stage under study. This scaling suggests that the time should scale as $t\rightarrow \lambda ^{-4-\mu }t$ for consistency. Since d $E\left( \vec{x}\right) /{\rm d}t\rightarrow \lambda ^{10+3\mu }{\rm d}E\left( \vec{x}\right) /{\rm d}t$ must be a constant $\varepsilon $, we have $\mu =-10/3$ and $\nu =-5/3$. Then, since $\varepsilon \propto $ $\left( v_{\vec{k}}^{\alpha }\right) ^{3}$, we have $v^{\alpha }\left( \vec{x}\right) =\left( \left\vert \vec{x}\right\vert \varepsilon \right) ^{1/3}f\left( \vec{x}/\left\vert \vec{x}\right\vert \right) $, where f is a function of only the direction $\vec{x}/\left\vert \vec{x}\right\vert $. Thus $v^{\alpha }\left( \vec{x}\right) $represents an average velocity difference or the velocity dispersion  $\sigma _{r}$ at the separation scale $r=\left\vert \vec{x}\right\vert $. Thus we obtain the relation, originally derived by Kolmogorov (1941),

\begin{displaymath}\sigma _{r}=\left( r\varepsilon \right) ^{1/3}, \end{displaymath} (3)

which claims that the velocity dispersion increases with scale. A possible numerical factor of $O\left( 1\right) $ is absorbed into the renormalized parameter  $\varepsilon $. By utilizing the local virial relation (Iguchi et al. 2006) with this equation, we have the mass at the scale r as

\begin{displaymath}M_{r}=\frac{r\sigma _{r}^{2}}{G}=\frac{\varepsilon ^{2/3}}{G}r^{5/3}{\rm ,} \end{displaymath} (4)

or equivalently, the mass density at the scale r as $\rho _{r}=M_{r}r^{-3}/\left( 4\pi /3\right) =G^{-1}\varepsilon ^{2/3}r^{-4/3}/\left( 4\pi /3\right) $, which is consistent with the scaling of $\delta _{\vec{k}}$ with $\nu =-5/3$.

It should be emphasized that the viscosity term does not dominate in the present collisionless DM and even in this collisionless case, the virial relation holds as a consequence of dynamical relaxation (Iguchi et al. 2006).

3 Observational tests

3.1 Mass-angular momentum relation

We examine the angular momentum-mass relation, which has been the starting point of the present study. By utilizing the rigid body approximation, virial relation, and Eq. (4), we have the expression

\begin{displaymath}\frac{J}{M^{2}}=\frac{2}{5}G^{4/5}\varepsilon ^{-1/5}M^{-1/5} \end{displaymath} (5)

with $\varepsilon =0.3[$cm2/s3], which is consistently suggested from several other observations (Nakamichi et al. 2008). It is interesting to notice that mass dependence of the angular momentum $J\propto M^{9/5}$ is very similar to the one predicted from the tidal torquing $J\propto M^{5/3}$. The above result, expressed as the solid line in Fig. 1, is compared with observations; simple points are from Muradian et al. (1999), and points with error bars are from Brosche (1986); and Brosche & Tassie (1989). Our result is consistent with the latter but not with the former.

3.2 The scale dependent magnetic field

Now we consider a possible relation between CDT and the large scale distribution of cosmic magnetic fields. The magnetic field $\vec{B}$ and the vorticity $\vec{\omega}\equiv rot\vec{v}$ actually satisfy very similar equations of motion and a rough argument based on this fact is found in Landau & Lifshits (1984), Sect. 74. Generation of the cosmic magnetic field is studied in Gnedin et al. (2000), and further development of the magnetic field is discussed in Schekochihin et al. (2005), for example. Magnetic fields at higher redshift are discussed in Kronberg (2005) and Kronberg et al. (2007).

However, a complete model and theory which systematically describe the generation and development of the cosmic magnetic field on all scales have not yet been established. Therefore we simply assume here the following conditions as a tentative starting point for discussions. (a) The dynamo mechanism is a general process to convert rotational energy into magnetic fields in various cosmic scales with a constant conversion rate $\Gamma $. (b) Baryons should faithfully follow the motion of DM, at least at later stages of the universe. The assumption (a) should be considered as a working hypothesis at present motivated from the similarity in the equations for $\vec{B}$ and $\vec{\omega}$. The assumption (b) may sound strange if one imagines a simple straight fall of baryons into a static potential well formed by DM. However, since the DM is moving according to Eq. (3), we cannot suppose a static potential well. Furthermore, in the case of galaxies, there is an empirical relation that DM has the same specific angular momentum as baryons,which is widely supported and adopted in the study of angular momentum of galaxies (Tonini & Salucci 2006). These facts may support the idea that the baryons are dynamically coupled to turbulent motions of DM.

Adopting the above assumptions, we consider that the portion of $\Gamma $ of the kinetic energy at scale r, $\rho _{\rm DM}\left\langle {v^{2}}\right\rangle /2=(3/(8\pi G))\varepsilon ^{4/3}r^{-2/3}$ is supposed to turn into the energy density of the magnetic field $\vec{B}^{2}/\left( 8\pi \right) $. This yields the relation

\begin{displaymath}\vec{B}_{\rm estimated}=\left( \frac{3\Gamma }{G}\right) ^{1/2}\varepsilon ^{2/3}r^{-1/3}. \end{displaymath} (6)

This result, expressed as the solid line in Fig. 2, is compared with observations (Vallee 1990, 1995). Guided by these data, we have chosen the value $\Gamma =0.02$. Reflecting the above bold assumptions, the fit is not so remarkable, although a general trend is not excluded by the observations. For the larger scales beyond about 10 Mpc, the dynamical time becomes larger than the Hubble time, where we cannot apply our argument.
 \begin{figure} \par\resizebox{90mm}{!}{\includegraphics{0687fig1.eps}} \par\end{figure} Figure 1:

The relation between J/M2 and M for various objects; simple points are from Muradian et al. (1999), and points with error bars are from Brosche (1986); Brosche et al. (1989). The solid line represents our relation Eq. (5) with $\protect\varepsilon =0.3$.
Open with DEXTER

4 Summary

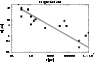 \begin{figure} \par\resizebox{90mm}{!}{\includegraphics{0687fig2.eps}} \end{figure} Figure 2:

Cosmic magnetic fields in various scales. The deta are from Vallee (1990), marked by stars; Vallee (1995), marked by squares and diamonds. The solid line represents Eq. (6) with parameter $\Gamma =0.02$. This fit is violated below the distance of about the parsec scale, and another power seems to develop below there.

Open with DEXTER
We proposed a possible origin of angular momentum and related scaling relations of SGS as the turbulent motion of DM after the shell crossing time. The scaling solution for the Fourier transformed Jeans equation and the assumption of a constant energy flow yield unique scaling relations, which explain the observed scaling of the angular momentum-mass J-M relation and the magnetic field -size B-r relation and others. All of them point to a concordant value for the constant energy flow per mass: $\varepsilon =0.3[$cm2/s3].

References

All Figures

  \begin{figure} \par\resizebox{90mm}{!}{\includegraphics{0687fig1.eps}} \par\end{figure} Figure 1:

The relation between J/M2 and M for various objects; simple points are from Muradian et al. (1999), and points with error bars are from Brosche (1986); Brosche et al. (1989). The solid line represents our relation Eq. (5) with $\protect\varepsilon =0.3$.
Open with DEXTER
In the text

  \begin{figure} \par\resizebox{90mm}{!}{\includegraphics{0687fig2.eps}} \end{figure} Figure 2:

Cosmic magnetic fields in various scales. The deta are from Vallee (1990), marked by stars; Vallee (1995), marked by squares and diamonds. The solid line represents Eq. (6) with parameter $\Gamma =0.02$. This fit is violated below the distance of about the parsec scale, and another power seems to develop below there.

Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.