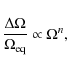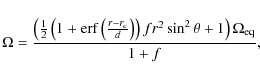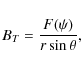| Issue |
A&A
Volume 497, Number 3, April III 2009
|
|
|---|---|---|
| Page(s) | 829 - 833 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200811426 | |
| Published online | 05 March 2009 | |
Dynamo generated toroidal magnetic fields in rapidly rotating stars
D. Moss1 - D. Sokoloff2
1 - School of Mathematics, University of Manchester,
Oxford Road, Manchester, M13 9PL, UK
2 -
Department of Physics, Moscow University, 119992 Moscow, Russia
Received 26 November 2008 / Accepted 16 February 2009
Abstract
Aims. Results presented in the recent observational paper by Petit et al. (2008, MNRAS, 388, 80) suggest that, for solar-like stars, the large-scale surface toroidal fields become strong for rotational periods less than about 12 d. We discuss this observation in the context of stellar dynamo theory, as a manifestation of a bifurcation in dynamo regimes occurring around this rotation period.
Methods. Working in the context of mean field theory, we first consider two options for such a bifurcation for a given stellar rotation law: (a) a bifurcation resulting in a sudden increase of the near-surface toroidal field, with all other details of the model being kept unaltered; (b) a new type of surface boundary condition at the stellar surface, forced by internal reorganization of magnetic field with increasing rotation rate, which causes a more-or-less abrupt increase in large-scale surface toroidal field.
Results. Neither of these options seem to provide anything like the reported behaviour of surface toroidal field for plausible choices of parameters, although we cannot conclusively eliminate a possible role for the latter mechanism. We conclude that any such bifurcation most plausibly is associated with some reorganization in the stellar hydrodynamics as the stellar rotation rate increases. The simplest suggestion, i.e. a transition from a solar-like rotation law (with spoke-like angular velocity contours through the bulk of the convection zone) to a law with quasi-cylindrical isorotation contours as thought to be appropriate to rapidly rotating stars, seems to reproduce the observed phenomenology reasonably well.
Conclusions. While we appreciate the manifold uncertainties in the available theory and observations, we thus suggest that the bifurcation deduced by Petit et al. (2008) is an observational manifestation of the transition between solar-like and quasi-cylindrical rotation laws, occuring near a rotational period of 12 d.
Key words: Sun: activity - Sun: magnetic fields - stars: magnetic fields - magnetic fields
1 Introduction
Historically the solar activity cycle was identified from sunspot data. Contemporary interpretation of the cycle identifies it as a magnetic phenomenon which involves toroidal as well as poloidal magnetic field components, where sunspots are considered as tracers for the toroidal magnetic field. Correspondingly, confrontation between theoretical findings and solar phenomenology based on sunspot data can only illuminate the situation from a very limited viewpoint. Specific dynamo models for the solar cycle suggest various relations between toroidal and poloidal dynamo generated solar magnetic fields (for example, phase shift between the components) which seem on first sight to be very attractive for confrontation between theory and observations. In practice however the available tracers for toroidal and poloidal solar magnetic fields are so physically different that their confrontation is quite nontrivial, and comparison between theory and observations is usually based primarily on the sunspot data. As far as it is known, the description of the solar cycle determined from data concerning tracers of poloidal magnetic field appears to be substantially different than the conventional description based on sunspot data (e.g. Obridko et al. 2006): specifically, the activity wave identified by the surface mean magnetic field appears as a system of standing waves rather than the traveling wave identified from the sunspot data.
Because the physical nature of stellar activity cycles appears
predominantly similar to that of the solar cycle, it is natural to
consider the relation between toroidal and poloidal magnetic fields
in a wider stellar perspective. The observational identifications of
toroidal and poloidal stellar magnetic components are then, however, even
more indirect than those for the Sun. Suitable observational results
concerning the relation between toroidal and poloidal magnetic
components are obviously desirable to clarify the general situation;
the recent paper by Petit et al. (2008) seems to provide some such
information. In a study of solar-like dwarfs, Petit et al. (2008)
estimate that large-scale surface toroidal fields become strong for rotational
periods less than about
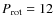 d, i.e. for
d, i.e. for
![]() .
They consider the phenomenon as a
bifurcation between regimes for slowly rotating stars, where the
surface magnetic field is presumably predominantly
poloidal, and rapidly rotating
stars where the surface toroidal component becomes substantial.
.
They consider the phenomenon as a
bifurcation between regimes for slowly rotating stars, where the
surface magnetic field is presumably predominantly
poloidal, and rapidly rotating
stars where the surface toroidal component becomes substantial.
Our aim here is to interpret this observational finding in the context of stellar dynamo theory. Such an interpretation is far from straightforward.
We can envisage, and discuss below, three broad possibilities; that the conventional surface boundary condition of the magnetic field needs modification (see, e.g., Moss 1977, in a rather different context), that there is a bifurcation in dynamo properties as the rotation rate (and thus dynamo number) increases, due solely to a reorganization of the dynamo (e.g. Brandenburg et al. 1989; Jennings & Weiss 1991), or that the increase in surface toroidal field is a consequence of a change of the underlying internal hydrodynamics. These possibilities are discussed in more detail in Sects. 4.1-4.3 respectively. There is also the possibility that the observed surface toroidal fields might be related to coronal fields with a systematic orientation, but even so their appearance at periods of about 12 d still needs explanation, and plausibly could still be associated with stronger interior toroidal fields, as discussed here. Our general conclusion, perhaps more important than the discussion of any particular dynamo model, is that the bifurcation suggested by Petit et al. has the potential to be very informative when confronting stellar dynamo theories with stellar activity observations.
2 Background
Observations of solar-type stars suggest that
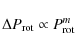 |
(1) |
where
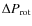 is the observed variation of rotation rate
over the surface (not extending above mid-latitudes) and
is the observed variation of rotation rate
over the surface (not extending above mid-latitudes) and
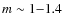 .
Thus
.
Thus
where
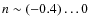 ,
and
,
and
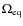 is the
equatorial rotation rate.
is the
equatorial rotation rate.
At the same time a number of observational studies are indicating
the presence of large-scale toroidal fields at the surfaces of
late-type stars, and Petit et al. (2008) in a study of solar-like
stars suggest the existence of a ``threshold'' for
their appearance around
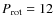 d. Conventional dynamo
models usually take as a boundary condition
d. Conventional dynamo
models usually take as a boundary condition
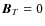 at the
stellar surface, matching the interior field to a vacuum
external field (but see Covas et al. 2005). There appear to be three
immediate possible theoretical explanations of the appearance of
strong surface toroidal field. It is possible that the zero boundary
condition on the surface toroidal field is inappropriate, and the
interior field should be fitted to a more general external force-free
field - this possibility attracted attention in the 1970 s in the
context of CP star modelling (e.g. Milsom & Wright 1976; Moss
1977). An alternative is that there is a bifurcation in the field
structure as the rotation period decreases, leading to a stronger
sub-surface toroidal field which becomes unstable and erupts through
the surface. A third possibility is that the underlying stellar
rotation law changes from a quasi-solar form, appropriate to
slower rotators, to a quasi-cylindrical form at higher rotation
rates, also leading to a sudden increase in sub-surface toroidal
field strength. We study all the above possibilities in the
framework of a conventional mean-field dynamo model in a stellar
convective shell. Note that we thus only discuss the large-scale
magnetic field.
at the
stellar surface, matching the interior field to a vacuum
external field (but see Covas et al. 2005). There appear to be three
immediate possible theoretical explanations of the appearance of
strong surface toroidal field. It is possible that the zero boundary
condition on the surface toroidal field is inappropriate, and the
interior field should be fitted to a more general external force-free
field - this possibility attracted attention in the 1970 s in the
context of CP star modelling (e.g. Milsom & Wright 1976; Moss
1977). An alternative is that there is a bifurcation in the field
structure as the rotation period decreases, leading to a stronger
sub-surface toroidal field which becomes unstable and erupts through
the surface. A third possibility is that the underlying stellar
rotation law changes from a quasi-solar form, appropriate to
slower rotators, to a quasi-cylindrical form at higher rotation
rates, also leading to a sudden increase in sub-surface toroidal
field strength. We study all the above possibilities in the
framework of a conventional mean-field dynamo model in a stellar
convective shell. Note that we thus only discuss the large-scale
magnetic field.
![\begin{figure}
\par\begin{tabular}{ll}
(a)\includegraphics[width=3.5cm]{solar.eps} (b)\includegraphics[width=3.5cm]{cyl.eps}\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/15/aa11426-08/Timg12.png) |
Figure 1: Equally spaced isorotation contours for a) the solar-like rotation law; b) the quasi-cylindrical rotation law. See text for details. |
| Open with DEXTER | |
3 Rotation laws
If we take standard
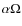 dynamo theory,
then
dynamo theory,
then
![]() and
and
 .
We can construct a series of ``solar type''
dynamo models, with the convection zone occupying approximately the
outer 30% by radius of the star, and
.
We can construct a series of ``solar type''
dynamo models, with the convection zone occupying approximately the
outer 30% by radius of the star, and 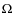 increasing from
increasing from
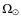 .
Taking a ``solar-like'' surface rotation law of the
form
.
Taking a ``solar-like'' surface rotation law of the
form
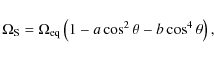
where
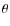 is polar angle and ``solar'' values are
a=0.126, b=0.159,
(cf. Tassoul 1978) we construct a plausible extrapolation
between the surface r=R and
the base of the overshoot region at r=r0R of the form
is polar angle and ``solar'' values are
a=0.126, b=0.159,
(cf. Tassoul 1978) we construct a plausible extrapolation
between the surface r=R and
the base of the overshoot region at r=r0R of the form
Here
 is taken as
is taken as 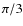 ,
and corresponds to the polar angle
at which the surface angular velocity is that of the base of the
tachocline, and
f(r) is a function that goes smoothly from unity at r=r0R to
zero at
,
and corresponds to the polar angle
at which the surface angular velocity is that of the base of the
tachocline, and
f(r) is a function that goes smoothly from unity at r=r0R to
zero at
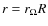 .
We take r0=0.64,
.
We take r0=0.64,
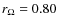 and
and
 .
Isorotation contours are shown in Fig. 1a.
Thus
.
Isorotation contours are shown in Fig. 1a.
Thus
This value of
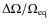 at
at
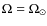 is used to determine
is used to determine
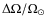 for all
for all
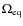 with both
n=-0.4 and n=0, using (2). Although this apparently
gives values that are too large compared with some observations we
note (i) the Sun is the only really well-determined case; (ii) non-solar
with both
n=-0.4 and n=0, using (2). Although this apparently
gives values that are too large compared with some observations we
note (i) the Sun is the only really well-determined case; (ii) non-solar
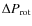 values are estimated from a limited
range of latitudes, not extending close to the poles, and so
probably underestimate
values are estimated from a limited
range of latitudes, not extending close to the poles, and so
probably underestimate
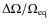 .
The stars
which really seem to have very small
.
The stars
which really seem to have very small
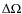 values are very
rapid rotators, and so outside of the range of periods of immediate
interest. In any case, if we have over-estimated
values are very
rapid rotators, and so outside of the range of periods of immediate
interest. In any case, if we have over-estimated
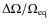 ,
then we have done so uniformly
across the range of rotation periods, and any differential effects
we observe should be valid.
,
then we have done so uniformly
across the range of rotation periods, and any differential effects
we observe should be valid.
For more rapid rotation we can expect the rotation law to be quasi-cylindrical,
and so adopt as an empirical law (cf. Covas et al. 2005)
where
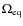 is the equatorial angular velocity and, rather
arbitrarily, d=0.05,
is the equatorial angular velocity and, rather
arbitrarily, d=0.05,
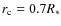 .
Then
.
Then
4 Results
4.1 Modification of surface boundary condition
We first summarize the general theory of toroidal fields in very
low density domains in the context of large-scale stellar
magnetic fields. This follows quite closely
the discussion in Raadu (1971), Milsom & Wright (1976), Moss (1977).
When modelling stellar magnetic fields it is necessary to ensure that the
field in the interior joins smoothly onto a force-free field in the
external, very low density, region. Splitting the magnetic field into
poloidal and toroidal parts,
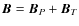 ,
the Lorentz
force can be written as
,
the Lorentz
force can be written as
Restricting consideration to axisymmetric fields, the last term is identically zero, the first two are poloidal vectors and the third is toroidal. In this case
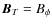 .
.
The condition
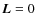 can be satisfied by setting
can be satisfied by setting
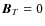 and
and
 ;
this provides the
usual boundary condition on the interior field at r=R.
Configurations with
;
this provides the
usual boundary condition on the interior field at r=R.
Configurations with
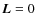 and
and
 are
also possible. Then a necessary condition is that
are
also possible. Then a necessary condition is that
![]() ,
which is the torque-free condition. If
,
which is the torque-free condition. If 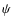 is the ``streamfunction'' for
the poloidal field (so
is the ``streamfunction'' for
the poloidal field (so
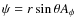 ,
where
,
where  is the toroidal
component of the vector potential,
is the toroidal
component of the vector potential,
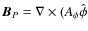 ),
so that
),
so that
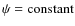 on fieldlines of poloidal field),
then
on fieldlines of poloidal field),
then
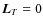 implies
implies
where F is an arbitrary function (e.g. Lüst & Schlüter 1954). For example, Raadu (1971) showed that if
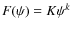 ,
then
k>2 for satisfactory behaviour at large distances. Thus the boundary
condition
,
then
k>2 for satisfactory behaviour at large distances. Thus the boundary
condition
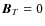 at r=R could be replaced by (7) -
of course the vacuum condition on the poloidal field would also need amendment
to give
at r=R could be replaced by (7) -
of course the vacuum condition on the poloidal field would also need amendment
to give
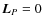 with
with
 .
Moss (1977) constructed models with steady fields
relevant to magnetic CP stars with such boundary
conditions, by arbitrarily specifying
.
Moss (1977) constructed models with steady fields
relevant to magnetic CP stars with such boundary
conditions, by arbitrarily specifying  and solving the equation
and solving the equation
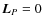 explicitly in r>R.
explicitly in r>R.
| |
Figure 2:
The dependence of |
| Open with DEXTER | |
This sort of formalism appears to work reasonably well when investigating
the time independent field structures of the CP stars, but encounters
difficulties when considering oscillatory dynamo fields -
there are difficult physical issues
connected with the properties of a time-varying external toroidal field
extending to large distances.
Moreover, in the case being discussed,
there is a direct link between toroidal and poloidal field components
via the alpha term in the dynamo equation. For example, a
dipole-like dynamo field (odd parity) has 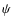 an even function with respect
to the equator, whereas
an even function with respect
to the equator, whereas 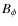 is odd (given that
is odd (given that 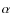 is
antisymmetric). But then any plausible
is
antisymmetric). But then any plausible  in (7)
insists that
in (7)
insists that 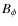 be an even function, in contradiction to the
assumption of an odd parity field structure. It is, of course,
quite implausible that the very low density environs of a late-type
star can alter significantly the gross structure of the internal
magnetic field (``the tail does not wag the dog''). We conclude that
the analysis is incomplete.
be an even function, in contradiction to the
assumption of an odd parity field structure. It is, of course,
quite implausible that the very low density environs of a late-type
star can alter significantly the gross structure of the internal
magnetic field (``the tail does not wag the dog''). We conclude that
the analysis is incomplete.
Putting all this on one side, the pragmatic question here is whether use of boundary condition such as (7) with the corresponding amendment to the poloidal field condition would change significantly the dependence of surface toroidal field on rotation rate. Very limited and approximate numerical experimentation (ignoring the modification to the poloidal boundary condition) did not support any strong effect, and a priori it is difficult to think of a strong physical argument that this would happen. Thus we did not pursue the matter further.
In summary, while it is clear that the surface boundary condition
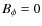 may be inappropriate, rigorous implementation of a more
general boundary condition in the context of an oscillatory dynamo
generated field requires resolution of difficult issues, which we
have not pursued. Our intuition is that these issues may not be
directly relevant to the problem addressed in this paper, but of
course we cannot rule out such a possibility.
may be inappropriate, rigorous implementation of a more
general boundary condition in the context of an oscillatory dynamo
generated field requires resolution of difficult issues, which we
have not pursued. Our intuition is that these issues may not be
directly relevant to the problem addressed in this paper, but of
course we cannot rule out such a possibility.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{en1.eps} %
\end{figure}](/articles/aa/full_html/2009/15/aa11426-08/Timg56.png) |
Figure 3: Dependence of measures of toroidal energy on rotation rate with fixed parity P=-1 for n=0. Asterisks denote results with the solar-like rotation law (3), diamonds those with the quasi-cylindrical law (4). |
| Open with DEXTER | |
4.2 Bifurcation due to more intensive dynamo action
We use the mean field dynamo model of Covas et al. (2005), implementing a naive
alpha-quenching nonlinearity rather than the feedback of the Lorentz force on
the differential rotation as used there. We write
![]() ,
where
,
where
 is given in Fig. 2.
The turbulent diffusivity
is given in Fig. 2.
The turbulent diffusivity 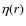 is taken as a constant,
is taken as a constant,  ,
except in
fractional radii
,
except in
fractional radii
![]() ,
where it changes smoothly so that
,
where it changes smoothly so that
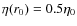 .
We start with a ``solar'' model that is about 20% supercritical.
Taking
.
We start with a ``solar'' model that is about 20% supercritical.
Taking
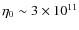 cm2 s-1 gives the dynamo number
cm2 s-1 gives the dynamo number
![]() .
The marginal value of
.
The marginal value of
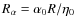 is then about -3.2,
and so we take
is then about -3.2,
and so we take
 for this baseline model.
Values of
for this baseline model.
Values of
 for larger values of
for larger values of
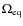 are determined by scaling from these values.
For each model we calculate the energies in the poloidal and toroidal
components of the (axisymmetric) magnetic field in the entire dynamo-active
region, the energies in the shell
are determined by scaling from these values.
For each model we calculate the energies in the poloidal and toroidal
components of the (axisymmetric) magnetic field in the entire dynamo-active
region, the energies in the shell
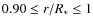 ,
and the energies in the immediately sub-surface region,
,
and the energies in the immediately sub-surface region,
![]() ,
respectively
,
respectively
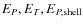 ,
,
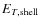 ,
,
 .
Specifically calculations were performed for the solar-like rotation
law for
.
Specifically calculations were performed for the solar-like rotation
law for
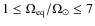 ,
and for the quasi-cylindrical
rotation law with
,
and for the quasi-cylindrical
rotation law with
![]() ,
for both n=-0.4 and n=0.
,
for both n=-0.4 and n=0.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{en2.eps} %
\end{figure}](/articles/aa/full_html/2009/15/aa11426-08/Timg75.png) |
Figure 4: Dependence of measures of toroidal energy on rotation rate with fixed parity P=-1 for n=-0.4. Notation is as in Fig. 3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{en3.eps} %
\end{figure}](/articles/aa/full_html/2009/15/aa11426-08/Timg76.png) |
Figure 5: Dependence of measures of toroidal energy on rotation rate with free parity for n=-0.4. Notation is as in Fig. 3. |
| Open with DEXTER | |
When we examine results for a fixed rotation law (i.e. only diamonds or
only asterisks in the figures), we see no evidence for a sudden bifurcation,
e.g. to a branch with markedly higher energies, as the rotation speed
increases. The only exception is in Fig. 3 (rotation law (3))
at
 .
However the magnetic fields of
the models with
.
However the magnetic fields of
the models with
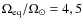 are steady, and so irrelevant to our investigation.
are steady, and so irrelevant to our investigation.
Table 1:
Mean parity versus rotation rate for models with solar-like
rotation-law and
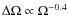 .
All models are
singly periodic.
.
All models are
singly periodic.
4.3 Transition from one rotation law to the other
If we now consider the results for the two rotation laws
together,
the graphs of
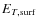 for both n=0 and
n=-0.4 show a displacement by a factor of about 4 at
for both n=0 and
n=-0.4 show a displacement by a factor of about 4 at
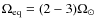 ,
and there is a similar, smaller, discontinuity in the graphs for
,
and there is a similar, smaller, discontinuity in the graphs for
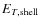 ,
see Figs. 3 and 4.
The other measures of magnetic energy are almost continuous
when switching from one rotation law to the other.
,
see Figs. 3 and 4.
The other measures of magnetic energy are almost continuous
when switching from one rotation law to the other.
Thus Figs. 3-5 give a
hint that the bifurcation under
discussion can be associated with a transition from a solar-like
rotation law with approximately radial contours through most
of the convection zone to a quasi-cylindrical law. Of course in ``reality'' a
gradual transition from a rotation law appropriate to slow rotators
to a rapid-rotator law could be expected. However, unless the
transition is over a wide range of rotation speeds, the above
treatment should be adequate to illustrate the behaviour of field
energies as
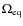 increases. In principle, it would be
trivial to compose a synthetic rotation law that was solar-like
for say
increases. In principle, it would be
trivial to compose a synthetic rotation law that was solar-like
for say
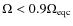 and quasi-cylindrical for
and quasi-cylindrical for
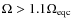 ,
where
,
where
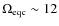 d,
with a smooth transition between. Then our results presented
in Sect. 4.2 would be valid
outside of this transition range, and would suggest a significant jump in
toroidal field, especially in the measures
d,
with a smooth transition between. Then our results presented
in Sect. 4.2 would be valid
outside of this transition range, and would suggest a significant jump in
toroidal field, especially in the measures
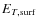 and
and
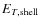 ,
as the rotation law changes.
,
as the rotation law changes.
5 Discussion
Our results presented in Figs. 3-5 show that there is no evidence for marked bifurcations in magnetic energy for given hydrodynamic flows that do not change with rotation rate - i.e. the relations defined by the asterisks and diamonds separately do not show any sudden changes of slope (except for the two most rapidly rotating models of Fig. 3 with the solar-like rotation law, where there has been a bifurcation from oscillatory to (physically irrelevant) steady solutions).
On the other hand there is a distinct jump in the large-scale toroidal energy
between the relations for solar-like and quasi-cylindrical
rotational laws. If we believe that these rotation laws are
more-or-less appropriate physically, then we have a possibility of
identifying the origin of the observed appearance of large-scale surface
toroidal fields around
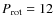 d, namely that it is a
result of a change in the internal azimuthal flows, as the
Taylor-Proudman constraint becomes important at shorter rotational
periods. We realise that our conclusions may be rather model
dependent, but would stress in conclusion our belief that
observations such as those of Petit et al. (2008) have considerable
potential for illuminating and discriminating between
various mechanisms for magnetic field generation.
d, namely that it is a
result of a change in the internal azimuthal flows, as the
Taylor-Proudman constraint becomes important at shorter rotational
periods. We realise that our conclusions may be rather model
dependent, but would stress in conclusion our belief that
observations such as those of Petit et al. (2008) have considerable
potential for illuminating and discriminating between
various mechanisms for magnetic field generation.
Acknowledgements
D.S. is grateful to financial support from RFBR under grant 07-02-00127a. We thank the referee, A. Brandenburg, for his constructive comments.
References
- Brandenburg, A., Krause, F., Meinel, R., Moss, D., & Tuominen, I. 1989, A&A, 213, 411 [NASA ADS] (In the text)
- Covas, E., Moss, D., & Tavakol, R. 2005, A&A, 429, 657 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jennings, R. L., & Weiss, N. O. 1991, MNRAS, 252, 249 [NASA ADS] (In the text)
- Lüst, R., & Schlüter, A. 1954, Z. Astrophys., 34, 263 [NASA ADS] (In the text)
- Milsom, F., & Wright, G. A. 1976, MNRAS, 174, 307 [NASA ADS] (In the text)
- Moss, D. 1977, MNRAS, 178, 51 [NASA ADS] (In the text)
- Obridko, V. N., Sokoloff, D. D., Kuzanyan, K. M., Shelting, B. D., & Zakharov, V. G. 2006, MNRAS, 365, 827 [NASA ADS] [CrossRef] (In the text)
- Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] (In the text)
- Tassoul, J.-L. 1978, Theory of Rotating Stars (Princeton, N.J.: Princeton Univ. Press) (In the text)
- Raadu, M. 1971, Ap&SS, 14, 464 [NASA ADS] [CrossRef] (In the text)
All Tables
Table 1:
Mean parity versus rotation rate for models with solar-like
rotation-law and
![]() .
All models are
singly periodic.
.
All models are
singly periodic.
All Figures
![\begin{figure}
\par\begin{tabular}{ll}
(a)\includegraphics[width=3.5cm]{solar.eps} (b)\includegraphics[width=3.5cm]{cyl.eps}\\
\end{tabular}
\end{figure}](/articles/aa/full_html/2009/15/aa11426-08/Timg12.png) |
Figure 1: Equally spaced isorotation contours for a) the solar-like rotation law; b) the quasi-cylindrical rotation law. See text for details. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
The dependence of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{en1.eps} %
\end{figure}](/articles/aa/full_html/2009/15/aa11426-08/Timg56.png) |
Figure 3: Dependence of measures of toroidal energy on rotation rate with fixed parity P=-1 for n=0. Asterisks denote results with the solar-like rotation law (3), diamonds those with the quasi-cylindrical law (4). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{en2.eps} %
\end{figure}](/articles/aa/full_html/2009/15/aa11426-08/Timg75.png) |
Figure 4: Dependence of measures of toroidal energy on rotation rate with fixed parity P=-1 for n=-0.4. Notation is as in Fig. 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{en3.eps} %
\end{figure}](/articles/aa/full_html/2009/15/aa11426-08/Timg76.png) |
Figure 5: Dependence of measures of toroidal energy on rotation rate with free parity for n=-0.4. Notation is as in Fig. 3. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.