| Issue |
A&A
Volume 497, Number 3, April III 2009
|
|
|---|---|---|
| Page(s) | 755 - 771 | |
| Section | Galactic structure, stellar clusters, and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200810870 | |
| Published online | 18 February 2009 | |
Multiple stellar populations in Magellanic Cloud clusters![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
I. An ordinary feature for intermediate age globulars in the LMC?
A. P. Milone1 - L. R. Bedin2 - G. Piotto1 - J. Anderson2
1 - Dipartimento di Astronomia, Università di
Padova, Vicolo dell'Osservatorio 3, 35122 Padova, Italy
2 -
Space Telescope Science Institute, 3700 San Martin Drive,
Baltimore, MD 21218, USA
Received 28 August 2008 / Accepted 14 October 2008
Abstract
Context. The discovery of multiple main sequences (MS) in the massive clusters NGC 2808 and Omega Centauri, along with multiple subgiant branches in NGC 1851 and NGC 6388 has challenged the long-held paradigm that globular clusters consist of simple stellar populations. This evolving picture has been further complicated by recent photometric studies of the Large Magellanic Cloud (LMC) intermediate-age clusters, where the main sequence turn-off (MSTO) was found to be bimodal (NGC 1806 and NGC 1846) or broadened (NGC 1783 and NGC 2173).
Aims. We undertook a study of archival HST images of Large and Small Magellanic Cloud clusters with the aim of measuring the frequency of clusters with evidence of multiple or prolonged star formation events and determining their main properties. We found useful images for 53 clusters that cover a wide range of ages. In this paper, we analyse the color-magnitude diagrams (CMD) of sixteen intermediate-age ( 1-3 Gyr) LMC clusters.
1-3 Gyr) LMC clusters.
Methods. The data were reduced and the photometry corrected for differential reddening (where required). We find that eleven clusters show an anomalous spread (or split) in colour and magnitude around the MSTO, even though the other main features of the CMD (MS, red giant branch, asymptotic giant branch) are narrow and the horizontal branch (HB) red clump well defined. By using the CMD of the stars in regions that surround the cluster, we demonstrate that the observed feature is unequivocally associated to the clusters. We use artificial-star tests to demonstrate that the spread (or split) is not an artifact due to photometric errors or binaries.
Results. We confirm that two clusters (NGC 1806 and NGC 1846) clearly exhibit two distinct MSTOs and observe, for the first time, a double MSTO in NGC 1751. In these three clusters, the population corresponding to the brighter MSTO includes more than two-thirds of the cluster stellar population. We confirm the presence of multiple stellar populations in NGC 1783. Our photometry strongly suggests that the MSTO of this cluster is formed by two distinct branches. In seven clusters (ESO057-SC075, HODGE7, NGC 1852, NGC 1917, NGC 1987, NGC 2108, and NGC 2154), we observed an intrinsic broadening of the MSTO that may suggest that these clusters have experienced a prolonged period of star formation that spans a period between 150 and 250 Myr. The CMDs of IC 2146, NGC 1644, NGC 1652, NGC 1795, and NGC 1978 show no evidence of spread or bimodality within our photometric precision. In summary, 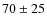 % of our sample are not consistent with the simple, single stellar population hypothesis.
% of our sample are not consistent with the simple, single stellar population hypothesis.
Key words: galaxies: star clusters - stars: Hertzprung-Russell (HR) and C-M diagram - Galaxy: globular clusters: general - galaxies: Magellanic Clouds
1 Introduction
Nearly all the clusters that have been resolved into individual stars exhibit a colour-magnitude diagram (CMD) consistent with the stars belonging to a single, simple stellar population. In recent years, however, thanks to the improving precision of instruments and techniques (mainly from space), the discovery of multiple populations of stars in stellar clusters is challenging this traditional picture and has led to new views on how clusters form and evolve.
Thus far, photometry has revealed multiple stellar populations in a few Galactic globular clusters (GGCs) i.e. Omega Centauri (Anderson 1997; Bedin et al. 2004; Piotto et al. 2005; Sollima et al. 2007, Villanova et al. 2007), NGC 2808 (D'Antona et al. 2005; Piotto et al. 2007), NGC 1851 (Milone et al. 2008a), and NGC 6388 (Piotto 2008), also in some intermediate-age Large Magellanic Cloud (LMC) clusters (Bertelli et al. 2003; Mackey & Broby Nielsen 2007 [M07]; Mackey et al. 2008 [M08]) and in the Small Magellanic Cloud (SMC) cluster NGC 419 (Glatt et al. 2008a). Each of the above clusters exhibits a different pattern of age spread and/or chemical enrichment. It is clear that the star-formation history differs from cluster to cluster (see Piotto 2008, for a review).
There is additional photometric evidence that other clusters exhibit
some kind of population multiplicity. Marino et al. (2008) find
photometric evidence of two distinct stellar populations among the
red giant branch (RGB) stars of M4. Yong et al. (2008) find
abundance variations in NGC 6752 that correlate with the Str
 mgren
cy index and show eight other clusters that present a similar cyspread in their giant branches.
mgren
cy index and show eight other clusters that present a similar cyspread in their giant branches.
In addition, many GGCs, including those with no photometric evidence
for multiple populations, exhibit large star-to-star variations in
their chemical abundances (see Gratton et al. 2004, for a review).
Almost all GGCs have homogeneous Fe-peak-element abundances (with the
only exception being Omega Centauri, hereafter 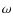 Cen), but they
show a significant dispersion in CNO, Na, Mg, Al, and s-process
elements. The pattern of chemical abundances in GGCs must be
primordial as it is observed not only among RGB or asymptotic giant
branch (AGB) stars, but also among the sub giant branch (SGB), and
most importantly among unevolved stars on the MS
(Gratton et al. 2001, 2004). The presence of a well-defined pattern
among Na, O, Mg, and Al suggests that most of the GGCs may have hosted
multiple episodes of star formation separated by a few hundred Myr
(D'Antona & Caloi 2008).
Cen), but they
show a significant dispersion in CNO, Na, Mg, Al, and s-process
elements. The pattern of chemical abundances in GGCs must be
primordial as it is observed not only among RGB or asymptotic giant
branch (AGB) stars, but also among the sub giant branch (SGB), and
most importantly among unevolved stars on the MS
(Gratton et al. 2001, 2004). The presence of a well-defined pattern
among Na, O, Mg, and Al suggests that most of the GGCs may have hosted
multiple episodes of star formation separated by a few hundred Myr
(D'Antona & Caloi 2008).
Unfortunately, in an old population, such a difference in age corresponds to a difference of a few hundredths of a magnitude at the level of the MS turn-off (TO) and SGB. At the moment, it is not possible to firmly establish a spread in a cluster's MSTO with this amplitude, given the presence of differential reddening and difficulties in doing systematically accurate crowded-field photometry at this level of precision.
The families of young and intermediate-age massive clusters that populate the Large and the Small Magellanic Clouds offer us precious opportunities for photometrically searching for multiple stellar populations because, in the CMD of a 1-3 Gyr old cluster, an age interval of 200-300 Myr corresponds to a magnitude difference of a few tenths of a magnitude. Two populations with such a difference could be distinguished easily even at the distance of the Magellanic Clouds (MC).
Indeed, recent photometric studies of LMC clusters have demonstrated
that the presence of multiple stellar populations is not a peculiarity
of the most massive Galactic GGCs. Bertelli et al. (2003)
compare a CMD of NGC 2173 from FORS/VLT data with Padova models and
suggest for this LMC cluster a prolonged star-formation episode
spanning a period of about 300 Myr. In a recent paper, M08 find
that the main-sequence turn off (MSTO) for NGC 1783 reveals a much
spread in colour wider than can be explained by photometric errors.
Both M07 and M08 also reveal the presence of a double MSTO in the rich
intermediate-age clusters NGC 1846 and NGC 1806 of the LMC, and
suggest that their CMDs unveil two populations with
an age difference of  300 Myr.
300 Myr.
Driven by these results on
Galactic and LMC clusters, we undertook an analysis of archival
HST images of LMC and SMC clusters with the purpose of measuring the
frequency of clusters with evidence of multiple or prolonged star
formation. The clusters that have been analysed cover a wide range of
ages, from  106 to
106 to  1010 yr. Since the search of
multiple populations is carried out through analysis of CMDs,
the study of clusters with different ages requires a different sort of
analysis.
1010 yr. Since the search of
multiple populations is carried out through analysis of CMDs,
the study of clusters with different ages requires a different sort of
analysis.
In this paper, which is the first of a series, we show our entire
sample of ACS/WFC CMDs for forty-seven LMC and SMC stellar clusters
and present a detailed study of sixteen intermediate-age LMC clusters
(between  1 and
1 and  3 Gyr). The paper is organised as follow.
Section 2 describes the data and the data reduction
techniques. In Sect. 3 we present the CMDs of the
sixteen intermediate-age clusters. In Sect. 4, we confirm the split
of the MSTO of NGC 1806 and NGC 1846 and observe, for the first time,
two distinct MSTOs in NGC 1751. We analyse the CMD of these
clusters in detail and measure the fraction of stars belonging to each of their
MSTO populations. We confirm the presence of multiple stellar
populations in NGC 1783 and suggest that the MSTO of this cluster
should be formed by two distinct branches. In Sect. 5 we note an
anomalous spread around the MSTO of seven clusters: ESO057-SC075,
HODGE 7, NGC 1852, NGC 1917, NGC 1987, NGC 2108, and NGC 2154. In
Sect. 6 we demonstrate that the observed spread in the MSTO region
of these clusters must be real, since it cannot stern from to differential
reddening, field contamination, photometric errors, or binary stars. In
Sect. 7 we determine the cluster ages and the age
differences among different stellar populations in the same cluster
through isochrone fitting. Finally, Sect. 8
includes a short summary of our results.
3 Gyr). The paper is organised as follow.
Section 2 describes the data and the data reduction
techniques. In Sect. 3 we present the CMDs of the
sixteen intermediate-age clusters. In Sect. 4, we confirm the split
of the MSTO of NGC 1806 and NGC 1846 and observe, for the first time,
two distinct MSTOs in NGC 1751. We analyse the CMD of these
clusters in detail and measure the fraction of stars belonging to each of their
MSTO populations. We confirm the presence of multiple stellar
populations in NGC 1783 and suggest that the MSTO of this cluster
should be formed by two distinct branches. In Sect. 5 we note an
anomalous spread around the MSTO of seven clusters: ESO057-SC075,
HODGE 7, NGC 1852, NGC 1917, NGC 1987, NGC 2108, and NGC 2154. In
Sect. 6 we demonstrate that the observed spread in the MSTO region
of these clusters must be real, since it cannot stern from to differential
reddening, field contamination, photometric errors, or binary stars. In
Sect. 7 we determine the cluster ages and the age
differences among different stellar populations in the same cluster
through isochrone fitting. Finally, Sect. 8
includes a short summary of our results.
2 Observation and data reduction
To investigate the presence of multiple stellar populations in Magellanic Cloud clusters we searched the MAST STScI-archive for HST images collected with the Wide Field Channel (WFC) of the Advanced Camera for Surveys (hereafter ACS/WFC). We found useful images for 53 clusters from GO 9891 (PI: G. F. Gilmore ), GO 10395 (PI: J. S. Gallagher) and GO 10595 (PI: P. Goudfrooij). The result of this search is presented in Table 1 for 47 clusters from GO 9891 and GO 10595, while the GO 10396 data set described in Table 1 of Glatt et al. (2008b) (which includes six SMC clusters) will be used in a future paper focused on SMC.
The photometric reduction of the ACS/WFC data was carried out using the software presented and described in detail in Anderson et al. (2008). It consists in a package that analyses all the exposures of each cluster simultaneously to generate a single list of stars for each field. Stars are measured independently in each image by using the best available PSF models from Anderson & King (2006).
This routine was designed to work well in both crowded and uncrowded fields, and it is able to detect almost every star that can be detected by eye. It takes advantage of the many independent dithered pointings of each scene and the knowledge of the PSF to avoid including artifacts in the list. Calibration of ACS photometry into the Vega-mag system was performed following recipes in Bedin et al. (2005) and using the zero points given in Sirianni et al. (2005).
![\begin{figure}
\par\includegraphics[width=8cm,height=9.5cm,clip]{0870f1-NEW.eps} %\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg12.png) |
Figure 1:
Diagnostic parameters used to select the stars with
the best photometry are plotted as a function of
|
| Open with DEXTER | |
2.1 Selection of the star sample
Stars can be poorly measured for several reasons: crowding by nearby neighbours, contamination by cosmic-rays (CRs), or image artifacts such as hot pixels or diffraction spikes. The goal of the present work is to clearly identify multi-populations. For this purpose we need to select the best-measured stars in the field (i.e., those with the lowest random and systematic errors), but we also need to have a large enough statistical sample to be able to identify secondary sequences that may have many fewer members than the primary ones.
The software presented by Anderson et al. (2008) provides very valuable tools for reaching this goal. In addition to the stellar fluxes and positions it provides a number of parameters that can be used as diagnostics of the reliability of photometric measurements. Specifically, these are,
- the rms of the magnitudes measured in different exposures
(rms
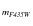 ,
rms
,
rms
 ,
and rms
,
and rms
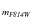 ,
available only for clusters with more than one exposure in the
same filter, cf. Table 1);
,
available only for clusters with more than one exposure in the
same filter, cf. Table 1);
- the rms of the positions measured in
different exposures transformed in a common distortion-free
reference frames (rms
 ,
and rms
,
and rms );
);
- the residuals to the PSF fit for each star (
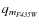 ,
,
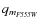 ,
and
,
and
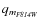 ;
what
Anderson et al. 2008
define as quality fit);
;
what
Anderson et al. 2008
define as quality fit);
- the ratio between the estimated flux of the star in a 0.5 arcsec
aperture, and the flux from neighbouring stars within the same
aperture (
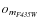 ,
,
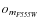 ,
and
,
and
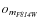 ,
again see Anderson et al. 2008, for details).
,
again see Anderson et al. 2008, for details).
In the five left hand panels of Fig. 1, we show the criteria
we used to select the sample of stars with the best
photometry in the F435W band for NGC 1806. The photometric system at
this stage is kept in instrumental magnitudes,
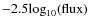 ,
where the flux is expressed in photo-electrons
recorded in the reference exposure.
,
where the flux is expressed in photo-electrons
recorded in the reference exposure.
We note a clear trend in the quality-fit and rms parameters as a
function of the magnitude due to the decreasing signal-to-noise ratio
(S/N). To select well-measured stars at different S/N we
adopted the following procedure.
We began by dividing all the stars into magnitude bins. The size of
each bin varied from one cluster to another depending on the number of
stars; for each of them, we computed the median rms (q) and the
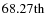 percentile (hereafter
percentile (hereafter 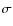 ). The median was
derived recursively: after each computation, all stars exceeding four
times
). The median was
derived recursively: after each computation, all stars exceeding four
times 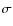 were provisionally rejected until the next iteration
and the median was recomputed. This procedure was repeated until two
subsequent measures of the median differ by less than the 1% of the
value.
were provisionally rejected until the next iteration
and the median was recomputed. This procedure was repeated until two
subsequent measures of the median differ by less than the 1% of the
value.
Finally, we arrived at the red line of Fig. 1 by adding
to the median of each bin N times 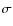 .
This gave us the red
circles, which we then fitted with a spline. All stars below the red
line in each plot were flagged as well-measured. The factor Nranges from 5 to 6, and was chosen to draw the
boundaries that follow the bulk of the distribution of each parameter
value.
.
This gave us the red
circles, which we then fitted with a spline. All stars below the red
line in each plot were flagged as well-measured. The factor Nranges from 5 to 6, and was chosen to draw the
boundaries that follow the bulk of the distribution of each parameter
value.
The neighbour-contamination parameters do not show a clear trend with
magnitude, so we simply flagged all the stars with
![]() as well-measured.
as well-measured.
Obviously, the rms of the magnitudes was not available in the case of clusters with only one image per band (HODGE 7, IC 2146, NGC 1644, NGC 1652, NGC 1795, NGC 1852, NGC 1917, NGC 1978, and NGC 2154). In such cases those selections were not applied. In the right panels of Fig. 1 we show the CMD of all the measured stars of NGC 1806 (top) and of stars that pass all the selection criteria (bottom).
2.2 Artificial-star tests
The artificial-star (AS) experiments used in this paper were run
following the procedures described in Anderson et al. (2008).
First of all, for each cluster, we produced an input list with about
105 stars located on the entire ACS field of view. It includes the
coordinates of the stars (
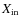 ,
,
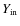 )
in the reference
frame, and the magnitudes in the F435W (or F555W) and
F814W bands
(
)
in the reference
frame, and the magnitudes in the F435W (or F555W) and
F814W bands
(
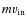 ,
,
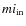 ). We generated the artificial stars
with a flat luminosity function in the F814W band and with
instrumental magnitudes from -5 to -14. We placed artificial
stars fainter than the MSTO on the MS ridge line that is determined as
described in Sect. 6.2.1 and added artificial stars
brighter than the MSTO along the isochrone that fits the observed
CMD best (see Sect. 7).
). We generated the artificial stars
with a flat luminosity function in the F814W band and with
instrumental magnitudes from -5 to -14. We placed artificial
stars fainter than the MSTO on the MS ridge line that is determined as
described in Sect. 6.2.1 and added artificial stars
brighter than the MSTO along the isochrone that fits the observed
CMD best (see Sect. 7).
The program described in Anderson et al. (2008) allows artificial-star tests to be performed for one star at a time and entirely in software guaranteeing that artificial stars will never interfere with each other, no matter how many tests are done. Therefore it makes it very simple to do artificial star tests because it is not necessary to add an array of non-interfering stars on the images, reducing all the images each time. For each star in the input list, the routine adds the star to each exposure at the appropriate place with the appropriate flux, and measures the images in the same manner as real stars, producing the same output parameters as in Sect. 2.1. If the input and the output positions differ by less than 0.5 pixel and the fluxes differ by less than 0.75 mag, then the artificial star is considered as found.
Artificial stars played a crucial role in this analysis by allowing us to determine the completeness level of our sample and to measure the fraction of chance-superposition ``binaries''. The completeness depends on the crowding conditions, as well as on stellar luminosity. Our procedures account for both of these. Our goal in the AS tests is to probe how incompleteness and photometric errors vary with crowding or brightness. As a result, we generated a list of artificial stars that had colours that placed them on the average cluster sequence and positions drawn from the overall cluster radial distribution.
We divided the ACS/WFC field for each cluster into 5 concentric annuli
centred on the cluster centre, and within each annulus we examined
the AS results in eight magnitude bins, from -14 to -5. For each
of these 5 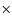 8 grid points, we then determined the average
completeness by taking the ratio of the recovered to input artificial
stars within that bin. This grid then allowed us to estimate the
completeness for any star at any position within the cluster. As an
example, the left panel of Fig. 2 shows the completeness as
a function of the instrumental
8 grid points, we then determined the average
completeness by taking the ratio of the recovered to input artificial
stars within that bin. This grid then allowed us to estimate the
completeness for any star at any position within the cluster. As an
example, the left panel of Fig. 2 shows the completeness as
a function of the instrumental
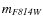 magnitude in each of
the five annuli used to divide the field of NGC 1806. Finally, we
interpolated the grid points and derived the completeness value
associated with each star. The right panel of Fig. 2 shows
the completeness contours in the radius versus
magnitude in each of
the five annuli used to divide the field of NGC 1806. Finally, we
interpolated the grid points and derived the completeness value
associated with each star. The right panel of Fig. 2 shows
the completeness contours in the radius versus
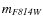 magnitude plane. Continuous lines correspond to completeness levels of 0.25, 0.50, and 0.75. Dotted lines indicate differences of completeness
of 0.05.
magnitude plane. Continuous lines correspond to completeness levels of 0.25, 0.50, and 0.75. Dotted lines indicate differences of completeness
of 0.05.
![\begin{figure}
\includegraphics[width=15.2cm,clip]{0870f2.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg33.png) |
Figure 2:
Left: completeness as a function of the
|
| Open with DEXTER | |
3 The cluster CMDs
In Fig. 3 we show the instrumental versus
versus
 1 to
1 to  3 Gyr). The other
clusters will be covered in forthcoming papers. All selected
intermediate age clusters are LMC members.
3 Gyr). The other
clusters will be covered in forthcoming papers. All selected
intermediate age clusters are LMC members.
![\begin{figure}
\par\includegraphics[width=\textwidth]{0870f3-NEW.eps} %\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg34.png) |
Figure 3:
Instrumental
|
| Open with DEXTER | |
Since most of the clusters of our sample cover a small portion of the ACS/WFC field of view, we can easily isolate a CMD that is representative of the field population surrounding the cluster by selecting the portion of the ACS/WFC image that is farthest from the cluster centre, so that the contamination of cluster members should be negligible and, in many cases, almost absent.
To minimize the fraction of field stars in the cluster CMD,
we selected two regions with the same area. The first region, which
below we call the ``cluster field'', is centred on the cluster and
includes the region with the highest density of cluster members (with
NGC 1978 the only exception, where we chose an annulus around the
cluster centre to exclude the crowded cluster core). The
second region is far enough from the cluster center that very few
cluster stars would be expected to be present there. We will call this
field ``reference field'' and its stars should be representative of the
typical population in front of and behind the cluster. Since cluster
stars in the vicinity of the MSTO are the main targets of the present
study, we defined the area of these regions such that the density of
stars within a magnitude from the TO, namely with
![]() ,
in the cluster field would be at
least a fixed number (N) of times that of the reference field. In
most cases we could set N=5, which would mean that, even without
field correction, we have at most a 20% contamination. An exception
is NGC 1917, which is projected upon a densely populated region of the
LMC. In this case we used N=3. For the most populated clusters
(IC 2146, NGC 1806, NGC 1846, and NGC 1978), we adopted N=10.
,
in the cluster field would be at
least a fixed number (N) of times that of the reference field. In
most cases we could set N=5, which would mean that, even without
field correction, we have at most a 20% contamination. An exception
is NGC 1917, which is projected upon a densely populated region of the
LMC. In this case we used N=3. For the most populated clusters
(IC 2146, NGC 1806, NGC 1846, and NGC 1978), we adopted N=10.
In Fig. 4, we compare the CMDs of the cluster and reference fields for the sixteen intermediate age clusters that have been studied in this paper.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f4.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg36.png) |
Figure 4: Comparison of the CMD of cluster and reference fields for the 16 selected intermediate-age clusters. |
| Open with DEXTER | |
 and populates
the evolved portions of the CMD. In Sect. 6.1
we use the CMDs of the reference field to decontaminate the CMD
of the cluster.
and populates
the evolved portions of the CMD. In Sect. 6.1
we use the CMDs of the reference field to decontaminate the CMD
of the cluster.
3.1 Differential reddening
It is well known that differential reddening causes a shift in all the CMD features parallel to the reddening line and tends to randomly broaden them. A quick look at the CMDs presented in this paper shows that most of the RGBs and AGBs are narrow and well defined, and that the HB red clump is compact. Moreover, we have divided the cluster field into many subregions (the exact number varies from one cluster to another, depending on the number of stars) and compared the CMDs of stars located in each of them. In most cases, we found no evidence of any offset among the CMDs, and so, any variations in reddening should be negligible.
Two exceptions to this reddening-free rule are NGC 1751 and NGC 2108. We show their CMD in Figs. 5 and 6. The confused shape of the HB red clumps and of other primary features suggests differential reddening. Since differential reddening acts along the direction of the reddening arrow shown at the lower left, sequences (such as the SGB) that are aligned perpendicular to the reddening line are most affected.
![\begin{figure}
\par\includegraphics[width=9.2cm]{0870f5.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg38.png) |
Figure 5: Comparison between the CMD of NGC 1751 before ( top panel) and after ( bottom panel) the correction for differential reddening. The arrow indicates the reddening direction. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=9.2cm]{0870f6.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg39.png) |
Figure 6: As in Fig. 5 for NGC 2108. |
| Open with DEXTER | |
For this reason, a search for a possible split or a spread around the MSTO requires an accurate correction of the effects produced by differential reddening on the observed CMD. To correct for differential reddening, we used the procedure described in Sarajedini et al. (2007). Briefly, we define the fiducial main sequence for the cluster and tabulate, with a grid of points across the field, how the observed stars in the vicinity of each grid point may systematically lie to the red or the blue of the fiducial sequence; this systematic colour offset is indicative of the local differential reddening.
In the lower panel of Fig. 5, we show the corrected CMD of
NGC 1751. It should be noted how, after the correction has been
applied, all the main features of the CMD become
narrower and clearly defined, confirming that most of the effects of
differential reddening have been removed. The improvement of the CMD
is particularly evident for the stars of the HB red clump; the tightness
along the reddening line of this clump means that
the spread (or split) we see in the MSTO cannot be due to differential
reddening. Figure 6 illustrates the effects of the
reddening correction in NGC 2108. The total amount of differential
reddening within the cluster region is
![]() for NGC 1751 and
for NGC 1751 and 
![]() for NGC 2108.
for NGC 2108.
The two clusters that suffer from sizable differential reddening are not at any particular angular distance from the centre of the LMC or with respect to the Milky Way, compared to the other fourteen clusters. They might just fall in some poorly known gas-dust complex structure, and/or with a limited spatial extension.
4 Clusters with a double MSTO: NGC 1806, NGC 1846, and NGC 1751
At least three clusters of our sample clearly show two distinct MSTOs: NGC 1846, NGC 1806, and NGC 1751. The split is evident in the CMDs of the cluster fields that are shown in Figs. 7-9, and is exalted by the Hess diagram in the inset. The presence of two, distinct TOs in NGC 1806 and NGC 1846 was discovered by M07 and M08, who also found no difference in the spatial distribution between the stars in the brighter and fainter MSTOs(hereafter bMSTO and fMSTO). ![\begin{figure}
\includegraphics[width=8.75 cm]{0870f7.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg42.png) |
Figure 7: CMD of NGC 1846. All detected sources in the inner field that successfully passed all the selection criteria have been plotted. In the inset we show the Hess diagram for the CMD region around the MSTO. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.75 cm]{0870f8.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg43.png) |
Figure 8: As in Fig. 7 for NGC 1806. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f9.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg44.png) |
Figure 9: As in Fig. 7 for NGC 1751. |
| Open with DEXTER | |
This procedure is illustrated in Fig. 10 for NGC 1806. We used the CMD of the cluster field, with foreground/background contamination removed as described in Sect. 6.1. We began by finding the isochrones that went through the two sequences and the giant branch (as will be described in detail in Sect. 7). These are the red and blue lines. We then defined by hand two pairs of reference points: P1,f and P2,f on the fMSTO isochrone and P1,b and P2,b on the bMSTO isochrone. The two pairs of points were chosen with the criterion of delimiting the region of the CMD where the split is more evident and were used to draw the grey lines in panel (a). Only stars contained in the region between these lines have been used for the following analysis.
In panel (b), we shifted and rotated the reference frame such that the new origin corresponds to P1,f and the abscissa goes from P1,b to P1,f. For simplicity, in the following, we refer to the abscissa and ordinate of this reference frame as ``colour'' and ``magnitude''. The red dashed line is a fiducial line through the region close to the fMSTO. We drew it by marking four points on the region close to the fMSTO, equally spaced in ``magnitude'' and drawing a line through them by means of a spline fit.
In panel (c) the ``colour'' of this line was subtracted from the colour of each star, and the ``magnitude'' of each star has been divided by the ``magnitude'' of a stars with the same ``colour'' that lies on the line that goes from P2,f to P2,b.
For the analysis that follows, we have divided the  ``magnitude'' range
into N bins. We used N=4 for NGC 1806 and NGC 1846 and N=2 for
the less populated NGC 1751. In each of them, we determined the
fraction of stars belonging to each MSTO as follows. Our aim was to
model the
``magnitude'' range
into N bins. We used N=4 for NGC 1806 and NGC 1846 and N=2 for
the less populated NGC 1751. In each of them, we determined the
fraction of stars belonging to each MSTO as follows. Our aim was to
model the  ``colour'' distribution by fitting the sum of two
partially overlapping Gaussians, but we need to reduce the influence
of outliers (such as stars with poor photometry, residual field stars,
and binaries). To this end, we did a preliminary fit of the Gaussians
using all available stars, then we rejected all the stars more
than two
``colour'' distribution by fitting the sum of two
partially overlapping Gaussians, but we need to reduce the influence
of outliers (such as stars with poor photometry, residual field stars,
and binaries). To this end, we did a preliminary fit of the Gaussians
using all available stars, then we rejected all the stars more
than two 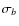 distant and less than 2
distant and less than 2 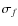 from the
fMSTO and repeated the fit (where the
from the
fMSTO and repeated the fit (where the 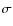 's are those of the best
fitting Gaussians in each
's are those of the best
fitting Gaussians in each 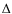 ``magnitude'' bin fitted to the fMSTO and
bMSTO respectively).
``magnitude'' bin fitted to the fMSTO and
bMSTO respectively).
The continuous vertical lines show the centres of the best-fitting
Gaussians in each 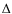 ``magnitude'' interval. The red dashed line
is located two
``magnitude'' interval. The red dashed line
is located two
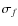 on the ``blue'' side of the fMSTO and the
blue line runs two
on the ``blue'' side of the fMSTO and the
blue line runs two
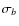 on the ``red'' side of the bMSTO.
on the ``red'' side of the bMSTO.
![\begin{figure}
\par\includegraphics[width=16.5cm, angle=0]{0870f10.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg47.png) |
Figure 10:
Procedure adopted to
measure the fraction of stars belonging to the bMSTO and fMSTO
in NGC 1806. Panel a) shows a zoom of the CMD from
Fig. 8 with the isochrones that best fits the
fMSTO and the bMSTO superimposed. The grey lines delimit the
portion of the CMD where the split is more evident. Only stars
from this region are used to measure the population ratio. In
Panel b) we shifted and rotated the reference frame of
Panel a). Red dashed line is the fiducial of the region around the
fMSTO. In Panel c) we plotted stars between the grey lines
but after the subtraction of the ``colour'' of the region around
the fMSTO fiducial from the ``colour'' of each star and the
division of the ``magnitude'' of each star by the ``magnitude'' of
the upper grey line. The four right bottom panels show the
|
| Open with DEXTER | |
It is important to notice here that, to each point (
P1,f(b),
P2,f(b)) that we have arbitrarely selected on the two isochrones
with the only purpose to disentangle the two SGBs, corresponds to a mass
(
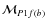 ,
,
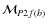 ). To obtain a more correct
measure of the fraction of stars in each of the two populations
(
). To obtain a more correct
measure of the fraction of stars in each of the two populations
(
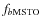 ,
,
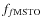 )
it must be noted that we are dealing with
two different mass intervals (
)
it must be noted that we are dealing with
two different mass intervals (
![]() )
and we have to compensate for two facts: first, more massive stars are
rarer, and second, more massive stars evolve faster.
)
and we have to compensate for two facts: first, more massive stars are
rarer, and second, more massive stars evolve faster.
We calculated the fraction of stars in each branch as,


where Ab and Af are the area of the Gaussians that best fit the bMSTO and the fMSTO, and
 the Salpeter (1955) IMF.
the Salpeter (1955) IMF.
We find that 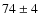 % of stars of NGC 1806 belong to the bMSTO and
% of stars of NGC 1806 belong to the bMSTO and
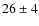 % to the fMSTO. In the case of NGC 1846, we have
% to the fMSTO. In the case of NGC 1846, we have
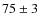 %
of stars in the bMSTO and
%
of stars in the bMSTO and 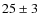 % in the fMSTO. Finally,
% in the fMSTO. Finally,
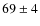 % of the NGC 1751 stars belong to the bMSTO and the
% of the NGC 1751 stars belong to the bMSTO and the
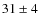 % to
the fMSTO. Interestingly enough, a similar population ratio
between the bright and the faint SGB ratios has been found in the
Galactic globular clusters NGC 1851 (Milone et al. 2008a) and
NGC 6388
(Piotto et al., in preparation). We note here that
D'Antona & Coloi (2008) predict
that more than 50% of the cluster stars must be coming from the
second (younger) population in their intermediate mass AGB ejecta
pollution scenario proposed to explain multiple populations in star
clusters.
% to
the fMSTO. Interestingly enough, a similar population ratio
between the bright and the faint SGB ratios has been found in the
Galactic globular clusters NGC 1851 (Milone et al. 2008a) and
NGC 6388
(Piotto et al., in preparation). We note here that
D'Antona & Coloi (2008) predict
that more than 50% of the cluster stars must be coming from the
second (younger) population in their intermediate mass AGB ejecta
pollution scenario proposed to explain multiple populations in star
clusters.
4.1 The (double?) MSTO of NGC 1783
A spread in colour around the MSTO of NGC 1783 was first noted by
Mucciarelli et al. (2007). Unfortunately their
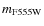 versus
versus
![]() CMD had low photometric accuracy,
because it was obtained from the GO 9891 images alone. Therefore,
they were unable to distinguish between the intrinsic spread in colour
and the broadening expected by photometric uncertainties. M08
obtained a CMD for this cluster from data with higher S/N (using both
GO 10595 and GO 9891 images) and demonstrated that NGC 1783 shows a
much wider spread in color than what would be expected by photometric
errors alone.
CMD had low photometric accuracy,
because it was obtained from the GO 9891 images alone. Therefore,
they were unable to distinguish between the intrinsic spread in colour
and the broadening expected by photometric uncertainties. M08
obtained a CMD for this cluster from data with higher S/N (using both
GO 10595 and GO 9891 images) and demonstrated that NGC 1783 shows a
much wider spread in color than what would be expected by photometric
errors alone.
Our CMD of NGC 1783 is shown in Fig. 11 and clearly confirms the anomalous spread around the MSTO. In addition, the Hess diagram in the inset reveals a split MSTO and strongly suggests that the apparent spread could be attributed to two distinct branches that are closely spaced and poorly resolved by the observations.
5 Possible evidence of prolonged star formation
The CMDs around the MSTO loci for the remaining twelve intermediate-age clusters that have been studied in this work are presented in Figs. 12-23. Unfortunately, being this an archive project, the photometric data set available for these twelve clusters is not homogeneous. One short and two deep images for each of the three filters: F435W, F555W, and F814W, were collected within program GO 10595, while one single deep image in both F555W and F814W bands were collected within the snap-shot program GO 9891. Only two clusters were observed by both programs (NGC 1987 and NGC 2108), one cluster (ESO057-SC075) only in GO-10595, and the remaining nine (HODGE 7, IC 2146, NGC 1644, NGC 1652, NGC 1795, NGC 1852, NGC 1917, NGC 1978, and NGC 2154) were observed within GO 9891 only (see Table 1 for more details).
We find that seven of these clusters show hints of an intrinsic spread around the MSTO: ESO057-SC075, HODGE 7, NGC 1852, NGC 1917, NGC 1987, NGC 2108, and NGC 2154. The CMDs of IC 2146, NGC 1644, NGC 1652, NGC 1795, and NGC 1978 show no evidence of such a spread and are all consistent with hosting stars with the same age and chemical composition, within our photometric precisions. When simulated CMDs are introduced, we will give a more objective criterion for distinguishing clusters with an intrinsic spread around the MSTO (at the end of Sect. 6.2.2).
It must be noted that, apart from the broadened MSTO region, the other primary features of the CMDs of these clusters (MS, RGB, and AGB) are narrow, and the HB red-clump is well-defined, thus the spread cannot be an artifact produced by differential reddening or variations in photometric zero points along the ACS field.
The limited statistic and photometric resolution do not allow us to establish whether these spreads are just unresolved splits -like those identified in the more populous clusters described in Sect. 4- or not.
In the following section, we show that the spread around the MSTO of the clusters mentioned above must be intrinsic. To do this, we demonstrate that the broadening we see cannot be explained by any combination of photometric errors, field-star contamination, or unresolved photometric binaries.
6 Does the spread MSTO reflect the presence of multiple stellar populations?
Globular-cluster systems with multiple populations manifest themselves
in many different photometric ways. In 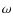 Cen we
(Anderson 1997; Bedin et al. 2004) detected a split of the MS, which can
only be explained by two stellar groups with different He content and
metallicity (Piotto et al. 2005), and also at least four distinct
SGBs (which may indicate age differences greater than 1 Gyr, see
Villanova et al. 2007, and references within). In NGC 2808 we
inferred the existence of three distinct stellar populations from the
three MSs (which is most easily explained by three groups
of stars with different helium content, see Piotto et al. 2007). In
the case of NGC 1851, two populations of stars are
inferred from the fact that the SGB splitting into two branches. This
feature can be explained either by two distinct bursts of star
formation with a time separation of about 1 Gyr or by two stellar
populations with distinct initial chemical composition and a much
smaller age difference (Milone et al. 2008a; Cassisi et al. 2008). A
split in the SGB has also been observed in NGC 6388 (Piotto 2008)
demonstrating that this massive GC hosts two distinct stellar groups.
In a spectro-photometric study of M4, Marino et al. (2008) detect a
bimodal RGBs, and demostrate that it is due to a bimodal distribution
of CN, Na, O, also indicating that this relatively-small cluster
contains multiple populations.
Cen we
(Anderson 1997; Bedin et al. 2004) detected a split of the MS, which can
only be explained by two stellar groups with different He content and
metallicity (Piotto et al. 2005), and also at least four distinct
SGBs (which may indicate age differences greater than 1 Gyr, see
Villanova et al. 2007, and references within). In NGC 2808 we
inferred the existence of three distinct stellar populations from the
three MSs (which is most easily explained by three groups
of stars with different helium content, see Piotto et al. 2007). In
the case of NGC 1851, two populations of stars are
inferred from the fact that the SGB splitting into two branches. This
feature can be explained either by two distinct bursts of star
formation with a time separation of about 1 Gyr or by two stellar
populations with distinct initial chemical composition and a much
smaller age difference (Milone et al. 2008a; Cassisi et al. 2008). A
split in the SGB has also been observed in NGC 6388 (Piotto 2008)
demonstrating that this massive GC hosts two distinct stellar groups.
In a spectro-photometric study of M4, Marino et al. (2008) detect a
bimodal RGBs, and demostrate that it is due to a bimodal distribution
of CN, Na, O, also indicating that this relatively-small cluster
contains multiple populations.
The Galactic clusters cited above variously exhibit broadening or bifurcation of the RGB, SGB, and lower MS populations. In the case of the intermediate-age LMC clusters we studied here, we detected both splits of the MSTO, as in NGC 1846 and NGC 1806 (Sect. 4, M07 and M08), in NGC 1751 and possibly NGC 1783 (Sect. 4), and a broadening of the MSTO as the clusters in Figs. 12-14 and NGC 2173 (Bertelli et al. 2003). The low numbers of stars on the RGB make it difficult to assess the presence of a split or anomalous broadening along this evolutionary sequence, and the distance of the LMC makes it impossible to detect splits in the lower MS population with the presently available data.
While the splits and broadening we have shown above look quite convincing, it is important to consider the possibility that photometric errors or other effects can generate anomalous spreads and bifurcations, which could be confused with differences in age and/or chemical composition. In addition, it is also important to consider that both binaries and field stars contaminate the CMD region around the MSTO where we are most sensitive to the presence of multiple stellar populations.
In Sect. 6.1, we demonstrate that the MSTO broadening visible in Figs. 12-14 is not due to field-star contamination by statistically subtracting field stars from the cluster CMD. In Sect. 6.2, we consider the influence that binary stars could have on the spread of the MSTO. To do this, we use of artificial stars to simulate the CMD of a single population plus a population of binaries such that visible in the lower main sequence. We then present the decontaminated cluster CMD and compare it with the simulated one that includes both realistic errors and binaries to show that the observed MSTO broadening cannot be explained by a single population.
![\begin{figure}
\par\includegraphics[width=8.75 cm]{0870f11.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg64.png) |
Figure 11: As in Fig. 7 for NGC 1783. |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.75cm]{0870f12.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg65.png) |
Figure 12: As in Fig. 7 for ESO057-SC075. |
| Open with DEXTER | |
6.1 A method to decontaminate the cluster CMD from field stars
We began our analysis looking at the original CMD from stars near the
cluster centre, where we estimated that the contamination by field
stars is at most at the level of  20% (see
Sect. 3).
20% (see
Sect. 3).
However, it is possible to reduce this contamination even further by
a statistical subtraction of those stars that are most likely to
be field stars. We used the following approach which is based on
the assumption that the distribution of field stars in the CMD of the
cluster and reference field is nearly the same. For each star in the
reference field CMD, we calculated the distance to all the cluster
field stars:
![]() (or
(or
![]() ). We then flagged the closest
cluster field star as a candidate to be subtracted.
We remind the reader that
cluster and reference fields cover the same area.
). We then flagged the closest
cluster field star as a candidate to be subtracted.
We remind the reader that
cluster and reference fields cover the same area.
We determined the ratio r between the completeness of this stars and the completeness of the reference field star. This ratio is always r<1.0. To avoid over-subtracting field stars, we generated a random number between 0 and 1, and removed the star from the cluster CMD whenever this random number was less than the ratio of the completenesses.
![\begin{figure*}
\par\includegraphics[width=8.75 cm]{0870f24.ps}
\end{figure*}](/articles/aa/full_html/2009/15/aa10870-08/Timg68.png) |
Figure 24: Statistical decontamination from field stars of the CMD of NGC 1806. Upper panels: CMD extracted from the reference ( left), and cluster fields ( right). Bottom panels: CMD of all the stars that have been subtracted from the reference field ( left) and decontaminated cluster CMD ( right). |
| Open with DEXTER | |
The main steps in this procedure are illustrated in Fig. 24 for NGC 1806. The upper panels show the CMD of stars in the reference (left) and cluster (right) field, the bottom ones the CMD of subtracted stars (left), and the decontaminated CMD (right). The statistical subtraction of field stars was not applied to the most populated clusters (NGC 1978, NGC 1783), which occupy most of the field of view and have the highest ratio of cluster to reference field stars. We note that there is an additional young stellar cluster within the ACS images of NGC 1852, so we were careful to select a reference field that was as far as possible from both clusters.
![\begin{figure}
\par\includegraphics[width=8.5cm,height=10cm,clip]{0870f25.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg69.png) |
Figure 25: Comparison of the CMD of the cluster field and those of four external reference regions (A, B, C and D) for NGC 1987. The values given in the bottom left corner of each CMD are the number of stars (corrected for incompleteness) in the box around the cluster MSTO. |
| Open with DEXTER | |
Obviously, small variations in the distribution of stars in the reference field are expected even within the small WFC/ACS field of view. To check whether the reference field star distribution can be reasonably assumed uniform, we defined four regions with the same area of the cluster field and the largest possible distance from the cluster centre. We extracted the CMD of each region and compared it with that of the cluster field. A typical example of this procedure is shown in Fig. 25 for NGC 1987. In particular, we compared the number of stars (corrected for completeness) in the boxed region around the MSTO. We found that, in most cases, the variation in the number of stars in this region is smaller than about 30%. Obviously, this procedure has been applied only to clusters that cover a sufficiently small fraction of the ACS field of view. We cannot exclude the possibility that the variation of the number of stars in reference field regions could be (partially) due to contamination of cluster members. However, we note that oversubtracting the cluster members does not affect our results for the morphology of the MSTO.
6.2 The synthetic CMD
The main goal of this section is to generate a synthetic CMD of a cluster with the same characteristics as the observed one, but hosting a single stellar population. This is a necessary step for demonstrating whether the observed spread in color around the MSTO is an intrinsic feature due to the multiple stellar populations or is an artifact produced by unresolved binaries or photometric errors.
To simulate a CMD that reproduces the main properties of the observed one well enough we must ensure that:
- the mass function of the synthetic CMD is as similar as possible to the observed one;
- simulated and observed stars have the same radial distribution, completeness, and photometric errors;
- the fraction and the mass ratio distribution of simulated photometric binaries are as close as possible to the real ones.
6.2.1 Step one: simulation of single stars
We separately simulated MS and evolved stars.
U NEVOLVED S TARS:
to generate single MS stars we started by selecting a subsample of
artificial stars with the following criterion. For each star in the
cluster field that survived to the statistical subtraction of reference
field stars of Sect. 6.1, we have assigned a
subsample of the artificial stars and randomly extracted a star from
it (see Sect. 2.2 for a description of how AS were
generated). The artificial-star subsample consists of all the
artificial stars with similar magnitudes (within 0.1
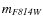 mag) and radial distances (less then 50 pixel from the observed
star). This method produces a catalogue of simulated stars with almost
the same luminosity, and radial distribution of the observed catalogue.
This procedure has been applied only to MS stars.
mag) and radial distances (less then 50 pixel from the observed
star). This method produces a catalogue of simulated stars with almost
the same luminosity, and radial distribution of the observed catalogue.
This procedure has been applied only to MS stars.
E VOLVED S TARS: things become more complicated for stars brighter than the MSTO where the complex shape of the CMD makes it harder to associate a star with the CMD sequence that corresponds to its evolutionary phase. For this reason, a different approach was used to simulate evolved stars (i.e. stars brighter than the MSTO).
First of all, we counted the number of MS stars (corrected for
completeness) with
![]() and calculated the average number of stars per
unit mass
and calculated the average number of stars per
unit mass
 in this range of luminosity. Next, we
obtained
in this range of luminosity. Next, we
obtained
 for stars brighter than the MSTO by using a
Salpeter (1955)
IMF and associated these stars to each portion of the CMD according to
the Pietrinferni et al. (2004) models.
for stars brighter than the MSTO by using a
Salpeter (1955)
IMF and associated these stars to each portion of the CMD according to
the Pietrinferni et al. (2004) models.
Since evolved stars should all have nearly the same mass, we would
expect them to also have the same radial distribution. For
this reason, we randomly associated the
radial distance of an observed star brighter than the MSTO
to each simulated evolved star. Finally,
for each simulated star, we selected the sample of artificial stars
with almost the same magnitude, colour and distance from the cluster
centre (we imposed that both input
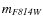 magnitude and colour
must differ by less than 0.01 mag and radial distance by less than
50 pixels) and randomly extracted a star from it.
magnitude and colour
must differ by less than 0.01 mag and radial distance by less than
50 pixels) and randomly extracted a star from it.
It must be noted that the simulated CMDs have photometric errors that are slightly smaller than the errors of real stars. This reflects a fundamental limitation of artificial-star tests. An artificial star is measured by using the same PSF as was used to generate it, while for the real stars we necessarely have an imperfect PSF. The PSF is constructed to fit the real stars as closely as possible, but there will invariably be errors in the PSF model for the real stars, which will not be present for the artificial stars. (However, it must be clearly stated that these differences are appreciable only for the stars with the highest S/N ratio.)
Below, we describe the method we used to estimate the difference between the photometric errors of real and artificial stars. This allows us to introduce an additional error component in to the artificial-star photometry so that the real and artificial sequences can be directly compared. We illustrate the procedure for the case of NGC 1806. The same procedure was applied for all clusters.
To determine how much artificial broadening of the error distribution
is necessary, we compare the color distribution of the observed and
simulated MS stars. Figure 26 shows the colour
distribution of MS stars for NGC 1806: the left panel contains the CMD
of all the stars contained in the cluster field after the subtraction
of the reference field stars. The red fiducial line (MSRL) is
computed by using the following procedure. We started by dividing the
CMD into bins of magnitude in the F814W band and, for each bin, we
calculated the median colour and magnitude and obtained a raw fiducial
line by fitting these points with a spline. Then for each star we
derived the absolute value of the difference between its colour and the
colour of the fiducial line, and calculated the  as the
as the
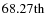 percentile. All the stars with distances greater than
percentile. All the stars with distances greater than
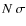 from the fiducial were rejected and the survivors used to
redetermine the median colour, magnitude, and
from the fiducial were rejected and the survivors used to
redetermine the median colour, magnitude, and 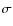 .
We iterated this
procedure five times with N going from 6 to 2 (integer numbers).
.
We iterated this
procedure five times with N going from 6 to 2 (integer numbers).
In the middle panel we show the straightened CMD obtained by
subtracting the color of the fiducial line from the color of each star.
In the right panel we show the histograms of the color
distribution in eight
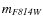 magnitude intervals. The
distribution in color is reproduced well by a Gaussian plus a tail on
the red side due to the conspicuous number of photometric binaries and
blends.
magnitude intervals. The
distribution in color is reproduced well by a Gaussian plus a tail on
the red side due to the conspicuous number of photometric binaries and
blends.
![\begin{figure}
\par\includegraphics[width=9 cm]{0870f26.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg73.png) |
Figure 26:
Left: CMD of NGC 1806 with the MSRL overplotted;
middle: the CMD rectified by subtraction of the MSRL;
right: color distribution of the rectified CMD. The |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9 cm]{0870f27.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg74.png) |
Figure 27: As in Fig. 26 but for artificial stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75 cm]{0870f28.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg75.png) |
Figure 28:
Comparison of the |
| Open with DEXTER | |
In Fig. 27 we also reproduce the distribution in colour for
the artificial star MS. As expected, the spread of the latter is
slightly less than that of the observed MS. We note that
this additional dispersion does not allow us to exclude
intrinsic dispersion of the MSs smaller than 0.03 mag in color, which
might result from dispersion of Z, Y, or a combination of the two (see
discussion in Milone et al. 2008a). In Fig. 28 we compare
the dispersions of the observed MS (
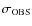 ,
circles) and
for artificial stars (
,
circles) and
for artificial stars (
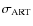 ,
triangles) as a function of
the
,
triangles) as a function of
the
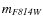 magnitude. The continuous lines are the
best-fitting fourth-order polynomials (
magnitude. The continuous lines are the
best-fitting fourth-order polynomials (
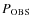 and
and
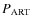 ).
Finally, we added to the color of each star of the artificial-star CMD
an error randomly extracted from a Gaussian distribution with
dispersion:
).
Finally, we added to the color of each star of the artificial-star CMD
an error randomly extracted from a Gaussian distribution with
dispersion:
![]() .
.
6.2.2 Step two: simulation of binary systems
It is clear from the excess of stars on the red side of the main sequence that many of these clusters have sizeable binary populations (compare Figs. 26 with 27). We expect that this binary population can have some effect on the distribution of stars around the turnoff, so we estimate the binary-contamination effect. Binary stars of LMC clusters will be unresolved even with HST, but the light from each star will combine and the binary system will appear as a single point-source object. These binaries can be discerned photometrically from the single stars along the MS as they are located brightward and to the red of the sequence. The position of the binary systems formed by two MS stars (MS-MS binaries) with different mass ratios in a typical CMD of an intermediate age LMC clusters are illustrated in Fig. 29.
![\begin{figure}
\par\includegraphics[width=8.8cm]{0870f29.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg81.png) |
Figure 29: CMD of NGC 1806. Grey area highlight the loci populated by MS-MS binaries. The levels of grey are proportional to the mass ratio. Red lines indicate the position of a MS-MS binary for six fixed values of the mass of the primary star (m1) and q ranging from 0 to 1. |
| Open with DEXTER | |
In the same region of the CMD, in addition to the true physically associated binaries, we also expect a few chance superpositions (blends). The artificial-star tests (see Fig. 27) show that this is a very weak effect.
It is important to note here that measuring the fraction of binaries is not the goal of this paper. Instead, our aim here is to estimate their fraction so that we can determine how much of the spread of the MSTO region can reasonably be attributed to them.
Binaries can be parametrized by their mass ratio,
q = m1/m2,
where
m1<m2. To estimate the fraction of MS-MS
photometric binaries with a mass ratio greater than a threshold value
(hereafter
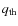 ,
see Table 2 for the adopted
,
see Table 2 for the adopted
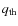 for
each cluster), we applied the methods described in Milone
et al. (2008b) and Bedin et al. (2008). We divided the CMD into two
regions: the first one (A) contains all the single MS stars and
binaries with a primary star with
for
each cluster), we applied the methods described in Milone
et al. (2008b) and Bedin et al. (2008). We divided the CMD into two
regions: the first one (A) contains all the single MS stars and
binaries with a primary star with
![]() (where
(where
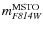 is the magnitude of the MSTO in the
F814W band). It corresponds to the light and dark grey areas of
Fig. 30. The second region (B) is the part of Athat contains MS-MS binaries with
is the magnitude of the MSTO in the
F814W band). It corresponds to the light and dark grey areas of
Fig. 30. The second region (B) is the part of Athat contains MS-MS binaries with
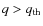 ,
and corresponds to
the dark grey area of Fig. 30. We adopted
,
and corresponds to
the dark grey area of Fig. 30. We adopted
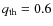 or
or
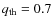 ,
as indicated in Table 2, depending on
the photometric quality of the data. The fraction of binaries with
,
as indicated in Table 2, depending on
the photometric quality of the data. The fraction of binaries with
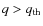 has been evaluated as
has been evaluated as

Table 2:
Fraction of photometric binaries with
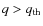 and total
fraction of binaries (Cols. 5 and 6) within the cluster field.
and total
fraction of binaries (Cols. 5 and 6) within the cluster field.
![\begin{figure}
\par\hspace*{3mm}\includegraphics[width=9cm,clip]{0870f30.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg91.png) |
Figure 30: The MS of NGC 1806 with the candidate binaries with mass ratio q>0.6 plotted as crosses. |
| Open with DEXTER | |
 is the number of stars (corrected
for completeness) observed in the region A (B) of the CMD extracted
from the cluster field,
is the number of stars (corrected
for completeness) observed in the region A (B) of the CMD extracted
from the cluster field,
 are the
corresponding numbers of stars in the CMD of the reference field and
account for the field contamination and
are the
corresponding numbers of stars in the CMD of the reference field and
account for the field contamination and
 refers
to artificial stars: their ratio indicates the fraction of blends.
Finally, we calculated the global fraction of binaries by
interpolation, assuming a flat mass-ratio distribution. The only
differences from Milone et al. (2008b) and Bedin
et al. (2008) is that in this paper we removed the contribution
from field stars by using the CMD observed in the reference region,
rather than by using a Galactic model or proper motions. The measured
fraction of binaries in each cluster are in Table 2.
refers
to artificial stars: their ratio indicates the fraction of blends.
Finally, we calculated the global fraction of binaries by
interpolation, assuming a flat mass-ratio distribution. The only
differences from Milone et al. (2008b) and Bedin
et al. (2008) is that in this paper we removed the contribution
from field stars by using the CMD observed in the reference region,
rather than by using a Galactic model or proper motions. The measured
fraction of binaries in each cluster are in Table 2.
We tried very hard to get a reliable binary fraction for those clusters, but unfortunately, their are just too big on ACS/WFC FOV. If we take the outskirts as representative of the field, we would end up subtracting cluster members from clusters, and since energy equipartion makes the binary sink into the cluster core, this could potentially generate dangerous biases in the relative fraction of a single to binary system. We avoid on purpose to giving numbers in Table 1 for those clusters, to avoid contamination of the literature with unreliable values of the binary fraction for those objects.
To simulate binary stars to be added to the simulated CMD described in Sect. 6.2 we adopted the following procedure:
- we selected a fraction
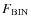 of single stars equal to the measured
fraction of binaries and derived their masses by using the
Pietrinferni et al. (2004) mass-luminosity relation. For the
clusters where the measure of the binary fraction is not available,
we assumed the average value of
of single stars equal to the measured
fraction of binaries and derived their masses by using the
Pietrinferni et al. (2004) mass-luminosity relation. For the
clusters where the measure of the binary fraction is not available,
we assumed the average value of
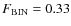 ;
;
- for each of them, we calculated the mass
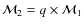 of the
secondary star and obtained the corresponding
of the
secondary star and obtained the corresponding
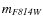 magnitude. Its colour was derived by the MSRL;
magnitude. Its colour was derived by the MSRL;
- finally, we summed up the F435W (or F555W) and F814W fluxes of the two components, calculated the corresponding magnitudes, added the corresponding photometric error, and replaced the original star in the CMD with this binary system.
Figures 35 and 36 illustrate the same exercise for the clusters with no
significant MSTO broadening.
Now that we have introduced the simulated CMDs, we can describe how we
distinguish between clusters that show evidence of hosting a multiple
population, and those that do not. First, we calculated the
dispersion of stars along the same direction perpendicular to the
obseverd spread (on the right of the MSTO) for real
(
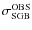 )
and artificial stars (
)
and artificial stars (
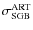 ).
Then, we considered a cluster as hosting a multiple population if the
dispersion of real stars was more than three times the dispersion of
the simulated CMD. This condition is verified for eleven out the
sixteen clusters. Although the exact position of the line along which
to measure the spread is not unique, it seemed to us a reasonably
solid approach.
).
Then, we considered a cluster as hosting a multiple population if the
dispersion of real stars was more than three times the dispersion of
the simulated CMD. This condition is verified for eleven out the
sixteen clusters. Although the exact position of the line along which
to measure the spread is not unique, it seemed to us a reasonably
solid approach.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f31.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg100.png) |
Figure 31: From left to right in each column: CMD of the cluster field for NGC 2154, HODGE 7, and NGC 1917, CMD of the reference field, CMD of the cluster field after the reference field stars have been statistically subtracted, simulated CMD. |
| Open with DEXTER | |
7 Isochrone fitting
Both M07 and M08 propose that the split of the MSTO of NGC 1846 and NGC 1806 is consistent with the presence of two distinct stellar populations with the same chemical composition and a difference in age of about 300
300  .
In addition, M08 suggest that the
spread of the MSTO of NGC 1783 can be attributed to a prolonged star
formation.
.
In addition, M08 suggest that the
spread of the MSTO of NGC 1783 can be attributed to a prolonged star
formation.
In the previous sections, we demonstrated that eight additional clusters show strong indications of an intrinsic spread or split of the CMD around the MSTO region. The remaining five objects of our sample show no significant evidence of a multiple stellar population within our photometric precision (see Figs. 35 and 36).
We note that in the clusters where a spread in the MSTO is claimed, the other evolutionary sequences are narrow and well defined, after a correction for differential reddening has been made. The tightness of these other sequences is also a strong indication that there is very little variation in metallicity among the stars.
Therefore, in the absence of any detailed chemical composition analysis, we will assume in what follows that any spread around the MSTO can be attributed to a difference in age alone. We derive the main parameters for each cluster (metallicity, age, and the maximum age spread among the populations) by fitting the data with the isochrones from the BaSTI evolutionary code (Pietrinferni et al. 2004, updated version of August 2008). Each of the isochrones has a solar-scaled distribution of metals and includes convective overshooting.
To determine the isochrone that best matches the observed CMD of our
clusters with no evidence of an intrinsic spread around the MSTO, we
followed a procedure similar to the one adopted by M07. We generated
a grid of isochrones using metallicities of
Z= 0.008 and 0.010,
sampling an age range between 1.0 and 3.0 Gyr at intervals of
0.05 Gyr. Then, we defined by hand the magnitude of the MSTO, the color
of the RGB at a level intermediate between that of the red end of the
SGB and that of the HB red-clump, and the magnitude of the HB
red-clump. In this way we calculated the difference in magnitude
between the MSTO and the HB red-clump (
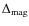 )
and the
difference in color between the MSTO and the fiducial points on the
RGB (
)
and the
difference in color between the MSTO and the fiducial points on the
RGB (
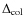 ). Then we calculated a value of
). Then we calculated a value of
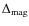 and
and
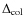 for each isochrone in the grid and
compared them with the observed ones. Finally, we selected all the
isochrones where
for each isochrone in the grid and
compared them with the observed ones. Finally, we selected all the
isochrones where
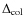 and
and
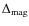 differ
respectively by less
differ
respectively by less 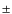 0.25 and
0.25 and 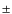 0.03 mag and fitted
them to the CMD by hand. To do this, we varied the distance modulus
in the range
18.30<(m-M)0<18.70 and the reddening between 0.00
and 0.30, both in steps of 0.01 mag and searched for the combination
that matches the cluster sequences best.
For clusters with a double or broadened MSTO, we used a similar
approach with the exception that, in this case, we first defined on
the observed CMD the magnitude of the MSTO and the values of
0.03 mag and fitted
them to the CMD by hand. To do this, we varied the distance modulus
in the range
18.30<(m-M)0<18.70 and the reddening between 0.00
and 0.30, both in steps of 0.01 mag and searched for the combination
that matches the cluster sequences best.
For clusters with a double or broadened MSTO, we used a similar
approach with the exception that, in this case, we first defined on
the observed CMD the magnitude of the MSTO and the values of
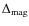 and
and
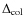 for the bMSTO and
determined the isochrone that best fits this younger population.
Then, we selected all the isochrones with the same metallicity,
distance modulus, and reddening, but different ages, and fitted the
fMSTO. For clusters with a broadened MSTO, we calculated those values
that correspond to the brighter and the fainter region of the MSTO.
for the bMSTO and
determined the isochrone that best fits this younger population.
Then, we selected all the isochrones with the same metallicity,
distance modulus, and reddening, but different ages, and fitted the
fMSTO. For clusters with a broadened MSTO, we calculated those values
that correspond to the brighter and the fainter region of the MSTO.
The best fitting distance modulus, reddening, metallicity, and age are
listed in Table 3. The last column indicates the maximum age
difference,
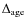 ,
for stars in clusters that show
possible evidence of multiple or prolonged star formation episodes.
In Figs. 37-39, we have
overplotted the best fitting isochrones to the observed CMDs.
Interestingly, the multiple (or prolonged) star-formation episodes
seem to lie between 150 and 250 Myr, which is very similar to the time interval
between successive star formation episodes in the intermediate-mass
AGB star ejecta pollution depicted by Ventura et al. (2001).
,
for stars in clusters that show
possible evidence of multiple or prolonged star formation episodes.
In Figs. 37-39, we have
overplotted the best fitting isochrones to the observed CMDs.
Interestingly, the multiple (or prolonged) star-formation episodes
seem to lie between 150 and 250 Myr, which is very similar to the time interval
between successive star formation episodes in the intermediate-mass
AGB star ejecta pollution depicted by Ventura et al. (2001).
8 Conclusions
High-precision HST ACS/HST photometry of sixteen intermediate age LMC
stellar clusters has revealed that eleven of them (i.e. about the
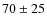 %
of the entire sample) host multiple stellar populations.
%
of the entire sample) host multiple stellar populations.
The CMDs of NGC 1806, NGC 1846, and NGC 1751 exhibit two dinstinct MSTOs, suggesting that these clusters have experienced (at least) two main episodes of star formation with a temporal separation of 200-250 Myr. For these three clusters, the high quality of our photometry enabled us not only to distinguish the two populations, but also to measure the fraction of stars belonging to each of them. In all these cases, the population corresponding to the brighter MSTO (the younger population) is the main population, and it includes more than two-thirds of the cluster stellar population, consistent with the intermediate mass AGB pollution scenario (See D'Antona & Caloi 2008, for a recent review).
Table 3: Parameters that have been used to obtain the best fit between the observed CMD and the BaSTI isochrones.
![\begin{figure}
\par\includegraphics[width=18cm]{0870f37.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg109.png) |
Figure 37: The best-fitting isochrones, obtained by using the distance modulus, reddening, metallicity, and age(s) of NGC 1846, NGC 1987, NGC 1783, NGC 1806, ESO057-SC075, and NGC 1751 listed in Table 3 and overplotted on the CMD of the cluster field of ( left). A zoom of the region around the MSTO is shown on the right. |
| Open with DEXTER | |
Our photometry strongly suggests that the intrinsic broadening of the MSTO of NGC 1783 observed by M08 could be attributed to the presence of two distinct branches that are closely spaced and poorly resolved by the observations.
In seven additional clusters, namely ESO057-SC075, HODGE7, NGC 1852, NGC 1917, NGC 1987, NGC 2108, and NGC 2154, we observed a wide spread in colour for the stars around the MSTO. In spite of this, the other main features of the CMD are narrow and well-defined, demonstrating that the spread cannot be an artifact produced by differential reddening, by variation in the photometric zero point along the chip, or by a relatively wide spread in metallicity. By using the CMD of the stars in the fields that surround the cluster, we demonstrated that the observed feature is unequivocally associated with the clusters. Finally, artificial stars and simulated CMDs show that the wide spread in colour observed around the MSTO cannot be produced by photometric errors or binaries. It is interesting to note that the age spreads observed in this sample appear to be quite similar, with all between 150 and 250 Myr.
Acknowledgements
We thank the anonymous referee for the careful reading of the manuscript and for the useful comments.
References
- Anderson, J. 1997, Ph.D. Thesis, Univ. California, Berkeley (In the text)
- Anderson, J., & King, I. R. 2006, ACS/ISR 2006-01, PSFs, Photometry and Astrometry for the ACS/WFC (In the text)
- Anderson, J., Sarajedini, A., Bedin, L. R., et al. 2008, AJ, 135, 2055 [NASA ADS] [CrossRef] (In the text)
- Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] (In the text)
- Bedin, L. R., Cassisi, S., Castelli, F., et al. 2005, MNRAS, 357, 1048 [NASA ADS] [CrossRef] (In the text)
- Bedin, L. R., Salaris, M., Piotto, G., et al. 2008, ApJ, 679, L29 [NASA ADS] [CrossRef] (In the text)
- Bertelli, G., Nasi, E., Girardi, L., et al. 2003, AJ, 125, 770 [NASA ADS] [CrossRef] (In the text)
- Cassisi, S., Salaris, M., Pietrinferni, A., et al. 2008, ApJ, 672, L115 [NASA ADS] [CrossRef] (In the text)
- D'Antona, F., & Caloi, V. 2008, MNRAS, accepted [arXiv:0807.4233] (In the text)
- D'Antona, F., Bellazini, M., Caloi, V., et al. 2005, ApJ, 631, 868 [NASA ADS] [CrossRef] (In the text)
- Glatt, K., Grebel, E. K., Sabbi, E., et al. 2008a, AJ, 136, 1703 [NASA ADS] [CrossRef] (In the text)
- Glatt, K., Grebel, E. K., Sabbi, E., et al. 2008b, AJ, 135, 1106 [NASA ADS] [CrossRef]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gratton, R. G., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] (In the text)
- Mackey, A. D., & Broby Nielsen, P. 2007, MNRAS, 369, 921 [CrossRef] (M07) (In the text)
- Mackey, A. D., Broby Nielsen, P., Ferguson, M. N., & Richardson, J. C. 2008, ApJ, 681, L17 [NASA ADS] [CrossRef] (M08) (In the text)
- Marino, A. F., Villanova, S., Piotto, G., et al. 2008, A&A, 490, 625 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Milone, A. P., Bedin, L. R., Piotto, G., et al. 2008a, ApJ, 673, 241 [NASA ADS] [CrossRef] (In the text)
- Milone, A. P., Piotto, G., Bedin, L. R., & Sarajedini, A. 2008b, in XXI Century Challenges for Stellar Evolution, Mem. Soc. Astron. Ital., 79/2, ed. S. Cassisi, & M. Salaris [arXiv:0801.3177] (In the text)
- Mucciarelli, A., Origlia, L., & Ferraro, F. R. 2007, AJ, 134, 1813 [NASA ADS] [CrossRef] (In the text)
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] (In the text)
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef]
- Piotto, G. 2008, in XXI Century Challenges for Stellar Evolution, Memorie della Societa Astronomica Italiana, vol. 79/2, ed. S. Cassisi, & M. Salaris [arXiv:0801.3175] (In the text)
- Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef] (In the text)
- Piotto, G., Villanova, S., Bedin, L. R., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] (In the text)
- Piotto, G. 2009, et al. in preparation
- Salpeter, E. 1955, ApJ, 121, 161 [NASA ADS] [CrossRef] (In the text)
- Sarajedini, A., Barker, M. K., Geisler, D., Harding, P., & Schommer, R. 2007, AJ, 133, 290 [NASA ADS] [CrossRef] (In the text)
- Sollima, A., Ferraro, F. R., Bellazzini, M., et al. 2007, ApJ, 654, 915 [NASA ADS] [CrossRef] (In the text)
- Sirianni, M., Jee, M. J., Beni'tez, N., et al. 2005, PASP, 117, 1049 [NASA ADS] [CrossRef] (In the text)
- Ventura, P., D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, 65 [NASA ADS] [CrossRef] (In the text)
- Villanova, S., Piotto, G., King, I. R., et al. 2007, ApJ, 663, 296 [NASA ADS] [CrossRef] (In the text)
- Yong, D., Grundahal, F., Johnson, J. A., & Asplund, M. 2008 [arXiv:0806.0187v1] (In the text)
Online Material
Table 1: Description of the data sets.
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f13.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg110.png) |
Figure 13: As in Fig. 7 for NGC 1987. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f14.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg111.png) |
Figure 14: As in Fig. 7 for NGC 2108. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f15.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg112.png) |
Figure 15: As in Fig. 7 for HODGE 7. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f16.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg113.png) |
Figure 16: As in Fig. 7 for NGC 1852. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f17.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg114.png) |
Figure 17: As in Fig. 7 for NGC 1917. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f18.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg115.png) |
Figure 18: As in Fig. 7 for NGC 2154. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f19.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg116.png) |
Figure 19: As in Fig. 7 for IC 2146. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f20.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg117.png) |
Figure 20: As in Fig. 7 for NGC 1644. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f21.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg118.png) |
Figure 21: As in Fig. 7 for NGC 1652. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f22.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg119.png) |
Figure 22: As in Fig. 7 for NGC 1795. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f23.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg120.png) |
Figure 23: As in Fig. 7 for NGC 1978. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm]{0870f32.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg121.png) |
Figure 32: As in Fig. 31 for NGC 1846, NGC 1806, and NGC 1751. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f33.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg122.png) |
Figure 33: As in Fig. 31 for NGC 1987, NGC 2108 and ESO057-SC075. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f34.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg123.png) |
Figure 34: As in Fig. 31 for NGC 1783 and NGC 1852. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f35.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg124.png) |
Figure 35: As in Fig. 31 for NGC 1975, NGC 1644, and NGC 1652. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm]{0870f36.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg125.png) |
Figure 36: As in Fig. 31 for NGC 1978 and IC 2146. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f38.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg126.png) |
Figure 38: As in Fig. 37 for NGC 1652, NGC 1644, NGC 1917, HODGE7, NGC 1852, and NGC 2154. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f39.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg127.png) |
Figure 39: As in Fig. 37 for IC 2146, NGC 2108, NGC 1978, and NGC 1795. |
| Open with DEXTER | |
Footnotes
- ... clusters
![[*]](/icons/foot_motif.png)
- Based on observations with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by AURA, Inc., under NASA contract NAS 5-26555.
- ...
![[*]](/icons/foot_motif.png)
- Table 1, Figs. 13-23, 32-36, 38, and 39 are only available in electronic form at http://www.aanda.org
All Tables
Table 2:
Fraction of photometric binaries with
![]() and total
fraction of binaries (Cols. 5 and 6) within the cluster field.
and total
fraction of binaries (Cols. 5 and 6) within the cluster field.
Table 3: Parameters that have been used to obtain the best fit between the observed CMD and the BaSTI isochrones.
Table 1: Description of the data sets.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,height=9.5cm,clip]{0870f1-NEW.eps} %\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg12.png) |
Figure 1:
Diagnostic parameters used to select the stars with
the best photometry are plotted as a function of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=15.2cm,clip]{0870f2.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg33.png) |
Figure 2:
Left: completeness as a function of the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=\textwidth]{0870f3-NEW.eps} %\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg34.png) |
Figure 3:
Instrumental
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f4.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg36.png) |
Figure 4: Comparison of the CMD of cluster and reference fields for the 16 selected intermediate-age clusters. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9.2cm]{0870f5.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg38.png) |
Figure 5: Comparison between the CMD of NGC 1751 before ( top panel) and after ( bottom panel) the correction for differential reddening. The arrow indicates the reddening direction. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=9.2cm]{0870f6.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg39.png) |
Figure 6: As in Fig. 5 for NGC 2108. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.75 cm]{0870f7.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg42.png) |
Figure 7: CMD of NGC 1846. All detected sources in the inner field that successfully passed all the selection criteria have been plotted. In the inset we show the Hess diagram for the CMD region around the MSTO. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.75 cm]{0870f8.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg43.png) |
Figure 8: As in Fig. 7 for NGC 1806. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f9.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg44.png) |
Figure 9: As in Fig. 7 for NGC 1751. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm, angle=0]{0870f10.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg47.png) |
Figure 10:
Procedure adopted to
measure the fraction of stars belonging to the bMSTO and fMSTO
in NGC 1806. Panel a) shows a zoom of the CMD from
Fig. 8 with the isochrones that best fits the
fMSTO and the bMSTO superimposed. The grey lines delimit the
portion of the CMD where the split is more evident. Only stars
from this region are used to measure the population ratio. In
Panel b) we shifted and rotated the reference frame of
Panel a). Red dashed line is the fiducial of the region around the
fMSTO. In Panel c) we plotted stars between the grey lines
but after the subtraction of the ``colour'' of the region around
the fMSTO fiducial from the ``colour'' of each star and the
division of the ``magnitude'' of each star by the ``magnitude'' of
the upper grey line. The four right bottom panels show the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75 cm]{0870f11.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg64.png) |
Figure 11: As in Fig. 7 for NGC 1783. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=8.75cm]{0870f12.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg65.png) |
Figure 12: As in Fig. 7 for ESO057-SC075. |
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
\par\includegraphics[width=8.75 cm]{0870f24.ps}
\end{figure*}](/articles/aa/full_html/2009/15/aa10870-08/Timg68.png) |
Figure 24: Statistical decontamination from field stars of the CMD of NGC 1806. Upper panels: CMD extracted from the reference ( left), and cluster fields ( right). Bottom panels: CMD of all the stars that have been subtracted from the reference field ( left) and decontaminated cluster CMD ( right). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,height=10cm,clip]{0870f25.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg69.png) |
Figure 25: Comparison of the CMD of the cluster field and those of four external reference regions (A, B, C and D) for NGC 1987. The values given in the bottom left corner of each CMD are the number of stars (corrected for incompleteness) in the box around the cluster MSTO. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9 cm]{0870f26.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg73.png) |
Figure 26:
Left: CMD of NGC 1806 with the MSRL overplotted;
middle: the CMD rectified by subtraction of the MSRL;
right: color distribution of the rectified CMD. The |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9 cm]{0870f27.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg74.png) |
Figure 27: As in Fig. 26 but for artificial stars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75 cm]{0870f28.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg75.png) |
Figure 28:
Comparison of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{0870f29.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg81.png) |
Figure 29: CMD of NGC 1806. Grey area highlight the loci populated by MS-MS binaries. The levels of grey are proportional to the mass ratio. Red lines indicate the position of a MS-MS binary for six fixed values of the mass of the primary star (m1) and q ranging from 0 to 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{3mm}\includegraphics[width=9cm,clip]{0870f30.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg91.png) |
Figure 30: The MS of NGC 1806 with the candidate binaries with mass ratio q>0.6 plotted as crosses. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f31.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg100.png) |
Figure 31: From left to right in each column: CMD of the cluster field for NGC 2154, HODGE 7, and NGC 1917, CMD of the reference field, CMD of the cluster field after the reference field stars have been statistically subtracted, simulated CMD. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{0870f37.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg109.png) |
Figure 37: The best-fitting isochrones, obtained by using the distance modulus, reddening, metallicity, and age(s) of NGC 1846, NGC 1987, NGC 1783, NGC 1806, ESO057-SC075, and NGC 1751 listed in Table 3 and overplotted on the CMD of the cluster field of ( left). A zoom of the region around the MSTO is shown on the right. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f13.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg110.png) |
Figure 13: As in Fig. 7 for NGC 1987. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f14.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg111.png) |
Figure 14: As in Fig. 7 for NGC 2108. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f15.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg112.png) |
Figure 15: As in Fig. 7 for HODGE 7. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f16.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg113.png) |
Figure 16: As in Fig. 7 for NGC 1852. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f17.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg114.png) |
Figure 17: As in Fig. 7 for NGC 1917. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f18.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg115.png) |
Figure 18: As in Fig. 7 for NGC 2154. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f19.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg116.png) |
Figure 19: As in Fig. 7 for IC 2146. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f20.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg117.png) |
Figure 20: As in Fig. 7 for NGC 1644. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f21.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg118.png) |
Figure 21: As in Fig. 7 for NGC 1652. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f22.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg119.png) |
Figure 22: As in Fig. 7 for NGC 1795. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.75cm]{0870f23.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg120.png) |
Figure 23: As in Fig. 7 for NGC 1978. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{0870f32.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg121.png) |
Figure 32: As in Fig. 31 for NGC 1846, NGC 1806, and NGC 1751. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f33.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg122.png) |
Figure 33: As in Fig. 31 for NGC 1987, NGC 2108 and ESO057-SC075. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f34.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg123.png) |
Figure 34: As in Fig. 31 for NGC 1783 and NGC 1852. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f35.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg124.png) |
Figure 35: As in Fig. 31 for NGC 1975, NGC 1644, and NGC 1652. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{0870f36.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg125.png) |
Figure 36: As in Fig. 31 for NGC 1978 and IC 2146. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f38.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg126.png) |
Figure 38: As in Fig. 37 for NGC 1652, NGC 1644, NGC 1917, HODGE7, NGC 1852, and NGC 2154. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0870f39.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10870-08/Timg127.png) |
Figure 39: As in Fig. 37 for IC 2146, NGC 2108, NGC 1978, and NGC 1795. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



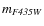 for NGC 1806. Red lines separate the well-measured
stars (thin points) from those that are more likely to have a
poorer photometry (thick points). On the right we compare the
CMD of all the measured stars ( top) and of stars that pass our
criteria of selection ( bottom).
for NGC 1806. Red lines separate the well-measured
stars (thin points) from those that are more likely to have a
poorer photometry (thick points). On the right we compare the
CMD of all the measured stars ( top) and of stars that pass our
criteria of selection ( bottom).