| Issue |
A&A
Volume 497, Number 3, April III 2009
|
|
|---|---|---|
| Page(s) | 851 - 867 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200810839 | |
| Published online | 18 February 2009 | |
Physical characteristics of very small meteoroids
J.-B. Kikwaya1,2 - M. Campbell-Brown2 - P. G. Brown2 - R. L. Hawkes3 - R. J. Weryk2
1 - Vatican Observatory, 00120, Vatican City State, Italy
2 - Department of Physics and Astronomy, University of Western Ontario,
1151 Richmond St., London, ON N6A 3K7, Canada
3 - Physics Department, Mount Allison University, 67 York St.,
Sackville, NB E4L 1E6, Canada
Received 21 August 2008 / Accepted 3 February 2009
Abstract
We have optically recorded faint meteors using a large aperture LLLTV (low light level television) system based on second generation image intensifiers. These data consist of 42 two-station meteors of which 13 were captured during an observing campaign near London, Ontario (Canada) in May 2004, and 29 during a campaign near Kiruna
(Sweden) in October 2007. Among 13 meteors recorded in the London campaign, where the baseline between the two sites was 5 km, only four meteors satisfied our requirement for complete lightcurves and deceleration profiles by starting in the field of view, of at least one station and also ending in the field of view of at least one station. From the second set of 29 meteors captured in Sweden, with
a baseline of 117.7 km, only two satisfied these criteria. The cameras used in both campaigns had fields of view of 6 degrees, which
with an assumed range of 100 km, gives a scale of 13 m/pixel at
 60 interlaced fields per second. This resolution allows precise
measurement of the deceleration of very faint meteors. The limiting magnitude for meteors on these
systems is near V = +8,
while +11th magnitude stars are visible in the individual fields. The meteors detected in these two campaigns have
peak brightnesses between absolute magnitude +6.2 and +7.4. Their photometric masses range from 4.2 mg to 0.35 mg. An ablation model was applied to fit each complete two-station event using the high-precision
metric and photometric data as a constraint, in an attempt to compute
bulk meteoroid densities. Interestingly, a large proportion of our faint meteor events were found to ablate at low altitudes, a result partly of our observing biases. The orbits of these events are consistent with either asteroidal or a Jupiter-family comet origin.
The meteoroids' physical properties, as determined through model fits, suggest high densities, which favors an asteroidal interpretation.
The high percentage of apparently dense asteroidal meteoroids at these small sizes may call into question earlier findings
that only
60 interlaced fields per second. This resolution allows precise
measurement of the deceleration of very faint meteors. The limiting magnitude for meteors on these
systems is near V = +8,
while +11th magnitude stars are visible in the individual fields. The meteors detected in these two campaigns have
peak brightnesses between absolute magnitude +6.2 and +7.4. Their photometric masses range from 4.2 mg to 0.35 mg. An ablation model was applied to fit each complete two-station event using the high-precision
metric and photometric data as a constraint, in an attempt to compute
bulk meteoroid densities. Interestingly, a large proportion of our faint meteor events were found to ablate at low altitudes, a result partly of our observing biases. The orbits of these events are consistent with either asteroidal or a Jupiter-family comet origin.
The meteoroids' physical properties, as determined through model fits, suggest high densities, which favors an asteroidal interpretation.
The high percentage of apparently dense asteroidal meteoroids at these small sizes may call into question earlier findings
that only  1% of meteoroids at these masses are asteroidal in origin. Our results are similar to others that find
1% of meteoroids at these masses are asteroidal in origin. Our results are similar to others that find 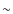 15% of faint TV meteors had spectra consistent with pure iron meteoroids. We find that many of these apparently asteroidal objects
also undergo extensive fragmentation, which may reflect melting and spraying of droplets rather than mechanical fragmentation. Some individual cases
in our small dataset will be highlighted where high bulk densities (approaching that of iron) are required to adequately match the end height,
peak brightness, and observed deceleration. We speculate that these meteoroids may represent metallic condensates from impact-processed asteroid regolith.
15% of faint TV meteors had spectra consistent with pure iron meteoroids. We find that many of these apparently asteroidal objects
also undergo extensive fragmentation, which may reflect melting and spraying of droplets rather than mechanical fragmentation. Some individual cases
in our small dataset will be highlighted where high bulk densities (approaching that of iron) are required to adequately match the end height,
peak brightness, and observed deceleration. We speculate that these meteoroids may represent metallic condensates from impact-processed asteroid regolith.
Key words: meteors, meteoroids
1 Introduction
An important physical property of meteoroids is their density. Knowing it can help determine the physical structure and potentially the chemical composition of their parent bodies. However, determining meteoroid density is not an easy task. It might be easy to find the density of a solid, uniform sphere ablating in the atmosphere (assuming the body enters the atmosphere as a solid with a spherical shape, ablates uniformly, and remains a single solid body during the whole of its flight), but ablation modeling is complicated by the fact that meteoroids fragment and have unknown shapes, structures, and chemical compositions.
When a meteoroid comes into contact with the earth's atmosphere, it ablates and generates electromagnetic radiation, including visible light. The height of ablation is influenced by many factors, including the entry angle, the speed of the meteoroid, its mass, the energy required to ablate the material of which it is composed, its boiling point, its structure, and its bulk density (Campbell-Brown & Koschny 2004).
It has long been known that the ablation behaviour among meteoroids differs considerably. These differences are reflected in different beginning heights, lightcurve shapes and, for larger meteoroids, in end height differences for meteoroids of similar speed and mass (cf. Ceplecha et al. 1998, for a complete discussion). It has long been assumed that these differences have to do with the physical characteristics of each meteoroid, including its composition, structure, bulk density and size: for example Koten et al. (2004) used the lightcurves and heights of video meteors to find significant differences among meteors from major showers. They argue that this suggests the parent bodies have different chemical compositions or physical structure.
The interpretation of all of these data is substantially complicated by the process of fragmentation. Besides the question of whether or not small meteoroids undergo fragmentation, the process of fragmentation itself remains an open question. Does fragmentation occur before the onset of, or during rapid vaporization? Does it happen at a critical temperature or a critical pressure?
Campbell et al. (2000) argued that fragmentation occurs before the process of ablation starts. Only after grains have been released from the main mass do they undergo intensive ablation. This is consistent with the dustball meteoroid model (Hawkes & Jones 1975), in which meteoric bodies are assumed to be composed of grains held together by a lower boiling point ``glue'': when the binding melts, the grains are released. Further support for the dustball model comes from the weak dependence of the beginning height, maximum height and trail length of the visible meteor on the mass of the meteoroid, as found in studies by Campbell et al. (2000), Koten et al. (2004), Hapgood et al. (1982) (for Perseids fainter than Mv = 0) and Beech (1986) (for Draconid meteors). The dustball model predicts that grains of different masses which are ejected from the meteoroid will decelerate at different rates, producing physical wake from the spread in the grains. Fisher et al. (2000) confirmed that half of the video meteors they investigated showed this wake when observed with short effective exposures.
Clearly, the mechanism of fragmentation for meteoroids is complex and much of contemporary meteoroid ablation modelling concentrates on attempting to formalize the process. Campbell-Brown & Koschny (2004) suggested that fragmentation occurs when the temperature of the surface is high enough to disrupt the binding matrix of the meteoroid; the top layer of the meteoroid (to a depth determined by the assumed thermal conductivity) is released all at once.
In a study of six Draconid meteors for which deceleration and photometric measurements were available for the first time, Borovicka et al. (2007) suggested that grain separation started after the surface of the meteoroid received a certain energy flux, calculated to be 106 J m-2; this is physically equivalent to requiring the surface to reach a particular temperature. The meteoroid then gradually fragments into grains over the first half of its trajectory, a process Borovicka et al. (2007) call thermal erosion. Meteoroids resistant to this process may disrupt at low dynamic pressures.
Beech & Murray (2003) used the dustball model to generate synthetic Leonid lightcurves. They matched different shapes of lightcurves to synthetic lightcurves generated by a power law distribution of grains, from 10-10 kg up to 10% of the total mass (which was taken to be 10-6 kg), varying the mass distribution index between 1.0 to 2.0. They suggested that the 1999 Leonid meteoroids were relatively rich in larger-mass fundamental grains.
While several studies of the overall physical structure of meteoroids have produced qualitative support for the dustball model, quantitative
measurements of the bulk density of meteoroids are more difficult to make, again due to the variety of ways fragmentation may be handled in modelling.
Ceplecha (1968) calculated the density of small meteoroids and classified them into four categories (A, B, C, D) based on a parameter, 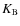 ,
which depends on the atmospheric density at the beginning of the luminous trajectory, the initial velocity and the elevation of the radiant. Categories A through D were attributed to meteoroids having densities from 2700 to
180 kg m-3.
,
which depends on the atmospheric density at the beginning of the luminous trajectory, the initial velocity and the elevation of the radiant. Categories A through D were attributed to meteoroids having densities from 2700 to
180 kg m-3.
Babadzhanov (2002) examined 413 photographic super-schmidt meteors and applied a model which assumed quasi-continuous fragmentation (QCF). They found meteoroid densities between 400 kg m-3 and 7800 kg m-3. Bellot Rubio et al. (2002) questioned the validity of these high densities for small meteoroids. He singled out two questionable assumptions which led Babadzhanov (2002) to these results. The first is the fact that QCF is based essentially on fitting a model to the lightcurve, without taking into consideration the dynamical properties of the meteoroids, particularly the deceleration. The second was that the specific energy of fragmentation used by Babazhanov (2002) was underestimated by at least a factor of 10. Bellot Rubio points out that, with such a small heat of fragmentation, the meteoroid will always fragment before reaching the ``real'' heat of ablation. Analyzing the same meteors using the single body theory (assuming none of the meteoroids fragment), Bellot Rubio et al. (2002) found densities ranging from 400 kg m-3 to 4800 kg m-3. Since the characteristics of fragmentation are often observed in the lightcurves of small meteoroids as transient increases in brightness (including in the sample analysed by Bellot-Rubio et al. 2002), Borovicka (2005) pointed out that this is a shortcoming of Bellot Rubio's work. Clearly, the lightcurves of meteoroids should be fit with a model that takes into account the dynamical properties of the meteoroids.
In this work, we adopt the dustball model as a first approximation to the physical structure of a meteoroid. We use the numerical model of ablation developed by Campbell-Brown & Koschny (2004). This model is applied to high resolution measurements of lightcurves and astrometry for a suite of faint meteors observed from two stations. In particular, our measurement precision is high enough to allow routine observation of deceleration for faint (magnitude +7) meteors. This particular model uses eight free parameters to produce a theoretical lightcurve, and allows the velocity to vary with height along the meteoroid trajectory. We explore the solution space of all possible parameters and compute for each meteor hundreds of thousands of solutions whose lightcurves and decelerations are then compared to those observed. We find density limits for each meteor within which a solution can be found; from the number of solutions at each modeled density, we get a statistical measure of the density for each meteoroid and a measure of its error.
2 Observations and equipment
Data were collected during two different observing runs; one over three nights in Canada in May 2004, and one over seven nights in Sweden in October 2007. Second generation (Gen II) Litton microchannel plate image intensifiers with S-20 spectral response were used. Gen II intensifiers have a spectral response from 340-870 nm and have less sensitivity in the red, and shorter tube lifetimes, than Gen III intensifiers but are otherwise comparable. They are significantly more sensitive than Gen I intensifiers, and less susceptible to blooming when imaging bright point objects. Gen II intensifiers were used simply because they were simpler to integrate with the large lenses used in these campaigns. We used catadioptric lenses with 155 mm focal length and f/0.75 for both stations.
In the first campaign, two Deep Gen II cameras were installed at two different sites, which we call Elginfield Observatory
(
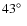
 N,
N,
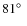
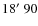 W) and the Silo site
(
W) and the Silo site
(
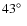
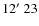 N,
N,
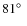
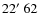 W).
The baseline between the two stations is 5.5 km and the cameras were pointed at the zenith, in order to cover a very large common
volume of the sky. The baseline is much shorter than that typically used in video meteor observations, where cameras with fields of view (FOV) of 25 to 40 degrees are separated by 30 to 60 km. This short baseline for our cameras, with their fields of view of 6 degrees, was motivated by the desire to maximize the number of two-station meteors completely observed by maximizing the common volume observed by the cameras: this also minimizes the height bias of the system. A longer baseline improves the precision, but produces almost no useful two station meteors, as seen by the results in the second campaign.
The computation of different height precisions from different baseline values for two different camera FOVs shows that the deep genII with a FOV of 6 degrees, a baseline of 5.5 km and resolution of 0.008 degrees per pixel produces a height precision within 10% of that obtained with a baseline of 45.5 km and a typical LLLTV resolution of 0.054 degrees per pixel corresponding to a FOV of 35 degrees. Recognizing that the height errors alone are not the only uncertainty and that geometry comes into play in the trajectory solution, we examined all four events in detail from the short baseline campaign and introduced typical meteor measurement errors (of order 1 pixel) to all measured points in a monte carlo simulation run 10 000 times. We find that in average the radiant error is 1.6 degrees; the height error 0.6 km and the velocity error 0.8 km s-1. This demonstrates that the shorter baseline is compensated by the higher resolution in terms of overall trajectory precision relative to typical LLLTV baselines.
W).
The baseline between the two stations is 5.5 km and the cameras were pointed at the zenith, in order to cover a very large common
volume of the sky. The baseline is much shorter than that typically used in video meteor observations, where cameras with fields of view (FOV) of 25 to 40 degrees are separated by 30 to 60 km. This short baseline for our cameras, with their fields of view of 6 degrees, was motivated by the desire to maximize the number of two-station meteors completely observed by maximizing the common volume observed by the cameras: this also minimizes the height bias of the system. A longer baseline improves the precision, but produces almost no useful two station meteors, as seen by the results in the second campaign.
The computation of different height precisions from different baseline values for two different camera FOVs shows that the deep genII with a FOV of 6 degrees, a baseline of 5.5 km and resolution of 0.008 degrees per pixel produces a height precision within 10% of that obtained with a baseline of 45.5 km and a typical LLLTV resolution of 0.054 degrees per pixel corresponding to a FOV of 35 degrees. Recognizing that the height errors alone are not the only uncertainty and that geometry comes into play in the trajectory solution, we examined all four events in detail from the short baseline campaign and introduced typical meteor measurement errors (of order 1 pixel) to all measured points in a monte carlo simulation run 10 000 times. We find that in average the radiant error is 1.6 degrees; the height error 0.6 km and the velocity error 0.8 km s-1. This demonstrates that the shorter baseline is compensated by the higher resolution in terms of overall trajectory precision relative to typical LLLTV baselines.
In the second campaign, cameras were placed at Peera in Finland (
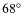
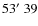 N,
N,
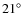
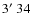 E)
and at Kiruna in Sweden (
E)
and at Kiruna in Sweden (
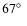
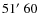 N,
N,
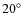
 E). The baseline between the two stations is 117 km.
The main purpose of the second campaign was to look for simultaneous events with the EISCAT tristatic radar, so the geometry was not optimal
for our purposes, but some of the data are still useful for this study.
E). The baseline between the two stations is 117 km.
The main purpose of the second campaign was to look for simultaneous events with the EISCAT tristatic radar, so the geometry was not optimal
for our purposes, but some of the data are still useful for this study.
The field of view of the images was
5.4
 4.1
4.1
 .
The pixel dimensions of the video system are
.
The pixel dimensions of the video system are
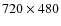 pixels, producing a resolution of
pixels, producing a resolution of  30
30
 /pixel.
/pixel.
For a meteor 100 km from the camera, the systems had a resolution of
 13 m per pixel with the full field of view being equivalent
to linear dimensions of
13 m per pixel with the full field of view being equivalent
to linear dimensions of
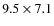 km. We find that this is
sufficient resolution at our small meteoroid sizes to show even very small decelerations. We used the CCD in an interlaced mode
with 60 video fields (or 30 video frames) per second. The limiting stellar magnitude of the video camera system was around +11 per field.
km. We find that this is
sufficient resolution at our small meteoroid sizes to show even very small decelerations. We used the CCD in an interlaced mode
with 60 video fields (or 30 video frames) per second. The limiting stellar magnitude of the video camera system was around +11 per field.
3 Data and analysis
In the first run in London Ontario (Canada), we detected a total of 17 meteors in almost 18 h, where 13 were simultaneous on both cameras. In the second run in October 2007, 35 meteors in 49 h were detected and among them, 29 were simultaneously seen on both stations. We examined data for each simultaneous meteor, took the time the event occurred and checked if the meteor ended on the field of view of at least one of the two stations. The end of the trail is particularly critical, since most of the deceleration occurs at the end of a meteor's trajectory. We add to this criterion the requirement that the event should start in the field of view of at least one station as this gives a complete lightcurve for better estimation of the photometric mass of the meteor.
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{0839fig1.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg26.png) |
Figure 1: Meteor captured in Kiruna (Sweden) on October 11 2007 at 02:55:32 UTC. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{0839fig2.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg27.png) |
Figure 2: Meteor captured in Kiruna (Sweden) on October 09 2007 at 01:37:25 UTC. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{0839fig3.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg28.png) |
Figure 3: Meteor captured in Kiruna (Sweden) on October 06 2007 at 01:54:42 UTC crossing the entire field of view. |
| Open with DEXTER | |
Most of the meteors, as seen from both sites, either started in the field of view but ended outside, or started outside and ended in the field of view of one camera (Figs. 1 and 2). Some completely crossed the field of view (Fig. 3). Some even crossed the entire field of view in just one frame, making it virtually impossible to get an astrometric solution. All these meteors failed to satisfy our two criteria and were eliminated. Among the 13 meteors seen simultaneously on both sites in the first observing run, only four satisfied the conditions of starting and ending in the field of view of at least one of the two cameras. From the second observing run, with the narrow field of view and the long baseline between the two stations, only two of the 29 simultaneous meteors satisfied the criteria and were selected.
The astrometric positions of meteors are calibrated using the stars in the field of view. The pixel locations of the stars are found
using a centre-of-mass algorithm, and are compared against the SKY2000v4 catalogue (Myers et al. 2001). The right ascension and declination
are converted into local zenith and azimuth angles (the camera is fixed to that reference frame). A third order linear least squares fit is used;
however, in order to fit a frame close to or including the zenith, rotation is used to re-reference each point so that no singularities occur.
All of the star coordinates are referenced about the centre of the frame. After this, they are projected onto an xy plane, and then fitted against
the pixel locations. While a second order fit may be adequate, a third order fit allows for better lens distortion corrections. Errors in the resulting fit are calculated based on the angular separation between the catalogue and fitted
coordinates, so that each star has a single error associated with it. This is more meaningful than quoting separate errors for azimuth and zenith
angles, since azimuth error is dependent on the zenith angle. On the GenII systems used in this study, typical errors of 0.002 degrees are found,
which corresponds according to our resolution to  0.3 pixels.
0.3 pixels.
The meteor positions are manually measured by selecting a point on the leading edge of the meteor. We find that selecting positions manually will result in errors (due to lack of sub-pixel precision) of order 1-2 pixels; this is the dominant source of error in our measurements.
After each frame has been flat fielded, the photometric magnitudes are computed by a log-sum-pixel approach with background subtraction (cf. Hawkes 2002). That is, each star has a defined disc covering the whole star and a surrounding ring representing the background. The median value in the ring is subtracted from the disc (taking into account pixel areas), and the magnitude of the star is computed as the logarithm of the sum of the pixel intensities in the disc. A typical error of 0.1-0.2 mag is found for each star. For all the stars in the image, a linear fit relates these magnitudes against catalogue visual magnitudes (from SKY2000v4 Myers et al. 2001). Because the magnitude base is fixed, the slope value of this fit is fixed at unity, and the offset determines the calibration.
The photometric mass is found using the standard integral of the lightcurve (cf. Hawkes 2002, for details). Here we use value for the luminous efficiency related to velocity from the study by Hill (Hill et al. 2005).
Photometric errors are determined using standard error techniques, where the standard deviation of the photon count is
governed by Poisson statistics. This gives an error in the photometric magnitude of 2.5/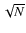 (where N is the
pixel intensity sum, proportional to the number of photons), to which the error from the photometric
calibration is added.
(where N is the
pixel intensity sum, proportional to the number of photons), to which the error from the photometric
calibration is added.
![\begin{figure}
\par\hspace*{3mm}\includegraphics[width=8cm,height=5.7cm]{0839fig4.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg30.png) |
Figure 4: An example showing the velocity of a meteor before and after the filtering (smoothing) technique. |
| Open with DEXTER | |
We used code from Borovicka (1990) called Milig to compute the in-atmosphere trajectory of all simultaneous meteors, providing the distance, the velocity and also the height of the meteor versus time along the trajectory. Once the trajectory line has been identified, the velocity can be computed from each station for each pair of points on the trajectory. Small errors in the determined position of the meteor in each frame will produce large random errors on the velocity at each point. In order to reduce this noise on the measurement of velocity versus time (or height), we use a filtering technique which consists of calculating the speed using every third or fourth point instead of every point in the original measurements (Fig. 4). The meteor clearly shows deceleration (Fig. 5) and the good agreement between the velocities from each site indicates the solution is robust.
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{0839fig5.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg31.png) |
Figure 5: The velocity of meteor ELSL11 as measured from both sites along its trajectory. |
| Open with DEXTER | |
To find the approximate initial, out-of-atmosphere velocity, which is needed as initial input into our model, we make use of the fact that the image resolution of our systems is similar to
that of the super-schmidt photographic meteors. Following
Whipple & Jacchia (1957) the pre-atmospheric velocity of the meteoroid was computed following
the empirical expression he suggested relating distance (D) to time (t)
(Eq. (1)).
The velocity at any time can be found from the time derivative of the expression, Eq. (2). The pre-atmospheric velocity can be found by evaluating the expression with t set to minus infinity. The second derivative of Eq. (1) gives the deceleration, and k is the slope of the logarithm of the deceleration. When k is known, B and C can be determined by the method of least squares. The velocity approaches the pre-atmospheric velocity asymptotically as t approaches minus infinity; the error in the fit can be estimated from the error in the fit parameter (Fig. 6).
From the positional measurements at each station, the pre-atmospheric velocity and the radiant were computed according to Borovicka (1990), while the heliocentric meteoroid orbits were computed using the methods of Ceplecha (1987). We note that, due to the geometry used, the meteors captured during the Swedish campaign have relatively greater uncertainty in their solutions due the fact of having only a few measured points for the entire trajectory.
![\begin{figure}
\par\includegraphics[width=5cm,height=5.2cm,clip]{0839fig6.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg34.png) |
Figure 6: Velocity of meteor ELSL11 from both sites along its trajectory. |
| Open with DEXTER | |
4 Ablation model
In our work, we use the dustball model of Campbell-Brown & Koschny (2004). Where the traditional dustball model suggests that the light production starts as soon as the small grains are all released, the heating of the meteoroid, modeled through Clausius-Clapeyron formalism by Campbell-Brown and Koschny, allows one to consider ablation even before the boiling temperature is reached. The dustball model of Campbell-Brown and Koschny allows the user to enter any number of grains and their masses, without necessarily assuming a power law distribution. This is a considerable advantage, since the computing time may be reduced significantly by representing a distribution of grain sizes as a small number of distinct sizes.
The model considers three sources of energy: energy imparted to the meteoroid by collisions with atmospheric atoms, the energy lost from the meteoroid by radiation, and the energy lost through evaporation of the meteor material. The mass loss is calculated using the Knudsen-Langmuir formula, combined with the Clausius-Clapeyron equation. A term proportional to kinetic energy transfer, like the classical formula, is also added to simulate spallation when the meteoroid is very hot. For more details the ablation model itself, see Campbell-Brown & Koschny (2004).
5 Results
For each meteor, we extracted the velocity and the radiant using the trajectory code of Borovicka (1990). We extracted the lightcurve of each of the six meteors with complete lightcurves. No correction for photometric saturation was needed since none of these six meteors were bright enough to have any saturated pixels. We applied our ablation model to simultaneously fit the observed lightcurve and deceleration.
Among the parameters used in the model, we have chosen some to remain fixed and some to remain free. Fixed parameters include the fusion point of the meteoroid
grains, which is taken to be 100 K less than the boiling point of the meteoroid grains (the boiling temperature remains free); the condensation
coefficient 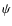 ,
which is fixed to 0.5 (condensation coefficient of stone), the emissivity of the meteoroid (fixed to 0.9), and the atmospheric
density, provided by the MSISE 90 model (Hedin 1991).
,
which is fixed to 0.5 (condensation coefficient of stone), the emissivity of the meteoroid (fixed to 0.9), and the atmospheric
density, provided by the MSISE 90 model (Hedin 1991).
To fit the observed decelerations and lightcurves, using the model output we search the entire free parameter space for each meteor. This first stage in the solution procedure helps to identify the regions in which solutions are concentrated. The main difficulty with this approach is the grain distribution; while the number of solutions covering a reasonable range of each of the other free parameters is merely prohibitive, the number of possible grain distributions is essentially infinite. As a first approximation, we have chosen to represent each meteor at this step as a collection of grains all having the same size. For each meteoroid, we chose masses of grains (from the smallest grains which will still ablate independently to the total meteoroid mass), and fixed the number of those grains so that the total mass of the meteoroid corresponded to the total photometric mass of the meteor. The shape of the lightcurves found in this way will almost certainly be wrong, but as we get close to a good solution, we expect one of the grain sizes will produce a curve with significant overlap to the measured lightcurve.
We extract from each solution set the best model fit, which we define here to mean the one with the smallest  value (the
value (the  here is the standard
one where the smallest number indicates the best fit). We allow the theoretical lightcurve and the measured lightcurve to have
one fourth of points which do not overlap to within the measured error margins.
At this stage, for each of these potential solutions, we adjust the mass and number of grains by hand in order to find the best fit to the
observed lightcurve and deceleration.
here is the standard
one where the smallest number indicates the best fit). We allow the theoretical lightcurve and the measured lightcurve to have
one fourth of points which do not overlap to within the measured error margins.
At this stage, for each of these potential solutions, we adjust the mass and number of grains by hand in order to find the best fit to the
observed lightcurve and deceleration.
5.1 Free parameters
The free parameters used in our ablation model include:
- grain mass (to which the number of grains is tied);
- density of the meteoroid;
- the heat of ablation (
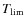 );
);
- the boiling point of the meteoroid grains (
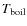 );
);
- the temperature at which the grains are released;
- the specific heat (Cp);
- the average molar mass of meteoroid material;
- the thermal conductivity of the meteoroid.
First, we allow the density to vary from 500 kg m-3 (very porous carbonaceous materials) to 8000 kg m-3 (iron meteoroid).
We used seven steps in the density. The heat of ablation is of the order of 106 J kg-1 (cf. Ceplecha et al. 1998). The actual value
depends on the composition of the meteoroid. Babadzhanov (2002) used
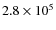 J kg-1 while Bellot Rubio et al. (2002) thought that it should be around
J kg-1 while Bellot Rubio et al. (2002) thought that it should be around
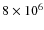 J kg-1. Following
Bellot Rubio et al. (2002), we allow the heat of ablation
to range from
J kg-1. Following
Bellot Rubio et al. (2002), we allow the heat of ablation
to range from
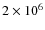 to
to
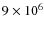 J kg-1.
J kg-1.
Physically, the fragmentation temperature (
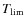 )
must be less than the boiling temperature (
)
must be less than the boiling temperature (
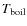 ), otherwise the grains will ablate before they
separate. Knowing that iron (the densest element we expect to encounter as a major element in the composition of the meteoroid) reaches its boiling
temperature around 2000 K, we choose fragmentation temperatures ranging from 900 K to 1600 K, and set the boiling temperature to vary between
1400 K to 2300 K.
), otherwise the grains will ablate before they
separate. Knowing that iron (the densest element we expect to encounter as a major element in the composition of the meteoroid) reaches its boiling
temperature around 2000 K, we choose fragmentation temperatures ranging from 900 K to 1600 K, and set the boiling temperature to vary between
1400 K to 2300 K.
The thermal conductivity is expected to be small considering the physics of small meteoroids with considerable porosity (Campbell-Brown & Koschny 2004; Popova 2005). We choose it to range between 0.1 to 1.0 W/m K.
We varied the molar mass from 20 to 56 atomic mass units (amu), covering atoms ranging from sodium to iron. We find that most solutions were not very sensitive to molar mass changes if the value was over 36 amu. The range of specific heat goes from 600 J/kg K to 1400 J/kg K, which correspond to the values used by Campbell-Brown & Koschny (2004).
In some ablation models, 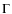 (drag coefficient) and
(drag coefficient) and 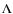 (heat transfer coefficient) are assumed from the beginning.
Examining the Draconids, Borovicka et al. (2007) set
(heat transfer coefficient) are assumed from the beginning.
Examining the Draconids, Borovicka et al. (2007) set 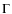 and
and 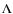 to 1. Fisher et al. (2000) assumed also
to 1. Fisher et al. (2000) assumed also 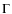 and
and
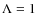 .
Campbell-Brown & Koschny (2004) assumed
.
Campbell-Brown & Koschny (2004) assumed
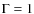 and
and
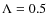 .
In our work, when doing
the huge search of solutions, we left
.
In our work, when doing
the huge search of solutions, we left 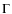 and
and 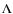 to be 1 following these earlier studies. After finding the regions near
the best solutions, we adjusted them in concert with the mass to improve the model fits. At this stage in our solution procedure, we allow
to be 1 following these earlier studies. After finding the regions near
the best solutions, we adjusted them in concert with the mass to improve the model fits. At this stage in our solution procedure, we allow 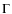 and
and 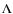 to vary from 0.7-0.9.
to vary from 0.7-0.9.
To demonstrate our procedure in detail we take meteor ELSL11 as a first example, showing explicitly how we evaluated the interval of possible values for each parameter. Other meteor events will be discussed only briefly.
5.2 Evaluation of density
5.2.1 Case study of meteor ELSL11
We start with the observed lightcurve and deceleration (plot of velocity versus height) of meteor ELSL11. The investigation will consist of finding all the modeled lightcurves and decelerations which will match the observed curves. The solution will combine the eight free parameters described above with those which have been fixed (air density, emissivity, etc.). A reasonable determination of each parameter is defined.
It is relatively easy to choose a range of values for each parameter, except for the grain mass. This fact will lead us to approach the real meteoroid grain mass distribution through two steps. We know that the reasonable number of grains in a meteoroid is in the thousands, and the mass of individual grains could range from 10-12 kg (approximately the smallest size which will ablate) to 10-8 kg (about one tenth the total mass for our sample events). The number of sizes of grains involved for any meteoroid is almost certainly more than one; however, in the first step, we consider the meteoroid to be composed of only one size of grain, the mass of which we can alter from 10-12 kg to 10-9 kg.
For meteor ELSL11, we present the grain mass distributions which were initially modeled in Table 1. The photometric mass was taken
to be the initial mass. Considering the grain mass ranging from 10-9 kg to 10-12, we divided the initial photometric mass to have the
number of grains. Our goal is to find
those grain mass distributions which offer good fits between the modeled lightcurve and deceleration curve, and the observed curves.
The second step will then be to use these solutions as starting points and to refine these solutions by finding a grain mass distribution which produces a good fit for the meteor event as defined by the  fit between the model and the observations. For ELSL11, the values of other parameters
used in the modelling are given in Table 2.
fit between the model and the observations. For ELSL11, the values of other parameters
used in the modelling are given in Table 2.
Table 1: Initial grain mass distributions used for meteor ELSL11 in the first stage of analysis.
Table 2:
Values for the parameters (other than grain mass) used in the modelling.
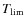 is the temperature at which fragmentation occurs,
is the temperature at which fragmentation occurs,
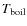 the boiling point of the grains,
the boiling point of the grains, 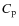 the specific heat, Mmass the molar mass, and Thermal Cond the thermal conductivity of the bulk meteoroid
(Meteor ELSL11).
the specific heat, Mmass the molar mass, and Thermal Cond the thermal conductivity of the bulk meteoroid
(Meteor ELSL11).
Using every combination of all these values of the free parameters, we generated 151 200 different theoretical lightcurves and decelerations. Each was then compared to the observed ones through the goodness-of-fit using standard  .
A perfect fit
to both curves would have a
.
A perfect fit
to both curves would have a  value equal to zero.
value equal to zero.
We sorted these 151 200 solutions by the  values, as compared to both the observed lightcurve and the observed deceleration curve.
For this event, we rejected any solution with
values, as compared to both the observed lightcurve and the observed deceleration curve.
For this event, we rejected any solution with  less than 0.016. This value is chosen by noting that for this particular event the
number of degrees of freedom is 51 and the average sigma (error bar) on the lightcurve is 0.15 mag. As such, this value for the
less than 0.016. This value is chosen by noting that for this particular event the
number of degrees of freedom is 51 and the average sigma (error bar) on the lightcurve is 0.15 mag. As such, this value for the  produces a statistically significant difference between the model and observed lightcurve values (cf. Bevington & Robinson 2003).
We ended up with two major concentrations of solutions: one around a density of 1000 kg m-3 and another around a density of 8000 kg m-3.
produces a statistically significant difference between the model and observed lightcurve values (cf. Bevington & Robinson 2003).
We ended up with two major concentrations of solutions: one around a density of 1000 kg m-3 and another around a density of 8000 kg m-3.
For each group of solutions, we find the one with the smallest  .
In our example, the first group of solutions, with densities concentrated
around 1000 kg m-3, has the best solution at model number 107935 with grain mass 1.78 E-10 kg, heat of ablation 7.0E6 J/kg,
fragmentation temperature 1700 K, boiling temperature 2000 K, specific heat
800 J/kg K, molar mass 30 atomic units, and thermal
conductivity 1.0 W/m K. The second set of solutions around 8000 kg m-3 has a grain mass bigger than the one for the low density
solution (1.32 E-09 kg). The heat of ablation is the same, the fragmentation temperature differs by just 100 K, as does the boiling
temperature. The specific heat is the same for both solutions. The best molar mass is 36 atomic units for the 8000 kg m-3 solution,
compared to 30 atomic units for the low density solution. For the thermal conductivity, the best value for the 8000 kg m-3 solution
is half that of the 1000 kg m-3 solution.
.
In our example, the first group of solutions, with densities concentrated
around 1000 kg m-3, has the best solution at model number 107935 with grain mass 1.78 E-10 kg, heat of ablation 7.0E6 J/kg,
fragmentation temperature 1700 K, boiling temperature 2000 K, specific heat
800 J/kg K, molar mass 30 atomic units, and thermal
conductivity 1.0 W/m K. The second set of solutions around 8000 kg m-3 has a grain mass bigger than the one for the low density
solution (1.32 E-09 kg). The heat of ablation is the same, the fragmentation temperature differs by just 100 K, as does the boiling
temperature. The specific heat is the same for both solutions. The best molar mass is 36 atomic units for the 8000 kg m-3 solution,
compared to 30 atomic units for the low density solution. For the thermal conductivity, the best value for the 8000 kg m-3 solution
is half that of the 1000 kg m-3 solution.
In examining the modelled lightcurves and velocity profiles for the two best solutions (a low density solution around 1000 kg m-3 and high density solution around 8000 kg m-3) we find that the high density solution matches the observed data better than the low density solution. The low density solution shows the light production stopping at 87 km; the observed data go down to 83 km. Figures 7 and 8 show the lightcurves of the high and low density solutions; Figs. 9 and 10 show the decelerations for the two solutions.
The next step in our solution procedure is to use these two best model fits as starting points, and to refine the grain masses, heat transfer and drag coefficients to find the best possible solution in the phase space region. This step was done by hand, adding and subtracting grains of different masses while keeping the other parameters constant. At each step, both the lightcurve and deceleration produced by the model were compared to the observed curves.
The starting values of the parameters for the high density solution were those of the best fit, listed in the previous section. The shape of the lightcurve is clearly not single body, meaning that more than one size of grain is needed to model it properly. We attempted to find a better solution using three different grain masses. We were able to find a model which is very close to the observed data (Figs. 11 and 12). The parameters for this fit are given in Table 3.
For the low density solution, we began by modifying the number and size of the grains involved. As with the high density solution, we used three
grain sizes. The initial attempt used the same parameters as the single grain size model, but had 450 grains with masses of
 kg,
430 grains with a mass of
kg,
430 grains with a mass of
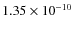 kg, and 30 grains with a mass of
kg, and 30 grains with a mass of
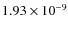 kg. The peak magnitude produced by this model
was too small, so we then increased the mass of the grains in the middle bin from
kg. The peak magnitude produced by this model
was too small, so we then increased the mass of the grains in the middle bin from
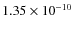 kg to
kg to
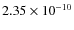 kg. This matched
the maximum magnitude, but the model produced more light than observed at higher and lower altitudes, and did not penetrate as far into the atmosphere
as the observed meteor. To correct for the latter, we increased the mass of the largest grains to
kg. This matched
the maximum magnitude, but the model produced more light than observed at higher and lower altitudes, and did not penetrate as far into the atmosphere
as the observed meteor. To correct for the latter, we increased the mass of the largest grains to
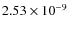 kg. The lightcurve for this
model is compared to the observed lightcurve in Fig. 13; the parameters used are given in Table 4.
kg. The lightcurve for this
model is compared to the observed lightcurve in Fig. 13; the parameters used are given in Table 4.
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{0839fig7.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg55.png) |
Figure 7: Lightcurve of the best single grain mass solution around 1000 kg m3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{0839fig8.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg56.png) |
Figure 8: Lightcurve of the best single grain mass solution around 8000 kg m3 for ELSL11. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{0839fig9.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg57.png) |
Figure 9: Deceleration of the best single grain mass solution around 1000 kg m3 for ELSL11. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{839fig10.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg58.png) |
Figure 10: Deceleration of the best single grain mass solution around 8000 kg m3 for ELSL11. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{839fig11.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg59.png) |
Figure 11: Lightcurve for ELSL11 with the model fit for a density of 8000 kg m-3 using parameters from Table 3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{839fig12.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg60.png) |
Figure 12: Deceleration for ELSL11 for a density of 8000 kg m-3 using parameters from Table 3. |
| Open with DEXTER | |
In all three of the solutions where grain numbers and masses were varied, the model solution reaches the detection threshold earlier than the observed lightcurve. This could be corrected if the fragmentation temperature is increased, releasing the grains just prior to the height where the meteor becomes visible. In order to match the observed starting height, it was necessary to raise the fragmentation temperature from 1700 K to 3000 K. In order to keep the fragmentation temperature lower than the boiling temperature, we also had to raise the boiling temperature to 3300 K, and we set the fusion temperature to 3200 K for consistency. We used the same grain mass distribution as in the previous solution. The parameters for this modified solution are given in Table 5, and the model is compared to the observed lightcurve in Fig. 14.
The solution around 1000 kg m-3 is still a poor fit, and it seems physically unrealistic to have a low density meteoroid with a fragmentation temperature as high as 3000 K. We therefore reject the low density solution, and proceed to refine the density measurement assuming that the meteoroid's density is close to 8000 kg m-3.
The point of the first search over the eight different parameters is to identify broadly the different regions where the possible solutions fall, to work on the best solution from each region, to determine where among all the different concentrations of solutions the best solution lies, and determine the likely mass distribution of the grains in the meteoroid. We will now fix the grain distribution, and perform a second search with greater resolution in the density parameter, which is the parameter of greatest interest to us. We allow the other parameters (apart from grain masses) to vary as shown in Table 6.
Table 3: Table summarizing parameters involved in the final stage of the high density solution model for ELSL11. Den is density, Qf is heat of ablation, Cps is specific heat, Thermal Cond is thermal conductivity.
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{839fig13.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg61.png) |
Figure 13: Modified solution for 1000 kg m-3 using three grain masses. The sudden jump in the predicted light output from the model indicates a sudden fragmentation event. |
| Open with DEXTER | |
Using every possible combination of the parameters in the table, we computed 432000 modeled solutions. We compared each of these to
the observed lightcurves and deceleration of ELSL11. For this search, we set a stricter limit on the  value of 0.08
for both the lightcurve and deceleration comparison; this roughly corresponds to a solution which fits inside the error bars of
both plots. We ended up with 234 different good solutions (solutions with
value of 0.08
for both the lightcurve and deceleration comparison; this roughly corresponds to a solution which fits inside the error bars of
both plots. We ended up with 234 different good solutions (solutions with  less than or equal to our limit) with
densities from 5000 kg m-3 to 8000 kg m-3 for ELSL11. The greatest number of good solutions falls between a density of 5500 kg m-3 and
6500 kg m-3. Among these 234 solutions,
the best one (with the smallest
less than or equal to our limit) with
densities from 5000 kg m-3 to 8000 kg m-3 for ELSL11. The greatest number of good solutions falls between a density of 5500 kg m-3 and
6500 kg m-3. Among these 234 solutions,
the best one (with the smallest  both on the lightcurve and the deceleration) has a density of 5500 kg m-3
with a total mass of
both on the lightcurve and the deceleration) has a density of 5500 kg m-3
with a total mass of
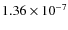 kg. All other parameters associated with this particular solution are summarized in Table 7.
kg. All other parameters associated with this particular solution are summarized in Table 7.
Table 4: Distribution of grains for the solution around 1000 kg m-3 using three grain masses.
Table 5: Distribution of grains for the solution around 1000 kg m-3, with three grain sizes and modified temperatures of fragmentation, boiling and fusion.
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{839fig14.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg63.png) |
Figure 14: Modified solution for 1000 kg m-3, with three grain sizes and modified temperatures of fragmentation, boiling and fusion. |
| Open with DEXTER | |
Table 6: Variation of parameters used modeling lightcurves and decelerations for ELSL11 in the second stage search. The mass column does not give the variation of grain sizes, but the actual grain distribution used in every model.
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{839fig15.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg70.png) |
Figure 15: Plot of the best density solutions for ELSL11. The best solution falls at 5500 kg m-3. The left bound is 5000 kg m-3 and the right bound is 8000 kg m-3. |
| Open with DEXTER | |
Table 7: Values of parameters producing the best model solution among 234 solutions found to describe meteor ELSL11.
Table 8: Summary table for the six meteors modelled in detail in this study. A value of 1 under the size column means there is only one size of grains used in the modelling, 1, 2 two sizes in the composition of the meteoroid and 1, 2, 3 three sizes of grains in the composition of the meteoroid.
Table 9: Summary table of the six meteors and their statistical densities as given by the method. A value of 1 in the size column means there is only one size of grains in the composition of the meteoroid, 1, 2 two sizes in the composition of the meteoroid and 1, 2, 3 three sizes of grains in the composition of the meteoroid.
Table 10: Sumary table for the first observing campaign near London Ontario (Canada). Hb is beginning height, Hi is initial height (actual height as appeared on the field of view) , He is ending height and Hf is final height (actual height as appeared on the field of view). The velocity is the no-atmosphere velocity computed as outlined in the text.
![\begin{figure}
\par\includegraphics[width=15cm,height=8cm]{839fig16.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg87.png) |
Figure 16: The best model of meteor ELSL11, with a density of 5500 kg m-3. |
| Open with DEXTER | |
To determine the range of probable densities in our final model fits, we adopt the best fit value and expressed the density
of ELSL11 by an asymmetrical error bar as
5500 + 2500/-500 kg m-3, expressing the full range of possible density fits
for our chosen  cut.
cut.
This detailed example serves to outline our methodology as we try to fit our model to the available metric and photometric observations. In the next sections, we will briefly summarize our findings for the additional 5 meteor events for which we were able to apply this detailed approach.
5.2.2 Meteor ELSL01
Using the mass distribution in Table 8, we modeled a 352 800 combinations of the free parameters, with densities concentrated around 7000 and
8000 kg m-3. For this event, statistically significance required the solutions to have a  less than or equal to 0.078 on the
lightcurve and less than or equal to 0.1 on deceleration; a total of 167 solutions matched the observed data (Fig. 17).
Among these solutions, the best one has a density of 7000 kg m-3 (plotted in Fig. 18); the values of the other parameters
are given in Table 9. The total mass of ELSL01, which had a velocity of 11.3 km s-1, close to the earth escape velocity, was
modeled to be
less than or equal to 0.078 on the
lightcurve and less than or equal to 0.1 on deceleration; a total of 167 solutions matched the observed data (Fig. 17).
Among these solutions, the best one has a density of 7000 kg m-3 (plotted in Fig. 18); the values of the other parameters
are given in Table 9. The total mass of ELSL01, which had a velocity of 11.3 km s-1, close to the earth escape velocity, was
modeled to be
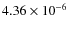 kg. The density of ELSL01 was found to be
7000 + 1500/-1500 kg m-3.
kg. The density of ELSL01 was found to be
7000 + 1500/-1500 kg m-3.
5.2.3 Meteor ELSL09
Using the grain mass distribution in Table 8, we computed 483 000 solutions with density ranging from
250 kg m-3 to 3000 kg m-3. We found 147 solutions whose lightcurves and decelerations
matched the observed ones with a statistically significant value of standard  of better than 0.06 on both lightcurve and deceleration
(Fig. 19). Among these good solutions, the one having the smallest standard chi-square had a density of 900 kg m-3
(Fig. 20) with a total modeled mass of
of better than 0.06 on both lightcurve and deceleration
(Fig. 19). Among these good solutions, the one having the smallest standard chi-square had a density of 900 kg m-3
(Fig. 20) with a total modeled mass of
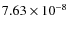 kg. Values of the other parameters for this particular
solution are summarized in Table 9. The best fit density for ELSL09 is 900 + 250/-150 kg m-3.
kg. Values of the other parameters for this particular
solution are summarized in Table 9. The best fit density for ELSL09 is 900 + 250/-150 kg m-3.
5.2.4 Meteor ELSL12
With the grain mass distribution in Table 8, we effected a search to find a more precise determination of the density which was computed using
a standard  cutoff of 0.15 or less on the lightcurve and 0.1 on the deceleration. This left 753 solutions and gives the density
distribution shown in Fig. 21. Among all of these solutions, the best one had a density of 4500 kg m-3
(shown in Fig. 22) with a total modeled mass of
cutoff of 0.15 or less on the lightcurve and 0.1 on the deceleration. This left 753 solutions and gives the density
distribution shown in Fig. 21. Among all of these solutions, the best one had a density of 4500 kg m-3
(shown in Fig. 22) with a total modeled mass of
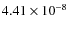 kg. The values of the other parameters
in the best model are specified in Table 9. The density of ELSL12 was found to be 4500 + 2000/-2500 kg m-3.
kg. The values of the other parameters
in the best model are specified in Table 9. The density of ELSL12 was found to be 4500 + 2000/-2500 kg m-3.
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{839fig17.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg89.png) |
Figure 17: Plot of accepted solutions for ELSL01. The best solution falls at 7000 kg m-3. The left bound is 5500 kg m-3 and the right bound is 8500 kg m-3. |
| Open with DEXTER | |
5.2.5 Meteor PEKI08
The second search was based on 330750 different models using the grain mass distribution in Table 8. The modeled densities ranged
from 200 kg m-3 to 1200 kg m-3. Only models having a standard  less than or equal to 0.04 on the lightcurve and 0.01 on the
deceleration were considered. 1525 solutions satisfied the conditions, shown in Fig. 23. Among them, the best one had a
density of 600 kg m-3 (Fig. 24) with a total modeled mass of
less than or equal to 0.04 on the lightcurve and 0.01 on the
deceleration were considered. 1525 solutions satisfied the conditions, shown in Fig. 23. Among them, the best one had a
density of 600 kg m-3 (Fig. 24) with a total modeled mass of
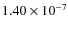 kg. Other parameter values are given
in Table 9. The density of PEKI 08 was found to be
600 + 200/-200 kg m-3.
kg. Other parameter values are given
in Table 9. The density of PEKI 08 was found to be
600 + 200/-200 kg m-3.
5.2.6 Meteor PEKI09
Using the mass distribution in Table 8 and the resolution on the density parameter from 200 kg m-3 to
1500 kg m-3 with a step of 50 kg m-3, 330 000 model solutions were computed. These were required to have a standard
 on lightcurve and deceleration less than or equal to 0.07. A total number of 2994 solutions satisfied this particular condition, and
the density distribution is plotted in Fig. 25. Among these good solutions, the best one
had a density of 500 kg m-3 (plotted in Fig. 26) and its total modeled mass was
on lightcurve and deceleration less than or equal to 0.07. A total number of 2994 solutions satisfied this particular condition, and
the density distribution is plotted in Fig. 25. Among these good solutions, the best one
had a density of 500 kg m-3 (plotted in Fig. 26) and its total modeled mass was
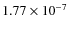 kg. Table 9 shows the values of other parameters of the best solution. The good solutions range from
200 kg m-3 to 800 kg m-3 and the best solution with the smallest
kg. Table 9 shows the values of other parameters of the best solution. The good solutions range from
200 kg m-3 to 800 kg m-3 and the best solution with the smallest  is 500 kg m-3. The density of PEKI09 is estimated as
500 + 300/-300 kg m-3.
is 500 kg m-3. The density of PEKI09 is estimated as
500 + 300/-300 kg m-3.
6 Discussion
Our analysis emphasizes that when it comes to modeling meteoroid behaviour, where many free parameters are involved, we should not in general expect to find a unique solution matching the lightcurve, or even both the lightcurve and the deceleration. Different combinations of free parameters can produce modeled lightcurves and decelerations falling within the observed error bars. If solutions closely matching the observations can be found for both high and low densities, the data often are not sufficiently restrictive to uniquely determine the meteoroid density. We found, for the six meteors we observed, that good solutions were concentrated in a relatively small portion of the density space, meaning that a meaningful density and an estimate of the error could be found. In our case, the fact that the number of good fits falls to zero for densities higher and lower than the best fit density gives the ultimate boundaries to the meteoroid density, though these may be somewhat conservative.
Our analysis revealed similar behaviour to that found by Borovicka et al. (2007). Both works showed that meteoroids fragment gradually near the onset of detectable light production into constituent grains whose masses vary in a very narrow range between 10-9 and 10-12. In both studies, the disruption occurs with an energy around 106 J kg-1. The grain distribution used in our study (between one and three discrete sizes of grain) is in contrast to that used in other studies, many of which use the more physical assumption of a power law (Borovicka et al. 2007; Beech 1986; Beech & Murray 2003). The lightcurves produced by this simplification are almost as smooth as the power-law generated curves, and deliver a considerable gain in computation time, since particles of the same size released at the same time can be simulated as a single particle and their luminosity later multiplied. Computation time was of critical importance in our study, since hundreds of thousands of models had to be run for each meteor.
![\begin{figure}
\par\includegraphics[width=15cm,height=8cm]{839fig18.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg90.png) |
Figure 18: Lightcurve and deceleration of ELSL01, with best model. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{839fig19.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg91.png) |
Figure 19: Plot of best solutions for ELSL09.The best solution falls at 900 kg m-3. The left bound is 750 kg m-3 and the right bound is 1150 kg m-3. |
| Open with DEXTER | |
In this work, we obtained the density of each meteoroid after fitting both its lightcurve and deceleration. This was done for first time by Borovicka et al. (2007) for six Draconids. They found an estimated density of 300 kg m-3 for Draconids in full agreement with Ceplecha (1988) and Revelle (2001). The meteoroids in our work had a range of densities going from 500 kg m-3 to 7000 kg m-3, overlapping with values obtained by Babadzhanov (2002) and Bellot Rubio et al. (2002).
![\begin{figure}
\par\includegraphics[width=15cm,height=8cm]{839fig20.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg92.png) |
Figure 20: Lightcurve and deceleration of ELSL09 together with the best model fit. |
| Open with DEXTER | |
Table 11: Summary table of the second observing campaign from Kiruna (Sweden) and Peera (Finland). Hb is beginning height, Hi is initial height (actual height as appeared on the field of view), He is ending height and Hf is final height (actual height as appeared on the field of view). The velocity is the no-atmosphere velocity computed as outlined in the text.
Table 12: Table summarizing orbital elements of all 42 meteors. alp geo and del geo are respectively geocentric right ascension and declination at the epoch J2000.0. TJ is Tisserand parameter with respect to Jupiter. PEKI20 is the case of meteors which crossed the entire field of view making it difficult to compute any trajectory solution.
Table 13:
Table showing where the best model fits occur among 151200 computed. Each model number
has a modeled lightcurve and a modeled deceleration computed with values of the free parameters as shown. The comparison of the
the modeled lightcurve with the observed one is represented by the value of the standard  in the last column. We show here only
the value of
in the last column. We show here only
the value of  of lightcurve. (Meteor ELSL11).
of lightcurve. (Meteor ELSL11).
Three of the six meteoroids have very high density (ELSL01, ELSL11, ELSL12). They fall well within the range of density defined by
Babazhanov (2002) whose investigation on density of meteoroids took into account the fragmentation process. But they are significantly higher than
the range defined by Bellot Rubio et al. (2002). Some of the ablation for these higher density meteoroids may be occurring as liquid droplets, rather
than as discrete grains (Lebedinets & Portnyagin 1968). Association of these high density meteoroids with asteroidal objects is further supported by
their orbits which have tisserand values greater than 3, consistent with an asteroidal origin. These events may represent the iron meteoroid
population identified at slightly larger sizes spectrally by Borovicka et al. (2005); our work suggests that this iron meteoroid population may
extend down to even smaller masses. Among the meteors we believe underwent fragmentation (and had more than one size of grain), ELSL09 does have
a low density. Thus, we cannot automatically associate fragmentation with high values of density. This suggests that when the model is based not
only on the observed lightcurve, but also on the observed deceleration behaviour of the meteoroid, there is no exclusive bias against finding low
densities with the model. We can also address the disagreement of Bellot Rubio et al. (2002) with Babazhanov's work (Babazhanov 2002)
concerning the value of heat of ablation. Babazhanov (2002) assumed the heat of ablation to be fixed to
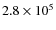 J kg-1
(latter, he brought it to
J kg-1
(latter, he brought it to
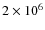 J kg-1), but in our study we found different heats of ablation involved in good model fits
of different meteoroids. This shows that the heat of ablation cannot be assumed, but should be fitted as a free parameter. The density of three other
meteoroids (ELSL09, PEKI08, PEKI09) fell well inside both the ranges defined by Bellot Rubio et al. (2002) and Babazhanov (2002). All of
these meteors fragmented, but had densities at the lower end.
J kg-1), but in our study we found different heats of ablation involved in good model fits
of different meteoroids. This shows that the heat of ablation cannot be assumed, but should be fitted as a free parameter. The density of three other
meteoroids (ELSL09, PEKI08, PEKI09) fell well inside both the ranges defined by Bellot Rubio et al. (2002) and Babazhanov (2002). All of
these meteors fragmented, but had densities at the lower end.
The heights of meteors of the Swedish campaign (at different season and latitude) are significantly higher than the Canadian one. This is partly the result of the observing geometry and may also reflect our detection bias given the volume sampled from both sites. While one of our six events has a nominally hyperbolic orbit, the precision of the velocity measurement (given the paucity of data points for the Swedish campaign data) together with the large extrapolation between the observed and extra-atmosphere velocity suggests to us rather that this is measurement uncertainty.
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.5cm]{839fig21.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg97.png) |
Figure 21: Plot of good solutions for ELSL12.The best solution falls at 4500 kg m-3. The left bound is 2000 kg m-3 and the right bound is 6500 kg m-3. |
| Open with DEXTER | |
7 Conclusion
In this work we have, for the first time for meteoroids in the size range of 10-7 to 10-8 kg, used both the dynamic and photometric observations of meteoroids to determine their densities, using a full simulation of ablation including fragmentation. We have exhaustively searched the parameter space to ensure that the density limits we determine from the model fully characterize the possible range of density. Previous studies of meteoroid density have relied on finding a single model which matches the observations, without searching for other combinations of the free parameters which might yield equally good fits. The number of meteors for which we have applied this modelling technique has been limited and we have analysed these in detail mainly to demonstrate the method at this stage. We note that our findings in terms of meteoroid physical properties should not be taken to represent the meteoroid population as a whole as our sampling is very biased by the requirements of complete trails.
Among 13 meteors in the first observing run and 29 meteors in the second run, only six satisfied the criteria of both starting and ending in the field of view of at least at one of the two stations (the necessary criteria to guarantee a complete lightcurve for an accurate photometric mass of the meteoroid). Among the six meteors, three with relatively low velocity were found to have very high densities. Taking into account fragmentation in determining the density of meteoroid does not, however, necessarily lead to higher values of meteoroid density, particularly when the heat of ablation of the meteoroid material is kept as a free parameter. The proportion of small meteoroids with high densities may be underestimated. It is possible these nearly pure iron meteoroids represent the impact pulverized remains from asteroids with ordinary chondrite compositions, a process which has been demonstrated in the lab to produce small, nearly pure iron particulates (Horz et al. 2005). Instruments with a narrow field of view and very high sensitivity are able to record these very faint meteoroids. Apart from the small number statistics in this study, our observations were biased toward slow, dense meteoroids which ablate low in the atmosphere and therefore have shorter trails, more likely to begin and end in the field of view.
![\begin{figure}
\par\includegraphics[width=12cm,height=7.3cm]{839fig22.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg98.png) |
Figure 22: Lightcurve and deceleration of ELSL12, shown together with the best fitting model. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10cm,height=6.5cm]{839fig23.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg99.png) |
Figure 23: Plot of good solutions for PEKI08. The best solution falls at 600 kg m-3. The left bound is 400 kg m-3 and the right bound is 800 kg m-3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,height=7.4cm]{839fig24.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg100.png) |
Figure 24: Lightcurve and deceleration of PEKI08, with the best fitting model. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10cm,height=6.5cm]{839fig25.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg101.png) |
Figure 25: Plot of good solutions for PEKI09. The best solution falls at 500 kg m-3. The left bound is 200 kg m-3 and the right bound is 800 kg m-3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,height=8cm]{839fig26.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg102.png) |
Figure 26: Lightcurve and deceleration of PEKI09, with the best fitting model. |
| Open with DEXTER | |
Precise measurements of deceleration provide a very important constraint in determining meteoroid density. For small meteoroids, both the photometric and dynamic data are needed to adequately constrain ablation models. High velocity meteoroids typically only show deceleration at the very end of their trajectory, with most of the energy transfer being used for ablation and very little going in to changing the velocity, making deceleration difficult to measure. The equipment used in this investigation is capable of detecting very small decelerations, but the number of usable meteors is small because of the very small fields of view. The next step will be to see if standard meteor video cameras, with fields of view in the 15 to 30 degree range, can measure the deceleration with enough accuracy to constrain the model parameters, particularly density. If so, many more meteor densities will be determined, giving the statistics needed for an analysis of the average composition of meteoroids.
Acknowledgements
J.B.K. thanks the Vatican Observatory for funding support and Guy Consolmagno for help in manuscript preparation. The authors also thank Kyle Hill, Ashley Faloon, Leslie Rogers and Nicole Kaiser for their help in collection of data as well as Jiri Borovicka and Zdenek Ceplecha for use of their software. P.G.B., MDC and R.L.H. thank the Natural Sciences and Engineering Research Council for funding support for this work.
References
- Babadzhanov, P. B. 2002, A&A, 384, 317 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Beech, M. 1986, AJ, 91, 159 [NASA ADS] [CrossRef] (In the text)
- Beech, M., & Murray, I. S. 2003, MNRAS, 345, 696 [NASA ADS] [CrossRef] (In the text)
- Beech, M., Illingworth, A., & Murray, I. S. 2003, M&PS, 38, 1045 [NASA ADS]
- Bellot Rubio, L. R., Martinez Gonzalez, M. J., Ruiz Herrera, L., et al. 2002, A&A, 389, 680 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bevington, P. R., & Robinson, D. K. 2003, Data Reduction and Error Analysis for the Physical Science (New York: McGraw-Hill), 313 (In the text)
- Borovicka, J. 1990, Bull. Astr. Inst. Czechosl., 41, 391 [NASA ADS]
- Borovicka, J. P., Koten, P., Spurny, P., Bocek, J., & Stork, R. 2005, Icarus, 174, 15 [NASA ADS] [CrossRef] (In the text)
- Borovicka, J. 2005, Proceedings of the International Astronomy Union (Cambridge University Press), 1, 249 [CrossRef]
- Borovicka, J., Spurny, P., & Koten, P. 2007, A&A, 473, 661 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Campbell, M. P., Brown, A., Leblanc, R., et al. 2000, M&PS, 35, 1259 [NASA ADS] (In the text)
- Campbell-Brown, M. D., & Koschny, D. 2004, A&A, 418, 751 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ceplecha, Z. 1968, SAO Special Rep., 279, 1 [NASA ADS] (In the text)
- Ceplecha, Z. 1987, Bull. Astron. Inst. Czech., 38, 4, 222 (In the text)
- Ceplecha, Z. 1988, Bull. Astron. Inst. Czech., 39, 4, 221 (In the text)
- Ceplecha, Z. J., Borovicka, W. G., Elford, D. O., et al. 1998, Space Sci. Rev., 84, 327 [NASA ADS] [CrossRef] (In the text)
- Fisher, A. A., Hawkes, R. L., Murray, I. S., Campbell, M. D., & LeBlanc, A. G. 2000, Planetary and Space Sci., 48, 911 [NASA ADS] [CrossRef] (In the text)
- Hapgood, M., Rothwell, P., & Royrvik, O. 1982, MNRAS, 201, 569 [NASA ADS] (In the text)
- Hawkes, R. L. 2002, Meteors in the Earth's atmosphere, ed. E. Murad, & I. P. Williams, 97 (In the text)
- Hawkes, R. L., & Jones, J. 1975, MNRAS, 173, 339 [NASA ADS] (In the text)
- Hedin, A. 1991, J. Geophys. Res. 96, 1154 (In the text)
- Hörz, F., Cintala, M. J., See, T. H., & Le, L. 2005, M&PS, 40, 1329 [NASA ADS] (In the text)
- Koten, P., Borovicka, J., Spurny, P., Betlem, H., & Evans, S. 2004, A&A, 428, 683 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lebedinets, V. N., & Portnyagin, Yu. I. 1968, SvA AJ, 11, 700 [NASA ADS] (In the text)
- Hill, K. A., Rogers, L. A., & Hawkes, R. L. 2005, A&A, 444, 615 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Myers, J. R., Sande, C. B., Miller, A. C., Warren, W. H., Jr, & Tracewell, D. A. 2001, yCat, 5109 (In the text)
- Popova, O. P. 2004, Earth, Moon, and Planets 95, 303
- Revelle, D. O. 2001, in Proc. Meteoroids 2001 Conf., ed. B. Warmbein, Kiruna, Sweden, ESA-SP, 495, 513 (In the text)
- Whipple, F. L., & Jacchia, L. G. 1957, Smithsonian Contr. Astrophysics, 1, 183 [NASA ADS] (In the text)
All Tables
Table 1: Initial grain mass distributions used for meteor ELSL11 in the first stage of analysis.
Table 2:
Values for the parameters (other than grain mass) used in the modelling.
![]() is the temperature at which fragmentation occurs,
is the temperature at which fragmentation occurs,
![]() the boiling point of the grains,
the boiling point of the grains, ![]() the specific heat, Mmass the molar mass, and Thermal Cond the thermal conductivity of the bulk meteoroid
(Meteor ELSL11).
the specific heat, Mmass the molar mass, and Thermal Cond the thermal conductivity of the bulk meteoroid
(Meteor ELSL11).
Table 3: Table summarizing parameters involved in the final stage of the high density solution model for ELSL11. Den is density, Qf is heat of ablation, Cps is specific heat, Thermal Cond is thermal conductivity.
Table 4: Distribution of grains for the solution around 1000 kg m-3 using three grain masses.
Table 5: Distribution of grains for the solution around 1000 kg m-3, with three grain sizes and modified temperatures of fragmentation, boiling and fusion.
Table 6: Variation of parameters used modeling lightcurves and decelerations for ELSL11 in the second stage search. The mass column does not give the variation of grain sizes, but the actual grain distribution used in every model.
Table 7: Values of parameters producing the best model solution among 234 solutions found to describe meteor ELSL11.
Table 8: Summary table for the six meteors modelled in detail in this study. A value of 1 under the size column means there is only one size of grains used in the modelling, 1, 2 two sizes in the composition of the meteoroid and 1, 2, 3 three sizes of grains in the composition of the meteoroid.
Table 9: Summary table of the six meteors and their statistical densities as given by the method. A value of 1 in the size column means there is only one size of grains in the composition of the meteoroid, 1, 2 two sizes in the composition of the meteoroid and 1, 2, 3 three sizes of grains in the composition of the meteoroid.
Table 10: Sumary table for the first observing campaign near London Ontario (Canada). Hb is beginning height, Hi is initial height (actual height as appeared on the field of view) , He is ending height and Hf is final height (actual height as appeared on the field of view). The velocity is the no-atmosphere velocity computed as outlined in the text.
Table 11: Summary table of the second observing campaign from Kiruna (Sweden) and Peera (Finland). Hb is beginning height, Hi is initial height (actual height as appeared on the field of view), He is ending height and Hf is final height (actual height as appeared on the field of view). The velocity is the no-atmosphere velocity computed as outlined in the text.
Table 12: Table summarizing orbital elements of all 42 meteors. alp geo and del geo are respectively geocentric right ascension and declination at the epoch J2000.0. TJ is Tisserand parameter with respect to Jupiter. PEKI20 is the case of meteors which crossed the entire field of view making it difficult to compute any trajectory solution.
Table 13:
Table showing where the best model fits occur among 151200 computed. Each model number
has a modeled lightcurve and a modeled deceleration computed with values of the free parameters as shown. The comparison of the
the modeled lightcurve with the observed one is represented by the value of the standard ![]() in the last column. We show here only
the value of
in the last column. We show here only
the value of ![]() of lightcurve. (Meteor ELSL11).
of lightcurve. (Meteor ELSL11).
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{0839fig1.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg26.png) |
Figure 1: Meteor captured in Kiruna (Sweden) on October 11 2007 at 02:55:32 UTC. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{0839fig2.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg27.png) |
Figure 2: Meteor captured in Kiruna (Sweden) on October 09 2007 at 01:37:25 UTC. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{0839fig3.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg28.png) |
Figure 3: Meteor captured in Kiruna (Sweden) on October 06 2007 at 01:54:42 UTC crossing the entire field of view. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{3mm}\includegraphics[width=8cm,height=5.7cm]{0839fig4.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg30.png) |
Figure 4: An example showing the velocity of a meteor before and after the filtering (smoothing) technique. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{0839fig5.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg31.png) |
Figure 5: The velocity of meteor ELSL11 as measured from both sites along its trajectory. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,height=5.2cm,clip]{0839fig6.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg34.png) |
Figure 6: Velocity of meteor ELSL11 from both sites along its trajectory. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{0839fig7.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg55.png) |
Figure 7: Lightcurve of the best single grain mass solution around 1000 kg m3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{0839fig8.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg56.png) |
Figure 8: Lightcurve of the best single grain mass solution around 8000 kg m3 for ELSL11. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{0839fig9.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg57.png) |
Figure 9: Deceleration of the best single grain mass solution around 1000 kg m3 for ELSL11. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{839fig10.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg58.png) |
Figure 10: Deceleration of the best single grain mass solution around 8000 kg m3 for ELSL11. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{839fig11.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg59.png) |
Figure 11: Lightcurve for ELSL11 with the model fit for a density of 8000 kg m-3 using parameters from Table 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm, height=5.7cm]{839fig12.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg60.png) |
Figure 12: Deceleration for ELSL11 for a density of 8000 kg m-3 using parameters from Table 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{839fig13.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg61.png) |
Figure 13: Modified solution for 1000 kg m-3 using three grain masses. The sudden jump in the predicted light output from the model indicates a sudden fragmentation event. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{839fig14.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg63.png) |
Figure 14: Modified solution for 1000 kg m-3, with three grain sizes and modified temperatures of fragmentation, boiling and fusion. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{839fig15.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg70.png) |
Figure 15: Plot of the best density solutions for ELSL11. The best solution falls at 5500 kg m-3. The left bound is 5000 kg m-3 and the right bound is 8000 kg m-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,height=8cm]{839fig16.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg87.png) |
Figure 16: The best model of meteor ELSL11, with a density of 5500 kg m-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{839fig17.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg89.png) |
Figure 17: Plot of accepted solutions for ELSL01. The best solution falls at 7000 kg m-3. The left bound is 5500 kg m-3 and the right bound is 8500 kg m-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,height=8cm]{839fig18.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg90.png) |
Figure 18: Lightcurve and deceleration of ELSL01, with best model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm]{839fig19.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg91.png) |
Figure 19: Plot of best solutions for ELSL09.The best solution falls at 900 kg m-3. The left bound is 750 kg m-3 and the right bound is 1150 kg m-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,height=8cm]{839fig20.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg92.png) |
Figure 20: Lightcurve and deceleration of ELSL09 together with the best model fit. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.5cm]{839fig21.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg97.png) |
Figure 21: Plot of good solutions for ELSL12.The best solution falls at 4500 kg m-3. The left bound is 2000 kg m-3 and the right bound is 6500 kg m-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,height=7.3cm]{839fig22.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg98.png) |
Figure 22: Lightcurve and deceleration of ELSL12, shown together with the best fitting model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=10cm,height=6.5cm]{839fig23.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg99.png) |
Figure 23: Plot of good solutions for PEKI08. The best solution falls at 600 kg m-3. The left bound is 400 kg m-3 and the right bound is 800 kg m-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,height=7.4cm]{839fig24.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg100.png) |
Figure 24: Lightcurve and deceleration of PEKI08, with the best fitting model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=10cm,height=6.5cm]{839fig25.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg101.png) |
Figure 25: Plot of good solutions for PEKI09. The best solution falls at 500 kg m-3. The left bound is 200 kg m-3 and the right bound is 800 kg m-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,height=8cm]{839fig26.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10839-08/Timg102.png) |
Figure 26: Lightcurve and deceleration of PEKI09, with the best fitting model. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.