| Issue |
A&A
Volume 497, Number 3, April III 2009
|
|
|---|---|---|
| Page(s) | 713 - 728 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200810352 | |
| Published online | 24 February 2009 | |
Frequency and properties of bars in cluster and field galaxies at intermediate redshifts![[*]](/icons/foot_motif.png)
F. D. Barazza1 - P. Jablonka1,2,3 - V. Desai4 - S. Jogee5 - A. Aragón-Salamanca6 - G. De Lucia7 - R. P. Saglia8 - C. Halliday9 - B. M. Poggianti10 - J. J. Dalcanton 11 - G. Rudnick12 - B. Milvang-Jensen13,14 - S. Noll8,15 - L. Simard16 - D. I. Clowe17 - R. Pelló18 - S. D. M. White7 - D. Zaritsky19
1 - Laboratoire d'Astrophysique, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
2 -
Université de Genève, Observatoire de Sauverny, 1290 Versoix, Switzerland
3 -
GEPI, CNRS-UMR8111, Observatoire de Paris, section de Meudon, 5 place Jules Janssen, 92195 Meudon Cedex, France
4 -
Spitzer Science Center, Caltech, Pasadena CA 91125, USA
5 -
Department of Astronomy, University of Texas at Austin, 1 University Station C1400, Austin, TX 78712-0259, USA
6 -
School of Physics and Astronomy, University of Nottingham, University Park, Nottingham NG7 2RD, UK
7 -
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Strasse 1, 85748 Garching bei München, Germany
8 -
Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse, 85748 Garching bei München, Germany
9 -
INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
10 -
Osservatorio Astronomico di Padova, Vicolo dell'Osservatorio 5, 35122 Padova, Italy
11 -
Astronomy Department, University of Washington, Box 351580, Seattle, WA 98195, USA
12 -
NOAO, 950 N. Cherry Avenue, Tucson, AZ 85719, USA
13 -
Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
14 -
The Royal Library/Copenhagen University Library, Research Dept., Box 2149, 1016 Copenhagen K, Denmark
15 -
Observatoire Astronomique de Marseille-Provence, 38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
16 -
Herzberg Institute of Astrophysics, National Research Council of Canada, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
17 -
Ohio University, Department of Physics and Astronomy, Clippinger Labs 251B, Athens, OH 45701, USA
18 -
Laboratoire d'Astrophysique de Toulouse-Tarbes, CNRS, Université de Toulouse, 14 avenue Édouard Belin, 31400 Toulouse, France
19 -
Steward Observatory, University of Arizona, 933 North Cherry Avenue, Tucson, AZ 85721, USA
Received 9 June 2008 / Accepted 29 January 2009
Abstract
We present a study of large-scale bars in field and cluster environments out to redshifts of  0.8 using a final sample of 945 moderately inclined disk galaxies drawn from the
EDisCS project. We characterize bars and their host galaxies and look for relations between the presence of a bar and the properties of the underlying disk. We investigate whether the fraction and
properties of bars in clusters are different from their counterparts in the field. The properties of bars and disks are determined by ellipse fits to the surface brightness distribution
of the galaxies using HST/ACS images in the F814W filter. The bar identification is based on quantitative criteria after highly inclined (>
0.8 using a final sample of 945 moderately inclined disk galaxies drawn from the
EDisCS project. We characterize bars and their host galaxies and look for relations between the presence of a bar and the properties of the underlying disk. We investigate whether the fraction and
properties of bars in clusters are different from their counterparts in the field. The properties of bars and disks are determined by ellipse fits to the surface brightness distribution
of the galaxies using HST/ACS images in the F814W filter. The bar identification is based on quantitative criteria after highly inclined (>
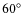 ) systems have been excluded. The total
optical bar fraction in the redshift range
z=0.4-0.8 (median z=0.60), averaged over the entire sample, is
) systems have been excluded. The total
optical bar fraction in the redshift range
z=0.4-0.8 (median z=0.60), averaged over the entire sample, is 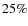 (
(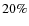 for strong bars). For the cluster and field subsamples, we measure bar fractions of
for strong bars). For the cluster and field subsamples, we measure bar fractions of 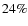 and
and 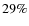 ,
respectively. We find that bars in clusters are on average longer than in the field and preferentially found close to the cluster center, where the bar fraction is somewhat higher (
,
respectively. We find that bars in clusters are on average longer than in the field and preferentially found close to the cluster center, where the bar fraction is somewhat higher ( 31%) than at larger distances (
31%) than at larger distances ( 18%). These findings however rely on a relatively small subsample and might be affected by small number statistics. In agreement with local studies, we find that disk-dominated galaxies have a higher optical bar fraction (
18%). These findings however rely on a relatively small subsample and might be affected by small number statistics. In agreement with local studies, we find that disk-dominated galaxies have a higher optical bar fraction ( 45%) than bulge-dominated galaxies (
45%) than bulge-dominated galaxies ( 15%). This result is based on Hubble types and effective radii and does not change with redshift. The latter finding implies that bar
formation or dissolution is strongly connected to the emergence of the morphological structure of a disk and is typically accompanied by a transition in the Hubble type. The question whether internal or external factors are more important for bar formation and evolution cannot be answered definitely. On the one hand, the bar fraction and properties of cluster and field samples of disk galaxies are quite similar, indicating that internal processes are crucial for bar formation. On the other hand, we find evidence that cluster centers are favorable locations for bars, which suggests that the internal processes responsible for bar growth are supported by the typical
interactions taking place in such environments.
15%). This result is based on Hubble types and effective radii and does not change with redshift. The latter finding implies that bar
formation or dissolution is strongly connected to the emergence of the morphological structure of a disk and is typically accompanied by a transition in the Hubble type. The question whether internal or external factors are more important for bar formation and evolution cannot be answered definitely. On the one hand, the bar fraction and properties of cluster and field samples of disk galaxies are quite similar, indicating that internal processes are crucial for bar formation. On the other hand, we find evidence that cluster centers are favorable locations for bars, which suggests that the internal processes responsible for bar growth are supported by the typical
interactions taking place in such environments.
Key words: galaxies: spiral - galaxies: structure - galaxies: clusters: general - galaxies: evolution - galaxies: formation
1 Introduction
There is evidence that the dynamical and secular evolution of disk galaxies is intimately connected with the presence of stellar bars. Theory and n-body simulations predict that bars transfer angular momentum to the outer disk, which causes the stellar orbits in the bar to become elongated and the bar amplitude to increase (Athanassoula 2003; Pfenniger & Friedli 1991; Sellwood & Wilkinson 1993; Lynden-Bell 1979). The growing bar becomes more and more efficient in driving gas inside the corotation radius towards the center of the disk, which can trigger starbursts (Regan et al. 1999; Sakamoto et al. 1999; Jogee et al. 2005; Sheth et al. 2005; Regan & Teuben 2004; Bournaud & Combes 2002; Hunt & Malkan 1999; Schinnerer et al. 2002) and contribute to the formation of disky bulges (Debattista et al. 2006; Sakamoto et al. 1999; Jogee et al. 2005; Kormendy & Kennicutt 2004; Athanassoula et al. 2005; Kormendy 1993; Sheth et al. 2005). The redistribution of angular momentum driven by bars is not restricted to the baryonic component, but also applies to dark matter (Berentzen et al. 2006; Combes et al. 1990; Weinberg 1985; Debattista & Sellwood 2000). Another indication of secular evolution induced by the orbital structure and resonances in a bar potential is provided by box- or peanut-shaped bulges in inclined galaxies (Debattista et al. 2006; Combes et al. 1990; Bureau & Freeman 1999; Pfenniger & Norman 1990; Kuijken & Merrifield 1995; Martinez-Valpuesta et al. 2006). These processes affect the properties of disk galaxies and therefore shape the diversity of morphologies.
While it is still unknown why a specific disk galaxy hosts a bar and an apparently similar galaxy is unbarred, it is clear that a significant fraction of bright disk galaxies appears barred in optical
observations (Reese et al. 2007; Eskridge et al. 2000; Marinova & Jogee 2007; Barazza et al. 2008). In studies carried out in the near-infrared (NIR) or in both, NIR and optical, the NIR bar fractions are typically higher (Laurikainen et al. 2004; Eskridge et al. 2000; Marinova & Jogee 2007; Menéndez-Delmestre et al. 2007; Knapen 1999). These findings indicate that bar detection is affected by dust extinction and that studies completed at different wavelengths cannot be readily compared. This caveat is important particularly when results from local bar studies are compared with the findings of investigations at intermediate redshifts, where issues such as band shifting, surface brightness dimming, and reduced resolution further decrease the bar detection rate. In earlier studies, it was found that the bar fraction undergoes a significant intrinsic decline out to 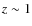 (van den Bergh et al. 2000; Abraham et al. 1999), which was confirmed by Sheth et al. (2008). Other studies report that the bar fraction is fairly constant out to
(van den Bergh et al. 2000; Abraham et al. 1999), which was confirmed by Sheth et al. (2008). Other studies report that the bar fraction is fairly constant out to 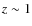 for strong bars (Jogee et al. 2004, bar ellipticity >0.4) or all bars (Elmegreen et al. 2004; Zheng et al. 2005, see also Sect. 7), once the aforementioned effects are taken
into account.
for strong bars (Jogee et al. 2004, bar ellipticity >0.4) or all bars (Elmegreen et al. 2004; Zheng et al. 2005, see also Sect. 7), once the aforementioned effects are taken
into account.
Table 1: Basic properties of clusters and the secondary structures.
To identify and characterize bars, different methods have been applied. The most straightforward approach is to inspect images visually and assign a bar class (e.g., weak/strong bars) to each galaxy (Eskridge et al. 2000; de Vaucouleurs et al. 1991). By adopting this approach, strong bars were detected twice as frequently in near-infrared data than optical data (Eskridge et al. 2000) and the bar fraction was found to increase between Sc galaxies and later types (Odewahn 1996). Apart from visual classification, a quantitative characterization of bars has been attempted using for instance, the gravitational torque method (Buta et al. 2005; Block et al. 2002; Laurikainen et al. 2002), Fourier dissection (Laurikainen et al. 2006; Buta et al. 2006), and ellipse fits to the galaxy isophotes (Sheth et al. 2000; Reese et al. 2007; Regan & Elmegreen 1997; Marinova & Jogee 2007; Erwin 2005; Abraham et al. 1999; Sheth et al. 2002; Knapen et al. 2000; Jogee et al. 2004; Whyte et al. 2002; Elmegreen et al. 2004; Jogee et al. 2002b; Erwin & Sparke 2002; Menéndez-Delmestre et al. 2007; Barazza et al. 2008; Jogee et al. 2002a; Sheth et al. 2008). These methods provide measurements of the bar length and shape and enable the impact of the bar on the disk to be assessed.
The vast majority of these bar studies have concentrated on field galaxy samples and estimated the bar fraction among disk galaxies and the general properties of bars and their host galaxies. First attempts have been made to relate the presence of a bar to its host galaxy properties, such as disk structure, central surface brightness, or color. On the other hand, there have been few studies of the relation between the occurrence of bars and environment. Kumai et al. (1986) studied the relative fractions of different disk galaxy types as a function of environment. They detected no increase in bar fraction inside galaxy clusters or groups, but measured a significantly higher fraction of barred disks in binary systems. This was confirmed by Elmegreen et al. (1990) and Giuricin et al. (1993), who both found that galaxies in binary systems are preferentially early type and barred. A similar result was reported by Varela et al. (2004). Interestingly, while the fraction of barred disks in clusters or groups is not higher than in the field (Marinova et al. 2009; van den Bergh 2002; Kumai et al. 1986; van den Bergh 2007), Thompson (1981) and Andersen (1996) presented evidence that barred galaxies in the Coma and Virgo clusters are more concentrated toward the cluster centers than unbarred disks.
We present the first study of bars in clusters at intermediate redshifts, which enables the properties of bars and their host galaxies to be studied in dense environments. We use a final sample of 945 moderately inclined disk galaxies drawn from a parent sample of 1906 disk galaxies from the ESO distant cluster survey (EDisCS, White et al. 2005). We use the available I-band HST/ACS images to identify and characterize bars, based on quantitative criteria. We use this sample to look for relations between the occurrence and the properties of bars and their host galaxies. For a subsample of 241 objects, for which spectroscopic redshifts and reliable cluster membership determinations are available, we look for relations between barred and unbarred galaxies and their environment. We also study a wide range of redshifts, which allows us to search for trends with increasing look-back time. The outline of the paper is as follows: in Sect. 2 we present
the available data and our sample selection. The method to identify and characterize bars as well as limits of the detectability of bars in our data is described in Sect. 3. Our results in terms of bar fractions and relations between bars and host galaxy properties are presented in Sect. 4. In Sect. 5 we discuss the properties of the bars in our sample galaxies, and in Sect. 6 look at the specific distribution of barred galaxies within the
clusters. The implications of our results are discussed in Sect. 7 and the summary and conclusions are given in Sect. 8. Throughout the paper, we assume a flat cosmology with
![]() and H0=70 km s-1 Mpc-1. Magnitudes are given in the Vega system.
and H0=70 km s-1 Mpc-1. Magnitudes are given in the Vega system.
2 Sample selection from EDisCS
The ESO Distant Cluster Survey is a study of 26 optically selected and spectroscopically confirmed galaxy systems, from rich groups to massive clusters, smoothly distributed between redshifts 0.39 and 0.96 (Milvang-Jensen et al. 2008; Halliday et al. 2004). For all systems, we have assembled three-band optical VLT
deep photometry, deep NTT/SOFI near-infrared imaging, and optical VLT/FORS2 spectroscopy (White et al. 2005). We also acquired HST/ACS images in the F814W filter for 10 fields containing the most distant clusters studied by EDisCS. The exposure time of these observations per pixel is 2040 s, except for the central
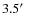
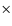
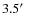 ,
which has an exposure time per pixel of 10 200 s. We completed both a visual classification of galaxy morphologies (see Sect. 2.1) and a quantitative analysis of their structural parameters (Desai et al. 2007; Simard et al. 2009). The visual classification was completed for all galaxies brighter than
,
which has an exposure time per pixel of 10 200 s. We completed both a visual classification of galaxy morphologies (see Sect. 2.1) and a quantitative analysis of their structural parameters (Desai et al. 2007; Simard et al. 2009). The visual classification was completed for all galaxies brighter than
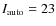 mag, where
mag, where
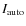 is the SExtractor AUTO magnitude measured on the I-band VLT images. In this work, we adopt the same magnitude cut at
is the SExtractor AUTO magnitude measured on the I-band VLT images. In this work, we adopt the same magnitude cut at
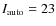 mag and consider only galaxies with Hubble types S0-Sm/Im, i.e. disk galaxies and lenticulars, which can also be barred
mag and consider only galaxies with Hubble types S0-Sm/Im, i.e. disk galaxies and lenticulars, which can also be barred![]() . For
. For 
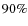 of the sample, a Sérsic fit to the surface brightness distribution (with GIM2D, Simard et al. 2009,2002) has been performed on the I-band HST/ACS images, providing the effective radius used in our analysis (see Sect. 4.3).
of the sample, a Sérsic fit to the surface brightness distribution (with GIM2D, Simard et al. 2009,2002) has been performed on the I-band HST/ACS images, providing the effective radius used in our analysis (see Sect. 4.3).
We select all galaxies meeting these criteria in ten fields regardless of whether they are cluster members or group/field galaxies. These fields encompass a total of 12 clusters and 4 groups. Structures with
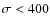 km s-1 are regarded as groups. Galaxies are considered to be cluster/group members if the integrated photometric redshift probability to be within z
km s-1 are regarded as groups. Galaxies are considered to be cluster/group members if the integrated photometric redshift probability to be within z 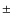 0.1 of the cluster redshift is greater than a specific limit. These limits are based on our spectroscopy and range from 0.1 to 0.35 depending on the filter set available for each particular field (Pelló et al. 2008; White et al. 2005). Cluster/group membership for objects with spectroscopic observations is defined as being within
0.1 of the cluster redshift is greater than a specific limit. These limits are based on our spectroscopy and range from 0.1 to 0.35 depending on the filter set available for each particular field (Pelló et al. 2008; White et al. 2005). Cluster/group membership for objects with spectroscopic observations is defined as being within 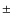
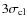 of
of
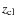 (Milvang-Jensen et al. 2008; Halliday et al. 2004). Photometric redshifts were determined using the methods described in Rudnick et al. (2001) and Pelló et al. (2008),
and were based on the optical+near-infrared photometry. The accuracy of photometric redshifts is typically
(Milvang-Jensen et al. 2008; Halliday et al. 2004). Photometric redshifts were determined using the methods described in Rudnick et al. (2001) and Pelló et al. (2008),
and were based on the optical+near-infrared photometry. The accuracy of photometric redshifts is typically
![]()
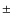 0.01 (Pelló et al. 2008). The rest-frame magnitudes and colors were computed using the method described in Rudnick et al. (2003). We restrict the cluster and field samples to the redshift range
z=0.4-0.8 in order to remain in the rest-frame optical. The median photometric redshift of the total sample is 0.60. The basic properties of the main and secondary structures and the number of objects found in these structures are given in Table 1. We show the distributions in redshift and absolute V magnitude in Figs. 1 and 2, respectively. These plots include the parent sample of 1906 galaxies, to which our bar classification method (see Sect. 3) was applied. Spectroscopic redshifts are available for a subsample of 459 galaxies. For the low redshift cluster fields (z<0.6) spectroscopic observations were restricted to objects with I<22 mag and for the high redshift cluster fields (z>0.6) to I<23 mag (Milvang-Jensen et al. 2008; Halliday et al. 2004). This ensures that the distribution in absolute magnitude for galaxies with spectroscopic redshifts remains roughly the same over the entire redshift range (
z=0.4-0.8). The distributions in Figs. 1 and 2 for the cluster and field subsamples are very similar. The arrows in Fig. 2 indicate the absolute
V-band magnitude for a Sa galaxy at z=0.8 corresponding to
0.01 (Pelló et al. 2008). The rest-frame magnitudes and colors were computed using the method described in Rudnick et al. (2003). We restrict the cluster and field samples to the redshift range
z=0.4-0.8 in order to remain in the rest-frame optical. The median photometric redshift of the total sample is 0.60. The basic properties of the main and secondary structures and the number of objects found in these structures are given in Table 1. We show the distributions in redshift and absolute V magnitude in Figs. 1 and 2, respectively. These plots include the parent sample of 1906 galaxies, to which our bar classification method (see Sect. 3) was applied. Spectroscopic redshifts are available for a subsample of 459 galaxies. For the low redshift cluster fields (z<0.6) spectroscopic observations were restricted to objects with I<22 mag and for the high redshift cluster fields (z>0.6) to I<23 mag (Milvang-Jensen et al. 2008; Halliday et al. 2004). This ensures that the distribution in absolute magnitude for galaxies with spectroscopic redshifts remains roughly the same over the entire redshift range (
z=0.4-0.8). The distributions in Figs. 1 and 2 for the cluster and field subsamples are very similar. The arrows in Fig. 2 indicate the absolute
V-band magnitude for a Sa galaxy at z=0.8 corresponding to
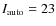 mag (
mag (
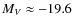 mag, taking into account a K-correction). The same calculation for a Sc galaxy would result in a slightly fainter absolute V-band magnitude. In the following, we present our main results for both the total sample and a sample restricted to
mag, taking into account a K-correction). The same calculation for a Sc galaxy would result in a slightly fainter absolute V-band magnitude. In the following, we present our main results for both the total sample and a sample restricted to
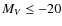 mag, which is our completeness limit (the complete sample). This shows that the incompleteness for galaxies with MV>-20 is not biasing our results. All numbers and fractions always refer to the total sample. In Sect. 4, results based on the separation between cluster/group and field galaxies are always based on our spectroscopic data. This reduces the sample size considerably, but ensures a
reliable cluster or field allocation. We estimate that a photometrically based cluster sample would have a field galaxy contamination of up to
mag, which is our completeness limit (the complete sample). This shows that the incompleteness for galaxies with MV>-20 is not biasing our results. All numbers and fractions always refer to the total sample. In Sect. 4, results based on the separation between cluster/group and field galaxies are always based on our spectroscopic data. This reduces the sample size considerably, but ensures a
reliable cluster or field allocation. We estimate that a photometrically based cluster sample would have a field galaxy contamination of up to 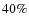 .
Finally, we emphasize that the number of objects in the four groups is rather small and that only three bars are found in group galaxies (see also Table 1). For the remainder of the paper, we therefore refer to the subsample of
cluster/group galaxies as the cluster subsample.
.
Finally, we emphasize that the number of objects in the four groups is rather small and that only three bars are found in group galaxies (see also Table 1). For the remainder of the paper, we therefore refer to the subsample of
cluster/group galaxies as the cluster subsample.
2.1 The visual classification of the galaxies
We visually classified all galaxies brighter than
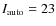 mag, where
mag, where
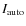 is the SExtactor (Bertin & Arnouts 1996) magnitude measured on the I-band VLT images and is an estimate of the total magnitude of a galaxy in the Vega system. This classification has been described in detail in Desai et al. (2007). We recall here its main features in particular those related to our purpose, i.e., the spiral galaxies. Each of the five classifiers (AAS, JJD, VD, PJ and BP) was trained on the HST WFPC2 images and visual morphological catalogs of the 0.3<z<0.5 MORPHS clusters, using the same procedure as described in Smail et al. (1997).
is the SExtactor (Bertin & Arnouts 1996) magnitude measured on the I-band VLT images and is an estimate of the total magnitude of a galaxy in the Vega system. This classification has been described in detail in Desai et al. (2007). We recall here its main features in particular those related to our purpose, i.e., the spiral galaxies. Each of the five classifiers (AAS, JJD, VD, PJ and BP) was trained on the HST WFPC2 images and visual morphological catalogs of the 0.3<z<0.5 MORPHS clusters, using the same procedure as described in Smail et al. (1997).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f1.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg40.png) |
Figure 1: Redshift distribution of the basic sample of 1906 disk galaxies. The solid line shows the distribution based on spectroscopic redshifts and the dashed line that based on photometric redshifts. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f2.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg41.png) |
Figure 2:
Distribution of absolute V magnitude for the cluster and field samples. The solid histograms show the distribution for the total sample of 1906 galaxies, whereas the dashed histograms represent the spectroscopic subsample. The arrows indicate the magnitude cut (at
|
| Open with DEXTER | |
Since, in this analysis, we consider possible trends of bar fraction with the Hubble type of the galaxies, we now investigate our ability to distinguish between adjacent types, e.g., Sa from Sb, Sc from Sd, etc. Galaxies in the cluster Cl1216-1201 (z=0.79) were classified by all five classifiers and the data set for this cluster can be used to complete the most reliable statistical analysis. We found that the mean dispersion between classifiers and for all spiral galaxies was 1.2 T-type. The fraction of galaxies with a dispersion of less than 2 T-types among galaxies was 66%, and increased to 89% for 3-types (Sa to Sb for example). These global numbers did not change if one considers early- or late-type spirals. Type 6 (Sd) galaxies were identified within 3 T-types at 88%, while type 1 (Sa) were at 91%. The rest of the clusters were analyzed by two classifiers. Their statistics is either identical to the one of Cl1216-1201 or have slightly lower success rates. However, the ability to agree to less than 3 T-type is never lower than 60%. This shows that our classification is robust and trends along the Hubble sequence can be reliably detected. In Fig. 3 we show examples of S0-Sc galaxies for cluster CL1232-1250 at z=0.54 and cluster CL1216-1201 at z=0.79. The image depth and resolution are sufficient to separate Hubble types even at z=0.79.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0352f3-1.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg43.png) |
Figure 3:
From left to right examples of S0, Sa, Sb, and Sc galaxies for cluster CL1232-1250 at z=0.54 (top row) and cluster CL1216-1201 at z=0.79 (bottom row). The images are |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0352f4.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg44.png) |
Figure 4:
This is an example of an inclined (
|
| Open with DEXTER | |
3 Bar characterization and detectability
We first describe our method to detect and characterize bars using the I-band HST/ACS images and then discuss the limitations of the detectability of bars imposed by the observations used in our study.
3.1 The detection and characterization of bars
Our method of finding bars relies on the fact that the isophotes of bars in moderately inclined disk galaxies (i.e., with disk inclination
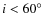 )
have much higher ellipticities than the isophotes of the underlying disk. The ellipticities of the isophotes are derived by fitting ellipses to the surface brightness distribution of the disks. The corresponding profiles of ellipticity (
)
have much higher ellipticities than the isophotes of the underlying disk. The ellipticities of the isophotes are derived by fitting ellipses to the surface brightness distribution of the disks. The corresponding profiles of ellipticity (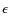 )
and position angle (PA) are investigated based on quantitative criteria. The method of ellipse fits has been used widely by observational studies of bars in disk galaxies
(Reese et al. 2007; Knapen et al. 2000; Sheth et al. 2000; Whyte et al. 2002; Laine et al. 2002; Regan & Elmegreen 1997; Elmegreen et al. 2004; Abraham et al. 1999; Friedli et al. 1996; Sheth et al. 2003; Jogee et al. 2002b,1999; Menéndez-Delmestre et al. 2007; Sheth et al. 2008; Jogee et al. 2002a).
There is also strong theoretical evidence supporting this approach (Shen & Sellwood 2004; Athanassoula 1992).
)
and position angle (PA) are investigated based on quantitative criteria. The method of ellipse fits has been used widely by observational studies of bars in disk galaxies
(Reese et al. 2007; Knapen et al. 2000; Sheth et al. 2000; Whyte et al. 2002; Laine et al. 2002; Regan & Elmegreen 1997; Elmegreen et al. 2004; Abraham et al. 1999; Friedli et al. 1996; Sheth et al. 2003; Jogee et al. 2002b,1999; Menéndez-Delmestre et al. 2007; Sheth et al. 2008; Jogee et al. 2002a).
There is also strong theoretical evidence supporting this approach (Shen & Sellwood 2004; Athanassoula 1992).
The specific method we use in this study has already been applied in earlier investigations and a detailed description can be found in the corresponding papers (Jogee et al. 2004; Marinova & Jogee 2007; Barazza et al. 2008). We start by fitting ellipses to the images using the standard IRAF task ``ellipse'' via an iterative wrapper developed by Jogee et al. (2004), which (a) refines the center of the galaxy using the IRAF routine ``imcenter''; (b) determines the maximum galaxy semi-major axis length (
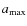 )
out to which
ellipses will be fitted by finding where the galaxy isophotes reach the sky level; (c) executes ``ellipse'' for a maximum number N of iterations, for each object, analyzing each output on the fly to guide the next fit. The wrapper stops either if all the isophotes can be fitted or if the maximum N of iterations is reached, where N is typically set to be 300. A fit is considered to be successful if all the isophotes can be fitted either in one single fit or via a combination of partial fits. The fitting process for an individual galaxy can fail completely if the center of an object cannot be found or if the surface brightness oscillates too strongly across the galaxy. This typically happens when a foreground star is present or when two objects overlap. For only
)
out to which
ellipses will be fitted by finding where the galaxy isophotes reach the sky level; (c) executes ``ellipse'' for a maximum number N of iterations, for each object, analyzing each output on the fly to guide the next fit. The wrapper stops either if all the isophotes can be fitted or if the maximum N of iterations is reached, where N is typically set to be 300. A fit is considered to be successful if all the isophotes can be fitted either in one single fit or via a combination of partial fits. The fitting process for an individual galaxy can fail completely if the center of an object cannot be found or if the surface brightness oscillates too strongly across the galaxy. This typically happens when a foreground star is present or when two objects overlap. For only 
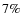 of objects in our initial sample, the ellipse fit failed and successful fits were obtained for 1906 galaxies. When using the IRAF task ``ellipse'' for ellipse fits, the goodness of the best-fit solution is measured by four harmonic amplitudes (A3, A4, B3, B4), which describe by how much the true isophote differs from the best-fit model ellipse (e.g., Jedrzejewski 1987). We find that the deviations from ellipses are typically small (<
of objects in our initial sample, the ellipse fit failed and successful fits were obtained for 1906 galaxies. When using the IRAF task ``ellipse'' for ellipse fits, the goodness of the best-fit solution is measured by four harmonic amplitudes (A3, A4, B3, B4), which describe by how much the true isophote differs from the best-fit model ellipse (e.g., Jedrzejewski 1987). We find that the deviations from ellipses are typically small (<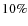 ).
).
Based on these fits, radial profiles of the surface brightness, 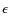 ,
and PA are derived, and the fitted ellipses are overplotted onto the galaxy images. Examples of these profiles and
overlays are shown in Figs. 4-6. These representations and the true images
are the primary tools for the classification. In a first step, the disk inclination (i) is determined using the
,
and PA are derived, and the fitted ellipses are overplotted onto the galaxy images. Examples of these profiles and
overlays are shown in Figs. 4-6. These representations and the true images
are the primary tools for the classification. In a first step, the disk inclination (i) is determined using the 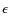 profile. For each galaxy, an interactive visualization tool (Jogee et al. 2004) is used to display the overlay and radial profiles, interactively determine the
disk parameters (ellipticity, PA) and bar parameters (maximum ellipticity, semi-major axis, PA), and assign the main classification of ``inclined'', ``unbarred'', and ``barred''. If the disk inclination, i.e., the inclination in the outer parts of the galaxy is higher than
profile. For each galaxy, an interactive visualization tool (Jogee et al. 2004) is used to display the overlay and radial profiles, interactively determine the
disk parameters (ellipticity, PA) and bar parameters (maximum ellipticity, semi-major axis, PA), and assign the main classification of ``inclined'', ``unbarred'', and ``barred''. If the disk inclination, i.e., the inclination in the outer parts of the galaxy is higher than
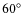 (or
(or
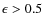 )
the galaxy is classified as being too inclined and excluded from further analysis. The galaxy shown in Fig. 4 is such an object. We find that
)
the galaxy is classified as being too inclined and excluded from further analysis. The galaxy shown in Fig. 4 is such an object. We find that 
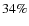 (652 objects) of the sample galaxies have
(652 objects) of the sample galaxies have
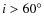 ,
which is similar to results for other samples (Jogee et al. 2004; Barazza et al. 2008), that are comparable in size and where the same method has been applied.
,
which is similar to results for other samples (Jogee et al. 2004; Barazza et al. 2008), that are comparable in size and where the same method has been applied.
The remaining galaxies were then classified as unbarred or barred, based on the following quantitative criteria: (1) 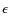 increases steadily to a global maximum higher than 0.25, while the PA value remains constant (within
increases steadily to a global maximum higher than 0.25, while the PA value remains constant (within
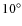 ); and (2)
); and (2) 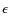 then drops by at least 0.1 and the PA changes at the transition between the bar to the disk region. Figure 6 shows a galaxy, which meets these two criteria. While unbarred spiral galaxies can also reach large
then drops by at least 0.1 and the PA changes at the transition between the bar to the disk region. Figure 6 shows a galaxy, which meets these two criteria. While unbarred spiral galaxies can also reach large 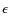 and exhibit prominent drops in their
and exhibit prominent drops in their 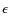 profiles in the region dominated by spiral arms, this is always accompanied by strong isophotal twists. Since we exclude too inclined
galaxies, criterion (2) is characteristic of a barred disk, because the disks are typically more circular than the bars for moderately inclined galaxies. After classifying a galaxy, we used our
interactive display tool to measure the ellipticity, PA, and semi-major axis of its outer disk. For galaxies classified as barred, we measure the same quantities, as well as the maximum ellipticity,
profiles in the region dominated by spiral arms, this is always accompanied by strong isophotal twists. Since we exclude too inclined
galaxies, criterion (2) is characteristic of a barred disk, because the disks are typically more circular than the bars for moderately inclined galaxies. After classifying a galaxy, we used our
interactive display tool to measure the ellipticity, PA, and semi-major axis of its outer disk. For galaxies classified as barred, we measure the same quantities, as well as the maximum ellipticity,
 ,
of the bar and the semi-major axis,
,
of the bar and the semi-major axis,
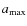 ,
of maximum bar ellipticity. We use
,
of maximum bar ellipticity. We use
 as a partial measure of the bar strength and
as a partial measure of the bar strength and
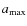 as an estimate for the semi-major axis of the bar,
as an estimate for the semi-major axis of the bar,
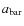 .
A detailed theoretical and empirical justification of this approach is provided in Marinova & Jogee (2007) and Menéndez-Delmestre et al. (2007) (see also the discussion in Sect. 5).
.
A detailed theoretical and empirical justification of this approach is provided in Marinova & Jogee (2007) and Menéndez-Delmestre et al. (2007) (see also the discussion in Sect. 5).
![\begin{figure}
\par\includegraphics[width=14.55cm,clip]{0352f5.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg52.png) |
Figure 5:
The same as Fig. 4, but for a galaxy classified as unbarred according to our ellipse fits. The images are roughly
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=14.55cm,clip]{0352f6.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg54.png) |
Figure 6:
The same as Fig. 4, but for a galaxy classified as barred from ellipse fits. The images are roughly
|
| Open with DEXTER | |
The classifications and quantities measured are based on the observed images and profiles and are therefore affected by projection effects (for a detailed discussion of how disk inclinations affect apparent bar sizes, see Barazza et al. 2008). We did not attempt to deproject our galaxies, since it is difficult to determine the PA in the outer disks accurately enough, particularly for galaxies at high redshifts. The resulting large errors in the PA would cause inaccurate deprojections. We also note that the statistical results before and after deprojection are very similar (Marinova & Jogee 2007).
Of the remaining 1254 moderately inclined (
 ) galaxies, we exclude another 309 objects for two reasons: i) the presence of a close neighbor, whose outer isophotes overlap with the
target galaxy, can cause ``ellipse'' to fit the two galaxies simultaneously. The number of these cases is relatively high, due to the fact that many galaxies in our sample are located in or close to cluster centers, where the galaxy density is high; ii) galaxies with very low surface brightnesses, resulting in very messy profiles, which could not be properly classified. Our final sample therefore comprises 945 disk galaxies, among which we find 238 to be barred.
) galaxies, we exclude another 309 objects for two reasons: i) the presence of a close neighbor, whose outer isophotes overlap with the
target galaxy, can cause ``ellipse'' to fit the two galaxies simultaneously. The number of these cases is relatively high, due to the fact that many galaxies in our sample are located in or close to cluster centers, where the galaxy density is high; ii) galaxies with very low surface brightnesses, resulting in very messy profiles, which could not be properly classified. Our final sample therefore comprises 945 disk galaxies, among which we find 238 to be barred.
3.2 The detectability of bars
As shown by several studies (e.g., Eskridge et al. 2000; Marinova & Jogee 2007; Knapen 1999), the detectability of bars improves at longer wavelengths. The bar fraction measured for near-infrared observational studies are typically slightly higher than for studies based on optical imaging. The main reason for this difference is extinction caused by dust absorption, which is less severe at longer wavelengths. Our sample of disk galaxies covers the redshift range z=0.4-0.8, where the I-band observations correspond to rest-frame B to V. Hence, band-shifting effects should not be so strong, but since the rest-frame range is rather blue, we should miss bars due to dust absorption, and the provided bar fractions must be considered as lower limits. In addition, enhanced star formation and dust obscuration further impede bar detection at higher redshifts.
Another factor affecting the identification of bars in disk galaxies is the resolution of the observations. We apply two requirements for bar detection: (1) a bar can only be detected if its angular diameter encompasses at least 4 PSFs; (2) the bar size (i.e., the bar radius,
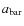 )
covers at least four pixels. Criterion (1) is based on the fact that we need at least one PSF for the bulge, two PSFs for the bar region, and one PSF for the disk beyond the bar. This resolution is
needed to detect reliably the quantitative bar signatures described in Sect. 3.1. The PSF on our images is
)
covers at least four pixels. Criterion (1) is based on the fact that we need at least one PSF for the bulge, two PSFs for the bar region, and one PSF for the disk beyond the bar. This resolution is
needed to detect reliably the quantitative bar signatures described in Sect. 3.1. The PSF on our images is
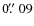 ,
which corresponds to
,
which corresponds to  675 pc at the highest redshift (
675 pc at the highest redshift (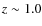 )
and 4 PSFs correspond to
)
and 4 PSFs correspond to  2.7 kpc at that redshift. In Fig. 7, we plot redshift versus the bar diameter in arcsec. The dotted line indicates 4 PSFs (i.e.,
2.7 kpc at that redshift. In Fig. 7, we plot redshift versus the bar diameter in arcsec. The dotted line indicates 4 PSFs (i.e.,
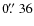 ). The second requirement for bar detection is illustrated in Fig. 8, where we plot
). The second requirement for bar detection is illustrated in Fig. 8, where we plot
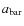 as a function of redshift. The dotted line indicates the lower limit for large-scale bars at 1 kpc (Laine et al. 2002) and the dashed line corresponds to the absolute size of
four pixels. For increasing redshifts higher than
as a function of redshift. The dotted line indicates the lower limit for large-scale bars at 1 kpc (Laine et al. 2002) and the dashed line corresponds to the absolute size of
four pixels. For increasing redshifts higher than  0.4, we begin to lose the smallest bars. However, based on both bar-detection criteria, we are complete for bars with
0.4, we begin to lose the smallest bars. However, based on both bar-detection criteria, we are complete for bars with
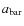
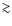 2 kpc.
2 kpc.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f7.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg59.png) |
Figure 7:
Plot showing the bar diameter in arcsec versus redshift. The filled points indicate spectroscopically based redshifts, while open points are for photometric redshifts. The dotted horizontal line marks 4 PSFs (i.e.
|
| Open with DEXTER | |
Besides resolution, other factors, such as increased obscuration due to both dust and star formation and surface-brightness dimming, can prevent bar detection at higher redshifts. Small bars are particularly affected by these factors. We point out that all results presented in this study have been checked with regard to a possible bias with respect to redshift (e.g., see Fig. 13).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f8.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg60.png) |
Figure 8:
The same as Fig. 7, but this time showing the bar size in terms of bar semi-major axis
|
| Open with DEXTER | |
4 The optical bar fraction and its dependence on galaxy properties
In the following, we discuss the properties of our disk galaxy sample based on our bar classification. We show how the presence of a bar is related to other characteristics of the galaxies and whether there is a difference between galaxies in clusters and the field. In general, we use the sample of 945 moderately inclined disk galaxies for our analysis, while when comparing cluster and field galaxies we restrict the sample to objects with spectroscopic observations (136 galaxies in clusters and 105 galaxies in the field). This reduces the size of the sample considerably, but ensures reliable membership assignment. In particular, the contamination of the cluster sample by field galaxies based on photometric redshifts impedes an accurate separation between cluster and field galaxies. The error bars in the following plots only include Poissonain errors. Specific factors affecting bar detection are discussed in Sect. 3.2.
![\begin{figure}
\par\mbox{
\includegraphics[width=9cm,clip]{0352f9a.ps}\includegraphics[width=9cm,clip]{0352f9b.ps} }
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg61.png) |
Figure 9:
The distribution of barred and unbarred disk galaxies as a function of Hubble type. a) The bar fraction as a function of Hubble type. The filled circles show the relation for our final sample of 945 disk galaxies. The open circles show the relation for the complete sample with
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{
\includegraphics[width=9cm,clip]{0352f10a.ps}\includegraphics[width=9cm,clip]{0352f10b.ps} }\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg62.png) |
Figure 10: The same as Fig. 9, but for the absolute V magnitude. In a) only bins with more than 25 objects are shown. |
| Open with DEXTER | |
Among the 945 disk galaxies in our sample, we find 238 to be barred, and hence derive an optical bar fraction (
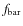 )
of
)
of 
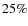 .
This is significantly lower than is typically found in optical studies of local galaxies (Aguerri et al. 2009; Reese et al. 2007; Eskridge et al. 2000; Marinova & Jogee 2007; Barazza et al. 2008), but in good agreement with studies at intermediate redshifts (Elmegreen et al. 2004; Sheth et al. 2008). This could indicate that the bar fraction is lower at higher redshifts, which would imply that we can detect nearly all bars in our sample. Possible other reasons for the difference compared to local studies have been given in Sect. 3.2. We also point out that the bar fraction for bulge-dominated galaxies is found to be significantly lower than for disk-dominated systems in studies of local galaxies (Aguerri et al. 2009; Barazza et al. 2008), a result confirmed by our own study (Sect. 4.1). Since our sample is
dominated by early-type disks (>
.
This is significantly lower than is typically found in optical studies of local galaxies (Aguerri et al. 2009; Reese et al. 2007; Eskridge et al. 2000; Marinova & Jogee 2007; Barazza et al. 2008), but in good agreement with studies at intermediate redshifts (Elmegreen et al. 2004; Sheth et al. 2008). This could indicate that the bar fraction is lower at higher redshifts, which would imply that we can detect nearly all bars in our sample. Possible other reasons for the difference compared to local studies have been given in Sect. 3.2. We also point out that the bar fraction for bulge-dominated galaxies is found to be significantly lower than for disk-dominated systems in studies of local galaxies (Aguerri et al. 2009; Barazza et al. 2008), a result confirmed by our own study (Sect. 4.1). Since our sample is
dominated by early-type disks (>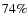 are earlier than Sc), a relatively low bar fraction might be expected. If we only consider strong bars (e>0.4), we obtain a bar fraction of
are earlier than Sc), a relatively low bar fraction might be expected. If we only consider strong bars (e>0.4), we obtain a bar fraction of 
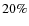 ,
which also agrees well with earlier studies (Jogee et al. 2004). For the spectroscopically confirmed cluster sample, we obtain
,
which also agrees well with earlier studies (Jogee et al. 2004). For the spectroscopically confirmed cluster sample, we obtain
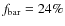 (136 objects/33 bars), and for the corresponding field sample, we derive
(136 objects/33 bars), and for the corresponding field sample, we derive
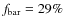 (105/30). These values agree within the uncertainties with the result for the complete sample and indicate that the frequency of bars in clusters is almost identical to that in the field. This finding indicates that bar formation, in general, is independent of environment, which was also found by van den Bergh (2002). On the other hand, Varela et al. (2004)
found twice as many bars in perturbed as in isolated galaxies. We investigate these results further in Sect. 7.
(105/30). These values agree within the uncertainties with the result for the complete sample and indicate that the frequency of bars in clusters is almost identical to that in the field. This finding indicates that bar formation, in general, is independent of environment, which was also found by van den Bergh (2002). On the other hand, Varela et al. (2004)
found twice as many bars in perturbed as in isolated galaxies. We investigate these results further in Sect. 7.
4.1 The bar fraction as a function of morphological type
In Fig. 9, we show the optical bar fraction as a function of Hubble type. The results for the total sample (Figs. 9a and b) indicate that the bar fraction increases towards
later Hubble types. Galaxies earlier than Sb have bar fractions below 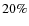 ,
while all later types exhibit higher bar fractions. The monotonically increasing bar fraction along the sequence and the
significant difference between those of S0s (
,
while all later types exhibit higher bar fractions. The monotonically increasing bar fraction along the sequence and the
significant difference between those of S0s (
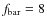
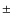
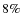 )
and Scs (
)
and Scs (
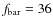
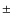
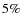 )
indicate that the effect is significant. Our results for Sd and Sm/Im types are less robust due to the smaller number of galaxies with these morphologies. Similar analyzes
(Elmegreen et al. 2004; Odewahn 1996) based on the Third Reference Catalog of Bright Galaxies (de Vaucouleurs et al. 1991), however, obtained different results. Their bar fraction was at its lowest for Sc galaxies and increased towards earlier and later types. We cannot compare the results for S0 galaxies, since these wre not included in the earlier investigations. On the other hand, our result is consistent with two
studies based on the Sloan Digitized Sky Survey (SDSS), where, however, no Hubble types were available: Barazza et al. (2008) showed that the bar fraction is significantly higher for disk-dominated galaxies than for galaxies hosting prominent bulges. Although the sample in that study was dominated by late-type disks, the connection found between the prominence of the bulge and the bar fraction can also be inferred from our result. In their analysis of bars in local disk galaxies, Aguerri et al. (2009) found that S0 galaxies have a significantly lower bar fraction (by
)
indicate that the effect is significant. Our results for Sd and Sm/Im types are less robust due to the smaller number of galaxies with these morphologies. Similar analyzes
(Elmegreen et al. 2004; Odewahn 1996) based on the Third Reference Catalog of Bright Galaxies (de Vaucouleurs et al. 1991), however, obtained different results. Their bar fraction was at its lowest for Sc galaxies and increased towards earlier and later types. We cannot compare the results for S0 galaxies, since these wre not included in the earlier investigations. On the other hand, our result is consistent with two
studies based on the Sloan Digitized Sky Survey (SDSS), where, however, no Hubble types were available: Barazza et al. (2008) showed that the bar fraction is significantly higher for disk-dominated galaxies than for galaxies hosting prominent bulges. Although the sample in that study was dominated by late-type disks, the connection found between the prominence of the bulge and the bar fraction can also be inferred from our result. In their analysis of bars in local disk galaxies, Aguerri et al. (2009) found that S0 galaxies have a significantly lower bar fraction (by 
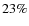 )
than galaxies of later types, which agrees well with our result. A somewhat different result was reported by Sheth et al. (2008), who found a slight preference for bars in bulge-dominated systems at high redshifts. We emphasize that the presence of a large bulge should not impede bar detection, since we are only interested in large-scale bars and exclude strongly inclined objects, for which a massive bulge could make bar detection difficult.
)
than galaxies of later types, which agrees well with our result. A somewhat different result was reported by Sheth et al. (2008), who found a slight preference for bars in bulge-dominated systems at high redshifts. We emphasize that the presence of a large bulge should not impede bar detection, since we are only interested in large-scale bars and exclude strongly inclined objects, for which a massive bulge could make bar detection difficult.
![\begin{figure}
\par\mbox{
\includegraphics[width=9cm,clip]{0352f11a.ps}\includegraphics[width=9cm,clip]{0352f11b.ps} }\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg72.png) |
Figure 11: The same as Fig. 10, but for rest-frame U-V color. |
| Open with DEXTER | |
Figures 9c and d show the same relations for our spectroscopic sample. The distributions indicate that early-type disks are more prominent in clusters, as expected, whereas the bar fractions in the field and in clusters are quite similar. On the other hand, we find differences in the bar fractions for individual Hubble types in clusters and the field, for instance for Sa galaxies (cluster: 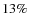 ,
field:
,
field: 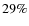 ). However, due to the small number of objects
involved (20-40 galaxies), the significance of this result cannot be assessed reliably.
). However, due to the small number of objects
involved (20-40 galaxies), the significance of this result cannot be assessed reliably.
4.2 The bar fraction as function of magnitude and color
In Fig. 10, we show how the optical bar fraction depends on the rest-frame total V-band magnitude of the galaxy, for both the full sample and the spectroscopic subsample. For cluster members, the rest-frame magnitudes are calculated based on the cluster redshift (as opposed to the galaxy redshift). The bar fraction remains relatively constant with galaxy magnitude. The slight decrease towards lower magnitudes lies within the uncertainties and is therefore insignificant. Early-type disks are generally more luminous than late-type disk and have a lower bar
fraction (Fig. 9). We may therefore naively expect that the bar fraction should increase toward lower magnitude. This trend could be erased, however, if the brighter galaxies in each morphological class had a higher bar fraction, which has been found in a study of barred disks in the Abell 901/902 supercluster environment (Marinova et al. 2009). To investigate this possibility, we split the morphological subsamples at MV=-21.0 mag, which is the mean V-band magnitude of the complete sample (
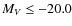 ), and determine the bar fractions for the brighter and fainter
parts of these subsamples. The result is shown in Table 2. For Hubble types S0-Sb, the bright subsample does indeed have a higher bar fraction than the faint subsample. For Sc disks, the
trend is, however, reversed. This explains the almost constant bar fraction as a function of magnitude. The result indicates that most bars in early-type disks have a relatively high surface brightness and therefore contribute significantly to the high luminosity.
), and determine the bar fractions for the brighter and fainter
parts of these subsamples. The result is shown in Table 2. For Hubble types S0-Sb, the bright subsample does indeed have a higher bar fraction than the faint subsample. For Sc disks, the
trend is, however, reversed. This explains the almost constant bar fraction as a function of magnitude. The result indicates that most bars in early-type disks have a relatively high surface brightness and therefore contribute significantly to the high luminosity.
Table 2: Bar fractions per Hubble type for bright and faint subsamples.
Figures 10c and d show the distributions for the cluster and field subsamples. The cluster sample is slightly brighter than the field sample, but in terms of bar fraction they are almost identical.
The corresponding relations with respect to rest-frame U-V color are shown in Fig. 11. The bar fraction declines toward redder colors (Figs. 11a and b), as expected from the relations found in terms of morphology. This finding emphasizes that late-type disks are more likely to host bars than early-type disks. The same trend is also found for the cluster and field subsamples (Figs. 11c and d), although the cluster sample is on average significantly redder than the field sample.
![\begin{figure}
\par\mbox{
\includegraphics[width=9cm,clip]{0352f12a.ps} \includegraphics[width=9cm,clip]{0352f12b.ps} }\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg83.png) |
Figure 12: The same as Fig. 10, but for the effective radius determined from a Sérsic fit. Galaxies in the clusters cl1227.9-1138 and cl1227.9-1138a are excluded, since Sérsic fits are unavailable. |
| Open with DEXTER | |
4.3 The bar fraction as a function of effective radius
The effective radius (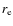 )
determined by applying a Sérsic fit to the entire galaxy is a measure of the concentration of the galaxy light and a partial measure of the prominence of the bulge. A relation between Hubble type and
)
determined by applying a Sérsic fit to the entire galaxy is a measure of the concentration of the galaxy light and a partial measure of the prominence of the bulge. A relation between Hubble type and 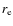 is therefore expected and also found in our sample. We computed the mean effective radius for each Hubble type and obtain the following result: S0:
is therefore expected and also found in our sample. We computed the mean effective radius for each Hubble type and obtain the following result: S0:
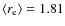 kpc; Sa:
kpc; Sa:
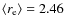 kpc; Sb:
kpc; Sb:
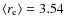 kpc; Sc:
kpc; Sc:
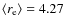 kpc; and Sd:
kpc; and Sd:
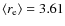 kpc. However, since
kpc. However, since 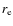 only indicates the distribution of the light in the galaxies, it is more related to the concentration of the light than the Hubble type. Figure 12 shows the bar fraction as a function of
only indicates the distribution of the light in the galaxies, it is more related to the concentration of the light than the Hubble type. Figure 12 shows the bar fraction as a function of 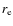 .
There is a continuous rise in the bar fraction with increasing
.
There is a continuous rise in the bar fraction with increasing 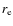 (Fig. 12a). This again seems to be just another representation of the effect already indicated in the relations based on morphology and color. Galaxies with larger central light (or mass) concentrations have less bars than disk-dominated galaxies with small central objects. The result also agrees with the findings of Barazza et al. (2008) where a similar plot is shown and with the results of Hernández-Toledo et al. (2008), which are based on the light concentration index. However, the apparent lack of the smallest bars at higher redshifts might contribute to this result. This could be the case if galaxies with small effective radii tend to have shorter bars. We therefore reproduce Fig. 12a for three different subsamples. The result is shown in Fig. 13. The solid line is for galaxies at
(Fig. 12a). This again seems to be just another representation of the effect already indicated in the relations based on morphology and color. Galaxies with larger central light (or mass) concentrations have less bars than disk-dominated galaxies with small central objects. The result also agrees with the findings of Barazza et al. (2008) where a similar plot is shown and with the results of Hernández-Toledo et al. (2008), which are based on the light concentration index. However, the apparent lack of the smallest bars at higher redshifts might contribute to this result. This could be the case if galaxies with small effective radii tend to have shorter bars. We therefore reproduce Fig. 12a for three different subsamples. The result is shown in Fig. 13. The solid line is for galaxies at 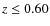 (the median redshift of the sample), the dotted line is for galaxies at z>0.60, and the dashed line shows the relation assuming that only bars with
(the median redshift of the sample), the dotted line is for galaxies at z>0.60, and the dashed line shows the relation assuming that only bars with
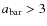 kpc can be detected (i.e., all bars with
kpc can be detected (i.e., all bars with
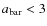 kpc are considered to be unbarred in this case). All subsamples clearly show that the bar
fraction increases towards galaxies with larger effective radii. We can therefore conclude that the result is real and not caused by the lower bar detection rate at higher redshift.
kpc are considered to be unbarred in this case). All subsamples clearly show that the bar
fraction increases towards galaxies with larger effective radii. We can therefore conclude that the result is real and not caused by the lower bar detection rate at higher redshift.
Finally, the same result is again found in the two subsamples in Figs. 12c and d. This finding supports the assumption that the presence of a bar is related to the disk structure and the magnitude of the central mass concentration.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f13.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg91.png) |
Figure 13:
The same as Fig. 12a, but for three different subsamples: the solid line is for galaxies at |
| Open with DEXTER | |
5 The properties of the bars
The two main properties of bars typically measured and analyzed in bar studies are the bar size and strength. Different methods are adopted to determine these quantities. In particular, the bar strength can be measured using the gravitational torque exerted by the bar (Buta et al. 2005; Block et al. 2002), the maximum ellipticity of the bar (Knapen et al. 2000; Jogee et al. 1999; Laine et al. 2002; Martin 1995; Marinova & Jogee 2007; Barazza et al. 2008), Fourier decomposition
(Elmegreen et al. 1996), and visual estimates of strength (Eskridge et al. 2002). As described in Sect. 3.1, our measurements are based on ellipse fitting. Since this fitting provide the basis of the classification, the determination of the maximum ellipticity (
 ,
interpreted as
the bar strength) and the radius (
,
interpreted as
the bar strength) and the radius (
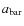 ,
interpreted as the bar size), at which this maximum occurs, is straightforward. However, we emphasize that the maximum bar ellipticity is only a partial
measure of the bar strength, because it provides no indication of the mass of the bar. However, Shen & Sellwood (2004) demonstrated that the maximum ellipticity correlates strongly with the relative
amplitude of the bisymmetric Fourier component of the mass density averaged over a certain inner radial range, where the bar dominates. In addition, the gravitational torque, on average,
correlates with the maximum ellipticity of the bar (Laurikainen et al. 2002). We can therefore regard the bar ellipticity to some extent as a measure of the bar strength.
,
interpreted as the bar size), at which this maximum occurs, is straightforward. However, we emphasize that the maximum bar ellipticity is only a partial
measure of the bar strength, because it provides no indication of the mass of the bar. However, Shen & Sellwood (2004) demonstrated that the maximum ellipticity correlates strongly with the relative
amplitude of the bisymmetric Fourier component of the mass density averaged over a certain inner radial range, where the bar dominates. In addition, the gravitational torque, on average,
correlates with the maximum ellipticity of the bar (Laurikainen et al. 2002). We can therefore regard the bar ellipticity to some extent as a measure of the bar strength.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f14.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg92.png) |
Figure 14: The bar size ( left) and bar ellipticity ( right) distributions for the total sample (solid lines) and the spectroscopic sample (dashed line). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f15.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg93.png) |
Figure 15: The same as Fig. 14, but only showing the spectroscopically defined cluster (solid lines) and field (dashed lines) subsamples. For readability, error bars are only shown for the cluster sample. |
| Open with DEXTER | |
In Fig. 14, we show the bar size and bar ellipticity distributions. A significant majority (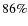 )
of bars have sizes
)
of bars have sizes  5 kpc, in agreement with un-deprojected results in earlier studies (Jogee et al. 2004; Marinova & Jogee 2007; Barazza et al. 2008). Similarly, the distribution of
5 kpc, in agreement with un-deprojected results in earlier studies (Jogee et al. 2004; Marinova & Jogee 2007; Barazza et al. 2008). Similarly, the distribution of
 is consistent with these earlier studies. Figure 15 shows the corresponding distributions for the cluster and field subsamples. The cluster sample exhibits no prominent peak in the bar size distribution (left panel), but is slightly skewed towards larger sizes. In contrast, the field sample shows a similar distribution to that of the total sample. Hence, bars in clusters tend to be longer than bars in field galaxies.
is consistent with these earlier studies. Figure 15 shows the corresponding distributions for the cluster and field subsamples. The cluster sample exhibits no prominent peak in the bar size distribution (left panel), but is slightly skewed towards larger sizes. In contrast, the field sample shows a similar distribution to that of the total sample. Hence, bars in clusters tend to be longer than bars in field galaxies.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f16.ps}
\par\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg95.png) |
Figure 16: The bar size as a function of normalized clustercentric distance for the spectroscopic cluster subsample. Filled points are for S0/Sa types and open point for Sb/Sc types. There are no other Hubble types in the sample. The dashed line indicates the mean bar size for this sample of 3.68 kpc. |
| Open with DEXTER | |
The differences that we observe between the bar size distributions of the field and cluster samples (Fig. 15) could indicate that the cluster environment has an impact on the bar sizes. In fact, numerical simulations show that tidally induced bars are on average longer than bars in isolated disks (Aguerri & González-García 2009). To
investigate this possibility, we measured the projected distances (
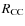 )
of the cluster galaxies from the corresponding cluster center, assuming that all galaxies are at the cluster redshift. This value was then normalized by
)
of the cluster galaxies from the corresponding cluster center, assuming that all galaxies are at the cluster redshift. This value was then normalized by
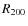 ,
the radius within which the average mass density is equal to 200 times the critical density. We use the definition given in Finn et al. (2005, Eq. (8)). In Fig. 16, we plot the bar size versus the normalized clustercentric distance. Larger bars tend to be located close to the cluster center. The majority of bars larger than the average size of 3.68 kpc (indicated by the dashed line) are located
within
,
the radius within which the average mass density is equal to 200 times the critical density. We use the definition given in Finn et al. (2005, Eq. (8)). In Fig. 16, we plot the bar size versus the normalized clustercentric distance. Larger bars tend to be located close to the cluster center. The majority of bars larger than the average size of 3.68 kpc (indicated by the dashed line) are located
within
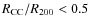 .
A KS-test indicates that there is a
.
A KS-test indicates that there is a 
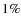 probability that the
probability that the
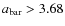 kpc sample stems from the same distribution as the complementary sample of small bars in terms of
kpc sample stems from the same distribution as the complementary sample of small bars in terms of
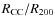 .
We must remember that we are using projected
distances, although this is unlikely to explain the trend entirely. It is also interesting that
most of the
.
We must remember that we are using projected
distances, although this is unlikely to explain the trend entirely. It is also interesting that
most of the
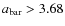 kpc bars are found in disks of intermediate Hubble type. However, we highlight that the number of objects (33) in the plot is small and the significance of this
finding is difficult to assess. We will nevertheless discuss possible origins of this effect in Sect. 7.
kpc bars are found in disks of intermediate Hubble type. However, we highlight that the number of objects (33) in the plot is small and the significance of this
finding is difficult to assess. We will nevertheless discuss possible origins of this effect in Sect. 7.
In Fig. 17, we show how the bar properties are related to Hubble type. The two panels show the mean bar size and bar ellipticity for each Hubble type. The mean bar sizes are in the range 2.5-3.5 kpc. For early-type disks (S0-Sb), this is consistent with the results of Erwin (2005), whereas the mean bar sizes in late-type disks are larger than those measured by Erwin (2005). However, the number of objects in the Sd and Sm/Im classes is rather small in our sample (see Fig. 9). On the other hand, there is an obvious relation between morphological type and mean bar ellipticity, which increases by more than 0.2 from early to late types. However, this result is at least in part due to the measurement including the bulge, which can lead to an underestimation of the bar ellipticity (Gadotti 2008). The measured bar ellipticity stems from the outermost isophote attributed to the bar. The bulge light contributes to the central part of this isophote. A large and luminous bulge will therefore widen this isophote at the center and, hence, lower the bar ellipticity. With the data available, it is impossible to estimate the impact that this effect could have on the relation in Fig. 17 (lower panel). An accurate bulge-bar-disk decomposition would be required to investigate the possibility that late-type disks indeed have stronger bars, on average. This is, however, beyond the scope of this analysis.
6 The distribution of barred galaxies within the clusters
In two studies of local galaxy clusters, evidence has been found that barred galaxies are preferentially located at the cluster core. An analysis of the clustercentric distances of barred galaxies in the Coma cluster (Thompson 1981) showed that a significantly larger fraction of barred galaxies are located at the cluster core than larger clustercentric distances (the adopted core radius for Coma was  784 kpc). In a similar study of the Virgo cluster, Andersen (1996) found
that the barred disk galaxies are more centrally concentrated than the unbarred disks. For S0 galaxies, the same study found that the distributions of barred and unbarred objects are the same. In Fig. 18, we show the bar fractions as a function of the clustercentric distances (absolute and normalized). We find the highest bar fraction in the central bin. For the
784 kpc). In a similar study of the Virgo cluster, Andersen (1996) found
that the barred disk galaxies are more centrally concentrated than the unbarred disks. For S0 galaxies, the same study found that the distributions of barred and unbarred objects are the same. In Fig. 18, we show the bar fractions as a function of the clustercentric distances (absolute and normalized). We find the highest bar fraction in the central bin. For the
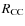 distribution, the bar fraction declines from
distribution, the bar fraction declines from 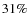 in the central bin to
in the central bin to 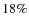 at
at  1 Mpc. (The corresponding values for the complete sample are
1 Mpc. (The corresponding values for the complete sample are 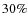 and
and 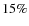 ,
respectively.) For the
,
respectively.) For the
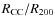 distribution, the corresponding values are
distribution, the corresponding values are 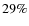 in the central bin and
in the central bin and 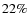 at R200. (The corresponding values for the complete sample are
at R200. (The corresponding values for the complete sample are 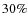 and
and 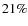 ,
respectively.) We emphasize again that the sample used is rather small, but we can safely say that barred galaxies do not avoid the cluster center. With the tendency for galaxy with large bars to be located close to cluster cores (Fig. 16), these findings indicate that regions of high galaxy density are favorable locations for bars.
,
respectively.) We emphasize again that the sample used is rather small, but we can safely say that barred galaxies do not avoid the cluster center. With the tendency for galaxy with large bars to be located close to cluster cores (Fig. 16), these findings indicate that regions of high galaxy density are favorable locations for bars.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f17.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg105.png) |
Figure 17: The average bar size ( top) and average bar ellipticity ( bottom) as a function of Hubble type. The number in brackets gives the number of objects in that bin. The error bars indicate standard deviations of the mean. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f18.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg106.png) |
Figure 18: The bar fraction as a function of the clustercentric distance ( left) and the normalized clustercentric distance ( right) for the spectroscopic subsample. |
| Open with DEXTER | |
7 Discussion
We have found the optical bar fraction averaged over our entire sample covering the redshift range
z=0.4-0.8 to be 
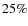 .
The median redshift of the sample is 0.60. In Sect. 3.2, we discussed how at these redshifts certain factors, such as reduced resolution, band shifting, enhanced obscuration by dust, could lead to a reduced bar detection rate. This could explain why the optical bar fraction of this sample is considerably lower than measured in local samples of disk
galaxies (Aguerri et al. 2009; Marinova & Jogee 2007; Barazza et al. 2008), but is in good agreement with studies at intermediate redshifts (Jogee et al. 2004; Elmegreen et al. 2004; Sheth et al. 2008). We note that all of these studies were based on samples primarily composed of galaxies in low density environments. A key question is whether the lower bar fraction at intermediate redshifts is primarily a result of the enhanced difficulty in identifying bars, or whether the number of barred disk galaxies was really lower at these redshifts. Several studies (van den Bergh et al. 2000; Abraham et al. 1999) claimed that the bar fraction was significantly lower at
.
The median redshift of the sample is 0.60. In Sect. 3.2, we discussed how at these redshifts certain factors, such as reduced resolution, band shifting, enhanced obscuration by dust, could lead to a reduced bar detection rate. This could explain why the optical bar fraction of this sample is considerably lower than measured in local samples of disk
galaxies (Aguerri et al. 2009; Marinova & Jogee 2007; Barazza et al. 2008), but is in good agreement with studies at intermediate redshifts (Jogee et al. 2004; Elmegreen et al. 2004; Sheth et al. 2008). We note that all of these studies were based on samples primarily composed of galaxies in low density environments. A key question is whether the lower bar fraction at intermediate redshifts is primarily a result of the enhanced difficulty in identifying bars, or whether the number of barred disk galaxies was really lower at these redshifts. Several studies (van den Bergh et al. 2000; Abraham et al. 1999) claimed that the bar fraction was significantly lower at 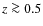 .
This was confirmed by Sheth et al. (2008). Only for a small subsample of large and massive galaxies was a constant bar fraction found (Sheth et al. 2008,2003). In other studies, a fairly constant bar fraction out to
.
This was confirmed by Sheth et al. (2008). Only for a small subsample of large and massive galaxies was a constant bar fraction found (Sheth et al. 2008,2003). In other studies, a fairly constant bar fraction out to 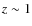 was found for strong bars (Jogee et al. 2004) or all bars (Elmegreen et al. 2004; Zheng et al. 2005). To determine the evolution in the bar fraction with redshift in our sample, we divided the sample into three redshift bins and measured the bar fraction and the mean bar sizes and ellipticities in each. The bin sizes were defined in order to obtain comparable numbers of objects in each bin. We only considered
galaxies with spectroscopic redshifts. The corresponding results are shown in Table 3.
The bar fraction was found to decline modestly from
was found for strong bars (Jogee et al. 2004) or all bars (Elmegreen et al. 2004; Zheng et al. 2005). To determine the evolution in the bar fraction with redshift in our sample, we divided the sample into three redshift bins and measured the bar fraction and the mean bar sizes and ellipticities in each. The bin sizes were defined in order to obtain comparable numbers of objects in each bin. We only considered
galaxies with spectroscopic redshifts. The corresponding results are shown in Table 3.
The bar fraction was found to decline modestly from 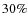 at
at
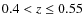 to
to 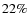 at
at
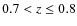 .
The average bar sizes in the lowest and highest redshift bins are roughly the same, and the average bar strength does not change within our redshift range. This indicates that we have not missed significant numbers of short or weak bars at higher redshifts. These results suggest that either the bar fraction decreases with increasing redshift, which would imply that we can nearly detect all bars in our sample, or that the decline is caused by the growing difficulty in identifying bars at higher redshifts. Reasons for the latter were given in Sect. 3.2. A detailed analysis of this issue was beyond the scope of this study.
.
The average bar sizes in the lowest and highest redshift bins are roughly the same, and the average bar strength does not change within our redshift range. This indicates that we have not missed significant numbers of short or weak bars at higher redshifts. These results suggest that either the bar fraction decreases with increasing redshift, which would imply that we can nearly detect all bars in our sample, or that the decline is caused by the growing difficulty in identifying bars at higher redshifts. Reasons for the latter were given in Sect. 3.2. A detailed analysis of this issue was beyond the scope of this study.
Table 3: Bar fractions and properties as a function of z.
The other results presented in the previous sections can be divided into two categories: (1) general relations between bars and the properties of their host galaxies, independent of whether the galaxies are cluster members or in the field; (2) relations regarding the specific locations of barred galaxies within the clusters.
7.1 Relating bar fraction and characteristics to host galaxy properties
We have found additional evidence that the bar fraction is related to the morphological structure of the host galaxies, which agrees with the results reported in Odewahn (1996), Barazza et al. (2008), and
Marinova et al. (2009). The bar fraction rises from early- to late-type disks, or in other words, from bulge-dominated galaxies to disk-dominated galaxies (Figs. 9a and 12a). This appears to indicate that bars in bulge-dominated disks are more likely to be dissolved. However, the processes responsible cannot have been important since z=0.8, because the difference in the bar fraction between bulge-dominated galaxies and disk-dominated galaxies (
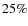 ,
Fig. 9) is much larger than the decline in the bar fraction with redshift (
,
Fig. 9) is much larger than the decline in the bar fraction with redshift (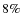 ,
Table 3). This is also illustrated in Fig. 19, where we plot the bar fraction as a function of Hubble type for a low and high redshift subsample. The figure shows that the bar fraction in bulge-dominated galaxies was already low at higher redshifts and implies that not many bars in these galaxies could have been dissolved since z>0.60. In addition, we observe that all morphological types contribute to the decline in the bar fraction by
,
Table 3). This is also illustrated in Fig. 19, where we plot the bar fraction as a function of Hubble type for a low and high redshift subsample. The figure shows that the bar fraction in bulge-dominated galaxies was already low at higher redshifts and implies that not many bars in these galaxies could have been dissolved since z>0.60. In addition, we observe that all morphological types contribute to the decline in the bar fraction by 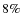 from higher to lower redshifts (see Table 3).
from higher to lower redshifts (see Table 3).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f19.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg114.png) |
Figure 19:
The bar fraction as a function of Hubble type, separated into a subsample at |
| Open with DEXTER | |
Figure 19 seems to indicate that the
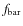 -morphology relation does not significantly change with redshift. This would suggest that bars are typically formed or destroyed during processes in which the morphology of the disk is emerging or changing. In other words, bars are not dissolved in, for instance, S0 galaxies, but can be destroyed during the processes in
which a disk galaxy is transformed into a S0. On the other hand, a scenario in which bars are constantly formed and dissolved without altering the relative fractions across the Hubble sequence would also be consistent with our data. However, this would require a high degree of fine tuning between formation and destruction processes and is rather unlikely.
-morphology relation does not significantly change with redshift. This would suggest that bars are typically formed or destroyed during processes in which the morphology of the disk is emerging or changing. In other words, bars are not dissolved in, for instance, S0 galaxies, but can be destroyed during the processes in
which a disk galaxy is transformed into a S0. On the other hand, a scenario in which bars are constantly formed and dissolved without altering the relative fractions across the Hubble sequence would also be consistent with our data. However, this would require a high degree of fine tuning between formation and destruction processes and is rather unlikely.
From a theoretical perspective, there are several studies indicating that present-day bars are rather robust and not easily destroyed (Debattista et al. 2006; Athanassoula et al. 2005; Shen & Sellwood 2004; Martinez-Valpuesta et al. 2006). Typically, a massive central mass concentration would be required to dissolve a bar. However, present-day super massive black holes, central dense stellar clusters, or the inner parts of bulges are not massive enough to affect bars significantly. However, it has been argued that a central mass concentration with the effects of gas inflows can lead to bar dissolution (Bournaud et al. 2005). In this picture, bars would become weaker and weaker and start to resemble lenses, which are preferentially found in early-type disks (Kormendy & Kennicutt 2004; Kormendy 1979) and can be interpreted as dissolving bars. In this context, it is interesting to note that we find, on average, weaker bars in early-type disks compared to late-type disks (Fig. 17, lower panel). However, our results appear to be consistent with a scenario in which bars are rather stable and long-lived, but the possibility that bar destruction and reformation also plays a crucial role cannot be ruled out.
7.2 The distribution of barred galaxies in clusters
In Sect. 4, we have shown that the bar fractions in clusters and in the field are essentially the same. This result indicates that clusters neither significantly foster nor prevent the formation of bars and if there are processes leading to the destruction of bars in clusters, they also act in the field. We point out that these results are based on relatively small samples and a confirmation with a larger sample would be desirable. Our findings are in agreement with the study by van den Bergh (2002), who investigated the bar fraction in field, group, and cluster environments. Considering the galaxy distribution in clusters, we have found that the bar fraction in the cluster center is higher than its average value (Fig. 18). Similar results were reported for local clusters (Andersen 1996; Thompson 1981). These findings indicate that the specific conditions in cluster centers support bar formation or help to avoid bar destruction. The large relative velocities of the galaxies in cluster centers prevent galaxy mergers, but galaxy flybys and the corresponding interactions are frequent. There is theoretical (Mihos & Hernquist 1994; Noguchi 1996; Gerin et al. 1990) and observational (Elmegreen et al. 1990; Giuricin et al. 1993; Varela et al. 2004) evidence that galaxy-galaxy interactions trigger bar formation.
The triggered formation of bars in the cluster center could also be responsible for the size distribution of bars. Most galaxies hosting bars with sizes larger than the mean bar size for cluster galaxies (3.68 kpc) are located within
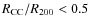 (Fig. 16). Although the number of objects studied is small, this is a remarkable result. Is it possible to relate the presence of these large bars at the cluster centers to the interactions proposed to
instigate bar formation? One plausible scenario would be that the formation of these large bars was triggered in the cluster center and that the bars are therefore rather young. The fact that most of
the host galaxies of these bars are of intermediate Hubble type appears to support this picture. Simulations of disk galaxies indicated that bars grow rapidly just after their formation (Berentzen et al. 2006) and become significantly shorter once the buckling instability occurs (Martinez-Valpuesta & Shlosman 2004). Conversely, large bar sizes can also be interpreted as signs of maturity (Valenzuela & Klypin 2003; Debattista & Sellwood 2000) or just as an intermediate stage during the evolution of a barred disk galaxy (Curir et al. 2006). However, it is
important to point out that the disk galaxies simulated in theoretical studies of bar formation and evolution are typically isolated or part of a cosmological simulation and the specific processes in clusters are not considered.
(Fig. 16). Although the number of objects studied is small, this is a remarkable result. Is it possible to relate the presence of these large bars at the cluster centers to the interactions proposed to
instigate bar formation? One plausible scenario would be that the formation of these large bars was triggered in the cluster center and that the bars are therefore rather young. The fact that most of
the host galaxies of these bars are of intermediate Hubble type appears to support this picture. Simulations of disk galaxies indicated that bars grow rapidly just after their formation (Berentzen et al. 2006) and become significantly shorter once the buckling instability occurs (Martinez-Valpuesta & Shlosman 2004). Conversely, large bar sizes can also be interpreted as signs of maturity (Valenzuela & Klypin 2003; Debattista & Sellwood 2000) or just as an intermediate stage during the evolution of a barred disk galaxy (Curir et al. 2006). However, it is
important to point out that the disk galaxies simulated in theoretical studies of bar formation and evolution are typically isolated or part of a cosmological simulation and the specific processes in clusters are not considered.
8 Summary and conclusions
We have searched for bars in 945 galaxies, drawn from a parent sample of 1906 disk galaxies from the EDisCS project. We used HST/ACS images taken in the F814W filter and restricted our sample to
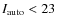 mag. The selection of disk galaxies (S0-Sm) was based on their visual classifications. We identified and characterized bars based on ellipse fits to the surface brightness distribution and quantitative criteria. After excluding unsatisfactory fits and highly inclined systems (>
mag. The selection of disk galaxies (S0-Sm) was based on their visual classifications. We identified and characterized bars based on ellipse fits to the surface brightness distribution and quantitative criteria. After excluding unsatisfactory fits and highly inclined systems (>
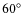 ), our bar analysis was performed for the remaining 945 disk galaxies. Spectroscopic observations were available for a subsample of 238 galaxies. Based on the corresponding redshifts and cluster assignments, we evaluated the distribution of barred disks in 11 galaxy clusters and 4 groups in the redshift range
), our bar analysis was performed for the remaining 945 disk galaxies. Spectroscopic observations were available for a subsample of 238 galaxies. Based on the corresponding redshifts and cluster assignments, we evaluated the distribution of barred disks in 11 galaxy clusters and 4 groups in the redshift range
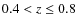 and analyzed the properties of their bars. Our main results were:
and analyzed the properties of their bars. Our main results were:
- 1.
- The total optical bar fraction, averaged over the entire sample covering the redshift range
z=0.4-0.8, is
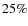 (
(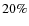 for strong bars, i.e., bar ellipticity >0.4). This is in good agreement with earlier studies at intermediate redshifts. The corresponding bar fractions for the spectroscopically based cluster and field samples are
for strong bars, i.e., bar ellipticity >0.4). This is in good agreement with earlier studies at intermediate redshifts. The corresponding bar fractions for the spectroscopically based cluster and field samples are 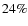 and
and 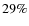 ,
respectively. Hence, the occurrence of bars in clusters is roughly the same as in the field.
,
respectively. Hence, the occurrence of bars in clusters is roughly the same as in the field.
- 2.
- We find that the bar fraction increases towards later Hubble types (form

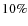 for S0 to >
for S0 to >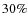 for Sc). Interpreting this relation as being due to the decreasing prominence of the bulge, our result is in close agreement with the findings of Barazza et al. (2008). It suggests
that the size (or mass) of the bulge has an impact on the probability that a bar forms or survives in a disk galaxy. The relation does not change with redshift, indicating that bars form or dissolve only when the disk changes its morphology.
for Sc). Interpreting this relation as being due to the decreasing prominence of the bulge, our result is in close agreement with the findings of Barazza et al. (2008). It suggests
that the size (or mass) of the bulge has an impact on the probability that a bar forms or survives in a disk galaxy. The relation does not change with redshift, indicating that bars form or dissolve only when the disk changes its morphology.
- 3.
- The bar fraction as a function of effective radius exhibits a striking increase (from

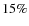 to
to 
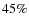 )
towards larger radii. This result is expected in view of the morphology-bar fraction relation (point 2), but is much more pronounced than the latter. This indicates
that it is really the structure of the disk that strongly affects bar formation and survival.
)
towards larger radii. This result is expected in view of the morphology-bar fraction relation (point 2), but is much more pronounced than the latter. This indicates
that it is really the structure of the disk that strongly affects bar formation and survival.
- 4.
- The bar size and bar ellipticity distributions of our sample galaxies are similar to those of other studies. The majority of bars have sizes <5 kpc, as expected for un-deprojected samples. The
average bar size is rather constant along the Hubble sequence (
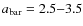 kpc), while the average bar ellipticity increases towards later Hubble types (from
kpc), while the average bar ellipticity increases towards later Hubble types (from
 for S0 to
for S0 to
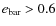 for Sd/Sm/Im). We suspect that this result is strongly affected by the fact that large and luminous bulges cause the ellipticities in the bar region to be lower.
for Sd/Sm/Im). We suspect that this result is strongly affected by the fact that large and luminous bulges cause the ellipticities in the bar region to be lower.
- 5.
- We find a somewhat higher bar fraction (

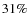 )
close to the centers of the clusters than at larger clustercentric distances (
)
close to the centers of the clusters than at larger clustercentric distances (
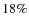 ). This is consistent with earlier results for the Virgo and Coma clusters. Moreover, bars in clusters are on average longer than in the field and preferentially located close to the cluster center. Most bars with sizes above the average (
). This is consistent with earlier results for the Virgo and Coma clusters. Moreover, bars in clusters are on average longer than in the field and preferentially located close to the cluster center. Most bars with sizes above the average (
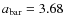 kpc) are located at
kpc) are located at
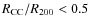 .
We have to point out that these results are based on the relatively small sample of spectroscopically confirmed cluster members and might therefore be affected by small number statistics.
.
We have to point out that these results are based on the relatively small sample of spectroscopically confirmed cluster members and might therefore be affected by small number statistics.
Acknowledgements
This paper is based on observations collected at the European Southern Observatory, Chile, as part of large program 166.A-0162 (the ESO Distant Cluster Survey). The Dark Cosmology Centre is funded by the Danish National Research Foundation.
References
- Abraham, R. G., Merrifield, M. R., Ellis, R. S., Tanvir, N. R., & Brinchmann, J. 1999, MNRAS, 308, 569 [NASA ADS] [CrossRef]
- Aguerri, J. A. L., & González-García, A. C. 2009, A&A, 494, 891 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Aguerri, J. A. L., Mendez-Abreu, J., & Corsini, E. M. 2009, A&A, 495, 491 [NASA ADS] [CrossRef] [EDP Sciences]
- Andersen, V. 1996, AJ, 111, 1805 [NASA ADS] [CrossRef] (In the text)
- Athanassoula, E. 1992, MNRAS, 259, 328 [NASA ADS]
- Athanassoula, E. 2003, MNRAS, 341, 1179 [NASA ADS] [CrossRef]
- Athanassoula, E., Lambert, J. C., & Dehnen, W. 2005, MNRAS, 363, 496 [NASA ADS]
- Barazza, F. D., Jogee, S., & Marinova, I. 2008, ApJ, 675, 1194 [NASA ADS] [CrossRef]
- Berentzen, I., Shlosman, I., & Jogee, S. 2006, ApJ, 637, 582 [NASA ADS] [CrossRef]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Block, D. L., Bournaud, F., Combes, F., Puerari, I., & Buta, R. 2002, A&A, 394, L35 [NASA ADS] [CrossRef] [EDP Sciences]
- Bournaud, F., & Combes, F. 2002, A&A, 392, 83 [NASA ADS] [CrossRef] [EDP Sciences]
- Bournaud, F., Combes, F., & Semelin, B. 2005, MNRAS, 364, L18 [NASA ADS] (In the text)
- Bureau, M., & Freeman, K. C. 1999, AJ, 118, 126 [NASA ADS] [CrossRef]
- Buta, R., Vasylyev, S., Salo, H., & Laurikainen, E. 2005, AJ, 130, 506 [NASA ADS] [CrossRef]
- Buta, R., Laurikainen, E., Salo, H., Block, D. L., & Knapen, J. H. 2006, AJ, 132, 1859 [NASA ADS] [CrossRef]
- Combes, F., Debbasch, F., Friedli, D., & Pfenniger, D. 1990, A&A, 233, 82 [NASA ADS]
- Curir, A., Mazzei, P., & Murante, G. 2006, A&A, 447, 453 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Debattista, V. P., & Sellwood, J. A. 2000, ApJ, 543, 704 [NASA ADS] [CrossRef]
- Debattista, V. P., Mayer, L., Carollo, C. M., et al. 2006, ApJ, 645, 209 [NASA ADS] [CrossRef]
- Desai, V., Dalcanton, J. J., Aragón-Salamanca, A., et al. 2007, ApJ, 660, 1151 [NASA ADS] [CrossRef]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., Jr., et al. 1991, Third Reference Catalogue of Bright Galaxies (Berlin, Heidelberg, New York: Springer-Verlag), Vol. 1-3, XII, 2069
- Elmegreen, D. M., Elmegreen, B. G., & Bellin, A. D. 1990, ApJ, 364, 415 [NASA ADS] [CrossRef] (In the text)
- Elmegreen, B. G., Elmegreen, D. M., Chromey, F. R., Hasselbacher, D. A., & Bissell, B. A. 1996, AJ, 111, 2233 [NASA ADS] [CrossRef] (In the text)
- Elmegreen, B. G., Elmegreen, D. M., & Hirst, A. C. 2004, ApJ, 612, 191 [NASA ADS] [CrossRef]
- Erwin, P. 2005, MNRAS, 364, 283 [NASA ADS] [CrossRef]
- Erwin, P., & Sparke, L. S. 2002, AJ, 124, 65 [NASA ADS] [CrossRef]
- Eskridge, P. B., Frogel, J. A., Pogge, R. W., et al. 2000, AJ, 119, 536 [NASA ADS] [CrossRef]
- Eskridge, P. B., Frogel, J. A., Pogge, R. W., et al. 2002, ApJS, 143, 73 [NASA ADS] [CrossRef] (In the text)
- Finn, R. A., Zaritsky, D., McCarthy, D. W., Jr., et al. 2005, ApJ, 630, 206 [NASA ADS] [CrossRef] (In the text)
- Friedli, D., Wozniak, H., Rieke, M., Martinet, L., & Bratschi, P. 1996, A&AS, 118, 461 [NASA ADS] [CrossRef] [EDP Sciences]
- Gadotti, D. A. 2008, MNRAS, 384, 420 [NASA ADS] [CrossRef] (In the text)
- Gerin, M., Combes, F., & Athanassoula, E. 1990, A&A, 230, 37 [NASA ADS]
- Giuricin, G., Mardirossian, F., Mezzetti, M., & Monaco, P. 1993, ApJ, 407, 22 [NASA ADS] [CrossRef] (In the text)
- Halliday, C., Milvang-Jensen, B., Poirier, S., et al. 2004, A&A, 427, 397 [NASA ADS] [CrossRef] [EDP Sciences]
- Hernández-Toledo, H. M., Vázquez-Mata, J. A., Martínez-Vázquez, L. A., et al. 2008, AJ, 136, 2115 [NASA ADS] [CrossRef] (In the text)
- Hunt, L. K., & Malkan, M. A. 1999, ApJ, 516, 660 [NASA ADS] [CrossRef]
- Jedrzejewski, R. I. 1987, MNRAS, 226, 747 [NASA ADS] (In the text)
- Jogee, S., Kenney, J. D. P., & Smith, B. J. 1999, ApJ, 526, 665 [NASA ADS] [CrossRef]
- Jogee, S., Knapen, J. H., Laine, S., et al. 2002a, ApJ, 570, L55 [NASA ADS] [CrossRef]
- Jogee, S., Shlosman, I., Laine, S., et al. 2002b, ApJ, 575, 156 [NASA ADS] [CrossRef]
- Jogee, S., Barazza, F. D., Rix, H.-W., et al. 2004, ApJ, 615, L105 [NASA ADS] [CrossRef] (In the text)
- Jogee, S., Scoville, N., & Kenney, J. D. P. 2005, ApJ, 630, 837 [NASA ADS] [CrossRef]
- Knapen, J. H. 1999, The Evolution of Galaxies on Cosmological Timescales, ASP Conf. Ser., 187, 72
- Knapen, J. H., Shlosman, I., & Peletier, R. F. 2000, ApJ, 529, 93 [NASA ADS] [CrossRef]
- Kormendy, J. 1979, ApJ, 227, 714 [NASA ADS] [CrossRef]
- Kormendy, J. 1993, Galactic Bulges, IAU Symp., 153, 209
- Kormendy, J., & Kennicutt, R. C., Jr. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef]
- Kuijken, K., & Merrifield, M. R. 1995, ApJ, 443, L13 [NASA ADS] [CrossRef]
- Kumai, Y., Taniguchi, Y., & Ishii, H. 1986, MNRAS, 223, 139 [NASA ADS] (In the text)
- Laine, S., Shlosman, I., Knapen, J. H., & Peletier, R. F. 2002, ApJ, 567, 97 [NASA ADS] [CrossRef]
- Laurikainen, E., Salo, H., & Rautiainen, P. 2002, MNRAS, 331, 880 [NASA ADS] [CrossRef]
- Laurikainen, E., Salo, H., & Buta, R. 2004, ApJ, 607, 103 [NASA ADS] [CrossRef]
- Laurikainen, E., Salo, H., Buta, R., et al. 2006, AJ, 132, 2634 [NASA ADS] [CrossRef]
- Lynden-Bell, D. 1979, MNRAS, 187, 101 [NASA ADS]
- Marinova, I., & Jogee, S. 2007, ApJ, 659, 1176 [NASA ADS] [CrossRef]
- Marinova, I., et al. 2009, ApJ, submitted
- Martin, P. 1995, AJ, 109, 2428 [NASA ADS] [CrossRef]
- Martinez-Valpuesta, I., & Shlosman, I. 2004, ApJ, 613, L29 [NASA ADS] [CrossRef] (In the text)
- Martinez-Valpuesta, I., Shlosman, I., & Heller, C. 2006, ApJ, 637, 214 [NASA ADS] [CrossRef]
- Menéndez-Delmestre, K., Sheth, K., Schinnerer, E., Jarrett, T. H., & Scoville, N. Z. 2007, ApJ, 657, 790 [NASA ADS] [CrossRef]
- Mihos, J. C., & Hernquist, L. 1994, ApJ, 431, L9 [NASA ADS] [CrossRef]
- Milvang-Jensen, B., Noll, S., Halliday, C., et al. 2008, A&A, 482, 419 [NASA ADS] [CrossRef] [EDP Sciences]
- Noguchi, M. 1996, ApJ, 469, 605 [NASA ADS] [CrossRef]
- Odewahn, S. C. 1996, Barred Galaxies, IAU Colloq., 157, ASP Conf. Ser., 91, 30 (In the text)
- Pelló, et al. 2008, A&A, submitted
- Pfenniger, D., & Norman, C. 1990, ApJ, 363, 391 [NASA ADS] [CrossRef]
- Pfenniger, D., & Friedli, D. 1991, A&A, 252, 75 [NASA ADS]
- Reese, A. S., Williams, T. B., Sellwood, J. A., Barnes, E. I., & Powell, B. A. 2007, AJ, 133, 2846 [NASA ADS] [CrossRef]
- Regan, M. W., & Elmegreen, D. M. 1997, AJ, 114, 965 [NASA ADS] [CrossRef]
- Regan, M. W., & Teuben, P. J. 2004, ApJ, 600, 595 [NASA ADS] [CrossRef]
- Regan, M. W., Sheth, K., & Vogel, S. N. 1999, ApJ, 526, 97 [NASA ADS] [CrossRef]
- Rudnick, G., Franx, M., Rix, H.-W., et al. 2001, AJ, 122, 2205 [NASA ADS] [CrossRef] (In the text)
- Rudnick, G., Rix, H.-W., Franx, M., et al. 2003, ApJ, 599, 847 [NASA ADS] [CrossRef] (In the text)
- Sakamoto, K., Okumura, S. K., Ishizuki, S., & Scoville, N. Z. 1999, ApJ, 525, 691 [NASA ADS] [CrossRef]
- Schinnerer, E., Maciejewski, W., Scoville, N., & Moustakas, L. A. 2002, ApJ, 575, 826 [NASA ADS] [CrossRef]
- Sellwood, J. A., & Wilkinson, A. 1993, Reports of Progress in Physics, 56, 173 [NASA ADS] [CrossRef]
- Shen, J., & Sellwood, J. A. 2004, ApJ, 604, 614 [NASA ADS] [CrossRef]
- Sheth, K., Regan, M. W., Vogel, S. N., & Teuben, P. J. 2000, ApJ, 532, 221 [NASA ADS] [CrossRef]
- Sheth, K., Vogel, S. N., Regan, M. W., et al. 2002, AJ, 124, 2581 [NASA ADS] [CrossRef]
- Sheth, K., Regan, M. W., Scoville, N. Z., & Strubbe, L. E. 2003, ApJ, 592, L13 [NASA ADS] [CrossRef]
- Sheth, K., Vogel, S. N., Regan, M. W., Thornley, M. D., & Teuben, P. J. 2005, ApJ, 632, 217 [NASA ADS] [CrossRef]
- Sheth, K., Elmegreen, D. M., Elmegreen, B. G., et al. 2008, ApJ, 675, 1141 [NASA ADS] [CrossRef] (In the text)
- Simard, L., Willmer, C. N. A., Vogt, N. P., et al. 2002, ApJS, 142, 1 [NASA ADS] [CrossRef]
- Simard, L., et al. 2009, A&A, submitted
- Smail, I., Dressler, A., Couch, W. J., et al. 1997, ApJS, 110, 213 [NASA ADS] [CrossRef] (In the text)
- Thompson, L. A. 1981, ApJ, 244, L43 [NASA ADS] [CrossRef] (In the text)
- Valenzuela, O., & Klypin, A. 2003, MNRAS, 345, 406 [NASA ADS] [CrossRef]
- van den Bergh, S. 2002, AJ, 124, 782 [NASA ADS] [CrossRef]
- van den Bergh, S. 2007, AJ, 134, 1508 [NASA ADS] [CrossRef]
- van den Bergh, S., Cohen, J. G., Hogg, D. W., & Blandford, R. 2000, AJ, 120, 2190 [NASA ADS] [CrossRef]
- Varela, J., Moles, M., Márquez, I., et al. 2004, A&A, 420, 873 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Weinberg, M. D. 1985, MNRAS, 213, 451 [NASA ADS]
- White, S. D. M., Clowe, D. I., Simard, L., et al. 2005, A&A, 444, 365 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Whyte, L. F., Abraham, R. G., Merrifield, M. R., et al. 2002, MNRAS, 336, 1281 [NASA ADS] [CrossRef]
- Zheng, X. Z., Hammer, F., Flores, H., Assémat, F., & Rawat, A. 2005, A&A, 435, 507 [NASA ADS] [CrossRef] [EDP Sciences]
Footnotes
- ... redshifts
![[*]](/icons/foot_motif.png)
- Based on observations collected at the European Southern Observatory, Chile, as part of large programme 166.A-0162 (the ESO Distant Cluster Survey). Also based on observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. These observations are associated with proposal 9476. Support for this porposal was provided by NASA through a grant from Space Telescope Science Institute.
- ... barred
![[*]](/icons/foot_motif.png)
- In the remainder of the paper, we use the terms disk-galaxy sample or disk galaxies for brevity including S0s.
All Tables
Table 1: Basic properties of clusters and the secondary structures.
Table 2: Bar fractions per Hubble type for bright and faint subsamples.
Table 3: Bar fractions and properties as a function of z.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f1.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg40.png) |
Figure 1: Redshift distribution of the basic sample of 1906 disk galaxies. The solid line shows the distribution based on spectroscopic redshifts and the dashed line that based on photometric redshifts. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f2.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg41.png) |
Figure 2:
Distribution of absolute V magnitude for the cluster and field samples. The solid histograms show the distribution for the total sample of 1906 galaxies, whereas the dashed histograms represent the spectroscopic subsample. The arrows indicate the magnitude cut (at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0352f3-1.eps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg43.png) |
Figure 3:
From left to right examples of S0, Sa, Sb, and Sc galaxies for cluster CL1232-1250 at z=0.54 (top row) and cluster CL1216-1201 at z=0.79 (bottom row). The images are |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0352f4.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg44.png) |
Figure 4:
This is an example of an inclined (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.55cm,clip]{0352f5.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg52.png) |
Figure 5:
The same as Fig. 4, but for a galaxy classified as unbarred according to our ellipse fits. The images are roughly
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[width=14.55cm,clip]{0352f6.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg54.png) |
Figure 6:
The same as Fig. 4, but for a galaxy classified as barred from ellipse fits. The images are roughly
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f7.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg59.png) |
Figure 7:
Plot showing the bar diameter in arcsec versus redshift. The filled points indicate spectroscopically based redshifts, while open points are for photometric redshifts. The dotted horizontal line marks 4 PSFs (i.e.
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f8.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg60.png) |
Figure 8:
The same as Fig. 7, but this time showing the bar size in terms of bar semi-major axis
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{
\includegraphics[width=9cm,clip]{0352f9a.ps}\includegraphics[width=9cm,clip]{0352f9b.ps} }
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg61.png) |
Figure 9:
The distribution of barred and unbarred disk galaxies as a function of Hubble type. a) The bar fraction as a function of Hubble type. The filled circles show the relation for our final sample of 945 disk galaxies. The open circles show the relation for the complete sample with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{
\includegraphics[width=9cm,clip]{0352f10a.ps}\includegraphics[width=9cm,clip]{0352f10b.ps} }\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg62.png) |
Figure 10: The same as Fig. 9, but for the absolute V magnitude. In a) only bins with more than 25 objects are shown. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{
\includegraphics[width=9cm,clip]{0352f11a.ps}\includegraphics[width=9cm,clip]{0352f11b.ps} }\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg72.png) |
Figure 11: The same as Fig. 10, but for rest-frame U-V color. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{
\includegraphics[width=9cm,clip]{0352f12a.ps} \includegraphics[width=9cm,clip]{0352f12b.ps} }\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg83.png) |
Figure 12: The same as Fig. 10, but for the effective radius determined from a Sérsic fit. Galaxies in the clusters cl1227.9-1138 and cl1227.9-1138a are excluded, since Sérsic fits are unavailable. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f13.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg91.png) |
Figure 13:
The same as Fig. 12a, but for three different subsamples: the solid line is for galaxies at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f14.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg92.png) |
Figure 14: The bar size ( left) and bar ellipticity ( right) distributions for the total sample (solid lines) and the spectroscopic sample (dashed line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f15.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg93.png) |
Figure 15: The same as Fig. 14, but only showing the spectroscopically defined cluster (solid lines) and field (dashed lines) subsamples. For readability, error bars are only shown for the cluster sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f16.ps}
\par\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg95.png) |
Figure 16: The bar size as a function of normalized clustercentric distance for the spectroscopic cluster subsample. Filled points are for S0/Sa types and open point for Sb/Sc types. There are no other Hubble types in the sample. The dashed line indicates the mean bar size for this sample of 3.68 kpc. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f17.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg105.png) |
Figure 17: The average bar size ( top) and average bar ellipticity ( bottom) as a function of Hubble type. The number in brackets gives the number of objects in that bin. The error bars indicate standard deviations of the mean. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f18.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg106.png) |
Figure 18: The bar fraction as a function of the clustercentric distance ( left) and the normalized clustercentric distance ( right) for the spectroscopic subsample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0352f19.ps}
\end{figure}](/articles/aa/full_html/2009/15/aa10352-08/Timg114.png) |
Figure 19:
The bar fraction as a function of Hubble type, separated into a subsample at |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



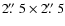 .
.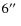 on a side. Right: the radial profiles of surface brightness ( top), ellipticity
on a side. Right: the radial profiles of surface brightness ( top), ellipticity 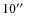 on a side.
on a side.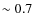 ,
while the PA remains approximately constant. After the end of the bar at the transition to the more circular disk, the ellipticity decreases sharply at
,
while the PA remains approximately constant. After the end of the bar at the transition to the more circular disk, the ellipticity decreases sharply at
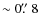 and the PA starts to change significantly at this point.
and the PA starts to change significantly at this point.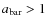 kpc) and nuclear bars (
kpc) and nuclear bars (