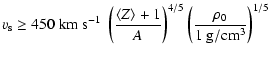EDP Sciences
Home All issues Volume 497 / No 1 (April I 2009) A&A, 497 1 (2009) 27-34 Full HTML
Free Access
Issue
A&A
Volume 497, Number 1, April I 2009
Page(s) 27 - 34
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/20079136
Published online 18 February 2009

2D numerical study of the radiation influence on shock structure relevant to laboratory astrophysics

M. González1,2,3 - E. Audit2,3 - C. Stehlé4


1 - Instituto de Fusión Nuclear, Universidad Politécnica de Madrid, Madrid, Spain
2 - Service d'Astrophysique, CEA/DSM/IRFU/SAp, Centre de Saclay, 91191 Gif-sur-Yvette, France
3 - Laboratoire AIM, CNRS, CEA/DSM, Université Paris Diderot, 91191 Gif-sur-Yvette, France
4 - LERMA, Observatoire de Paris, Université Paris VI, CNRS, 5 place J. Janssen, 92195 Meudon, France

Received 23 November 2007 / Accepted 9 January 2009

Abstract
Context. Radiative shocks are found in various astrophysical objects and particularly at different stages of stellar evolution. Studying radiative shocks, their topology, and thermodynamical properties is therefore a starting point to understanding their physical properties. This study has become possible with the development of large laser facilities, which has provided fresh impulse to laboratory astrophysics.
Aims. We present the main characteristics of radiative shocks modeled using cylindrical simulations. We focus our discussion on the importance of multi-dimensional radiative-transfer effects on the shock topology and dynamics.
Methods. We present results obtained with our code HERACLES for conditions corresponding to experiments already performed on laser installations. The multi-dimensional hydrodynamic code HERACLES is specially adapted to laboratory astrophysics experiments and to astrophysical situations where radiation and hydrodynamics are coupled.
Results. The importance of the ratio of the photon mean free path to the transverse extension of the shock is emphasized. We present how it is possible to achieve the stationary limit of these shocks in the laboratory and analyze the angular distribution of the radiative flux that may emerge from the walls of the shock tube.
Conclusions. Implications of these studies for stellar accretion shocks are presented.

Key words: hydrodynamics - radiative transfer - shock waves - plasmas - stars: formation - methods: numerical

1 Introduction

Radiative shocks are shocks in which the structure of the flow is affected by radiation, either because the radiative energy density cannot be neglected or because the energy transport by radiation (i.e., the radiative flux) is significant. For densities relevant to laboratory astrophysics, the radiative flux becomes important at temperature of a few tens of eV. The temperature has to be about one order of magnitude higher before the radiative energy becomes important. In astrophysics and in particular stellar physics, the density can be far lower and radiation therefore becomes important at lower temperatures.

A characteristic of radiative shocks is that at high shock speeds, the shocked matter is strongly heated and radiates energy. Unless the cold upstream gas is completely transparent, it absorbs this radiation creating a hot radiative precursor in front of the shock where the matter is generally ionized. We focus hereafter on shocks that exhibit a developed radiative precursor.

The modeling of these radiative shocks is difficult because of the nonlocal coupling between hydrodynamics and radiation, of the different scales important to radiation and hydrodynamics (Sincell et al. 1999b; Zel'dovich & Raizer 1967; Sincell et al. 1999a), and of multi-dimensional effects (Leygnac et al. 2006; González et al. 2006b).

The topology and evolution of radiative shocks depend on several factors, such as the geometry (from 1D, as in shock tubes, to more complex geometries), the energy deposition (impulsive, as for radiative blast waves, or continuously driven by a constant piston velocity), the optical depth of the downstream and upstream regions relative to the shock, and the possible contribution of a magnetic field. A detailed description of radiative shocks is given by Zel'dovich & Raizer (1967), Mihalas & Mihalas (1984), and Drake (2005).

These strong radiative shocks are found at different stages of stellar evolution: from star formation, when the accreting gas falls onto the protostellar forming object; during the accretion - ejection process, which manifests itself in terms of the jets of Young Stellar Objects (YSO) and stellar disks, in the atmospheres of evolved stars, when shocks drive pulsation (Fadeyev & Gillet 1998; Chadid et al. 2000; Fadeyev & Gillet 2000); and in the last stages of supernovae explosions.

Spherical or 1D symmetry is the usual obvious approximation, which prevails in the lack of further information about the geometry of these astrophysical shocks. However, if this approximation is reasonable as a first step for pulsating stars, accretion shocks, and supernovae explosions, it may become questionable in the case of accretion funnels of classical T-Tauri stars, where the matter is supposed to fall from the stellar disk to the stellar surface by means of channels that follow the magnetic-field lines. Accretion in Classical T-Tauri stars is inferred from veiling in the spectrum and also from signatures in the spectral lines. Simulations indicate that the topology of the accretion funnels is strongly dependent on the relative orientation of the magnetic-field symmetry and rotation axis (Romanova et al. 2003). At the base (on the stellar surface), the column may vary from compact circular to ring geometries, whereas the upper part (connected to the disk) may exhibit various fold-like, or more compact topologies driven by instabilities. This topic is still the subject of much debate and controversy.

Both the complexity in the structure of the radiative shocks, even for a 1D approximation, and the lack of angular resolution, require accurate simulations coupling radiation transport with hydrodynamics. This motivates the study of radiative shocks in 2D simple cylindrical geometries, to analyze the effect of the finite lateral size of the radiative shock, on its structure and luminosity. One should not use identical simulations to both check with and analyze observations. Experimental validation of these complex hydrodynamic features is thus required.

Obviously, the typical dimensions of astrophysical radiative shocks ensure that they cannot be studied directly in the laboratory. The study of radiative shocks on Earth thus require different gases and physical conditions, which can be recreated by high energy installations such as laser or pulsed electric installations (Remington et al. 2006). Radiative shock experiments have been performed with high power lasers (Bozier et al. 1986,2000; Bouquet et al. 2004; Busquet et al. 2007; Reighard et al. 2006; Busquet et al. 2006; Keiter et al. 2002; González et al. 2006b). Typically, a 200 J laser in about 1 ns can launch a shock at about 60 km s-1 in targets of millimeter size (Bouquet et al. 2004) filled with xenon at pressures of some fractions of bars, whereas supercritical shocks at 100 km s-1 in SiO2 aerogel, argon, and xenon have been produced at the OMEGA laser (5 kJ). Strong shocks have also been generated by a compact pulse-power device (Kondo et al. 2006), producing shocks at 45 km s-1 in xenon with different gas pressures of up to 10-2 bars. We see below that, for a fixed shock velocity accessible to a laser installation, the radiative regime is more easily achieved with a low-density, high-atomic-mass gas, which explains why low-density xenon is often used in these studies.

These experiments enable one to examine the physics of the radiative precursor (dynamics and density) by visible interferometry and provide information about the temperature of the shock front, by visible emissivity. Studies of the dynamics of the precursor of xenon radiative shocks by interferometry (Bouquet et al. 2004), and shadowgraphy (González et al. 2006b), and of its topology by instantaneous X-ray imaging (Vinci et al. 2006) indicate that multi-dimensional effects can affect the shock wave, and, in particular, its precursor. This was attributed to the lateral radiation losses (through the walls of the shock tube), which reduce the amount of radiation heating the precursor and thus affect its structure (Leygnac et al. 2006; González et al. 2006b).

Keilty et al. (2000), Shigemori et al. (2000), Edwards et al. (2001), Calder et al. (2002), and Laming & Grun (2002) focused their studies on the spherical, radiative, blast waves, which are similar to those studied in the previous 1D cases, in terms of the development of radiative precursor, but also exhibit strong differences, such as the importance of radiative cooling and the development of various instabilities. The study of these experimental blast waves is linked to the problem of the evolution and stability of supernova remnants.

After the presentation of the typical structure of 1D radiative shocks, we present a numerical study of laboratory radiative shocks that can be generated by medium-power laser facilities, such as PALS (Prague, Czech Republic), LULI (Palaiseau, France), and similar lasers. The numerical code (HERACLES) used in this work is first briefly presented. We then study the effect of the duration of the shock driven by the piston (Sect. 4). In Sect. 5, we consider the effects of multi-dimensional radiative transfer and their correlation with the width of the shock tube. In Sect. 6, we examine the influence of the radiation boundary-conditions, which are inferred from the albedo of the cell wall, on the topology and propagation of the shock. Finally, we present the perspectives and conditions for obtaining an experimental stationary radiative shock and present the angular dependence of the emerging radiative flux of such a shock.

2 Structure of a 1D radiative shock

In this section, we present the typical features of a radiative shock in terms of 1D geometry. When the flow passes through the shock, it is heated and it re-emits a fraction of its energy by radiation processes. These emitted photons are then absorbed by the cold and opaque unshocked gas. This preheated upstream gas is called the radiative precursor. When the stationary regime is reached, a radiative shock is then composed of both a purely hydrodynamical shock (which consists of a discontinuity in the hydrodynamical quantities) and a radiative precursor, whose length is directly correlated with both the mean free path of photons in the gas and the shock velocity. One usually considers two classes of shocks depending on the temperature reached just ahead of the hydrodynamical discontinuity. If it is lower than the post-shock temperature, the shock is called subcritical, and if it is equal the shock is called supercritical.

By assuming that a strong shock develops in an initially cold gas of density $\rho_0$ (mass number A) and solving the Rankine-Hugoniot relations, one can show that the temperature reached in the shock equals

$\displaystyle % T = 120.27 \; {\rm K} \; \frac{A}{\langle Z \rangle+1} \; \left... ...\gamma-1)}{(\gamma+1)^2} \left[1 + \sqrt{1+(\gamma^2-1)X} -(\gamma+1)X \right],$     (1)

where $\langle Z \rangle$ is the mean ionization stage in the shocked material, $X = \frac{e_{\rm i}}{\frac12 \mu u_{\rm s}^2}$ is the ratio of the ionization energy per atom to the initial kinetic energy per atom, and $\mu=$ the mean molecular weight of the non-ionized gas). The photons escaping from the shock front are used to heat the cold gas, incoming onto the front, to a temperature of T- (which is lower than T). Neglecting the gas compression in the precursor, one has (Zel'dovich & Raizer 1967):
$\displaystyle % \sigma T^4 = \rho_0 u_{\rm s} \epsilon (T_{-}, \rho_0),$     (2)

where $\epsilon=\frac{kT(1+Z)}{\mu(\gamma-1)}+\frac{e_{\rm i}}{\mu}$ is the internal specific energy (erg/g) after taking into account the ionization.

When T- equals T, the shock enters the supercritical regime, which is characterized by an extended precursor. The corresponding critical velocity is obtained formally by resolving the coupled set of Eqs. (1) and (2). This system must be solved numerically because one needs to take account of the temperature dependence of both the internal energy and ionic charge. Using the atomic-physics model described by Michaut et al. (2004) and for xenon of density 10-3 g/cm3, we found a critical velocity around 30 km s-1, achieving a shock temperature of 12 eV and average ionic charge of 8. In the particular case of a perfect gas with $\gamma =5/3$, and neglecting the ionization-energy term in Eqs. (1) and (2), one obtains the following approximate value of

$\displaystyle % v_{\rm s} \ge 450 \; {\rm km~s^{-1}} \; \left(\frac{\langle Z \rangle+1}{A}\right)^{4/5} \left(\frac{\rho_0}{1~{\rm g/cm^3}}\right)^{1/5}$     (3)

which illustrates that the supercritical regime is more easily obtained at low density and for high-mass gases. Using 1D hydro-radiative simulations, Ensman (1994) found a supercritical regime at 20 km s-1 for hydrogen at 8 $\times $ 10-10 g/cm3 in qualitative agreement with Eq. 3.

The precursor extension, L, can be approximated with a radiative heat-conduction model. One then finds that L is about several photon mean-free-paths close to the supercritical limit (Penzo & Tassart 1984; Nemchinov & Shuvalov 1980).

A typical 1D supercritical shock structure is shown in Fig. 1. These academic profiles were obtained using xenon with a constant ionisation charge of 5, a perfect-gas equation-of-state with $\gamma $ = 1.1, and analytic opacities (Bozier et al. 1986). The velocity of the shock is 65 km s-1 and the initial density and temperature are 1.3 $\times $ 10-3 g/cm3 and 300 K, respectively. The radiative precursor is clearly evident in the radiative flux and temperature profiles but, at this moderate shock speed, the density and velocity are only slightly affected.

 \begin{figure*} \par\includegraphics[angle=90,width=8.8cm,clip]{9136fg1.ps} \end{figure*} Figure 1:

Typical profiles of a 1D radiative shock: density ( upper left), velocity ( upper right), radiative and gas temperature ( lower left), and radiative flux ( lower right).
Open with DEXTER

  3 The HERACLES code

The simulations presented in this paper were completed using the three-dimensional radiation-hydrodynamics code HERACLES (González et al. 2007). This code solves the Euler equations for hydrodynamics coupled with the moment equations of the transfer equation. The original closure relation used for the radiative model (M1 model) allows one to be exact both in the diffusive and transport limit regimes. This code output data was verified by analytic models and compared with other codes. It can study a wide variety of astrophysical problems (González et al. 2007). Furthermore, it was used to develop and analyze a laboratory experiment of radiative shocks (González et al. 2006b). This cross-validation between experiment and simulation illustrates the relevance of HERACLES to both laboratory astrophysics and classical astrophysical situations.

The strength of HERACLES is that it can deal with multi-dimensional problems. Until now, radiative shocks have been studied by 1D geometry models, multi-D models with hydrostatic flows, or by adopting the flux-limited diffusion approximation (Bouquet et al. 2004; Drake 2007, and reference therein). On the one hand, the multi-D effects (such as lateral losses) can determine the structure of the flow, and on the other hand, at the foot of the radiative precursor, the reduced flux (ratio of the radiative flux to the product of the radiative energy and the light speed) is nearly one so that we are in the transport limit. In this context, HERACLES is of particular relevance to the study of multi-D radiative shocks.

Although all shocks in reality propagate within 3D media, we performed 2D axisymmetric simulations. As a first step, we considered only the determination of the theoretical influence of different parameters on the shock propagation. Furthermore, we verified that 2D axisymmetric and 3D Cartesian simulations produced identical results (e.g., speeds, positions) if one is careful to ensure that the surface-to-volume ratio is equal in both cases. Our results are therefore relevant to the case of radiative shocks propagating in a rectangular medium, as in most laboratory experiments.

Hereafter, all simulations presented are for shocks propagating in cylindrical cells with the left vertical boundary corresponding to the symmetry axis and the lateral losses located at the right vertical boundary. They are filled with xenon, which is initially at ambient temperature and a pressure of 0.2 bar (i.e., this corresponds to a density of 1.3 $\times $ 10-3 g/cm3). These values are typical of laboratory experiments (Bouquet et al. 2004; González et al. 2006b) where a high molecular weight and a low density are chosen to maximize radiative effects. If not specified, we use a realistic equation of state and opacities. The equation of state of xenon was computed using the OPA-CS code of Stehlé, which uses a screened hydrogenic model and is described in Michaut et al. (2004). The opacities were kindly provided by Busquet, who computed them using the STA code (Bar-Shalom et al. 1989). The shock is driven at a speed of 65 km s-1 which is a typical of present-day laser experiments. The boundary of the cells can have a variable albedo, defined as the fraction of the incident radiative flux re-emitted by the wall. We demonstrated in previous work (González et al. 2006b) that this parameter has a strong influence on the precursor propagation. We therefore performed simulations for albedos between 0$\%$(fully transparent or fully absorbing boundaries) and 100$\%$ (total reemission).

  4 Launching effect

The dynamics of the shock propagation depend strongly on the launching procedure. In laser driven shocks, the conversion of the laser energy to the piston mechanical energy is performed by the shock generated in the piston during the laser ablation (Bouquet et al. 2004; Drake 2005). In this paragraph we compare the dynamics of the shock for two launching scenarios. In the first, the piston moves at a constant velocity. The second corresponds to the case where the piston decelerates with time. Hereafter, we denote these two driving cases as continuous and impulsive respectively.

Figure 2a shows the difference between a shock with a launching phase of the shock that is impulsive and one for which the driving is continuous. In both cases, the lateral albedo is 40%. When the shock driver (``piston'') is continuous, the shock propagates at constant velocity equal to the initial velocity of 65 km s-1. In the impulsive case, the driver of 65 km s-1 is continuous during 0.3 ns and then decreases with a temporal dependence that reproduces qualitatively the velocities of the experimental shocks (González et al. 2006b). In that case, the shock decelerates as soon as the drive stops because it has little inertia. Regardless of the drive duration, one can observe three different stages in the precursor dynamics. In the first stage, the precursor moves faster than the shock. The photons emitted by the shock propagate in the upstream fluid, which is optically thick, where they are absorbed. This induces a warm, ionized, radiative precursor in the upstream part of the shock. In a second phase, the precursor decelerates (it can be even slower than the shock front). Finally, it reaches a constant speed equal to that of the shock front. This is the stationary regime.

These three stages are clearly seen in Fig. 2b which shows the distance separating the shock from the precursor leading-edge versus time. Since the precursor goes faster than the shock, this distance increases to a maximum value. Then, as the precursor slows down, this distance decreases until reaching an asymptotic value (stationary limit), when both the shock and precursor leading-edge travel at the same speed.

In a laboratory experiment, the duration of the driving is not a parameter that one can vary simply. It is easier to modify the shock dynamics by changing the radiative lateral losses, which can be achieved by varying the width of the canal or by modifying the albedo of the cells walls. This albedo can be specially adapted by choosing properly the material of the cell or by choosing special coating on these walls.

In the following sections, we examine the influence of these parameters on the dynamics of the shock precursor and in particular on the delay before the stationary regime.

   \begin{figure} \par\subfigure[Shock and precursor absolute positions]{\includegr... ...ursor]{\includegraphics[angle=90,width=4.2cm,clip] {9136fg2b.ps} }\end{figure} Figure 2:

Influence of the dynamics of the piston launching on the shock dynamics. The shock is driven in xenon at 0.2 bar at room temperature. The shock tube is a cylindrical cell with a 0.7 cm diameter and albedo of 40%. The full line refers to the impulsive lanching whereas the dotted line refers to a shock driven by a piston at constant velocity of 65 km s-1 (cf. Sects. 3 and 4).
Open with DEXTER

  5 Effect of a 2D radiation field

We define R to be the ratio of the transverse width l to the photon mean-free-path $\lambda$ in the unshocked medium ( $\lambda \simeq 1$ mm). In this section, we present the influence of R on the radiative shock structure and evolution. In our bi-dimensional and axisymmetric simulations, the gas is driven at a speed of 35 km s-1, constant both in time and across the cell. Since we impose lateral reflecting boundaries on the hydrodynamics, the shock would remain planar without accounting for the radiative transfer. It would be transversally homogeneous, and temperature and density would vary only with y-position (along the canal axis). However, when accounting for radiative transfer with lateral losses through partially reflective walls, 2D effects can be observed. Density and temperature vary with x-position (perpendicular to the axis) and, in some conditions, curvature of the shock front may even be observed. The influence of the radiation on the shock structure is directly correlated with the possibility of photon escape from the medium, which can be estimated from the dimensionless number $R=l/\lambda$.

The importance of radiative losses on the shock structure, which depends strongly on R, has not been considered in detail by many laboratory experiments nor in the study of radiative shocks encountered in astrophysical objects. For example, the mean free path in xenon at 300 K and 10-3 g/cm3, which is typical of laboratory experiments, is about 0.1 mm whereas the canal width is about 1 mm. For a typical stellar atmosphere (T=5000 K and $\rho$ = 5 $\times $ 10-11 g/cm3), the typical mean free path is 4 $\times $ 1011 cm and decreases rapidly when the temperature increases (Seaton et al. 1994) whereas the radius of a classical T Tauri star is about 2 $\times $ 1011 cm.

Figure 3 shows bi-dimensional maps at the same time for three different canal widths (i.e., three values of R). The shock position is marked by the jump in density and by the temperature peak. The precursor is located in the lower part of the figure below the shock. Its extension is particularly visible in the maps of temperature and radiative flux.

If R is small (cf. Fig. 3a), the photons don't interact with the gas and they escape freely from the system. As the radiation escapes laterally, the shock loses some part of its energy, it decelerates rapidly, and the precursor remains thin. Since the photons emitted at any point of the downstream medium escape freely, the shock remains planar. In contrast, if R is large (cf. Fig. 3c), the photons cannot escape because they are reabsorbed over a short distance. The shock travels faster than in the first case. In the limit where R tends to infinity, we recover the uni-dimensional case with a planar shock except for a small layer along the walls, similar to a boundary layer. In the intermediate case (cf. Fig. 3b), the shock is curved, since only photons close to the walls escape, and photons emitted on the axis are trapped. The shock then decelerates more close to the walls than on the axis, which tends to bend the shock. Shock curvatures have already been observed experimentally by imaging techniques (Reighard et al. 2006; Vinci et al. 2006), although the dynamical origin of the curvature can be of many different natures.

    \begin{figure} \par\subfigure[R=0.5]{ \includegraphics[angle=90,width=8cm,clip] ... ...R=10]{ \includegraphics[angle=90,width=8cm,clip] {9136fg3c.eps} }\end{figure} Figure 3:

At a same instant, snapshots of the maps of density, temperature, radial, and axial radiative flux showing the influence of the canal width compared to the photon mean free path (R=0.5 top panel, R=1 middle panel and R=10 bottom panel). Case of xenon initially at 1.3 $\times $ 10-3 g/cm3 and 300 K, using perfect-gas equation-of-state ($\gamma $ = 5/3 and mean molecular weight $\mu $ = 20 equivalent to a mean ionization stage of 5), and analytic opacities (Bozier et al. 1986). The shock propagates from top to bottom.
Open with DEXTER

  6 Effect of radiative losses

In the previous section, we showed that the ratio R of the photon mean free path to the canal width was a key parameter for the radiative losses. In this section, we study in more detail the influence of the lateral radiative losses on the shock and precursor dynamics. We therefore consider a canal of fixed width but with walls of variable albedo a, which varies between 0 (no wall reflexion) and 1 (purely reemitting walls).

This wall albedo is a crucial point in the laboratory experiments. Varying the element used for the cells or covering the cell walls with layers of different elements (e.g., gold, aluminium), one can test the radiative-loss effects.

We study the influence of the albedo on the dynamical properties of the shock at short and long times. To illustrate the effect, we have chosen to focus the analysis on the case of impulsive launching. We concentrate our study on the positions of the shock front and of the leading edge of the precursor (defined as the point, on the cell symmetry axis, where the temperature reaches the threshold value of 5 eV). The value of the temperature threshold influences the extension of the precursor only slightly.

  \begin{figure} \par\subfigure[]{\includegraphics[width=7.5cm,clip]{9136fg4a.ps} ... ...cm} \subfigure[]{\includegraphics[width=7.5cm,clip]{9136fg4b.ps} }\end{figure} Figure 4:

a) Influence of the walls albedo upon the shock (dashed line) and precursor (solid line) positions. b) Influence of the albedo upon the distance between the precursor and the shock. Comparison for an albedo of 0%, 40%, 50%, 60%, 70%, 80%, 90%, and 100% (from bottom to top).
Open with DEXTER

Figure 4 shows the shock dynamics obtained with an albedo of 0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 100%. One can see that the wall albedo has almost no effect on the shock velocity, at least for the evolution times considered here. However, the precursor is strongly affected by the albedo. As can be seen in Fig. 4b, for small values of the albedo (for important lateral losses), when most of the photons escape, the precursor extension remains small and its deceleration increases. This dependence is non-linear (cf. Sect. 7 below for the dependence of the time needed to reach the stationary limit on the albedo). The extension of the precursor relative to the shock front reduces slowly with time, as a consequence of the weakening of the shock and the slow deceleration of the piston. This evolution at later times differs from the case where the piston moves at a constant velocity, as can be seen from Fig. 2, which converges at long times towards a stationary limit, where precursor and shock front move at the same velocity. At early times, the precursor front moves far more rapidly than the shock front, and we expect that this regime is close to the case of a Marshak wave (a radiation-driven thermal wave without coupling to hydrodynamics). For t below 5 ns, and a=1, one thus recovers the well-known 1D-Marshak-wave time-dependence of $\sqrt{t}$. For smaller values of the albedo, the structure of the 2D-bent Marshak waves is more complex, even supposing a constant opacity, as one can see from Hurricane & Hammer (2006), who studied the bending and slowing of the front by radiative losses. However, even if similarities exist between the dynamics and topologies of a Marshak wave and those of a radiative precursor at early times, the two processes differ physically, especially at late times where the stationary limit is reached in one process and not in the other.

  7 Toward stationary shock

In the case of a shock with continuous driving, the typical evolution of the radiative shocks exhibits, as in the previous case, a first phase of development of the precursor, where the ionization-front velocity exceeds the shock velocity. After this phase, the ionization-front velocity decelerates until it becomes equal to the front velocity. At this time, the stationary limit is reached. The corresponding time at which this stationary radiative shock is formed, $t_{\rm stat}$, is of the order of the ratio of the precursor extension to the shock velocity.

The stationary shock limit is usually assumed for astrophysical flows, because $t_{\rm stat}$ is less than the typical hydrodynamical time, $t_{\rm hyd}$. For instance, in the case of pulsating stars, $t_{\rm hyd}$, which is roughly equal to the ratio of the atmosphere width to the shock velocity, varies between 1500 s for RR Lyrae and 106 s for cooler giants such as RV Tauri, whereas $t_{\rm stat}$ is of the order of 50 s for a shock velocity around 10 km s-1 (Fokin et al. 2004). In accretion shocks along magnetospheric columns, this time is approximately equal to the ratio of the column length to the shock velocity, or 104-105 s for classical T Tauri stars (of about 3 solar radius and 300 km s-1). Thus, in the absence of any shorter timescale of hydrodynamical motion (e.g., instabilities), these astrophysical shock waves can be supposed to be stationary from the radiative point of view.

Associated with the 1D approximation, this stationary limit also offers the advantage of simplicity in the observational diagnostics with the help of published stationary-shock structure tabulations (Fadeyev & Gillet 2000).

In the experimental cases, the piston velocity decreases slowly with time. However, as in the academic case of continuously sustained shock, the precursor extension relative to the shock front increases at early times until reaching a maximum value. We have chosen to define the time interval to form a stationary shock, $t_{\rm stat}$, as the time of maximum extension of the precursor because it unambiguously delimits the short accelerating and long decelerating phases of the precursor dynamics.

Using this definition, and in the launching case, which is close to that of previous experiments (González et al. 2006b), we find $t_{\rm stat}=5.6$ ns, 6.1 ns, 7.1 ns, 7.6 ns, 8.6 ns, 10.6 ns, 13.1 ns, 18.7 ns, 32.3 ns, and 409 ns for wall albedos of 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 percent, respectively (cf. Fig. 5). Thus, high lateral radiation losses (small albedo) not only decelerate the radiative precursor, but also strongly decrease the time to reach the stationary limit. From these numerical simulations, we derive an analytical fit

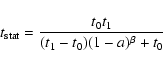\begin{displaymath}% t_{\rm stat} = \frac{t_0 t_1}{(t_1-t_0)(1-a)^\beta+t_0} \end{displaymath} (4)

where a is the wall albedo, t0 and t1 are the stationary times for a=0 and a=1, respectively, and $\beta$ is a constant. Their values are $t_0=5.6~{\rm ns}$, $t_1= 409~{\rm ns}$, and $\beta=0.84$.

 \begin{figure} \par\includegraphics[width=8cm,clip]{9136fg5.ps} \end{figure} Figure 5:

Influence of the albedo upon the time interval to form a stationary radiative shock, $t_{\rm stat}$ (points: numerical simulations results, line: fit).
Open with DEXTER

In all of these simulations, the shock position is insensitive to the albedo of the tube walls. However, even if the shock speed is constant, the density and temperature of the post-shock matter are sensitive to the radiative losses. Higher losses (smaller albedo) result in a higher density and a lower temperature. As a consequence, the precursor extension tends to be lower in the case of higher losses because the emissivity of the shock front is proportional to T4 and also because a large fraction of the photons escapes without contributing to the precursor extension.

Until now, we have emphasized the strong dependence of the stationary-shock structure on its radiative parameters (e.g., ratio R of the transverse width to the photon mean free path, and the percentage of radiative losses at the walls of the shock tube), or equivalently to departures from the 1D approximation. Another interesting quantity is the radiation flux, since it is used, for instance, as a tracer of accretion rate. In Fig. 6, we plot, for different tube-wall albedos, the variations in the luminosity as a function of the angle of observation $\theta$ ($\theta=0$ corresponds to a forward flux, $\theta=\pi/2$ to a perpendicular flux, and $\theta=\pi$ to a backward flux). The plotted profiles correspond to the luminosity integrated from the beginning of the radiative precursor to the shock front at time t=50 ns. The integral is evaluated by calculating the photon angular distribution function, which is known from the M1 model, at each point along the cell wall. We plot a normalized luminosity because we are interested only in the angular distribution and not in the absolute value, which is more difficult to compare. One can see that with increasing lateral losses the angle corresponding to the maximum of the luminosity increases and the distribution sharpens around this angle. This is due to the fact that when the losses are high, the radiative reduced flux is higher, and the luminosity tends to become almost mono-directional (in the limiting case of a unit-reduced flux) rather than an isotropic Planck function (in the limiting case of diffusion). The luminosity is much more directional and the dispersion around the preferred direction is lower. Figure 7 shows that this angle is approximately a linear function of the lateral albedo of the tube walls. All these points illustrate the strong anisotropy of the flux in the radiative shock. Although illustrated for a given time, the conclusions about the influence of the albedo on the peak of the angular distribution and on the dispersion about this value are of a quite general character during the shock propagation.

 \begin{figure} \par\includegraphics[width=7.5cm,clip]{9136fg6.ps} \end{figure} Figure 6:

Normalized luminosities for different values of albedo (80% in yellow solid line, 70% in red dotted line, 50% in green dashed line, 20% in blue dashed-dotted line and 0% in black dashed-double-dotted line).
Open with DEXTER

 \begin{figure} \par\includegraphics[width=8cm,clip]{9136fg7.ps} \end{figure} Figure 7:

Angle corresponding to the maximum of the luminosity as a function of the albedo (points: numerical simulation results, line: fit).
Open with DEXTER

8 Conclusion

We have illustrated how radiation influences the radiative-shock topology and structure. These effects can be observed with experimental results and used to interpret observational data.

We have in particular shown that lateral radiative losses induce a curvature in the shock front and a strong shortening of the radiative precursor. For laboratory experiments, it means that the tube geometry and the opacities play a key role in the shock propagation and topology. In astrophysical cases, this suggests that the link between accretion rate and photometric observation is strongly dependent on the gas conditions and the possible presence of dust.

Lateral radiative losses through the walls of the tube lead to a weakening of the shock, and a reduction in the precursor extension and temperature. They also strongly reduce the time needed to reach the stationary limit.

The radiative flux that emerges from the tube boundaries evolves from an isotropic situation in the case of low radiation losses to a more anisotropic distribution in the case of strong radiative losses. This effect may have a strong impact on photometric observations of anisotropic accretion flows, such as in the case of T Tauri star accretion through funnels.

High-energy, high-power installations, such as lasers, allow generation of strong radiative shocks with extended precursors. Most studies have focused on the global characterization of the radiative precursor. Only a few have attempted to study the shock front, which requires X-ray diagnostics of high temporal and spatial resolution and is thus very challenging. An important result of our study is the reduction with radiative losses in the time needed to reach the stationary limit. Although some experiments have been close to reaching this limit (González et al. 2006b), this has not been studied until now experimentally.

Shock velocities of 60-80 km s-1 are accessible with kJ class lasers. Using more powerful laser-energy installations such as the NIF (Haynam et al. 2007) at Livermore (USA) or the LMJ (Ebrardt & Chaput 2008; Besnard 2008; Bettinger & Decroisette 1999) at Bordeaux (France) will allow us to explore the effects of the radiation pressure on the structure of the shock wave. Using xenon at densities of the order of 5 $\times $ 10-4 g/cm3, such effects start to be visible for shock velocities of the order of 200 km s-1 (Michaut et al. 2004).

Another interesting topic that could be addressed is the eventual development of radiative instabilities. These ``thermal'' instabilities have been studied theoretically and numerically for optically thin radiative shocks, in the context of, for example, accretion onto white dwarfs, and colliding radiative flows (Walder & Folini 1996; Chevalier & Imamura 1982; Ryu & Vishniac 1987; Bertschinger 1986; Mignone 2005; Falle 1975; Laming & Grun 2002). Such an instability was observed experimentally in 3D blast-wave development over a few hundreds of nanoseconds (Grun et al. 1991), although other experiments failed to reproduce it on a shorter timescale (Edwards et al. 2001). The development of these instabilities in an optically-thicker radiative shock (with a radiative precursor) has, to our knowledge, not been studied theoretically. The multidimensional effects, by deforming the front and allowing a transition towards an optically thin case, could be favorable to the development of such instabilities, and this will be the subject of future studies.

These laboratory studies allow us to test the adequacy of modern codes in dealing with astrophysical, hypersonic radiative flows. The HERACLES 3D radiation hydrodynamics code is well adapted to the study of these anisotropic radiative flows. It allows us to test together the cases of both optically thick and optically thin regimes. It has been already used in modeling the propagation of astrophysical radiative jets in the ISM (González 2006; González et al. 2006a). Future improvements will include the inclusions of multigroup radiative-transport (which may influence the fine structure of the shock precursor), the decoupling of ionic and electronic temperatures (which affect the shock front), and non-LTE effects, which play a role in the optically thin regions of the shock structure.

Acknowledgements
The authors are indebted to M. Busquet and to the anonymous referee for valuable comments and suggestions leading to an improvement of this manuscript. This work was carried out under the EU funded RTN JETSET (contract MRTN-CT-2004 005592). The authors acknowledge the financial support of CNRS program PNPS and ANR grant SiNERGHy (ANR-06-CIS6-009-01) and would like to thanks the CEA computing center (CCRT) where all the simulations were done. M.G. acknowledges the financial support provided by the European Commission TUIXS project and the French Ministry of Foreign Affairs through the Lavoisier grant.

References

All Figures

  \begin{figure*} \par\includegraphics[angle=90,width=8.8cm,clip]{9136fg1.ps} \end{figure*} Figure 1:

Typical profiles of a 1D radiative shock: density ( upper left), velocity ( upper right), radiative and gas temperature ( lower left), and radiative flux ( lower right).
Open with DEXTER
In the text

    \begin{figure} \par\subfigure[Shock and precursor absolute positions]{\includegr... ...ursor]{\includegraphics[angle=90,width=4.2cm,clip] {9136fg2b.ps} }\end{figure} Figure 2:

Influence of the dynamics of the piston launching on the shock dynamics. The shock is driven in xenon at 0.2 bar at room temperature. The shock tube is a cylindrical cell with a 0.7 cm diameter and albedo of 40%. The full line refers to the impulsive lanching whereas the dotted line refers to a shock driven by a piston at constant velocity of 65 km s-1 (cf. Sects. 3 and 4).
Open with DEXTER
In the text

     \begin{figure} \par\subfigure[R=0.5]{ \includegraphics[angle=90,width=8cm,clip] ... ...R=10]{ \includegraphics[angle=90,width=8cm,clip] {9136fg3c.eps} }\end{figure} Figure 3:

At a same instant, snapshots of the maps of density, temperature, radial, and axial radiative flux showing the influence of the canal width compared to the photon mean free path (R=0.5 top panel, R=1 middle panel and R=10 bottom panel). Case of xenon initially at 1.3 $\times $ 10-3 g/cm3 and 300 K, using perfect-gas equation-of-state ($\gamma $ = 5/3 and mean molecular weight $\mu $ = 20 equivalent to a mean ionization stage of 5), and analytic opacities (Bozier et al. 1986). The shock propagates from top to bottom.
Open with DEXTER
In the text

   \begin{figure} \par\subfigure[]{\includegraphics[width=7.5cm,clip]{9136fg4a.ps} ... ...cm} \subfigure[]{\includegraphics[width=7.5cm,clip]{9136fg4b.ps} }\end{figure} Figure 4:

a) Influence of the walls albedo upon the shock (dashed line) and precursor (solid line) positions. b) Influence of the albedo upon the distance between the precursor and the shock. Comparison for an albedo of 0%, 40%, 50%, 60%, 70%, 80%, 90%, and 100% (from bottom to top).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{9136fg5.ps} \end{figure} Figure 5:

Influence of the albedo upon the time interval to form a stationary radiative shock, $t_{\rm stat}$ (points: numerical simulations results, line: fit).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{9136fg6.ps} \end{figure} Figure 6:

Normalized luminosities for different values of albedo (80% in yellow solid line, 70% in red dotted line, 50% in green dashed line, 20% in blue dashed-dotted line and 0% in black dashed-double-dotted line).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{9136fg7.ps} \end{figure} Figure 7:

Angle corresponding to the maximum of the luminosity as a function of the albedo (points: numerical simulation results, line: fit).
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.