EDP Sciences
Home All issues Volume 497 / No 1 (April I 2009) A&A, 497 1 (2009) 167-176 Full HTML
Free Access
Issue
A&A
Volume 497, Number 1, April I 2009
Page(s) 167 - 176
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200811385
Published online 18 February 2009

Observational and theoretical constraints for an H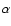$\alpha $-halo around the Crab nebula[*],[*]

A. Tziamtzis1 - M. Schirmer2,3 - P. Lundqvist1 - J. Sollerman1


1 - Department of Astronomy, AlbaNova University Center, Stockholm University, 106 91 Stockholm, Sweden
2 - Isaac Newton Group of Telescopes, Calle Alvarez Abreu 68 2, 38700 Santa Cruz de La Palma, Spain
3 - Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany

Received 20 November 2008 / Accepted 5 February 2009

Abstract
Aims. We searched for a fast moving H$\alpha $ shell around the Crab nebula. Such a shell could account for this supernova remnant's missing mass, and carry enough kinetic energy to make SN 1054 a normal type II event.
Methods. Deep H$\alpha $ images were obtained with WFI at the 2.2 m MPG/ESO telescope and with MOSCA at the 2.56 m NOT. The data are compared with theoretical expectations derived from shell models with ballistic gas motion, constant temperature, constant degree of ionisation, and a power law for the density profile.
Results. We reach a surface brightness limit of $5~\times~10^{-8}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$. A halo is detected, but at a much higher surface brightness than our models of recombination emission and dust scattering predict. Only collisional excitation of Ly$\beta$ with partial de-excitation to H$\alpha $ could explain such amplitudes. We show that the halo seen is caused by PSF scattering and thus not related to a real shell. We also investigated the feasibility of a spectroscopic detection of high-velocity H$\alpha $ gas towards the centre of the Crab nebula. Modelling the emission spectra shows that such gas easily evades detection in the complex spectral environment of the H$\alpha $-line.
Conclusions. PSF scattering significantly contaminates our data, preventing a detection of the predicted fast shell. A real halo with observed peak flux of about $2~\times~10^{-7}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ could still be accomodated within our error bars, but our models predict a factor 4 lower surface brightness. Eight meters class telescopes could detect such fluxes unambiguously, provided that a sufficiently accurate PSF model is available. Finally, we note that PSF scattering also affects other research areas where faint haloes are searched for around bright and extended targets.

Key words: ISM: supernova remnants - stars: supernovae: individual: SN1054

1 Introduction

According to historical records, SN 1054 was visible during daytime for more than three weeks and for almost two years during night-time (see e.g. Clark & Stephenson 1977). Its light curve (e.g. Sollerman et al. 2001), hydrogen-rich nebula, and the presence of a central neutron star (Comella et al. 1969; Staelin & Reifenstein 1968) are all compatible with a normal core-collapse event. However, the velocities of the filaments in the Crab nebula are rather low ($\sim$ $1400 \rm ~km~s^{-1}$, Woltjer 1972), as is the observed ejecta mass of $4.6\pm1.8~{M}_\odot$ (Fesen et al. 1997).

The elemental abundances and the low velocity and mass of the filaments may be accomplished by a low-energy explosion of a 8- $13 ~{M}_\odot$ star (Kitaura et al. 2006; Nomoto 1987,1985). Indeed, supernovae with very low kinetic energies are known, such as SN 1997D with (1- $4) \times 10^{50}$ erg (Turatto et al. 1998; Chugai & Utrobin 2000). However, no events with as little kinetic energy as SN 1054 ( $1.5~\times~10^{49}$erg) have yet been identified.

Chevalier (1977,1985) suggested that a hydrogen-rich shell of a few solar masses could carry most of the kinetic energy. Such a shell could be observed as extended optical emission, or as non-thermal radio and thermal X-ray emission caused by a shock front advancing through the interstellar medium such as in the case of SNR G21.5-0.9 (in X-ray, Matheson & Safi-Harb 2005).

Searches for such emission around the Crab nebula have been performed at radio wavelengths (Velusamy 1985; Trushkin 1986; Frail et al. 1995; Wilson & Weiler 1982; Velusamy 1984; Velusamy et al. 1992), in the optical (e.g. Fesen & Ketelsen 1985; Gull & Fesen 1982), and in X-rays (Mauche & Gorenstein 1989; Predehl & Schmitt 1995; Seward et al. 2006; Mauche & Gorenstein 1985), yielding negative results. Possibly the Crab nebula expands into a local bubble of the ISM with correspondingly low interaction rates (see Wallace et al. 1999, and references therein).

The first evidence for the existence of a shell was reported by Hester et al. (1996), in the form of [O III] emission surrounding the outer boundaries of the nebula. Sankrit et al. (1998) interpreted this emission as due to radiative shocks at the outer edge where the synchrotron nebula accelerates the hypothetical shell. Sollerman et al. (2000) detected a blue shifted absorption feature in C IV $\lambda$1550 in a far-UV HST spectrum, extending up to $\sim$ $2500 \rm ~km~s^{-1}$. Such a feature of the shell was predicted by Lundqvist et al. (1986) using photoionisation models. Lower limits of $0.3 ~{M}_\odot$ and $1.5~\times~10^{49}$ erg were derived for the mass of the shell and its kinetic energy, respectively. This is significantly below the canonical value of 1051 erg, but the results of Sollerman et al. (2000) do not rule out a normal type II explosion. For a comprehensive summary of the search for a halo and for a general overview of the Crab nebula see Hester (2008).

By means of sufficiently deep H$\alpha $ surface brightness maps strong constraints can be put on the shell mass and its radial density profile. Sollerman et al. (2000) showed that a fast shell with 4 $~{M}_\odot$ would escape the deepest H$\alpha $ search so far, reaching a surface brightness limit of $1.5~\times~10^{-7}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ (Fesen et al. 1997, using spectroscopy). In this paper we describe our attempts to image an H$\alpha $ halo with the Wide Field Imager (WFI) (Baade et al. 1999) at the 2.2 m MPG/ESO telescope and the Mosaic Camera (MOSCA) at the 2.56 m Nordic Optical Telescope, reaching a sensitivity of $5.0~\times~10^{-8}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$. The observations and data reduction are summarised in Sect. 2. We analyse the images in Sect. 3 and link the results to theoretical models in Sect. 4. The feasibility of a direct spectroscopic detection towards the centre of the Crab nebula is evaluated in Sect. 5. Our results are discussed in Sect. 6, followed by our conclusions. Throughout this paper we use the term shell for actual physical material around the Crab nebula, and the term halo for its appearance in images and spectra.

Table 1:   Summary of the WFI, MOSCA and FORS1 observations.

2 Observations and data reduction

2.1 Imaging data

WFI covers 34 $^{\prime}\;$$\times$ 33 $^{\prime}\;$with a pixel scale of 0 $.\!\!^{\prime\prime}$238. We observed in the H$\alpha $ filter ( $\lambda_{\rm c}=6588$ Å, FWHM=74 Å) using a very wide dither pattern (see Fig. 1) in order to suppress instrumental effects and to obtain a good superflat. This is especially important when searching for low surface brightness features (see Erben et al. 2005, and in particular their Fig. 8). Observations were carried out in service mode in dark and grey time (see Sect. 2.2.1 for details).

Independent H$\alpha $ images ( $\lambda_{\rm c}=6564$ Å, FWHM=33 Å, NOT filter code #21) were taken with MOSCA in dark time. MOSCA has 4 CCDs and offers in this filter a comparatively small, 5 $.\!\!^{\prime}$5 diameter circular field with 0 $.\!\!^{\prime\prime}$217 per pixel. It was centred on the north-western part of the Crab nebula (see Fig. 2).

2.2 Data reduction

We processed the multi-chip camera data with the THELI[*] pipeline (Erben et al. 2005). The images were overscan corrected (not for MOSCA, which does not have an overscan), debiased, flatfielded, gain-corrected, and in case of WFI also superflatted. The MOSCA data could not be superflatted as the target covered most of the field of view. One of the MOSCA CCDs (#4) did not flatfield properly and was partially masked (see also Fig. 3). The images were then individually weighted and we determined the relative photometric zeropoints between them. After sky subtraction and a full astrometric calibration the images were coadded. The photometric zeropoint is constant across the stacked mosaic images with an error of $\sim$0 $~.\!\!^{\rm {m}}$07.

In the following we describe the superflatting and sky subtraction. These two steps are critical as they must not suppress or enhance a halo while correcting for flat field residuals and inhomogeneous sky background.

2.2.1 Superflatting

Three main dither positions (Fig. 1) were chosen for the WFI observations. Dither offsets of $4^{\prime}$- $5^{\prime}$ were made at each one. Since the Crab nebula is 6 $^{\prime}\;$in size, this approach ensured that every pixel saw the sky much more often than the object, which is the basic requirement when making superflats. We first run SExtractor (Bertin & Arnouts 1996) to detect all objects consisting of at least 5 connected pixels, each of which having a minimum S/N-ratio of 2. In this manner stars and the Crab nebula were masked out. Lower detection thresholds would have removed sky features as well which must be preserved. The masked images of a given CCD were then scaled to the same mode and median-combined using a 2.5$\sigma $outlier rejection. This is the standard approach in THELI.

 \begin{figure} \par\includegraphics[width=9cm]{crabfig1.eps} \end{figure} Figure 1:

The WFI detector layout and the dither pattern. The Crab nebula was placed on three main positions on the detector and is represented to scale by the solid circles. At each of these main positions random dither offsets of up to $\pm 2\hbox{$.\!\!^{\prime}$ }5$ were applied (small dashed circles).
Open with DEXTER

11 of the 36 images were taken in grey conditions, with the moon 12 degrees or less above the horizon and 80 to 110 degrees away from the target. 7 of these exposures were significantly affected by uneven sky background or reflections and removed from further processing. In the remaining 4 grey exposures only one or two of the chips were affected (none with the Crab nebula inside) and not used for the superflat.

The superflats were then smoothed with a 1 $^{\prime}\;$wide kernel in order to suppress small scale noise. Since CCDs 1 and 8 still showed significant, time-variable background features in all exposures, they were excluded at this stage.

2.2.2 Sky subtraction

After superflatting and rejecting CCDs 1 and 8, only small (1-3%) and large-scale ($\sim$10 $^{\prime}\;$) gradients were left in the exposures. They are larger in size than the Crab nebula and a possible halo. The outermost 2 $^{\prime}\;$of the right edges of CCDs 4 and 5 are occasionally brighter by about 2%. This is not a cause of concern as the dithering never moved the target close to this region.

THELI uses a similar approach for background subtraction as for the superflat. All objects with at least 5 connected pixels and 2$\sigma $ above the sky noise were replaced with the mode of the remaining pixels. This intermediate image was then smoothed and subtracted. We tested two different smoothing scales of 1 $.\!\!^{\prime}$8 and 3 $.\!\!^{\prime}$0, and as an additional check also created a coadded image where only a constant sky was subtracted from each CCD. A very similar halo around the Crab nebula is detected in all three coadded images, thus it was not artificially introduced by the data reduction. In fact, we show below that it is caused purely by PSF scattering. The coadded images with the 1 $.\!\!^{\prime}$8 and 3 $.\!\!^{\prime}$0 background smoothing scales are very similar, and we conservatively chose the latter for further analysis. A comparison with the constant sky subtraction image shows that the modelling lowered the halo's brightness by less than $\sim$10%.

The sky background of the MOSCA data was not modelled, as only small areas of sky were available between the Crab nebula and the edge of the field. We subtracted constant estimates obtained from empty areas located $\sim$2 $^{\prime}\;$from the nebula's outer edge. Some particular issues with the MOSCA reductions are explained in the Appendix.

 \begin{figure} \par\includegraphics[width=9cm]{crabfig2.eps} \end{figure} Figure 2:

Part of the coadded WFI image. For clarity we did not invert the centre of the nebula. A faint halo around the SNR is visible. Superimposed is the slit position for the FORS1 spectra, together with the location where we tested the feasibilty of a spectroscopic detection of a fast shell. The large circle shows the MOSCA field of view.
Open with DEXTER

2.2.3 Absolute photometric calibration

We used the Crab pulsar and its flux-calibrated spectrum (from Sollerman et al. 2000) for the absolute photometric calibration of the WFI data. Since the pulsar lies within a complex nebular environment, we must remove the contribution of the latter from the pulsar's flux. We obtained a DAOPHOT PSF model from isolated, bright but unsaturated, field stars and subtracted it from the pulsar's PSF. In this way the nebular contribution could be quantified and removed. The pulsar's magnitude was then aperture corrected, using the same field stars. The differences between aperture and PSF photometry were then $\leq$0.01 mag, and the final photometric zeropoint became ZP $_{\rm WFI}=21.42\pm0.15$.

Flux-calibration for the MOSCA data was based on DAOPHOT aperture photometry of the spectro-photometric standard star HD 93521. After application of the MOSCA filter transmission curve to the reference spectrum, the photometric zeropoint became ZP $_{\rm MOSCA}=21.5\pm0.10$. With this calibration there was a constant offset of 0.07 mag in field stars seen by MOSCA as compared to WFI. The Carlsberg Meridian Archive[*] shows increased extinction levels for the corresponding week in La Palma, however without a measurement for our night. The observations were thus probably not made in photometric conditions, and we corrected the MOSCA zeropoint for this offset.

 \begin{figure} \par\includegraphics[width=9cm]{crabfig3.eps} \end{figure} Figure 3:

The coadded MOSCA image. The missing part to the upper right is due to a partially masked CCD.
Open with DEXTER

3 Observational results

In this section we present the results from our imaging campaigns. We trace clear but inconsistent signals in both the WFI and MOSCA data and discuss them in Sect. 4.

Our halo detection strategy is described in the following based on the WFI data. It was done in a similar way for MOSCA. We

  • mask all stellar flux so that it does not contribute to the halo;
  • define an outer boundary of the Crab nebula;
  • measure and average the halo brightness as a function of distance from this boundary in many different sectors.

3.1 Masking the image

In order to mask any unwanted light, we ran SExtractor with a detection threshold of $2\sigma$ and a minimum number of 15 connected pixels. The noise in coadded mosaic images is very uneven due to the dither pattern and the gaps between the CCDs, and this fact must be taken into account in the detection process. The coadded weight map reflects these noise properties and was therefore slotted into SExtractor as well. In this way stars, filter ghosts, and the Crab Nebula itself were masked while the halo was preserved. Some residuals of scattered light were still visible around brighter stars and masked manually. These masks are shown as black regions in Fig. 5. Also shown in this figure is the contribution of PSF scattering mimicking a halo, which we discuss in Sect. 4.1.

3.2 Defining the boundary around the Crab nebula

We measure the halo brightness as a function of distance from the nebula in several sectors protruding outwards from the explosion centre. Once the sectors cross the edge of the nebula, the radial coordinate (distance) is set to zero, and we begin integrating the halo flux. However, the edge's fractal-like appearance (Fig. 4) makes the determination of the zero-point of the radial coordinate difficult. Isolated or half-connected groups of pixels still reside inside, leading to an underestimation of the distance between the explosion centre and the outer edge. As a result, the stack of individual profiles is not properly aligned, leading to increased scatter in the result. To avoid this, we defined the manual mask indicated by the solid line in Fig. 4.

 \begin{figure} \par\includegraphics[width=9cm]{crabfig4.eps} \end{figure} Figure 4:

Defining the boundary (mask) of the Crab nebula. Only the south-eastern area is shown. The automatic masking with SExtractor left a fractal-like border which hampers the determination of the starting point for the halo measurement in a sector. The solid line shows the manual re-definition of the mask. Most of the stellar flux was automatically masked, but remaining residuals around brighter stars had to be covered manually. These masks can be seen in Fig. 5.
Open with DEXTER

3.3 The radial halo profile

We assume the centre of the halo to coincide with the explosion centre, located at $\alpha_{\rm J2000}= 05^{\rm h} 34^{\rm m} 32.7^{\rm s}$, $\delta_{\rm J2000}= +22^{\circ} 00^{\prime} 48\hbox{$.\!\!^{\prime\prime}$ }7$ (back-projecting the pulsar proper motion as given by Kaplan et al. 2008). The exact position is not a critical parameter for our analysis, the measured halo profile changes negligably when the assumed explosion centre is shifted by a few arcseconds. We defined 72 sectors, each 5 degrees wide, emerging from this centre. Those sectors that covered the jet-like Crab chimney (see Rudie et al. 2008, for details) were excluded from our analysis, hence 68 (MOSCA: 20) sectors remain.

 \begin{figure} \par\includegraphics[width=9cm]{crabfig5.eps} \end{figure} Figure 5:

Masks for the field stars, together with two of the 72 measurement sectors. These converge towards the explosion centre and are drawn to scale. The density of the radial bins is four times higher than indicated, and the field of view is similar to that in Fig. 2. The brightening in the immediate surrounding of the Crab nebula shows the amount of PSF scattering expected for WFI (see Sect. 4.1).
Open with DEXTER

In order to scan the profile in each sector, we divided them into 29 (MOSCA: 19) equidistant radial bins 24 pixels in length corresponding to 5 $.\!\!^{\prime\prime}$7 (5 $.\!\!^{\prime\prime}$2) for WFI (MOSCA). Their mean brightness was calculated using an interative 2.5$\sigma $ outlier rejection. This clipping procedure reduced the error bars of the final radial profile by just 5%, indicating that our masks are already very efficient.

Figure 6 shows the results. The error bars represent the standard deviation of the mean surface brightness and are dominated by brightness fluctuations as a function of azimuthal angle. We can trace the haloes to distances of $1\hbox{$.\!\!^{\prime}$ }9$ and $1\hbox{$.\!\!^{\prime}$ }3$ for WFI and MOSCA, respectively. The MOSCA signal peaks at $2.5~\times~10^{-6} \rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ and is twice as high as that for WFI, but it also decays faster. If x is the distance from the outer edge of the nebula in arcminutes, then the profiles are proportional to 10-0.88 x (WFI) and 10-1.12 x (MOSCA). These inconsistencies are investigated in Sect. 4. The sensitivity limit reached is $5~\times~10^{-8}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$, corresponding to 31.2 mag per square arcsecond.

 \begin{figure} \par\includegraphics[width=9cm]{crabfig6.ps} \end{figure} Figure 6:

The halo profiles observed. They fall off following power laws with slopes of -0.88 (WFI) and -1.12 (MOSCA).
Open with DEXTER

4 Analysis

We show here that the haloes are caused by PSF scattering, and we infer upper limits to the surface brightness of a real shell. We present model calculations for three different physical processes that can lead to H$\alpha $emission in the shell and compare them to our observations.

4.1 PSF scattering

Figure 7 shows filter ghosts and other scattered light around stars. In order to evaluate how much this effect contributes to the haloes, we obtained azimuthally averaged PSF models for both data sets (see Fig. 8).

The PSF model for WFI extends to a radius of 2 $.\!\!^{\prime}$7 and was created from very bright stars in the coadded image. The saturated core was replaced by one obtained from unsaturated stars. During the construction of the model a strict $1\sigma$ rejection threshold was applied to suppress contamination from field stars. The resulting PSF profile exhibits several bumps due to the filter ghosts which make simple mathematical fits inadequate. We also created a second PSF model with reduced wing amplitude, by subtracting the rms value of the sky background on a large scale from the first model. In this way we could evaluate how sensitive light scattering is to small changes in the amplitude of the PSF wings.

The PSF model for MOSCA was obtained in a similar way from two moderately bright stars in a single 600 s blank field exposure taken in the same night. The model's empirical part extends out to 0 $.\!\!^{\prime}$85, beyond which it is extrapolated by a power law with index $\beta=-2.4\pm0.4$. The slope was determined from the profile between 0 $.\!\!^{\prime}$45 and 0 $.\!\!^{\prime}$85. Note that the uncertainty of this model at a radius of 0 $.\!\!^{\prime}$2 is already larger than that for the WFI PSF at 2 $.\!\!^{\prime}$0.

To evaluate the PSF contribution, we zeroed all pixels in the coadded images having values less than 5 times the sky noise, keeping only the cores of stars and the Crab nebula. These images were then convolved with the PSF models, and the profile measurements were repeated with identical settings and masks. The result for WFI is shown in Fig. 9 (dotted line), together with the contribution from the PSF model with lowered wing amplitude (dashed line). The latter significantly underestimates the halo flux as compared to the unaltered model. Residual light from field stars contributes to the halo only for radii larger than 1 $.\!\!^{\prime}$5. We evaluated this by convolving an image where all field stars were masked out. Within the error bars of the best-fitting PSF and of the measurement, a real halo with an H$\alpha $ peak flux of $2~\times~10^{-7}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ can still be accomodated, comparable to the upper limit of $1.5~\times~10^{-7}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ obtained by Fesen et al. (1997).

Figure 10 shows the corresponding result for MOSCA. The halo is very well explained by PSF scattering (dotted line). The other two lines represent the $1\sigma$ uncertainty of the power-law fit to the PSF wing. Due to the less reliable MOSCA PSF model we could not improve the upper flux limit obtained with WFI.

We stress that simplified approaches such as a comparison of the slope of the PSF with the slope of the halo, or of the brightness ratios between inner and outer part of the PSF and inner and outer part of the Crab nebula, are insufficient. In these ways PSF scattering would have been underestimated by about 3 orders of magnitude. Only full 2D convolutions can quantify the effect accurately. It appears plausible that an earlier detection made in H$\alpha $on a photographic plate (Murdin 1994; Murdin & Clark 1981) also shows this effect. Davidson & Fesen (1985) argued that the detection made was of instrumental nature, but the subject was not investigated further.

 \begin{figure} \par\includegraphics[width=9cm]{crabfig7.eps} \end{figure} Figure 7:

Illustrates the WFI filter ghosts. The star shown is the brightest seen in the lower left edge of Fig. 2. The core of the PSF is labelled as 1, followed by three filter ghosts of decreasing intensity, labelled 2-4.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=9cm]{crabfig8.ps} \end{figure} Figure 8:

The two PSF models for WFI (solid line) and MOSCA (dotted line). The bumps in the WFI PSF at 0.15, 0.4 and 0.8 arcmin reflect the various filter ghosts. The MOSCA PSF is extrapolated for radii larger than 0 $.\!\!^{\prime}$85 by a power law with index $\beta =-2.4$ (not shown). MOSCA has a significantly more compact PSF than WFI for radii larger than about 4 $^{\prime \prime }$ (0 $.\!\!^{\prime}$06), which explains the steeper slope of the halo in that data.
Open with DEXTER

4.2 Theoretical models for H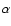$\alpha $ emission from a fast shell

Our data still allows for a peak H$\alpha $ surface brightness of $2~\times~10^{-7}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ through the WFI H$\alpha $-filter. The upper limit of $1.5~\times~10^{-7}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ by Fesen et al. (1997) refers to the total unfiltered surface brightness. We compare these values below with predictions based upon the shell models of Sollerman et al. (2000). Therein, the shell is of spherical shape and expands freely outside the Crab nebula with $V\propto R$. It has an inner minimum radius of $R_{\rm min}=5.0\times10^{18}$ cm corresponding to a minimum velocity of $1680\rm ~km~s^{-1}$. Unlike the Crab nebula the shell is not affected by the pulsar wind. The mass of the shell is set to $M_{\rm sh} = 4.5 ~{M}_\odot$, it has a fixed electron temperature of $T_{\rm e}= 2~\times~10^{4}$ K (Lundqvist et al. 1986), and a radial density profile $\rho \propto R^{-\eta}$, with $\eta = 3$ or $\eta = 4$. Smaller values for $\eta $ do not fit the profile of the C IV absorption (see Sollerman et al. 2000), and values $\eta\gtrsim5$ would make the H$\alpha $ surface brightness surpass our detection limit.

All fluxes determined from the models must be corrected for galactic extinction before they can be compared to observations, using the reddening parameters E(B-V)=0.52 and R=3.1 (Sollerman et al. 2000). Our dereddened upper limit of the H$\alpha $ surface brightness through the WFI H$\alpha $-filter becomes $6.6~\times~10^{-7}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$.

4.2.1 Recombination emission

For the modelling of the recombination emission we furthermore assume that hydrogen in the shell is fully ionised and that the gas has a He/H-ratio of 0.1 by number. Figure 11 shows the modelled surface brightness profile as a function of distance from the edge of the nebula for two cases: $\eta = 3$ (top panel) and $\eta = 4$ (bottom). The solid lines describe the surface brighness captured by the WFI H$\alpha $-filter.

For comparison we also plot the signals expected through the WFI red continuum filter (dashed line) and for unfiltered observations (dotted line). The continuum filter selects ${\rm H\alpha}$-emission from shell gas receding from the observer with 2000-6000  $\rm ~km~s^{-1}$. The advantage is that the Crab nebula is much less bright in these wavelengths and thus the amount of scattered light is reduced, which favours a detection. On the other hand, the gas seen in this filter is actually at significantly larger distance behind the Crab nebula and just projected next to the nebula's edge. The densities in these parts of the shell are much smaller and thus the emission is significantly reduced (see Fig. 11). The dotted line represents the fluxes expected for unfiltered observations which we need later on for comparison with spectroscopy.

Peak surface brightness for the H$\alpha $-filter occurs at the edge of the nebula with $1.5~\times~10^{-7}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ for $\eta = 4$. For comparison, the observed WFI halo peaks at $1.2~\times~10^{-6}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ which translates into a dereddened value of $4.0~\times~10^{-6}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$, $\sim$26 times higher than the prediction. Taking the PSF scattering into account, the $\eta = 4$ (3) model is 4 (14) times below our dereddened upper limit. A similar relation emerges for the upper limit of $1.5~\times~10^{-7}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ by Fesen et al. (1997). Their result is based on unfiltered spectra and must therefore be compared with the dotted lines in Fig. 11 at roughly 0.3 arcmin from the edge of the nebula. Including reddening, the $\eta = 4$ (3) model is 4 (10) times below their detection limit. For a temperature of the shell of $7.5~\times~10^{3}$ K, as assumed by Fesen et al. (1997), the modelled surface brightness is $\sim$2.7 times higher than for $2~\times~10^{4}$ K. This brings the predicted surface brightness closer to the imaging and spectroscopic upper limits by the same factor. For the $\eta = 4$ (3) model the limits would only be a factor of $\sim$1.5 larger than the emitted surface brightness. The recombination emission can also be enhanced to some degree if the gas is clumpy and has a higher gas density. The latter, however, would quickly exceed a sensible value for the shell mass, make the C IV $\lambda$1550 absorption seen by Sollerman et al. (2000) too high, and contradict the findings of Sankrit et al. (1998).

 \begin{figure} \par\includegraphics[width=9cm]{crabfig9.ps} \end{figure} Figure 9:

The WFI halo profile with the contributions from the PSF (dotted line), and from the PSF with reduced wing amplitude (dashed).
Open with DEXTER

 \begin{figure} \par\includegraphics[width=9cm]{crabfig10.ps} \end{figure} Figure 10:

The MOSCA halo profile and the best fit PSF contribution (dotted line). The other lines show the 1$\sigma $ uncertainty of the fit.
Open with DEXTER

The slope of the haloes expected from recombination emission is close to exponential with 10-0.60 x for $\eta = 3$ and 10-0.82 x for $\eta = 4$. We note that the latter is coincidentally very similar to the slope for the WFI halo caused by PSF scattering. The MOSCA data would require steeper density profiles than $\eta = 4$.

 \begin{figure} \center \includegraphics[width=85mm, angle=0, clip]{crabfig11.eps} \end{figure} Figure 11:

H$\alpha $ halo surface brightness using the model described in Sect. 4.2. The dotted lines show the unfiltered total H$\alpha $ surface brightness, whereas the solid and dashed lines show what is captured through H$\alpha $ and continuum ESO/WFI filters, respectively. Note how the surface brightness falls off rapidly with distance from the edge of the nebula. As discussed in the text, the $\eta = 4$ model provides an adequate fit to the shape of the fall-off, but it cannot explain the flux amplitude.
Open with DEXTER

4.2.2 Dust scattering

Scattering by interstellar dust can contribute to the shell flux, too. The Crab nebula is an isolated object, and its dust density is nearly equal to the surrounding ISM, as was found by observations from the optical to sub-millimeter wavelengths (Green et al. 2004; Temim et al. 2006; Fesen & Blair 1990). The latter authors also showed that small-grain dust is entirely absent inside the nebula, and that larger grains amount to only 10-3- $10^{-2}~{M}_\odot$. Hence a normal dust-to-gas ratio can be assumed and an analysis similar to that in (Osterbrock 1989, Chap. 7) is valid. We adopt an H$\alpha $ luminosity of $7~\times~10^{34}$ erg s-1 for the nebula (Davidson 1987) and take the electron density to be $3 \rm ~cm^{-3}$ close to it, as is appropriate for the $\eta = 4$ model described above. In this way one obtains a ratio of emissivities (scattered emission on dust to recombination emission) $j_{\rm D} / j_{{\rm H}\alpha}\lesssim1$. Thus dust scattering will contribute about the same amount to the peak halo surface brightness as recombination emission.

The ratio $j_{\rm D} / j_{{\rm H}\alpha}$ has a radial dependence of $\propto$ $(R / R_{\rm min})^{\eta - 2}$. For $\eta = 4$ this means that dust scattering will dominate over recombination emission for increasing distances, effectively lowering the steepness of the halo profile. This can be used to discriminate scattering from recombination emission. Such an attempt should be complemented by deep observations in [O III], as the Crab nebula is bright in this line and dust scattering more efficient for shorter wavelengths.

4.2.3 Collisional excitation

One way to significantly enhance H$\alpha $ emission is collisional excitation of Ly$\beta$, followed by part of the radiative de-excitation going into H$\alpha $. This only works for temperatures well above 104 K, agreeing with our assumptions of $2~\times~10^{4}$ K. A neutral fraction of hydrogen of 10% is then enough to increase H$\alpha $ by a factor of $\sim$10 compared to pure recombination emission. If the shell gas was clumpy it is likely that such conditions prevail. However, our observations and those of Fesen et al. (1997) demand collisional excitation to be less dominant, as otherwise the halo would have been detected unamiguously. It remains unclear though if this effect will be constant with distance from the edge of the nebula, which could alter both the halo's slope and amplitude. Detailed modelling is required to test this.

5 Prospects for a spectroscopic halo detection

Direct imaging is not the only option for detecting a fast shell. Fesen et al. (1997) took 9 ks spectra with a 2.4 m telescope of regions outside the nebula, but could not detect any emission lines. Such emission would only have small Doppler shifts as the gas in this area moves mainly perpendicular to the line of sight. Another way would be spectroscopy of objects near the explosion centre, where the gas moves mainly along the line of sight and hence has a very large Doppler shift. In this way Sollerman et al. (2000) detected blue-shifted C IV absorption which is currently the best observational evidence for a fast shell.

Below we evaluate the chances of detecting the H$\alpha $ footprint of a shell towards the centre of the nebula. It would appear as emission on both sides of the H$\alpha $ line, serving as an additional verification of an expanding shell. Yet such an observation would be made against a complex and bright H$\alpha $ background, and thus the location where the spectra are taken must be picked carefully. A good choice will maximise the contrast as well as the spectroscopic separation of the shell and the nebula emission.

A set of FORS1 (Appenzeller et al. 1998) VLT spectra of the pulsar, taken for a different programme, serves as our testbed. The total exposure time was 600 s through a 1 $.\!\!^{\prime\prime}$0 wide slit, the dispersion is 2.7 Å$\;$pixel-1. We identified an area 10 $\;\!\!^{\prime\prime}\;$north of the pulsar which is largely free of bright filaments (see Fig. 2). The spectrum around the H$\alpha $ line is shown in Fig. 12.

 \begin{figure} \par\includegraphics[width=9cm]{crabfig12.eps} \end{figure} Figure 12:

Dereddened spectrum around H$\alpha $ 10 $\;\!\!^{\prime\prime}\;$north of the pulsar. In the lower panel we have inflated the flux scale and added the $\eta = 4$ model spectrum from Fig. 13. A constant of $10^{-17}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ was included, simulating the continuum emission from the pulsar wind nebula. Note that the model spectrum has been multiplied by a factor of 100 to be distinguishable in this plot.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=9cm]{crabfig13.eps} \end{figure} Figure 13:

Line profiles for the H$\alpha $ recombination emission of a fast shell, based on the models of Sect. 4.2. Note the gap in halo emission between $\pm 1680 \rm ~km~s^{-1}$ for lines of sight close to the explosion centre. The smaller the slope $\eta $ of the density profile, the less pronounced is the intensity fall off with increasing absolute velocity. The dotted line shows the filter curve of the WFI red continuum filter.
Open with DEXTER

We base our analysis on the shell models from Sect. 4.2 and their recombination emission. The H$\alpha $ line profile from such a shell depends strongly on the positioning of the spectroscopic slit, as gas with different velocities is projected along different lines of sight. For example, as the shell has an inner radius $R_{\rm min}$, no emission close to the pulsar will be seen for velocities $\vert V\vert<1680\rm ~km~s^{-1}$ ($\pm37$ Å) from the rest wavelength of H$\alpha $. This gap decreases for lines of sight further away from the centre. At the edge of the nebula the halo emission peaks at the rest wavelength of H$\alpha $. The corresponding spectra are shown in Fig. 13.

In Fig. 12 we overplotted the emission expected for the $\eta = 4$ model over the H$\alpha $ line observed. The model was increased by a factor of 100 compared to the data in order to make it visible. Even if collisional excitation was very important and boosted the halo's surface brightness by a factor 100, the emission would still be undetectable in these spectra. The main problem are the neighbouring [N II] lines at 6548 Å and 6583 Å  corresponding to $-675 \rm ~km~s^{-1}$ and $+944 \rm ~km~s^{-1}$, respectively. Their rest wavelengths are close to the expected H$\alpha $ peak emissions of the shell. The motions of the H$\alpha $ filaments with $\sim$ $\pm1400 \rm ~km~s^{-1}$contaminate the halo signal further. Increasing the integration times significantly would not help to resolve this issue. We tested other areas along the slit as well and they produce no better results than this one. We therefore conclude that a search for H$\alpha $ shell emission inside the Crab nebula is unfeasible.

6 Discussion

6.1 PSF scattering and haloes around galaxies

Our findings concerning the PSF scattering are applicable to other situations where very faint haloes are searched for around bright extended targets. The effect is easily overlooked, as the PSF is often thought of in scales of arcseconds rather than of arcminutes. The PSF can be very efficient in scattering light from far inside a bright target into its outskirts.

Observations of the extraplanar gas around edge-on galaxies are particularily affected by this, as galaxies can have high central surface brightnesses and small minor axes. Wu et al. (2002) recognised this effect in their work on NGC 4565 and constructed large PSF models based on separate observations of isolated bright stars. Their models extend to $28^{\prime}$ (corresponding to 1000 pixels), and they find that PSF scattering in their data is measurable but negligible. Wu et al. (2002) are cited by several authors working on similar subjects, yet PSF scattering appears to be largely ignored.

Zibetti et al. (2004) take this effect into account in their analysis of the stacked halo of 1047 edge-on galaxies taken from SDSS. They find a maximum contamination of about 30%. However, their PSF extends only to about 20 pixels ( $8^{\prime\prime}$) and is then extrapolated by an exponential function. de Jong (2008) investigated this in detail and reconstructed the SDSS PSF out to 180 pixels. Beyond that, the PSF is extrapolated with a power law index of -2.6 as obtained from the inner 40 to 180 pixels. Using a full 2D convolution of the stacked galaxy image, de Jong (2008) shows that the PSF contributes 50% in g and r, and up to 80% in i-band to the signal measured by Zibetti et al. (2004).

Even though this is an entirely different field of astrophysics, it suffers from the same observational effect. In our case the situation is rather extreme as the Crab nebula is of effectively constant surface brightness over its $5^{\prime}\times7^{\prime}$ area when smoothing out the filaments. Thus PSF scattering is very effective as the entire object contributes. The conclusions of de Jong (2008) are in excellent agreement with our own:

  • extrapolating a PSF to large radii can be very misleading as a small change in the wing amplitude can have a large effect on the amount of scattered light;
  • the PSF wings should ideally be constructed from extremely bright isolated stars and be joined with a core determined from bright but unsaturated stars;
  • the amount of scattering is very difficult to judge based just upon the PSF profile. Only a full 2D convolution will reveal its overall effect.

6.2 Prospects for future observations

Our images are strongly affected by PSF contamination. This also applies for similar attempts at other telescopes, and can only be overcome by large and accurate PSF models. These must be created by means of a very bright star that by far dominates all other flux in the image. Ideally, the star should be positioned on the same detector area as the target. It should be bright enough so that the PSF can be modelled without using azimuthal averaging, which destroys asymmetries in the PSF wings. Such a star should ideally be observed close to the target and in the same night, bracketing the target observations in time. The detector must be given sufficient time for recovery after such observations so that charge persistencies can decay. Dark conditions are required to keep the sky background as low as possible.

Observations through a red continuum filter would significantly minimise the contamination by scattered light. We investigated the efficiency of this approach based on the WFI continuum filter. As can be seen from Figs. 11 and 13, the flux expected in that filter would be 5 (8) times lower for the $\eta = 3$ (4) models as compared to H$\alpha $. This will be very difficult to record on 8m class telescopes. On the other hand, the combined emission from the processes discussed in Sect. 4.2, or from its constituents alone, would become visible in several hours H$\alpha $ exposure with e.g. FORS2 on the VLT, provided that good PSF models are available. For an optimum comparison of such data with model predictions one would subtract the 2D PSF-convolved image from the original image, and then integrate over the halo in concentric rings around the explosion centre.

On the spectroscopic side, the most promising approach is to search for Doppler shifted absorption features in a relatively uncontaminated spectral region against the central part of the nebula. However, care has to be taken in the interpretation of the result, as a chimney-like structure extending towards us may contain gas at velocities similar to those in the shell. This can be tested by searching for fast ($\sim$ $2000\rm ~km~s^{-1}$) blueshifted [O III] $\lambda 4959$ emission as [O III] is bright in the Crab chimney. This would lead to emission at around 4925-4935 Å and could be difficult to disentangle from He I 4921. Adding information from other emission lines seen in the chimney may be useful.

Finally, deep 21 cm radio observations outside the nebula may be useful. The main difficulty here is the uncertain degree of ionisation of hydrogen in the shell. If collisional excitation of H-alpha is important, then a good fraction of neutral hydrogen is implied which may show up in 21 cm line emission. Hence observations of the H$\alpha $ surface brightness of the shell can help to estimate the radio flux.

7 Summary

We have presented WFI and MOSCA images in H$\alpha $ to search for a high velocity shell around the Crab nebula. Our detection limit in both data sets is $5~\times~10^{-8}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$, three times deeper than the previously deepest study by Fesen et al. (1997). However, our measurement of an H$\alpha $ halo is corrupted by PSF contamination which can account for all of the signal. A real halo with an observed (i.e. reddened) peak brightness of $2~\times~10^{-7}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ could still be accomodated within the error bars. Thus we could not improve on the limits set by Fesen et al. (1997). Deep imaging with 8 m class telescopes, together with good PSF models, could yield progress in this field.

We discuss three different processes that could power H$\alpha $ emission from a fast shell: recombination emission, dust scattering, and collisional excitation. All but the latter yield flux levels about one order of magnitude below the one observed. As the halo flux in two independent imaging data sets is well described by PSF scattering, we can rule out collisional excitation to play a dominant role in the shell gas.

We argue that a spectroscopic detection of H$\alpha $ emission towards the centre of the nebula is unfeasible. The emission is very weak and buried in the complex spectral environment of the H$\alpha $ and [N II] lines. The prospects of detecting blueshifted absorption features in the pulsar or other background sources are significantly better and were already demonstrated by Sollerman et al. (2000). A deeper spectrum outside the Crab nebula could still be very useful, as the recombination level is below the upper value from Fesen et al. (1997). However, the amount of PSF scattering needs to be quantified also for spectroscopy. This problem could be avoided by looking only at emission further away than about $2200 \rm ~km~s^{-1}$ from H$\alpha $. However, the flux expected for density profiles steeper than $\eta\sim2$ is so low that a positive detection appears unfeasible.

Acknowledgements
We are grateful to Andrew Cardwell, Roger Chevalier and Rob Fesen for comments on an early version of this manuscript. We thank Göran Olofsson for crucial discussions of scattered light, and the anonymous referee for very useful suggestions. This work was supported by the Swedish Research Council. At the start of this project P.L. was, and J.S. currently is, a Research Fellow at the Royal Swedish Academy supported by a grant from the Wallenberg Foundation.

Appendix A: MOSCA peculiarities

We discovered that the gains of the individual chips in the MOSCA array depend on the illumination level. The gain ratios are different by up to 20% in flat fields with approximately 30 kADU as compared to the observations with very low background level ($\sim$100 ADU). The same behaviour was observed in data taken through two other filters about two months later.

The THELI pipeline assumes that all chips of a mosaic camera are brought to the same gain during flatfielding. This is not the case for MOSCA. We circumvented the problem by switching off THELI's gain adjustment and processed and stacked the data from each CCD independently. The 4 stacked images were then run again through the astrometric and photometric part of THELI, being interpreted as 4 dithered exposures coming from a single-chip camera. Given the overlap sources, relative photometric zeropoints could be calculated and thus the gain differences were removed. Upon comparing the fluxes of 74 common stars in the MOSCA and WFI data, we find a scattering of 0.08 mag without systematic trends as a function of position in the MOSCA mosaic.

References

Footnotes

... nebula[*]
Based on observations made with ESO Telescopes at the La Silla and Paranal Observatories, Chile (ESO Programmes 66.D-0489, 68.D-0096 and 170.A-0519).
...[*]
Based on observations made with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias.
... THELI[*]
Available at http://www.astro.uni-bonn.de/~mischa/theli.html
... Archive[*]
http://www.ast.cam.ac.uk/~dwe/SRF/camc_extinction.html

All Tables

Table 1:   Summary of the WFI, MOSCA and FORS1 observations.

All Figures

  \begin{figure} \par\includegraphics[width=9cm]{crabfig1.eps} \end{figure} Figure 1:

The WFI detector layout and the dither pattern. The Crab nebula was placed on three main positions on the detector and is represented to scale by the solid circles. At each of these main positions random dither offsets of up to $\pm 2\hbox{$.\!\!^{\prime}$ }5$ were applied (small dashed circles).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig2.eps} \end{figure} Figure 2:

Part of the coadded WFI image. For clarity we did not invert the centre of the nebula. A faint halo around the SNR is visible. Superimposed is the slit position for the FORS1 spectra, together with the location where we tested the feasibilty of a spectroscopic detection of a fast shell. The large circle shows the MOSCA field of view.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig3.eps} \end{figure} Figure 3:

The coadded MOSCA image. The missing part to the upper right is due to a partially masked CCD.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig4.eps} \end{figure} Figure 4:

Defining the boundary (mask) of the Crab nebula. Only the south-eastern area is shown. The automatic masking with SExtractor left a fractal-like border which hampers the determination of the starting point for the halo measurement in a sector. The solid line shows the manual re-definition of the mask. Most of the stellar flux was automatically masked, but remaining residuals around brighter stars had to be covered manually. These masks can be seen in Fig. 5.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig5.eps} \end{figure} Figure 5:

Masks for the field stars, together with two of the 72 measurement sectors. These converge towards the explosion centre and are drawn to scale. The density of the radial bins is four times higher than indicated, and the field of view is similar to that in Fig. 2. The brightening in the immediate surrounding of the Crab nebula shows the amount of PSF scattering expected for WFI (see Sect. 4.1).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig6.ps} \end{figure} Figure 6:

The halo profiles observed. They fall off following power laws with slopes of -0.88 (WFI) and -1.12 (MOSCA).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig7.eps} \end{figure} Figure 7:

Illustrates the WFI filter ghosts. The star shown is the brightest seen in the lower left edge of Fig. 2. The core of the PSF is labelled as 1, followed by three filter ghosts of decreasing intensity, labelled 2-4.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig8.ps} \end{figure} Figure 8:

The two PSF models for WFI (solid line) and MOSCA (dotted line). The bumps in the WFI PSF at 0.15, 0.4 and 0.8 arcmin reflect the various filter ghosts. The MOSCA PSF is extrapolated for radii larger than 0 $.\!\!^{\prime}$85 by a power law with index $\beta =-2.4$ (not shown). MOSCA has a significantly more compact PSF than WFI for radii larger than about 4 $^{\prime \prime }$ (0 $.\!\!^{\prime}$06), which explains the steeper slope of the halo in that data.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig9.ps} \end{figure} Figure 9:

The WFI halo profile with the contributions from the PSF (dotted line), and from the PSF with reduced wing amplitude (dashed).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig10.ps} \end{figure} Figure 10:

The MOSCA halo profile and the best fit PSF contribution (dotted line). The other lines show the 1$\sigma $ uncertainty of the fit.
Open with DEXTER
In the text

  \begin{figure} \center \includegraphics[width=85mm, angle=0, clip]{crabfig11.eps} \end{figure} Figure 11:

H$\alpha $ halo surface brightness using the model described in Sect. 4.2. The dotted lines show the unfiltered total H$\alpha $ surface brightness, whereas the solid and dashed lines show what is captured through H$\alpha $ and continuum ESO/WFI filters, respectively. Note how the surface brightness falls off rapidly with distance from the edge of the nebula. As discussed in the text, the $\eta = 4$ model provides an adequate fit to the shape of the fall-off, but it cannot explain the flux amplitude.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig12.eps} \end{figure} Figure 12:

Dereddened spectrum around H$\alpha $ 10 $\;\!\!^{\prime\prime}\;$north of the pulsar. In the lower panel we have inflated the flux scale and added the $\eta = 4$ model spectrum from Fig. 13. A constant of $10^{-17}\rm ~erg~s^{-1}~cm^{-2}~sr^{-1}$ was included, simulating the continuum emission from the pulsar wind nebula. Note that the model spectrum has been multiplied by a factor of 100 to be distinguishable in this plot.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{crabfig13.eps} \end{figure} Figure 13:

Line profiles for the H$\alpha $ recombination emission of a fast shell, based on the models of Sect. 4.2. Note the gap in halo emission between $\pm 1680 \rm ~km~s^{-1}$ for lines of sight close to the explosion centre. The smaller the slope $\eta $ of the density profile, the less pronounced is the intensity fall off with increasing absolute velocity. The dotted line shows the filter curve of the WFI red continuum filter.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.