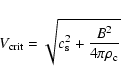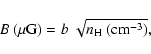| Issue |
A&A
Volume 497, Number 1, April I 2009
|
|
|---|---|---|
| Page(s) | 145 - 153 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200811115 | |
| Published online | 09 February 2009 | |
Shocks in dense clouds
II. Dust destruction and SiO formation in J shocks
V. Guillet - A. P. Jones - G. Pineau des Forêts
Institut d'Astrophysique Spatiale (IAS), Bâtiment 121, Université Paris-Sud 11 and CNRS, 91405 Orsay, France
Received 9 October 2008 / Accepted 28 January 2009
Abstract
Context. Observations of SiO line emission in shocks in star-forming regions indicate that silicate dust destruction must be occurring in these dense regions. Current models rely on predictions for dust destruction by sputtering in C-type shock waves. However, J-type shocks may also be relevant for interpreting the widely-observed optical line emission from species such as O I and Fe II.
Aims. In this work we explore, for the first time, dust destruction in J-type shocks slower than 50 km s-1.
Methods. We follow the dust trajectories throughout the shock using a model for the dust dynamics that allows us to solve the shock structure and at the same time calculate the degree of dust processing. We include the effects of sputtering in gas-grain collisions, and vaporisation and shattering in grain-grain collisions.
Results. We find that the amount of silicon released into the gas phase is a few percent. The dominant destructive process is vaporisation, not sputtering. The degree of dust destruction increases with the shock velocity but decreases as the Phys. Rev. E density increases.
Conclusions. Our results compare well with that of C-type shock models. J-type shocks are therefore reasonable candidates for an interpretation of SiO line emission in molecular outflows and jets.
Key words: shock waves - magnetohydrodynamics (MHD) - dust, extinction - ISM: clouds - ISM: jets and outflows - ISM: evolution
1 Introduction
Dust constituents such as Fe, Mg and Si are known to be heavily depleted in diffuse and dense clouds. However, observations of supersonic jets and molecular outflows around YSOs attest to the presence of these refractory species in the gas phase, e.g. in the form of SiO or Fe II (Giannini et al. 2006; Nisini et al. 2007; Giannini et al. 2004). This can be explained by models in which dust is destroyed in the shock waves initiated by jets and outflows.
Previous studies have only considered the destruction of dust in multi-fluid MHD shocks, namely C-type shocks, where the neutral gas is decoupled from the charged fluid composed of ions, electrons and charged grains (for a review of the different shock types, see Draine & McKee 1993). It has been shown that such shocks can form SiO through the sputtering of Si from silicate grains, followed by gas-phase reactions between the released Si and gas phase O2 or OH (Gusdorf et al. 2008a,b; Schilke et al. 1997).
In this study we focus on the processing of dust grains in J-type shocks, i.e. mono-fluid shocks characterised by discontinuities (shock fronts) and high postshock temperatures. Such shocks can exist even in the presence of a transverse magnetic field, provided that the shock velocity is higher than a critical velocity. They are indeed expected to exist at the apex of bow shocks around YSOs where the observed strong lines of Fe II can not be explained within the framework of a C shock model (McCoey et al. 2004) but with J shocks modelling (e.g. Hartigan et al. 2004). For the first time, we show that dust destruction occurs in J-type shocks at levels comparable to that of C-type shocks of the same velocity, and that this destruction is dominated by vaporisation in grain-grain collisions.
Our paper is organised as follows: Sect. 2 describes the ingredients needed to calculate the dynamics of dust grains through J shocks, as presented in Guillet et al. (2007, hereafter Paper I). Section 3 details our model for the processing of dust in gas-grain and grain-grain collisions. Our main results are presented in Sect. 4. In Sect. 5, we conclude and compare our predictions for silicate dust destruction with that for C-type shocks.
2 Dust dynamics in J shocks
A molecular cloud is a partially ionised medium embedded in a magnetic field that allows the propagation of various types of MHD waves. Among them, magnetosonic waves can propagate in the charged component of the gas transverse to the magnetic field lines at a velocity:
where
with b = 1, which at densities of 104 and 106 cm-3 yields a magnetic field intensity of 100
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=8cm,clip]{1115fg1t.eps}\par\vspace*{2mm}
\includegraphics[width=8.2cm,clip]{1115fg1b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg15.gif) |
Figure 1:
(top) The temperature profiles for J shocks propagating at 35 and 50 km s-1 through a molecular cloud (
|
| Open with DEXTER | |
Figure 1 presents the temperature and density profiles for transverse J shocks with velocities of 35 and 50 km s-1, as obtained with our updated version of the Flower et al. (2003) shock code![]() . When the gas crosses the shock front it is compressed and heated on a lengthscale approximately equal to the mean free path. The shock discontinuity (
. When the gas crosses the shock front it is compressed and heated on a lengthscale approximately equal to the mean free path. The shock discontinuity (
![]() cm for the 104 cm-3 J shocks) is resolved here by using an artificial viscosity (see Flower et al. 2003, Sect. 2 therein). Radiative emission in the shock cools and further compresses the gas and the magnetic field lines. The increasing magnetic pressure eventually limits the final compression ratio that can be achieved in the postshock. Note that the temperature reached at the shock front and the final compression ratio do not depend on the Phys. Rev. E density.
cm for the 104 cm-3 J shocks) is resolved here by using an artificial viscosity (see Flower et al. 2003, Sect. 2 therein). Radiative emission in the shock cools and further compresses the gas and the magnetic field lines. The increasing magnetic pressure eventually limits the final compression ratio that can be achieved in the postshock. Note that the temperature reached at the shock front and the final compression ratio do not depend on the Phys. Rev. E density.
2.1 Grain charge model
The trajectories of dust grains through a magnetohydrodynamic (MHD) shock strongly depend on the evolution of their charge because of the presence of the magnetic field. In Paper I we presented a model for the grain charge calculation, based on the work by Draine & Sutin (1987). Grains are charged by the competition between the collection of free electrons and the recombination of ions on their surfaces.
This stochastic process of ion and electron collection results in an average charge which is negative and proportional to both the temperature and the grain radius.
The sticking coefficient for electrons, ![]() ,
is taken to be 0.5 so as to take account of the scattering of electrons at low energies, while the recombination of ions is taken to be 100% efficient when ions hit a grain (
,
is taken to be 0.5 so as to take account of the scattering of electrons at low energies, while the recombination of ions is taken to be 100% efficient when ions hit a grain (![]() = 1). An effective ion temperature has been defined to enable us to approximately model the effect of grain gyration on the ion collection rate (see Paper I for further details).
= 1). An effective ion temperature has been defined to enable us to approximately model the effect of grain gyration on the ion collection rate (see Paper I for further details).
Our grain charge model is valid for shocks where secondary electron emission, i.e. the ejection of electrons from the grains by primary electrons impacting at energies higher than ![]() 20-30 eV, is negligible.
In this study we assume that secondary electron emission can be neglected for the shock velocities considered (
20-30 eV, is negligible.
In this study we assume that secondary electron emission can be neglected for the shock velocities considered (![]() 50 km s-1).
50 km s-1).
2.2 The dynamics of test grains
The dynamics of grains was extensively analysed in Paper I, where we focused on C-type shocks. Here we present the detailed trajectories of grains, which are considered as test particles, in J-type shocks. The trajectories of three representative silicate grains in a 35 km s-1 J shock propagating through a cloud of density 104 cm-3 are plotted in Fig. 2. These trajectories and velocity profiles are obtained by simultaneously integrating the laws of motion for the grains and the evolution of their (average) charge through the shock profile given in Fig. 1. The grains enter the shock at a velocity equal to the shock velocity, as measured in the shock frame, and start gyrating around the magnetic field lines perpendicular to the plane of the figure. The 400 and 800 Å grains are first reflected back into the Phys. Rev. E gas by the magnetic field gradient arising from the gas compression (e.g. Woitke et al. 1993). The reflected grains then undergo a Fermi I acceleration of their gyration velocity (e.g. Slavin et al. 2004) and eventually penetrate into the shock with a velocity higher than the shock velocity. The grains are then progressively brought to rest with respect to the gas on a timescale that is roughly proportional to the grain radius and the grain material density. The gyration timescale scales as a2 while the damping timescale scales as a (see Paper I): the longer gyration phase of large grains therefore corresponds to fewer gyrations than for smaller grains (Fig. 2).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg2t.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{1115fg2b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg20.gif) |
Figure 2:
(top) The trajectories of three silicate test grains of radii 400, 800 and 1600 Å through a 35 km s-1 J shock propagating in a molecular cloud (
|
| Open with DEXTER | |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=8.3cm,clip]{1115fg3t.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{1115fg3b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg21.gif) |
Figure 3:
Same as Fig. 2 but for a denser cloud (
|
| Open with DEXTER | |
The situation is different at higher densities because the gyration timescale scales as
![]() while the gyration damping timescale scales as
while the gyration damping timescale scales as
![]() (Paper I). At a density of 106 cm-3 (Fig. 3) and for the same shock velocity of 35 km s-1 as in Fig. 2, the grains enter the shock without experiencing any magnetic reflection: the stronger gas drag slows down the grains so efficiently that they can not move upstream into the Phys. Rev. E medium. It now takes fewer gyrations to bring the grains to rest with respect to the gas. The larger grains do not even complete their first gyration before being fully coupled to the gas.
(Paper I). At a density of 106 cm-3 (Fig. 3) and for the same shock velocity of 35 km s-1 as in Fig. 2, the grains enter the shock without experiencing any magnetic reflection: the stronger gas drag slows down the grains so efficiently that they can not move upstream into the Phys. Rev. E medium. It now takes fewer gyrations to bring the grains to rest with respect to the gas. The larger grains do not even complete their first gyration before being fully coupled to the gas.
3 Dust processing model
In slow J shocks (![]() 100 km s-1) it is the gyration of grains around magnetic field lines, not the shock temperature, which is responsible for their destruction through both erosion by the gas and vaporisation in grain-grain collisions. During the damping of their gyration grains experience supersonic impacts of gas particles which may erode their surfaces if the relative velocity is high enough, a process called inertial sputtering. Thermal sputtering is not important here because the postshock gas temperatures are too low. Grain gyration also favours high-velocity (head-on) collisions between grains and, therefore, grain destruction by vaporisation, i.e. a partial atomisation of the colliding grains. Vaporisation is always accompagnied by the shattering of both grains, which creates a high abundance of very small grains. Shattering is the dominant process in grain-grain collisions and acts as a limiter to grain vaporisation (Jones et al. 1996).
100 km s-1) it is the gyration of grains around magnetic field lines, not the shock temperature, which is responsible for their destruction through both erosion by the gas and vaporisation in grain-grain collisions. During the damping of their gyration grains experience supersonic impacts of gas particles which may erode their surfaces if the relative velocity is high enough, a process called inertial sputtering. Thermal sputtering is not important here because the postshock gas temperatures are too low. Grain gyration also favours high-velocity (head-on) collisions between grains and, therefore, grain destruction by vaporisation, i.e. a partial atomisation of the colliding grains. Vaporisation is always accompagnied by the shattering of both grains, which creates a high abundance of very small grains. Shattering is the dominant process in grain-grain collisions and acts as a limiter to grain vaporisation (Jones et al. 1996).
3.1 The Phys. Rev. E dust size distribution
The efficiency of dust destruction in shocks depends on the composition and size distribution of grains in the Phys. Rev. E cloud. Following Paper I we consider two distinct populations of non-porous, spherical grain cores of silicate (MgFeSiO4) and carbon (graphite), covered by icy mantles. The mantles are predominantly composed of H2O, CO2, NH3 and CH3OH, with an average specific density taken to be 1 g cm-3. For a comparaison with other works we represent each grain core size distribution as an MRN-type distribution (Mathis et al. 1977):
![]() for 100 Å
< a < 3000 Å, where
for 100 Å
< a < 3000 Å, where
![]() .
Although, our code can be run with any power law or log-normal size distribution. With the MRN-type core size distribution that we adopt all the grains are assumed to be covered, in the Phys. Rev. E medium, with an icy mantle of thickness
.
Although, our code can be run with any power law or log-normal size distribution. With the MRN-type core size distribution that we adopt all the grains are assumed to be covered, in the Phys. Rev. E medium, with an icy mantle of thickness ![]() 150 Å independent of their radius (Paper I).
To compute the evolution of the dust size distribution, as well as the degree of dust destruction, we must calculate the charge, dynamics and processing of a range of grain sizes. In this study each silicate and carbon dust size distribution is modelled with 8 size bins, with radii running from 3000 Å to 100 Å. Five empty bins are added to each distribution to collect fragments smaller than 100 Å that are produced by the shattering of dust grains. The smallest fragment allowed has a radius of
150 Å independent of their radius (Paper I).
To compute the evolution of the dust size distribution, as well as the degree of dust destruction, we must calculate the charge, dynamics and processing of a range of grain sizes. In this study each silicate and carbon dust size distribution is modelled with 8 size bins, with radii running from 3000 Å to 100 Å. Five empty bins are added to each distribution to collect fragments smaller than 100 Å that are produced by the shattering of dust grains. The smallest fragment allowed has a radius of ![]() 5 Å, a value that is not critical for the intensity of dust destruction in our slow J shocks. See Paper I for further details on the management of size bins.
5 Å, a value that is not critical for the intensity of dust destruction in our slow J shocks. See Paper I for further details on the management of size bins.
3.2 Grain mantle and core erosion
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg4t.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{1115fg4b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg27.gif) |
Figure 4: (top) The H2O ice sputtering yield for incident H, H2 and He as a function of impact velocity, for the models of Tielens et al. (1994) and Barlow (1978). (bottom) The sputtering yield for Si atoms from silicate (MgFeSiO4, olivine-type) grain cores by the dominant sputtering species, He and O, for the models of Tielens et al. (1994) and May et al. (2000). |
| Open with DEXTER | |
Icy species such as H2O, which constitute the mantles covering the grain cores, are the first to be removed by sputtering in the shock. If the mantles are completely eroded, and the gyration velocity is higher than ![]() 30 km s-1 (Tielens et al. 1994), inertial sputtering of the grain cores can result in the release of atoms (e.g. C, Fe, Mg and Si) from the dust and into the gas phase.
30 km s-1 (Tielens et al. 1994), inertial sputtering of the grain cores can result in the release of atoms (e.g. C, Fe, Mg and Si) from the dust and into the gas phase.
The sputtering efficiency is determined by the sputtering yield, i.e. the probability for an atom to be ejected from the grain surface by an impinging atom or ion. Sputtering yields depend on the atom or ion impact velocity, on the nature of the incident particle as well as the stoichiometric composition of the grain material. In calculating the sputtering of the grain cores we take account of the incident atoms, principally He, O, C and N. For the mantles only the main contributors, H, H2 and He, are considered. The sputtering of grain cores by molecules proved to be negligible because the molecules are dissociated in shocks where core sputtering can be significant. He turns out to be the dominant sputtering species for the grain cores, a result already found by Jones et al. (1994).
We adopt two limiting cases for the sputtering yields: an upper limit based on the model by Tielens et al. (1994), and a lower limit based on the models by Barlow (1978) for the erosion of the ice mantles and May et al. (2000) for the erosion of cores. These yields are compared in Fig. 4. As Si represents only one atom out of 7 in MgFeSiO4, the yields from Tielens et al. (1994) averaged over all incident angles (twice the value for normal incidence) are divided by 7 to be coherent with the formalism developed in May et al. (2000).
The relative gas-grain velocity in the shock, which determines the sputtering rate, varies with grain size (see Figs. 2 and 3). The evolution of the mantle thickness is therefore integrated separately for each grain size (i.e. each bin), starting with a thickness of ![]() 150 Å for all grains (see Sect. 3.1). Only once the mantles have been fully eroded can the grain cores be
eroded. The
evolution of the size distribution of grain cores is
calculated using the method of Mizuno et al. (1988) as presented in Paper I.
150 Å for all grains (see Sect. 3.1). Only once the mantles have been fully eroded can the grain cores be
eroded. The
evolution of the size distribution of grain cores is
calculated using the method of Mizuno et al. (1988) as presented in Paper I.
3.3 Shattering and vaporisation of grain cores
Tielens et al. (1994) and Jones et al. (1996) present an extensive theoretical study of the vaporisation and shattering of spherical grains, based on an analysis of the propagation of shock waves in solid materials. They compare their results with laboratory experiments and study the effect of this dust processing in J shocks propagating in the Warm Intercloud Medium.
They find that the nature of the outcome of a grain-grain collision depends on the relative velocity of the colliding partners, not on the energy involved. Below a threshold velocity of a few km s-1 the colliding grains will bounce and above this velocity the grains will be shattered![]() . If the impact velocity exceeds
. If the impact velocity exceeds ![]() 20 km s-1, part or all of the colliding grains can be vaporised. The mass fraction of the grains vaporised and/or shattered in the collision is a function of the relevant threshold pressure, energy density, impact velocity, grain specific density and the grain radius-ratio (Jones et al. 1996; Tielens et al. 1994). We adopt this model for grain-grain collisional processing in our study, reminding the reader that the slope of the shattered fragment size distribution, -3.3, is slightly less than the input MRN slope (-3.5).
Based on the results of laboratory experiments (Wang 1999; Nagahara & Ozawa 1996), we further assume that the vaporisation of silicate grains leads to the direct formation of SiO, unlike sputtering which releases Si.
20 km s-1, part or all of the colliding grains can be vaporised. The mass fraction of the grains vaporised and/or shattered in the collision is a function of the relevant threshold pressure, energy density, impact velocity, grain specific density and the grain radius-ratio (Jones et al. 1996; Tielens et al. 1994). We adopt this model for grain-grain collisional processing in our study, reminding the reader that the slope of the shattered fragment size distribution, -3.3, is slightly less than the input MRN slope (-3.5).
Based on the results of laboratory experiments (Wang 1999; Nagahara & Ozawa 1996), we further assume that the vaporisation of silicate grains leads to the direct formation of SiO, unlike sputtering which releases Si.
To calculate the collision rate between grains we use a statistical approach similar to that of Jones et al. (1996) but adapted to the context of dense clouds. Based on the detailled trajectories of test grains through the shock (e.g. Figs. 2 and 3) we model the gyration velocity and calculate the average number of grains per unit volume at any point in the shock, taking into account the fact that dust grains can be reflected back into the Phys. Rev. E gas at the shock front (Fig. 2) or may not have the time to complete their first gyration in the shock before being stoppped by the gas (Fig. 3). The details and justification of this modelling can be found in Appendix A.
3.4 Limitations of our numerical treatment
Our treatment of grain-grain collisions ignores some aspects of dust processing in the shock. Firstly, and unlike Jones et al. (1996), we do not follow the processing of fragments from the time they are formed in the collision until they are brought to rest with respect to the gas. This approximation is justified because we do not expect the processing of small fragments,during their gyration phase, to be significant for shocks with velocities less than 50 km s-1, either by sputtering (Jones et al. 1996, Fig. 11 therein) or shattering and vaporisation (Borkowski & Dwek 1995; Jones et al. 1996). Secondly, we ignore the destruction of the mantles by shattering and vaporisation in grain-grain collisions. Our numerical model is currently unable to handle this because it would require us to track the history of each colliding grain. Thus, we consider that all grains of a given size carry a mantle of the same thickness, whatever their history, and that this mantle is only removed by sputtering. Fragments smaller than 100 Å, which are absent from the initial distribution and are only created by the shattering of grains, are assumed to carry no mantles. Finally, we are forced to ignore the processing of the reflected grains during their first gyration, i.e. before they enter the shock for the second time. This is a numerical limitation due to the fact that we need to assign a unique average gyration velocity to each grain size at any position in the shock (see Appendix A for more details).
4 Results
The quantity of silicon and carbon released into the gas phase, as a result of dust destruction in J shocks with velocities ![]() 50 km s-1, is shown in Fig. 5. The degree of destruction is about a few percent and increases with the shock velocity but decreases with increasing Phys. Rev. E density. Vaporisation is the dominant destruction process, not sputtering, and is effective at destroying grains at velocities <30 km s-1 where sputtering is insignificant.
50 km s-1, is shown in Fig. 5. The degree of destruction is about a few percent and increases with the shock velocity but decreases with increasing Phys. Rev. E density. Vaporisation is the dominant destruction process, not sputtering, and is effective at destroying grains at velocities <30 km s-1 where sputtering is insignificant.
Dust vaporisation increases approximately linearly with shock velocity (Fig. 5) because the gyration damping timescale, i.e. the time during which grain-grain processing occurs, is roughly proportional to the shock velocity. The decrease in dust vaporisation with increasing Phys. Rev. E density is due to the fact that high-velocity (head-on) collisions between large grains, which mostly contribute to the vaporisation, tend to disappear at high densities where the large grains hardly gyrate at all (see Fig. 3).
When no magnetic field is present (B=0) the grains do not gyrate and the impact of collisions is therefore minimised. Such a model give results that are found to be independent of the preshock density. We can therefore consider the results for B=0 as the minimal dust destruction in J shocks for a given shock velocity, whatever the Phys. Rev. E conditions.
The sputtering of grain cores with the May et al. (2000) yields turns out to be negligible (
![]() )
at all shock velocities and Phys. Rev. E densities considered here (Fig. 5). With the Tielens et al. (1994) yields sputtering is only efficient for shocks faster than 35 km s-1 (the threshold velocity for inertial sputtering is approximately 30 km s-1, see Fig. 4). In this case the dust destruction by sputtering is higher at lower densities (
)
at all shock velocities and Phys. Rev. E densities considered here (Fig. 5). With the Tielens et al. (1994) yields sputtering is only efficient for shocks faster than 35 km s-1 (the threshold velocity for inertial sputtering is approximately 30 km s-1, see Fig. 4). In this case the dust destruction by sputtering is higher at lower densities (
![]() cm-3) because in shocks faster than 35 km s-1 some grains are reflected, highly accelerated at the shock front and therefore subject to more erosion (Fig. 2). When no reflected grains are present (Fig. 3), the level of sputtering is roughly independent of the Phys. Rev. E density and the magnetic field intensity (e.g. B=0). From now, and unless otherwise stated, the May et al. (2000) are used so that dust destruction in the forecoming results is only caused by vaporisation in grain-grain collisions.
cm-3) because in shocks faster than 35 km s-1 some grains are reflected, highly accelerated at the shock front and therefore subject to more erosion (Fig. 2). When no reflected grains are present (Fig. 3), the level of sputtering is roughly independent of the Phys. Rev. E density and the magnetic field intensity (e.g. B=0). From now, and unless otherwise stated, the May et al. (2000) are used so that dust destruction in the forecoming results is only caused by vaporisation in grain-grain collisions.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg5t.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{1115fg5b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg29.gif) |
Figure 5: (top) The percentage of silicon released into the gas phase from dust (in the form of atomic Si by sputtering and SiO by vaporisation) as a function of the shock velocity for 3 Phys. Rev. E densities ( 104, 105, 106 cm-3) and for the particular case of a pure hydrodynamical shock (B=0) where the amount of vaporisation is independent of the Phys. Rev. E density. For sputtering, two models are presented: the May et al. (2000) sputtering yields (black solid), which result in negligible erosion, and the Tielens et al. (1994) yields (red dashed). (bottom) Same results for vaporisation and sputtering of carbon (graphite) grains. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg6.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg31.gif) |
Figure 6:
The percentage of silicon released into gas phase, for 35 and 50 km s-1 J shocks propagating into a cloud of Phys. Rev. E density 104 cm-3, as a function of the factor
|
| Open with DEXTER | |
Figure 6 shows the percentage of silicon released into the gas phase as a function of the transverse magnetic field intensity (through the parameter b of Eq. (2)). The factor b can not be much higher than 1 for the propagation of J shocks (
![]() )
in the velocity range considered here. Dust is less readily destroyed in J shocks propagating through weaker transverse magnetic fields. As the magnetic field intensity decreases the grain dynamics more closely resemble that of Fig. 3 rather than Fig. 2: large grains hardly gyrate, thereby limiting the head-on collisions responsible for grain vaporisation.
)
in the velocity range considered here. Dust is less readily destroyed in J shocks propagating through weaker transverse magnetic fields. As the magnetic field intensity decreases the grain dynamics more closely resemble that of Fig. 3 rather than Fig. 2: large grains hardly gyrate, thereby limiting the head-on collisions responsible for grain vaporisation.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg7.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg33.gif) |
Figure 7:
(left) The silicate dust mass distribution before (MRN) and after the passage of 30, 40 and 50 km s-1 J shocks propagating through a cloud of density
|
| Open with DEXTER | |
The size distributions of silicate and carbon grains are clearly affected by the shock, Fig. 7 shows the results of our model. From this it can be seen that numerous small grains are produced by grain shattering and that the slope of the distribution is slightly modified, reaching a flatter mass distribution (
![]() for silicate dust) between 100 and 3000 Å for a 50 km s-1 shock. The results are almost identical for denser clouds (
for silicate dust) between 100 and 3000 Å for a 50 km s-1 shock. The results are almost identical for denser clouds (
![]() and 106 cm-3). Carbon (graphite) grains are not as resistant to fragmentation as silicates (see Sect. 3.3). Their size distribution is therefore more affected by the passage of the shock.
and 106 cm-3). Carbon (graphite) grains are not as resistant to fragmentation as silicates (see Sect. 3.3). Their size distribution is therefore more affected by the passage of the shock.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg8.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg36.gif) |
Figure 8:
Chemical evolution in a 25 km s-1 J shock propagating through a molecular cloud (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg9t.eps}\par\includeg...
...{1115fg9m.eps}\par\includegraphics[width=8.65cm,clip]{1115fg9b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg37.gif) |
Figure 9: Same as Fig. 8 but for a dissociative 35 km s-1 J shock. |
| Open with DEXTER | |
In a shock SiO can be produced directly in vaporising grain-grain collisions and may subsequently be dissociated in the hot (
![]() K) postshock gas. In Figs. 8 and 9 we compare the production of SiO in a 25 km s-1 shock, which dissociates H2 (binding energy
K) postshock gas. In Figs. 8 and 9 we compare the production of SiO in a 25 km s-1 shock, which dissociates H2 (binding energy ![]() 4.5 eV) but not SiO (binding energy
4.5 eV) but not SiO (binding energy ![]() 8 eV), with that in a 35 km s-1 shock where both molecules are dissociated. In the 25 km s-1 shock (Fig. 8) the SiO is produced directly by the vaporisation of the silicate grains and remains in the gas phase. Gas phase chemistry does not intervene in this case in the production of SiO. However, in the 35 km s-1 shock (Fig. 9) the SiO produced by vaporisation is soon destroyed by H+ ions.
SiO can be produced by Si + O2 reactions (Le Picard et al. 2001), the reactant O2 being itself produced by the reaction between O with OH.
But only when the recombination of H+ on grain surfaces becomes important can the SiO survive.
In both shocks (Figs. 8 and 9) the gas phase abundance of SiO diminishes when SiO starts to deplete into mantles on the surfaces of grains in the high density postshock gas.
In our work we have adopted an initial gas-phase fractional abundance for O2 of X(O
2) = 10-7, in accordance with the recent SWAS results (Larsson et al. 2007). This initial value has no impact on our results because O2 has to be reformed in dissociative shocks (Fig. 9), and does not intervene in SiO formation in non-dissociative shocks (Fig. 8).
8 eV), with that in a 35 km s-1 shock where both molecules are dissociated. In the 25 km s-1 shock (Fig. 8) the SiO is produced directly by the vaporisation of the silicate grains and remains in the gas phase. Gas phase chemistry does not intervene in this case in the production of SiO. However, in the 35 km s-1 shock (Fig. 9) the SiO produced by vaporisation is soon destroyed by H+ ions.
SiO can be produced by Si + O2 reactions (Le Picard et al. 2001), the reactant O2 being itself produced by the reaction between O with OH.
But only when the recombination of H+ on grain surfaces becomes important can the SiO survive.
In both shocks (Figs. 8 and 9) the gas phase abundance of SiO diminishes when SiO starts to deplete into mantles on the surfaces of grains in the high density postshock gas.
In our work we have adopted an initial gas-phase fractional abundance for O2 of X(O
2) = 10-7, in accordance with the recent SWAS results (Larsson et al. 2007). This initial value has no impact on our results because O2 has to be reformed in dissociative shocks (Fig. 9), and does not intervene in SiO formation in non-dissociative shocks (Fig. 8).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1115fg10.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg39.gif) |
Figure 10: Derivative of the column density of SiO with respect to the logarithm of the temperature showing the temperature range where the SiO is the most abundant, for 30-50 km s-1 J shocks with a Phys. Rev. E density of 104 cm-3. |
| Open with DEXTER | |
Figure 10 shows our calculations for the colum density of SiO formed in 30-50 km s-1 J shocks with a Phys. Rev. E density of 104 cm-3.
Figure 10 is presented as a function of decreasing gas temperature, i.e. increasing flow time, and provides first order estimates for the column density of SiO at a given temperature. In all the shocks considered here, the column density for SiO peaks at temperatures ![]() 500 K.
500 K.
5 Concluding remarks
Table 1: Percentage of Si, Fe, Mg and C released into the gas phase in transverse J shocks.
Table 1 summarises our results for the percentage of destruction of silicate and carbon dust in J shocks. For silicate dust these results are valid not only for Si but also for Mg and Fe because both the vaporisation and sputtering (with the Tielens et al. 1994 yields) respect the stoichiometric composition of the material (here MgFeSiO4). A range of values is given for each shock velocity and Phys. Rev. E density. The lower value indicates the amount of vaporisation, the upper value the amount of vaporisation and sputtering when the Tielens et al. (1994) yields are used. If only one value is given, then sputtering is insignificant.
Vaporisation slowly increases with shock velocity but decreases with increasing cloud density. Dust sputtering is always negligible (<![]() )
with the May et al. (2000) yields, but not with the Tielens et al. (1994) yields for shock velocities higher than 35 km s-1. However, even in the more favorable case, sputtering is always dominated by vaporisation for shocks slower than 50 km s-1.
Our main conclusion is therefore that dust destruction in slow J shocks (
)
with the May et al. (2000) yields, but not with the Tielens et al. (1994) yields for shock velocities higher than 35 km s-1. However, even in the more favorable case, sputtering is always dominated by vaporisation for shocks slower than 50 km s-1.
Our main conclusion is therefore that dust destruction in slow J shocks (![]() 50 km s-1) is significant (at the level of a few percent) and is mainly caused by vaporisation in grain-grain collisions.
50 km s-1) is significant (at the level of a few percent) and is mainly caused by vaporisation in grain-grain collisions.
Our shock model also includes the evolution of the dust size distribution as a result of the production of abundant small grains through the shattering of large grains in grain-grain collisions. Shattering tends to fragment predominantly large grains and steepen the dust size distribution of the smaller grains, a results already found by Jones et al. (1996) for (faster) shocks propagating in the Warm Intercloud Medium.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1115fig11-New.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg43.gif) |
Figure 11:
Percentage of Si released into the gas phase as a function of the shock velocity for C-type shocks (Gusdorf et al. 2008a) and J-type
shocks (this study) propagating in a molecular cloud (
|
| Open with DEXTER | |
The efficiency of dust destruction in C shocks was one of the strong arguments in favor of these models in the interpretation of the SiO observed in molecular outflows around new-born stars. As shown in Fig. 11 our results for silicate destruction in J shocks are of the same order of magnitude as those of Gusdorf et al. (2008a) for C shocks, though somewhat lower but still within a factor of 2-3 (Fig. 11).
The similarity of our results is a coincidence because the underlying physics is different in each case: Gusdorf et al. (2008a) only include the destruction of dust through sputtering with the May et al. (2000) yields, whereas in our model dust is destroyed by vaporisation in grain-grain collisions, sputtering being negligible with these yields.
Note that in the work by Gusdorf et al. (2008a), a fractional abundance
![]() of PAHs was necessary to raise the magnetosonic velocity to
of PAHs was necessary to raise the magnetosonic velocity to ![]() 60 km s-1 (see Paper I, Table 1 therein) and allow for the existence of C-shocks as fast as 50 km s-1 with b=1.
60 km s-1 (see Paper I, Table 1 therein) and allow for the existence of C-shocks as fast as 50 km s-1 with b=1.
Unlike in C shocks, grains can be destroyed in ![]() 25 km s-1 J shocks due to their high-velocity gyration around the magnetic field lines. J-type shocks therefore seem to also be a reasonable candidate for the interpretation of SiO observations from outflows, even at low shock velocities. In order to better compare our results with observations we are currently planning to calculate SiO emissivities and line profiles using a Large Velocity Gradient model (Gusdorf et al. 2008a,b).
25 km s-1 J shocks due to their high-velocity gyration around the magnetic field lines. J-type shocks therefore seem to also be a reasonable candidate for the interpretation of SiO observations from outflows, even at low shock velocities. In order to better compare our results with observations we are currently planning to calculate SiO emissivities and line profiles using a Large Velocity Gradient model (Gusdorf et al. 2008a,b).
Acknowledgements
We wish to thank Hugues Leroux for useful discussions on the erosion and vaporisation of silicate materials. We also wish to thank the referee, J. Slavin, for a carefull reading of the manuscript, and S. Cabrit for meaningful suggestions.
Appendix A: Modelling grain-grain collisions
In this paper we calculate the intensity of gas-grain and grain-grain processing at the same time we solve the shock structure from the Phys. Rev. E to the postshock medium. A given position, z, in the shock must therefore correspond to a unique value for each integrated variable. The true dynamics of grains of Figs. 2 and 3, where z alternately decreases and increases due to the grain gyration around the magnetic field lines, can therefore not be used ``as is'' in our integration scheme. In this appendix, we detail our method for the integration of an average gyration velocity of each grain size, which allows us to follow the average motion of grains downstream through the shock and to calculate the impact velocities in grain-grain collisions. This model is specifically designed for J shocks propagating in high density clouds (
![]() cm-3) where the damping of grain gyration is very efficient.
cm-3) where the damping of grain gyration is very efficient.
In our model the dynamics of the grains of a given size is divided into two phases (see Fig. A.1): 1) an inertial phase, where the grain velocities are directed downstream in the shock propagation direction; followed by 2) a gyration phase, where the gyration velocities have become isotropic in the gas frame. We choose to distinguish these two phases at the point where grains complete their first gyration in the shock. Figure A.1 shows how our model can reproduce the average evolution of the gyration velocity of all dust grains through the shock, both at low (
![]() cm-3) and high (
cm-3) and high (
![]() cm-3) Phys. Rev. E densities.
cm-3) Phys. Rev. E densities.
This model allows us to compute the impact velocity in grain-grain collisions.
When the two colliding grains are in their inertial phase, there exist no head-on collisions because all grains basically move forward, so that impact velocities are low. The grains move faster than the gas during this phase and the compression ratio of the grain fluids is therefore lower than the compression of the gas by a factor
![]() ,
where
,
where ![]() is the velocity of the gas and
is the velocity of the gas and ![]() the component of the grain velocity
the component of the grain velocity ![]() in the shock direction. Both these effects tend to reduce the intensity of vaporisation in this phase compared to a model where the gyration phases of grains would be randomly distributed.
in the shock direction. Both these effects tend to reduce the intensity of vaporisation in this phase compared to a model where the gyration phases of grains would be randomly distributed.
When grains are in their gyration phase, their velocities can be considered isotropic in the gas frame and the compression of their fluid therefore follows that of the gas. When at least one of the colliding grains is in its gyration phase, we must treat grain-grain collisions with a statistical method. The processing resulting from the collisions of grains with gyration velocities v1 and v2 is therefore calculated as the average processing resulting from four collisions with relative velocities v1 + v2, |v2 - v1| and (v12 + v22)0.5 counted twice.
The presence of reflected, and therefore accelerated, grains tends to increase dust destruction. Modelling the average dynamics we have to ignore the first gyration of the grains and apply the two grain dynamic phases from the moment they definitively enter the shock (see the 400 and 800 Å grains in Fig. A.1). With this approximation we however underestimate the number of grains per unit volume at the shock front. This slightly lowers our results for the intensity of dust processing by vaporisation, shattering and inertial sputtering.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1115f12t.eps}\par\vspace*{2mm}
\includegraphics[width=8.3cm,clip]{1115f12b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg50.gif) |
Figure A.1: The results of our model for the gyration velocity of dust grains (dashed lines) compared to the gyration velocity presented in Figs. 2 and 3 (solid lines) for 35 km s-1 shocks. The reflected grains are injected into the shock with the velocity they have when they finally enter the shock. Here we distinguish two phases: 1) an inertial phase where the grain is launched in the shock and our model strictly follows the detailed dynamics of grains; which is followed by 2) a gyration phase where our model only represents the average gyration velocity. |
| Open with DEXTER | |
Our calculation of the shock structure therefore coherently takes into account the dust charging, dynamics and processing. This is done in five steps:
- 1.
- We solve the steady-state chemistry and grain charge for the Phys. Rev. E cloud, assuming a gas temperature of 10 K and a fixed dust mantle composition (see Paper I).
- 2.
- We calculate the shock profile with the Flower et al. (2003) shock code, starting from the Phys. Rev. E steady-state conditions and assuming that the dust follows the motion of ions with no processing (Fig. 1).
- 3.
- We integrate the dynamics of the silicate and carbon grains as test particles through this shock profile in order to allow backward motion of the dust grains (Figs. 2 and 3).
- 4.
- The resulting trajectories and velocity profiles are used to define the relevant parameters for the integration of the average gyration velocity of the grains through the shock (Fig. A.1): their position in the shock separating the inertial phase from the gyration phase and their entrance velocity for the reflected grains.
- 5.
- We integrate the shock structure using the conservation equations governing the physics and chemistry in the shock and couple them with the calculation of grain charge, average dynamics and processing of two size distributions of carbon and silicate grains covered with mantles.
References
- Barlow, M. J. 1978, MNRAS, 183, 367 [NASA ADS] (In the text)
- Borkowski, K. J., & Dwek, E. 1995, ApJ, 454, 254 [NASA ADS] [CrossRef]
- Draine, B. T., & Sutin, B. 1987, ApJ, 320, 803 [NASA ADS] [CrossRef] (In the text)
- Draine, B. T., & McKee, C. F. 1993, ARA&A, 31, 373 [NASA ADS] [CrossRef] (In the text)
- Flower, D. R., Le Bourlot, J., Pineau des Forêts, G., & Cabrit, S. 2003, MNRAS, 341, 70 [NASA ADS] [CrossRef] (In the text)
- Giannini, T., McCoey, C., Caratti o Garatti, A., et al. 2004, A&A, 419, 999 [NASA ADS] [CrossRef] [EDP Sciences]
- Giannini, T., McCoey, C., Nisini, B., et al. 2006, A&A, 459, 821 [NASA ADS] [CrossRef] [EDP Sciences]
- Guillet, V., Pineau des Forêts, G., & Jones, A. P. 2007, A&A, 476, 263 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I) (In the text)
- Gusdorf, A., Cabrit, S., Flower, D. R., & Pineau des Forêts, G. 2008a, A&A, 482, 809 [NASA ADS] [CrossRef] [EDP Sciences]
- Gusdorf, A., Pineau des Forêts, G., Cabrit, S., & Flower, D. R. 2008b, A&A, 490, 695 [NASA ADS] [CrossRef] [EDP Sciences]
- Hartigan, P., Raymond, J., & Pierson, R. 2004, ApJ, 614, L69 [NASA ADS] [CrossRef] (In the text)
- Jones, A. P., Tielens, A. G. G. M., Hollenbach, D. J., & McKee, C. F. 1994, ApJ, 433, 797 [NASA ADS] [CrossRef] (In the text)
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] (In the text)
- Larsson, B., Liseau, R., Pagani, L., et al. 2007, A&A, 466, 999 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Le Picard, S. D., Canosa, A., Pineau des Forêts, G., Rebrion-Rowe, C., & Rowe, B. R. 2001, A&A, 372, 1064 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] (In the text)
- May, P. W., Pineau des Forêts, G., Flower, D. R., et al. 2000, MNRAS, 318, 809 [NASA ADS] [CrossRef] (In the text)
- McCoey, C., Giannini, T., Flower, D. R., & Caratti o Garatti, A. 2004, MNRAS, 353, 813 [NASA ADS] [CrossRef] (In the text)
- Mizuno, H., Markiewicz, W. J., & Voelk, H. J. 1988, A&A, 195, 183 [NASA ADS] (In the text)
- Nagahara, H., & Ozawa, K. 1996, Geochim. Cosmochim. Acta, 60, 1445 [NASA ADS] [CrossRef]
- Nisini, B., Codella, C., Giannini, T., et al. 2007, A&A, 462, 163 [NASA ADS] [CrossRef] [EDP Sciences]
- Schilke, P., Walmsley, C. M., Pineau des Forêts, G., & Flower, D. R. 1997, A&A, 321, 293 [NASA ADS]
- Slavin, J. D., Jones, A. P., & Tielens, A. G. G. M. 2004, ApJ, 614, 796 [NASA ADS] [CrossRef] (In the text)
- Tielens, A. G. G. M., McKee, C. F., Seab, C. G., & Hollenbach, D. J. 1994, ApJ, 431, 321 [NASA ADS] [CrossRef] (In the text)
- Wang, J. 1999, Geochim. Cosmochim. Acta, 63, 953 [NASA ADS] [CrossRef]
- Woitke, P., Dominik, C., & Sedlmayr, E. 1993, A&A, 274, 451 [NASA ADS] (In the text)
Footnotes
- ... code
![[*]](/icons/foot_motif.gif)
- Our model includes
 130 chemical species, more than 900 chemical reactions and 50 levels for the population of H2.
130 chemical species, more than 900 chemical reactions and 50 levels for the population of H2.
- ... shattered
![[*]](/icons/foot_motif.gif)
- The threshold velocities for shattering are of 1.2 km s-1 for carbon-carbon collisions and 2.7 km s-1 for silicate-silicate collisions (Jones et al. 1996, Table 1 therein).
All Tables
Table 1: Percentage of Si, Fe, Mg and C released into the gas phase in transverse J shocks.
All Figures
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=8cm,clip]{1115fg1t.eps}\par\vspace*{2mm}
\includegraphics[width=8.2cm,clip]{1115fg1b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg15.gif) |
Figure 1:
(top) The temperature profiles for J shocks propagating at 35 and 50 km s-1 through a molecular cloud (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg2t.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{1115fg2b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg20.gif) |
Figure 2:
(top) The trajectories of three silicate test grains of radii 400, 800 and 1600 Å through a 35 km s-1 J shock propagating in a molecular cloud (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\hspace*{2mm}\includegraphics[width=8.3cm,clip]{1115fg3t.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{1115fg3b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg21.gif) |
Figure 3:
Same as Fig. 2 but for a denser cloud (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg4t.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{1115fg4b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg27.gif) |
Figure 4: (top) The H2O ice sputtering yield for incident H, H2 and He as a function of impact velocity, for the models of Tielens et al. (1994) and Barlow (1978). (bottom) The sputtering yield for Si atoms from silicate (MgFeSiO4, olivine-type) grain cores by the dominant sputtering species, He and O, for the models of Tielens et al. (1994) and May et al. (2000). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg5t.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{1115fg5b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg29.gif) |
Figure 5: (top) The percentage of silicon released into the gas phase from dust (in the form of atomic Si by sputtering and SiO by vaporisation) as a function of the shock velocity for 3 Phys. Rev. E densities ( 104, 105, 106 cm-3) and for the particular case of a pure hydrodynamical shock (B=0) where the amount of vaporisation is independent of the Phys. Rev. E density. For sputtering, two models are presented: the May et al. (2000) sputtering yields (black solid), which result in negligible erosion, and the Tielens et al. (1994) yields (red dashed). (bottom) Same results for vaporisation and sputtering of carbon (graphite) grains. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg6.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg31.gif) |
Figure 6:
The percentage of silicon released into gas phase, for 35 and 50 km s-1 J shocks propagating into a cloud of Phys. Rev. E density 104 cm-3, as a function of the factor
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg7.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg33.gif) |
Figure 7:
(left) The silicate dust mass distribution before (MRN) and after the passage of 30, 40 and 50 km s-1 J shocks propagating through a cloud of density
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg8.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg36.gif) |
Figure 8:
Chemical evolution in a 25 km s-1 J shock propagating through a molecular cloud (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1115fg9t.eps}\par\includeg...
...{1115fg9m.eps}\par\includegraphics[width=8.65cm,clip]{1115fg9b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg37.gif) |
Figure 9: Same as Fig. 8 but for a dissociative 35 km s-1 J shock. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1115fg10.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg39.gif) |
Figure 10: Derivative of the column density of SiO with respect to the logarithm of the temperature showing the temperature range where the SiO is the most abundant, for 30-50 km s-1 J shocks with a Phys. Rev. E density of 104 cm-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1115fig11-New.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg43.gif) |
Figure 11:
Percentage of Si released into the gas phase as a function of the shock velocity for C-type shocks (Gusdorf et al. 2008a) and J-type
shocks (this study) propagating in a molecular cloud (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1115f12t.eps}\par\vspace*{2mm}
\includegraphics[width=8.3cm,clip]{1115f12b.eps}
\end{figure}](/articles/aa/full_html/2009/13/aa11115-08/Timg50.gif) |
Figure A.1: The results of our model for the gyration velocity of dust grains (dashed lines) compared to the gyration velocity presented in Figs. 2 and 3 (solid lines) for 35 km s-1 shocks. The reflected grains are injected into the shock with the velocity they have when they finally enter the shock. Here we distinguish two phases: 1) an inertial phase where the grain is launched in the shock and our model strictly follows the detailed dynamics of grains; which is followed by 2) a gyration phase where our model only represents the average gyration velocity. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.