| Issue |
A&A
Volume 496, Number 1, March II 2009
|
|
|---|---|---|
| Page(s) | 57 - 75 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361:200811443 | |
| Published online | 14 January 2009 | |
The 0.4 <z< 1.3 star formation history of the Universe as viewed in the far-infrared
B. Magnelli1 - D. Elbaz1 - R. R. Chary2 - M. Dickinson3 - D. Le Borgne1,4 - D. T. Frayer2 - C. N. A. Willmer5
1 - Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot, IRFU/Service d'Astrophysique, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
2 -
Spitzer Science Center, California Institute of Technology, Pasadena, CA 91125, USA
3 -
National Optical Astronomy Observatory, Tucson, AZ 85719, USA
4 -
Institut d'Astrophysique de Paris, UMR7095 CNRS, UPMC, 98bis boulevard Arago, 75014 Paris, France
5 -
Steward Observatory, University of Arizona, 933 North Cherry Avenue, Tucson, AZ 85721, USA
Received 28 November 2008 / Accepted 20 December 2008
Abstract
Aims. We use the deepest existing mid- and far-infrared observations (reaching ![]() 3 mJy at 70
3 mJy at 70 ![]() m) obtained with Spitzer in the Great Observatories Origins Deep Survey (GOODS) and Far Infrared Deep Extragalactic Legacy survey (FIDEL) fields to derive the evolution of the rest-frame 15
m) obtained with Spitzer in the Great Observatories Origins Deep Survey (GOODS) and Far Infrared Deep Extragalactic Legacy survey (FIDEL) fields to derive the evolution of the rest-frame 15 ![]() m, 35
m, 35 ![]() m, and total infrared luminosity functions of galaxies spanning z<1.3. We thereby quantify the fractional contribution of infrared luminous galaxies to the comoving star formation rate density over this redshift range. In comparison with previous studies, the present one takes advantage of deep 70
m, and total infrared luminosity functions of galaxies spanning z<1.3. We thereby quantify the fractional contribution of infrared luminous galaxies to the comoving star formation rate density over this redshift range. In comparison with previous studies, the present one takes advantage of deep 70 ![]() m observations that provide a more robust infrared luminosity indicator than 24
m observations that provide a more robust infrared luminosity indicator than 24 ![]() m affected by the emission of PAHs at high redshift (
m affected by the emission of PAHs at high redshift (
![]() ), and we use several independent fields to control cosmic variance.
), and we use several independent fields to control cosmic variance.
Methods. We used a new extraction technique based on the well-determined positions of galaxies at shorter wavelengths to extract the 24 and 70 ![]() m flux densities of galaxies. It is found that sources separated by a minimum of 0.5
m flux densities of galaxies. It is found that sources separated by a minimum of 0.5 ![]() FWHM are deblended by this technique, which facilitates multi-wavelength associations of counterparts. Using a combination of photometric and spectroscopic redshifts that exist for
FWHM are deblended by this technique, which facilitates multi-wavelength associations of counterparts. Using a combination of photometric and spectroscopic redshifts that exist for ![]() 80% of the sources in our sample, we are able to estimate the rest-frame luminosities of galaxies at 15
80% of the sources in our sample, we are able to estimate the rest-frame luminosities of galaxies at 15 ![]() m and 35
m and 35 ![]() m. By complementing direct detections with a careful stacking analysis, we measured the mid- and far-infrared luminosity functions of galaxies over a factor
m. By complementing direct detections with a careful stacking analysis, we measured the mid- and far-infrared luminosity functions of galaxies over a factor ![]() 100 in luminosity (
100 in luminosity (
![]()
![]()
![]() )
at z<1.3. A stacking analysis was performed to validate the bolometric corrections and to compute comoving star-formation rate densities in three redshift bins 0.4<z<0.7, 0.7<z<1.0 and, 1.0<z<1.3.
)
at z<1.3. A stacking analysis was performed to validate the bolometric corrections and to compute comoving star-formation rate densities in three redshift bins 0.4<z<0.7, 0.7<z<1.0 and, 1.0<z<1.3.
Results. We find that the average infrared spectral energy distribution of galaxies over the last 2/3 of the cosmic time is consistent with that of local galaxies, although individual sources do present significant scatter. We also measured both the bright and faint ends of the infrared luminosity functions and find no evidence for a change in the slope of the double power law used to characterize the luminosity function. The redshift evolution of infrared luminous galaxies is consistent with pure luminosity evolution proportional to
![]() up to
up to
![]() .
We do not find evidence of differential evolution between LIRGs and ULIRGs up to
.
We do not find evidence of differential evolution between LIRGs and ULIRGs up to
![]() ,
in contrast with previous claims. The comoving number density of infrared luminous galaxies has increased by a factor of
,
in contrast with previous claims. The comoving number density of infrared luminous galaxies has increased by a factor of ![]() 100 between 0<z<1. By
100 between 0<z<1. By ![]() ,
LIRGs produce half of the total comoving infrared luminosity density.
,
LIRGs produce half of the total comoving infrared luminosity density.
Key words: galaxies: evolution - infrared: galaxies - galaxies: starburst - cosmology: observations
1 Introduction
Constraining the star formation history of galaxies as a function of redshift is a key to understanding galaxy formation. To estimate the ongoing star formation rate (SFR) of galaxies one needs to measure direct and re-radiated stellar emission of young stars which correspond to the rest-frame UV and IR light, respectively. Due to the difficulties and the only recent possibility to obtain deep infrared observations, first studies which have estimated SFR evolution with redshift have only used UV observations corrected for dust extinction (Madau et al. 1999). However dust extinction correction suffers from various uncertainties and it is well known that local galaxies harboring strong dusty star formation are opaque to UV radiation (Buat et al. 2005). Hence to obtain a complete understanding of these dusty star forming galaxies, deep infrared observations are required.
Taking advantage of infrared capabilities such as the Infrared Space Observatory (ISO), several teams have confirmed the importance of infrared galaxies for the understanding of SFR evolution (Lagache et al. 2004; Franceschini et al. 2001; Aussel et al. 1999; Xu et al. 2001; Elbaz et al. 1999; Metcalfe et al. 2003; Elbaz et al. 2002; Chary & Elbaz 2001). Indeed they all found that the contribution of luminous infrared galaxies to the SFR density increases with redshift up to ![]() and that at high redshift the bulk of the SFR density occurs in luminous infrared galaxies (i.e.
and that at high redshift the bulk of the SFR density occurs in luminous infrared galaxies (i.e.
![]()
![]() LIRGs <
LIRGs <
![]() ,
,
![]()
![]() ULIRGs) which are relatively rare in the local Universe.
ULIRGs) which are relatively rare in the local Universe.
The Spitzer Space Telescope made it possible to obtain a complete census of the SFR density evolution up to
![]() using deep 24
using deep 24 ![]() m Multiband Imaging Photometer (MIPS; Rieke et al. 2004) observations. Many authors (Xu 2000; Le Floc'h et al. 2005; Lagache et al. 2003; Chary & Elbaz 2001) have studied the evolution of the rest-frame 15
m Multiband Imaging Photometer (MIPS; Rieke et al. 2004) observations. Many authors (Xu 2000; Le Floc'h et al. 2005; Lagache et al. 2003; Chary & Elbaz 2001) have studied the evolution of the rest-frame 15 ![]() m or 8
m or 8 ![]() m luminosity function (LF) based on MIPS 24
m luminosity function (LF) based on MIPS 24 ![]() m data. Then using empirical SED libraries (Lagache et al. 2003; Dale & Helou 2002; Chary & Elbaz 2001) to derive the total infrared luminosities of galaxies from these monochromatic luminosities, they were able to constrain the evolution of the total infrared LF. They all found a strong evolution with cosmic time of the relative contributions of normal, LIRG and ULIRG galaxies to the SFR density. At
m data. Then using empirical SED libraries (Lagache et al. 2003; Dale & Helou 2002; Chary & Elbaz 2001) to derive the total infrared luminosities of galaxies from these monochromatic luminosities, they were able to constrain the evolution of the total infrared LF. They all found a strong evolution with cosmic time of the relative contributions of normal, LIRG and ULIRG galaxies to the SFR density. At
![]() ,
the SFR density is dominated by quiescent galaxies whereas at
,
the SFR density is dominated by quiescent galaxies whereas at
![]() it is dominated by LIRGs. They also found that the contribution of ULIRGs to the SFR density rises steeply from z=0 to z=1 but still remains negligible at
it is dominated by LIRGs. They also found that the contribution of ULIRGs to the SFR density rises steeply from z=0 to z=1 but still remains negligible at
![]() (i.e. less than 10%). More recently, studies using MIPS 24
(i.e. less than 10%). More recently, studies using MIPS 24 ![]() m (Caputi et al. 2007) data have extended previous works to higher redshift and found that ULIRGs may dominate the SFR density at
m (Caputi et al. 2007) data have extended previous works to higher redshift and found that ULIRGs may dominate the SFR density at
![]() .
.
All these studies, based on 24 ![]() m observations, are strongly dependent on the SED library (Lagache et al. 2003; Dale & Helou 2002; Chary & Elbaz 2001) used to derive the total infrared luminosity of galaxies.
Moreover significant uncertainties on the bolometric correction are implied by the redshifting of the strong PAH and silicate emission into the 24
m observations, are strongly dependent on the SED library (Lagache et al. 2003; Dale & Helou 2002; Chary & Elbaz 2001) used to derive the total infrared luminosity of galaxies.
Moreover significant uncertainties on the bolometric correction are implied by the redshifting of the strong PAH and silicate emission into the 24 ![]() m bandwidth.
m bandwidth.
At
![]() ,
Calzetti et al. (2007) have proven that the rest-frame 24
,
Calzetti et al. (2007) have proven that the rest-frame 24 ![]() m luminosity is a robust SFR estimator. Moreover using deep radio observations Appleton et al. (2004) have proven that observed 70
m luminosity is a robust SFR estimator. Moreover using deep radio observations Appleton et al. (2004) have proven that observed 70 ![]() m flux was a more robust SFR estimator than the observed 24
m flux was a more robust SFR estimator than the observed 24 ![]() m flux. Hence using the observed MIPS 70
m flux. Hence using the observed MIPS 70 ![]() m data for galaxies below
m data for galaxies below ![]() ,
as in the present study, will strongly reduce the bolometric correction uncertainties since this emission corresponds to the rest-frame 35
,
as in the present study, will strongly reduce the bolometric correction uncertainties since this emission corresponds to the rest-frame 35 ![]() m luminosity at
m luminosity at
![]() which is produced by dust of about the same temperature (
which is produced by dust of about the same temperature (
![]() )
as that responsible for the 24
)
as that responsible for the 24 ![]() m emission in local galaxies. The aim of the present paper is to take advantage of the deepest 70
m emission in local galaxies. The aim of the present paper is to take advantage of the deepest 70 ![]() m observations currently available to strongly constrain the bright end slope of the 35
m observations currently available to strongly constrain the bright end slope of the 35 ![]() m and the total infrared LFs up to
m and the total infrared LFs up to
![]() .
These far-infrared data, as part of the Far Infrared Deep Extragalactic Survey (FIDEL) and the Great Observatories Origin Deep Survey (GOODS), cover 4 fields (Extended Groth Strip, Extended Chandra Deep Field South, GOODS-N and, GOODS-S) which are wide enough (
.
These far-infrared data, as part of the Far Infrared Deep Extragalactic Survey (FIDEL) and the Great Observatories Origin Deep Survey (GOODS), cover 4 fields (Extended Groth Strip, Extended Chandra Deep Field South, GOODS-N and, GOODS-S) which are wide enough (![]() 1400 total arcmin2) and deep enough (
1400 total arcmin2) and deep enough (![]() 3 mJy at 70
3 mJy at 70 ![]() m) to obtain a good constraint on the bright end slope of these LFs. By complementing direct 70
m) to obtain a good constraint on the bright end slope of these LFs. By complementing direct 70 ![]() m detections with a careful stacking analysis, we also constrain the faint end slope of these LFs.
Finally, by studying the redshift evolution of the total infrared LF, we derive the evolution of the SFR density and the relative contributions of normal, LIRG and ULIRG galaxies to the total comoving infrared luminosity density as a function of redshift.
m detections with a careful stacking analysis, we also constrain the faint end slope of these LFs.
Finally, by studying the redshift evolution of the total infrared LF, we derive the evolution of the SFR density and the relative contributions of normal, LIRG and ULIRG galaxies to the total comoving infrared luminosity density as a function of redshift.
The layout of the paper is as follows: in Sect. 2, we present the mid- and far-infrared observations as well as all the ancillary data used in this study. We also present in this section the new extraction technique used to extract infrared sources and the simulations made to characterize the limits of our infrared catalogs. In Sect. 3, we present the rest-frame 15 ![]() m LF inferred in three redshift bins center at z=0.55, 0.85 and, 1.15 using MIPS 24
m LF inferred in three redshift bins center at z=0.55, 0.85 and, 1.15 using MIPS 24 ![]() m data. The rest-frame 35
m data. The rest-frame 35 ![]() m LF inferred in these three redshift bins using the MIPS 70
m LF inferred in these three redshift bins using the MIPS 70 ![]() m data is presented in Sect. 4. In this section we also measure, using a stacking analysis, the observed 24/70
m data is presented in Sect. 4. In this section we also measure, using a stacking analysis, the observed 24/70 ![]() m correlation which enables us to constrain the faint end slope of the rest frame 35
m correlation which enables us to constrain the faint end slope of the rest frame 35 ![]() m LF. In Sect. 5 we present the total infrared LF function and its evolution up to
m LF. In Sect. 5 we present the total infrared LF function and its evolution up to
![]() .
Finally in Sect. 6 we discuss the evolution of the rest-frame 35
.
Finally in Sect. 6 we discuss the evolution of the rest-frame 35 ![]() m and total infrared LF in terms of the cosmic SFR history and the relative contributions of normal and luminous infrared galaxies.
m and total infrared LF in terms of the cosmic SFR history and the relative contributions of normal and luminous infrared galaxies.
Throughout this paper we will use a cosmology with
![]() ,
,
![]() ,
,
![]() .
.
2 The Data
2.1 Infrared imaging
2.1.1 EGS
The Extended Groth Strip field (
![]() )
was observed at 24 and 70
)
was observed at 24 and 70 ![]() m with the MIPS instrument on board the Spitzer Space Telescope as part of the Far Infrared Deep Extragalactic Legacy program (FIDEL, PI: Dickinson). These observations cover a total area of 900 arcmin2 using the scan mode AOT of Spitzer (see Spitzer observer's manual for more information).
m with the MIPS instrument on board the Spitzer Space Telescope as part of the Far Infrared Deep Extragalactic Legacy program (FIDEL, PI: Dickinson). These observations cover a total area of 900 arcmin2 using the scan mode AOT of Spitzer (see Spitzer observer's manual for more information).
The data were coadded using the MOPEX mosaicing software provided by the Spitzer Science Center. The final 24 ![]() m mosaic has a pixel scale of 1.2
m mosaic has a pixel scale of 1.2
![]() pixel and an effective integration time per sky pixel of
pixel and an effective integration time per sky pixel of ![]() 14 000 s. The final 70
14 000 s. The final 70 ![]() m mosaic has a pixel scale of 4.0
m mosaic has a pixel scale of 4.0
![]() pixel and an effective integration time per sky pixel of
pixel and an effective integration time per sky pixel of ![]() 7200 s.
For both wavelengths the calibration factor used to convert digital units (
7200 s.
For both wavelengths the calibration factor used to convert digital units (
![]() )
to flux (
)
to flux (
![]() )
was taken from the MIPS data handbook (see SSC MIPS Data Handbook v3.3.1 Sect. 3.7.2). At these wavelengths the point spread functions (PSF) are characterized by a FWHM of
)
was taken from the MIPS data handbook (see SSC MIPS Data Handbook v3.3.1 Sect. 3.7.2). At these wavelengths the point spread functions (PSF) are characterized by a FWHM of ![]()
![]() and
and ![]()
![]() at 24 and 70
at 24 and 70 ![]() m observations, respectively. These FWHM were measured on the empirical PSF used to perform our PSF fitting analysis (see Sect. 2.2).
m observations, respectively. These FWHM were measured on the empirical PSF used to perform our PSF fitting analysis (see Sect. 2.2).
The 24 and 70 ![]() m observations reach a point source sensitivity of
m observations reach a point source sensitivity of ![]()
![]() Jy and
Jy and ![]()
![]() Jy respectively. These point source sensitivities include effects of background and confusion noise and were derived using extensive simulations (see Sect. 2.2 for a complete definition). For both wavelengths, source extraction was first performed with a PSF fitting technique using the positions of IRAC sources as priors (see Sect. 2.2). This procedure leads to a total of 8457 sources at 24
Jy respectively. These point source sensitivities include effects of background and confusion noise and were derived using extensive simulations (see Sect. 2.2 for a complete definition). For both wavelengths, source extraction was first performed with a PSF fitting technique using the positions of IRAC sources as priors (see Sect. 2.2). This procedure leads to a total of 8457 sources at 24 ![]() m (
m (![]()
![]() Jy) and 669 sources at 70
Jy) and 669 sources at 70 ![]() m (
m (![]() 3 mJy).
3 mJy).
2.1.2 GOODS-North & South
Infrared imaging of the GOODS-N field (
![]() )
was obtained at 24
)
was obtained at 24 ![]() m as part of the GOODS Legacy program (PI: Dickinson). The 70
m as part of the GOODS Legacy program (PI: Dickinson). The 70 ![]() m data were obtained as part of the GO-3325 (PI: Frayer et al. 2006b) program for the
m data were obtained as part of the GO-3325 (PI: Frayer et al. 2006b) program for the
![]()
![]()
![]() central region and as part of the FIDEL legacy program for the northeast and southwest regions in order to cover the entire GOODS-N area (i.e.
central region and as part of the FIDEL legacy program for the northeast and southwest regions in order to cover the entire GOODS-N area (i.e.
![]()
![]()
![]() ).
Infrared imaging of the GOODS-S field (
).
Infrared imaging of the GOODS-S field (
![]() )
was obtained at 24 and 70
)
was obtained at 24 and 70 ![]() m as part of the GOODS legacy program (PI: Dickinson) and the GO-20147 (PI: Frayer) program respectively. We note that even if the GOODS-S 24
m as part of the GOODS legacy program (PI: Dickinson) and the GO-20147 (PI: Frayer) program respectively. We note that even if the GOODS-S 24 ![]() m field covers a
m field covers a
![]()
![]()
![]() area, the deep 70
area, the deep 70 ![]() m observations only cover a
m observations only cover a
![]()
![]()
![]() area. Thus the GOODS-N and the GOODS-S fields cover respectively a total area of 194 arcmin2 and 91 arcmin2.
area. Thus the GOODS-N and the GOODS-S fields cover respectively a total area of 194 arcmin2 and 91 arcmin2.
Final mosaics, obtained using MOPEX, have the same pixel scale as the EGS (i.e. 1.2
![]() pixel at 24
pixel at 24 ![]() m and 4.0
m and 4.0
![]() pixel at 70
pixel at 70 ![]() m). In both fields observations reach point source sensitivity of
m). In both fields observations reach point source sensitivity of ![]()
![]() Jy and
Jy and ![]()
![]() Jy at 24 and 70
Jy at 24 and 70 ![]() m respectively (i.e. an effective integration time per sky pixel of
m respectively (i.e. an effective integration time per sky pixel of ![]() 35 000 s and
35 000 s and ![]() 10 800 s respectively). Source extraction was carried out using our method with prior positions, leading to a total of 2151 sources at 24
10 800 s respectively). Source extraction was carried out using our method with prior positions, leading to a total of 2151 sources at 24 ![]() m (
m (![]()
![]() Jy, 5
Jy, 5![]() )
and 119 sources at 70
)
and 119 sources at 70 ![]() m (
m (![]() 2.5 mJy) in GOODS-N and 870 sources at 24
2.5 mJy) in GOODS-N and 870 sources at 24 ![]() m (
m (![]()
![]() Jy) and 44 sources at 70
Jy) and 44 sources at 70 ![]() m (
m (![]() 2.5 mJy) in GOODS-S.
2.5 mJy) in GOODS-S.
2.1.3 ECDF-S
The ECDF-S (
![]() )
was observed with the MIPS instrument as part of the FIDEL legacy program (PI: Dickinson) and covers a total area of 900 arcmin2.
In the following we refer to the ECDF-S field as the outer part of this
)
was observed with the MIPS instrument as part of the FIDEL legacy program (PI: Dickinson) and covers a total area of 900 arcmin2.
In the following we refer to the ECDF-S field as the outer part of this
![]()
![]()
![]() area while the central part (
area while the central part (
![]()
![]()
![]() )
is refered to as the GOODS-S field (see Sect. 2.1.2). Reduced to its outer part, the ECDF-S field covers a total area of 520 arcmin2 (hereafter ECDFS-O). The choice to treat separately the GOODS-S and the ECDFS-O data is driven by the difference in the 70
)
is refered to as the GOODS-S field (see Sect. 2.1.2). Reduced to its outer part, the ECDF-S field covers a total area of 520 arcmin2 (hereafter ECDFS-O). The choice to treat separately the GOODS-S and the ECDFS-O data is driven by the difference in the 70 ![]() m coverage (the central part being deeper than the outer part). The final 70
m coverage (the central part being deeper than the outer part). The final 70 ![]() m mosaic, obtained using MOPEX, has the same pixel scale as the EGS and reaches a point source sensitivity of
m mosaic, obtained using MOPEX, has the same pixel scale as the EGS and reaches a point source sensitivity of ![]() 3.5 mJy (i.e. an effective integration time per sky pixel of
3.5 mJy (i.e. an effective integration time per sky pixel of ![]() 5750 s). At 24
5750 s). At 24 ![]() m, the effective integration time per sky pixel being inhomogeneous, the final mosaic reaches point source sensitivity values which are function of the source positions. It spans the range of
m, the effective integration time per sky pixel being inhomogeneous, the final mosaic reaches point source sensitivity values which are function of the source positions. It spans the range of ![]()
![]() Jy over the whole mosaic.
Jy over the whole mosaic.
Using our extraction method we obtained 2474 sources at 24 ![]() m (
m (![]()
![]() Jy) and 195 sources at 70
Jy) and 195 sources at 70 ![]() m (
m (![]() 3.5 mJy).
3.5 mJy).
2.2 Infrared source detection
Since most sources in these fields were unresolved, we performed a PSF fitting technique to extract their photometry. Nevertheless, to be able to deal with blending issues and to go down to the limit of the data, we used, as a prior information, the expected position of the sources. We assume that all sources present in the mid-infrared images have already been detected at other wavelengths where the depth and the resolution of the data are higher.
For the 24 ![]() m data, we choose to use the position of the IRAC-3.6
m data, we choose to use the position of the IRAC-3.6 ![]() m sources. This choice was motivated by the depth of the IRAC-3.6
m sources. This choice was motivated by the depth of the IRAC-3.6 ![]() m data which is on average a factor of 30 deeper than MIPS 24
m data which is on average a factor of 30 deeper than MIPS 24 ![]() m data in every field used in this study. Hence since we know that the typical
m data in every field used in this study. Hence since we know that the typical
![]() ratio spans the range [3-20] (Chary et al. 2004), the IRAC data are deep enough to contain every 24
ratio spans the range [3-20] (Chary et al. 2004), the IRAC data are deep enough to contain every 24 ![]() m source. Moreover the resolution of the IRAC-3.6
m source. Moreover the resolution of the IRAC-3.6 ![]() m data (FWHM
m data (FWHM ![]()
![]() )
being 3 times sharper than the MIPS 24
)
being 3 times sharper than the MIPS 24 ![]() m data, blended sources separable in the 24
m data, blended sources separable in the 24 ![]() m MIPS images (i.e. sources separated by more than
m MIPS images (i.e. sources separated by more than ![]()
![]() in the 24
in the 24 ![]() m data) are unblended in the IRAC catalog.
m data) are unblended in the IRAC catalog.
For the GOODS-N field, we used the publicly available IRAC catalog released as part of the GOODS legacy program (Dickinson et al., in preparation). This catalog contains 19 437 objects detected at 3.6 ![]() m with a 50% completeness limit of 0.5
m with a 50% completeness limit of 0.5 ![]() Jy and an astrometric accuracy of
Jy and an astrometric accuracy of
![]() .
For the EGS, we used the publicly available IRAC EGS catalog released by the AEGIS collaboration (Barmby et al. 2008). This catalog contains 57 434 objects detected at 3.6
.
For the EGS, we used the publicly available IRAC EGS catalog released by the AEGIS collaboration (Barmby et al. 2008). This catalog contains 57 434 objects detected at 3.6 ![]() m with a 50% completeness limit of 1.5
m with a 50% completeness limit of 1.5 ![]() Jy. The astrometric accuracy of this catalog is estimated to be close to
Jy. The astrometric accuracy of this catalog is estimated to be close to
![]() .
Finally, for the GOODS-S/ECDF-S region, we used the SIMPLE catalog (Spitzer IRAC/MUSYC Public Legacy in ECDF-S; Gawiser et al. 2006). This catalog contains 61 233 objects detected at 3.6
.
Finally, for the GOODS-S/ECDF-S region, we used the SIMPLE catalog (Spitzer IRAC/MUSYC Public Legacy in ECDF-S; Gawiser et al. 2006). This catalog contains 61 233 objects detected at 3.6 ![]() m with a 50% completeness limit of 1.5
m with a 50% completeness limit of 1.5 ![]() Jy. The astrometric accuracy is the same as in the EGS catalog.
Jy. The astrometric accuracy is the same as in the EGS catalog.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1443f1a.eps}\hspace*{3mm}
\includegraphics[width=8.8cm,clip]{1443f1b.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg65.gif) |
Figure 1:
Photometric accuracy, [S(out) - S(in)]/S(out), derived from the simulation as a function of measured flux density, S(out), for the GOODS-N 24 |
| Open with DEXTER | |
Table 1: Catalog properties.
An empirical 24 ![]() m PSF was constructed with isolated point like objects present in the mosaic and was then fitted to all IRAC positions in the map. The photometry of each 24
m PSF was constructed with isolated point like objects present in the mosaic and was then fitted to all IRAC positions in the map. The photometry of each 24 ![]() m source is defined as the scaled fitted PSF. Then, as for a standard aperture correction, the photometry is corrected to account for the finite size of the empirical PSF. A residual image was created by subtracting from the original image the detected 24
m source is defined as the scaled fitted PSF. Then, as for a standard aperture correction, the photometry is corrected to account for the finite size of the empirical PSF. A residual image was created by subtracting from the original image the detected 24 ![]() m sources. Finally we check in this residual image the presence of 24
m sources. Finally we check in this residual image the presence of 24 ![]() m sources missed by the lack of IRAC position using DAOPHOT detection. We find no residual sources.
m sources missed by the lack of IRAC position using DAOPHOT detection. We find no residual sources.
For the 70 ![]() m data, we choose to start from our previous 24
m data, we choose to start from our previous 24 ![]() m detections. This choice is straightforward since the typical
m detections. This choice is straightforward since the typical
![]() ratio spans the range [2-100] (Papovich et al. 2007) and that the 24
ratio spans the range [2-100] (Papovich et al. 2007) and that the 24 ![]() m observations are about 100 times deeper.
No reliable empirical PSF can be constructed at 70
m observations are about 100 times deeper.
No reliable empirical PSF can be constructed at 70 ![]() m since only a few isolated sources can be found in each map. We decided to use the appropriate 70
m since only a few isolated sources can be found in each map. We decided to use the appropriate 70 ![]() m Point Response Function (PRF) estimated on the extragalactic First Look Survey (xFLS; Frayer et al. 2006a) mosaic and available on the Spitzer web site. Then as for the 24
m Point Response Function (PRF) estimated on the extragalactic First Look Survey (xFLS; Frayer et al. 2006a) mosaic and available on the Spitzer web site. Then as for the 24 ![]() m detection, we fit the 70
m detection, we fit the 70 ![]() m maps with this synthetic PSF at each 24
m maps with this synthetic PSF at each 24 ![]() m position. Once again we then check the residual image but no residual sources where found, i.e. we did not see any evidence for the existence of 70
m position. Once again we then check the residual image but no residual sources where found, i.e. we did not see any evidence for the existence of 70 ![]() m sources with no 24
m sources with no 24 ![]() m counterpart at these depths.
m counterpart at these depths.
The advantage of this method of priors is principally to resolve a large part of the blending issue.
Moreover this method reduces the cross-matching issue since for each IRAC position we directly have a 24 and 70 ![]() m flux. Then to cross-match our mid-infared detections with any other catalog, we can use the IRAC astrometry which is more accurate than any 24 or 70
m flux. Then to cross-match our mid-infared detections with any other catalog, we can use the IRAC astrometry which is more accurate than any 24 or 70 ![]() m centroid position.
m centroid position.
To estimate completeness and photometric reliability we performed extensive simulations for each field and at each wavelength. We added artificial sources in the image with a flux distribution matching approximately the measured number counts (see Frayer et al. 2006b; Papovich et al. 2004).
In order to preserve the original statistics of the image (especially the crowding properties) the numbers of artificial objects added in the image was kept small (as an example for GOODS-N we only added 40 sources into the 24 ![]() m image and 4 sources into 70
m image and 4 sources into 70 ![]() m images). Moreover as the photon noise of the MIPS 24 and 70
m images). Moreover as the photon noise of the MIPS 24 and 70 ![]() m data is dominated by the background emission we do not need to introduce any additional Poisson noise due to the photon statistics of the object itself. We then performed the source extraction again to compare the resulting photometry to the input values. To increase the statistics we used repeatedly the same procedure with different positions in the same field. For each field we introduced a total of 20 000 artificial objects.
m data is dominated by the background emission we do not need to introduce any additional Poisson noise due to the photon statistics of the object itself. We then performed the source extraction again to compare the resulting photometry to the input values. To increase the statistics we used repeatedly the same procedure with different positions in the same field. For each field we introduced a total of 20 000 artificial objects.
In Fig. 1 we show the results of one of the simulations obtained for the GOODS-N 24 ![]() m and 70
m and 70 ![]() m data. We plot for each wavelength the photometric accuracy derived from the simulation as a function of measured flux density. We defined the completeness as the fraction of sources with a flux accuracy better than 50%. To estimate the contamination of our catalog by spurious sources (i.e. sources arising from the noise properties of the image and not from real sources) we simulated very faint sources which were normally undetectable since they were introduced with a flux density fainter than the background noise. The contamination was then defined as the fraction of these undetectable sources that were extracted by our method. Using these simulations we defined the flux density limits of the final catalogs as those above which we simultaneously get:
m data. We plot for each wavelength the photometric accuracy derived from the simulation as a function of measured flux density. We defined the completeness as the fraction of sources with a flux accuracy better than 50%. To estimate the contamination of our catalog by spurious sources (i.e. sources arising from the noise properties of the image and not from real sources) we simulated very faint sources which were normally undetectable since they were introduced with a flux density fainter than the background noise. The contamination was then defined as the fraction of these undetectable sources that were extracted by our method. Using these simulations we defined the flux density limits of the final catalogs as those above which we simultaneously get:
- a photometric error better than 33% for at least 68% of the sources;
- a completeness of at least
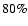 (to minimize future completeness correction);
(to minimize future completeness correction);
- a contamination by artificial sources lower than 15%.
For the 70 ![]() m data of GOODS-N and S, the catalog flux density limit is 2.5 mJy. For the EGS 70
m data of GOODS-N and S, the catalog flux density limit is 2.5 mJy. For the EGS 70 ![]() m data, the flux limit of our catalog is 3 mJy and for the ECDFS-O 70
m data, the flux limit of our catalog is 3 mJy and for the ECDFS-O 70 ![]() m data the detection limit of the catalog is 3.5 mJy.
m data the detection limit of the catalog is 3.5 mJy.
We would like to emphasize that the calibration factor taken to generate the final 24 and 70 ![]() m mosaics are derived from stars, whose SED at these wavelengths are generally very different from those of distant galaxies. Hence color corrections may be necessary to these fluxes (at most
m mosaics are derived from stars, whose SED at these wavelengths are generally very different from those of distant galaxies. Hence color corrections may be necessary to these fluxes (at most ![]()
![]() ). Nevertheless, since these color corrections are highly dependent on the redshift and the intrinsic SED of the sources, we decided to introduce these color corrections directly in the k-correction used to estimate the LF (see Sect. 3.1) since both quantities are taken into account in this computation.
). Nevertheless, since these color corrections are highly dependent on the redshift and the intrinsic SED of the sources, we decided to introduce these color corrections directly in the k-correction used to estimate the LF (see Sect. 3.1) since both quantities are taken into account in this computation.
2.3 Spectroscopic redshifts
2.3.1 EGS
The optical spectroscopic redshifts of the EGS field were taken from the DEEP2 data release 3 catalog (Davis et al. 2007). This survey targeted ![]() 50 000 distant galaxies with R<24.5, using the DEIMOS spectrograph on the Keck II telescope. In the EGS, unlike the other DEEP2 fields, objects at z < 0.7 were not excluded from the selection. The data release 3 catalog contains about 31 600 reliable redshifts with
18.5<R<24.5. For more details on the selection criteria of the DEEP 2 program see Davis et al. (2007).
50 000 distant galaxies with R<24.5, using the DEIMOS spectrograph on the Keck II telescope. In the EGS, unlike the other DEEP2 fields, objects at z < 0.7 were not excluded from the selection. The data release 3 catalog contains about 31 600 reliable redshifts with
18.5<R<24.5. For more details on the selection criteria of the DEEP 2 program see Davis et al. (2007).
2.3.2 GOODS-North/South & ECDF-S
A large number of spectroscopic redshifts has been measured for galaxies in the GOODS regions.
In GOODS-N a total of 2376 spectroscopic redshifts come from a combination of various studies (Wirth et al. 2004; Cowie et al. 2004; Cohen et al. 2000, Stern et al., in prep.). In the GOODS-S/ECDF-S region, 2547 spectroscopic redshifts were also combined from various studies (Vanzella et al. 2006; Mignoli et al. 2005; Le Fèvre et al. 2004). Although these spectroscopic redshift catalogs were obtained from several campaigns with diverse selection criteria, when combined together, they provide a rather homogeneous sampling. In GOODS-N and GOODS-S, respectively 60% and 50% of the galaxies brighter than
zAB=23.5 and with a photometric redshift lower than
![]() ,
have a spectroscopic redshift (see Elbaz et al. 2007).
,
have a spectroscopic redshift (see Elbaz et al. 2007).
2.4 Photometric redshifts
2.4.1 EGS
In addition to the spectroscopic redshifts we also need reliable photometric redshifts. We used publicly available photometric redshifts provided by the TERAPIX and the VVDS consortia (Ilbert et al. 2006) using the Canada-Hawai-France Telescope Legacy Survey (CFHT-LS).
The CFHTLS D3 survey consists of a 1 square degree region centered at
![]() ,
,
![]() observed through the u, g, r, i and z CFHTLS filters. Using this set of photometric magnitudes and appropriate spectral energy distributions (SED), the "Le Phare" photometric code provided a redshift probability distribution for each source (Ilbert et al. 2006).
observed through the u, g, r, i and z CFHTLS filters. Using this set of photometric magnitudes and appropriate spectral energy distributions (SED), the "Le Phare" photometric code provided a redshift probability distribution for each source (Ilbert et al. 2006).
The final
![]() selected catalog contains 366 030 sources with a magnitude limit of
selected catalog contains 366 030 sources with a magnitude limit of
![]() .
For galaxies with
.
For galaxies with
![]() and z<1.5, these redshifts have an accuracy of
and z<1.5, these redshifts have an accuracy of
![]() with 3.8% of catastrophic errors (Ilbert et al. 2006). As recommended in Ilbert et al. (2006), we excluded all sources with a double peak in their redshift probability distribution function (PDF) since most of them did not have a reliable redshift. The overlap region between the EGS and the CFHTLS D3 reduces the EGS area from 900 arcmin2 down to 548 arcmin2.
with 3.8% of catastrophic errors (Ilbert et al. 2006). As recommended in Ilbert et al. (2006), we excluded all sources with a double peak in their redshift probability distribution function (PDF) since most of them did not have a reliable redshift. The overlap region between the EGS and the CFHTLS D3 reduces the EGS area from 900 arcmin2 down to 548 arcmin2.
2.4.2 GOODS-North & South
For the GOODS fields, we complemented the spectroscopic redshifts with photometric redshifts estimated using Z-PEG (Le Borgne & Rocca-Volmerange 2002). For both fields we used some of the deepest data currently available in the GOODS region (UBVRIzJHK, 3.6 ![]() m, 4.5
m, 4.5 ![]() m) to derive photometric redshifts with an accuracy of
m) to derive photometric redshifts with an accuracy of
![]() .
For more detail on the complete multi-lambda catalog used in the computation of the photometric redshifts see Le Borgne et al. (in prep.).
.
For more detail on the complete multi-lambda catalog used in the computation of the photometric redshifts see Le Borgne et al. (in prep.).
Table 2: Redshift catalog properties.
2.4.3 ECDF-S
For the ECDF-S we used the catalog of photometric redshifts from the COMBO-17 survey (Classifying Objects by Medium-Band Observations in 17 filters; Wolf et al. 2004). The COMBO-17 survey observed a 31.5 ![]() 30 arcmin2 area with 5 broadband and 12 narrowband filters.
The catalog contains 63 501 objects selected on the deep R-band image (R<26) carried out with the Wide Field Imager (WFI) at the MPG/ESO 2.2-m telescope in La Silla. Using an extensive SED library, they fitted the photometry of each object to compute its redshift probability distribution.
Finally the COMBO-17 catalog contains 24 216 objects with a reliable photometric redshift.
30 arcmin2 area with 5 broadband and 12 narrowband filters.
The catalog contains 63 501 objects selected on the deep R-band image (R<26) carried out with the Wide Field Imager (WFI) at the MPG/ESO 2.2-m telescope in La Silla. Using an extensive SED library, they fitted the photometry of each object to compute its redshift probability distribution.
Finally the COMBO-17 catalog contains 24 216 objects with a reliable photometric redshift.
For sources with R<24 and z<1.2, these redshifts have an accuracy of
![]() .
For sources fainter than R=24 the redshift accuracy drops dramatically, therefore we did not consider in the following such faint objects.
.
For sources fainter than R=24 the redshift accuracy drops dramatically, therefore we did not consider in the following such faint objects.
2.5 Removing Active galaxies
The infrared luminosity of a normal star-forming galaxy can be severely affected by the presence of an Active Galactic Nucleus (AGN). Hence to study the star formation history of normal galaxies it is necessary to identify and remove these AGNs.
In order to test the presence of AGNs in the GOODS field, we used the deepest Chandra X-ray observations i.e. the 1 Ms maps for the CDF-S and the 2 Ms maps for the CDF-N (Alexander et al. 2003). For both fields we used the corresponding public X-ray catalog. For the EGS field we also used Chandra observations taken from the public AEGIS-X data release 2 point source catalog which has a 200 Ks coverage (Laird et al. 2008). Finally for the ECDF-S we used the 250 Ks Chandra observations, which flank the 1 Ms CDF-S observations (Lehmer et al. 2005).
AGNs were identified as galaxies with either
![]()
![]() 3
3 ![]()
![]() and/or a hardness ratio greater than 0.8 (ratio of the counts in the 2-8 keV to 0.5-2 keV passbands) (Bauer et al. 2004). As mentioned in Bauer et al. (2004), some AGNs might be missed by this technique. The fraction of such galaxies remains a matter of debate until today but the global consistency of the 24-70
and/or a hardness ratio greater than 0.8 (ratio of the counts in the 2-8 keV to 0.5-2 keV passbands) (Bauer et al. 2004). As mentioned in Bauer et al. (2004), some AGNs might be missed by this technique. The fraction of such galaxies remains a matter of debate until today but the global consistency of the 24-70 ![]() m color of the galaxies studied here (as discussed in Sect. 4.2) suggests that they should not play a dominant role (see also Fadda et al. 2002). We did not subtract the AGN contribution to the IR light of those galaxies harboring an AGN, instead we conservatively assumed that any galaxy contaminated by an AGN was not forming stars. It is well-known that AGNs do also harbor star formation, especially those emitting strongly at IR wavelengths, but such subtraction would be highly speculative at the present level of our knowledge.
m color of the galaxies studied here (as discussed in Sect. 4.2) suggests that they should not play a dominant role (see also Fadda et al. 2002). We did not subtract the AGN contribution to the IR light of those galaxies harboring an AGN, instead we conservatively assumed that any galaxy contaminated by an AGN was not forming stars. It is well-known that AGNs do also harbor star formation, especially those emitting strongly at IR wavelengths, but such subtraction would be highly speculative at the present level of our knowledge.
2.6 The final IR galaxy sample
To construct our final catalog, we first truncated our mid-infrared catalog to the region covered by both Spitzer and the optical redshift surveys used in this study. This step was especially important for the EGS field where the total FIDEL area of 900 arcmin2 is reduced to 548 arcmin2 to overlap the CFHT-LS survey (i.e. the photometric redshift survey). We then cross-matched the 24 ![]() m catalog with the X-ray observations to exclude AGNs. We found that
m catalog with the X-ray observations to exclude AGNs. We found that ![]()
![]() (
(![]()
![]() )
of the 24
)
of the 24 ![]() m (70
m (70 ![]() m) sources were affected by an X-ray AGN and hence removed from our catalog. The rest of the data was then cross-matched with the different spectroscopic catalogs and finally the remaining sources were matched with the photometric catalogs. All these cross-matching steps were made using the IRAC astrometry of the mid-infrared sample and a matching radius of 1.5 arcsec. The choice of 1.5 arcsec is motivated by the size of the IRAC-
m) sources were affected by an X-ray AGN and hence removed from our catalog. The rest of the data was then cross-matched with the different spectroscopic catalogs and finally the remaining sources were matched with the photometric catalogs. All these cross-matching steps were made using the IRAC astrometry of the mid-infrared sample and a matching radius of 1.5 arcsec. The choice of 1.5 arcsec is motivated by the size of the IRAC-![]() m PSF FWHM (
m PSF FWHM (![]()
![]() ). In case of multiple associations we selected the closest optical counterparts to the IRAC centroid. We found that 8%, 10% and 9% of the MIPS 24
). In case of multiple associations we selected the closest optical counterparts to the IRAC centroid. We found that 8%, 10% and 9% of the MIPS 24 ![]() m sources have multiple associations with optical sources brighter than I <26 mag for the EGS, GOODS-N, GOODS-S. For the ECDFS-O we found that 1% of sources have a multiple association with optical sources brigther than
m sources have multiple associations with optical sources brighter than I <26 mag for the EGS, GOODS-N, GOODS-S. For the ECDFS-O we found that 1% of sources have a multiple association with optical sources brigther than
![]() .
.
All the different steps described previously and applied to the different fields of our study are listed in the Table 2. The redshift completeness is larger than 90% (70% except for the ECDFS-O) at 70 ![]() m (24
m (24 ![]() m) for the sources with no AGN contribution.
m) for the sources with no AGN contribution.
2.7 Redshift uncertainties and sample completeness
One of the major concern of all studies heavily relying on photometric redshift is their possible redshift incompleteness for distant and/or faint galaxies. As these issues may have a nonnegligible effect when estimating luminosity functions as a function of redshift, one should pay attention to the consequence of these limitations.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f2.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg112.gif) |
Figure 2:
Comparison between photometric and spectroscopic redshift for 2406 galaxies of our 24 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1443f3a.eps}\vspace*{5mm}
\i...
...f3b.eps}\vspace*{5mm}
\includegraphics[width=8cm,clip]{1443f3c.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg113.gif) |
Figure 3:
Fraction of 24 |
| Open with DEXTER | |
In Sect. 2.4 we have quoted the accuracy of all photometric redshift catalogs used in this work. Nevertheless since these accuracies were based on an optically-selected sample we need to characterize the typical uncertainties of our 24 ![]() m-selected sample. In Fig. 2 we compare the spectroscopic and photometric redshifts of all 24
m-selected sample. In Fig. 2 we compare the spectroscopic and photometric redshifts of all 24 ![]() m sources with a spectroscopic redshift after combining the four fields (2406 sources, see Table 2). We observe a very good agreement between the photometric and spectroscopic redshifts with an accuracy of
m sources with a spectroscopic redshift after combining the four fields (2406 sources, see Table 2). We observe a very good agreement between the photometric and spectroscopic redshifts with an accuracy of
![]() and a median value of -0.005. We notice that this accuracy is not statistically larger than the accuracy quoted for the optically-selected sample. We also found
and a median value of -0.005. We notice that this accuracy is not statistically larger than the accuracy quoted for the optically-selected sample. We also found ![]() of catastrophic objects defined as those objects with
of catastrophic objects defined as those objects with
![]() .
Even if those galaxies are statistically rare, they could have a major effect on the estimates of the LF by boosting the bright end slope. Therefore in the following study we will pay close attention to quantify their effect on the estimates of the total infrared LF (see Sect. 3.1).
.
Even if those galaxies are statistically rare, they could have a major effect on the estimates of the LF by boosting the bright end slope. Therefore in the following study we will pay close attention to quantify their effect on the estimates of the total infrared LF (see Sect. 3.1).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f4.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg116.gif) |
Figure 4:
Redshift distributions of 24 |
| Open with DEXTER | |
As previously mentioned and quoted in Table 2 a high fraction (![]()
![]() )
of our final IR galaxy sample have been associated with a spectroscopic and/or a photometric redshift. Nevertheless the remaining fraction of sources with no redshift association are not randomly distributed in the redshift space. As a result, we need to quantify the redshift above which the photometric redshift incompleteness affects our study. In Fig. 3 we present the photometric redshift completeness as a function of the optical magnitude (solid lines). These histograms allow us to estimate the optical magnitude above which the determination of a reliable photometric redshift start to be problematic. Independently, we also present in Fig. 3 the optical magnitude distribution of the 24
)
of our final IR galaxy sample have been associated with a spectroscopic and/or a photometric redshift. Nevertheless the remaining fraction of sources with no redshift association are not randomly distributed in the redshift space. As a result, we need to quantify the redshift above which the photometric redshift incompleteness affects our study. In Fig. 3 we present the photometric redshift completeness as a function of the optical magnitude (solid lines). These histograms allow us to estimate the optical magnitude above which the determination of a reliable photometric redshift start to be problematic. Independently, we also present in Fig. 3 the optical magnitude distribution of the 24 ![]() m sources for different redshift bins. For clarity these optical magnitude distributions have been scaled with an arbitrary factor. By combining these two informations (i.e. the redshift determination completeness as a function of the optical magnitude and optical magnitude distribution) one can have an estimates of the redshift incompleteness of his sample. For example, if the photometric redshift catalog is highly incomplete for sources fainter than R>24 and in the same time a large fraction of the 24
m sources for different redshift bins. For clarity these optical magnitude distributions have been scaled with an arbitrary factor. By combining these two informations (i.e. the redshift determination completeness as a function of the optical magnitude and optical magnitude distribution) one can have an estimates of the redshift incompleteness of his sample. For example, if the photometric redshift catalog is highly incomplete for sources fainter than R>24 and in the same time a large fraction of the 24 ![]() m sources that lie at 1<z<1.3 have
m sources that lie at 1<z<1.3 have
![]() ,
one can expect a large redshift incompleteness in this redshift bin.
,
one can expect a large redshift incompleteness in this redshift bin.
As already discussed in Le Floc'h et al. (2005) we observe that sources situated at higher redshift have fainter optical counterpart and that the redshift determination completeness decreases at faint magnitudes. For the GOODS fields we notice that the depth of optical observations and the use of deep near infrared data allow us to have a complete redshift association up to
![]() .
Indeed we notice that the redshift completeness of the GOODS field falls at optical magnitudes (i.e. R>27.5) where the distribution of 24
.
Indeed we notice that the redshift completeness of the GOODS field falls at optical magnitudes (i.e. R>27.5) where the distribution of 24 ![]() m sources that lie at 1.3<z<2.5 is already low.
Therefore for the GOODS fields, sources with no redshift association (
m sources that lie at 1.3<z<2.5 is already low.
Therefore for the GOODS fields, sources with no redshift association (![]()
![]() )
are likely located at z>2 and hence should not affect the study of the evolution of the total infrared LF up to z=1.3. For the EGS the redshift determination completeness highly decreases at an optical magnitude range (i.e. I-mag
)
are likely located at z>2 and hence should not affect the study of the evolution of the total infrared LF up to z=1.3. For the EGS the redshift determination completeness highly decreases at an optical magnitude range (i.e. I-mag ![]() 22.5) where a large fraction of sources are located at z<1.3. This trend can lead to a high incompleteness of sources located at 1<z<1.3. However we notice that the decrease of this redshift determination is driven by sources with a double peak in their probability distribution functions (PDF; see the dash lines in Fig. 3). All galaxies for which we have both a double peak distribution in their photometric redshift and a spectroscopic redshift are located at z>1. The minor effect of ``double peak'' galaxies on the redshift distribution can be inferred by the comparison of the redshift distribution of the EGS and the GOODS fields (for which we expect no redshift incompleteness up to
22.5) where a large fraction of sources are located at z<1.3. This trend can lead to a high incompleteness of sources located at 1<z<1.3. However we notice that the decrease of this redshift determination is driven by sources with a double peak in their probability distribution functions (PDF; see the dash lines in Fig. 3). All galaxies for which we have both a double peak distribution in their photometric redshift and a spectroscopic redshift are located at z>1. The minor effect of ``double peak'' galaxies on the redshift distribution can be inferred by the comparison of the redshift distribution of the EGS and the GOODS fields (for which we expect no redshift incompleteness up to
![]() ;
see Figs. 4 and 3). Indeed we do not observe large differences in the redshift distribution of these two fields between 0<z<1.3, whereas at z>1.3 the number of sources in the EGS drops to zero likely due to redshift incompleteness. Finally for the ECDFS-O field we find the same results than Le Floc'h et al. (2005), i.e. the magnitude distribution of the two highest redshift bins (i.e. 0.7<z<1.0 and 1.0<z<1.3) are truncated at the faint end which indicate that these redshift bins are affected by incompleteness. Nevertheless we can estimate from the shape of the magnitude distribution that only
;
see Figs. 4 and 3). Indeed we do not observe large differences in the redshift distribution of these two fields between 0<z<1.3, whereas at z>1.3 the number of sources in the EGS drops to zero likely due to redshift incompleteness. Finally for the ECDFS-O field we find the same results than Le Floc'h et al. (2005), i.e. the magnitude distribution of the two highest redshift bins (i.e. 0.7<z<1.0 and 1.0<z<1.3) are truncated at the faint end which indicate that these redshift bins are affected by incompleteness. Nevertheless we can estimate from the shape of the magnitude distribution that only ![]()
![]() of sources should be affected by this incompleteness and hence no large effects are expected on the estimates of the infrared LFs.
Indeed we will see in the following that the infrared LFs inferred from the ECDFS-O and GOODS fields are, within the error bars, in very good agreement (see Sects. 3-5).
To conclude we infer that the redshift incompleteness should not affect the conclusions of our study since the uncertainties corresponding to this misidentification are lower than the uncertainties introduced by the k-correction and the photometric redshift measurements.
of sources should be affected by this incompleteness and hence no large effects are expected on the estimates of the infrared LFs.
Indeed we will see in the following that the infrared LFs inferred from the ECDFS-O and GOODS fields are, within the error bars, in very good agreement (see Sects. 3-5).
To conclude we infer that the redshift incompleteness should not affect the conclusions of our study since the uncertainties corresponding to this misidentification are lower than the uncertainties introduced by the k-correction and the photometric redshift measurements.
Assuming that our photometric redshift catalogs do not suffer from incompleteness up to z=1.3, we can construct a reference sample of galaxies located at z<1.3. When compared to this reference sample, we find that the fraction of sources with a spectroscopic redshift is ![]() ,
,
![]() and,
and, ![]() for the GOODS, the EGS and the ECDFS-O fields respectively.
for the GOODS, the EGS and the ECDFS-O fields respectively.
3 The rest-frame 15 micron luminosity functions
Table 3: 15 microns k-correction of the sample.
In this section, we present the redshift evolution of the rest-frame 15 ![]() m luminosity function (LF) that we derive from the catalogs described in the previous section using the observed MIPS 24
m luminosity function (LF) that we derive from the catalogs described in the previous section using the observed MIPS 24 ![]() m flux density. The 15
m flux density. The 15 ![]() m LF is computed for three redshift bins centered at z=0.55, 0.85 and 1.15 (same bins as in Fig. 3) for which the 24
m LF is computed for three redshift bins centered at z=0.55, 0.85 and 1.15 (same bins as in Fig. 3) for which the 24 ![]() m observations correspond to the rest-frame 15, 13 and 11
m observations correspond to the rest-frame 15, 13 and 11 ![]() m wavelengths respectively. The extrapolation that needs to be applied to compute the 15
m wavelengths respectively. The extrapolation that needs to be applied to compute the 15 ![]() m luminosity is therefore negligible in the first two redshift bins (still it is carefully computed here) and becomes larger in the highest redshift bin due to the fact that the observed 24
m luminosity is therefore negligible in the first two redshift bins (still it is carefully computed here) and becomes larger in the highest redshift bin due to the fact that the observed 24 ![]() m is more distant from the rest-frame 15
m is more distant from the rest-frame 15 ![]() m. While the derivation of the rest-frame 15
m. While the derivation of the rest-frame 15 ![]() m LF has already been addressed in some previous studies (Le Floc'h et al. 2005), this is done here for two reasons.
m LF has already been addressed in some previous studies (Le Floc'h et al. 2005), this is done here for two reasons.
First, we wish to check and demonstrate the consistency of our technique and catalogs with those previous studies at a common wavelength before deriving the rest-frame 35 ![]() m LF. As we show it here, our results are not only consistent with those previous studies but even extend them to fainter luminosities as well as they provide a more robust constraint on the 15
m LF. As we show it here, our results are not only consistent with those previous studies but even extend them to fainter luminosities as well as they provide a more robust constraint on the 15 ![]() m LF because our catalogs are three times deeper at 24
m LF because our catalogs are three times deeper at 24 ![]() m than the one used in Le Floc'h et al. (2005). We are also able to validate the results against the effects of cosmic variance by comparing three independent fields: the EGS, the GOODS and the ECDFS-O fields.
m than the one used in Le Floc'h et al. (2005). We are also able to validate the results against the effects of cosmic variance by comparing three independent fields: the EGS, the GOODS and the ECDFS-O fields.
Second, this study will serve as a basis for the extension of the derivation of the faint end of the 35 ![]() m LF. For that purpose, we will first determine the typical ratio of the observed 70 over 24
m LF. For that purpose, we will first determine the typical ratio of the observed 70 over 24 ![]() m flux densities per redshift and flux density bins in order to associate 24
m flux densities per redshift and flux density bins in order to associate 24 ![]() m sources to a given flux density bin at 70
m sources to a given flux density bin at 70 ![]() m. Then we will derive the contribution of this bin to the 35
m. Then we will derive the contribution of this bin to the 35 ![]() m LF.
m LF.
The sizes of the redshift bins [0.4-0.7], [0.7-1.0], [1.0-1.3] were defined such as to encompass a large enough number of sources in the computation of the 35 ![]() m LF. For consistency, we used the same redshift bins here for the 15
m LF. For consistency, we used the same redshift bins here for the 15 ![]() m LF.
m LF.
3.1 Methodology
We define here the k-correction as the ratio between the rest-frame 15 and
![]() m luminosities as in Eq. (1).
m luminosities as in Eq. (1).
where
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f5.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg130.gif) |
Figure 5:
15 |
| Open with DEXTER | |
In the following, the 15 microns luminosity (
![]() )
of each galaxy is derived using the CE01 library. This choice was made to be homogeneous with the rest of the study since we will also use the CE01 templates to derive the total infrared luminosity of galaxies.
Indeed, as illustrated in Sect. 4.2, the CE01 library appears to best reproduce the observed luminosity-luminosity correlations even at high redshift (i.e.
)
of each galaxy is derived using the CE01 library. This choice was made to be homogeneous with the rest of the study since we will also use the CE01 templates to derive the total infrared luminosity of galaxies.
Indeed, as illustrated in Sect. 4.2, the CE01 library appears to best reproduce the observed luminosity-luminosity correlations even at high redshift (i.e.
![]() ).
).
The LF are derived using the
![]() method (Schmidt 1968) which does not require any assumption on the shape of the LF. The LF is then directly derived from the data. The comoving volume associated to any source of a given luminosity is defined as
method (Schmidt 1968) which does not require any assumption on the shape of the LF. The LF is then directly derived from the data. The comoving volume associated to any source of a given luminosity is defined as
![]() where
where
![]() is the lower limit of the redshift bin, and
is the lower limit of the redshift bin, and
![]() is the maximum redshift at which the object could be seen given the flux density limit of the sample, with a maximum value corresponding to the upper redshift of the redshift bin. For each luminosity bin, the LF is then given by
is the maximum redshift at which the object could be seen given the flux density limit of the sample, with a maximum value corresponding to the upper redshift of the redshift bin. For each luminosity bin, the LF is then given by
where
The four different fields studied here (EGS, GOODS-N, GOODS-S and ECDFS-O) have different flux density limits, therefore we will treat separately the GOODS-N and S (
![]() Jy), the EGS (
Jy), the EGS (
![]() Jy) and the ECDFS-O (
Jy) and the ECDFS-O (
![]() Jy). This will allow us to test the role of cosmic variance.
Jy). This will allow us to test the role of cosmic variance.
The uncertainties of the LF values depend on the numbers of sources in each luminosity bin, on the photometric redshifts uncertainties, the k-correction uncertainties and finally on the 24 and 70 ![]() m flux uncertainties. To compute these errors we performed Monte Carlo simulations by creating 1000 simulated catalogs. These simulated catalogs contain the same number of sources as the original one but we attributed to each source with a photometric redshift a new redshift randomly selected within its probability distribution function. Sources with a spectroscopic redshift have been left unchanged. To take into account the redshift catastrophic errors we randomly selected
m flux uncertainties. To compute these errors we performed Monte Carlo simulations by creating 1000 simulated catalogs. These simulated catalogs contain the same number of sources as the original one but we attributed to each source with a photometric redshift a new redshift randomly selected within its probability distribution function. Sources with a spectroscopic redshift have been left unchanged. To take into account the redshift catastrophic errors we randomly selected ![]() of sources with a photometric redshift (corresponding to the fraction of catastrophic sources found in Sect. 2.7) and then attributed to these sources a random redshift selected assuming a flat distribution between 0<z<3. We notice that assuming a flat distribution may not be totally realistic since catastrophic errors are generally bimodal (e.g., assigning to a low redshift galaxy a much higher redshift due to mistaking one spectral break for another).
Nevertheless the sample that we use to compare the photometric and spectroscopic redshifts is not large enough to describe rigorously this bimodality. However, assuming a flat distribution may be a more conservative assumption since this can yield an overestimation of the uncertainties due to redshift catastrophic errors. Indeed if the bimodal distribution of the catastrophic errors is characterized by
of sources with a photometric redshift (corresponding to the fraction of catastrophic sources found in Sect. 2.7) and then attributed to these sources a random redshift selected assuming a flat distribution between 0<z<3. We notice that assuming a flat distribution may not be totally realistic since catastrophic errors are generally bimodal (e.g., assigning to a low redshift galaxy a much higher redshift due to mistaking one spectral break for another).
Nevertheless the sample that we use to compare the photometric and spectroscopic redshifts is not large enough to describe rigorously this bimodality. However, assuming a flat distribution may be a more conservative assumption since this can yield an overestimation of the uncertainties due to redshift catastrophic errors. Indeed if the bimodal distribution of the catastrophic errors is characterized by
![]() (i.e. due to mistaking the Lyman break for a Balmer break) then it will only affect the estimates of the LF at z>3. To take into account flux uncertainties we attributed to each source a new flux selected into a Gaussian distribution centered at the original flux of the source and with a dispersion computed as
(i.e. due to mistaking the Lyman break for a Balmer break) then it will only affect the estimates of the LF at z>3. To take into account flux uncertainties we attributed to each source a new flux selected into a Gaussian distribution centered at the original flux of the source and with a dispersion computed as
![]() where
where
![]() is the calibration uncertainty estimated to be
is the calibration uncertainty estimated to be ![]()
![]() of the source flux density and
of the source flux density and
![]() is the source photometric uncertainty computed on the residual image. Finally to take into account the k-correction uncertainties, we selected the source luminosity assuming a Gaussian distribution centered at the original source luminosity and with a dispersion of 0.05 dex. Using these 1000 simulated catalogs, we then computed again the rest frame 15
is the source photometric uncertainty computed on the residual image. Finally to take into account the k-correction uncertainties, we selected the source luminosity assuming a Gaussian distribution centered at the original source luminosity and with a dispersion of 0.05 dex. Using these 1000 simulated catalogs, we then computed again the rest frame 15 ![]() m LF and defined the total uncertainty in each luminosity bin as the quadratic sum of the Poissonian error (
m LF and defined the total uncertainty in each luminosity bin as the quadratic sum of the Poissonian error (![]()
![]() )
and the dispersion given by the Monte-Carlo simulations.
We found that the Poisson statistics dominate the total uncertainties at the bright luminosity bin whereas at faint luminosities the total uncertainty is dominated by the Monte Carlo uncertainty.
)
and the dispersion given by the Monte-Carlo simulations.
We found that the Poisson statistics dominate the total uncertainties at the bright luminosity bin whereas at faint luminosities the total uncertainty is dominated by the Monte Carlo uncertainty.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{1443f6.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg148.gif) |
Figure 6:
Rest-frame 15 microns LF estimated for three redshift bins with the
|
| Open with DEXTER | |
To study the evolution of the rest-frame 15 microns LF between
![]() and
and
![]() we used as a local reference the local 15 microns LF of Xu (2000) derived using the bivariate (15
we used as a local reference the local 15 microns LF of Xu (2000) derived using the bivariate (15 ![]() m vs. 60
m vs. 60 ![]() m luminosity) method and based on ISOCAM observations. This LF is then fitted with a double power law function. This choice is driven by the fact that the ultimate goal of this paper is to derive the evolution of the total infrared LF which is itself best fitted with a double power law function (Sanders et al. 2003). Hence to be homogeneous we have made the choice, in the following, to fit the 15, 35
m luminosity) method and based on ISOCAM observations. This LF is then fitted with a double power law function. This choice is driven by the fact that the ultimate goal of this paper is to derive the evolution of the total infrared LF which is itself best fitted with a double power law function (Sanders et al. 2003). Hence to be homogeneous we have made the choice, in the following, to fit the 15, 35 ![]() m and total infrared LFs with double power laws. Using the Sanders et al. (2003) best-fit (i.e.
m and total infrared LFs with double power laws. Using the Sanders et al. (2003) best-fit (i.e.
![]() for log(
for log(
![]() ) < 10.5 and
) < 10.5 and
![]() for log(
for log(
![]() ) > 10.5) and a bivariate method, we derived the values of the two power laws for the 15
) > 10.5) and a bivariate method, we derived the values of the two power laws for the 15 ![]() m LF. We find that
m LF. We find that
![]() for log(
for log(
![]() ) <
) <
![]() and
and
![]() for log(
for log(
![]() ) >
) >
![]() .
Then, using a
.
Then, using a ![]() minimization, we fitted the Xu (2000) observations with this function, leaving
minimization, we fitted the Xu (2000) observations with this function, leaving
![]() and the normalization as free parameters. We also fit independently, with the same method and the same function, the rest-frame 15 microns LF derived in the three redshift bins (see Table 5).
and the normalization as free parameters. We also fit independently, with the same method and the same function, the rest-frame 15 microns LF derived in the three redshift bins (see Table 5).
In Fig. 6 we present the rest-frame 15 ![]() m LF derived with the
m LF derived with the
![]() method for the three redshift bins considered in this study. As already mentioned, these LFs have been derived jointly for the GOODS-N and S fields and separately for the EGS and ECDFS-O fields. The negligible role of cosmic variance is illustrated by the very good agreement between the three solutions in the derived 15
method for the three redshift bins considered in this study. As already mentioned, these LFs have been derived jointly for the GOODS-N and S fields and separately for the EGS and ECDFS-O fields. The negligible role of cosmic variance is illustrated by the very good agreement between the three solutions in the derived 15 ![]() m LF.
m LF.
3.2 Results
The resulting rest-frame 15 ![]() m LFs are presented in Fig. 6. They provide three significant results.
m LFs are presented in Fig. 6. They provide three significant results.
First, as written in the previous section, no strong effect of cosmic variance (i.e. ![]() 0.05-0.1 dex) is found between the three fields, which provide the same 15
0.05-0.1 dex) is found between the three fields, which provide the same 15 ![]() m LF within the error bars. This observed estimate of the cosmic variance is totally consistent with theoretical estimates of
m LF within the error bars. This observed estimate of the cosmic variance is totally consistent with theoretical estimates of ![]() 0.07 dex based on the area of our fields (see Trenti & Stiavelli 2008).
0.07 dex based on the area of our fields (see Trenti & Stiavelli 2008).
Second, the comparison of the rest-frame 15 ![]() m LF obtained in this study and the ones inferred by Le Floc'h et al. (2005) are in agreement for all 3 redshift bins. We note that the inferred LF was here extended to fainter luminosities using our
m LF obtained in this study and the ones inferred by Le Floc'h et al. (2005) are in agreement for all 3 redshift bins. We note that the inferred LF was here extended to fainter luminosities using our ![]() 3 times deeper catalog which allowed us to obtain better constraints on the faint end slope of the LF.
3 times deeper catalog which allowed us to obtain better constraints on the faint end slope of the LF.
Third, we find a substantial evolution of the LF with redshift. This evolution, already revealed by previous studies (Xu 2000; Franceschini et al. 2001; Le Floc'h et al. 2005; Caputi et al. 2007; Lagache et al. 2003; Chary & Elbaz 2001) is usually expressed through an evolution both in density and in luminosity of the local LF (i.e. ![]() ). Assuming that the shape of the LF remains the same since
). Assuming that the shape of the LF remains the same since
![]() ,
these studies express the evolution as
,
these studies express the evolution as
![]() ,
where g(z) and f(z) describe the density and the luminosity evolution through
g(z)=(1+z)p and
f(z)=(1+z)q. The weakness of this parameterization is that it assumes a monotonic evolution of the LF preventing any turn-over in the evolution (e.g. an increase in density that would be followed by a decrease). This kind of turn-over has already been seen at other infrared wavelengths (e.g. Caputi et al. 2007).
Therefore, we chose to fit independently the 3 different redshift bins with double power laws.
Then tracking the value of
,
where g(z) and f(z) describe the density and the luminosity evolution through
g(z)=(1+z)p and
f(z)=(1+z)q. The weakness of this parameterization is that it assumes a monotonic evolution of the LF preventing any turn-over in the evolution (e.g. an increase in density that would be followed by a decrease). This kind of turn-over has already been seen at other infrared wavelengths (e.g. Caputi et al. 2007).
Therefore, we chose to fit independently the 3 different redshift bins with double power laws.
Then tracking the value of
![]() and
and
![]() (see Sect. 3.1) as a function of redshift enabled us to constrain the evolution of the LF. We find that the variation of
(see Sect. 3.1) as a function of redshift enabled us to constrain the evolution of the LF. We find that the variation of
![]() with redshift is not large and starts with a small rise from
with redshift is not large and starts with a small rise from
![]() to
to
![]() followed by a small fall up to
followed by a small fall up to
![]() .
Hence the 15
.
Hence the 15 ![]() m LF appears to be rather consistent with the standard definition of a pure, monotonic, luminosity evolution in this redshift range, proportional to
m LF appears to be rather consistent with the standard definition of a pure, monotonic, luminosity evolution in this redshift range, proportional to
![]() .
We note that the variations in density or of
.
We note that the variations in density or of
![]() are small and of the same order than the difference in the galaxy number densities found between the GOODS and EGS fields in the faint end of the LF. Such small variations could well be produced by cosmic variance.
are small and of the same order than the difference in the galaxy number densities found between the GOODS and EGS fields in the faint end of the LF. Such small variations could well be produced by cosmic variance.
4 The rest-frame 35 microns luminosity functions
We now compute the rest-frame 35 ![]() m LF, based on 70
m LF, based on 70 ![]() m observations, to minimize k-correction in the z<1.2 range and hence reduce the dependency of the LF on the assumed SED library.
m observations, to minimize k-correction in the z<1.2 range and hence reduce the dependency of the LF on the assumed SED library.
Table 4: 35 microns k-correction of the sample.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f7.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg158.gif) |
Figure 7:
35 |
| Open with DEXTER | |
4.1 Methodology
In order to minimize k-correction uncertainties due to potentially evolving SED with redshift, we chose to derive the FIR LF at the closest rest-frame wavelength associated to the MIPS 70 ![]() m filter in the two most distant redshift bins (i.e. 0.7<z<1.0, 1.0<z<1.3), which translate into the rest-frame 30-40
m filter in the two most distant redshift bins (i.e. 0.7<z<1.0, 1.0<z<1.3), which translate into the rest-frame 30-40 ![]() m wavelength range. Therefore we chose to derive the rest-frame LF at 35 microns. In the lowest redshift bin (i.e. 0.4<z<0.7), the MIPS 70
m wavelength range. Therefore we chose to derive the rest-frame LF at 35 microns. In the lowest redshift bin (i.e. 0.4<z<0.7), the MIPS 70 ![]() m filter probes the rest-frame 40-50
m filter probes the rest-frame 40-50 ![]() m wavelength range where the k-correction is larger but local SEDs such as those used here were proved to be quite robust at these low redshifts (Bavouzet et al. 2008).
m wavelength range where the k-correction is larger but local SEDs such as those used here were proved to be quite robust at these low redshifts (Bavouzet et al. 2008).
As already discussed in this paper, the three different SED libraries give k-corrections which agree within 10% on average and up to 20% at most around
![]() (see Fig. 7 and Table 4). In the following we use the CE01 library and we will show in Sect. 4.2 that this is indeed the best one, among the three considered here, for our purpose.
(see Fig. 7 and Table 4). In the following we use the CE01 library and we will show in Sect. 4.2 that this is indeed the best one, among the three considered here, for our purpose.
The rest-frame 35 ![]() m LF was derived using the
m LF was derived using the
![]() method and the k-corrected 70
method and the k-corrected 70 ![]() m data. The completeness correction factors were derived using the simulations described in Sect. 2.2. The GOODS-S and N fields are treated jointly (flux limit
m data. The completeness correction factors were derived using the simulations described in Sect. 2.2. The GOODS-S and N fields are treated jointly (flux limit ![]() 2.5 mJy), the EGS and the ECDFS-O were treated separately (flux limit
2.5 mJy), the EGS and the ECDFS-O were treated separately (flux limit ![]() 3 mJy and
3 mJy and ![]() 3.5 mJy). As for the 15 microns LF, to take into account most of the uncertainties, we performed Monte Carlo simulations. For these Monte Carlo simulations the 35
3.5 mJy). As for the 15 microns LF, to take into account most of the uncertainties, we performed Monte Carlo simulations. For these Monte Carlo simulations the 35 ![]() m k-correction uncertainties were assumed to be of 0.08 dex. This conservative value was derived using the largest disagreement observed between the three SED libraries. Indeed, as shown in Fig. 7, we observe at
m k-correction uncertainties were assumed to be of 0.08 dex. This conservative value was derived using the largest disagreement observed between the three SED libraries. Indeed, as shown in Fig. 7, we observe at ![]() a disagreement of 0.08 dex between the LDP and DH libraries.
a disagreement of 0.08 dex between the LDP and DH libraries.
There is no direct local reference available in the literature for the 35 ![]() m LF. Therefore we constructed a local reference from the rest-frame 25 microns LF of Shupe et al. (1998) derived using the IRAS Faint Source Survey. Using a bivariate method and the CE01 library, we converted the 25 microns LF into a rest-frame 35 microns LF. As already mentioned, in the sake of consistency all along this study, we fitted this local reference and the three other LFs (corresponding to our three redshift bins) with double power laws with fixed slopes, i.e.
m LF. Therefore we constructed a local reference from the rest-frame 25 microns LF of Shupe et al. (1998) derived using the IRAS Faint Source Survey. Using a bivariate method and the CE01 library, we converted the 25 microns LF into a rest-frame 35 microns LF. As already mentioned, in the sake of consistency all along this study, we fitted this local reference and the three other LFs (corresponding to our three redshift bins) with double power laws with fixed slopes, i.e.
![]() for log(
for log(
![]() ) <
) <
![]() and
and
![]() for log(
for log(
![]() ) >
) >
![]() (see Table 5).
(see Table 5).
We have computed the rest-frame 35 ![]() m LF in two successive steps. As discussed above, we started with the same technique as for the rest-frame 15
m LF in two successive steps. As discussed above, we started with the same technique as for the rest-frame 15 ![]() m LF, using the catalog of sources detected at 70
m LF, using the catalog of sources detected at 70 ![]() m and correcting for incompleteness, k-correction and 1/Vmax. The results are presented in the Fig. 9 with filled stars for the EGS, GOODS (N and S) and ECDFS-O fields.
For each redshift bin, we fitted the rest-frame 35
m and correcting for incompleteness, k-correction and 1/Vmax. The results are presented in the Fig. 9 with filled stars for the EGS, GOODS (N and S) and ECDFS-O fields.
For each redshift bin, we fitted the rest-frame 35 ![]() m LF using the local double power law reference with fixed slopes. In Fig. 9 the light shaded areas represent the areas spanned by all the parametric solutions which are compatible within 1
m LF using the local double power law reference with fixed slopes. In Fig. 9 the light shaded areas represent the areas spanned by all the parametric solutions which are compatible within 1![]() with the rest-frame 35
with the rest-frame 35 ![]() m derived using the 70
m derived using the 70 ![]() m observations. Here again, we find that the bright end of the LF is well constrained and does not show any evidence for a change of slope. The regime that we were able to probe down to the 70
m observations. Here again, we find that the bright end of the LF is well constrained and does not show any evidence for a change of slope. The regime that we were able to probe down to the 70 ![]() m detection limit of 2 mJy corresponds to total IR luminosities of 0.7, 2 and 5
m detection limit of 2 mJy corresponds to total IR luminosities of 0.7, 2 and 5 ![]() 10
10
![]() computed from the CE01 library. Hence, apart from the upper redshift bin, this luminosity domain covers the full range of LIRGs and ULIRGs. This brings direct constraints, at these redshifts, to the relative contributions of LIRGs and ULIRGs to the comoving SFR density. Previous studies, based either on extrapolations from the mid-IR or on uncertain dust extinction corrections from the UV, were likely less robust than the derivation of a total IR luminosity from rest-frame 35
computed from the CE01 library. Hence, apart from the upper redshift bin, this luminosity domain covers the full range of LIRGs and ULIRGs. This brings direct constraints, at these redshifts, to the relative contributions of LIRGs and ULIRGs to the comoving SFR density. Previous studies, based either on extrapolations from the mid-IR or on uncertain dust extinction corrections from the UV, were likely less robust than the derivation of a total IR luminosity from rest-frame 35 ![]() m luminosities. In a second step, presented in the next section, we extend our derivation of the 35
m luminosities. In a second step, presented in the next section, we extend our derivation of the 35 ![]() m LF below its knee by using a stacking analysis.
m LF below its knee by using a stacking analysis.
Table 5:
Parameter values of the 15 ![]() ,
35
,
35 ![]() and total infrared LF
and total infrared LF
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{1443f8.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg190.gif) |
Figure 8:
The 70 vs. 24 |
| Open with DEXTER | |
4.2 Constraining the faint end 35 microns LF through stacking
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{1443f9.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg191.gif) |
Figure 9:
Rest-frame 35 microns LF estimated independently in three redshift bins with the
|
| Open with DEXTER | |
In order to stack positions of 35 ![]() m sources below the detection limit, it is necessary to adopt some prior positions. The 24
m sources below the detection limit, it is necessary to adopt some prior positions. The 24 ![]() m catalogs provide the best proxy for this purpose since the 24
m catalogs provide the best proxy for this purpose since the 24 ![]() m images are two orders of magnitudes deeper than the 35
m images are two orders of magnitudes deeper than the 35 ![]() m ones and the two wavelengths are the closest available. If the IR SED of galaxies of a given luminosity would not vary much since
m ones and the two wavelengths are the closest available. If the IR SED of galaxies of a given luminosity would not vary much since ![]() ,
we would expect a direct correlation between the 24
,
we would expect a direct correlation between the 24 ![]() m/(1+z) and 70
m/(1+z) and 70 ![]() m/(1+z) luminosities since local galaxies do follow tight correlations between their 6.75, 12, 15, 25, 60 and 100
m/(1+z) luminosities since local galaxies do follow tight correlations between their 6.75, 12, 15, 25, 60 and 100 ![]() m luminosities (see e.g. Chary & Elbaz 2001). We have tested the existence of such correlations both in the bright luminosity range where galaxies are detected at 24 and 70
m luminosities (see e.g. Chary & Elbaz 2001). We have tested the existence of such correlations both in the bright luminosity range where galaxies are detected at 24 and 70 ![]() m and in the lower luminosity range by stacking 70
m and in the lower luminosity range by stacking 70 ![]() m images on the positions of sources detected only at 24
m images on the positions of sources detected only at 24 ![]() m.
m.
We started by dividing the 24 ![]() m catalogs into three sub-samples, one for each redshift bin.
Then, we separated 24
m catalogs into three sub-samples, one for each redshift bin.
Then, we separated 24 ![]() m sources per luminosity bins of 0.4 dex. For each 24
m sources per luminosity bins of 0.4 dex. For each 24 ![]() m luminosity bin we stacked on the residual 70
m luminosity bin we stacked on the residual 70 ![]() m image all sources with no 70
m image all sources with no 70 ![]() m detection. The photometry of the stacked image was then measured using an aperture of 16
m detection. The photometry of the stacked image was then measured using an aperture of 16
![]() ,
a background within annuli of 40 and 60
,
a background within annuli of 40 and 60
![]() and an aperture correction factor of 1.705 (as discussed in the Spitzer observer's manual). Finally, the mean 70
and an aperture correction factor of 1.705 (as discussed in the Spitzer observer's manual). Finally, the mean 70 ![]() m flux density (
m flux density (
![]() )
for a given 24
)
for a given 24 ![]() m bin was computed following Eq. (3).
m bin was computed following Eq. (3).
where
Uncertainties of stacking values depend on the homogeneity of the underlying sample and on background fluctuations. To estimate the uncertainties related to the sample inhomogeneity (i.e.
![]() )
we perform a standard bootstrap analysis. To estimate the uncertainties due to background fluctuations (i.e.
)
we perform a standard bootstrap analysis. To estimate the uncertainties due to background fluctuations (i.e.
![]() )
we perform a stacking analysis at random positions using the same numbers of stacked elements. This stacking analysis at random positions is repeated 100 times and then
)
we perform a stacking analysis at random positions using the same numbers of stacked elements. This stacking analysis at random positions is repeated 100 times and then
![]() is given by the dispersion of these stacking fluxes. Finally the total uncertainty is defined as the quadratic sum of
is given by the dispersion of these stacking fluxes. Finally the total uncertainty is defined as the quadratic sum of
![]() and
and
![]() .
These uncertainties are shown in Fig. 8.
.
These uncertainties are shown in Fig. 8.
The first result that we find here is that in both regimes - i.e. where sources are strong enough to be detected at both wavelengths and where sources are only seen at 24 ![]() m - the two luminosities in the rest-frame wavelengths 24
m - the two luminosities in the rest-frame wavelengths 24 ![]() m/(1+z) and 70
m/(1+z) and 70 ![]() m/(1+z) do follow a correlation. This correlation is in agreement with the CE01 library but is a factor of two below predictions from the LDP and DH libraries. This correlation being found in the three redshift bins it confirms that one can complement the 70
m/(1+z) do follow a correlation. This correlation is in agreement with the CE01 library but is a factor of two below predictions from the LDP and DH libraries. This correlation being found in the three redshift bins it confirms that one can complement the 70 ![]() m LF at the faint end based on 24
m LF at the faint end based on 24 ![]() m detections.
Therefore using the inferred 24/70
m detections.
Therefore using the inferred 24/70 ![]() m correlation (red line in Fig. 8) we have derived the 70
m correlation (red line in Fig. 8) we have derived the 70 ![]() m luminosity of each source starting from their 24
m luminosity of each source starting from their 24 ![]() m flux density and then produced the full 35
m flux density and then produced the full 35 ![]() m LFs. These LFs are represented with filled squares in Fig. 9. Using the local double power law reference with fixed slopes, we then fitted these rest-frame 35
m LFs. These LFs are represented with filled squares in Fig. 9. Using the local double power law reference with fixed slopes, we then fitted these rest-frame 35 ![]() m LFs and all solutions of this fit compatible, within 1
m LFs and all solutions of this fit compatible, within 1![]() ,
with the data are presented as the dark shaded area of Fig. 9. As revealed by the overlapping of the light and dark shaded areas, the resulting 35
,
with the data are presented as the dark shaded area of Fig. 9. As revealed by the overlapping of the light and dark shaded areas, the resulting 35 ![]() m LF are fully consistent with the ones based on direct 70
m LF are fully consistent with the ones based on direct 70 ![]() m detections and extend them far below the knee of the LF.
m detections and extend them far below the knee of the LF.
4.3 Results
We used the combination of direct 70 ![]() m detections and 24
m detections and 24 ![]() m-derived luminosities, converted into 35
m-derived luminosities, converted into 35 ![]() m luminosities from stacked 70
m luminosities from stacked 70 ![]() m images, to derive 35
m images, to derive 35 ![]() m LF over more than two orders of magnitude, allowing us to position the knee of the LF in all three redshift bins (see Fig. 9). The data do not show any obvious sign for a change of slope of the LF both at the faint and bright ends, from
m LF over more than two orders of magnitude, allowing us to position the knee of the LF in all three redshift bins (see Fig. 9). The data do not show any obvious sign for a change of slope of the LF both at the faint and bright ends, from ![]() to 1.3. This confirms that our choice to keep the same double power-law slopes than the ones used locally is pertinent. Like for the 15
to 1.3. This confirms that our choice to keep the same double power-law slopes than the ones used locally is pertinent. Like for the 15 ![]() m LF, we only find marginal evidence for a variation of
m LF, we only find marginal evidence for a variation of
![]() with redshift, while
with redshift, while
![]() follows a rapid evolution proportional to
follows a rapid evolution proportional to
![]() law from
law from
![]() to
to
![]() ,
consistent with pure luminosity evolution. The flat slope of the bright end of the LF, typical of the IR LF, and its rapid evolution with redshift clearly illustrates the rising power of luminous galaxies over less luminous ones when going to higher redshifts. In the following section, we discuss the implications of the redshift evolution of the 35
,
consistent with pure luminosity evolution. The flat slope of the bright end of the LF, typical of the IR LF, and its rapid evolution with redshift clearly illustrates the rising power of luminous galaxies over less luminous ones when going to higher redshifts. In the following section, we discuss the implications of the redshift evolution of the 35 ![]() m LF on the total IR LF.
m LF on the total IR LF.
5 Total infrared luminosity function
In this section, we use the best proxy to compute the total IR luminosity of galaxies (
![]() ), i.e. the observed 70
), i.e. the observed 70 ![]() m data when available or else the 24
m data when available or else the 24 ![]() m data.
m data.
![]() is computed over the wavelength range 8-1000
is computed over the wavelength range 8-1000 ![]() m. Under this definition, the SFR and
m. Under this definition, the SFR and
![]() are related by Eq. (4) (Kennicutt 1998) for a Salpeter IMF (
are related by Eq. (4) (Kennicutt 1998) for a Salpeter IMF (![]()
![]() m-2.35, between 0.1-100
m-2.35, between 0.1-100 ![]() ). Note that we integrate the SED curve to derive
). Note that we integrate the SED curve to derive
![]() instead of using the classical approximation using the four IRAS broadband filters as defined in Sanders & Mirabel (1996).
instead of using the classical approximation using the four IRAS broadband filters as defined in Sanders & Mirabel (1996).
Up to a redshift of
5.1 Luminosity function
The total infrared luminosity function is derived using the
![]() method and the completeness correction factor derived from our simulations. The two GOODS fields were combined and then the EGS, ECDFS-O and GOODS fields were treated separately. Error bars were derived using Monte Carlo simulations to take into account most of the uncertainties. For these Monte Carlo simulations the total infrared k-correction uncertainties were assumed to be of 0.11 dex.
method and the completeness correction factor derived from our simulations. The two GOODS fields were combined and then the EGS, ECDFS-O and GOODS fields were treated separately. Error bars were derived using Monte Carlo simulations to take into account most of the uncertainties. For these Monte Carlo simulations the total infrared k-correction uncertainties were assumed to be of 0.11 dex.
We use as a local reference for the total IR LF, the Sanders et al. (2003) LF derived from the analytical fit to the IRAS Revised Bright Galaxy Sample, i.e.
![]() for log(
for log(
![]() ) <
) <
![]() and
and
![]() for log(
for log(
![]() ) >
) >
![]() with
with
![]() ) = 10.5 (
) = 10.5 (![]() ).
).
As for the rest-frame 35 ![]() m LF, we use the observed 24
m LF, we use the observed 24 ![]() m to constrain the faint end slope of the LF. For each source we first derived its 70
m to constrain the faint end slope of the LF. For each source we first derived its 70 ![]() m flux density using the 24-70
m flux density using the 24-70 ![]() m correlations that we obtained from our stacking analysis (see Sect. 4.2).
Then, as for direct 70
m correlations that we obtained from our stacking analysis (see Sect. 4.2).
Then, as for direct 70 ![]() m detections, we used the CE01 SEDs to derive
m detections, we used the CE01 SEDs to derive
![]() from the 70
from the 70 ![]() m flux density.
m flux density.
We separate the values of the LF derived from observed 70 ![]() m (stars) and stacked 70
m (stars) and stacked 70 ![]() m (squares) in the resulting total IR LF (Fig. 11). Using the Sanders et al. (2003) local reference with fixed slopes we fit independently the total infrared LF derived using direct 70
m (squares) in the resulting total IR LF (Fig. 11). Using the Sanders et al. (2003) local reference with fixed slopes we fit independently the total infrared LF derived using direct 70 ![]() m observations (light shaded area) and the one derived using the stacking analysis (dark shaded area). We note that direct 70
m observations (light shaded area) and the one derived using the stacking analysis (dark shaded area). We note that direct 70 ![]() m observations allow us to sharply constrain the evolution of LIRGs and ULIRGs up to
m observations allow us to sharply constrain the evolution of LIRGs and ULIRGs up to
![]() but fail to constrain the knee of the total IR LF which requires to rely on stacking (see light shaded area). In the regime where direct 70
but fail to constrain the knee of the total IR LF which requires to rely on stacking (see light shaded area). In the regime where direct 70 ![]() m data is available, we find that the two techniques (starting from either 24
m data is available, we find that the two techniques (starting from either 24 ![]() m + stacking or 70
m + stacking or 70 ![]() m) provide consistent bright sides of the LF. The resulting parametric fits (using the parametric form of the local reference at all redshifts) are summarized in Table 5.
m) provide consistent bright sides of the LF. The resulting parametric fits (using the parametric form of the local reference at all redshifts) are summarized in Table 5.
The total IR LF is found to exhibit a rapid evolution with redshift (Fig. 11) nearly consistent with a pure luminosity evolution proportional to
![]() from
from
![]() to
to
![]() .
Marginal evidence for a decrease of
.
Marginal evidence for a decrease of
![]() is found proportional to
is found proportional to
![]() when fitting all fields, but staying consistent with a flat behavior when accounting for cosmic variance (see Fig. 11).
when fitting all fields, but staying consistent with a flat behavior when accounting for cosmic variance (see Fig. 11).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1443f10.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg208.gif) |
Figure 10:
The k-correction between the observed 24 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{1443f11.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg209.gif) |
Figure 11:
Total infrared LF estimated for three redshift bins with the
|
| Open with DEXTER | |
Table 6: Parameters leading the total infrared LF evolution.
Such decrease of
![]() was also found by previous studies such as Pérez-González et al. (2005) for the rest-frame 12
was also found by previous studies such as Pérez-González et al. (2005) for the rest-frame 12 ![]() m LF and Caputi et al. (2007) for the rest-frame 8
m LF and Caputi et al. (2007) for the rest-frame 8 ![]() m and the total infrared LF. Nevertheless this decrease has to be taken with caution since incompleteness in the faint luminosity bins could mimic this evolution (Pérez-González et al. 2005).
m and the total infrared LF. Nevertheless this decrease has to be taken with caution since incompleteness in the faint luminosity bins could mimic this evolution (Pérez-González et al. 2005).
Finally, we also notice that the redshift evolution of the rest-frame 35 ![]() m and total IR LF are in agreement, i.e. a pure luminosity evolution proportional to
m and total IR LF are in agreement, i.e. a pure luminosity evolution proportional to
![]() and
and
![]() for the rest-frame 35
for the rest-frame 35 ![]() m and total IR LF respectively. This consistency arises from the quasi-linearity between L35 and
m and total IR LF respectively. This consistency arises from the quasi-linearity between L35 and
![]() .
.
5.2 Comparison with previous work
As revealed in Table 6 the global evolution of the total infrared LF inferred in this study is broadly consistent with previous studies (Huynh et al. 2007; Le Floc'h et al. 2005; Caputi et al. 2007). However slight differences appear between in the LIRG and ULIRG regimes. In Fig. 11 we compare the LF inferred in our study with the work of Le Floc'h et al. (2005) and Huynh et al. (2007).
We notice that the LF inferred by Le Floc'h et al. (2005) is consistent with our values at low luminosities. However, above log
![]() > 11.5, Le Floc'h et al. (2005) obtained higher values, with a discrepancy increasing with luminosity. These differences, which affect the relative contributions of LIRGs and ULIRGs to the total infrared luminosity density, might be explained by the fact that we removed AGNs from our catalogs while Le Floc'h et al. (2005) did not.
However we checked that keeping AGNs to derive the total infrared LF only reduces part of the discrepancy. Hence the main explanation of these differences is the method used to convert monochromatic luminosities into total infrared luminosities. Le Floc'h et al. (2005) used a combination of SED libraries to derive the total infrared luminosity from 24
> 11.5, Le Floc'h et al. (2005) obtained higher values, with a discrepancy increasing with luminosity. These differences, which affect the relative contributions of LIRGs and ULIRGs to the total infrared luminosity density, might be explained by the fact that we removed AGNs from our catalogs while Le Floc'h et al. (2005) did not.
However we checked that keeping AGNs to derive the total infrared LF only reduces part of the discrepancy. Hence the main explanation of these differences is the method used to convert monochromatic luminosities into total infrared luminosities. Le Floc'h et al. (2005) used a combination of SED libraries to derive the total infrared luminosity from 24 ![]() m observations while we used the CE01 library and either direct or stacked 70
m observations while we used the CE01 library and either direct or stacked 70 ![]() m observations for the bright and faint end slopes of the LF, respectively. The latter should provide more robust estimates of
m observations for the bright and faint end slopes of the LF, respectively. The latter should provide more robust estimates of
![]() since the rest-frame 35
since the rest-frame 35 ![]() m luminosity is produced by similar carriers as the rest-frame 24
m luminosity is produced by similar carriers as the rest-frame 24 ![]() m one which was proven to be a robust SFR indicator by Calzetti et al. (2007).
m one which was proven to be a robust SFR indicator by Calzetti et al. (2007).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f12.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg225.gif) |
Figure 12:
Total infrared LF estimated at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f13.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg229.gif) |
Figure 13:
Evolution of the comoving number density up to
|
| Open with DEXTER | |
We notice in Fig. 11 that our LF is, within the error bars, in agreement with Huynh et al. (2007). Nevertheless we also notice that at low luminosities, their values are slightly lower than ours. We interpret this discrepancy as a difference in the treatment of incompleteness. Our multi-wavelengths catalogs being computed with a new extraction technique based on prior positions, we are able to extract blended sources and hence reduce incompleteness corrections. We conclude that at low luminosities the LFs measured in this study should be more robust than the ones derived by Huynh et al. (2007).
The total IR LF derived here is noticeably different from the one previously obtained by Caputi et al. (2007) at
![]() (see Fig. 12) who used 24
(see Fig. 12) who used 24 ![]() m images in the CDFS. There are two possible explanations for this difference: it could either result from cosmic variance or from the method that they used to derive
m images in the CDFS. There are two possible explanations for this difference: it could either result from cosmic variance or from the method that they used to derive
![]() and which does not take into account 70
and which does not take into account 70 ![]() m observations as in our study. To exclude the first possibility, we computed the total IR LF from our EGS 24
m observations as in our study. To exclude the first possibility, we computed the total IR LF from our EGS 24 ![]() m catalog. Depending on the SED library that we used, we either find an IR LF overlapping ours (using the CE01 SEDs) or matching the Caputi et al. (2007) one (using the
m catalog. Depending on the SED library that we used, we either find an IR LF overlapping ours (using the CE01 SEDs) or matching the Caputi et al. (2007) one (using the
![]() correlation of Bavouzet et al. 2008; as in Caputi et al. 2007). This shows that the difference between the two studies does not come from cosmic variance but rather from the choice of the SED library. As we showed earlier, the CE01 SED turned out to fit better the 24 versus 70
correlation of Bavouzet et al. 2008; as in Caputi et al. 2007). This shows that the difference between the two studies does not come from cosmic variance but rather from the choice of the SED library. As we showed earlier, the CE01 SED turned out to fit better the 24 versus 70 ![]() m correlation down to the faintest luminosities using stacking. Since the 70
m correlation down to the faintest luminosities using stacking. Since the 70 ![]() m band provides a more accurate estimate of the total infrared luminosity than the 24
m band provides a more accurate estimate of the total infrared luminosity than the 24 ![]() m one and since the LDP library does not reproduce the observed 24-70
m one and since the LDP library does not reproduce the observed 24-70 ![]() m correlation at
m correlation at ![]() (see Fig. 8), we conclude that our inferred LFs should be more robust.
(see Fig. 8), we conclude that our inferred LFs should be more robust.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{1443f14.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg235.gif) |
Figure 14:
Evolution of the comoving IR energy density up to
|
| Open with DEXTER | |
6 Discussion
The redshift evolution of the comoving number density of LIRGs and ULIRGs is derived by integrating the infrared LF in each redshift bin, 0.4<z<0.7, 0.7<z<1.0 and 1.0<z<1.3. The number density of LIRGs and ULIRGs appear to be 40 and 100 times larger at
![]() than in the local Universe, respectively (see Fig. 13). Hence we confirm the rapid evolution of these extremely luminous dusty galaxies over the last 8 billion years. The evolution is at a slightly more moderate pace than previous studies since Le Floc'h et al. (2005) and Chary & Elbaz (2001) found a factor 70 for LIRGs. This correction towards a larger contribution of the remaining lower luminosity galaxies, that we name here ``normal'' galaxies, comes from the faint part of the LF that we were able to constrain through our stacking analysis. It must be noted that at the highest redshifts, we are only sensitive to the LIRG and ULIRG population. Thus the extrapolation to fainter luminosities (illustrated by the green filled circles in Fig. 13) assumes the same faint end slope for the LF seen at lower redshifts and could be uncertain. Finally, we note that the number density of ULIRGs at
than in the local Universe, respectively (see Fig. 13). Hence we confirm the rapid evolution of these extremely luminous dusty galaxies over the last 8 billion years. The evolution is at a slightly more moderate pace than previous studies since Le Floc'h et al. (2005) and Chary & Elbaz (2001) found a factor 70 for LIRGs. This correction towards a larger contribution of the remaining lower luminosity galaxies, that we name here ``normal'' galaxies, comes from the faint part of the LF that we were able to constrain through our stacking analysis. It must be noted that at the highest redshifts, we are only sensitive to the LIRG and ULIRG population. Thus the extrapolation to fainter luminosities (illustrated by the green filled circles in Fig. 13) assumes the same faint end slope for the LF seen at lower redshifts and could be uncertain. Finally, we note that the number density of ULIRGs at
![]() is nearly equal to that of LIRGs at
is nearly equal to that of LIRGs at
![]() .
In order to detect 10 ULIRGs at
.
In order to detect 10 ULIRGs at ![]()
![]() 0.2 (892 Mpc3/arcmin2), one would need to cover more than 3 GOODS fields.
0.2 (892 Mpc3/arcmin2), one would need to cover more than 3 GOODS fields.
In Fig. 14, we compare the comoving IR luminosity density (or equivalently SFR density due to obscured star formation, using Eq. (4)) produced by normal galaxies, LIRGs and ULIRGs to that obtained by Le Floc'h et al. (2005). Note that X-ray AGN have already been removed from the LF.
We also notice that at
![]() values quoted in Le Floc'h et al. (2005) need to be corrected by a factor 2.5 (empty triangles of Fig. 14). The total infrared LF taken as their local reference was derived in Sanders et al. (2003) by bins of magnitude but used in Le Floc'h et al. (2005) as if it was derived by bins of luminosity. This error does not change the LFs derived at higher redshift by Le Floc'h et al. (2005) but could have affected their estimates of
values quoted in Le Floc'h et al. (2005) need to be corrected by a factor 2.5 (empty triangles of Fig. 14). The total infrared LF taken as their local reference was derived in Sanders et al. (2003) by bins of magnitude but used in Le Floc'h et al. (2005) as if it was derived by bins of luminosity. This error does not change the LFs derived at higher redshift by Le Floc'h et al. (2005) but could have affected their estimates of
![]() and
and
![]() and hence their estimates of the evolution of the infrared luminosity density. The discrepancy found between the
and hence their estimates of the evolution of the infrared luminosity density. The discrepancy found between the
![]() derived in this study and the one derived in Le Floc'h et al. (2005) can be partly due to this error since starting from an erroneous local LF would yield to an overestimate of
derived in this study and the one derived in Le Floc'h et al. (2005) can be partly due to this error since starting from an erroneous local LF would yield to an overestimate of
![]() .
.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{1443f15.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg238.gif) |
Figure 15:
Evolution of the comoving star formation rate density up to
|
| Open with DEXTER | |
As observed in Fig. 14 we confirm the transition between a regime dominated by normal galaxies at low redshift and by LIRGs at high redshift. The transition occurred at
![]() compared to
compared to
![]() derived by Le Floc'h et al. (2005). While LIRGs and ULIRGs altogether produce less than 2
derived by Le Floc'h et al. (2005). While LIRGs and ULIRGs altogether produce less than 2![]() of the present-day bolometric luminosity density of galaxies, they produced half of it 8 billion years ago. Indeed, the contribution of unobscured UV light to the comoving SFR density was lower than that of LIRGs/ULIRGs by a factor of about
of the present-day bolometric luminosity density of galaxies, they produced half of it 8 billion years ago. Indeed, the contribution of unobscured UV light to the comoving SFR density was lower than that of LIRGs/ULIRGs by a factor of about ![]() 3 (see Fig. 15). Although the luminosity density of ULIRGs was much larger at
3 (see Fig. 15). Although the luminosity density of ULIRGs was much larger at
![]() than today, their contribution to the total IR energy density was still rather low (i.e.
than today, their contribution to the total IR energy density was still rather low (i.e. ![]()
![]() ). We find it to be lower than Le Floc'h et al. (2005) by a factor of
). We find it to be lower than Le Floc'h et al. (2005) by a factor of ![]() 2 which may partly be explained by the fact that unlike Le Floc'h et al. (2005) we have removed the contribution of X-ray AGN which becomes large among ULIRGs. Furthermore, by using the observed 70
2 which may partly be explained by the fact that unlike Le Floc'h et al. (2005) we have removed the contribution of X-ray AGN which becomes large among ULIRGs. Furthermore, by using the observed 70 ![]() m data instead of extrapolating from 24
m data instead of extrapolating from 24 ![]() m, we have reduced the uncertainty in the estimates of the bolometric luminosity.
m, we have reduced the uncertainty in the estimates of the bolometric luminosity.
In order to get a complete census on the SFR history we need to take into account the contribution of unobscured UV light. The unobscured SFR density (dot line in Fig. 15) is taken from a GALEX study (Schiminovich et al. 2005) which yield an evolution following a
(1+z)2.5 law and a local star formation density of
![]() (
(![]() ) = 4
) = 4 ![]() 10-3
10-3
![]() .
The total SFR density (dashed line in Fig. 15) was then defined as the sum of the unobscured SFR density traced by the direct UV light and the dusty SFR density traced by the infrared emission. We find that the relative contribution of unobscured UV light to the cosmic SFR density evolves nearly in parallel with the total one and accounts for
.
The total SFR density (dashed line in Fig. 15) was then defined as the sum of the unobscured SFR density traced by the direct UV light and the dusty SFR density traced by the infrared emission. We find that the relative contribution of unobscured UV light to the cosmic SFR density evolves nearly in parallel with the total one and accounts for ![]() 20% of the local SFR density and
20% of the local SFR density and ![]() 20% of the
20% of the
![]() (
(![]() ) = 0.15
) = 0.15
![]() .
Globally, the cosmic star-formation history that we derived using data at 24 and 70
.
Globally, the cosmic star-formation history that we derived using data at 24 and 70 ![]() m is consistent with the combination of indicators, either unobscured or corrected for dust extinction, as compiled by Hopkins & Beacom (2006). We also notice a very good agreement between the cosmic star-formation history derived in our work and the ones derived by Seymour et al. (2008) and Smolcic et al. (2009) using deep radio observations. Especially, it is very encouraging to see that the star formation history for ULIRGs obtained using deep radio data is in very good agreement with our independent measurements.
m is consistent with the combination of indicators, either unobscured or corrected for dust extinction, as compiled by Hopkins & Beacom (2006). We also notice a very good agreement between the cosmic star-formation history derived in our work and the ones derived by Seymour et al. (2008) and Smolcic et al. (2009) using deep radio observations. Especially, it is very encouraging to see that the star formation history for ULIRGs obtained using deep radio data is in very good agreement with our independent measurements.
7 Conclusion
We make use of the deep 24 ![]() m and 70
m and 70 ![]() m surveys in the Great Observatories Origins Deep Survey (GOODS) and Extended Groth Strip (EGS) fields to characterize the evolution of the comoving star-formation rate density at 0.4<z<1.3 which corresponds to 2/3 of cosmic time.
The data span a total area of
m surveys in the Great Observatories Origins Deep Survey (GOODS) and Extended Groth Strip (EGS) fields to characterize the evolution of the comoving star-formation rate density at 0.4<z<1.3 which corresponds to 2/3 of cosmic time.
The data span a total area of ![]() 800 arcmin2 and a comoving volume of 1.4
800 arcmin2 and a comoving volume of 1.4 ![]() 106 Mpc3. Thanks to the wealth of multiwavelength data,
106 Mpc3. Thanks to the wealth of multiwavelength data, ![]() 80% of the sources are associated with either a photometric or spectroscopic redshift.
80% of the sources are associated with either a photometric or spectroscopic redshift.
The exquisite depth of the data results in a high surface density of sources. In order to alleviate the effects of confusion, we have developed a technique which uses the prior positional information of sources at shorter wavelengths to extract the flux density of sources at 24 ![]() m and 70
m and 70 ![]() m. We have undertaken extensive simulations to quantify flux errors and biases which might be associated with this technique. The relative depth of the 24 and 70
m. We have undertaken extensive simulations to quantify flux errors and biases which might be associated with this technique. The relative depth of the 24 and 70 ![]() m survey results in only 7% of 24
m survey results in only 7% of 24 ![]() m sources being detected at 70
m sources being detected at 70 ![]() m.
m.
By associating the redshifts with the sources in the mid- and far-infrared catalogs, we are able to measure the rest-frame 15 ![]() m and 35
m and 35 ![]() m luminosities of galaxies out to
m luminosities of galaxies out to ![]() .
We use a stacking procedure to measure the evolution of the 24 to 70
.
We use a stacking procedure to measure the evolution of the 24 to 70 ![]() m luminosity ratio for sources which are undetected at 70
m luminosity ratio for sources which are undetected at 70 ![]() m. We find that the average observed 24
m. We find that the average observed 24 ![]() m and 70
m and 70 ![]() m properties of both the detected and stacked sources are in excellent agreement with correlations derived from local galaxy samples. However, the 24/70 micron flux ratios of individual galaxies do show a significant scatter of 0.2 dex.
m properties of both the detected and stacked sources are in excellent agreement with correlations derived from local galaxy samples. However, the 24/70 micron flux ratios of individual galaxies do show a significant scatter of 0.2 dex.
By complementing the direct detections with the stacking analysis, we are able to measure a 15 ![]() m, 35
m, 35 ![]() m and total infrared luminosity function for star forming galaxies between 0.4<z<1.3. We measure both the bright end and faint end slope of the luminosity functions, which span a factor of
m and total infrared luminosity function for star forming galaxies between 0.4<z<1.3. We measure both the bright end and faint end slope of the luminosity functions, which span a factor of ![]() 100 in luminosity (
100 in luminosity (
![]() ), a substantial improvement over previous works. We find no evidence for a change in slope of the double power-law used to characterize the local IR LF of galaxies. However, we confirm the strong evolution in the number density of infrared luminous galaxies between 0<z<1.
), a substantial improvement over previous works. We find no evidence for a change in slope of the double power-law used to characterize the local IR LF of galaxies. However, we confirm the strong evolution in the number density of infrared luminous galaxies between 0<z<1.
LIRGs and ULIRGs evolve at about the same rate over this redshift, having increased by a factor of ![]() 40 and
40 and ![]() 100 in number density, respectively. LIRGs contribute about
100 in number density, respectively. LIRGs contribute about ![]() 50% to the comoving star-formation rate density at
50% to the comoving star-formation rate density at ![]() ,
comparable to the contribution of lower luminosity star-forming galaxies. The infrared luminosity density is a factor of five higher than the UV luminosity density at
,
comparable to the contribution of lower luminosity star-forming galaxies. The infrared luminosity density is a factor of five higher than the UV luminosity density at ![]() confirming that the bulk of the star-formation is dust obscured.
confirming that the bulk of the star-formation is dust obscured.
Acknowledgements
This work is based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by NASA through an award issued by JPL/Caltech. This paper makes use of photometric redshifts produced jointly by Terapix and VVDS teams. Funding for the DEEP2 survey has been provided by NSF grants AST95-09298, AST-0071048, AST-0071198, AST-0507428, and AST-0507483 as well as NASA LTSA grant NNG04GC89G. Some of the data presented herein were obtained at the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation. The DEEP2 team and Keck Observatory acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community and appreciate the opportunity to conduct observations from this mountain. D. Le Borgne and D. Elbaz wish to thank the Centre National d'Etudes Spatiales (CNES) for their support.
References
- Alexander, D. M., Bauer, F. E., Brandt, W. N., et al. 2003, AJ, 125, 383 [NASA ADS] [CrossRef] (In the text)
- Appleton, P. N., Fadda, D. T., Marleau, F. R., et al. 2004, ApJS, 154, 147 [NASA ADS] [CrossRef] (In the text)
- Aussel, H., Cesarsky, C. J., Elbaz, D., & Starck, J. L. 1999, A&A, 342, 313 [NASA ADS]
- Barmby, P., Huang, J., Ashby, M. L. N., et al. 2008, ArXiv e-prints, 803 (In the text)
- Bauer, F. E., Alexander, D. M., Brandt, W. N., et al. 2004, AJ, 128, 2048 [NASA ADS] [CrossRef] (In the text)
- Bavouzet, N., Dole, H., Le Floc'h, E., et al. 2008, A&A, 479, 83 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [NASA ADS] [CrossRef] (In the text)
- Caputi, K. I., Lagache, G., Yan, L., et al. 2007, ApJ, 660, 97 [NASA ADS] [CrossRef] (In the text)
- Chary, R., & Elbaz, D. 2001, ApJ, 556, 562 [NASA ADS] [CrossRef]
- Chary, R., Casertano, S., Dickinson, M. E., et al. 2004, ApJS, 154, 80 [NASA ADS] [CrossRef] (In the text)
- Cohen, J. G., Hogg, D. W., Blandford, R., et al. 2000, ApJ, 538, 29 [NASA ADS] [CrossRef]
- Cowie, L. L., Barger, A. J., Hu, E. M., Capak, P., & Songaila, A. 2004, AJ, 127, 3137 [NASA ADS] [CrossRef]
- Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef]
- Dale, D. A., Bendo, G. J., Engelbracht, C. W., et al. 2005, ApJ, 633, 857 [NASA ADS] [CrossRef]
- Davis, M., Guhathakurta, P., Konidaris, N. P., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] (In the text)
- Elbaz, D., Cesarsky, C. J., Fadda, D., et al. 1999, A&A, 351, L37 [NASA ADS]
- Elbaz, D., Cesarsky, C. J., Chanial, P., et al. 2002, A&A, 384, 848 [NASA ADS] [CrossRef] [EDP Sciences]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Fadda, D., Flores, H., Hasinger, G., et al. 2002, A&A, 383, 838 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Franceschini, A., Aussel, H., Cesarsky, C. J., Elbaz, D., & Fadda, D. 2001, A&A, 378, 1 [NASA ADS] [CrossRef] [EDP Sciences]
- Frayer, D. T., Fadda, D., Yan, L., et al. 2006a, AJ, 131, 250 [NASA ADS] [CrossRef] (In the text)
- Frayer, D. T., Huynh, M. T., Chary, R., et al. 2006b, ApJ, 647, L9 [NASA ADS] [CrossRef] (In the text)
- Gawiser, E., van Dokkum, P. G., Herrera, D., et al. 2006, ApJS, 162, 1 [NASA ADS] [CrossRef] (In the text)
- Hopkins, A. M. 2004, ApJ, 615, 209 [NASA ADS] [CrossRef]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] (In the text)
- Huynh, M. T., Frayer, D. T., Mobasher, B., et al. 2007, ApJ, 667, L9 [NASA ADS] [CrossRef] (In the text)
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lagache, G., Dole, H., & Puget, J.-L. 2003, MNRAS, 338, 555 [NASA ADS] [CrossRef]
- Lagache, G., Dole, H., Puget, J.-L., et al. 2004, ApJS, 154, 112 [NASA ADS] [CrossRef]
- Laird, E. S., Nandra, K., Georgakakis, A., et al. 2008, ArXiv e-prints (In the text)
- Le Borgne, D., & Rocca-Volmerange, B. 2002, A&A, 386, 446 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Le Fèvre, O., Vettolani, G., Paltani, S., et al. 2004, A&A, 428, 1043 [NASA ADS] [CrossRef] [EDP Sciences]
- Le Floc'h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef]
- Lehmer, B. D., Brandt, W. N., Alexander, D. M., et al. 2005, ApJS, 161, 21 [NASA ADS] [CrossRef] (In the text)
- Madau, P., Haardt, F., & Rees, M. J. 1999, ApJ, 514, 648 [NASA ADS] [CrossRef] (In the text)
- Marcillac, D., Elbaz, D., Charlot, S., et al. 2006, A&A, 458, 369 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Metcalfe, L., Kneib, J.-P., McBreen, B., et al. 2003, A&A, 407, 791 [NASA ADS] [CrossRef] [EDP Sciences]
- Mignoli, M., Cimatti, A., Zamorani, G., et al. 2005, A&A, 437, 883 [NASA ADS] [CrossRef] [EDP Sciences]
- Nandra, K., Laird, E. S., Adelberger, K., et al. 2005, MNRAS, 356, 568 [NASA ADS] [CrossRef]
- Papovich, C., Dole, H., Egami, E., et al. 2004, ApJS, 154, 70 [NASA ADS] [CrossRef]
- Papovich, C., Rudnick, G., Le Floc'h, E., et al. 2007, ApJ, 668, 45 [NASA ADS] [CrossRef] (In the text)
- Pérez-González, P. G., Rieke, G. H., Egami, E., et al. 2005, ApJ, 630, 82 [NASA ADS] [CrossRef] (In the text)
- Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] (In the text)
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] (In the text)
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [NASA ADS] [CrossRef] (In the text)
- Schiminovich, D., Ilbert, O., Arnouts, S., et al. 2005, ApJ, 619, L47 [NASA ADS] [CrossRef] (In the text)
- Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] (In the text)
- Seymour, N., Dwelly, T., Moss, D., et al. 2008, MNRAS, 386, 1695 [NASA ADS] [CrossRef] (In the text)
- Shupe, D. L., Fang, F., Hacking, P. B., & Huchra, J. P. 1998, ApJ, 501, 597 [NASA ADS] [CrossRef] (In the text)
- Smolcic, V., Schinnerer, E., Zamorani, G., et al. 2009, ApJ, 690, 610 [NASA ADS] [CrossRef] (In the text)
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef]
- Trenti, M., & Stiavelli, M. 2008, ApJ, 676, 767 [NASA ADS] [CrossRef] (In the text)
- Vanzella, E., Cristiani, S., Dickinson, M., et al. 2006, A&A, 454, 423 [NASA ADS] [CrossRef] [EDP Sciences]
- Wirth, G. D., Willmer, C. N. A., Amico, P., et al. 2004, AJ, 127, 3121 [NASA ADS] [CrossRef]
- Wolf, C., Meisenheimer, K., Kleinheinrich, M., et al. 2004, A&A, 421, 913 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Xu, C. 2000, ApJ, 541, 134 [NASA ADS] [CrossRef]
- Xu, C., Lonsdale, C. J., Shupe, D. L., O'Linger, J., & Masci, F. 2001, ApJ, 562, 179 [NASA ADS] [CrossRef]
All Tables
Table 1: Catalog properties.
Table 2: Redshift catalog properties.
Table 3: 15 microns k-correction of the sample.
Table 4: 35 microns k-correction of the sample.
Table 5:
Parameter values of the 15 ![]() ,
35
,
35 ![]() and total infrared LF
and total infrared LF
Table 6: Parameters leading the total infrared LF evolution.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1443f1a.eps}\hspace*{3mm}
\includegraphics[width=8.8cm,clip]{1443f1b.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg65.gif) |
Figure 1:
Photometric accuracy, [S(out) - S(in)]/S(out), derived from the simulation as a function of measured flux density, S(out), for the GOODS-N 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f2.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg112.gif) |
Figure 2:
Comparison between photometric and spectroscopic redshift for 2406 galaxies of our 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1443f3a.eps}\vspace*{5mm}
\i...
...f3b.eps}\vspace*{5mm}
\includegraphics[width=8cm,clip]{1443f3c.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg113.gif) |
Figure 3:
Fraction of 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f4.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg116.gif) |
Figure 4:
Redshift distributions of 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f5.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg130.gif) |
Figure 5:
15 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{1443f6.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg148.gif) |
Figure 6:
Rest-frame 15 microns LF estimated for three redshift bins with the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f7.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg158.gif) |
Figure 7:
35 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{1443f8.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg190.gif) |
Figure 8:
The 70 vs. 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{1443f9.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg191.gif) |
Figure 9:
Rest-frame 35 microns LF estimated independently in three redshift bins with the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1443f10.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg208.gif) |
Figure 10:
The k-correction between the observed 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{1443f11.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg209.gif) |
Figure 11:
Total infrared LF estimated for three redshift bins with the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f12.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg225.gif) |
Figure 12:
Total infrared LF estimated at
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1443f13.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg229.gif) |
Figure 13:
Evolution of the comoving number density up to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{1443f14.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg235.gif) |
Figure 14:
Evolution of the comoving IR energy density up to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{1443f15.eps}
\end{figure}](/articles/aa/full_html/2009/10/aa11443-08/Timg238.gif) |
Figure 15:
Evolution of the comoving star formation rate density up to
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



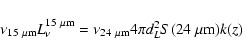
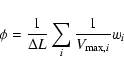
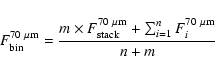
![\begin{displaymath}%
{\it SFR}~ [{M}_{\odot}~{\rm yr}^{-1}] = 1.72 \times 10^{-10} L_{\rm IR} ~[{L}_{\odot}].
\end{displaymath}](/articles/aa/full_html/2009/10/aa11443-08/img204.gif)