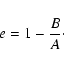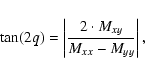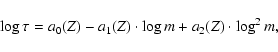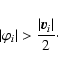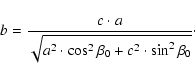EDP Sciences
Home All issues Volume 495 / No 3 (March I 2009) A&A, 495 3 (2009) 807-818 Full HTML
Free Access
Issue
A&A
Volume 495, Number 3, March I 2009
Page(s) 807 - 818
Section Galactic structure, stellar clusters, and populations
DOI https://doi.org/10.1051/0004-6361/200810407
Published online 30 January 2009

Shape parameters of Galactic open clusters[*]

N. V. Kharchenko1,2,3 - P. Berczik1,2 - M. I. Petrov2,4 - A. E. Piskunov1,3,5 - S. Röser1 - E. Schilbach1 - R.-D. Scholz3


1 - Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg (ZAH), Mönchhofstraße 12-14, 69120 Heidelberg, Germany
2 - Main Astronomical Observatory, 27 Academica Zabolotnogo Str., 03680 Kiev, Ukraine
3 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
4 - Institut für Astronomie der Universität Wien, Türkenschanzstraße 17, 1180 Wien, Austria
5 - Institute of Astronomy of the Russian Acad. Sci., 48 Pyatnitskaya Str., 109017 Moscow, Russia

Received 17 June 2008 / Accepted 25 November 2008

Abstract
Context. Ellipticities have been determined for only a few tens of open clusters.
Aims. We derive the observed and modelled shape parameters (apparent ellipticity and orientation of the ellipse) of 650 Galactic open clusters identified in the ASCC-2.5 catalogue.
Methods. We compute the observed shape parameters of Galactic open clusters with a multi-component analysis. For the vast majority of clusters, these parameters are determined for the first time. High resolution (``star by star'') N-body simulations are carried out with a specially developed $\phi $GRAPE code providing models of clusters of different initial masses, Galactocentric distances, and rotation velocities.
Results. By comparing models and observations for about 150 clusters, we find that the ellipticities of observed clusters are too low (0.2 vs. 0.3), and take a first step in identifying the main reason for this discrepancy. After $\approx$50 Myr, the models predict that clusters exhibit an oblate shape with an axis ratio of 1.65:1.35:1, and a major axis tilt by an angle of $q_{XY} \approx 30^\circ$ with respect to the Galactocentric radius due to the differential rotation of the Galaxy.
Conclusions. Unbiased estimates of cluster shape parameters require reliable membership determination in large cluster areas out to 2-3 tidal radii, where the density of cluster stars is considerably lower than the background. Although dynamically bound stars beyond the tidal radius contribute insignificantly to the cluster mass, knowledge of their distribution is essential for a correct determination of cluster shape parameters. In contrast, a restricted mass range of cluster stars does not play such a dramatic role, although deep surveys allow us to identify more cluster members and, therefore, to increase the accuracy of the observed shape parameters.

Key words: Galaxy: open clusters and associations: general - Galaxy: solar neighbourhood - Galaxy: stellar content

1 Introduction

We aim to study the properties of the local population of Galactic open clusters. The sample contains 650 open clusters and cluster-like associations identified in the all-sky compiled catalogue of 2.5 million stars ASCC-2.5 (Kharchenko 2001). For each cluster, a combined spatio-kinematic-photometric membership analysis was performed (Kharchenko et al. 2004) and a homogeneous set of different cluster parameters was derived (Kharchenko et al. 2005a,b). Piskunov et al. (2007) and Piskunov et al. (2008a) determined tidal radii and masses of open clusters and briefly discussed their relation to cluster ellipticity. In the present study, we discuss in detail all the issues related to the shape of local clusters.

The shape of a star cluster, as well as its size and mass, are the most important dynamical parameters. They are already predesignated at the stage of the cluster formation, when the cluster retains the memory of the size and shape of the parent cloud. In addition to internal processes (self-gravitation and rotation), a considerable role in cluster shaping is played by external forces, e.g. by the Galactic tidal field, which acts in two ways (cf. Wielen 1985,1974): a) stretching the cluster into an ellipsoid directed towards the Galactic centre, and b) producing cluster tails outpouring from the ellipsoid endpoints (cluster Lagrangian points). The tails consist of stars lost by the cluster, which lead and/or trail the cluster along its orbit due to differential rotation of the Galactic disk (see e.g. Chumak & Rastorguev 2006). The encounters of star clusters with giant molecular clouds randomize the regular effect of the Galactic field (Gieles et al. 2006). Additionally, molecular clouds produce a screening effect, as they partly overlap the clusters.

Most of the above reasons lead to deviations from cluster sphericity with different effects on the cluster core and corona. The analysis of such violations and their comparison with predictions of N-body models can shed light on the dynamical history of open clusters. We assume in the following that open clusters can be represented by triaxial ellipsoids.

The deviations of the globular clusters from sphericity are evident and their ellipticities were determined for the first time already at the beginning of the last century. For example, Shapley & Sawyer (1927) published the ellipticity estimates of 75 globular clusters. Shape parameters have been determined for one hundred Galactic globular clusters (White & Shawl 1987), i.e., according to Harris' on-line catalogue[*], for about two thirds of the known objects in the Galaxy.

For open clusters, the status of the shape measurements is much poorer; flattening estimates have been obtained only for a few tens of open clusters. Raboud & Mermilliod (1998b,a) and Adams et al. (2002,2001) found evidence of flattening in the Pleiades and in Praesepe. Their results support the predictions of Wielen's model (Wielen 1985,1974), which explains the ellipsoidal form of clusters by tidal coupling with the Galaxy. In contrast, the flattening measured for the Hyades (Oort 1979) deviates from theoretical expectations. Chen et al. (2004) published morphological parameters, including cluster ellipticities, for 31 Galactic open clusters, located preferentially in the anticentre direction of the Galaxy.

With this paper, we attempt to fill this gap in the parameter list of open clusters and determine the shape parameters for all 650 open clusters in our sample (Kharchenko et al. 2005a,b). To be able to compare theoretical predictions with these observed shape parameters, we carried out a set of high resolution (``star by star'') N-body dynamical calculations of cluster models with different initial angular momenta located at different Galactocentric distances in the Milky Way.

The paper has the following structure. In Sect. 2, we provide the basic equations used in the present work; in Sect. 3, we describe the N-body models; in Sect. 4, we compare the observed shape parameters with model calculations and with literature data; and in Sect. 5, we summarize our results.

2 Calculation of observed cluster shape parameters

In this study, we use the following coordinate systems: spherical Galactic coordinates (l, b); the rectangular Galactocentric system (X, Y, Z), with origin in the Galactic centre, and axes directed to the Sun (X), along the Galactic rotation at the Sun's location (Y), and to the North Galactic Pole (Z); and a proper rectangular coordinate system (X', Y', Z') with origin at the centre of the cluster under consideration. The X'-axis is directed along the projection of the cluster Galactocentric vector onto the Galactic plane, Y' points to the direction of Galactic rotation and Z' is directed towards the North Galactic Pole.

Only for the two nearest clusters (Ursa Majoris and the Hyades) do sufficiently accurate distances of individual stars exist, allowing direct determination of the 3D structure parameters of these clusters. For other clusters, we can only consider the stellar distributions in projection onto the celestial sphere.

To derive the shape parameters of clusters (ellipticity, lengths, and directions of the ellipse axes), we applied a multicomponent analysis to the positions of cluster members in the standard (or tangential) coordinate system x, y in each sky area containing a cluster. For each cluster member, the positions x, y were computed from its Galactic coordinates l, b as:

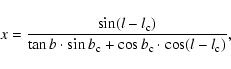
\begin{displaymath}x = \frac{\sin (l - l_{\rm c})} {\tan b \cdot \sin b_{\rm c} + \cos b_{\rm c} \cdot \cos (l - l_{\rm c})}, \end{displaymath}


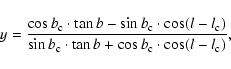
\begin{displaymath}y = \frac{\cos b_{\rm c} \cdot \tan b - \sin b_{\rm c} \cdot ... ...m c} \cdot \tan b + \cos b_{\rm c} \cdot \cos(l - l_{\rm c})}, \end{displaymath}

where $l_{\rm c}, b_{\rm c}$ are the Galactic coordinates of the cluster centre. The axis x is parallel to the Galactic plane, and the axis y points towards the North Galactic Pole; positive directions of x, y coincide with positive directions of l and b, and at the cluster centre $x_{\rm c} = 0$, $y_{\rm c} = 0$. The 2nd order momenta of standard coordinates are given by

\begin{displaymath}M_{xx} = \frac{\sum_i x_i^2}{N},~~~ M_{yy} = \frac{\sum_i y_i^2}{N},~~~ M_{xy} = \frac{\sum_i x_i y_i}{N}, \end{displaymath}

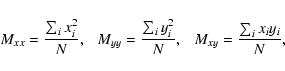
where i = 1, 2,... N, and N is the number of cluster members, which form the basis for the characteristic equation:

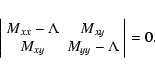
\begin{displaymath}\left\vert \begin{array}{cc} M_{xx}- \Lambda & M_{xy}\\ M_{xy} & M_{yy}- \Lambda \end{array}\right\vert = 0. \end{displaymath}

The roots of this equation, $A=\sqrt {\Lambda_1},~B= \sqrt {\Lambda_2}$, define the scaling of the principal semi-major and semi-minor axes of an apparent ellipse given by the distribution of cluster members over the sky area. An apparent ellipticity e (ellipticity hereafter) is then computed as

\begin{displaymath}e = 1 - \frac{B}{A}\cdot \end{displaymath} (1)

The orientation of the ellipse is defined by the parameter q, which is the angle between the Galactic plane and the longest principal axis of the ellipse:

\begin{displaymath}\tan (2q) = \left \vert \frac{2 \cdot M_{xy}}{M_{xx} - M_{yy}} \right \vert , \end{displaymath} (2)

varying between $0^\circ$ and $90^\circ$.

The rms errors of these values are computed from:

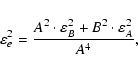
\begin{displaymath}\varepsilon_e^2 = \frac{A^2 \cdot \varepsilon^2_B + B^2 \cdot \varepsilon^2_A} {A^4}, \end{displaymath}


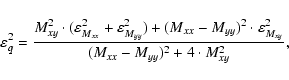
\begin{displaymath}\varepsilon_q^2 = \frac{M_{xy}^2 \cdot (\varepsilon^2_{M_{xx}... ...arepsilon^2_{M_{xy}}} {( M_{xx}- M_{yy})^2 + 4\cdot M_{xy}^2}, \end{displaymath}

where

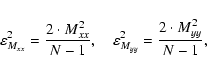
\begin{displaymath}\varepsilon_{M_{xx}}^2 = \frac{2 \cdot M_{xx}^2}{N-1},~~~~ \varepsilon_{M_{yy}}^2 = \frac{2 \cdot M_{yy}^2}{N-1}, \end{displaymath}


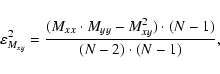
\begin{displaymath}\varepsilon_{M_{xy}}^2 = \frac{(M_{xx} \cdot M_{yy} - M_{xy}^2) \cdot (N-1)}{(N-2) \cdot (N-1)}, \end{displaymath}

and $\varepsilon_A$ and $\varepsilon_B$ (as well as $\varepsilon_e$ and $\varepsilon_q$) are calculated by applying the law of error propagation.

If the orientations of cluster ellipses are not random, one expects to observe a longitudinal dependence of e. Since clusters reside at different heliocentric distances d, it would be more convenient to consider a related angle $\lambda $ instead of l, where $\lambda $ is the angle between the projections of the heliocentric and Galactocentric vectors of a cluster onto the Galactic plane, and can be determined from:

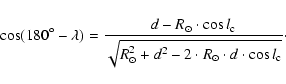
\begin{displaymath}\cos (180^\circ - \lambda) = \frac{d - R_{\odot} \cdot \cos l... ... + d^2 - 2 \cdot R_{\odot} \cdot d \cdot \cos l_{\rm c}}}\cdot \end{displaymath}

The angle $\lambda $ varies between $0^\circ$ and $180^\circ$. Similarly, $\beta $ is the angle between the projections of the two vectors onto the meridional plane of a cluster:

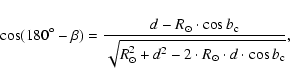
\begin{displaymath}\cos (180^\circ - \beta) = \frac{d - R_{\odot} \cdot \cos b_{... ...dot} + d^2 - 2 \cdot R_{\odot} \cdot d \cdot \cos b_{\rm c}}}, \end{displaymath}

the angle $\beta $ varies between $0^\circ$ and $90^\circ$. Here d is the distance of the cluster from the Sun, $R_{\odot} = 8.5$ kpc is the distance of the Sun from the Galactic centre. We define $\lambda $ and $\beta $ to be $\lambda = 180^{\circ}$ at $l = 180^{\circ}$ and $\beta =0^\circ $ at $b = 0^{\circ}$. In Fig. 1, we show the values of $\lambda $ and $\beta $ for all 650 clusters.

 \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig01.eps} \end{figure} Figure 1:

Aspect angles $\lambda $ and $\beta $ versus Galactic coordinates l and b, respectively, for all 650 clusters.
Open with DEXTER

Using the equations above, one can compute shape parameters (principal semi-axes A and B, ellipticity e, and angles q, $\beta $), both for real and modelled clusters.

3 Numerical modeling

A non-sphericity of star clusters is predicted by both theory and numerical simulations. Wielen (1985,1974) predicted that the ratios of the three orthogonal axes of the cluster ellipsoid should exhibit the ratio (a:b:c)=(2.0:1.4:1.0). The longest axis points towards the Galactic centre and the shortest one is directed towards the North Pole. These results were derived from N-body calculations of 500 particles and confirmed later with more sophisticated models including up to 1000 particles (Terlevich 1987), and up to 2500 particles (Chumak & Rastorguev 2006). These numbers of particles correspond to clusters of initial mass below $10^3~M_{\odot}$. There is evidence, however, that the average masses of forming star clusters are higher. For example, Piskunov et al. (2008b) found that the average mass of the Galactic open clusters at birth equaled $4.5\times 10^3~M_\odot$. Therefore, it is necessary to consider models with higher numbers of particles than developed before.

3.1 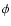$\phi $GRAPE N-body code

For our high-resolution N-body simulations, we use a specially developed $\phi $GRAPE code. The code itself and the GRAPE hardware that we used were described in detail by Harfst et al. (2007). Here, we briefly mention a few of the special features of our code. The program has already been thoroughly tested with different N-body applications, including the high resolution, direct study of the dynamical evolution of the Galactic centre with Binary (or Single) Black Holes (Berczik et al. 2006; Merritt et al. 2007; Berczik et al. 2005)[*].

The program acronym $\phi $GRAPE means: Parallel Hermite Integration with GRAPE. The serial and parallel versions of the program are written from scratch in ANSI-C and use the standard MPI library for communication. For the integration of the star cluster's dynamical evolution inside the Galactic potential, we use the parallel GRAPE systems developed at ARI Heidelberg (GRACE - year 2005) and at MAO Kiev (GRAPE/GRID - year 2007).

The code uses the 4th order Hermite integration scheme for the particles with the hierarchical individual block timesteps, together with the parallel usage of GRAPE6a cards for the hardware calculation of the acceleration $\vec{a}$, and the first time-derivative of the acceleration $\vec{\dot{a}}$(this term is usually called ``jerk'' in the N-body community).

We study in particular the effect of N-body softening, suppressing the hard binary formation in our code, on the evolution of the cluster model. We vary the softening parameter from a few hundreds to a few astronomical units, and find no significant difference in the evolution of the cluster mass and shape. We also consider the role of a possible initial mass segregation and do not observe any dependence of the evolution of the semimajor axis on this value.

Compared with the previous public version we add two major changes to the code. First of all, we add the possibility of having some external potential, acceleration, and also ``jerk''. For the external potential, we choose the form proposed by Miyamoto & Nagai (1975). Using such a multi-mass component potential, we can easily approximate the Galaxy's external force, acting on our star cluster in the Galactic disk at different Galactocentric distances. The second change includes the possibility of switching on the mass loss due to the stellar evolution for every modelled star particle. For metallicity-dependent stellar lifetimes, we use the approximation formula proposed by Raiteri et al. (1996):

\begin{displaymath}\log \tau = a_0(Z) - a_1(Z) \cdot \log m + a_2(Z) \cdot \log^2 m, \end{displaymath}

where $\tau$ is expressed in years and the stellar mass m in solar masses, and where Z is the abundance of heavy elements. The coefficients are defined to be:

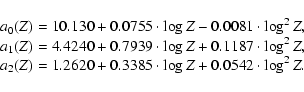
\begin{displaymath}\begin{array}{lllll} a_0(Z)= 10.130 + 0.0755 \cdot \log Z - 0... ...+ 0.3385 \cdot \log Z + 0.0542 \cdot \log^2 Z. \\ \end{array} \end{displaymath}

The mass lost by stars during their evolution is calculated with the help of tables from van den Hoek & Groenewegen (1997) and approximated analytically by the metallicity-dependent formula:

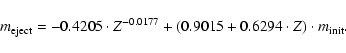
\begin{displaymath}m_{\rm eject}= -0.4205 \cdot Z^{-0.0177} + (0.9015 + 0.6294 \cdot Z) \cdot m_{\rm init}. \end{displaymath}

For simplicity in our model, we assume that stars lose their masses permanently at a constant rate of $-m_{\rm eject}/\tau$.

Since stars lose the bulk of their masses at the end of their evolution, we also test an alternative mass-loss scenario, where we reduce the stellar masses just in one timestep at the end of the star life. We find that the models have almost identical evolutionary patterns of shape parameters and mass loss of clusters, independent of the version of stellar mass loss used.

3.2 Initial conditions for the star cluster

Table 1:   The parameters of the Galactic potential components.

To generate the initial position and velocity distributions of cluster particles, we use the standard King model. The code for the generation of the initial rotating star cluster is described in detail by Einsel & Spurzem (1999). We also use their notation to parametrize our rotating King model family with the concentration parameter W0 and the dimensionless angular velocity $\omega_0$. Thus, each model can be parametrized by the combination of these two numbers. The larger the value of W0, the larger the central concentration, and the larger $\omega_0$, the larger is the angular momentum of the model.

For the present simulations we study the variation in the output parameters for only three basic King models. We vary only the rotation parameter $\omega_0 = (0.0,~0.3,~0.6)$. According to Table 1 in Einsel & Spurzem (1999), the ratio of the ``pure'' rotational energy to the total kinetic energy in the models for these three cases is $E_{\rm rot}/E_{\rm kin} = (0.0,~0.105,~0.278)$. The concentration parameter was always set to be W0 = 6.0 (which corresponds to the models with medium concentration).

As a next step, taking the Salpeter (1955) initial mass function (IMF) $f(m)={\rm d}N/{\rm d}m$, we create the random particle mass distribution:

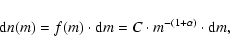
\begin{displaymath}{\rm d}n(m) = f(m)\cdot {\rm d}m = {\it C} \cdot m^{-(1+\alpha)} \cdot {\rm d}m, \end{displaymath}

with the lower and upper mass limits of $m_{\rm l} = 0.08~M_\odot$, and $m_{\rm u} = 8.0~M_\odot$, respectively, and with a Salpeter slope of $\alpha = 1.35$. We use the upper mass limit of 8.0 $M_\odot$, because we consider a ``pure/classical'' open cluster (older than 30-40 Myr), when all high mass stars have already completed their life as a SNII, and swept out all the residual gas left from the cluster formation process.

The number of particles required to model a given initial mass of the cluster $M_{\rm c}(0)$, can be computed from the assumed IMF to be

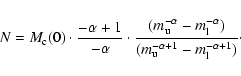
\begin{displaymath}N = M_{\rm c}(0) \cdot \frac{-\alpha+1}{-\alpha} \cdot \frac... ...alpha})}{(m_{\rm u}^{-\alpha+1} - m_{\rm l}^{-\alpha+1})}\cdot \end{displaymath}

With the adopted IMF parameters for the model cluster and initial masses $M_{\rm c}(0) = (10^4, 5\times10^3, 10^3)~M_\odot$, we have the following particle numbers N = (40 404, 20 202, 4040).

After setting the initial masses, positions, and velocities of every particle in the model, we complete the standard N-body normalization (Aarseth et al. 1974) of the model, and rescale the initial cluster data to place our system in virial equilibrium $E_{\rm gra} = -2 \cdot E_{\rm kin} = 2 \cdot E_{\rm tot}$with the following parameters: $G = M_{\rm c} = 1$ and $E_{\rm tot} = -0.25$. This step does not alter any physical quantity of the modelled star cluster, but is useful for numerical reasons. For a King model with W0 = 6.0, such a normalization produces a half-mass radius of about 0.8 (in dimensionless units).

After constructing the dimensionless parameters of our model, we can easily extend them to a different physical cluster mass and half-mass radius. In principle, these two parameters can be set independently, but to reduce the number of independent initial parameters we decided to use some physically motivated relation between initial mass and initial half-mass radius. For this purpose, we used the extension of the well-known mass versus radius relation for molecular clouds and clumps in the Galaxy (see Theis & Hensler 1993 and Inoue & Kamaya 2000), which can be scaled to:

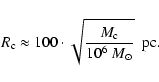
\begin{displaymath}R_{\rm c} \approx 100 \cdot \sqrt{\frac {M_{\rm c}} {10^6 ~M_\odot}}~~{\rm pc}. \end{displaymath}

For the three physical masses chosen, we set the corresponding radii to $R_{\rm c} = (10$, 7, 3) pc.

To confirm the dependence of the computed evolution of cluster shape on the adopted mass versus radius relation, we developed a series of models where we set the normalising factor to 100, 71, and 43 pc. We find that, for typical model parameters, the evolution in the cluster shape does not in practice depend on this factor.

3.3 Galactic rotation curve

For the external Galactic potential shaping a cluster, we choose the combined ``Plummer-Kuzmin disk'' form (see Miyamoto & Nagai 1975):

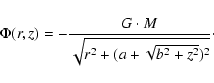
\begin{displaymath}\Phi(r,z) = - \frac{ G \cdot M }{ \sqrt{r^2 + (a + \sqrt{b^2 + z^2} )^2} }\cdot \end{displaymath}

Coupling this potential with a three-component Galactic mass-distribution model consisting of ``Bulge'', ``Disk'', and ``Halo'' components (Douphole & Colin 1995), one can easily reproduce the observed rotation curve of the Galaxy

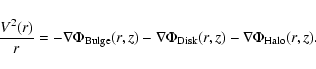
\begin{displaymath}\frac{V^2(r)}{r} = -\nabla\Phi_{\rm Bulge}(r,z) -\nabla\Phi_{\rm Disk}(r,z) -\nabla\Phi_{\rm Halo}(r,z). \end{displaymath}

To bring this into agreement with the kinematics of the open cluster subsystem in the Solar neighbourhood, we slightly modify the Douphole & Colin (1995) parameters. The parameter values consistent with the observed Oort constants $(A, B) = (14.5 \pm 0.8, -13.0 \pm 1.1)$ km s-1 kpc-1 derived by Piskunov et al. (2006) are shown in Table 1. The adopted values of Oort constants correspond to $V/R_\odot = 27.5 \pm 1.3$ km s-1 kpc-1, which at $R_{\odot} = 8.5$ kpc correspond to $V \approx 233$ km s-1. Using these data, we derive circular velocities also at distances of 7.5 kpc and 10.0 kpc from the Galactic centre.

3.4 Model list and model cluster memberships

Table 2:   Model parameters.

As a starting point for our model cluster, we select the position inside the Galactic disk (R0, 0.0, 0.0) with the corresponding circular velocity (0.0, -V0, 0.0). For the set of our runs, we use three values for the positions inside the Galactic disk: R0 = (7.0, 8.5, 10.0) kpc with corresponding circular velocities V0 = (236, 233, 231) km s-1. Together with the three initial masses $M_{\rm c}(0)$ of clusters and the three rotational parameters $\omega_0$, these three positions create the set of $3 \times 3 \times 3$, i.e. in total 27 models (see the full list of model parameters in Table 2). Each model comprises a few hundred ``snapshots'' made at different moments of time equally spaced from t=0 to $t \ga 1$ Gyr. For each model particle, every snapshot displays its initial and current mass, coordinates, and velocities in the rectangular Galactocentric coordinate system.

To complete a detailed analysis of star cluster shapes, we must first identify the cluster centre position. This issue requires special attention, since particles that have left the cluster during the evolution should for this purpose not be taken into account. For this, we use our own iterative routine, considering the distributions of positions and velocities of particles and apply this to every snapshot. We find that we are able to determine the centre even for models with the highest mass loss, which lose more than half of their initial content during the evolution.

As a next step in our analysis, we convert the positions and velocities of the particles into the proper coordinate system of the cluster related to the local density centre and define the list of particles that are still bound to the cluster. We use the particle kinetic and gravitational energy as criteria for belonging to the cluster. The kinetic energy is computed from the velocity of every particle in the proper system of the cluster. For the gravitational energy, we use the value of the cluster's self-gravity potential, determined as the sum of all interactions between a selected particle and the remaining particles. We assume that only the particles that have a negative relative energy are still bound to the cluster:

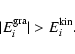
\begin{displaymath}\vert E^{\rm gra}_i\vert > E^{\rm kin}_i. \end{displaymath}

In other words, for bound particles, we can write:

\begin{displaymath}\vert\varphi_i\vert > \frac{\vert\vec{v}_i\vert}{2}\cdot \end{displaymath} (3)

Using this condition for the definition of cluster membership, we exclude particles that have relatively large velocities compared with the cluster centre and compile a list of particles that we select to be ``dynamical'' cluster members.

 \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig02.eps} \end{figure} Figure 2:

The evolution of the mass of dynamically bound particles for three cases of the initial mass of the cluster models (three columns with masses shown at the top of each column). The upper panels are constructed for non-rotating models ( $\omega _0 = 0.0$) and show the effect of the Galactocentric distance. The dotted (red), solid (black), and dashed-dotted (blue) curves are models at R0 = 7, 8.5, and 10 kpc. The bottom panels illustrate the effect of cluster rotation at the Solar Galactocentric distance. The solid (black), dashed (green), and long dashed (magenta) curves show models with $\omega _0 = 0.0$, 0.3, and 0.6.
Open with DEXTER

We define the current mass of the cluster $M_{\rm c}(t)$ to be the sum of masses of all bound particles. In Fig. 2, we show the evolution of $M_{\rm c}(t)$ for a set of selected models. The evolution shows a behaviourb similar to that of the models of Ernst et al. (2007) and Kim et al. (2008). Figure 2 indicates that a star cluster loses between 35% and 70% of its initial mass during the first 1 Gyr and the mass loss decreases with increasing distance of the clusters from the Galactic centre and with increasing cluster rotation velocity.

We double-check our mass-loss sequences by comparing with results that we obtain with other fully independent and also publicly available N-body codes (N-body4 (with GRAPE6) & N-body6++). All the models exhibit the same evolution patterns of mass loss.

4 Shape parameters of observed and modelled clusters

4.1 Shape parameters of the cluster models

 \begin{figure} \par\includegraphics[width=8.8cm,clip]{10407_fig03.eps} \end{figure} Figure 3:

The particle distribution in the X'Y'- and Z'Y'-planes of a model with initial mass $M_{\rm c}(0) = 10^3~M_\odot$ and distance from the Galactic centre R0 = 8.5 kpc at different moments of time. The cluster age is indicated in the right corner of each panel. Cyan dots - all particles, red dots and red-color labels - dynamically bound particles, black dots and labels - massive particles ( $m> 1~M_\odot$), black labels in brackets - dynamically bound massive particles. Arrows indicate the limits of cluster tails when they do not fit to the frame.
Open with DEXTER

 \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig04.eps} \end{figure} Figure 4:

The evolution in ratios of the model ellipsoidal axes a:cand b:c for bound particles for models of different initial mass (three columns with masses shown at the panel top). In every panel the upper triplet of the curves indicates the a:c ratio and the lower triplet corresponds to b:c. The designations are the same as in Fig. 2.
Open with DEXTER

We first consider how the cluster model, initialized as a spheroid, changes its shape and orientation with time. The evolution of a selected model in the planes X'Y' and Y'Z' is shown in Fig. 3. With time, the cluster elongates along the line of the Galactocentric radius, and begins to ``leak'' losing low-mass particles from the limits corresponding to the Lagrangian points, farthest and nearest to the Galactic centre. Due to the differential rotation, the particles overtake the cluster at the end nearest to the Galactic centre and lag at the farthest end. The tails contain stars, which do no longer belong to the cluster. The dynamical members form an ellipsoid projected onto the X'Y' and Z'Y'planes as ellipses. In the X'Y' plane, the ellipse is tilted with respect to the X'-axis at an angle qXY, whereas in the Z'Y'-plane it follows the Y'-axis.

These details about the distribution of N-body particles arise due to interaction with the Galactic tidal field. They are found in all N-body simulations of open clusters (see, e.g., Fig. 7 of Terlevich 1987; Chumak & Rastorguev 2006).

In Fig. 3, one can also clearly see the so-called ``tidal tail clumps'' (star density enhancements) at about 150 pc from the cluster centre. These clumps were mentioned probably for the first time in Capuzzo Dolcetta et al. (2005) and discussed in more detail by Küpper et al. (2008). We observe these clumps in all our models (see the model videos at the FTP link shown in the footnote to page [*]). They can be explained by a simple theory (Just et al. 2009).

In Figs. 4 and 5, we show the evolution in the axis ratios a:c and b:c and of the tilt angle qXY for selected models. After a few tens of Myrs, the initially spherical cluster transforms into an ellipsoid tilted with respect to the Galactocentric radius, the semi-major axis being about twice as long as the minor axis, and a tilt of between $30^{\circ}$ and $40^{\circ}$. The shape parameters are almost independent of the Galactocentric distance of the model clusters, but the ellipsoid becomes flatter with increasing cluster rotation.

 \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig05.eps} \end{figure} Figure 5:

The evolution of the tilt angle qXY computed for dynamically bound particles for three cases of the initial mass of the cluster models (three columns with masses shown in the top of the panels). The designations are the same as in Fig. 2.
Open with DEXTER

 \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig06.eps} \end{figure} Figure 6:

Dependence of the shape of a model cluster on the sampling constraints. Bottom: cluster ellipticity e and semiaxes A and B as functions of lower mass limit ( left) and radius of the considered area ( right). The circles show the major semiaxes, the triangles are for the minor one, and short (red) horizontal bars mark the ellipticity. Vertical bars indicate the statistical uncertainties. The upper row shows the numbers of particles participating in the construction of the corresponding values.
Open with DEXTER

N-body models offer good possibilities for studying various biases that can occur in cluster ellipticities derived from observations. In Fig. 6, we show the dependence of the ellipticity of a model cluster on sampling constraints due to the mass and the distances from the cluster centre of the particles considered. In this way we mimic the usual selection effects, which impact the observations of true clusters. Removing the model particles below a certain mass limit simulates a possible bias due to the limited deepness of a survey. The restriction of the models by distances of particles from the cluster centre simulates the bias arising due to underestimation of cluster size. Hereafter, we call the latter effect a ``restricted area bias''. We consider a cluster model, where both major and minor semi-axes of the ellipsoid are observed to be at right angles, i.e. the projected ellipticity is at its maximum. The model cluster is 150 Myr old, its current mass is $4.2\times10^3~ M_\odot$, and, as a consequence, its tidal radius is $r_{\rm t}=22.5$ pc. The number of dynamically bound particles is $N_{\rm c}=19~371$.

The tidal radius of the model cluster was computed from the current total mass of member particles with the well-known relation of King (1962). This places the model tidal radii into the same system as the observed tidal radii of open clusters. We note that for about 1/3 of our clusters, we determined tidal radii by fitting the cluster radial density distribution with a King profile (Piskunov et al. 2007), and for the remaining clusters we used a proper calibration to estimate their tidal radii (Piskunov et al. 2008a). Then, assuming that clusters fill up their potential well, the cluster ``tidal'' masses were computed from the King (1962) formula for all 650 clusters.

From Fig. 6, we conclude that excluding low-mass particles from consideration has a much smaller impact on the resulting ellipticity than excluding the external parts of the model cluster. Indeed, removing low-mass particles causes the axes A and B to decrease slightly. Since they change, however, in coordination with each other, the ellipticity is almost constant within the statistical uncertainties. In contrast, by including more and more distant particles in the ellipticity calculation, the ellipticity increases steadily. At a distance of two tidal radii, the corresponding ellipticity is close to the limiting value achieved if all bound particles within about three tidal radii are taken into account.

This behaviour can be easily understood if one considers the dependences of the axes A and B on the cluster radius. The minor axis B reaches its maximum value within $r_{\rm t}$ and increases no more, whereas the major axis Acontinues to rise beyond the tidal radius. One should note that the cluster flatness is produced by a relatively small number of cluster particles: only 2% of bound particles occupy a zone beyond $1~r_{\rm t}$, and only 0.1% of them can be found at $r>2~r_{\rm t}$. In contrast, a few tens of the most massive particles, which are not constrained spatially, produce about the same ellipticity as the rest of the low mass members. A consequence of a smaller sample is, however, a considerably higher statistical uncertainty in the resulting ellipticity. A comparison with older models shows that the above conclusions remain valid for cluster ages up to one Gyr.

In summary, we conclude that the determination of cluster ellipticity is not influenced strongly by the survey's deepness, but rather by the extent of the surveyed areas around the clusters. By restricting ourselves to areas smaller than the corresponding tidal radius, one runs the risk of introducing a ``restricted area bias'' into the resulting cluster ellipticities, and hence making clusters more circular than they are in reality.

4.2 Determination of the uniform shape parameters of the observed and modelled clusters

To compare observations with models, one needs to define parameters adequately describing both entities. From observations, we compute the apparent ellipticities e and orientation parameters q of each cluster in our sample using the approach presented in Sect. 2 and adopting the apparent cluster radius r2 from Kharchenko et al. (2005a,b). The observed shape parameters e and q for each of the 650 open clusters are listed in a table available in electronic form only from the CDS. To compute the parameters, we consider only the most probable members with kinematic and photometric probabilities higher than 61% (see Kharchenko et al. 2004). This decision was guided simply by the fact that a sample was stronger contaminated if we included stars with a lower membership probability. Since field stars tend to be represented by a random distribution, the contamination leads to a bias, evident as a fictitious decrease in the observed ellipticity.

 \begin{figure} \par\includegraphics[angle=270,width=7.8cm,clip]{10407_fig07.eps} \end{figure} Figure 7:

Dependence of the apparent ellipticity e on the probability threshold for cluster membership of the open cluster Stock 2. The bars correspond to mean errors. Large open circles indicate the apparent ellipticities based on the sample of stars with membership probability higher than 1% ( the left circle), higher than 14% ( the middle circle), and higher than 61% ( the right circle).

Open with DEXTER

For illustration purposes, we completed the ellipticity calculation by considering cluster stars with different membership probabilities. For our basic sample of 152 clusters (see Sect. 4.3 for definition), we derived an average ellipticity of $\overline{e}=0.18$ when considering stars with a membership probability higher than 61%, $\overline{e}=0.14$ for membership probability higher than 14%, $\overline{e}=0.12$ for membership probability higher than 1%, and $\overline{e}=0.09$ if we consider all stars projected onto the cluster area. A probability threshold of 61% is a compromise between a possible bias due to backgroud contamination and the number of stars included in the ellipticity calculation.

On the other hand, one must ensure that stars of membership probability higher than 61% adequately describe the cluster properties. In Fig. 7, we show the variations in the apparent ellipticity with the probability threshold in the case for example of the cluster Stock 2. This cluster is a well populated cluster, so we derive satisfactory statistics even for the smallest star samples containing the most probable cluster members. The effect of the contamination by field stars is significant if the probability threshold P is less than 30%, but becomes almost insignificant (although still systematic) at $40\% \leqslant P <60\%$. If we consider stars with membership probabilities higher than 60%, the variations in the resulting apparent ellipticity have a random character. Although the sample of stars with membership probability over the 61% threshold may contain a number of field stars, this indicates that they do not introduce a bias in the apparent ellipticity determination. A further increase in the probability threshold does not improve the results significantly, but the mean error in the apparent ellipticities becomes larger due to poor statistics. Therefore, we consider a 61% threshold to be the optimal choice.

From the models, we obtain the axes a, b, and c, and the tilt angle qXY describing the shape and orientation of a cluster in the proper coordinate system (X',Y',Z'). To compare them with the observed parameters e and q, we must ``view'' the models under the same conditions applicable to the observed clusters. First, one must remember that the limiting magnitude of the ASCC-2.5 is about V=12, and even in the nearest clusters we can, therefore, observe only stars more massive than $0.7~M_{\odot}$, i.e. one order of magnitude higher than the lower mass limit of model particles. Further, the resulting shape parameters are strongly dependent on the size of the area around the cluster centre included in the computations. Therefore, a model cluster must be scaled to the apparent cluster radius r2 of its observed counterpart.

For each observed cluster, we first selected its theoretical counterpart from Table 2 at the Galactocentric distance that is closest to the location of the observed cluster. For a given model, we then selected the snapshot that had an age closest in value to the observed age. This snapshot was placed at the position of the true cluster, and the model particles were projected onto the face-on plane (i.e. for every particle, the standard coordinates x,ywere computed). From the complete list of model particles, we selected the true members of the cluster by applying Eq. (3). We used this list to compute ``true'' model parameters of the cluster's shape with the formulae from Sect. 2.

The models contain particles down to relatively low masses, which cannot always be detected in real observations. To reproduce the observed conditions (i.e. to obtain the ``observed'' model parameters), we further reduced the list of dynamical members by selecting particles in the observed mass range and obeying the condition that the number of modelled and observed members within the cluster area r2 is approximately the same.

As a result, we consider four different sets of input data. The first set includes real observations of clusters, which we call ``OC''. The following three sets are related to the models. The set ``MC'' represents the models, which reproduce ``true'' clusters containing all the dynamical members in the complete range of particle masses. The third set `` ${\rm MC_{m}}$'' includes only ``massive'' dynamical members of given clusters above the limiting magnitude of ASCC-2.5 . Finally, the set `` $\rm {MC_{mr}}$'' completely reproduces the observed sample: it includes the same number of particles selected in the same mass range $\Delta m$ as we observe in real clusters. As for the observed clusters, the $\rm {MC_{mr}}$ models contain only those particles, which reside within the apparent cluster radius r2. Since the sets ${\rm MC_{m}}$ and $\rm {MC_{mr}}$ bridge the sets MC and OC, they are introduced to investigate the biases in the observed shape parameters, which may occur due to the limitations of the mass ranges and spatial distribution of cluster stars described in Sect. 4.1.

4.3 Comparison of shape parameters of the modelled and observed clusters

For comparison with the model data, we consider only clusters with more than 20 most probable members. We also exclude the two densely populated clusters NGC 869 (h Per) and NGC 884 ($\chi$ Per), since they overlap in projection on the sky, and have a large number (more than 50%) of members in common, making an accurate determination of their individual shape parameters rather difficult. Hereafter, we refer to the resulting sample as the ``basic sample'' comprising 152 objects.

According to the mass estimates of open clusters given in Piskunov et al. (2008a), the average tidal mass of clusters in the basic sample is about $10^3~M_{\odot}$, which is comparable to the average cluster mass of $700~M_\odot$ determined by Piskunov et al. (2008b) for the complete cluster sample of 650 clusters. Therefore, we assume that the basic sample represents the typical cluster population in the Solar vicinity sufficiently well, having typical initial masses of about $4.5\times 10^3~M_\odot$ as determined in Piskunov et al. (2008b). For this reason, we select the cluster models with initial mass of $5\times10^3~M_{\odot}$ as the most suitable for comparison with observations. According to Fig. 4, the shape parameters do not change considerably for models with larger initial masses, whereas the ellipticity becomes more prominent in clusters with initial masses considerably lower than the adopted $5\times10^3~M_{\odot}$. In the following, we consider the non-rotating models of open clusters keeping in mind that, with increasing rotation velocity, clusters also become flatter.

The distributions of ellipticities e and orientation angles q of the observed and modelled clusters of the basic sample are shown in Fig. 8. The distribution of ellipticity shows a clear maximum for the complete cluster models (the set MC) at $e\approx 0.25{-}0.35$, and the corresponding ellipsoids are elongated parallel to the Galactic plane (the orientation angle $q \approx 0^\circ$). For the models ${\rm MC_{m}}$ and $\rm {MC_{mr}}$ that account for the restrictions set by observations, the ellipticity decreases, while the spread in q increases indicative of a more random orientation of the apparent ellipses. The observed clusters (the set OC) exhibit relatively small ellipticities with a peak between 0.075-0.175. Although a peak at q = 0 is still observed, the orientation angles q are distributed over the entire range. This is simply a consequence of the small ellipticities, since apparently circular clusters have no orientation angle.

 \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig08.eps} \end{figure} Figure 8:

Distributions of ellipticities e ( left panels) and orientation angles q ( right panels) for 152 clusters. The panels are marked with the identifiers of the set.
Open with DEXTER

We show the dependence of ellipticities e on cluster age in Fig. 9 for all four sets. We limit our consideration to 144 clusters with $\beta <20^\circ $ to minimize the impact of the projection on the smallest axis of the ellipsoid occurring for clusters at large galactic latitudes. According to the model set MC, clusters change their initially circular shapes into ellipsoids during the first 50 Myr and retain this form thereafter. This behaviour can be also inferred from Fig. 3. The small scatter around the average ellipticity for clusters older than 50 Myr is defined by their location in the Galactic plane relative to the Sun and to the Galactic centre, i.e. by the aspect angle $\lambda $. When we reduce the number of observable members by excluding model particles of low masses (the set ${\rm MC_{m}}$), the average ellipticity does not vary, although the distribution shows a larger scatter, which arises due to the poorer quality of the data for remaining dynamical members. When further excluding model particles located outside the apparent radius assumed for the clusters, the average ellipticity becomes significantly lower. The observed clusters show a similar ellipticity distribution as the model set $\rm {MC_{mr}}$. These features confirm the results of the analysis carried out in Sect. 4.1.

 \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig09.eps} \end{figure} Figure 9:

Ellipticities e of 144 low-latitude open clusters ( $\beta <20^\circ $) versus age t. The panels are marked with the identifiers of the set. The dotted vertical line marks t = 50 Myr. In each panel, the horizontal lines show the corresponding average ellipticity for clusters older than 50 Myr. The dashed lines indicate their standard deviations. Vertical bars for a cluster at t = 2.46 Gyr show typical rms errors of the ellipticity estimates.
Open with DEXTER

Table 3:   Projected semi-axes A and B in selected directions of the sky for the model of preferentially orientated cluster ellipsoids.

The following statistical results illustrate the decisive role of spatial limitation ($r \le r_2$) in causing difficulty in measuring the true ellipticity of clusters. The average ellipticities of 103 clusters with t > 50 Myr are equal to $0.328 \pm 0.004$, $0.322 \pm 0.013$, $0.184 \pm 0.010$, and $0.186 \pm 0.010$ for MC, ${\rm MC_{m}}$, $\rm {MC_{mr}}$, and CO, respectively. The similar average ellipticities of the sets $\rm {MC_{mr}}$ and OC indicate that a possible bias due to background contamination is small if the ellipticity calculation is based on cluster stars with membership probabilities higher than 61%. We conclude, also, that a spatial limitation of cluster members introduces a significant bias in the determination of ellipticities, whereas a mass limitation increases mainly the random uncertainties in the results. The lower ellipticities of the sets $\rm {MC_{mr}}$ and OC are due to too small radii r2 ibeing assumed for the clusters. We note that, on average, the ASCC-2.5 -based estimates of cluster radii r2 (Kharchenko et al. 2005a) are already larger by a factor of two compared to previously published values. More reliable estimates of cluster radii are possible only if a proper separation of cluster members from the numerous field stars can be achieved in the outer cluster regions. This would require more accurate surveys of proper motions and photometric data all over the sky. On the other hand, surveys deeper than the ASCC-2.5 would increase the random accuracy of the ellipticity determination of open clusters.

4.4 Distribution of the cluster ellipticity over the sky

Ellipticities of open clusters have been studied either for individual objects (Raboud & Mermilliod 1998b,a), or towards selected positions of the Galactic disk (Chen et al. 2004). In the present study, we determined the apparent shape parameters for clusters observed all over the sky. Therefore, it appears useful to derive geometric relations between the apparent ellipticity of clusters and their spatial location in the Galaxy. A regular dependence can of course only be expected if cluster ellipsoids are not orientated randomly in space but show a certain orientation with respect to the Galactic centre.

The model calculations indicate that the Galactic tidal field and differential rotation quickly align clusters along a preferential direction, and the resulting ellipsoids always show the same axis ratios. We define a, b, c be the semi-axes of these three-axial ellipsoids with the semi-major axis a tilted with respect to the Galactocentric radii of the clusters by an angle qXY. For simplicity, we further assume that the major axis is parallel to the Galactic plane. Hereafter, we call this approach the model of preferentially-oriented ellipsoids, and the ellipsoid itself is the ``reference'' one.

From observations, however, we can only see a two-dimensional projection of the reference ellipsoid on the sky that is an ellipse with the semi-axes Aand B. The ratio B/A varies from c/a to 1, depending on the aspect angles $\lambda $ and $\beta $ describing the cluster location with respect to the Sun and the Galactic centre. The apparent ellipticity e changes from 0 to 1 - c/a, respectively.

 \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig10.eps} \end{figure} Figure 10:

Ellipticity e versus aspect angle $\lambda $ for 103 clusters with $\beta <20^\circ $ and t > 50 Myr. The left panel corresponds to the Galactic longitude range $l = 0^{\circ }{-}180^{\circ }$, the right panel to $l = 180^{\circ }{-}360^{\circ }$. The curves show the $e(\lambda ,\beta )$-relations for $\beta =0^\circ $ ( upper curve) and $\beta =20^\circ $ ( lower curve) constructed for the reference ellipsoid tilted to the direction to the Galactic centre by angle $q_{XY} = 30^\circ $, having axis ratios (1.65:1.35:1). Short horizontal bars (red): set MC (complete models), open circles: set OC (observations). The vertical bars drawn for one object show the typical rms error of the observed ellipticity. The dashed vertical lines mark  $\lambda _{ac}$, the dotted ones $\lambda _{bc}$.

Open with DEXTER

When a cluster is located in the Galactic plane ( $b = \beta = 0^{\circ}$), B = c is always valid, and A varies from b to a. The apparent ellipticity reaches the maximum e = 1 - c/a at aspect angles $\lambda_{ac}=90^\circ+q_{XY}$ (for $l = 0^{\circ }{-}180^{\circ }$) and at $\lambda_{ac}=90^\circ-q_{XY}$ (for $l = 180^{\circ }{-}360^{\circ }$). In contrast, the apparent ellipticity reaches the minimum e = 1 - c/b at $\lambda_{bc}=q_{XY}$ (for $l = 0^{\circ }{-}180^{\circ }$) and $\lambda_{bc}=180^\circ- q_{XY}$ (for $l = 180^{\circ }{-}360^{\circ }$). For all other directions, the apparent ellipticities can be computed from the equations given in the first row of Table 3.

Although the majority of star clusters is located close to the Galactic plane, there is a number of clusters at higher galactic latitudes. In a special case, when clusters are located directly at the Galactic Poles, one observes A = a and B = b. For all other clusters outside the Galactic plane, the projection of the reference ellipsoid is defined by both aspect angles. For example, at $\lambda =\lambda _{ac}$ the ellipticity decreases monotonically from 1-c/aat $\beta =0^\circ $ to 1-b/a at $\beta=90^\circ$. The corresponding expression is given in the second row of Table 3. At $\lambda =\lambda _{bc}$, this relation is different since the projected ellipse changes its orientation at some angle $\beta_0$. Thus, the ellipticity first decreases from 1-c/b at $\beta =0^\circ $ to 0 at $\beta=\beta_0$, and then increases to 1-b/a at $\beta=90^\circ$. The corresponding equations are listed in the last two rows of Table 3. The aspect angle $\beta_0$ where the projection becomes a circle (A = B) is determined by the semi-axes a, b, c of the reference ellipsoid from the equality condition

\begin{displaymath}b = \frac{c \cdot a} {\sqrt{a^2 \cdot \cos^2 \beta_0 + c^2 \cdot \sin^2 \beta_0}}\cdot \end{displaymath} (4)

For given parameters of the reference ellipsoid, the Galactic meridian at $\lambda _{ac}$ defines a locus of maximum ellipticities $e(\lambda_{ac},\beta)$ over the sky, whereas the Galactic meridian at $\lambda _{bc}$ corresponds to a locus of minimum ellipticities $e(\lambda_{bc},\beta)$.

In Figs. 10 and 11, we plot the analytical relations from Table 3 together with the model and observed data on ellipticities, versus the aspect angles for ``relaxed'' clusters, which are older than 50 Myr. Although a few observed ellipticities fit the predicted values, the majority of the observed clusters show, as expected, too low ellipticities due to the restricted area bias described above. Therefore, we cannot use the observations for deriving the parameters of the reference ellipsoid. The parameters a, b, c and qXYwere instead found by fitting the relations from Table 3 to the data points of the complete models (MC) as (a:b:c) =(1.65:1.35:1) and $q_{XY} = 30^\circ $. These parameters are based on the non-rotating models assuming the same initial masses ( $5\times10^3~M_{\odot}$) but different location of clusters from the Galactic centre (see also Figs. 4 and 5). For this reference ellipsoid, the angle $\beta_0$ is determined from Eq. (4) to be $\beta_0 = 57.6^{\circ}$.

4.5 Comparison with the literature

There have been only a few studies about the ellipticity of Galactic open clusters. Raboud & Mermilliod (1998a) and Raboud & Mermilliod (1998b) studied the shape of the Pleiades and Praesepe using the most accurate available data on astrometric and photometric membership for these open clusters. For the Pleiades, Raboud & Mermilliod (1998a) determined $e = 0.17\pm0.05$. Since Raboud & Mermilliod (1998b) do not provide the ellipticity for Praesepe, we computed this value ( $e=0.05\pm0.07$) based on data for the cluster membership from their Table 2. Chen et al. (2004) published morphological parameters, including the ellipticity, of 31 Galactic open clusters, residing basically in the Galactic anticentre direction. They used the 2MASS catalogue and segregated clusters from the background with the help of an equidensity method. We compare our results with the above studies in Fig. 12.

Our results for the two nearest clusters ( $e=0.16\pm0.09$ for the Pleiades, and $e=0.14\pm0.09$ for Praesepe) are in good agreement with the ellipticities derived by Raboud & Mermilliod (1998a) and Raboud & Mermilliod (1998b). This is expected since both studies are based on the catalogues of the Hipparcos-Tycho family, and the member lists of Raboud and Mermilliod practically coincide with our membership for these clusters. Since Pleiades and Praesepe are at small distances from the Sun and exhibit large proper motions, one can reliably determine membership in these clusters out to relatively large distances from the cluster centres and down to stars of relatively low masses. Therefore, these clusters are most suitable candidates for obtaining realistic ellipticities from observations. The complete models (MC) provide e=0.30 and 0.12 for the Pleiades and Praesepe, respectively, and reproduce the observations reasonably well.

 \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig11.eps} \end{figure} Figure 11:

Ellipticity e versus aspect angle $\beta $ for 110 clusters with t>50 Myr. The curves show the $e(\lambda ,\beta )$-relations for $\lambda =\lambda _{ac}$ (dashed curve) and $\lambda =\lambda _{bc}$ (dotted curve) constructed for the reference ellipsoid tilted in the direction of the Galactic centre by an angle $q_{XY} = 30^\circ $, and with axis ratios (1.65:1.35:1). Short horizontal bars (red): MC (complete models), open circles: OC (observations). The vertical bars drawn for one object show the typical rms error of the observed ellipticity. The dashed vertical line marks $\beta =20^\circ $.
Open with DEXTER

 \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig12.eps} \end{figure} Figure 12:

Comparison of our results with data from the literature. The left panel compares ellipticities of selected clusters. The clusters from Chen et al. (2004) are shown with open circles, the Pleiades (Raboud & Mermilliod 1998a) with a red square, and Praesepe (Raboud & Mermilliod 1998b) with a blue triangle. The dotted line is the bisector. Right panel: comparison of distributions with e for 21 clusters with t>50 Myr within the Galactic longitude range $144^{\circ }{-}250^{\circ }$ of Chen et al. (2004) - filled histogram, and our 27 clusters within the same longitude and age ranges (hatched histogram). The dashed (red) histogram is the distribution of full models (set MC) of 27 clusters. See details in the text.
Open with DEXTER

A comparison with the results of Chen et al. (2004) is expected to be instructive, since different techniques and sets of input data have been used in ellipticity determinations. Unfortunately, both studies have only 13 clusters in common, and 12 of them do not belong to the basic sample since the number of their most probable members is less than 20 stars in our data. Nevertheless, the agreement between both results is reasonable: the ellipticities of 11 of 13 clusters deviate from the bisector by less than one rms-error in Fig. 12 (left panel).

In Fig. 12 (right panel), we compare the distributions of the cluster ellipticities of Chen et al. (2004) with our models (MC) and observations (OC). To avoid coordinate-dependent misinterpretations, we consider only these clusters in our basic sample that are located in the same area of the sky as the clusters in the sample of Chen et al. (2004), i.e. $l=144^\circ{-}250^\circ,~b=-18^\circ{-}+20^\circ$. We also exclude all clusters younger than 50 Myr from the comparison. The restricted samples include 21 clusters of Chen et al. (2004) and 27 of our clusters with observed and model ellipticities. Whereas N-body models forecast an average ellipticity of $e\approx 0.3$ and a narrow spread of ellipticities in this Galactic direction, our observations show a much wider distribution enhanced at smaller ellipticities ( e = 0.06-0.29). Provided that the peak in the distribution of Chen et al. (2004) data at low ellipticities ( $e\approx 0.10{-}0.15$) is not random, we conclude that their data suffer even more from the restricted area bias than our observations do. The large spread in the data of Chen et al. (2004) can be explained by larger random errors of their ellipticities.

We briefly mention here results concerning the ellipticities of Galactic globular clusters. White & Shawl (1987) determined shape parameters of globular clusters with the equidensity contours method for the data from the Palomar and SRC Sky surveys. They found that, for 99 globular clusters, the average ellipticity was only $0.07\pm 0.01$, and the orientation angles were distributed randomly (because the clusters are almost round). White & Shawl (1987) proposed that interstellar extinction is a probable reason for this unexpected result.

5 Conclusion

Based on a multicomponent analysis of the coordinates of the most probable cluster members, we have determined the shape parameters of 650 Galactic open clusters. Ellipticities and orientation angles complete the list of morphological and dynamical parameters (core sizes and apparent cluster radii, indicators of mass segregation, tidal radii) determined and analysed in a series of previous papers (Piskunov et al. 2008a; Schilbach et al. 2006; Piskunov et al. 2007).

We have carried out high resolution N-body simulations with the specially developed $\phi $GRAPE code on the parallel GRAPE systems developed at ARI Heidelberg and MAO Kiev. The set of 27 cluster models (3 initial masses $\times$ 3 Galactocentric distances $\times$ 3 rotation parameters) with a maximum number of particles of 40 404 was evolved during 1 Gyr. The cluster particles are initially distributed according to a Salpeter IMF in the mass range $0.08{-}8.0~M_\odot$. For each particle, the decision about its cluster membership was made by comparing its potential and kinetic energies.

The calculations of the apparent shape parameters of the modelled and observed clusters were carried out with the same technique. The selection of suitable models was based on initial cluster masses that were estimated from the earlier studies of our cluster sample (Piskunov et al. 2008a,2007). This enabled us to realize a self-consistent approach in comparing model and observed shape parameters using the data of 152 of the most populated Galactic clusters from our sample.

N-body calculations show that all the models lose more than about 50% of their initial mass during the first Gyr of the evolution only due to two-body encounters. A model cluster older than $\approx$50 Myr retains an oblate shape, with the major axis a tilted with respect to the Galactocentric radius at an angle of $\approx$30-40 degrees. The model counterparts corresponding to 152 observed clusters have an ellipticity distribution with a peak in the range $e \approx 0.3{-}0.4$, and, on average, the ellipticity becomes even higher for rotating model clusters.

However, the observed clusters exhibit significantly lower ellipticity, typically of about e=0.2. A comparison of observed cluster shapes with those of detailed models allowed us to realize that the observed lower ellipticities are only apparent. We explain this disagreement by a bias of observations due to underestimated cluster sizes r2 based on the ASCC-2.5 data and used in the determination of cluster ellipticities. According to the models, the ellipticity of the central region of a cluster is low, it increases if outer layers are taken into account, and approaches asymptotically the highest value at 2-3 tidal radii $r_{\rm t}$. Particles outside the tidal radius contribute negligibly to the cluster mass, although their spatial distribution a critical factor in determining the cluster ellipticity. Due to a relatively low density of cluster members above the background level in outer cluster regions, true clusters are usually observable only within distances smaller than $r_{\rm t}$ from the cluster centres. Although the apparent cluster sizes r2 based on the ASCC-2.5 are twice as large as previously published in the literature, the ratio $r_2/r_{\rm t}$ was found to be, on average, only 0.5 (Piskunov et al. 2008a).

In contrast, the deepness of the survey does not play a significant role in the ellipticity determination. Although deeper surveys offer the possibility of identifying more numerous cluster members of lower masses and, consequently, to increase the random accuracy of the ellipticity determination, this alone is insufficient to avoid the ``restricted area bias''.

We adopted the assumption of Wielen (1985,1974) about the preferential shape and orientation of cluster ellipsoids in the Galaxy, and derived simple formulae giving a relation between the apparent ellipticity and spatial location of clusters of our sample. Due to relatively high systematic and random errors in observed ellipticities, however, we were unable to use the present observations for estimating the parameters of the reference ellipsoid. According to N-body calculations, the cluster ellipsoid has an axis ratio of a:b:c=1.65:1.35:1, and is tilted by an angle $q_{XY} \approx 30^\circ$ with respect to the Galactocentric radius.

To test the models with real observations, the ellipticity determination for clusters must be based on data from sufficiently large areas (up to two to three tidal radii) around the clusters. From this point of view, equidensity methods are hardly useful in determining true cluster sizes, especially due to a low density contrast of cluster members above the background at large distances from the cluster centres. Membership determination with kinematic and photometric criteria resolves the problem more successfully but requires surveys of higher proper motion accuracy than available in the ASCC-2.5 .

Acknowledgements

We would like to thank Rob Jeffries, the referee, for his useful comments and suggestions, which helped us to improve the paper.

This study was supported by DFG grant 436 RUS 113/757/0-2, and RFBR grants 06-02-16379, 07-02-91566.

P. Berczik and M. Petrov thank for the special support of his work by the Ukrainian National Academy of Sciences under the Main Astronomical Observatory GRAPE/GRID computing cluster project.

P. Berczik acknowledges his support from the German Science Foundation (DGF) under SFB 439 (sub-project B11) ``Galaxies in the Young Universe'' at the University of Heidelberg. His work was also supported by the Volkswagen Foundation ``Volkswagenstiftung'' under GRACE Project and grant No. I80 041-043 of the Ministry of Science, Education and Arts of the state of Baden-Württemberg, Germany.

References

Footnotes

... clusters[*]
The determined shape parameters for 650 clusters are listed in a table that is available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/495/807
... catalogue[*]
http://www.physics.mcmaster.ca/resources/globular.html
...)[*]
The present version of the code and the full snapshot datasets analyzed in the paper are publicly available from: ftp://ftp.ari.uni-heidelberg.de/pub/staff/berczik/phi-GRAPE-cluster/.

All Tables

Table 1:   The parameters of the Galactic potential components.

Table 2:   Model parameters.

Table 3:   Projected semi-axes A and B in selected directions of the sky for the model of preferentially orientated cluster ellipsoids.

All Figures

  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig01.eps} \end{figure} Figure 1:

Aspect angles $\lambda $ and $\beta $ versus Galactic coordinates l and b, respectively, for all 650 clusters.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig02.eps} \end{figure} Figure 2:

The evolution of the mass of dynamically bound particles for three cases of the initial mass of the cluster models (three columns with masses shown at the top of each column). The upper panels are constructed for non-rotating models ( $\omega _0 = 0.0$) and show the effect of the Galactocentric distance. The dotted (red), solid (black), and dashed-dotted (blue) curves are models at R0 = 7, 8.5, and 10 kpc. The bottom panels illustrate the effect of cluster rotation at the Solar Galactocentric distance. The solid (black), dashed (green), and long dashed (magenta) curves show models with $\omega _0 = 0.0$, 0.3, and 0.6.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{10407_fig03.eps} \end{figure} Figure 3:

The particle distribution in the X'Y'- and Z'Y'-planes of a model with initial mass $M_{\rm c}(0) = 10^3~M_\odot$ and distance from the Galactic centre R0 = 8.5 kpc at different moments of time. The cluster age is indicated in the right corner of each panel. Cyan dots - all particles, red dots and red-color labels - dynamically bound particles, black dots and labels - massive particles ( $m> 1~M_\odot$), black labels in brackets - dynamically bound massive particles. Arrows indicate the limits of cluster tails when they do not fit to the frame.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig04.eps} \end{figure} Figure 4:

The evolution in ratios of the model ellipsoidal axes a:cand b:c for bound particles for models of different initial mass (three columns with masses shown at the panel top). In every panel the upper triplet of the curves indicates the a:c ratio and the lower triplet corresponds to b:c. The designations are the same as in Fig. 2.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig05.eps} \end{figure} Figure 5:

The evolution of the tilt angle qXY computed for dynamically bound particles for three cases of the initial mass of the cluster models (three columns with masses shown in the top of the panels). The designations are the same as in Fig. 2.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig06.eps} \end{figure} Figure 6:

Dependence of the shape of a model cluster on the sampling constraints. Bottom: cluster ellipticity e and semiaxes A and B as functions of lower mass limit ( left) and radius of the considered area ( right). The circles show the major semiaxes, the triangles are for the minor one, and short (red) horizontal bars mark the ellipticity. Vertical bars indicate the statistical uncertainties. The upper row shows the numbers of particles participating in the construction of the corresponding values.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=7.8cm,clip]{10407_fig07.eps} \end{figure} Figure 7:

Dependence of the apparent ellipticity e on the probability threshold for cluster membership of the open cluster Stock 2. The bars correspond to mean errors. Large open circles indicate the apparent ellipticities based on the sample of stars with membership probability higher than 1% ( the left circle), higher than 14% ( the middle circle), and higher than 61% ( the right circle).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig08.eps} \end{figure} Figure 8:

Distributions of ellipticities e ( left panels) and orientation angles q ( right panels) for 152 clusters. The panels are marked with the identifiers of the set.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig09.eps} \end{figure} Figure 9:

Ellipticities e of 144 low-latitude open clusters ( $\beta <20^\circ $) versus age t. The panels are marked with the identifiers of the set. The dotted vertical line marks t = 50 Myr. In each panel, the horizontal lines show the corresponding average ellipticity for clusters older than 50 Myr. The dashed lines indicate their standard deviations. Vertical bars for a cluster at t = 2.46 Gyr show typical rms errors of the ellipticity estimates.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig10.eps} \end{figure} Figure 10:

Ellipticity e versus aspect angle $\lambda $ for 103 clusters with $\beta <20^\circ $ and t > 50 Myr. The left panel corresponds to the Galactic longitude range $l = 0^{\circ }{-}180^{\circ }$, the right panel to $l = 180^{\circ }{-}360^{\circ }$. The curves show the $e(\lambda ,\beta )$-relations for $\beta =0^\circ $ ( upper curve) and $\beta =20^\circ $ ( lower curve) constructed for the reference ellipsoid tilted to the direction to the Galactic centre by angle $q_{XY} = 30^\circ $, having axis ratios (1.65:1.35:1). Short horizontal bars (red): set MC (complete models), open circles: set OC (observations). The vertical bars drawn for one object show the typical rms error of the observed ellipticity. The dashed vertical lines mark  $\lambda _{ac}$, the dotted ones $\lambda _{bc}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig11.eps} \end{figure} Figure 11:

Ellipticity e versus aspect angle $\beta $ for 110 clusters with t>50 Myr. The curves show the $e(\lambda ,\beta )$-relations for $\lambda =\lambda _{ac}$ (dashed curve) and $\lambda =\lambda _{bc}$ (dotted curve) constructed for the reference ellipsoid tilted in the direction of the Galactic centre by an angle $q_{XY} = 30^\circ $, and with axis ratios (1.65:1.35:1). Short horizontal bars (red): MC (complete models), open circles: OC (observations). The vertical bars drawn for one object show the typical rms error of the observed ellipticity. The dashed vertical line marks $\beta =20^\circ $.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{10407_fig12.eps} \end{figure} Figure 12:

Comparison of our results with data from the literature. The left panel compares ellipticities of selected clusters. The clusters from Chen et al. (2004) are shown with open circles, the Pleiades (Raboud & Mermilliod 1998a) with a red square, and Praesepe (Raboud & Mermilliod 1998b) with a blue triangle. The dotted line is the bisector. Right panel: comparison of distributions with e for 21 clusters with t>50 Myr within the Galactic longitude range $144^{\circ }{-}250^{\circ }$ of Chen et al. (2004) - filled histogram, and our 27 clusters within the same longitude and age ranges (hatched histogram). The dashed (red) histogram is the distribution of full models (set MC) of 27 clusters. See details in the text.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.