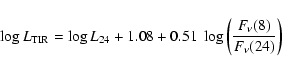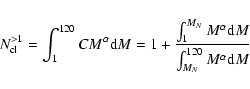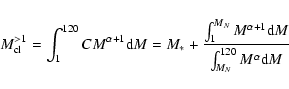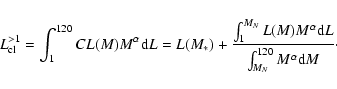| Issue |
A&A
Volume 495, Number 2, February IV 2009
|
|
|---|---|---|
| Page(s) | 479 - 490 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361:200811086 | |
| Published online | 14 January 2009 | |
The cluster birthline in M 33
E. Corbelli1 - S. Verley1 - B. G. Elmegreen2 - C. Giovanardi1
1 - INAF-Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125
Firenze, Italy
2 -
IBM Research Division, T.J. Watson Research Center, 1101 Kitchawan Road,
Yorktown Hts., NY 10598, USA
Received 3 October 2008 / Accepted 12 December 2008
Abstract
Aims. The aim of this paper is twofold: (a) to determine the reliability of infrared (IR) emission to trace star formation in individual star-forming sites of M 33, and (b) to outline a new method for testing the distribution function of massive stars in newly formed clusters.
Methods. We select 24 ![]() m IR sources from the Spitzer survey of M 33 with H
m IR sources from the Spitzer survey of M 33 with H![]() counterparts and show that the IR luminosities have a weak dependence on galactocentric radius. The IR and H
counterparts and show that the IR luminosities have a weak dependence on galactocentric radius. The IR and H![]() luminosities are not correlated. Complementing the infrared photometry with GALEX-UV data, we estimate the bolometric luminosities to investigate how they are related to the H
luminosities are not correlated. Complementing the infrared photometry with GALEX-UV data, we estimate the bolometric luminosities to investigate how they are related to the H![]() luminosities. We simulate a theoretical diagram for the expected bolometric-to-H
luminosities. We simulate a theoretical diagram for the expected bolometric-to-H![]() luminosity ratio,
luminosity ratio,
![]() /
/
![]() ,
of young clusters as a function of the cluster luminosity. We then compare the observed
,
of young clusters as a function of the cluster luminosity. We then compare the observed
![]() /
/
![]() ratios with the theoretical predictions.
ratios with the theoretical predictions.
Results. In the log(L
![]() /
/
![]() )
plane, stellar clusters should be born along a curve that we call the cluster birthline. The birthline depends on the stellar initial mass function (IMF) at the high-mass end, but not on the cluster mass function. For an upper stellar mass limit of
)
plane, stellar clusters should be born along a curve that we call the cluster birthline. The birthline depends on the stellar initial mass function (IMF) at the high-mass end, but not on the cluster mass function. For an upper stellar mass limit of
![]() ,
the birthline is flat for
,
the birthline is flat for
![]() erg s-1 because all clusters fully sample the IMF. It increases toward lower luminosities as the upper end of the IMF becomes incompletely sampled. Aging moves clusters above the birthline. The observations of M 33 show that young isolated clusters lie close to the theoretical birthline for a wide range of
erg s-1 because all clusters fully sample the IMF. It increases toward lower luminosities as the upper end of the IMF becomes incompletely sampled. Aging moves clusters above the birthline. The observations of M 33 show that young isolated clusters lie close to the theoretical birthline for a wide range of
![]() .
The observed
.
The observed
![]() /
/
![]() ratio increases toward low
ratio increases toward low
![]() like the theoretical curve, indicating that luminosity is not proportional to H
like the theoretical curve, indicating that luminosity is not proportional to H![]() emission for low mass clusters. The best fit to the birthline is for a randomly sampled IMF, in which the mass of most massive star in a cluster is not strictly limited by the cluster's mass, but can have any value up to the maximum stellar mass with a probability determined by the IMF. We also find that the IR luminosity of young stellar clusters in M 33 is not proportional to their bolometric luminosity. This irregularity could be the result of low and patchy dust abundance. In M 33 dust absorbs and re-radiates in the IR only part of the UV light from young clusters.
emission for low mass clusters. The best fit to the birthline is for a randomly sampled IMF, in which the mass of most massive star in a cluster is not strictly limited by the cluster's mass, but can have any value up to the maximum stellar mass with a probability determined by the IMF. We also find that the IR luminosity of young stellar clusters in M 33 is not proportional to their bolometric luminosity. This irregularity could be the result of low and patchy dust abundance. In M 33 dust absorbs and re-radiates in the IR only part of the UV light from young clusters.
Key words: stars: luminosity function, mass function - dust, extinction - galaxies: star clusters - galaxies: individual: M 33
1 Introduction
Our knowledge of interstellar conditions that favor the
birth of stars and clusters is mostly based on the Milky Way, but
these studies are ill-suited for examining
massive stars, which are an embedded population with a short lifetime.
The number of Milky Way
clusters that one can sample is also limited by extinction
and distance uncertainties. These problems are somewhat diminished in
studies of other galaxies, where imaging with high sensitivity
and resolution is possible thanks to
space observatories such as Spitzer, HST and GALEX. Soon we shall be able
to know if the IMF and extinction in star-forming sites varies
along the Hubble
sequence, and if ISM perturbations from
these sites vary with cluster position and mass.
In the mean time, the best galaxies for study are in the Local Group.
M 33, at a distance D=840 kpc (Freedman et al. 1991), has a higher SFR
per unit area than M 31 (3.4 versus 0.74 ![]() Gyr-1 pc-2, Kennicutt 1998) and a lower extinction towards star-forming regions
because of its lower inclination
(e.g. Magrini et al. 2007b; Israel & Kennicutt 1980, and references therein).
Bearing no prominent bulge and no signs of recent mergers, M 33 is a prototype for
star formation in a quiescent galaxy and for evolutionary
scenarios in blue, low luminosity systems. Observations of the molecular,
atomic and ionized gas in M 33 have been carried out in the past years (e.g.
Corbelli & Schneider 1997; Deul & van der Hulst 1987;Heyer et al. 2004; Corbelli 2003; Engargiola et al. 2003; Hoopes & Walterbos 2000).
Together with recent works on the metallicity content of the young and
old stellar population across the M 33 disk, they allow us to trace the global
formation and evolution history of the nearest blue disk galaxy
(Magrini et al. 2007a, and references therein).
Gyr-1 pc-2, Kennicutt 1998) and a lower extinction towards star-forming regions
because of its lower inclination
(e.g. Magrini et al. 2007b; Israel & Kennicutt 1980, and references therein).
Bearing no prominent bulge and no signs of recent mergers, M 33 is a prototype for
star formation in a quiescent galaxy and for evolutionary
scenarios in blue, low luminosity systems. Observations of the molecular,
atomic and ionized gas in M 33 have been carried out in the past years (e.g.
Corbelli & Schneider 1997; Deul & van der Hulst 1987;Heyer et al. 2004; Corbelli 2003; Engargiola et al. 2003; Hoopes & Walterbos 2000).
Together with recent works on the metallicity content of the young and
old stellar population across the M 33 disk, they allow us to trace the global
formation and evolution history of the nearest blue disk galaxy
(Magrini et al. 2007a, and references therein).
Verley et al. (2008,2007)
have shown that the recent Spitzer images of M 33 allow us
to study the average radial variation of star formation properties across the disk,
and to locate stellar clusters and individual stars with
infrared luminosities as low as
![]() erg s-1 (corresponding to
a B2 spectral type star on the main sequence). M 33 therefore gives us
a unique opportunity to study the properties of many individual star-forming
sites, containing a range of populations from
single O and B-type stars to young stellar clusters and associations. The observable
luminosity range
extends up to
erg s-1 (corresponding to
a B2 spectral type star on the main sequence). M 33 therefore gives us
a unique opportunity to study the properties of many individual star-forming
sites, containing a range of populations from
single O and B-type stars to young stellar clusters and associations. The observable
luminosity range
extends up to
![]() for NGC 604
(Israel et al. 1982,1986; Hippelein et al. 2003),
the second brightest HII complex in the Local Group.
for NGC 604
(Israel et al. 1982,1986; Hippelein et al. 2003),
the second brightest HII complex in the Local Group.
The aim of this paper is to examine the conditions of the interstellar medium
where stellar clusters are born, to define stellar
cluster properties related to the birth and death of massive stars,
and to examine star formation rate (SFR) diagnostics of individual complexes in M 33.
We will show the importance of complementing infrared photometry with photometry at
optical and ultraviolet wavelengths. Previous papers outlined the
need for infrared photometry to supplement H![]() in determining the SFR (e.g. Calzetti et al. 2005; Kennicutt et al. 2007, for M 51).
In bright star-forming regions of more distant and brighter galaxies,
such as M 51, there is a tight linear relation between IR luminosity and the
strength of extinction-corrected, optical recombination lines
(e.g. Calzetti et al. 2005). On the other hand, in late-type galaxies
there are strong variations in the H
in determining the SFR (e.g. Calzetti et al. 2005; Kennicutt et al. 2007, for M 51).
In bright star-forming regions of more distant and brighter galaxies,
such as M 51, there is a tight linear relation between IR luminosity and the
strength of extinction-corrected, optical recombination lines
(e.g. Calzetti et al. 2005). On the other hand, in late-type galaxies
there are strong variations in the H![]() -to-infrared flux ratio, which limits
our ability to trace star formation via infrared
photometry alone (e.g. Cannon et al. 2006, for the metal deficient Local dwarf
NGC 6822, where the H
-to-infrared flux ratio, which limits
our ability to trace star formation via infrared
photometry alone (e.g. Cannon et al. 2006, for the metal deficient Local dwarf
NGC 6822, where the H![]() -to-IR flux ratio
variations are as high as a factor 10).
UV observations are also needed
to trace the properties of star formation, particularly where the HII regions are
density bounded or the O-type stars have evolved off the main sequence.
GALEX observations of M 33 have shown that the UV
luminosity of a region is comparable to the IR luminosity (Verley et al. 2008),
and is therefore a significant contribution to the total.
-to-IR flux ratio
variations are as high as a factor 10).
UV observations are also needed
to trace the properties of star formation, particularly where the HII regions are
density bounded or the O-type stars have evolved off the main sequence.
GALEX observations of M 33 have shown that the UV
luminosity of a region is comparable to the IR luminosity (Verley et al. 2008),
and is therefore a significant contribution to the total.
Here we employ a new
technique to extract and measure sources from M 33 images.
Because dust and its associated IR emission are distributed in both star-forming
complexes and the diffuse interstellar medium,
we do photometry with varying apertures to match the source size at each wavelength.
We also combine IR, UV and H![]() fluxes to give source properties
down to very faint emission levels.
fluxes to give source properties
down to very faint emission levels.
It is currently unknown if IR fluxes are good diagnostics for
the SFR in areas where the bolometric luminosity of the newborn cluster
is below 1040 erg s-1. M 33 is an excellent candidate for studying
individual low-mass clusters because its proximity minimizes
contamination from the surrounding ISM.
Whether low-mass clusters contribute substantially to the SFR of a galaxy
depends on the initial cluster mass function (ICMF).
In M 33 the fragmentation process seems to favor
small masses: the mass spectrum slope for giant molecular clouds (GMCs) is steeper
than -2, as is
the HII region luminosity function determined from H![]() emission
(e.g. Wyder et al. 1997). Verley et al. (2007) have shown that
the luminosity function at 24
emission
(e.g. Wyder et al. 1997). Verley et al. (2007) have shown that
the luminosity function at 24 ![]() m can be described by a double power-law
that is shallower than -2 at its faint end. While a change of slope like this
could mark the transition between poor and rich clusters, occurring at the
luminosity of the brightest star formed, a shallow slope at the low
luminosity end can also indicate a decreasing dust abundance for lower masses.
Giant complexes may form primarily in dust-rich environments, e.g. close to spiral
arms, while low-mass clusters may form everywhere, also in low-dust environments.
If some low-mass clusters are born in a low or patchy dust environment, then we cannot
use IR luminosities alone to infer the SFR.
m can be described by a double power-law
that is shallower than -2 at its faint end. While a change of slope like this
could mark the transition between poor and rich clusters, occurring at the
luminosity of the brightest star formed, a shallow slope at the low
luminosity end can also indicate a decreasing dust abundance for lower masses.
Giant complexes may form primarily in dust-rich environments, e.g. close to spiral
arms, while low-mass clusters may form everywhere, also in low-dust environments.
If some low-mass clusters are born in a low or patchy dust environment, then we cannot
use IR luminosities alone to infer the SFR.
In this paper we will study the large
scatter in the IR-to-H![]() ratio that is observed when young, low-luminosity
stellar clusters are selected in M 33. We show that
complementing the IR photometry with UV photometry helps recover the total
cluster luminosity and improves the correlation between
stellar continuum and gas recombination lines from star-forming regions.
We will examine in detail the theoretical and observed relation
between
ratio that is observed when young, low-luminosity
stellar clusters are selected in M 33. We show that
complementing the IR photometry with UV photometry helps recover the total
cluster luminosity and improves the correlation between
stellar continuum and gas recombination lines from star-forming regions.
We will examine in detail the theoretical and observed relation
between
![]() and
and
![]() ,
the deviations from the linear
regime, and some properties of the massive stellar population in young clusters.
,
the deviations from the linear
regime, and some properties of the massive stellar population in young clusters.
We shall also investigate the 8 ![]() m emission from PAHs in individual HII regions.
Generally, PAH emission is low in dwarf and low-luminosity blue galaxies
compared to other IR radiation. This may be related
to the low metallicity and intense stellar radiation field in these
systems relative to those in spiral galaxies
(e.g. Houck et al. 2004; Hogg et al. 2005; Lu et al. 2003; Rosenberg et al. 2006; Galliano et al. 2003). Hunter et al. (2001)
for example, used Infrared Space Observatory (ISO) mid-IR imaging and
far-IR (FIR) spectroscopy to examine the properties of five dwarf
irregular systems. They found that PAH emission, which is associated only
with the brightest H II regions, is depressed relative to that of small
grains and far-IR. In addition, the integrated [C II] emission
relative to PAH emission is high in dwarfs compared to spiral
galaxies, suggesting that atomic carbon is elevated
relative to PAHs in dwarfs. Engelbracht et al. (2005) also examined
low-metallicity systems and found that 8.0
m emission from PAHs in individual HII regions.
Generally, PAH emission is low in dwarf and low-luminosity blue galaxies
compared to other IR radiation. This may be related
to the low metallicity and intense stellar radiation field in these
systems relative to those in spiral galaxies
(e.g. Houck et al. 2004; Hogg et al. 2005; Lu et al. 2003; Rosenberg et al. 2006; Galliano et al. 2003). Hunter et al. (2001)
for example, used Infrared Space Observatory (ISO) mid-IR imaging and
far-IR (FIR) spectroscopy to examine the properties of five dwarf
irregular systems. They found that PAH emission, which is associated only
with the brightest H II regions, is depressed relative to that of small
grains and far-IR. In addition, the integrated [C II] emission
relative to PAH emission is high in dwarfs compared to spiral
galaxies, suggesting that atomic carbon is elevated
relative to PAHs in dwarfs. Engelbracht et al. (2005) also examined
low-metallicity systems and found that 8.0 ![]() m emission decreases abruptly relative to 24
m emission decreases abruptly relative to 24 ![]() m dust emission when
the metallicity is less than one-third to one-fifth solar.
M 33 is a low-luminosity galaxy hosting HII regions with metallicities
between solar and one-fifth solar and a shallow radial
gradient (Rosolowsky & Simon 2008; Magrini et al. 2007b).
PAHs are not globally underabundant
in M 33 although there is a faster decline of 8
m dust emission when
the metallicity is less than one-third to one-fifth solar.
M 33 is a low-luminosity galaxy hosting HII regions with metallicities
between solar and one-fifth solar and a shallow radial
gradient (Rosolowsky & Simon 2008; Magrini et al. 2007b).
PAHs are not globally underabundant
in M 33 although there is a faster decline of 8 ![]() m emission
relative to longer wavelengths beyond 3.5 kpc
(Verley et al. 2008).
It is of interest then to examine possible metallicity and
radial dependences of PAH features in individual HII regions.
m emission
relative to longer wavelengths beyond 3.5 kpc
(Verley et al. 2008).
It is of interest then to examine possible metallicity and
radial dependences of PAH features in individual HII regions.
In Sect. 2 we define young stellar cluster samples in M 33
and analyze their IR properties. In
Sect. 3 we study their UV luminosities and colors and define the
cluster bolometric luminosities. The concept of cluster birthline is
given in Sect. 4 and tested using M 33 young clusters.
In Sect. 4 we discuss the implications of our results relative to
the dust abundance, to the bolometric to H![]() luminosity ratio,
and to the population of massive stars in
star-forming sites of M 33. In the Appendix we analyze
possible metallicity dependencies using a small sample of young clusters
for which gas metal abundances are known, as well as dependencies of
cluster properties on the mass of the associated giant molecular cloud.
luminosity ratio,
and to the population of massive stars in
star-forming sites of M 33. In the Appendix we analyze
possible metallicity dependencies using a small sample of young clusters
for which gas metal abundances are known, as well as dependencies of
cluster properties on the mass of the associated giant molecular cloud.
2 Multiwavelength observations of star-forming sites
The closest star-forming galaxies offer a unique opportunity
to resolve individual star-forming regions. In M 33,
the star formation process can be investigated not only by
averaging over selected areas of the disk or by using very bright complexes,
but also by observing individual star clusters of moderate size. The sensitivity
of telescopes such as Spitzer in the IR and GALEX in the UV allows us to
sample clusters over 4 orders of magnitude in brightness: from the second
brightest HII region of the Local Group (NGC 604) down to clusters of about 1000 ![]() .
We can look in detail at the
site properties where clusters of different masses are born,
and at the emission properties of young clusters.
We will use photometric information on sources
across the M 33 disk as given by the Spitzer 8
.
We can look in detail at the
site properties where clusters of different masses are born,
and at the emission properties of young clusters.
We will use photometric information on sources
across the M 33 disk as given by the Spitzer 8 ![]() m and 24
m and 24 ![]() m images
described in Verley et al. (2007), by the GALEX FUV and NUV images
from the GALEX Atlas (Gil de Paz et al. 2007), and by the H
m images
described in Verley et al. (2007), by the GALEX FUV and NUV images
from the GALEX Atlas (Gil de Paz et al. 2007), and by the H![]() image
of Hoopes & Walterbos (2000).
image
of Hoopes & Walterbos (2000).
2.1 The main sample
We define a sample of young stellar clusters and isolated massive stars
using the IR catalog of 515 sources extracted from the 24 ![]() m
Spitzer map by Verley et al. (2007).
This catalog has a completeness limit of
m
Spitzer map by Verley et al. (2007).
This catalog has a completeness limit of
![]() erg s-1(this limiting luminosity refers to the 90
erg s-1(this limiting luminosity refers to the 90![]() level of completeness
computed by extrapolation of the observed cumulative luminosity function at
L24 > 1037 erg s-1).
We remind the reader that the photometry for these sources has
been done with a varying aperture to match the source size.
From the catalog we select only sources
that have an H
level of completeness
computed by extrapolation of the observed cumulative luminosity function at
L24 > 1037 erg s-1).
We remind the reader that the photometry for these sources has
been done with a varying aperture to match the source size.
From the catalog we select only sources
that have an H![]() counterpart. We search for H
counterpart. We search for H![]() counterparts to 24
counterparts to 24 ![]() m sources as follows. We first define a sample of H
m sources as follows. We first define a sample of H![]() sources
by extracting 413 sources from the H
sources
by extracting 413 sources from the H![]() image using the SExtractor
software with no specified sky coordinate list and with varying aperture
(Bertin & Arnouts 1996; specific inputs given in Verley et al. 2007).
For any source in the IR catalog we then
define a searching radius,
image using the SExtractor
software with no specified sky coordinate list and with varying aperture
(Bertin & Arnouts 1996; specific inputs given in Verley et al. 2007).
For any source in the IR catalog we then
define a searching radius, ![]() ,
equal to the radius of the source
in the 24
,
equal to the radius of the source
in the 24 ![]() m image (minor axis if the source PSF is elliptical). This radius
is derived by Verley et al. (2007) using SExtractor in the framework of
the ``hybrid'' method and varies between 12 and 200 pc.
If at least one of the sources in
the H
m image (minor axis if the source PSF is elliptical). This radius
is derived by Verley et al. (2007) using SExtractor in the framework of
the ``hybrid'' method and varies between 12 and 200 pc.
If at least one of the sources in
the H![]() sample is at a distance less than or equal to the searching radius
of an IR source, then this infrared source is selected and its H
sample is at a distance less than or equal to the searching radius
of an IR source, then this infrared source is selected and its H![]() flux is set equal to the sum of the fluxes of all H
flux is set equal to the sum of the fluxes of all H![]() sources within
sources within
![]() .
If no H
.
If no H![]() sources are found within
sources are found within ![]() ,
then we attempt to measure
the H
,
then we attempt to measure
the H![]() flux using the ``hybrid'' photometric method devised by
Verley et al. (2007). With the ``hybrid'' photometric method, we search for
H
flux using the ``hybrid'' photometric method devised by
Verley et al. (2007). With the ``hybrid'' photometric method, we search for
H![]() emission in the circular area of radius
emission in the circular area of radius ![]() around the positions of IR sources (specifying the
source coordinates to the SExtractor software).
If again an H
around the positions of IR sources (specifying the
source coordinates to the SExtractor software).
If again an H![]() feature is found within the
searching area, then this source is selected and its H
feature is found within the
searching area, then this source is selected and its H![]() flux set equal to the ``hybrid'' photometric flux. If H
flux set equal to the ``hybrid'' photometric flux. If H![]() emission
is found at a distance larger than
emission
is found at a distance larger than ![]() ,
then the IR source is not selected
for our sample.
The use of the hybrid method allows us to recover many faint H
,
then the IR source is not selected
for our sample.
The use of the hybrid method allows us to recover many faint H![]() counterparts because their approximate positions are entered into SExtractor.
From both methods we have a final sample of 355 sources that have been selected
from the 24
counterparts because their approximate positions are entered into SExtractor.
From both methods we have a final sample of 355 sources that have been selected
from the 24 ![]() m Spitzer map and have an H
m Spitzer map and have an H![]() counterpart.
Of these, only 3 have a double counterpart in H
counterpart.
Of these, only 3 have a double counterpart in H![]() ,
less than 1
,
less than 1![]() .
We estimate the completeness limit of the survey to be
.
We estimate the completeness limit of the survey to be
![]() erg s-1 in H
erg s-1 in H![]() (90
(90![]() level of completeness).
level of completeness).
Using the 8 ![]() m Spitzer map, we also search for 8
m Spitzer map, we also search for 8 ![]() m counterparts to all 24
m counterparts to all 24 ![]() m sources. We employ the same method used
for finding H
m sources. We employ the same method used
for finding H![]() counterparts.
We find that 491 of the 515 sources in the 24
counterparts.
We find that 491 of the 515 sources in the 24 ![]() m catalog
have an 8
m catalog
have an 8 ![]() m counterpart. For the subsample of interest in this paper
(the 355 IR sources with an H
m counterpart. For the subsample of interest in this paper
(the 355 IR sources with an H![]() counterpart), 349, or almost all, have
a clear detection at 8
counterpart), 349, or almost all, have
a clear detection at 8 ![]() m. To the limit of our completeness for 8
m. To the limit of our completeness for 8 ![]() m,
estimated to be 1037 erg s-1 (90
m,
estimated to be 1037 erg s-1 (90![]() level of completeness),
we find that 8
level of completeness),
we find that 8![]() of the sources have multiple counterparts at 8
of the sources have multiple counterparts at 8 ![]() m.
If the associated PAHs are located along the photodissociation regions and
HII shells, then more than one 8
m.
If the associated PAHs are located along the photodissociation regions and
HII shells, then more than one 8 ![]() m bright rim might be detected per source
even if one stellar cluster is powering the 24
m bright rim might be detected per source
even if one stellar cluster is powering the 24 ![]() m emission at the
center.
m emission at the
center.
In Fig. 1 we show that the source sizes
are always much smaller than their average separations, so the sources are distinct.
The scatter around the average source size is small, comparable to the size of the
symbols used in the plot. Source sizes decrease radially outward and
their average separations increase.
The 8 ![]() m and H
m and H![]() images are used at
the original resolution, higher than that of the 24
images are used at
the original resolution, higher than that of the 24 ![]() m image.
The use of images smoothed to the spatial resolution of the 24
m image.
The use of images smoothed to the spatial resolution of the 24 ![]() m image, 6 arcsecs,
would have more firmly constrained the total flux at 8
m image, 6 arcsecs,
would have more firmly constrained the total flux at 8 ![]() m and H
m and H![]() for some
cases, but it would also have diluted the fainter sources in the midst of high
diffuse emission, making them harder to detect.
The presence of elliptical source PSFs also makes it difficult to match the
source fluxes at all wavelengths. Also, for the main sample, the 8
for some
cases, but it would also have diluted the fainter sources in the midst of high
diffuse emission, making them harder to detect.
The presence of elliptical source PSFs also makes it difficult to match the
source fluxes at all wavelengths. Also, for the main sample, the 8 ![]() m and H
m and H![]() fluxes might be slightly higher in crowded fields than what we derive
(i.e., we might be missing some multiple faint components with luminosities on the order
of our completeness limit).
However, as we shall see later, this will not affect the main results derived
using the isolated source sample. This sample, defined more precisely later in
this Section, consists of round, compact sources without multiple counterparts;
they are found by visually inspecting the images at all wavelengths.
fluxes might be slightly higher in crowded fields than what we derive
(i.e., we might be missing some multiple faint components with luminosities on the order
of our completeness limit).
However, as we shall see later, this will not affect the main results derived
using the isolated source sample. This sample, defined more precisely later in
this Section, consists of round, compact sources without multiple counterparts;
they are found by visually inspecting the images at all wavelengths.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg01.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg23.gif) |
Figure 1:
The average distance between sources, d, and the average source size, s,
are shown as a function of galctocentric radius. The dispersions around the average
source sizes are comparable to the symbol sizes. Different symbols refer to measurements
at different wavelengths: 24 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1086fg02.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg24.gif) |
Figure 2:
The ratio
|
| Open with DEXTER | |
In Fig. 2 we show source luminosities, the 24 ![]() m-to-H
m-to-H![]() ratio and the
24
ratio and the
24 ![]() m-to-8
m-to-8 ![]() m ratio as functions of the galactocentric
radius R. The 24
m ratio as functions of the galactocentric
radius R. The 24 ![]() m and 8
m and 8 ![]() m luminosities are defined as
m luminosities are defined as ![]() ,
where
,
where ![]() is the luminosity per unit frequency at 24 and 8
is the luminosity per unit frequency at 24 and 8 ![]() m, i.e.
m, i.e.
![]() ,
,
![]() being the IR flux measured
and D the distance to M 33.
L24, L8, and
being the IR flux measured
and D the distance to M 33.
L24, L8, and
![]() (uncorrected for
extinction) are in units of erg s-1.
The ratio
(uncorrected for
extinction) are in units of erg s-1.
The ratio
![]() has a high dispersion and is consistent with
having no radial dependence. The slope of the linear fit in the
log(
has a high dispersion and is consistent with
having no radial dependence. The slope of the linear fit in the
log(
![]() plane
is
plane
is
![]() with a Pearson linear correlation coefficient
of -0.14. Brighter IR sources lie preferentially at smaller radii,
but the radial dependence is not strong enough to be dominant when the ratio of 24
with a Pearson linear correlation coefficient
of -0.14. Brighter IR sources lie preferentially at smaller radii,
but the radial dependence is not strong enough to be dominant when the ratio of 24 ![]() m to H
m to H![]() luminosity is considered. H
luminosity is considered. H![]() emission appears to
have a very marginal radial dependence and a higher dispersion than the IR luminosities.
If extinction corrections, generally higher at smaller radii, were applied to the
H
emission appears to
have a very marginal radial dependence and a higher dispersion than the IR luminosities.
If extinction corrections, generally higher at smaller radii, were applied to the
H![]() source luminosities, then the sign of the poor correlation found between
source luminosities, then the sign of the poor correlation found between
![]() and R might be reversed.
However, we show in the rest of this paper that extinction corrections are
small; M 33 is a galaxy with low dust content (see also Verley et al. 2008).
and R might be reversed.
However, we show in the rest of this paper that extinction corrections are
small; M 33 is a galaxy with low dust content (see also Verley et al. 2008).
The ratio
L24/L8 has a radial dependence that is weak but
undoubtedly exists: the slope of the linear fit shown in Fig. 2
is
![]() and the Pearson linear correlation coefficient is
0.34. The radial dependence of the 8
and the Pearson linear correlation coefficient is
0.34. The radial dependence of the 8 ![]() m source luminosity
is stronger than that of the 24
m source luminosity
is stronger than that of the 24 ![]() m luminosity, so the 24-to-8
m luminosity, so the 24-to-8 ![]() m
luminosity ratio increases at large galactocentric radii.
Because PAHs are likely responsible for the 8
m
luminosity ratio increases at large galactocentric radii.
Because PAHs are likely responsible for the 8 ![]() m emission in M 33,
it might be that in the outer disk the lower ISM pressure pushes the
photodissociation regions, where PAHs reside, further from the bulk of the 24
m emission in M 33,
it might be that in the outer disk the lower ISM pressure pushes the
photodissociation regions, where PAHs reside, further from the bulk of the 24 ![]() m
emission. Then our algorithm for finding 8
m
emission. Then our algorithm for finding 8 ![]() m counterparts to 24
m counterparts to 24 ![]() m sources
would fail at large galactocentric radii.
However, Verley et al. (2008)
have found that the average radial profile at 8
m sources
would fail at large galactocentric radii.
However, Verley et al. (2008)
have found that the average radial profile at 8 ![]() m in
M 33 falls off more steeply than that at 24, 70 and 160
m in
M 33 falls off more steeply than that at 24, 70 and 160 ![]() m, and at UV wavelengths.
Hence PAH carriers seem effectively underabundant at large radii.
There have been claims in other
galaxies that this might be due to the low metal content of the outermost regions,
but it is unclear if this applies to M 33 because of its
very shallow metallicity gradient (Magrini et al. 2007b).
m, and at UV wavelengths.
Hence PAH carriers seem effectively underabundant at large radii.
There have been claims in other
galaxies that this might be due to the low metal content of the outermost regions,
but it is unclear if this applies to M 33 because of its
very shallow metallicity gradient (Magrini et al. 2007b).
2.2 Total IR luminosities
Verley et al. (2007) have already pointed
out the large scatter between the SFR
in selected HII regions of M 33
computed via the H![]() optical recombination
line and that inferred from the 24
optical recombination
line and that inferred from the 24 ![]() m infrared flux.
We shall show that this cannot be
from extinction affecting the H
m infrared flux.
We shall show that this cannot be
from extinction affecting the H![]() line because M 33 has
a globally low dust content. Nor does it result from
total IR luminosities of star-forming sites in M 33 that are not well
represented by 24
line because M 33 has
a globally low dust content. Nor does it result from
total IR luminosities of star-forming sites in M 33 that are not well
represented by 24 ![]() m luminosities.
m luminosities.
Verley et al. (2008) have shown that the total
infrared luminosity (hereafter TIR, defined as the emission between 3-1100 ![]() m)
in star-forming regions correlates with
the 24
m)
in star-forming regions correlates with
the 24 ![]() m emission, with a weak additional dependence on the 8-to-24
m emission, with a weak additional dependence on the 8-to-24 ![]() m ratio.
They show that for a sample of sources selected at 160
m ratio.
They show that for a sample of sources selected at 160![]() m, the
m, the
![]() varies between -0.8 and -1.2 when
varies between -0.8 and -1.2 when
![]() varies between -0.5 and 0.3.
The best fitting relation is
varies between -0.5 and 0.3.
The best fitting relation is
where the 24
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg03.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg36.gif) |
Figure 3:
The total infrared luminosity of sources in the main sample
as a function of the 24 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1086fg04.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg37.gif) |
Figure 4:
Ratio of the TIR
to H |
| Open with DEXTER | |
The TIR-to-H![]() luminosity ratio for our main sample
has a large dispersion and shows no dependence on galactocentric radius or
source brightness.
In the next Sextion we will use UV photometry to compute H
luminosity ratio for our main sample
has a large dispersion and shows no dependence on galactocentric radius or
source brightness.
In the next Sextion we will use UV photometry to compute H![]() extinction corrections for each source in the round and isolated samples. The results
prove that the large scatter we observe in Fig. 4 is intrinsic
to the sources and is not the result of measurement errors.
extinction corrections for each source in the round and isolated samples. The results
prove that the large scatter we observe in Fig. 4 is intrinsic
to the sources and is not the result of measurement errors.
We shall show in the rest of the paper that the scatter in Fig. 4
is related to three effects:
(a) a varying dust opacity around sources, which implies that the TIR is not
proportional to the cluster bolometric luminosity; (b) a non linear relation
between the bolometric and H![]() luminosity of newly born clusters
when the cluster luminosity is below a certain threshold, and (c) cluster aging.
luminosity of newly born clusters
when the cluster luminosity is below a certain threshold, and (c) cluster aging.
2.3 UV photometry: the round sample and the isolated sample
We now complement the infrared and H![]() photometry with the far- and
near-UV data. UV colors can also be used to infer the age of 24
photometry with the far- and
near-UV data. UV colors can also be used to infer the age of 24 ![]() m
selected sources. GALEX-UV images of M 33 are
available (Gil de Paz et al. 2007) and we shall use them at the original
resolution (1.5 arcsec) to measure the FUV
and NUV luminosities of 24
m
selected sources. GALEX-UV images of M 33 are
available (Gil de Paz et al. 2007) and we shall use them at the original
resolution (1.5 arcsec) to measure the FUV
and NUV luminosities of 24 ![]() m sources with H
m sources with H![]() counterparts.
Because we perform
the UV photometry using a circular aperture, we select 106 sources at 24
counterparts.
Because we perform
the UV photometry using a circular aperture, we select 106 sources at 24 ![]() m
using the requirement that the PSF ellipticity is less than 0.2.
We shall call this the round sample. We set the
radius of the UV photometric aperture equal to the source size at 24
m
using the requirement that the PSF ellipticity is less than 0.2.
We shall call this the round sample. We set the
radius of the UV photometric aperture equal to the source size at 24 ![]() m
and consider an annulus with a width equal to 2 pixels (3 arcsec for GALEX) around
sources for background removal.
It is not desirable to perform individual UV source extraction
because of crowding due to the high density of UV sources.
As pointed out already in
previous papers (e.g. Calzetti et al. 2005), the UV emission peaks are
sometimes displaced with respect to the infrared emission peaks.
Stellar complexes can be made of 2 or more populations of different ages,
both visible in the UV, with the older ones more extended than the
young ones. In this case the old ones should be included in the background.
We would like to
measure only the UV flux coming from the same area covered by IR emission.
To strengthen our results we have selected a clean sample, made of 26 sources
that have a clean annulus in both the FUV and NUV images, i.e. no source
contamination for background subtraction. We shall call this
the isolated sample.
Briefly, the sources in the isolated sample are sources from the main
sample which satisfy the following criteria:
(i) the PSF of the source at 24
m
and consider an annulus with a width equal to 2 pixels (3 arcsec for GALEX) around
sources for background removal.
It is not desirable to perform individual UV source extraction
because of crowding due to the high density of UV sources.
As pointed out already in
previous papers (e.g. Calzetti et al. 2005), the UV emission peaks are
sometimes displaced with respect to the infrared emission peaks.
Stellar complexes can be made of 2 or more populations of different ages,
both visible in the UV, with the older ones more extended than the
young ones. In this case the old ones should be included in the background.
We would like to
measure only the UV flux coming from the same area covered by IR emission.
To strengthen our results we have selected a clean sample, made of 26 sources
that have a clean annulus in both the FUV and NUV images, i.e. no source
contamination for background subtraction. We shall call this
the isolated sample.
Briefly, the sources in the isolated sample are sources from the main
sample which satisfy the following criteria:
(i) the PSF of the source at 24 ![]() m is
nearly circular i.e. the ellipticity is <0.2
and all of the UV flux is inside
m is
nearly circular i.e. the ellipticity is <0.2
and all of the UV flux is inside ![]() ;
(ii) the source
has one H
;
(ii) the source
has one H![]() counterpart (as defined earlier in this paper);
(iii) in the far- and near-UV maps, an annulus of 2 pixels around the
emitting source is devoid of any sources.
counterpart (as defined earlier in this paper);
(iii) in the far- and near-UV maps, an annulus of 2 pixels around the
emitting source is devoid of any sources.
We will use the round sample, which includes the isolated sample, in the rest of the paper to understand some basic properties of young stellar clusters in M 33. To check that we are not oversubtracting the background in the case of sources which do not have a clean annulus, we compute the average UV luminosities for the isolated sample and for the ensemble of sources in the round sample which are not in the isolated sample. The ratio between the two average luminosities is close to unity, being 38.556 and 38.365 the FUV and NUV logarithmically averaged luminosities (in erg s-1) in the round and non-isolated sample, and 38.563 and 38.377 respectively for the isolated sample. We are therefore confident in the ability of our technique for UV background removal to recover the UV luminosities associated with young clusters.
The UV AB-magnitudes were converted to luminosities
using:
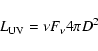 |
(2) |
with D the distance to M 33,
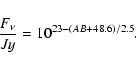 |
(3) |
Considering that the GALEX flux calibration has been revised after the early data release, we apply the recommended 0.12 mag offset to the FUV-NUV color defined as
3 UV colors, opacity and bolometric luminosities of star-forming regions
The TIR luminosity of HII regions is radiation from young stars absorbed and re-emitted by dust grains. The leftover cluster radiation, not absorbed by grains, is mostly emitted in the UV. We now infer the extinction of the radiation coming from the gas and the stars in the HII regions using the observed infrared-to-far UV ratio. As in Calzetti (2001), we shall use the factor 1.68 to account for the bolometric correction of the stellar emission relative to the FUV.
Since our IR and UV data refer to clusters still embedded in HII regions, the dust optical depth for the stellar continuum radiation is
similar to that for the H![]() line emission. We are not considering
the UV light from previous generations of stars.
We infer the FUV extinctions after
measuring the TIR and FUV source luminosities, and then we relate this to the
extinction at other wavelengths as in Calzetti (2001):
line emission. We are not considering
the UV light from previous generations of stars.
We infer the FUV extinctions after
measuring the TIR and FUV source luminosities, and then we relate this to the
extinction at other wavelengths as in Calzetti (2001):
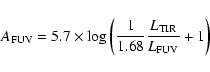 |
(4) |
| (5) |
| (6) |
| (7) |
We show in Fig. 5 the ratio
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1086fg05.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg52.gif) |
Figure 5: Opacity expressed as infrared-to-FUV luminosity ratio versus the observed UV color for all sources in the round sample. Circles indicates sources in the isolated sample. All sources to the left of the line marked 10 Myrs are younger than 10 Myrs according to the instantaneous burst model. All sources below the mark AV=1.7 have visual extinction AV<1.7 mag. |
| Open with DEXTER | |
We estimate the bolometric luminosity of our sources as:
where
We apply extinction corrections to the FUV and H![]() luminosities
of sources in the round sample according to the model described earlier
in this Section.
The good correlation between extinction corrected UV luminosities
and 8
luminosities
of sources in the round sample according to the model described earlier
in this Section.
The good correlation between extinction corrected UV luminosities
and 8 ![]() m luminosities is evident in Fig. 6.
This is expected since PAHs are excited by the UV radiation of the
nearest star-forming region. This
nice correlation confirms the goodness of our extinction corrections.
Thilker et al. (2007) have found that
PAH emission at 8
m luminosities is evident in Fig. 6.
This is expected since PAHs are excited by the UV radiation of the
nearest star-forming region. This
nice correlation confirms the goodness of our extinction corrections.
Thilker et al. (2007) have found that
PAH emission at 8 ![]() m is suppressed within strong star-forming regions.
The linear correlation between extinction corrected far-UV luminosities
and 8
m is suppressed within strong star-forming regions.
The linear correlation between extinction corrected far-UV luminosities
and 8 ![]() m luminosities, which does not break at high
luminosities, suggests that this is not happening in M 33.
m luminosities, which does not break at high
luminosities, suggests that this is not happening in M 33.
A correlation between FUV and H![]() luminosities is also present.
Given the different dependencies of these two luminosities on cluster
mass and age, the presence of some scatter in their relation is
not surprising. The next section will better address this issue.
luminosities is also present.
Given the different dependencies of these two luminosities on cluster
mass and age, the presence of some scatter in their relation is
not surprising. The next section will better address this issue.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1086fg06.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg56.gif) |
Figure 6:
H |
| Open with DEXTER | |
4 The cluster birthline: from bright to dim candles
Because we resolve stars
and clusters in M 33 at IR and optical wavelengths when the brightest member
is earlier than a B2 type star, the
expected relation between IR and H![]() emission is far from
linear even under the circumstance that most of the
bolometric luminosity of massive stars is absorbed by dust and re-emitted
in the IR. This is a result of the different dependencies of the
bolometric and H
emission is far from
linear even under the circumstance that most of the
bolometric luminosity of massive stars is absorbed by dust and re-emitted
in the IR. This is a result of the different dependencies of the
bolometric and H![]() luminosities on the stellar mass
(Panagia 1973; Vacca et al. 1996; Sternberg et al. 2003),
considering the lack of the highest mass stars in some clusters.
In this Section we would like to investigate in detail the emission
by individual clusters at different wavelengths to
judge the reliability of using infrared and H
luminosities on the stellar mass
(Panagia 1973; Vacca et al. 1996; Sternberg et al. 2003),
considering the lack of the highest mass stars in some clusters.
In this Section we would like to investigate in detail the emission
by individual clusters at different wavelengths to
judge the reliability of using infrared and H![]() emission as a
quantitative tracer of recent star formation for a range of luminosities.
emission as a
quantitative tracer of recent star formation for a range of luminosities.
4.1 Modelling cluster birthlines
To compute the H![]() luminosity of a stellar cluster, one needs to
know the mass distribution at the upper end of the IMF. Even though
the stellar IMF is well known for intermediate stellar masses,
where the original exponent derived by Salpeter (1955)
is now widely tested and used, uncertainties remain at the high-
and low-mass ends.
luminosity of a stellar cluster, one needs to
know the mass distribution at the upper end of the IMF. Even though
the stellar IMF is well known for intermediate stellar masses,
where the original exponent derived by Salpeter (1955)
is now widely tested and used, uncertainties remain at the high-
and low-mass ends.
The IMF may be interpreted as a probability distribution
function that specifies the probability for a randomly chosen
star to lie within a certain mass range
(e.g. Barker et al. 2008; Cerviño & Luridiana 2006, for stochasticity in the IMF).
The absence of stars with very high masses suggests there is
a fundamental upper limit to the IMF
(>120-150 ![]() see Weidner & Kroupa 2004; Koen 2006; Hoversten & Glazebrook 2008; Oey & Clarke 2005; Massey & Hunter 1998; Elmegreen 2000; Figer 2005).
The most massive clusters sample the IMF out to this maximum possible stellar mass
and no further, even though there are enough stars to do so if the IMF continued
with the same slope.
Low and intermediate mass clusters do not generally have stars near the maximum
possible mass, but their most massive stars tend to have a mass that increases
with the cluster mass (Larson 1982). This trend leads to the question of
whether the upper limit to the stellar mass in a particular cluster depends on the
cluster mass because of some physically limiting process, or whether it follows only
from randomly sampling the IMF. In the first case, low mass clusters could not
make high mass stars. In the second case they could, as long as there is enough gas,
and intermediate-mass clusters should occasionally be found with unusually massive stars
- ``outliers'' in the IMF. An important difference arises for the summed IMF from many
clusters: it should be steeper than any cluster IMF in the
first case and the same as the average cluster IMF in the second case. The summed IMF
is the basis for the present day mass function in whole galaxies and is therefore
important to understand for population models and studies of galaxy evolution.
A recent debate in the literature suggests the question about maximum stellar mass
should be settled observationally
(Weidner & Kroupa 2004,2006; Elmegreen 2006).
see Weidner & Kroupa 2004; Koen 2006; Hoversten & Glazebrook 2008; Oey & Clarke 2005; Massey & Hunter 1998; Elmegreen 2000; Figer 2005).
The most massive clusters sample the IMF out to this maximum possible stellar mass
and no further, even though there are enough stars to do so if the IMF continued
with the same slope.
Low and intermediate mass clusters do not generally have stars near the maximum
possible mass, but their most massive stars tend to have a mass that increases
with the cluster mass (Larson 1982). This trend leads to the question of
whether the upper limit to the stellar mass in a particular cluster depends on the
cluster mass because of some physically limiting process, or whether it follows only
from randomly sampling the IMF. In the first case, low mass clusters could not
make high mass stars. In the second case they could, as long as there is enough gas,
and intermediate-mass clusters should occasionally be found with unusually massive stars
- ``outliers'' in the IMF. An important difference arises for the summed IMF from many
clusters: it should be steeper than any cluster IMF in the
first case and the same as the average cluster IMF in the second case. The summed IMF
is the basis for the present day mass function in whole galaxies and is therefore
important to understand for population models and studies of galaxy evolution.
A recent debate in the literature suggests the question about maximum stellar mass
should be settled observationally
(Weidner & Kroupa 2004,2006; Elmegreen 2006).
In order to model
the distribution of stellar masses within a young cluster,
we follow two different approaches using the same IMF.
In one case we assume that each
cluster has a maximum stellar mass that is explicitly related to
the cluster mass. We call this the
maximum mass case. In the second case, we assume that stars of all masses
can form in clusters of all masses, provided there is enough gas, and that
the choice of a particular stellar mass is random, following the IMF. We call this
the randomly sampled case.
Once we specify how a cluster is built we need to establish
![]() and
and
![]() ,
the
cluster bolometric and H
,
the
cluster bolometric and H![]() luminosity.
This is done by summing the contributions of all stars in the cluster
using stellar masses, Ly-continuum, and bolometric luminosities
tabulated
by Vacca et al. (1996) for stellar masses
luminosity.
This is done by summing the contributions of all stars in the cluster
using stellar masses, Ly-continuum, and bolometric luminosities
tabulated
by Vacca et al. (1996) for stellar masses
![]() and
by Panagia (1973) for
and
by Panagia (1973) for
![]() .
We extrapolate
luminosity values logarithmically if stellar masses
are outside these mass ranges and interpolate logarithmically for
masses that are intermediate to those shown in their tables.
We assume ZAMS (Zero Age Main Sequence) and solar metallicity and
divide the number of Ly-continuum photon
rates by
.
We extrapolate
luminosity values logarithmically if stellar masses
are outside these mass ranges and interpolate logarithmically for
masses that are intermediate to those shown in their tables.
We assume ZAMS (Zero Age Main Sequence) and solar metallicity and
divide the number of Ly-continuum photon
rates by
![]() ph erg-1 to obtain H
ph erg-1 to obtain H![]() luminosities.
luminosities.
In what follows we compute the theoretical cluster birthline
in the plane log(
![]() )
using a stellar IMF with a
Salpeter slope
)
using a stellar IMF with a
Salpeter slope
![]() between 1 and 120
between 1 and 120 ![]() .
No stars with mass
lower than 1
.
No stars with mass
lower than 1 ![]() or higher
than 120
or higher
than 120 ![]() will be considered. The IMF in stellar clusters
extends down to masses lower than 1
will be considered. The IMF in stellar clusters
extends down to masses lower than 1 ![]() but these stars
give a negligible contribution to the cluster luminosity, which is
the relevant quantity for this paper.
but these stars
give a negligible contribution to the cluster luminosity, which is
the relevant quantity for this paper.
In the maximum mass case, given a number N of cluster members with
masses above 1 ![]() ,
there will be a certain mass limit MN above
which the probability of finding one star is unity and this star will
be of mass M*.
If
,
there will be a certain mass limit MN above
which the probability of finding one star is unity and this star will
be of mass M*.
If ![]() is the number of stars produced per unit mass,
is the number of stars produced per unit mass,
then the number of cluster members with masses above 1
We computed the normalization constant C by assuming that the number of stars between 120
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg07.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg70.gif) |
Figure 7:
Filled circles mark the expected values of the bolometric-to-H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg08.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg71.gif) |
Figure 8:
The distribution of the ratio of the bolometric-to-H |
| Open with DEXTER | |
In the randomly sampled case,
there is no explicit relationship between cluster mass and maximum stellar mass
as in Eqs. (10)-(12).
Even though MN is the most
likely mass for the cluster's most-massive member, the actual mass can be as large as
120 ![]() ,
although the probability that such a massive star actually forms
decreases as the cluster mass decreases.
To model this case, we simulate 40 000 clusters that
are distributed in number according to their mass between 20
and 10 000
,
although the probability that such a massive star actually forms
decreases as the cluster mass decreases.
To model this case, we simulate 40 000 clusters that
are distributed in number according to their mass between 20
and 10 000 ![]() as
as
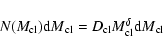 |
(13) |
where
If low mass stars form first, a cluster enters the
birthline from the top left and follows it down and to the right as
![]() increases. If, instead, massive
stars are born at random times during cluster formation,
then the cluster can jump down on the simulated birthline and then move
towards slightly higher values of
increases. If, instead, massive
stars are born at random times during cluster formation,
then the cluster can jump down on the simulated birthline and then move
towards slightly higher values of
![]() and
and
![]() /
/
![]() .
This happens until all of the gas available to fuel star formation is used
or SF is quenched by feedback.
Cluster aging from the death of massive stars increases
the
.
This happens until all of the gas available to fuel star formation is used
or SF is quenched by feedback.
Cluster aging from the death of massive stars increases
the
![]() /
/
![]() ratio and then the cluster moves upward from the birthline.
This is because the death of massive stars makes the cluster H
ratio and then the cluster moves upward from the birthline.
This is because the death of massive stars makes the cluster H![]() luminosity fade away more rapidly than bolometric luminosity.
Using the public code Starburst 99, we evaluate how the clusters evolve off
the birthline. The vertical dashed lines in Fig. 8 show the
aging effect. A cluster reaches the top of the Figure in about 10 Myrs.
Two fundamental properties of the predicted cluster
birthline are: (a) the linear correlation between
luminosity fade away more rapidly than bolometric luminosity.
Using the public code Starburst 99, we evaluate how the clusters evolve off
the birthline. The vertical dashed lines in Fig. 8 show the
aging effect. A cluster reaches the top of the Figure in about 10 Myrs.
Two fundamental properties of the predicted cluster
birthline are: (a) the linear correlation between
![]() and
and
![]() ,
which holds for very young massive clusters (the horizontal part of the birthline),
breaks down below a critical value of
the cluster bolometric luminosity, depending on the stellar
IMF at the high mass-end; (b)all stellar clusters should lie on or above the birthline shown
in Fig. 7 for the two cases examined.
,
which holds for very young massive clusters (the horizontal part of the birthline),
breaks down below a critical value of
the cluster bolometric luminosity, depending on the stellar
IMF at the high mass-end; (b)all stellar clusters should lie on or above the birthline shown
in Fig. 7 for the two cases examined.
4.2 The M 33 test case for the birthline
If most of the luminosity of young clusters were absorbed by
dust and re-irradiated in the IR, then the
![]() data points in the log(
data points in the log(
![]() /
/
![]() )
plane should all lie
above the birthline sequence. However, by looking at Fig. 9,
which plots the observed values on the birthline plane,
we see a clear discrepancy with the birthline theoretical prediction. Many
clusters lie below the birthline, for both the maximum mass case and the
randomly sampled case. It has to be pointed out that
any heavier extinction correction, as well as corrections due to the loss
of ionizing photons leaking out
of the HII regions, will move the data points further down, toward lower
values of
)
plane should all lie
above the birthline sequence. However, by looking at Fig. 9,
which plots the observed values on the birthline plane,
we see a clear discrepancy with the birthline theoretical prediction. Many
clusters lie below the birthline, for both the maximum mass case and the
randomly sampled case. It has to be pointed out that
any heavier extinction correction, as well as corrections due to the loss
of ionizing photons leaking out
of the HII regions, will move the data points further down, toward lower
values of
![]() /
/
![]() .
Since any data point
below the birthline is unexplained we must conclude
that our assumption, namely that the TIR luminosity traces the bolometric
luminosity, is not correct for most of the clusters observed. This discrepancy
with the birthline cannot be the result of an unreliable 24
.
Since any data point
below the birthline is unexplained we must conclude
that our assumption, namely that the TIR luminosity traces the bolometric
luminosity, is not correct for most of the clusters observed. This discrepancy
with the birthline cannot be the result of an unreliable 24 ![]() m - TIR conversion
because the dispersion in the 24
m - TIR conversion
because the dispersion in the 24 ![]() m to TIR luminosity ratio is only about 0.1
in the log. Also recall that individual extinction
corrections have been applied to H
m to TIR luminosity ratio is only about 0.1
in the log. Also recall that individual extinction
corrections have been applied to H![]() luminosities (see Sect. 3).
luminosities (see Sect. 3).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg09.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg80.gif) |
Figure 9:
The total infrared-to-H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg10.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg81.gif) |
Figure 10:
Bolometric to H |
| Open with DEXTER | |
As outlined in the previous Section, we now complement IR with UV photometry
to derive the cluster bolometric luminosity.
In Fig. 10 we plot the
![]() -to-
-to-
![]() ratio as a function
of
ratio as a function
of
![]() for the round sample marking (with circles) members of the isolated
sample. Clusters in
the round and isolated samples lie above the birthline predicted by the
randomly sampled case with a very few exceptions. Members of the isolated sample,
for which UV photometry is more accurate, follow closely the birthline and
this underlines their young age. Only one cluster in the isolated sample with
for the round sample marking (with circles) members of the isolated
sample. Clusters in
the round and isolated samples lie above the birthline predicted by the
randomly sampled case with a very few exceptions. Members of the isolated sample,
for which UV photometry is more accurate, follow closely the birthline and
this underlines their young age. Only one cluster in the isolated sample with
![]() erg s-1 seems to lie below the birthline,
having a lower value of
erg s-1 seems to lie below the birthline,
having a lower value of
![]() /
/
![]() .
The most likely explanation of the H
.
The most likely explanation of the H![]() excess is that
this cluster has formed a star more massive
than 120
excess is that
this cluster has formed a star more massive
than 120 ![]() ,
but additional analysis is needed before drawing any
definitive conclusion on this.
In general the agreement is good also for the round sample: almost all of the
clusters lie above the birthline for the randomly sampled case. This
implies that the round sample is made up of relatively young clusters too.
In Fig. 10 we add the main sequence
boundary (dash-dotted line). This
marks the value of
,
but additional analysis is needed before drawing any
definitive conclusion on this.
In general the agreement is good also for the round sample: almost all of the
clusters lie above the birthline for the randomly sampled case. This
implies that the round sample is made up of relatively young clusters too.
In Fig. 10 we add the main sequence
boundary (dash-dotted line). This
marks the value of
![]() /
/
![]() for a cluster at the end of the main sequence
lifetime for single massive stars (e.g. Stahler & Palla 2005).
It is impressive how the isolated sample is bounded by the
birthline at the bottom and by the main sequence boundary at the top.
That means that effectively we have traced the sequence of young compact
clusters before supernovae disrupt them and blow away dust grains.
for a cluster at the end of the main sequence
lifetime for single massive stars (e.g. Stahler & Palla 2005).
It is impressive how the isolated sample is bounded by the
birthline at the bottom and by the main sequence boundary at the top.
That means that effectively we have traced the sequence of young compact
clusters before supernovae disrupt them and blow away dust grains.
If the birth of stars in clusters is
regulated by the statistical character of the IMF and there is no
physical or absolute relation between the maximum stellar mass in a cluster and
the cluster mass, then the predicted
cluster birthline is in good agreement with the data.
This agreement is illustrated by
the relative number of sources below the birthline, where there should be none. Only
5![]() of the clusters are more than 3-
of the clusters are more than 3-![]() below the birthline in the
randomly-sampled case, whereas 25% of the clusters are more than
3-
below the birthline in the
randomly-sampled case, whereas 25% of the clusters are more than
3-![]() below the birthline in the maximum-mass case.
This result
favours the randomly sampled model for the
stellar population in clusters.
below the birthline in the maximum-mass case.
This result
favours the randomly sampled model for the
stellar population in clusters.
We infer that some of the clusters with the lowest
![]() /
/
![]() ratios for their
ratios for their
![]() values
have outlier massive stars, i.e. massive stars without their usual proportion of
low mass stars. In these cases, a
star has formed with a mass that is larger than the average upper mass
limit for a cluster of that mass. It would be interesting to study these cases more
to see if there are other unusual characteristics, such as extreme mass segregation,
cloud disruption, or cloud temperatures.
values
have outlier massive stars, i.e. massive stars without their usual proportion of
low mass stars. In these cases, a
star has formed with a mass that is larger than the average upper mass
limit for a cluster of that mass. It would be interesting to study these cases more
to see if there are other unusual characteristics, such as extreme mass segregation,
cloud disruption, or cloud temperatures.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1086fg11.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg83.gif) |
Figure 11:
Median values for the randomly sampled case obtained using
different indices for the cluster distribution function:
open squares, filled squares
and open triangles correspond to
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1086fg12.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg84.gif) |
Figure 12:
Median values for the randomly sampled case obtained using
different index for the stellar IMF: filled triangles, filled squares
and open square correspond to
|
| Open with DEXTER | |
The simulated
![]() /
/
![]() distribution is very marginally dependent
on the value of
distribution is very marginally dependent
on the value of ![]() for the cluster mass function. For
for the cluster mass function. For
![]() the distribution of
the median value is within the 1-
the distribution of
the median value is within the 1-![]() error bar values of the more
widely used
error bar values of the more
widely used ![]() distribution (see Fig. 11)
(Hunter et al. 2003; Dowell et al. 2008; Chandar et al. 2006).
Figure 12 shows
the effect of using an IMF index steeper or flatter than the classical
Salpeter value. There is a better agreement of some cluster data with a steeper
IMF at the high-mass end, but the number of clusters below the birthline increases.
So, we favor a Salpeter IMF with some cluster aging to bring them above
the birthline. A diagram of
distribution (see Fig. 11)
(Hunter et al. 2003; Dowell et al. 2008; Chandar et al. 2006).
Figure 12 shows
the effect of using an IMF index steeper or flatter than the classical
Salpeter value. There is a better agreement of some cluster data with a steeper
IMF at the high-mass end, but the number of clusters below the birthline increases.
So, we favor a Salpeter IMF with some cluster aging to bring them above
the birthline. A diagram of
![]() versus UV colors
shows that the most luminous sources are also the oldest in our isolated
sample. This accounts for the slight rise in plotted points above the birthline for
large
versus UV colors
shows that the most luminous sources are also the oldest in our isolated
sample. This accounts for the slight rise in plotted points above the birthline for
large
![]() in Fig. 10. Additional data is
needed to better constrain the ages of those clusters.
in Fig. 10. Additional data is
needed to better constrain the ages of those clusters.
5 Summary and discussion
M 33 is ideal for deriving the properties of young star-forming
clusters and their massive stellar populations. It contains star-forming complexes
with a wide range of luminosities, and it is close enough that even clusters
with one O- or B-type star can be localized.
We have examined in this paper young stellar clusters selected
in the 24 ![]() m map of M 33 that have H
m map of M 33 that have H![]() counterparts.
The 8-to-24
counterparts.
The 8-to-24 ![]() m luminosity ratio has a small dispersion and
shows a dependence on the galactocentric radius.
The total IR-to-H
m luminosity ratio has a small dispersion and
shows a dependence on the galactocentric radius.
The total IR-to-H![]() luminosity ratio,
luminosity ratio,
![]() /
/
![]() ,
shows a larger dispersion, especially towards
faint sources,
and no correlation with galactocentric distance or source IR luminosity.
The large scatter in the TIR-to-H
,
shows a larger dispersion, especially towards
faint sources,
and no correlation with galactocentric distance or source IR luminosity.
The large scatter in the TIR-to-H![]() flux
arises mostly because of variations in the local dust abundance which adds to
some aging effect.
Only a certain fraction of the bolometric luminosity of 24
flux
arises mostly because of variations in the local dust abundance which adds to
some aging effect.
Only a certain fraction of the bolometric luminosity of 24 ![]() m-selected sources
can be absorbed by grains and re-emitted locally at IR wavelengths. This fraction
might be small for low-luminosity sources that are not born along
the spiral arms of M 33.
m-selected sources
can be absorbed by grains and re-emitted locally at IR wavelengths. This fraction
might be small for low-luminosity sources that are not born along
the spiral arms of M 33.
We have calculated the bolometric luminosity for 106 ``round'' stellar
clusters,
![]() ,
using UV and IR photometry. This has allowed us to
test the concept of the cluster birthline introduced in this paper.
The cluster birthline, defined in the parameter space
log(
,
using UV and IR photometry. This has allowed us to
test the concept of the cluster birthline introduced in this paper.
The cluster birthline, defined in the parameter space
log(
![]() /
/
![]() ), is the line of birth of
young clusters, a theoretical lower boundary for the ratio
), is the line of birth of
young clusters, a theoretical lower boundary for the ratio
![]() /
/
![]() for each
for each
![]() .
We show that along the cluster birthline the relation between
.
We show that along the cluster birthline the relation between
![]() and
and
![]() is linear for high-
is linear for high-
![]() clusters but
is non-linear for clusters with
clusters but
is non-linear for clusters with
![]() erg s-1.
Deviations from linearity are expected because of two effects: the IMF is not fully
sampled in low mass clusters, and the
number of photons emitted by a star with energies above the hydrogen ionization
threshold has a stronger dependence on
stellar mass than does the stellar bolometric luminosity
(e.g. Panagia 1973; Vacca et al. 1996).
For high
erg s-1.
Deviations from linearity are expected because of two effects: the IMF is not fully
sampled in low mass clusters, and the
number of photons emitted by a star with energies above the hydrogen ionization
threshold has a stronger dependence on
stellar mass than does the stellar bolometric luminosity
(e.g. Panagia 1973; Vacca et al. 1996).
For high
![]() clusters, the IMF is usually sampled out to the highest possible
stellar mass and then the ratio of high-to-low mass stars is constant, making the
clusters, the IMF is usually sampled out to the highest possible
stellar mass and then the ratio of high-to-low mass stars is constant, making the
![]() to
to
![]() ratio constant. For low
ratio constant. For low
![]() clusters, the IMF becomes
depleted of the highest mass stars; these stars have the lowest
ratio of
clusters, the IMF becomes
depleted of the highest mass stars; these stars have the lowest
ratio of
![]() /
/
![]() and their depletion raises the average ratio.
The observed flatness of
and their depletion raises the average ratio.
The observed flatness of
![]() /
/
![]() for luminous sources
implies either that there is a maximum possible stellar mass equal to
for luminous sources
implies either that there is a maximum possible stellar mass equal to ![]()
![]() ,
as assumed in our models, or that the
,
as assumed in our models, or that the
![]() -to-
-to-
![]() ratio for individual stars
becomes constant at
ratio for individual stars
becomes constant at
![]() .
.
We modeled the cluster birthline by populating clusters of various
masses with stars having masses selected from an IMF. Several cluster mass
function slopes and IMF slopes were used for comparison. We modeled the
upper end of the IMF in two cases. The maximum mass case assumed that each
cluster produced stars with masses only up to a maximum value that equals the
average maximum stellar mass for a cluster of that mass. In this case, low mass clusters
can produce only low mass stars. The randomly sampled case assumed that
each cluster can produce stars over the full range of the IMF, in which case a low
mass cluster can occasionally produce a high mass star (provided the cluster mass
exceeds the stellar mass, of course). Both cases have the same average maximum stellar
mass for clusters of each mass, but only the second case can produce outlier stars -
stars with masses significantly above the average maximum for that cluster, which means
above the upper end of the smooth and declining part of the IMF that is observed
at intermediate stellar mass. Comparing the two cases, the clusters birthline in the
maximum mass case has a higher value of
![]() /
/
![]() over the range of
over the range of
![]() where O- and B-type stars are starting to populate the upper end of the IMF. This range extends
from
where O- and B-type stars are starting to populate the upper end of the IMF. This range extends
from
![]() slightly less than 1038 erg s-1 to
slightly less than 1038 erg s-1 to
![]() slightly larger
than 1040 erg s-1. At smaller
slightly larger
than 1040 erg s-1. At smaller
![]() ,
stars producing H
,
stars producing H![]() emission
do not form in the maximum mass case and are highly unlikely in the randomly sampled case.
At larger
emission
do not form in the maximum mass case and are highly unlikely in the randomly sampled case.
At larger
![]() ,
the IMF is fully sampled in both cases.
,
the IMF is fully sampled in both cases.
From the round sample we selected 26 sources which appear isolated and
compact in the UV maps
i.e. the annular region around them, used for background
subtraction, is not contaminated by UV sources.
All but one of the stellar clusters in this sample, called the isolated sample
are compatible with
cluster birthline predicted in the randomly sampled case for the Salpeter IMF
with maximum stellar mass limit of 120 ![]() .
For the isolated sample in fact 25 out of 26 clusters lie on or above this birthline.
Considering the whole round sample we find similar fractions:
100 over 106 clusters are compatible with the same birthline.
In contrast, 25% of the clusters in the round sample lie below the theoretical
birthline in the maximum mass case, and hence are incompatible with this cluster
population model. M 33 has therefore provided a positive test to the cluster
birthline concept introduced in this paper. Stellar clusters are born
along the birthline and aging moves the clusters above it.
The observations also suggest that
stars randomly sample the IMF and that clusters occasionally have outlier massive stars.
Clusters in the isolated sample lie below the upper main sequence boundary
(
.
For the isolated sample in fact 25 out of 26 clusters lie on or above this birthline.
Considering the whole round sample we find similar fractions:
100 over 106 clusters are compatible with the same birthline.
In contrast, 25% of the clusters in the round sample lie below the theoretical
birthline in the maximum mass case, and hence are incompatible with this cluster
population model. M 33 has therefore provided a positive test to the cluster
birthline concept introduced in this paper. Stellar clusters are born
along the birthline and aging moves the clusters above it.
The observations also suggest that
stars randomly sample the IMF and that clusters occasionally have outlier massive stars.
Clusters in the isolated sample lie below the upper main sequence boundary
(
![]() Myr), which is consistent with their compactness and young age. Below this
boundary, the most massive stars that a cluster formed are still present (assuming
that all stars form at about the same time), so
Myr), which is consistent with their compactness and young age. Below this
boundary, the most massive stars that a cluster formed are still present (assuming
that all stars form at about the same time), so
![]() /
/
![]() remains low, and
supernovae have not yet disrupted the cluster or blown
away the dust. No cluster in the isolated sample lies
above the upper main sequence boundary, but some clusters in the more numerous
round sample do. This difference might indicate that some members of the round sample have
lost their most massive stars (e.g. Pflamm-Altenburg & Kroupa 2006).
However, in the opacity-UV-color diagram, the two samples occupy the same
area so their ages are about the same.
An alternative explanation for the high
remains low, and
supernovae have not yet disrupted the cluster or blown
away the dust. No cluster in the isolated sample lies
above the upper main sequence boundary, but some clusters in the more numerous
round sample do. This difference might indicate that some members of the round sample have
lost their most massive stars (e.g. Pflamm-Altenburg & Kroupa 2006).
However, in the opacity-UV-color diagram, the two samples occupy the same
area so their ages are about the same.
An alternative explanation for the high
![]() /
/
![]() ratio is then
leakage of ionizing photons from HII regions.
Clusters in the round sample are in fact not as compact and isolated as the
clusters in the isolated sample, so the non-isolated clusters could be more prone to leakage.
Future studies that resolve individual
stars should help to answer this age-versus-leakage question.
If massive stars are observed directly, and in proportional to the IMF, then leakage must be
the cause of the higher
ratio is then
leakage of ionizing photons from HII regions.
Clusters in the round sample are in fact not as compact and isolated as the
clusters in the isolated sample, so the non-isolated clusters could be more prone to leakage.
Future studies that resolve individual
stars should help to answer this age-versus-leakage question.
If massive stars are observed directly, and in proportional to the IMF, then leakage must be
the cause of the higher
![]() /
/
![]() ratio.
ratio.
Luminosities at 8 and 24 ![]() m correlate with gas metal abundances;
the dispersion is large because there are
few sources with an accurate metal abundance determination.
While we did not find a significative sample of 24
m correlate with gas metal abundances;
the dispersion is large because there are
few sources with an accurate metal abundance determination.
While we did not find a significative sample of 24 ![]() m sources embedded in
GMCs which are not detected in H
m sources embedded in
GMCs which are not detected in H![]() ,
we find 34 sources
associated with GMCs which have an H
,
we find 34 sources
associated with GMCs which have an H![]() counterpart.
The 24
counterpart.
The 24 ![]() m luminosities of these sources
correlate with associated GMC masses, even though with a large scatter.
m luminosities of these sources
correlate with associated GMC masses, even though with a large scatter.
From studies in the solar neighborhood we know that a stellar cluster in its
youngest stage is likely to be deeply embedded in molecular clouds. Later,
mechanical and radiative effects of
the most massive stars disrupt the cloud, the extinction decreases and the cluster
becomes visible in the ultraviolet. The time interval in which massive
stars are detectable through IR, H![]() and UV emission
depends not only on stellar lifetimes but also on the opacity of the
parent cloud and on its
time evolution. The characteristics of molecular
clouds seem linked to the large-scale morphology of the galaxy.
Earlier studies of a radio-selected sample of thermal sources in M 33
have provided 11 young, optically-visible stellar clusters but no embedded
star cluster (Buckalew et al. 2006). A small sample of compact infrared
selected sources with no H
and UV emission
depends not only on stellar lifetimes but also on the opacity of the
parent cloud and on its
time evolution. The characteristics of molecular
clouds seem linked to the large-scale morphology of the galaxy.
Earlier studies of a radio-selected sample of thermal sources in M 33
have provided 11 young, optically-visible stellar clusters but no embedded
star cluster (Buckalew et al. 2006). A small sample of compact infrared
selected sources with no H![]() counterpart has been observed in the
CO J=1-0 and J=2-1 lines (Corbelli et al. 2009, in preparation). The
weakness or absence of CO lines suggests that these sources are not
embedded proto-stellar clusters in the process of formation but a more
evolved population.
In M 33 the amount of extinction seems generally lower than in the Milky Way.
The absence of large molecular complexes and a steeper mass spectrum
implies that even in an early SF phase many
stellar complexes may not be highly obscured. Later,
winds and SN explosions remove efficiently the dusty envelope
and the cluster fades away in the IR before less massive stars
get off the main sequence.
counterpart has been observed in the
CO J=1-0 and J=2-1 lines (Corbelli et al. 2009, in preparation). The
weakness or absence of CO lines suggests that these sources are not
embedded proto-stellar clusters in the process of formation but a more
evolved population.
In M 33 the amount of extinction seems generally lower than in the Milky Way.
The absence of large molecular complexes and a steeper mass spectrum
implies that even in an early SF phase many
stellar complexes may not be highly obscured. Later,
winds and SN explosions remove efficiently the dusty envelope
and the cluster fades away in the IR before less massive stars
get off the main sequence.
The concept of a cluster birthline together with the high resolution of future telescopes seems a promising way to analyze star formation in external galaxies.
Acknowledgements
We would like to thank R. Walterbos for providing us the Himage of M 33, R. Bandiera, L. Hunt, P. Lenzuni, and F. Palla for stimulating discussion on the Cluster Birthline and the referee, R. de Grijs, for his criticism to an earlier version of the paper. The work of S. V. is supported by a INAF-Osservatorio Astrofisico di Arcetri fellowship. This research has made use of Spitzer Space Telescope data and of GALEX mission data. We acknowledge Spitzer Space Telescope center operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration, and NASA's support for the construction, operation, and science analysis of the GALEX mission, developed in cooperation with the Center National d'Etudes Spatiales of France.
Appendix A: The metallicity and GMC samples
We now investigate if properties of star-forming sites in M 33
are related to the host gas metallicity or to the parent molecular cloud mass.
We first consider a sample of HII regions observed by Magrini et al. (2007b)
for which metallicities have been determined via optical spectroscopy.
Extinction can be estimated via the Balmer decrement, even though this is
only an upper limit to the overall extinction through a whole HII region.
Unfortunately the sample of HII regions with known metallicity for which
radio continuum or Paschen lines are available for determining the extinction
deeply into the star-forming region is limited to 5 bright sources and therefore
the sample is not statistically meaningful.
Our metallicity sample is made of 31 HII regions with known O/H abundance,
Balmer decrement,
and accurate IR photometry at 8 and 24 ![]() m. H
m. H![]() emission has
been corrected for extinction using the Balmer decrement and the relation
emission has
been corrected for extinction using the Balmer decrement and the relation
![]() .
The extinction (which gives values
AV< 1.7 in the whole sample) is comparable to what has
been derived with more accurate estimates. There is no trend of extinction with
metallicity or with gas column density that is associated with the source site.
Low column density gas hosts preferentially low metallicity HII regions.
.
The extinction (which gives values
AV< 1.7 in the whole sample) is comparable to what has
been derived with more accurate estimates. There is no trend of extinction with
metallicity or with gas column density that is associated with the source site.
Low column density gas hosts preferentially low metallicity HII regions.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1086app1.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg92.gif) |
Figure A.1:
Metallicity as a function of galactocentric radius for sources
with IR counterparts. Filled dots represent sources where the electron
temperature diagnostic lines have been detected. The metallicity measured
in terms of O/H from a compilation by Magrini et al. (2007b,a)
is also plotted as a function of the ratios of the 24 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1086app2.eps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg93.gif) |
Figure A.2:
The metallicity measured
in terms of O/H from a compilation of Magrini et al. (2007b,a)
is plotted as a function of the 24 |
| Open with DEXTER | |
The sample of sources with IR counterparts shows a shallow radial metallicity
gradient (Fig. A.1).
If we restrict our sample to sources where the electron
temperature diagnostic lines have been detected, and hence the
electron temperature can be measured (filled dots in Figs. A.1
and A.2), then the gradient is compatible with that derived by
Magrini et al. (2007b)
using the same selection criteria. The
L24/L8 and
![]() ratios do not show any
clear metallicity dependence because sources with high metallicity (say
O/H above -3.5)
have high luminosities at optical and IR wavelengths (Fig. A.2).
The dependence is however very marginal if we consider only sources with electron
temperature determinations, whose metallicities are more certain.
The scatter around the mean values increases
as the metallicity decreases, but this might be an effect of
large galactocentric radii, where most of the low metallicity
regions are found.
ratios do not show any
clear metallicity dependence because sources with high metallicity (say
O/H above -3.5)
have high luminosities at optical and IR wavelengths (Fig. A.2).
The dependence is however very marginal if we consider only sources with electron
temperature determinations, whose metallicities are more certain.
The scatter around the mean values increases
as the metallicity decreases, but this might be an effect of
large galactocentric radii, where most of the low metallicity
regions are found.
IR luminosities show a dependence on metallicity.
Bright sources at 8 and 24 ![]() m are born where metallicity is high while
low metallicity
gas host a wider range of source luminosities. However uncertainties in the
metallicities of bright sources that have no detections of the electron
temperature diagnostic lines are large and do not allow us to
draw firm conclusions.
m are born where metallicity is high while
low metallicity
gas host a wider range of source luminosities. However uncertainties in the
metallicities of bright sources that have no detections of the electron
temperature diagnostic lines are large and do not allow us to
draw firm conclusions.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1086app3.eps}
\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg94.gif) |
Figure A.3:
The molecular cloud masses associated with the IR selected
sources are shown versus the 24 |
| Open with DEXTER | |
We also analyze the BIMA giant molecular cloud dataset
(13'' spatial resolution; Engargiola et al. 2003) to see
if any sources in the main sample are associated with GMCs and
in these cases if the source luminosities are related to the parent GMC masses.
Figure A.3 shows the GMC masses as functions of the L24 and
![]() values for sources within 6.5 arcseconds of a GMC.
This limiting radius was chosen to
match the BIMA spatial resolution of the Engargiola et al. (2003) GMCs survey
that was used to identify the clouds.
There is a dependence of the IR source luminosity on the GMC mass, despite the
large scatter. The slope of the correlation is
values for sources within 6.5 arcseconds of a GMC.
This limiting radius was chosen to
match the BIMA spatial resolution of the Engargiola et al. (2003) GMCs survey
that was used to identify the clouds.
There is a dependence of the IR source luminosity on the GMC mass, despite the
large scatter. The slope of the correlation is
![]() with Pearson linear
correlation coefficient of 0.53. The ratio
with Pearson linear
correlation coefficient of 0.53. The ratio
![]() for the GMC sample
varies by about 1.5 order of magnitudes for sources associated with small clouds,
and by even less for sources associated with the most massive clouds.
Sources in the GMC sample are then confined to a smaller range of
for the GMC sample
varies by about 1.5 order of magnitudes for sources associated with small clouds,
and by even less for sources associated with the most massive clouds.
Sources in the GMC sample are then confined to a smaller range of
![]() than that reported in Fig. A.3 for the full sample. The ratio
than that reported in Fig. A.3 for the full sample. The ratio
![]() shows no clear dependence on the GMC mass.
shows no clear dependence on the GMC mass.
References
- Barker, S., de Grijs, R., & Cerviño, M. 2008, A&A, 484, 711 [NASA ADS] [CrossRef] [EDP Sciences]
- Bell, E. F., Papovich, C., Wolf, C., et al. 2005, ApJ, 625, 23 [NASA ADS] [CrossRef]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bianchi, L., & Efremova, B. V. 2006, AJ, 132, 378 [NASA ADS] [CrossRef] (In the text)
- Buckalew, B. A., Kobulnicky, H. A., Darnel, J. M., et al. 2006, ApJS, 162, 329 [NASA ADS] [CrossRef] (In the text)
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] (In the text)
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [CrossRef] (In the text)
- Calzetti, D., Kennicutt, Jr., R. C., Bianchi, L., et al. 2005, ApJ, 633, 871 [NASA ADS] [CrossRef]
- Cannon, J. M., Walter, F., Armus, L., et al. 2006, ApJ, 652, 1170 [NASA ADS] [CrossRef] (In the text)
- Cerviño, M., & Luridiana, V. 2006, A&A, 451, 475 [NASA ADS] [CrossRef] [EDP Sciences]
- Chandar, R., Fall, S. M., & Whitmore, B. C. 2006, ApJ, 650, L111 [NASA ADS] [CrossRef]
- Corbelli, E. 2003, MNRAS, 342, 199 [NASA ADS] [CrossRef]
- Corbelli, E., & Schneider, S. E. 1997, ApJ, 479, 244 [NASA ADS] [CrossRef]
- de Grijs, R., & Parmentier, G. 2007, Chin. J. Astron. Astrophys., 7, 155 [NASA ADS] [CrossRef] (In the text)
- Deul, E. R., & van der Hulst, J. M. 1987, A&AS, 67, 509 [NASA ADS]
- Dowell, J. D., Buckalew, B. A., & Tan, J. C. 2008, AJ, 135, 823 [NASA ADS] [CrossRef]
- Elmegreen, B. G. 2000, ApJ, 539, 342 [NASA ADS] [CrossRef]
- Elmegreen, B. G. 2006, ApJ, 648, 572 [NASA ADS] [CrossRef]
- Engargiola, G., Plambeck, R. L., Rosolowsky, E., & Blitz, L. 2003, ApJS, 149, 343 [NASA ADS] [CrossRef]
- Engelbracht, C. W., Gordon, K. D., Rieke, G. H., et al. 2005, ApJ, 628, L29 [NASA ADS] [CrossRef] (In the text)
- Figer, D. F. 2005, Nature, 434, 192 [NASA ADS] [CrossRef]
- Freedman, W. L., Wilson, C. D., & Madore, B. F. 1991, ApJ, 372, 455 [NASA ADS] [CrossRef] (In the text)
- Galliano, F., Madden, S. C., Jones, A. P., et al. 2003, A&A, 407, 159 [NASA ADS] [CrossRef] [EDP Sciences]
- Gil de Paz, A., Boissier, S., Madore, B. F., et al. 2007, ApJS, 173, 185 [NASA ADS] [CrossRef] (In the text)
- Heyer, M. H., Corbelli, E., Schneider, S. E., & Young, J. S. 2004, ApJ, 602, 723 [NASA ADS] [CrossRef]
- Hippelein, H., Haas, M., Tuffs, R. J., et al. 2003, A&A, 407, 137 [NASA ADS] [CrossRef] [EDP Sciences]
- Hogg, D. W., Tremonti, C. A., Blanton, M. R., et al. 2005, ApJ, 624, 162 [NASA ADS] [CrossRef]
- Hoopes, C. G., & Walterbos, R. A. M. 2000, ApJ, 541, 597 [NASA ADS] [CrossRef]
- Houck, J. R., Charmandaris, V., Brandl, B. R., et al. 2004, ApJS, 154, 211 [NASA ADS] [CrossRef]
- Hoversten, E. A., & Glazebrook, K. 2008, ApJ, 675, 163 [NASA ADS] [CrossRef]
- Hunter, D. A., Kaufman, M., Hollenbach, D. J., et al. 2001, ApJ, 553, 121 [NASA ADS] [CrossRef] (In the text)
- Hunter, D. A., Elmegreen, B. G., Dupuy, T. J., & Mortonson, M. 2003, AJ, 126, 1836 [NASA ADS] [CrossRef]
- Israel, F. P., & Kennicutt, R. C. 1980, Astrophys. Lett., 21, 1 [NASA ADS]
- Israel, F. P., Gatley, I., Matthews, K., & Neugebauer, G. 1982, A&A, 105, 229 [NASA ADS]
- Israel, F. P., de Boer, K. S., & Bosma, A. 1986, A&AS, 66, 117 [NASA ADS]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] (In the text)
- Kennicutt, Jr., R. C., Calzetti, D., Walter, F., et al. 2007, ApJ, 671, 333 [NASA ADS] [CrossRef]
- Koen, C. 2006, MNRAS, 365, 590 [NASA ADS] [CrossRef]
- Larson, R. B. 1982, MNRAS, 200, 159 [NASA ADS] (In the text)
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [CrossRef] (In the text)
- Lu, N., Helou, G., Werner, M. W., et al. 2003, ApJ, 588, 199 [NASA ADS] [CrossRef]
- Magrini, L., Corbelli, E., & Galli, D. 2007a, A&A, 470, 843 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Magrini, L., Vílchez, J. M., Mampaso, A., Corradi, R. L. M., & Leisy, P. 2007b, A&A, 470, 865 [NASA ADS] [CrossRef] [EDP Sciences]
- Massey, P., & Hunter, D. A. 1998, ApJ, 493, 180 [NASA ADS] [CrossRef]
- Oey, M. S., & Clarke, C. J. 2005, ApJ, 620, L43 [NASA ADS] [CrossRef]
- Panagia, N. 1973, AJ, 78, 929 [NASA ADS] [CrossRef]
- Pflamm-Altenburg, J., & Kroupa, P. 2006, MNRAS, 373, 295 [NASA ADS] [CrossRef] (In the text)
- Rosenberg, J. L., Ashby, M. L. N., Salzer, J. J., & Huang, J.-S. 2006, ApJ, 636, 742 [NASA ADS] [CrossRef]
- Rosolowsky, E., & Simon, J. D. 2008, ApJ, 675, 1213 [NASA ADS] [CrossRef]
- Salpeter, E. E. 1955, ApJ, 121, 161 [NASA ADS] [CrossRef] (In the text)
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [CrossRef] (In the text)
- Stahler, S. W., & Palla, F. 2005, The Formation of Stars, ed. S. W. Stahler, & F. Palla (Wiley-VCH), 865 (In the text)
- Sternberg, A., Hoffmann, T. L., & Pauldrach, A. W. A. 2003, ApJ, 599, 1333 [NASA ADS] [CrossRef]
- Thilker, D. A., Boissier, S., Bianchi, L., et al. 2007, ApJS, 173, 572 [NASA ADS] [CrossRef]
- Vacca, W. D., Garmany, C. D., & Shull, J. M. 1996, ApJ, 460, 914 [NASA ADS] [CrossRef]
- Verley, S., Hunt, L. K., Corbelli, E., & Giovanardi, C. 2007, A&A, 476, 1161 [NASA ADS] [CrossRef] [EDP Sciences]
- Verley, S., Corbelli, E., Giovanardi, C., & Hunt, L. K. 2008, ArXiv e-prints
- Weidner, C., & Kroupa, P. 2004, MNRAS, 348, 187 [NASA ADS] [CrossRef]
- Weidner, C., & Kroupa, P. 2006, MNRAS, 365, 1333 [NASA ADS]
- Wyder, T. K., Hodge, P. W., & Skelton, B. P. 1997, PASP, 109, 927 [NASA ADS] [CrossRef] (In the text)
All Figures
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg01.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg23.gif) |
Figure 1:
The average distance between sources, d, and the average source size, s,
are shown as a function of galctocentric radius. The dispersions around the average
source sizes are comparable to the symbol sizes. Different symbols refer to measurements
at different wavelengths: 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1086fg02.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg24.gif) |
Figure 2:
The ratio
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg03.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg36.gif) |
Figure 3:
The total infrared luminosity of sources in the main sample
as a function of the 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1086fg04.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg37.gif) |
Figure 4:
Ratio of the TIR
to H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1086fg05.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg52.gif) |
Figure 5: Opacity expressed as infrared-to-FUV luminosity ratio versus the observed UV color for all sources in the round sample. Circles indicates sources in the isolated sample. All sources to the left of the line marked 10 Myrs are younger than 10 Myrs according to the instantaneous burst model. All sources below the mark AV=1.7 have visual extinction AV<1.7 mag. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1086fg06.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg56.gif) |
Figure 6:
H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg07.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg70.gif) |
Figure 7:
Filled circles mark the expected values of the bolometric-to-H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg08.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg71.gif) |
Figure 8:
The distribution of the ratio of the bolometric-to-H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg09.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg80.gif) |
Figure 9:
The total infrared-to-H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1086fg10.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg81.gif) |
Figure 10:
Bolometric to H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1086fg11.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg83.gif) |
Figure 11:
Median values for the randomly sampled case obtained using
different indices for the cluster distribution function:
open squares, filled squares
and open triangles correspond to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1086fg12.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg84.gif) |
Figure 12:
Median values for the randomly sampled case obtained using
different index for the stellar IMF: filled triangles, filled squares
and open square correspond to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1086app1.eps}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg92.gif) |
Figure A.1:
Metallicity as a function of galactocentric radius for sources
with IR counterparts. Filled dots represent sources where the electron
temperature diagnostic lines have been detected. The metallicity measured
in terms of O/H from a compilation by Magrini et al. (2007b,a)
is also plotted as a function of the ratios of the 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1086app2.eps}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg93.gif) |
Figure A.2:
The metallicity measured
in terms of O/H from a compilation of Magrini et al. (2007b,a)
is plotted as a function of the 24 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1086app3.eps}
\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2009/08/aa11086-08/Timg94.gif) |
Figure A.3:
The molecular cloud masses associated with the IR selected
sources are shown versus the 24 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.