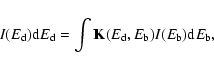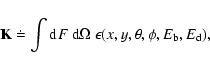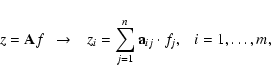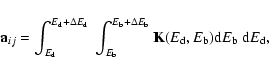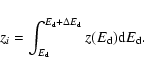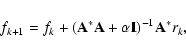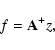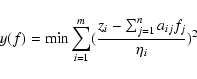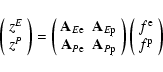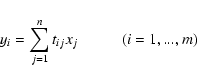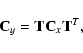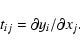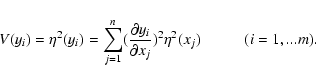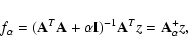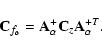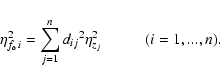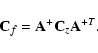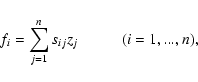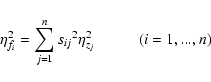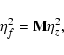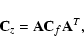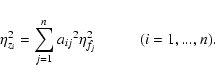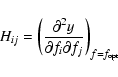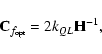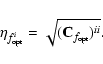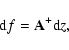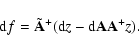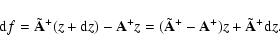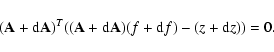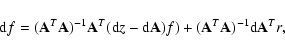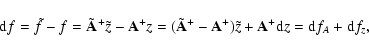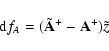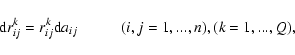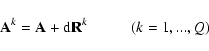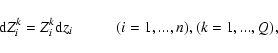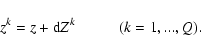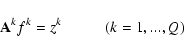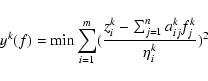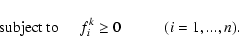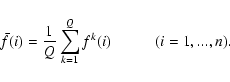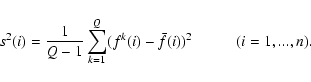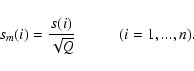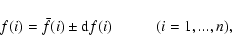Regularization methods used in error analysis of solar particle spectra measured on SOHO/EPHIN

A. Kharytonov; E. Böhm; R. F. Wimmer-Schweingruber

doi:10.1051/0004-6361:200810854

Home

All issues

Volume 495 / No 2 (February IV 2009)

A&A, 495 2 (2009) 663-675

Full HTML

Free Access

Issue		A&A Volume 495, Number 2, February IV 2009


Page(s)		663 - 675
Section		Astronomical instrumentation
DOI		https://doi.org/10.1051/0004-6361:200810854
Published online		22 December 2008

Regularization methods used in error analysis of solar particle spectra measured on SOHO/EPHIN

A. Kharytonov - E. Böhm - R. F. Wimmer-Schweingruber

Institute of Experimental and Applied Physics, Kiel University, Leibnizstrasse 11, 24118 Kiel, Germany

Received 25 August 2008 / Accepted 9 December 2008

Abstract
Context. The telescope EPHIN (Electron, Proton, Helium INstrument) on the SOHO (SOlar and Heliospheric Observatory) spacecraft measures the energy deposit of solar particles passing through the detector system. The original energy spectrum of solar particles is obtained by regularization methods from EPHIN measurements. It is important not only to obtain the solution of this inverse problem but also to estimate errors or uncertainties of the solution.
Aims. The focus of this paper is to evaluate the influence of errors or noise in the instrument response function (IRF) and in the measurements when calculating energy spectra in space-based observations by regularization methods.
Methods. The basis of solar particle spectra calculation is the Fredholm integral equation with the instrument response function as the kernel that is obtained by the Monte Carlo technique in matrix form. The original integral equation reduces to a singular system of linear algebraic equations. The nonnegative solution is obtained by optimization with constraints. For the starting value we use the solution of the algebraic problem that is calculated by regularization methods such as the singular value decomposition (SVD) or the Tikhonov methods. We estimate the local errors from special algebraic and statistical equations that are considered as direct or inverse problems. Inverse problems for the evaluation of errors are solved by regularization methods.
Results. This inverse approach with error analysis is applied to data from the solar particle event observed by SOHO/EPHIN on day 1996/191. We find that the various methods have different strengths and weaknesses in the treatment of statistical and systematic errors.

Key words: Sun: particle emissi on - methods: data analysis - interplanetary medium - methods: numerical

1 Introduction

In many cases the measurements of a physical process is described by the Fredholm integral equation of the first kind

$\begin{displaymath}% \int^b_a K(x,s)f(s) {\rm d}s=z(x), \hspace{4mm} x \in [c,d], \end{displaymath}$

(1)

where f is the unknown and the kernel K and the righthand side z are given functions. The usual approach to solving this inverse problem is the discretization and formulation as a numerical algebra problem (Hansen 1998; Neumaier 1998; Tikhonov & Arsenin 1977). We have a system of linear algebraic equations that is often singular or ill-conditioned

$\begin{displaymath}% {\bf A}f = z, \end{displaymath}$

(2)

where ${\bf A}\in R^{m\times n}$ is a matrix or discrete forward operator with elements a_ij, which describe the measurement process, $f\in R^n$ is the unknown vector with components f_i, and $z\in R^m$ is the known vector with measured components z_i.

When solving this discretized inverse problem with noisy data one must perform the error analysis. For this we consider two approaches.

1): In the statistical approach, we find the error propagation or the covariance matrix from statistical equations. Errors are as a rule in the vector z.
2): In the algebraic approach we find errors from algebraic equations. Errors (called perturbations in this case) can be both in the vector z and in the matrix $\bf A$ .

The statistical error propagation from the input data to the output function are interesting and practical. Those questions for general physical problems are considered in e.g. Bevington (1969), Bock & Krischer (1998), Brandt (1999), Branham (1990), Lyons (1989), Tellinghuisen (2001).

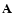Error propagation for solving inverse problems is considered in Hansen (1998), Neumaier (1998), and van Wijk et al. (2002).

After Wilkinson (1965), the perturbation theory was developed in numerical linear algebra, covering linear systems, the matrix inverse, the least square problem, and singular value problems. One can refer to all those problems as the error estimation. Most of those results are discussed in Wilkinson (1965), Björck (1991), Higham (1996), Lawson & Hanson (1974), Neumaier (1998), Wedin (1973), and they also contain the information about error bounds for the case when the matrix $\bf A$ is square or nonsingular. The error estimation for the singular matrix $\bf A$ and discrete inverse problems is considered in Neumaier (1998) and Hansen (1998). Lefebvre et al. (2000) present a method of error propagation for matrix inversion, applicable to a non singular matrix A, including errors in the matrix A. This method may be extended to ill-posed problems, but is not investigated here. The detailed mathematical and physical description of the solar particle spectra computation from the SOHO/EPHIN data have been presented in Böhm et al. (2007), showing the value of the method of regularization, and a comparison of various methods. Missing there was the estimation of uncertainties in the intensities. Thus, in this paper, we focus on the analysis of uncertainties in general and applying various methods to data obtained with the SOHO/EPHIN sensor. Therefore, we give only a brief formulation of this problem in Sect. 3. In Sect. 2 we summarize the telescope EPHIN details, its modeling and experimental data used in the paper. We focus on the error propagation in Sect. 4.1 and consider the error estimation in Sect. 4.3. The statistical approach to the error analysis in perturbed equations is used in Sect. 4.4. The numerical results of the solar energetic particles spectra and errors in solutions obtained by various methods are represented in Sect. 5.

2 Description of EPHIN modeling and measurements

2.1 Instrument and Monte Carlo simulation

The Electron Proton Helium Instrument (EPHIN), part of the Comprehensive Suprathermal and Energetic Particle Analyzer (COSTEP) (Müller-Mellin et al. 1995), on ESA's Solar and Heliospheric Observatory (SOHO) measures solar energetic electrons, protons, and alpha particles in the energy range 150 keV to >5 MeV (electrons) and 4 MeV/n to > 53 MeV/n (protons and helium). EPHIN consists of a stack of five silicon detectors, surrounded by an anti-coincidence shield, a plastic scintillator and sixth silicon detector to distinguish between stopping and penetrating particles (Fig. 1). Two passivated ion-implanted detectors (A and B) define the large (83 $^\circ$ ) field of view with a geometric factor of 5.1 cm² sr. The lithium-drifted silicon detectors C, D, and E stop electrons up to 10 MeV and hydrogen and helium nuclei up to 53 MeV/n. We will only discuss electrons and protons. The generalization to inclusion of helium ions is straightforward. For data analysis the energy deposit is pulse-height analyzed. On-board processing includes classification into E- and P-channels, depending on the energy deposit in each detectors A-E. Thus, the E-channels measure predominantly electrons, the P-channels predominantly protons, but with cross contamination which can be appreciable, depending on the electron-to-proton ratio. The pulse-height-analyzed data contain information on the energy deposit of single particles in detectors A-E in a total of 256 energy bins, and the depth in the sensor head reached (B, C, D, or E). For this work, we have rebinned this energy information into 30 logarithmically equidistantly spaced energy intervals. The sensitivity of each of these energy bins has been modeled as discussed in Sect. 2.2. Together, pulse-height words and energy bin sensitivities allow us to reconstruct the original particle spectra. This paper addresses the accuracy of the energy spectrum calculations achievable with the regularization technique.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{854fig01.eps} \end{figure}$	Figure 1: Side view of the EPHIN-sensor, a telescope consisting of 6 Si-solid state detectors A-F (in green) surrounded by an active anticonincidence scintillator G (in red). 10 simulated beam electrons of 4 MeV are shown in red as well as a pair of generated secondary gamma rays in blue.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=13cm,clip]{854fig02.eps} \end{figure}$

Figure 2:

Matrix A of geometric factors in dependence of the energy deposit $E_{\rm d}$ and the energy of the beam particle $E_{\rm b}$ , with ${\bf A}_{E{\rm e}}$ , ${\bf A}_{E{\rm p}}$ , ${\bf A}_{P{\rm e}}$ , and ${\bf A}_{P{\rm p}}$ in the different quadrants, as derived from the Monte-Carlo simulation of the EPHIN instrument. The scale in energy 0-30 is equivalent to a logarithmic scale 0.1 to 100 MeV, which is repeated from 30 to 60, so displaying the full matrix for electrons and protons. We have applied logarithmic binning in the energies $E_{\rm d}$ and $E_{\rm b}$ to account for the power-law particle spectra that are expected in particle acceleration processes in the heliosphere.

Open with DEXTER

We used GEANT-3 (GEANT3 2006) and GEANT-4 (GEANT4 collaboration 2006) of the CERN program library to simulate the detector response of EPHIN to ions and electrons. The experimental data were analyzed with the PAW package of the CERN program library (PAW 1993), and information about energy resolution and triggering requirements of EPHIN were added at this stage. Final graphics were produced by ROOT from the CERN program library (ROOT 2000). Figure 2 shows the matrix $\bf A$ as obtained from the Monte Carlo simulation, subdivided into four parts. ${\bf A}_{E{\rm e}}$ and ${\bf A}_{P{\rm p}}$ are nearly diagonal energy deposit $\approx$ beam energy, ( $E_{\rm d} \approx E_{\rm b}$ ), with some leakage towards lower energy deposits due to insensitive material and other losses. The cross-talk channels ${\bf A}_{E{\rm p}}$ and ${\bf A}_{P{\rm e}}$ show much lower response than ${\bf A}_{E{\rm e}}$ and ${\bf A}_{P{\rm p}}$ and are considerably less diagonal. Figure 3 shows the matrix of uncertainties corresponding to the geometric factors as given in Fig. 2. For small geometric factors the relative errors may reach 100%, as demonstrated in Fig. 4, displaying the relative error in the geometric factor for the matrix elements on the diagonal. Included is the interval in which there is a null row vector in matrix A (no entries in the beam energy for any energy deposit interval). dA was derived from a combination of statistical uncertainty in Monte Carlo simulation and considerations about the uncertainty in the instrument, such as uniformity of dead layers, and energy resolution.

$\begin{figure} \par\includegraphics[width=13cm,clip]{854fig03.eps} \end{figure}$	Figure 3: Errors on geometric factors ${\bf A}_{E{\rm e}}$ , ${\bf A}_{E{\rm p}}$ , ${\bf A}_{P{\rm e}}$ , and ${\bf A}_{P{\rm p}}$ as derived from the Monte-Carlo simulation of the EPHIN instrument. The description is analogous to Fig. 2. Note the different z-axis scales of Figs. 2 and 3.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig04.eps} \end{figure}$	Figure 4: Relative errors of geometric factors for the diagonal elements of matrix A, null row vector in matrix A means (no entries in the beam energy for any energy deposit interval) (see Figs. 2, 3).
Open with DEXTER

2.2 Data used in analysis

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig05.eps} \end{figure}$

Figure 5:

Time series of E-channel ( upper panel) and P-channel ( lower panel) count rates during the solar particle event of days 188 to 192 in 1996. The various curves (red, green, black and blue) show count rates in the energy intervals, as recorded by the SOHO-EPHIN-sensor. Day 1996/191, 16-17 h, has been chosen for a detailed analysis: a 24-h pre-event period on day 1996/188 has been taken as solar and non-solar interplanetary event background measurement.

Open with DEXTER

The solar energetic particle event of day 191 in 1996 has been chosen in this analysis, to illustrate again the regularization method in this work, but with putting main effort into uncertainty estimation. We have analyzed other time periods (Böhm et al. 2007; and Gòmez-Herrero et al. 2006), but will limit ourselves here to the time period defined above in this work.

Figure 5 shows the count rate in that time period for the E-channels, supposed to be mainly electrons, and the P-channels, supposed to be mainly protons. Day 188 has been taken to represent the background for quiet times and has been used to correct the solar event count rates. Error analysis has been performed for day 191, 16-17 h. Figure 6 shows the total pulse height distribution in the E- and P-channel, which is used as the z-vector in Eq. (2). For the uncertainty, $\eta$ , we use the rule of quadratic addition of errors (see Bock & Krischer 1998) in the optimization approach. The terms $\eta_i$ are the purely statistical errors associated with each data point (omitting uncertainties in the matrix elements of A).

$\begin{displaymath}% \eta_i^2 = (\eta_{\rm ev})^2_i + (\eta_{\rm back})^2_i, \end{displaymath}$

(3)

where $(\eta_{\rm ev})_i$ is the error in the experimental data day 191, 16-17 h, in the event, and $(\eta_{\rm back})_i$ is the error in the background observation (day 188) (see Fig. 5).

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig06.eps} \end{figure}$	Figure 6: Measured pulse height (energy deposit) distribution on day 191/1996, 16-17 h, all E-channels have been combined and all P-channels have been combined too. The background as measured on day 188/1996 has been subtracted (see Fig. 5). The binning is equidistant in logarithmic scale, 10 bins per decade, corresponding to the energy deposit $E_{\rm d}$ , see Fig. 2.
Open with DEXTER

Note that the validity of this background estimate for our investigated time period hinges on the observation that other background sources, especially X-ray-induced background, are normally concentrated around the onset of solar particle events. To reduce the influence of such background, we have chosen a part of the event, which is late in its sequence, and by using the coincidence technique X- and $\gamma$ -rays only contribute to the count rate by chance coincidences.

3 The basic integral equation and its solution

The basic integral equation (Eq. (4)) connects the intensity of the energy deposit $I(E_{\rm d})$ and the intensity of the original beam energy $I(E_{\rm b})$ of particles. A particle entering the instrument deposits an energy $E_{\rm d}$ in the instrument. Because of incomplete charge collection and insensitive material (such as dead layers), $E_{\rm d}$ is lower than the original energy of the particle $E_{\rm b}$ . Since the energy deposit is a stochastic process, the statistical and experimental accuracy limits the resolution in $E_{\rm d}$ . In addition, because of the different ionization cross sections of electrons and protons (and of other ions), $E_{\rm d}$ not only depends on $E_{\rm b}$ , but also on particle species. Other important factors determining $E_{\rm d}$ given $E_{\rm b}$ are angles, dead layers, detector arrangements, etc., and need to be taken into account when simulating detector response to a beam of particles with energy $E_{\rm b}$ and intensity $I(E_{\rm b})$ . Thus, the intensity of the energy deposit, $I(E_{\rm d})$ , is generally given by

$\begin{displaymath}% I(E_{\rm d}){\rm d}{E_{\rm d}} = \int {\bf K}(E_{\rm d}, E_{\rm b}) I(E_{\rm b}) {\rm d}{E_{\rm b}}, \end{displaymath}$

(4)

which is the Fredholm integral equation (Eq. (1)) that needs to be solved for the unknown quantity $I(E_{\rm b})$ . Here, ${\bf K}(E_{\rm d}, E_{\rm b})$ , the kernel of the integral equation, is the instrument sensitivity to measure $E_{\rm d}$ given a particle of energy $E_{\rm b}$ . The kernel, ${\bf K}$ , is then given by

$\begin{displaymath}% {\bf K} \doteq \int {\rm d}F~ {\rm d}\Omega ~ \epsilon (x, y, \theta, \phi, E_{\rm b}, E_{\rm d}), \end{displaymath}$

(5)

where $\epsilon$ is the efficiency of detecting a particle with energy in $[E_{\rm b}, E_{\rm b} + {\rm d} E_{\rm b}]$ that deposits energy in the range $[E_{\rm d}, E_{\rm d} + {\rm d} E_{\rm d}]$ , hitting the detector in the area element ${\rm d} F$ at position (x,y) within the solid angle element ${\rm d} \Omega$ from the direction given by $\theta$ and $\phi$ . $\epsilon$ and ${\bf K}$ need to be calculated using a Monte-Carlo simulation that is described below. We will assume an isotropic angular distribution of the beam and a homogeneous (uniform) distribution on the sensor area. Equation (4) may also be interpreted as an algebraic equation if the kernel ${\bf K}$ is known in discrete intervals, just as Eq. (1) may be interpreted as Eq. (2),

$\begin{displaymath}% z = {\bf A}f \ \ \rightarrow\ \ \ z_i = \sum_{j=1}^n {\bf a}_{ij} \cdot f_j, \ \ \ i = 1, \ldots, m, \end{displaymath}$

(6)

where

$\begin{displaymath}% {\bf a}_{ij} = \int_{E_{\rm d}}^{E_{\rm d} + \Delta E_{\rm ... ... K}(E_{\rm d}, E_{\rm b}) {\rm d}E_{\rm b} \ {\rm d}E_{\rm d}, \end{displaymath}$

(7)

and

$\begin{displaymath}% z_i = \int_{E_{\rm d}}^{E_{\rm d} + \Delta E_{\rm d}} z(E_{\rm d}) {\rm d}E_{\rm d}. \end{displaymath}$

(8)

We solve Eq. (6) by the following regularization methods:

a)

The iterated Tikhonov method: the iterated Tikhonov regularization method using the scheme

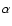$\begin{displaymath}% f_{k+1} = f_{k} + ({\bf A^{\ast}A} + {\alpha}{\bf I})^{-1}{\bf A^{\ast}}r_{k}, \end{displaymath}$

(9)

where $\alpha$ is the regularization parameter 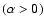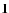$(\alpha>0)$ , $\bf I$ is the identity matrix, 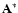${\bf A^{\ast}}$ is the adjoint matrix and r_k is the residual

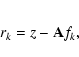
$\begin{eqnarray*}r_{k} = z - {\bf A}f_k, \end{eqnarray*}$

with f₀ = 0 gives the solution of the Tikhonov method,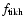 $f_{\rm tikh}$ .

b)

Singular value decomposition (SVD) method: it is known that the minimum norm solution of the least square problem 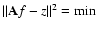$\vert\vert{\bf A}f-z\vert\vert^{2} = \min$ is given by the vector

$\begin{displaymath}% f = {\bf A^{+}}z, \end{displaymath}$

(10)

and is called a pseudo-solution of the system Eq. (6), the matrix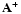 ${\bf A^{+}}$ is the Moore-Penrose pseudo-inverse of $\bf A$ .

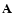This solution, 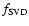$f_{\rm SVD}$ , is completely congruent with the solution of the Tikhonov method 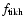$f_{\rm tikh}$ , Eq. (9).

c)

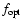Optimization with constraints: the nonnegative solution $f_{\rm opt}$ is obtained by optimization with constraints

$\begin{displaymath}% y(f) = \min \sum_{i=1}^m(\frac{z_{i} - \sum_{j=1}^{n}{a_{ij}f_{j}}} {\eta_{i}})^2 \end{displaymath}$

(11)

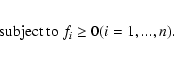
$\begin{eqnarray*}{\rm subject~to}\; f_{i} \geq 0 (i = 1,...,n). \end{eqnarray*}$

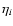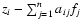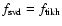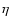and with $\eta_i$ (Eq. (3)) desribing the uncertainty in the numerator, $z_{i} - \sum_{j=1}^{n}{a_{ij}f_{j}}$ . $f_{\rm {svd}} = f_{\rm {tikh}}$ is used as the starting value. Here we use the non-standard notation for the deviation $\eta$ instead of the standard symbol 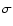$\sigma$ , to avoid any confusion with singular value of the matrices. For more details see Böhm et al. (2007).

The response functions, $\bf A$ , for the E- and P-channels can be presented in following decomposed form. The matrix elements ${\bf a}_{ij}$ in the E-channels for electrons are ${\bf A}_{E{\rm e}}$ and for protons ${\bf A}_{E{\rm p}}$ , and in the P-channels for electrons are ${\bf A}_{P{\rm e}}$ and for protons ${\bf A}_{P{\rm p}}$ .

Then Eq. (6) can be rewritten in the form

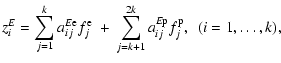		$\displaystyle z_i^E = \sum_{j=1}^k a_{ij}^{E{\rm e}} f_j^{\rm e} \ + \ \sum_{j = k+1}^{2 k} a_{ij}^{E{\rm p}} f_j^{\rm p}, \ \ (i=1,\ldots,k),$	(12)
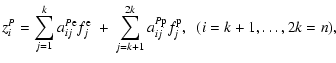		$\displaystyle z_i^P = \sum_{j=1}^k a_{ij}^{P{\rm e}} f_j^{\rm e} \ + \ \sum_{j = k+1}^{2 k} a_{ij}^{P{\rm p}} f_j^{\rm p}, \ \ (i=k+1,\ldots,2k = n),$	(13)

or, in matrix form,

$\begin{displaymath}% \left( \begin{array}{c} z^E \\ z^P \end{array}\right) = \l... ...eft( \begin{array}{c} f^{\rm e}\\ f^{\rm p}\end{array}\right) \end{displaymath}$

(14)

where $f^{\rm e}$ and $f^{\rm p}$ are the electron and proton distributions, and z^E and z^P are the measured count rates in the E- and P-channels.

4 Error analysis

In this section we consider the well-known and newly developed methods for the estimation of errors in the solution of the discrete inverse problems.

4.1 Error propagation

We will use the general error propagation law that is known from the theory of linear transformations of random variables and in multi variate statistics (Brandt 1999).

For m linear functions ${\bf y} = (y_1, y_2, ..., y_m)$ of random variables ${\bf x} = (x_1, x_2, ..., x_n)$ with the covariance matrix ${\bf C}_x(n\times n)$

$\begin{displaymath}% y_i = \sum_{j=1}^{n}{t_{ij}x_{j}} \hspace*{1cm} (i = 1,...,m) \end{displaymath}$

(15)

or in matrix form

$\begin{displaymath}% {\bf y} = {\bf Tx} \end{displaymath}$

(16)

one can obtain the covariance $(m\times m)$ matrix ${\bf C}_y$

$\begin{displaymath}% {\bf C}_y = {\bf TC}_x{\bf T}^T, \end{displaymath}$

(17)

where $\bf T$ is the matrix of derivatives or the Jacobi matrix. Furthermore we assume that the errors are small,

$\begin{displaymath}% t_{ij} = {\partial y_{i}}/{\partial x_{j}}. \end{displaymath}$

(18)

Equation (17) is known as the general error propagation law.

If all x_i are independent, i.e. if ${\bf C}_x$ is diagonal, the variances of y_i are given by the law of error propagation in the well-known form

$\begin{displaymath}% V(y_i) = {\eta}^2(y_i) = \sum_{j=1}^{n}(\frac{\partial y_{i}}{\partial x_{j}})^2 {\eta}^2(x_j) \hspace*{1cm} (i = 1,...m). \end{displaymath}$

(19)

4.1.1 Tikhonov method

The error propagation problem with the Tikhonov regularization method is presented in van Wijk et al. (2002). The regularized solution of Eq. (2) by the Tikhonov method is

$\begin{displaymath}% f_{\alpha} = ({\bf A}^{T}{\bf A} + {\alpha}{\bf I})^{-1}{\bf A}^{T}z = {\bf A}^{+}_{\alpha}z, \end{displaymath}$

(20)

where ${\bf A}^{+}_{\alpha}$ is the regularized pseudo-inverse

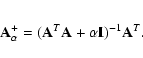
$\begin{eqnarray*}{\bf A}^{+}_{\alpha} = ({\bf A}^{T}{\bf A} + {\alpha}{\bf I})^{-1}{\bf A}^{T}. \end{eqnarray*}$

From Eq. (17) one can obtain the variance-covariance matrix of $f_{\alpha}$

$\begin{displaymath}% {\bf C}_{f_{\alpha}} = {\bf A}^{+}_{\alpha}{\bf C}_z{\bf A}^{+T}_{\alpha}. \end{displaymath}$

(21)

Let ${\bf A}^{+}_{\alpha} = \bf D$ . If all z_i are independent, i.e. if C_z is diagonal, the law of error propagation has the form

$\begin{displaymath}% \eta_{f_{\alpha}{i}}^2 = \sum_{j=1}^{n}{d_{ij}}^2 \eta_{z_{j}}^2 \hspace{1cm} (i = 1,...,n). \end{displaymath}$

(22)

4.1.2 SVD method

Formally we obtain the variance $\eta^2_{f}$ from the direct problem, using the minimum norm solution of the least square problem

$\begin{displaymath}% f = {\bf A^{+}}z, \end{displaymath}$

(23)

where the matrix ${\bf A^{+}}$ is the pseudo-inverse of the matrix $\bf A$ . The general error propagation law for this case is

$\begin{displaymath}% {\bf C}_{f} = {\bf A}^{+}{\bf C}_z{\bf A}^{+T}. \end{displaymath}$

(24)

Let $\bf A^{+} = \bf S$ , then Eq. (23) in the component form is

$\begin{displaymath}% f_{i} = \sum_{j=1}^{n}{s_{ij}z_{j}} \hspace*{1cm} (i = 1,...,n), \end{displaymath}$

(25)

where s_ij are components of ${\bf S}\in R^{n\times n}$ .

For all z_i independent the law of error propagation is

$\begin{displaymath}% \eta_{f_{i}}^2 = \sum_{j=1}^{n}{s_{ij}}^2 \eta_{z_{j}}^2 \hspace{1cm} (i = 1,...,n) \end{displaymath}$

(26)

or in matrix form

$\begin{displaymath}% \eta_{f}^2 = {\bf M}{\eta_{z}^2}, \end{displaymath}$

(27)

where ${\bf M}\in R^{n\times n}$ is a matrix with elements m_ij=s_ij², and $\eta_{f}^2\in R^n$ is the unknown vector with components $\eta_{f_{i}}^2$ , and ${\eta_{z}^2}\in R^n$ is defined as $\eta_{i}^2$ in Eq. (11).

4.1.3 Minimum variance method

Now consider f as the known vector and Eq. (2) as the direct problem of a calculating z. We define the variance $\eta_{z}^2$ with components $\eta_{z_{i}}^2$ from the general error propagation law Eq. (17)

$\begin{displaymath}% {\bf C}_z = {\bf A}{\bf C}_{f}{\bf A}^T, \end{displaymath}$

(28)

where ${\bf C}_z$ and ${\bf C}_f$ are variance-covariance matrices.

For statistically independent random variables f and z, matrices ${\bf C}_z$ , ${\bf C}_f$ are diagonal and the law of error propagation is

$\begin{displaymath}% \eta_{z_{i}}^2 = \sum_{j=1}^{n}{a_{ij}}^2 \eta_{f_{j}}^2 \hspace{1cm} (i = 1,...,n). \end{displaymath}$

(29)

Equation (29) in the matrix form is

$\begin{displaymath}% {\bf B}x = y, \end{displaymath}$

(30)

where ${\bf B}\in R^{n\times n}$ is a matrix with elements b_ij=a_ij², $x\in R^n$ is the unknown vector with components $x_{i}=\eta_{f_{i}}^2$ , $y\in R^n$ is the known vector with components $y_{i}=\eta_{z_{i}}^2$ . Thus we have system of linear algebraic equations for finding the unknown vector $x=\eta_{f}^2$ . For this, one must solve the inverse problem with singular matrix $\bf B$ . Algebraic and optimization approaches are used for solving this problem. The algebraic solution can be obtained by the SVD method and the iterated Tikhonov regularization method.

In the optimization approach we must find the minimum of a multivariable function.

4.2 Using MATLAB functions in error analysis

In data analysis the MATLAB function fmincon (Matlab 2006) is used for determining the best estimate $f_{\rm opt}$ for unknown values f from Eq. (11). Information on the errors of $f_{\rm opt}$ is obtained from the Hessian matrix $\bf H$ with components

$\begin{displaymath}% H_{ij} = \left(\frac{\partial^2 {y}}{\partial {f_i}\partial {f_j}}\right)_{f=f_{\rm opt}} \end{displaymath}$

(31)

as the elements of the symmetric matrix of second derivatives of the minimization function.

The covariance matrix of $f_{\rm opt}$ is

$\begin{displaymath}% {\bf C}_{f_{\rm opt}} = 2k_{QL}{\bf H}^{-1}, \end{displaymath}$

(32)

where the numerical value k_QL = 1, when the function being minimized is a sum of squares (Eq. (11)). The square roots of the diagonal elements are the symmetric errors

$\begin{displaymath}% \eta_{f_{\rm opt}^{i}} = \sqrt{({\bf C}_{f_{\rm opt}})^{ii}}. \end{displaymath}$

(33)

The MATLAB function lscov allows us to obtain standard errors ${\rm d}f$ and the covariance matrix of the function f.

4.3 Error estimation

We first consider the sensitivity of the solution of Eq. (2) to the perturbations in the right-hand side z. If z is changed to $z + {\rm d}z$ then f is changed to $f + {\rm d}f$ and Eq. (2) is

$\begin{displaymath}% {\bf A}(f + {\rm d}f) = z + {\rm d}z. \end{displaymath}$

(34)

Subtracting Eq. (2) from Eq. (34), we have

$\begin{displaymath}% {\bf A}{\rm d}f = {\rm d}z. \end{displaymath}$

(35)

The solution of Eq. (35) is the perturbation ${\rm d}f$

$\begin{displaymath}% {\rm d}f = {\bf A}^{+}{\rm d}z, \end{displaymath}$

(36)

where ${\bf A^{+}}$ is the pseudo-inverse of matrix $\bf A$ .

Now consider the effect of perturbations in $\bf A$ and z. For the perturbed solution $\tilde{f} = f + {\rm d}f$ we have the equation

$\begin{displaymath}% \tilde{\bf A}\tilde{f} = \tilde{z}, \end{displaymath}$

(37)

where $\tilde{\bf A} = {\bf A} + {\rm d}{\bf A}$ and $\tilde{z} = z +{\rm d}z$ . Then the solution of Eq. (37) is

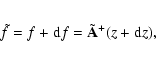
$\begin{eqnarray*}\tilde{f} = f + {\rm d}f = \tilde{\bf A}^{+}(z + {\rm d}z), \end{eqnarray*}$

where $\tilde{\bf A}^{+}$ is the pseudo-inverse of matrix $\tilde{\bf A}$ .

The value ${\rm d}f$ from Eq. (37) or the difference between the perturbed solution $\tilde{f}$ and the unperturbed f can be computed by various means. We can write one solution as

$\begin{displaymath}% {\rm d}f = \tilde{\bf A}^{+}({\rm d}z - {\rm d}{\bf A}{\bf A}^{+}z). \end{displaymath}$

(38)

Another expression for ${\rm d}f$ is presented in Lawson & Hanson (1974)

$\begin{displaymath}% {\rm d}f = \tilde{\bf A}^{+}(z + {\rm d}z) - {\bf A}^{+}z = (\tilde{\bf A}^{+} - {\bf A}^{+})z + \tilde{\bf A}^{+}{\rm d}z. \end{displaymath}$

(39)

The case when ${\rm rank}({\bf A}) = {\rm rank}({\bf A} + {\rm d}{\bf A}) = n$ is considered in Björck (1996). The perturbed solution $\tilde{f} = f + {\rm d}f$ satisfies the normal equations

$\begin{displaymath}% ({\bf A} + {\rm d}{\bf A})^{T}(({\bf A} + {\rm d}{\bf A})(f + {\rm d}f) - (z +{\rm d}z)) = 0. \end{displaymath}$

(40)

Subtracting ${\bf A}^{T}({\bf A}f - z) = 0$ , and neglecting second-order terms, one finds

$\begin{displaymath}% {\rm d}f = ({\bf A}^{T}{\bf A})^{-1}{\bf A}^{T}({\rm d}z - ... ... d}{\bf A})f) + ({\bf A}^{T}{\bf A})^{-1}{\rm d}{\bf A}^{T}r, \end{displaymath}$

(41)

where $r = z - {\bf A}f$ .

Wedin & Wikström (2002) use the following formula

$\begin{displaymath}% {\rm d}f = \tilde{f} - f = \tilde{\bf A}^{+}\tilde{z} - {\b... ...{+})\tilde{z} + {\bf A}^{+}{\rm d}z = {\rm d}f_A + {\rm d}f_z, \end{displaymath}$

(42)

where the first term

$\begin{displaymath}% {\rm d}f_A = (\tilde{\bf A}^{+} - {\bf A}^{+})\tilde{z} \end{displaymath}$

(43)

correspond to perturbations in $\bf A$ and the second one, ${{\rm d}f_z} = {\bf A}^{+}{\rm d}z$ , to perturbations in z (see Eq. (35)). We use Eqs. (36), (42), and (43) in uncertainty calculations described in this subsection.

4.4 Monte Carlo method with random perturbations (Method of numerical ``measurements'')

We consider the perturbations in $\bf A$ and z as a random process. For our case we have ${\rm rank}({\bf A}) = {\rm rank}({\rm d}{\bf A}) < n$ . The matrices $\bf A$ and ${\rm d}\bf A$ are nonnegative ( $a_{ij}\geq 0$ and ${\rm d}a_{ij}\geq 0$ ). Let Q be the number of calculations that one can consider as the number of ``measurements'' or the sample of a size Q. Then for every calculation k from this set Q the random perturbations matrix ${\rm d}{\bf R}^{k}$ is obtained by the following method. We use the random matrix ${\bf R}^{k}$ with components r_ij^k and ${\rm rank}({\bf R}^{k}) = n$ . Random numbers in this matrix have a normal distribution with mean 0 and standard deviation 1. Then we obtain the matrix ${\rm d}{\bf R}^{k}$ with components ${\rm d}r_{ij}^{k}$ as

$\begin{displaymath}% {\rm d}r_{ij}^{k} = r_{ij}^{k}{\rm d}a_{ij} \hspace*{1cm} (i,j = 1,...,n),(k = 1,...,Q), \end{displaymath}$

(44)

where ${\rm d}a_{ij}$ are components of the matrix ${\rm d}\bf A$ . Then we form the matrix

$\begin{displaymath}% {\bf A}^{k} = {\bf A} + {\rm d}{\bf R}^{k} \hspace*{1cm} (k = 1,...,Q) \end{displaymath}$

(45)

with the necessary condition that these new matrices ${\bf A}^{k}$ must be nonnegative. We obtain the random perturbations vector ${\rm d}Z^{k}_{i}$ by the similar method

$\begin{displaymath}% {\rm d}Z^{k}_{i} = Z^{k}_{i}{\rm d}z_{i} \hspace*{1cm} (i = 1,...,n), (k = 1,...,Q), \end{displaymath}$

(46)

where Z^k is an array of random numbers with mean 0 and standard deviation 1 that has the same size as z. The vector z^k must be nonnegative

$\begin{displaymath}% z^{k} = z +{\rm d}Z^{k} \hspace*{1cm} (k = 1,...,Q). \end{displaymath}$

(47)

If $\bf A$ and z for every k (k = 1,...,Q) are changed to ${\bf A}^{k}$ and z^k then the solution f is changed to $f^{k} = f + {\rm d}f^{k}$ .

We solve the algebraic equations

$\begin{displaymath}% {\bf A}^{k}f^{k} = z^{k} \hspace*{1cm} (k = 1,...,Q) \end{displaymath}$

(48)

and the optimization problem as the minimum of a constrained nonlinear multi-variable function for every k (k = 1,...,Q)

$\begin{displaymath}% y^{k}(f) = \min \sum_{i=1}^m(\frac{z^{k}_{i} - \sum_{j=1}^{n}{a^{k}_{ij}f^{k}_{j}}}{\eta^{k}_{i}})^2 \end{displaymath}$

(49)

$\begin{displaymath}% {\rm subject~to} \hspace*{0.5cm} f^{k}_{i} \geq 0 \hspace*{1cm}(i = 1,...,n). \end{displaymath}$

(50)

Here z^k_i are the components of $z^{k}\in R^m$ , a^k_ij are the components of ${\bf A}^{k}\in R^{m\times n}$ , and $\eta^{k}_{i}>0 \ (i = 1,...,m)$ are given numbers.

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig07.eps} \end{figure}$

Figure 7:

Energy distribution for day 191/1996, 16-17 h, solutions $f_{\rm alg}$ and $f_{\rm opt}$ are obtained by applying Eqs. (10), (11). Null row vector in matrix A means: no entries in the beam energy for any energy deposit interval, creating unphysical results, but still producing mathematically correct numbers, small positive or even large negative numbers and uncertainties (see Figs. 2, 3). Points at 10^-2 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.

Open with DEXTER

Solving these problems we obtain 2Q solutions.

The arithmetic mean of all Q calculations for the function f is

$\begin{displaymath}% \bar{f}(i) = \frac{1}{Q}\sum_{k=1}^Q f^{k}(i) \hspace*{1cm} (i = 1,...,n). \end{displaymath}$

(51)

We define the sample standard deviation s(i) for each point i of the solution f as

$\begin{displaymath}% s^2(i) = \frac{1}{Q-1}\sum_{k=1}^Q (f^{k}(i) - \bar{f} (i))^{2} \hspace*{1cm} (i = 1,...,n). \end{displaymath}$

(52)

The error or uncertainty in the mean value $\bar{f}(i)$ in general is the standard error, s_m(i), which is defined as

$\begin{displaymath}% s_{m}(i) = \frac{s(i)}{\sqrt{Q}} \hspace*{1cm} (i = 1,...,n). \end{displaymath}$

(53)

Here, we use this statistical method to get the distribution of values f_i with uncertainties in z_i and/or a_ik that is we use

$\begin{displaymath}% s_{m}(i) = s(i) \hspace*{1cm} (i = 1,...,n). \end{displaymath}$

(54)

We can quote the resultant calculations of the solar energy spectra as

$\begin{displaymath}% f(i) = \bar{f}(i) \pm {\rm d}f(i) \hspace*{1cm} (i = 1,...,n), \end{displaymath}$

(55)

where ${\rm d}f(i) = s(i)$ .

This method allows us to consider random perturbations either only in the matrix $\bf A$ or only in the vector z or in $\bf A$ and z. Besides we can combine the method of random perturbations with the error propagation law. In this case we must use Eq. (24) for every k from Q computations and then evaluate mean values for all three variants of perturbations.

5 Numerical results

Figure 7 shows the energy distribution corresponding to the day 191/1996 event obtained by the regularization methods using algebraic (Eq. (10)) and optimization (Eq. (11)) approaches. These methods produce different and incompatible solutions partly related to the constraints applied in the optimization approach (see Eq. (11)).

Table 1: Summary of error analysis methods.

The algebraic approach produces underflows, small positive values, and even (unreasonably) large negative and positive values. These values are partly due to bins with z_i=0 and(or) a_ik=0 in a complete column or row (null row vector, see Fig. 7) (see Figs. 2-4). Underflows in the optimization approach are consistent with f_i=0. These energy distributions from Fig. 7 are used in the following as the reference, when displaying relative errors.

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig08.eps} \end{figure}$

Figure 8:

Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by various methods: the Tikhonov method with $\alpha = 10^{-9}$ , Eq. (21); the SVD method, Eq. (24). Null row vector in matrix A means (no entries in the beam energy for any energy deposit interval). (see Figs. 2, 3) Points at 10^-3 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig09.eps} \end{figure}$

Figure 9:

Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using the minimum variance method, Eq. (30), with using algebraic ${\rm d}f_{\rm alg}/f_{\rm alg}$ and optimization ${\rm d}f_{\rm opt}/f_{\rm opt}$ approaches. The SVD method, ${\rm d}f_{\rm SVD}/f_{\rm alg}$ Eq. (24), is placed for the comparison. Null row vector in matrix A means (no entries in the beam energy for any energy deposit interval). (see Figs. 2, 3) Points at 10^-3 display underflows. Points at 10 display overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig10.eps} \end{figure}$

Figure 10:

Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using the MATLAB functions: fmincon, Eq. (33), ${\rm d}f_{\rm fmincon}/f_{\rm opt}$ , and lscov, ${\rm d}f_{\rm lscov}/f_{\rm opt}$ . Points at 10^-3 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig11.eps} \end{figure}$

Figure 11:

Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using errors in z and $\bf A$ ( ${\rm d}f_{z{\bf A}}/f_{\rm alg}$ ) (Eq. (42)), in $\bf A$ ( ${\rm d}f_{\bf A}/f_{\rm alg}$ ) (Eq. (43)), and in z ( ${\rm d}f_z/f_{\rm alg})$ (Eq. (35)). Points at 10^-3 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=13cm,clip]{854fig12.eps} \end{figure}$

Figure 12:

Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using the error propagation method (see Sect. 4.1) with random perturbations: in z and $\bf A$ ( ${\rm d}f_{z{\bf A}}/f_{z{\bf A}-{\rm alg}}$ ), in $\bf A$ ( ${\rm d}f_{\bf A}/f_{{\bf A}-{\rm alg}}$ ), and in z ( ${\rm d}f_z/f_{z-{\rm alg}}$ ), Eq. (48). Null row vector in matrix A means (no entries in the beam energy for any energy deposit interval). (see Figs. 2, 3) Points at 10^-3 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to $E_{\rm b}$ , see Fig. 2.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig13.eps} \end{figure}$

Figure 13:

Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using the Monte Carlo method (see Sect. 4.4) with random perturbations: in z and $\bf A$ ( ${\rm d}f_{z{\bf A}}/f_{z{\bf A}-{\rm alg}}$ ), in $\bf A$ ( ${\rm d}f_{\bf A}/f_{{\bf A}-{\rm alg}}$ ), and in z ( ${\rm d}f_z/f_{z-{\rm alg}}$ ) for the algebraic approach, Eq. (48). Null row vector in matrix A means (no entries in the beam energy for any energy deposit interval). (see Figs. 2, 3) Points at 10^-4 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to $E_{\rm b}$ , see Fig. 2.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig14.eps} \end{figure}$

Figure 14:

Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using the Monte Carlo method (see Sect. 4.4) with random perturbations: in z and $\bf A$ $({\rm d}f_{z{\bf A}}/f_{z{\bf A}-{\rm opt}}$ ), in $\bf A$ ( ${\rm d}f_{\bf A}/f_{{\bf A}-{\rm opt}}$ ), and in z ( ${\rm d}f_z/f_{z-{\rm opt}}$ ) for the optimization approach, Eqs. (49), (50). Null row vector in matrix A means (no entries in the beam energy for any energy deposit interval) (see Figs. 2, 3). Points at 10^-4 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig15.eps} \end{figure}$	Figure 15: Energy spectrum obtained by the Monte Carlo method (see Sect. 4.4), algebraic solution, with uncertainties in z and $\bf A$ . errors taken from Eq. (54). The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig16.eps} \end{figure}$	Figure 16: Energy spectrum obtained by the Monte Carlo method (see Sect. 4.4), optimization solution, with uncertainties in z and $\bf A$ . Errors taken from Eq. (54). The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.
Open with DEXTER

We consider solutions and the error analysis for Eq. (2). Errors in the vector z and in the matrix $\bf A$ cause errors in the solution f. Poissonian errors go with the vector z, the experimental data. Errors in the matrix $\bf A$ are the result of the Monte Carlo modeling of processes, the modeling of the sensor head, and the statistical accuracy in the sensor response to the particle beam from the Monte Carlo simulation. In all following calculations we define the changes ${\rm d}f$ in the solution f caused by statistical errors in experimental data and errors in the matrix ${\rm d}\bf A$ represented in Fig. 3. In all results obtained by the optimization approach we use errors ${\rm d}z$ only ( $\eta _{i}={\rm d}z_i$ in Eq. (11)).

In the following, we compare the various methods for error estimation outlined in Sect. 4 combined with the analysis method explained in Sect. 3. Table 1 gives an overview of the different combinations and methods investigated here and maps them to the figures in this paper.

Figure 8 shows the relative errors in the regularized energy distribution from the error propagation law Eq. (17) obtained by the Tikhonov method and the SVD method. The solution for the Tikhonov method with the regularization parameter $\alpha = 10^{-9}$ is the same as for the SVD method. The errors of the methods coincide where they do not underflow. The errors increase with channel number that is with energy for electrons as well as for protons, and are all below 1 (100%). The SVD-method produces reasonable errors even in the ``null vector range'', which should not be meaningful.

Figure 9 presents solutions of the inverse problem for error propagation Eq. (30) using algebraic and optimization approaches. For this case the relative errors from the optimization approach are smaller than from the algebraic approach. The errors are on a 10% level, increasing with energy (channel number).

Figure 10 is a plot of relative errors in the energy distribution obtained by using MATLAB functions. The function fmincon allows us to compute the Hessian matrix that is connected with the covariance matrix by Eq. (32). The function lscov allows us to obtain the least square solution in presence of known covariance. We use the following variant of this function $[f,{\rm d}f,mse,S] = {\rm lscov}(A,z)$ (that means optimization with $\eta_i={\rm d}z_i=1$ ), here mse is the mean squared error, S is the estimated covariance matrix of f. Errors below channel number 15 for electrons, and number 55 for protons look reliable, staying below 1 (100%). The results with lscov here are not a good measure of the errors ( ${\rm d}z_i=1$ is used), and should be taken as an example of bad adjustment of the optimization approach with ${\rm d}z_i=1$ .

Figure 11 shows the relative errors in the energy distribution obtained by using perturbations in the matrix $\bf A$ and vector z (Eq. (42)). The main contribution to the errors is produced by errors in the matrix A. It would be possible to improve the calculation of the matrix A, from a purely statistical point of view, but that does not help to avoid systematic errors in modeling the geometry, the materials and in the energy calibration of the sensor head, and in modeling interaction processes in the Monte Carlo program GEANT4. Therefore, we have retained the current uncertainties in A as representative of other systematic unknowns.

Figure 12 illustrates the error propagation law with random perturbations both in the matrix $\bf A$ and vector z. The results show that the measurement errors ${\rm d}z$ play only a secondary role compared with the uncertainties in the matrix $\bf A$ . The relative errors ${\rm d}f_z/f_{z-{\rm alg}}$ from this figure are the same as the relative errors ${\rm d}f_{\rm SVD}/f_{\rm alg}$ from Fig. 8. Again errors are obtained in the ``null vector range'' range, here for all variants in ${\rm d}f_{i}$ calculations.

Figure 13 shows the relative errors obtained by using the Monte Carlo method with random perturbations in the matrix $\bf A$ and vector z for the algebraic approach (Q = 100, see Eqs. (51), (55)). Large errors are caused by uncertainties in the matrix A in a wide region.

In Fig. 14 we plot of relative errors obtained by using the Monte Carlo method with random perturbations in the matrix $\bf A$ and vector z for the optimization approach (Q = 100, see Eqs. (51), (55)).

The results presented in Figs. 13, 14 were obtained for relative errors $\vert\vert{\rm d}{\bf A}\vert\vert _{2}/\vert\vert{\bf A}\vert\vert _{2} = 0.0609$ and $\vert\vert{\rm d}z\vert\vert _{2}/\vert\vert z\vert\vert _{2} = 0.0189$ . Here $\vert\vert{\bf A}\vert\vert _{2}$ is the largest singular value of $\bf A$ , ||z||₂ is the Euclidean length of a vector z. At low channel numbers the uncertainty in f is dominated by the matrix A, where threshold fluctuations in determination of the geometric factor are important, while at high channel numbers the statistical uncertainties in the experimental date z are dominant.

For the algebraic approach (see Fig. 13) the uncertainties in the matrix $\bf A$ play the larger role than in the vector z. For the optimization approach (see Fig. 14) the uncertainties in the vector z play the larger role than in the matrix $\bf A$ .

In the case of relative errors $\vert\vert{\rm d}{\bf A}_{1}\vert\vert _{2}/\vert\vert{\bf A}\vert\vert _{2} = 0.6089$ and $\vert\vert{\rm d}z\vert\vert _{2}/\vert\vert z\vert\vert _{2} = 0.0189$ for the optimization approach the uncertainties in the vector z play the insignificant role compared with errors in the matrix $\bf A$ . These results are not presented in this paper.

Figures 15 and 16 show our final results. Energy distributions (rate/bin/hour) are transformed to energy spectra ( $\rm intensity/cm^2/sr/h/MeV$ ) and included are the errors according to the MC-perturbation method using ${\rm d}\bf A$ and ${\rm d}z$ (Eq. (3)). The algebraic approach (Fig. 15) seems extremely unreliable, according to the errors, across the energy range >1 MeV, the optimization approach (Fig. 16) displays large errors at high energies, as expected due to low event rate z and low accuracy in the matrix A (because of low acceptance).

6 Discussion

The uncertainties df_i in the spectrum f_i depend on the statistical accuracy of the data and on the uncertainties in the matrix of geometrical factors. Qualitatively the statistical uncertainties increase with increasing energy due to the generally steep energy spectrum and reduced count rate. But the detection efficiency is small at low energies, despite the high rate, giving rise to large uncertainties, and the efficiency is low at high energies, because of triggering conditions with anticoincidence, again with small geometrical factors and thus large uncertainties. So we expect large uncertainties from the matrix at low energies, and from the matrix and the data (low statistics) at high energies, especially for electrons.

All distributions of relative uncertainties show this behavior, a decrease at low energies (channel number) and a rise after a minimum, but that does not continue to high energies in the SVD- and the Tikhonov approaches, instead staying constant (Figs. 8, 9).

There are energy intervals giving unreasonable (unphysical) intensities and uncertainties, which nevertheless produce reasonable absolute uncertainties, from a mathematical point of view, e.g., in the algebraic approach (Fig. 11), and even in the error propagation method (Fig. 12).

In the optimization approach with constraints (intensity nonnegative) the uncertainties get larger than 100% at high energies, indicating that the error propagation method is not applicable any more. The contribution of statistical uncertainties in the experimental data seems to be less important than the uncertainties in the matrix elements, as can be seen in all methods of error analysis, applying the MC(dz, dA) technique (Figs. 11-14). This gives a hint to the fact that the response matrix may show systematic errors, despite producing the matrix to the best of our sensor knowledge. Approximations used in the construction of the geometrical model of the EPHIN sensor, as well as inaccuracies in energy calibration and energy resolution may be the cause of those systematic errors.

The energy spectrum obtained by the algebraic approach shows large errors, when using the MC(dz, dA) technique. These are caused by partly negative values in the intensities f_i at higher energies (Fig. 15). This deficiency of the algebraic approach does not appear in the optimization approach (Fig. 16), which gives more realistic values of the uncertainties in the regularization method of data analysis in this experiment.

7 Conclusions

In this paper we have studied the impact of various error sources on the quantity of uncertainties in the solution of the ill-posed problem Eq. (2). We considered errors in the experimental data (vector z) and the discrete forward operator (matrix A). In the error analysis we use well-known and newly developed methods, such as the inverse problem for error propagation and the Monte Carlo method with random perturbations in the matrix $\bf A$ and vector z. The results for the various methods are presented in this paper.

The algebraic methods, Eq. (10), in general show unphysical negative values in some components f_i of the solution f, and in some components of ${\rm d}f_{i}$ as well. The optimization approach seems to be reliable and stable. The error estimation obtained here correlates with the statistical accuracy in the components z_i and the discrete forward operator A.

We find that the various methods have different strengths and weaknesses in the treatment of statistical and systematic errors. Using the Monte-Carlo method with random perturbations we managed to include errors in both, vector z as well as in matrix A in our analysis. Based on results shown in Figs. 15 and 16 we claim that this MC-method provides the best error estimation.

Acknowledgements

We wish to thank the anonymous referee for comments that helped us to improve this paper.

References

Bevington, P. R. 1969, Data Reduction and Error Analysis for Physical Sciences (New York: McGraw-Hill) (In the text)
Björck, A. 1991, BIT, 31, 238 [CrossRef] (In the text)
Björck, A. 1996, Numerical Methods for Least Squares Problems (Philadelphia: SIAM) (In the text)
Bock, R. K., & Krischer, W. 1998, The Data Analysis BriefBook (Berlin: Springer-Verlag) (In the text)
Böhm, E., Kharytonov, A., & Wimmer-Schweingruber, R. F. 2007, A&A, 473, 673 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Brandt, S. 1999, Data Analysis: Statistical and Computational Methods for Scientists and Engineers (New York: Springer-Verlag) (In the text)
Branham, R. L. 1990, Scientific Data Analysis: an Introduction to Overdetermined Systems (New York: Springer-Verlag) (In the text)
GEANT3 2006, CERN Program Library W5013, CERN-CN division, see also: http://wwwinfo.cern.ch/geant3 (In the text)
GEANT4 collaboration 2006, An Object-Oriented Toolkit for Simulation in HEP, CERN-LHCC 98-44, see also: http://wwwinfo.cern.ch/asd/geant4/geant4.html (In the text)
Gòmez-Herrero, R., Klassen, A., Heber, B., et al. 2006, Second Solar Orbiter Workshop, Athens, 16-20 October (In the text)
Hansen, P. C. 1998, Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion (Philadelphia: SIAM)
Higham, N. J. 1996, Accuracy and Stability of Numerical Algorithms (Philadelphia: SIAM) (In the text)
Lawson, C. L., & Hanson, R. J. 1974, Solving Least Squares Problems (Eaglewood Cliffs, New Jersey: Prentice Hall, Inc.) (In the text)
Lefebvre, M., Keeler, R. K., Sobie, R., & White, J. 2000, Nuclear Instruments and Methods in Physics research, Section A, 451, 520 (In the text)
Lyons, L. 1989, Statistics for Physicists (Cambridge: Cambridge University Press) (In the text)
Matlab 2006, Optimization Toolbox User's Guide, The MathWorks, Inc., see also: http://www.mathworks.com (In the text)
Müller-Mellin, R., Kunow, H., Fleißner, V., et al. 1995, Sol. Phys., 162, 483 [NASA ADS] [CrossRef] (In the text)
Neumaier, A. 1998, SIAM Rev., 40, 636 [CrossRef]
PAW 1993, Paw Analysis Workstation, CERN Program Library Q121, CERN-CN division, see also: http://cern.ch/paw (In the text)
ROOT, Brun, R. 2000, An Object-Oriented Data Analysis Framework, CERN-CN division, see also: http://root.cern.ch (In the text)
Tellinghuisen, J. 2001, J. Phys. Chem. A, 105, 3917 [CrossRef] (In the text)
Tikhonov, A. N., & Arsenin, V. Y. 1977, Solution of Ill-Posed Problems (New York: Wiley)
van Wijk, K., Scales, J. A., Navidi, W., & Tenorio, L. 2002, Geophys. J. Int., 149, 625 [NASA ADS] [CrossRef] (In the text)
Wedin, P.-A. 1973, BIT, 13, 217 [CrossRef] (In the text)
Wedin, P.-A., & Wikström, G. 2002, Technical Report, UMINF:02.16, 1 (In the text)
Wilkinson, J. H. 1965, The Algebraic Eigenvalue Problem (Oxford: Clarendon Press) (In the text)

Footnotes

... spectra: During times of high fluxes, the pulse height words need to be weighted according to another data type, the so-called histograms to account for the limited telemetry to earth.

All Tables

Table 1: Summary of error analysis methods.

All Figures

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{854fig01.eps} \end{figure}$	Figure 1: Side view of the EPHIN-sensor, a telescope consisting of 6 Si-solid state detectors A-F (in green) surrounded by an active anticonincidence scintillator G (in red). 10 simulated beam electrons of 4 MeV are shown in red as well as a pair of generated secondary gamma rays in blue.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=13cm,clip]{854fig02.eps} \end{figure}$	Figure 2: Matrix A of geometric factors in dependence of the energy deposit $E_{\rm d}$ and the energy of the beam particle $E_{\rm b}$ , with ${\bf A}_{E{\rm e}}$ , ${\bf A}_{E{\rm p}}$ , ${\bf A}_{P{\rm e}}$ , and ${\bf A}_{P{\rm p}}$ in the different quadrants, as derived from the Monte-Carlo simulation of the EPHIN instrument. The scale in energy 0-30 is equivalent to a logarithmic scale 0.1 to 100 MeV, which is repeated from 30 to 60, so displaying the full matrix for electrons and protons. We have applied logarithmic binning in the energies $E_{\rm d}$ and $E_{\rm b}$ to account for the power-law particle spectra that are expected in particle acceleration processes in the heliosphere.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=13cm,clip]{854fig03.eps} \end{figure}$	Figure 3: Errors on geometric factors ${\bf A}_{E{\rm e}}$ , ${\bf A}_{E{\rm p}}$ , ${\bf A}_{P{\rm e}}$ , and ${\bf A}_{P{\rm p}}$ as derived from the Monte-Carlo simulation of the EPHIN instrument. The description is analogous to Fig. 2. Note the different z-axis scales of Figs. 2 and 3.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig04.eps} \end{figure}$	Figure 4: Relative errors of geometric factors for the diagonal elements of matrix A, null row vector in matrix A means (no entries in the beam energy for any energy deposit interval) (see Figs. 2, 3).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig05.eps} \end{figure}$	Figure 5: Time series of E-channel ( upper panel) and P-channel ( lower panel) count rates during the solar particle event of days 188 to 192 in 1996. The various curves (red, green, black and blue) show count rates in the energy intervals, as recorded by the SOHO-EPHIN-sensor. Day 1996/191, 16-17 h, has been chosen for a detailed analysis: a 24-h pre-event period on day 1996/188 has been taken as solar and non-solar interplanetary event background measurement.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig06.eps} \end{figure}$	Figure 6: Measured pulse height (energy deposit) distribution on day 191/1996, 16-17 h, all E-channels have been combined and all P-channels have been combined too. The background as measured on day 188/1996 has been subtracted (see Fig. 5). The binning is equidistant in logarithmic scale, 10 bins per decade, corresponding to the energy deposit $E_{\rm d}$ , see Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig07.eps} \end{figure}$	Figure 7: Energy distribution for day 191/1996, 16-17 h, solutions $f_{\rm alg}$ and $f_{\rm opt}$ are obtained by applying Eqs. (10), (11). Null row vector in matrix A means: no entries in the beam energy for any energy deposit interval, creating unphysical results, but still producing mathematically correct numbers, small positive or even large negative numbers and uncertainties (see Figs. 2, 3). Points at 10^-2 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig08.eps} \end{figure}$	Figure 8: Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by various methods: the Tikhonov method with $\alpha = 10^{-9}$ , Eq. (21); the SVD method, Eq. (24). Null row vector in matrix A means (no entries in the beam energy for any energy deposit interval). (see Figs. 2, 3) Points at 10^-3 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig09.eps} \end{figure}$	Figure 9: Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using the minimum variance method, Eq. (30), with using algebraic ${\rm d}f_{\rm alg}/f_{\rm alg}$ and optimization ${\rm d}f_{\rm opt}/f_{\rm opt}$ approaches. The SVD method, ${\rm d}f_{\rm SVD}/f_{\rm alg}$ Eq. (24), is placed for the comparison. Null row vector in matrix A means (no entries in the beam energy for any energy deposit interval). (see Figs. 2, 3) Points at 10^-3 display underflows. Points at 10 display overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig10.eps} \end{figure}$	Figure 10: Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using the MATLAB functions: fmincon, Eq. (33), ${\rm d}f_{\rm fmincon}/f_{\rm opt}$ , and lscov, ${\rm d}f_{\rm lscov}/f_{\rm opt}$ . Points at 10^-3 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig11.eps} \end{figure}$	Figure 11: Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using errors in z and $\bf A$ ( ${\rm d}f_{z{\bf A}}/f_{\rm alg}$ ) (Eq. (42)), in $\bf A$ ( ${\rm d}f_{\bf A}/f_{\rm alg}$ ) (Eq. (43)), and in z ( ${\rm d}f_z/f_{\rm alg})$ (Eq. (35)). Points at 10^-3 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=13cm,clip]{854fig12.eps} \end{figure}$	Figure 12: Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using the error propagation method (see Sect. 4.1) with random perturbations: in z and $\bf A$ ( ${\rm d}f_{z{\bf A}}/f_{z{\bf A}-{\rm alg}}$ ), in $\bf A$ ( ${\rm d}f_{\bf A}/f_{{\bf A}-{\rm alg}}$ ), and in z ( ${\rm d}f_z/f_{z-{\rm alg}}$ ), Eq. (48). Null row vector in matrix A means (no entries in the beam energy for any energy deposit interval). (see Figs. 2, 3) Points at 10^-3 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to $E_{\rm b}$ , see Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig13.eps} \end{figure}$	Figure 13: Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using the Monte Carlo method (see Sect. 4.4) with random perturbations: in z and $\bf A$ ( ${\rm d}f_{z{\bf A}}/f_{z{\bf A}-{\rm alg}}$ ), in $\bf A$ ( ${\rm d}f_{\bf A}/f_{{\bf A}-{\rm alg}}$ ), and in z ( ${\rm d}f_z/f_{z-{\rm alg}}$ ) for the algebraic approach, Eq. (48). Null row vector in matrix A means (no entries in the beam energy for any energy deposit interval). (see Figs. 2, 3) Points at 10^-4 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to $E_{\rm b}$ , see Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig14.eps} \end{figure}$	Figure 14: Absolute of relative errors $\vert{\rm d}f_i/f_i\vert$ in the energy distribution obtained by using the Monte Carlo method (see Sect. 4.4) with random perturbations: in z and $\bf A$ $({\rm d}f_{z{\bf A}}/f_{z{\bf A}-{\rm opt}}$ ), in $\bf A$ ( ${\rm d}f_{\bf A}/f_{{\bf A}-{\rm opt}}$ ), and in z ( ${\rm d}f_z/f_{z-{\rm opt}}$ ) for the optimization approach, Eqs. (49), (50). Null row vector in matrix A means (no entries in the beam energy for any energy deposit interval) (see Figs. 2, 3). Points at 10^-4 display underflows. There are no overflows. The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig15.eps} \end{figure}$	Figure 15: Energy spectrum obtained by the Monte Carlo method (see Sect. 4.4), algebraic solution, with uncertainties in z and $\bf A$ . errors taken from Eq. (54). The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=12cm,clip]{854fig16.eps} \end{figure}$	Figure 16: Energy spectrum obtained by the Monte Carlo method (see Sect. 4.4), optimization solution, with uncertainties in z and $\bf A$ . Errors taken from Eq. (54). The binning is equidistant in logarithmic scale, 10 bins per decade corresponding to the beam energy $E_{\rm b}$ , see Fig. 2.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.