Gamma-ray spectrum of RX J1713.7-3946 in the Fermi era and future detection of neutrinos

R. Yamazaki; K. Kohri; H. Katagiri

doi:10.1051/0004-6361:200810845

Home

All issues

Volume 495 / No 1 (February III 2009)

A&A, 495 1 (2009) 9-13

Full HTML

Free Access

Issue		A&A Volume 495, Number 1, February III 2009


Page(s)		9 - 13
Section		Astrophysical processes
DOI		https://doi.org/10.1051/0004-6361:200810845
Published online		14 January 2009

A&A 495, 9-13 (2009)

Gamma-ray spectrum of RX J1713.7-3946 in the Fermi era and future detection of neutrinos

R. Yamazaki¹ - K. Kohri² - H. Katagiri¹

1 - Department of Physical Science, Hiroshima University, Higashi-Hiroshima, Hiroshima 739-8526, Japan
2 - Physics Department, Lancaster University, LA1 4YB, UK

Received 22 August 2008 / Accepted 5 December 2008

Abstract
The recently launched satellite, Fermi Gamma-ray Space Telescope, is expected to find out if cosmic-ray (CR) protons are generated from supernova remnants (SNRs), especially RX J1713.7-3946, by observing the GeV-to-TeV $\gamma$ -rays. The GeV emission is thought to be bright if the TeV emission is hadronic, i.e., of proton origin, while dim if leptonic. We reexamine the above view using a simple theoretical model of nonlinear acceleration of particles to calculate the gamma-ray spectrum of Galactic young SNRs. If the nonlinear effects of CR acceleration are considered, it may be impossible to distinguish the evidence of proton acceleration from leptonic in the $\gamma$ -ray spectrum of Galactic young SNRs like RX J1713.7-3946. On the other hand, future km³-class neutrino observations will likely find a clear evidence of the proton acceleration there.

Key words: acceleration of particles - ISM: supernova remnants - gamma rays: theory

1 Introduction

Recently, Fermi Gamma-ray Space Telescope (Fermi), observing GeV $\gamma$ -ray photons, has been launched. The GeV $\gamma$ -ray observations with Fermi are expected to identify the accelerators of Galactic cosmic-ray (CR) protons whose energy extends up to the ``knee'' energy ( $\approx$ 10^15.5 eV). At present, the most probable candidate for the CR accelerator is a young supernova remnant (SNR). Since the detections of synchrotron X-rays in some SNRs show evidence of electron acceleration (Koyama et al. 1995), the current unsolved issue is whether the SNRs produce high-energy protons or not. TeV $\gamma$ -ray observations are important to address this problem. So far, TeV $\gamma$ -rays have been detected from several young SNRs (Enomoto et al. 2002; Katagiri et al. 2005; Aharonian et al. 2005,2004). They arise from either leptonic (CMB photons up-scattered by high energy electrons) or hadronic ( $\pi ^0$ -decay photons generated via accelerated protons) processes, and it is generally difficult to separate these processes using only the TeV energy band; the study of wide-band, GeV-to-TeV spectra is necessary.

RX J1713.7-3946 (hereafter RXJ1713) is a representative SNR from which bright TeV $\gamma$ -rays have been detected. The HESS experiment measured the TeV spectrum and claimed that its shape was better explained by the hadronic model (Aharonian et al. 2006,2007). So far, compared with other young SNRs, the TeV $\gamma$ -ray spectrum of RXJ1713 is the most precisely measured and the energy coverage is wide, from 0.3 to 100 TeV, so that we can obtain the best constraints on theoretical models.

Recently, time variation of synchrotron X-rays was discovered in RXJ1713 (Uchiyama et al. 2007). If the variation timescale is determined from the synchrotron cooling of X-ray emitting electrons, the magnetic field is estimated to be $B\sim$ mG. If so, the leptonic, one-zone emission model (e.g., Aharonian & Atoyan 1999) cannot explain the TeV-to-X-ray flux ratio, supporting the hadronic origin of TeV $\gamma$ -rays. It should be noted that the amplified magnetic field is theoretically expected (e.g., Giacalone & Jokipii 2007; Lucek & Bell 2000). In this case, according to the standard diffusive shock acceleration theory, the maximum energy of accelerated protons is estimated as (Aharonian & Atoyan 1999)

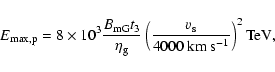$\begin{displaymath}E_{{\rm max},{\rm p}}=8\times10^3 \frac{B_{\rm mG}t_3}{\eta_{... ...rac{v_{\rm s}}{4000~{\rm km}~{\rm s}^{-1}}\right)^2 {\rm TeV}, \end{displaymath}$

(1)

which can be comparable to the knee energy. Here, $B_{\rm mG}$ , $v_{\rm s}$ , t₃, and $\eta_{\rm g}$ are the magnetic field strength in units of mG, the shock velocity, the age of the SNR in units of 10³ yr, and the gyrofactor, respectively.

However, at present, there are several issues to be addressed, as the above picture on RXJ1713 is not yet proved. First, if $B\sim{\rm mG}$ and TeV emission is hadronic, then in order to explain the measured flux of radio synchrotron emitted by primary electrons, the electron-to-proton ratio at the SNR should be anomalously small, $K_{\rm ep}\sim10^{-6}$ (Uchiyama et al. 2003; Butt 2008), which is far below the observed value at the earth and estimated values in the nearby galaxy (Katz & Waxman 2008). This might be resolved if the electrons are accelerated in the later stages of SNR evolution, when the value of $K_{\rm ep}$ is different from the present value (Tanaka et al. 2008), although further discussions are necessary. Second, the hadronic scenario may be inconsistent with the molecular cloud (MC) observations (Fukui et al. 2003). RXJ1713 is surrounded by MCs, which might suggest collision with them and high target number density. If the TeV $\gamma$ -rays are hadronic, such a region should be brighter than observed (Plaga 2008).

In addition, if the measured width of the synchrotron X-ray filaments at the shock front of SNRs is determined by the synchrotron cooling effect (Bamba et al. 2005b; Uchiyama et al. 2003; Bamba et al. 2005a,2003; Vink & Laming 2003), the magnetic field is independently estimated as $B\approx0.1$ mG (Parizot et al. 2006), which is an order of magnitude smaller than that estimated by Uchiyama et al. (2007). Also, the cutoff energy of TeV $\gamma$ -ray spectrum is low, so that in the one-zone hadronic scenario $E_{{\rm max},{\rm p}}$ is estimated as 30-100 TeV (Villante & Vissani 2007), which is approximately two orders of magnitude lower than the knee energy. If $E_{{\rm max},{\rm p}}<100$ TeV and $B\approx1$ mG, then Eq. (1) tells us $\eta_{\rm g}\ga80$ , implying far from the ``Bohm limit'' ( $\eta_{\rm g}\approx1$ ) which is inferred from the X-ray observation (Yamazaki et al. 2004; Parizot et al. 2006) or expected theoretically (Giacalone & Jokipii 2007; Lucek & Bell 2000). This statement is recast if we involve recent results of X-ray observations. The precise X-ray spectrum of RXJ1713 is revealed, which gives $v_{\rm s}=3.3\times10^8\eta_{\rm g}^{1/2}$ cm s^-1 (Tanaka et al. 2008). Then, Eq. (1) can be rewritten as $E_{{\rm max},{\rm p}}=5\times10^3B_{\rm mG}t_3$ TeV. Hence, in order to obtain $E_{{\rm max},{\rm p}}<100$ TeV, we need $B\la20~\mu$ G in the context of the hadronic scenario of TeV $\gamma$ -rays. One might think that the volume filling factor of the region with $B\approx1$ mG is small and that the average field strength is smaller, e.g., $B\approx0.1$ mG. However, even in this case, $E_{{\rm max},{\rm p}}$ is more than 100 TeV, which contradicts the observed $\gamma$ -ray spectrum beyond 10 TeV.

In these circumstances, Fermi will give us important information on the $\gamma$ -ray emission mechanism. So far, the GeV emission has been thought to be bright if the TeV emission is hadronic, while dim if leptonic. However, this argument is not so straightforward if the nonlinear model of CR acceleration is considered. In the next section, we calculate the photon spectrum using a simple semi-analytic model taking into account nonlinear effects. Indeed, we show that in a certain case, the hadronic emission spectrum in the GeV-to-TeV band is similar to the leptonic one.

2 Hadronic gamma-rays in the efficient acceleration case

If a large amount of protons are accelerated, their momentum flux is large, so that the back-reaction of them is significant and the background shock structure is modified (Blandford & Eichler 1987; Malkov & Drury 2001; Drury 1983). Compared with the test-particle (inefficient acceleration) case in which the back-reaction effects are neglected, the background plasma is more compressed at the shock due to the additional CR pressure, which leads to a harder CR spectrum. Hence the hadronic emission becomes harder. At present, there is no reliable theory to determine the acceleration efficiency, and it is not clear whether this nonlinear model is correct or not. Thus, the observations to determine the acceleration efficiency and the CR spectrum at the acceleration site are important. It is widely expected that RXJ1713 with precise studies in the $\gamma$ -ray and X-ray bands is one of the best laboratories to investigate theories of nonlinear acceleration.

There are several models of nonlinear CR acceleration (Berezhko et al. 1994; Malkov 1997; Kang et al. 2001; Amato & Blasi 2005; Blasi 2002; Blasi et al. 2005; Ellison et al. 1996). Here, we adopt the one-dimensional, semi-analytic model (Blasi 2002; Blasi et al. 2005). In the following, we briefly summarize the formalism. The accelerated CR protons are described by the distribution function, f(x,p), where x is the spatial coordinate and p is the momentum of the accelerated proton. We derive stationary solutions to the set of an equation for f(x,p) that describes the diffusive transport equation of accelerated protons, and equations for the background thermal plasma that is treated as a fluid. The velocity, density, and thermodynamic properties of the fluid can be determined by the mass and momentum conservation equations, with the inclusion of the CR pressure calculated as

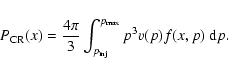$\begin{displaymath}P_{\rm CR}(x)=\frac{4\pi}{3}\int_{p_{\rm inj}} ^{p_{\rm max}}p^3v(p)f(x,p)~{\rm d}p. \end{displaymath}$

(2)

The injection of accelerated particles is assumed to occur at the shock front (x=0), and mono-energetic injection with the injection momentum $p_{\rm inj}$ is adopted. This is because at present we do not understand the injection process from first principles, hence we take a simple injection recipe. We assume $p_{\rm inj}=\xi p_{\rm th}$ , where $p_{\rm th}=(2m_{\rm p}k_{\rm B}T_2)^{1/2}$ is the momentum of particles in the thermal peak of the Maxwellian distribution of the background plasma in the downstream region, having temperature T₂. Furthermore, we assume the continuity of the distribution function of accelerated particles and the background thermal plasma at $p=p_{\rm inj}$ and x=0, namely $f(0,p_{\rm inj})=(n_2/\pi^{3/2}p_{\rm th}^3) {\rm e}^{-(p_{\rm inj}/p_{\rm th})^2}$ , where n₂ is the downstream number density of the background fluid. In this formalism, input parameters are the maximum momentum $p_{\rm max}$ , the upstream Mach number M₀, upstream fluid velocity u₀, and the injection parameter $\xi$ . Given these parameters, the distribution function of accelerated protons at the shock front f₀(p) is calculated, and various physical quantities are obtained such as the injection rate $\eta$ , the total compression ratio $R_{\rm tot}$ , the fraction of the CR pressure at the shock $\xi_c(0)=P_{\rm CR}(0) /\rho_0u_0^2$ .

Note that recent nonlinear models of CR acceleration have been developed taking into account the magnetic field amplification (Vladimirov et al. 2006) and its influence on turbulent heating (Vladimirov et al. 2008), fluid compression (Caprioli et al. 2008a,b; Terasawa et al. 2007), and Alfvénic drift (Zirakashvili & Ptuskin 2008), which are neglected in the model considered in this paper. These effects lead to less spectral hardening of accelerated particles and smaller compression ratios, and might be important in order to calculate the $\gamma$ -ray spectrum (Morlino et al. 2009). However, at present, it is not certain whether or not the magnetic field is strongly amplified in the acceleration region; although streaming instabilities between accelerated protons and background plasma may occur, the nonlinear evolution of the instability and the saturation level are highly uncertain. Although the magnetic field amplification is potentially coupled to the high injection rate of protons, they should, in principle, be treated separately. In this sense, our model is the extreme limit of the nonlinear acceleration theory, which predicts the hardest spectrum of accelerated particles.

In this paper, we adopt M₀=100, $p_{\rm max}=1\times10^5m_{\rm p}c$ , $u_0=5\times10^8$ cm s^-1, and $\xi=3.6$ . Then, we obtain $p_{\rm inj}=3.74\times10^{-3}m_{\rm p}c$ , $\eta=2.03\times10^{-4}$ , $R_{\rm tot}=36.2$ , and $\xi_{\rm c}(0)=0.902$ . While the total number of CR protons is much smaller than that of the background plasma ( $\eta\ll1$ ), the CR pressure is dominant (Amato & Blasi 2005). We find that the CR energy spectrum is asymptotically $N_p(p)\propto p^2f_0(p)\propto p^{-1.5}$ , which is harder than in the case of inefficient acceleration. This result on the asymptotic form has been analytically derived, which does not depend on the shock parameters such as M₀ and u₀ in the large-M₀ limit (Malkov 1999,1997).

Using the derived distribution function of CR protons, we calculate the $\gamma$ -ray spectrum produced by $\pi ^0$ -decay process. We used the PYTHIA Monte-Carlo event generator (Sjostrand et al. 2006), which fits existing experimental data well, to calculate the pp scattering processes and detailed distributions of the daughter particles such as $\pi ^0$ and $\pi^{\pm}$ . We have also obtained the distribution functions of emitted photons and neutrinos which are produced by subsequent decays of those mesons and muons in the same code (Yamazaki et al. 2006). The result is shown in Fig. 1.

$\begin{figure} \par\includegraphics[width=20pc]{0845fig1.eps} \end{figure}$

Figure 1:

$\nu F_\nu$ -spectra in $\gamma$ -ray band, predicted by hadronic $\pi ^0$ -decay model in the efficient acceleration case (solid line) and leptonic IC model in the inefficient case (dashed line). The dot-dashed curve shows the 1 year, 5 $\sigma$ sensitivity for the Fermi LAT taking into account the Galactic diffuse background (Higashi et al. 2008). The observed spectrum in the TeV band is shown (Aharonian et al. 2007).

Open with DEXTER

So far, we have considered the hadronic $\gamma$ -ray spectrum in the context of the efficient acceleration scenario. For comparison, we show, in Fig. 1, the spectrum of leptonic inverse-Compton (IC) radiation via accelerated electrons in the case of inefficient acceleration, where back reaction effects of accelerated protons are neglected. Throughout the paper, we take into account the Klein-Nishina effect in calculating the IC spectrum. The assumed form of the electron distribution is $N_{\rm e}(E_{\rm e})\propto E_{\rm e}^{-s_{\rm e}}\exp(-E_{\rm e}/E_{\rm max})$ , and we adopt $s_{\rm e}=2.0$ and $E_{\rm max}=28$ TeV. This case can be realized if the magnetic field is weak enough for the synchrotron cooling effect to be insufficient, whose condition is written as $t_{\rm age}<t_{\rm synch}=6\pi m_{\rm e}^2c^3/\sigma_TE_{\rm max}B^2$ , where $t_{\rm age}=t_3\times10^3$ yr is the age of the SNR. Solving this equation with $E_{\rm max}=28$ TeV, we derive $B<26t_3^{-1/2}\mu$ G. If the magnetic field is strong ( $B\gg26t_3^{-1/2}\mu$ G), the spectral deformation occurs, which will be discussed in Sect. 4. One can find from Fig. 1 that the $\pi ^0$ -decay $\gamma$ -ray emission in the efficient acceleration model coincides with the leptonic IC model in the inefficient case. The reason is simple. Let s_i be the index of the energy spectrum of accelerated particles i ( $i={\rm p}$ or ${\rm e}$ ), so that $N_i(E_i)\propto E_i^{-s_i}$ . Then, the radiation spectrum of $\pi ^0$ -decay $\gamma$ -rays is in the form $\nu F_\nu\propto\nu^{2-s_{\rm p}}$ , while the spectrum of IC radiation is given by $\nu F_\nu\propto\nu^{-(s_{\rm e}-3)/2}$ . Hence, hadronic emission with $s_{\rm p}\approx1.5$ and IC emission with $s_{\rm e}\approx2.0$ give the same spectral slope. This is summarized in Table 1.

Below several hundreds of MeV, hadronic $\gamma$ -ray emission is dimmer than leptonic IC emission because $\pi ^0$ creation reaction does not occur for low-energy (<70 MeV in the center-of-mass frame) protons. Unfortunately, Fermi sensitivity is not high enough to recognize this decline below $\sim$ GeV.

One can find that both models slightly deviate from the observed spectrum in the sub-TeV energy range. The significance of this is sometimes strengthened, because the leptonic one-zone IC model is unlikely (Aharonian et al. 2007). However, as will be seen in the next section, it is not serious if the two-zone models are considered.

Table 1: Spectral index of $\nu F_\nu$ spectrum of gamma-rays ( $\nu F_\nu \propto \nu ^\alpha$ ) for various cases. Hadronic emission model in the case of efficient acceleration (Ia) predicts similar $\gamma$ -ray spectral slope with the leptonic, inefficient acceleration model with weak magnetic field (IIIb). On the other hand, hadronic inefficient acceleration models (IIa and IIIa) predict similar $\gamma$ -ray spectral slope with the leptonic, moderate magnetic field model (IIb).

3 Two-zone models

Here, we consider simple two-zone models to better explain the observed TeV spectrum (Aharonian & Atoyan 1999). RXJ1713 is interacting with MCs, so that the environment around the shock producing high-energy particles may be inhomogeneous. In this case, the one-zone approximation is too simplified, which motivates us to investigate the two-zone model as the next-order approximation.

3.1 Hadronic two-zone model

In this model, two independent regions, j (j=1,2), are considered. For each component, we independently calculate the proton spectrum again using the semi-analytic model of nonlinear CR acceleration considered in the previous section. The region j has parameters M₀^(j), $p_{\rm max}{}^{(j)}$ , u₀^(j), and $\xi^{(j)}$ . Then, we derive the hadronic $\gamma$ -ray spectrum produced by $\pi ^0$ -decay process. The total emission spectrum from the SNR is simply given by the sum of the emissions from two regions.

Figure 2 shows the result where we adopt $p_{\rm max}{}^{(1)}=2\times10^4m_{\rm p}c$ and $p_{\rm max}{}^{(2)}=2\times10^5m_{\rm p}c$ . The rest of the parameters are the same as those of the previous section: M₀⁽¹⁾=M₀⁽²⁾=100, $u_0^{(1)}=u_0^{(2)}=5\times10^8$ cm s^-1, and $\xi^{(1)}=\xi^{(2)}=3.6$ . The normalization of the $\pi ^0$ -decay emission is proportional to the product of the amount of the accelerated protons, which is represented by $N_{\rm p}(p=mc)$ , and the target number density, n_t. Here, we adjust $n_{\rm t}^{(1)}N_{\rm p}^{(1)}(p=mc)/n_{\rm t}^{(2)}N_{\rm p}^{(2)}(p=mc)=0.56$ in order to explain the observed $\gamma$ -ray spectrum. Then, one can see that the fit becomes better compared with the one-zone hadronic model.

$\begin{figure} \par\includegraphics[width=20pc]{0845fig2.eps} \end{figure}$	Figure 2: $\nu F_\nu$ -spectra in the $\gamma$ -ray band, predicted by the two-zone hadronic model (solid line). The dashed and dotted lines represent fluxes from region 1 and 2, respectively. Others are the same as in Fig. 1.
Open with DEXTER

3.2 Leptonic two-zone model

The observed correlation between TeV $\gamma$ -ray and synchrotron X-rays (Aharonian et al. 2006) may suggest that they have the same origin. Then, since synchrotron X-rays arise from accelerated electrons, one may expect that the leptonic model is likely (Ogasawara et al. 2007; Lazendic et al. 2004; Porter et al. 2006).

Similar to the hadronic two-zone model, two independent regions are considered. The region j (j=1,2) has a magnetic field B^(j)and the electron spectrum $N^{(j)}(E_{\rm e})=A^{(j)}E_{\rm e}^{-s_{\rm e}^{(j)}}\exp(-E_{\rm e}/E_{\rm max}^{(j)})$ , where A^(j) is the normalization constant. Here, the electron spectra are given by a single power-law form, because the inefficient acceleration is adopted. We consider synchrotron emission and IC emission in which the target photon is the CMB. The total emission spectrum from the SNR is given by the sum of the emissions from two regions.

Figures 3 and 4 show the result where we adopt $B^{(1)}=2.1~\mu$ G, $B^{(2)}=10~\mu$ G, $s_{\rm e}^{(1)}=s_{\rm e}^{(2)}=2.0$ , $E_{\rm max}^{(1)}=10$ TeV, $E_{\rm max}^{(2)}=40$ TeV, and A⁽¹⁾/A⁽²⁾=2.74. The observed spectrum, including radio and X-ray bands, can be explained by this model. Note that in the leptonic model, the magnetic field strength must be much less than the observationally inferred values (Uchiyama et al. 2007; Parizot et al. 2006) in order to fit the radio and X-ray synchrotron spectrum - if the magnetic field were larger than 10 $\mu$ G, the predicted synchrotron radiation would be much brighter than observed (Aharonian & Atoyan 1999). Hence, other explanations for the observations of rapid time variability and thin width of synchrotron filaments may be necessary (Katz & Waxman 2008; Pohl et al. 2005; Butt 2008).

$\begin{figure} \par\includegraphics[width=20pc]{0845fig3.eps} \end{figure}$	Figure 3: $\nu F_\nu$ -spectra in the $\gamma$ -ray band, predicted by a two-zone leptonic IC model (solid line). The dashed and dotted lines represent fluxes from region 1 and 2, respectively. Others are the same as in Fig. 1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=20pc]{0845fig4.eps} \end{figure}$	Figure 4: The same as in Fig. 3, but in the wide-band energy range from radio to TeV $\gamma$ -rays. Radio and X-ray data are taken from Aharonian et al. (2006) and Takahashi et al. (2008), respectively.
Open with DEXTER

Comparing Fig. 2 with Fig. 3, we find that the predicted spectrum of the hadronic two-zone model in the efficient acceleration case is similar to that of the leptonic two-zone model in the case of inefficient acceleration. This conclusion is the same as that for one-zone models in Sect. 2.

4 Conclusion

Some models predict relatively bright GeV $\gamma$ -rays compared with those considered above. If the CR back-reaction effect on the particle spectrum is small (inefficient-acceleration case), then the energy spectral index of protons is $s_{\rm p}\approx2$ , and the $\pi ^0$ -decay $\gamma$ -ray emission shows a roughly flat $\nu F_\nu$ -spectrum, $\nu F_\nu\propto\nu^0$ , in the GeV-TeV band (model IIa/IIIa in Table 1). The predicted flux is marginally consistent with the EGRET upper limit, $\nu F_\nu\approx5\times10^{-11}$ erg s^-1cm^-2 at 1-10 GeV (Hartman et al. 1999; Aharonian et al. 2006). On the other hand, if the magnetic field is moderately strong, the synchrotron cooling effect causes steepening of the electron spectrum over a wide energy range - typically $s_{\rm e}\approx3$ (e.g., see Sect. 19.3, Eq. (19.16) of Longair 1994). In this case, leptonic IC emission in the GeV-TeV band again shows a nearly flat $\nu F_\nu$ -spectrum (model IIb in Table 1). Therefore, these $\gamma$ -ray emission models (IIa/IIIa and IIb) cannot be distinguished. This has been discussed in Ellison et al. (2007), where $B\approx60~\mu$ G.

In summary, it may be difficult to differentiate between hadronic and leptonic emission by the spectral shape of the GeV-to-TeV $\gamma$ -ray emission of Galactic young SNRs like RXJ1713 (Table 1). As shown in this paper, when the GeV $\gamma$ -ray flux is relatively low (e.g., $\nu F_\nu\propto\nu^{0.5}$ ), both an efficient acceleration model with hadronic $\gamma$ -ray emission (model Ia) and a leptonic, weak magnetic-field model with inefficient acceleration (model IIIb) may give similar spectral shapes. On the other hand, as already pointed out in Ellison et al. (2007), when the GeV emission is relatively bright (e.g., $\nu F_\nu\propto\nu^0$ ), one may not be able to distinguish the hadronic model in the inefficient case (models IIa/IIIa) from the leptonic one with a moderately strong magnetic field (model IIb). This conclusion may, at least qualitatively, be applicable to other young SNRs emitting TeV gamma-rays, such as RX J0852.0-4622 (Aharonian et al. 2005; Katagiri et al. 2005). Fermi will likely provide us with rich information on the emission mechanism of RXJ1713 and other young SNRs. However, one should only draw conclusions with great care, even in the Fermi era. Probably, neutrino observation with km³-class detectors such as IceCube (Achterberg et al. 2007) or KM3NeT (Kappes & Consortium 2007) will finally resolve the problem (Crocker et al. 2002; Kistler & Beacom 2006; Alvarez-Muñiz & Halzen 2002; Huang & Pohl 2008; Halzen et al. 2008; Vissani & Villante 2008). As shown in Fig. 5, if the observed TeV $\gamma$ -ray emission is hadronic, then the expected neutrino spectrum at the source is above the atmospheric neutrino background at around 5-10 TeV, which may become the smoking gun of proton acceleration in Galactic young SNRs.

$\begin{figure} \par\includegraphics[width=20pc]{0845fig5.eps}\end{figure}$

Figure 5:

$\nu F_\nu$ -spectra of TeV $\gamma$ -rays (solid line) and $\mu$ -neutrinos (dashed line) calculated within the hadronic two-zone model in the efficient acceleration case. The solid line is the same as in Fig. 2. We have averaged the vacuum oscillation effects among neutrinos. The dotted line shows the daily averaged atmospheric neutrino flux expected in KM3NeT (Kappes et al. 2007; Kappes & Consortium 2007).

Open with DEXTER

Acknowledgements

We are grateful to the referee for useful comments. This work was supported in part by a Grant-in-aid from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan, No. 18740153, No. 19047004 (R.Y.) and No. 19740143 (H.K.), and in part by PPARC grant, PP/D000394/1, EU grant MRTN-CT-2006-035863, the European Union through the Marie Curie Research and Training Network ``UniverseNet'', MRTN-CT-2006-035863 (K.K.)

References

Achterberg, A., Ackermann, M., Adams, J., et al. 2007, PRD, 76, 042008 [NASA ADS] [CrossRef] [Erratum: PRD, 77, 089904 (2008)] (In the text)
Aharonian, F. A., & Atoyan, A. M. 1996, A&A, 309,917
Aharonian, F. A., & Atoyan, A. M. 1999, A&A, 351, 330 (In the text)
Aharonian, F. A., Akhperjanian, A. G., Aye, K.-M., et al., 2004, Nature, 432, 75 [NASA ADS] [CrossRef]
Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al., 2005, A&A, 437, L7 [NASA ADS] [CrossRef] [EDP Sciences]
Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al., 2006, A&A, 449, 223 [NASA ADS] [CrossRef] [EDP Sciences]
Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R, et al. 2007, A&A, 464, 235 [NASA ADS] [CrossRef] [EDP Sciences]
Alvarez-Muñiz, J., & Halzen, F. 2002, ApJ, 576, L33 [NASA ADS] [CrossRef]
Amato, E., & Blasi, P. 2005, MNRAS, 364, L76 [NASA ADS]
Bamba, A., Yamazaki, R., Ueno, M., & Koyama, K., 2003, ApJ, 589, 827 [NASA ADS] [CrossRef]
Bamba, A., Yamazaki, R., Yoshida, T., Terasawa, T., & Koyama, K. 2005a, ApJ, 621, 793 [NASA ADS] [CrossRef]
Bamba, A., Yamazaki, R., & Hiraga, J. S. 2005b, ApJ, 632, 294 [NASA ADS] [CrossRef]
Berezhko, E. G., et al. 1994, Astropart. Phys., 2, 215 [NASA ADS] [CrossRef]
Blandford, R. D., & Eichler, D. 1987, Phys. Rep., 154, 1 [NASA ADS] [CrossRef]
Blasi, P. 2002, Astropart. Phys., 16, 429 [NASA ADS] [CrossRef]
Blasi, P., Gabici, S., & Vannoni, G. 2005, MNRAS, 361, 907 [NASA ADS] [CrossRef]
Butt, Y. 2008, MNRAS, 386, L20 [NASA ADS]
Caprioli, D., Blasi, P., Amato, E., & Vietri, M. 2008a, ApJ, 679, L139 [NASA ADS] [CrossRef]
Caprioli, D., et al. 2008b, [arXiv:0807.4261]
Crocker, R. M., Melia, F., & Volkas, Raymond R. 2002, ApJS, 141, 147 [NASA ADS] [CrossRef]
Drury, L.O'C. 1983, Rep. Prog. Phys, 46, 973 [NASA ADS] [CrossRef]
Ellison, D. C., Baring, M. G., & Jones, F. C. 1996, ApJ, 473, 1029 [NASA ADS] [CrossRef]
Ellison, D. C., Patnaude, D. J., Slane, P., Blasi, P., & Gabici, S. 2007, ApJ, 661, 879 [NASA ADS] [CrossRef] (In the text)
Enomoto, R., Tanimori, T., Naito, T., et al. 2002, Nature, 416, 823 [NASA ADS] [CrossRef]
Fukui, Y., Moriguchi, Y., Tamura, K., et al. 2003, PASJ, 55, L61 [NASA ADS] (In the text)
Gabici, S., Aharonian, F. A., & Blasi, P. 2007, Ap&SS, 309, 365 [NASA ADS] [CrossRef]
Giacalone, J., & Jokipii, J. A. 2007, ApJ, 663, L41 [NASA ADS] [CrossRef]
Halzen, F., et al. 2008, PRD, 78, 063004 [NASA ADS] [CrossRef]
Hartman, R. C., Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 79 [CrossRef]
Higashi, Y., Kubo, H., Yoshida, T., et al. 2008, ApJ, 683, 957 [NASA ADS] [CrossRef] (In the text)
Huang, C.-Y., & Pohl, M. 2008, Astropart. Phys., 29, 282 [NASA ADS] [CrossRef]
Kang, H., Jones, T. W., LeVeque, R. J., & Shyue, K. M. 2001, ApJ, 550, 737 [NASA ADS] [CrossRef]
Kappes, A., Hinton, J., Stegmann, C., & Aharonian, F. A. 2007, ApJ, 656, 870 [NASA ADS] [CrossRef]
Kappes, A. 2007, [arXiv:0711.0563] (In the text)
Katagiri, H., Enomoto, R., Ksenofontov, L. T., et al. 2005, ApJ, 619, L163 [NASA ADS] [CrossRef]
Katz, B., & Waxman, E. 2008, JCAP, 01, 018 [NASA ADS] (In the text)
Kistler, M. D., & Beacom, J. F. 2006, PRD, 74, 063007 [NASA ADS] [CrossRef]
Koyama, K., Petre, R., Gotthelf, E. V., et al. 1995, Nature, 378, 255 [NASA ADS] [CrossRef] (In the text)
Lazendic, J. S., Slane, P. O., Gaensler, B. M., et al. 2004, ApJ, 602, 271 [NASA ADS] [CrossRef]
Longair, M. S. 1994, High Energy Astrophysics, 2, Stars, the Galaxy and the interstellar medium (Cambridge: Cambridge University Press) (In the text)
Lucek, S. G., & Bell, A. R. 2000, MNRAS, 314, 65 [NASA ADS] [CrossRef]
Malkov, M. A. 1997, ApJ, 485, 638 [NASA ADS] [CrossRef]
Malkov, M. A. 1999, ApJ, 511, L53 [CrossRef]
Malkov, E., & Drury, L.O'C. 2001, Rep. Prog. Phys., 64, 429 [NASA ADS] [CrossRef]
Morlino, G., Amato, E., & Blasi, P. 2009, MNRAS, 392, 240 [NASA ADS] [CrossRef] (In the text)
Ogasawara, T., Yoshida, T., Yanagita, S., & Kifune, T. 2007, Ap&SS, 309, 401 [NASA ADS] [CrossRef]
Parizot, E., Yoshida, T., Yanagita, S., & Kifune, T. 2006, A&A, 453, 387 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Plaga, R. 2008, New Astron., 13, 73 [NASA ADS] [CrossRef] (In the text)
Pohl, M., et al. 2005, ApJ, 626, L101 [NASA ADS] [CrossRef]
Porter, T. A., Moskalenko, I. V., & Strong, A. W. 2006, ApJ, 648, L29 [NASA ADS] [CrossRef]
Sjostrand, T., Mrenna, S., & Skands, P. 2006, JHEP, 0605, 026 [NASA ADS] (In the text)
Takahashi, T., Tanaka, T., Uchiyama, Y., et al. 2008, PASJ, 60, S131 (In the text)
Tanaka, T., Uchiyama, Y., Aharonian, F. A., et al. 2008, ApJ, 685, 988 [NASA ADS] [CrossRef] (In the text)
Terasawa, T., Hada, T., Matsukiyo, S., et al. 2007, Prog. Theor. Phys. Suppl., 169, 146 [NASA ADS] [CrossRef]
Uchiyama, Y., Aharonian, F. A., & Takahashi, T. 2003, A&A, 400, 567 [NASA ADS] [CrossRef] [EDP Sciences]
Uchiyama, Y., Aharonian, F. A., Tanaka, T., Takahashi, T., & Maeda, Y. 2007, Nature, 449, 576 [NASA ADS] [CrossRef] (In the text)
Villante, F. L., & Vissani, F. 2007, PRD, 76, 125019 [NASA ADS] [CrossRef] (In the text)
Vink, J., & Laming, J. M. 2003, ApJ, 584, 758 [NASA ADS] [CrossRef]
Vissani, F., & Villante, F. L. 2008, Nucl. Inst. Meth. Phys. Res. A, 588, 123 [NASA ADS] [CrossRef]
Vladimirov, A., Ellison, D. C., & Bykov, A., et al. 2006, ApJ, 652, 1246 [NASA ADS] [CrossRef] (In the text)
Vladimirov, A., Bykov, A. M., & Ellison, D. C. 2008, ApJ, 688, 1084 [NASA ADS] [CrossRef] (In the text)
Yamazaki, R., et al. 2004, A&A, 416, 595 [NASA ADS] [CrossRef] [EDP Sciences]
Yamazaki, R., Kohri, K., Bamba, A., et al. 2006, MNRAS, 371, 1975 [NASA ADS] [CrossRef] (In the text)
Zirakashvili, V. N., & Ptuskin, V. S. 2008, [arXiv:0807.2754] (In the text)

Footnotes

... (Fermi): http://fermi.gsfc.nasa.gov/
... harder: Another kind of formation of a hard $\gamma$ -ray spectrum from accelerated protons is the SNR-MC interaction system with appropriate separation (e.g., Aharonian & Atoyan 1996; Gabici et al. 2007). The slower propagation of the low-energy protons toward the cloud makes the $\gamma$ -ray spectrum hard.

All Tables

Table 1: Spectral index of $\nu F_\nu$ spectrum of gamma-rays ( $\nu F_\nu \propto \nu ^\alpha$ ) for various cases. Hadronic emission model in the case of efficient acceleration (Ia) predicts similar $\gamma$ -ray spectral slope with the leptonic, inefficient acceleration model with weak magnetic field (IIIb). On the other hand, hadronic inefficient acceleration models (IIa and IIIa) predict similar $\gamma$ -ray spectral slope with the leptonic, moderate magnetic field model (IIb).

All Figures

$\begin{figure} \par\includegraphics[width=20pc]{0845fig1.eps} \end{figure}$	Figure 1: $\nu F_\nu$ -spectra in $\gamma$ -ray band, predicted by hadronic $\pi ^0$ -decay model in the efficient acceleration case (solid line) and leptonic IC model in the inefficient case (dashed line). The dot-dashed curve shows the 1 year, 5 $\sigma$ sensitivity for the Fermi LAT taking into account the Galactic diffuse background (Higashi et al. 2008). The observed spectrum in the TeV band is shown (Aharonian et al. 2007).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=20pc]{0845fig2.eps} \end{figure}$	Figure 2: $\nu F_\nu$ -spectra in the $\gamma$ -ray band, predicted by the two-zone hadronic model (solid line). The dashed and dotted lines represent fluxes from region 1 and 2, respectively. Others are the same as in Fig. 1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=20pc]{0845fig3.eps} \end{figure}$	Figure 3: $\nu F_\nu$ -spectra in the $\gamma$ -ray band, predicted by a two-zone leptonic IC model (solid line). The dashed and dotted lines represent fluxes from region 1 and 2, respectively. Others are the same as in Fig. 1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=20pc]{0845fig4.eps} \end{figure}$	Figure 4: The same as in Fig. 3, but in the wide-band energy range from radio to TeV $\gamma$ -rays. Radio and X-ray data are taken from Aharonian et al. (2006) and Takahashi et al. (2008), respectively.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=20pc]{0845fig5.eps}\end{figure}$	Figure 5: $\nu F_\nu$ -spectra of TeV $\gamma$ -rays (solid line) and $\mu$ -neutrinos (dashed line) calculated within the hadronic two-zone model in the efficient acceleration case. The solid line is the same as in Fig. 2. We have averaged the vacuum oscillation effects among neutrinos. The dotted line shows the daily averaged atmospheric neutrino flux expected in KM3NeT (Kappes et al. 2007; Kappes & Consortium 2007).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.