| Issue |
A&A
Volume 494, Number 3, February II 2009
|
|
|---|---|---|
| Page(s) | 1083 - 1090 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361:200810894 | |
| Published online | 22 December 2008 | |
Evolution of the barium abundance in the early Galaxy from a NLTE analysis of the Ba lines in a homogeneous sample of EMP stars![[*]](/icons/foot_motif.gif)
S. M. Andrievsky1,2 -
M. Spite1 -
S. A. Korotin2 -
F. Spite1 -
P. François1 -
P. Bonifacio1,3,![]() -
R. Cayrel1 -
V. Hill1
-
R. Cayrel1 -
V. Hill1
1 -
GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 92125 Meudon Cedex, France
2 -
Department of Astronomy and Astronomical Observatory, Odessa National University, Isaac Newton Institute of Chile, Odessa branch, Shevchenko Park, 65014 Odessa, Ukraine
3 -
Istituto Nazionale di Astrofisica, Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
Received 1 September 2008 / Accepted 18 November 2008
Abstract
Context. Barium is a key element in constraining the evolution of the (not well understood) r-process in the first galactic stars and currently the Ba abundances in these very metal-poor stars were mostly measured under the Local Thermodynamical Equilibrium (LTE) assumption, which may lead in general to an underestimation of Ba.
Aims. We present here determinations of the barium abundance taking into account the non-LTE (NLTE) effects in a sample of extremely metal-poor stars (EMP stars): 6 turnoff stars and 35 giants.
Methods. The NLTE profiles of the three unblended Ba II lines (4554 Å, 5853 Å, 6496 Å) have been computed. The computations were made with a modified version of the MULTI code, applied to an atomic model of the Ba atom with 31 levels of Ba I, 101 levels of Ba II, and compared to the observations.
Results. The ratios of the NLTE abundances of barium relative to Fe are slightly shifted towards the solar ratio. In the plot of [Ba/Fe] versus [Fe/H], the slope of the regression line is slightly reduced as is the scatter. In the interval
![]() ,
[Ba/Fe] decreases with a slope of about 1.4 and a scatter close to 0.44. For
,
[Ba/Fe] decreases with a slope of about 1.4 and a scatter close to 0.44. For
![]() the number of stars is not sufficient to decide whether [Ba/Fe] keeps decreasing (and then CD-38:245 should be considered as a peculiar ``barium-rich star'') or if a plateau is reached as soon as
the number of stars is not sufficient to decide whether [Ba/Fe] keeps decreasing (and then CD-38:245 should be considered as a peculiar ``barium-rich star'') or if a plateau is reached as soon as
![]() .
In both cases the scatter remains quite large, larger than what can be accounted for by the measurement and determination errors, suggesting the influence of a complex process of Ba production, and/or inefficient mixing in the early Galaxy.
.
In both cases the scatter remains quite large, larger than what can be accounted for by the measurement and determination errors, suggesting the influence of a complex process of Ba production, and/or inefficient mixing in the early Galaxy.
Key words: stars: general - stars: abundances - Galaxy: halo - Galaxy: evolution - stars: supernovae: general - Galaxy: abundances
1 Introduction
In the framework of the ESO ``large programme First stars'', very high quality spectra of extremely metal-poor (EMP) giants and turnoff stars were obtained with the high resolution spectrograph UVES fed with the VLT.
In this sample, 33 giants and 18 turnoff stars are
``normal metal-poor stars'' (not carbon-rich). Among them 22 giants and 10 turnoff stars have
![]() .
The main parameters of these stars can be found in Cayrel et al. (2004: ``First stars V'') and Bonifacio et al. (2007: ``First stars VII'', 2008: ``First stars XII'').
In François et al. (2007, ``First stars VIII'') the abundance of the neutron capture elements has been studied in the sample of EMP giants.
From an LTE analysis, it has been found that, generally speaking, the abundance ratios of these elements relative to iron ([X/Fe]) are very scattered, with sometimes a factor of more than one hundred between the abundance ratios of two stars with equal [Fe/H].
Moreover, on average, [Ba/Fe] increases from about -1.5 to +0.2 while [Fe/H] increases from -3.6 to -2.6.
The important scatter of [Ba/Fe] (and [Sr/Fe]) vs. [Fe/H] has been confirmed by Bonifacio et al. (2008, ``First stars XII'') where the abundances in the sample of giants are compared to the abundances in a sample of turnoff stars obtained in the same conditions.
On the other hand, from a similar LTE analysis, e.g. Burris et al. (2000), Honda et al. (2004) or Lai et al. (2008) found abundance ratios that, in the same range of metallicity, show a similar behaviour. This general trend can also be traced from the rather low S/N measurements of Barklem et al. (2005) in a very large sample of 373 metal-poor stars, albeit with a larger scatter.
.
The main parameters of these stars can be found in Cayrel et al. (2004: ``First stars V'') and Bonifacio et al. (2007: ``First stars VII'', 2008: ``First stars XII'').
In François et al. (2007, ``First stars VIII'') the abundance of the neutron capture elements has been studied in the sample of EMP giants.
From an LTE analysis, it has been found that, generally speaking, the abundance ratios of these elements relative to iron ([X/Fe]) are very scattered, with sometimes a factor of more than one hundred between the abundance ratios of two stars with equal [Fe/H].
Moreover, on average, [Ba/Fe] increases from about -1.5 to +0.2 while [Fe/H] increases from -3.6 to -2.6.
The important scatter of [Ba/Fe] (and [Sr/Fe]) vs. [Fe/H] has been confirmed by Bonifacio et al. (2008, ``First stars XII'') where the abundances in the sample of giants are compared to the abundances in a sample of turnoff stars obtained in the same conditions.
On the other hand, from a similar LTE analysis, e.g. Burris et al. (2000), Honda et al. (2004) or Lai et al. (2008) found abundance ratios that, in the same range of metallicity, show a similar behaviour. This general trend can also be traced from the rather low S/N measurements of Barklem et al. (2005) in a very large sample of 373 metal-poor stars, albeit with a larger scatter.
Generally, the barium abundance in metal-poor stars has been investigated under the LTE approximation. However, the NLTE corrections can be very significant, in particular at low metallicity (see Asplund 2005; Short & Hauschildt 2006) they could be at least partly responsible for the large scatter of the abundance ratios of the heavy elements at low metallicity. In order to determine reliable trends and scatters, and to properly trace the history of nucleosynthesis processes in the first stars, it is highly desirable to perform NLTE analyses.
There are several studies devoted to the determination of the NLTE barium abundance in metal-poor stars. Gigas (1988) performed NLTE modeling of the barium lines in the spectrum of the mildly metal deficient dwarf star Vega. Later, Mashonkina & Bikmaev (1996), and Mashonkina et al. (1999) estimated abundance correction for the cooler and more metal deficient dwarfs (down to [Fe/H] = -2.5). This work was continued by Mashonkina & Gehren (2000), Mashonkina et al. (2003) and more recently by Mashonkina et al. (2008).
In this last paper the authors study the abundance of the heavy elements in four very metal-poor stars with
![]() :
one giant, HD 122 563, and three turnoff stars.
Moreover Short & Hauschildt (2006), performed a theoretical analysis of the non-LTE effects on the Ba lines (
:
one giant, HD 122 563, and three turnoff stars.
Moreover Short & Hauschildt (2006), performed a theoretical analysis of the non-LTE effects on the Ba lines (
![]() ,
5853, 6141, 6496 Å) for metallicities between
,
5853, 6141, 6496 Å) for metallicities between
![]() and -5. They used NLTE models for these computations, but an interesting point is that they could show that the NLTE profiles based on NLTE models differ negligibly from the NLTE profiles computed from LTE models (as is generally done).
and -5. They used NLTE models for these computations, but an interesting point is that they could show that the NLTE profiles based on NLTE models differ negligibly from the NLTE profiles computed from LTE models (as is generally done).
We present here the results of a direct application of an NLTE analysis to the sample of extremely metal-poor stars (turnoff stars and giants) previously analyzed in the ``First stars'' programme. In our previous papers (Andrievsky et al. 2007, 2008) we reported the sodium and aluminium NLTE abundances in these same stars.
This sample covers the region of metallicities from
![]() .
Such metal-poor stars have not been investigated up to now with the aim of deriving their NLTE barium abundances.
.
Such metal-poor stars have not been investigated up to now with the aim of deriving their NLTE barium abundances.
2 Observations and reduction
The sample of stars and the observational data are the same as dicussed in previous papers: First Stars V, VII, VIII and XII (Cayrel et al. 2004; Bonifacio
et al. 2007;
François et al. 2007; and Bonifacio et al. 2008). In brief, the observations were performed with the VLT-UT2 and UVES (Dekker et al. 2000) with a resolving power
![]() .
The signal-to-noise ratio in the spectra of the giants is very high:
.
The signal-to-noise ratio in the spectra of the giants is very high:
![]() 130 per pixel (with an average of 5 pixels per resolution element) but it is lower for the turnoff stars (generally fainter), in particular in the
130 per pixel (with an average of 5 pixels per resolution element) but it is lower for the turnoff stars (generally fainter), in particular in the
![]() region where the strongest Ba line is located, at the very end of the spectra obtained with the ``blue'' camera.
region where the strongest Ba line is located, at the very end of the spectra obtained with the ``blue'' camera.
The spectra were reduced using the UVES context (Ballester et al. 2000) within MIDAS.
Table 1 gives the NLTE barium abundances for our sample. They could be determined for only six (out of 18) turnoff stars, because even their strongest lines of Ba are very weak.
The
![]() value, given in Col. 6 for comparison, has been borrowed from François et al. (2007) for the giants and Bonifacio et al. (2008) for the turnoff stars.
In the last column is given the total number of Ba lines used for the computation. If n=3, all the three lines 4554, 5853, and 6496 Å have been computed, if
n=2 only 4554 and 6496 Å could be used and if n=1 only 4554 Å. For the giants, an ``m'' indicates that the star has been found ``mixed'' in Spite et al. (2005). In this table, for the determination of the relative LTE and NLTE values we have adopted for the solar values
value, given in Col. 6 for comparison, has been borrowed from François et al. (2007) for the giants and Bonifacio et al. (2008) for the turnoff stars.
In the last column is given the total number of Ba lines used for the computation. If n=3, all the three lines 4554, 5853, and 6496 Å have been computed, if
n=2 only 4554 and 6496 Å could be used and if n=1 only 4554 Å. For the giants, an ``m'' indicates that the star has been found ``mixed'' in Spite et al. (2005). In this table, for the determination of the relative LTE and NLTE values we have adopted for the solar values
![]() (Asplund et al. 2005) at variance with François et al. 2007 who adopted
(Asplund et al. 2005) at variance with François et al. 2007 who adopted
![]() (Grevesse & Sauval 2000).
(Grevesse & Sauval 2000).
3 NLTE calculations
The NLTE profiles of the barium lines were computed using a modified version of the MULTI code (Carlsson 1986). The modifications are described in Korotin et al. (1999).
For these computations we used Kurucz's (1992) models (ATLAS9), after checking on some typical stars that the use of MARCS models (Gustafsson et al. 2008) as in Cayrel et al. (2004) would not introduce any significant difference.
As a rule, in the turnoff stars with
![]() ,
the barium abundance can be determined only from the resonance line at 4554 Å, but even this line becomes too weak at
,
the barium abundance can be determined only from the resonance line at 4554 Å, but even this line becomes too weak at
![]() .
In the giants, three lines can be traced down to
.
In the giants, three lines can be traced down to
![]() ,
the resonance line and the two subordinate lines at 5853 and 6496 Å; at still lower metallicity only two lines (4554 and 6496 Å) are still detectable.
,
the resonance line and the two subordinate lines at 5853 and 6496 Å; at still lower metallicity only two lines (4554 and 6496 Å) are still detectable.
3.1 Atomic model of Ba
Our barium model contains 31 levels of Ba I, 101
levels of Ba II with n < 50, and the ground level of Ba III ion.
In the detailed consideration we included 91 bound-bound transitions between the first 28 levels of Ba II with n < 12 and l < 5.
The other levels were used for the particle number conservation. The fine structure of the levels ![]() and
and
![]() was taken into account; the other levels were treated as single.
The corresponding Grotrian diagram is shown in Fig. 1. Only those transitions that were considered in detail, are indicated. The energies of the levels are from Curry (2004). The oscillator strengths of the bound-bound transitions are from Wiese & Martin (1980), Warner (1968), and Miles & Wiese (1969). For the transitions between the seven low-lying levels we used the data from Davidson et al. (1992).
was taken into account; the other levels were treated as single.
The corresponding Grotrian diagram is shown in Fig. 1. Only those transitions that were considered in detail, are indicated. The energies of the levels are from Curry (2004). The oscillator strengths of the bound-bound transitions are from Wiese & Martin (1980), Warner (1968), and Miles & Wiese (1969). For the transitions between the seven low-lying levels we used the data from Davidson et al. (1992).
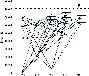 |
Figure 1: The Grotrian diagramme for Ba II, only those transitions that were considered in detail, are indicated. |
| Open with DEXTER | |
3.2 The different constants
A cause of uncertainty in the NLTE analysis of the barium spectrum is the scarce information about the photoionization cross-sections for the different levels. For the majority of the levels we used the results of the scaled Thomas-Fermi method application (Hofsaess 1979). For g-levels and levels with n = 11 we used the hydrogen-like approximation (Lang 1998, Eq. (1.230)).
Effective excitation electron collisional strengths for the
transitions between the first levels (![]() ,
,
![]() and
and
![]() )
were used following Schoening & Butler (1998).
Experimental cross-sections for the transitions
)
were used following Schoening & Butler (1998).
Experimental cross-sections for the transitions
![]() and
and
![]() were taken from Crandall et al. (1974). Collisional
rates for the transitions between sublevels
were taken from Crandall et al. (1974). Collisional
rates for the transitions between sublevels ![]() ,
,
![]() and
and
![]() ,
,
![]() ,
and between
,
and between ![]() and
and ![]() were estimated
with the help of the corresponding formula from Sobelman et al. (1981). For
the rest of the allowed transitions, we used the van Regemorter (1962)
formula, while for the forbidden transitions the Allen's (1973) formula
was used.
were estimated
with the help of the corresponding formula from Sobelman et al. (1981). For
the rest of the allowed transitions, we used the van Regemorter (1962)
formula, while for the forbidden transitions the Allen's (1973) formula
was used.
The rate of the collisional ionization from the ground level of Ba II was calculated using the corresponding formula in Sobelman et al. (1981). The use of experimental data of Peart et al. (1989) and Feeney et al. (1972) give the same results. For the other levels, Drawin's (1961) formula was used.
Inelastic collisions of barium atoms with hydrogen atoms may play a significant role in the cool star atmospheres. They have been taken into account through the formula of Steenbock & Holweger (1984). A correcting factor of 0.1 was derived as a result of the experimental fitting of the barium lines in solar spectrum. Collisions with atomic hydrogen for the forbidden transitions were not taken into account, but we checked that the resulting uncertainty about the equivalent width of the lines, computed by the method of Takeda (1991), does not exceed 0.5%.
The odd barium isotopes have hyper-fine splitting of their levels and thus several HFS components for each line. As was demonstrated by Mashonkina et al. (1999), a three-component structure is sufficient to describe the 4554 Å barium line (see also Rutten 1978). This line was fitted in the solar spectrum by adopting the even-to-odd abundance ratio of 82:18 (Cameron 1982). Since metal deficient stars are supposed to include a larger fraction of the material synthesized in SNe II through the pure r-process, we used an even-to-odd ratio 50:50 for the stars. Nevertheless, we checked that the resulting difference in the equivalent widths of the 4554 Å line due to this change in the even-to-odd ratio is very small. (As a consequence, from our spectra it is not possible to estimate the abundance ratios of the different isotopes of Ba from our spectra, higher resolution would be necessary.)
Radiative damping constants are from Mashonkina & Bikmaev (1996), Stark broadening parameters are from the VALDatabase (http://ams.astro.univie.ac.at/~vald). Since the classical van der Waals formula underestimates the effect of the interaction with neutral particles, the broadening parameters were found by comparing the observed lines in the solar spectrum (Kurucz et al. 1984) with a synthetic spectrum computed with the solar model of Kurucz (1996).
The best agreement was obtained for
![]() (Fig. 2), in good agreement with the estimation of the solar abundance of barium of Asplund et al. (2005).
(Fig. 2), in good agreement with the estimation of the solar abundance of barium of Asplund et al. (2005).
The oscillator strengths of the lines components and the corresponding HFS shifts,
as well as the broadening parameters are given in Table 2. For the
Van der Waals constant C6 we have adopted the definition of Unsöld (1968, Eqs. (82), (47)):
![]() .
.
3.3 Non-LTE effects
The profiles of the barium lines are rather sensitive to the NLTE effects, in particular in metal-poor stars with rather high temperature. The NLTE correction sign changes when the temperature and the metallicity change. Mashonkina et al. (1999) discuss in detail this behaviour in detail for turnoff metal-poor stars. Since the abundance of barium at a given metallicity is very scattered, it is important to note that the NLTE corrections are very sensitive not only to the metallicity of the model but also to the barium abundance itself (the equivalent width of the line).
- -
- The resonance line or the low excitation subordinate lines that are used for the determination of the barium abundance can show substantial nonequilibrium excitation effects.
In a metal-poor atmosphere, since there are few electrons and thus few collisions, the radiative processes cause the departure from equilibrium in the atomic level populations even in the deep atmospheric layers. If the mean intensity of the radiative field in the line frequencies
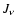 exceeds the Planck intensity
exceeds the Planck intensity 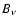 ,
then an enhanced photoexcitation depopulates the lower atomic levels and overpopulates the upper ones (this ``pumping'' is described e.g. in Bruls et al. 1992, or Asplund 2005).
The depth of the effective formation of the radiation in b-b transitions changes significantly with the metallicity (and the corresponding barium abundance) of the star (Fig. 3). This explains the dependence of the NLTE correction on [Fe/H] (Figs. 4 and 5). The lower the metallicity of the model, the deeper in the atmosphere is the line formation level (Fig. 3).
,
then an enhanced photoexcitation depopulates the lower atomic levels and overpopulates the upper ones (this ``pumping'' is described e.g. in Bruls et al. 1992, or Asplund 2005).
The depth of the effective formation of the radiation in b-b transitions changes significantly with the metallicity (and the corresponding barium abundance) of the star (Fig. 3). This explains the dependence of the NLTE correction on [Fe/H] (Figs. 4 and 5). The lower the metallicity of the model, the deeper in the atmosphere is the line formation level (Fig. 3).
- -
- Another mechanism causing the deviations from LTE is the so called UV overionization from the 6p level.
In the atmosphere of turnoff or RGB stars, Ba II is the dominant species and generally this implies that overionization does not significantly affect the line formation.
But for extremely metal-poor stars, already at
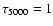 the mean intensity exceeds the Planck intensity at the frequency of the ionization threshold of the 6p level. As a result this level is significantly depopulated.
the mean intensity exceeds the Planck intensity at the frequency of the ionization threshold of the 6p level. As a result this level is significantly depopulated.
| |
Figure 2:
Profile fitting for the barium lines in the solar spectrum with
|
| Open with DEXTER | |
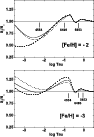 |
Figure 3:
Ratio
|
| Open with DEXTER | |
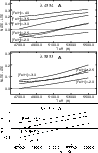 |
Figure 4:
NLTE corrections computed as a function of the temperature
of the model, for several metallicities. The calculations are performed for
|
| Open with DEXTER | |
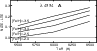 |
Figure 5:
NLTE corrections computed as a function of the temperature of the dwarf models, for several metallicities. All calculations are performed with [Ba/Fe] = 0.0 and
|
| Open with DEXTER | |
 |
Figure 6:
LTE (dashed lines) and NLTE (solid lines) profiles calculated for
|
| Open with DEXTER | |
 |
Figure 7: Profile fitting for the barium lines in two giant stars (BS 17569-049 and CS 22891-209) and a turnoff star (BS 17570-063). In this last case only the 4554 Å line is visible. |
| Open with DEXTER | |
As an illustration we show in Figs. 4 (giants), and 5 (turnoff stars) how the NLTE correction depends on the metallicity for different effective temperatures. For the giant stars we used [Ba/Fe] = -0.5, while for dwarfs [Ba/Fe] = 0.0. These values are typical of the observations. (In turnoff stars if [Fe/H] = -3.0 and [Ba/Fe] = -0.5, the strongest barium line is very weak (
![]() )
and since it is located at the end of the spectra it is generally not detectable).
In fact the main parameter which determines the NLTE correction is [Ba/H], as can be seen in Fig. 4.
Our corrections for the 4554 Å line are in good agreement with those of Mashonkina & Bikmaev (1996) computed for dwarfs and [Fe/H] = -2.
)
and since it is located at the end of the spectra it is generally not detectable).
In fact the main parameter which determines the NLTE correction is [Ba/H], as can be seen in Fig. 4.
Our corrections for the 4554 Å line are in good agreement with those of Mashonkina & Bikmaev (1996) computed for dwarfs and [Fe/H] = -2.
In giant stars (Fig. 4), the NLTE correction for the two lines at 4554 and 5853 Å can be positive or negative depending on the effective temperature. A similar conclusion was obtained by Short & Hauschildt (2006). For the line 4554 Å we found that LTE and NLTE profiles coincide at [Fe/H] = -2.5, while Short & Hauschildt (2006) found such a coincidence at [Fe/H] = -3.0. Our computations (NLTE line transfer with an LTE background model) cannot be directly compared to those of Short & Hauschildt who used NLTE line transfer on an NLTE background model. In spite of this, the predictions of the two are qualitatively similar, with moderate quantitative disagreement. Part of the disagreement may, indeed, be due to the difference in the adopted background models, but part of it may also be due to the differences in the model atoms employed in the two computations. Some examples of the calculated profiles are given in Fig. 6.
3.4 Line profile fitting
It should be stressed that the NLTE corrections given in
Figs. 4 or 5 should not be used to determine a precise value of the NLTE abundance of barium in metal-poor stars, since this correction depends critically on several parameters ([Ba/H], ![]() ). The best way to determine the Ba abundance is to calculate the NLTE profiles directly, and to compare them to the observed profiles. Such an approach was used in this paper. The profile fitting for some stars is displayed in Fig. 7.
). The best way to determine the Ba abundance is to calculate the NLTE profiles directly, and to compare them to the observed profiles. Such an approach was used in this paper. The profile fitting for some stars is displayed in Fig. 7.
The mean NLTE barium abundances of the stars are listed in Table 1 .
The small difference between the [Ba/Fe] ratio found for HD 122 563 in Mashonkina et al. (2008) and in our paper, can be explained by the different values adopted for the gravity.
When several Ba lines are detected in the spectra of a star, the abundances deduced from the different lines agree within ![]()
![]() .
This value can be considered as the observational error. The total error is the quadratic sum of this error and of the error due to the stellar parameter uncertainties. The largest uncertainty arises from the uncertainties in the temperature and the gravity of the stars. We estimate that the total error on [Ba/Fe] is close to 0.2 dex.
.
This value can be considered as the observational error. The total error is the quadratic sum of this error and of the error due to the stellar parameter uncertainties. The largest uncertainty arises from the uncertainties in the temperature and the gravity of the stars. We estimate that the total error on [Ba/Fe] is close to 0.2 dex.
4 Discussion
4.1 Global trend
The behavior of the ratio [Ba/Fe] vs. metallicity for the investigated stars is displayed in Fig. 8.
The turnoff and the giant stars show a similar behaviour (as judged from the few dwarfs for which Ba was measurable). There is no difference in the behaviour of mixed giants (stars located above the Luminosity Function Bump: Spite et al. 2005, 2006) and the low RGB giants. Barium is not affected by mixing along the RGB.
In François et al. (2007) it has been shown from an LTE analysis that in the interval
![]() ,
the abundance of barium decreases rapidly with the metallicity, in agreement with previous works in the literature.
Our NLTE analysis of the barium lines in the same extremely metal-poor star spectra has led to some slight shifts of the derived individual LTE [Ba/Fe] ratios toward the solar ratio, but the main tendency is only slightly changed.
,
the abundance of barium decreases rapidly with the metallicity, in agreement with previous works in the literature.
Our NLTE analysis of the barium lines in the same extremely metal-poor star spectra has led to some slight shifts of the derived individual LTE [Ba/Fe] ratios toward the solar ratio, but the main tendency is only slightly changed.
Globally the results may be summarised as follows (see Fig. 8):
Below the metallicity
![]() ,
the mean value of [Ba/Fe] is negative as found in François et al. (2007).
,
the mean value of [Ba/Fe] is negative as found in François et al. (2007).
The slope of the NLTE value of [Ba/Fe] vs. [Fe/H] is a little shallower than in LTE: the slope of the regression computed in the interval
![]() is about
is about
![]() in NLTE rather than
in NLTE rather than
![]() under LTE assumption (Fig. 8). This small variation of the slope was expected by Mashonkina
et al. (2008). The slope is compatible with a secondary production of Ba.
under LTE assumption (Fig. 8). This small variation of the slope was expected by Mashonkina
et al. (2008). The slope is compatible with a secondary production of Ba.
Table 1: Adopted model and NLTE barium abundance for our sample of stars.
In the region
![]() ,
the scatter around the regression line of the [Ba/Fe] vs. [Fe/H] plot (Fig. 8) is a little smaller (0.44) for the NLTE values than for the LTE values (0.52), but it remains very large, much larger than observed for the abundances of other elements (where it is generally smaller than 0.2 dex). This scatter strongly exceeds what is expected from the measurement and determination errors, and illustrates the decoupling between iron and Ba nucleosyntheses. This point remains valid when using Mg (rather than Fe) as a reference element, suggesting also a decoupling between the production of Mg (hydrostatic burning) and Ba (r-process).
,
the scatter around the regression line of the [Ba/Fe] vs. [Fe/H] plot (Fig. 8) is a little smaller (0.44) for the NLTE values than for the LTE values (0.52), but it remains very large, much larger than observed for the abundances of other elements (where it is generally smaller than 0.2 dex). This scatter strongly exceeds what is expected from the measurement and determination errors, and illustrates the decoupling between iron and Ba nucleosyntheses. This point remains valid when using Mg (rather than Fe) as a reference element, suggesting also a decoupling between the production of Mg (hydrostatic burning) and Ba (r-process).
In the extremely low metallicity domain (
![]() ), the mean behaviour of [Ba/Fe] is not clear. At this very low metallicity, the barium abundance could be estimated in only three ``normal'' stars. (CD -38:245, CS 22172-002 and CS 22885-096). In these stars [Ba/Fe] is around -0.7 suggesting that a
``plateau'' of [Ba/Fe] is reached. But for two other stars, only limits could be measured and for one of them it is rather low:
), the mean behaviour of [Ba/Fe] is not clear. At this very low metallicity, the barium abundance could be estimated in only three ``normal'' stars. (CD -38:245, CS 22172-002 and CS 22885-096). In these stars [Ba/Fe] is around -0.7 suggesting that a
``plateau'' of [Ba/Fe] is reached. But for two other stars, only limits could be measured and for one of them it is rather low:
![]() .
.
4.2 A complex trend?
At very low metallicity (
![]() ), the behaviour of [Ba/Fe] with [Fe/H] (Fig. 8) can be interpreted in three different ways:
), the behaviour of [Ba/Fe] with [Fe/H] (Fig. 8) can be interpreted in three different ways:
- 1.
-
Our Fig. 8 can be interpreted, as proposed by François et al. (2007), by a very large scatter of [Ba/Fe] in the region
![$\rm -3.2 <[Fe/H]<-2.8$](/articles/aa/full_html/2009/06/aa10894-08/img69.gif) :
a factor of about 1000 from star to star, and (for
:
a factor of about 1000 from star to star, and (for
![$\rm [Fe/H] <-3.3$](/articles/aa/full_html/2009/06/aa10894-08/img13.gif) )
a plateau close to the value
)
a plateau close to the value
![$\rm [Ba/Fe]=-1.$](/articles/aa/full_html/2009/06/aa10894-08/img70.gif)
This interpretation was suggested by François et al. (2007) after merging their measurements with those of Honda et al. (2004). But it seems that there is a systematic difference between these two sets of measurements: in Fig. 10 of François et al. the data points from Honda et al. seem to be systematically offsetted in [Fe/H] and [Ba/Fe] compared to the points of François et al. (2007). The difference is mainly due to the adoption of a lower microturbulent velocity by Honda et al. (2004). This systematic shift could be responsible, at least partly, for the very large scatter without any defined trend, suggested by François et al. (2007) in the region![$\rm -3.2 <[Fe/H]<-2.8$](/articles/aa/full_html/2009/06/aa10894-08/img69.gif) .
.
- 2.
-
When only our measurements are taken into account (Fig. 8), and as a consequence, all the stars in the graph are studied in a very homogeneous way, it becomes clear that in the interval
![$\rm -3.6<[Fe/H]<2.5$](/articles/aa/full_html/2009/06/aa10894-08/img71.gif) ,
[Ba/Fe] increases with [Fe/H] with a slope close to
,
[Ba/Fe] increases with [Fe/H] with a slope close to
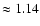 (when the non-LTE effects are taken into account).
(when the non-LTE effects are taken into account).
A problem is to know what happens at lower metallicity. For
![$\rm [Fe/H]<-3.6$](/articles/aa/full_html/2009/06/aa10894-08/img73.gif) the decrease of [Ba/Fe] could continue and then 5 stars would seem Ba-rich with the definition
the decrease of [Ba/Fe] could continue and then 5 stars would seem Ba-rich with the definition
![$\rm [Ba/Fe]> \overline{[Ba/Fe]} + 2 \sigma$](/articles/aa/full_html/2009/06/aa10894-08/img74.gif) :
:
- the two carbon rich stars (CS 22892-052 (Sneden et al. 1996, and CS 22949-037 Depagne et al. 2002);
- the well known r-rich star CS 31082-001 (see Cayrel et al. 2001; Hill et al. 2002);
- CD-38:245, the most metal-poor star of the sample. In this star François
et al. measured an upper limit of the europium abundance:
![$\rm [Eu/Fe]<+0.38$](/articles/aa/full_html/2009/06/aa10894-08/img75.gif) .
According to the definition (Barklem et al. 2005; Beers & Christlieb 2005) of the r-I class of ``moderately r-rich stars''
(
.
According to the definition (Barklem et al. 2005; Beers & Christlieb 2005) of the r-I class of ``moderately r-rich stars''
(
![$\rm +0.3 <[Eu/Fe]< +1.0$](/articles/aa/full_html/2009/06/aa10894-08/img76.gif) )
the upper limit of the Eu abundance may bring CD-38:245 in this class;
)
the upper limit of the Eu abundance may bring CD-38:245 in this class;
- a turnoff star, CS 22948-093. In this kind of star it would be impossible to measure the europium abundance even if it is r-rich with [Eu/Fe] = 1.
However if we suppose that in ``normal'' stars [Ba/Fe] decreases continuously in the interval
![$\rm -4.2<[Fe/H]<-2.5$](/articles/aa/full_html/2009/06/aa10894-08/img78.gif) with a uniform scatter (sigma = 0.44), then 4 stars
(over 38) are outside the two sigma limits (3 on one side and 1 on the other side). This is more than what it is expected for a Gaussian population (only 5%).
with a uniform scatter (sigma = 0.44), then 4 stars
(over 38) are outside the two sigma limits (3 on one side and 1 on the other side). This is more than what it is expected for a Gaussian population (only 5%).
- 3.
-
A third interpretation would combine a decrease of [Ba/Fe] only in the range
![$\rm -3.3 <[Fe/H]<-2.5$](/articles/aa/full_html/2009/06/aa10894-08/img79.gif) and then a plateau which would determine the mean value of the ratio [Ba/Fe] in the early Galaxy:
and then a plateau which would determine the mean value of the ratio [Ba/Fe] in the early Galaxy:
![$\rm [Ba/Fe]\approx -0.7$](/articles/aa/full_html/2009/06/aa10894-08/img80.gif) from this
NLTE analysis.
The value of this plateau would define the yields of barium (relative to iron) in the massive primitive supernovae. If we consider only the stars with
from this
NLTE analysis.
The value of this plateau would define the yields of barium (relative to iron) in the massive primitive supernovae. If we consider only the stars with
![$\rm [Fe/H] < -3.7$](/articles/aa/full_html/2009/06/aa10894-08/img81.gif) ,
the scatter around [Ba/Fe] = -0.7 is rather small, but there are
2 stars with upper limits that increase this scatter.
If a plateau exists, it could suggest a production of Ba independent of the metallicity in the primitive supernovae.
,
the scatter around [Ba/Fe] = -0.7 is rather small, but there are
2 stars with upper limits that increase this scatter.
If a plateau exists, it could suggest a production of Ba independent of the metallicity in the primitive supernovae.
Table 2:
Parameters of the barium lines.
![]() ,
following (Unsöld 1968), in
,
following (Unsöld 1968), in
![]() .
.
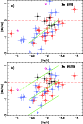 |
Figure 8:
[Ba/Fe] vs. [Fe/H] in our sample of stars computed with the LTE
hypothesis (plot a)) and taking into account the NLTE effects (plot b)).
The values of [Ba/Fe] have been computed with
|
| Open with DEXTER | |
5 Conclusion
We present here a homogeneous determination of the abundance of Ba in a sample of extremely metal-poor stars (turnoff and giant stars) taking into account the non-LTE effects.
There is a good agreement between the abundances of turn off stars, unmixed giants (low RGB) and ``mixed'' giants (stars located in the HR diagram higher than the Luminosity function bump). In the giant stars the abundance of barium does not depend on the deep mixing inside the star.
The NLTE abundances are free from the approximations made in the LTE determinations. The trend of [Ba/Fe] versus [Fe/H] is refined: less scatter, and a better defined and shallower slope. The slope is compatible with a secondary process. The general behaviour would be the same if Mg (rather than Fe) was the reference element.
The scatter of [Ba/Fe], although reduced, is large, and cannot be explained by the determination errors: it suggests the influence of several factors. The contribution of one (or more) additional ``r'' process has been invoked in the literature (see François et al. and references therein 2007; Travaglio et al. 2004; Wasserburg & Qian 2008). Also, an extremely efficient galactic mixing is excluded.
The behaviour of [Ba/Fe] with [Fe/H] (Fig. 8) could be described in two different ways. For a decreasing metallicity:
- 1.
- the mean value of [Ba/Fe] decreases linearly with a large (uniform) scatter and a few outliers;
- 2.
- the mean value of [Ba/Fe] decreases linearly in the interval
![$\rm -2.5>[Fe/H]<-3.6$](/articles/aa/full_html/2009/06/aa10894-08/img90.gif) ,
and then reaches a plateau.
,
and then reaches a plateau.
Acknowledgements
The authors thank the referee for a very careful reading of the manuscript and for useful suggestions. S.M.A. kindly acknowledges the support and hospitality of the Paris-Meudon Observatory. P.B. acknowledges financial support from EU contract MEXT-CT-2004-014265(CIFIST). M.S., R.C., F.S., P.B., V.H., P.F. acknowledge the support of CNRS (PNG and PNPS).
References
- Allen, C. W. 1973, Astrophysical Quantities (London: Athlone Press) (In the text)
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2007, A&A, 464, 1081 [NASA ADS] [CrossRef] [EDP Sciences]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2008, A&A 481, 481 [NASA ADS]
- Asplund, M. 2005, Ann. Rev. Astro. Astrophys., 43, 481 [NASA ADS] [CrossRef] (In the text)
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, ASP Conf. Ser., 336, 25 [NASA ADS] (In the text)
- Ballester, P., Modigliani, A., Boitiquin, O., et al. 2000, ESO Messenger, 101, 31 [NASA ADS] (In the text)
- Barklem, P. S., Christlieb, N., Beers, T. C., et al. 2005, A&A, 439, 129 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] (In the text)
- Bonifacio, P., Molaro, P., Sivarani, T., et al. 2007, A&A, 462, 851 [NASA ADS] [CrossRef] [EDP Sciences] (First stars VII) (In the text)
- Bonifacio, P., Spite, M., Cayrel, R., et al. 2009, A&A, submitted (First stars XII) (In the text)
- Bruls, J. H., Rutten, R. J., & Shchukina, N. 1992, A&A, 265, 237 [NASA ADS] (In the text)
- Burris, D. L., Pilachowski, C. A., Armandro, T. A., et al. 2000, ApJ, 544, 302 [NASA ADS] [CrossRef] (In the text)
- Carlsson, M. 1986, Uppsala Obs. Rep. 33 (In the text)
- Cameron, A. G. W. 1982, Ap&SS, 82, 123 [NASA ADS] [CrossRef] (In the text)
- Cayrel, R., Hill, V., Beers, T. C., et al. 2001, Nature, 409, 691 [NASA ADS] [CrossRef] (In the text)
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars V) (In the text)
- Crandall, D. H., Dunn, G. H., Gallagher, A., et al. 1974, ApJ, 191, 789 [NASA ADS] [CrossRef] (In the text)
- Curry, J. J. 2004, J. Phys. Chem. Ref. Data, 33, 725 [NASA ADS] [CrossRef] (In the text)
- Davidson, M. D., Snoek, L. C., Volten, H., & Doenszelmann, A. 1992, A&A, 255, 457 [NASA ADS] (In the text)
- Dekker, H., D'Odorico, S., Kaufer, A., et al. 2000, in Optical and IR Telescopes Instrumentation and Detectors, ed. I. Masanori, & A. F. Morwood, Proc. SPIE, 4008, 534 (In the text)
- Depagne, E., Hill, V., Spite, M., et al. 2002, A&A, 390, 187 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars II) (In the text)
- Drawin, H.-W. 1961, ZPhy, 164, 513 [NASA ADS] (In the text)
- Feeney, R. K., Hooper, J. W., & Elford, M. T. 1972, PhRvA, 6, 1469 [NASA ADS] (In the text)
- François, P. 1996, A&A, 313, 229 [NASA ADS]
- François, P., Depagne, E., Hill, V., et al. 2007, A&A, 476, 935 [NASA ADS] [CrossRef] [EDP Sciences] (First stars VIII) (In the text)
- Gigas, D. 1988, A&A, 192, 264 [NASA ADS]
- Grevesse, N., & Sauval, A. J. 2000, Origin of the elements in the Solar system, ed. O. Manuel, 261 (In the text)
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hill, V., Plez, B., Cayrel, R., et al. 2002, A&A, 387, 560 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars I) (In the text)
- Hofsaess, D. 1979, ADNDT, 24, 285 [NASA ADS] [CrossRef] (In the text)
- Honda, S., Aoki, W., Kajino, T., et al. 2004, ApJ, 607, 474 [NASA ADS] [CrossRef] (In the text)
- Korotin, S. A., Andrievsky, S. M., & Luck, R. E. 1999, A&A, 351, 168 (In the text)
- Kurucz, R. L. 1992, The Stellar Population of Galaxies, ed. B. Barbuy, & A. Renzini, IAU Symp., 149, 225
- Kurucz, R. L. 1996, Model Atmospheres and Spectrum Synthesis, ed. S. J. Adelman, F. Kupka, & W. W. Weiss, San Francisco, ASP Conf. Ser., 108, 2 (In the text)
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar Flux Atlas from 296 [NASA ADS] to 1300 nm, New Mexico, National Solar Observatory (In the text)
- Lai, D. K., Bolte, M., Johnson, J. A., et al. 2008 [arXiv:0804.1370v1] (In the text)
- Lang, K. 1998, Astrophysical formulae (Berlin - Heidelberg - New York: Springer-Verlag), 52 (In the text)
- Mashonkina, L., & Bikmaev, I. 1996, ARep, 40, 94 [NASA ADS] (In the text)
- Mashonkina, L., & Gehren, T. 2000, A&A, 364, 249 [NASA ADS]
- Mashonkina, L., & Gehren, T. 2001, A&A, 376, 232 [NASA ADS] [CrossRef] [EDP Sciences]
- Mashonkina, L., & Zhao, G. 2006, A&A, 456, 313 [NASA ADS] [CrossRef] [EDP Sciences]
- Mashonkina, L., Gehren, T., & Bikmaev, I. 1999, A&A, 343, 519 (In the text)
- Mashonkina, L., Gehren, T., Travaglio, C., & Borkova, T. 2003, A&A, 397, 275 [NASA ADS] [CrossRef] [EDP Sciences]
- Mashonkina, L., Zhao, G., Gehren, T., et al. 2008, A&A, 478, 529 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Miles, B. M., & Wise, W. L. 1969, ADNDT, 1, 1 [NASA ADS] [CrossRef] (In the text)
- Peart, B., Underwood, J. R. A., & Dolder, K. 1989, JPhB, 22, 1679 [NASA ADS] (In the text)
- Peterson, R. C., Kurucz, R. L., & Carney, B. W. 1990, ApJ, 350, 173 [NASA ADS] [CrossRef]
- Rutten, R. J. 1978, SoPh, 56, 237 [NASA ADS]
- Schoening, T., & Butler, K. 1998, A&AS, 128, 581 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Short, C. I., & Hauschildt, P. H. 2006, ApJ, 641, 494 [NASA ADS] [CrossRef] (In the text)
- Sneden, C., McWilliam, A., Preston, G. W., et al. 1996, ApJ, 467, 819 [NASA ADS] [CrossRef] (In the text)
- Sobelman, I. I., Vainshtein, L. A., & Yukov, E. 1981, Excitation of Atoms and Broadening of Spectral Lines, Springer Ser. in Chem. Phys. (Berlin: Springer) (In the text)
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars VI) (In the text)
- Spite, M., Cayrel, R., Hill, V., et al. 2006, A&A, 455, 291 [NASA ADS] [CrossRef] [EDP Sciences] (First Stars IX) (In the text)
- Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] (In the text)
- Takeda, Y. 1991, A&A, 242, 455 [NASA ADS] (In the text)
- Travaglio, C., Gallino, R., Arnone, E., et al. 2004, ApJ, 601, 864 [NASA ADS] [CrossRef] (In the text)
- Unsöld, A. 1968, Physik der Sternatmosphären (Berlin, Heidelberg, New York: Springer-Verlag), 332 (In the text)
- van Regemorter, H. 1962, ApJ, 136, 906 [NASA ADS] [CrossRef] (In the text)
- Warner, B. 1968, MNRAS, 139, 115 [NASA ADS] (In the text)
- Wasserburg, G. J., & Qian, Y. Z. 2008 [arXiv:0809.2827] (In the text)
- Wiese, W. L., & Martin, G. A. 1980, NSRDS-NBS 68, P.II (In the text)
Footnotes
- ... stars
![[*]](/icons/foot_motif.gif)
- Based on observations obtained with the ESO Very Large Telescope at Paranal Observatory (Large Programme ``First Stars'', ID 165.N-0276; P.I.: R. Cayrel.
- ...
![[*]](/icons/foot_motif.gif)
- CIFIST Marie Curie Excellence Team.
All Tables
Table 1: Adopted model and NLTE barium abundance for our sample of stars.
Table 2:
Parameters of the barium lines.
![]() ,
following (Unsöld 1968), in
,
following (Unsöld 1968), in
![]() .
.
All Figures
 |
Figure 1: The Grotrian diagramme for Ba II, only those transitions that were considered in detail, are indicated. |
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
Profile fitting for the barium lines in the solar spectrum with
|
| Open with DEXTER | |
| In the text | |
 |
Figure 3:
Ratio
|
| Open with DEXTER | |
| In the text | |
 |
Figure 4:
NLTE corrections computed as a function of the temperature
of the model, for several metallicities. The calculations are performed for
|
| Open with DEXTER | |
| In the text | |
 |
Figure 5:
NLTE corrections computed as a function of the temperature of the dwarf models, for several metallicities. All calculations are performed with [Ba/Fe] = 0.0 and
|
| Open with DEXTER | |
| In the text | |
 |
Figure 6:
LTE (dashed lines) and NLTE (solid lines) profiles calculated for
|
| Open with DEXTER | |
| In the text | |
 |
Figure 7: Profile fitting for the barium lines in two giant stars (BS 17569-049 and CS 22891-209) and a turnoff star (BS 17570-063). In this last case only the 4554 Å line is visible. |
| Open with DEXTER | |
| In the text | |
 |
Figure 8:
[Ba/Fe] vs. [Fe/H] in our sample of stars computed with the LTE
hypothesis (plot a)) and taking into account the NLTE effects (plot b)).
The values of [Ba/Fe] have been computed with
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


