| Issue |
A&A
Volume 494, Number 3, February II 2009
|
|
|---|---|---|
| Page(s) | 879 - 890 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361:200810756 | |
| Published online | 11 December 2008 | |
Deceleration of arbitrarily magnetized GRB ejecta: the complete evolution
P. Mimica1 - D. Giannios2 - M. A. Aloy1
1 - Departamento de Astronomía y Astrofísica, Universidad
de Valencia, 46100 Burjassot, Spain
2 - Max Planck Institute for
Astrophysics, Box 1317, 85741 Garching, Germany
Received 6 August 2008 / Accepted 4 November 2008
Abstract
Context. The role of magnetic fields in gamma-ray burst (GRB) flows remains debated. If of sufficient strength, they can leave their signature on the initial phases of the afterglow by substantially changing the backreaction of the flow as a consequence of its interaction with the external medium.
Aims. We attempt to understand quantitatively the dynamical effect and observational signatures of GRB ejecta magnetization on the onset of the afterglow.
Methods. We perform ultrahigh-resolution, one-dimensional, relativistic MHD simulations of the interaction between a radially expanding, magnetized ejecta with the interstellar medium. We require ultrahigh numerical resolution because of the extreme jump conditions in the region of interaction between the ejecta and the circumburst medium. We study the complete evolution of an ultrarelativistic shell to the self-similar asymptotic phase.
Results. Our simulations demonstrate that the complete evolution can be characterized in terms of two parameters, the ![]() parameter introduced by Sari and Piran and the magnetization
parameter introduced by Sari and Piran and the magnetization ![]() .
We use this fact in producing numerical models in which the shell Lorentz factor
.
We use this fact in producing numerical models in which the shell Lorentz factor ![]() is between 10 and 20 and rescaling the results to arbitrarily large values of
is between 10 and 20 and rescaling the results to arbitrarily large values of ![]() .
We find that the reverse shock is typically weak or absent for ejecta characterized by
.
We find that the reverse shock is typically weak or absent for ejecta characterized by
![]() .
The onset of the forward shock emission is strongly dependent on the magnetization. On the other hand, the magnetic energy of the shell is transferred into the external medium on a short timescale (of several times the duration of the burst). The later forward shock emission contains no information about the initial magnetization of the flow. The asymptotic evolution of strongly magnetized shells, after experiencing significant deceleration, resembles that of hydrodynamic shells, i.e. they enter fully into the Blandford-McKee self-similar regime.
.
The onset of the forward shock emission is strongly dependent on the magnetization. On the other hand, the magnetic energy of the shell is transferred into the external medium on a short timescale (of several times the duration of the burst). The later forward shock emission contains no information about the initial magnetization of the flow. The asymptotic evolution of strongly magnetized shells, after experiencing significant deceleration, resembles that of hydrodynamic shells, i.e. they enter fully into the Blandford-McKee self-similar regime.
Key words: gamma rays: bursts - methods: numerical - magnetohydrodynamics (MHD) - shock waves
1 Introduction
Gamma ray bursts (GRBs) are understood to be produced by the energy release in an ultrarelativistic outflow. The mechanisms responsible for launching, accelerating the flow and powering the GRB emission are still not well understood. Two alternative sources of the energy content of the flow have been considered. The GRB flow may be dominated initially by thermal energy density creating a fireball (Paczynski 1986; Goodman 1986) or by the energy stored in magnetic fields giving rise to a Poynting-flux dominated flow (PDF, Usov 1992; Thompson 1994; Meszaros & Rees 1997).
In fireball models, magnetic fields are not dynamically important at any stage of the flow evolution. On the other hand, models of MHD jet acceleration indicate that the conversion of Poynting flux to kinetic energy is partial (Giannios & Spruit 2006; Beskin et al. 1998; Li et al. 1992; Michel 1969; Vlahakis & Königl 2003). As a result, the flow remains rather strongly magnetized at large distances where it interacts with the circumburst medium.
The interaction of the fast flow with the external medium is probably responsible the afterglow emission. The initial phases of this interaction depend, to a large extent, on the magnetization of the flow. Strong magnetic fields affect the shock conditions and the internal dynamics of the ejecta. Rees & Gunn (1974) and Kennel & Coroniti (1984) presented the first attempts to understand the effect of the magnetization on the shock conditions. In the ideal MHD limit, they showed that shocks in magnetically dominated flows cannot dissipate energy efficiently. This particular effect was studied recently by examining the shock conditions of the (reverse) shock that propagates into the GRB flow and the resulting emission (Fan et al. 2004; Zhang & Kobayashi 2005). By accounting for the internal evolution of the magnetized shell, Giannios et al. (2008) argued that even moderately strong magnetic fields can suppress the reverse shock completely and explain the observed paucity of reverse-shock signature in the early afterglow.
We continue previous (semi-)analytical studies of the afterglow phase
of magnetized ejecta with relativistic MHD simulations. We follow the
deceleration of magnetized ejecta from the initial phases of
interaction to the self similar regime in which all energy is
transferred to the shocked, external medium. These simulations clarify
the dynamical effects of GRB ejecta magnetization and their
observational implications for the forward and reverse shock emission.
We present a new set of scaling laws that enable us to extrapolate the
results of numerical models with moderate values of the initial bulk
Lorentz factor (![]() 15) of the ejecta to equivalent models
with much larger Lorentz factors
15) of the ejecta to equivalent models
with much larger Lorentz factors ![]() 100.
100.
2 Ejecta-medium interaction
At large distances from the central engine, there is significant interaction between the relativistic ejecta and the external medium. This interaction is believed to produce afterglow emission. An important difference between fireballs and PDFs is related to the magnetization of the ejecta at the onset of the afterglow phase. In fireball models, the energy of the flow is dominated by the kinetic energy of baryons at large distances from the central engine. If the flow is launched being Poynting-flux dominated, it is expected to retain a significant fraction of its energy in the form of magnetic energy, the remainder being in kinetic form (Beskin et al. 1998; Drenkhahn & Spruit 2002; Lyutikov & Blandford 2003; Li et al. 1992; Michel 1969). Since at least the initial phases of the ejecta-external medium interaction depend on the magnetization of the ejecta (Kennel & Coroniti 1984; Fan et al. 2004; Genet et al. 2007; Zhang & Kobayashi 2005), it is possible to differentiate between fireballs and PDF models from afterglow observations. As we show in this work, early afterglow observations are particularly promising in this respect.
2.1 Previous studies
The deceleration of non-magnetized ejecta has been studied with both analytical (Sari & Piran 1995; Rees & Meszaros 1992) and numerical approaches in one dimension (1D) (Kobayashi et al. 1999) and two dimensions (2D) (Meliani et al. 2007; Granot et al. 2001). The 2D studies are important to follow the late-time lateral spreading of collimated ejecta (Rhoads 1999). On the other hand, the initial phases of ejecta deceleration, in which we are interested, are unaffected by 2D effects and can be studied by assuming a spherically symmetric flow.
Sari & Piran (1995) considered the case of non-magnetized ejecta
assuming a cold shell with (isotropic equivalent) kinetic energy E,
Lorentz factor ![]() ,
and width
,
and width ![]() ,
which
moves against an external medium of density
,
which
moves against an external medium of density
![]() .
This
interaction leads to a pair of shocks: one that propagates in the
external medium (forward shock) and one that decelerates the ejecta
(reverse shock). The strength of the reverse shock depends on the
ratio of the density of the shell to the external medium and on the
bulk Lorentz factor of the flow. It can be shown that the strength of
the reverse shock can be conveniently parametrized by
.
This
interaction leads to a pair of shocks: one that propagates in the
external medium (forward shock) and one that decelerates the ejecta
(reverse shock). The strength of the reverse shock depends on the
ratio of the density of the shell to the external medium and on the
bulk Lorentz factor of the flow. It can be shown that the strength of
the reverse shock can be conveniently parametrized by
where
The dynamics of the deceleration of strongly magnetized ejecta have
not been studied in similar detail. In addition to the ![]() parameter, the ejecta are characterized by the magnetization
parameter, the ejecta are characterized by the magnetization ![]() defined to be the ratio of magnetic to kinetic energy in
the flow. Kennel & Coroniti (1984) considered ideal MHD shock conditions
in arbitrarily magnetized ejecta with a dominant toroidal field, and
showed that the dissipation by the shock becomes weaker as
defined to be the ratio of magnetic to kinetic energy in
the flow. Kennel & Coroniti (1984) considered ideal MHD shock conditions
in arbitrarily magnetized ejecta with a dominant toroidal field, and
showed that the dissipation by the shock becomes weaker as ![]() increases (e.g. Lyutikov & Blandford 2003). They applied their analysis
to the standing shock of pulsar winds. Zhang & Kobayashi (2005) focused on
the effect of magnetization in the context of GRB afterglows. They
ignored the internal evolution of the shell prior to interaction with
the external medium and studied the reverse-shock-crossing phase
(provided that a reverse shock formed). They found distinct features
in the early time light curves because of the magnetization. The
shocks from the interaction of the GRB ejecta with the external medium
propagate forwards and the shock conditions depend on the distance
from the central engine. The Zhang & Kobayashi (2005) analysis was
criticized by Lyutikov (2005) for the assumption about the
distance where the ejecta decelerate. Giannios et al. (2008)
accounted for the internal evolution of the ejecta and derived an
analytic condition for the existence of a reverse shock depending on
increases (e.g. Lyutikov & Blandford 2003). They applied their analysis
to the standing shock of pulsar winds. Zhang & Kobayashi (2005) focused on
the effect of magnetization in the context of GRB afterglows. They
ignored the internal evolution of the shell prior to interaction with
the external medium and studied the reverse-shock-crossing phase
(provided that a reverse shock formed). They found distinct features
in the early time light curves because of the magnetization. The
shocks from the interaction of the GRB ejecta with the external medium
propagate forwards and the shock conditions depend on the distance
from the central engine. The Zhang & Kobayashi (2005) analysis was
criticized by Lyutikov (2005) for the assumption about the
distance where the ejecta decelerate. Giannios et al. (2008)
accounted for the internal evolution of the ejecta and derived an
analytic condition for the existence of a reverse shock depending on ![]() and
and ![]() in a parameter space relevant to GRB flows
in a parameter space relevant to GRB flows![]() .
.
After the reverse shock (if there is one) reaches the back part of the
ejecta, there is a transient phase of interaction during which
rarefaction waves cross the shocked ejecta and shocked external
medium. Gradually most of the energy is transferred into the shocked
external medium and the entire structure relaxes to the self-similar
blast wave described in Blandford & McKee (1976). The evolution of the
blast wave then depends only on the total energy E and density of
the external medium ![]() and not on
and not on ![]() .
After the
self-similar evolution has been reached, nothing can be inferred about
the initial magnetization of the flow.
.
After the
self-similar evolution has been reached, nothing can be inferred about
the initial magnetization of the flow.
However, none of these studies have addressed two important questions. First, there is the question of which stage of the interaction a reverse shock forms (if it forms at all). At a short distance from the central engine, the magnetic pressure of the shell is sufficiently high for the shell to rarefy upon interacting with the external medium. This rarefaction may develop into a (reverse) shock at larger distance where the magnetic pressure in the shell drops. Second, although it is clear ignoring radiative losses that the total energy initially in the shell is passed onto the external medium at a distance approximately similar to the Sedov length, which is independent of the magnetization of the flow (Lyutikov 2005), the details of how exactly this occurs depend on the magnetization. These two aspects are closely connected to the energy dissipated in the (forward and reverse) shocks as a function of distance, and consequently, to the afterglow emission from particles accelerated in these shocks. We address this issue by studying the full dynamical interaction from the initial stages to the establishment of the self-similar evolution. To this end, we perform ultra-high-resolution, one-dimensional relativistic MHD simulations of shell-medium interaction.
3 The model for the ejecta
We focus on the GRB flow at a distance at which there is substantial
interaction with the external medium. This interaction probably occurs
a considerable time after the acceleration, collimation, and prompt
emission phases are completed. After the internal dissipation phase
(believed to power the ![]() -ray emission) ends, the flow expands
radially and cools down. The expansion also produces a dominant
toroidal component of the magnetic field. At the so-called Alfvén
point, the poloidal
-ray emission) ends, the flow expands
radially and cools down. The expansion also produces a dominant
toroidal component of the magnetic field. At the so-called Alfvén
point, the poloidal ![]() and toroidal
and toroidal ![]() field
components are expected to be of similar magnitude. At larger
distances, the flux freezing condition corresponds to
field
components are expected to be of similar magnitude. At larger
distances, the flux freezing condition corresponds to
![]() while the induction equation predicts slower
decline for
while the induction equation predicts slower
decline for
![]() .
The same scalings would hold if the
initial B-field was random with
.
The same scalings would hold if the
initial B-field was random with
![]() at large
distance from the central engine.
at large
distance from the central engine.
We consider radially moving, cold shell of ejecta of width ![]() ,
total (kinetic and magnetic) energy E that coasts with a bulk
Lorentz factor
,
total (kinetic and magnetic) energy E that coasts with a bulk
Lorentz factor ![]() .
The magnetic content of the flow is
parametrized with the magnetization parameter
.
The magnetic content of the flow is
parametrized with the magnetization parameter ![]() ,
which
represents the magnetic-to-kinetic energy ratio in the shell. The
flow is assumed to move with super-fast magnetosonic speeds (i.e.
,
which
represents the magnetic-to-kinetic energy ratio in the shell. The
flow is assumed to move with super-fast magnetosonic speeds (i.e.
![]() ;
for studies of the opposite limit, see
Lyutikov 2006; and Genet et al. 2007). For the
simulations presented below, the shell is located at an initial
distance r0 from the central engine. The choice of r0 is
important, since r0 should be sufficiently small not to affect the
subsequent interaction of the ejecta with the external medium. We must
set r0 to be smaller than any of the characteristic radii that
appear when considering the deceleration of magnetized ejecta. These
radii are the ``contact'' radius and the ``reverse-shock crossing'' radius
to be defined in the next section.
;
for studies of the opposite limit, see
Lyutikov 2006; and Genet et al. 2007). For the
simulations presented below, the shell is located at an initial
distance r0 from the central engine. The choice of r0 is
important, since r0 should be sufficiently small not to affect the
subsequent interaction of the ejecta with the external medium. We must
set r0 to be smaller than any of the characteristic radii that
appear when considering the deceleration of magnetized ejecta. These
radii are the ``contact'' radius and the ``reverse-shock crossing'' radius
to be defined in the next section.
3.1 Characteristic distances
In the super-fast magnetosonic flow under consideration, the various
parts along the radial direction drop out of MHD contact
during the acceleration phase. It can be shown that for a cold flow
that coasts with constant speed with dominant toroidal field the
magnetization remains constant. The time it takes for a fast MHD wave
to cross the width of the shell is therefore fixed. The expansion
timescale
![]() is initially much shorter than
that of MHD waves but increases linearly with distance from the
central engine. At the so-called ``contact'' radius
is initially much shorter than
that of MHD waves but increases linearly with distance from the
central engine. At the so-called ``contact'' radius ![]() ,
MHD
waves cross the width of the shell on a timescale comparable to the
expansion timescale (Giannios et al. 2008)
,
MHD
waves cross the width of the shell on a timescale comparable to the
expansion timescale (Giannios et al. 2008)
After contact is established, the shell is no longer in pure ballistic motion and internal evolution because MHD forces can no longer be ignored. On the other hand, in non-magnetized ejecta the sound speed declines sharply with distance due to adiabatic expansion, and the motion is unaffected by the pressure of the shell.
A second important radius is that at which the reverse shock reaches
the rear part of the ejecta. This radius can be identified using the
formulation of Zhang & Kobayashi (2005) by solving the ideal MHD shock
conditions for arbitrarily magnetized ejecta (see also
Fan et al. 2004, for the case of mildly magnetized ejecta). Their
analysis describes the reverse-shock crossing-phase provided that
there is a reverse-shock forming. The reverse-shock crossing radius
can be expressed approximately as (Giannios et al. 2008)
The Zhang & Kobayashi (2005) analysis does not take into account the internal evolution of the shell. It is thus accurate when such evolution insignificant, i.e. when
The initial distance r0 where the shell is set up up must be
![]() so that the simulation begins sufficiently early
to follow both any rarefaction waves within the shell, and
shocks caused by the interaction with the external medium.
so that the simulation begins sufficiently early
to follow both any rarefaction waves within the shell, and
shocks caused by the interaction with the external medium.
3.2 Characteristic quantities
In this paper, we frequently use the following definition
of the normalized time of observation for a model with parameters
![]() ,
,
![]() ,
and r0:
,
and r0:
where
We also often base our arguments on the relative Lorentz factor
![]() between two parts of the fluid separated by the
shock front. For ultrarelativistic flows, we use
between two parts of the fluid separated by the
shock front. For ultrarelativistic flows, we use
where
3.3 Numerical models
Although the problem is characterized by several parameters E,
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() ,
to complete a
systematic study of the shell-medium interaction, we need to focus on
the combination of the first four parameters that are given by
,
to complete a
systematic study of the shell-medium interaction, we need to focus on
the combination of the first four parameters that are given by
 |
(6) |
and
As in the case of unmagnetized ejecta, we use the Sari-Piran
parameter ![]() to characterize partly the strength of the reverse shock. In the
magnetized case, the shock strength is certainly not uniquely
constrained by
to characterize partly the strength of the reverse shock. In the
magnetized case, the shock strength is certainly not uniquely
constrained by ![]() .
An additional parameter,
.
An additional parameter, ![]() ,
must be
introduced to describe fully the reverse-shock strength of arbitrarily
magnetized flows. Thus, one deals with a
,
must be
introduced to describe fully the reverse-shock strength of arbitrarily
magnetized flows. Thus, one deals with a
![]() plane in
exploring different cases for the initial phases of shell-external
medium interaction. Here, we explore the
plane in
exploring different cases for the initial phases of shell-external
medium interaction. Here, we explore the
![]() regime that is
relevant to typical GRB parameters. Numerical reasons limit us to the
regime that is
relevant to typical GRB parameters. Numerical reasons limit us to the
![]() range of the magnetization parameter.
range of the magnetization parameter.
Our different models are summarized in Table 1. The
![]() models (thin shells) are characterized by
models (thin shells) are characterized by
![]() erg,
erg,
![]() cm,
cm,
![]() ,
,
![]() cm-3. The
cm-3. The ![]() models (thick shells) have a factor of ten
higher total energy E and the shell width
models (thick shells) have a factor of ten
higher total energy E and the shell width ![]() ,
while
,
while
![]() and
and ![]() remain fixed. The ``continuous flow''
model (to be discussed in more detail in Sect. 4.3) describes a flow
of constant total (kinetic + Poynting) luminosity of L=1049 erg/s
that moves with
remain fixed. The ``continuous flow''
model (to be discussed in more detail in Sect. 4.3) describes a flow
of constant total (kinetic + Poynting) luminosity of L=1049 erg/s
that moves with
![]() and collides with an external medium of
number density
and collides with an external medium of
number density
![]() cm-3. In all models,
cm-3. In all models,
![]() cm.
cm.
Table 1: Parameters of the numerical models.
One may notice that the models are characterized by an unrealistically
low Lorentz factor
![]() and wide shells
and wide shells
![]() cm with respect to that expected for a GRB flow
(i.e.
cm with respect to that expected for a GRB flow
(i.e.
![]() ,
,
![]() cm). These parameters were chosen so that the problem was resolved
reliably with our RMHD code. While models with
cm). These parameters were chosen so that the problem was resolved
reliably with our RMHD code. While models with
![]() in combination with extreme density and magnetic field jumps at the
edge of the ejecta shell are not feasible at this stage, we propose a
method to extrapolate the results of the
in combination with extreme density and magnetic field jumps at the
edge of the ejecta shell are not feasible at this stage, we propose a
method to extrapolate the results of the
![]() simulation by
rescaling appropriately the initial conditions. Furthermore, we
completed simulations with
simulation by
rescaling appropriately the initial conditions. Furthermore, we
completed simulations with
![]() ,
where we demonstrate the
accuracy of the rescaling procedure (see Sect. 4.4).
,
where we demonstrate the
accuracy of the rescaling procedure (see Sect. 4.4).
4 Results
To derive the results presented in this Section, we solve the
equations of RMHD in 1D spherical geometry with a magnetic field
perpendicular to the direction of propagation of the fluid, i.e., with
a purely toroidal magnetic field. The system of RMHD equations, and
the numerical tests we have completed to identify the appropriate
numerical resolution for our experiments (between 104 and
![]() cells to resolve the initial radial width of the ejecta)
are shown in Appendix A. Finally, all our models have were
executed until the bulk Lorentz factor behind the forward shock had
declined to
cells to resolve the initial radial width of the ejecta)
are shown in Appendix A. Finally, all our models have were
executed until the bulk Lorentz factor behind the forward shock had
declined to
![]() .
By that time, the shell had experienced
a substantial deceleration and fully entered into the Blandford-MacKee
self-similar regime.
.
By that time, the shell had experienced
a substantial deceleration and fully entered into the Blandford-MacKee
self-similar regime.
4.1 Non-magnetized shells
The
![]() models exhibit the well known features expected from
analytical results (Sari & Piran 1995) and simulations
(Kobayashi et al. 1999). The thin shell (
models exhibit the well known features expected from
analytical results (Sari & Piran 1995) and simulations
(Kobayashi et al. 1999). The thin shell (![]() )
model is
characterized by a Newtonian-to-mildly-relativistic reverse shock.
The reverse shock crosses the shell at a distance
)
model is
characterized by a Newtonian-to-mildly-relativistic reverse shock.
The reverse shock crosses the shell at a distance
![]() cm, which agrees to within
cm, which agrees to within ![]() 10% with the analytical
estimate from Eq. (3). At this distance, the relative
Lorentz factor of the shocked ejecta with respect to the unshocked
shell is
10% with the analytical
estimate from Eq. (3). At this distance, the relative
Lorentz factor of the shocked ejecta with respect to the unshocked
shell is
![]() .
The thick shell (
.
The thick shell (![]() ) model
finds itself closer to the ``relativistic reverse shock'' regime with
) model
finds itself closer to the ``relativistic reverse shock'' regime with
![]() cm (to within
cm (to within ![]() 10% of the
initial estimate) and
10% of the
initial estimate) and
![]() .
In both runs, after
the reverse shock crosses the shell, a rarefaction begins at the rear
part of the shell and propagates forwards (a similar rarefaction
happens in the magnetized case, which we label R2 in
Fig. 1). The rarefaction crosses the contact
discontinuity, generated in the leading radial edge of the shell (an
equivalent contact-discontinuity arises in the magnetized case: see
``CD'' in Fig. 1), and reaches the forward shock as
the shell approaches
.
In both runs, after
the reverse shock crosses the shell, a rarefaction begins at the rear
part of the shell and propagates forwards (a similar rarefaction
happens in the magnetized case, which we label R2 in
Fig. 1). The rarefaction crosses the contact
discontinuity, generated in the leading radial edge of the shell (an
equivalent contact-discontinuity arises in the magnetized case: see
``CD'' in Fig. 1), and reaches the forward shock as
the shell approaches
![]() cm
and
cm
and
![]() cm, in the thin-
and in the thick-shell case, respectively. At this stage,
cm, in the thin-
and in the thick-shell case, respectively. At this stage, ![]() 90%
of the energy of the shell has been transferred into the shocked
external medium. Within a factor of
90%
of the energy of the shell has been transferred into the shocked
external medium. Within a factor of ![]() 2 in radius, the blastwave
fully relaxes to the Blandford-McKee self-similar solution.
2 in radius, the blastwave
fully relaxes to the Blandford-McKee self-similar solution.
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg01.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg81.gif) |
Figure 1:
Snapshot of the thin magnetized shell evolution taken after
the RS has formed and before it has crossed the shell. Full and
dashed black lines show the logarithms of the rest-mass density
(normalized to the initial shell density |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg02.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg82.gif) |
Figure 2:
Energy in different components (normalized to the initial
total energy in the shell) as a function of the radius of the
FS. Upper and lower panels show the thin ( |
| Open with DEXTER | |
The different components of the total energy (see
e.g., Mimica et al. 2007) as function of radius of the front shock (FS)
are shown in Fig. 2. For the thin-shell model, the peak
of the thermal energy of the shell (approximately 9% of the total
energy contained in the ejecta) identifies the position of the
reverse shock (RS) crossing of the shell. Beyond
![]() cm,
most of the energy that was initially in the shell is transferred into
the shocked external medium. The apparent ``disappearance'' of the
shell at
cm,
most of the energy that was initially in the shell is transferred into
the shocked external medium. The apparent ``disappearance'' of the
shell at
![]() cm is a numerical artifact of
the grid remapping
cm is a numerical artifact of
the grid remapping![]() . However, this effect is
irrelevant to the discussion of the features in which we are
interested, since all occur before the shell
``disappears'', both in non-magnetized and magnetized models. For the
unmagnetized thick-shell runs, we see that the reverse shock dissipates
more energy from the shell, reaching approximately 18% of the total
shell energy by the time it crosses the shell.
. However, this effect is
irrelevant to the discussion of the features in which we are
interested, since all occur before the shell
``disappears'', both in non-magnetized and magnetized models. For the
unmagnetized thick-shell runs, we see that the reverse shock dissipates
more energy from the shell, reaching approximately 18% of the total
shell energy by the time it crosses the shell.
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg03.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg85.gif) |
Figure 3:
Relative Lorentz factor at the FS
( upper panel) and RS
( lower panel) as a function of the normalized observer time
|
| Open with DEXTER | |
In Fig. 3, we show the relative Lorentz factor at the
FS and the RS as a function of observer time. Both shocks form
immediately after allowing the initial shell to evolve. The RS becomes
stronger with distance, as evident in the increase of
![]() with
with
![]() .
This strengthening continues until it reaches the
rear part of the shell, where it encounters a far less dense medium,
resulting in a kink in the RS curves (marked with vertical black lines
in Fig. 3). The peak of the emission associated with
the RS is expected to occur at the moment the RS breaks out of the
shell, since afterwards the density, pressure, and velocity of the
shocked medium decrease abruptly, and precisely there it reaches its
maximum strength. For the thin-shell case, this happens slightly after
the burst, i.e. at observer time
.
This strengthening continues until it reaches the
rear part of the shell, where it encounters a far less dense medium,
resulting in a kink in the RS curves (marked with vertical black lines
in Fig. 3). The peak of the emission associated with
the RS is expected to occur at the moment the RS breaks out of the
shell, since afterwards the density, pressure, and velocity of the
shocked medium decrease abruptly, and precisely there it reaches its
maximum strength. For the thin-shell case, this happens slightly after
the burst, i.e. at observer time
![]() .
For the thick
shell, the peak of the RS emission appears at the end of the burst, at
a time
.
For the thick
shell, the peak of the RS emission appears at the end of the burst, at
a time
![]() .
.
The Lorentz factor of the external medium just behind the FS declines
as a function of radius. An interesting feature is the change in the
slope of
![]() at time
at time
![]() for the thin shell (at time
for the thin shell (at time
![]() for the thick
shell), which is a result of the rarefaction R2(Fig. 1) reaching the forward shock. For a short
transient period, the FS reduces its strength because the density
behind it is reduced by the action of the rarefaction R2. The decay
of
for the thick
shell), which is a result of the rarefaction R2(Fig. 1) reaching the forward shock. For a short
transient period, the FS reduces its strength because the density
behind it is reduced by the action of the rarefaction R2. The decay
of
![]() is more rapid for a time
interval
is more rapid for a time
interval
![]() after the rarefaction R2catches up with the FS. Thus, we expect the early afterglow emission
to weaken transiently more rapidly with time. Later, the time
dependence of
after the rarefaction R2catches up with the FS. Thus, we expect the early afterglow emission
to weaken transiently more rapidly with time. Later, the time
dependence of
![]() expected from the self-similar solution, is gradually established.
expected from the self-similar solution, is gradually established.
4.2 Magnetized shells
The initial phases of deceleration of strongly magnetized ejecta distinctly differ from those that are unmagnetized in a way related to the magnetic pressure of the ejecta. As discussed in Giannios et al. (2008), the discontinuity in the physical conditions between the shell and the external medium results in the development of two Riemann structures, each every radial (rear and forward) edge of the shell. The waves into which each of these Riemann structures decompose are combinations of shocks and/or rarefactions separated by contact discontinuities. If the magnetic pressure is sufficiently high, instead of a typical double-shock structure, a right-going shock (FS) and a left-going rarefaction (R1) develop from the forward edge of the shell (Fig. 1). Similarly, at the backward edge of the shell, a rarefaction (not shown in Fig. 1) moving backwards (in the shell comoving-frame) into the external medium develops, as well as a rarefaction that penetrates the shell.
The expansion of the shell produces a decrease in the magnetic
pressure and the Lorentz factor of contact until the ``transition''
radius,
![]() ,
is reached, where
,
is reached, where
![]() .
This
distance can be estimated by balancing between the pressure of the
shocked external medium
.
This
distance can be estimated by balancing between the pressure of the
shocked external medium
![]() and the magnetic
pressure of the shell
and the magnetic
pressure of the shell
![]() ,
and solving for the radius
,
and solving for the radius
 |
(7) |
From this distance onwards, the shell decelerates with respect to its initial
The shock is initially weak (
![]() )
and
remains so during the period in which it sweeps up the entire (thin)
shell (Fig. 3). When it reaches the back edge of the
shell,
)
and
remains so during the period in which it sweeps up the entire (thin)
shell (Fig. 3). When it reaches the back edge of the
shell,
![]() ,
i.e., it remains Newtonian. The
reverse shock dissipates a negligible amount of energy (
,
i.e., it remains Newtonian. The
reverse shock dissipates a negligible amount of energy (![]() 0.1% of
the total energy in the shell). It becomes stronger when a thick
shell is considered, reaching
0.1% of
the total energy in the shell). It becomes stronger when a thick
shell is considered, reaching
![]() by the time it
reaches the rear radial edge of the shell (Fig. 3,
lower panel). Thus, this RS sweeping a thick shell leads to a higher
dissipation of energy (
by the time it
reaches the rear radial edge of the shell (Fig. 3,
lower panel). Thus, this RS sweeping a thick shell leads to a higher
dissipation of energy (![]() 1% of the total). However, the
dissipated energy is still a factor of
1% of the total). However, the
dissipated energy is still a factor of ![]() 20 lower than in the
non-magnetized thick-shell model. In the thin-shell case, the local
maximum of the thermal energy at
20 lower than in the
non-magnetized thick-shell model. In the thin-shell case, the local
maximum of the thermal energy at
![]() cm
(Fig. 2 upper panel) corresponds to the RS
crossing. Afterwards, most of the energy concentrates into the shocked
external medium at distance
cm
(Fig. 2 upper panel) corresponds to the RS
crossing. Afterwards, most of the energy concentrates into the shocked
external medium at distance
![]() cm, when the
evolution becomes similar to that of the unmagnetized shell.
cm, when the
evolution becomes similar to that of the unmagnetized shell.
At early times, the Lorentz factor of the medium just behind the
forward shock is higher than that of the shell, due to the initial
rarefaction. This initially leads to
![]() until the
``transition'' radius is reached (Fig. 3). The fact
that initially
until the
``transition'' radius is reached (Fig. 3). The fact
that initially
![]() is a unique feature of
magnetized ejecta (in unmagnetized ejecta
is a unique feature of
magnetized ejecta (in unmagnetized ejecta
![]() always). This initial phase also appears in the early afterglow of the
electromagnetic model (Genet et al. 2007; Lyutikov 2006).
always). This initial phase also appears in the early afterglow of the
electromagnetic model (Genet et al. 2007; Lyutikov 2006).
The magnetization affects the (reverse) shock conditions and, as a result, the reverse shock crosses a magnetized shell more rapidly than an unmagnetized one (the vertical blue lines appear to the left of the vertical black lines in the lower panel of Fig. 3). This feature was revealed in the study of Fan et al. (2004). Our simulations demonstrate that the rarefaction R2 also crosses (in observer time) a magnetized more rapidly shell than a unmagnetized one.
On a timescale of a few (thick shell) or several (thin shell) times
that of the duration of the burst, the ![]() and
and ![]() models exhibit similar evolution. At this stage, almost all the shell
energy has been transferred to the shocked external medium
(Fig. 2). The two models have the same total energy and
relax to identical asymptotic self-similar solutions (note the
similarity between the rising parts of the solid thin blue and black
lines in Fig. 2). The forward shock emission beyond
this time reveals nothing about the initial magnetization. We note,
however, that there is a prolonged RS crossing phase at the tail of
the magnetized ejecta, and some residual energy remains in the form
of Poynting flux at later times that may power some (energetically
weak) afterglow features.
models exhibit similar evolution. At this stage, almost all the shell
energy has been transferred to the shocked external medium
(Fig. 2). The two models have the same total energy and
relax to identical asymptotic self-similar solutions (note the
similarity between the rising parts of the solid thin blue and black
lines in Fig. 2). The forward shock emission beyond
this time reveals nothing about the initial magnetization. We note,
however, that there is a prolonged RS crossing phase at the tail of
the magnetized ejecta, and some residual energy remains in the form
of Poynting flux at later times that may power some (energetically
weak) afterglow features.
4.3 Dissipation by the reverse shock
Our simulations can quantitatively answer the question of how much
energy is dissipated when the reverse shock propagates into ejecta of
different magnetization ![]() and parameter
and parameter ![]() .
For practical
reasons, the simulations were limited to a few models
.
For practical
reasons, the simulations were limited to a few models![]() .
On the other hand, they can be used in evaluating the accuracy and
limitations of previous (semi-)analytical studies
(Fan et al. 2004; Giannios et al. 2008; Zhang & Kobayashi 2005) and exploring a larger
parameter space of
.
On the other hand, they can be used in evaluating the accuracy and
limitations of previous (semi-)analytical studies
(Fan et al. 2004; Giannios et al. 2008; Zhang & Kobayashi 2005) and exploring a larger
parameter space of ![]() and
and ![]() .
.
The ``continuous flow'' models with
![]() and
and
![]() describe spherical flows of constant (as functions of radius)
luminosity L, magnetization
describe spherical flows of constant (as functions of radius)
luminosity L, magnetization ![]() ,
and Lorentz factor
,
and Lorentz factor
![]() that collide with a uniform external medium of number
density
that collide with a uniform external medium of number
density ![]() .
Initially, the interface between the two media is
set to be at some distance r0 (see Sect. 3 for the choice of r0)
and the system is allowed to evolve. With these models, we can focus
on the interface of interaction between the shell and external medium
and, therefore, track in significant detail the formation and
strengthening of the reverse shock with time (or equivalently
radius). This configuration allows us to follow the strength of the
reverse shock for different ``equivalent thickness'' of shells in a
single simulation.The idea behind the equivalent thickness is to
measure the penetration distance from the contact discontinuity to the
reverse shock, and assume a shell whose initial thickness
.
Initially, the interface between the two media is
set to be at some distance r0 (see Sect. 3 for the choice of r0)
and the system is allowed to evolve. With these models, we can focus
on the interface of interaction between the shell and external medium
and, therefore, track in significant detail the formation and
strengthening of the reverse shock with time (or equivalently
radius). This configuration allows us to follow the strength of the
reverse shock for different ``equivalent thickness'' of shells in a
single simulation.The idea behind the equivalent thickness is to
measure the penetration distance from the contact discontinuity to the
reverse shock, and assume a shell whose initial thickness ![]() is equal to this distance. We can then use Eq. (1) to obtain
the equivalent
is equal to this distance. We can then use Eq. (1) to obtain
the equivalent ![]() of the assumed shell. The consequence of this is
that the more the reverse shock penetrates the flow, the thicker
equivalent shell it probes for the fixed magnetization
of the assumed shell. The consequence of this is
that the more the reverse shock penetrates the flow, the thicker
equivalent shell it probes for the fixed magnetization ![]() .
We
define equivalent
.
We
define equivalent ![]() (taking into account that
(taking into account that
![]() )
)
for which it is evident that a thicker equivalent shell corresponds to a lower
![\begin{figure}
\includegraphics[scale=0.45]{figures/0756fg04.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg109.gif) |
Figure 4:
Energy dissipation in the reverse shock in
|
| Open with DEXTER | |
A convenient measure of the strength of the reverse shock is the
relative Lorentz factor
![]() of the unshocked ejecta
with respect to the shocked ejecta (Eq. (5)). In
Fig. 4, we mark the locations where the
of the unshocked ejecta
with respect to the shocked ejecta (Eq. (5)). In
Fig. 4, we mark the locations where the
![]() becomes 1.04, 1.1, and 1.25. We have argued in
(Giannios et al. 2008) that for
becomes 1.04, 1.1, and 1.25. We have argued in
(Giannios et al. 2008) that for
![]() ,
the
magnetization of the flow cannot prevent the formation of a shock in
the ejecta and vice versa. The curve defined by setting
,
the
magnetization of the flow cannot prevent the formation of a shock in
the ejecta and vice versa. The curve defined by setting
![]() (thick black line in Fig. 4) can thus
be used as a proxy to mark the region where a reverse shock forms.
(thick black line in Fig. 4) can thus
be used as a proxy to mark the region where a reverse shock forms.
As one can see in Fig. 4, the region in which a reverse
shock exists is larger than that estimated by
(Giannios et al. 2008). This is due to the late RS formation that has
been revealed by the numerical simulations. This effect was
unaccounted for in our previous analytic estimates. However, the
analytic prediction that the reverse shock emission from models whose
parameters are in the region
![]() would not be
observed is still qualitatively valid, since the dissipation from the
shock is weak. On the solid line,
would not be
observed is still qualitatively valid, since the dissipation from the
shock is weak. On the solid line,
![]() and
becomes higher only for lower values of
and
becomes higher only for lower values of ![]() .
For
.
For
![]() ,
the shock converts only a fraction of
,
the shock converts only a fraction of ![]()
![]() of the energy of the
shell into heat. Here
of the energy of the
shell into heat. Here
![]() for
for
![]() (see e.g., Zhang & Kobayashi 2005). Integrating the thermal energy in
the shocked shell for the snapshot for which
(see e.g., Zhang & Kobayashi 2005). Integrating the thermal energy in
the shocked shell for the snapshot for which
![]() ,
we find that it accounts only for
,
we find that it accounts only for ![]() 0.3% and
0.3% and ![]() 0.1% of the
total energy of the shocked shell in the
0.1% of the
total energy of the shocked shell in the
![]() and
and
![]() models respectively. This reveals that a shock, though there, still
dissipates weakly ``above'' the solid line of Fig. 4.
models respectively. This reveals that a shock, though there, still
dissipates weakly ``above'' the solid line of Fig. 4.
4.4 Rescaling of the results to arbitrarily high 
Our simulations correspond to an ultrarelativistic shell of material
interacting with the external medium that has the qualitative
characteristics expected at the onset of the afterglow phase of the
GRB ejecta. Nevertheless, they have two parameters that are
unrealistic with respect to that expected in a GRB, namely the initial
bulk Lorentz factor ![]() and the thickness of the shell
and the thickness of the shell
![]() .
GRBs are believed to originate from flows with
.
GRBs are believed to originate from flows with
![]() ,
while the flow thickness is probably connected
to the observed duration of the burst by
,
while the flow thickness is probably connected
to the observed duration of the burst by
![]() cm. However, numerical reasons compel us to
simulate shells which have
cm. However, numerical reasons compel us to
simulate shells which have
![]() and
and
![]() cm. In this section we present a method in which our
results can reliably be rescaled to GRB-relevant parameters.
cm. In this section we present a method in which our
results can reliably be rescaled to GRB-relevant parameters.
4.4.1 Motivation for the proposed rescaling
We first focus on unmagnetized GRB ejecta and then extend our
discussion to include magnetization. For
![]() ,
the problem of
the interaction between an ultrarelativistic and thin cold shell with
an external medium is defined by four parameters E,
,
the problem of
the interaction between an ultrarelativistic and thin cold shell with
an external medium is defined by four parameters E, ![]() ,
,
![]() ,
and
,
and ![]() .
The evolution of this configuration does
not depend on the individual parameters but a specific combination of
them can be expressed by
.
The evolution of this configuration does
not depend on the individual parameters but a specific combination of
them can be expressed by
![]() .
The parameter
.
The parameter ![]() determines, for example, the relative Lorentz factor
determines, for example, the relative Lorentz factor
![]() of the reverse shock (Sari & Piran 1995). For the
ultrarelativistic flow under consideration,
of the reverse shock (Sari & Piran 1995). For the
ultrarelativistic flow under consideration,
![]() (see Eq. (5)), where
(see Eq. (5)), where
![]() represents the Lorentz factor of the shocked ejecta
when the shock reaches their rear part. For fixed
represents the Lorentz factor of the shocked ejecta
when the shock reaches their rear part. For fixed ![]() ,
this means
that
,
this means
that
![]() is a fixed fraction of
is a fixed fraction of ![]() independently of the value of
independently of the value of ![]() .
For example, since in our
.
For example, since in our
![]() model we found that
model we found that
![]() ,
one can predict that a non-magnetized shell
with
,
one can predict that a non-magnetized shell
with ![]() and arbitrary
and arbitrary
![]() is characterized by
is characterized by
![]() at the moment of the
RS crossing.
at the moment of the
RS crossing.
The idea behind rescaling is to solve (numerically) the evolution of a
shell with
![]() and
and
![]() ,
and then predict
(without simulating) the evolution of a second shell with
,
and then predict
(without simulating) the evolution of a second shell with
![]() (usually higher than
(usually higher than
![]() )
and
)
and
![]() which
has the same
which
has the same ![]()
![]() .
The distance from the central engine at which the reverse
shock crosses the second shell is
.
The distance from the central engine at which the reverse
shock crosses the second shell is
![]() (see Eq. (3)). The
same relation connects the distances given by
(see Eq. (3)). The
same relation connects the distances given by
![]() (see Sari & Piran 1995) where the shells ``1''
and ``2'' enter the deceleration phase after accumulating a fraction
(see Sari & Piran 1995) where the shells ``1''
and ``2'' enter the deceleration phase after accumulating a fraction
![]() of their own initial mass M0. This indicates that
the characteristic distances of the shell-medium interaction for the
shell ``2'' are shifted by a factor
of their own initial mass M0. This indicates that
the characteristic distances of the shell-medium interaction for the
shell ``2'' are shifted by a factor
![]() with respect to those of the shell
``1''. We postulate that the same is true throughout the
evolution of the system. More precisely, we claim that by
rescaling the Lorentz factor from
with respect to those of the shell
``1''. We postulate that the same is true throughout the
evolution of the system. More precisely, we claim that by
rescaling the Lorentz factor from
![]() to
to
![]() one
can predict the evolution of a shell ``2'' by using that of the
shell ``1'' providing that one also rescales the distance to
one
can predict the evolution of a shell ``2'' by using that of the
shell ``1'' providing that one also rescales the distance to
![]() .
.
We further extend the previous postulate by adding up the possibility
that the shell was magnetized, i.e., we extend the previous claim to
the case
![]() .
The evolution of a thin,
ultrarelativistic shell of thickness
.
The evolution of a thin,
ultrarelativistic shell of thickness
is self-similar to that of a shell with the same
4.4.2 Mathematical description of the rescaling
Here, we provide the expressions for transformation of the
solutions for models with the same total energy E and density
of the external medium ![]() .
On more mathematical terms, the
postulated recipe for transforming from one solution to another is the
following. Suppose the bulk Lorentz factor
.
On more mathematical terms, the
postulated recipe for transforming from one solution to another is the
following. Suppose the bulk Lorentz factor
![]() of the
shell ``1'' at is known (t1 is the time in the rest frame of the
GRB engine or laboratory frame), and we define the quantity
of the
shell ``1'' at is known (t1 is the time in the rest frame of the
GRB engine or laboratory frame), and we define the quantity
![]() .
We further assume that the bulk
Lorentz factors of both shells at any time other than the initial one
are linked by
.
We further assume that the bulk
Lorentz factors of both shells at any time other than the initial one
are linked by
where
Here
There are several interesting properties of the proposed recipe. First, the magnetizations of both ejecta are the same (
4.4.3 Invariance of the time of observation
An important byproduct of the transformations provided by
Eqs. (10) and (11) is that the time of
observation defined by Eq. (4) is invariant. The only
assumption that we make is that the motions of both shells ``1''
and ``2'' are ultrarelativistic, so that the position of the FS can,
generally, be written as
We first demonstrate the invariance of
We transform the integral as

and insert it into Eq. (14). After transforming
 |
(15) |
For a point inside the shell ``2'', that differs from the FS, we have
We can see that the second term on the right hand side is also invariant to the scaling, since
4.4.4 Verification by test simulations
We tested numerically the postulate stated in the previous section for
both unmagnetized and magnetized flows, and found that it is correct
to within a few percent accuracy. In the following, we present three
numerical models that share a common magnetization
![]() and
and
![]() .
The remainder of the parameters are: 1)
.
The remainder of the parameters are: 1)
![]() and
and
![]() cm; 2)
cm; 2)
![]() and
and
![]() cm; and iii) 3)
cm; and iii) 3)
![]() and
and
![]() cm. We use the scaling relations
given in Eqs. (10)-(12) to conform
models 1 and 3 to the model 2. In Fig. 5, we show
the density, magnetization, and Lorentz factor after applying
the scaling laws Eqs. (10)-(12) to the
models.
cm. We use the scaling relations
given in Eqs. (10)-(12) to conform
models 1 and 3 to the model 2. In Fig. 5, we show
the density, magnetization, and Lorentz factor after applying
the scaling laws Eqs. (10)-(12) to the
models.
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg05.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg166.gif) |
Figure 5:
Results of a test of the rescaling with |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg06.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg169.gif) |
Figure 6:
Similar to Fig. 3, but for the models used
in the test of the rescaling hypothesis. Black, blue, and red lines
in the upper (lower) panel show the relative Lorentz factor of the
fluid at the FS (RS) as a function of the normalized time of
observation for models with
|
| Open with DEXTER | |
4.5 Extrapolation to

 100 and ``bolometric''
light curves
100 and ``bolometric''
light curves
The MHD calculations presented here do not suffice to calculate the expected emission in detail. Such a calculation of the afterglow emission in different observed bands needs additional assumptions related to the, poorly known, shock microphysics. These include, for example, the energy distribution of the accelerated electrons and the generation of magnetic fields in the shock front. Furthermore, one needs to include radiative mechanisms such as synchrotron and inverse Compton and allow for adiabatic losses. This detailed calculation falls beyond the scope of this work. Instead, we apply a simple method to obtain a rough estimate of the bolometric emission expected from the different models. To make predictions about the properties of the afterglow light curves associated with our numerical models, we extrapolate them to the conventionally accepted parameter regime where GRBs occur. To achieve this, we apply the rescaling described in the previous section.
We assume that in both reverse and forward shocks a fraction
![]() of the dissipated energy ins transferred to
high-energy electrons, and that the electrons are in the fast-cooling
regime (as is usually the case during the initial afterglow
phases). The resulting total emission then is given by the rate at
which the shocks heat the external medium and the shell.
of the dissipated energy ins transferred to
high-energy electrons, and that the electrons are in the fast-cooling
regime (as is usually the case during the initial afterglow
phases). The resulting total emission then is given by the rate at
which the shocks heat the external medium and the shell.
From the shock conditions at the FS (Sari & Piran 1995), we derive the
thermal energy (in the laboratory frame) dissipated by the FS when it
moves from r to
![]() to be
to be
 |
(17) |
where we assume that
For the reverse shock, we estimate its luminosity by assuming that a fraction
where
The luminosities
![]() and
and
![]() can be normalized to
the initial shell luminosity defined by
can be normalized to
the initial shell luminosity defined by
 |
(20) |
In this way, we obtain the dimensionless luminosities
We have checked that the normalized and conveniently scaled light
curves for the test models from Sect. 4.4.4 agree to
within a few percent of each other. This means that we can use this
normalized light curves to predict the bolometric luminosity observed
from a shell with, e.g.,
![]() ,
and the same value
,
and the same value ![]() and 0.5 as our thin and thick shell models, respectively. The
light curves computed for the reference models with
and 0.5 as our thin and thick shell models, respectively. The
light curves computed for the reference models with
![]() and
scaled to ejecta of Lorentz factors
and
scaled to ejecta of Lorentz factors
![]() (thin shell;
Fig. 7) and
(thin shell;
Fig. 7) and
![]() (thick model shell;
Fig. 8) differ fundamentally between thin and thick
magnetized shells. The luminosity of the RS of magnetized thin shells
is much smaller than the luminosity of the corresponding RS in the
hydrodynamic case (we note that in Fig. 7 the light
curve of the magnetized RS is not evident on the scale we are
considering). For thick shells, the luminosity of the RS shock is
about 10 times smaller than that of the corresponding thick shell with
(thick model shell;
Fig. 8) differ fundamentally between thin and thick
magnetized shells. The luminosity of the RS of magnetized thin shells
is much smaller than the luminosity of the corresponding RS in the
hydrodynamic case (we note that in Fig. 7 the light
curve of the magnetized RS is not evident on the scale we are
considering). For thick shells, the luminosity of the RS shock is
about 10 times smaller than that of the corresponding thick shell with
![]() .
Hence, the detection of the RS will, in general, be far
more difficult if the shell ejecta is magnetized than if it is
unmagnetized. Indeed, if the magnetized ejecta is thin, it is
likely that the RS will not be detected at all.
.
Hence, the detection of the RS will, in general, be far
more difficult if the shell ejecta is magnetized than if it is
unmagnetized. Indeed, if the magnetized ejecta is thin, it is
likely that the RS will not be detected at all.
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg07.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg187.gif) |
Figure 7:
Light curves for non-magnetized (black) and magnetized
(blue line) thin shell models after scaling the
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg08.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg188.gif) |
Figure 8:
Same as Fig. 7, but for a thick
shell model ( |
| Open with DEXTER | |
5 Discussion and comparison with previous work
GRB outflows may be launched by strong fields resulting in a Poynting-flux-dominated wind. In this case, the flow can remain strongly magnetized throughout the acceleration, collimation, and GRB emission phases, all the way to the onset of the afterglow. This is in sharp contrast to expectations for a flow initially dominated by thermal energy (fireball) in which magnetic fields are dynamically unimportant. Magnetization is expected to affect the initial phase of interaction between the GRB ejecta and the external medium. Since early afterglow observations are now possible for many bursts, it has become topical to study the effect of the ejecta magnetization in the early afterglow in more detail.
Here we perform ultra-high resolution 1D RMHD simulations of the interaction between a radially expanding magnetized ejecta and the interstellar medium. We study the complete evolution of an ultrarelativistic, initially-uniform, ejecta shell, all the way to a self-similar, asymptotic phase. We explicitly show the resolution of numerical simulations required to resolve appropriately all the discontinuities in the flow, and to be free of numerical artifacts. The main findings of the work are the following:
- 1.
- the complete evolution can be characterized in terms of two
parameters, namely, the Sari-Piran parameter
 and the
magnetization
and the
magnetization  .
Since both parameters are defined from
combinations of basic physical properties of the ejecta (e.g.,
.
Since both parameters are defined from
combinations of basic physical properties of the ejecta (e.g.,
 ,
E, and
,
E, and  ), a single point in the
), a single point in the
 -plane can be used to probe a variety of
equivalent combinations of basic physical parameters. A useful
byproduct of this degeneracy is that one can produce numerical
models where the shell Lorentz factor is
-plane can be used to probe a variety of
equivalent combinations of basic physical parameters. A useful
byproduct of this degeneracy is that one can produce numerical
models where the shell Lorentz factor is  is of the order
of 10, and rescale the results to arbitrarily high values
is of the order
of 10, and rescale the results to arbitrarily high values
 .
Certainly, the numerical difficulty of simulations with
moderate Lorentz factor (namely,
.
Certainly, the numerical difficulty of simulations with
moderate Lorentz factor (namely,
 )
is smaller
than those with a large one (see Appendix A.1). The
later type of simulations are prone to a number of numerical
artifacts that hinder an appropriate comprehension of the physics we
are dealing with. The method of rescaling our reference numerical
models to the conditions expected to occur in GRB afterglows is
described in Sect. 4.4;
)
is smaller
than those with a large one (see Appendix A.1). The
later type of simulations are prone to a number of numerical
artifacts that hinder an appropriate comprehension of the physics we
are dealing with. The method of rescaling our reference numerical
models to the conditions expected to occur in GRB afterglows is
described in Sect. 4.4;
- 2.
- the amounts of energy dissipated in the reverse shock depend
strongly on the magnetization of the flow. The reverse shock is weak
or absent for ejecta characterized by
 (thin
shells) and
(thin
shells) and
 .
The emission from the reverse
shock is suppressed strongly for
.
The emission from the reverse
shock is suppressed strongly for
 ,
except for
high
,
except for
high
 flows (or, equivalently, low
flows (or, equivalently, low  flows). More moderate values of the magnetization
flows). More moderate values of the magnetization
 can lead to powerful emission, in excess of that expected for
can lead to powerful emission, in excess of that expected for
 ejecta, since there is both a strong shock and strong
magnetic field for efficient synchrotron emission. The last
statement assumes that is particle acceleration occurs in magnetized
shocks with an efficiency similar to that of unmagnetized shocks;
ejecta, since there is both a strong shock and strong
magnetic field for efficient synchrotron emission. The last
statement assumes that is particle acceleration occurs in magnetized
shocks with an efficiency similar to that of unmagnetized shocks;
- 3.
- magnetically dominated (
 )
ejecta are
characterized by an initial rarefaction that originates in the
leading radial edge of the shell and results in a Lorentz factor of
the front shock
)
ejecta are
characterized by an initial rarefaction that originates in the
leading radial edge of the shell and results in a Lorentz factor of
the front shock
 .
The energy dissipated by the
forward shock and the expected emission at the onset of the
afterglow are much higher for
.
The energy dissipated by the
forward shock and the expected emission at the onset of the
afterglow are much higher for
 ejecta than for
the weakly magnetized ones. ``Bolometric'' light curves were
presented in Sect. 4.5;
ejecta than for
the weakly magnetized ones. ``Bolometric'' light curves were
presented in Sect. 4.5;
- 4.
- the magnetic energy of the shell is increased by shock
compression during the reverse-shock crossing in agreement with the
findings of Zhang & Kobayashi (2005). We have found that the bulk of
the magnetic energy is transferred into the shocked external medium
on a short timescale (a few to several times the burst duration) for
the
 and
and  models that we have simulated. Several
light-crossing times of the initial ejecta width suffice for the
evolution of ejecta of
models that we have simulated. Several
light-crossing times of the initial ejecta width suffice for the
evolution of ejecta of
 to become similar to that of
the
to become similar to that of
the
 simulation. At this stage almost, all the energy
has been transferred into the shocked external medium and the
forward-shock emission is practically independent of the initial
magnetization of the flow. One should observe the onset of the
afterglow to identify effects connected to the magnetization.
simulation. At this stage almost, all the energy
has been transferred into the shocked external medium and the
forward-shock emission is practically independent of the initial
magnetization of the flow. One should observe the onset of the
afterglow to identify effects connected to the magnetization.
Modelling of the emission associated with the forward and reverse shock can be used to compare the magnetization of the shocked external medium with that of the shocked ejecta (e.g, Zhang et al. 2003). This method was applied to a number of bursts (Kumar & Panaitescu 2003; Fan et al. 2002; Gomboc et al. 2008; Mundell et al. 2007b). We caution here that such an approach considers hydrodynamical shock conditions and is therefore unreliable when the magnetization of the ejecta is sufficiently high to alter the dynamics of the deceleration. In that a full MHD calculation (such as that presented here) is needed for accurate comparison to observations.
There are aspects of the problem of interaction between magnetized ejecta and the external medium that have not been settled by this work. Although we solved the dynamical evolution of the ejecta, and the strength of the shocks as a function of time, and computed approximate ``bolometric'' light curves, we did not calculate detailed light curves for different observed bands. For this calculation, additional assumptions would have been required related to the shock microphysics and inclusion of radiative processes such as synchrotron and inverse Compton emission.
Furthermore, we have not explored the high ![]() (or Newtonian reverse
shock) regime. In this regime, shell-spreading due to the presence of
both slower and faster parts within the shell has to be
considered. For
(or Newtonian reverse
shock) regime. In this regime, shell-spreading due to the presence of
both slower and faster parts within the shell has to be
considered. For ![]() ,
the onset of the afterglow occurs at
a later observer time and can be used to infer physical quantities
such as the Lorentz factor of the flow
,
the onset of the afterglow occurs at
a later observer time and can be used to infer physical quantities
such as the Lorentz factor of the flow ![]() (Mundell et al. 2007a; Sari & Piran 1999). The slope of the initial rising
part and the peak of the curve depend on the external medium density
profile and probably the magnetization of the ejecta. These features
are worth investigation in more detail. Finally, since the initial
interaction (as seen by the observer) lasts longer, substantial
magnetic energy remains in the shell. It is possible that dissipation
of this magnetic energy in localized active regions produces late-time
flares as proposed by Giannios (2006).
(Mundell et al. 2007a; Sari & Piran 1999). The slope of the initial rising
part and the peak of the curve depend on the external medium density
profile and probably the magnetization of the ejecta. These features
are worth investigation in more detail. Finally, since the initial
interaction (as seen by the observer) lasts longer, substantial
magnetic energy remains in the shell. It is possible that dissipation
of this magnetic energy in localized active regions produces late-time
flares as proposed by Giannios (2006).
Acknowledgements
The authors thank the referee for his thoughtful comments and suggestions for improvements of this work. P.M. was at the University of Valencia with a European Union Marie Curie Incoming International Fellowship (MEIF-CT-2005-021603). M.A.A. is a Ramón y Cajal Fellow of the Spanish Ministry of Education and Science. P.M. and M.A.A. also acknowledge the partial support from the Spanish Ministry of Education and Science (AYA2007-67626-C03-01, CSD2007-00050). P.M. thanks Jose-Maria Martí and Jose-Maria Ibañez for support and critical discussions. D.G. thanks Henk Spruit for useful discussions. The authors thankfully acknowledge the computer resources, technical expertise and assistance provided by the Barcelona Supercomputing Center - Centro Nacional de Supercomputación.
Appendix A: Numerical method
We solve equations of RMHD in 1D spherical geometry assuming that the
fluid moves only in the radial direction. The magnetic field is purely
toroidal magnetic, i.e., the magnetic field is perpendicular to the
direction of fluid propagation. The system of RMHD equations is (with
the speed of light set to be c=1)
where the vector of unknown or conserved variables is given by
 |
(A.2) |
The fluxes in Eq. (A.1) are
![\begin{displaymath}\vec{F} = \left(
\rho \gamma v,
\rho h^* \gamma^2 v^2 + p^*, \left[\rho h^*\gamma^2 - \rho\gamma\right] v, vB
\right) ,
\end{displaymath}](/articles/aa/full_html/2009/06/aa10756-08/img200.gif) |
(A.3) |
and the source terms read
 |
(A.4) |
Here
Romero et al. (2005) discussed the solution to the Riemann problem in
for when the magnetic field is perpendicular to the fluid velocity and
a Cartesian geometry. They showed that the ratio
![]() is
constant everywhere except across contact discontinuity. An analogous
expression in spherical geometry,
is
constant everywhere except across contact discontinuity. An analogous
expression in spherical geometry,
![]() can be
derived by assuming a cold magnetized fluid. In this case, the system of
equations given by Eq. (A.1) reduces to three equations. From the
continuity and induction equations one can easily derive the
desired relation.
can be
derived by assuming a cold magnetized fluid. In this case, the system of
equations given by Eq. (A.1) reduces to three equations. From the
continuity and induction equations one can easily derive the
desired relation.
We use the relativistic magnetohydrodynamic code MRGENESIS (Mimica et al. 2005,2007), a high-resolution shock capturing scheme based on GENESIS (Leismann et al. 2005; Aloy et al. 1999). In our code, the fluid is discretized in spherical shells (zones). We use the PPM (Colella & Woodward 1984) scheme for the spatial interpolation of variables within numerical zones, and a HLLC (Mignone & Bodo 2006) approximate Riemann solver to compute numerical fluxes across zone boundaries. The time integration is performed using a third-order Runge-Kutta method.
A.1 Numerical resolution
For the simulation results to be as free as possible of numerical artifacts a sufficiently high resolution is needed. Of particular concern is the minimum number of iterations necessary to resolve the initial evolution of the discontinuity separating the shell from the external medium (that forms a Riemann problem). This information is required since almost all RMHD codes based on approximate Riemann solvers develop initial transient spurious behaviors at the location of the original discontinuity. These spurious behaviors relax with time to the correct physical solution. Therefore, since the problem is self-similar in Cartesian coordinates, almost independently of the initial resolution, our numerical code recovers correctly (i.e., within the accuracy of our method) the physical solution. However, in spherical symmetry the problem is not strictly self-similar. Thus, the break up of an initial discontinuity may lead to the formation of additional discontinuities (inside of the Riemann fan but not directly emerging from the contact discontinuity) at later times. This is precisely what happens in the rarefaction R1 in our magnetized models (see Sect. 4.2), where the RS forms. If the formation of the shock happens close to the location of the contact discontinuity, the initial transient artifacts in numerical simulations may pollute the formation of the RS and produce an incorrect numerical solution, where, e.g., the RS does not form. The way to diminish the effect of these initial transients is to increase the numerical resolution around the initial discontinuity.
To eliminate the effects of the spherical geometry on the solution of
the Riemann problem, and in view of the fact that our initial shells
start at distances of
![]() cm, where the local effects of
the spherical geometry are practically negligible, we
study both exact and numerical solutions of the following Riemann
problem in planar coordinates:
cm, where the local effects of
the spherical geometry are practically negligible, we
study both exact and numerical solutions of the following Riemann
problem in planar coordinates:
- left state:
 ,
p=10-2,
,
p=10-2,
 and B = 15,
and B = 15,
- right state:
 ,
p=10-6,
,
p=10-6,
 and B = 0.
and B = 0.
![\begin{figure}
\par\includegraphics[scale=0.3]{figures/0756fg09.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg213.gif) |
Figure A.1:
Time |
| Open with DEXTER | |
Figure A.1 shows the results of the test for seven
different simulations whose zone sizes have values
![]() ,
and
,
and
![]() .
By fitting to the data points in the plot, we find
.
By fitting to the data points in the plot, we find
![]() .
This linear dependence can be seen
in the lower panel of Fig. A.1, where we see that
.
This linear dependence can be seen
in the lower panel of Fig. A.1, where we see that
![]() is roughly independent of the resolution
(Fig. A.1 lower panel). We find that
is roughly independent of the resolution
(Fig. A.1 lower panel). We find that
![]() .
.
Of equal importance is the dependence of ![]() and
and
![]() on
the initial Lorentz factor. We modify the Riemann problem by changing
on
the initial Lorentz factor. We modify the Riemann problem by changing
![]() of the left state and the magnetic field, such that
the ratio
of the left state and the magnetic field, such that
the ratio
![]() For this test, we use the finest
resolution
For this test, we use the finest
resolution
![]() for all models. Results
are shown in Fig. A.2. We find
for all models. Results
are shown in Fig. A.2. We find
![]() .
Due to the constant
.
Due to the constant ![]() ,
this means
that
,
this means
that
![]() also depends almost linearly on
also depends almost linearly on ![]() .
Combining results shown in Fig. A.1 with those
of Fig. A.2 and assuming linear dependences of
.
Combining results shown in Fig. A.1 with those
of Fig. A.2 and assuming linear dependences of ![]() on
on
![]() and
and ![]() ,
we conclude that the required spatial
discretization for Riemann problems similar to those discussed in this
paper follows the relation
,
we conclude that the required spatial
discretization for Riemann problems similar to those discussed in this
paper follows the relation
We emphasize that the constants implicit to Eq. (A.5) depend on the initial density and pressure ratio, as well as the magnetization of the fluid. The result expressed by Eq. (A.5) can also be interpreted in the following way: at a fixed numerical resolution, if the Lorentz factor of the problem to be solved increases, the time needed to relax any initial numerical pathology also increases.
We use Eq. (A.5) to determine the maximum ![]() (or,
conversely, the minimum resolution) needed to complete our simulations
such that
(or,
conversely, the minimum resolution) needed to complete our simulations
such that ![]() is far shorter than any of the characteristic
hydrodynamic timescales in our models. In articular, we require
that
is far shorter than any of the characteristic
hydrodynamic timescales in our models. In articular, we require
that ![]() is shorter than the time needed to form the RS in
the rarefaction fan R1.
is shorter than the time needed to form the RS in
the rarefaction fan R1.
| |
Figure A.2:
Time needed to resolve the Riemann problem in planar
coordinates as a function of the initial Lorentz factor |
| Open with DEXTER | |
A reduced density jump between the shell
![]() and the
external medium
and the
external medium
![]() reduces drastically the numerical
complexity of the break up of the Riemann problem. Our choice of the
density jump
reduces drastically the numerical
complexity of the break up of the Riemann problem. Our choice of the
density jump
![]() attempts to reach the
large density contrast expected in the conditions found in GRB
afterglows (although it is still lower than what an optimal modeling
demands). We point out that a much reduced value of
attempts to reach the
large density contrast expected in the conditions found in GRB
afterglows (although it is still lower than what an optimal modeling
demands). We point out that a much reduced value of
![]() (as considered by Mizuno et al. 2009)
could be too low for the conditions in this
astrophysical context.
(as considered by Mizuno et al. 2009)
could be too low for the conditions in this
astrophysical context.
References
- Aloy, M. A., Ibáñez, J. M., Martí, J. M., & Müller, E. 1999, ApJS, 122, 151 [CrossRef]
- Beskin, V. S., Kuznetsova, I. V., & Rafikov, R. R. 1998, MNRAS, 299, 341 [CrossRef]
- Blandford, R. D., & McKee, C. F. 1976, Physics of Fluids, 19, 1130 [NASA ADS] [CrossRef] (In the text)
- Colella, P., & Woodward, P. R. 1984, J. Comp. Phys., 54, 174 [CrossRef] (In the text)
- Drenkhahn, G., & Spruit, H. C. 2002, A&A, 391, 1141 [NASA ADS] [CrossRef] [EDP Sciences]
- Fan, Y.-Z., Dai, Z.-G., Huang, Y.-F., & Lu, T. 2002, Chinese J. Astron. Astrophys., 2, 449 [NASA ADS]
- Fan, Y. Z., Wei, D. M., & Wang, C. F. 2004, A&A, 424, 477 [NASA ADS] [CrossRef] [EDP Sciences]
- Genet, F., Daigne, F., & Mochkovitch, R. 2007, MNRAS, 381, 732 [NASA ADS] [CrossRef]
- Giannios, D. 2006, A&A, 455, L5 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Giannios, D., & Spruit, H. C. 2006, A&A, 450, 887 [NASA ADS] [CrossRef] [EDP Sciences]
- Giannios, D., Mimica, P., & Aloy, M. A. 2008, A&A, 478, 747 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gomboc, A., Kobayashi, S., Guidorzi, C., et al. 2008 [arXiv:0804.1727]
- Goodman, J. 1986, ApJ, 308, L47 [NASA ADS] [CrossRef]
- Granot, J., Miller, M., Piran, T., Suen, W. M., & Hughes, P. A. 2001, in Gamma-ray Bursts in the Afterglow Era, ed. E. Costa, F. Frontera, & J. Hjorth, 312
- Kennel, C. F., & Coroniti, F. V. 1984, ApJ, 283, 694 [NASA ADS] [CrossRef] (In the text)
- Kobayashi, S., Piran, T., & Sari, R. 1999, ApJ, 513, 669 [CrossRef] (In the text)
- Kumar, P., & Panaitescu, A. 2003, MNRAS, 346, 905 [NASA ADS] [CrossRef]
- Leismann, T., Antón, L., Aloy, M. A., et al. 2005, A&A, 436, 503 [NASA ADS] [CrossRef] [EDP Sciences]
- Li, Z.-Y., Chiueh, T., & Begelman, M. C. 1992, ApJ, 394, 459 [NASA ADS] [CrossRef]
- Lyutikov, M. 2005 [arXiv:astro-ph/0503505] (In the text)
- Lyutikov, M. 2006, New J. Phys., 8, 119 [CrossRef] (In the text)
- Lyutikov, M., & Blandford, R. 2003, ArXiv Astrophysics e-prints
- Meliani, Z., Keppens, R., Casse, F., & Giannios, D. 2007, MNRAS, 376, 1189 [NASA ADS] [CrossRef]
- Meszaros, P., & Rees, M. J. 1997, ApJ, 482, L29 [NASA ADS] [CrossRef]
- Michel, F. C. 1969, ApJ, 158, 727 [NASA ADS] [CrossRef]
- Mignone, A., & Bodo, G. 2006, MNRAS, 368, 1040 [NASA ADS] [CrossRef] (In the text)
- Mimica, P., Aloy, M. A., Müller, E., & Brinkmann, W. 2005, A&A, 441, 103 [NASA ADS] [CrossRef] [EDP Sciences]
- Mimica, P., Aloy, M. A., & Müller, E. 2007, A&A, 466, 93 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mizuno, Y., Zhang, B., Giacomazzo, B., et al. 2009, ApJ, 690, L47 [NASA ADS] [CrossRef] (In the text)
- Mundell, C. G., Melandri, A., Guidorzi, C., et al. 2007a, ApJ, 660, 489 [NASA ADS] [CrossRef]
- Mundell, C. G., Steele, I. A., Smith, R. J., et al. 2007b, Science, 315, 1822 [NASA ADS] [CrossRef]
- Paczynski, B. 1986, ApJ, 308, L43 [NASA ADS] [CrossRef]
- Rees, M. J., & Gunn, J. E. 1974, MNRAS, 167, 1 [NASA ADS] (In the text)
- Rees, M. J., & Meszaros, P. 1992, MNRAS, 258, 41P [NASA ADS]
- Rhoads, J. E. 1999, ApJ, 525, 737 [CrossRef] (In the text)
- Romero, R., Martí, J. M., Pons, J. A., Ibáñez, J. M., & Miralles, J. A. 2005, J. Fluid Mechanics, 544, 323 [NASA ADS] [CrossRef] (In the text)
- Sari, R., & Piran, T. 1995, ApJ, 455, L143 [NASA ADS]
- Sari, R., & Piran, T. 1999, A&AS, 138, 537 [CrossRef] [EDP Sciences]
- Thompson, C. 1994, MNRAS, 270, 480
- Usov, V. V. 1992, Nature, 357, 472 [NASA ADS] [CrossRef]
- Vlahakis, N., & Königl, A. 2003, ApJ, 596, 1080 [NASA ADS] [CrossRef]
- Zhang, B., & Kobayashi, S. 2005, ApJ, 628, 315 [NASA ADS] [CrossRef]
- Zhang, B., Kobayashi, S., & Mészáros, P. 2003, ApJ, 595, 950 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ... GRB flows
![[*]](/icons/foot_motif.gif)
- While this work was being refereed,
Mizuno et al. (2009) published a work addressing the problem of the
deceleration of arbitrary magnetized ejecta into an unmagnetized
medium, and discussed its implications for GRBs and active galactic
nuclei. However, in spite of the undoubtable importance of their
studies, the conditions set by these authors (particularly, the use
of planar symmetry, and the low density contrast between the
magnetized shell and the external medium
 100) are far from
those typical of GRB afterglows, especially during the early
afterglow propagation.
100) are far from
those typical of GRB afterglows, especially during the early
afterglow propagation.
- ... remapping
![[*]](/icons/foot_motif.gif)
- As described by Mimica et al. (2007), grid remapping enables us to follow the evolution of a localized shell over large distance by repeated remapping of the numerical grid. In this work the grid always follows the front shock, so that, once the shell has been slowed down by the reverse shock, it is eventually ``lost'' from the grid.
- ...
forms
![[*]](/icons/foot_motif.gif)
- We thank the referee for pointing out that, without this decrease of the fast speed, a shock would form either immediately or never at all.
- ... models
![[*]](/icons/foot_motif.gif)
- Each simulation takes between 50 and 200 thousand hours of computer time using between 32 and 320 processors (depending whether we compute thin, thick, or continuous flow models) on Mare Nostrum (http://www.bsc.es/plantillaA.php?cat_id=5). The typical external storage requirements of one model vary between 10 (thin) and 100 (thick models) gigabytes, since relatively frequent output of the fluid state is needed to obtain a satisfactory coverage of the fluid evolution needed for the post-processing calculations.
- ...

![[*]](/icons/foot_motif.gif)
- For the simplicity of the discussion, we fix E
and
 for the two shells. We generalize our expressions to arbitrary
values of E and
for the two shells. We generalize our expressions to arbitrary
values of E and  in the Appendix B.
in the Appendix B.
All Tables
Table 1: Parameters of the numerical models.
All Figures
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg01.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg81.gif) |
Figure 1:
Snapshot of the thin magnetized shell evolution taken after
the RS has formed and before it has crossed the shell. Full and
dashed black lines show the logarithms of the rest-mass density
(normalized to the initial shell density |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg02.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg82.gif) |
Figure 2:
Energy in different components (normalized to the initial
total energy in the shell) as a function of the radius of the
FS. Upper and lower panels show the thin ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg03.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg85.gif) |
Figure 3:
Relative Lorentz factor at the FS
( upper panel) and RS
( lower panel) as a function of the normalized observer time
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[scale=0.45]{figures/0756fg04.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg109.gif) |
Figure 4:
Energy dissipation in the reverse shock in
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg05.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg166.gif) |
Figure 5:
Results of a test of the rescaling with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg06.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg169.gif) |
Figure 6:
Similar to Fig. 3, but for the models used
in the test of the rescaling hypothesis. Black, blue, and red lines
in the upper (lower) panel show the relative Lorentz factor of the
fluid at the FS (RS) as a function of the normalized time of
observation for models with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg07.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg187.gif) |
Figure 7:
Light curves for non-magnetized (black) and magnetized
(blue line) thin shell models after scaling the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\includegraphics[scale=0.32]{figures/0756fg08.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg188.gif) |
Figure 8:
Same as Fig. 7, but for a thick
shell model ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[scale=0.3]{figures/0756fg09.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10756-08/Timg213.gif) |
Figure A.1:
Time |
| Open with DEXTER | |
| In the text | |
| |
Figure A.2:
Time needed to resolve the Riemann problem in planar
coordinates as a function of the initial Lorentz factor |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.






![\begin{displaymath}
t_{\rm obs} := \Delta_0^{-1} \left[ct - r\right] ,
\end{displaymath}](/articles/aa/full_html/2009/06/aa10756-08/img53.gif)







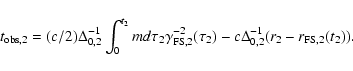

![\begin{displaymath}
L_{\rm RS} : =(\Delta t)^{-1}\ \max\left[0, \epsilon_{\rm e...
...a r}4 \gamma^2
p - \int_{{\rm shell}\ r}4 \gamma^2 p\right] ,
\end{displaymath}](/articles/aa/full_html/2009/06/aa10756-08/img179.gif)

