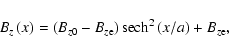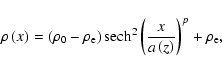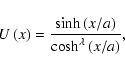| Issue |
A&A
Volume 494, Number 3, February II 2009
|
|
|---|---|---|
| Page(s) | 1119 - 1125 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361:200810541 | |
| Published online | 11 December 2008 | |
Sausage oscillations in loops with a non-uniform cross-section
D. J. Pascoe1 - V. M. Nakariakov2 - T. D. Arber2 - K. Murawski3
1 - School of Mathematics and Statistics, University of St Andrews, St Andrews, KY16 9SS, UK
2 - Physics Department, University of Warwick, Coventry, CV4 7AL, UK
3 - Institute of Physics, UMCS, ul. Radziszewskiego 10, 20-031 Lublin, Poland
Received 8 July 2008 / Accepted 27 November 2008
Abstract
Context. Flaring coronal loops are often observed in microwave and sometimes in soft X-rays, as extended structures of variable cross-section or width. The quasi-periodic pulsations associated with flaring coronal loops have been interpreted in terms of standing, fast sausage magnetoacoustic modes and suggested for the diagnostics of the magnetic field outside the oscillating loop.
Aims. We investigate the effects of a non-uniform cross-section on a coronal loop with respect to the standing sausage modes it supports.
Methods. Numerical simulations of standing sausage modes are performed for a straight, zero-![]() coronal loop with a varying cross-section. The global sausage mode and higher harmonics are considered, and simulations were performed for a range of density contrast ratios and loop divergence parameter. We consider modifications of the period of oscillation and the spatial profile of the standing modes.
coronal loop with a varying cross-section. The global sausage mode and higher harmonics are considered, and simulations were performed for a range of density contrast ratios and loop divergence parameter. We consider modifications of the period of oscillation and the spatial profile of the standing modes.
Results. As the loop divergence parameter increases, the period of the standing modes decreases. The fractional change period is independent of the density contrast ratio. The spatial profiles of the standing modes are modified by the cross-section inhomogeneity, but this effect is too weak to be observable by modern instruments. For the global sausage mode, the cross-section radius divergence by a factor of 2 is found to cause the decrease in the period of about 5%.
Key words: Sun: corona - Sun: oscillations - Sun: flares - magnetohydrodynamics (MHD)
1 Introduction
Quasi-periodic pulsations observed in the light curves of solar and stellar flares attract intensive attention in the context of coronal seismology as a promising tool for the diagnostics of flaring plasmas (Nakariakov 2006). Quasi-periodic pulsations observed in the microwave and hard X-ray bands can be produced by several mechanisms, in particular by the periodic generation of plasmoids (e.g. Ofman & Sui 2006) or with the sausage magnetoacoustic mode (e.g. Nakariakov et al. 2003). As the period of the sausage mode is determined, in particular, by the value of the Alfvén speed outside the oscillating loop, this mode provides us with a tool for estimating this parameter (Nakariakov et al. 2003). Sausage oscillations have also been observed in a cool post-flare loop (Srivastava et al. 2008). Recent numerical simulations of the sausage mode performed in terms of a straight magnetic slab model demonstrated the applicability of this mode for estimating the magnetic field outside the oscillating loop by the oscillation period and the loop length (Pascoe et al. 2007). Also, it was found that the period of the sausage mode is not sensitive to fine multi-shell radial structuring (Pascoe et al. 2007), which strengthens the seismological potential of this mode. However, the effect of longitudinal stratification on the sausage mode period remains to be studied.
Flaring coronal loops are often observed in microwave and sometimes in soft X-rays as extended structures of variable cross-section or width (Melnikov et al. 2005). This contrasts with EUV and SXR loops in quiet active regions, which are seen to have a constant cross-section. This difference in shape can be understood in terms of the model for a flaring coronal loop, as suggested by Zaitsev & Stepanov (1982) to explain the quasi-periodic modulation of hard X-rays. Flaring energy release near the loop apex increases the gas pressure there, causing the loop to expand and the magnetic field strength to decrease from its original value ![]() to
to
![]() .
This sets up a magnetic trap, confining fast electrons. The impulsive energy release also generates fast magnetoacoustic waves, which perturb the value of the magnetic field and hence the ratio
.
This sets up a magnetic trap, confining fast electrons. The impulsive energy release also generates fast magnetoacoustic waves, which perturb the value of the magnetic field and hence the ratio
![]() which determines the minimal pitch angle of trapped electrons. Modulation of the pitch angle therefore causes a variation in the flux of electrons escaping the magnetic trap and hence the intensity of hard X-rays generated by fast electrons reaching the loop footpoints.
which determines the minimal pitch angle of trapped electrons. Modulation of the pitch angle therefore causes a variation in the flux of electrons escaping the magnetic trap and hence the intensity of hard X-rays generated by fast electrons reaching the loop footpoints.
In the context of the kink mode, the effect of structuring in the longitudinal direction on the kink mode has received thorough attention in several recent studies. Andries et al. (2005a) and McEwan et al. (2006) investigated the effect of longitudinal structuring on the ratio of the fundamental oscillation period, P1, to its first harmonic, P2. Due to dispersion, the ratio P1 / 2 P2 departs from unity even in the case of a straight homogeneous loop. The extent of the departure can be used as a seismological tool to deduce the density scale height in the corona. An analytical expression describing the shift in P1 / 2 P2 in terms of the loop length and density scale height was derived by McEwan et al. (2008) for the thin tube approximation.
Donnelly et al. (2006) investigated the influence of longitudinal structuring on the modes of oscillation of a coronal flux tube by incorporating a dense chromospheric layer. It was found that environmental structuring changes the cut-off frequency, enhancing leakage such that even the fundamental kink mode may become leaky. However, for realistic chromospheric depths the mode remains trapped but with a shift in frequency. This work was extended by Díaz et al. (2007) who considered continuous exponential structuring profiles rather than piecewise uniform profiles. They found that the frequency shift due to structuring for the fundamental period is small, but the ratio between the periods of the fundamental mode and higher harmonics can be used as a diagnostic tool.
Erdélyi & Verth (2007) investigated the effect of longitudinal density stratification on the amplitude profile of the standing kink mode of a TRACE 171 Å temperature loop (approximately 1 MK). They found that stratification changed the amplitude profile from one of constant longitudinal density, but that the effect was too subtle for such observational signatures to be detectable by EUV imagers.
Safari et al. (2007) also considered standing kink modes of longitudinally stratified coronal loops. They found changes in amplitude profiles of a few percent, consistent with Erdélyi & Verth (2007), and showed that the predicted departure of P1 / 2 P2 from unity was in good agreement with the observational data of Verwichte et al. (2004). The latter result was also found by Karami & Asvar (2007), who considered the effects of longitudinal density stratification on the frequencies of standing kink and fluting modes.
Andries et al. (2005b) examined how longitudinal density stratification alters the oscillation frequencies and damping rates by resonant absorption of a zero ![]() cylindrical flux tube. It was found numerically that, for homogeneous stratification, both period and damping time are affected in the same way so that the ratio of the two remains unaffected. Dymova & Ruderman (2006) also obtained this result analytically.
cylindrical flux tube. It was found numerically that, for homogeneous stratification, both period and damping time are affected in the same way so that the ratio of the two remains unaffected. Dymova & Ruderman (2006) also obtained this result analytically.
Arregui et al. (2005) also studied the effects of both radial and longitudinal density stratification on the frequency and damping rate of resonantly damped kink modes. Their numerical solutions indicate the period and damping of oscillations mainly depend on the density contrast ratio between the loop apex and footpoints, and the inhomogeneity length scale, and are insensitive to the details of longitudinal stratification.
Verth & Erdélyi (2008) derived the governing equation of the fast kink mode in a coronal loop modelled as an expanding magnetic flux tube with arbitrary longitudinal plasma density. They found that even a relatively small loop expansion can have a significant effect on the accuracy of density scale heights derived from loop oscillations.
The aim of this paper is to study the effect of the longitudinal variation of the loop cross-section on the sausage mode period in terms of a modified slab model. In this study we neglect the effects of finite plasma ![]() ,
of fine transverse structuring, and of curvature. The paper is organised as follows: the method of generating an equilibrium state is described in Sect. 2. In Sect. 3 the results of sausage mode perturbations are presented and Sect. 4 contains discussion and conclusions.
,
of fine transverse structuring, and of curvature. The paper is organised as follows: the method of generating an equilibrium state is described in Sect. 2. In Sect. 3 the results of sausage mode perturbations are presented and Sect. 4 contains discussion and conclusions.
2 The model
In the simplest approximation, the sausage mode is adequately described by a slab model (see e.g., discussions in Edwin & Roberts 1983; Nakariakov et al. 2003; Pascoe et al. 2007). In this study, we modify the slab model, considering a slab of variable width. As we are not familiar with any analytical magnetostatic solution to use for the equilibrium magnetic field, we construct the equilibrium in our numerical simulations using the LARE2 D code (Arber et al. 2001). In the following, we model a coronal loop as a straight slab, having an internal Alfvén speed lower than the external Alfvén speed and therefore able to act as a waveguide. We start with a uniform, zero ![]() plasma, with a straight, constant magnetic field in the z direction. We then apply an enhancement to the magnitude of the straight magnetic field, directed along the z axis, using the symmetric Epstein profile (Nakariakov & Roberts 1995)
plasma, with a straight, constant magnetic field in the z direction. We then apply an enhancement to the magnitude of the straight magnetic field, directed along the z axis, using the symmetric Epstein profile (Nakariakov & Roberts 1995)
where Bz0 is the magnetic field at the loop axis,
The length of the loop is defined by the size of the numerical domain in the z direction and was chosen to be 10 Mm, which corresponds, e.g., to a short flaring loop. Line-tied boundary conditions were used for all quantities to simulate the loop footpoints. In the direction transverse to the loop axis (x direction), the size of the numerical domain was chosen to be 40 Mm, with open boundary conditions, to simulate the open external coronal environment.
Since the plasma ![]() is zero, the only contribution to total pressure is the magnetic pressure, which is proportional to the magnitude of the magnetic field (
is zero, the only contribution to total pressure is the magnetic pressure, which is proportional to the magnitude of the magnetic field (
![]() ). The magnetic field enhancement is therefore a non-equilibrium state and will undergo expansion. However, the constraint of line-tied boundary conditions at the loop footpoints leads to a non-uniformity in the z direction, with the expansion maximum at the loop apex and minimum at the footpoints. This produces an equilibrium with curved field lines in which the magnetic pressure and tension forces are in balance. The extent of this non-uniformity depends upon the size of the applied magnetic field enhancement in relation to the uniform background field.
). The magnetic field enhancement is therefore a non-equilibrium state and will undergo expansion. However, the constraint of line-tied boundary conditions at the loop footpoints leads to a non-uniformity in the z direction, with the expansion maximum at the loop apex and minimum at the footpoints. This produces an equilibrium with curved field lines in which the magnetic pressure and tension forces are in balance. The extent of this non-uniformity depends upon the size of the applied magnetic field enhancement in relation to the uniform background field.
To reach the equilibrium state, simulations were run for 2000 s (corresponding to 200 loop transit times at the external Alfvén speed). After this time, any remaining plasma motions were gradually and artificially damped to produce the final equilibrium state of the magnetic field. This damping was removed before the wave modes were studied. The initial and final magnetic field configurations are shown in Fig. 1 for a magnetic field enhancement of
![]() .
This method allows us to control the degree of divergence of the loop width by varying the initial ratio of
.
This method allows us to control the degree of divergence of the loop width by varying the initial ratio of
![]() with
with
![]() held constant. Figure 1 shows only the central part of the computational domain; the full size is 10 Mm in the z direction and 40 Mm in the x direction, with a numerical resolution of 200 by 800 pixels respectively. Convergence tests were performed by varying the resolution.
held constant. Figure 1 shows only the central part of the computational domain; the full size is 10 Mm in the z direction and 40 Mm in the x direction, with a numerical resolution of 200 by 800 pixels respectively. Convergence tests were performed by varying the resolution.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg01.eps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{0541fg02.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg19.gif) |
Figure 1: The initial ( top) and final ( bottom) configurations of the magnetic field lines. The equilibrium is obtained by allowing an enhancement to a straight, constant magnetic field to evolve subject to the constraint of line-tied boundary conditions at the loop footpoints. Distances are in Mm. |
| Open with DEXTER | |
The density profile then added to form the loop has the form of a generalised symmetric Epstein profile
where
![\begin{figure}
\par {\hspace*{6mm}\includegraphics[width=6.8cm,clip]{0541fg03.ps...
...ar\vspace*{2mm}
\par\includegraphics[width=8cm,clip]{0541fg04.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg26.gif) |
Figure 2:
Top: contour plot of the density profile that is added on top of the magnetic field profile shown in the bottom panel of Fig. 1. A generalised symmetric Epstein profile with steepness parameter p=10 is used, along with a varying semi-width parameter
|
| Open with DEXTER | |
In our simulations we use a density profile steepness parameter p=10. This increases the profile steepness without introducing a discontinuity into the simulations. Figure 2 shows a contour plot of the density profile corresponding to the equilibrium magnetic field profile shown in Fig. 1. Also shown in Fig. 2 is the Alfvén speed profile along the loop axis. The Alfvén speed is lower at the loop apex due to the lower magnetic field strength there. For a straight slab, analytical solutions for the dispersion relation exist for the generalised symmetric Epstein profile in the cases of p=1 and
![]() ,
but solutions must be obtained numerically for cases in between these limits.
,
but solutions must be obtained numerically for cases in between these limits.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg05.eps}\par\vspace*{2m...
...s}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{0541fg07.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg28.gif) |
Figure 3:
Phase speed dispersion curves for the generalised symmetric Epstein density profile with steepness parameter p=10 for density contrast ratios of 50 ( top), 30 ( middle) and 20 ( bottom). The vertical lines correspond to the solution for the global sausage mode with |
| Open with DEXTER | |
Figure 3 shows the phase speed dispersion curves for the density contrast ratios of
![]() ,
30 and 20 used in our simulations. To differentiate the simulations by the non-uniformity of the magnetic field we introduce a loop divergence parameter
,
30 and 20 used in our simulations. To differentiate the simulations by the non-uniformity of the magnetic field we introduce a loop divergence parameter
![]() ,
where
,
where
![]() .
Figure 4 shows how the maximum, minimum and arithmetic mean values of the loop semi-width parameter are related to the loop divergence parameter.
.
Figure 4 shows how the maximum, minimum and arithmetic mean values of the loop semi-width parameter are related to the loop divergence parameter.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg08.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg31.gif) |
Figure 4:
The variation of the loop semi-width with the loop divergence parameter (
|
| Open with DEXTER | |
3 Sausage perturbations of a flaring loop
We performed simulations investigating the effect of the non-uniformity in the loop width upon the resonant period of the standing modes. For this, we excite sausage perturbations of the equilibrium configuration reached by the method described in Sect. 2.
3.1 Global sausage mode
In the zero ![]() case and an Epstein density profile (Eq. (2) with p=1), the fast magnetoacoustic eigenfunctions (Cooper et al. 2003b) which describe the perturbation of the transverse component of the plasma velocity of the sausage mode are given by the expression
case and an Epstein density profile (Eq. (2) with p=1), the fast magnetoacoustic eigenfunctions (Cooper et al. 2003b) which describe the perturbation of the transverse component of the plasma velocity of the sausage mode are given by the expression
where
For the equilibrium structure described in the previous section, the perturbation given by Eq. (3) is not an eigenmode because of the divergence of the flux tube cross-section. However, this perturbation is sufficiently close to the sausage mode we are interested in. Thus, we excite the global sausage mode of the non-uniform structure by perturbing the transverse plasma velocity as
where
Figure 5 shows the longitudinal dependence of the amplitude of the global sausage mode. This is determined by considering the perturbation of the magnetic field strength at many points along the loop axis. At each point the spectral amplitude of the global sausage mode is calculated from the magnetic field time series by use of a periodogram routine. This method allows us to identify the particular harmonic corresponding to a given frequency and examine its spatial profile in detail for modifications introduced by the cross-section non-uniformity. In the case of a the straight-slab model (
![]() ), the dependence exactly corresponds to the expected
), the dependence exactly corresponds to the expected
![]() profile, where
profile, where
![]() ,
which has a maximum (anti-node) at the loop apex and tends to zero at the loop footpoints. For higher values of loop divergence parameter, the profile is increasingly modified and becomes more localised to the loop apex. However, this modification of the profile for the global standing mode is relatively small and its direct detection would be beyond the resolution of modern instruments, especially taking into account the uncertainty connected with geometrical and LOS effects.
,
which has a maximum (anti-node) at the loop apex and tends to zero at the loop footpoints. For higher values of loop divergence parameter, the profile is increasingly modified and becomes more localised to the loop apex. However, this modification of the profile for the global standing mode is relatively small and its direct detection would be beyond the resolution of modern instruments, especially taking into account the uncertainty connected with geometrical and LOS effects.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg09.eps}\par\vspace*{2m...
...s}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{0541fg11.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg41.gif) |
Figure 5:
Profiles of the amplitude of the global sausage mode, measured along the loop axis for the cases of
|
| Open with DEXTER | |
Figure 6 shows the dependence of the change in period (![]() )
of the global sausage upon the loop divergence parameter (
)
of the global sausage upon the loop divergence parameter (
![]() ). The change in period is defined as
). The change in period is defined as
![]() ,
where P is the period measured by the variation of the magnetic field strength at the loop apex, and
,
where P is the period measured by the variation of the magnetic field strength at the loop apex, and ![]() is the period for the case of a straight slab (
is the period for the case of a straight slab (
![]() ). For the density contrast ratios of 50, 30 and 20, the period of oscillation for the global sausage mode in a straight slab is 44.8, 35.1 and 29.0 s, respectively. In Fig. 6 the crosses, squares and triangle show the results for simulations with density contrast ratios of 50, 30 and 20, respectively. The upper and lower curves show the change in period estimated for a straight slab model with a width given by the maximum and minimum values, respectively, as shown in Fig. 4. The solid, dashed and dotted lines are for density contrast ratios of 50, 30 and 20, respectively. When calculating the straight-slab estimates, the variation of the internal magnetic field was found to be unimportant, as the modes considered are near the sausage mode cut-off and so weakly dependent upon the internal Alfvén speed.
). For the density contrast ratios of 50, 30 and 20, the period of oscillation for the global sausage mode in a straight slab is 44.8, 35.1 and 29.0 s, respectively. In Fig. 6 the crosses, squares and triangle show the results for simulations with density contrast ratios of 50, 30 and 20, respectively. The upper and lower curves show the change in period estimated for a straight slab model with a width given by the maximum and minimum values, respectively, as shown in Fig. 4. The solid, dashed and dotted lines are for density contrast ratios of 50, 30 and 20, respectively. When calculating the straight-slab estimates, the variation of the internal magnetic field was found to be unimportant, as the modes considered are near the sausage mode cut-off and so weakly dependent upon the internal Alfvén speed.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg12.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg44.gif) |
Figure 6:
The dependence of the change in period ( |
| Open with DEXTER | |
The main effect seen is the decrease of the period with increasing non-uniformity of the loop semi-width, and that the decrease is independent of the density contrast ratio. Figure 3 shows that a higher phase speed corresponds to a lower normalised wavenumber k a. Since Fig. 5 shows there is no significant change in the wavenumber k, the decrease in period is a result of a lower loop semi-width a. From Fig. 4 we may conclude that the period is therefore being most strongly influenced by the minimum loop width at the footpoints, rather than the width at the loop apex where the loop width and oscillation amplitude are largest. However, the period is still higher than the change calculated for a straight slab with a decreased width. This can be explained by the effective shortening of the non-uniform loop from the point of view of the global sausage oscillation. Indeed, according to Fig. 5 in the case of the nonuniform cross-section, the wavelength of the global sausage mode is shorter than in the uniform case.
3.2 Third harmonic
Simulations were also performed for the third longitudinal harmonic, for which
![]() .
As in the case of the global mode, the initial perturbation was setup according to the analytical expression given by Eq. (4) with the appropriate value of kz.
.
As in the case of the global mode, the initial perturbation was setup according to the analytical expression given by Eq. (4) with the appropriate value of kz.
Figure 7 shows the longitudinal dependence of the absolute value of the amplitude of the third harmonics, calculated in the same way as above for the global sausage mode. In the case of a the straight-slab model (
![]() ), the dependence exactly corresponds to the expected
), the dependence exactly corresponds to the expected
![]() profile, where
profile, where
![]() ,
which has three anti-nodes; one at the loop apex and two at the the loop legs. For higher values of loop divergence parameter, the profile increasingly departs from the cosine distribution, and again becomes more localised to the loop apex. The modification to the mode profiles by the increasing loop width non-uniformity is the decrease of the distance between the inner and outer anti-nodes and a decrease in the size of the inner anti-node relative to the outer ones. The shift in the maxima is not present in the case of the straight loop and so is not due to the boundary conditions.
,
which has three anti-nodes; one at the loop apex and two at the the loop legs. For higher values of loop divergence parameter, the profile increasingly departs from the cosine distribution, and again becomes more localised to the loop apex. The modification to the mode profiles by the increasing loop width non-uniformity is the decrease of the distance between the inner and outer anti-nodes and a decrease in the size of the inner anti-node relative to the outer ones. The shift in the maxima is not present in the case of the straight loop and so is not due to the boundary conditions.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg13.eps}\par\vspace*{2m...
...}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{0541fg15.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg46.gif) |
Figure 7:
Profiles of the absolute spectral amplitude measured along the loop axis for the cases of
|
| Open with DEXTER | |
Figure 8 shows the dependence of the change in period of the third harmonic upon the loop divergence parameter. For the density contrast ratios of 50, 30 and 20, the period of oscillation for the third harmonic sausage mode in a straight slab is 30.1, 23.4 and 19.1 s, respectively. As with the global sausage mode, the period decreases with increasing loop width non-uniformity and the change is independent of the density contrast ratio. However, the period decrease is much stronger, and is greater than the change calculated due to the decreasing minimum loop width.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg16.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg47.gif) |
Figure 8:
The dependence of the change in period ( |
| Open with DEXTER | |
As the loop width non-uniformity increases, it is observed in the simulations that the applied third harmonic perturbation generates also a global mode oscillation. Figure 9 shows the relative spectral amplitude of the global sausage mode to the third longitudinal harmonic. For low values of loop divergence parameter,
![]() ,
the third harmonic alone is excited. This is consistent with our expectations as we would not expect coupling of the harmonics in the limit of a straight coronal loop. The generation of the global sausage mode is very efficient for the higher values of loop divergence parameter,
,
the third harmonic alone is excited. This is consistent with our expectations as we would not expect coupling of the harmonics in the limit of a straight coronal loop. The generation of the global sausage mode is very efficient for the higher values of loop divergence parameter,
![]() ,
suggesting the importance of loop geometry in the selection of modes of oscillation.
,
suggesting the importance of loop geometry in the selection of modes of oscillation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg17.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg50.gif) |
Figure 9: The ratio of the amplitudes of the global sausage mode to the third longitudinal harmonic for an applied perturbation corresponding to the third harmonic in a straight slab. The solid, dashed and dotted lines are for density contrast ratios of 50, 30 and 20, respectively. |
| Open with DEXTER | |
Figure 10 shows the change in period of the global sausage mode upon the loop divergence parameter when the mode is generated by applying a third harmonic perturbation as demonstrated in Fig. 9. By comparison with Fig. 6 in which the global sausage mode is excited directly, it is seen that the change in period is a robust feature of the loop geometry and not dependent upon the excitation mechanism.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg18.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg51.gif) |
Figure 10:
The dependence of the change in period ( |
| Open with DEXTER | |
4 Conclusions
We have investigated the effects of a non-uniform cross-section for a coronal loop with respect to the standing sausage modes it supports. This investigation is relevant, in particular, to the case of flaring coronal loops which have been observed to exhibit such a variation in cross-section. The model also improves the explanation of quasi-periodic pulsations regularly observed in flaring loops by means of modulation of the number of magnetically-trapped, non-thermal electrons. Standing sausage modes are an ideal candidate for this modulation since they perturb the absolute value of the magnetic field and hence the magnetic trap mirror ratio. In both trapped and leaky regimes this mode is found to provide us with the information about the Alfvén speed and the magnetic field value outside the oscillating loop. In order to use this kind of observation as a diagnostic tool in MHD coronal seismology it is necessary to develop an understanding of how the observed period depends upon the coronal loop parameters.
In a flaring coronal loop, the variation of the loop cross-section arises due to the increased gas pressure at the loop apex, which causes the loop to expand at the apex with a corresponding decrease in the magnetic field strength. This increase in gas pressure also implies a higher value of plasma ![]() at the loop apex than the footpoints, but the effects of finite
at the loop apex than the footpoints, but the effects of finite ![]() were not considered in this study. This can be justified as follows: even in a flaring loop, the characteristic periods of sausage oscillations, determined by the phase speed close to the Alfvén speed outside the oscillating loop, are much shorter than the characteristic periods of acoustic (or longitudinal) oscillations, determined by the sound speed in the loop. Even if the plasma
were not considered in this study. This can be justified as follows: even in a flaring loop, the characteristic periods of sausage oscillations, determined by the phase speed close to the Alfvén speed outside the oscillating loop, are much shorter than the characteristic periods of acoustic (or longitudinal) oscillations, determined by the sound speed in the loop. Even if the plasma ![]() reaches unity in the loop, the sound speed in the loop remains much slower than the Alfvén speed outside the loop.
reaches unity in the loop, the sound speed in the loop remains much slower than the Alfvén speed outside the loop.
We considered the effect of the loop cross-section non-uniformity on the global sausage mode and the third spatial harmonics. We found that as the loop divergence parameter was increased, the global sausage mode continued to be supported with an increasing distortion of the longitudinal profile of the perturbation. However, these changes are far smaller than one would expect to be able to observe with current or future instruments.
As the loop divergence parameter increases, the period of the global sausage mode decreases. The period lies in between the estimates made for straight-slab models with the maximum and minimum widths, corresponding to the widths at the loop apex and footpoints, respectively, and was closer to the estimate made using the minimum width. This implies the period of the global sausage mode is being most strongly influenced by the width at the loop footpoint even though the mode itself produces no perturbation there. Another effect which explains the decrease in the mode period is the decrease in the effective longitudinal wavelength. The fractional change period is found to be practically independent of the density contrast ratio. The increase in the loop minor radius with the distance along the loop by a factor of two causes the decrease in the period of the global sausage mode less than 5%. Hence the staight cylinder model describes the global sausage mode adequately.
When applying a perturbation with the spatial dependence corresponding to the third longitudinal harmonic, it was again seen that the mode continued to be supported with only small changes to its spatial profile along the loop. The change in period, relative to the straight-slab model, was again negative (the period is shorter in the non-uniform case), but in this case wasmuch stronger than for the global sausage mode, and in fact so strong that it does not lie in between the estimates made for a straight slab with the maximum and minimum values of loop width. The reason for such a strong modulation of the period is not clear at this point in time, but the inadequacy of these straight-slab estimates suggests the curvature of the loop flux tube may be relevant to this case.
Another strong effect seen when applying a third harmonic perturbation to a loop with non-uniform cross-section was the generation of the global sausage mode. In the case of real coronal loops, the excitation mechanism is likely to be of a impulsive nature rather than the artificial ones used in these numerical simulations. However, this result implies the global sausage mode can be very effectively excited in flaring loops. When the global sausage mode was excited by means of the third harmonic perturbation, the change in period was the same as when it was excited directly, indicating the robustness of the result.
For these simulations, we chose a loop length that was sufficiently short that the standing sausage modes were always located in the trapped regime for the range of parameters considered. This is appropriate to the quasi-periodic pulsations observed in flaring loops since they are observed to have a high signal quality. Gravity was also ignored in these simulations as we do not expect stratification to have an important effect in flaring loops which are short and consequently have practically uniform density.
Acknowledgements
D.J.P. was supported by a PPARC studentship at University of Warwick and by STFC at University of St Andrews. A part of the work was done during D.J.P. visit to UMCS, supported by the Polish Ministry of Science and Education. V.M.N. acknowledges the support from ISSI.
References
- Andries, J., Arregui, I., & Goossens, M. 2005a, ApJ, 624, L57 [NASA ADS] [CrossRef] (In the text)
- Andries, J., Goossens, M., Hollweg, J. V., Arregui, I., & Van Doorsselaere, T. 2005b, A&A, 430, 1109 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, JCP, 171, 151 [NASA ADS] [CrossRef] (In the text)
- Arregui, I., Van Doorsselaere, T., Andries, J., Goossens, M., & Kimpe, D. 2005, A&A, 441, 361 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cooper, F. C., Nakariakov, V. M., & Williams, D. R. 2003, A&A, 409, 325 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Díaz, A. J., Donnelly, G. R., & Roberts, B. 2007, A&A, 476, 359 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Donnelly, G. R., Díaz, A. J., & Roberts, B. 2006, A&A, 457, 707 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dymova, M. V., & Ruderman, M. S. 2006, A&A, 457, 1059 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] (In the text)
- Erdélyi, R., & Verth, G. 2007, A&A, 462, 743 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Karami, K., & Asvar, A. 2007, MNRAS, 381, 97 [NASA ADS] [CrossRef] (In the text)
- McEwan, M. P., Donnelly, G. R., Díaz, A. J., & Roberts, B. 2006, A&A, 460, 893 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- McEwan, M. P., Díaz, A. J., & Roberts, B. 2008, A&A, 481, 819 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Melnikov, V. F., Reznikova, V. E., Shibasaki, K., & Nakariakov, V. M. 2005, A&A, 439, 727 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Nakariakov, V. M. 2007, Adv. Space Res., 39, 1804 [NASA ADS] [CrossRef]
- Nakariakov, V. M., & Roberts, B. 1995, Sol. Phys., 159, 399 [NASA ADS] [CrossRef] (In the text)
- Nakariakov, V. M., Melnikov, V. F., & Reznikova, V. E. 2003, A&A, 412, L7 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ofman, L., & Sui, L. 2006, ApJ, 644, L149 [NASA ADS] [CrossRef] (In the text)
- Pascoe, D. J., Nakariakov, V. M., & Arber, T. D. 2007a, Sol. Phys., 246, 165 [NASA ADS] [CrossRef] (In the text)
- Pascoe, D. J., Nakariakov, V. M., & Arber, T. D. 2007b, A&A, 461, 1149 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Safari, H., Nasiri, S., & Sobouti, Y. 2007, A&A, 470, 1111 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Srivastava, A. K., Zaqarashvili, T. V., Uddin, W., Dwivedi, B. N., & Kumar, P. 2008, MNRAS, 388, 1899 [NASA ADS] [CrossRef] (In the text)
- Verth, G., & Erdélyi, R. 2008, A&A, 486, 1015 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 223, 77 [CrossRef] (In the text)
- Zaitsev, V. V., & Stepanov, A. V. 1982, Sov. Astron. Lett., 8, 132 [NASA ADS] (In the text)
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg01.eps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{0541fg02.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg19.gif) |
Figure 1: The initial ( top) and final ( bottom) configurations of the magnetic field lines. The equilibrium is obtained by allowing an enhancement to a straight, constant magnetic field to evolve subject to the constraint of line-tied boundary conditions at the loop footpoints. Distances are in Mm. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\hspace*{6mm}\includegraphics[width=6.8cm,clip]{0541fg03.ps...
...ar\vspace*{2mm}
\par\includegraphics[width=8cm,clip]{0541fg04.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg26.gif) |
Figure 2:
Top: contour plot of the density profile that is added on top of the magnetic field profile shown in the bottom panel of Fig. 1. A generalised symmetric Epstein profile with steepness parameter p=10 is used, along with a varying semi-width parameter
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg05.eps}\par\vspace*{2m...
...s}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{0541fg07.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg28.gif) |
Figure 3:
Phase speed dispersion curves for the generalised symmetric Epstein density profile with steepness parameter p=10 for density contrast ratios of 50 ( top), 30 ( middle) and 20 ( bottom). The vertical lines correspond to the solution for the global sausage mode with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg08.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg31.gif) |
Figure 4:
The variation of the loop semi-width with the loop divergence parameter (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg09.eps}\par\vspace*{2m...
...s}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{0541fg11.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg41.gif) |
Figure 5:
Profiles of the amplitude of the global sausage mode, measured along the loop axis for the cases of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg12.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg44.gif) |
Figure 6:
The dependence of the change in period ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg13.eps}\par\vspace*{2m...
...}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{0541fg15.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg46.gif) |
Figure 7:
Profiles of the absolute spectral amplitude measured along the loop axis for the cases of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg16.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg47.gif) |
Figure 8:
The dependence of the change in period ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg17.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg50.gif) |
Figure 9: The ratio of the amplitudes of the global sausage mode to the third longitudinal harmonic for an applied perturbation corresponding to the third harmonic in a straight slab. The solid, dashed and dotted lines are for density contrast ratios of 50, 30 and 20, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0541fg18.eps}
\end{figure}](/articles/aa/full_html/2009/06/aa10541-08/Timg51.gif) |
Figure 10:
The dependence of the change in period ( |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.